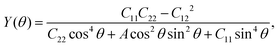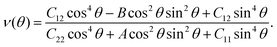Prediction of two-dimensional antiferromagnetic ferroelasticity in an AgF2 monolayer†
Xilong
Xu
,
Yandong
Ma
*,
Ting
Zhang
,
Chengan
Lei
,
Baibiao
Huang
 and
Ying
Dai
and
Ying
Dai
 *
*
School of Physics, State Key Laboratory of Crystal Materials, Shandong University, Jinan, Shandong 250100, China. E-mail: yandong.ma@sdu.edu.cn; daiy60@sina.com
First published on 1st July 2020
Abstract
Two-dimensional multiferroics, simultaneously harboring antiferromagneticity and ferroelasticity, are essential and highly sought for miniaturized device applications, such as high-density data storage, but thus far they have rarely been explored. Herein, using first principles calculations, we identified two-dimensional antiferromagnetic ferroelasticity in an AgF2 monolayer that is dynamically and thermally stable, and can be easily fabricated from its bulk. The AgF2 monolayer is an antiferromagnetic semiconductor with large spin polarization, and with great structural distortion due to its intrinsic Jahn–Teller effect when thinning the AgF2 down to a monolayer. Additionally, it features excellent ferroelasticity with high transition signal and a low switching barrier, rendering the room-temperature nonvolatile memory accessible. Such coexistence of antiferromagneticity and ferroelasticity is of great significance to the study of two-dimensional multiferroics and also renders the AgF2 monolayer a promising platform for future multifunctional device applications.
New conceptsIn this work, we propose a novel two-dimensional multiferroic material consisting of single-layer AgF2 that can be used for next-generation information storage applications. We suggest that single-layer AgF2 is an antiferromagnetic ferroelastic semiconductor with large spin polarization. It experiences a structural distortion when AgF2 is thinned down to a monolayer, which is attributed to the Jahn–Teller effect. The AgF2 monolayer features excellent ferroelasticity with high transition signal and low switching barrier, enabling potential applications in room-temperature nonvolatile memory. Such coexistence of antiferromagneticity and ferroelasticity is of great significance to the study of two-dimensional multiferroics and also renders the AgF2 monolayer a promising platform for future multifunctional device applications. |
Introduction
Multiferroics are singular materials1 that possess two or three of the so-called ferroic orders: ferromagnetism, ferroelectricity, and ferroelasticity. Their roles are crucial in a great deal of device applications, such as information storage, spintronic devices, non-volatile memory, and magnetic sensors.2–10 Moreover, exploiting several functionalities in a single material provides an unprecedented opportunity to develop new applications, such as high-density multiscale data storage. For example, Gajek et al.11 demonstrated four-state memory based on multiferroics in La0.1Bi0.9MnO3, which in principle permits data to be electrically written and magnetically read. This not only takes advantage of the best aspects of magnetic data storage and ferroelectric random access memory, but also avoids the shortcomings related to producing the giant local electric fields required to write and read ferroelectric random memory. Therefore, the existence of multiferroics in two-dimensional (2D) materials would be more attractive for miniaturized device applications. Thus far, research on 2D multiferroics has mainly focused on ferromagnetic ferroelectricity,12–16 and many systems have been identified that belong to this class, such as (CrBr3)2Li,17 CrI3,18 Hf2VC2F2,19 and CuCrP2S6.20There has recently been great interest in 2D ferroelastic materials due to their novel properties that are suitable for a significant number of promising applications such as shape memory, templating electronic nanostructures, superelasticity, and mechanical switches.21–26 The unique fingerprint of ferroelasticity is the existence of two or more equally stable orientation variants that can be transformed to each other without diffusion by applying external stress.27,28 Typical examples include phosphorene, phosphorene analogues,29 t-TiN,30 t-YN,31 BP5,32 AgCl,33 borophane,34 and SnO.35 Furthermore, some of them have demonstrated ferroelectric ferroelasticity or ferromagnetic ferroelasticity.29,32,33,35,36 Also, antiferromagnetism has recently been achieved in 2D materials, such as MnPSe337 and MnBi2Te4.38 Compared with conventional antiferromagnets, 2D antiferromagnetic materials exhibit many emergent behaviors, such as magnon condensates, exotic magnetism, quantum phase transitions, and criticality.39 Considering the merits of 2D ferroelasticity and antiferromagnetism, as well as the fact that multiferroics have been extended to include antiferroic orders in three-dimensional materials,1 it would be highly interesting to explore whether antiferromagnetic ferroelasticity can exist in 2D materials.40
In the present work, on the basis of first principles calculations, we report the discovery of such 2D multiferroics in an AgF2 monolayer that was found to be dynamically and thermally stable, and required only a small energetic cost to be derived from its bulk, suggesting its high possibility of experimentally achieving exfoliation. An AgF2 monolayer is an intrinsic magnetic semiconductor with large spin polarization, and its ground state is antiferromagnetic. Moreover, due to its unique structure stemming from the Jahn–Teller distortion, strain-driven 120° variant switching was achieved in an AgF2 monolayer with a high transition signal, suggesting intrinsic ferroelasticity. The low ferroelastic switching barrier enables 2D ferroelasticity in the AgF2 monolayer to be eminently accessible in experiments. Therefore, the AgF2 monolayer is expected to be a promising 2D antiferromagnetic ferroelastic multiferroic. Because of these combined properties, the AgF2 monolayer is an excellent candidate for future multifunctional applications in a wide range of technologies, in particular, for high-density multiscale data storage.
Method
All calculations based on density functional theory (DFT) were performed using the Vienna ab initio Simulation Package (VASP).41 The exchange–correlation interaction was treated by generalized gradient approximation (GGA) parametrized by Perdew, Burke, and Ernzerhof (PBE). The ion-electron interaction was treated by the projector augmented wave method (PAW).42,43 The Monkhorst–Pack k-mesh was set to 5 × 9 × 1, and the kinetic cutoff energy was set to 550 eV. All structures were fully relaxed until the force on each atom was less than 0.01 eV Å−1. The electronic iteration convergence criterion was set to 1 × 10−6 eV. To avoid spurious interactions between periodic images, a vacuum space of at least 15 Å was introduced. The energy barriers were calculated using the nudged elastic band (NEB) method. The phonon band was calculated using the PHONOPY code.44Ab initio molecular dynamics (AIMD) simulations were performed at 500 K and for 3 ps with a time step of 3 fs using a NVT ensemble.Results
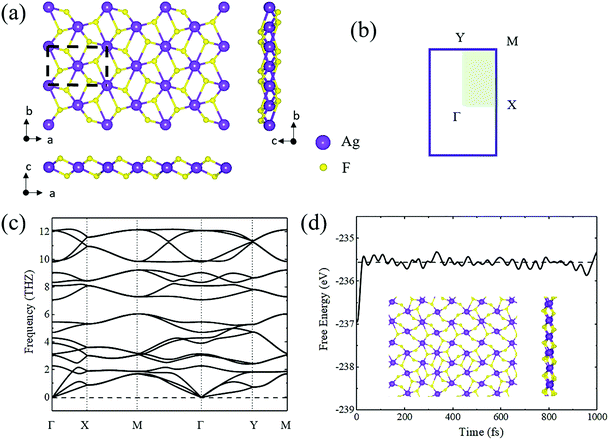
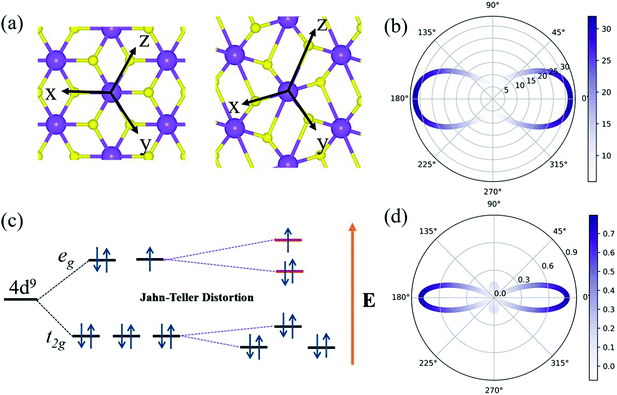
Bulk AgF2 has been synthesized since 1971 and has also been previously examined.45 Fig. S1a (ESI†) shows the crystal structure of bulk AgF2. The lattice constants were optimized to be a = 5.327 Å, b = 5.733 Å, and c = 5.968 Å, which are consistent with the experimental results (a = 5.073 Å, b = 5.529 Å, and c = 5.813 Å).45 The band structure and phonon bands of bulk AgF2 are shown in Fig. S1b and S3 (ESI†). As shown in Fig. S1a (ESI†), bulk AgF2 exhibits a layered structure in which the layers are stacked along the c axis by van der Waals interaction. Such a particular structure strongly implies that single-layer AgF2 might be peeled off from the bulk in a manner similar to that of graphene from graphite.To quantitatively estimate the experimental feasibility of exfoliating single-layer AgF2 from its bulk, we calculated the cleavage energy, which was found to be 28 meV Å−2. This value is quite close to that of graphene (23 meV Å−2) and MoS2 (26 meV Å−2),46 indicating that the exfoliation of single-layer AgF2 is highly possible in experiments. Fig. 1a shows the optimized crystal structure of the AgF2 monolayer. Clearly, its single-layer structure taken from the bulk experiences a significant distortion, leading to the structure shown in Fig. 1a. The AgF2 monolayer exhibits a tetragonal lattice with the space group of P2_1/c. The lattice constants were found to be a = 6.02 Å and b = 4.15 Å.
It is interesting to stress that the cleavage energy for single-layer AgF2 is small, although there is significant distortion in the single-layer structure. To understand this feature, we also calculated the cleavage energy of single-layer AgF2 without the distortion, which was estimated to be only 36.2 meV Å−2. This value is also small and comparable to that of graphene and MoS2. The structural distortion further decreases the cleavage energy to 28 meV Å−2. Such structural distortion arises from the particular structure of bulk AgF2. As shown in Fig. S2 (ESI†), in bulk AgF2, each Ag atom is surrounded by six F atoms, wherein four F atoms at 2.12 Å are from the same sheet, and two apical F atoms at 2.75 Å are from two neighboring sheets. When thinning down to a single layer, the absence of two apical F atoms from the neighboring sheets results in the structural distortion.
To verify the stability of the AgF2 monolayer, we performed phonon spectra calculations and AIMD simulations. As shown in Fig. 1c, the monolayer phonon spectrum shows no obvious imaginary frequency in the entire Brillouin region except for the tiny imaginary frequency (approximately 0.16 THz) near the Γ point, which is negligible. During the AIMD simulation (3 ps at 500 K), neither broken bond nor geometry reconstruction was observed; see Fig. 1d. The fluctuation of total free energy with time is also shown in the inset in Fig. 1d. Based on these results, we confirmed that the AgF2 monolayer is dynamically and thermally stable. To reflect the bonding characteristic in the AgF2 monolayer, we calculated its electron localization function (ELF) map, which is plotted in Fig. S5 (ESI†). We found that the electron localizations were mainly distributed around the Ag and F atoms as well as the centers between them, indicating the covalent bonding characteristic for the Ag–F bond.
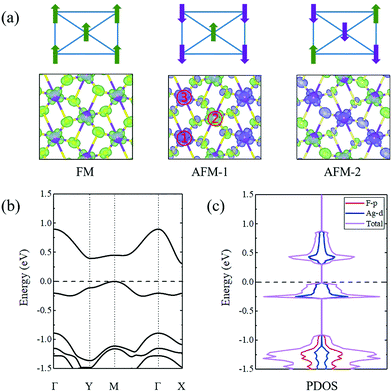
Due to the spontaneous structural distortion, the crystal structure of the AgF2 monolayer is significantly different from that of the single layer in bulk AgF2, which is expected to achieve distinct properties in the AgF2 monolayer. To this end, we first investigated the magnetic properties of the AgF2 monolayer. We found that in contrast to the case of bulk AgF2, interestingly, the AgF2 monolayer is spin polarized. The magnetic moments are mainly contributed by Ag atoms, while a tiny part originates from F atoms. The local magnetic moment of an Ag atom was found to be 0.39 μB. It should be noted that the existence of a magnetic moment does not guarantee the formation of magnetic coupling. Then, we studied the magnetic coupling in the lattice of the AgF2 monolayer. Because each Ag atom has four nearest-neighboring and two next-neighboring Ag atoms, we considered the following three different magnetic configurations: (1) ferromagnetic coupling (FM) – all magnetic moments are spin-parallel; (2) antiferromagnetic coupling (AFM-1) – the magnetic moments of Ag atom and its nearest-neighboring Ag atoms are spin-antiparallel; (3) antiferromagnetic coupling (AFM-2) – the magnetic moments of Ag atoms and its two next-neighboring Ag atoms are spin-antiparallel.
The spin density distributions for these three magnetic configurations are calculated following the equation: Δρ = ρ↑ − ρ↓, wherein ρ↑ and ρ↓ represent the spin-up and spin-down charge density, respectively. The corresponding results are shown in Fig. 2a. Among these three considered magnetic configurations for the AgF2 monolayer, the ground state with the lowest energy is AFM-1. It is energetically more stable than the FM (AFM-2) state by 39.3 (36.7) meV per f.u. The underlying mechanism for the AFM-1 coupling in the AgF2 monolayer is sought in the competition between the through-bond (super-exchange) and through-space (direct-exchange) interactions,47,48 which have been widely adopted in many previous works on 2D magnetic systems.49–52 This mechanism can qualitatively describe the interactions between the magnetic moments. For the through-bond (super-exchange) interaction, one Ag atom with down-spin (up-spin) density would induce up-spin (down-spin) density on the adjacent F atom, leading to a ferromagnetic coupling between the adjacent Ag atoms. For the through-space (direct-exchange) interaction, one Ag atom with down-spin (up-spin) density would directly induce up-spin (down-spin) density on the adjacent Ag atom, without the mediation of F atoms, which gives rise to an antiferromagnetic coupling between the adjacent Ag atoms. Both through-bond (super-exchange) and through-space (direct-exchange) interactions sensitively depend on the distance between the adjacent Ag atoms. As shown in Fig. 2a, due to the shorter distance of Ag1 (Ag3)–Ag2 (3.65 Å), the through-space (direct-exchange) interaction plays a dominant role in the magnetic coupling between Ag1 (Ag3) and Ag2. For Ag1–Ag3, the through-bond (super-exchange) interaction plays a dominant role in the magnetic coupling between Ag1 and Ag3, which results from their longer distance (4.14 Å). Based on these results, we can easily understand why the magnetic ground state for AgF2 monolayer is AFM-1.
Fig. 2b shows the band structures of the AgF2 monolayer with the AFM-1 state. Clearly, the AgF2 monolayer exhibits semiconducting behavior with an indirect bandgap of 0.31 eV, wherein the conduction band minimum (CBM) is located at the X point and the valence band maximum (VBM) lies at the M point. It should be noted that this value is based on the PBE functional, which might be smaller than the experimental value. We further employed the HSE06 functional to obtain a more precise band gap. As listed in Table S1 (ESI†), the band gap based on the HSE06 functional is estimated to be 2.87 eV. Based on the projected density of states shown in Fig. 2c, we found that the VBM and CBM of AgF2 monolayer are mainly contributed by d orbitals of Ag atoms and p orbitals of F atoms. Accordingly, we demonstrated that the AgF2 monolayer is a 2D antiferromagnetic semiconductor, which is highly sought for spintronic device applications.
To obtain further insight into this behavior, we also investigated the corresponding properties of single-layer AgF2 isolated from the bulk without optimization, which is referred to as h-AgF2. We found that the ground state for the h-AgF2 monolayer is nonmagnetic. The band structures in Fig. S4 (ESI†) show that it is a conductor. Therefore, the h-AgF2 monolayer is a nonmagnetic conductor, which is similar to that of its bulk phase; see Fig. S1 (ESI†). The discrepancy between the AgF2 and h-AgF2 monolayers can thus be attributed to the spontaneous structural distortion. Upon considering the distortion, it was determined that the coordinated environment of the Ag atoms as well as the ground state were modified.
Considering the particular structure, we next studied the mechanical properties of the AgF2 monolayer. The AgF2 monolayer has four independent elastic constants, which are found to be C11 = 36.2 N m−1, C12 = 5.3 N m−1, C22 = 6.65 N m−1, and C66 = 7.61 N m−1. They meet the Born criteria: C11C22 − C122 > 0 and C66 > 0, indicating that the AgF2 monolayer is mechanically stable. On the basis of the elastic constants, the Young's modulus and Poisson ratio of the AgF2 monolayer along the in-plane θ can be obtained by the following expression:53
Here,
| A = (C11C22 − C122)/C66 − 2C12, |
| B = C11 + C22 − (C11C22 − C122)/C66. |
The corresponding angle-dependent Young's modulus and Poisson's ratio of the AgF2 monolayer are presented in Fig. 3b and d. It can be seen that Y(θ) for the AgF2 monolayer varies from 6 N m−1 to 32 N m−1, suggesting the significant mechanical anisotropy. Moreover, these values are comparable to that of phosphorene (24–102 N m−1), but remarkably smaller than that of MoS2 (120–240 N m−1) and graphene (340 N m−1), which ensures their mechanical flexibility and is beneficial for the ferroelastic transition induced by external strain. The Poisson's ratio ν(θ) is used to characterize the transverse synthetic strain of materials under the corresponding axial strain. As shown in Fig. 3d, Poisson's ratio of the AgF2 monolayer also shows strong anisotropy, and interestingly, a negative Poisson's ratio of −0.075 is achieved.
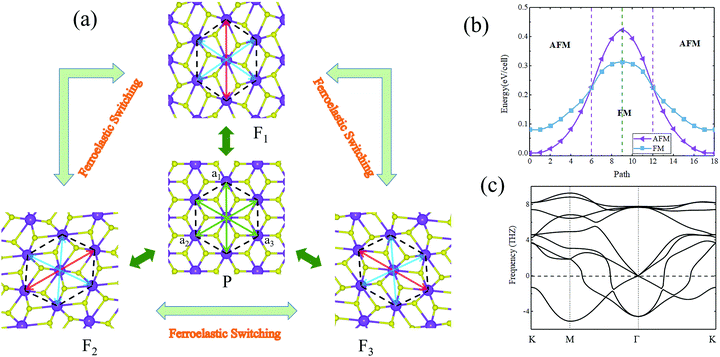
When taking into account its crystal symmetry, 2D ferroelasticity is also expected in the AgF2 monolayer. For convenience in our discussion, we consider the basic building block, namely the deformed hexagon of the AgF2 monolayer, as the structural unit. We define three diagonal lines of the deformed hexagon as a1, a2, and a3, respectively, as shown in Fig. 4a. According to the relationship of a1, a2, and a3, three energetically equivalent orientation states can be achieved for the AgF2 monolayer, i.e., F1 (a1 = 8.30 Å and a2 = a3 = 7.31 Å), F2 (a2 = 8.30 Å and a1 = a3 = 7.31 Å), and F3 (a3 = 8.30 Å and a1 = a2 = 7.31 Å) (Fig. 4a), which can be considered as the three ferroelastic ground states for the AgF2 monolayer. These three ground states can be transformed into each other. If we take F1 as the initial ferroelastic ground state, when applying an external stress along the a1 direction, the longer lattice switches to the a2 or a3 axis, that is, the AgF2 monolayer transforms into the ground state F2 or F3. Such behavior does not result in any bond breaking and only imposes a variant transformation, which is equivalent to asymmetry operations, namely a 120° rotation. The T phase of the AgF2 monolayer was determined as the paraelastic state, which is referred to as the P state (Fig. 4a), with lattice parameters of a1 = a2 = a3 = 7.20 Å. The phonon spectra of the P state are shown in Fig. 4c, from which we can see that it is unstable. This suggests that it would experience spontaneous lattice relaxation and transform into the ground state F1, F2, or F3.
The underlying mechanism for the spontaneous lattice relaxation can be attributed to the Jahn–Teller distortion. As shown in Fig. 3a, the Ag atom in T-AgF2 conforms to the octahedral coordination, and the five degenerate d orbitals split into two subsets (i.e., the eg levels with higher energy and t2g levels with lower energy) because of the disruption of symmetry under the octahedral crystal field. For one Ag2+, there are nine d electrons: six electrons fully occupy the three t2g orbitals, two electrons fully occupy one eg orbital, and one electron half-occupies one eg orbital. This results in one local magnetic moment for one Ag atom. Moreover, the unequivalent distribution of the electrons on the two eg orbitals would result in the Jahn–Teller distortions, forming a system with lower symmetry and thus further splitting the energy levels; see Fig. 3c. Therefore, the structural phase transition from T-AgF2 to AgF2 monolayers spontaneously occurs, exhibiting barrier-free behavior. Due to its three equivalent axes, there are three equivalent distorted ground states for the AgF2 monolayers.
One important factor that determines the ferroelastic performance of the AgF2 monolayer is the reversible strain, which relates to the signal intensity of ferroelastic switching. Here, ferroelastic reversible strain is defined as (ai/aj − 1) × 100, where ai ≠ aj and i/j = 1, 2, and 3. The ferroelastic reversible strain for the AgF2 monolayer is calculated to be 13.5%, compared with that of t-YN (14.4%)31 and GeS (17.8%),29 but significantly smaller than that of BP5 (41.4%),32 borophane (42%),34 and phosphorene (37.9%).29 It should be mentioned that typical 3D ferroelastic materials normally exhibit a reversible strain ranging from 0.5% to 3%. Such a large value of the AgF2 monolayer indicates that the 2D ferroelasticity would exhibit a strong ferroelastic switching signal, which is beneficial for practical ferroelastic applications.
To further understand the ferroelastic behaviors of the AgF2 monolayer, we investigated the ferroelastic transformation pathway using the nudged elastic band (NEB) method. Because the transformation pathways between any two of these three ground states are identical for the AgF2 monolayer, we will only consider the process from initial state F1 to final state F2 as an example. All intermediate states with different lattice sizes between the ferroelastic ground and paraelastic states are automatically created by NEB, and the obtained result is shown in Fig. 4b. Clearly, the paraelastic state P bridges the F1 and F2 states. In the interconversion, there is no other metastable state. The overall activation barrier for ferroelastic switching in the AgF2 monolayer was found to be 51 meV per atom. This value is larger than those of phosphorene analogues (1.3–4.2 meV per atom)29 and t-YN (33 meV per atom),31 but smaller than those of phosphorene (200 meV per atom)29 and borophane (100 meV per atom).34 Such a moderate activation barrier suggests that the AgF2 monolayer would exhibit fast ferroelastic switching when external strain is introduced. This feature, combined with the strong switching signal, enables its excellent 2D ferroelasticity. We thus can conclude that the AgF2 monolayer is a long-sought 2D antiferromagnetic ferroelastic multiferroic. Concerning the ferroelastic transition process shown in Fig. 4b, we can see another interesting point; that is, the magnetic ground state of the AgF2 monolayer will be changed during this process. Around the initial state F1 to final state F2, the magnetic ground state is AFM-1, while it is FM for the states around the paraelastic state P. It is interesting that the paraelastic structure might be established when including a square substrate with appropriate lattice parameters.
At last, we discuss the ferroelastic domain boundaries of the AgF2 monolayer. Similar to ferroelectricity and ferromagnetism, the ferroelastic transition is generally subjected to the domain-wall motion.54 Additionally, the formation of domain boundaries between adjacent variants might result in intriguing properties. Because there are three different variants for the AgF2 monolayer, three possible types of boundaries will be produced: F1–F2, F1–F3, and F2–F3. The atomic structures of these three domain boundaries are shown in Fig. 5, in which different ferroelastic domains are highlighted in different colors. These three types of ferroelastic domain boundaries are equivalent and can be transformed to each other by rotating 120 degrees. Unlike two-dimensional domain boundaries in three-dimensional materials, these domain boundaries are quasi-one-dimensional. The formation energy of the domain boundaries was found to be 56 meV Å−1, which is comparable with that of T′-TMDs (27–52 meV Å−1),55 indicating that the formation of such a type of domain boundary is possible and stable.
 | ||
| Fig. 5 Crystal structures of the ferroelastic domain boundaries between (a) F1–F2, (b) F1–F3, and (c) F2–F3. Different colors highlight the different ferroelastic domains. | ||
Conclusion
In summary, we systematically investigated the multiferronic properties of an AgF2 monolayer on the basis of first principles calculations. The AgF2 monolayer was found to be dynamically and thermally stable, and required only a small energetic cost to be obtained from its bulk. We found that the AgF2 monolayer is an intrinsic magnetic semiconductor with large spin polarization, and its ground state is antiferromagnetic. The AFM-1 coupling was attributed to the combined effects of through-bond and through-space interaction. Additionally, arising from the structural distortion, the AgF2 monolayer exhibited a strain-driven 120° variant switching, with a high transition signal and low ferroelastic switching barrier. This enables the 2D ferroelasticity in the AgF2 monolayer that is desirable for practical applications. We thus demonstrated a 2D antiferromagnetic ferroelastic multiferroic in an AgF2 monolayer, which holds great potential for multifunctional applications in a wide range of technologies.Conflicts of interest
The authors declare no competing financial interests.Acknowledgements
This work is supported by the National Natural Science Foundation of China (No. 11804190), Shandong Provincial Natural Science Foundation of China (No. ZR2019QA011 and ZR2019MEM013), Shandong Provincial Key Research and Development Program (Major Scientific and Technological Innovation Project) (No. 2019JZZY010302), Shandong Provincial Key Research and Development Program (No. 2019RKE27004), Qilu Young Scholar Program of Shandong University, and the Taishan Scholar Program of Shandong Province.References
- H. Schmid, Multi-ferroic magnetoelectrictrics, Ferroelectrics, 1994, 162, 317–338 CrossRef.
- Z. Tu, et al., 2D Diluted multiferroic semiconductors upon intercalation, Adv. Electron. Mater., 2019, 1800960 CrossRef.
- S. S. Lee, et al., Correlation between geometrically induced oxygen octahedral tilts and multiferroic behaviors in BiFeO3 films, Adv. Funct. Mater., 2018, 28, 1800839 CrossRef.
- Y. Zhao, et al., Nonvolatile electrical control and heterointerface-induced half-metallicity of 2D ferromagnets, Adv. Funct. Mater., 2019, 29, 1901420 CrossRef.
- C.-G. Duan, et al., Tailoring magnetic anisotropy at the ferromagnetic/ferroelectric interface, Appl. Phys. Lett., 2008, 92, 122905 CrossRef.
- J. Qi, et al., Two-dimensional multiferroic semiconductors with coexisting ferroelectricity and ferromagnetism, Appl. Phys. Lett., 2018, 113, 043102 CrossRef.
- Z. Tu, et al., Two-dimensional metal-free organic multiferroic material for design of multifunctional integrated circuits, J. Phys. Chem. Lett., 2017, 8, 1973–1978 CrossRef CAS PubMed.
- W. Wang, et al., Magnetic domain-wall induced ferroelectric polarization in rare-earth orthoferrites AFeO3 (A = Lu, Y, Gd): first-principles calculations, J. Mater. Chem. C, 2019, 7, 10059–10065 RSC.
- W. Sun, et al., Valence mediated tunable magnetism and electronic properties by ferroelectric polarization switching in 2D FeI2/In2Se3 van der Waals heterostructures, Nanoscale, 2019, 11, 9931–9936 RSC.
- C. Gong, et al., Multiferroicity in atomic van der Waals heterostructures, Nat. Commun., 2019, 10, 2657 CrossRef PubMed.
- M. Gajek, et al., Tunnel junctions with multiferroic barriers, Nat. Mater., 2007, 6, 296–302 CrossRef CAS PubMed.
- N. Benedek, et al., Hybrid improper ferroelectricity: a mechanism for controllable polarization-magnetization coupling, Phys. Rev. Lett., 2011, 106, 107204 CrossRef PubMed.
- W. Luo, et al., Two-dimensional hyperferroelectric metals: A different route to ferromagnetic-ferroelectric multiferroics, Phys. Rev. B, 2017, 96, 235415 CrossRef.
- S. Dong, et al., Full control of magnetism in a manganite bilayer by ferroelectric polarization, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 140404 CrossRef.
- X. Wang, et al., Observation of magnetoelectric multiferroicity in a cubic perovskite system: LaMn3Cr4O12, Phys. Rev. Lett., 2015, 115, 087601 CrossRef PubMed.
- N. Feng, et al., Superior properties of energetically stable La2/3Sr1/3MnO3/tetragonal BiFeO3 multiferroic superlattices, ACS Appl. Mater. Interfaces, 2015, 7, 10612–10616 CrossRef CAS PubMed.
- C. Huang, et al., Prediction of intrinsic ferromagnetic ferroelectricity in a transition-metal halide monolayer, Phys. Rev. Lett., 2018, 120, 147601 CrossRef PubMed.
- Y. Zhao, et al., Surface vacancy-induced switchable electric polarization and enhanced ferromagnetism in monolayer metal trihalides, Nano Lett., 2018, 18, 2943–2949 CrossRef CAS PubMed.
- J.-J. Zhang, et al., Type-II multiferroic Hf2VC2F2 MXene monolayer with high transition temperature, J. Am. Chem. Soc., 2018, 140, 9768–9773 CrossRef CAS PubMed.
- Y. Lai, et al., Two-dimensional ferromagnetism and driven ferroelectricity in van der Waals CuCrP2S6, Nanoscale, 2019, 11, 5163–5170 RSC.
- J.-X. Gao, et al., High-Temperature Ferroelastic Phase Transition in an Organic–Inorganic Hybrid: [(CH3)3NCH2Br]2–ZnBr4, J. Phys. Chem. C, 2018, 122, 23111–23116 CrossRef CAS.
- N. A. Spadin, et al., The renaissance of magnetoelectric multiferroics, Science, 2005, 309, 391–392 CrossRef PubMed.
- R. Ramesh, et al., Multiferroics: progress and prospects in thin films, Nat. Mater., 2007, 6, 20–28 CrossRef PubMed.
- W. Eerenstein, et al., Multiferroic and magnetoelectric materials, Nature, 2006, 442, 759–765 CrossRef CAS PubMed.
- E. K. H. Salje, et al., Ferroelastic Materials, Annu. Rev. Mater. Res., 2012, 42, 265–283 CrossRef CAS.
- M. D. Hollingsworth, et al., Memory and perfection in ferroelastic inclusion compounds, Cryst. Growth Des., 2005, 5, 2100–2116 CrossRef CAS.
- E. K. H. Salje, Ferroelastic materials, Annu. Rev. Mater. Res., 2012, 42, 265–283 CrossRef CAS.
- B. D. Poquette, et al., Domain reorientation as a damping mechanism in ferroelastic-reinforced metal matrix composites, Metall. Mater. Trans. A, 2011, 42, 2833–2842 CrossRef CAS.
- M. Wu, et al., Intrinsic ferroelasticity and/or multiferroicity in two-dimensional phosphorene and phosphorene analogues, Nano Lett., 2016, 16, 3236–3241 CrossRef CAS PubMed.
- L. Zhou, et al., Computational dissection of two-dimensional rectangular titanium mononitride TiN: auxetics and promises for photocatalysis, Nano Lett., 2017, 17, 4466–4472 CrossRef CAS PubMed.
- B. Xu, et al., A two-dimensional tetragonal yttrium nitride monolayer: a ferroelastic semiconductor with switchable anisotropic properties, Nanoscale, 2018, 10, 215–221 RSC.
- H. Wang, et al., BP5 monolayer with multiferroicity and negative Poisson's ratio: a prediction by global optimization method, 2D Mater., 2017, 4, 045020 CrossRef.
- Y. Gao, M. Wu and X. Zeng, Phase transitions and ferroelasticity–multiferroicity in bulk and two-dimensional silver and copper monohalides, Nanoscale Horiz., 2019, 4, 1106–1112 RSC.
- L. Kou, et al., Auxetic and ferroelastic borophane: a novel 2D material with negative Possion's ratio and switchable Dirac transport channels, Nano Lett., 2016, 16, 7910–7914 CrossRef CAS PubMed.
- L. Seixas, et al., Multiferroic two-dimensional materials, Phys. Rev. Lett., 2016, 116, 206803 CrossRef CAS PubMed.
- C. Zhang, et al., First-Principles prediction of a Room-Temperature ferromagnetic Janus VSSe monolayer with piezoelectricity, ferroelasticity, and large valley polarization, Nano Lett., 2019, 19, 1366–1370 CrossRef PubMed.
- R. Gusmão, et al., Exfoliated layered manganese trichalcogenide phosphite (MnPX3, X = S, Se) as electrocatalytic van der Waals materials for hydrogen evolution, Adv. Funct. Mater., 2019, 29, 1805975 CrossRef.
- P. Rani, et al., Crystal growth and basic transport and magnetic properties of MnBi2Te4, J. Supercond. Novel Magn., 2019, 1–5 Search PubMed.
- V. Baltz, et al., Antiferromagnetic spintronics, Rev. Mod. Phys., 2018, 90, 015005 CrossRef CAS.
- L. Yang, et al., Two-dimensional Cu2Si monolayer with planar hexacoordinate copper and silicon bonding, J. Am. Chem. Soc., 2015, 7, 2757–2762 CrossRef PubMed.
- G. Kresse, et al., Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS PubMed.
- K. Burke, et al., Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77, 3865 CrossRef PubMed.
- G. Kresse, et al., From ultrasoft pseudopotentials to the projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758 CrossRef CAS.
- A. Togo, et al., First-principles calculations of the ferroelastic transition between rutile-type and CaCl2-type SiO2 at high pressures, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 134106 CrossRef.
- P. Fischer, et al., Crystal and magnetic structure of silver difluoride: I. Determination of the AgF2 structure, J. Phys. Chem. Solids, 1971, 32, 543–550 CrossRef CAS.
- Y. Ma, et al., Double Dirac point semimetal in 2D material: Ta2Se3, 2D Mater., 2017, 4, 025111 CrossRef.
- K. Yoshizawa, et al., Through-Bond and Through-Space Interactions of Organic Radicals Coupled by m-Phenylene, Bull. Chem. Soc. Jpn., 1996, 69, 3443–3450 CrossRef CAS.
- Y. Ma, et al., Evidence of the existence of magnetism in pristine VX2 monolayers (X = S, Se) and their strain-induced tunable magnetic properties, ACS Nano, 2012, 6, 1695–1701 CrossRef CAS PubMed.
- Y. Zhou, et al., Tensile Strain Switched Ferromagnetism in Layered NbS2 and NbSe2, ACS Nano, 2012, 6, 9727–9736 CrossRef CAS PubMed.
- Q. Peng, et al., First-principles study of the effects of mechanical strains on the radiation hardness of hexagonal boron nitride monolayers, Nanoscale, 2013, 5, 695–703 RSC.
- H. Shi, et al., Strong ferromagnetism in hydrogenated monolayer MoS2 tuned by strain, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 205305 CrossRef.
- H. Y. Lv, et al., Strain-controlled switch between ferromagnetism and antiferromagnetism in 1T-CrX2 (X = Se, Te) monolayers, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 214419 CrossRef.
- E. Cadelano, et al., Elastic properties of hydrogenated graphene, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 235414 CrossRef.
- H. Wang, et al., Two-dimensional multiferroics in monolayer group IV monochalcogenides, 2D Mater., 2017, 4, 015042 CrossRef.
- W. Li, et al., Ferroelasticity and domain physics in two-dimensional transition metal dichalcogenide monolayers, Nat. Commun., 2016, 7, 10843 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0nh00362j |
| This journal is © The Royal Society of Chemistry 2020 |