Machine learning reveals multiple classes of diamond nanoparticles
Amanda J.
Parker
*a and
Amanda S.
Barnard
 b
b
aData61 CSIRO, Door 34 Goods Shed Village St, Docklands, Victoria, Australia. E-mail: amanda.parker@data61.csiro.au
bANU Research School of Computer Science, Acton, ACT 2601, Australia
First published on 20th August 2020
Abstract
Generating samples of nanoparticles with specific properties that allow for structural diversity, rather than requiring structural precision, is a more sustainable prospect for industry, where samples need to be both targeted to specific applications and cost effective. This can be better enabled by defining classes of nanoparticles and characterising the properties of the class as a whole. In this study, we use machine learning to predict the different classes of diamond nanoparticles based entirely on the structural features and explore the populations of these classes in terms of the size, shape, speciation and charge transfer properties. We identify 9 different types of diamond nanoparticles based on their similarity in 17 dimensions and, contrary to conventional wisdom, find that the fraction of sp2 or sp3 hybridized atoms are not strong determinants, and that the classes are only weakly related to size. Each class has been describe in such way as to enable rapid assignment using microanalysis techniques.
New conceptsUnlike chemical systems, nanoparticles cannot be perfectly purified, so measurements of the properties of samples are averages over distributions in size, shape, defect type and concentration. This makes the tailoring of nanoparticle samples challenging, and often increases the cost of production when structural precision is required. This expensive prerequisite can be alleviated by instead considering classes of nanoparticles, and their class-dependent properties, which can be aligned to specific applications. In this paper have used sophisticated clustering and classification machine learning methods to identify 9 classes of diamond nanoparticles; a particularly challenging and important materials that has a complicated aromatic and aliphatic surface structure that determines it suitability for drug delivery applications. We have identified 9 classes of diamond nanoparticles using a general approach that is entirely interpretable, but does not depend on the speciation, as has been assumed for over a decade. We report the expectation values for charge transfer properties of each class as a whole, which fall in distinct energy ranges, making class-dependent separation of diamond nanoparticle samples a viable target for industry, who cannot afford to make perfect samples every time. |
Introduction
Machine learning is a valuable enabling technology,1–5 but nanomaterials present a particularly challenging domain, since they include the finite size, restructuring and (surface) chemical complexity of macromolecules, combined with the variety of crystal lattices, planar and point defects of extended materials;6 they can even be amorphous. Characterisation of nanomaterials can include hundreds of structural features,7 and structure/property relationship can be difficult to extract.8For this reason one of the aims in nanoscience is to obtain perfectly monodispersed samples of nanoparticles, both in terms of their size and their shape. In some cases it is possible to approach this goal, but in other cases (such as diamond nanoparticles) lack of control during formation hinders progress, and polydispersivity is persistent.9 Using modern separation techniques the ability to perfectly purify samples based on structural or chemical characteristics is highly desirable,10,11 but to date has yet to be realised. This is in part due to the extreme complexity of these particles that include both aromatic and aliphatic carbon at the surface, which has an important impact on the charge transfer properties12 and the surface electrostatic potential that drives aggregation.13 These properties are important in determining their usefulness as a drug delivery platform. They are currently proving invaluable in the fields of biotechnology and medicine,14–26 since in most cases the controlled binding and release of functional agents are moderated by surface charge transfer. The direction and efficiency of charge transfer depends on the sign and value of the ionization potential (the donation of an electron) and the electron affinity (the accepting of an electron) and the band gap (the energy barrier).
To create bespoke samples of diamond nanoparticles targeted to specific biomedical applications, or with different reaction energies, an alternative approach is to abandon monodispersivity and allow for particle diversity where it is not detrimental to performance. This can be done by defining classes of nanoparticles based on structural similarity and characterising the properties of the class. In this way nanoparticles can be synthesised or separated by class, and the need for perfect samples is reduced or even eliminated. A class of particle with a certain size range and speciation (for example) is also a more realistic prospect for industry, where samples need to be both targeted to specific application and cost effective. Machine learning (ML) is ideally suited to identifying classes of structures in multiple dimensions, and it has been previously established that combining a sufficiently large and diverse ensemble of candidate nanostructures generated using conventional simulations with ML is an effective way of handling nanocarbon complexity.8
In this study, we use ML to predict the different classes of diamond nanoparticles based entirely on the structural features and explore the populations of these classes in terms of the size, shape, speciation and charge transfer properties. We have used sophisticated clustering and classification algorithms to reveal different types of nanoparticles based on their similarity in sixteen dimensions. The results show that there are 9 classes of diamond nanoparticles, based on a limited set of structural and morphological characteristics that do not include the fraction of sp2 or sp3 atoms, and is only weakly related to size.
Data set and methods
In this study we have used an ensemble data set of 500 diamond nanoparticles simulated using electronic structure modelling methods and numerically characterised using statistical analyses to define structural features.30 The set contains face centred cubic and twinned structures spanning the experimentally observed sizes between 0.97 nm and 4.25 nm, and a range of different shapes enclosed by {111}, {110}, {100}, {210}, {113}, {311} and {123} surface facets. These include the octahedron, truncated octahedron, cuboctahedron, truncated cube, cube (or regular hexahedron), great rhombicuboctahedron, small rhombicuboctahedron, modified-truncated octahedron, rhombi-truncated octahedron, rhombi-truncated hexahedron, rhombic dodecahedron, tetrakis hexahedron, deltoidal icositetrahedron, triakis octahedron, hexakis octahedron, and 5-fold multi-twinned particle with the simple, Ino and Marks decahedral morphologies.31 Both hydrogenated and clean (reconstructed) versions are included, and can be obtained online.32,33The features of these structures included in the present study are listed in Table 1, described as structural, chemical and statistical, depending on how they were measured. Structural features are a result of input decisions, while chemical and statistical feature are results of the electronic structure simulations. All features were calculated based on the atomic positions as implemented in the program “statix” by Jungnickel,34,35 where the uncertainties are the standard deviation in the corresponding measured quantities. Together they encompass atomic, crystallographic and morphological descriptors.
| Feature | Description | Type |
|---|---|---|
| D_nm | Average particle diameter (nm) | Structural |
| Sphericity | Morphological anisotropy | Structural |
| H_conc | Concentration of hydrogen atoms (%) | Structural |
| FCC_conc | Concentration of fcc C atoms (%) | Structural |
| HCP_conc | Concentration of hcp C atoms (%) | Structural |
| F_100 | Fraction of {100} surface facets (%) | Structural |
| F_110 | Fraction of {110} surface facets (%) | Structural |
| F_111 | Fraction of {111} surface facets (%) | Structural |
| sp1 | Concentration of sp1-hybridised atoms (%) | Chemical |
| sp2 | Concentration of sp2-hybridised atoms (%) | Chemical |
| sp2x | Concentration of sp2+x-hybridised atoms (%) | Chemical |
| sp3 | Concentration of sp3-hybridised atoms (%) | Chemical |
| CC_coord | Average coordination number of C atoms | Statistical |
| dCC | Average C–C bond length (nm) | Statistical |
| dCCe | Uncertainty in the C–C bond length (nm) | Statistical |
| aCCC | Average C–C–C bond angle (degrees) | Statistical |
| aCCCe | Uncertainty in the C–C–C bond angle (degrees) | Statistical |
After feature extraction, feature selection and engineering is extremely important36,37 and can assist in reducing the number of dimensions by eliminating features that are already well described by others. Strongly correlated features should be avoided as they overly complicate models and can introduce bias. In our case redundant features were identified using correlation matrices, and we removed features with over 95% correlation. Property labels included in this data set are the ionisation potential (calculated as the difference between the neutral particle and its cation), the electron affinity and the electronic band gap. The shape of the nanoparticles is categorical, making it an external label.
Clustering
Clustering methods are unsupervised pattern recognition techniques that group samples based on a similarity index, without reference to target labels. There are many different clustering methods available, each with advantages and disadvantages.27 In this study we have used a new clustering method that has the advantage of including hyper-parameter optimization.28 Iterative label spreading (ILS) is based on a general definition of a cluster and the quality of a clustering result, and is capable of predicting the number and type of clusters and outliers in advance of clustering, regardless of the complexity of the distribution of the data. ILS can be used to evaluate the results from other clustering algorithms, or perform clustering directly. It has been shown to be more reliable than alternative approaches for simple and challenging cases (such as the null and chain cases) and to be ideal for studying noisy data with high dimensionality and high variance, as is typical for nanoparticle systems. This software is freely available online.29Direct clustering is achieved using this algorithm by initializing one labeled point and applying ILS to obtain the ordered minimum distance (Rmin(i)) plot, as described in detail in ref. 28. The number of clusters can be automatically extracted by identifying peaks in the Rmin(i) plot (due to density discontinuities between clusters) that divide the plot into n regions. This can be automated using a continuous wavelet transform peak finding algorithm with smoothing over p points. The smoothing essentially sets the minimum cluster size to identify clusters of no smaller than p. Alternatively, if clear peaks are present they can be identified by hand. One point can be relabelled in each region (preferably in a dense region i.e. several grouped minima) to run ILS again, and obtain a fully labeled data set with n clusters defined. ILS can also be applied to each individual cluster to confirm that each region is a single cluster that should not be divided further.
Classifier
Classification is a type of supervised learning where the target labels are also provided with the features. A classifier is trained (using input training data) to recognise how unseen instances relate to some known classes of instances and assigns them accordingly. There are numerous classification algorithms available, and the superiority of one over another depends on the application and the data set.In this study we have used the non-linear, non-parametric Decision Tree Classifier (DTC) to train model that predicts different types of diamond nanoparticles based on simple decision rules inferred from the structural features. Decision trees are trained by recursively splitting the data, and are able to handle multi-output problems. They are simple to understand, and an explanation for the condition is easily explained by boolean logic. Advantages of a decision tree classifier is that they require little data preparation, they can be validated using statistical tests, they are interpretable and can be visualised. This method was chosen for its intuitive interpretability. The hyper-parameters of the DTC were optimised using a grid search (criterion = ‘entropy’, splitter = ‘best’, max_depth = 6, min_samples_leaf = 3, max_features = none, min_impurity_split = 0.0000001, ccp_alpha = 0, class_weight = none, random_state = 42) and applied using 10-fold cross validation, and a 20/80 test/train split. Disadvantages include possible instability with respect to small variation in the data, locally optimal decision at nodes dominating since they are based on heuristic algorithms (given an optimal decision tree is known to be NP-complete), biased trees can be created if some classes dominate, and they are prone to over-fitting (do not generalise well). For this reason, we calculated the learning curve to confirm accuracy and generalisable, and that the size of the data set was sufficient to avoid these issues.
Results and discussion
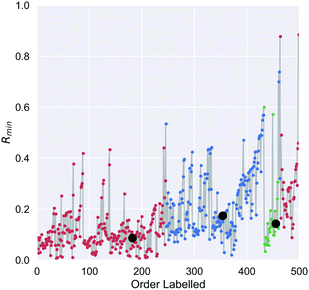
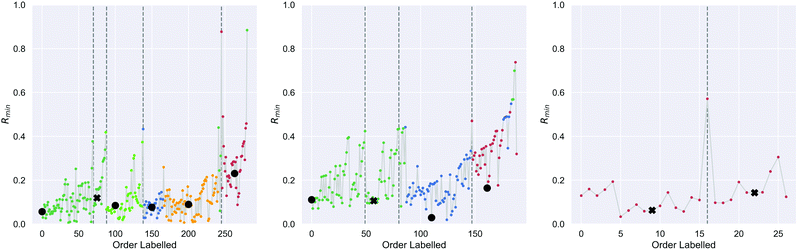
On the first pass ILS we identified three clusters in the diamond nanoparticle ensemble, as shown by the arrows in Fig. 1 using automated peak finding with smoothing over 25 points. Unlike other types of nanoparticles where the clustering results are quite distinct,38 these results are indistinct and suggest that sub-clusters may be present.We then applied ILS again to each the of the primary clusters individually, generated the Rmin(i) plot in each case (see Fig. 2), and confirmed that each cluster contained sub-clusters that could not be further devolved. We identified peaks and chose an initial minima to label in a dense region between each pair. Four of the resulting sub-clusters contained less than 25 nanoparticles and so were removed. For example, primary cluster 3 contained insufficient nanoparticles to be split, even though a peak in the Rmin(i) plot suggests there could two types of particles, and was therefore retained as one cluster. This resulted in 9 clusters containing at least 25 nanoparticles.
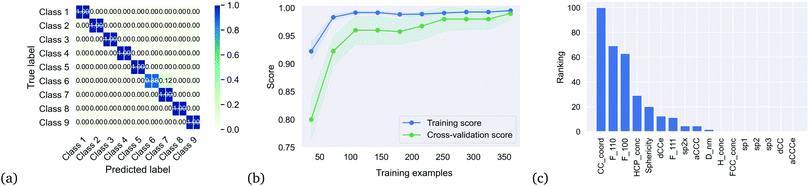
We then applied the DTC to determine if the clusters represented separable classes, and obtained an excellent result with a coefficient of determination Rtrain2 = 0.995 for the training set, 0.990 for the testing set, and a cross-validation score of 0.99 ± 0.025. Table 2 summaries the accuracy, precision and recall for each class, which is also captured in the multi-class confusion matrix in Fig. 3(a). Fig. 3(b) provides the learning curve for the DTC model, confirming the high accuracy and generalisability with no under-fitting or over-fitting over a training sample size of 350 nanoparticles. These classes are separated based on only 10 of the 17 features as shown in the feature importance histogram in Fig. 3(c), including the average C–C coordination number (CC_coord, which is 4 in bulk diamond), the fraction of {110} surface area (F_110), the fraction of {100} surface area (F_100), the concentration of atomic with HCP packing (HCP_conc, lonsdaelite structure associated with twinning), the shape anisotropy (Sphericity), the uncertainty in the C–C bond length (dCCe), the fraction of {111} surface area (F_111), the fraction of strained sp2+x atoms (sp2x), the average C–C–C angle (aCCC), and the diameter of the nanoparticle (D_nm).
| Precision | Recall | Accuracy | |
|---|---|---|---|
| Class 1 | 1.00 | 1.00 | 1.00 |
| Class 2 | 1.00 | 1.00 | 1.00 |
| Class 3 | 1.00 | 1.00 | 1.00 |
| Class 4 | 1.00 | 1.00 | 1.00 |
| Class 5 | 1.00 | 1.00 | 1.00 |
| Class 6 | 1.00 | 0.88 | 0.93 |
| Class 7 | 0.92 | 1.00 | 0.96 |
| Class 8 | 1.00 | 1.00 | 1.00 |
| Class 9 | 1.00 | 1.00 | 1.00 |
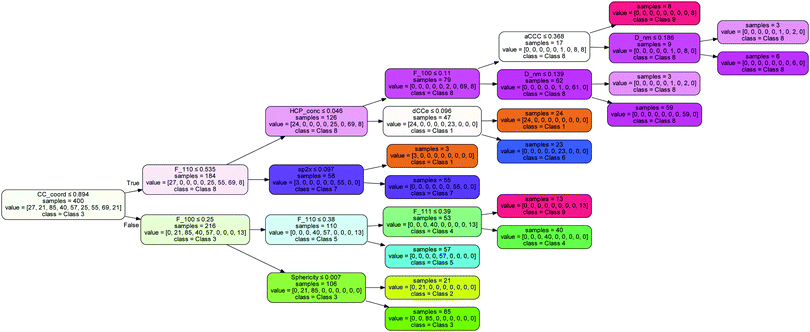
Notable omissions from this list are the concentration of hydrogen, which is associated with the passivation of the surfaces, and the fraction of sp2 atoms and sp3 atoms, which is associated with surface graphitization. The results indicate that this surface structure information can be entirely captured by the C–C coordination number (which is 3 for sp2 atoms and H-terminated atoms, and 4 for sp3 atoms), the C–C–C angle (which is ∼120° for sp2 atoms and ∼109° for sp3 atoms) and the uncertainty in the C–C bond length (which is ∼1.42 Å for sp2 atoms and ∼1.54 Å for sp3 atoms). The decision tree used by the model to separate these 9 classes is shown in Fig. 4, indicating the normalised values that split each node.
The information in this high-scoring decision tree can be used to confidently place any diamond nanoparticle into its class, C. The remaining questions, however, are what does each class look like, and what are its properties? To capture the averaged structure and properties of each class we have used ensemble filtering, which is a statistical screening method used to predict the impact of purifying samples based on design decisions.31 Ensemble filtering requires that each instance be assigned a probability, which can reflect any observable distribution. We have calculated the thermodynamic probability (p(n)) for each nanoparticle (n) in our ensemble of N = 500 instances at room temperature and atmospheric pressure with respect to bulk diamond and H2, as outlined in ref. 7 and 31, using the free software QuickThermo.39 We then individually applied 9 binary filters (F) such that ∀n ∈ N: p(n) = (F = 1 ∧ p(n)) ∨ (F = 0 ∧ 0), and F = (C ∧ 1) ∨ (¬C ∧ 0), where C ∈ {1,2,3,4,5,6,7,8,9} is the class label. This means that for a given class, if a nanoparticle is a member of the class its probability is unaffected, else it is set to zero.
Using these filtered samples the expectation values for each feature was then calculated to characterise each class as a whole. These results are provided in Table 3, where we can see that the nanoparticles in the classes are very different. Class 1 are heavily twinned and anisotropic, with hydrogenated surfaces (sp2x = 0%, aCCC ∼ 109°). Class 2 are un-twinned, hydrogenated compound shapes dominated by {110} facets. Class 3 are un-twinned, hydrogenated compound shapes dominated by {100} facets. Class 4 are un-twinned, hydrogenated shapes with almost entirely {111} facets. Class 5 are un-twinned, hydrogenated compound shapes with almost entirely {110} facets. Class 6 are twinned, reconstructed shapes with almost entirely {111} facets that have graphitized (sp2x > 27%); similar to class 1, but without the surface passivation. Class 7 are un-twinned, reconstructed shapes with almost entirely {110} facets; similar to class 5, but without the surface passivation. Class 8 are un-twinned, reconstructed compound shapes; similar to class 3, but without the surface passivation. Finally, class 9 are high index shapes with {210}, {331}, {113} or {123} facets, with and without surface passivation. Comparing these classes we can also see similarities that reflect the original primary clusters.
| Feature | Class 1 | Class 2 | Class 3 | Class 4 | Class 5 | Class 6 | Class 7 | Class 8 | Class 9 |
|---|---|---|---|---|---|---|---|---|---|
| CC_coord | 3.61 | 4.00 | 4.00 | 4.00 | 4.00 | 3.36 | 3.72 | 3.60 | 3.92 |
| F_110 (%) | 7.86 | 56.0 | 12.7 | 0 | 83.34 | 5.60 | 77.96 | 6.71 | 0 |
| F_100 (%) | 14.30 | 28.0 | 54.3 | 17.73 | 8.27 | 10.09 | 11.43 | 38.32 | 0 |
| HCP_conc (%) | 18.92 | 0 | 0 | 0 | 0 | 0 | 8.79 | 0 | 0 |
| Sphericity | 3.11 | 1.05 | 1.10 | 1.12 | 1.057 | 3.46 | 1.06 | 1.11 | 1.05 |
| dCCe (Å) | 0.010 | 0.013 | 0.017 | 0.009 | 0.011 | 0.054 | 0.049 | 0.046 | 0.024 |
| F_111 (%) | 75.68 | 16.0 | 33.04 | 82.27 | 8.39 | 82.44 | 10.6 | 54.97 | 0 |
| sp2x (%) | 0 | 0 | 0.01 | 0 | 0.01 | 27.15 | 18.92 | 17.33 | 5.49 |
| aCCC (deg.) | 109.6 | 109.5 | 109.5 | 109.5 | 109.5 | 112.3 | 110.2 | 111.0 | 109.6 |
| D_nm (nm) | 2.23 | 3.41 | 3.23 | 3.50 | 3.43 | 2.10 | 3.39 | 3.28 | 2.971 |
| 〈IP〉 (eV) | 4.90 | 4.39 | 4.20 | 4.42 | 4.36 | 5.43 | 5.54 | 5.37 | 4.62 |
| 〈EA〉 (eV) | −4.18 | −2.66 | −2.95 | −3.29 | −2.94 | 4.18 | 4.73 | 4.55 | 0.17 |
| 〈Egap〉 (eV) | 9.09 | 7.04 | 7.14 | 7.71 | 7.30 | 1.25 | 0.81 | 0.82 | 4.47 |
In addition to this is the same procedure has been used to calculate the expectation values of three electronic properties for each class. We can see from the final rows of Table 3 that the hydrogenated classes 1, 2, 3, 4 and 5 have similar ionization potential (IP) and negative electron affinities (EA). The reconstructed classes 6, 7, an 8 have higher IP and positive EA. Class 9 has an IP similar to the hydrogenated classes but and EA that is in between the hydrogenated and the reconstructed classes. The band gap (Egap) is very sensitive to the class. Hydrogenated classes have wider band gaps, reconstructed classes have small band gaps, and twinned classes are always wider gaps than their un-twinned counterpart. These results suggest it may be possible to select diamond nanoparticle samples for different applications by purifying based on class.
Conclusions
In this paper we have used a combination of computational data describing a diverse set of diamond nanoparticles and machine learning to identify 9 classes based on their similarity in 17 dimensions. The 17 dimensional feature space includes structural, chemical and statistical features and the set contains 500 particles that span the entire experimentally observed size range. The 9 classes are largely determined by the C–C coordination number, which is affected by the presence of hydrogen passivation or aromatic reconstructions at the surfaces, the fraction of {110} and {100} facets and the presence of twin planes. This is contrary to conventional wisdom that diamond nanoparticles be categorised based on the fraction of sp2 or sp3 hybridized atoms or particle sizes, which are not found to be strong determinants. Each of the classes can be conveniently summarised using three characteristics that can be determined using microanalysis techniques: with or without twinning, with or without surface passivation, and the orientation of the dominant surface facet ({110}, {100}, {111} or a higher index {hkl}). This enables rapid assignment of the diamond nanoparticle samples to a class, which correspond to different ranges of ionization potential, electron affinity and band gap.This approach is entirely general, and future work is planned to identify and characterise the various classes of other important nanomaterials.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
Computational resources for this project have been supplied by the National Computing Infrastructure (NCI) national facility under partner Grant q27.References
- K. Rajan, Annu. Rev. Mater. Res., 2008, 38, 299–322 CrossRef CAS.
- J. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, APL Mater., 2013, 1, 011002 CrossRef.
- T. Lookman, F. J. Alexander and K. Rajan, Information science for materials discovery and design, Springer Series in Materials Science, Springer International Publishing, Switzerland, 2016 Search PubMed.
- L. Ward and C. Wolverton, Curr. Opin. Solid State Mater. Sci., 2017, 21, 167–176 CrossRef CAS.
- D. M. Dimiduk, E. A. Holm and S. R. Niezgoda, Int. Matter. Manufact. Innov., 2018, 7, 157–172 CrossRef.
- A. S. Barnard, B. Motevalli, A. J. Parker, J. M. Fisher, C. A. Feigl and G. Opletal, Nanoscale, 2019, 11, 19190–19201 RSC.
- B. Motevalli, A. J. Parker, B. Sun and A. S. Barnard, Nano Futures, 2019, 3, 045001 CrossRef.
- B. Motevalli, B. Sun and A. S. Barnard, J. Phys. Chem. C, 2020, 124, 7404–7413 CrossRef CAS.
- V. N. Mochalin, O. Shenderova, D. Ho and Y. Gogotsi, Nat. Nanotechnol., 2012, 7, 11–23 CrossRef CAS.
- E. Ōsawa, Single-Nano Buckydiamond Particles-Synthetic strategies, characterization methodologies and emerging applications, in Nanodiamonds: Applications in Biology and Nanoscale Medicine, ed. D. Ho, Springer Science + Business Media, Inc., Norwell, MA, 2010, ch. 1, pp. 1–33 Search PubMed.
- Rediscovery of Detonation Nanodiamond: 3 nm Bucky Diamond in Aqueous Dispersion, S. Sasaki, S. Chang, A. S. Barnard and E. Ōsawa, presented before 2013 JSAP-MRS Joint Symposia, Doshisha Univ., Sept. 17. Abst. No. 17p-PM3-8.
- B. Sun and A. S. Barnard, Nanoscale, 2016, 8, 14264–14270 RSC.
- A. S. Barnard and E. Ōsawa, Nanoscale, 2014, 6, 1188–1194 RSC.
- Nanodiamonds: Applications in Biology and Nanoscale Medicine, ed. D. Ho, Springer Science + Business Media, New York, 2009 Search PubMed.
- R. Lam, M. Chen, E. Pierstorff, H. Huang, E. Ōsawa and D. Ho, ACS Nano, 2008, 2, 2095–2102 CrossRef CAS.
- A. M. Schrand, S. A. C. Hens and O. A. Shenderova, Crit. Rev. Solid State Mater. Sci., 2009, 34, 18–74 CrossRef CAS.
- E. Chow, E. Pierstorff, G. Cheng and D. Ho, ACS Nano, 2008, 2, 33–40 CrossRef CAS.
- R. Shimkunas, E. Robinson, X. Zhang, R. Lam, X. Xu, E. Osawa and D. Ho, Biomaterials, 2009, 30, 5720–5728 CrossRef CAS PubMed.
- M. Chen, E. Robinson, H. Huang, E. Pierstorff and D. Ho, Ann. Biomed. Eng. Soc., 2009, 37, 2003–2017 CrossRef.
- A. Smith, E. Robinson, X. Zhang, E. Chow, E. Osawa and D. Ho, Nanoscale, 2011, 3, 2844–2848 RSC.
- X. Zhang, R. Lam, X. Xu, E. K. Chow, H. Kim and D. Ho, Adv. Mater., 2011, 23, 4770–4775 CrossRef CAS PubMed.
- V. N. Mochalin, A. Pentecost, X.-M. Li, I. Neitzel, M. Nelson, C. Wei, T. He, F. Guo and Y. Gogotsi, Mol. Pharmaceutics, 2013, 10, 3728–3735 CrossRef CAS PubMed.
- D. Ho, C.-H. K. Wang and E. K.-H. Chow, Sci. Adv., 2015, 1, e1500439 CrossRef PubMed.
- D. K. Lee, T. Kee, Z. Liang, D. Hsiou, D. Miya, B. Wu, E. Osawa, E. K.-H. Chow, E. C. Sung, M. K. Kang and D. Ho, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, E9445–E9454 CrossRef CAS PubMed.
- U. Roy, V. Drozd, A. Durygin, J. Rodriguez, P. Barber, V. Atluri, X. Liu, T. G. Voss, S. Saxena and M. Nair, Sci. Rep., 2018, 8, 1603 CrossRef PubMed.
- S. Chauhan, N. Jain and U. Nagaich, J. Pharm. Anal., 2020, 10, 1–12 CrossRef.
- D. Xu and Y. Tian, Ann. Data Sci., 2015, 2, 165 CrossRef.
- A. J. Parker and A. S. Barnard, Adv. Theory Simul., 2019, 2, 1900145 CrossRef CAS.
- A. Barnard and A. Parker, Iterative Label Spreading, v1. CSIRO Software Collection, 2019 DOI:10.25919/5d806280b91a9.
- A. S. Barnard and G. Opletal, Nanoscale, 2019, 11, 23165–23172 RSC.
- A. S. Barnard, G. Opletal and S. L. Y. Chang, J. Phys. Chem. C, 2019, 123, 11207–11215 CrossRef CAS.
- A. Barnard, Nanodiamond Data Set, v1. CSIRO Data Collection, 2016 DOI:10.4225/08/571F076D050B1.
- A. Barnard, Twinned Nanodiamond Data Set, v2. CSIRO Data Collection, 2018 DOI:10.25919/5be375f444e69.
- G. Jungnickel, unpublished.
- G. Jungnickel, T. Frauenheim, D. Porezag, P. Blaudeck and U. Stephan, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 6709 CrossRef CAS PubMed.
- L. Ward, A. Dunn, A. Faghaninia, N. E. R. Zimmermann, S. Bajaj, Q. Wang, J. Montoya, J. Chen, K. Bystrom, M. Dylla, K. Chard, M. Astad, K. A. Persson, G. J. Snyder, I. Foster and A. Jain, Comput. Mater. Sci., 2018, 152, 60–69 CrossRef.
- N. Wagner and J. M. Rondinelli, Front. Mater., 2016, 3, 28 Search PubMed.
- A. J. Parker, G. Opletal and A. S. Barnard, J. Appl. Phys., 2020, 128, 014301 CrossRef CAS.
- B. Motevalli Soumehsaraei and A. Barnard, QuickThermo, v1. CSIRO Software Collection, 2019 DOI:10.25919/5d39589c523d4.
| This journal is © The Royal Society of Chemistry 2020 |