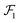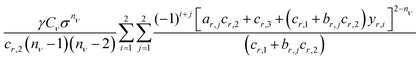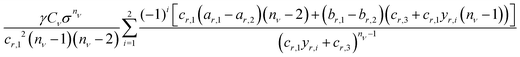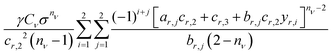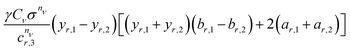Analytical van der Waals interaction potential for faceted nanoparticles†
Brian Hyun-jong
Lee
 and
Gaurav
Arya
and
Gaurav
Arya
 *
*
Department of Mechanical Engineering and Materials Science, Duke University, Durham, NC 27708, USA. E-mail: gaurav.arya@duke.edu; Fax: +1 (919) 660-8963; Tel: +1 (919) 660-5435
First published on 30th October 2020
Abstract
Our ability to synthesize faceted nanoparticles of tunable shapes and sizes has opened up many intriguing applications of such particles. However, our progress in understanding, modeling, and simulating their collective rheology, phase behavior, and self-assembly has been hindered by the lack of analytical interparticle interaction potentials. Here, we present one of the first analytical models for the van der Waals interaction energy between faceted nanoparticles. The model was derived through various approximations that reduce the usual six-dimensional integral over particle volumes to a series of two-dimensional integrals over particle interaction areas with closed-form solutions. Comparison and analyses of energies obtained from the analytical model with those computed from exact atomistic calculations show that the model approximations lead to insignificant errors in predicted energies across all relevant particle configurations. We demonstrate that the model yields accurate energies for diverse particle shapes including nanocubes, triangular prisms, faceted rods, and square pyramids, while yielding many orders of magnitude improvement in computational efficiency compared to atomistic calculations. To make the model more accessible and to demonstrate its applicability, an open-source graphical user interface application implementing the model for nanocubes in arbitrary configurations has been developed. We expect that the analytical model will accelerate future investigations of faceted nanoparticles that require accurate calculation of interparticle interactions.
New conceptsThere is tremendous interest in understanding the interaction forces acting between faceted nanoparticles because of their ability to self-assemble into novel higher-order architectures with unique optical and mechanical properties. One of the most fundamental components of such interactions acting between nanoparticles is the van der Waals (vdW) forces. While vdW forces can be rapidly calculated using analytical models for simple and symmetric particle geometries, no such models exist for faceted particles. In this work, we develop an analytical model for the vdW interaction potential between faceted nanoparticles. The model was derived by reducing the usual six-dimensional integral over particle volumes to a series of two-dimensional integrals over particle interaction areas with closed-form solutions. The model can accurately capture the vdW energy landscape of diverse particle shapes, while providing many orders of magnitude improvement in computational efficiency compared to brute-force atomistic calculations. The model's accuracy, efficiency, and ease of implementation will allow researchers to rapidly explore vdW energy landscapes of faceted nanoparticles and enable many future investigations on the rheology, phase behavior, and self-assembly of such particles through simulations that have so far been impeded by the prohibitive costs of accurately evaluating vdW energies. |
Introduction
Advancements in solution-based synthesis techniques have enabled researchers to produce faceted nanoparticles (NPs) of various shapes and sizes.1,2 Because of their sharp edges and flat surfaces, faceted NPs exhibit useful properties such as enhanced catalytic activity,3,4 improved cellular uptake,5–7 and unusual plasmonic resonances.8,9 In addition, faceted NPs can be used as building blocks for assembly of particle clusters and superlattices with new and complex arrangements that cannot be achieved by spherical NPs. Such assembled states of NPs could have potential applications in plasmonics,10–12 metamaterials,13–15 chiroptical sensors,16,17 photovoltaics,18,19 and quantum-dot solids.20,21 A key quantity that determines the morphology of structures formed by NPs is their pairwise interaction potential energy, and one of the most fundamental component of interparticle interactions is the van der Waals (vdW) forces. These forces are almost always attractive and arise from the dipole–dipole interactions acting between atoms across NPs. In general, vdW forces encompass not only interactions between instantaneous dipoles and induced dipoles, but also interactions between permanent dipoles and between permanent dipoles and induced dipoles. In some definitions, vdW forces also include the short-range repulsion arising from Pauli exclusion principle, which prevents atoms and particles from overlapping. Though vdW interactions are much weaker than covalent, ionic, or metallic bonds and typically have a shorter range than charge–charge interactions, they are ubiquitous as they act across all atomic species. As a result, the collective vdW interactions between NPs can become substantial (≫thermal energy kBT) and are often the main driving force for particle assembly and aggregation.A common approach for calculating the vdW interaction energy UvdW between two NPs involves summing up vdW energies contributed by all pairs of atoms interacting across the two particles, as given by 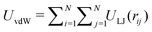 . Here, rij is the distance between atoms i and j on separate NPs and N is the number of atoms in each NP, assumed to be identical here. The pairwise interactions are usually treated using the Lennard-Jones (LJ) potential ULJ = 4ε[(σ/r)12 − (σ/r)6], in which σ represents the atomic size, the first term accounts for the attractive vdW interactions due to dipoles, and the second term empirically models the electron–electron repulsion due to Pauli exclusion principle. The interaction energy parameter ε can be related to the Hamaker constant obtained from experiments22,23 or from Lifshitz theory.24 While such “atomistic summation” approach does not properly account for retardation and many-body effects, it provides a straightforward means to calculating vdW interactions between NPs of arbitrary shapes. However, because NPs contain many atoms (N ∼ 104 to 108) and each vdW energy calculation requires
. Here, rij is the distance between atoms i and j on separate NPs and N is the number of atoms in each NP, assumed to be identical here. The pairwise interactions are usually treated using the Lennard-Jones (LJ) potential ULJ = 4ε[(σ/r)12 − (σ/r)6], in which σ represents the atomic size, the first term accounts for the attractive vdW interactions due to dipoles, and the second term empirically models the electron–electron repulsion due to Pauli exclusion principle. The interaction energy parameter ε can be related to the Hamaker constant obtained from experiments22,23 or from Lifshitz theory.24 While such “atomistic summation” approach does not properly account for retardation and many-body effects, it provides a straightforward means to calculating vdW interactions between NPs of arbitrary shapes. However, because NPs contain many atoms (N ∼ 104 to 108) and each vdW energy calculation requires 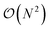 LJ energy evaluations, this approach becomes computationally expensive for exploring energy landscapes of NPs, where energy needs to be computed as a function of particle position and orientation, and prohibitive for simulations, where interactions between NPs need to computed over hundreds of particles and millions of time steps. For this reason, researchers have attempted to obtain analytical solutions to UvdW by replacing the summation over interatomic LJ interactions with an integral of the LJ potential over the volumes V1 and V2 of the interacting NPs, that is,
LJ energy evaluations, this approach becomes computationally expensive for exploring energy landscapes of NPs, where energy needs to be computed as a function of particle position and orientation, and prohibitive for simulations, where interactions between NPs need to computed over hundreds of particles and millions of time steps. For this reason, researchers have attempted to obtain analytical solutions to UvdW by replacing the summation over interatomic LJ interactions with an integral of the LJ potential over the volumes V1 and V2 of the interacting NPs, that is, 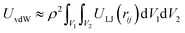 , where ρ is the number density of atoms in the NPs.25 For spherical particles, this integral can be solved exactly by taking advantage of the geometric symmetry of the particles.26 Analytic solutions also exist for other simple and symmetric shapes such as spherical shells, parallel flat surfaces, and parallel cylinders in close proximity.25,27 However, no such closed-form solutions exist for vdW interactions between faceted NPs whose asymmetric shape and finite span along each dimension render the above integral analytically intractable.
, where ρ is the number density of atoms in the NPs.25 For spherical particles, this integral can be solved exactly by taking advantage of the geometric symmetry of the particles.26 Analytic solutions also exist for other simple and symmetric shapes such as spherical shells, parallel flat surfaces, and parallel cylinders in close proximity.25,27 However, no such closed-form solutions exist for vdW interactions between faceted NPs whose asymmetric shape and finite span along each dimension render the above integral analytically intractable.
Because of the lack of analytic expressions for vdW interactions between faceted NPs, simulation studies using accurate descriptions of UvdWvia atomistic summation have been limited to small system sizes.28,29 For larger systems, researchers have resorted to approximate descriptions of UvdW to reduce the computational cost. For instance, the NPs could be constructed out of much fewer coarse beads, each intended to represent a large group of atoms.30,31 However, the vdW energy, including its distance and orientational dependence, obtained by summing over interbead LJ interactions across the NPs can differ significantly from that obtained from atomistic summation. In many cases, researchers choose to neglect attractive vdW interactions altogether,32–36 retaining only the excluded-volume interactions, which can be more efficiently implemented by using algorithms that check for geometric overlaps between NPs37,38 or by representing NPs using shells of short-range repulsive beads.39,40 While approximating or neglecting vdW interactions between particles may be acceptable for exploring granular packing in macroscopic particles or for studying entropy-driven crystallization of NPs, a proper and accurate description of vdW interactions between faceted NPs is necessary for studying their self-assembly and phase behavior, as evident from past work on spherical NPs.41–45 Hence, there is tremendous interest in accurately and efficiently accounting for vdW interactions in studies involving faceted NPs.
Here we present an analytical model for calculating vdW interaction energies between faceted NPs. The model was achieved by discretizing the volume of one of the NPs into parallel rods and deriving a simplified potential for the vdW interactions between a rod and a NP, allowing us to convert the usual vdW integral of interatomic potential over particle volumes into a series of analytically solvable area integrals of the rod–NP potential over the interacting facets of the NP. The resulting expressions are able to accurately describe the full vdW energy landscape for a range of faceted NPs, including cubes, triangular prisms, faceted rods, and square pyramids. The analytical model can be easily coded into computational routines, and as demonstration we provide an open-source graphical user interface application for calculating the vdW energy of nanocubes in arbitrary configurations. The accuracy and computational efficiency of the analytical model developed here should enable a range of simulation studies on the rheology, self-assembly, and phase behavior of faceted NPs, previously found to be computationally prohibitive.
Results
Model development
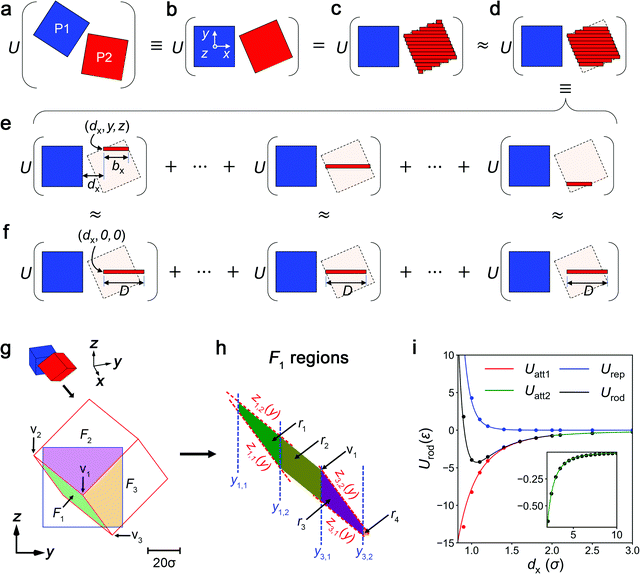
Our approach for deriving analytical vdW potentials for faceted particle, using nanocubes as the example, is summarized in Fig. 1. Given two NPs in arbitrary orientations (Fig. 1a), we first transform the coordinate frame of reference so that one particle (P1) is at the origin with one of its faces denoted by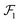 oriented perpendicular to the x-axis as shown in Fig. 1b. The configuration R of this two-particle system is then fully described by the position vector and orientation of the other particle (P2). Next, we discretize the volume of P2 into a collection of parallel rod elements oriented normal to the interacting face of P1 as depicted in Fig. 1c. (Henceforth, we use the term “interacting face” to refer to all facets of P1 and P2 that face each other.) The rods are characterized by their length bx, separation distance dx from P1, and lateral position in the y and z directions. The rod separation distance and length are both functions of their lateral position and particle configuration, that is, dx ≡ dx(y, z; R) and bx ≡ bx(y, z; R).
oriented perpendicular to the x-axis as shown in Fig. 1b. The configuration R of this two-particle system is then fully described by the position vector and orientation of the other particle (P2). Next, we discretize the volume of P2 into a collection of parallel rod elements oriented normal to the interacting face of P1 as depicted in Fig. 1c. (Henceforth, we use the term “interacting face” to refer to all facets of P1 and P2 that face each other.) The rods are characterized by their length bx, separation distance dx from P1, and lateral position in the y and z directions. The rod separation distance and length are both functions of their lateral position and particle configuration, that is, dx ≡ dx(y, z; R) and bx ≡ bx(y, z; R).
Consider now that each rod has a cross-section so small that it contains a single line of atoms of size σ. If the vdW interaction energy between a rod and P1 can be described by an interaction potential Urod ≡ Urod(y, z, dx, bx), then the total vdW energy of interaction UvdW ≡ UvdW(R) between the two particles can be written as an area integral of this potential over the entire projected area of P2 (onto the y–z plane) denoted by 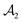 :
:
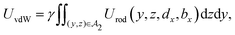 | (1) |
To obtain an analytical solution for UvdW, we simplify the integrand and limits in eqn (1) through approximations based on observations that are described and justified in more detail later. Briefly, the first observation is that the rods whose y–z projections fall outside the boundary of 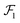 contribute negligibly to UvdW, an effect that arises due to the short-ranged nature of the interatomic vdW potential. This allows us to discard integration over such rods that fall outside
contribute negligibly to UvdW, an effect that arises due to the short-ranged nature of the interatomic vdW potential. This allows us to discard integration over such rods that fall outside 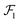 's boundaries (Fig. 1d and e), which simplifies the integration limits in eqn (1). For instance, both the y and z integration limits for nanocubes in the configuration shown in the figure are simply given by −D/2 and D/2, where D is the edge length of the cube. The second observation is that the interaction energy Urod is insensitive to both the length of the rods beyond a cutoff length smaller than D and the lateral position of the rods except those outside
's boundaries (Fig. 1d and e), which simplifies the integration limits in eqn (1). For instance, both the y and z integration limits for nanocubes in the configuration shown in the figure are simply given by −D/2 and D/2, where D is the edge length of the cube. The second observation is that the interaction energy Urod is insensitive to both the length of the rods beyond a cutoff length smaller than D and the lateral position of the rods except those outside 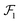 's boundary. Consequently, the vdW energy contributed by a rod of length bx whose P1-proximal end is located at (dx, y, z) can be approximated as equal to that of a rod of length D located at the origin of the y–z axes, (dx, 0, 0) (see Fig. 1f). This then allows us to eliminate Urod's dependency on y, z, and bx without much loss in accuracy, making Urod solely a function of separation distance dx(y, z). These approximations help convert the original integral in eqn (1) into a more manageable form:
's boundary. Consequently, the vdW energy contributed by a rod of length bx whose P1-proximal end is located at (dx, y, z) can be approximated as equal to that of a rod of length D located at the origin of the y–z axes, (dx, 0, 0) (see Fig. 1f). This then allows us to eliminate Urod's dependency on y, z, and bx without much loss in accuracy, making Urod solely a function of separation distance dx(y, z). These approximations help convert the original integral in eqn (1) into a more manageable form:
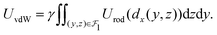 | (2) |
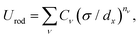 | (3) |
Given that both particles are faceted, the distance dx between the two interacting facets is always a linear function of y and z as given by
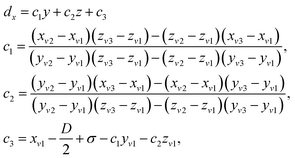 | (4) |
While this simple linear form of dx and the power-law form of Urod make eqn (2) always analytically solvable, two geometrical aspects of the system require the integral to be solved in a piecewise manner. First, the function dx(y, z) is different for each interacting face of P2, where there could be up to three such facets depending on particle position and orientation. Second, the y and z integration limits for each facet, which are not constants but functions of each other, need to be defined in a way that yields an analytical solution to the integral eqn (2). Therefore, we segment the area integral into multiple regions r in which the y integral limits are constants and the z integral limits are linear functions of y. For two interacting cubes, we first define the intersection area of the y–z projections of P1 and P2 faces as depicted by the shaded regions in Fig. 1g. Then, we divide the intersection area from each face of P2 into separate regions at all y positions where the z integral limits change their dependency on y, for example, at vertex positions where the edges change their slope (Fig. 1h). This choice makes eqn (2) analytically solvable and the region definition process can be automated into a computational routine. The final form of the vdW energy integral for each region r and rod interaction component ν is then given by
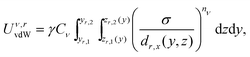 | (5) |
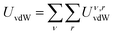 . The analytical solution to this integral depends on the particle orientations as dr,x of a region may or may not be a function of both y and z. For example, parallel facets lead to a constant dr,x while their rotation about axes parallel to the y- and z-axis leads to dr,x ≡ dr,x(z) and dr,x ≡ dr,x(y), respectively. Table 1 provides the analytical solutions to the general case in which dr,x is a function of both y and z and to these three special cases. We refer readers to see Fig. S1 and ESI† for complete derivation of these solutions.
. The analytical solution to this integral depends on the particle orientations as dr,x of a region may or may not be a function of both y and z. For example, parallel facets lead to a constant dr,x while their rotation about axes parallel to the y- and z-axis leads to dr,x ≡ dr,x(z) and dr,x ≡ dr,x(y), respectively. Table 1 provides the analytical solutions to the general case in which dr,x is a function of both y and z and to these three special cases. We refer readers to see Fig. S1 and ESI† for complete derivation of these solutions.
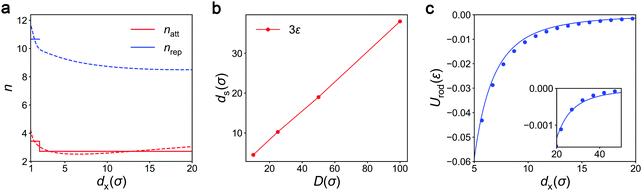
The last remaining task involves establishing suitable values of the unknown parameters Cν and nν that describe the strength and distance scaling of the attractive and repulsive portions of the rod potential Urod (eqn (3)). To obtain these parameters, we attempted power-law fits to the distance dx-dependent vdW interaction energies computed between a rod and a NP (of similar dimension D) using atomistic descriptions of the two bodies. In particular, the NP was modeled as a simple-cubic lattice of atoms of size and lattice spacing σ, the rod was modeled as a linear array of atoms of same size and spacing, and the interaction energy Urod was obtained by summing the interatomic LJ potential with parameters σ and ε across all atoms of the rod and NP. For fitting purposes, we decomposed Urod into attractive and repulsive contributions Uatt and Urep arising from the two terms in the LJ potential.
Fig. 1i presents Urod(dx), Uatt(dx), and Urep(dx) plots computed for a representative nanocube of edge length D = 50σ (which corresponds to a particle of size ∼17 nm if it were made of metal atoms typically of size 3.4 Å) along with power-law fits to the attractive and repulsive energies. The energies and fits for other cube sizes (D = 25σ, 75σ, and 100σ) are provided in Fig. S2 (ESI†). The repulsive vdW interactions for all four systems could be fitted by a single power-law (Table 2). The attractive vdW energies, however, could not be fitted using a single power-law, but separating the interactions into a short-range portion Uatt1(dx ≤ dcut) and a long-range portion Uatt2(dx > dcut) using dcut = 2σ allowed accurate fits using two separate power laws for all studied NPs. The obtained fit parameters, as listed in Table 2, show that the short-range portions exhibit nearly identical scalings for all nanocubes, but the long-range portions displayed some dependence on particle size. These results suggest that the rod potential needs to be treated as a piecewise continuous function:
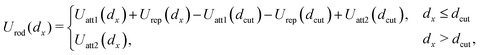 | (6) |
| Shape | D(σ) | C att1(ε) | n att1 | C att2(ε) | n att2 | C rep(ε) | n rep |
|---|---|---|---|---|---|---|---|
| Cube | 25 | −7.76 | 3.45 | −5.87 | 3.00 | 3.86 | 10.66 |
| Cube | 50 | −7.76 | 3.43 | −4.65 | 2.72 | 3.86 | 10.66 |
| Cube | 75 | −7.76 | 3.43 | −4.03 | 2.58 | 3.86 | 10.66 |
| Cube | 100 | −7.76 | 3.43 | −3.65 | 2.50 | 3.86 | 10.66 |
| Triangular prism | 50 | −7.76 | 3.44 | −4.69 | 2.73 | 3.86 | 10.66 |
| Square rod | 50 | −7.75 | 3.44 | −4.61 | 2.71 | 3.86 | 10.66 |
| Square pyramid | 50 | −7.76 | 3.44 | −4.72 | 2.74 | 3.86 | 10.67 |
Model predictions and accuracy
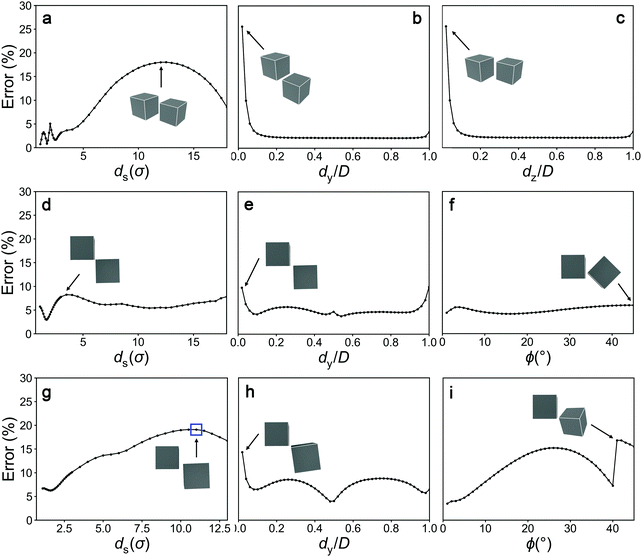
To evaluate the accuracy of our analytical model, we compared its energy predictions for a range of NP shapes and sizes to energies computed atomistically via summation of interatomic LJ interactions. For a two-particle system, the energy landscape can be conveniently described in terms of the position and orientation of one NP (P2) relative to the other (P1) in a coordinate frame in which one of P1's faces ( ) points in the +x direction (as in Fig. 1b). The orientation of P2 was described using 3 Euler angles (ϕ,θ,ψ) and its position was described using 3 Cartesian coordinates (ds,dy,dz). We chose to define P2's position not by its center of mass but by its vertex closest to
) points in the +x direction (as in Fig. 1b). The orientation of P2 was described using 3 Euler angles (ϕ,θ,ψ) and its position was described using 3 Cartesian coordinates (ds,dy,dz). We chose to define P2's position not by its center of mass but by its vertex closest to 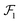 , with ds denoting the distance of this vertex from
, with ds denoting the distance of this vertex from 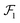 and dy and dz representing the vertex's lateral offset from the edges of
and dy and dz representing the vertex's lateral offset from the edges of 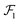 . Hence, ds represents the closest separation distance between the two NPs, wherein ds = 0 signifies contact. Using this set of coordinates, we sought to assess the ability of our model to capture the entire vdW energy landscape, especially its distance dependence UvdW(ds) for arbitrary NP configurations (dy,dz,ϕ,θ,ψ).
. Hence, ds represents the closest separation distance between the two NPs, wherein ds = 0 signifies contact. Using this set of coordinates, we sought to assess the ability of our model to capture the entire vdW energy landscape, especially its distance dependence UvdW(ds) for arbitrary NP configurations (dy,dz,ϕ,θ,ψ).
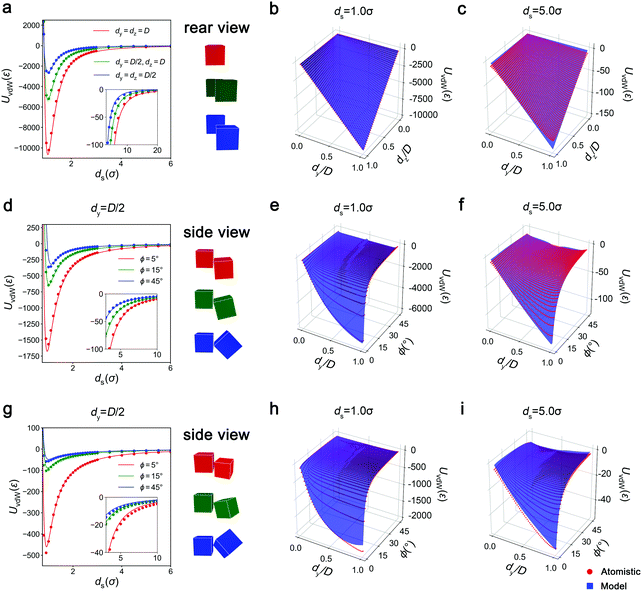
Next, we examined tilted coplanar configurations, where nanocubes lie flat on a plane and translate and rotate only within that plane, configurations relevant to particles confined in thin films or those deposited on flat substrates.10,28 Such configurations are characterized by the separation distance ds between nanocubes, their lateral offset dy, and their tilt angle ϕ, assuming that particles lie flat on the x–y plane (θ = ψ = 0°,dz = D). Fig. 2d–f presents model predictions for UvdW(ds) at representative dy and ϕ values and for UvdW(dy,ϕ) at the two representative ds values considered above. We find that the model is able to quantitatively capture the distance dependence of the vdW energy and its dependence on the relative offset and tilt for these nanocube configurations. The UvdW(dy,ϕ) landscapes also reveal that the vdW energy rises with increasing dy, as expected, but unlike the linear dependence observed for parallel configurations, the energies for tilted cubes display increasingly weaker dependence on dy with increasing ϕ. The reason is that the larger the ϕ, the more the total energy is dominated by the interactions mediated by the leading edge of P2 (closest to P1) which are unaffected by changes in ϕ at fixed ds. The landscapes also show the energy decreasing more sharply with increasing ϕ at smaller ϕ than larger ϕ. This effect may be explained by considering the incremental change in vdW interactions mediated by a rod element on P2 (any rod not associated with the closest vertex) that moves away from P1 by a small distance due to a small increase in angle ϕ. Because Urod(dx) decays more sharply at smaller distances, rods that are located closer to P1 at small ϕ will incur a sharper drop in vdW interactions compared to those further away at large ϕ. Both of these effects are accurately captured by the analytical model.
Lastly, we tested our model for the more general case wherein nanocubes are able to rotate or translate along all six degrees of freedom. Given the enormity of this configurational space, we chose to focus on configurations with ϕ = θ = ψ and dz = 0.5D as we found these to be general enough to capture the model's accuracy for any configuration. UvdW(ds) plotted for several representative orientations in Fig. 2g shows that the model can accurately describe the depth of the energy minimum and the long-range interactions. However, the location of the repulsive barrier at small distances is slightly overpredicted at large ϕ. This is because the model treats NPs as macroscopic bodies with flat surfaces while the actual particles have atomically corrugated surfaces that may allow closer separation distances, as P2's leading vertex could be accommodated within the atomic interstices of P1's interacting face. This discrepancy in barrier location is however smaller than 0.1σ, so quite negligible. The model also reproduces well the atomistically computed UvdW(dy,ϕ) landscapes at small and large separation distances (Fig. 2h and i). Similar to coplanar configurations, the energies for these general configurations also vary highly nonlinearly with the relative offset and tilt of the nanocubes, and the model is again able to quantitatively capture all these variations spanning at least three orders of magnitude in energy.
 in the predicted energies of all configurations with that specified coordinate value, where Umodel and Uatomistic are the energies calculated by the model and by atomistic summation. For example, the data point marked with a blue square in Fig. 3g represents the collective error in the energy of all general configurations (0 < dy ≤ D and 0° < ϕ ≤ 45°) with ds = 11σ. We have computed these errors with respect to ds, dy, and dz for parallel configurations, and ds, dy, and ϕ with fixed dz of D and 0.5D for the coplanar and the general configurations, respectively. To exclude configurations with negligible interactions, we only considered those with Uatomistic > 3ε. By analyzing the error associated with each coordinate in this manner, we were able examine the strengths and weaknesses of the model for particular types of configurations.
in the predicted energies of all configurations with that specified coordinate value, where Umodel and Uatomistic are the energies calculated by the model and by atomistic summation. For example, the data point marked with a blue square in Fig. 3g represents the collective error in the energy of all general configurations (0 < dy ≤ D and 0° < ϕ ≤ 45°) with ds = 11σ. We have computed these errors with respect to ds, dy, and dz for parallel configurations, and ds, dy, and ϕ with fixed dz of D and 0.5D for the coplanar and the general configurations, respectively. To exclude configurations with negligible interactions, we only considered those with Uatomistic > 3ε. By analyzing the error associated with each coordinate in this manner, we were able examine the strengths and weaknesses of the model for particular types of configurations.
Our results demonstrate that the model is accurate for most configurations and the errors are generally less than 15%. The largest errors are observed for parallel configuration of nanocubes interacting with their edges (dy or dz ≈ 0) or interacting at large separation distances (ds > 10σ), and for strongly tilted configurations of nanocubes interacting via vertex-edge contacts (ϕ > 40°). These larger errors arise due to two factors. First, the magnitude of the energy for these configurations are generally much smaller than for the nanocubes interacting with small ds, small ϕ, or large dy or dz. For instance, the average energy of parallel configurations at ds = 1.5σ is equal to 1140ε while those at ds = 10σ exhibit an energy of only 9ε. Therefore, even small differences between Umodel and Uatomistic will result in large percentage errors for configurations with large ds. Second, several assumptions of our model become less valid for these configurations. For instance, we assumed that all rods making up particle P2, even those facing P1's edges, interact with particle P1 as if they were facing its center. For the configurations with dy or dz ≈ 0, the interaction energies between the particles are dominated by the energies of the edges and our assumption could lead to errors in such cases.
Although these results point out certain weaknesses of the analytical model due to its assumptions, it is noteworthy that all of the configurations with large individual errors are those in which the particles are interacting very weakly. In fact, almost all configurations of nanocubes with the largest individual percentage errors had |Uatomistic| < 4ε. Therefore, we can conclude that while our model may deviate from atomistic energy calculations for some weakly interacting configurations, the model is accurate for most configurations and especially for those with significant interaction strengths.
We finally investigated the ability of our model to describe the vdW interactions between other types of faceted NPs. For this purpose, we examined triangular prisms (of dimensions 50σ × 50σ × 70.7σ), square rods (50σ × 50σ × 500σ), and square pyramids (50σ × 50σ × 50σ), as shown in Fig. 4b. These particular NP shapes were chosen as they have been extensively explored in the literature for studying packing behavior and self-assembly,49–51 and for creating devices with unique plasmonic52,53 and chiroptical properties.54,55 We restricted our analysis to particle configurations most relevant to their application, namely, tilted coplanar configurations for triangular prisms (that yield distance- and angle-dependent plasmonic hotspots), twisted configurations for square rods (used for chiroptical sensing), and face-tip configurations for square pyramids (commonly observed during assembly and packing). Fig. 4c–e presents representative UvdW(ds) for the three NP shapes in various configurations calculated using the parameters listed in Table 2. We observe that for all three NPs our model accurately reproduces the distance and orientation dependence of the vdW energies obtained from atomistic summation. The model's accuracy is especially reassuring for triangular prism and square pyramid configurations exhibiting small tilt angles θ that most strongly challenge the fixed rod-length approximation in our model. For these configurations, rod elements at the leading edge (in case of triangular prisms) or leading vertex (square pyramids) of P2 are actually only a single atom long. This indicates that our rod-length approximation may not be as erroneous as it appears at first glance. For parallel rods, the variation in vdW energy with twist angle was found to match the variation in surface area of interaction with angle, which also our model predicted very well. Taken together, our results demonstrate that our analytical model is applicable to faceted NPs of various shapes and sizes.
Analysis of model assumptions
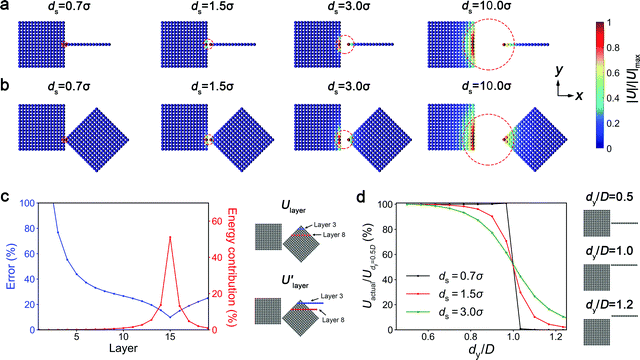
In deriving our analytical model for vdW interaction energies between faceted NPs, we made the following four assumptions: (1) all rod elements irrespective of their lateral position are of length equal to the characteristic size of the NP (rod length approximation); (2) each rod element irrespective of its lateral position contributes an interaction energy equal to that of a rod facing the center of reference particle P1 (edge approximation); (3) energies from all rod elements that are not within the boundary of the interacting face of P1 in the y–z axes are ignored (cutoff assumption); and (4) the rod–NP interaction potential Urod can be described by power-law functions of fixed coefficients and exponents (power-law approximation). Despite these assumptions, we found that the analytical model provides remarkably accurate predictions for the vdW interaction energy between nanocubes in almost every possible configuration. The model also makes accurate predictions for other faceted particles like rods, prisms and pyramids in relevant configurations. Thus, several of the model assumptions, which appear to become worse with tilted configurations of nanocubes and glancing tip-face configurations of prisms and pyramids, do not lead to significant errors in net energy.As dx becomes larger, the number of atoms contributing significant interaction energies increases. The data in Fig. 5a indicates that these atoms can be enclosed by a sphere centered around the rod atom closest to the nanocube. As this sphere gets larger with increasing dx, the assumptions become worse. For example, at dx = 1.5σ and 3σ, the energies contributed by nanocube atoms in the immediate vicinity of the central atom facing the rod also become significant. In this case, if the rod was facing the edges of the nanocube, our model would overestimate the rod's energy by an amount equal to the energy contributed by some of these vicinity atoms that the model assumes to exist. However, we find that the energy is still dominated by the energy of the single atom closest to the cube, and, therefore, the rod length, edge, and cutoff assumptions still remain quite valid. When dx increases further to 10σ, almost the entire interacting face of the nanocube makes significant contribution to the energy of the system. Thus, if distant rods facing the edges of the nanocube are made to interact at the nanocube center based on the edge approximation, we would overestimate the total energy by adding contributions from many nanocube atoms that do not actually exist. Furthermore, the rod atoms make significant energy contributions up to the fourth layer. Therefore, for highly slanted cubes or triangular prisms that are one-atom thick in the x-axis at the tips, the rod-length assumption would lead to excess energy from the fictitious layers of added rod atoms. Finally, as the volume of sphere of influential atoms increases, the cutoff assumption also becomes worse, as rods above or below the nanocubes top or bottom edges, currently neglected in our model, start to make more significant contributions.
To assess the impact of the rod-length, edge, and cutoff assumptions at the level of interparticle interactions, we analyzed the interatomic LJ interactions between two 15σ nanocubes in a tilted coplanar configuration at varying separation distances ds, as depicted in Fig. 5b. We chose this configuration in which NPs interact mostly via their edges, as it invokes some of the largest errors from these assumptions. As observed in the rod-cube system, the number of atoms contributing significant energies expanded with increasing ds. For example, while the total energy of the system could be almost entirely described by the interaction energy of the overlapping atoms at ds = 0.7σ, the total energy for ds = 10σ required consideration of a larger number of atoms from both NPs. This means that our rod-cube model for this well-separated configuration would treat particle P1 as if it had many more atoms that fill up the red dotted circle drawn in the figure. However, it is important to note that the majority of the total energy is still contributed by atoms around the closest vertex of P2 and P1 atoms facing this vertex. Though the model is expected to yield large errors for rods corresponding to the upper and lower edges of P2 which are actually only one atom long in the x-axis and have large dx, the contribution of these atoms to the overall energy is negligible. Since the model calculates the contribution from the atoms around the closest vertex accurately, the net error in vdW energy, even for this highly slanted nanocube P2 interacting near the edge of P1, remains small.
To gain a more quantitative understanding of the error introduced by the rod length assumption, we compared in Fig. 5c the energies contributed by each layer of atoms in P2, from top to bottom. In the figure, layer 1 corresponds to the single atom on the top edge of the cube, layer 2 represents the next layer of atoms immediately below that edge, and so on, with layer 15 denoting the layer of atoms containing the P1-proximal vertex. The blue curve represents the percentage error  in the energy of each layer measured as the deviation of its energy
in the energy of each layer measured as the deviation of its energy 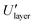 calculated using full-length rods of atoms (of length D as assumed in our model) from the true energy Ulayer calculated using the actual atomic positions in each layer, and the red curve represents the percentage energy contribution of each layer as given by
calculated using full-length rods of atoms (of length D as assumed in our model) from the true energy Ulayer calculated using the actual atomic positions in each layer, and the red curve represents the percentage energy contribution of each layer as given by 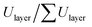 . The results show that the error is indeed very large for the topmost layers (>100% for layer 1) and dips to small values for layers involving or adjacent to the closest vertex (≈10% for layer 15). However, the energies contributed by the topmost layers are only a tiny fraction of the total energy (0.016% for layer 1), as most of the energy is contributed by layer 15 (≈51%) and its adjacent layers. This explains why the cumulative error in total energy remains quite small, at only 14.4%, even though the percentage errors in energy are quite large for layers close to the edges of the nanocube. These results demonstrate that the rod length assumption has a small negative impact on the total energy of particles, as the portions of P2 that most violate this assumption are almost always the farthest from P1 (e.g., at the tips of particles in highly slanted configurations where the rod lengths deviate the most from the assumed length D) and hence contribute the least to the total energy.
. The results show that the error is indeed very large for the topmost layers (>100% for layer 1) and dips to small values for layers involving or adjacent to the closest vertex (≈10% for layer 15). However, the energies contributed by the topmost layers are only a tiny fraction of the total energy (0.016% for layer 1), as most of the energy is contributed by layer 15 (≈51%) and its adjacent layers. This explains why the cumulative error in total energy remains quite small, at only 14.4%, even though the percentage errors in energy are quite large for layers close to the edges of the nanocube. These results demonstrate that the rod length assumption has a small negative impact on the total energy of particles, as the portions of P2 that most violate this assumption are almost always the farthest from P1 (e.g., at the tips of particles in highly slanted configurations where the rod lengths deviate the most from the assumed length D) and hence contribute the least to the total energy.
To quantify the errors arising from the edge and cutoff assumptions, we examined how the rod–nanocube interaction energy varies as a function of the rod's lateral position. Fig. 5d plots the LJ interaction energy between the 15σ nanocube and a same-length rod as a function of its normalized lateral coordinate dy/D, where dy/D = 0.5 and 1 correspond to a rod facing the nanocube's center and upper edge, and dy/D > 1 indicates a rod going beyond the upper edge; we held the other lateral coordinate fixed at dz = D/2 and compared the energy variation at three different fixed values of the separation distance dx. For a rod with dx = 0.7σ that overlaps with the nanocube, the energy remains unchanged from the center to the edge of the nanocube and becomes negligible immediately after the rod crosses the edge. The edge and cutoff assumptions are thus valid for small separation distances, and should lead to negligible errors for NP configurations at small separation distances. At larger dx, the energies start to deviate as dy/D exceeds 0.8 and becomes ≈70% of the energy of the centrally-located rod once the rod gets to the edge of the nanocube. Beyond the edge, the energy quickly reduces to ≈15% of the energy of the central rods. This means that the edge assumption may overestimate the vdW energy of a rod at the edge by 30%, and the cutoff assumption may underestimate its energy slightly below the edges by 15%. The net impact of the two kinds of errors on interparticle energy will obviously be much smaller because: the errors partly cancel out due to their opposite sign, they diminish with rod distance from edges, and the percentage contribution of energy from rods close to edges to the net energy is typically small. Thus, similar to the rod length assumption, the edge and cutoff assumptions also lead to small errors in the total energy.
The above analysis shows that distance-dependent scaling exponents might be required to accurately model Urep and Uatt across all dx, though this would make the model analytically intractable. Thus, our strategy of modeling these potentials using one or two power-laws with constant exponents to permit analytical solution is approximate. Given that Urep needs to be modeled accurately only over small distances (dx ≤ 2σ) due to the short-ranged nature of this potential and that its true exponent shows only a small variation in this distance range, the power-law approximation turns out to be very accurate for Urep (see Fig. 1i). The power-law used for modeling Uatt at short distances is similarly a good approximation as this power-law also is required to operate over a short range of distances (1σ ≤ dx < 2σ). However, the power-law used for modeling the long-range behavior of Uatt needs to be accurate over broader range of distances (dx > 2σ). Clearly, this power-law is neither expected nor required to accurately model interactions at large distances where the fitted exponent departs strongly from the true exponent and the interaction energies become very small. We therefore set the range of validity of this power law as the distance range over which the particles still interact with significant energies that we want our model to accurately predict; in this study, we set this energy threshold to be equal to 3ε, which is 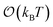 .
.
To determine roughly the distance range for which the total interparticle energy |UvdW| > 3ε, we calculated via atomistic summation the interaction energies of face–face nanocubes for a range of cube sizes D. We chose this configuration, as it yields the largest energies for a given ds. Interestingly, the energies decayed to 3ε at ds ≈ 0.38D, a distance range proportional to particle size (Fig. 6b). For nanocubes with ϕ > 0° or dy < D, the relevant ds would be even smaller. Therefore, our model is only required to be accurate for ds ≤ 0.38D. As demonstrated in our results in Fig. 3, our model using only the two sets of power laws described above could accurately predict vdW interaction energies within this distance range. In fact, the single power-law used for describing the long-range portion of Uatt in our model could accurately describe Urod at distances as large as ds = 1D (Fig. 6c). Therefore, we can assume that our current model with two sets of parameters can predict the vdW interactions between faceted NPs over a significant range of separation distances. Additional power-laws could potentially be included in the model if greater accuracy is required for predicting small interparticle energies at larger ds.
Computational implementation
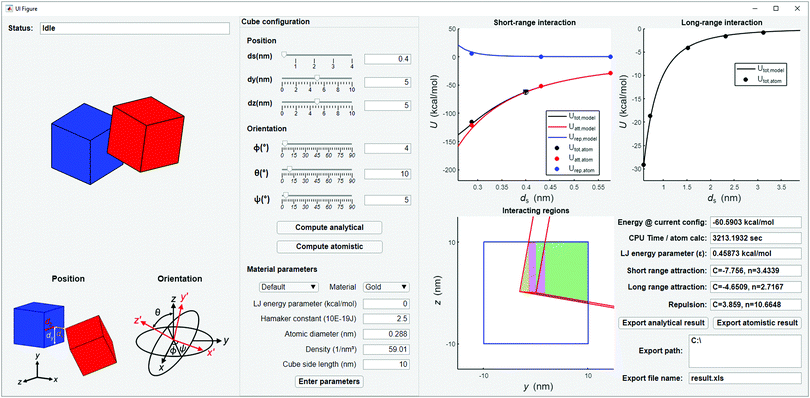
To make the model more accessible to researchers and demonstrate its applicability, we developed an open-source MATLAB application with a graphical user interface (GUI) that implements the model for arbitrary nanocube sizes and configurations. The user interface is shown in Fig. 7. In this application, the user can input the configuration (ds, dy, dz, ϕ, θ, ψ) and material properties (σ, ε, D) of the nanocubes. In addition to utilizing the user-provided values of ε, the application can also infer ε from the Hamaker constant, atomic diameter, and number density of atoms constituting the material (see ESI† and Fig. S4 for examples of application of the model to specific materials). From these input parameters, the application calculates and outputs the following: the power-law scaling coefficients and exponents that best describe the short- and long-range portions of the rod potential; the y–z projection of the interacting regions of the facets used for calculating total energy; and the vdW energies as a function of particle separation distance ds, including the value at the inputted distance. The potential energy obtained from the analytical model can also be compared with energy computed from atomistic calculations. Detailed description of the computational implementation of our model is provided in ESI† and Fig. S5, and the application and its source codes are available on GitHub.56Discussion
In this study, we developed an accurate analytical model for calculating vdW interaction energies between faceted NPs. This work is motivated by the high computational costs of calculating vdW energies through atomistic summation of interatomic potentials and the inability of coarser-grained models of particles to capture various features of the vdW energy landscape (comparison between UvdW obtained from atomistic models and coarse-grained models is provided in Fig. S6, ESI†). Our model was derived by discretizing the volume of one of the interacting particles into rod-shaped volume elements and casting the interparticle vdW energy of interaction as an area integral over rod-particle interactions. Through several approximations and atomistic calculations, we were able to derive and parameterize power-law functions for the rod-particle potential. Segmentation of the vdW energy area integral into sub-integrals with constant or linearly-varying integration limits then allowed us to derive closed-form solutions for the vdW energy. We found that the resulting analytical expressions were able to quantitatively capture the distance- and orientation-dependent vdW interactions for a range of faceted NPs, including cubes, square rods, triangular prisms, and square pyramids. Extensive analysis of errors resulting from approximations of the model revealed that the percentage errors in calculated energies were minimal for most particle configurations and that the small fraction of configurations that exhibited larger errors represented weakly interacting particles that have a much lower bar for accuracy.The obvious benefit of this model over atomistic summation is its computational efficiency. The cost of atomistic energy calculations rises sharply with the particle size, and, for the nanocubes studied here, the CPU time rises as ≈2.6 × 10−7D6 seconds per energy evaluation on an Intel Core i7-7700 processor (Fig. S7, ESI†). In contrast, our model takes only ≈7 × 10−4 seconds of CPU time per evaluation independent of the particle size. For 100σ nanocubes, this translates to more than 8 orders of magnitude reduction in computational costs. The model's efficiency would be especially valuable in simulations that require repeated calculation of interparticle energies. Consider, for instance, a Monte Carlo simulation of commonly studied 40 nm (∼100σ) silver nanocubes47 with a typical system size of N = 100 particles and simulation length of 107 steps. Assuming 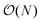 energy evaluations per step, the simulation would require ∼200 hours as opposed to ∼106 years of CPU time if the simulation used our model instead of atomistic summation for calculating energies.
energy evaluations per step, the simulation would require ∼200 hours as opposed to ∼106 years of CPU time if the simulation used our model instead of atomistic summation for calculating energies.
The development of an analytical model for vdW interactions that is both accurate and efficient should enable many problems involving faceted NPs to be studied by simulations that would otherwise have had to resort to inaccurate treatment of vdW interactions via coarse-grained models. The vast literature on spherical NPs has shown that the strength and range of attractive forces between particles, including those arising from vdW interactions, significantly impact the rheology, phase behavior, and microstructure of fluid-particle systems. For example, the strength of vdW interactions between particles has been shown to strongly impact their jamming transition41 and the type of anisotropic phase that they form when grafted with polymers.57,58 Simulation studies of faceted NPs using purely-repulsive potentials have demonstrated that the particles organize into novel arrangements under compression as a result of the anisotropy in their excluded volume.33,34 One can expect that the introduction of attractive forces between such NPs would cause them to self-assemble (as opposed to pack) into new and complex equilibrium and nonequilibrium (trapped) structural phases. Thus, the ability to accurately and efficiently model vdW forces between faceted NPs would enable researchers to explore their phase behavior and rheology. Such studies have the potential to reveal previously unseen phases and phenomena that may be of interest to basic science or engineering applications.
Several extensions of the model that may enhance its applicability but have not been investigated in the current study could become topics of future investigation. First, while we showed that the model provides excellent energy predictions for simple faceted geometries like cuboids, pyramids, and prisms, the range of particle shapes for which the model remains accurate needs to be further investigated. An inherent assumption of our model is that the interactions between two particles is dominated by a single interacting facet of one of the particles (P1's face normal to the x-axis), which holds true for all shapes whose adjoining facets subtend an angle equal to or smaller than 90°. However, this assumption becomes invalid for shapes exhibiting larger angles, or in other words, shapes with more facets than cubes. For these shapes, other P1 facets also exhibit overlap with P2 facets in their y–z projections and their interactions must be accounted for as well. Thus, the model is expected to lose accuracy with increasing number of facets (beyond cubes) to the point of becoming invalid for spheres that effectively possess an infinite number of facets. Thus, additional work is required to determine particle shapes for which the model remains accurate and to revise the model to improve its accuracy for other faceted geometries.
Second, we did not investigate in this study the model's accuracy for particles larger than D = 100σ (∼40 nm). Based on our earlier analysis of the rod potential, the power-law describing its long-range attraction is required to be valid to a distance of 0.38D (at which point the interparticle interactions are deemed to be insignificant). Thus, the larger the particle, the larger the range over which the power-law is required to be accurate. This means that for large NPs, of sizes 100 nm to several microns, a single power-law may not be sufficient to accurately model the rod potential over this entire range. Future studies would thus benefit from exploring the accuracy of the current version of the model to larger particles and investigating the ability of employing additional power-laws to improve model accuracy for large NPs.
Lastly, the model currently only calculates vdW energies between particles and not forces or torques, which requires additional and more complex considerations of energy gradients and interaction site positions. Therefore, the model in its current form can only be used in “static” simulations such as Monte Carlo and energy-minimization methods, and not in “dynamic” simulations such as molecular dynamics or Brownian dynamics methods. While static simulations can be used to investigate many particle-related phenomena such as self-assembly and phase behavior, expansion of the model to dynamic simulations would enable other particle-related topics such as assembly dynamics, rheology, and nonequilibrium effects to be studied.
Conclusions
We developed an analytical model for calculating the vdW interaction potential between faceted NPs. The model is able to accurately predict the vdW energy landscape across all relevant particle configurations for a range of NP shapes. A computational implementation of this method demonstrated that the model can bring orders of magnitude improvement in computational efficiency over the atomistic summation approach for calculating vdW energies. We expect that the model's accuracy, efficiency, and ease of implementation will allow researchers to rapidly explore vdW energy landscapes of faceted NPs, and, more importantly, enable many future investigations of faceted NPs through simulations that have so far been impeded by the prohibitive costs of accurately evaluating vdW energies.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by a grant from the National Science Foundation (CMMI award 1636356) and Duke University. Computational resources were provided by the Duke Computing Cluster (DCC) and the Extreme Science and Engineering Discovery Environment (XSEDE) Program supported by the National Science Foundation (ACI-1053575). We thank Dr Michael Rubinstein and Dr Stefan Zauscher for useful discussions.References
- Y. Sun and Y. Xia, Shape-controlled synthesis of gold and silver nanoparticles, Science, 2002, 298, 2176–2179 CrossRef CAS.
- J. Pal and T. Pal, Faceted metal and metal oxide nanoparticles: design, fabrication and catalysis, Nanoscale, 2015, 7, 14159–14190 RSC.
- N. Tian, Z.-Y. Zhou, S.-G. Sun, Y. Ding and Z. L. Wang, Synthesis of tetrahexahedral platinum nanocrystals with high-index facets and high electro-oxidation activity, Science, 2007, 316, 732–735 CrossRef CAS.
- X. Huang, Z. Zhao, J. Fan, Y. Tan and N. Zheng, Amine-assisted synthesis of concave polyhedral platinum nanocrystals having {411} high-index facets, J. Am. Chem. Soc., 2011, 133, 4718–4721 CrossRef CAS.
- Y. Qi, T. Zhang, C. Jing, S. Liu, C. Zhang, P. J. Alvarez and W. Chen, Nanocrystal facet modulation to enhance transferrin binding and cellular delivery, Nat. Commun., 2020, 11, 1–10 Search PubMed.
- C. Graf, D. Nordmeyer, C. Sengstock, S. Ahlberg, J. Diendorf, J. Raabe, M. Epple, M. Köller, J. Lademann and A. Vogt, et al., Shape-dependent dissolution and cellular uptake of silver nanoparticles, Langmuir, 2018, 34, 1506–1519 CrossRef CAS.
- S. Nangia and R. Sureshkumar, Effects of nanoparticle charge and shape anisotropy on translocation through cell membranes, Langmuir, 2012, 28, 17666–17671 CrossRef CAS.
- A.-Q. Zhang, D.-J. Qian and M. Chen, Simulated optical properties of noble metallic nanopolyhedra with different shapes and structures, Eur. Phys. J. D, 2013, 67, 231 CrossRef.
- B. J. Wiley, S. H. Im, Z.-Y. Li, J. McLellan, A. Siekkinen and Y. Xia, Maneuvering the Surface Plasmon Resonance of Silver Nanostructures through Shape-Controlled Synthesis, J. Phys. Chem. B, 2006, 32, 15666–15675 CrossRef.
- B. Gao, G. Arya and A. R. Tao, Self-orienting nanocubes for the assembly of plasmonic nanojunctions, Nat. Nanotechnol., 2012, 7, 433–437 CrossRef CAS.
- K. L. Gurunatha, S. Marvi, G. Arya and A. R. Tao, Computationally Guided Assembly of Oriented Nanocubes by Modulating Grafted Polymer–Surface Interactions, Nano Lett., 2015, 15, 7377–7382 CrossRef CAS.
- M. Gao, X. Zheng, I. Khan, H. Cai, J. Lan, J. Liu, J. Wang, J. Wu, S. Huang and S. Li, et al., Resonant light absorption and plasmon tunability of lateral triangular Au nanoprisms array, Phys. Lett. A, 2019, 383, 125881 CrossRef CAS.
- Q. Wang, Z. Wang, Z. Li, J. Xiao, H. Shan, Z. Fang and L. Qi, Controlled growth and shape-directed self-assembly of gold nanoarrows, Sci. Adv., 2017, 3, e1701183 CrossRef.
- Y. Nagaoka, R. Tan, R. Li, H. Zhu, D. Eggert, Y. A. Wu, Y. Liu, Z. Wang and O. Chen, Superstructures generated from truncated tetrahedral quantum dots, Nature, 2018, 561, 378 CrossRef CAS.
- J. Gong, R. S. Newman, M. Engel, M. Zhao, F. Bian, S. C. Glotzer and Z. Tang, Shape-dependent ordering of gold nanocrystals into large-scale superlattices, Nat. Commun., 2017, 8, 14038 CrossRef CAS.
- Y. Zhu, L. Xu, W. Ma, Z. Xu, H. Kuang, L. Wang and C. Xu, A one-step homogeneous plasmonic circular dichroism detection of aqueous mercury ions using nucleic acid functionalized gold nanorods, Chem. Commun., 2012, 48, 11889–11891 RSC.
- W. Ma, H. Kuang, L. Xu, L. Ding, C. Xu, L. Wang and N. A. Kotov, Attomolar DNA detection with chiral nanorod assemblies, Nat. Commun., 2013, 4, 1–8 Search PubMed.
- A. Lin, S.-M. Fu, Y.-K. Chung, S.-y. Lai and C.-W. Tseng, An optimized surface plasmon photovoltaic structure using energy transfer between discrete nano-particles, Opt. Express, 2013, 21, A131–A145 CrossRef.
- N. Kholmicheva, P. Moroz, U. Rijal, E. Bastola, P. Uprety, G. Liyanage, A. Razgoniaev, A. D. Ostrowski and M. Zamkov, Plasmonic nanocrystal solar cells utilizing strongly confined radiation, ACS Nano, 2014, 8, 12549–12559 CrossRef CAS.
- C. R. Kagan and C. B. Murray, Charge transport in strongly coupled quantum dot solids, Nat. Nanotechnol., 2015, 10, 1013 CrossRef CAS.
- W. J. Baumgardner, K. Whitham and T. Hanrath, Confined-but-connected quantum solids via controlled ligand displacement, Nano Lett., 2013, 13, 3225–3231 CrossRef CAS.
- S. Biggs and P. Mulvaney, Measurement of the forces between gold surfaces in water by atomic force microscopy, J. Chem. Phys., 1994, 100, 8501–8505 CrossRef CAS.
- C. Argento and R. French, Parametric tip model and force-distance relation for Hamaker constant determination from atomic force microscopy, J. Appl. Phys., 1996, 80, 6081–6090 CrossRef CAS.
- E. Lifshitz, The theory of molecular attractive forces between solids, Sov. Phys. JETP, 1956, 2, 73–83 Search PubMed.
- J. N. Israelachvili, Intermolecular and Surface Forces, Academic Press, 2015 Search PubMed.
- H. C. Hamaker, The London-van der Waals attraction between spherical particles, Physica, 1937, 4, 1058–1072 CrossRef CAS.
- R. Tadmor, The London-van der Waals interaction energy between objects of various geometries, J. Phys.: Condens. Matter, 2001, 13, L195 CrossRef CAS.
- B. H. Lee and G. Arya, Orientational Phase Behavior of Polymer-Grafted Nanocubes, Nanoscale, 2019, 11, 15939–15957 RSC.
- Y. Takato, M. E. Benson and S. Sen, Rich collision dynamics of soft and sticky crystalline nanoparticles: Numerical experiments, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 92, 032403 CrossRef.
- Z. Zhang, M. A. Horsch, M. H. Lamm and S. C. Glotzer, Tethered nano building blocks: Toward a conceptual framework for nanoparticle self-assembly, Nano Lett., 2003, 3, 1341–1346 CrossRef CAS.
- Z. Tang, Z. Zhang, Y. Wang, S. C. Glotzer and N. A. Kotov, Self-assembly of CdTe nanocrystals into free-floating sheets, Science, 2006, 314, 274–278 CrossRef CAS.
- P. F. Damasceno, M. Engel and S. C. Glotzer, Predictive self-assembly of polyhedra into complex structures, Science, 2012, 337, 453–457 CrossRef CAS.
- E. G. Teich, G. van Anders, D. Klotsa, J. Dshemuchadse and S. C. Glotzer, Clusters of polyhedra in spherical confinement, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, E669–E678 CrossRef CAS.
- B. S. John, C. Juhlin and F. A. Escobedo, Phase behavior of colloidal hard perfect tetragonal parallelepipeds, J. Chem. Phys., 2008, 128, 044909 CrossRef.
- U. Agarwal and F. A. Escobedo, Mesophase behaviour of polyhedral particles, Nat. Mater., 2011, 10, 230 CrossRef CAS.
- S. E. Ilse, C. Holm and J. de Graaf, Surface roughness stabilizes the clustering of self-propelled triangles, J. Chem. Phys., 2016, 145, 134904 CrossRef.
- E. G. Gilbert, D. W. Johnson and S. S. Keerthi, A fast procedure for computing the distance between complex objects in three-dimensional space, IEEE J. Robotics and Automation, 1988, 4, 193–203 CrossRef.
- S. Gottschalk, M. C. Lin and D. Manocha, OBBTree: A hierarchical structure for rapid interference detection, Proc. of ACM Siggraph'96, 1996, pp. 171–180.
- J. Ghaboussi and R. Barbosa, Three-dimensional discrete element method for granular materials, Int. J. Numer. Anal. Methods Geomech., 1990, 14, 451–472 CrossRef.
- M. Spellings, R. L. Marson, J. A. Anderson and S. C. Glotzer, GPU accelerated Discrete Element Method (DEM) molecular dynamics for conservative, faceted particle simulations, J. Comput. Phys., 2017, 334, 460–467 CrossRef.
- V. Trappe, V. Prasad, L. Cipelletti, P. Segre and D. A. Weitz, Jamming phase diagram for attractive particles, Nature, 2001, 411, 772 CrossRef CAS.
- T. Lafitte, S. K. Kumar and A. Z. Panagiotopoulos, Self-assembly of polymer-grafted nanoparticles in thin films, Soft Matter, 2014, 10, 786–794 RSC.
- C. Allain, M. Cloitre and M. Wafra, Aggregation and sedimentation in colloidal suspensions, Phys. Rev. Lett., 1995, 74, 1478 CrossRef CAS.
- H. Tanaka, Y. Nishikawa and T. Koyama, Network-forming phase separation of colloidal suspensions, J. Phys.: Condens. Matter, 2005, 17, L143 CrossRef CAS.
- T.-Y. Tang, Y. Zhou and G. Arya, Interfacial Assembly of Tunable Anisotropic Nanoparticle Architectures, ACS Nano, 2019, 13, 4111–4123 CrossRef CAS.
- M. C. Weidman, D.-M. Smilgies and W. A. Tisdale, Kinetics of the self-assembly of nanocrystal superlattices measured by real-time in situ X-ray scattering, Nat. Mater., 2016, 15, 775 CrossRef CAS.
- A. Klinkova, H. Thérien-Aubin, A. Ahmed, D. Nykypanchuk, R. M. Choueiri, B. Gagnon, A. Muntyanu, O. Gang, G. C. Walker and E. Kumacheva, Structural and optical properties of self-assembled chains of plasmonic nanocubes, Nano Lett., 2014, 14, 6314–6321 CrossRef CAS.
- M. N. O’Brien, M. Girard, H.-X. Lin, J. A. Millan, M. O. de la Cruz, B. Lee and C. A. Mirkin, Exploring the zone of anisotropy and broken symmetries in DNA-mediated nanoparticle crystallization, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 10485–10490 CrossRef.
- E. S. Harper, B. Waters and S. C. Glotzer, Hierarchical self-assembly of hard cube derivatives, Soft Matter, 2019, 15, 3733–3739 RSC.
- E. G. Teich, G. van Anders, D. Klotsa, J. Dshemuchadse and S. C. Glotzer, Clusters of polyhedra in spherical confinement, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, E669–E678 CrossRef CAS.
- M. Yang, K. Sun and N. A. Kotov, Formation and assembly- disassembly processes of ZnO hexagonal pyramids driven by dipolar and excluded volume interactions, J. Am. Chem. Soc., 2010, 132, 1860–1872 CrossRef CAS.
- Z. Fang, L. Fan, C. Lin, D. Zhang, A. J. Meixner and X. Zhu, Plasmonic coupling of bow tie antennas with Ag nanowire, Nano Lett., 2011, 11, 1676–1680 CrossRef CAS.
- S. Kim, J. Jin, Y.-J. Kim, I.-Y. Park, Y. Kim and S.-W. Kim, High-harmonic generation by resonant plasmon field enhancement, Nature, 2008, 453, 757 CrossRef CAS.
- M. Sun, L. Xu, J. H. Bahng, H. Kuang, S. Alben, N. A. Kotov and C. Xu, Intracellular localization of nanoparticle dimers by chirality reversal, Nat. Commun., 2017, 8, 1847 CrossRef.
- B. Auguié, J. L. Alonso-Gómez, A. Guerrero-Martnez and L. M. Liz-Marzán, Fingers crossed: Optical activity of a chiral dimer of plasmonic nanorods, J. Phys. Chem. Lett., 2011, 2, 846–851 CrossRef.
- vdWnano, https://github.com/BrianHLeeProjects/vdWnano.
- T.-Y. Tang and G. Arya, Anisotropic three-particle interactions between spherical polymer-grafted nanoparticles in a polymer matrix, Macromolecules, 2017, 50, 1167–1183 CrossRef CAS.
- V. Pryamtisyn, V. Ganesan, A. Z. Panagiotopoulos, H. Liu and S. K. Kumar, Modeling the anisotropic self-assembly of spherical polymer-grafted nanoparticles, J. Chem. Phys., 2009, 131, 221102 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0nh00526f |
| This journal is © The Royal Society of Chemistry 2020 |