Open Access Article
Open Access ArticleNegative effective excitonic diffusion in monolayer transition metal dichalcogenides†
Roberto
Rosati
 *,
Raül
Perea-Causín
*,
Raül
Perea-Causín
 ,
Samuel
Brem
,
Samuel
Brem
 and
Ermin
Malic
and
Ermin
Malic
Chalmers University of Technology, Department of Physics, 412 96 Gothenburg, Sweden. E-mail: roberto.rosati@chalmers.se
First published on 27th November 2019
Abstract
While exciton relaxation in monolayers of transition metal dichalcogenides (TMDs) has been intensively studied, spatial exciton diffusion has received only a little attention – in spite of being a key process for optoelectronics and having already shown interesting unconventional behaviours (e.g. spatial halos). Here, we study the spatiotemporal dynamics in TMD monolayers and track optically excited excitons in time, momentum, and space. In particular, we investigate the temperature-dependent exciton diffusion including the remarkable exciton landscape constituted by bright and dark states. Based on a fully quantum mechanical approach, we show at low temperatures an unexpected negative effective diffusion characterized by a shrinking of the spatial exciton distributions. This phenomenon can be traced back to the existence of dark exciton states in TMD monolayers and is a result of an interplay between spatial exciton diffusion and intervalley exciton–phonon scattering.
Monolayers of transition metal dichalcogenides (TMDs) have attracted much attention1–14 in particular due to their remarkable exciton landscape including bright and momentum- and spin-dark exciton states.1,6,8,12 Recently, their spatiotemporal exciton dynamics has been studied,15–22 showing peculiar effects including a distinct diffusion of bright and spin-dark excitons at low temperatures20 as well as the formation of spatial halos at higher excitation densities.21 The latter has been suggested to stem from phonon winds23 or efficient thermal drifts.24
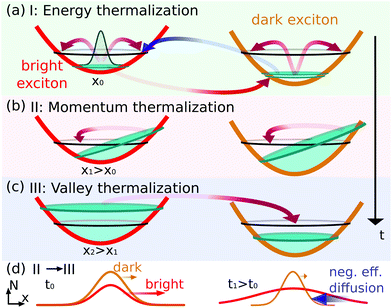
In this work, we shed light on the impact of the versatile exciton landscape including bright and momentum-dark states on spatiotemporal exciton dynamics in TMD monolayers in different temperature regimes. The resulting evolution is a complicated process with the coexistence of several many-particle mechanisms, showing in particular the appearance of different phases which will be addressed in the following. At a more simplified level, one expects that after optical excitation the excitons thermalize in energy on a quick timescale of hundreds of femtoseconds at room temperature10,11 [Fig. 1(a)]. However, spatial propagation can also result on longer timescales in anisotropic exciton occupations, since excitons with the same energy but different momentum orientation propagate towards different spatial directions – similarly to electrons in quantum wells.25,26 Momentum thermalization at each space point drives toward an isotropic distribution [Fig. 1(b)]. During this evolution, the excitonic spatial distribution undergoes an effective diffusion, i.e. it broadens in space while preserving the position of the maximum distribution and rotational symmetry. Here effective diffusion refers to the transient evolution, whereas the conventional diffusion refers to the steady-state regime.18,20 Furthermore, different diffusion characteristics of bright and dark states can result in a local non-equilibrium among different valleys. Here, a space-dependent equilibration of bright and dark states leads toward a valley-thermalized occupation [Fig. 1(c)].
Based on a fully quantum mechanical approach,10,11,14 this work provides microscopic insights into the interplay of spatiotemporal exciton dynamics and thermalization. We resolve the evolution of optically excited, spatially localized excitons in time, momentum, energy, and space taking into account bright and momentum-dark excitonic states. We predict unexpected spatiotemporal dynamics including the emergence of a negative effective diffusion, where the spatial profiles of the excitonic distribution shrink in space, apparently moving back towards the excitation center [cf. blue arrow in Fig. 1(d)].
1. Theoretical approach
Our goal is to study on a microscopic footing the spatiotemporal dynamics of excitons in the exemplary hBN-encapsulated tungsten disulfide (WS2) monolayers. Considering the single-particle dispersion27 and solving the exciton Wannier equation10,11,28,29 with a non-local screening in analogy to recent studies,30 we obtain a set of exciton states |α〉 ≡ |Q, v〉 characterized by the valley index v, the center-of-mass momentum Q and the exciton energy εα = Ev + ħ2|Q|2/(2Mv) with Mv as the total valley-dependent mass. Due to considerable energy separations, we restrict our attention to the 1s states of the bright excitons (KK) and the momentum-dark excitons (KK′, KΛ) lying approximately 51.5 and 30.5 meV below KK, respectively. These values have been obtained by solving the Wannier equation and are in good qualitative agreement with recent ab initio studies.12 Spin-dark states20,31 have not been taken into account, as they are not expected to qualitatively affect the main message of this work, i.e. the transient spatiotemporal dynamics of spin-allowed states. The former states in fact interact with the latter via less-effective carrier-spin-flipping processes.32,33 Moreover, spin-dark KK states have similar properties to the KK′ excitons (in terms of dispersion relation) and are hence expected to lead at first approximation only to quantitative changes. Furthermore, in this work we focus on the intrinsic undoped regime, where the effect of trions18,20,34,35 is negligible.Taking states |α〉 ≡ |Q, v〉 as a basis, we introduce the coefficients ραα′ of the single-particle density matrix36–38 of incoherent excitons, ραα′ = ρvv′QQ′ = 〈![[X with combining circumflex]](https://www.rsc.org/images/entities/i_char_0058_0302.gif) †α′Xα〉, where X(†)α are annihilation (creation) operators for the state |α〉. Then, we introduce the excitonic intravalley Wigner function
†α′Xα〉, where X(†)α are annihilation (creation) operators for the state |α〉. Then, we introduce the excitonic intravalley Wigner function 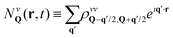 , which summed over Q provides the intravalley spatial density
, which summed over Q provides the intravalley spatial density 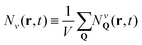 . The total excitonic density nv(t) in valley v reads
. The total excitonic density nv(t) in valley v reads 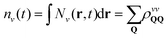 and is determined by the diagonal density matrix elements. In contrast, the off-diagonal terms induce an explicit dependence on r, i.e. they result in a spatial inhomogeneity.
and is determined by the diagonal density matrix elements. In contrast, the off-diagonal terms induce an explicit dependence on r, i.e. they result in a spatial inhomogeneity.
Now, we introduce an equation of motion for the spatiotemporal dynamics of excitons by exploiting the Heisenberg equation and the many-particle Hamilton operator.28,37,38 The derived semiconductor Bloch equation10,14 can then be transformed in the Wigner representation39,40 and reads in the low excitation regime:
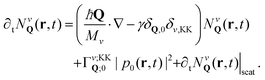 | (1) |
The first term indicates the free evolution of excitons ∇QεQ,v = ħQ/Mv, while the second term takes into account the losses due to the direct photoluminescence IPL(r, t) = γNKKQ≈0(r, t). Here, γ describes the radiative recombination rate within the light cone (δQ,0δv,KK).10,11,29 The effects of phonon-assisted radiative recombination are beyond the scope of this work.41
The first contribution in the second line of eqn (1) describes the formation of incoherent excitons due to phonon-driven transfer from the excitonic polarization pQ≈0(r, t) (referred to in the literature as coherent excitons10). The latter are optically excited by an electromagnetic field A(r, t) through ∂tpQ(r, t)|opt ∝ M·A(r, t)δQ,0, with M depending on optical matrix elements and excitonic wave functions.10,11 The process is driven by exciton–phonon scattering with the rates Γvv′QQ′ describing scattering from state |Q′v′〉 to |Qv〉 via interaction with phonons.10,11 We take into account longitudinal and transverse acoustic (LA, TA) and optical (LO, TO) modes as well as the out-of-plane A1 optical mode, which provide the most efficient scattering channels.42 Phonon energies and carrier-phonon scattering coefficients within the deformation potential approximation are extracted from density functional theory studies.42 Since coherent excitons decay on an ultrafast timescale of 10–100 fs,10 it is the incoherent exciton distribution that determines the spatiotemporal dynamics of the photoluminescence.
Finally, the last term in eqn (1) describes the scattering contribution. In this work we focus on high-quality hBN-encapsulated TMD monolayer samples, where disorder does not play a large role. The encapsulation with hBN has been applied as a key strategy to prepare high-quality TMD samples, resulting in strong linewidth narrowings,43,44 ascribed to shielding of the material from the substrate and surface defects as well as to mitigation of the effect of dielectric disorder.45 We restrict our attention to the low-excitation regime, where the main source of scattering is given by exciton–phonon interactions. The intra- (v = v′) and inter-valley (v ≠ v′) contribution can be written as 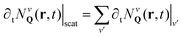 , where ∂tNvQ(r, t)|v′ indicates the dynamics of Nv induced by the interaction with Nv′. The corresponding equation of motion reads:
, where ∂tNvQ(r, t)|v′ indicates the dynamics of Nv induced by the interaction with Nv′. The corresponding equation of motion reads:
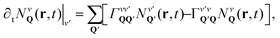 | (2) |
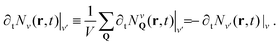 It follows immediately that intravalley scattering does not change Nv(r, t), i.e. ∂tNv(r, t)|v = 0, as expected for broad densities.46,47 Although having no direct contribution, the intravalley scattering may have a considerable impact on the spatial distribution Nv(r), since locally (i.e. in every position r) these scattering channels redistribute the Wigner function NvQ in the momentum Q toward the local equilibrium distribution NvoQ(r, t) ∝ exp[−εQv/(kBT)]. By studying how the difference between NvQ and NvoQ evolves,39 it can be shown that the dynamics of the spatial distribution Nv is given in the absence of intervalley scattering mechanisms and in the steady-state regime by Fick's law
It follows immediately that intravalley scattering does not change Nv(r, t), i.e. ∂tNv(r, t)|v = 0, as expected for broad densities.46,47 Although having no direct contribution, the intravalley scattering may have a considerable impact on the spatial distribution Nv(r), since locally (i.e. in every position r) these scattering channels redistribute the Wigner function NvQ in the momentum Q toward the local equilibrium distribution NvoQ(r, t) ∝ exp[−εQv/(kBT)]. By studying how the difference between NvQ and NvoQ evolves,39 it can be shown that the dynamics of the spatial distribution Nv is given in the absence of intervalley scattering mechanisms and in the steady-state regime by Fick's law| ∂tNv(r, t) = DvΔrNv(r, t). | (3) |
Here decaying mechanisms have been omitted18,20 and Dv = 1/2〈τvQħ2Q2/Mv2〉|vQ is the diffusion coefficient, with 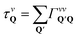 providing the Q-dependent relaxation time induced by intravalley processes. The introduced expectation value 〈fQ〉|vQ provides the average of fQ assuming a (local) thermalized distribution
providing the Q-dependent relaxation time induced by intravalley processes. The introduced expectation value 〈fQ〉|vQ provides the average of fQ assuming a (local) thermalized distribution 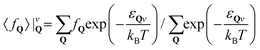 . Under the assumption of constant relaxation times τQvv ≈ τv the well-known steady-state relation Dv = τvkBT/Mv can be recovered.
. Under the assumption of constant relaxation times τQvv ≈ τv the well-known steady-state relation Dv = τvkBT/Mv can be recovered.
The evolution of Nv(r, t) undergoes a so-called effective diffusion, i.e. (i) it preserves the location of its center (in contrast to transport studies involving a shift of the occupation peak48), (ii) it is rotationally symmetric, and (iii) it broadens in space. In order to quantify this effective diffusion process, we introduce a width wv of the distribution Nv which is proportional to the variance, 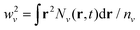 . According to Fick's law [eqn (3)], confined spatial distributions would behave as Nv(r, t) ∝ exp [−r2/wv2(t)] with w2v(t) = w2v,0 + 4Dvt,17,21 where w2v,0 is the initial width. It follows that one can define an effective diffusion coefficient (or diffusivity) as Dv = ¼∂tw2v, i.e. as the slope of the temporal evolution of the squared width w2v. In the so-called conventional diffusion, Dv is a constant. This behaviour occurs in the steady-state regime and can be described by the conventional Fick's law [eqn (3)]. However, before the steady-state regime is reached, the spatial distribution is expected to undergo a non-trivial evolution, which can be interpreted in terms of a modified Fick's law with a time-dependent effective diffusion coefficient Dv(t).49–51 As a remarkable example, in the so-called ballistic scenario, where many-particle scattering is negligible, the effective diffusion coefficient Dv(t) increases linearly with time t.25 The intravalley scattering leads the system from a ballistic regime to a conventional diffusion by acting as a frictional mechanism counteracting the free evolution. When the intervalley contribution becomes of the same order of magnitude as the intravalley one, intriguing phenomena are expected including negative effective diffusion effects – as will be discussed below. Since we will mostly focus on transient phenomena, for the sake of simplicity and unless otherwise specified below we will simply write diffusion when referring to effective diffusion.
. According to Fick's law [eqn (3)], confined spatial distributions would behave as Nv(r, t) ∝ exp [−r2/wv2(t)] with w2v(t) = w2v,0 + 4Dvt,17,21 where w2v,0 is the initial width. It follows that one can define an effective diffusion coefficient (or diffusivity) as Dv = ¼∂tw2v, i.e. as the slope of the temporal evolution of the squared width w2v. In the so-called conventional diffusion, Dv is a constant. This behaviour occurs in the steady-state regime and can be described by the conventional Fick's law [eqn (3)]. However, before the steady-state regime is reached, the spatial distribution is expected to undergo a non-trivial evolution, which can be interpreted in terms of a modified Fick's law with a time-dependent effective diffusion coefficient Dv(t).49–51 As a remarkable example, in the so-called ballistic scenario, where many-particle scattering is negligible, the effective diffusion coefficient Dv(t) increases linearly with time t.25 The intravalley scattering leads the system from a ballistic regime to a conventional diffusion by acting as a frictional mechanism counteracting the free evolution. When the intervalley contribution becomes of the same order of magnitude as the intravalley one, intriguing phenomena are expected including negative effective diffusion effects – as will be discussed below. Since we will mostly focus on transient phenomena, for the sake of simplicity and unless otherwise specified below we will simply write diffusion when referring to effective diffusion.
2. Results
2.1. Spatiotemporal photoluminescence
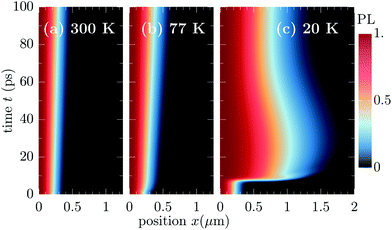
Now, we exploit the theoretical approach discussed above to describe the spatiotemporal dynamics in monolayer TMDs. First, we create a non-equilibrium through an optical excitation which is resonant to the A exciton and centered in time (around t0 = 0.2 ps with A(r, t) having an amplitude FWHM of 100 fs) and space (around r = 0 with amplitude FWHM of 0.5 μm and associated width w of about 0.3 μm). We emphasize that although the size of the intensity affects the initial width of the distribution, its impact on the evolution of Dv(t) is found to be negligible, as far as no additional effects induced by stronger localizations are considered.46,47 Then, we evaluate eqn (1) and (2) to describe transient changes of the effective diffusion coefficients Dv(t) including phonon-assisted transfer between bright and momentum-dark excitons.We start considering the direct PL spatial distribution IPL, which remains rotationally symmetric with respect to its center r = 0, hence we plot only the values along the x-axis. We show in Fig. 2 normalized PL distributions, from which the change of the spatial profile can be better understood, while the unnormalized PL can be found in the ESI.† Note that IPL undergoes decaying processes similar to the case of spatially homogeneous optical excitation.10 Such decays are dominated by shape-preserving mechanisms (e.g. radiative recombination or fast intervalley thermalization), hence affecting the total exciton density but not the profile of its spatial distribution. While in Fig. 2 the initial shape of IPL follows the intensity of the exciting optical field, its evolution illustrates the increase of the lateral size of the spatial exciton distribution at different temperatures. At 300 K, there is only a modest and constant broadening, while at 77 K, one can see a more pronounced increase of the spatial size due to the weaker counteracting exciton–phonon scattering at lower temperatures. Interestingly, different timescales are observable, exhibiting a much faster effective diffusion in the first few picoseconds followed by a slower broadening.
Further decreasing the temperature to 20 K, we find in addition to an unexpected fast broadening between approximately 4 and 8 ps an even more surprising behaviour: after approximately 30 ps, the PL spatial distribution starts to shrink, i.e. the normalized PL profile apparently goes back in space towards the center of the distribution rather than diffusing away from it. This indicates an effective back-diffusion (in the sense of reduction of second moment) or according to a modified Fick's law [see eqn (3)], negative diffusion. Although also observed in single-species studies,50,52 negative diffusions appear usually in multi-component systems (also called uphill diffusion, see e.g.ref. 53–55). Negative carrier diffusions have been shown e.g. in scanning ultrafast electron microscopy studies56 as a result of spatial separation of electrons and holes and the resulting (Coulomb-induced) interaction. In our case, the multi-component nature is induced by the remarkable multi-valley exciton landscape displayed in TMD monolayers. We will show below that the efficient intervalley exciton–phonon scattering is the origin of both the back-diffusion and the sharp increase at about 4–8 ps. In particular, we will discuss how the observed diffusion delay stems from the interplay of initial valley-intrinsic diffusion (with the appearance of cold/hot energy distribution in bright and dark valleys, respectively) and time required to absorb (acoustic) intervalley phonons from higher-energy dark exciton states.
2.2. Valley-dependent exciton diffusion
To understand the interesting spatiotemporal evolution of the PL, we perform now a quantitative analysis of the shape of excitonic densities including bright and dark states. Fig. 3 illustrates the time evolution of the squared spatial width w2v and the resulting diffusion coefficient Dv for KK, KK′ and KΛ excitons. In addition we plot the analogous variables for the total spatial density N(r, t) obtained by summing over the three intravalley spatial densities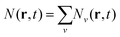 (dotted lines). The PL (dashed lines) follows the dynamics of NKK while N follows the dynamics of the most occupied valley, i.e. KΛ at 300 K and KK′ at the two lowest temperatures. At room temperature [Fig. 3(a)] we observe an almost identical behavior for all three types of excitons. The diffusion coefficients Dv become very quickly time-independent and reach a stationary value of almost 1 cm2 s−1. This is the consequence of a very efficient exciton–phonon scattering at 300 K that results in an ultrafast equilibration of all intra- and intervalley exciton states, before a considerable spatial separation between valleys could appear. This is not the case anymore at 77 K [Fig. 3(b)], where we observe valley-dependent values.
(dotted lines). The PL (dashed lines) follows the dynamics of NKK while N follows the dynamics of the most occupied valley, i.e. KΛ at 300 K and KK′ at the two lowest temperatures. At room temperature [Fig. 3(a)] we observe an almost identical behavior for all three types of excitons. The diffusion coefficients Dv become very quickly time-independent and reach a stationary value of almost 1 cm2 s−1. This is the consequence of a very efficient exciton–phonon scattering at 300 K that results in an ultrafast equilibration of all intra- and intervalley exciton states, before a considerable spatial separation between valleys could appear. This is not the case anymore at 77 K [Fig. 3(b)], where we observe valley-dependent values.
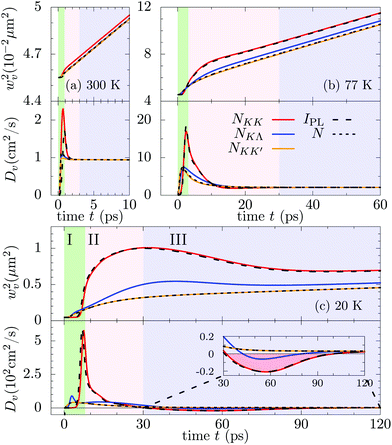 | ||
Fig. 3 Temporal evolution of squared spatial width w2v of excitonic distributions and the associated transient diffusion coefficient Dv of KK, KK′ and KΛ excitons shown at (a) 300 K, (b) 77 K, and (c) 20 K. The evolution of the direct PL is illustrated with the dashed black line while the one associated with the total spatial density 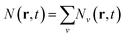 is indicated by the dotted black line. The three phases characterizing the spatiotemporal dynamics are denoted with green, red and blue background colors, respectively (as introduced in Fig. 1). is indicated by the dotted black line. The three phases characterizing the spatiotemporal dynamics are denoted with green, red and blue background colors, respectively (as introduced in Fig. 1). | ||
In Fig. 3(b) we find three well-distinguished phases determining the temporal evolution of exciton diffusion in TMD monolayers: (I) an initial phase with a valley-dependent fast increase of diffusion coefficients (green-shaded background), (II) a transient phase where the differences between valleys decrease (red-shaded background), and (III) a final phase, where an effective stationary diffusion coefficient is reached (blue-shaded background). It is the relatively long duration of phase II, where the diffusion coefficients are still valley-intrinsic, that gives rise to the observed different widths w2v for different exciton densities. These differences are essentially preserved in phase III, i.e. the w2v trajectories tend to be parallel resulting in similar diffusion coefficients Dv.
Decreasing the temperature to 20 K [Fig. 3(c)], both the maximal values of coefficients Dv and the spatial separation between valley-dependent widths w2v further increase, reflecting the strongly reduced efficiency of exciton–phonon scattering counteracting diffusion and valley redistribution of excitons. After the initial steep increase, the diffusion coefficients of both KK and KΛ excitons undergo a subsequent decrease eventually leading to negative values at around 30–100 ps for KK excitons (see the inset). The appearance of negative effective diffusion explains the features observed in the PL in Fig. 2. Although a thorough microscopic description of other interaction mechanisms, such as disorder, has not been considered, we find that on slightly increasing the scattering rates (i.e. somehow mimicking the presence of additional scattering channels), the qualitative aspects of the evolution of DKK at 20 K would still be present. Furthermore, in the considered WS2 monolayer we find that the radiative recombination [see rate γ in eqn (1)] has a negligible effect on DKK. As we will see in the next subsection, the evolution of DKK is in fact ruled by the energetically lowest dark excitonic states, the latter being affected by γ only via second order processes (i.e. refilling of valley KK).
2.3. Intervalley exciton–phonon scattering
To better understand the mechanism underlying the predicted negative diffusion, we investigate the role of intervalley exciton–phonon scattering. Fig. 4 illustrates the full temporal evolution of Dv at 300 K in the Gedanken experiments, where we artificially switch off the intervalley scattering after 10 ps. We clearly observe that without intervalley scattering one would have pronounced valley-dependent diffusion coefficients Dv reflecting different effective masses of the involved valleys. Recalling the discussed steady-state relation between Dv and intravalley τv, this implies scattering rates of approximately 84 (omitting the radiative decay γ), 66 and 43 fs for KK, KK′ and KΛ excitons, respectively. Fig. 4 already shows the crucial role of intervalley scattering for exciton diffusion even at room temperature.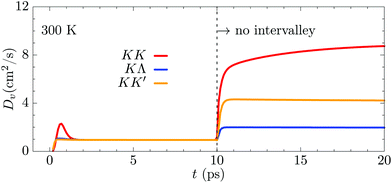 | ||
| Fig. 4 Diffusion coefficient of KK, KK′ and KΛ excitons at 300 K, where intervalley channels are switched off after 10 ps. | ||
To be able to quantitatively understand how the intervalley scattering affects the diffusion at low temperatures, we introduce the scattering-induced shape variation:
| ηv(r, t) = ∂tNv(r, t)|scat − cvNv(r, t), | (4) |
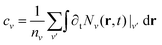 . The shape variation ηv(r, t) is the difference between full scattering-induced density dynamics ∂tNv(r, t)|scat and shape-preserving change of exciton amount. The latter only induces a variation of amplitude Nv(r, t + Δt) = (1 + cvΔt)Nv(r, t) in the limit Δt → 0. The quantity η alone, in contrast, would induce Nv(r, t + Δt) = Nv(r, t) + Δt
. The shape variation ηv(r, t) is the difference between full scattering-induced density dynamics ∂tNv(r, t)|scat and shape-preserving change of exciton amount. The latter only induces a variation of amplitude Nv(r, t + Δt) = (1 + cvΔt)Nv(r, t) in the limit Δt → 0. The quantity η alone, in contrast, would induce Nv(r, t + Δt) = Nv(r, t) + Δt![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) ηv(r, t). Since
ηv(r, t). Since 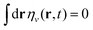 , it follows that ηv may describe amount-preserving variations of density Nv, i.e. ηv extracts the changes in shape of Nv from ∂tNv(r, t)|scat, while the variation of nv is described by cvNv. The shape variation ηv describes scattering-induced spatial redistribution of density Nv(r) from e.g. position r1 toward r2 by assuming negative (positive) values in the regions where the distribution is lost (gained). Thus, η directly affects the exciton diffusion process. Exploiting the general definition of the diffusion coefficient Dv below eqn (3), we introduce a scattering-induced diffusion coefficient
, it follows that ηv may describe amount-preserving variations of density Nv, i.e. ηv extracts the changes in shape of Nv from ∂tNv(r, t)|scat, while the variation of nv is described by cvNv. The shape variation ηv describes scattering-induced spatial redistribution of density Nv(r) from e.g. position r1 toward r2 by assuming negative (positive) values in the regions where the distribution is lost (gained). Thus, η directly affects the exciton diffusion process. Exploiting the general definition of the diffusion coefficient Dv below eqn (3), we introduce a scattering-induced diffusion coefficient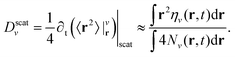 This quantity provides the contribution of spatial density redistribution induced by exciton–phonon scattering to the exciton diffusion. Recalling that for broad distributions46,47 the intravalley scattering mechanisms do not contribute to the scattering-induced dynamics of Nv, i.e.
This quantity provides the contribution of spatial density redistribution induced by exciton–phonon scattering to the exciton diffusion. Recalling that for broad distributions46,47 the intravalley scattering mechanisms do not contribute to the scattering-induced dynamics of Nv, i.e.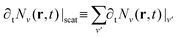 , the scattering-induced diffusion coefficient Dscatv can also be seen as the direct measure for the intervalley scattering-induced diffusion Dintervv.
, the scattering-induced diffusion coefficient Dscatv can also be seen as the direct measure for the intervalley scattering-induced diffusion Dintervv.
Fig. 5(a) shows a direct comparison between scattering-induced (DintervKK) and full diffusion coefficient DKK at 20 K. We find strong similarities between the two lines, indicating that the scattering-induced diffusion dominates the transient features of DKK. These include e.g. the high peak at about 8 ps, which can be explained as follows: due to the low temperature the momentum-dark excitons have not fully thermalized yet, having an overpopulation of states with energies high enough to scatter into KK states (cf. blue arrow in Fig. 1(a)).
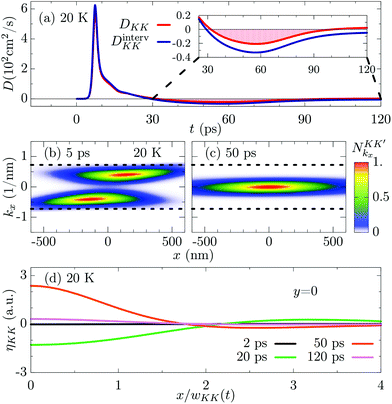 | ||
Fig. 5 Illustration of the mechanism behind negative diffusion. (a) Intervalley scattering-induced diffusion coefficient DintervKK (see the definition in the text) in direct comparison with the full diffusion coefficient DKK at 20 K illustrating the crucial contribution of intervalley scattering. (b and c) Wigner distribution 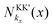 for KK′ excitons plotted at 5 and 50 ps as a function of k ≡ (kx, 0) and r ≡ (x, 0). The dotted line indicates the minimum wave-vector modulus required for the intervalley process into valley KK via absorption of acoustic modes. (d) Normalized scattering-induced shape variation [cf. eqn (4)] for KK excitons at four different times. for KK′ excitons plotted at 5 and 50 ps as a function of k ≡ (kx, 0) and r ≡ (x, 0). The dotted line indicates the minimum wave-vector modulus required for the intervalley process into valley KK via absorption of acoustic modes. (d) Normalized scattering-induced shape variation [cf. eqn (4)] for KK excitons at four different times. | ||
This can be observed also in Fig. 5(b), where the Wigner distribution 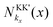 for KK′ excitons is plotted at 5 ps, i.e. during the steep increase. Due to the reduced temperature, both energy and momentum thermalizations are not finished yet. We find a clear anisotropy in momentum, such that there is a higher exciton occupation at positive (negative) momenta for x > 0 (x < 0). The energy distribution is not thermalized around kx ≈ 0, but exhibits peaks at finite momenta indicating a hot exciton distribution.
for KK′ excitons is plotted at 5 ps, i.e. during the steep increase. Due to the reduced temperature, both energy and momentum thermalizations are not finished yet. We find a clear anisotropy in momentum, such that there is a higher exciton occupation at positive (negative) momenta for x > 0 (x < 0). The energy distribution is not thermalized around kx ≈ 0, but exhibits peaks at finite momenta indicating a hot exciton distribution.
The non-equilibrium excess-energy is induced by the polarization-to-population transfer, implying that the incoherent dark states formed directly after the optical excitation lay one intervalley phonon energy below the KK minimum (i.e. the energy of coherent excitons). This creates an initial hot distribution of dark excitons, which subsequently relaxes toward the corresponding ground state. In contrast, the initial distribution in KK is even colder than 20 K, resulting in a very slow effective diffusion in the bright valley before the steep increase. Note that these hot dark excitons can scatter back into KK exciton states via absorption of intervalley phonons. As a guide to the eye, the dotted line in Fig. 5(b and c) indicates the minimum wave-vector modulus required for such an intervalley process via absorption of acoustic modes. As shown in Fig. 5(b), the distribution of these KK′ states with high-enough energy is mostly located away from the initial excitation spot, while the other KK′ states with smaller energies are distributed closer to r = 0. Once these spatially wide-spread hot states scatter into KK valley, the density of the latter undergoes a steep extension of its spatial broadening, resulting in the increase of the squared width w2KK in Fig. 3(c). The absorption of phonons with finite energy is less effective at small temperatures, thus inducing the time delay of Fig. 2–4, whose duration is found to be directly affected by acoustic-phonon-induced intervalley scattering. Once occupied mostly via scattering from high-energy dark states, the KK excitons thermalize. It is during this valley-thermalization phase [cf. also Fig. 1(c and d)] that the negative transient diffusion in DKK appears. When the diffusion of KK excitons shows the highest negative values, the distribution of KK′ excitons is already quasi-thermalized both in energy and momentum, cf. Fig. 5(c). It is crucial to have a dark state well below the bright one, so that a hot dark excitonic distribution can be formed giving rise to the steep increase of DKK on a few picosecond timescale, cf. Fig. 5(a and b). This behaviour is expected to change qualitatively in semiconductors where the bright exciton is the energetically lowest state.
The driving force behind the remarkable negative diffusion is intervalley exciton–phonon scattering processes, as the similarity of Dinterv to the scattering-induced diffusion D shows in Fig. 5(a) (see also the inset). Note that the effect of Dintervv becomes smaller for excitons with a higher population, i.e., the energetically lowest and thus the highest occupied KK′ excitons have a negligible Dinterv (not shown), resulting in a smoother evolution of w2KK′ and DKK′ [Fig. 3(c)]. In fact, it can be shown that the mutual interaction between two valleys v1 and v2 leads to ηv1 ≈ −ηv2. Inserting the last approximation in the η-dependent definition of Dinterv, one finds 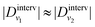 nv2/nv1. As a consequence, for nv1 ≪ nv2 it follows that
nv2/nv1. As a consequence, for nv1 ≪ nv2 it follows that 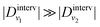 . This explains why the negative diffusion region only appears for lower-populated exciton valleys [Fig. 3(c)].
. This explains why the negative diffusion region only appears for lower-populated exciton valleys [Fig. 3(c)].
The different temporal behaviour displayed by DintervKK is induced by different qualitative trends of the shape variation ηKK, cf. Fig. 5(d). Here, we have normalized ηKK with respect to nKK(0, t) and considered the dimension-free position x/wKK(t) to compare spatial distributions with different height and width. At 2 ps, the timescale is too short for the absorption of phonons, hence both Dinterv and η are negligible. In contrast, at 20 ps Dinterv is very high. Accordingly, η shows the conventional diffusive shape with a transfer of density from the center [η(x) < 0 for x ≈ 0] toward the tails (η > 0 for x ≳ 2wKK). However, at 50 ps there is a remarkable change of sign in η, which is now positive in the center and negative in the tail. This implies an uphill transfer of density from the tails toward the center, i.e. a negative diffusion, which is in fact displayed in Fig. 5(d) at 50 ps. At 120 ps, there is a similar behaviour of η, however with a reduced magnitude. This implies Dinterv with a reduced negativity (in agreement with Fig. 5(a)) that is overcompensated for by other mechanisms resulting in an overall positive diffusion, cf. the red line in Fig. 5(a).
3. Conclusions
We have shown that the spatiotemporal exciton dynamics in transition metal dichalcogenides can result in an unexpected negative exciton diffusion, i.e. a shrinking of the spatial exciton density. Based on a fully quantum mechanical approach providing microscopic insights into time-, momentum- and space-resolved exciton dynamics, we ascribe this behaviour to the interplay of valley-intrinsic diffusion and intervalley thermalization processes. The key ingredient is the remarkable excitonic landscape of TMD monolayers containing bright and lower-lying dark states. Our work sheds light on the emerging field of spatiotemporal dynamics in atomically thin materials and may trigger new experimental and theoretical studies on valley-dependent exciton diffusion.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This project has received funding from the Swedish Research Council (VR, project number 2018-00734) and the European Union's Horizon 2020 research and innovation programme under grant agreement no. 785219 (Graphene Flagship).References
- T. Mueller and E. Malic, npj 2D Mater. Appl., 2018, 2, 29 CrossRef.
- G. Wang, A. Chernikov, M. M. Glazov, T. F. Heinz, X. Marie, T. Amand and B. Urbaszek, Rev. Mod. Phys., 2018, 90, 021001 CrossRef CAS.
- D. Xiao, G.-B. Liu, W. Feng, X. Xu and W. Yao, Phys. Rev. Lett., 2012, 108, 196802 CrossRef PubMed.
- A. Chernikov, T. C. Berkelbach, H. M. Hill, A. Rigosi, Y. Li, O. B. Aslan, D. R. Reichman, M. S. Hybertsen and T. F. Heinz, Phys. Rev. Lett., 2014, 113, 076802 CrossRef PubMed.
- K. He, N. Kumar, L. Zhao, Z. Wang, K. F. Mak, H. Zhao and J. Shan, Phys. Rev. Lett., 2014, 113, 026803 CrossRef PubMed.
- H. Yu, X. Cui, X. Xu and W. Yao, Natl. Sci. Rev., 2015, 2, 57 CrossRef CAS.
- A. Steinhoff, M. Florian, M. Rösner, M. Lorke, T. O. Wehling, C. Gies and F. Jahnke, 2D Mater., 2016, 3, 031006 CrossRef.
- G. Wang, C. Robert, M. M. Glazov, F. Cadiz, E. Courtade, T. Amand, D. Lagarde, T. Taniguchi, K. Watanabe, B. Urbaszek and X. Marie, Phys. Rev. Lett., 2017, 119, 047401 CrossRef CAS PubMed.
- T. Deilmann and K. S. Thygesen, Phys. Rev. B, 2017, 96, 201113(R) CrossRef.
- M. Selig, G. Berghäuser, M. Richter, R. Bratschitsch, A. Knorr and E. Malic, 2D Mater., 2018, 5, 035017 CrossRef.
- S. Brem, M. Selig, G. Berghaeuser and E. Malic, Sci. Rep., 2018, 8, 8238 CrossRef PubMed.
- T. Deilmann and K. S. Thygesen, 2D Mater., 2019, 6, 035003 CrossRef.
- N. Lundt, L. Dusanowski, E. Sedov, P. Stepanov, M. M. Glazov, S. Klembt, M. Klaas, J. Beierlein, Y. Qin, S. Tongay, M. Richard, A. V. Kavokin, S. Höfling and C. Schneider, Nat. Nanotechnol., 2019, 14, 770–775 CrossRef CAS PubMed.
- P. Merkl, F. Mooshammer, P. Steinleitner, A. Girnghuber, K. Lin, P. Nagler, J. Holler, C. Schüller, J. Lupton, T. Korn, S. Ovesen, S. Brem, E. Malic and R. Huber, Nat. Mater., 2019, 18, 691 CrossRef CAS PubMed.
- N. Kumar, Q. Cui, F. Ceballos, D. He, Y. Wang and H. Zhao, Nanoscale, 2014, 6, 4915 RSC.
- S. Mouri, Y. Miyauchi, M. Toh, W. Zhao, G. Eda and K. Matsuda, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 155449 CrossRef.
- J. He, D. He, Y. Wang, Q. Cui, F. Ceballos and H. Zhao, Nanoscale, 2015, 7, 9526 RSC.
- T. Kato and T. Kaneko, ACS Nano, 2016, 10, 9687 CrossRef CAS PubMed.
- L. Yuan, T. Wang, T. Zhu, M. Zhou and L. Huang, J. Phys. Chem. Lett., 2017, 8, 3371 CrossRef CAS PubMed.
- F. Cadiz, C. Robert, E. Courtade, M. Manca, L. Martinelli, T. Taniguchi, K. Watanabe, T. Amand, A. Rowe, D. Paget, B. Urbaszek and X. Marie, Appl. Phys. Lett., 2018, 112, 152106 CrossRef.
- M. Kulig, J. Zipfel, P. Nagler, S. Blanter, C. Schüller, T. Korn, N. Paradiso, M. M. Glazov and A. Chernikov, Phys. Rev. Lett., 2018, 120, 207401 CrossRef CAS PubMed.
- J. Zipfel, M. Kulig, R. Perea-Causín, S. Brem, J. D. Ziegler, R. Rosati, T. Taniguchi, K. Watanabe, M. M. Glazov, E. Malic and A. Chernikov, arXiv:1911.02909, 2019.
- M. M. Glazov, Phys. Rev. B, 2019, 100, 045426 CrossRef CAS.
- R. Perea-Causín, S. Brem, R. Rosati, R. Jago, M. Kulig, J. D. Ziegler, J. Zipfel, A. Chernikov and E. Malic, Nano Lett., 2019, 19, 7317 CrossRef PubMed.
- F. Steininger, A. Knorr, P. Thomas and S. W. Koch, Z. Phys. B: Condens. Matter, 1997, 103, 45 CrossRef CAS.
- A. Knorr, F. Steininger, B. Hanewinkel, S. Kuckenburg, P. Thomas and S. W. Koch, Phys. Status Solidi B, 1998, 206, 139 CrossRef CAS.
- A. Kormányos, G. Burkard, M. Gmitra, J. Fabian, V. Zólyomi, N. D. Drummond and V. Fal'ko, 2D Mater., 2015, 2, 022001 CrossRef.
- H. Haug and S. W. Koch, Quantum Theory of the Optical and Electronic Properties of Semiconductors: Fifth Edition, World Scientific Publishing Company, 2009 Search PubMed.
- M. Selig, G. Berghäuser, A. Raja, P. Nagler, C. Schüller, T. F. Heinz, T. Korn, A. Chernikov, E. Malic and A. Knorr, Nat. Commun., 2016, 7, 13279 CrossRef CAS PubMed.
- S. Brem, J. Zipfel, M. Selig, A. Raja, L. Waldecker, J. D. Ziegler, T. Taniguchi, K. Watanabe, A. Chernikov and E. Malic, Nanoscale, 2019, 11, 12381–12387 RSC.
- M. R. Molas, C. Faugeras, A. O. Slobodeniuk, K. Nogajewski, M. Bartos, D. M. Basko and M. Potemski, 2D Mater., 2017, 4, 021003 CrossRef.
- Y. Song and H. Dery, Phys. Rev. Lett., 2013, 111, 026601 CrossRef PubMed.
- L. Wang and M. W. Wu, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 115302 CrossRef.
- F. Gao, Y. Gong, M. Titze, R. Almeida, P. M. Ajayan and H. Li, Phys. Rev. B, 2016, 94, 245413 CrossRef.
- M. Titze, B. Li, X. Zhang, P. M. Ajayan and H. Li, Phys. Rev. Mater., 2018, 2, 054001 CrossRef CAS.
- F. Rossi and T. Kuhn, Rev. Mod. Phys., 2002, 74, 895 CrossRef CAS.
- M. Kira and S. W. Koch, Prog. Quantum Electron., 2006, 30, 155 CrossRef.
- E. Malic and A. Knorr, Graphene and Carbon Nanotubes: Ultrafast Optics and Relaxation Dynamics, Wiley, John & Sons, 2013 Search PubMed.
- O. Hess and T. Kuhn, Phys. Rev. A, 1996, 54, 3347 CrossRef CAS PubMed.
- R. Jago, R. Perea-Causín, S. Brem and E. Malic, Nanoscale, 2019, 11, 10017 RSC.
- S. Brem, A. Ekman, D. Christiansen, F. Katsch, M. Selig, C. Robert, X. Marie, B. Urbaszek, A. Knorr and E. Malic, arXiv:1904.04711, 2019.
- Z. Jin, X. Li, J. T. Mullen and K. W. Kim, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 045422 CrossRef.
- F. Cadiz, E. Courtade, C. Robert, G. Wang, Y. Shen, H. Cai, T. Taniguchi, K. Watanabe, H. Carrere, D. Lagarde, M. Manca, T. Amand, P. Renucci, S. Tongay, X. Marie and B. Urbaszek, Phys. Rev. X, 2017, 7, 021026 Search PubMed.
- O. A. Ajayi, J. V. Ardelean, G. D. Shepard, J. Wang, A. Antony, T. Taniguchi, K. Watanabe, T. F. Heinz, S. Strauf, X.-Y. Zhu and J. C. Hone, 2D Mater., 2017, 4, 031011 CrossRef.
- A. Raja, L. Waldecker, J. Zipfel, Y. Cho, S. Brem, J. D. Ziegler, M. Kulig, T. Taniguchi, K. Watanabe, E. Malic, T. F. Heinz, T. C. Berkelbach and A. Chernikov, Nat. Nanotechnol., 2019, 14, 832–837 CrossRef CAS PubMed.
- R. Rosati and F. Rossi, Appl. Phys. Lett., 2013, 103, 113105 CrossRef.
- R. Rosati and F. Rossi, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 205415 CrossRef.
- R. Rosati, F. Lengers, D. E. Reiter and T. Kuhn, Phys. Rev. B, 2018, 98, 195411 CrossRef CAS.
- D. F. Cordovilla Leon, Z. Li, S. W. Jang, C.-H. Cheng and P. B. Deotare, Appl. Phys. Lett., 2018, 113, 252101 CrossRef.
- H. Zhao, B. D. Don, S. Moehl, H. Kalt, K. Ohkawa and D. Hommel, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 035306 CrossRef.
- D. F. Cordovilla Leon, Z. Li, S. W. Jang and P. B. Deotare, arXiv:1908.07648, 2019.
- H. Zhao, B. D. Don, G. Schwartz and H. Kalt, Phys. Rev. Lett., 2005, 94, 137402 CrossRef PubMed.
- P. K. Gupta and A. R. Cooper, Physica, 1971, 54, 39 CrossRef.
- M. B. Wolf and D. London, Geochim. Cosmochim. Acta, 1994, 58, 4127 CrossRef CAS.
- A. Lauerer, T. Binder, C. Chmelik, E. Miersemann, J. Haase, D. M. Ruthven and J. Kärger, Nat. Commun., 2015, 6, 7697 CrossRef CAS PubMed.
- E. Najafi, A. Jafari, B. Liao and A. Zewail, arXiv:1909.06338, 2019.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/C9NR07056G |
| This journal is © The Royal Society of Chemistry 2020 |