Nano-makisu: highly anisotropic two-dimensional carbon allotropes made by weaving together nanotubes

Abstract

Graphene and carbon nanotubes (CNT) are the representatives of two-dimensional (2D) and one-dimensional (1D) forms of carbon, both exhibiting unique geometric structures and peculiar physical and chemical properties. Herein, we propose a family or series of 2D carbon-based highly anisotropic Dirac materials by weaving together an array of CNTs by direct C–C bonds or by graphene ribbons. By employing first-principles calculations, we demonstrate that these nano-makisus are thermally and dynamically stable and possess unique electronic properties. These 2D carbon allotropes are all metals and some nano-makisus show largely anisotropic Dirac cones, causing very different transport properties for the Dirac fermions along different directions. The Fermi velocities in the k_x direction could be ∼170 times higher than those in the k_y direction, which is the strongest anisotropy among 2D carbon allotropes to the best of our knowledge. This intriguing feature of the electronic structure has only been observed in heavy element materials with strong spin–orbit coupling. These results indicate that carbon based materials may have much broader applications in future nanoelectronics.

---

Introduction

Carbon is the most versatile element, forming a plethora of compounds and allotropes, because it can form bonds in various hybridizations of atomic orbitals. Hence, it is one of the most common components in matter, and it comprises a wide range of systems from living tissues, minerals, to functional materials.^1–3 The discovery of fullerenes in 1985 set off a tide of new research devoted towards the synthesis of novel carbon allotropes, including the synthesis of carbon nanotubes and the exfoliation of graphene.^4–7 As the most stable two-dimensional (2D) carbon material, graphene exhibits many unusual physical properties such as ballistic carrier transport, room-temperature quantum Hall effect, ambipolar field effect and extremely high conductivity, etc.^7–10 These peculiar properties render graphene as a promising candidate for applications in many future technologies.^11,12 The success of graphene has inspired the search for other novel 2D carbon materials with very different structures and lattice topologies. Although most of the 2D carbon allotropes are energetically metastable, many of them, such as graphdiyne, have been realized experimentally.^13,14 Furthermore, the new 2D carbon allotropes often exhibit unique properties that might outperform graphene in various aspects, including potential superconductivity, a negative Poisson's ratio, and possess distorted or anisotropic Dirac cones, etc.,^14–17 which are associated with their unique lattice topologies. These results illustrate the importance of the structure–property relationship in carbon allotropes.

For many years, it was believed that many geometric features of graphene are necessary preconditions for the existence of a Dirac cone. However, after the discovery of several new 2D Dirac carbon allotropes, such as α-, β-, and 6,6,12-graphyne,¹⁴ phagraphene,¹⁷ and S-, D-, E-, and r-graphene,^18,19 it turns out that a strictly planar structure, chemically equivalent and sp²-hybridized carbon atoms, a honeycomb lattice, and even a hexagonal symmetry are not prerequisites for the existence of Dirac cones. Many of these 2D carbon allotropes show largely distorted Dirac cones leading to electronic properties that are complementary to that of graphene.^14,20,21 In some Dirac materials, the Dirac cones are remarkably anisotropic, causing very different transport properties of the Dirac fermions in different directions.^20,22–27 Such unique properties can provide more tunability for novel properties and applications.^28,29 However, such largely anisotropic Dirac cones are rare in carbon based materials.²⁰

Carbon nanotubes (CNTs), as a one-dimensional (1D) form of carbon, are cylindrical carbon allotropes composed of sp²-hybridized carbon atoms that form hexagonal networks.³⁰ They exhibit many novel properties such as extraordinary strength, as well as unique electronic, thermal and mechanical properties, which give them great potential in a wide range of applications.^31,32 CNTs have been widely used in composite and coating materials, drug delivery, heterogeneous catalysis, energy storage and biotechnology.^33–36 Furthermore, the hollow tubular structure enables CNTs to be used as effective gas and metal containers, as well as host nanoreactors to promote some chemical reactions through nanoscale confinement.^37,38 Hydrostatic/non-hydrostatic pressure was applied on CNTs to build new carbon allotropes both experimentally and theoretically.^39–45 Due to the unique tubular structure, CNTs usually have a very high length-to-diameter ratio, which makes many properties of CNTs extremely anisotropic.

In this work, we propose a family of carbon allotropes, by interlinking an array of zigzag single-walled carbon nanotubes (SWNTs), whose structures are analogous to makisu, a mat woven from bamboo and cotton string and used in Japanese cuisine. These nano-makisus might combine the advantages of both graphene and CNTs. Using density functional theory calculations, their stability and electronic properties are studied thoroughly. The results show that these carbon allotropes are dynamically stable, and they are all metallic. Moreover, highly anisotropic Dirac cones are found in their band structures. The unusual electronic transport properties predicted by the calculations suggest that nano-makisus could be a new family of candidate materials for future nanoelectronics.

Methodology

The calculations were performed using first-principles density functional theory (DFT) as implemented in the Vienna ab initio simulation package (VASP).^46–48 The exchange and correlation were obtained within the generalized gradient approximation (GGA), using the functional of Perdew, Burke, and Ernzerhof (PBE).⁴⁹ The projector augmented wave (PAW) method was used to treat the core states.^50,51 Periodic boundary conditions (PBC) were applied, and the vacuum between sheets in neighboring cells along the (001) direction was set to be larger than 15 Å to avoid spurious interactions between periodic images. For the electronic structure calculations, plane waves with a kinetic energy cutoff of 500 eV were adopted to expand the valence electron (2s²2p²) wavefunctions. Brillouin zone (BZ) integrations were carried out using Γ-centered sampling grids with a resolution of 2π × 0.2 Å⁻¹. Structural relaxation was performed using the conjugate gradient (CG) scheme until the force components were converged to within 0.01 eV Å⁻¹, and the self-consistent field calculations were stopped when the energy difference between two steps was smaller than 1 × 10⁻⁸ eV per atom. First-principles molecular dynamic simulations under constant temperature and volume (NVT) were performed to examine thermal stability. The phonon spectra were recorded to examine dynamical stability using the PHONOPY package.⁵²

Results and discussion

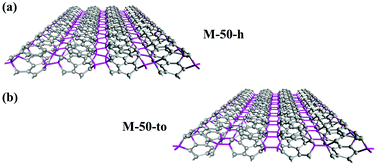
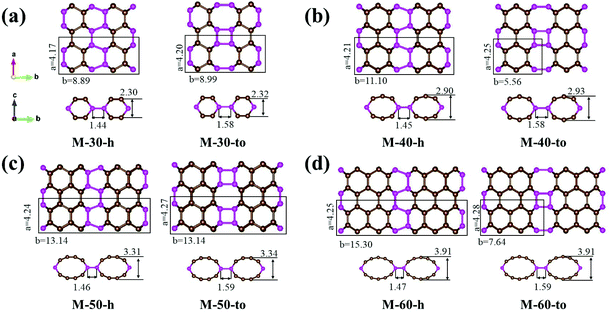
Nano-makisus are constructed by connecting zigzag (n,0), n = 3–6, SWNTs along the radial directions of the nanotubes. The neighboring nanotubes are connected by sp³-carbons. The structures of two representative nano-makisus connected by direct C–C bonds are shown in Fig. 1a and b. Two different ways of connecting the neighboring zigzag SWNTs are studied in this work. In one style, the SWNTs are linked together via hexagonal rings alone (shown in Fig. 1a), while in the other style, the nanotubes are linked via a combination of tetragons and octagons (shown in Fig. 1b). Similar connectivities can be found in previously reported structures (bct C₄, Cco-C₈, etc.).^53–55 The constructed structures are denoted by the chiral indices (n,m) of the SWNTs, together with the way in which the neighboring nanotubes are connected. Accordingly, we obtained M-30-h/to, M-40-h/to, M-50-h/to and M-60-h/to nano-makisus, where “M” represents nano-makisu, the numbers correspond to the chiral indices of the nanotubes, “h” represents the hexagon connection and “to” represents the tetragon-octagon connection.

Fig. 1 Two-dimensional structures of (a) M-50-h, and (b) M-50-to, gray and pink atoms are carbons.

The top and side views of the optimized atomic configurations of eight nano-makisus are shown in Fig. 2a–d. The pristine SWNTs only consist of sp²-hybridized carbon atoms located in a honeycomb lattice, corresponding to a coordination number of 3. When two neighbouring nanotubes are connected, the connecting carbon atoms will have 4 neighbouring atoms, and therefore are in a sp³ hybridized state. As shown in Fig. 2, in each nano-makisu, the pink-coloured sp³-hybridized carbon atoms are on the same plane and sandwiched between the sp²-hybridized carbon atoms. After optimization, the cross sections of carbon nanotubes will change from circular to elliptical to reduce the stress caused by the sp³ hybridization of the connecting carbon atoms. The nanotubes with larger radii also show larger deformation. In most cases, the nano-makisu unit cell consists of two SWNTs, namely, the number of carbon atoms per nano-makisu unit cell is twice as many as that in the unit cell of the nanotube as shown in Table 1. However, nano-makisu M-40-to and M-60-to are exceptions, due to the fact that zigzag (4,0), (6,0) SWNTs and the connecting tetragons and octagons have a mirror symmetry. Therefore, the unit cells of nano-makisu M-40-to and M-60-to consist of only one SWNT, and they have the same number of carbon atoms per unit cell as that in zigzag (4,0) and (6,0) SWNTs, respectively. The distance between two neighbouring nanotubes in nano-makisu mainly depends on the connection style and is slightly affected by the size of the nanotubes. In “to”-type nano-makisu, the distance between two nanotubes is 1.58–1.59 Å, which is slightly further than that of typical sp³–sp³ C–C bonds, while the distances between nanotubes in “h”-type nano-makisu are much shorter, ranging from 1.44–1.47 Å, rendering strong sp² components in these C atoms.

Fig. 2 Top and side views of the optimized structures of nano-makisu (a) M-30-h and M-30-to, (b) M-40-h and M-40-to, (c) M-50-h and M-50-to, (d) M-60-h and M-60-to. Unit cells are marked with gray lines. The lattice parameters, distances between two neighbouring nanotubes, and thickness of nano-makisus are provided in angstrom (Å). Brown balls represent sp²-hybridized carbon atoms and pink balls represent sp³-hybridized carbon atoms.

Table 1 Summary of the total number of carbon atoms per unit cell, calculated energy difference per atom relative to graphene, percentage of sp³-hybridized carbon atoms in each unit cell, and average bond length of sp²–sp², sp²–sp³ and sp³–sp³ C–C bonds for graphene, various SWNTs and nano-makisus. “—” means there is no corresponding value

System	Carbons	ΔE/atom (eV)	sp^3 (%)	C–C (sp^2–sp^2)	C–C (sp^2–sp^3)	C–C (sp^3–sp^3)
Graphene	2	0	0	1.42	—	—
SWNT (3,0)	12	1.29	0	1.49	—	—
SWNT (4,0)	16	0.77	0	1.46	—	—
SWNT (5,0)	20	0.49	0	1.44	—	—
SWNT (6,0)	24	0.35	0	1.43	—	—
M-30-h	24	0.80	0.17	1.49	1.57	1.54
M-30-to	24	0.89	0.17	1.49	1.56	1.58
M-40-h	32	0.55	0.13	1.47	1.56	1.55
M-40-to	16	0.60	0.13	1.45	1.54	1.58
M-50-h	40	0.39	0.10	1.45	1.55	1.56
M-50-to	40	0.43	0.10	1.45	1.53	1.57
M-60-h	48	0.29	0.08	1.44	1.54	1.57
M-60-to	24	0.32	0.08	1.44	1.53	1.59

---

To further study the bonding between two neighbouring nanotubes, the electron localization function (ELF) was calculated and the detailed results are shown in Fig. S1.† The electrons between two nanotubes are highly localized, indicating the formation of covalent bonds. The nano-makisu structures are composed of both sp²-hybridized tube and sp³-hybridized connecting carbon atoms, shown in brown and pink in Fig. 2, respectively. Therefore, there are three types of carbon–carbon bonds in nano-makisus, namely, sp²–sp², sp²–sp³ and sp³–sp³ bonds. As the diameter of the nanotubes increases, the curvature of the nanotube surface becomes smaller. When the nanotubes are connected to form nano-makisus, the deformation of nanotubes will also reduce the surface curvature. This will make the three C–C bonds formed by sp²-hybridized carbon atoms closer to the ideal trigonal planar geometry. Therefore, as the nanotubes become larger, the average bond lengths of sp²–sp² and sp²–sp³ C–C bonds in nano-makisus will gradually approach the typical bond length without any tension (1.40 and 1.51 Å). The sp³–sp³ bond length in “h”-type nano-makisu is much closer to the typical sp³–sp³ bond length (1.54 Å) than that in “to”-type nano-makisu, which can be attributed to the formation of large tension tetragons in “to”-type nano-makisu. The detailed data are shown in Table 1. From M-30-h/to to M-60-h/to, the average sp²–sp² and sp²–sp³ carbon bond lengths decrease, while the average bond length of sp³–sp³ increases, which clearly demonstrates the stretching process of carbon nanotubes.

The thermodynamic stability of nano-makisus was investigated by calculating their total energies using first-principles calculations. The obtained results are shown in Table 1. Compared with graphene, the most stable 2D carbon allotrope, nano-makisus are 0.29–0.89 eV per carbon higher in energy. However, nano-makisus possess lower energies than many previously reported carbon allotropes, such as α-graphyne and penta-graphene.^14,56 Meanwhile, the energies of nano-makisus are comparable with two carbon allotropes previously proposed by our group, bubble-wrap carbons (0.36–0.81 eV per atom less stable than graphene) and egg-tray graphenes (0.22–0.33 eV per atom less stable than graphene), as listed in Table S1.† With increasing diameter of the nanotubes, nano-makisus become more planar and the energy differences relative to graphene tend to become smaller due to the smaller tension in larger nanotubes. Moreover, the energies of “to”-type nano-makisus are somewhat higher than that of “h”-type, which can be attributed to the fact that hexagons are more stable than tetragons and octagons. It is noteworthy that the energies of nano-makisus are lower than that of the corresponding pristine SWNTs, which means pristine SWNTs, especially those with small radii, tend to connect with each other spontaneously and form nano-makisus. For example, the reactions from separated SWNTs to M-30-h/to and M-40-h/to show no barrier (Fig. S2†). This is partially because the connection between two neighbouring nanotubes can relieve the strain inside carbon nanotubes. In particular, the energy reduction from SWNT (3,0) to M-30-h/to is the largest (Fig. S3†). Fig. 3 shows how the energy difference per atom relative to graphene changes as a function of the percentage of sp³-hybridized carbon atoms in each unit cell for each nano-makisu. We found that the energies of nano-makisus possess a proportional relationship with the ratio of sp³ carbon atoms, that is, a nano-makisu with a higher sp³ carbon ratio will have a higher energy.

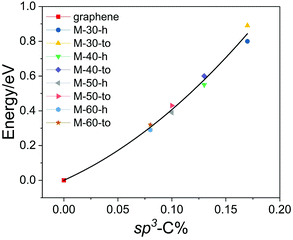Fig. 3 The energy difference per atom relative to graphene and how it changes as a function of the percentage of sp³-hybridized carbon atoms in each unit cell for each nano-makisu.

To examine the dynamic stability of nano-makisus, we calculated the phonon band structure along high-symmetry directions, and the results are shown in Fig. S4.† The phonon spectra of all nano-makisus with the exception of one, M-50-h, show no imaginary frequencies, indicating they are dynamically stable.

The imaginary frequencies in the phonon spectrum of M-50-h are extremely small and are likely artefacts present from the convergence of the phonon calculation, since the calculations of the force constants for a two-dimensional carbon allotrope usually require better convergence and larger supercells for frozen phonons, and the unit cell of M-50-h is already quite large. However, positive phonon frequencies cannot ensure that the material is stable at finite temperatures. In order to further confirm the thermal stability of these predicted structures, ab initio molecular dynamics simulations (AIMD) were carried out. The simulations were run for 6 ps containing 4000 MD steps at temperatures up to 1000 K. The nano-makisu structures did not experience serious disruption or dissociation, indicating that these 2D carbon materials possess good stability. The final configurations for each molecular dynamic simulation are shown in Fig. S5.†

Although the total energy calculations and the MD simulations indicate that nano-makisus could stay stable, their synthesis remains a challenging task. However, recently there has been extensive experimental progress in the fabrication of low dimensional carbon allotropes via several routes, including bottom-up chemical synthesis⁵⁷ and the compression of bundles of zigzag SWNTs. The latter route is more promising. As a matter of fact, the studies of SWNTs under high pressures and high temperatures have shown the conversion of the sp² carbons to sp³ carbons.^44,58–60 Besides, the simulated X-ray diffraction patterns of the theoretically predicted bct C4 ⁵³ and Cco-C8 ⁵⁴ structures are in good agreement with the experimental data, revealing the 4-, 6- and 8-member carbon rings in bct C4 and Cco-C8 and the presence of the sp³ interlinking carbons that are very similar to those found in nano-makisus. These experimental studies strongly suggest that the proposed nano-makisus could be fabricated, and as shown by our calculations they can remain stable once they are made. Indeed, many allotropes with energies higher than nano-makisus such as graphdiyne,¹³ a C₂₀ cage⁶¹ and the smallest carbon nanotube⁶² (0.77, 1.14 and 1.15 eV per atom less stable than graphene, respectively) have already been synthesized.

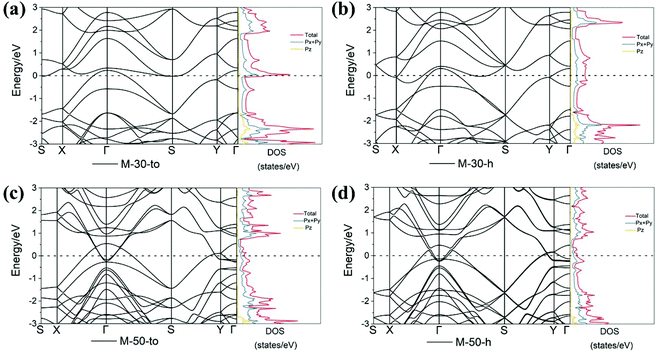
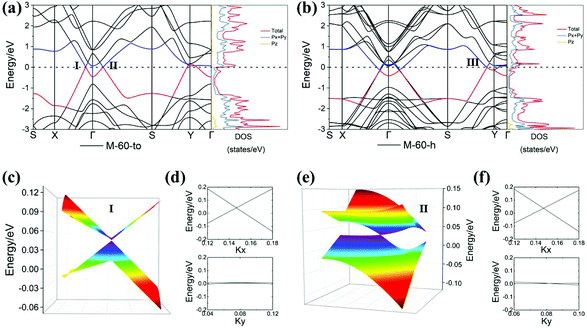
Next, we turn our attention to study the electronic properties of nano-makisus. The obtained band structures and density of states (DOS) calculated at the PBE level of theory are shown in Fig. 4–6, and the results reveal that all the nano-makisus are metallic. By comparing the band structures of different nano-makisus, we find that the connecting style of two neighbouring nanotubes (“h” and “to”) in nano-makisus has little impact on the electronic properties of M-30-to/h and M-50-to/h. For example, the band structures of M-30-to and M-30-h are very similar (Fig. 4a and b). The same is found for M-50-to and M-50-h (Fig. 4c and d).

Fig. 4 Band structures and DOS of (a) M-30-to, (b) M-30-h, (c) M-50-to and (d) M-50-h.

Fig. 5 Band structures and DOS of (a) M-40-to and (b) M-40-h. The Fermi level, E_F, is set to 0. (c) 3D Dirac cone formed by valence and conduction bands in the vicinity of the Dirac point I in M-40-to; (d) Dispersions near the Dirac point I parallel and perpendicular to the X–Γ symmetry line; (e) 3D Dirac cone formed by valence and conduction bands in the vicinity of the Dirac point II in M-40-to; (f) Dispersions near the Dirac point II parallel and perpendicular to the Γ–S symmetry line.

Fig. 6 Band structures and DOS of (a) M-60-to and (b) M-60-h. The Fermi level E_F is set to 0. (c) 3D Dirac cone formed by valence and conduction bands in the vicinity of the Dirac point I in M-60-to; (d) dispersions near the Dirac point I parallel and perpendicular to the X–Γ high symmetry line; (e) 3D Dirac cone formed by valence and conduction bands in the vicinity of the Dirac point II in M-60-to; (f) dispersions near the Dirac point II parallel and perpendicular to the Γ–S high symmetry line.

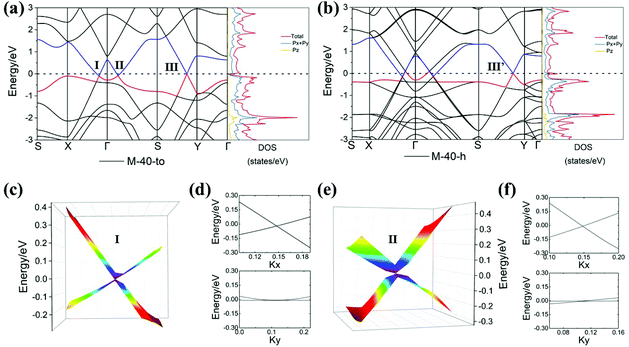
The band structures and DOS of M-40-to/h are shown in Fig. 5a and b. Interestingly, crossing points with linear bands were found in both band structures, indicating possible Dirac points in the first BZ. In M-40-to, two crossing points, denoted as I and II, are found at (0.1033, 0.0, 0.0) along the line from X to Γ and at (0.1077, 0.1097, 0.0) along the line from Γ to S, respectively. The 3D band structures around these two crossing points (Fig. 5c and e) clearly reveal that they are indeed Dirac points. The two Dirac cones lie slightly below the Fermi level, which indicates that M-40-to is a self-doped Dirac material and the electrons act as charge carriers at both Dirac point I and II. Remarkably, these two Dirac cones show a highly anisotropic character. In order to further study its effects on transport properties, we obtained the Fermi velocities by calculating the slope of the linear bands along two perpendicular directions (x and y) using the expression v_f = E(q)/ħ|q|. For Dirac cone I, the slopes of the two crossing bands in the k_x direction in reciprocal space are equal to −33.52 and +13.30 eV Å, which correspond to Fermi velocities of 8.11 × 10⁵ and 3.22 × 10⁵ m s⁻¹. These two velocities are close to that of 8.22 × 10⁵ m s⁻¹ in graphene, while in the k_y direction, the slopes are −0.74 and +0.70 eV Å, which correspond to the Fermi velocities of 1.80 × 10⁴ and 1.68 × 10⁴ m s⁻¹. The Fermi velocities in the k_x direction are 19 to 45 times higher than that in the k_y direction, indicating the highly anisotropic transport properties. The anisotropy is also confirmed by the band dispersions near point I parallel or perpendicular to the high symmetry X–Γ line as shown in Fig. 5d and f. For Dirac cone II, the slopes in the k_x direction are −32.24 (v_fx = 7.80 × 10⁵ m s⁻¹) and +16.57 eV Å (v_fx = 4.01 × 10⁵ m s⁻¹), and in the k_y direction they are −0.19 (v_fy = 4.56 × 10³ m s⁻¹) and +4.46 eV Å (v_fy = 1.08 × 10⁵ m s⁻¹). The Fermi velocities in the k_x direction are 4 to 171 times higher than that in the k_y direction, which shows a stronger anisotropy when compared with other 2D Dirac carbon allotropes reported previously^{14,17,19–21,63–65} (Table S2†). M-40-h possesses four Dirac cones at positions similar to those of M-40-to (Fig. 5b). This is caused by the fact that M-40-h is lower in symmetry, and this doubles the size of its unit cell and correspondingly the bands are “folded”. Partial charge density distributions of the two Dirac bands in the proximity of the Fermi level demonstrate that point I and II have similar charge distribution and the electron densities in the highest occupied band (VBM) are delocalized, while the electron densities in the lowest unoccupied band (CBM) are highly localized at sp² carbons in the nanotubes (Fig. S7b†).

Besides, there is another crossing point of linear bands in both M-40-to and M-40-h. They are located at (0.1270, 0.5, 0.0) (Dirac point III) as shown in Fig. 5a and (0.1247, 0.5, 0.0) (Dirac point III′) as shown in Fig. 5b along the line from S to Y in the first BZ, respectively. The 3D band structures of these two points (Fig. S6a and S6c†) also reveal that they are Dirac points. For Dirac cone III in M-40-to, the slopes of the band energies and the corresponding Fermi velocities of the two crossing bands in the k_x direction are −34.87 (v_fx = 8.43 × 10⁵ m s⁻¹) and +29.42 eV Å (v_fx = 7.11 × 10⁵ m s⁻¹), and in the k_y direction the values are −0.88 (v_fy = 2.14 × 10⁴ m s⁻¹) and +0.90 eV Å (v_fy = 2.18 × 10⁴ m s⁻¹). The Fermi velocities in the k_x direction are 33 to 39 times higher than that in the k_y direction. The corresponding values in M-40-h are −34.91 (v_fx = 8.44 × 10⁵ m s⁻¹) and +23.71 eV Å (v_fx = 5.73 × 10⁵ m s⁻¹) in the k_x direction, and −32.61 (v_fy = 7.89 × 10⁵ m s⁻¹) and +19.62 eV Å (v_fy = 4.74 × 10⁵ m s⁻¹) in the k_y direction. These values are comparable with that of graphene and other carbon Dirac allotropes predicted in previous studies.^14,17,19 Partial charge density distributions of the highest occupied band show that the holes are delocalized at Dirac point III in M-40-to, and localized at the sp² carbons at Dirac point III′ in M-40-h. In contrast, the electron density in the lowest unoccupied bands shows that the electrons are localized at sp² carbons in M-40-to and partially localized in sp² nanotube carbons in M-40-h (Fig. S7c and d†).

The electronic structures of M-60-to/h are shown in Fig. 6. Similar to M-40-to, two crossing points of linear bands are found along the high symmetry line X–Γ at (0.0909, 0.0, 0.0) (denoted as point I) and along the high symmetry line Γ–S at (0.0889, 0.0884, 0.0) (denoted as point II) in the first BZ.

Different to M-40-to, these two points lie slightly above the Fermi level, causing self-doped holes to be charge carriers. As shown in Fig. 6c and e, the calculated 3D band structures around points I and II clearly reveal that they are anisotropic Dirac points. For Dirac cone I, the slopes of the band energies of the two bands in reciprocal space and the corresponding Fermi velocities are equal to −34.73 (v_fx = 8.40 × 10⁵ m s⁻¹) and +27.97 eV Å (v_fx = 6.76 × 10⁵ m s⁻¹) in the k_x direction, and −0.69 (v_fy = 1.67 × 10⁴ m s⁻¹) and +0.62 eV Å (v_fy = 1.49 × 10⁴ m s⁻¹) in the k_y direction. For Dirac cone II, the slopes and the Fermi velocities are −34.18 (v_fx = 8.26 × 10⁵ m s⁻¹) and +26.57 eV Å (v_fx = 6.42 × 10⁵ m s⁻¹) in the k_x direction, and −3.81 (v_fy = 9.20 × 10⁴ m s⁻¹) and +0.38 eV Å (v_fy = 9.20 × 10³ m s⁻¹) in the k_y direction. The Fermi velocities in the k_x direction are 9 to 70 times higher than that in the k_y direction. The highly anisotropic properties can also be inferred from Fig. 6d and f. The partial charge densities show that the electrons at point I and II are both highly localized at sp² carbons as shown in Fig. S9a.†

Similar to M-40-h, M-60-h possesses one Dirac point (denoted as point III) located at (0.0773, 0.5, 0.0) along the line from S to Y. The calculated 3D bands in the vicinity of this point reveal that it is a highly anisotropic Dirac cone as displayed in Fig. S8.† The slopes of the crossing bands and the Fermi velocities are −33.21 (v_fx = 8.03 × 10⁵ m s⁻¹) and −12.77 eV Å (v_fx = 3.09 × 10⁵ m s⁻¹) in the k_x direction, and −2.20 (v_fy = 5.32 × 10⁴ m s⁻¹) and −1.79 eV Å (v_fy = 4.34 × 10⁴ m s⁻¹) in the k_y direction, which also illustrates the anisotropy of M-60-h. The partial charge density distributions of the two Dirac bands in the proximity of the Fermi level at Dirac point III in M-60-h show that the electrons at both the lower and upper cones are partially localized at sp² carbons in nanotubes, as seen in Fig. S9b.† Interlinked carbon nanotubes and fullerenes have been observed or predicted before.^66,67 In comparison with those allotropes, nano-makisus are two dimensional materials featuring anisotropic Dirac cones. It is interesting that the electronic structure of bct-C12,⁶⁸ a three-dimensional interlinked nanotube allotrope, is also very anisotropic. It shows linear dispersion (for Dirac particles) in one direction (k_z) and conventional metallic bands in the other two directions.

Conclusions

In summary, we proposed a series of 2D carbon materials with orderly arranged hollow tubular structures named nano-makisus. Their stabilities, structural features and electronic properties are studied by means of first-principles calculations. Depending on the size of the tubes, many nano-makisus are energetically very stable compared to other 2D carbon allotropes. Molecular dynamics calculations indicated that nano-makisus can withstand temperatures up to 1000 K. The electronic structure calculations demonstrated that these 2D carbon allotropes are all metallic. Some nano-makisus possess highly anisotropic Dirac cones with Fermi velocities varying from 4.56 × 10³ to 8.44 × 10⁵ m s⁻¹ along different k directions. The Fermi velocities in the k_x direction could be ∼170 times higher than that in the k_y direction, which is the largest anisotropy among 2D carbon allotropes. The strong propensity of the nanotubes toward interlinking under high pressure might provide a feasible route to fabricate this new family of 2D carbon allotropes. The high and direction-dependent Fermi velocities give nano-makisus great potential for future use in direction-dependent electronic devices. Furthermore, the hollow tubular structures may also enable nano-makisus to effectively constrain gas and metal species, and promote some chemical reactions through nanoscale confinement.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

M. M. acknowledges the support of the NSF CAREER award 1848141 and ACF PRF fund 50249-UN16. This work was also supported by the National Natural Science Foundation of China (61604101), the Scientific Research Foundation of UESTC for Young Teacher (ZYGX2016KYQD134). W. L. acknowledges the Scientific Research and Developed Fund of Zhejiang A&F University (No. 2019FR005 and 2019FR006), the National Natural Science Foundation of China (11975206) for financial support. E. Z. acknowledges the NSF (DMR-1827815) for financial support. Part of the calculations are performed on NSF-funded XSEDE resources (TGDMR130005) especially on the Stampede cluster run by Texas Advanced Computing Centre.

References

1. A. Hirsch, Nat. Mater., 2010, 9, 868.
2. K. Kinoshita, Carbon – Electrochemical and Physicochemical properties, John Wiley and Sons, Inc., 1st edn, 1988.
3. E. Frackowiak, Phys. Chem. Chem. Phys., 2007, 9, 1774–1785.
4. H. W. Kroto, J. R. Heath, S. C. O'Brien, R. F. Curl and R. E. Smalley, Nature, 1985, 318, 162.
5. S. Iijima, Nature, 1991, 354, 56.
6. S. Iijima and T. Ichihashi, Nature, 1993, 363, 603.
7. K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Science, 2004, 306, 666–669.
8. K. S. Novoselov, A. K. Geim, S. Morozov, D. Jiang, M. Katsnelson, I. Grigorieva, S. Dubonos and A. A. Firsov, Nature, 2005, 438, 197.
9. Y. Zhang, Y.-W. Tan, H. L. Stormer and P. Kim, Nature, 2005, 438, 201.
10. A. K. Geim and K. S. Novoselov, Nat. Mater., 2007, 6, 183–191.
11. P. Avouris and F. Xia, MRS Bull., 2012, 37, 1225–1234.
12. A. K. Geim, Science, 2009, 324, 1530–1534.
13. G. Li, Y. Li, H. Liu, Y. Guo, Y. Li and D. Zhu, Chem. Commun., 2010, 46, 3256–3258.
14. D. Malko, C. Neiss, F. Viñes and A. Görling, Phys. Rev. Lett., 2012, 108, 086804.
15. H. Terrones, M. Terrones, E. Hernández, N. Grobert, J.-C. Charlier and P. Ajayan, Phys. Rev. Lett., 2000, 84, 1716.
16. W. Liu, J.-Y. Liu, J. Xia, H.-Q. Lin and M.-S. Miao, Nanoscale, 2018, 10, 11328–11334.
17. Z. Wang, X.-F. Zhou, X. Zhang, Q. Zhu, H. Dong, M. Zhao and A. R. Oganov, Nano Lett., 2015, 15, 6182–6186.
18. W. Liu, M. Miao and J.-Y. Liu, J. Mater. Chem. C, 2015, 3, 9921–9927.
19. L.-C. Xu, R.-Z. Wang, M.-S. Miao, X.-L. Wei, Y.-P. Chen, H. Yan, W.-M. Lau, L.-M. Liu and Y.-M. Ma, Nanoscale, 2014, 6, 1113–1118.
20. C. Su, H. Jiang and J. Feng, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 075453.
21. L. Zhang, Z. Wang, Z. M. Wang, S. Du, H.-J. Gao and F. Liu, J. Phys. Chem. Lett., 2015, 6, 2959–2962.
22. V. Pardo and W. E. Pickett, Phys. Rev. Lett., 2009, 102, 166803.
23. V. Pardo and W. E. Pickett, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 035111.
24. G. Lee, M. A. Farhan, J. S. Kim and J. H. Shim, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 245104.
25. J. Park, G. Lee, F. Wolff-Fabris, Y. Koh, M. Eom, Y. Kim, M. Farhan, Y. Jo, C. Kim and J. Shim, Phys. Rev. Lett., 2011, 107, 126402.
26. Z. Liu, B. Zhou, Y. Zhang, Z. Wang, H. Weng, D. Prabhakaran, S.-K. Mo, Z. Shen, Z. Fang and X. Dai, Science, 2014, 343, 864–867.
27. B. Feng, J. Zhang, S. Ito, M. Arita, C. Cheng, L. Chen, K. Wu, F. Komori, O. Sugino and K. Miyamoto, Adv. Mater., 2018, 30, 1704025.
28. Y. Feng, Z. Wang, C. Chen, Y. Shi, Z. Xie, H. Yi, A. Liang, S. He, J. He and Y. Peng, Sci. Rep., 2014, 4, 5385.
29. T. Wehling, A. M. Black-Schaffer and A. V. Balatsky, Adv. Phys., 2014, 63, 1–76.
30. T. W. Odom, J.-L. Huang, P. Kim and C. M. Lieber, J. Phys. Chem. B, 2000, 104, 2794–2809.
31. V. N. Popov, Mater. Sci. Eng., R, 2004, 43, 61–102.
32. M. F. De Volder, S. H. Tawfick, R. H. Baughman and A. J. Hart, Science, 2013, 339, 535–539.
33. E. Bekyarova, Y. Ni, E. B. Malarkey, V. Montana, J. L. McWilliams, R. C. Haddon and V. Parpura, J. Biomed. Nanotechnol., 2005, 1, 3–17.
34. A. Bianco, K. Kostarelos and M. Prato, Curr. Opin. Chem. Biol., 2005, 9, 674–679.
35. D. N. Futaba, K. Hata, T. Yamada, T. Hiraoka, Y. Hayamizu, Y. Kakudate, O. Tanaike, H. Hatori, M. Yumura and S. Iijima, Nat. Mater., 2006, 5, 987.
36. J. Planeix, N. Coustel, B. Coq, V. Brotons, P. Kumbhar, R. Dutartre, P. Geneste, P. Bernier and P. Ajayan, J. Am. Chem. Soc., 1994, 116, 7935–7936.
37. J. Hu, Y. Bando, J. Zhan, C. Zhi and D. Golberg, Nano Lett., 2006, 6, 1136–1140.
38. J. Zhang, D. Zhao, D. Xiao, C. Ma, H. Du, X. Li, L. Zhang, J. Huang, H. Huang and C. L. Jia, Angew. Chem., Int. Ed., 2017, 56, 1850–1854.
39. M. Hu, Z. Zhao, F. Tian, A. R. Oganov, Q. Wang, M. Xiong, C. Fan, B. Wen, J. He and D. Yu, Sci. Rep., 2013, 3, 1331.
40. T. Yildirim, O. Gülseren, Ç. Kılıç and S. Ciraci, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, 12648.
41. Z. Zhao, X.-F. Zhou, M. Hu, D. Yu, J. He, H.-T. Wang, Y. Tian and B. Xu, J. Superhard Mater., 2012, 34, 371–385.
42. S. Saxena and T. A. Tyson, ACS Nano, 2010, 4, 3515–3521.
43. Q. Li, Y. Ma, A. R. Oganov, H. Wang, H. Wang, Y. Xu, T. Cui, H.-K. Mao and G. Zou, Phys. Rev. Lett., 2009, 102, 175506.
44. A. Merlen, N. Bendiab, P. Toulemonde, A. Aouizerat, A. San Miguel, J.-L. Sauvajol, G. Montagnac, H. Cardon and P. Petit, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 035409.
45. J. Proctor, M. Halsall, A. Ghandour and D. Dunstan, Phys. Status Solidi B, 2007, 244, 147–150.
46. W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133.
47. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50.
48. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169.
49. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
50. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953.
51. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758.
52. A. Togo, F. Oba and I. Tanaka, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 134106.
53. K. Umemoto, R. M. Wentzcovitch, S. Saito and T. Miyake, Phys. Rev. Lett., 2010, 104, 125504.
54. Z. Zhao, B. Xu, X.-F. Zhou, L.-M. Wang, B. Wen, J. He, Z. Liu, H.-T. Wang and Y. Tian, Phys. Rev. Lett., 2011, 107, 215502.
55. H. Cheng, G. P. Pez and A. C. Cooper, Nano Lett., 2003, 3, 585–587.
56. Z. Shunhong, Z. Jian, W. Qian, C. Xiaoshuang, K. Yoshiyuki and J. Puru, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 2372–2377.
57. S. Hitosugi, T. Yamasaki and H. Isobe, J. Am. Chem. Soc., 2012, 134, 12442–12445.
58. V. N. Khabashesku, Z. Gu, B. Brinson, J. L. Zimmerman, J. L. Margrave, V. A. Davydov, L. S. Kashevarova and A. V. Rakhmanina, J. Phys. Chem. B, 2002, 106, 11155–11162.
59. P. V. Teredesai, A. Sood, D. Muthu, R. Sen, A. Govindaraj and C. Rao, Chem. Phys. Lett., 2000, 319, 296–302.
60. M. Yao, Z. Wang, B. Liu, Y. Zou, S. Yu, W. Lin, Y. Hou, S. Pan, M. Jin and B. Zou, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 205411.
61. H. Prinzbach, A. Weiler, P. Landenberger, F. Wahl, J. Wörth, L. T. Scott, M. Gelmont, D. Olevano and B. v. Issendorff, Nature, 2000, 407, 60.
62. X. Zhao, Y. Liu, S. Inoue, T. Suzuki, R. Jones and Y. Ando, Phys. Rev. Lett., 2004, 92, 125502.
63. M. Zhao, W. Dong and A. Wang, Sci. Rep., 2013, 3, 3532.
64. W.-J. Yin, Y.-E. Xie, L.-M. Liu, R.-Z. Wang, X.-L. Wei, L. Lau, J.-X. Zhong and Y.-P. Chen, J. Mater. Chem. A, 2013, 1, 5341–5346.
65. L. Li, X. Kong and F. M. Peeters, Carbon, 2019, 141, 712–718.
66. Z. Zhao, B. Xu, L.-M. Wang, X.-F. Zhou, J. He, Z. Liu, H.-T. Wang and Y. Tian, ACS Nano, 2011, 5, 7226–7234.
67. L. Wang, B. Liu, H. Li, W. Yang, Y. Ding, S. V. Sinogeikin, Y. Meng, Z. Liu, X. C. Zeng and W. L. Mao, Science, 2012, 337, 825–828.
68. X. Dong, M. Hu, J. He, Y. Tian and H.-T. Wang, Sci. Rep., 2015, 5, 10713.

---

Footnote

† Electronic supplementary information (ESI) available: Electron localization function (ELF), phonon spectra, ab initio molecular dynamics simulations (AIMD), band structure of Dirac point III in M-40-to, Dirac point III’ in M-40-h, Dirac point III in M-60-h and partial charge densities of M-40-to/h and M-60-to/h. See DOI: 10.1039/c9nr08069d

---