A polyesteramide library from dicarboxylic acids and 2,2′-bis(2-oxazoline): synthesis, characterization, nanoparticle formulation and molecular dynamics simulations†
Irina
Muljajew
ab,
Andreas
Erlebach
 bc,
Christine
Weber
bc,
Christine
Weber
 ab,
Johannes R.
Buchheim
ab,
Johannes R.
Buchheim
 d,
Marek
Sierka
d,
Marek
Sierka
 bc and
Ulrich S.
Schubert
bc and
Ulrich S.
Schubert
 *ab
*ab
aLaboratory of Organic and Macromolecular Chemistry (IOMC), Friedrich Schiller University Jena, Humboldtstr. 10, 07743 Jena, Germany. E-mail: ulrich.schubert@uni-jena.de
bJena Center for Soft Matter (JCSM), Friedrich Schiller University Jena, Philosophenweg 7, 07743 Jena, Germany
cOtto Schott Institute of Materials Research (OSIM), Friedrich Schiller University Jena, Löbdergraben 32, 07743 Jena, Germany
dInstitute for Technical Chemistry and Environmental Chemistry, Center for Energy and Environmental Chemistry Jena (CEEC Jena), Friedrich Schiller University Jena, Philosophenweg 7a, 07743 Jena, Germany
First published on 20th November 2019
Abstract
The step growth polyaddition of a variety of dicarboxylic acids and 2,2′-bis(2-oxazoline) enabled access to a library of polyesteramides (PEA) with different linker lengths or bulkiness. PEA with alkylene spacers represented semicrystalline materials due to hydrogen bond formation between the oxamide moieties, as is evident from dynamic scanning calorimetry and wide-angle X-ray scattering (145 °C < Tm < 225 °C). In contrast, PEAs comprising substituted spacers resulted in amorphous materials suitable for the preparation of nanoparticle dispersions by means of direct nanoprecipitation from hexafluoroisopropanol into water. Strong intermolecular interactions that were evident from Hildebrand solubility parameters δ resulted in the formation of aggregates for the semi-crystalline materials. Although Hildebrand parameters alone provided less accurate solubility predictions of the PEAs in acetone and THF, the Flory–Huggins parameters χPS revealed pronounced changes of intermolecular interactions with variation of the polymer structure, clearly demonstrating a tunable hydrophobicity of the synthesized PEAs.
Introduction
Polymeric nanoparticles have great potential to increase the bioavailability of hydrophobic drugs.1–3 Mainly FDA-approved Resomer® materials, i.e. block copolymers composed of poly(ethylene oxide), and a polyester based on lactic acid and glycolic acid, are applied for this purpose. Although the variation of the monomer fractions allows for a certain tailoring of the nanoparticle properties, such as encapsulation efficiency or drug release, these materials are often not suited for specific cargos because of a low thermodynamic compatibility between the host and guest. An optimum carrier material for a given drug would require a targeted tailoring of the compatibility. Intrinsically, this has to be optimized for each individual active pharmaceutical ingredient (API) and requires access to a multitude of different polymers to match its hydrophilicity. As many drugs contain functional groups, specific interactions with functional groups of the polymer carrier could furthermore be exploited in the development of an optimum carrier material.Nanoprecipitation represents an easy method for the formulation of aqueous nanoparticle dispersions.4 Despite the relatively simple experimental procedure, the process has to be optimized for each polymer with regard to variables such as the concentration, solvent to non-solvent ratio, stirring speed, or addition of surfactants. Encapsulation of an API further increases the complexity of the process.5 Combining all these experimental possibilities with a variety of polymers results in a multidimensional parameter space that is difficult to handle by experiment alone, making the optimization of the carrier material, in fact, a trial and error process.
In silico predictions are able to accelerate this process, guiding the design of polymeric nanocarriers with tailored properties. Notably, atomistic simulations can be used to predict the thermodynamic properties of the polymer materials, avoiding nanoformulation trials of thermodynamically incompatible materials. In addition, understanding the underlying intermolecular interactions and structure–property relationships represents the key step towards a targeted development of nanocarriers tailor-made for a specific API.6,7 Solubility parameters (SP), which can be obtained from atomistic molecular dynamics (MD) simulations, are useful for rapid ranking of polymers and can be applied to predict solvent compatibility and bulk properties. However, SP do not account for entropic effects, concentration dependence and unique interactions between molecules.8 The description can be refined by combination with the Flory–Huggins (FH) theory, which includes enthalpic and entropic factors for the mixing of two components. In addition, specific interactions such as hydrogen bonding can be considered by performing simulations of polymer mixtures.8–11
Aiming towards the development of such a combined experimental and in silico approach, we selected polyesteramides (PEA) as a polymer class. Besides enabling the degradation of the polymeric nanoparticle by hydrolysis of the ester moieties,12–14 the amide functionalities might induce specific interactions via hydrogen bonding. These properties are, e.g., exploited in the commercial BAK® materials based on 1,4-butanediol, adipic acid and ε-caprolactam.15,16 PEAs can be synthesized by ring opening polymerization (ROP) of cyclic morpholinediones17,18 or, traditionally, by polycondensation of diols, dicarboxylic acids and amino acids yielding PEAs with randomly distributed amide and ester functionalities.19 The laborious monomer synthesis ruled out the ROP as a synthetic strategy for tailoring of the polymer properties via high-throughput experimentation (HTE) approaches.
Although bis(2-oxazoline)s are often used as coupling agents for chain extension of, e.g., polyamide20,21 or polyester20,22–24 prepolymers, comparably little attention has been paid towards their direct application for PEA synthesis. A nucleophilic attack of a carboxylic acid at the 2-oxazoline ring results in its opening and the formation of a diamide structure.25,26 Alternating diester and diamide moieties can hence be realized by the AA/BB polyaddition of dicarboxylic acids and bis(2-oxazolines).25,27 Benefitting from the experimental simplicity and a wide range of carboxylic acids commercially available to serve as monomers, this synthetic approach fulfills the basic requirements for the adjustment of the hydrophilicity of PEA materials in a HTE fashion.
Mostly, the reaction of aromatic bis(2-oxazoline)s such as 1,3- and 1,4-phenylene bis(2-oxazoline)s with dicarboxylic acids has been studied.25,28–31 Further examples include other aromatic bisoxazolines based on 2,5-furandicarboxylic acid,32 2,6-pyridine dicarboxylic acid,33 (1,1′-biphenyl)-4,4′-dicarboxylic acid,30,34 bis(4-carboxyphenyl)phenylphosphine oxide,35 or phenolphthalein.36 However, simple 2,2′-bis(2-oxazoline) (BisOx) has, to the best of our knowledge, not been utilized so far, and the reported polymers have not been applied for the formulation of nanoparticles. As depicted in Scheme 1, the resulting PEAs feature a diethylene oxamide moiety, whereas the spacer between the alternating ester functionalities is determined by the dicarboxylic acid employed for the polyaddition. It should be noted that two similarly structured oligomers with C4 and C8 alkylene spacers have been reported by Yin et al., however via a more complicated synthesis route.37
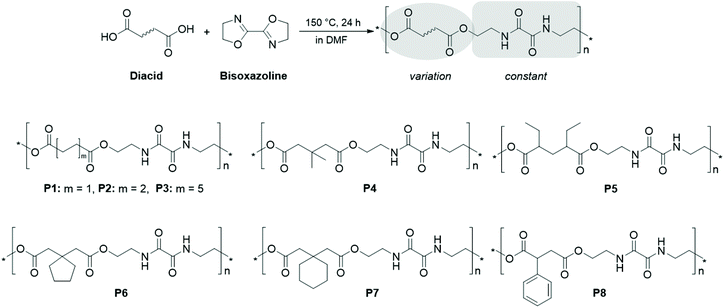 | ||
| Scheme 1 Schematic representation of the polymerization approach and the structures of the obtained polyesteramides P1 to P8. | ||
In order to facilitate the integration of a general experimental and in silico methodology for polymeric nanoparticles in an aqueous dispersion, we employed a range of dicarboxylic acids, also including substituted aliphatic spacers. This resulted in a broad variation of the hydrophilicity, the solid state properties and nanoprecipitation characteristics within the PEA library. The feasibility of the concept was consistently evaluated throughout the workflow by comparison of experimental results from wide-angle X-ray scattering (WAXS), solubility and nanoprecipitation with in silico predictions based on SP and FH theory combined with atomistic MD simulations.
Experimental section
Materials
Succinic acid (99.0%), 2,4-diethylglutaric acid (DL- and meso-mixture, 98.0%), 1,1-cyclopentanediacetic acid (98.0%), 1,1-cyclohexanediacetic acid (98.0%), and 2,2′-bis(2-oxazoline) (BisOx, 97.0%) were obtained from Tokyo Chemical Industry (TCI). Adipic acid (99.0%), dodecanedioic acid (99.0%), 3,3-dimethylglutaric acid (98.0%), (±)-phenylsuccinic acid (98.0%), and 1,1,1,3,3,3-hexafluro-2-propanol (HFiP, 99.0%) were purchased from Sigma Aldrich (now MERCK). N,N-Dimethylformamide (DMF, 99.8%, extra dry over molecular sieves) was purchased from ACROS Organics. All other chemicals and solvents were obtained from common commercial sources and used without further purification, unless otherwise stated.Instruments
Proton nuclear magnetic resonance (1H NMR) spectra and diffusion ordered NMR spectroscopy (DOSY) spectra were recorded at room temperature in 1,1,1,3,3,3-hexafluro-2-propanol-D2 (HFiP-d2) on a Bruker Avance 400 MHz spectrometer using the residual solvent resonance as an internal standard. The chemical shifts are given in ppm. For infrared spectroscopy, an IRAffinity-1 CE system from Shimadzu, equipped with a quest ATR diamond extended range X – single-reflection-ATR cuvette, was used.Size exclusion chromatography (SEC) was performed on an Agilent 1200 series system equipped with a PSS degasser, a G1310A pump, a G1329A auto sampler, a Techlab oven, a G1362A RI detector, and a PSS GRAM guard/30/1000 Å (10 μm particle size) column. The system was run with an eluent composed of N,N-dimethylacetamide (DMAc) with 0.21 wt% LiCl at a flow rate of 1 mL min−1 at 40 °C and was calibrated with polystyrene (PS) standards (400 to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 g mol−1) purchased from Polymer Standards Services GmbH (PSS).
000 g mol−1) purchased from Polymer Standards Services GmbH (PSS).
For the measurement of the matrix-assisted laser desorption/ionization (MALDI) spectra, an Ultraflex III TOF/TOF from Bruker Daltonics was used. The instrument was equipped with a Nd:YAG laser and a collision cell. All spectra were measured in the positive reflector mode using 2,5-dihydroxybenzoic acid (DHB) as a matrix. Ionization occurred readily from the sodium and potassium ions naturally present. The instrument was calibrated prior to each measurement with an external PMMA standard from PSS. Data were processed via Bruker Data Analysis software version 4.2.
Thermogravimetric analysis (TGA) was performed under a N2 atmosphere on a Netzsch TG 209 F1 Iris from 30 to 600 °C at a heating rate of 20 K min−1. Differential scanning calorimetry (DSC) measurements were performed on a Netzsch DSC 204 F1 Phoenix under a N2 atmosphere from −50 to 120 °C or 260 °C. Three cycles were recorded for each sample. The first and the second heating runs were conducted at a heating rate of 20 K min−1. For the third heating run, a heating rate of 10 K min−1 was applied. A cooling rate of 20 K min−1 between the heating runs was applied at all times. The glass transition temperature (Tg, inflection value) and the melting temperature (Tm) values are reported from the second heating run.
The X-ray diffraction studies were performed using a Bruker Phaser D2 diffractometer in reflection mode with Cu-Kα radiation (λ = 1.54056 Å) over a range of 2θ from 5 to 50° with a scanning rate of 0.015° s−1. Structure refinement of P1 was realized by the Rietveld method using Maud software.38 The background was determined using a fifth-order polynomial. LaB6 was used as a standard material to investigate the instrumental broadening. The degree of crystallinity was calculated with the integrated intensities of the amorphous and crystalline scattering curve in a range of 2θ from 15 to 30°.39,40
Dynamic light scattering (DLS) and ζ-potential measurements were performed on a Zetasizer Nano ZS from Malvern Instruments at 25 °C (λ = 633 nm) at an angle of 173°. Each measurement was performed five times for DLS and thrice for the ζ-potential. The mean particle size was approximated as the effective (Z-average) diameter and the width of the distribution as the polydispersity index (PDI) of the particles obtained by the method of cumulants assuming a spherical shape.
Polyesteramide synthesis
The respective diacid (1 mmol) and BisOx (641 mg, 1 mmol) were dissolved or suspended in 0.5 mL DMF. The vial was closed and the solution was degassed by gently bubbling with argon. The polymerization was performed at 150 °C for 24 h, and the reaction solution was cooled to room temperature. Because P1–P3 precipitated, HFiP was added to the reaction mixtures to dissolve the polyersteramides prior to precipitation into methanol at room temperature. All other PEAs were precipitated into cold (−20 °C) methanol. The obtained polymeric materials were dried at 40 °C in a vacuum oven and characterized by IR spectroscopy, 1H and DOSY NMR spectroscopy, MALDI-ToF mass spectrometry, SEC, TGA, DSC and wide-angle X-ray scattering experiments.Poly{succinic acid-alt-[bis(2-oxazoline)]} P1: 1H NMR (400 MHz, HFiP-d2): δ/ppm = 8.05 (2 × ![[N with combining low line]](https://www.rsc.org/images/entities/char_004e_0332.gif)
![[H with combining low line]](https://www.rsc.org/images/entities/char_0048_0332.gif) ); 4.28 (2 × CH2, –
); 4.28 (2 × CH2, –![[C with combining low line]](https://www.rsc.org/images/entities/char_0043_0332.gif)
![[H with combining low line]](https://www.rsc.org/images/entities/char_0048_0332.gif) 2–OOCR); 3.85 (2 × CH2, –
2–OOCR); 3.85 (2 × CH2, –![[C with combining low line]](https://www.rsc.org/images/entities/char_0043_0332.gif)
![[H with combining low line]](https://www.rsc.org/images/entities/char_0048_0332.gif) 2–OH); 3.66 (2 × CH2, –
2–OH); 3.66 (2 × CH2, –![[C with combining low line]](https://www.rsc.org/images/entities/char_0043_0332.gif)
![[H with combining low line]](https://www.rsc.org/images/entities/char_0048_0332.gif) 2–NHCOR); 3.55 (2 × CH2, HO–CH2–
2–NHCOR); 3.55 (2 × CH2, HO–CH2–![[C with combining low line]](https://www.rsc.org/images/entities/char_0043_0332.gif)
![[H with combining low line]](https://www.rsc.org/images/entities/char_0048_0332.gif) 2–NHCOR–); 2.76 (2 × CH2, –
2–NHCOR–); 2.76 (2 × CH2, –![[C with combining low line]](https://www.rsc.org/images/entities/char_0043_0332.gif)
![[H with combining low line]](https://www.rsc.org/images/entities/char_0048_0332.gif) 2–COOR).
2–COOR).
Poly{adipic acid-alt-[bis(2-oxazoline)]} P2: 1H NMR (400 MHz, HFiP-d2): δ/ppm = 8.04 (2 × ![[N with combining low line]](https://www.rsc.org/images/entities/char_004e_0332.gif)
![[H with combining low line]](https://www.rsc.org/images/entities/char_0048_0332.gif) ); 4.26 (2 × CH2, –
); 4.26 (2 × CH2, –![[C with combining low line]](https://www.rsc.org/images/entities/char_0043_0332.gif)
![[H with combining low line]](https://www.rsc.org/images/entities/char_0048_0332.gif) 2–OOCR); 3.85 (2 × CH2, –
2–OOCR); 3.85 (2 × CH2, –![[C with combining low line]](https://www.rsc.org/images/entities/char_0043_0332.gif)
![[H with combining low line]](https://www.rsc.org/images/entities/char_0048_0332.gif) 2–OH); 3.65 (2 × CH2, –
2–OH); 3.65 (2 × CH2, –![[C with combining low line]](https://www.rsc.org/images/entities/char_0043_0332.gif)
![[H with combining low line]](https://www.rsc.org/images/entities/char_0048_0332.gif) 2–NHCOR); 3.55 (2 × CH2, HO–CH2–
2–NHCOR); 3.55 (2 × CH2, HO–CH2–![[C with combining low line]](https://www.rsc.org/images/entities/char_0043_0332.gif)
![[H with combining low line]](https://www.rsc.org/images/entities/char_0048_0332.gif) 2–NHCOR); 2.48 (2 × CH2, –
2–NHCOR); 2.48 (2 × CH2, –![[C with combining low line]](https://www.rsc.org/images/entities/char_0043_0332.gif)
![[H with combining low line]](https://www.rsc.org/images/entities/char_0048_0332.gif) 2–COOR); 1.71 (2 × CH2, –
2–COOR); 1.71 (2 × CH2, –![[C with combining low line]](https://www.rsc.org/images/entities/char_0043_0332.gif)
![[H with combining low line]](https://www.rsc.org/images/entities/char_0048_0332.gif) 2–CH2–COOR).
2–CH2–COOR).
Poly{dodecanedioic acid-alt-[bis(2-oxazoline)]} P3: 1H NMR (400 MHz, HFiP-d2): δ/ppm = 8.05 (2 × ![[N with combining low line]](https://www.rsc.org/images/entities/char_004e_0332.gif)
![[H with combining low line]](https://www.rsc.org/images/entities/char_0048_0332.gif) ); 4.25 (2 × CH2, –
); 4.25 (2 × CH2, –![[C with combining low line]](https://www.rsc.org/images/entities/char_0043_0332.gif)
![[H with combining low line]](https://www.rsc.org/images/entities/char_0048_0332.gif) 2–OOCR); 3.85 (2 × CH2, –
2–OOCR); 3.85 (2 × CH2, –![[C with combining low line]](https://www.rsc.org/images/entities/char_0043_0332.gif)
![[H with combining low line]](https://www.rsc.org/images/entities/char_0048_0332.gif) 2–OH); 3.65 (2 × CH2, –
2–OH); 3.65 (2 × CH2, –![[C with combining low line]](https://www.rsc.org/images/entities/char_0043_0332.gif)
![[H with combining low line]](https://www.rsc.org/images/entities/char_0048_0332.gif) 2–NHCOR); 3.55 (2 × CH2, HO–CH2–
2–NHCOR); 3.55 (2 × CH2, HO–CH2–![[C with combining low line]](https://www.rsc.org/images/entities/char_0043_0332.gif)
![[H with combining low line]](https://www.rsc.org/images/entities/char_0048_0332.gif) 2–NHCOR); 2.43 (2 × CH2, –
2–NHCOR); 2.43 (2 × CH2, –![[C with combining low line]](https://www.rsc.org/images/entities/char_0043_0332.gif)
![[H with combining low line]](https://www.rsc.org/images/entities/char_0048_0332.gif) 2–COOR); 1.68 (2 × CH2, –
2–COOR); 1.68 (2 × CH2, –![[C with combining low line]](https://www.rsc.org/images/entities/char_0043_0332.gif)
![[H with combining low line]](https://www.rsc.org/images/entities/char_0048_0332.gif) 2–CH2–COOR); 1.36 (5 × CH2, –(
2–CH2–COOR); 1.36 (5 × CH2, –(![[C with combining low line]](https://www.rsc.org/images/entities/char_0043_0332.gif)
![[H with combining low line]](https://www.rsc.org/images/entities/char_0048_0332.gif) 2)5–CH2–CH2–COOR).
2)5–CH2–CH2–COOR).
Poly{dimethylglutaric acid-alt-[bis(2-oxazoline)]} P4: 1H NMR (400 MHz, HFiP-d2): δ/ppm = 8.05 (2 × ![[N with combining low line]](https://www.rsc.org/images/entities/char_004e_0332.gif)
![[H with combining low line]](https://www.rsc.org/images/entities/char_0048_0332.gif) ); 4.26 (2 × CH2, –
); 4.26 (2 × CH2, –![[C with combining low line]](https://www.rsc.org/images/entities/char_0043_0332.gif)
![[H with combining low line]](https://www.rsc.org/images/entities/char_0048_0332.gif) 2–OOCR); 3.85 (2 × CH2, –
2–OOCR); 3.85 (2 × CH2, –![[C with combining low line]](https://www.rsc.org/images/entities/char_0043_0332.gif)
![[H with combining low line]](https://www.rsc.org/images/entities/char_0048_0332.gif) 2–OH); 3.66 (2 × CH2, –
2–OH); 3.66 (2 × CH2, –![[C with combining low line]](https://www.rsc.org/images/entities/char_0043_0332.gif)
![[H with combining low line]](https://www.rsc.org/images/entities/char_0048_0332.gif) 2–NHCOR); 3.54 (2 × CH2, HO–CH2–
2–NHCOR); 3.54 (2 × CH2, HO–CH2–![[C with combining low line]](https://www.rsc.org/images/entities/char_0043_0332.gif)
![[H with combining low line]](https://www.rsc.org/images/entities/char_0048_0332.gif) 2–NHCOR); 2.53 (2 × CH2, –
2–NHCOR); 2.53 (2 × CH2, –![[C with combining low line]](https://www.rsc.org/images/entities/char_0043_0332.gif)
![[H with combining low line]](https://www.rsc.org/images/entities/char_0048_0332.gif) 2–COOR); 1.17 (2 ×
2–COOR); 1.17 (2 × ![[C with combining low line]](https://www.rsc.org/images/entities/char_0043_0332.gif)
![[H with combining low line]](https://www.rsc.org/images/entities/char_0048_0332.gif) 3). SEC (DMAc, RI detection, PS calibration): Mn = 5200 g mol−1, Đ = 1.26.
3). SEC (DMAc, RI detection, PS calibration): Mn = 5200 g mol−1, Đ = 1.26.
Poly{diethylglutaric acid-alt-[bis(2-oxazoline)]} P5: 1H NMR (400 MHz, HFiP-d2): δ/ppm = 8.11–7.89 (2 × ![[N with combining low line]](https://www.rsc.org/images/entities/char_004e_0332.gif)
![[H with combining low line]](https://www.rsc.org/images/entities/char_0048_0332.gif) ); 4.36–4.18 (2 × CH2, –
); 4.36–4.18 (2 × CH2, –![[C with combining low line]](https://www.rsc.org/images/entities/char_0043_0332.gif)
![[H with combining low line]](https://www.rsc.org/images/entities/char_0048_0332.gif) 2–OOCR); 3.85 (2 × CH2, –
2–OOCR); 3.85 (2 × CH2, –![[C with combining low line]](https://www.rsc.org/images/entities/char_0043_0332.gif)
![[H with combining low line]](https://www.rsc.org/images/entities/char_0048_0332.gif) 2–OH); 3.68 (2 × CH2, –
2–OH); 3.68 (2 × CH2, –![[C with combining low line]](https://www.rsc.org/images/entities/char_0043_0332.gif)
![[H with combining low line]](https://www.rsc.org/images/entities/char_0048_0332.gif) 2–NHCOR); 3.54 (2 × CH2, HO–CH2–
2–NHCOR); 3.54 (2 × CH2, HO–CH2–![[C with combining low line]](https://www.rsc.org/images/entities/char_0043_0332.gif)
![[H with combining low line]](https://www.rsc.org/images/entities/char_0048_0332.gif) 2–NHCOR); 2.55–2.31 (2 × CH, –
2–NHCOR); 2.55–2.31 (2 × CH, –![[C with combining low line]](https://www.rsc.org/images/entities/char_0043_0332.gif)
![[H with combining low line]](https://www.rsc.org/images/entities/char_0048_0332.gif) –COOR); 2.11–1.54 (3 × CH2, –
–COOR); 2.11–1.54 (3 × CH2, –![[C with combining low line]](https://www.rsc.org/images/entities/char_0043_0332.gif)
![[H with combining low line]](https://www.rsc.org/images/entities/char_0048_0332.gif) 2–CHR–COOR); 0.94 (2 ×
2–CHR–COOR); 0.94 (2 × ![[C with combining low line]](https://www.rsc.org/images/entities/char_0043_0332.gif)
![[H with combining low line]](https://www.rsc.org/images/entities/char_0048_0332.gif) 3). SEC (DMAc, RI detection, PS calibration): Mn = 6200 g mol−1, Đ = 1.26.
3). SEC (DMAc, RI detection, PS calibration): Mn = 6200 g mol−1, Đ = 1.26.
Poly{cyclopentanediacetic acid-alt-[bis(2-oxazoline)]} P6: 1H NMR (400 MHz, HFiP-d2): δ/ppm = 8.05 (2 × ![[N with combining low line]](https://www.rsc.org/images/entities/char_004e_0332.gif)
![[H with combining low line]](https://www.rsc.org/images/entities/char_0048_0332.gif) ); 4.26 (2 × CH2, –
); 4.26 (2 × CH2, –![[C with combining low line]](https://www.rsc.org/images/entities/char_0043_0332.gif)
![[H with combining low line]](https://www.rsc.org/images/entities/char_0048_0332.gif) 2–OOCR); 3.85 (2 × CH2, –
2–OOCR); 3.85 (2 × CH2, –![[C with combining low line]](https://www.rsc.org/images/entities/char_0043_0332.gif)
![[H with combining low line]](https://www.rsc.org/images/entities/char_0048_0332.gif) 2–OH); 3.67 (2 × CH2, –
2–OH); 3.67 (2 × CH2, –![[C with combining low line]](https://www.rsc.org/images/entities/char_0043_0332.gif)
![[H with combining low line]](https://www.rsc.org/images/entities/char_0048_0332.gif) 2–NHCOR); 3.55 (2 × CH2, HO–CH2–
2–NHCOR); 3.55 (2 × CH2, HO–CH2–![[C with combining low line]](https://www.rsc.org/images/entities/char_0043_0332.gif)
![[H with combining low line]](https://www.rsc.org/images/entities/char_0048_0332.gif) 2–NHCOR); 2.64 (2 × CH2, –
2–NHCOR); 2.64 (2 × CH2, –![[C with combining low line]](https://www.rsc.org/images/entities/char_0043_0332.gif)
![[H with combining low line]](https://www.rsc.org/images/entities/char_0048_0332.gif) 2–COOR); 1.84–1.58 (4 × CH2,
2–COOR); 1.84–1.58 (4 × CH2, ![[c with combining low line]](https://www.rsc.org/images/entities/char_0063_0332.gif)
![[y with combining low line]](https://www.rsc.org/images/entities/char_0079_0332.gif)
![[c with combining low line]](https://www.rsc.org/images/entities/char_0063_0332.gif)
![[l with combining low line]](https://www.rsc.org/images/entities/char_006c_0332.gif)
![[o with combining low line]](https://www.rsc.org/images/entities/char_006f_0332.gif)
![[p with combining low line]](https://www.rsc.org/images/entities/char_0070_0332.gif)
![[e with combining low line]](https://www.rsc.org/images/entities/char_0065_0332.gif)
![[n with combining low line]](https://www.rsc.org/images/entities/char_006e_0332.gif)
![[t with combining low line]](https://www.rsc.org/images/entities/char_0074_0332.gif)
![[a with combining low line]](https://www.rsc.org/images/entities/char_0061_0332.gif)
![[n with combining low line]](https://www.rsc.org/images/entities/char_006e_0332.gif)
![[e with combining low line]](https://www.rsc.org/images/entities/char_0065_0332.gif) ). SEC (DMAc, RI detection, PS calibration): Mn = 4200 g mol−1, Đ = 1.36.
). SEC (DMAc, RI detection, PS calibration): Mn = 4200 g mol−1, Đ = 1.36.
Poly{cyclohexanediacetic acid-alt-[bis(2-oxazoline)]} P7: 1H NMR (400 MHz, HFiP-d2): δ/ppm = 8.08–7.94 (2 × ![[N with combining low line]](https://www.rsc.org/images/entities/char_004e_0332.gif)
![[H with combining low line]](https://www.rsc.org/images/entities/char_0048_0332.gif) ); 4.25 (2 × CH2, –
); 4.25 (2 × CH2, –![[C with combining low line]](https://www.rsc.org/images/entities/char_0043_0332.gif)
![[H with combining low line]](https://www.rsc.org/images/entities/char_0048_0332.gif) 2–OOCR); 3.85 (2 × CH2, –
2–OOCR); 3.85 (2 × CH2, –![[C with combining low line]](https://www.rsc.org/images/entities/char_0043_0332.gif)
![[H with combining low line]](https://www.rsc.org/images/entities/char_0048_0332.gif) 2–OH); 3.66 (2 × CH2, –
2–OH); 3.66 (2 × CH2, –![[C with combining low line]](https://www.rsc.org/images/entities/char_0043_0332.gif)
![[H with combining low line]](https://www.rsc.org/images/entities/char_0048_0332.gif) 2–NHCOR); 3.55 (2 × CH2, HO–CH2–
2–NHCOR); 3.55 (2 × CH2, HO–CH2–![[C with combining low line]](https://www.rsc.org/images/entities/char_0043_0332.gif)
![[H with combining low line]](https://www.rsc.org/images/entities/char_0048_0332.gif) 2–NHCOR); 2.73–2.52 (2 × CH2, –
2–NHCOR); 2.73–2.52 (2 × CH2, –![[C with combining low line]](https://www.rsc.org/images/entities/char_0043_0332.gif)
![[H with combining low line]](https://www.rsc.org/images/entities/char_0048_0332.gif) 2–COOR); 1.80–1.35 (5 × CH2,
2–COOR); 1.80–1.35 (5 × CH2, ![[c with combining low line]](https://www.rsc.org/images/entities/char_0063_0332.gif)
![[y with combining low line]](https://www.rsc.org/images/entities/char_0079_0332.gif)
![[c with combining low line]](https://www.rsc.org/images/entities/char_0063_0332.gif)
![[l with combining low line]](https://www.rsc.org/images/entities/char_006c_0332.gif)
![[o with combining low line]](https://www.rsc.org/images/entities/char_006f_0332.gif)
![[h with combining low line]](https://www.rsc.org/images/entities/char_0068_0332.gif)
![[e with combining low line]](https://www.rsc.org/images/entities/char_0065_0332.gif)
![[x with combining low line]](https://www.rsc.org/images/entities/char_0078_0332.gif)
![[a with combining low line]](https://www.rsc.org/images/entities/char_0061_0332.gif)
![[n with combining low line]](https://www.rsc.org/images/entities/char_006e_0332.gif)
![[e with combining low line]](https://www.rsc.org/images/entities/char_0065_0332.gif) ). SEC (DMAc, RI detection, PS calibration): Mn = 4400 g mol−1, Đ = 1.49.
). SEC (DMAc, RI detection, PS calibration): Mn = 4400 g mol−1, Đ = 1.49.
Poly{phenylsuccinic acid-alt-[bis(2-oxazoline)]} P8: 1H NMR (400 MHz, HFiP-d2): δ/ppm = 8.10–7.88 (2 × ![[N with combining low line]](https://www.rsc.org/images/entities/char_004e_0332.gif)
![[H with combining low line]](https://www.rsc.org/images/entities/char_0048_0332.gif) ); 7.53–7.00 (5 × CH,
); 7.53–7.00 (5 × CH, ![[A with combining low line]](https://www.rsc.org/images/entities/char_0041_0332.gif)
![[r with combining low line]](https://www.rsc.org/images/entities/char_0072_0332.gif) –
–![[H with combining low line]](https://www.rsc.org/images/entities/char_0048_0332.gif) ); 4.36–4.09 (2 × CH2, –
); 4.36–4.09 (2 × CH2, –![[C with combining low line]](https://www.rsc.org/images/entities/char_0043_0332.gif)
![[H with combining low line]](https://www.rsc.org/images/entities/char_0048_0332.gif) 2–OOCR); 3.90–3.81 (2 × CH2, –
2–OOCR); 3.90–3.81 (2 × CH2, –![[C with combining low line]](https://www.rsc.org/images/entities/char_0043_0332.gif)
![[H with combining low line]](https://www.rsc.org/images/entities/char_0048_0332.gif) 2–OH); 3.72–3.44 (4 × CH2, –
2–OH); 3.72–3.44 (4 × CH2, –![[C with combining low line]](https://www.rsc.org/images/entities/char_0043_0332.gif)
![[H with combining low line]](https://www.rsc.org/images/entities/char_0048_0332.gif) 2–NHCOR, HO–CH2–
2–NHCOR, HO–CH2–![[C with combining low line]](https://www.rsc.org/images/entities/char_0043_0332.gif)
![[H with combining low line]](https://www.rsc.org/images/entities/char_0048_0332.gif) 2–NHCOR); 3.35–3.18 (CH, –
2–NHCOR); 3.35–3.18 (CH, –![[C with combining low line]](https://www.rsc.org/images/entities/char_0043_0332.gif)
![[H with combining low line]](https://www.rsc.org/images/entities/char_0048_0332.gif)
![[A with combining low line]](https://www.rsc.org/images/entities/char_0041_0332.gif)
![[r with combining low line]](https://www.rsc.org/images/entities/char_0072_0332.gif) –); 3.07–2.80 (CH2, –
–); 3.07–2.80 (CH2, –![[C with combining low line]](https://www.rsc.org/images/entities/char_0043_0332.gif)
![[H with combining low line]](https://www.rsc.org/images/entities/char_0048_0332.gif) 2–COOR). SEC (DMAc, RI detection, PS calibration): Mn = 2500 g mol−1, Đ = 1.85.
2–COOR). SEC (DMAc, RI detection, PS calibration): Mn = 2500 g mol−1, Đ = 1.85.
Nanoparticle preparation
Aqueous nanoparticle suspensions were prepared by the nanoprecipitation method. 1 mg of polymer was dissolved in 1 mL of HFiP. 0.5 mL of this solution was slowly injected into 5 mL of MilliQ water under stirring (1000 rpm) at room temperature. The open vial was left stirring overnight in order to evaporate the HFiP. DLS measurements were performed 24 h after preparation.The Flory–Huggins theory
Solubility predictions using the FH theory41–43 are based on a mean-field lattice approach, which divides the mixed state into equally sized segments with a molar volume υm. Each of these segments represents subunits of a polymer (1) or solvent (2) molecule, which interact with an average energy per segment pair εij. The FH parameter χFH is defined as44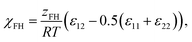 | (1) |
| Δem,FH = RTx1x2χFH. | (2) |
Note that in FH theory every segment occupies the same volume and, therefore, the segment mole fractions xi are the same as the volume fractions of the components. For small mixing volume changes, the segment molar Gibbs energy of mixing Δgm for the polymer and solvent molecules consisting of r1 and r2 segments, respectively, is given as
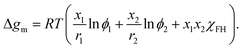 | (3) |
The original definition of the FH parameter does not account for the actual atomic structure of polymer–solvent mixtures.44 Here, we derive a modified formula for χFH, which includes the structural information through the radial distribution functions (RDF) of segment pairs obtained from atomistic simulations. The self-energy per segment pair εii is calculated from the Hildebrand solubility parameter δi of the pure substances (i = 1, 2), the molar volume υi of segment i and the coordination number zii obtained from the corresponding RDF (see the ESI†)45,46
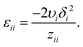 | (4) |
Similarly, the interaction energy between segments ε12 is calculated using the solubility parameter of the binary mixture δm and the average coordination number ![[z with combining macron]](https://www.rsc.org/images/entities/i_char_007a_0304.gif) 12 of the polymer and solvent segments (see the ESI†)
12 of the polymer and solvent segments (see the ESI†)
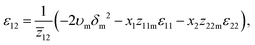 | (5) |
![[z with combining macron]](https://www.rsc.org/images/entities/i_char_007a_0304.gif) 12.
12.
Further improvement of thermodynamic modeling of polymer mixtures can be achieved employing composition dependent FH interaction parameters.47 So far, such parameters have been derived by fitting experimental phase diagrams.47 Here, we present an approach which derives the composition dependent FH interaction parameter directly from atomistic simulations. For this purpose, the coordination number zFH in eqn (1) is replaced with linear model functions Fi(xi) = Ai(1 − xi) + Bi and a parameter F12 that takes into account the structural changes with varying mixture compositions. The resulting FH parameter χz is given as (see the ESI†)
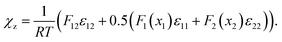 | (6) |
The composition independent parameters Ai, Bi and F12 are adjusted to yield the coordination numbers of the segments in the mixed state z11m, z22m and ![[z with combining macron]](https://www.rsc.org/images/entities/i_char_007a_0304.gif) 12 that correspond to the intermolecular structure obtained from atomistic simulations (see the ESI† for details). In contrast to the original definition of χFH, (eqn (2)), χz yields the FH energy of mixing Δem,z = RTx1x2χz that has the same value as the energy of mixing Δem,sim derived directly from atomistic simulations, i.e.
12 that correspond to the intermolecular structure obtained from atomistic simulations (see the ESI† for details). In contrast to the original definition of χFH, (eqn (2)), χz yields the FH energy of mixing Δem,z = RTx1x2χz that has the same value as the energy of mixing Δem,sim derived directly from atomistic simulations, i.e.
| Δem,z = Δem,sim = x1υ1δ12 + x2υ2δ22 − υmδm2. | (7) |
Computational procedure
Atomistic simulations were performed employing the Materials Studio (Version 17.1) program suite48 along with the COMPASSII force field.49 All materials were modelled as three-dimensional periodic amorphous cells constructed using a configurational bias Monte Carlo procedure50 implemented in the Amorphous Cell module based on the algorithm of Theodorou and Suter.51The unit cells of PEAs P1 to P8 (Scheme 1) contained 50 polymer chains with a degree of polymerization (DP) of 10, which is close to the experimentally determined values (cf.Table 1). The same DP was chosen for all models to facilitate a direct comparison and analysis of simulation results for different PEA structures. The unit cells of pure solvents, tetrahydrofuran (THF) and acetone (ACE), contained 800 molecules. In order to test the thermodynamic models described above, structure models for four different polymer–solvent mixtures with an approximate solvent content of 10 wt% were created. P4 and P8 were chosen as test cases. For both, the unit cells contained 50 polymer chains (DP = 10) as well as 232 and 258 THF molecules for P4 and P8, respectively. The structure models of the ACE-P4 and ACE-P8 mixtures comprised 288 and 320 acetone molecules, respectively.
| PEA | Diacid |
M
n(NMR)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a [g mol−1] a [g mol−1] |
DPa |
M
n(SEC)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b [g mol−1] b [g mol−1] |
Đ |
T
g![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c [°C] c [°C] |
T
m![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c [°C] c [°C] |
X
c![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) d [%] d [%] |
|---|---|---|---|---|---|---|---|---|
| a Determined by 1H NMR spectroscopy (400 MHz, HFiP-d2). b Determined by SEC (DMAc, 0.21 wt% LiCl, RI detection, PS calibration). c Determined by DSC in the 2nd heating run, inflection values are reported for Tg. d The degree of crystallinity determined by WAXS. | ||||||||
| P1 | Succinic acid | 1200 | 4 | n.a. | n.a. | n.a. | 152/211/222 | 50 |
| P2 | Adipic acid | 5000 | 17 | n.a. | n.a. | n.a. | 181/189 | 18 |
| P3 | Dodecanedioic acid | 7600 | 20 | n.a. | n.a. | n.a. | 149/168 | 39 |
| P4 | Dimethylglutaric acid | 4400 | 14 | 5200 | 1.26 | 21 | n.a. | n.a. |
| P5 | Diethylglutaric acid | 7100 | 21 | 6200 | 1.26 | 14 | n.a. | n.a. |
| P6 | Cyclopentanediacetic acid | 3800 | 11 | 4200 | 1.36 | 25 | n.a. | n.a. |
| P7 | Cyclohexanediacetic acid | 4600 | 13 | 4400 | 1.49 | 26 | n.a. | n.a. |
| P8 | Phenylsuccinic acid | 2600 | 8 | 2500 | 1.90 | 50 | n.a. | n.a. |
For each unit cell, three amorphous initial structures were constructed and geometrically optimized. Next, the lowest energy minima were refined employing MD simulations along with a simulated annealing procedure for generation of energetically more stable configurations. For this, the structure models were equilibrated at T = 300 K using the canonical (NVT) ensemble followed by a stepwise temperature increase up to 1000 K and a later decrease back to 300 K. In each step, the temperature was increased (decreased) by 100 K and, subsequently, the structure was equilibrated for 5 ps.
Next, MD simulations using the isothermal-isobaric (NPT) ensemble at zero target pressure and T = 300 K were performed with an equilibration for 100 ps employing the Berendsen barostat52 and a further simulation using the the Parrinello–Rahman barostat53–55 with a duration of 300 ps. The average cell parameters of the structure models were evaluated for the last 200 ps of the NPT simulations. The unit cells of the final structures of the NPT trajectories were scaled to the average cell parameters and the structure models were again equilibrated for 250 ps employing the NVT ensemble with a target temperature of 300 K. Average values of properties such as cohesive energy densities C, which are related to the Hildebrand solubility parameters with C = δ2, were calculated from the last 200 ps of the NVT simulations. All MD simulations employed the module Forcite along with a time step of 1 fs and the Nosé–Hoover thermostat.56,57
The total equilibration time in our simulations including the initial annealing procedure and following NPT and NVT MD simulations is 725 ps. This time is certainly not sufficient to describe full relaxation of polymer conformations, which takes place on at least the μs scale. However, the Monte Carlo algorithm of Theodorou and Suter50,51 used to generate initial polymer models was demonstrated51 to yield already well-relaxed amorphous glassy polymer models. The subsequent MD simulations are used only to sample the local atomic and vibrational motions, which take place at the fs to ps scale. In addition, for each model used in our simulations we have generated three fully independent initial structures, which yield virtually the same cohesive energy densities and RDF, in particular of the first coordination sphere.
Calculations of the RDF used coarse grained models of the final, geometrically optimized structures of the last NVT trajectory. Generation of coarse grained models used the module Mesostructure Builder approximating one polymer repeating unit (cf.Scheme 1) and solvent molecule as one coarse grained bead, respectively. The coarse grained models obtained were then used for the calculation of the intermolecular RDFs and coordination numbers zij used in eqn (3) and (4) (see the ESI†).
For elucidation of the crystal structure of P1, 16 initial structures assuming an infinite chain length were constructed similar to previous theoretical studies on the crystal structure of Nylon 6 (see the ESI†).58 All initial structures were geometrically optimized under constant (zero) pressure conditions. Subsequently, the X-ray diffraction patterns were calculated employing the module Reflex (Materials Studio, Version 17.1). Finally, three crystal structures showing diffraction peak positions similar to the experimentally observed X-ray diffractogram of P1 were chosen for the structure refinement (cf. Experimental section and Fig. S13†).
Results and discussion
Polymer synthesis and characterization
A PEA library was synthesized by polyaddition of 2,2′-bis(2-oxazoline) as an AA monomer and eight different dicarboxylic acids acting as the BB monomers. The bisoxazoline monomer was kept constant throughout the study to explore the impact of different diacid structures on the properties of the resulting PEAs. The utilized dicarboxylic acids are indicated in the corresponding PEA structures depicted in Scheme 1 and were commercially available, being therefore ideally suitable for a screening approach. The polymerization followed an AA + BB step-growth mechanism, including the opening of the 2-oxazoline rings by a nucleophilic attack of the carboxylic acid.25,27,28,59 As both monomers were bifunctional, this yielded a repetitive oxalamide unit and two ester moieties in the main chain of the PEA. For P1–P3, unsubstituted aliphatic dicarboxylic acids were used, aiming towards information regarding the influence of the spacer length between the diamide groups on the polymer properties. In addition, a C3 spacer between the ester moieties was kept constant, whereas the substitution pattern was varied: dimethyl and diethyl residues were introduced to alter the hydrophobicity of P4 and P5, whereas P6 and P7 were obtained from diacids with aliphatic cyclic substituents, i.e. cyclopentyl and cyclohexyl moieties. It should be noted that the carbon atom number is the same for P5 and P6. P8 included an aromatic moiety to further investigate the effect of the additional electron density. The syntheses were performed in a straightforward manner by simply adding the monomers in equimolar amounts in DMF and heating the reaction mixture at 150 °C overnight. An overview of the synthesized PEAs and their characterization results is provided in Table 1.IR spectroscopy provided initial confirmation of the functional groups present in the PEAs (Fig. S1 and S2†). All IR spectra clearly revealed the presence of ester moieties, as indicated by the ester carbonyl bands around 1730 cm−1. Also the amide I and amide II bands around 1650 cm−1 and 1530 cm−1, respectively, were detected for all PEAs, thereby indicating a successful polyaddition reaction. The spectra also hinted towards the absence of a starting material, as neither ν OH stretching bands of the dicarboxylic acid, nor ether (1110 cm−1) or imine (1621 cm−1) bands deriving from the 2-oxazoline were detected. In particular, the area increase of the ν –CH2– stretching band was consistent with the increased length of the aliphatic linker between the ester groups in the PEA series P1 to P3. Besides, the IR spectrum of P8 exhibited the sharp ν (![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH–) aromatic band.
CH–) aromatic band.
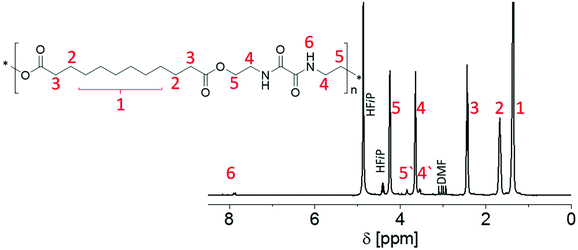
Presumably due to hydrogen bonds forming between the amide moieties, in particular the PEAs containing unsubstituted aliphatic spacers P1 to P3 were not readily soluble in a range of common deuterated solvents. However, HFiP is well-known to break such hydrogen bonds. As all synthesized PEAs were soluble in HFiP, the deuterated form of the solvent was applied for 1H NMR spectroscopy, enabling further structural insight into the new materials. Fig. 1 exemplarily depicts the 1H NMR spectrum of P3. The spectra of all other synthesized PEAs are provided in the ESI (Fig. S3–S9†).
In particular, peaks 4 and 5 in Fig. 1 confirmed the opening of both oxazoline rings forming amide and ester moieties with the dicarboxylic acids. The respective signals labelled 4′ and 5′ were associated with the polymer end groups functionalized with a –CONH–CH2–CH2–OH moiety (see below), as confirmed by additional DOSY experiments (data not shown). As no carboxylic acid protons were detected in the 1H NMR spectra for any PEA, the peak integrals of these signals were utilized to estimate the DP. The resulting molar masses Mn(NMR) varied between 1200 and 7100 g mol−1 for P1 to P8 and corresponded to DP values between 4 and 21. A clear correlation between the utilized diacid and the DP of the PEA could not be found. It should be noted that all other signals in the spectra of the different PEAs could be unambiguously assigned to the spacers between the ester moieties that result from the use of various dicarboxylic acids for the polyadditions.
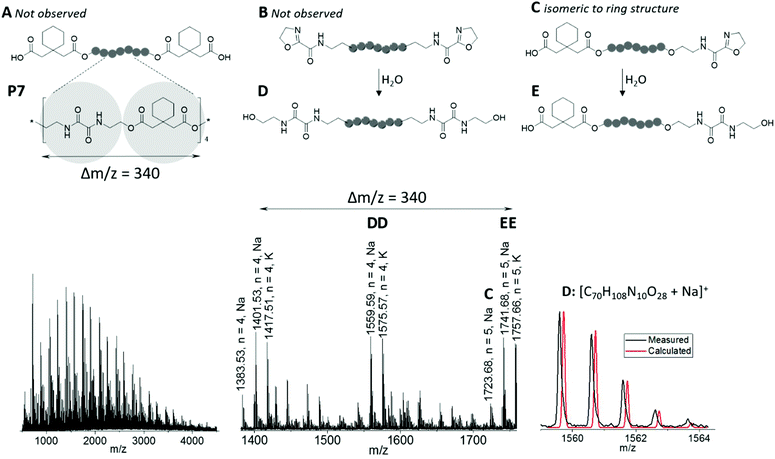
MALDI-ToF mass spectrometry investigation provided further insight into the polymer end groups present in the samples, as exemplarily shown for P7 in Fig. 2. In accordance with the repeating unit of the PEA obtained from BisOx and cyclohexanediacetic acid, the spectrum featured peaks spaced by regular m/z intervals of Δm/z = 340. Besides several less abundant m/z series, four main distributions were assigned. Because ionization occurred with both, sodium and potassium cations, these corresponded to two different PEA species. Three species would be expected from the polyaddition mechanism: chains functionalized with two 2-oxazoline end groups, chains comprising two carboxylic acid end groups, and chains carrying one 2-oxazoline and one carboxylic acid end group. It should be noted that the latter are isobaric to cyclic species and, surprisingly, represented the only one of these structures that could be assigned to less intense peaks in the MALDI-ToF mass spectrum (species C in Fig. 2). Instead of 2-oxazoline terminated macromolecules, –CO–NH–CH2CH2–OH end groups were found, either on both chain ends of P7 (species D in Fig. 2), or in combination with a carboxylic acid end group (species E in Fig. 2). Exemplarily, an overlay of calculated and measured isotopic patterns is depicted for the sodium adduct of the former. These end groups were presumably formed by opening of the 2-oxazoline rings by a nucleophilic attack of water. In fact, similar structures appeared during attempts to recrystallize BisOx from methanol, or were present in batches of BisOx that were stored for a long time. Although alcohols can also act as nucleophiles to attack 2-oxazoline moieties,60 none of the resulting macromolecules were found in the MALDI-ToF mass spectra.
As P4 to P8 were soluble in DMAc, these PEAs were further investigated by SEC to obtain information regarding the molar mass distribution (Fig. S10†). The obtained molar masses Mn(SEC) from 2500 to 6200 g mol−1 were in reasonable agreement with values obtained from 1H NMR spectroscopy. The purified polymers featured unimodal molar mass distribution with dispersity values (Đ) from 1.3 to 1.9, as expected for a step-growth polymerization with limited control over the DP.
Bulk properties
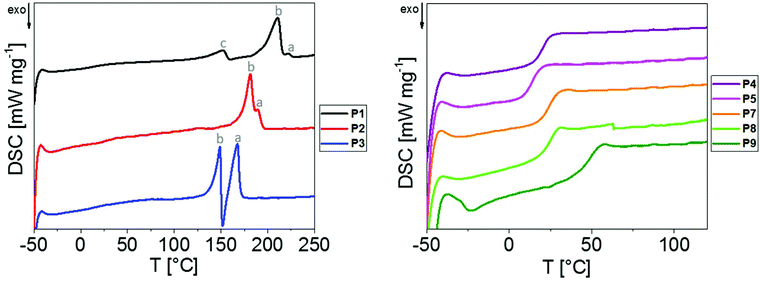
Despite the rather oligomeric nature of the PEAs, detailed investigations regarding their structures in solid state were performed. Thereby, it was possible to gain access to qualitative information regarding the presence of strong intermolecular interactions between the macromolecules in a straightforward manner. Enabling the formation of crystallites in bulk materials, these interactions might also complicate the formation of nanoparticle dispersions. The PEAs were hence investigated by means of DSC and WAXS. TGA measurements were performed to ensure the thermal stability during the course of the measurements (Fig. S11†).DSC measurements were performed using the bulk materials in the temperature range from −50 to 260 °C for P1 to P3 and from −50 to 120 °C for P4 to P8 (Table 1 and Fig. 3). For P1 to P3 comprising linear aliphatic spacers of various lengths, the DSC thermograms revealed melting peaks ranging from 149 to 222 °C, indicating the presence of semi-crystalline materials.
Exclusively the thermogram of P1, i.e. the PEA synthesized from the shortest dicarboxylic acid, revealed a third peak (labelled with “c” in Fig. 3) at 152 °C, which might have resulted from less perfect crystals in the form of “bundle chains” due to decreased chain flexibility. Two distinct melting peaks at higher temperatures (labelled as “a” and “b” in Fig. 3) were observed for P1 to P3, which might indicate the presence of two modifications in the bulk materials. The corresponding Tm values decreased with the increase in the length of the alkylene spacer between the ester moieties, which is consistent with observations made for aliphatic/aromatic PEAs by Kronek et al.30 In addition, the fraction of crystalline domains melting at higher temperatures (“a” Fig. 3) increased with the increase in the linker length.
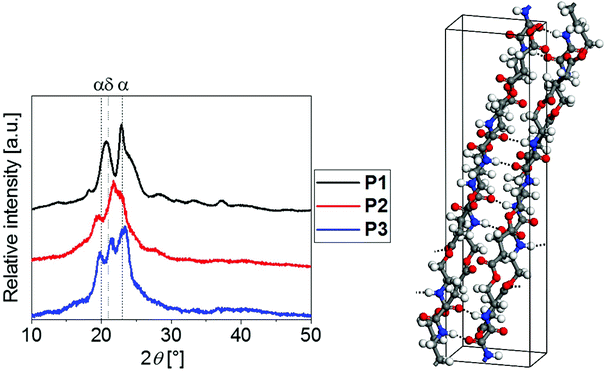
To gain deeper insight into their crystalline structures, P1 to P3 were hence further analyzed by means of WAXS (Fig. 4). The corresponding lattice parameters for P1 and P3 are listed in the ESI.†
The similar positions of the diffraction peak maxima for P1 to P3 hinted towards the presence of similar crystalline phases. The well-studied polyamides with alkylene spacers between the amide moieties, i.e., Nylon 6 or 11, are known to crystallize in a triclinic α-form (2θ ≈ 20°, 2θ ≈ 23°) and a hexagonal δ-form (2θ ≈ 21°), among others.61–65 Similar modifications were found for the investigated PEAs. In agreement with the melting peak observed from DSC, P1 crystallized predominantly in an α-form (2θ ≈ 21°, 2θ ≈ 23°, compare Fig. 4). In contrast, P3 clearly revealed the additional Bragg reflection at 2θ ≈ 21.4° that is associated with the δ modification, which is consistent with the two melting events observed using DSC. Unfortunately, the degree of crystallinity of P2 was not sufficient for drawing analogous conclusions.
One would expect that the hydrogen bond interactions between the amide moieties of the PEAs represent the major driving force for crystallization. The higher mass fraction of amide moieties for PEAs with shorter alkylene spacers explained the high degree of crystallinity of P1 (Xc = 50%). This PEA was hence selected for computational studies aiming to elucidate the intermolecular structure and interactions at the atomic level. The structure model depicted in Fig. 4 was successfully employed for Rietveld refinement of the experimentally determined diffractogram. Excellent agreement between the calculated and refined lattice parameters support the reliability of the structure model obtained (see the ESI†). Two hydrogen bonds per repeating unit were formed between the amide groups between neighboring polymer chains. Such directional intermolecular interactions are expected to promote ordering of polymer chains during crystallization rationalizing the comparatively high degree of crystallinity of P1.
The PEAs P4 to P8 containing substituted spacers were found to be amorphous, as only glass transitions were detected by DSC with Tg values ranging from 14 to 50 °C (Table 1 and Fig. 3). Due to an increase in the free volume induced by the larger ethyl substituents of P5, its Tg of 14 °C was lower than that of the methyl substituted P4 (Tg = 21 °C). For the cyclopentyl and cyclohexyl substituted P6 and P7, respectively, similar Tg values of 25 °C and 26 °C were found. The aromatic residue of P8 led to a significantly increased Tg of 50 °C. It should be noted that neither DSC investigations conducted up to 260 °C nor WAXS studies indicated the presence of any crystalline domains, showing that all substituents effectively prevented the crystallization of the PEAs P4 to P8.
Computational solubility predictions
Having successfully gained access to eight PEAs with various structures based on the dicarboxylic acid utilized, their applicability to form nanoparticles in aqueous dispersions was targeted. Nanoprecipitation represents a straightforward method to obtain these, in the best case avoiding the addition of emulsifiers or harsh formulation conditions.4 A volatile and water-miscible solvent that is able to dissolve the polymer is required for this purpose. THF and acetone are the most commonly used ones. Having realized solubility issues with the PEA series, we employed atomistic simulations to analyze their solubility behavior.In order to facilitate the analysis, the cohesive energy densities C calculated by MD simulations can be separated into the electrostatic Cel and the van der Waals CvdW contributions. The fraction of van der Waals interactions in the total intermolecular energy density is defined as
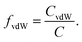 | (8) |
f vdW is used to characterize the intermolecular interactions of the PEAs. In a similar way, the Hilderbrand solubility parameter δ can be decomposed into the electrostatic δel and the van der Waals δvdW contributions, with δ2 = δel2 + δvdW2. Fig. 5 and Table 2 compare the total Hildebrand δ and van der Waals interaction parameters δvdW for P1 to P8 as well as THF and acetone. In addition, Table 2 shows the electrostatic interaction parameter δel, the fraction of the van der Waals interactions fvdW and the calculated mass densities.
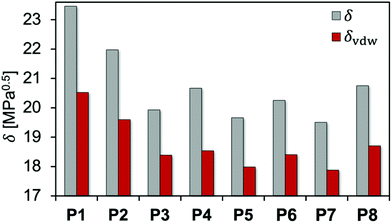 | ||
| Fig. 5 Total δ and van der Waals δvdW interaction parameters calculated for all polyesteramides P1 to P8. | ||
| PEA | δ [MPa0.5] | δ vdW [MPa0.5] | δ el [MPa0.5] | f vdW [%] | ρ [g cm−3] |
|---|---|---|---|---|---|
| P1 | 23.5 | 20.5 | 11.4 | 76.5 | 1.296 |
| P2 | 22.0 | 19.6 | 10.0 | 79.5 | 1.237 |
| P3 | 19.9 | 18.4 | 7.7 | 85.1 | 1.117 |
| P4 | 20.7 | 18.5 | 9.1 | 80.4 | 1.214 |
| P5 | 19.7 | 18.0 | 8.0 | 83.7 | 1.167 |
| P6 | 20.3 | 18.4 | 8.5 | 82.6 | 1.222 |
| P7 | 19.5 | 17.9 | 7.8 | 84.0 | 1.200 |
| P8 | 20.8 | 18.7 | 9.0 | 81.2 | 1.253 |
| THF | 18.3 | 17.7 | 4.9 | 93.0 | 0.850 |
| ACE | 19.3 | 16.9 | 9.3 | 76.7 | 0.784 |
For the PEA comprising linear aliphatic spacers of various lengths between the ester moieties, P1 showed the strongest intermolecular interaction among the investigated PEAs. δ considerably decreased while fvdW continuously increased with the number of backbone carbon atoms in the polymer repeating unit (P2 and P3). This is connected with an increase of the hydrophobicity of the PEAs when additional CH2 groups are incorporated, while larger repeating units favor steric effects leading to weaker intermolecular interactions. The same trend was observed on comparing P4 and P5 (methyl vs. ethyl substituents) as well as P6 and P7 (cyclopentyl vs. cyclohexyl substituents), respectively. Introducing an aromatic moiety in P8 leads to a slightly higher δ and lower fvdW compared to P6 and P7. This indicates that the presence of aromatic groups has only minor influence on the polymer–polymer interactions for the investigated PEAs.
The variation of δ and fvdW calculated for the PEAs clearly indicates differences in solubilities. In previous studies, solubility predictions using Hildebrand parameters calculated using MD simulations were successfully correlated with experimental data for several compounds.10,11
However, the general applicability of atomistic simulations combined with the FH theory for reliable predictions of the thermodynamic compatibility between polymers and low molar mass compounds has been questioned recently.66–68 In contrast to the previous models, our approach explicitly considers the intermolecular structure obtained from atomistic simulations for calculation of the FH interaction parameter χFH (eqn (1)) and its composition dependent counterpart χz (eqn (6)). In order to test the accuracy of both models for solubility predictions, the solubility of P4 and P8 in THF and acetone was tested experimentally. At a polymer concentration of 5 mg mL−1, P4 was soluble whereas P8 was insoluble in both solvents. Table 3 compares the corresponding values of the energies of mixing Δem at solvent concentrations of about 10 wt% (x1 ≈ 0.65) used for the atomistic simulations. In addition, the Gibbs energies of mixing Δgm for a polymer concentration of 5 mg mL−1 (x1 ≈ 0.004) used for the experimental solubility tests are displayed. All calculations are performed at 300 K.
| x 1 | 0.04 | 0.65 | ||||||
|---|---|---|---|---|---|---|---|---|
| Exp. | χ FH | χ z | Δgm,z | Δgm,FH | χ FH | χ z | Δem,sim | |
| THF-P4 | Soluble | −13.3 | −6.9 | −96 | −160 | −13.3 | 1.0 | 0.53 |
| THF-P8 | Insoluble | 35.5 | 26.5 | 235 | 324 | 35.5 | −6.2 | −3.49 |
| ACE-P4 | Soluble | −7.4 | −3.0 | −59 | −103 | −7.4 | −4.0 | −2.33 |
| ACE-P8 | Insoluble | 34.4 | 25.2 | 221 | 312 | 34.4 | −7.6 | −4.51 |
Both solubility predictions using χFH and χz agreed with the experimental observations, since P4 is predicted to be soluble in THF and acetone (Δgm < 0), whereas P8 is insoluble in both solvents (Δgm > 0). However, the energy of mixing obtained from atomistic simulations and Δem,z (Δem,z = Δem,sim, eqn (7)) was negative at x1 ≈ 0.65 for the mixtures THF-P8 and ACE-P8, but the FH theory along with χFH predicted strongly endothermic mixtures at this composition. Consequently, considerable deviations between Δgm,z and Δgm,FH were observed for the mixtures containing P8. In contrast, smaller differences between the predictions using χFH and χz were found for the tested P4 solutions.
For comparison, some previous studies calculated the FH interaction parameter from atomistic simulations without consideration of the actual intermolecular structure, e.g., using the formula8
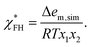 | (9) |
In the case of the P8 mixtures for which Δem,sim < 0, eqn (9) would yield negative FH parameters and, therefore, incorrectly predict complete solubility of P8 in THF and acetone. In contrast, our definition of the FH parameters χFH and χz explicitly takes into account the intermolecular structure obtained from atomistic simulations. This leads to correct predictions for dilute polymer solutions. For such low polymer concentrations, Δgm,z and Δgm,FH differ only slightly indicating that a random mean-field lattice along with a composition independent coordination number zFH reasonably approximates dilute polymer solutions (Fig. S15†). However, for higher polymer concentrations, calculations using χFH considerably deviated from predictions using the composition dependent χz and yielded energies of mixing inconsistent with the simulation results (see the ESI†). This applied in particular to the solutions containing P8, which is probably connected with steric effects and specific interactions originating from the phenyl groups. Thus, the use of the composition dependent χz was of central importance to achieve satisfactory agreement with both simulations and experimental results in the case of the investigated PEA solutions, since χz implicitly includes the deviations of the polymer mixture from the random mean-field lattice. However, directional interactions such as hydrogen bonding are not explicitly considered in FH theory.69 As a consequence, more accurate thermodynamic models are required for reliable solubility predictions of polymers showing pronounced specific interactions. This applies in particular to P1 for which WAXS experiments and the calculated crystal structure showed a strong influence of H-bonds on the polymer properties.
Aqueous nanoparticle dispersions
As the MD simulations indicated that the most commonly used solvents, i.e. THF and acetone, were not applicable for the entire series of the PEAs due to solubility restrictions, HFiP was applied as an alternative solvent for nanoprecipitation. HFiP is volatile (boiling temperature of 58 °C at ambient pressure), miscible with water and solubilizes all of the investigated PEAs P1 to P8, therefore meeting all the requirements for nanoprecipitation.Although the nanoparticle formation by means of nanoprecipitation can in general be optimized for individual polymers by variation of, e.g., the polymer concentration or solvent/non-solvent ratios, constant formulation parameters (c(P1 to P8) = 1 mg mL−1, volume ratio of HFiP/water = 1/10) were applied in this study to compare the influence of the PEA structure on the capability to easily form nanoparticles in aqueous dispersions. Accordingly, a solution of each polymer in HFiP was slowly injected into water under vigorous stirring, maintaining these concentrations and subsequently letting the organic solvent evaporate under ambient conditions. The obtained dispersions were analyzed by means of DLS (Fig. S11† and Table 4).
| P1 | P2 | P3 | P4 | P5 | P6 | P7 | P8 | |
|---|---|---|---|---|---|---|---|---|
| D h [nm] | Aggregation | 114 | 143 | 227 | 160 | 76 | ||
| PDI | 0.13 | 0.05 | 0.13 | 0.05 | 0.18 | |||
| ζ [mV] | −33 | −37 | −36 | −35 | −44 | |||
Despite the variation of the alkylene spacer length between the ester moieties, all semi-crystalline PEAs (P1 to P3) resulted in aggregation during nanoprecipitation attempts, presumably due to the strong intermolecular interactions that were also evident from the Hildebrand solubility parameters. In particular, P1 and P2 formed macroscopic precipitates. In contrast, aqueous nanoparticle dispersions were successfully obtained from HFiP solutions of the amorphous PEAs P4 to P8, irrespective of the increased or decreased number of carbon atoms compared to the semi-crystalline P1 to P3 (Fig. S12†). Except for the phenyl substituted P8 that produced smaller nanoparticles, the nanoparticle sizes varied from 160 to 230 nm, with batch to batch differences of ± 25 nm. All nanoparticles exhibited negative zeta potentials ζ between −33 and −44 mV, indicating the stability of the aqueous dispersions (Table 4). Those PEAs that successfully formed nanoparticles showed lower particle size with the increase in the Hildebrand solubility parameter with the exception of P6. Similarly, it has been shown recently that the polymer nanoparticle size decreases with the increase in the FH parameter of the polymer and solvent used for nanoparticle preparation.69 However, aggregation of P1 to P3 and considerably higher particle size of P6 demonstrate that accurate modeling of polymer nanoparticle formation requires, as mentioned above, the consideration of specific interactions such as hydrogen bonding and, moreover, precipitation kinetics.
Conclusions
The polyaddition polymerization of 2,2′-bis(2-oxazoline) and dicarboxylic acids with different aliphatic substituents enabled straightforward access to a PEA library. PEA with linear alkylene spacers between the ester moieties represented semi-crystalline materials, as confirmed by means of WAXS and DSC. Substituents at the spacer prevented the formation of crystallites through hydrogen bonding between the amide moieties of the material. These amorphous PEAs successfully formed aqueous nanoparticle dispersions by simple nanoprecipitation from HFiP into water. In contrast, strong intermolecular interactions that were evident from Hildebrand solubility parameters resulted in the formation of aggregates for the semi-crystalline materials. Although the predictability via Hildebrand parameters alone is to be taken into consideration with more than a grain of salt, MD simulations in combination with our improved FH theory provided accurate solubility predictions for the PEAs in THF and acetone.However, in order to verify the general applicability of this theory along with χz for at least qualitative solubility predictions of polymers with low molar mass compounds of interest for nanomedicine, i.e. drugs, more test simulations are required, which will be the subject of a future publication. These will guide our future research regarding detailed formulation studies including a variety of solvents, concentrations and anti-inflammatory APIs to be encapsulated into polymeric nanoparticles formed from the developed PEAs.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This project forms part of the Collaborative Research Centre PolyTarget (SFB 1278, projects A01 and Z01) funded by the German Research Foundation (DFG).References
- A. Bhakay, M. Rahman, R. N. Dave and E. Bilgili, Pharmaceutics, 2018, 10, 86 CrossRef CAS.
- E. Lepeltier, C. Bourgaux and P. Couvreur, Adv. Drug Delivery Rev., 2014, 71, 86–97 CrossRef CAS.
- S. Guo and L. Huang, Biotechnol. Adv., 2014, 32, 778–788 CrossRef CAS.
- S. Schubert, J. T. Delaney Jr. and U. S. Schubert, Soft Matter, 2011, 7, 1581–1588 RSC.
- C. J. M. Rivas, M. Tarhini, W. Badri, K. Miladi, H. Greige-Gerges, Q. A. Nazari, S. A. G. Rodríguez, R. Á. Román, H. Fessi and A. Elaissari, Int. J. Pharm., 2017, 532, 66–81 CrossRef.
- S. Sen, Y. Han, P. Rehak, L. Vuković and P. Král, Chem. Soc. Rev., 2018, 47, 3849–3860 RSC.
- A. Gooneie, S. Schuschnigg and C. Holzer, Polymer, 2017, 9, 16 Search PubMed.
- L. Huynh, C. Neale, R. Pomès and C. Allen, Nanomedicine, 2012, 8, 20–36 CrossRef CAS.
- X. D. Guo, L. J. Zhang and Y. Qian, Ind. Eng. Chem. Res., 2012, 51, 4719–4730 CrossRef CAS.
- A. Erlebach, T. Ott, C. Otzen, S. Schubert, J. Czaplewska, U. S. Schubert and M. Sierka, J. Comput. Chem., 2016, 37, 2220–2227 CrossRef CAS.
- A. O. Kasimova, G. M. Pavan, A. Danani, K. Mondon, A. Cristiani, L. Scapozza, R. Gurny and M. Moeller, J. Phys. Chem. B, 2012, 116, 4338–4345 CrossRef CAS.
- K. Herzog, R.-J. Mueller and W.-D. Deckwer, Polym. Degrad. Stab., 2006, 91, 2486–2498 CrossRef CAS.
- Y. Ikada and H. Tsuji, Macromol. Rapid. Commun., 2000, 21, 117–132 CrossRef CAS.
- L. N. Woodard and M. A. Grunlan, ACS Macro Lett., 2018, 7, 976–982 CrossRef CAS.
- S. Mecking, Angew. Chem., Int. Ed., 2004, 43, 1078–1085 CrossRef CAS.
- E. Grigat, R. Koch and R. Timmermann, Polym. Degrad. Stab., 1998, 59, 223–226 CrossRef CAS.
- N. Franz and H. A. Klok, Macromol. Chem. Phys., 2010, 211, 809–820 CrossRef CAS.
- Y. Feng, J. Lu, M. Behl and A. Lendlein, Macromol. Biosci., 2010, 10, 1008–1021 CrossRef CAS.
- A. Rodriguez-Galan, L. Franco and J. Puiggali, Polymer, 2011, 3, 65–99 CAS.
- L. Néry, H. Lefebvre and A. Fradet, Macromol. Chem. Phys., 2004, 205, 448–455 CrossRef.
- A. Douhi and A. Fradet, J. Polym. Sci., Part A: Polym. Chem., 1995, 33, 691–699 CrossRef CAS.
- J. V. Seppälä, A. O. Helminen and H. Korhonen, Macromol. Biosci., 2004, 4, 208–217 CrossRef.
- S. Y. Xu, Y. H. Shi, J. B. Zhao, S. L. Jiang and W. T. Yang, Polym. Adv. Technol., 2011, 22, 2360–2367 CrossRef CAS.
- C. Q. Huang, S. Y. Luo, S. Y. Xu, J. B. Zhao, S. L. Jiang and W. T. Yang, J. Appl. Polym. Sci., 2010, 115, 1555–1565 CrossRef CAS.
- B. M. Culbertson, Prog. Polym. Sci., 2002, 27, 579–626 CrossRef CAS.
- C. Weber, T. Neuwirth, K. Kempe, B. Ozkahraman, E. Tamahkar, H. Mert, C. R. Becer and U. S. Schubert, Macromolecules, 2011, 45, 20–27 CrossRef.
- K. Kempe, Macromol. Chem. Phys., 2017, 218, 1700021 CrossRef.
- T. Kagiya, S. Narisawa, T. Maeda and K. Fukui, J. Polym. Sci., Part B: Polym. Lett., 1966, 4, 257–260 CrossRef CAS.
- J. Lustoň, J. Kronek, O. Markus, I. Janigová and F. Böhme, Polym. Adv. Technol., 2007, 18, 165–172 CrossRef.
- J. Kronek, J. Nedbal, H. Valentová, M. Neubert, I. Janigová, N. Petrenčíková, P. Šrámková, K. Csomorová and L. Petra, Polym. Test., 2018, 68, 1–7 CrossRef CAS.
- Y. Sano, J. Polym. Sci., Part A: Polym. Chem., 1989, 27, 2749–2760 CrossRef CAS.
- C. H. Wilsens, N. J. Wullems, E. Gubbels, Y. Yao, S. Rastogi and B. A. Noordover, Polym. Chem., 2015, 6, 2707–2716 RSC.
- P. Chevallier, J.-C. Soutif, J.-C. Brosse and A. Rincón-Guerrero, Eur. Polym. J., 1998, 34, 767–778 CrossRef CAS.
- J. Lustoň, J. Kronek, A. Kleinová, I. Janigová, H. Valentová and J. Nedbal, J. Polym. Sci., Part A: Polym. Chem., 2012, 50, 3936–3943 CrossRef.
- I. B. Mansour, K. Alouani, E. Chauveau, V. Martin, F. Schiets and R. Mercier, Eur. Polym. J., 2010, 46, 814–820 CrossRef CAS.
- S. Li and M. Tao, J. Therm. Anal. Calorim., 2013, 113, 633–639 CrossRef CAS.
- T. Yin, H. Y. Sun, J. B. Zhao, Z. Y. Zhang and W. T. Yang, Polym. Eng. Sci., 2014, 54, 756–765 CrossRef CAS.
- P. Scardi, L. Lutterotti and P. Maistrelli, Powder Diffr., 1994, 9, 180–186 CrossRef CAS.
- J. B. Nichols, J. Appl. Phys., 1954, 25, 840–847 CrossRef CAS.
- J. E. Johnson, J. Appl. Polym. Sci., 1959, 2, 205–209 CrossRef CAS.
- P. J. Flory, J. Chem. Phys., 1942, 10, 51–61 CrossRef CAS.
- M. L. Huggins, J. Phys. Chem., 1942, 46, 151–158 CrossRef CAS.
- M. L. Huggins, J. Am. Chem. Soc., 1942, 64, 1712–1719 CrossRef CAS.
- I. Teraoka, in Polymer Solutions: An Introduction to Physical Properties, John Wiley & Sons, Inc., New York, 2002 Search PubMed.
- G. A. Mansoori, Fluid Phase Equilib., 1993, 87, 1–22 CrossRef CAS.
- J. H. Hildebrand, in The Solubility of Nonelectrolytes, Dover Publications, Inc., New York, 1964 Search PubMed.
- B. A. Wolf, in Making Flory–Huggins Practical: Thermodynamics of Polymer-Containing Mixtures, Springer-Verlag, Berlin, Heidelberg, 2011 Search PubMed.
- Dassault Systèmes BIOVIA, Materials Studio, 17.1.0.48, Dassault Systèmes, San Diego, 2017 Search PubMed.
- H. Sun, Z. Jin, C. Yang, R. L. C. Akkermans, S. H. Robertson, N. A. Spenley, S. Miller and S. M. Todd, J. Mol. Model., 2016, 22, 47 CrossRef.
- R. L. C. Akkermans, N. A. Spenley and S. H. Robertson, Mol. Simul., 2013, 39, 1153–1164 CrossRef CAS.
- D. N. Theodorou and U. W. Suter, Macromolecules, 1985, 18, 1467–1478 CrossRef CAS.
- H. J. C. Berendsen, J. P. M. Postma, W. F. v. Gunsteren, A. DiNola and J. R. Haak, J. Chem. Phys., 1984, 81, 3684–3690 CrossRef CAS.
- M. Parrinello and A. Rahman, Phys. Rev. Lett., 1980, 45, 1196–1199 CrossRef CAS.
- M. Parrinello and A. Rahman, J. Appl. Phys., 1981, 52, 7182–7190 CrossRef CAS.
- G. J. Martyna, D. J. Tobias and M. L. Klein, J. Chem. Phys., 1994, 101, 4177–4189 CrossRef CAS.
- S. Nosé, J. Chem. Phys., 1984, 81, 511–519 CrossRef.
- W. G. Hoover, Phys. Rev. A, 1985, 31, 1695–1697 CrossRef PubMed.
- Y. Li and W. A. Goddard, Macromolecules, 2002, 35, 8440–8455 CrossRef CAS.
- P. A. Gunatillake, G. Odian and D. A. Tomalia, Macromolecules, 1988, 21, 1556–1562 CrossRef CAS.
- T. Huber, F. Böhme, H. Komber, J. Kronek, J. Luston, D. Voigt and B. Voit, Macromol. Chem. Phys., 1999, 200, 126–133 CrossRef CAS.
- H. Arimoto, M. Ishibashi, M. Hirai and Y. Chatani, J. Polym. Sci., Part A: Gen. Pap., 1965, 3, 317–326 CrossRef CAS.
- J. P. Parker and P. H. Lindenmeyer, J. Appl. Polym. Sci., 1977, 21, 821–837 CrossRef CAS.
- Q. Zhang, Z. Mo, H. Zhang, S. Liu and S. Z. Cheng, Polymer, 2001, 42, 5543–5547 CrossRef CAS.
- J. Fernandez, G. Swallowe and S. Lee, J. Appl. Polym. Sci., 2001, 80, 2031–2038 CrossRef CAS.
- H. Shanak, K.-H. Ehses, W. Götz, P. Leibenguth and R. Pelster, J. Mater. Sci., 2009, 44, 655–663 CrossRef CAS.
- B. D. Anderson, J. Pharm. Sci., 2018, 107, 24–33 CrossRef CAS.
- A. D. Glova, S. G. Falkovich, D. I. Dmitrienko, A. V. Lyulin, S. V. Larin, V. M. Nazarychev, M. Karttunen and S. V. Lyulin, Macromolecules, 2018, 51, 552–563 CrossRef CAS.
- E. R. Turpin, V. Taresco, W. A. Al-Hachami, J. Booth, K. Treacher, S. Tomasi, C. Alexander, J. Burley, C. A. Laughton and M. C. Garnett, Mol. Pharmaceutics, 2018, 15, 4654–4667 CrossRef CAS PubMed.
- T. Cowen, K. Karim and S. A. Piletsky, Polym. Chem., 2018, 9, 4566–4573 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9py01293a |
| This journal is © The Royal Society of Chemistry 2020 |