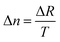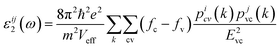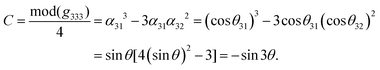RbNa(HC₃N₃O₃)·2H₂O exhibiting a strong second harmonic generation response and large birefringence as a new potential UV nonlinear optical material

Abstract

A new mixed alkali hydro-isocyanurate, RbNa(HC₃N₃O₃)·2H₂O, with the noncentrosymmetric space group Pna2₁ (No. 33), has been successfully grown by a hydrothermal method. The structure can be described as 2D wavy [Na(HC₃N₃O₃)O₄]_∞ layers separated by Rb atoms. The UV-vis diffuse reflection measurement revealed that RbNa(HC₃N₃O₃)·2H₂O has a large band gap of 5.10 eV, corresponding to the UV cutoff edge of 241 nm. The polarizing microscope measurement of a micron-sized single crystal shows that RbNa(HC₃N₃O₃)·2H₂O has a large birefringence of 0.194. The powder SHG measurement indicated that RbNa(HC₃N₃O₃)·2H₂O exhibits a strong SHG effect that is 5.3 times that of KH₂PO₄ (KDP) and can realize phase-matching in the visible and UV region. Moreover, the differences in the SHG responses between RbNa(HC₃N₃O₃)·2H₂O and two isostructural compounds have been investigated, which depend heavily on the structural modulation of the (HC₃N₃O₃)²⁻ group by cations. Meanwhile, the electronic structures and optical properties were well analyzed using DFT methods.

---

Introduction

Nonlinear optical (NLO) crystals that can generate ultraviolet (UV) coherent light are of considerable interest in the fields of laser processing, optical communication and photoetching.^1–7 To date, the most famous UV NLO crystal is β-BaB₂O₄ (BBO)⁸ due to its strong SHG effect (∼5 × KDP), short UV cutoff edge (190 nm) and large birefringence (Δn = 0.12@1064 nm), which has been widely used in second-, third-, fourth-, and fifth-harmonic generation. According to the anionic group theory, the superior linear and nonlinear properties of BBO should originate from its large π-conjugated delocalized (B₃O₆)³⁻ anionic group, which suggests that introducing large π-conjugated groups into NLO crystals would be a very efficient way for achieving excellent NLO performance. However, it is noteworthy that non-centrosymmetric (NCS) borates containing a large π-conjugated (B₃O₆)³⁻ group are rarely reported. In addition to BBO, there are only γ-KBe₂B₃O₇,⁹ CsZnB₃O₇,^10,11 LiB₆O₉F,¹² CsB₄O₆F ¹³ and Cs₂Al₂(B₂O₆)₂O.¹⁴ Therefore, this urges materials scientists to expand the research scope of large π-conjugated groups to search for new high performance UV NLO crystals.

In 2013, the Meyer group first found that the (C₃N₃O₃)³⁻ group has a highly similar structure to the (B₃O₆)³⁻ group. Then, they successfully synthesized the first NLO-active cynaurates, M₃(C₃N₃O₃) (M = Ca, Sr), containing the (C₃N₃O₃)³⁻ group, via cyclo-trimerization of linear (CNO)⁻ groups under vacuum conditions, which are isostructural to BBO but exhibit more superior linear and nonlinear optical properties than BBO.^15,16 In 2017, the Lin group confirmed that the large π-conjugated (C₃N₃O₃)³⁻ group is an ideal fundamental building block for UV NLO crystals in theory.¹⁷ These studies show that cynaurates have potential applications as UV NLO crystals.

More recently, our group further proposed that hydroisocyanurates may be more suitable candidates for UV NLO crystals because they not only have the large π-conjugated (HC₃N₃O₃)²⁻ and (H₂C₃N₃O₃)⁻ groups with high nonlinearity and strong optical anisotropy, the same as the (C₃N₃O₃)³⁻ group, but more importantly, their bulk single crystals are easy to grow via a simple water solution method. Accordingly, we successfully found the first hydro-isocyanurate NLO crystal, KLi(HC₃N₃O₃)·2H₂O, via a solvent-drop grinding method and grew bulk single crystals through the water solution technique.¹⁸ Afterward, several hydroisocyanurate crystals have been reported including K₂(HC₃N₃O₃),¹⁹ M₂N(H₂C₃N₃O₃)₄·6H₂O (M/N = Li/Ca and Na/Ba),²⁰ RE(H₂C₃N₃O₃)₂·(OH)·nH₂O (RE = La, Y and Gd),²¹ A₂B(H₂C₃N₃O₃)₄·nH₂O (A = K, Rb, Cs; B = Mg, Ca; n = 4, 10),²² RbLi(HC₃N₃O₃)·2H₂O ²³ and Cs₃Na(H₂C₃N₃O₃)₄·3H₂O.²⁴ Among them, however, only RbLi(HC₃N₃O₃)·2H₂O and Cs₃Na(H₂C₃N₃O₃)₄·3H₂O are NLO-active. Thus, it is very essential to find more hydro-isocyanurates or dihydro-isocyanurates as UV-NLO materials.

In this work, we have selected the RbOH–NaOH–H₃C₃N₃O₃ system to further search for promising hydroisocyanurate NLO crystals. As a result, a new mixed alkali NCS isocyanurate, RbNa(HC₃N₃O₃)·2H₂O, with a strong SHG effect and large birefringence, has been successfully grown through the hydrothermal method. Detailed in this study are the syntheses, crystal structures, and the relationship between the structure and NLO properties.

Experimental

Reagents and synthesis

In the synthesis of RbNa(HC₃N₃O₃)·2H₂O, the reaction mixture of RbOH·H₂O (2.41 g, 0.02 mol, 99%, Alfa), NaOH (0.80 g, 0.02 mol, 96%, Sinopharm), H₃C₃N₃O₃ (2.58 g, 0.02 mol, 98%, Adamas) and H₂O (5.0 mL) was sealed in an autoclave with a Teflon liner (200 mL). After heating at 120 °C for 2 hours, the mixture was slowly cooled down to ambient temperature at a rate of 20 °C h⁻¹. The product was washed with acetone, and then dried in air. Colorless rod-like millimeter-sized crystals were obtained (as shown in Fig. 1).

Fig. 1 Photos of RbNa(HC₃N₃O₃)·2H₂O crystals.

Single crystal X-ray diffraction

Single crystal X-ray diffraction data of the title compounds were collected at room temperature on a Rigaku Mercury CCD diffractometer with graphite-monochromatic Mo Kα radiation (λ = 0.71073 Å). A transparent block of the crystal was mounted on a glass fiber with epoxy for structure determination. The intensity data sets were corrected with the ω-scan technique. The data were integrated with the CrystalClear program. The intensities were corrected for Lorentz polarization, air absorption, and absorption attributable to the variation in the path length through the detector faceplate. Absorption corrections were also applied based on the multi-scan technique. The structures were solved using direct methods, refined with difference Fourier maps and full-matrix least-squares fitting on F² using SHELXL-97.²⁵ In addition, the PLATON²⁶ program was used for checking all the structures. The details of the crystallographic data and structure refinement information for the title compounds are listed in Table 1. Atomic coordinates and isotropic displacement coefficients are listed in Table S1, and bond lengths are listed in Table S2 of the ESI.†

Table 1 Crystal data and structure refinement of RbNa(HC₃N₃O₃)·2H₂O

Formula	C6H10N6Na2O10Rb2
a R(F) = ∑‖Fo| − |Fc‖/∑|Fo|·wR(Fo^2) = [∑w(Fo^2 − Fc^2)^2/∑w(Fo^2)^2]^1.
Formula weight (g mol^−1)	543.10
Crystal system	Orthorhombic
Space group	Pna21 (33)
a (Å)	15.829(18)
b (Å)	3.964(5)
c (Å)	13.068(16)
α = β = γ	90
Cell volume (Å^3)	819.8(17)
Z	2
ρ (calcd) (g cm^−3)	2.200
T (K)	293(2)
λ (Å)	0.71073
F(000)	552
μ (mm^−1)	6.087
R/wR^a (I > 2σ(I))	0.0458/0.1061
R/wR^a (all data)	0.0532/0.1085
GOF on F^2	1.044

---

Powder X-ray diffraction

Powder X-ray diffraction (PXRD) patterns of the polycrystalline title compounds were collected at room temperature on a Mini-flex 600 Powder X-ray diffractometer using Cu Kα radiation (λ = 1.540598 Å) in the 2θ = 10–70° range. The PXRD patterns of the pure powder samples of all compounds showed good agreement with the calculated PXRD patterns from the single crystal models (see Fig. S1†).

Thermal analysis

Thermogravimetric analyses (TGA) were carried out using a NETZSCH STA449F3 simultaneous thermal analyser. The reference (Al₂O₃) and crystal samples (5–15 mg) were enclosed in Al₂O₃ crucibles and heated from 30 °C to 1000 °C at a heating rate of 10 °C min⁻¹ under a constant flow of nitrogen gas.

UV-vis diffuse reflectance spectroscopy

The UV-vis diffuse reflectance powder spectra of the sample were measured at room temperature with BaSO₄ as the standard with 100% reflectance. Data were collected on a PerkinElmer Lamda-950 UV/vis/NIR spectrophotometer scanning in the range of 190–800 nm. Reflectance values were converted into absorbance according to the Kubelka–Munk function.^27,28

Infrared spectroscopy

IR spectra were recorded as KBr pellets on a Magna 750 Fourier transform infrared (FT-IR) spectrometer in the range of 4000–400 cm⁻¹ (see Fig. S9†).

Birefringence

The retardation and thickness of the title compound were measured using a Nikon ECLIPSE LV100 POL polarizing microscope with 589.6 nm light. The formula for calculating birefringence was as follows:
Δn represents the birefringence, ΔR denotes the optical path difference, and T indicates the thickness of the crystal.

Second harmonic generation

Powder SHG responses were investigated using a Q-switched Nd:YAG solid-state laser with a fundamental wavelength of 1064 nm with frequency doubling at 532 nm, for visible and UV SHG, respectively. According to the model source by Kurtz–Perry,²⁹ SHG responses depend strongly on the particle size. Polycrystalline samples of the title compounds were ground and sieved into the following particle size ranges: 25–45, 45–62, 62–75, 75–109, 109–150, and 150–212 μm. Cover slides were secured with tape in 1 mm thick plastic holders with an 8 mm diameter hole. KDP and BBO as the standard samples were prepared through grinding and sieving into identical particle size ranges in the same way. The ground samples were pressed into 1 mm thick aluminum holders containing a hole with a diameter of 8 mm and covered by glass microscope cover slides. Then these samples were put in an antiglare box and irradiated with laser waves at 1064 nm and 532 nm, respectively. In order to avoid the effect of the background flash lamp, a cutoff filter was employed. Furthermore, the second harmonic signal was selected by an interference filter (530 ± 10 nm), and then detected using a photomultiplier tube attached to a RIGOL DS1052E 50 MHz oscilloscope. The above procedures were repeated for the reference samples KDP and BBO. The proportion of the second harmonic intensity signal outputs between the title compounds and reference samples was calculated. All experiments were performed without an index-matching fluid.

Electronic structure calculations

Band structure and density of states (DOS) were determined using density functional theory (DFT) calculations provided by the CASTEP³⁰ code in the Material Studio package. The experimental crystal structure was used without further optimization. The exchange correlation interaction was treated by the generalized gradient approximation (GGA) of Perdew–Burke–Ernzerhof (PBE).³¹ The energy cutoff for the plane wave was chosen as 780 eV, and the self-consistent convergence of the total energy was set to 2.0 × 10⁻⁵ eV per atom. The Monkhorst–Pack³²k-point sampling of 2 × 2 × 4 in the Brillouin zone of the unit cell was selected for calculation. The interactions between the core and valence electrons were represented by the norm-conserving pseudopotentials, and the following valence configurations were observed: Na, 2s²2p⁶3s¹; Rb, 4s²4p⁶5s¹; C, 2s²2p²; N, 2s²2p³; O, 2s²2p⁴.

SHG coefficient calculations

The classical anharmonic oscillator (AHO) model³³ was adopted to calculate the SHG coefficients. The formula of the calculated second-order susceptibilities derived from the AHO model can be expressed in terms of the first-order susceptibilities as follows:

χ_ijk⁽²⁾(−ω₃;ω₁;ω₂) = F⁽²⁾χ_ii⁽¹⁾(ω₃)χ_jj⁽¹⁾(ω₁)χ_kk⁽¹⁾(ω₂).

The first-order susceptibility χ_ii⁽¹⁾ in the low-frequency region is given by χ⁽¹⁾(ω)_ii = [ε(ω)_ii − 1]/4π where the dielectric function

δ[E_c(k) − E_v(k) − ℏω]

where δ[E_c(k) − E_v(k) − ℏω] denotes the energy difference between the conduction and valence bands at the k point with absorption of a quantum ℏω. f_c and f_v represent the Fermi distribution functions of the conduction and valence bands, respectively. It is well acknowledged that DFT-GGA calculations commonly underestimate the band gap of the crystal. Consequently, to match the experimental band gap, the scissor operation should be employed to shift up the conduction band energy.

Results and discussion

Crystal structure

RbNa(HC₃N₃O₃)·2H₂O crystallizes into an orthorhombic crystal system with a non-centrosymmetric space group Pna2₁ (no. 33). In the structure, the fundamental building blocks are the (HC₃N₃O₃)²⁻ groups. The bond distances of C–N and C–O vary from 1.31 to 1.38 Å and 1.20 to 1.29 Å, respectively, which accord with the values in the reported cyanurates. Also, there is one crystallographically independent Na atom in its unit cell, which is coordinated to five O atoms to form a distorted trigonal bi-pyramidal NaO₅ configuration with Na–O bond lengths of 2.28–2.53 Å. The adjacent NaO₅ polyhedra connect each other to form a 1D chain via sharing the common oxygen atom (Fig. 2b). Furthermore, 1D NaO₅ chains were bridged via (HC₃N₃O₃)²⁻ groups to construct intricate 2D wavy [Na(HC₃N₃O₃)O₄]_∞ layers (Fig. 2c), which were separated by Rb atoms.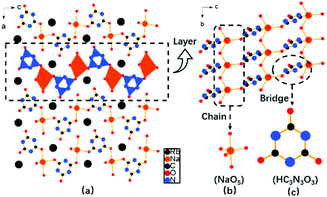

Fig. 2 (a) Crystal structure of RbNa(HC₃N₃O₃)·2H₂O; (b) layers consisting of a 1D (NaO₅) chain and (c) (HC₃N₃O₃) triangular entities.

Thermal analysis

As shown in Fig. S3,† RbNa(HC₃N₃O₃)·2H₂O exhibits two-step decomposition in the range of 30–600 °C. The first weight loss in the temperature range of 181–151 °C was 13.30% (cal. 13.30%), which can be assigned to the removal of two water molecules from the crystal structure. The second weight loss in the temperature ranging from 385 to 396 °C was 15.14% (cal. 15.80%), accounting for the loss of a cyanic acid molecule from the (HC₃N₃O₃)²⁻ group.

Birefringence

As shown in Fig. S4,† the measured retardation was approximately 1922 nm. Furthermore, the measured thickness was 9.86 μm. Accordingly, the derived birefringence was 0.194. In addition, the energy dependent refractive index curves in three polarization directions, x, y and z, were calculated by DFT and are presented in Fig. S5.† The calculated birefringence value was 0.239, which is in good agreement with the experimental one, indicating that our measurement is reliable. The large birefringence values could ensure that the crystal realizes phase-matching in the UV region as short as possible. Besides, it is noteworthy that the birefringence of RbNa(HC₃N₃O₃)·2H₂O is comparable to those of typical commercial birefringent materials including CaCO₃ (0.172@589 nm)³⁴ and YVO₄ (0.226@590 nm),³⁵ and it is larger than those of the reported UV birefringent materials such as Ba₂Ca(B₃O₆)₂ (0.124@589 nm),³⁶ Na₃Ba₂(B₃O₆)₂F (0.115@532 nm),³⁷ Ca₃(BO₃)₂ (0.097@589 nm),³⁸ BBO (0.119@546 nm)³⁹ and Ca(BO₂)₂ (0.2471@193 nm).⁴⁰

UV-Vis diffuse reflectance spectra

The UV-Vis diffuse reflectance spectra are shown in Fig. S6.† Obviously, the title compound exhibited wide transparency windows, >95%, from 266 to 800 nm, indicating that it could generate coherent light above 266 nm through direct SHG without absorption loss. Additionally, according to the Kubelka–Munk function, the optical band gap of RbNa(HC₃N₃O₃)·2H₂O can be deduced as 5.10 eV.

NLO properties

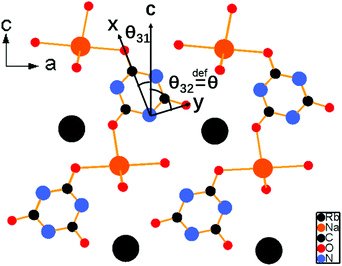
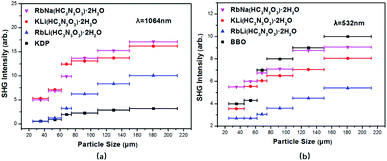
As shown in Fig. 4, the second-harmonic signals of RbNa(HC₃N₃O₃)·2H₂O were found to be about 5.3 times those of KDP at 1064 nm and 0.9 times those of BBO at 532 nm. Considering that the d₃₆ coefficient for KDP is 0.39 pm V⁻¹,⁴¹ the derived d_eff coefficient for RbNa(HC₃N₃O₃)·2H₂O is 2.07 pm V⁻¹. In addition, since RbNa(HC₃N₃O₃)·2H₂O is isostructural to MLi(HC₃N₃O₃)·2H₂O (M = K, Rb), the SHG measurements on MLi(HC₃N₃O₃)·2H₂O (M = K, Rb) were also performed under the same conditions as with RbNa(HC₃N₃O₃)·2H₂O. It is clear that the SHG signal of RbNa(HC₃N₃O₃)·2H₂O is larger than those of the isostructural MLi(HC₃N₃O₃)·2H₂O (M = K, Rb). Therefore, it is interesting to investigate the SHG difference among these isostructural compounds.

According to the anionic group theory,^42–44 the macroscopic SHG coefficients for these title compounds should originate from a geometrical addition of the microscopic second-order susceptibility of the planar (HC₃N₃O₃)²⁻ group. For these compounds, although only one crystallographically independent (HC₃N₃O₃)²⁻ group exists in the unit cell, it is clear that there are four kinds of (HC₃N₃O₃)²⁻ groups presenting different orientations due to the n slip plane and a slip plane of the space group. Because the four kinds of (HC₃N₃O₃)²⁻ groups exhibit opposite orientation in the a axis and b axis (see Fig. S2†), respectively, the contribution of NLO susceptibility mainly originates from the polarization of the (HC₃N₃O₃)²⁻ group along the c axis. It is noteworthy that though (HC₃N₃O₃)²⁻ groups present different orientations, they form the same angles θ₃₁ and θ₃₂ along the c axis (see Fig. 3). Since the (HC₃N₃O₃)²⁻ groups are approximately parallel to the a–c plane, we can define angle θ₃₂, reflecting the level of the (HC₃N₃O₃)²⁻ groups parallel to the c axis, as the rotational angles θ. The rotational angles θ of KLi(HC₃N₃O₃)·2H₂O, RbLi(HC₃N₃O₃)·2H₂O and RbNa(HC₃N₃O₃)·2H₂O are 72.34°, 70.57° and 75.45°, respectively.

Fig. 3 Rotational angles θ = θ₃₂ of RbNa(HC₃N₃O₃)·2H₂O.

Fig. 4 (a) SHG measurements of ground crystals of the title compounds with KDP as the reference at 1064 nm wavelength. (b) SHG measurements of ground crystals of the title compounds with BBO as the reference at 532 nm wavelength.

Further structural analysis of these crystals revealed that the different alignments among the (HC₃N₃O₃)²⁻ groups originated from the coordination behaviors of the counter cations, which can be distinguished by the ratios of ionic radii between the A⁺ (K⁺, Rb⁺) and B⁺ (Li⁺, Na⁺) cations. With the ratio ranging from 2.58 (Rb⁺/Li⁺) to 1.52 (Rb⁺/Na⁺), the rotational angle of (HC₃N₃O₃)²⁻ groups changed from 70.57° to 75.45°. These different arrangements resulted in different SHG effects due to the structural modulation of the anion groups. For the smallest ratios of ionic radii among the title compounds, all (HC₃N₃O₃)²⁻ groups in RbNa(HC₃N₃O₃)·2H₂O were parallel to each other, which contributed to the biggest SHG coefficient. These structures agreed well with the powder SHG experiment (see Table 2), which will be discussed in detail in a later section.

Table 2 NLO effects of RbLi(HC₃N₃O₃)·2H₂O, KLi(HC₃N₃O₃)·2H₂O and RbNa(HC₃N₃O₃)·2H₂O

Crystals	Radius ratio of cations (A^+/B^+)	Rotational angles (θ32) of (HC3N3O3)^2− (deg.)	Structural criterion C	Densities of the (HC3N3O3)^2− (N/V) (A^−3)	(N/V) × C (A^−3)	SHG coefficient (×KDP)
RbLi(HC3N3O3)·2H2O (2)	2.58	70.57	0.373	0.00533	0.00199	3.2
KLi(HC3N3O3)·2H2O (1)	2.34	72.34	0.469	0.00558	0.00262	5.1
RbNa(HC3N3O3)·2H2O (3)	1.52	75.05	0.569	0.00488	0.00277	5.3

---

Relationship between the structure and NLO properties

In order to investigate the relationship between the NLO properties and structure, the calculation methods reported in ref. 35 have been employed, which are described in detail in the ESI.†

Based on our previous studies,^45–48 one can know that the overall nonlinear coefficients of isomorphic compounds are highly dependent on the structural criterion C. Because the C factor was determined by the arrangement of the anionic group, one can establish a relationship between the structural criterion C and the rotational angle θ. In these examples, the arrangement of (HC₃N₃O₃)²⁻ groups gave the greatest contribution to g₃₃₃ (see Table 3), which revealed that the macroscopic SHG coefficient of the title compounds was mainly from the contribution of g₃₃₃. Furthermore, we calculated the structural criterion C by the following equation:

Table 3 Geometrical factors (g) of the title compounds

Crystals	g 311/N	g 322/N	g 333/N
1	0.353	0.112	−0.469
2	0.264	0.112	−0.373
3	0.453	0.123	−0.569

---

Further structural analysis revealed the key role of cations in modulating the arrangement of the (HC₃N₃O₃)²⁻ groups, which was strongly related to the cation size and variable coordination environment of the cations. According to the coordination environment, hexa-coordinated atoms K⁺ and Rb⁺ were classified into A⁺ type while Li⁺ and Na⁺ were classified into B⁺ type. With the decrease in the ratios of ionic radii between the A⁺ (K⁺, Rb⁺) and B⁺ (Li⁺, Na⁺) cations, the rotational angles of 2, 1 and 3 (70.57°, 72.34°, and 75.05°, respectively) increased gradually. The structural criterion C of 2, 1 and 3 (0.373, 0.469, and 0.569, respectively) increased gradually with the changes of the rotational angles. Considering the structural factor (C) and the density of the (HC₃N₃O₃)²⁻ group (N/V), the macroscopic SHG effect of 2 was the smallest among these three NLO crystals. Although 3 had the smallest density, the macroscopic SHG effect was still the largest due to its largest rotational angles. The relationship between the structure and NLO properties was in good agreement with the PSHG measurements (shown in Table 2).

Theoretical calculations

The calculated band structure is presented in Fig. S7.† RbNa(HC₃N₃O₃)·2H₂O exhibited a direct band gap of 4.70 eV at the G point, which was underestimated compared with the experimental results of 5.10 eV due to the underestimation of the band gap with the DFT methods. Therefore, the scissor operator values of 0.11 eV were applied to the subsequent SHG calculations.

The total and partial densities of states (DOS and PDOS) for the title compound are plotted in Fig. S8.† Because the optical properties mainly originate from the electronic transition between the states close to the Fermi level, only the upper region of the valence band (VB) and the bottom region of the conduction band (CB) were presented. It is clear that the VB spreading from about −2.4 eV to the Fermi level was mostly contributions of the O 2p and N 2p orbitals and the CB between 5.1 and 5.8 eV was mainly due to the C 2p orbital. This calculated result indicated that the optical properties of the title compound are primarily due to the (HC₃N₃O₃)²⁻ groups.

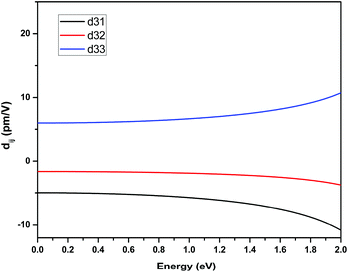
The space group of RbNa(HC₃N₃O₃)·2H₂O belongs to class mm2; three independent SHG tensor components (d₃₁, d₃₂ and d₃₃) should be taken into account. Theoretical values for the SHG coefficients were calculated using the “velocity-gauge” formula derived by Sipe et al. and are plotted in Fig. 5. The largest tensor component is d₃₃ of 6.98 pm V⁻¹ at a wavelength of 1064 nm (1.165 eV), which agreed well with the geometrical factor calculated by the anionic group theory. This further demonstrated that the (HC₃N₃O₃)²⁻ groups play a crucial role in the total SHG response.

Fig. 5 Calculated frequency-dependent SHG coefficient of RbNa(HC₃N₃O₃)·2H₂O.

Conclusions

A new mixed alkali isocyanurate, RbNa(HC₃N₃O₃)·2H₂O, has been successfully grown via a hydrothermal method. UV-Vis diffuse reflectance spectroscopy revealed that the title compound has a short UV cutoff edge of 243 nm. Additionally, linear and non-linear optical measurements showed that RbNa(HC₃N₃O₃)·2H₂O not only has a large birefringence of 0.194, but also a strong SHG effect that is 5.3 times that of KDP. These superior optical features suggest that RbNa(HC₃N₃O₃)·2H₂O may have promising applications in the UV region.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (Grant No 21975255, 51890862, U1605245, and 51425205), the National Key Research and Development Plan of Ministry of Science and Technology (Grant No 2016YFB0402104), the Strategic Priority Research Program of the Chinese Academy of Sciences (Grant No XDB20000000), the NSF of Fujian Province (2019J01020758) and the Youth Innovation Promotion Association CAS (303).

Notes and references

1. M. Razeghi, Proc. IEEE, 2002, 90, 1006.
2. V. Petrov, Prog. Quantum Electron., 2015, 42, 1.
3. Y. N. Xia, C. T. Chen, D. Y. Tang and B. C. Wu, Adv. Mater., 1995, 7, 79.
4. P. Becker, Adv. Mater., 1998, 10, 979.
5. X. L. Wang, L. K. Chen, W. Li, H. L. Huang, C. Liu, C. Chen, Y. H. Luo, Z. E. Su, D. Wu, Z. D. Li, H. Lu, Y. Hu, X. Jiang, C. Z. Peng, L. Li, N. L. Liu, Y. A. Chen, C. Y. Lu and J. W. Pan, Phys. Rev. Lett., 2016, 117, 210502.
6. X. Dong, L. Huang, C. Hu, H. Zeng, Z. Lin, X. Wang, K. M. Ok and G. Zou, Angew. Chem., 2019, 58, 6528–6534.
7. G. H. Zou, C. S. Lin, H. Jo, G. Nam, T. S. You and K. M. Ok, Angew. Chem., 2016, 128, 12257.
8. C. T. Chen, B. C. Wu, A. D. Jiang and G. M. You, Sci. China, Ser. B: Chem., Life Sci., Earth Sci., 1985, 28, 235.
9. S. Wang, N. Ye, W. Li and D. Zhao, J. Am. Chem. Soc., 2010, 132, 8779.
10. S. Zhao, J. Zhang, S. Q. Zhang, Z. Sun, Z. Lin, Y. Wu, M. Hong and J. Luo, Inorg. Chem., 2014, 53, 2521.
11. H. Yu, H. Wu, S. Pan, Z. Yang, X. Hou, X. Su, Q. Jing, K. R. Poeppelmeier and J. M. Rondinelli, J. Am. Chem. Soc., 2014, 136, 1264.
12. G. Cakmak, J. Nuss and M. Jansen, Z. Anorg. Allg. Chem., 2009, 635, 631.
13. X. Wang, Y. Wang, B. Zhang, F. Zhang, Z. Yang and S. Pan, Angew. Chem., Int. Ed., 2017, 56, 14119–14123.
14. Z. Fang, X. Jiang, M. Duan, Z. Hou, C. Tang, M. Xia, L. Liu, Z. Lin, F. Fan, L. Bai and C. Chen, Chem. – Eur. J., 2018, 24, 7856–7860.
15. M. Kalmutzki, M. Strobele, F. Wackenhut, A. J. Meixner and H. J. Meyer, Angew. Chem., Int. Ed., 2014, 53, 14260.
16. M. Kalmutzki, M. Strobele, F. Wackenhut, A. J. Meixner and H. J. Meyer, Inorg. Chem., 2014, 53, 12540.
17. F. Liang, L. Kang, X. Zhang, M.-H. Lee, Z. Lin and Y. Wu, Cryst. Growth Des., 2017, 17, 4015–4020.
18. D. Lin, M. Luo, C. Lin, F. Xu and N. Ye, J. Am. Chem. Soc., 2019, 141, 3390.
19. N. Wang, F. Liang, Y. Yang, S. Zhang and Z. Lin, Dalton Trans., 2019, 48, 2271–2274.
20. X. Meng, F. Liang, J. Tang, K. Kang, W. Yin, T. Zeng, B. Kang, Z. Lin and M. Xia, Inorg. Chem. Front., 2019, 6, 2850–2854.
21. X. Hao, M. Luo, C. Lin, D. Lin, L. Cao and N. Ye, Dalton Trans., 2019, 48, 12296–12302.
22. X. Meng, F. Liang, K. Kang, J. Tang, Q. Huang, W. Yin, Z. Lin and M. Xia, Dalton Trans., 2019, 48, 9048–9052.
23. X. Meng, F. Liang, K. Kang, J. Tang, T. Zeng, Z. Lin and M. Xia, Inorg. Chem., 2019, 58, 11289–11293.
24. X. Meng, F. Liang, J. Tang, K. Kang, Q. Huang, W. Yin, Z. Lin and M. Xia, Eur. J. Inorg. Chem., 2019, 2019, 2791.
25. G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Crystallogr., 2008, 64, 112–122.
26. A. L. Spek, J. Appl. Crystallogr., 2003, 36, 7–13.
27. J. Tauc, Mater. Res. Bull., 1970, 5, 721–729.
28. P. Kubelka and F. Munk, Z. Tech. Phys., 1931, 12(1), 886–892.
29. S. K. Kurtz and T. T. Perry, J. Appl. Phys., 1968, 39, 3798–3813.
30. S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. J. Probert, K. Refson and M. C. Payne, Z. Kristallogr., 2005, 220, 567–570.
31. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
32. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192.
33. R. W. Boyd, Nonlinear Opt., 1992, 21.
34. G. Ghosh, Opt. Commun., 1999, 163, 95–102.
35. L. G. DeShazer, Proc. SPIE, 2002, 10, 4481.
36. Z. Jia, N. Zhang, Y. Ma, L. Zhao, M. Xia and R. Li, Cryst. Growth Des., 2017, 17, 558–562.
37. X. Wang, M. Xia and R. K. Li, Opt. Mater., 2014, 38, 6–9.
38. S. Zhang, X. Wu, Y. Song, D. Ni, B. Hu and T. Zhou, J. Cryst. Growth, 2003, 252, 246–250.
39. R. Appel, C. D. Dyer and J. N. Lockwood, Appl. Opt., 2002, 41, 2470–2480.
40. X. Chen, B. Zhang, F. Zhang, Y. Wang, M. Zhang, Z. Yang, K. R. Poeppelmeier and S. Pan, J. Am. Chem. Soc., 2018, 140, 16311–16319.
41. R. C. Eckardt, H. Masuda, Y. X. Fan and R. L. Byer, IEEE J. Quantum Electron., 1990, 26, 922–933.
42. N. Ye, Q. X. Chen, B. C. Wu and C. T. Chen, J. Appl. Phys., 1998, 84, 555–558.
43. C. T. Chen, Y. C. Wu and R. K. Li, Int. Rev. Phys. Chem., 1989, 8, 65–91.
44. C. Chen, Sci. Sin., 1979, 22, 756–776.
45. Y. Song, M. Luo, C. Lin and N. Ye, Chem. Mater., 2017, 29, 896–903.
46. G. Yang, G. Peng, N. Ye, J. Wang, M. Luo, T. Yan and Y. Zhou, Chem. Mater., 2015, 27, 7520–7530.
47. M. Luo, F. Liang, Y. Song, D. Zhao, F. Xu, N. Ye and Z. Lin, J. Am. Chem. Soc., 2018, 140, 3884.
48. G. Zou, N. Ye, L. Huang and X. Lin, J. Am. Chem. Soc., 2011, 133, 20001.

---

Footnote

† Electronic supplementary information (ESI) available. CCDC 1953902. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c9qi01198f

---