Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A review of fibrous materials for soft body armour applications
Unsanhame Mawkhlieng
 a,
Abhijit Majumdar
*a and
Animesh Laha
ab
a,
Abhijit Majumdar
*a and
Animesh Laha
ab
aDepartment of Textile and Fibre Engineering, Indian Institute of Technology Delhi, India 110016. E-mail: majumdar@textile.iitd.ac.in
bBusiness Development Division, Reliance Industries, Mumbai, India
First published on 8th January 2020
Abstract
A critical review on the factors affecting the impact resistance behaviour of soft body armour is presented here. The effect of several material and structural parameters of fibrous assemblies used in soft armour is dealt with in depth. The standards of performance evaluation of soft body armour and modes of energy absorption are elucidated. The paper also reviews different approaches resorted to by the researchers to enhance the ballistic or stab resistance performance of these soft body armour materials. These approaches include surface treatments and modifications of the base material to increase yarn to yarn friction as well as implementation of 3D woven fabrics to enhance structural integrity. Among these, the effect of shear thickening fluid (STF) is discussed extensively. The review concludes with the future directions of research in the area of soft body armour.
1 Introduction
Body armour is a protective gear which is used to protect the human body against attacks of various kinds of sharp objects or projectiles. Body armour is broadly classified into two categories, namely hard body armour and soft body armour.1 Hard body armour, with protection of levels III and IV according to the National Institute of Justice (NIJ) standard,2 is reinforced with metal, ceramic (B4C) or fibre based composite plates within layers of fabric. They are used by military personnel in high risk operations for protection against high speed bullets or projectiles fired from weapons like AK-47s. They are heavy and rigid and thus, they restrict wearer's movement. In contrast, soft body armour is made of multiple layers of high-performance fabrics, making it lighter in weight and more flexible. Police, security personnel, riot officers, etc., use this type of armour against low velocity projectile attacks from handguns, pistols, shotguns, etc., for lower levels (NIJ levels II-A, II, and III-A) of ballistic protection.2,3 In general, 20–40 layers of woven or unidirectional fabrics, made from high performance fibres, are stitched together to prepare the soft body armour panels. Therefore, they are still bulky and heavy enough to restrict the agility of the wearer. Consequently, these limitations present several challenges when it comes to reduction of armour weight, effective improvement in terms of handling multiple ballistic shots and back face signature or BFS reduction.4The history of body armour materials is as old as human civilization. Their evolution with time has been briefly reviewed by Yadav et al.5 First generation soft body armour was prepared from silk by the medieval Japanese.6 Used during the World War I, this armour provided good protection against very low velocity projectiles (up to ≈120 m s−1) but not so, against projectiles having higher velocity (≈180 m s−1). Second generation soft body armour, prepared from nylon flak,7,8 was introduced during the World War II. Although it proved to be a very good barrier against munition fragments, it, however, failed against most of the pistol and rifle threats. Besides, it was bulky and heavy. The next generation of soft body armour development started with the invention of high-performance p-aramid fibre (Kevlar®) by DuPont, back in the 1960s. Presently, high-performance fibre based soft body armour are used as routine wear by police officers and security personnel to achieve protection against low speed ballistic threats including hand grenades, spike attacks and ice picks. High performance fibres used for such purposes include p-aramid (Kevlar®, Technora®, Twaron® etc.), ultra-high molecular weight polyethylene or UHMWPE (Dyneema®, Spectra® etc.), poly p-phenylene benzobisoxazole or PBO (Zylon®), polyhydroquinone-diimidazopyridine or PIPD fibres (M5), etc.9–11 The essential properties of the above fibres are low density (0.97 to 1.6 g cm−3), high tenacity (2.5–5.8 GPa) and high modulus (70–270 GPa).12 Several attempts have been made by fibre manufacturers and material researchers to develop new materials and improved structures so that the efficacy of soft body armour can be enhanced. Researchers have also explored the possibility of using multi-axial warp knitted fabrics and 3D woven fabrics in soft body armour.13,14 In the last two decades, the idea of using shear thickening fluid (STF) to improve the energy absorption capability of soft body armour has interested many researchers. The pioneer work in this area was done by Lee et al.15–17 in the early 2000s. They demonstrated that the impact resistance of woven fabrics can be enhanced significantly with STF treatment. Some reviews on body armour systems,1 ballistic protective clothing,12 evolution of soft body armour18 and body armour for stab and spike protection19 have been presented by researchers to provide a proper understanding of the field. This review presents the material (fibre) and structural (yarn and fabric) parameters influencing impact energy absorption in Section 2. Standards for evaluation of soft body armour is shown in Section 3. Mechanism of impact energy absorption is presented in Section 4. A detailed review of approaches to enhance the performance of soft body armour materials is highlighted in Section 5. Section 6 deals with some of the future trends in soft armour development.
2 Parameters influencing impact energy absorption
Arora and Ghosh18 collectively summarised the various parameters which contribute to the impact performance of soft armour panel. They classified these parameters into four categories – material parameters, structural parameters, projectile parameters and testing parameters. Material parameters include fibre density, fibre tenacity, fibre modulus and yarn to yarn friction. Structural parameters include yarn twist, weave, thread density, number of layers, etc. Projectile related parameters such as mass, shape and velocity, and testing related parameters such as shot location, number of shots, angle at which the bullet strikes the target and boundary conditions can affect the ballistic performance greatly. However, in-depth discussion of projectile and testing parameters is out of the scope of this review. Material and structure related parameters are discussed in the following section.2.1 Material properties
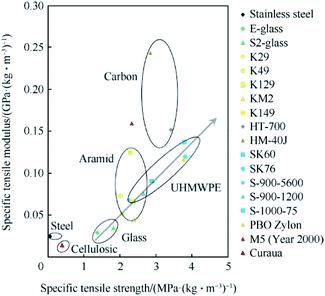 | ||
| Fig. 1 Relationship between specific tensile modulus and specific tensile strength of high-performance fibres1 (this figure has been reproduced from ref. 1 with permission from Elsevier). | ||
The ballistic performance of a woven fabric may be evaluated from its single yarn component.25 When a single fibre is hit by a projectile transversely, two waves simultaneously propagate-one, longitudinally and the other, transversely as shown in Fig. 2. While the longitudinal waves travel at the speed of sound, the transverse waves travel at a much slower speed. This is because, as the impact progresses, the yarn deflects itself in the direction of impact. The velocity of the longitudinal strain wave generated in a fibre due to impact can be determined by using eqn (1).
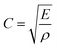 | (1) |
Transverse stress wave speed (u), on the other hand, is dependent on the tensile strain (ε) of the filament or yarn during impact and is related to the longitudinal stress wave velocity. Mathematically, it is given by eqn (2).
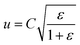 | (2) |
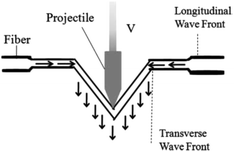 | ||
| Fig. 2 Pictorial representation of projectile impacting a single yarn6 (this figure has been reproduced from ref. 6 with permission from Elsevier). | ||
Cunniff,25 deduced a dimensionless fibre property U (defined as the product of specific fibre toughness and its strain wave velocity) as given in eqn (3).
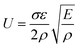 | (3) |
This equation shows that for better impact resistance, tensile strength and modulus of the fibre should be high whereas fibre density should be low. Besides, the fibres intended for body armour applications should also have properties like low moisture retention, high resistance to heat, high limiting oxygen index, etc.
According to Zeng et al.,30 coefficient of friction can be divided into three distinct ranges, namely, low (μ = 0.0–0.06), moderate (μ = 0.06–0.2) and high (μ = 0.2–1).30 Very low coefficient of friction results in poor integrity of the structure and thus, the projectile resisting power is reduced. It was observed that the increase of energy absorption is highly ‘sensitive’ to this given low range of friction, i.e., even with slight increase in friction coefficient, the energy absorption increased markedly. Moderate coefficient of friction (μ = 0.2) caused maximum energy absorption, while at coefficient of friction higher than 0.2, the energy absorption tended to fall, as shown in Fig. 3, due to localised stress concentration. Thus, the role and amount of friction can be seen to be very influential in energy absorption during ballistic impact.
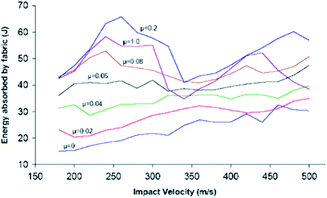 | ||
| Fig. 3 Effect of yarn to yarn friction on energy absorption during impact30 (this figure has been reproduced from ref. 30 with permission from John Wiley and Sons). | ||
With this understanding in mind, many researchers worked towards improving the friction by using resins, polymeric coatings and additives such as nanostructures for more energy absorption.31 As a matter of fact, the use of STF itself, as believed by many researchers32,33 helps in improved performance majorly through friction enhancement. Nanorods of metal oxides are also used to intensify friction between yarns. The development and use of such nanorods is described in greater detail in Section 5.7. The work by Gawandi et al.34 on the influence of polymeric coating on tow pull-out response of Kevlar showed enhanced friction, and hence, pull-out force. Here, it is important to note that relative humidity can greatly influence the coefficient of friction of hydrophilic fibres. For hydrophobic fibres, water can act as a lubricant, reducing the yarn pull-out force. Similarly, softening treatments drastically reduce the yarn to yarn friction.35,36
2.2 Structural parameters
For ballistic applications, fabrics must have an optimum level of thread density. Very tight fabrics will cause the yarns to deteriorate during weaving, while too loose a construction will not be able to stop the bullet from piercing through; a phenomenon commonly called as ‘wedge through’. In fact, it has been reported that fabric cover should have a value ranging from 0.6 to 0.95 for effective ballistic performance.48,49 Bajaj and Sriram12 reviewed that tight structures woven from yarns consisting of large number of filaments with finer denier are beneficial for efficient ballistic protection, particularly for finer projectiles. Laha et al.45 reported the influence of fabric construction for ballistic protection and found that jammed fabrics inhibited movement of yarns during impact, consequently, preventing the critical shear rate, needed for STF, from being achieved.
2.3 Number of fabric layers and stitching
A single layer of high-performance fabric is insufficient to ensure protection against high velocity impact.18 Therefore, a soft body armour against high velocity impact is generally comprised of several layers of high-performance fabrics sewn or stitched together.39 Expectedly, as the number of layers increases, the trauma depth and diameter decrease. The supportive findings of Karahan et al.53 also showed that with the increase in the number of layers (from 20 to 32), trauma depth (by 35.4%) and trauma diameter (by 12.7%) decreased (Fig. 4).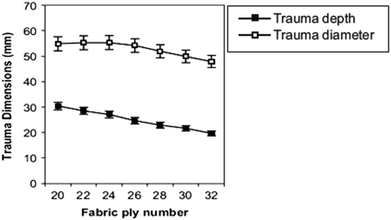 | ||
| Fig. 4 Effect of number of fabric layers on the trauma depth and diameter53 (this figure has been reproduced from ref. 53 with permission from Elsevier). | ||
The requirement of multiple layers necessitates adhesion or stitching of layers for considerable thickness. This extra adhesion or stitching process increases the stiffness of the fabric assembly which reduces the mobility of wearer. Although it is known that stitching partly damages the yarns55 and generates local stress-concentrated points on the fabric, however, stitching also plays the important role of binding the layers together, thus preventing delamination from occurring. An experiment conducted by Ahmad et al.56 on unstitched and stitched neat and natural rubber coated fabrics showed that, in general, stitched fabrics performed better than the unstitched ones. Stitch patterns like one inch field diamond, two inches field diamond, diagonal and perimeter stitching were used, and except for the one inch diamond stitched fabrics, unstitched samples showed lower ballistic limit. On the other hand, two inches field pattern gave the highest ballistic limit.
2.4 Orientation of fabric layers
As discussed in the previous section, multiple layers of high-performance fabric are required to get enough protection against high velocity impact. Stacking of multiple layers to make a single panel can be done in different ways. As shown in Fig. 5, Chen et al. and Wang et al.57,58 carried out detailed study on the effect of orientation of fabric laying on impact energy absorption. They found that impact energy absorption was always lower when all the fabric layers were aligned in 0°. The highest impact energy absorption was obtained for two, three, four and eight layered fabric panels using the angle of orientations [0/45], [0/30/60], [0/22.5/45/67.5] and [(0/22.5/45/67.5) × 2], respectively. Overall 11.4 to 18.5% increase in the impact energy absorption was obtained by using different orientations of fabrics in different layers. This is because as the different fabric layers are oriented along different axes, the assembly approaches isotropy. Post impact, the pyramid formed has a quadrilateral base because of the two principal axes along which the diagonals of the base align. Hence, if there are more than two sets of perpendicular axes, as in the case of a multi-layered fabric with angle ply orientation, the base may tend to be circular, so that the pyramid approximately becomes a cone and hence, the energy absorption increases.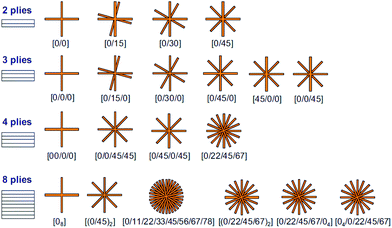 | ||
| Fig. 5 Ply orientations of ballistic panels57 (this figure has been reproduced from ref. 57 with permission from Elsevier). | ||
3 Standards for body armour evaluation
There are different standards for evaluating the performance of body armour. Standards form National Institute of Justice (NIJ), USA: NIJ 0101.06, NATO STANAG 4569, Home Office Scientific Development Branch (UK), European Ballistic Standards (EU), GOST Ballistic Standards (Russia), German SCHUTZKLASSE standard, International Ballistic Standards, are some of the available options. However, NIJ 0101.06 (ref. 2) is the most widely used standard for body armour evaluation. According to this standard, body armour is categorised into five classes based on the level of protection they provide – IIA, II, IIIA, III and IV. Type IIA, II and IIIA provide lower level of protection corresponding to different projectile type and mass and different projectile velocities of 355 m s−1 ± 9 m s−1 to 448 ± 9 m s−1. A new unworn armour is subjected to higher velocity as compared to a conditioned armour. Type III and IV, however, provide protection against projectiles having higher velocity of 847 m s−1 ± 9.1 m s−1 and 878 m s−1 ± 9.1 m s−1, respectively. Unlike type IIA, II and IIIA, both new and conditioned type III and IV armour are subjected to the same projectile velocity. Additionally, the formers are subjected to two test rounds, whereas the latter, to one. The number of shots per panel in all cases is standardised to 6. NIJ has also come up with a revised version NIJ 0101.07 which has been propounded for scrutiny and comments.3 Recently, the Bureau of Indian Standards has published a standard for ballistic evaluation (IS17051:2018), categorised in six levels (Level 1 to Level 6) based on the bullet weight, type and velocity.60 The permissible BFS as per the requirement of Indian army is 25 mm.61During ballistic evaluation, energy absorption by the test panel can be determined by using pre-impact and post-impact residual velocities of the projectile which are measured with the help of two chronographs positioned before and after the panel being tested (Fig. 6). This method is useful in case of complete perforation of the test panel by the projectile. The energy absorbed by the test panel is calculated by using eqn (4).
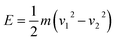 | (4) |
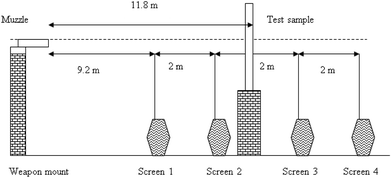 | ||
| Fig. 6 Impact velocity determination using chronograph59 (this figure has been reproduced from ref. 59 with permission from Elsevier). | ||
V0 and V50 are also used as parameters to evaluate the performance of body armour. V0 and V50 signify the bullet velocities at which the probability of penetration is 0 and 0.5, respectively. After firing a series of bullets, the bullet with the minimum velocity which perforates the armour and the bullet with the maximum velocity which is stopped by the armour are taken for consideration. The velocity for 0.5 probability of perforation is then determined normally by considering at least two cases of complete penetration and two cases of stoppage (Fig. 7).
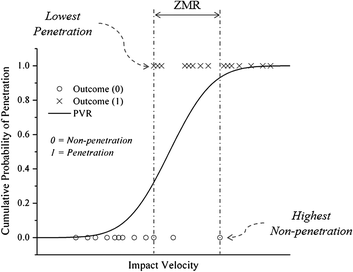 | ||
| Fig. 7 Determination of V50 (ref. 63) (this figure has been reproduced from ref. 63 with permission from Elsevier). | ||
Another important aspect of soft armour evaluation is blunt trauma or back face signature (BFS) which is usually measured for a non-perforation type impact.62 When a bullet is stopped by the armour, a trauma or crater is formed on the backing material with a certain diameter, depth and volume which represent the transmission of energy to the back side of armour. Therefore, after ballistic testing, the depth, diameter and volume of trauma is measured as shown in the Fig. 8.53 According to NIJ standard, the maximum permissible BFS is 44 mm. For measuring the trauma, the test panel is backed or supported with an easily deformable substance. Clay backing (Roma Plastilina) readily supports post-test linear and volumetric measurements and therefore, it is popularly used for blunt trauma evaluation. Other resilient materials, such as ballistic gelatin do not retain the deformation after impact. Therefore, in such cases, the trauma should be characterised with photographic equipment, force gauges, etc.64
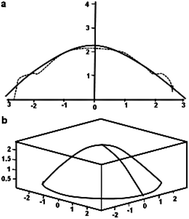 | ||
| Fig. 8 Evaluation of back face deformation. (a) Comparison of measured and fitted curves, (b) view of 3-D model of trauma obtained by a curve fitted using spline curve fitting method53 (this figure has been reproduced from ref. 53 with permission from Elsevier). | ||
4 Energy absorption mechanisms of soft body armour
When a high-performance fabric is hit by a projectile, energy is absorbed through various mechanisms, depending on both material and projectile parameters.12,59,65–67 During impact, the bullet can either completely or partially pierce through or can be entirely halted by the target. The fabric target absorbs energy through the following mechanisms:65,66,68• Yarn decrimping
• Fibre and yarn extension
• Yarn pull-out
• Fibre and yarn rupture
The relationships between these mechanisms and the ultimate ballistic performance of high-performance fabrics is yet to be understood fully. When a bullet strikes a fabric, crimp removal, yarn extension, pyramid formation by primary and secondary yarns, fibrillation and fibre breakage happens in sequence absorbing significant amount of energy. Fibre fusing is also observed in case of thermoplastic materials. It is generally accepted that yarn pull-out (Fig. 9) is a consequence of low yarn to yarn friction17,69,70 and hence, yarn pull-out test is a good step towards understanding the role of friction during impact.
 | ||
| Fig. 9 Fabric failure mechanisms during impact (a) yarn pull-out and (b) fibre and yarn rupture68 (this figure has been reproduced from ref. 68 with permission from Elsevier). | ||
4.1 Yarn pull-out
The earliest studies on yarn pull-out was reported by Sebastian et al. on plain woven cotton fabrics.71,72 In a typical yarn pull-out test, single or multiple yarns are pulled out from a high-performance woven fabric to measure of yarn to yarn friction. Fig. 10 shows two distinct regions in a yarn pull-out force vs. displacement graph, namely static friction region or crimp removal region and dynamic friction region or stick-slip region. In Region I, with the application of pull-out force, the yarn starts to straighten via the irreversible process of crimp removal. The peak force is reached when yarn crimp becomes zero. Thereafter, dynamic friction comes into play in the ‘yarn translation’ region which witnesses stick-slip effect.28,73 ‘Stick’ occurs when the yarn being pulled out is held by the transverse yarns, while ‘slip’ takes place when the yarn slides over the transverse yarns35,70,74–77 as depicted in Region II and III of Fig. 10. The plateau region in Region II is where the pulled yarn begins to slide relative to the fabric and the Region III is where the yarn starts to disengage from the fabric.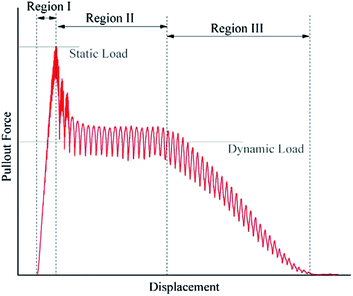 | ||
| Fig. 10 Pull-out response of a single yarn from a woven fabric36 (this figure has been reproduced from ref. 36 with permission from Elsevier). | ||
There are various factors which influence yarn pull-out results. The physical state, linear density, surface texture and surface treatment of the yarn play great roles during yarn pull-out. Other influencing factors are sample dimensions and thread density. Martinez et al.73 carried out friction and wear experiment on three variants of Kevlar fabrics and found that the static coefficient of friction (defined as the ratio of frictional force to contact force) was the highest in the tightest fabric sample, i.e., the sample with the highest thread density. Similarly, the pull-out force, defined in terms of frictional force per yarn crossover and frictional force per unit length of the yarn drawn out, were found to be highest for the same densest sample, clearly indicating that pull-out force increases as the thread density increases.
On a similar but different note, Bilisik et al.77 conducted single and multiple yarn pull-out experiments on Twaron fabrics and found supporting results in which the fabric sample with the highest thread density showed the highest pull-out force for single yarn pull-out.
However, for multiple yarn pull-out, the same translation was not observed because with the denser fabric, excess fibre breakage was observed. Bazhenov28 and Bilisik et al.77 showed that pull-out force also increased with increasing specimen length and in general, the same trend was also observed with increasing sample width. Weave, out-of-plane deformation, shear and transverse tension also influence yarn pull-out force. A two-dimensional finite element model developed by Dong and Sun74 also showed that thread density, yarn waviness, yarn friction and modulus are factors affecting yarn pull-out force. The parametric study gave rise to the simple eqn (5) that can be used for a fair estimation of pull-out force:
| F = C × TD4 × D2 × M × W × Fc | (5) |
Pull-out force decreases with the increase in pull-out speed, the reduction being higher for static pull-out loads than it is for dynamic pull-out loads.36 Pull-out force and crimp extension are higher in case of multiple yarn pull-out tests.
5 Approaches to improve the impact resistance
Researchers have explored different approaches to improve the impact resistance of woven fabrics as soft body armour material. Among these approaches, use of natural latex, use of shear thickening fluid (STF), fabric surface modification by developing nanorods of metal oxides and use of 3D woven fabrics are the few important ones. The idea of using STF or even surface modification is to enhance structural integrity through friction. On the other hand, the purpose of employing 3D woven structures is to enhance through-thickness mechanical properties. Because 2D woven structures are devoid of components in the Z-direction, hence, the load bearing capacity along the thickness can be improved by making use of 3D woven structures. The aspect of 3D woven fabrics and their role in ballistic applications will be discussed later in more detail.5.1 Use of latex/natural rubber coating
Ahmad et al.78 coated the Twaron fabrics with high modulus pre-vulcanised natural rubber by simple dipping technique. The ballistic performance of the all-neat samples was inferior to that of the composite system of neat and coated fabrics. Additionally, the number of layers penetrated by the projectile was less in the case of coated samples for the same projectile velocity. A related work done by Roy et al.79 also showed similar findings, besides showing that the energy absorption increased with increasing add-on percentage. Hassim et al.80 carried out puncture resistance test of unidirectional fabric after single dipping (SD), double dipping (DD) and triple dipping (TD) of samples with oily and dry probe and observed that the puncture resistance increased with increasing number of dipping, i.e., with increasing amount of natural latex.5.2 Use of shear thickening fluids (STF)
The application of shear thickening fluid (STF) for ballistic protection has attracted several research groups in recent years. Gürgen et al.32 has thoroughly reviewed the applications of STF for protective applications and therefore, the present work will only briefly describe this aspect. STF has been explored and used for low velocity impact applications,81,82 stab and spike protection83–92 as well as for high velocity ballistic impact applications.17,93,94 Shear thickening fluid (STF) is a non-Newtonian fluid having two phases, namely dispersed phase and dispersion medium. Initially with the application of shear, STF shows shear thinning behaviour. However, after achieving a particular shear rate, called critical shear rate, viscosity increases abruptly and the liquid suspension attains an almost solid like state.15,21,94–99 Fig. 11 shows the phenomenon of shear thickening. The dispersed phase of STF consists of nano-scale or sub-micron particles of silica, calcium carbonate or polymethylmethacrylate (PMMA), etc., while the dispersion medium of STF can be water, silicon oils, polyethylene glycol (PEG), polypropylene glycol (PPG) or 1-butyl-3-methylimidazolium tetrafluoroborate.100–105 In most of the reported literature, researchers have used colloidal silica nanoparticles or fumed silica as dispersed phase and PEG as dispersion medium.17,106–111 The choice of PEG is probably due to its non-toxicity, ease of handle and thermal stability. Sonochemical technique, high speed homogenization, use of magnetic stirrer, ultrasound sonication (using water bath or probe), etc., have been used by researchers for proper dispersion of particles in STF by breaking intermolecular interactions of nano particles.108,112–114 The phenomenon of shear thickening, fabrication method, rheological response and applications of STF have also been reviewed by Ding et al.115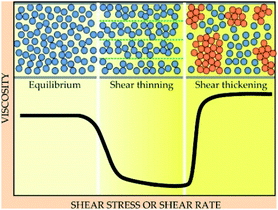 | ||
| Fig. 11 Schematic representation of shear thickening behaviour96 (this figure has been reproduced from ref. 96 with permission from American Institute of Physics). | ||
Hasanzadeh et al.110 and Srivastava et al.21 also reviewed the significance of STF and its influence on ballistic, stab, impact and puncture resistance of high performance textile materials.
5.3 Theories of shear thickening
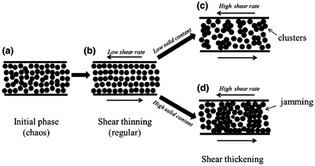
A few theories, namely, order–disorder transition (ODT), hydrocluster theory, jamming and dilation theory have been proposed by researchers to explain the shear thickening behaviour.At low shear rate, Brownian motion is prevalent and hence the particles are in equilibrium as shown in Fig. 12(a). With the application of very low shear rate, particles organise themselves in various layers resulting in shear thinning as shown in Fig. 12(b). On further increase in shear rate, formation of self-organised microstructures takes place which are bonded by hydrodynamic forces. These microstructures, known as hydroclusters, are a small, irregularly shaped clustered mass composed of particles which are momentarily compressed together. The particles within the momentarily formed hydroclusters itself are so minutely spaced that the assembly as a whole is incompressible, rendering the solid like behaviour that governs the shear thickening phenomenon. As a result shear thickening is obtained as shown in Fig. 12(c).104,123–127 Cheng et al.128 was able to visualise the formation of hydroclusters during shear thickening in concentrated colloidal suspensions with the help of fast confocal microscopy. This theory is able to predict the onset of shear thickening for a wide range of continuous and discontinuous shear thickening fluids, although simulations are not able to produce the same level of high viscosity observed in experiments.
Thereafter, explanation of shear thickening as a mechanism leans towards the hydrocluster theory. However, more recently, dilatancy in the volumetric sense, as a possible explanation to shear thickening was proposed by Brown and Jaeger.131 When volumetric dilation of a granular shear flow is confined by boundary conditions, internal stresses develop in the system. Equal and opposite forces are then transmitted to the particles which then come in contact with each other, contributing to the frictional contact forces. This, in accordance to the latest theory of contact rheology, contributes to the abrupt rise in viscosity of the system under high shear rate.131,132
5.4 Parameters influencing shear thickening behaviour
It has been observed that the behaviour of shear thickening fluid primarily depends on particle related parameters like solid content, particle aspect ratio, particle shape, particle size and its distribution, and so on. Other parameters like temperature and pH and carrier fluid properties are also influential.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) diameter) also critically affects the shear thickening behaviour of concentrated colloidal suspensions. It has been observed that with increase in particle aspect ratio, critical shear rate reduces, and viscosity increases probably because of the manner in which these particles interact. Besides, the minimum solid content required to achieve shear thickening also decreases with increasing particle aspect ratio. Wetzel et al.135 used spherical silica particles and CaCO3 particles of different aspect ratios ranging from 2
diameter) also critically affects the shear thickening behaviour of concentrated colloidal suspensions. It has been observed that with increase in particle aspect ratio, critical shear rate reduces, and viscosity increases probably because of the manner in which these particles interact. Besides, the minimum solid content required to achieve shear thickening also decreases with increasing particle aspect ratio. Wetzel et al.135 used spherical silica particles and CaCO3 particles of different aspect ratios ranging from 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 to 7
1 to 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and found that as the aspect ratio increases, requirement of solid volume fraction to reach the critical shear rate decreases.
1 and found that as the aspect ratio increases, requirement of solid volume fraction to reach the critical shear rate decreases.Particle shape has considerable influence on flow properties of concentrated colloidal suspensions. Although it is well established that particle shape is an important influential parameter as far as shear thickening is concerned, it is however, unclear as to what contributes to the effect. Whether it is the shape on its own that plays a role, or the combined effect of shape and other parameters such as size, volume fraction and so on, is still not fully understood. However, in general, it is observed that anisotropic particles more readily give shear thickening, and hence, suspensions with rod shaped or needle shaped particles have greater propensity for shear thickening behaviour than particles with plate, grains or sphere shapes.110,125,135
Another factor which has decisive influence in determining the critical shear rate and peak viscosity of STF is particle size. Barnes125 and Lee et al.136 showed that as particle size increases the onset of shear thickening moves towards lower shear rate (Fig. 14). This is probably because for a given volume fraction, the number of smaller size particles increases and so is the interaction among these particles.
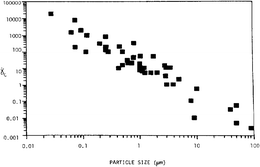 | ||
| Fig. 14 Effect of particle size on shear thickening behaviour of STF125 (this figure has been reproduced from ref. 125 with permission from AIP Publishing). | ||
Particle size distribution also impacts shear thickening behaviour. A wide continuous particle size distribution causes the critical shear rate to rise, while a narrower distribution causes the thickening to occur at lower shear rates.32
5.5 Effect of STF on failure mechanism of fabrics
The mechanism of STF–fabric interaction during impact has long been debated. Unfortunately, thorough understanding of the exact role of STF to enhance the impact resistance of high-performance fabrics is still quite obscure. Some researchers argue that increased friction is responsible for enhanced impact performance,32,33,90,147 while others believe that the inherent shear thickening phenomenon also plays a vital role in energy absorption.16,82,83,137,148–150In their attempt to understand the STF–fabric interaction mechanism, Majumdar et al.68 studied the stage-wise deformation pattern on neat and STF treated fabrics. Three distinct zones were observed in the force/energy plots against time as depicted in Fig. 18. Zone 1 or elastic zone was found to be linear in both untreated and STF treated fabrics, though longer in time in the case of the latter. Zone 2 or slippage/breakage zone was different for untreated and STF treated fabrics. For untreated fabrics, there was a fluctuation of force due to slippage and breakage of yarns which precluded any further increase in force in this zone. On the contrary, STF treated fabrics showed further increase in force in zone 2. The STF treated fabrics showed lesser yarn pull-out and more contribution from secondary yarns in energy absorption during impact. It was also observed that zone 1 and 2 collectively contributed about 40% of the total energy absorption in untreated fabrics and about 80% in STF treated fabrics. For untreated fabrics, zone 3 or failure zone was longer as compared to that of STF treated fabrics due to yarn pull-out in case of the former.
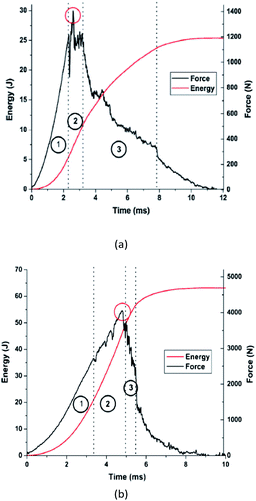 | ||
| Fig. 18 Force vs. time and energy vs. time graphs of (a) untreated and (b) STF treated Kevlar fabrics68 (this figure has been reproduced from ref. 68 with permission from Elsevier). | ||
A study by Kalman et al.137 showed that yarn pull-out is the most prevalent mode of failure for neat and PMMA treated fabrics. However, fibre and yarn rupture are the primary modes of failure and energy absorption for both silica-dry and silica-STF treated fabrics (Fig. 19).
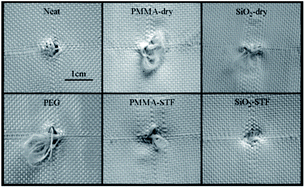 | ||
| Fig. 19 Failure modes of fabric during impact137 (this figure has been reproduced from ref. 137 with permission from American Chemical Society). | ||
5.6 Chemical modification of silica nanoparticles
Silica particles in nano dimension are very active particles. Thus, it is very difficult to obtain very high weight fraction of silica in STF due to particle aggregation. Surface modifications can be done to improve the dispersion of silica nanoparticles in dispersing medium. For example, the use of silane coupling agents is very common. They have a unique bi-functional structure with one group capable of reacting with silica and the other group compatible with the dispersing medium151 The bonding between the silane and the silica surface changes the hydrophilic surface into a hydrophobic one. The Si–O–Si–C moiety formed by this reaction not only provides a chemically stable attachment to the silica matrix, but also allows further modification with high chemical stability.152 Radhakrishnan et al.153 used polymer grafting technique to modify the surface of the silica nanoparticles (Fig. 20). Yu et al.109 used ethylene glycol (EG) as the surface modifying agent for silica (Fig. 21).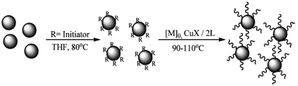 | ||
| Fig. 20 Surface modification of silica nanoparticles using polymer grafting technique153 (this figure has been reproduced from ref. 153 with permission from The Royal Society of Chemistry). | ||
 | ||
| Fig. 21 Reactions of silica nanoparticles with EG109 (this figure has been reproduced from ref. 109 with permission from Springer Nature). | ||
5.7 Use of nanorods of metal oxides
Surface modification by generating zinc oxide (ZnO) nanorods on high performance fabrics, a technique used to increase interfacial strength, have been explored by various researchers.156–162 It becomes clear from the works of Galan et al.,156 Ehlert et al.,159 Majumdar et al.161 and Hwang et al.155,160 that ZnO nanostructures developed on the surface of high-performance fabrics help to improve both the yarn pull-out and impact energy absorption, due to improved inter-yarn friction, without any deterioration in tensile strength. Various methods can be adopted to grow nanostructures on high performance fabrics. However, the most sought after one is the hydrothermal method163,164 because it is relatively simple and causes minimum damage to the fibre due to low processing temperature. Fig. 22(a) shows the growth of ZnO nanorods on Kevlar fabric surface whereas Fig. 22(b) presents the SEM images of ZnO nanorod coated Kevlar fabric.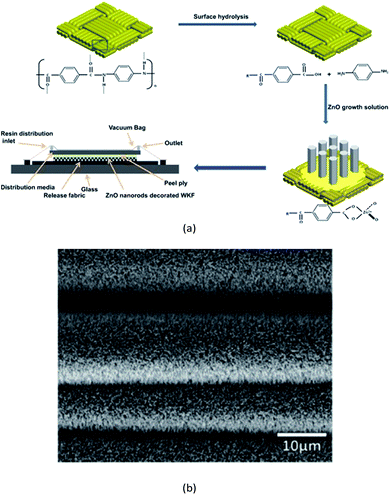 | ||
| Fig. 22 (a) ZnO nanorod formation on Kevlar fabric,154 (b) ZnO coated fabric155 (these figures have been reproduced from ref. 154 and 155, respectively with permission from Elsevier). | ||
5.8 Use of three dimensional (3D) fabrics
Multiple layers of stitched two dimensional (2D) plain woven fabrics are generally used for body armour applications. The disadvantages of this assembly are the adverse effects of stress concentration at crossover points of yarns in fabrics and poor layer to layer stress transfer. To overcome these problems, three dimensional (3D) woven fabrics may be used as an alternative.165–167 3D woven fabrics have several advantages over 2D fabrics like improved mechanical properties in through-thickness direction, better structural integrity and good layer to layer stress transfer.168 It is believed by many researchers that the presence of yarns in Z direction in 3D woven fabrics increases the stiffness, strength and compactness of the structure and its composite.167,169 Chevalier et al.170 concluded that for the same weight per unit area, stacked 2D fabrics absorb more energy than a 3D (warp interlock) fabric owing to higher volume fraction of yarn inside the 2D structures.Composites made of 3D structures offer several advantages over 2D laminates as evident by the results of a comparative study between 2D and 3D woven fabrics on compressive strength, post impact flexural strength and damage area after impact. Composites made of 3D woven fabrics are found to be superior, with reduced possibility of delamination and smaller failure zone.171 Different variants of 3D woven structures have been reported by different researchers for ballistic applications.55,170,172,173 The general definition and classification of 3D woven fabrics have been given in great detail by Boussu et al.174 and Fig. 23 shows the structural difference as per this classification.
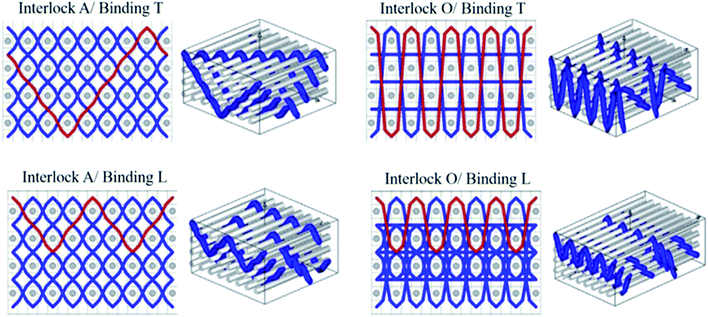 | ||
| Fig. 23 Classification of 3D woven structures (A = angle, O = orthogonal, L = layer to layer, T = through-thickness)174 (these figures have been reproduced from ref. 174 with permission from Elsevier). | ||
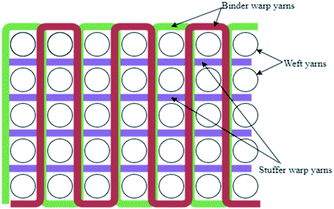
Fig. 24 shows an orthogonal interlock fabric with the three different sets of yarns used in 3D structures, namely binder warp, stuffer warp and weft yarns. As such, structures vary according to the binding depth of the binder warp and angle at which it binds the layers.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 was able to stop all bullets from piercing. At higher impact velocity (430 ± 10 m s−1) also, panels containing 3D fabrics with stuffer to binder ratio of 4
1 was able to stop all bullets from piercing. At higher impact velocity (430 ± 10 m s−1) also, panels containing 3D fabrics with stuffer to binder ratio of 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 performed better. Some researchers observed that orthogonal fabrics absorb the more energy when compared to other 3D structures in terms of peak force and total energy.181,182 This may be because of the absence of crimp, thereby permitting maximum utilisation of yarn properties. Structural stability is another advantage of orthogonal structures. This may stem from the fact that, for the same conditions, a higher fibre volume fraction can be expected for an orthogonal interlock binding than for an angle interlock binding, particularly in the thickness direction.183
1 performed better. Some researchers observed that orthogonal fabrics absorb the more energy when compared to other 3D structures in terms of peak force and total energy.181,182 This may be because of the absence of crimp, thereby permitting maximum utilisation of yarn properties. Structural stability is another advantage of orthogonal structures. This may stem from the fact that, for the same conditions, a higher fibre volume fraction can be expected for an orthogonal interlock binding than for an angle interlock binding, particularly in the thickness direction.183Due to this specific bonding arrangement between layers, 3D warp interlock fabrics are reported to show a small damaged zone, good resistance to delamination and multiple hits when subjected to impact.179 The stiffness and structural stability increase with the increase in number of layers while the crimp of the wavy yarns varies according to the interlacement pattern. Stuffer warp yarns are generally inserted to increase the structural stability and fibre volume fraction in composites.170,178,184 The mechanical and structural properties of these 3D fabrics can be altered by changing the stuffer to binder ratio, number of layers and by changing the binding depth of the binder warps.185 Of these, the binding depth has been reported to be one of the major parameters contributing to degradation of tow strength inside the woven structure.186 Higher values of number of layers and thread density seem to have a positive effect. It has been seen that better impact resistance can be anticipated with balanced or equilibrated structures wherein similar warp and weft densities are employed.179,187
6 Future trends
The constant need for reduced weight and enhanced performance has marked a shift in the choice of material for ballistic applications. UHMWPE fibres are now being explored more extensively than aramids due to lower density of the former. Hence, in the near future, one might expect UHMWPEs to replace aramids altogether. Another observable trend is the application of multi-phase STF with the addition of nanofillers such as carbon nanotubes and graphene instead of a single phase STF. In general, multi-phase STFs show higher peak viscosity, which is a requirement for ballistic resistance. Yet another trend that may take precedence in the coming years is the use of STF treated 3D structures in lieu of the currently used 2D structures. The use of carbon nanotubes in impact and ballistic applications at different stages, i.e., as an additive to the matrix or as a reinforcement to high-performance yarn may be exploited to greater extent as research progresses.191–1937 Summary
The present review critically analyses the vast body of research pursued to understand the roles of fibrous materials on ballistic impact resistance behaviour of soft body armour. Fibre and yarn properties are of paramount importance and UHMWPE fibres, due to their low density and very high modulus, seem to surpass aramids. Fabric constructions also play decisive roles as UD, 2D, 3D, triaxial and knitted fabrics behave differently during impact. For impact applications, crimpless UD fabric structures facilitate faster and wider dissipation of stress waves and the former is replacing the woven 2D fabrics to a great extent. Standards and evaluation techniques have also progressed to keep pace with the stringent requirement of body armour users. The use of shear thickening fluids has shown promising results at least against low velocity impact as well as against stab and puncture. Surface modification by developing nanorods of metal oxides have also shown potential in imparting additional energy absorption capacity to the base fibrous structure. Similarly, judicious selection of 3D woven construction may lead to improved impact energy absorption. Hybridization of different materials and structures for synergistic benefits is yet another approach that has been explored and the results are often very promising. The application of carbon nanotubes is also being explored to develop next generation light-weight body armour.Conflicts of interest
There is no conflict to declare.Acknowledgements
The authors are thankful to the Defence Research and Development Organization (DRDO), India and Terminal Ballistics Research Laboratory (TBRL), Chandigarh, India for providing financial assistance for this work through Grant No. DFTM/03/3203/M/01/JATC and ST-13/TBR-1298, respectively.References
- I. G. Crouch, Body armour – New materials, new systems, Def. Technol., 2019, 15(3), 241–253, DOI:10.1016/j.dt.2019.02.002.
- U.S. Department of Justice, Ballistic Resistance of Body Armor NIJ Standard-0101.06, 2008 Search PubMed.
- National Institute of Justice, Draft NIJ Standard 0101.07 Ballistic Resistance of Body Armor, 2018 Search PubMed.
- K. Horn, K. Biever, K. Burkman, et al., Lightening Body Armor, Pittsburg, 2012 Search PubMed.
- R. Yadav, M. Naebe, X. Wang and B. Kandasubramanian, Body armour materials: from steel to contemporary biomimetic systems, RSC Adv., 2016, 6(116), 115145–115174, 10.1039/C6RA24016J.
- B. A. Cheeseman and T. A. Bogetti, Ballistic impact into fabric and compliant composite laminates, Compos. Struct., 2003, 61(1–2), 161–173, DOI:10.1016/S0263-8223(03)00029-1.
- J. R. Vinson and J. A. Zukas, On the ballistic impact of textile body armor, J. Appl. Mech., 1975, 42(2), 263–268, DOI:10.1115/1.3423564.
- R. A. Prosser, Penetration of nylon ballistic panels by fragment-simulating projectiles Part II: Mechanism of penetration, Text. Res. J., 1988, 58(3), 161–165 CrossRef.
- High-Performance Fibres, ed. J. W. S. Hearle, Woodhead Publishing Limited, Cambridge, 1st edn, 2001 Search PubMed.
- J. Van Dingenen, High performance dyneema fibres in composites, Mater. Des., 1989, 10(2), 101–104, DOI:10.1016/S0261-3069(89)80021-4.
- P. M. Cunniff and M. A. Auerbach, High performance “M5” fiber for ballistics/structural composites, 23rd Army Sci Conf., 2002, pp. 1–8 Search PubMed.
- P. Bajaj and Sriram, Ballistic protective clothing: An overview, Indian J. Fibre Text. Res., 1997, 22(4), 274–291 CAS.
- A. Bhatnagar and E. S. Parrish, Bi-directional and multi-axial fabrics and fabric composites, US Pat., 6 841 492 B2, 2005.
- X. Chen and D. Yang, Use of 3D angle-interlock woven fabric for seamless female body armor: Part 1: Ballistic evaluation, Text. Res. J., 2010, 80(15), 1581–1588, DOI:10.1177/0040517510363187.
- Y. S. Lee, E. D. Wetzel Jr, R. G. Egres and N. J. Wagner, Advanced body armor utilizing shear thickening fluids, in 23rd Army Science Conference, Orlando, FL, December 2–5, 2002, pp. 1–6 Search PubMed.
- N. J. Wagner and E. D. Wetzel, Advanced body armor utilizing shear thickening fluids, US Pat., 7 498 276 B2, 2009.
- Y. S. Lee, E. D. Wetzel and N. J. Wagner, The ballistic impact characteristics of Kevlar woven fabrics impregnated with a colloidal shear thickening fluid, J. Mater. Sci., 2003, 38(13), 2825–2833, DOI:10.1023/A:1024424200221.
- S. Arora and A. Ghosh, Evolution of soft body armor, in Advanced Textile Engineering Materials, 2018, pp. 499–552, DOI:10.1002/9781119488101.ch13.
- R. Nayak, I. Crouch and S. Kanesalingam, et al., Body armor for stab and spike protection, Part 1: Scientific literature review, Text. Res. J., 2018, 88(7), 812–832, DOI:10.1177/0040517517690623.
- Kevlar® fibers, DuPont, http://www.dupont.co.in/products-and-services/fabrics-fibers-nonwovens/fibers/brands/kevlar/products/dupont-kevlar-fiber.html.
- A. Srivastava, A. Majumdar and B. S. Butola, Improving the impact resistance of textile structures by using shear thickening fluids: A review, Crit. Rev. Solid State Mater. Sci., 2012, 37(2), 115–129, DOI:10.1080/10408436.2011.613493.
- V. P. W. W. Shim, C. T. Lim and K. J. Foo, Dynamic mechanical properties of fabric armour, Int. J. Impact Eng., 2001, 25(1), 1–15, DOI:10.1016/S0734-743X(00)00038-5.
- Bladebuster®, http://bladebuster.ca/our-products/cut-resistant-clothing/dyneema-vs-kevla, accessed October 20, 2019.
- A. R. Gonzales, R. B. Schofield and S. V. Hart, Third Status Report of the Attorney General on Body Armor Safety Initiative Testing and Activities, 2005 Search PubMed.
- P. M. Cunniff, An analysis of the system effects in woven fabrics under ballistic impact, Text. Res. J., 1992, 62(9), 495–509, DOI:10.1177/004051759206200902.
- B. Pargalanda and F. Hernandezolivares, An analytical model to predict impact behavior of soft armors, Int. J. Impact Eng., 1995, 16(3), 455–466 CrossRef.
- B. J. Briscoe and F. Motamedi, The ballistic impact characteristics of aramid fabrics: The influence of interface friction, Wear, 1992, 158(1–2), 229–247, DOI:10.1016/0043-1648(92)90041-6.
- S. Bazhenov, Dissipation of energy by bulletproof aramid fabric, J. Mater. Sci., 1997, 32(15), 4167–4173, DOI:10.1007/BF02806188.
- Y. Duan, M. Keefe, T. A. Bogetti, B. A. Cheeseman and B. Powers, A numerical investigation of the influence of friction on energy absorption by a high-strength fabric subjected to ballistic impact, Int. J. Impact Eng., 2006, 32(8), 1299–1312, DOI:10.1016/j.ijimpeng.2004.11.005.
- X. S. Zeng, V. B. C. Tan and V. P. W. Shim, Modelling inter-yarn friction in woven fabric armour, Int. J. Numer. Methods Eng., 2006, 66(8), 1309–1330, DOI:10.1002/nme.1596.
- B. L. Lee, T. F. Walsh, S. T. Won, H. M. Patts, J. W. Song and A. H. Mayer, Penetration failure mechanisms of armor-grade fiber composites under impact, J. Compos. Mater., 2001, 35(18), 1605–1633, DOI:10.1177/002199801772661551.
- S. Gürgen, M. C. Kushan and W. Li, Shear thickening fluids in protective applications: A review, Prog. Polym. Sci., 2017, 75, 48–72, DOI:10.1016/j.progpolymsci.2017.07.003.
- A. Khodadadi, G. H. Liaghat and A. R. Sabet, et al., Experimental and numerical analysis of penetration into Kevlar fabric impregnated with shear thickening fluid, J. Thermoplast. Compos. Mater., 2018, 31(3), 392–407, DOI:10.1177/0892705717704485.
- A. Gawandi, E. T. Thostenson and J. W. Gilllespie, Tow pullout behavior of polymer-coated Kevlar fabric, J. Mater. Sci., 2011, 46(1), 77–89, DOI:10.1007/s10853-010-4819-3.
- K. Bilisik, Properties of yarn pull-out in para-aramid fabric structure and analysis by statistical model, Composites, Part A, 2011, 42(12), 1930–1942, DOI:10.1016/j.compositesa.2011.08.018.
- G. Nilakantan and J. W. Gillespie, Yarn pull-out behavior of plain woven Kevlar fabrics: Effect of yarn sizing, pullout rate, and fabric pre-tension, Compos. Struct., 2013, 101, 215–224, DOI:10.1016/j.compstruct.2013.02.018.
- N. Pan, Y. Lin, X. Wang and R. Postle, An oblique fiber bundle test and analysis, Text. Res. J., 2000, 70(8), 671–674, DOI:10.1177/004051750007000803.
- Y. Rao and R. J. Farris, Modeling and experimental study of the influence of twist on the mechanical properties of high-performance fiber yarns, J. Appl. Polym. Sci., 2000, 77(9), 1938–1949, DOI:10.1002/1097-4628(20000829)77:9<1938::aid-app9>3.0.co;2-d.
- M. V. Hosur, U. K. Vaidya, C. Ulven and S. Jeelani, Performance of stitched/unstitched woven carbon/epoxy composites under high velocity impact loading, Compos. Struct., 2004, 64(3–4), 455–466, DOI:10.1016/j.compstruct.2003.09.046.
- C. K. Chu and Y. L. Chen, Ballistic-proof effects of various woven constructions, Fibres Text. East. Eur., 2010, 6(83), 63–67 Search PubMed.
- X. Miao, G. Jiang and X. Kong, Experimental investigation on the stab resistance of warp knitted fabrics, Fibres Text. East. Eur., 2014, 22(5(107)), 65–70 Search PubMed.
- M. E. Messiry and E. Eltahan, Stab resistance of triaxial woven fabrics for soft body armor, J. Ind. Text., 2016, 45(5), 1062–1082, DOI:10.1177/1528083714551441.
- M. Karahan, Comparison of ballistic performance and energy absorption capabilities of woven and unidirectional aramid fabrics, Text. Res. J., 2008, 78(8), 718–730, DOI:10.1177/0040517508090487.
- C. C. Lin, C. M. Lin and C. C. Huang, et al., Elucidating the design and impact properties of composite nonwoven fabrics with various filaments in bulletproof vest cushion layer, Text. Res. J., 2009, 79(3), 268–274, DOI:10.1177/0040517507097515.
- A. Laha and A. Majumdar, Interactive effects of p-aramid fabric structure and shear thickening fluid on impact resistance performance of soft armor materials, Mater. Des., 2016, 89(5), 286–293, DOI:10.1016/j.matdes.2015.09.077.
- A. K. Bandaru, Y. Sachan, S. Ahmad, R. Alagirusamy and N. Bhatnagar, On the mechanical response of 2D plain woven and 3D angle-interlock fabrics, Composites, Part B, 2017, 118, 135–148, DOI:10.1016/j.compositesb.2017.03.011.
- A. K. Bandaru, V. V. Chavan, S. Ahmad, R. Alagirusamy and N. Bhatnagar, Low velocity impact response of 2D and 3D Kevlar/polypropylene composites, Int. J. Impact Eng., 2016, 93, 136–143, DOI:10.1016/j.ijimpeng.2016.02.016.
- M. Chitrangad, Hybrid Ballistic Fabric, US Pat., 5 187 003 A, 1993.
- C. R. Cork and P. W. Foster, The ballistic performance of narrow fabrics, Int. J. Impact Eng., 2007, 34(3), 495–508, DOI:10.1016/j.ijimpeng.2005.10.006.
- S. Sockalingam, S. C. Chowdhury, J. W. Gillespie Jr and M. Keefe, Recent advances in modeling and experiments of Kevlar ballistic fibrils, fibers, yarns and flexible woven textile fabrics – a review, Text. Res. J., 2016, 87(8), 984–1010, DOI:10.1177/0040517516646039.
- V. B. C. Tan, V. P. W. Shim and X. Zeng, Modelling crimp in woven fabrics subjected to ballistic impact, Int. J. Impact Eng., 2006, 32(1–4), 561–574, DOI:10.1016/j.ijimpeng.2005.06.008.
- V. B. C. Tan, V. P. W. Shim and T. E. Tay, Experimental and numerical study of the response of flexible laminates to impact loading, Int. J. Solids Struct., 2003, 40(23), 6245–6266, DOI:10.1016/S0020-7683(03)00413-X.
- M. Karahan, A. Kuş and R. Eren, An investigation into ballistic performance and energy absorption capabilities of woven aramid fabrics, Int. J. Impact Eng., 2008, 35(6), 499–510, DOI:10.1016/j.ijimpeng.2007.04.003.
- A. M. Sadegh and P. V. Cavallaro, Mechanics of energy absorbability in plain-woven fabrics: An analytical approach, J. Eng. Fibers Fabr., 2012, 7(1), 10–25 Search PubMed . http://www.jeffjournal.org/papers/Volume7/7.1.2Sadegh.pdf.
- W. Shi, H. Hu, B. Sun and B. Gu, Energy absorption of 3D orthogonal woven fabric under ballistic penetration of hemispherical-cylindrical projectile, J. Text. Inst., 2011, 102(10), 875–889, DOI:10.1080/00405000.2010.525815.
- M. R. Ahmad, W. Yunus, W. Ahmad, J. Salleh and A. Samsuri, Effect of fabric stitching on ballistic impact resistance of natural rubber coated fabric systems, Mater. Des., 2008, 29, 1353–1358, DOI:10.1016/j.matdes.2007.06.007.
- Y. Wang, X. Chen, R. Young, I. Kinloch and G. Wells, A numerical study of ply orientation on ballistic impact resistance of multi-ply fabric panels, Composites, Part B, 2015, 68, 259–265, DOI:10.1016/j.compositesb.2014.08.049.
- X. Chen, D. Sun, Y. Wang and Y. Zhou, 2D/3D Woven Fabrics for Ballistic Protection, in 4th World Conference on 3D Fabrics and Their Applications, 2012, pp. 1–12 Search PubMed.
- A. Majumdar, B. S. Butola and A. Srivastava, Development of soft composite materials with improved impact resistance using Kevlar fabric and nano-silica based shear thickening fluid, Mater. Des., 2014, 54, 295–300, DOI:10.1016/j.matdes.2013.07.086.
- Standard B of I, Textiles—Bullet Resistant Jackets—Performance Requirements, 2019.
- Technical Specifications of Light Weight Bullet Proof Jackets, New Delhi, 2009, https://mha.gov.in/sites/default/files/BPJacket.pdf.
- H. L. Gower, D. S. Cronin and A. Plumtree, Ballistic impact response of laminated composite panels, Int. J. Impact Eng., 2008, 35(9), 1000–1008, DOI:10.1016/j.ijimpeng.2007.07.007.
- G. Nilakantan, R. L. Merrill, M. Keefe, J. W. Gillespie and E. D. Wetzel, Experimental investigation of the role of frictional yarn pull-out and windowing on the probabilistic impact response of kevlar fabrics, Composites, Part B, 2015, 68, 215–229, DOI:10.1016/j.compositesb.2014.08.033.
- Military Textiles, ed. E. Wilusz, Woodhead Publishing Limited, Cambridge, 1st edn, 2008 Search PubMed.
- D. J. Carr, Failure mechanisms of yarns subjected to ballistic impact, J. Mater. Sci. Lett., 1999, 18, 585–588, DOI:10.1023/a:1006655301587.
- N. K. Naik and P. Shrirao, Composite structures under ballistic impact, Compos. Struct., 2004, 66(1–4), 579–590, DOI:10.1016/j.compstruct.2004.05.006.
- T. G. Montgomery, P. L. Grady and C. Tomasino, The effects of projectile geometry on the performance of ballistic fabrics, Text. Res. J., 1982, 52(7), 442–450, DOI:10.1177/004051758205200703.
- A. Majumdar, B. S. Butola and A. Srivastava, An analysis of deformation and energy absorption modes of shear thickening fluid treated Kevlar fabrics as soft body armour materials, Mater. Des., 2013, 51, 148–153, DOI:10.1016/j.matdes.2013.04.016.
- J. E. Kirkwood, K. M. Kirkwood and Y. S. I. L. Lee, et al., Yarn pull-out as a mechanism for dissipating ballistic iimpact energy in Kevlar KM-2 fabric: Part I: Producing ballistic performance, Text. Res. J., 2004, 74(10), 920–928 CrossRef.
- J. E. Kirkwood, K. M. Kirkwood, Y. S. Lee, R. G. Egres, N. J. Wagner and E. D. Wetzel, Yarn pull-out as a mechanism for dissipating ballistic impact energy in Kevlar(R) KM-2 fabric: Part II: Predicting ballistic performance, Text. Res. J., 2004, 74(11), 939–948, DOI:10.1177/004051750407401101.
- S. A. R. D. Sebastian, A. I. Bailey, B. J. Briscoe and D. Tabor, Effect of a softening agent on yarn pull-out force of a plain weave fabric, Text. Res. J., 1986, 56(10), 604–611 CrossRef CAS.
- S. A. R. D. Sebastian, A. I. Bailey, B. J. Briscoe and D. Tabor, Extensions, displacements and forces associated with pulling a single yarn from a fabric, J. Phys. D: Appl. Phys., 1987, 20(1), 130–139, DOI:10.1088/0022-3727/20/1/020.
- M. Martinez, C. Navarro, R. Cortes, J. Rodriguez and V. Sanchez-Galvez, Friction and wear behaviour of Kevlar fabrics, J. Mater. Sci., 1993, 28, 1305–1311 CrossRef CAS.
- Z. Dong and C. T. Sun, Testing and modeling of yarn pull-out in plain woven Kevlar fabrics, Composites, Part A, 2009, 40(12), 1863–1869, DOI:10.1016/j.compositesa.2009.04.019.
- K. Bilisik, Experimental determination of yarn pull-out properties of para-aramid (Kevlar®) woven fabric, J. Ind. Text., 2012, 41(3), 201–221, DOI:10.1177/1528083711413411.
- K. Bilisik, Stick-slip behavior of para-aramid (Twaron®) fabric in yarn pull-out, Text. Res. J., 2013, 83(1), 13–33, DOI:10.1177/0040517512449052.
- K. Bilisik and M. Korkmaz, Single and multiple yarn pull-outs on aramid woven fabric structures, Text. Res. J., 2011, 81(8), 847–864, DOI:10.1177/0040517510391703.
- M. R. Ahmad, W. Y. Wan Ahmad, J. Salleh and A. Samsuri, Performance of Natural Rubber Coated Fabrics under Ballistic Impact, Malaysian Polymer Journal, 2007, 2(1), 39–51 Search PubMed.
- R. Roy, A. Laha, N. Awasthi, A. Majumdar and B. S. Butola, Multi layered natural rubber coated woven p-aramid and UHMWPE fabric composites for soft body armor application, Polym. Compos., 2017, 39(10), 3636–3644, DOI:10.1002/pc.24391.
- N. Hassim, M. R. Ahmad, W. Y. W. Ahmad, A. Samsuri and M. H. M. Yahya, Puncture resistance of natural rubber latex unidirectional coated fabrics, J. Ind. Text., 2012, 42(2), 118–131, DOI:10.1177/1528083711429144.
- A. Majumdar and A. Laha, Effects of fabric construction and shear thickening fluid on yarn pull-out from high-performance fabrics, Text. Res. J., 2016, 86(9), 2056–2066, DOI:10.1177/0040517515619357.
- M. Soutrenon and V. Michaud, Impact properties of shear thickening fluid impregnated foams, Smart Mater. Struct., 2014, 23(3), 035022, DOI:10.1088/0964-1726/23/3/035022.
- R. G. Egres, M. J. Decker and C. J. Halbach, et al., Stab resistance of shear thickening fluid (STF) – Kevlar composites for body armor applications, in 24th Army Science Conference, 2004, DOI:10.1142/9789812772572_0034.
- D. Zielinska, B. Delczyk-Olejniczak, L. Wierzbicki, B. Z. E. Wilbik-Ha gas, M. H. Struszczyk and M. Leonowicz, Investigation of the effect of para-aramid fabric impregnation with shear thickening fluid on quasi-static stab resistance, Text. Res. J., 2014, 84(15), 1569–1577, DOI:10.1177/0040517514525881.
- W. Li, D. Xiong, X. Zhao, L. Sun and J. Liu, Dynamic stab resistance of ultra-high molecular weight polyethylene fabric impregnated with shear thickening fluid, Mater. Des., 2016, 102, 162–167, DOI:10.1016/j.matdes.2016.04.006.
- M. J. Decker, C. J. Halbach, C. H. Nam, N. J. Wagner and E. D. Wetzel, Stab resistance of shear thickening fluid (STF)-treated fabrics, Compos. Sci. Technol., 2007, 67, 565–578, DOI:10.1016/j.compscitech.2006.08.007.
- J. M. Houghton, B. A. Schiffman, D. P. Kalman, E. D. Wetzel and N. J. Wagner, Hypodermic needle puncture of shear thickening fluid (STF)-treated fabrics, in Proceedings of SAMPE, 2007, pp. 1–11, https://sites.udel.edu/wagnergroup/files/2015/03/Houghton_SAMPE07-needle-FINAL_pub-2gbvb2l.pdf Search PubMed.
- H. Mahfuz, F. Clements, V. Rangari, V. Dhanak and G. Beamson, Enhanced stab resistance of armor composites with functionalized silica nanoparticles, J. Appl. Phys., 2009, 105(6) DOI:10.1063/1.3086431.
- S. Gürgen and M. C. Kus, The stab resistance of fabrics impregnated with shear thickening fluids including various particle size of additives, Composites, Part A, 2017, 94, 50–60, DOI:10.1016/j.compositesa.2016.12.019.
- S. Gürgen and M. C. Kuşhan, The effect of silicon carbide additives on the stab resistance of shear thickening fluid treated fabrics, Mech. Adv. Mater. Struct., 2017, 24(16), 1381–1390, DOI:10.1080/15376494.2016.1231355.
- J. Gu, X. C. Huang, Y. Li, X. L. Wang, M. W. Shi and Z. Zheng, Improving the stab-resistance performance of ultra high molecular weight polyethylene fabric intercalated with nano-silica-fluid, J. Shanghai Jiaotong Univ., 2014, 19(1), 102–109, DOI:10.1007/s12204-013-1467-1.
- J. Qin, G. Zhang, L. Zhou, J. Li and X. Shi, Dynamic/quasi-static stab-resistance and mechanical properties of soft body armour composites constructed from Kevlar fabrics and shear thickening fluids, RSC Adv., 2017, 7, 39803–39813, 10.1039/c7ra07549a.
- J. L. Park, B. I. Yoon, J. G. Paik and T. J. Kang, Ballistic performance of p-aramid fabrics impregnated with shear thickening fluid; Part I – Effect of laminating sequence, Text. Res. J., 2012, 82(6), 527–541, DOI:10.1177/0040517511420765.
- J. L. Park, B. I. Yoon, J. G. Paik and T. J. Kang, Ballistic performance of p-aramid fabrics impregnated with shear thickening fluid; Part II – Effect of fabric count and shot location, Text. Res. J., 2012, 82(6), 542–557, DOI:10.1177/0040517511420765.
- A. Majumdar, B. S. Butola and A. Srivastava, Impact performance and energy absorption modes of kevlar fabrics treated with shear thickening fluid, in Fiber Society 2012 Spring Conference: Fiber Research for Tomorrow's Applications, 2012 Search PubMed.
- N. J. Wagner and J. F. Brady, Shear thickening in colloidal dispersions, Phys. Today, 2009, 62(10), 27–32, DOI:10.1063/1.3248476.
- L. Sun, D. Xiong and C.-Y. Xu, Application of shear thickening fluid in ultra high molecular weight polyethylene fabric, J. Appl. Polym. Sci., 2013, 129(4), 1922–1928, DOI:10.1002/app.38844.
- S. Li, Y. Wang, J. Ding, H. Wu and Y. Fu, Effect of shear thickening fluid on the sound insulation properties of textiles, Text. Res. J., 2014, 84(9), 897–902, DOI:10.1177/0040517513512395.
- M. Fahool and A. R. Sabet, Parametric study of energy absorption mechanism in Twaron fabric impregnated with a shear thickening fluid, Int. J. Impact Eng., 2016, 90, 61–71, DOI:10.1016/j.ijimpeng.2015.11.016.
- R. L. Hoffman, Discontinuous and dilatant viscosity behavior in concentrated suspensions. I. Observation of a flow instability, Trans. Soc. Rheol., 1972, 16(1), 155–173, DOI:10.1016/0021-9797(74)90059-9.
- R. L. Hoffman, Explanations for the cause of shear thickening in concentrated colloidal suspensions, J. Rheol., 1998, 42, 111–123, DOI:10.1122/1.550884.
- R. L. Hoffman, Discontinuous and dilatant viscosity behavior in concentrated suspensions. II. Theory and experimental tests, J. Colloid Interface Sci., 1974, 46(3), 491–506, DOI:10.1122/1.549250.
- E. Brown, N. A. Forman and C. S. Orellana, et al., Generality of shear thickening in dense suspensions, Nat. Mater., 2010, 9, 220–224, DOI:10.1038/nmat2627.
- J. Qin, G. Zhang and X. Shi, Study of a shear thickening fluid: the suspensions of monodisperse polystyrene microspheres in polyethylene glycol, J. Dispersion Sci. Technol., 2017, 38(7), 935–942, DOI:10.1080/01932691.2016.1216435.
- Y. Lee, R. Egres and K. M. Kirkwood, The effect of rheological parameters on the ballistic properties of shear thickening fluid (STF) – Kevlar composites, in NUMIFORM, Columbus, 2004, DOI:10.1063/1.1766538.
- X. Z. Zhang, W. H. Li and X. L. Gong, The rheology of shear thickening fluid (STF) and the dynamic performance of an STF-filled damper, Smart Mater. Struct., 2008, 17, 035027, DOI:10.1088/0964-1726/17/3/035027.
- T. J. Kang, K. H. Hong and M. R. Yoo, Preparation and properties of fumed silica/Kevlar composite fabrics for application of stab resistant material, Fibers Polym., 2010, 11(5), 719–724, DOI:10.1007/s12221-010-0719-z.
- T. J. Kang, C. Y. Kim and K. H. Hong, Rheological behavior of concentrated silica suspension and its application to soft armor, J. Appl. Polym. Sci., 2012, 124, 1534–1541, DOI:10.1002/app.
- K. Yu, H. Cao, K. Qian, X. Sha and Y. Chen, Shear-thickening behavior of modified silica nanoparticles in polyethylene glycol, J. Nanopart. Res., 2012, 14, 747 CrossRef.
- M. Hasanzadeh and V. Mottaghitalab, The role of shear-thickening fluids (STFs) in ballistic and stab-resistance improvement of flexible armor, J. Mater. Eng. Perform., 2014, 23(4), 1182–1196, DOI:10.1007/s11665-014-0870-6.
- M. Hasanzadeh, V. Mottaghitalab and M. Rezaei, Rheological and viscoelastic behavior of concentrated colloidal suspensions of silica nanoparticles: A response surface methodology approach, Adv. Powder Technol., 2015, 26(6), 1570–1577, DOI:10.1016/j.apt.2015.08.011.
- T. A. Hassan, V. K. Rangari and S. Jeelani, Synthesis, processing and characterization of shear thickening fluid (STF) impregnated fabric composites, Mater. Sci. Eng., A, 2010, 527(12), 2892–2899, DOI:10.1016/j.msea.2010.01.018.
- T. A. Hassan, V. K. Rangari and S. Jeelani, Sonochemical synthesis and rheological properties of shear thickening silica dispersions, Ultrason. Sonochem., 2010, 17(5), 947–952, DOI:10.1016/j.ultsonch.2010.02.001.
- Y. Park, Y. Kim, A. H. Baluch and C.-G. Kim, Empirical study of the high velocity impact energy absorption characteristics of shear thickening fluid (STF) impregnated Kevlar fabric, Int. J. Impact Eng., 2014, 72, 67–74, DOI:10.1016/j.ijimpeng.2014.05.007.
- J. Ding, P. Tracey, W. Li, G. Peng, P. G. Whitten and G. G. Wallace, Review on shear thickening fluids and applications, Textiles and Light Industrial Science and Technology, 2013, 2(4), 161–173 Search PubMed.
- J. Qin, G. Zhang, X. Shi and M. Tao, Study of a shear thickening fluid: the dispersions of silica nanoparticles in 1-butyl-3-methylimidazolium tetrafluoroborate, J. Nanopart. Res., 2015, 17(8), 333, DOI:10.1007/s11051-015-3144-9.
- W. H. Boersma, J. Laven and H. N. Stein, Shear thickening (dilatancy) in concentrated dispersions, Am. Inst. Chem. Eng., 1990, 36(3), 321–332, DOI:10.1002/aic.690360302.
- A. K. Gurnon and N. J. Wagner, Microstructure and rheology relationships for shear thickening colloidal dispersions, J. Fluid Mech., 2015, 769, 242–276, DOI:10.1017/jfm.2015.128.
- R. G. Egres, F. Nettesheim and N. J. Wagner, Rheo-SANS investigation of acicular-precipitated calcium carbonate colloidal suspensions through the shear thickening transition, J. Rheol., 2006, 50(5), 685–709, DOI:10.1122/1.2213245.
- R. G. Egres and N. J. Wagner, The rheology and microstructure of acicular precipitated calcium carbonate colloidal suspensions through the shear thickening transition, J. Rheol., 2005, 49(3), 719–746, DOI:10.1122/1.1895800.
- J. F. Brady and G. Bossis, The rheology of concentrated suspensions of spheres in simple shear flow by numerical simulation, J. Fluid Mech., 1985, 155, 105–129, DOI:10.1017/S0022112085001732.
- X.-Q. Liu, R.-Y. Bao, X.-J. Wu, W. Yang, B.-H. Xie and M.-B. Yang, Temperature induced gelation transition of a fumed silica/PEG shear thickening fluid, RSC Adv., 2015, 5(24), 18367–18374, 10.1039/c4ra16261g.
- B. J. Maranzano and N. J. Wagner, The effects of interparticle interactions and particle size on reversible shear thickening: Hard-sphere colloidal dispersions, J. Rheol., 2001, 45(5), 1205–1222, DOI:10.1122/1.1392295.
- G. Bossis and J. F. Brady, The rheology of brownian suspensions, J. Chem. Phys., 1989, 91, 1866–1874, DOI:10.1063/1.457091.
- H. A. Barnes, Shear-thickening (“Dilatancy”) in suspensions of nonaggregating solid particles dispersed in Newtonian liquids, J. Rheol., 1989, 33, 329–366, DOI:10.1122/1.550017.
- W. H. Boersma, J. Laven and H. N. Stein, Computer simulations of shear thickening of concentrated dispersions, J. Rheol., 1995, 39, 841, DOI:10.1122/1.550621.
- R. G. Egres Jr, Y. S. Lee and J. E. Kirkwood, et al., “Liquid armor”: Protective fabrics utilizing shear thickening fluids, in 4th Int. Conf. on Safety and Protective Fabrics, 2004, pp. 1–8 Search PubMed.
- X. Cheng, J. H. McCoy, J. N. Israelachvili and I. Cohen, Imaging the microscopic structure of shear thinning and thickening colloidal suspensions, Science, 2011, 333(6047), 1276–1279, DOI:10.1126/science.1207032.
- Dilatancy (granular material), https://en.wikipedia.org/wiki/Dilatancy_(granular_material), accessed March 24, 2018.
- A. B. Metzner and M. Whitlock, Flow behavior of concentrated (dilatant) suspensions, Trans. Soc. Rheol., 1958, 2(1), 239–254, DOI:10.1122/1.548831.
- E. Brown and H. M. Jaeger, The role of dilation and confining stresses in shear thickening of dense suspensions, J. Rheol., 2010, 56(4), 875–923, DOI:10.1122/1.4709423.
- E. Brown and H. M. Jaeger, Shear thickening in concentrated suspensions: phenomenology, mechanisms and relations to jamming, Rep. Prog. Phys., 2014, 77(4), 1–23, DOI:10.1088/0034-4885/77/4/046602.
- R. Seto, R. Mari, J. F. Morris and M. M. Denn, Discontinuous shear thickening of frictional hard-sphere suspensions, Phys. Rev. Lett., 2013, 111(21), 218301, DOI:10.1103/PhysRevLett.111.218301.
- N. Y. C. Lin, B. M. Guy and M. Hermes, et al., Hydrodynamic and contact contributions to continuous shear thickening in colloidal suspensions, Phys. Rev. Lett., 2015, 115(22), 228304, DOI:10.1103/PhysRevLett.115.228304.
- E. D. Wetzel, Y. S. Lee, R. G. Egres, K. M. Kirkwood, J. E. Kirkwood and N. J. Wagner, The effect of rheological parameters on the ballistic properties of shear thickening fluid (STF)-Kevlar composites, in AIP Conference Proceedings, 2004, pp. 288–293, DOI:10.1063/1.1766538.
- B.-W. Lee, I.-J. Kim and C.-G. Kim, The influence of the particle size of silica on the ballistic performance of fabrics impregnated with silica colloidal suspension, J. Compos. Mater., 2009, 43(23), 2679–2698, DOI:10.1177/0021998309345292.
- D. P. Kalman, R. L. Merrill, N. J. Wagner and E. D. Wetzel, Effect of particle hardness on the penetration behavior of fabrics intercalated with dry particles and concentrated particle-fluid suspensions, ACS Appl. Mater. Interfaces, 2009, 1(11), 2602–2612, DOI:10.1021/am900516w.
- J. Warren, S. Offenberger, H. Toghiani, C. U. Pittman, T. E. Lacy and S. Kundu, Effect of temperature on the shear-thickening behavior of fumed silica suspensions, ACS Appl. Mater. Interfaces, 2015, 7(33), 18650–18661, DOI:10.1021/acsami.5b05094.
- T. Tian, W. Li, J. Ding, G. Alici and H. Du, Study of the temperature effect of shear thickening fluid, in 2013 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM), Wollongong, Australia, 2013, pp. 833–837 Search PubMed.
- Q. Chen, W. Zhu, F. Ye, X. Gong, W. Jiang and S. Xuan, pH effects on shear thickening behaviors of polystyrene-ethylacrylate colloidal dispersions, Mater. Res. Express, 2014, 1(1), 015303, DOI:10.1088/2053-1591/1/1/015303.
- L. Shan, Y. Tian, J. Jiang, X. Zhang and Y. Meng, Effects of pH on shear thinning and thickening behaviors of fumed silica suspensions, Colloids Surf., A, 2015, 464, 1–7, DOI:10.1016/j.colsurfa.2014.09.040.
- Y. Wang, Y. Zhu and Y. Fu, Preparation and properties of HNT-SiO2 compounded shear thickening fluid, Nano brief reports and reviews, 2014, 9(8), 1450100, DOI:10.1142/S1793292014501008.
- W. Huang, Y. Wu, L. Qiu, C. Dong, J. Ding and D. Li, Tuning rheological performance of silica concentrated shear thickening fluid by using graphene oxide, Adv. Condens. Matter Phys., 2015, 2015, 1–5, DOI:10.1155/2015/734250.
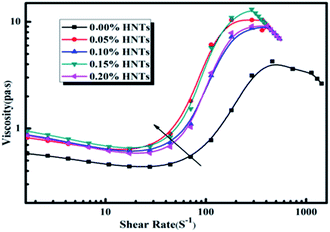
- A. Laha and A. Majumdar, Shear thickening fluids using silica-halloysite nanotubes to improve the impact resistance of p-aramid fabrics, Appl. Clay Sci., 2016, 132–133, 468–474, DOI:10.1016/j.clay.2016.07.017.
- X. Sha, K. Yu and H. Cao, Shear thickening behavior of nanoparticle suspensions with carbon nanofillers, J. Nanopart. Res., 2013, 15(7), 1816, DOI:10.1007/s11051-013-1816-x.
- M. Hasanzadeh and V. Mottaghitalab, Tuning of the rheological properties of concentrated silica suspensions using carbon nanotubes, Rheol. Acta, 2016, 55(9), 759–766, DOI:10.1007/s00397-016-0950-7.
- X. Gong, Y. Xu, W. Zhu, S. Xuan, W. Jiang and W. Jiang, Study of the knife stab and puncture-resistant performance for shear thickening fluid enhanced fabric, J. Compos. Mater., 2014, 48(6), 641–657, DOI:10.1177/0021998313476525.
- A. Srivastava, A. Majumdar and B. S. Butola, Improving the impact resistance performance of Kevlar fabrics using silica based shear thickening fluid, Mater. Sci. Eng., A, 2011, 529(25), 224–229, DOI:10.1016/j.msea.2011.09.021.
- V. B. C. Tan, T. E. Tay and W. K. Teo, Strengthening fabric armour with silica colloidal suspensions, Int. J. Solids Struct., 2005, 42(5–6), 1561–1576, DOI:10.1016/j.ijsolstr.2004.08.013.
- U. Mawkhlieng and A. Majumdar, Deconstructing the role of shear thickening fluid in enhancing the impact resistance of high-performance fabrics, Composites, Part B, 2019, 175, 107167, DOI:10.1016/j.compositesb.2019.107167.
- Y. Sun, Z. Zhang and C. P. Wong, Study on mono-dispersed nano-size silica by surface modification for underfill applications, J. Colloid Interface Sci., 2005, 292, 436–444, DOI:10.1016/j.jcis.2005.05.067.
- S. Ghosh, S. K. Goswami and L. J. Mathias, Surface modification of nano-silica with amides and imides for use in polyester nanocomposites, J. Mater. Chem. A, 2013, 1(19), 6073–6080, 10.1039/c3ta10381a.
- B. Radhakrishnan, R. Ranjan and W. J. Brittain, Surface initiated polymerizations from silica nanoparticles, Soft Matter, 2006, 2, 386–396, 10.1039/b516508c.
- A. Hazarika, B. K. Deka, D. Y. Kim, K. Kong, Y. B. Park and H. W. Park, Growth of aligned ZnO nanorods on woven Kevlar® fiber and its performance in woven Kevlar® fiber/polyester composites, Composites, Part A, 2015, 78, 284–293, DOI:10.1016/j.compositesa.2015.08.022.
- H. S. Hwang, M. H. Malakooti, B. A. Patterson and H. A. Sodano, Increased interyarn friction through ZnO nanowire arrays grown on aramid fabric, Compos. Sci. Technol., 2015, 107, 75–81, DOI:10.1016/j.compscitech.2014.12.001.
- U. Galan, Y. Lin, G. J. Ehlert and H. A. Sodano, Effect of ZnO nanowire morphology on the interfacial strength of nanowire coated carbon fibers, Compos. Sci. Technol., 2011, 71(7), 946–954, DOI:10.1016/j.compscitech.2011.02.010.
- Y. Lin, G. Ehlert and H. A. Sodano, Increased interface strength in carbon fiber composites through a ZnO nanowire interphase, Adv. Funct. Mater., 2009, 19(16), 2654–2660, DOI:10.1002/adfm.200900011.
- G. J. Ehlert, U. Galan and H. A. Sodano, Role of surface chemistry in adhesion between ZnO nanowires and carbon fibers in hybrid composites, ACS Appl. Mater. Interfaces, 2013, 5(3), 635–645, DOI:10.1021/am302060v.
- G. J. Ehlert and H. A. Sodano, Zinc oxide nanowire interphase for enhanced interfacial strength in lightweight polymer fiber composites, ACS Appl. Mater. Interfaces, 2009, 1(8), 1827–1833, DOI:10.1021/am900376t.
- H. S. Hwang, B. A. Patterson, M. H. Malakooti and H. A. Sodano, Modification of pullout behavior of Kevlar fabric by zinc oxide nanowire reinforcement, ASME 2013 Int Mech Eng Congr Expo IMECE2013, 2013, pp. 1–6 Search PubMed.
- A. Majumdar, B. S. Butola, N. Awasthi, I. Chauhan and P. Hatua, Improving the mechanical properties of p-aramid fabrics and composites by developing ZnO nanostructures, Polym. Compos., 2018, 39(9), 3300–3306, DOI:10.1002/pc.24346.
- P. Dixit, A. Ghosh and A. Majumdar, Hybrid approach for augmenting the impact resistance of p-aramid fabrics: grafting of ZnO nanorods and impregnation of shear thickening fluid, J. Mater. Sci., 2019, 54(20), 13106–13117, DOI:10.1007/s10853-019-03830-z.
- S. H. Lee, T. Minegishi and J. S. Park, et al., Ordered arrays of ZnO nanorods grown on periodically polarity-inverted surfaces, Nano Lett., 2008, 8(8), 2419–2422, DOI:10.1021/nl801344s.
- R. S. Sabry and O. AbdulAzeez, Hydrothermal growth of ZnO nano rods without catalysts in a single step, Manuf. Lett., 2014, 2(2), 69–73, DOI:10.1016/j.mfglet.2014.02.001.
- N. Khokar, 3D-Weaving: Theory and practice, J. Text. Inst., 2001, 92(2), 193–207, DOI:10.1080/00405000108659570.
- B. K. Behera and R. Mishra, 3-Dimensional weaving, Indian J. Fibre Text. Res., 2008, 33(3), 274–287 CAS.
- R. Ghosh and S. De, Z-fiber influence on high speed penetration of 3D orthogonal woven fiber composites, Mech. Mater., 2014, 68, 147–163, DOI:10.1016/j.mechmat.2013.06.008.
- M. P. Rao, B. V. Sankar and G. Subhash, Effect of Z-yarns on the stiffness and strength of three-dimensional woven composites, Composites, Part B, 2009, 40, 540–551, DOI:10.1016/j.compositesb.2009.01.011.
- M. Ansar, W. Xinwei and Z. Chouwei, Modeling strategies of 3D woven composites: A review, Compos. Struct., 2011, 93(8), 1947–1963, DOI:10.1016/j.compstruct.2011.03.010.
- C. Chevalier, F. Boussu and J. Nussbaum, 3D warp interlock fabric as an efficient flexible solution for impact protection, in, LWAG 2012 Lugano Workshop, Opportunities and Challenges of Light-Weight Armour-Failure Mechanisms, Materials, Experiments and Modeling, At Lugano, Switzerland, 2012 Search PubMed.
- J. Hu, 3-D Fibrous Assemblies: Properties, Applications and Modelling of Three-Dimensional Textile Structures, Woodhead Publishing Limited, Cambridge, 1st edn, 2008 Search PubMed.
- F. Boussu, B. Provost, D. Coutelier, D. Vallee and F. Rondot, New 3D textile composite hybrid solutions against high velocity impact, in International SAMPE Technical Conference, 2012 Search PubMed.
- Y. Mahadik and S. R. Hallett, The effect of compaction on the compressive properties of a 3D woven interlock fabric, in Proceedings of the 10th International Conference on Textile Composites – TEXCOMP 10: Recent Advances in Textile Composites, 2010 Search PubMed.
- F. Boussu, I. Cristian and S. Nauman, General definition of 3D warp interlock fabric architecture, Composites, Part B, 2015, 81, 171–188, DOI:10.1016/j.compositesb.2015.07.013.
- X. Wang, B. Hu and Y. Feng, et al., Low velocity impact properties of 3D woven basalt/aramid hybrid composites, Compos. Sci. Technol., 2008, 68, 444–450, DOI:10.1016/j.compscitech.2007.06.016.
- Y. Yu, X. Wang, Y. Li and Z. Wang, Numerical simulation of 3D orthogonal woven composite impacted by a spherical bullet, Chin. J. Comput. Phys., 2009, 879–886 Search PubMed.
- Y. Mahadik and S. R. Hallett, Effect of fabric compaction and yarn waviness on 3D woven composite compressive properties, Composites, Part A, 2011, 42(11), 1592–1600, DOI:10.1016/j.compositesa.2011.07.006.
- C. Dufour, P. Wang, F. Boussu and D. Soulat, Experimental investigation about stamping behaviour of 3D warp interlock composite preforms, Appl. Compos. Mater., 2014, 21(5), 725–738, DOI:10.1007/s10443-013-9369-9.
- B. Provost, F. Boussu, D. Coutellier, D. Vallee, F. Rondot and J. Nussbaum, Armouring solutions against high-velocity impact using 2D laminates and 3D warp interlock composites, J. Ind. Text., 2014, 43(4), 606–626, DOI:10.1177/1528083713498914.
- A. Majumdar, A. Laha, D. Bhattacharjee and I. Biswas, Tuning the structure of 3D woven aramid fabrics reinforced with shear thickening fluid for developing soft body armour, Compos. Struct., 2017, 178, 415–425, DOI:10.1016/j.compstruct.2017.07.018.
- R. Mishra, V. Baheti, B. K. Behera and J. Militky, Novelties of 3-D woven composites and nanocomposites, J. Text. Inst., 2014, 105(1), 84–92, DOI:10.1080/00405000.2013.812266.
- B. K. Behera and B. P. Dash, Mechanical behavior of 3D woven composites, J. Mater., 2015, 67, 261–271, DOI:10.1016/j.matdes.2014.11.020.
- H. L. Yi and X. Ding, Conventional approach on manufacturing 3D woven preforms used for composites, J. Ind. Text., 2004, 34(1), 39–50, DOI:10.1177/1528083704045847.
- C. Ha-Minh, F. Boussu, T. Kanit, D. Crépin and A. Imad, Effect of frictions on the ballistic performance of a 3D warp interlock fabric: Numerical analysis, Appl. Compos. Mater., 2012, 19(3–4), 333–347, DOI:10.1007/s10443-011-9202-2.
- C. Ha-Minh, A. Imad, F. Boussu and T. Kanit, Experimental and numerical investigation of a 3D woven fabric subjected to a ballistic impact, Int. J. Impact Eng., 2016, 88, 91–101, DOI:10.1016/j.ijimpeng.2015.08.011.
- F. Boussu, I. Cristian, S. Nauman, P. Lapeyronnie, C. Binetruy and X. Legrand, Effect of 3D-weave architecture on strength transfer from tow to textile composite, in 2nd World Conference on 3D Fabrics and Their Applications, 2009, pp. 2–8 Search PubMed.
- C. Chevalier, J. Nussbaum, D. Coutellier and F. Boussu, Experimental study on the influence of weaving parameters on the ballistic performances of 3D fabrics, in International Symposium on Ballistics, 2013 Search PubMed.
- K. Luan, B. Sun and B. Gu, Ballistic impact damages of 3-D angle-interlock woven composites based on high strain rate constitutive equation of fiber tows, Int. J. Impact Eng., 2013, 57, 145–158, DOI:10.1016/j.ijimpeng.2013.02.003.
- D. Yang, X. Chen and D. Sun, et al., Ballistic performance of angle-interlock woven fabrics, J. Text. Inst., 2016, 108(4), 586–596, DOI:10.1080/00405000.2016.1176622.
- X. Chen, W. Lo and A. E. Tayyar, Mouldability of angle-interlock woven fabrics for technical applications, Text. Res. J., 2002, 72(3), 195–200 CrossRef CAS.
- Y. R. Mahajan, Carbon nanotubes and the pursuit of the ultimate body armor, 2006, https://www.nanowerk.com/spotlight/spotid=17548.php, accessed February 19, 2019 Search PubMed.
- S. Sharma, S. R. Dhakate, A. Majumdar and B. P. Singh, Improved static and dynamic mechanical properties of multiscale bucky paper interleaved Kevlar fiber composites, Carbon, 2019, 152, 631–642, DOI:10.1016/j.carbon.2019.06.055.
- Nanocomp Technologies, Inc, http://www.miralon.com/, accessed February 19, 2019.
| This journal is © The Royal Society of Chemistry 2020 |