Open Access Article
Open Access ArticleChemical stability of Ca3Co4−xO9+δ/CaMnO3−δ p–n junction for oxide-based thermoelectric generators
Anette Eleonora Gunnæsa,
Raluca Tofana,
Kristian Berlanda,
Sandeep Gorantlaab,
Thomas Storaasa,
Temesgen Debelo Desissa cd,
Matthias Schrade
cd,
Matthias Schrade ae,
Clas Perssona,
Mari-Ann Einarsrud
ae,
Clas Perssona,
Mari-Ann Einarsrud f,
Kjell Wiikf,
Truls Norbyc and
Nikola Kanas
f,
Kjell Wiikf,
Truls Norbyc and
Nikola Kanas *f
*f
aDepartment of Physics, University of Oslo, SMN, FERMiO, NO-0349 Oslo, Norway
bŁUKASIEWICZ Research Network – PORT Polish Center for Technology Development, 54-066 Wrocław, Poland
cDepartment of Chemistry, University of Oslo, SMN, FERMiO, NO-0349 Oslo, Norway
dDepartment of Materials Science and Engineering, Adama Science and Technology University, 1888 Adama, Ethiopia
eDepartment of Sustainable Energy Technology, SINTEF, 0314 Oslo, Norway
fDepartment of Material Science and Engineering, NTNU Norwegian University of Science and Technology, 7491 Trondheim, Norway. E-mail: nikola.kanas@ntnu.no
First published on 30th January 2020
Abstract
An all-oxide thermoelectric generator for high-temperature operation depends on a low electrical resistance of the direct p–n junction. Ca3Co4−xO9+δ and CaMnO3−δ exhibit p-type and n-type electronic conductivity, respectively, and the interface between these compounds is the material system investigated here. The effect of heat treatment (at 900 °C for 10 h in air) on the phase and element distribution within this p–n junction was characterized using advanced transmission electron microscopy combined with X-ray diffraction. The heat treatment resulted in counter diffusion of Ca, Mn and Co cations across the junction, and subsequent formation of a Ca3Co1+yMn1−yO6 interlayer, in addition to precipitation of Co-oxide, and accompanying diffusion and redistribution of Ca across the junction. The Co/Mn ratio in Ca3Co1+yMn1−yO6 varies and is close to 1 (y = 0) at the Ca3Co1+yMn1−yO6–CaMnO3−δ boundary. The existence of a wide homogeneity range of 0 ≤ y ≤ 1 for Ca3Co1+yMn1−yO6 is corroborated with density functional theory (DFT) calculations showing a small negative mixing energy in the whole range.
Introduction
For waste heat harvesting at high temperatures and oxidizing conditions, thermoelectric generators (TEGs) based on oxides represent an interesting technology, enabling increased energy efficiency of any high-temperature process where heat harvesting is viable.1 Oxide-based thermoelectrics exhibit modest efficiencies compared with state-of-the-art non-oxides, but offer in principle superior stability at high temperatures in air (oxidizing conditions). The stability is however jeopardized by the need for metallic interconnects to form well-conducting contacts between the oxide p- and n-type legs, since the metals are noble (rare and expensive) or they will oxidize over time. Cracking or exfoliation due to differences in coefficients of thermal expansion (CTEs) between ceramic conductors and metal interconnects represent additional challenges.2 TEGs with direct contact between the p- and n-type legs without metallic interconnects in between have however been proposed.3–5 By avoiding the metallic interconnects, manufacturing becomes both simpler and less expensive. Such a direct oxide p–n junction faces however not only challenges in terms of high contact resistances from charge carrier depletion, but also stability issues related to interdiffusion and formation of new phases at the interface region. These stability issues are addressed in the present investigation for the specific case of Ca3Co4−xO9+δ–CaMnO3−δ.The recently reported all-oxide TEG made of p-type Ca3Co4−xO9+δ and n-type CaMnO3−δ introduced a new concept where a new phase with favorable thermoelectric properties is formed in situ at the interface between the p- and n-type conductors.6 Herein, we further study the materials and present a detailed analysis of the interdiffusion and formation of the secondary phases at the p–n interface in air and typical operating temperature of 900 °C.
According to Woermann et al., Ca3Co4−xO9+δ is stable up to 926 °C in air, at which it decomposes to Ca3Co2O6 and a Co1−zCazO (ss).7 Ca3Co4−xO9+δ is described with a homogeneity range (Ca3Co3.9+xO9+δ) with x between −0.03 and +0.17 at 900 °C.8 The homogeneity range increases towards Co-rich compositions with increasing temperatures and becomes narrowly sharp, where it ends at a single point.8 The stoichiometry of Ca3Co4−xO9+δ in our investigation corresponds to x within the homogeneity range as mentioned above, giving a maximum operating temperature of 900 °C.6,8,9
Ca3Co4−xO9+δ has a superlattice-misfit structure consisting of two monoclinic subsystems: a triple rock salt (RS)-type slab of Ca2CoO3 and a single CdI2-type CoO2 slab. The subsystems have identical a, c, and β parameters, but different b parameters: a = 4.8376 Å, c = 10.833 Å, β = 98.06, b1 = 4.5565 Å, and b2 = 2.8189 Å.10–13
CaMnO3−δ has an orthorhombic perovskite type structure, with lattice constants a = 5.279 Å, b = 7.448 Å and c = 5.264 Å at room temperature.14 Upon heating in air, the oxygen content is reduced and structural phase transitions occur at 893 and 913 °C with resulting tetragonal and cubic structural modifications, respectively.15 However, the phase transition temperatures are strongly dependent on the oxygen stoichiometry.16 According to the CaMnO3−δ phase diagram the cubic-to-tetragonal and tetragonal-to-orthorhombic transformations occur when 3 − δ ≈ 2.965 and 2.98, respectively, at 900 °C.17 Oxygen stoichiometry in air is reported to be 2.94 at 900 °C,17 and hence CaMnO3−δ should be in the cubic phase domain considering the heat treatment used in this work.
Golovkin et al. have reported phase diagrams of the system Ca–Mn–Co–O.18 Ca3Co4−xO9+δ exhibits a certain solid solubility of Mn,19,20 and the formation of a quaternary phase Ca3Co1+yMn1−yO6 is described by several authors.21–23 This phase has been reported to have a K4CdCl6 type of structure, the same as the pristine Ca3Co2O6 phase, with space group R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c. Both Hervoches et al.22 and Kanas et al.24 have confirmed a wide homogeneity range for Ca3Co1+yMn1−yO6, extending from y = 0 to 1.
c. Both Hervoches et al.22 and Kanas et al.24 have confirmed a wide homogeneity range for Ca3Co1+yMn1−yO6, extending from y = 0 to 1.
To establish all-oxide thermoelectric generators for operation in air at high temperatures, a detailed understanding of the processes taking place at the p–n junction at typical operating temperatures is decisive. In this investigation, we present a comprehensive study of the interdiffusion and formation of secondary phases at the Ca3Co4−xO9+δ/CaMnO3−δ interface in air at 900 °C.
Results and discussion
The SEM cross section view of the specimen in Fig. 1 shows the interface between the relatively dense CaMnO3−δ and the porous Ca3Co4−xO9+δ layer after heat treatment at 900 °C for 10 h. The distribution of Co (pink), Mn (blue) and Ca (green) at and in the vicinity of the interface between Ca3Co4−xO9+δ and CaMnO3−δ is visualized in the bottom left inset in Fig. 1.Two distinctly different regions are identified at the junction: “Region (a)” which is a ∼10 μm thick porous region at the porous Ca3Co4−xO9+δ side with a high density of Co-rich grains (pink in Fig. 1, bottom right inset).
“Region (b)” is a ∼2 μm thick dense interphase region with a significantly higher Ca/Mn ratio compared to the bulk CaMnO3−δ (green layer in Fig. 1, bottom right inset). Chemical analysis, topographically performed across the junction (Fig. 2), is in agreement with the observations from Fig. 1. The variations in the concentration of Ca, Mn and Co across the interface are given in Fig. 2b. Mn is seen to diffuse far into the porous Ca3Co4−xO9+δ, while the Mn concentration in Region (b) is lower than in the main bulk phase of CaMnO3−δ. Enhanced level of Ca is observed in Region (b) (interphase region) while a depletion in Ca is obvious in Region (a) (porous region). There is a moderate gradient in the Co concentration all through the Ca3Co4−xO9+δ layer until we reach the boundary between Region (a) and (b), followed by a steep decrease across Region (b).
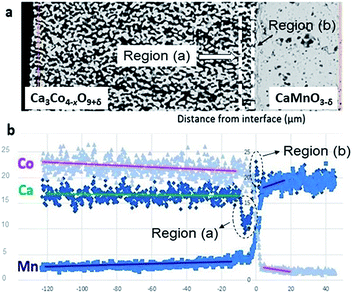 | ||
| Fig. 2 (a) SEM micrograph of the area analyzed by EDS. (b) Corresponding EDS diffusion profiles of Co, Mn and Ca. Unit of abscissa in μm and unit of ordinate in at%. | ||
Co is also seen to diffuse rather far into the CaMnO3−δ phase. This is in agreement with our recent data on bulk and enhanced grain boundary diffusivity of Co into CaMnO3−δ,25 where the bulk diffusivity at 900 °C would predict a diffusion length of 0.1 μm, while the enhanced grain boundary diffusion can explain the length closer to 10 μm in Fig. 2b. The faster diffusion of Mn into Ca3Co4−xO9+δ is most probably related to the porosity promoting enhanced surface diffusion. After careful surface polishing from the Ca3Co4−xO9+δ side (Fig. 3a), the polished surface was subjected to SEM/EDS analysis.
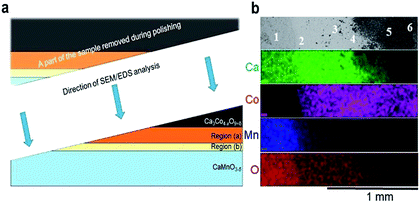 | ||
| Fig. 3 (a) A schematic illustration of the polished sample prior to SEM/EDS analysis. The figure is not drawn to scale, and Regions (a) and (b) are extended for the sake of clarity. (b) Plane view of back scattered electron image (uppermost section) followed by corresponding EDS maps of Ca (green), Co (pink), Mn (blue) and O (red). The assessment of the chemical composition was supplemented by spot EDS analysis according to the positions numbered from 1 to 6 in the uppermost section, and the results are given in Table 1. | ||
EDS elemental maps were taken along the surface (4 lowermost sections in Fig. 3b) and quantitative EDS analyses were made at 6 positions (“spots”) according to the numbering given in Fig. 3b (uppermost section). The results of the quantitative EDS analysis are given in Table 1. The compositions in positions 1 and 5 correspond to CaMnO3−δ and Ca3Co4−xO9+δ, respectively, while position 6 most probably correspond to mixture of Ca3Co4−xO9+δ and Co3O4. Position 3 (Region (b)) correspond to the quaternary phase, Ca3Co1+yMn1−yO6,22–24 where the ratio between Ca and the sum of Mn and Co is 1.53 which is close to 1.5 as expected in Ca3Co1+yMn1−yO6. We suggest that position 4 is representative for the porous region (Region (a)) due to the ratio Ca/(Mn + Co) is 1.33, which is between Ca3Co4−xO9+δ (≈0.75) and Ca3Co1+yMn1−yO6 (1.53), hence a mixture of Ca3Co1+yMn1−yO6 and Ca3Co4−xO9+δ. Position 2 shows a cation ratio between CaMnO3−δ and Ca3Co1+yMn1−yO6 and may be a mix of these two phases. It should be emphasized that there are uncertainties related to these calculations, both in the accuracy of the measurement as well as the fact that spot analysis also may include elements from phases below the point of analysis. Besides Ca redistribution, a thin densified reaction layer of Ca3Co1+yMn1−yO6 is formed as a result of Co entering into CaMnO3−δ. Variations in the Co/Mn ratio across the Ca3Co1+yMn1−yO6 reaction layer is expected as this forms a diffusion barrier for both cations and allows a wide range of mixing ratios, as seen from the steepness of both the Mn- and Co-profiles in Region (b) (Fig. 2).
| Spot | Ca | Co | Mn | O | Co + Mn | Ca/(Co + Mn) | Phase | Region |
|---|---|---|---|---|---|---|---|---|
| 1 | 20 | 0–1 | 20 | 60 | 20 | 1.00 | CaMnO3−δ | — |
| 2 | 28 | 6 | 14 | 53 | 20 | CaMnO3−δ/Ca3Co1+yMn1−yO6 | — | |
| 3 | 29 | 11 | 8 | 53 | 19 | Ca3Co1+yMn1−yO6 | (b) | |
| 4 | 28 | 13 | 8 | 52 | 21 | Ca3Co1+yMn1−yO6/Ca3Co4−xO9+δ | (a) | |
| 5 | 20 | 22 | 3 | 57 | 25 | Ca3Co4−xO9+δ | — | |
| 6 | 16 | 23 | 2 | 60 | 25 | Ca3Co4−xO9+δ | — | |
| CaMnO3−δ | 1 | — | ||||||
| Ca3Co1+yMn1−yO6 | 1.5 | — | ||||||
| Ca3Co4−xO9+δ | 0.75 | — |
Besides, a thermopower across the Ca3Co1+yMn1−yO6 reaction layer in TEG is directly affected by the Co/Mn ratio in Ca3Co1+yMn1−yO6, where the thermopower increases as Co/Mn ratio decreases.24
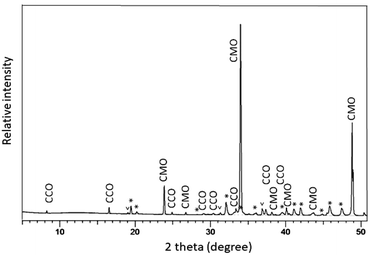
The polished plane view surface was further analyzed by XRD for phase clarification, where the main reflections corresponded to CaMnO3−δ and Ca3Co4−xO9+δ (Fig. 4).
With respect to the annealing temperature (900 °C), which is close to the Co3O4/CoO phase transition in air,26 Co will definitely be oxidized during cooling and at room temperature to exist as Co3O4. The broad and unsymmetrical set of reflections marked with “*” fits well to the trigonal structure of Ca3Co1+yMn1−yO6 with space group R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c.22 These results are in good agreement with our EDS compositional analysis (Fig. 3 and Table 1).
c.22 These results are in good agreement with our EDS compositional analysis (Fig. 3 and Table 1).
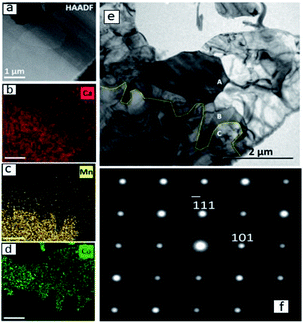
A detailed TEM/EDS analysis of the interface between CaMnO3−δ and Region (b) is presented in Fig. 5, where (a) to (d) are STEM-image and EDS analysis, while (e) and (f) are TEM-image and SAD zone axis patterns, respectively. The most striking feature is the sharp boundary between CaMnO3−δ and Region (b) shown by the yellow line in Fig. 5(e). Above the yellow line the Ca3Co1+yMn1−yO6 phase is confirmed by the SAD [12−1] zone axis patterns shown in (f), and further supported by the EDS analysis in (b)–(d) showing the presence of Ca, Co and Mn. The absence of Co and presence of Ca and Mn below the yellow line ((b)–(d)) confirm the presence of only CaMnO3−δ in this region. Although we expect some diffusion of Co into the CaMnO3−δ phase (Fig. 2), the concentration is below the detection limit in (d).
The CaMnO3−δ grains are identified as the low temperature (LT) orthorhombic CaMnO3−δ phase (Fig. 4) and the appearance of the CaMnO3−δ grains in Fig. 5(e) indicate high defect concentration appearing as a line pattern.
The high defect concentration is probably due to tensile stresses in CaMnO3−δ originating from the phase transition between the high temperature cubic phase (HT) to the LT phase, which is followed by a significant volume contraction.
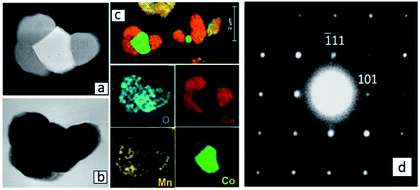
A detailed TEM/EDS analysis of Region (a) is given in Fig. 6. The EDS analysis in Fig. 6(c) confirms the formation of a Co-oxide rich phase, however connected to a phase containing Ca, Co and Mn. SAD [12−1] zone axis patterns identified this phase to be Ca3Co1+yMn1−yO6 (Fig. 6(d)) showing that Ca3Co1+yMn1−yO6 also may be formed quite far from the initial interface between Ca3Co4−xO9+δ and CaMnO3−δ. The reason for the formation of Ca3Co1+yMn1−yO6 far into Region (a) is a combination of Co depletion of the Ca3Co4−xO9+δ phase, due to diffusion of Co towards CaMnO3−δ, and counter diffusion of Mn into the Ca3Co4−xO9+δ phase (some solid solubility19,20). At some critical composition, Ca3Co4−xO9+δ will decompose and form Ca3Co1+yMn1−yO6 and a Co-oxide rich phase. The depletion of Ca in Region (a) (Fig. 2b) suggests that Ca diffuses towards Region (b), which is intuitively surprising since diffusion seemingly takes place against its concentration gradient.
However, assuming that the thermodynamic activity (chemical potential) of calcium in the Ca3Co4−xO9+δ-phase is much higher than in the Ca3Co1+yMn1−yO6-phase there will be a thermodynamic driving force for Ca-diffusion from Region (a) to Region (b). This explains the enhanced Ca concentration in Region (b) and Ca depletion in Region (a) (Fig. 2b). However, the formation of Ca3Co1+yMn1-yO6 depends on diffusion of Mn through the increasing layer of dense Ca3Co1+yMn1−yO6, which is expected to follow the parabolic law. Hence, the formation of Ca3Co1+yMn1−yO6 will virtually stop with time, corresponding to a fixed thickness of the Ca3Co1+yMn1−yO6 layer. The effect of counter diffusion and the formation of Ca3Co1+yMn1−yO6 on TEG performance is thoroughly elaborated in a previous paper by Kanas et al.6 Ca3Co1+yMn1−yO6 forms together with Ca3Co4−xO9+δ and CaMnO3−δ a p–p–n junction which exhibits ohmic behavior and a transverse thermoelectric effect, boosting the open-circuit voltage of the module. Furthermore, the electron energy levels of Ca3Co1+yMn1−yO6 are located intermediate of those of Ca3Co4−xO9+δ and CaMnO3−δ, which reduces the depletion of charge carriers at the Ca3Co4−xO9+δ–Ca3Co1+yMn1−yO6 and Ca3Co1+yMn1−yO6–CaMnO3−δ interfaces, as compared to initial Ca3Co4−xO9+δ–CaMnO3−δ p–n interface.6
DFT results for the mixing energy of Ca3Co1+yMn1−yO6 depicted in Fig. 7 show small negative values for the entire composition range, with a shallow minimum at y = 0.25, corresponding to a mixing energy of −5 meV per formula unit. According to the DFT calculations the most stable Ca3Co1+yMn1−yO6 composition should be in the vicinity of y ∼ 0.25, corresponding to a [Co]/[Mn] ratio of ∼1.67.
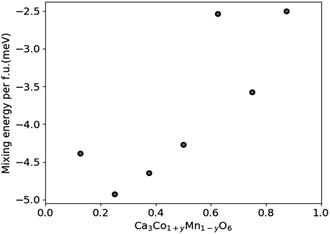 | ||
| Fig. 7 Calculated mixing energies of Ca3Co1+yMn1−yO6 as a function of y in Ca3Co1+yMn1−yO6. The scatter may reflect the limited size and number of atoms of the computational cell. | ||
Nevertheless, the negative mixing energy obtained in the entire range from y = 0.1 to 0.9 supports the existence of solid solubility in the whole range from y = 0 to 1, as confirmed by Hervoches et al.22 and Kanas et al.24 A small mixing energy is reasonable given that Co and Mn have similar atom sizes, and the DFT result serves to confirm that the nature of chemical bonding is not greatly affected by the substitution. At finite temperature the free energy would clearly show a broad minimum dominated by the entropy term which was not considered in these 0 K calculations.
All in all, the comprehensive structural analysis of the Ca3Co4−xO9+δ/CaMnO3−δ p–n junction gives an important overview of the complexity, described by counter diffusion and formation of several reaction products at the interface. In high-temperature applications the hot side of this TEG boosts the overall performance through a high open circuit voltage which occurs due to counter diffusion of cations resulting in formation of Ca3Co1+yMn1−yO6 with a high thermopower.6,24
Conclusions
The Ca3Co4−xO9+δ/CaMnO3−δ p–n junction is not stable at 900 °C as a new Ca3Co1+yMn1−yO6 intermediate phase forms through counter diffusion of Ca, Co and Mn. On the CaMnO3−δ side, a thin dense layer of Ca3Co1+yMn1−yO6 with variable composition forms, in which further in-diffusion of Co is slow. On the Ca3Co4−xO9+δ side, Mn diffusion into Ca3Co4−xO9+δ together with Co deficiency gives decomposition into Ca3Co1+yMn1−yO6 and Co-oxide. The diffusion profiles are in qualitative agreement with our recently published data on Co diffusion in CaMnO3−δ. DFT calculations and experimental evidence support the wider homogeneity range (0 ≤ y ≤ 1) of Ca3Co1+yMn1−yO6.Experimental
Phase-pure CaMnO3−δ powder was synthesized by solid-state reaction using a stoichiometric ratio of CaCO3 (Inframat Advanced Materials, >99% purity) and MnO2 (Sigma Aldrich, >99% purity) precursors, mixed and heated twice at 1200 °C for 14 h in air with grinding in between. A dense CaMnO3−δ pellet (diameter 12 mm, thickness 4 mm) was formed by cold isostatic pressing (CIP) at 200 MPa followed by sintering at 1300 °C for 14 h in air using a heating rate of 200 K h−1 and cooling rate of 100 K h−1. The dense CaMnO3−δ pellet was ground and polished with SiC papers and diamond paste to 1 μm. Ca3Co4−xO9+δ powder, with the nominal stoichiometry Ca3Co4O9+δ, was prepared by spray pyrolysis (CerPoTech AS, Norway), and a Ca3Co4−xO9+δ layer was produced by tape casting according to ref. 6. The tape was cast, laminated, and attached onto the polished CaMnO3−δ surface by pressing at 10 MPa and 80 °C for 3 min. The sample was then calcined at 450 °C for 1 h in air to remove organics and further heated at 900 °C for 10 h. Firm adhesion between Ca3Co4−xO9+δ and CaMnO3−δ was obtained after the heat treatment.The sample was subsequently embedded in epoxy and divided in pieces for both cross section and plane view examinations. The specimens were ground with SiC paper, and final polishing was done with colloidal Al2O3 (0.05 μm). For the plane view examination, the specimen was polished down stepwise from the Ca3Co4−xO9+δ side. The exposed area was analyzed by scanning electron microscopy (SEM) with energy dispersive X-ray energy dispersive spectroscopy (EDS) and X-ray diffraction (XRD) in between each polishing step. Cross section specimens were examined by a combination of SEM and transmission electron microscopy (TEM) enabling structural studies at both micro- and nanoscale. The TEM specimen, covering a ∼15 μm long region across the CaMnO3−δ/Ca3Co4−xO9+δ interface, was cut out by use of a focused ion beam (FIB) and thinned down to about 100 nm. EDS was conducted to map and quantify the elemental composition globally and locally by SEM and TEM, respectively. To improve statistics, line scan data sets were added after aligning the onset of the dense interface region.
A Rigaku MiniFlex600 system using Cu Kα radiation and florescence correction was used for the XRD investigation, while a Hitachi TM3000 SEM, a JEOL2010F TEM operated at 200 kV and a Cs probe corrected FEI Titan G2 60-300 TEM operated at 300 kV were used for the SEM and TEM studies.
The mixing energy of Ca3Co1+yMn1−yO6 was calculated within the spin-polarized density functional theory (DFT) utilizing the projector-augmented-plane wave method as implemented in VASP,27,28 and choosing the generalized-gradient approximation functional PBE.29 A supercell consisting of 2 × 2 × 2 primitive unit cells was used to emulate the solid solution, which was set up by randomly replacing 2, 4, 6, 8, 10, 12, and 14 of the 16 Mn atoms with Co atoms in the Ca3Co1+yMn1−yO6 supercell. To obtain an estimate of the mixing energy, we rely on a ferromagnetic ordering with spin aligned in intra-chain (111) direction. The plane-wave energy cutoff was set to 520 eV with a 2 × 2 × 2 Monkhorst–Pack k-point sampling of the Brillouin zone. Atomic coordinates and unit cell were relaxed until the total energy varied by less than 0.03 meV per formula unit.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
Financial support from the Research Council of Norway under the program Nano2021 to the project (number 228854) “Thermoelectric materials: Nanostructuring for improving the energy efficiency of thermoelectric generators and heat-pumps” (THELMA) conducted by NTNU, UiO, SINTEF, FFI, UiS and UiA.References
- S. Twaha, J. Zhu, Y. Yan and B. Li, Renewable Sustainable Energy Rev., 2016, 65, 698–726 CrossRef CAS.
- W. Liu, Q. Jie, S. E. Kim and Z. Ren, Acta Mater., 2015, 87, 357–376 CrossRef CAS.
- A. Becker, R. Chavez, N. Petermann, G. Schierning and R. Schmechel, J. Electron. Mater., 2013, 42, 2297–2300 CrossRef CAS.
- R. Chavez, S. Angst, J. Hall, F. Maculewicz, J. Stoetzel, H. Wiggers, L. T. Hung, N. Van Nong, N. Pryds, G. Span, D. E. Wolf, R. Schmechel and G. Schierning, J. Phys. D Appl. Phys., 2018, 51, 014005 CrossRef.
- G. Span, M. Wagner, S. Holzer and T. Grasser, 25th International Conference on Thermoelectrics, ICT, Vienna, 6–10 August, 2006 Search PubMed.
- N. Kanas, M. Bittner, S. P. Singh, T. D. Desissa, T. Norby, A. Feldhoff, T. Grande, K. Wiik and M.-A. Einarsrud, ACS Omega, 2018, 3, 9899–9906 CrossRef CAS.
- E. Woermann and A. Muan, J. Inorg. Nucl. Chem., 1970, 32, 1455–1459 CrossRef CAS.
- D. Sedmidubsky, V. Jakes, O. Jankovsky, J. Leitner, Z. Sofer and J. Hejtmanek, J. Solid State Chem., 2012, 194, 199–205 CrossRef CAS.
- N. Kanas, S. P. Singh, M. Rotan, M. Saleemi, M. Bittner, A. Feldhoff, T. Norby, K. Wiik, T. Grande and M.-A. Einarsrud, J. Eur. Ceram. Soc., 2018, 38, 1592–1599 CrossRef CAS.
- Y. Miyazaki, Solid State Ionics, 2004, 172, 463–467 CrossRef CAS.
- Y. Miyazaki, M. Onoda, T. Oku, M. Kikichi, Y. Ishii, Y. Ono, Y. Morii and T. Kajitani, J. Phys. Soc. Jpn., 2002, 71, 491–497 CrossRef CAS.
- A. C. Masset, C. Michel, A. Maignan, M. Hervieu, O. Toulemonde, F. Studer and B. Raveau, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, 166–175 CrossRef CAS.
- M. Schrade, H. Fjeld, T. G. Finstad and T. Norby, J. Phys. Chem. C, 2014, 118, 2908–2918 CrossRef CAS.
- K. R. Poeppelmeier, M. E. Leonowicz, J. C. Scanlon, J. M. Longo and W. B. Yelon, J. Solid State Chem., 1982, 45, 71–79 CrossRef CAS.
- H. Taguchi, M. Nagao, T. Sato and M. Shimada, J. Solid State Chem., 1989, 78, 312–315 CrossRef CAS.
- E. I. Goldyreva, I. A. Leonidov, M. V. Patrakeev and V. L. Kozhevnikov, J. Solid State Electrochem., 2016, 16, 1187–1191 CrossRef.
- E. I. Leonidova, I. A. Leonidov, M. V. Patrakeev and V. L. Kozhevnikov, J. Solid State Electrochem., 2011, 15, 1071–1075 CrossRef CAS.
- B. V. Golovkin and G. V. Bazuev, Russ. J. Gen. Chem., 2010, 80, 213–218 CrossRef CAS.
- A. Bhaskar, C.-J. Liu and L.-C. Huang, J. Electroceram., 2013, 31, 129–133 CrossRef CAS.
- J. L. Chen, Y. S. Liu, C.-J. Liu, L.-C. Huang, C. L. Dong, S. S. Chen and C. L. Chang, J. Phys. D: Appl. Phys., 2009, 42, 135418–135423 CrossRef.
- V. G. Zubkov, G. V. Bazuev, A. P. Tyutyunnik and I. F. Berger, J. Solid State Chem., 2001, 160, 293–301 CrossRef CAS.
- C. H. Hervoches, H. Okamoto, A. Kjekshus, H. Fjellvåg and B. C. Hauback, J. Solid State Chem., 2009, 182, 331–338 CrossRef CAS.
- G. V. Bazuev, V. G. Zubkov, I. F. Berger and V. N. Krasil’nikov, Russ. J. Inorg. Chem., 2001, 46, 317–322 Search PubMed.
- N. Kanas, S. P. Singh, T. D. Desissa, T. Norby, K. Wiik, T. Grande and M.-A. Einarsrud, Materials, 2019, 12, 497–507 CrossRef CAS.
- T. D. Desissa, N. Kanas, S. P. Singh, K. Wiik, M.-A. Einarsrud and T. Norby, Phys. Chem. Chem. Phys., 2018, 20, 2754–2760 RSC.
- M. Chen, B. Hallstedt and L. J. Gauckler, J. Phase Equilib., 2003, 24, 212–227 CrossRef CAS.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2020 |