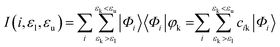Open Access Article
Open Access ArticleA first-principles computational comparison of defect-free and disordered, fluorinated anatase TiO2 (001) interfaces with water†
Kyle G. Reeves *ab,
Damien Dambournet
*ab,
Damien Dambournet ab,
Christel Laberty-Robert
ab,
Christel Laberty-Robert bc,
Rodolphe Vuilleumier
bc,
Rodolphe Vuilleumier d and
Mathieu Salanne
d and
Mathieu Salanne ab
ab
aSorbonne Université, CNRS, UMR 7574, Physico-chimie des électrolytes et nanosystèmes interfaciaux, PHENIX, Paris, France. E-mail: kyle.reeves@sorbonne-universite.fr
bRéseau sur le Stockage Electrochimique de L'Energie (RS2E), FR CNRS 3459, 80039 Amiens, France
cSorbonne Université, CNRS, UMR 7574, Collège de France, LCMCP, Paris, France
dPASTEUR, Département de Chimie, École Normale Supérieure, PSL University, Sorbonne Université, CNRS, 75005 Paris, France
First published on 2nd March 2020
Abstract
Chemical doping and other surface modifications have been used to engineer the bulk properties of materials, but their influence on the surface structure and consequently the surface chemistry are often unknown. Previous work has been successful in fluorinating anatase TiO2 with charge balance achieved via the introduction of Ti vacancies rather than the reduction of Ti. Our work here investigates the interface between this fluorinated titanate with cationic vacancies and a monolayer of water via density functional theory based molecular dynamics. We compute the projected density of states for only those atoms at the interface and for those states that fall within 1 eV of the Fermi level for various steps throughout the simulation, and we determine that the variation in this visualization of the density of states serves as a reasonable tool to anticipate where surfaces are most likely to be reactive. In particular, we conclude that water dissociation at the surface is the main mechanism that influences the anatase (001) surface whereas the change in the density of states at the surface of the fluorinated structure is influenced primarily through the adsorption of water molecules.
1. Introduction
Investigating clean energy systems is becoming increasingly important in order to address future energy and environmental demands. Hydrogen generation from liquid water using sunlight at catalytic interfaces is a promising approach to generate large volumes of carbon-free chemical fuels that can be used in photo-electrochemical cells (PECs).1–3 This process of water splitting was first demonstrated by Fujishima and Honda in their work with aqueous rutile titanium dioxide (TiO2) interface.4 Despite successfully having split water, the efficiency of the reaction remains low. Photo-reactivity on various surfaces of other polymorphs (e.g. anatase and brookite) suggests that challenges associated with the rutile structure may be better understood by further investigating the dynamics at these alternative TiO2 surfaces.5One such challenge is the optical bandgap of the material. Electron–hole pairs generated following photo-absorption migrate to the material's surface and are the species that ultimately drive the photocatalytic reactions. The size of a material's bandgap therefore limits the amount of the solar spectrum that can be absorbed by the material, and consequently the number of electron–hole pairs that can be generated. Thus, one approach to improving the photocatalytic efficiency of a material is to reduce the optical bandgap, often via chemical doping. This approach has been used widely in semiconductor physics to influence carrier concentrations and energetics, and in particular, this approach is useful to influence the material's bandgap.6–8
Physical processes in heterogeneous photocatalysis occur at material interfaces. Thus, while the bulk properties play a key role in the initial step of photo-absorption, examining only the bulk properties of the material will fall short of capturing the essential physics at the interface that drives the catalysis. Moreover, the electronic structure is sensitive to the surface structure and termination. The position and character of the band edges, for example, are sensitive to the surface structure, composition and termination.9 This complex relationship of surface structure and composition makes it less obvious which substitutions and subsequent reconstructions of the surface may lead to an increased photocatalytic activity. This relationship between surface structure and the dynamics of liquid water has been studied for the pristine rutile TiO2 (001) surface by Michaelides et al. who concluded that the distinct layers of water with differing dynamics can be generated as a result of interactions with the varying features of the surface (e.g. bridging oxygen atoms, five-fold coordinated Ti sites, etc.).10
Amongst the many polymorphs of TiO2, rutile and anatase have been the most extensively studied for use in photocatalytic water splitting.11–15 In the case of anatase, the (101) has been shown to be the majority surface in anatase nanoparticles. Unlike rutile TiO2 (110) surface and anatase (101), less is known about how water behaves at the anatase (001) surface. While the surface energy of this surface is larger than that of the (101), we investigate this (001) because of its reported greater photocatalytic activity.16 In this work, we therefore investigate the anatase TiO2 (001) surface. Additionally, this facet has been known to contribute a greater percentage of the TiO2 surfaces following fluorination.17 Fluorination of anatase has commonly been used as a means to stabilize the (001) facet via surface interactions during synthesis, but the role of fluorine atoms that have been incorporated into the anatase lattice remains poorly understood.18,19 Previously, work investigating the influence of fluorine doping in titanium dioxide suggested that the presence of fluorine atoms led to the reduction of Ti4+ to Ti3+.18 Contrary to this study, another material that incorporates fluorine into the lattice was recently synthesized where cationic vacancies are incorporated in the lattice to balance the additional charge of the fluorine dopant ions.20 This alternative mechanism for the incorporation of fluorine atoms into the lattice likely has a significant impact on the surface of the fluorinated titanate and therefore the chemistry that may occur at the surface.
In order to explore the implications of cationic vacancies at the surface, we begin our investigation from another theoretical work performed by Corradini et al.21 who proposed a possible atomistic structure for the bulk fluorinated titanate which was corroborated via synchrotron data on the experimental material. This investigation identified the lowest energy candidate structures by rigorously varying compositions and arrangements of the fluorinated titanate (1.5 × 105 configurations) with additional steps to consider variations in the lattice constants. Moreover, as the collection of candidate structures was narrowed down, density functional theory molecular dynamics (DFT-MD) simulations were performed to follow the evolution of the structure over 10 ps at 300 K. Given this extensive work, we assume a structure taken from the end of the DFT-MD simulation would be a reasonable first guess to begin this study. The material synthesized in the previous work showed roughly 22% vacancies. From their result, it was clear that the fluorination led to a greater degree of structural disorder in the material. This distortion to the lattice was due to the introduction of titanium vacancies required to maintain charge balance: every four oxygens that are substituted by fluorine must also be accompanied by a titanium(IV) vacancy. While the general structure of the anatase is identifiable, the large number of vacancies generate a noticeable amount of distortion in the system. Moreover, the slight mismatch in the Ti–O and Ti–F bond lengths (∼1.8 Å and ∼2.0 Å respectively) lead to an additional contribution to the distortion of the overall structure. As a result of the previously mentioned differences in the bulk structure, the surface of the fluorinated titanate also shows a greater variation in both the structural arrangement of atoms and the chemical composition.
Ultimately, the proposed structure for this work is one for the bulk material. It remains unclear, however, what the interfacial structure and the surface termination might be (i.e. the role of new elements and defects). It is the aim of this work, therefore, to provide insight into the nature of the fluorinated anatase surface and how the variation in the surface in both terms of chemistry and structure can influence the reactivity and chemical nature of the surface. For comparison, we will use the anatase (001) as a reference interface. We will systematically explore these two surfaces by considering the electronic structure of the interface of each material with vacuum and then later with a monolayer of water molecules.
2. Methodology
Density functional theory calculations
The DFT-MD simulations were performed using the CP2K code22 via the Quickstep algorithm.23 For both systems, we perform the density functional theory calculations using via Γ-point sampling, and periodic boundary conditions were applied. The simulations were performed at the generalized-gradient approximation level using the PBE exchange-correlation functional.24 For the basis set, we used DZVP-MOLOPT-SR-GTH to construct the Kohn–Sham wavefunctions with a plane wave cut-off of 400 Rydberg. Goedecker–Teter–Hutter pseudopotentials25 were used to describe core electrons, where Ti atoms were represented explicitly using 3s23p63d24s2 electronic orbitals, and O atoms were represented using 2s22p4 electronic orbitals. We performed our simulations at a temperature of 330 K with a Nosé–Hoover thermostat26,27 with a time constant of 25 fs. The integration timestep was 0.5 fs. The molecular dynamics simulations were performed each for 1.5 ps, for which we observed the initial local rearrangement of the first water layer. Longer simulations may be performed in the future to understand the nature of the surface beyond this initial rearrangement. To compute the density of states, atomic positions were taken for time steps in the DFT-MD trajectories indicated in each additional figure. The density of states calculations and atomic orbital projections were performed with the Quantum Espresso package.28,29 DFT+U30,31 was used with U = 3.3 eV, a value used in previous work on anatase.16Electronic structure of the vacuum interface
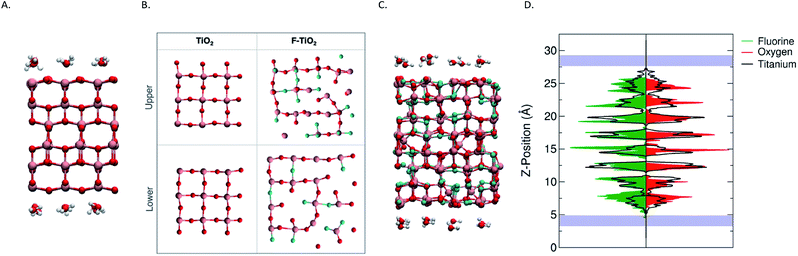
The slabs of the pristine anatase TiO2 and the fluorinated TiO2 were constructed such that the (001) surfaces were perpendicular to the z-axis of the simulation cell, producing two different surfaces to investigate. To construct the simulation cell for the pure anatase, the coordinates and lattice parameters for anatase TiO2 were taken from experiment, and a 3 × 3 × 2 supercell was constructed. The supercell was then cleaved on both the top and bottom (z-direction) of the cell to expose the (001) surface, leaving intact the rows of 2-fold coordinated oxygens and coordinating the layer of Ti atoms adjacent to them. It is known from previous studies of the (001) surface that these oxygens that play the dominant role in the water splitting surface reactions.32 The slab was then centred in the z-direction of the simulation cell with approximately 12.5 Å of vacuum above and below the slab for a final simulation cell size of 11.3535 Å × 11.3535 Å × 32.500 Å. The surface energy for the pure anatase (001) interface was computed to be 1.19 J m−2, which we note is slightly higher than existing literature values.33 The simulation cell for the fluorinated TiO2 was constructed by starting with the structure proposed by Corradini et al. This proposed structure was derived from a 4 × 4 × 2 supercell and represents the likely structure of the fluorinated anatase in bulk. The surface energy for the fluorinated system was computed to be 1.70 J m−2.Despite the different elemental composition and the presence of vacancies in the material, the proposed relaxed structure remains identifiable as the anatase structure. Ti layers in the (001) remain distinctly separate, and, therefore, it is still possible to identify and to construct the (001) surface by defining a plane that separates these parallel Ti layers. After computing the forces for the initial structure, we do not observe a compression nor tensile force at the interface. Larger forces are observed initially on titanium atom, however the direction of the forces appear to be influenced primarily by the local atomic environment. Again, the slab was centred in the simulation cell and a vacuum of ∼10 Å was added above and below for a final simulation cell size of 15.078 Å × 15.078 Å × 30.00 Å. It should be noted that because of the variability in the distribution of cationic vacancies in the material, the plane through which the material is cleaved results in different exposed surfaces and this consequently influences the relative numbers of interfacial oxygens and fluorine atoms as well as the number of cationic vacancies at the interface. The atoms shown in Fig. 1B represent only the top-most layers.
During the simulations, the layers of both oxygen and titanium atoms in the centre of the slab were frozen to keep the slab from drifting during the simulation as well as to approximate the more rigid mechanical properties of the bulk material away from the surface. In the case of the fluorinated TiO2 system, the atoms were not fix. In the case of the pure anatase, it is obvious that the upper and lower surfaces (Fig. 1B) resemble one another due to the periodicity of the material. The advantage of constructing the simulation cell in this way is clearer when we compare the two fluorinate surfaces. The bulk structure was cleaved in an effort to generate the greatest variety in local environments at the fluorinated surfaces. The initial surface stoichiometry of the top and bottom surfaces (defined as those atoms within 2.5 Å of the outermost atom) are TiO1.667F0.733 and TiO1.692F1.2308, respectively in comparison to the overall TiO1.44F1.12 stoichiometry of the overall simulation cell. Thus, one surface represents a slightly fluorine-rich surface while the other surface represents a slightly fluorine-poor surface with respect to the overall fluorinate material. These stoichiometries while a reasonable approximation will vary slightly depending on the choice of the cut-off distance. Moreover, the broad distributions of elements at the surface support our interpretation that the surface structure of the fluorinated titanate is relatively flexible. One feature that is clear is the presence of cationic vacancies at the surface. This creates areas of the surface that are under-coordinated. The variation in the local chemical environment (i.e. Ti atoms surrounded by oxygen or fluorine) is also apparent when comparing the upper and lower slab surfaces. This variety of local environments provides us with a broader insight into the nature of the fluorinated surface and how these variations influence the interface's reactivity. While these two surfaces are indeed limited in the chemical environments which are represented, we believe that the variety observed at the interfaces shown in Fig. 1B may serve as a reasonable starting point.
In this work, we focus on the interfacial electronic structure for each system in order to understand its response when exposed to solvent molecules. We, therefore, propose an approach which investigates the electronic structure of the surface by constructing a two-dimensional map of the density of states that corresponds only to those contributions from surface atoms. Not only does this approach give us some spatial resolution (e.g. atoms within a cut-off depth normal to the interface), but we also have the ability to identify contributions from specific elements. Moreover, given our interest in the reactivity of the surface, we also seek a tool that allows us to visualize only certain electronic states within a particular energy range, namely those states that fall at the band edges.
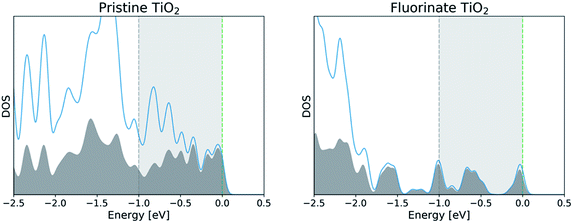
Atomic orbital projection34 is a well-known approach used to decompose electronic wavefunctions to understand the contributions from the hydrogenic wavefunctions corresponding to each of the atoms in the system. Assuming that the projection is able to account for a majority of the electron density (i.e. limiting electronic spilling), the projection of Kohn–Sham (KS) wave functions onto atomic orbitals can help to achieve our first goal of being able to partition and select for contributions from individual atoms. To achieve the energy selectivity, we project only those KS-wavefunctions that have corresponding eigenvalues that fall within an energy range of our choosing, here within 1 eV of the Fermi level. This approach can be formalized with the expression below,
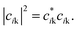
Given that we are interested in a two-dimensional cross-section of atoms (or a three-dimensional region with a shallow depth) of the simulation cell, we visualize this value of I2 as a two-dimensional plot by mapping the atom index i to its corresponding coordinates (xi, yi).
3. Results and discussion
Interfacial density of states: TiO2-vacuum interface
To characterize each surface's interface with the vacuum, we perform a density functional theory (DFT) calculation to determine the ground state electronic structure. We plot the density of states computed using CP2K for the full pristine and fluorinated TiO2 systems in Fig. 2. The contribution from the surface layers as previously defined are also noted in order to provide a greater context for the two-dimensional plot of the density of states that can be seen in Fig. 3. We show only one of the two layers for each slab for and electronic states that fall 1 eV below the computed Fermi level of the system to investigate the highest-energy valence states. In Fig. 3 (upper), we compute the greatest contribution of the density of states for the clean surface. We observe that the greatest contribution comes from the titanium atoms at the surface. Whereas previous studies that have investigated the density of states for anatase suggest a large Op character for the band edge,21 these calculations were performed for the bulk structure in which all titanium atoms were six-fold coordinated. In the case of the anatase (001) interface, the titanium atoms are under-coordinated with only five nearest oxygen atoms, and thus the additional electrons associated with the titanium are the highest energy, and therefore the most reactive.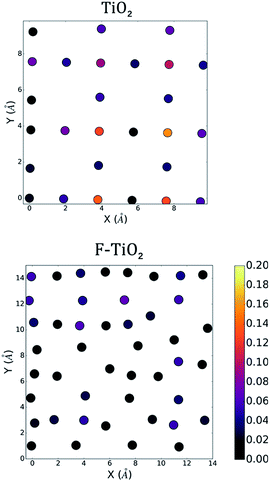 | ||
| Fig. 3 The density of states (HOMO-1 eV to HOMO) projected onto the surface atoms for the pure anatase and the fluorinated anatase interfaces. Positions of atoms are consistent with those found in Fig. 1B. Both surfaces, shown in the centre, are in contact with vacuum. Colour bar in units of states/eV unit cell. | ||
In Fig. 3 (lower), we see a similar case for the fluorinated anatase. The greatest contribution to the density of states again comes from under-coordinated titanium. We additionally observe a large contribution to the surface density of states from fluorine atoms. Visualizing the highest occupied molecular orbitals (HOMO) for each system, we observe a similar result (iso-surface plots in the ESI†). In the case of anatase, the five highest-energy Kohn–Sham single-particle wavefunctions are all localized at the surface of the system with strong d-orbital character, although not localized specifically on any one titanium atom. The case of the fluorinated anatase is less clear, however. Only one of the highest energy Kohn–Sham wavefunctions is localized at the surface. Thus, the highest reactivity in the structure can be attributed to the localized disorder within the structure, and in particular the titanium (cationic) vacancies in the centre of the simulation cell.
Water monolayer structure at TiO2 surfaces
In applications of photocatalysis such as water splitting, the interface is not exposed to vacuum, but instead solvated, likely by water. Water molecules adjacent to the surface are influenced by the electronic structure at the surface of the metal oxide, and similarly, the solvent molecules at the surface also influence the electronic structure at the surface. In the case of both rutile and anatase titanium dioxide, depending on the exposed facet, molecular dissociation and physisorption have been observed when the surface is exposed to water.32,35 Thus, in order to capture the possible changes to surface reactivity following the addition of a monolayer of H2O, we use density functional theory molecular dynamics (DFT-MD) simulations.It is known that solvent molecules at different distances away from metal oxide interfaces can have significantly different dynamics, and in particular, the first layer can be involved in very strong interactions or dissociative reactions.36 We limit our investigation to the monolayer as a means to understand how the surface is likely initially stabilized. The results of this preliminary simulation would likely serve as a reasonable starting point for longer simulations with bulk water.
We initialize the simulation cell by adding a single monolayer of water adjacent to each surface of the slab. We assume that no more than one titanium atom will interact with each interfacial water molecule at a given instant, and thus the number of water molecules in each monolayer is equal to the number of titanium atoms at the surface. In the case of the fluorinated anatase with titanium vacancies at the surface, a water molecule was nonetheless placed over the site where the titanium atom is replaced by a vacancy. Each layer was placed 2.5 Å away from the TiO2 surface, a distance greater than a typical Ti–O bond length yet small enough for water molecules to interact with the interface at the very beginning of the simulation. Each molecule was randomly oriented in space.
In the case of the monolayer of water on anatase (001), we immediately notice a large fluctuation in the density of states at the surface. At 45 fs (Fig. 4), we see a large increase in the density of states associated with one of the two-fold coordinate oxygen atoms at the surface but with the greatest increases associated with the Ti atoms along the line defined by x = 4 Å in the two-dimensional cross section (notably Ti atoms at y = 0 Å and 4 Å). This fluctuation is accompanied with the movement of water molecules in the direction of the surface, followed by a proton transfer from the water molecule to the bridging oxygen. The structure at 45 fs is associated with coordination of a water molecule to the Ti atom labelled as A in Fig. 4. This dissociative event is illustrated in the ESI† and is consistent with previously observed dissociative mechanism observed in previous works.32 We continued to run the TiO2/H2O monolayer simulation for roughly 1 ps at which point we determined that no further reactions were taking place. On the right-hand side of Fig. 4, we observe that the density of states has become more uniform and no longer shows the strong contribution from the titanium atoms. At the end of the simulation, we observed that on average 50% of the under-coordinated titanium atoms had bonded to a new OH– group at the surface as a result of the dissociation of water. This is consistent with the previous work of Sumita et al.32 Since one of the bridging oxygens atoms accepts a proton from one water, only one water molecule is needed to dissociate at the service to generate two hydroxyl groups coordinated to surface titanium atoms. After 500 fs, we also observe that those titanium atoms that have not formed a bond with a hydronium atom are instead coordinated by a water molecule.
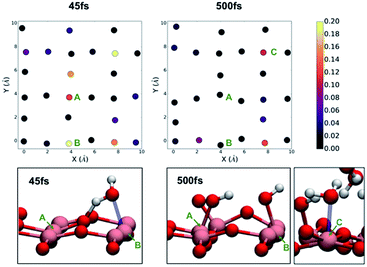 | ||
| Fig. 4 The density of states projected on the atoms of the anatase (001) surface after exposure to a monolayer of water at 45 fs (left) and 500 fs (right) into the DFT molecular dynamics simulations. | ||
In the case of the fluorinated anatase, we first visualize the density of states at the beginning of the simulation by parsing out individual contributions from each element. Along the left-hand side of Fig. 5, we can see that, as before, there is a large contribution to the density of states from the titanium atoms, although we now also observe an oxygen atom and several fluorine atoms that also contribute to the density of states associated with the valence band edge. Throughout the simulation, we observe three distinct categories of waters. First, there are water molecules that interact so weakly with the surface that they move away from the surface and into the vacuum. This accounts for 37.5% of the water molecules. A majority of the waters (62.5%) however remain close to the surface but do not dissociate. Throughout the simulation, we observe just two molecular dissociation events of the 32 water molecules in the simulation cell. In both of these cases, unlike the pristine TiO2, the dissociative event does not involve the bridging oxygens. Instead, we observed a different mechanism where the oxygen atoms adjacent to the cationic vacancy (O−) accept a proton from the water molecule, and in each case this dissociation results in one of the two titanium atoms bonding to the remaining OH− and changing from five-fold coordinated to six-fold coordinated. We can see from Fig. 5 that the density of states associated with the titanium atoms subsequently reduces after 750 fs into the simulation. Given that there are only two water molecules that reacted with the surface, we conclude from these results that it is not strictly dissociative events that lead to a reduced and more evenly distributed density of states at the surface as was the case in the pristine anatase, but rather this stabilization is likely due to a large extent to the physisorption of water molecules at the surface. This lack of reactivity at the fluorinated interface is also consistent with the previously mentioned observation that only one of the five highest occupied Kohn–Sham orbitals is localised at the interface.
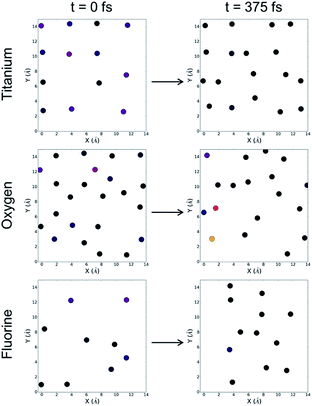 | ||
| Fig. 5 The density of states (HOMO-1 eV to HOMO) for the fluorinated anatase. Contributions are limited to titanium (top), oxygen (middle) and fluorine (bottom) atoms. The density of states at the surface are visualized at time 0 fs (left) and time 375 fs (right). The color bar is consistent with Fig. 3 and 4. | ||
Further examining Fig. 5, it becomes clear that the flexibility (i.e. the displacement of surface atoms throughout the simulation) of the pristine anatase and the fluorinated anatase interfaces represents one distinct difference between the two systems. The positions of the atoms at the fluorinated surface move significantly, both laterally and normal to the surface. This flexibility is directly related to the under-coordination introduced at the surface as a result of the presence of cationic vacancies. Ultimately, both the flexibility and rearrangement of the surface modulates the density of the states, so therefore it becomes challenging to identify the contribution of each of these two factors. Following the initial reactions and adsorption of molecules at the fluorinated surface, the density of states still has localized regions of higher energy electronic states. In particular, we see that some fluorine atoms retain high-energy electrons suggesting that they may be likely sites at the surface for oxidation to occur. Future work should also investigate the possible role of cationic defect sites in possible long-range reconstructions.
4. Conclusions
In conclusion, we first suggest that computing the density of states at material surfaces is a reasonable first step in determining reactivity of the surface. We visualized the surface states by projecting a narrow range of KS-wavefunctions below the Fermi level onto an atomic orbital basis set in order to localize the contributions spatially while only considering the electrons that are most likely to participate in the surface chemistry. We determined that the stabilization of the anatase is a result of water dissociation at the surface, whereas the stabilization of the fluorinated anatase is due to a single-layer of tightly-bound water molecules at the surface. In both cases, the water molecules played a key role in stabilizing the under-coordinated titanium atoms at the surface. Although via a different mechanism, we observe that cationic vacancies at the surface in the fluorinated system participate directly in the relatively rare instances of water dissociation. Additionally, these cationic vacancies lead to under-coordinated atoms at the surface which introduce greater flexibility at the surface. Future work naturally extends from this work to explore how additional layers of water (i.e. solid–liquid interfaces with bulk water) may be influenced by the new surface termination, and additionally to investigate the extent that the surface water molecules, particularly in the case of the fluorinated TiO2, exchange with water molecules in the bulk. This new understanding of the anatase and fluorinated anatase structures may also serve as a starting place for further studies investigating electron and hole localization at these interfaces.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The research leading to these results has received funding the cluster of excellence MATeriaux Interfaces Surfaces Environnement (MATISSE). We are grateful for the computing resources on MESU via the High-Performance Computing and Visualisation platform (HPCave) hosted by UPMC-Sorbonne Université and operated by the Institut des Sciences du Calcul et des Données (ISCD).References
- K. Sivula and R. van de Krol, Nat. Rev. Mater., 2016, 1, 15010 CrossRef CAS.
- C. Jiang, S. J. A. Moniz, A. Wang, T. Zhang and J. Tang, Chem. Soc. Rev., 2017, 46, 4645–4660 RSC.
- J. Joy, J. Mathew and S. C. George, Int. J. Hydrogen Energy, 2018, 43, 4804–4817 CrossRef CAS.
- A. Fujishima and K. Honda, Nature, 1972, 238, 37–38 CrossRef CAS.
- A. Vittadini, M. Casarin and A. Selloni, Theor. Chem. Acc., 2007, 117, 663–671 Search PubMed.
- T. Morikawa, R. Asahi, T. Ohwaki, K. Aoki and Y. Taga, Jpn. J. Appl. Phys., 2001, 40, L561 CrossRef.
- T. Umebayashi, T. Yamaki, H. Itoh and K. Asai, Appl. Phys. Lett., 2002, 81, 454–456 CrossRef.
- A. Walsh and A. Zunger, Nat. Mater., 2017, 16, 964–967 CrossRef.
- W. A. Smith, I. D. Sharp, N. C. Strandwitz and J. Bisquert, Energy Environ. Sci., 2015, 8, 2851–2862 RSC.
- L.-M. Liu, C. Zhang, G. Thornton and A. Michaelides, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 161415 CrossRef.
- M. Ni, M. K. H. Leung, D. Y. C. Leung and K. Sumathy, Renew. Sustain. Energy Rev., 2007, 11, 401–425 CrossRef CAS.
- T. A. Pham, Y. Ping and G. Galli, Nat. Mater., 2017, 16, 401 CrossRef CAS.
- E. Berardo and M. A. Zwijnenburg, J. Phys. Chem. C, 2015, 119, 13384–13393 CrossRef CAS.
- M. A. Henderson, Surf. Sci. Rep., 2011, 66, 185–297 CrossRef CAS.
- A. Fujishima, X. Zhang and D. A. Tryk, Surf. Sci. Rep., 2008, 63, 515–582 CrossRef CAS.
- S. Selcuk and A. Selloni, Nat. Mater., 2016, 15, 1107 CrossRef CAS.
- C. Sun, A. Selloni, A. Du and S. C. Smith, J. Phys. Chem. C, 2011, 115, 17092–17096 CrossRef CAS.
- A. M. Czoska, S. Livraghi, M. Chiesa, E. Giamello, S. Agnoli, G. Granozzi, E. Finazzi, C. D. Valentin and G. Pacchioni, J. Phys. Chem. C, 2008, 112, 8951–8956 CrossRef CAS.
- S. Yang and L. E. Halliburton, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 035204 CrossRef.
- W. Li, D. Corradini, M. Body, C. Legein, M. Salanne, J. Ma, K. W. Chapman, P. J. Chupas, A.-L. Rollet, C. Julien, K. Zhagib, M. Duttine, A. Demourgues, H. Groult and D. Dambournet, Chem. Mater., 2015, 27, 5014–5019 CrossRef.
- D. Corradini, D. Dambournet and M. Salanne, Sci. Rep., 2015, 5, 11553 CrossRef.
- J. Hutter, M. Iannuzzi, F. Schiffmann and J. Vandevondele, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 15–25 Search PubMed.
- J. VandeVondele and J. Hutter, J. Chem. Phys., 2007, 127, 114105 CrossRef PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef.
- S. Goedecker, M. Teter and J. Hutter, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 1703–1710 CrossRef.
- S. Nosé, J. Chem. Phys., 1984, 81, 511–519 CrossRef.
- S. Nosé, Mol. Phys., 1984, 52, 255–268 CrossRef.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. D. Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, K. Anton, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef.
- P. Giannozzi, O. Andreussi, T. Brumme, O. Bunau, M. B. Nardelli, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, M. Cococcioni, N. Colonna, I. Carnimeo, A. D. Corso, S. de Gironcoli, P. Delugas, R. A. DiStasio, A. Ferretti, A. Floris, G. Fratesi, G. Fugallo, R. Gebauer, U. Gerstmann, F. Giustino, T. Gorni, J. Jia, M. Kawamura, H.-Y. Ko, A. Kokalj, E. Küçükbenli, M. Lazzeri, M. Marsili, N. Marzari, F. Mauri, N. L. Nguyen, H.-V. Nguyen, A. Otero-de-la-Roza, L. Paulatto, S. Poncé, D. Rocca, R. Sabatini, B. Santra, M. Schlipf, A. P. Seitsonen, A. Smogunov, I. Timrov, T. Thonhauser, P. Umari, N. Vast, X. Wu and S. Baroni, J. Phys.: Condens. Matter, 2017, 29, 465901 CrossRef.
- M. Cococcioni and S. de Gironcoli, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 035105 CrossRef.
- V. I. Anisimov, J. Zaanen and O. K. Andersen, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 44, 943–954 CrossRef.
- M. Sumita, C. Hu and Y. Tateyama, J. Phys. Chem. C, 2010, 114, 18529–18537 CrossRef.
- H. Xu, P. Reunchan, S. Ouyang, H. Tong, N. Umezawa, T. Kako and J. Ye, Chem. Mater., 2013, 25, 405–411 CrossRef.
- D. Sanchez-Portal, E. Artacho and J. M. Soler, Solid State Commun., 1995, 95, 685–690 CrossRef CAS.
- F. De Angelis, C. Di Valentin, S. Fantacci, A. Vittadini and A. Selloni, Chem. Rev., 2014, 114, 9708–9753 CrossRef.
- H.-W. Wang, M. J. DelloStritto, N. Kumar, A. I. Kolesnikov, P. R. C. Kent, J. D. Kubicki, D. J. Wesolowski and J. O. Sofo, J. Phys. Chem. C, 2014, 118, 10805–10813 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9ra10415a |
| This journal is © The Royal Society of Chemistry 2020 |