Ab initio study on the excited states of pyrene and its derivatives using multi-reference perturbation theory methods

Abstract

Low-lying singlet excited states of pyrene derivatives originated from the ¹L_a and ¹L_b states of pyrene have decisive influences on their absorption and fluorescence emission behaviors. Calculation of these excited states with quantitative accuracy is required for the theoretical design of pyrene derivatives tailored to target applications; this has been a long-standing challenge for ab initio quantum chemical calculations. In this study, we explore an adequate computational scheme through calculations of pyrene and its phenyl-substituted derivatives using multi-reference perturbation theory (MRPT) methods. All valence π orbitals on the pyrene moiety were assigned to the active orbitals. Computational load was reduced by restricting the electron excitations within the active orbitals in the preparation of reference configuration space. A generalized multi-configuration quasi-degenerate perturbation theory (GMCQDPT) was adopted to treat the reference space other than the complete active space. The calculated ¹L_a and ¹L_b excitation energies of pyrene are in good agreement with the experimental values. Calculations of 1,3,6,8-tetraphenyl pyrene suggest that the energetic ordering of ¹L_a and ¹L_b is inverted through tetraphenyl substitution and its lowest singlet excited state is the ¹L_a parentage of pyrene, which is consistent with the experimentally deduced scheme. These results are not readily obtained by MRPT calculations with a limited number of active orbitals and single-reference theory calculations. Diphenyl pyrenes (DPPy) were also calculated at the same level of theory to investigate the dependence on the substitution positions of phenyl groups.

---

1. Introduction

Pyrene is one of the most well-studied polycyclic aromatic hydrocarbons (PAHs) because of its characteristic photophysical properties, such as prominent absorption bands and a fluorescence emission.¹ These properties can be tailored to meet specific requirements through modifications of its chemical structure;^2–11 therefore, pyrene derivatives are recognized as promising materials for organic light-emitting devices.^12–25 Pyrene is also well known for the formation of an excimer.^26–29 An aromatic excimer is a dimeric complex of the same aromatic molecules that is formed in the excited state. The fluorescence emission of an excimer was firstly observed for a pyrene solution by Förster and Kasper in 1954.²⁷ The excimer fluorescence emission band is significantly red-shifted, broad, and structureless, so that it is clearly distinguishable from that of the monomer. Given the substantial distinction between monomer and excimer emissions, as well as their sensitivity to the surrounding environments, pyrene is used to study the molecular structural properties of polymers^30–34 and macromolecules, such as proteins^35,36 and DNA.^37–42 It is also used as a probe in chemosensors that detect particular metal ions^43–51 and molecules.^52–55 The properties of an excimer are closely related to those of the monomer.^56–58 Thus, the excited states of pyrene and its derivatives have been vigorously investigated and still continue to attract much interest from scientists with respect to both fundamental studies and practical applications.^59–64

Pyrene has two important excited states, ¹L_a and ¹L_b in Platt's notation.⁶⁵ These excited states are closely relevant to the absorption and fluorescence emission behavior of pyrene. Excitation from the ground state to the ¹L_a state gives a prominent absorption band around 340 nm in the UV/Vis spectrum because of its large oscillator strength. In contrast, the oscillator strength of the ¹L_b state is negligibly small; the ¹L_b absorption band is barely visible in the absorption spectrum.⁶⁶ The ¹L_b state is the lowest singlet excited state and the ¹L_a state is the second lowest; therefore, the fluorescence emission of pyrene is of ¹L_b parentage according to Kasha's rule.⁶⁷ In substituted pyrene derivatives, the excitation energies and absorbance of these excited states are perturbed by the substituents. In some cases, even an energetic ordering of the ¹L_a and ¹L_b states is inverted as a result of the energy-level shifts of these excited states. 1,3,6,8-Tetraphyenyl pyrene (TPPy) is recognized as a typical example.^68,69 TPPy exhibits a relatively short fluorescence lifetime (τ ≈ 3 ns)^68,69 and a high fluorescence quantum yield (q_F = 0.9)⁷⁰ compared to pyrene (τ > 300 ns and q_F = 0.32).^68,69,71 These conspicuous changes in the photophysical properties can be attributed to an inversion of the energetic ordering of the ¹L_a and ¹L_b states through tetraphenyl substitution. Assuming the ¹L_a–¹L_b inversion, the fluorescence emission from TPPy originates from the ¹L_a-derived excited state of pyrene with a large oscillator strength, which is consistent with the experimental results.^68–70 Although this hypothetical mechanism based on the experimental findings was supported by theoretical studies that employed semi-empirical methods^68,69,72 and has been widely accepted, the ¹L_a–¹L_b inversion in TPPy still remains to be corroborated by ab initio calculations. Given such a background, a dependable computational scheme that enables accurate calculations of these excited states is required for the theoretical design of pyrene derivatives customized to target applications; therefore, the prediction of their energetic ordering is of particular importance.

Calculation of the ¹L_a and ¹L_b excited states of pyrene with quantitative accuracy has been a long-term challenge for ab initio quantum chemistry.⁷³ Time-dependent density functional theory (TDDFT)^74–78 has been recognized as an efficient approach to the excited states of large molecules^79,80 and is thus utilized in investigations of pyrene and its derivatives. Behind numerous successful results, comprehensive assessments indicate that TDDFT calculations yield inconsistencies in accuracy between the ¹L_a and ¹L_b excitation energies; in the worse cases, even the energetic ordering is incorrectly predicted.^73,81,82 Similar problems are known for TDDFT calculations of some other PAHs.^83–90 The second-order approximate coupled cluster singles and doubles (CC2) method is also widely used in the calculation of large molecules as an ab initio wave function approach.⁹¹ The energetic ordering of ¹L_a and ¹L_b of pyrene given by CC2 calculation is generally consistent with the experimental results. However, the incorporation of multi-configuration characters of excited states using single-reference methods such as CC2 is possibly insufficient, and could thus be responsible for the calculation errors. In this regard, multi-reference methods are expected to make up for this shortcoming.⁹² Bito et al. conducted multi-reference configuration interaction (MRCI) calculations as pioneering work,⁹³ followed by theoretical studies that utilized multi-reference perturbation theory (MRPT) methods,^73,81,94 such as multi-configuration quasi-degenerate perturbation theory (MCQDPT)⁹⁵ and complete active space second-order perturbation theory (CASPT2).⁹⁶ These methods adopt a complete active space self-consistent field (CASSCF) wavefunction⁹⁷ as their reference. The CAS involves all electron configurations generated by distributing active electrons among active orbitals. Consequently, the dimension rapidly increases with the number of active orbitals and electrons, which makes the routine computation impossible. Therefore, in these studies, a limited number of π orbitals and π electrons were selected from a total of 16 valence π orbitals and 16 valence π electrons to construct the reference CAS. Although the energetic ordering of ¹L_a and ¹L_b is correctly predicted in most of these calculations, absolute errors in the excitation energies of 0.2–0.7 eV remain, and the calculation accuracy is inconsistent between the ¹L_a and ¹L_b states. The discrepancies at the CASSCF level are much larger because dynamical electron correlation is not sufficiently incorporated.

Recent advances in theory and computational techniques have yielded significant progress. Freidzon et al. demonstrated that the ¹L_a and ¹L_b excitation energies of pyrene can be accurately predicted⁹⁸ using extended MCQDPT (XMCQDPT) method.⁹⁹ Nenov et al. performed second-order perturbation theory restricted active space (RASPT2) calculations¹⁰⁰ with the reference configuration space constructed using 16 π orbitals and 16 π electrons.¹⁰¹ The calculated excitation energies were in good agreement with the experimental values, even though the computational load was reduced by restricting the electron excitations within the active orbitals. Most recently, Noble et al. conducted multi-state CASPT2 calculations with the Cholesky decomposition technique^102,103 in their study of electronic relaxations from the S₃ state of pyrene.¹⁰⁴ The reference configuration space was prepared using 16 π orbitals and 16 π electrons, and the results were quite accurate. Lischka et al. carried out the calculations of paradigmatic aromatic molecules including pyrene using both multi-reference and single-reference methods.¹⁰⁵ In their results, the ¹L_a and ¹L_b excitation energies of pyrene calculated using the DFT/MRCI method¹⁰⁶ were in good agreement with the experimental values. The same authors successfully applied their calculation scheme to the study of large-sized aromatic dimers.¹⁰⁷ These studies suggest that the excited states of pyrene derivatives could also be calculated with quantitative accuracy by utilizing these advanced methods. Successful results with the full π valence reference space also imply that the incorporation of multi-configuration character is of key importance for accurate calculation.

In this study, we explore an adequate computational scheme that is suitable for the excited states of pyrene derivatives through calculations of pyrene and its phenyl substituted-derivatives shown in Fig. 1. Generalized multi-configuration quasi-degenerate perturbation theory (GMCQDPT)¹⁰⁸ was adopted in addition to the original MCQDPT. In contrast to the conventional multi-reference theories where the reference space is limited to the CAS, GMCQDPT allows more general types of reference. Accordingly, it has the potential to reduce the computational load without a significant decrease of accuracy and could enable the handling of pyrene derivatives with large system sizes.

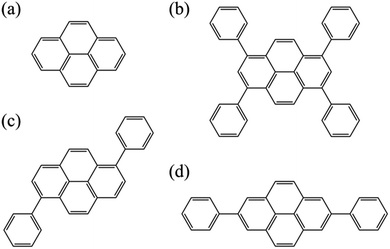Fig. 1 Molecular structures of (a) pyrene, (b) 1,3,6,8-tetraphenylpyrene (TPPy), (c) 1,6-diphenylpyrene (1,6-DPPy), and (d) 2,7-diphenylpyrene (2,7-DPPy).

2. Computational details

2.1. Reference wave functions for GMCQDPT

In the preparation of the reference wave function for GMCQDPT, the molecular orbitals are divided into three groups: inactive, active, and external orbitals. Whereas the inactive orbitals are always doubly occupied, external orbitals are always vacant. The electrons involved in the active orbitals are regarded as active electrons and the electron configurations are generated by distributing active electrons among active orbitals. The procedure so far is the same as that adopted in the construction of the CAS. Although any types of reference configuration space are available in GMCQDPT, the following three are proposed as typical examples: multi-reference determinant list plus excitations (MRX), restricted active space (RAS), and occupation restricted multiple active space (ORMAS).^109–111 In this study, the MRX type of reference was employed because of its simplicity. In the MRX framework, parent configurations and the electron excitation level, n, are defined. The excited configurations having n or less excited electrons from the parent configurations are involved into the reference space, in addition to the parent configurations themselves. If n is equal to the number of active electrons, then the reference space is identical with the CAS. The dimension of the reference space can be reduced by limiting the number of parent configurations and specifying n less than the number of active electrons.

In the GMCQDPT calculations of pyrene in this study, all 16 valence π orbitals were selected as active orbitals. Similarly, in the calculations of phenyl-substituted derivatives, the 16 π orbitals on their pyrene moieties were treated as active orbitals. The Hartree–Fock type ground state configuration with eight doubly-occupied π orbitals and eight unoccupied π* orbitals was defined as a parent configuration, and the n value was set at 2, 3 and 4. Henceforth, these reference spaces are denoted as MRX(n). GMCQDPT calculations were performed in the following two steps as well as the conventional CASSCF–MCQDPT procedure: multi-configuration self-consistent field (MCSCF) calculation with MRX(n) configuration space was firstly performed; the second-order perturbation calculation was subsequently conducted employing the obtained MCSCF function as its reference.

2.2. Calculations

The molecular geometrical structures were optimized using DFT with the B3LYP functional.^112,113 The ground and excited states were subsequently calculated at the optimized geometries. The absence of an imaginary number frequency was confirmed for all optimized structures by vibrational analyses. In addition to the GMCQDPT calculations, conventional CASSCF–MCQDPT calculations were also performed for comparison; CAS(4πe, 4πo), CAS(8πe, 8πo), and CAS(12πe, 12πo) were used as reference spaces. CAS{(2m)πe, (2m)πo} (m = 2, 4, and 6) was constructed using the m highest occupied and the m lowest unoccupied π orbitals on the pyrene moiety. The ground state, and the ¹L_a and ¹L_b excited states were averaged with even weights in the MCSCF calculations, and these three states were simultaneously perturbed in the MRPT calculations. Equations of motion coupled cluster singles and doubles (EOM-CCSD),^114,115 and TDDFT calculations with B3LYP, CAM-B3LYP,¹¹⁶ and ωB97XD¹¹⁷ functionals were also performed. The DPPy derivatives were calculated using GMCQDPT with MRX(4) and TDDFT. The cc-pVDZ basis set was used throughout the calculations.¹¹⁸ The molecular symmetries assumed were D_2h, D₂, C₂, and C_2h for pyrene,¹¹⁹ TPPy,¹²⁰ 1,6-DPPy, and 2,7-DPPy,¹²¹ respectively. MCSCF and MRPT calculations were performed using the GAMESS program.^122,123 Other calculations were conducted using Gaussian09.¹²⁴

3. Results and discussion

3.1. Calculation results

The calculated excitation energies and oscillator strengths are summarized in Table 1 along with available experimental values.^{119–121,125–128} According to the previous studies, the ¹L_a state of pyrene is characterized by two singly excited configurations: one is the highest occupied molecular orbital (HOMO) → the lowest unoccupied molecular orbital (LUMO) single excitation, and the other is the HOMO−1 → LUMO+1 single excitation. In contrast, HOMO−1 → LUMO and HOMO → LUMO+1 single excitations are dominant in the ¹L_b state.^119,129 The excited states were then identified on the basis of these configurations and related molecular orbitals. Fig. 2 shows the natural orbitals from HOMO−1 to LUMO+1 obtained using MCSCF with the MRX(4) configuration space. All natural orbitals from the MCSCF wave functions are presented in Fig. S1–S3.† Electronic state total energies and MCSCF excitation energies are listed in Table S1.†

Table 1 Calculated excitation energies and oscillator strengths. Available experimental values are also presented

Molecule	Method	Reference space	Number of electron configurations	^1La		^1Lb
				Excitation energy (eV)	Oscillator strength^a	Excitation energy (eV)	Oscillator strength^a
a Values are rounded off to four decimal places.b Ref. 125; adiabatic transition energies in vapor.c Ref. 126; gas-phase fluorescence excitation spectrum.d Ref. 127; λmax in acetonitrile.e Ref. 119; gas-phase fluorescence excitation spectrum.f Ref. 128; λmax in CH2Cl2.g Ref. 120; λmax in CH2Cl2.h Ref. 121; λmax in dilute CH2Cl2 (ca. 1 × 10^−5 M).
Pyrene	GMCQDPT	MRX(2)	4349	3.75	0.2030	3.17	0.0000
		MRX(3)	84 317	3.82	0.2511	3.31	0.0000
		MRX(4)	853 785	3.84	0.2308	3.40	0.0000
	MCQDPT	CAS(4πe, 4πo)	28	3.55	0.2170	2.83	0.0007
		CAS(8πe, 8πo)	3684	3.75	0.3997	3.26	0.0000
		CAS(12πe, 12πo)	640 432	3.83	0.3668	4.01	0.0001
	EOM-CCSD			4.45	0.3443	3.82	0.0001
	TD-B3LYP			3.68	0.2534	3.74	0.0001
	TD-CAM-B3LYP			3.98	0.3169	3.95	0.0001
	TD-ωB97XD			3.99	0.3216	3.96	0.0001
	Exptl.			3.85^b, 3.87^c, 3.71^d		3.41^b, 3.37^c^,^e
TPPy	GMCQDPT	MRX(2)	4349	3.11	0.2748	2.96	0.0000
		MRX(3)	84 317	3.27	0.3607	3.12	0.0001
		MRX(4)	853 785	3.07	0.2853	3.24	0.0000
	MCQDPT	CAS(4πe, 4πo)	28	2.92	0.3832	2.60	0.0028
		CAS(8πe, 8πo)	3684	3.15	0.5360	3.04	0.0003
		CAS(12πe, 12πo)	640 432	3.69	0.5381	3.58	0.0000
	EOM-CCSD			3.91	0.9563	3.65	0.0001
	TD-B3LYP			3.13	0.7128	3.49	0.0003
	TD-CAM-B3LYP			3.47	0.8555	3.76	0.0008
	TD-ωB97XD			3.50	0.8649	3.77	0.0007
	Exptl.			3.24^f, 3.15^g
1,6-DPPy	GMCQDPT	MRX(4)	1 138 281	3.39	0.2438	3.31	0.0169
	TD-B3LYP			3.35	0.6050	3.61	0.0025
	TD-CAM-B3LYP			3.69	0.7010	3.85	0.0085
	TD-ωB97XD			3.71	0.7009	3.86	0.0093
2,7-DPPy	GMCQDPT	MRX(4)	853 785	3.64	0.1487	3.30	0.0001
	TD-B3LYP			3.59	0.1276	3.38	0.0000
	TD-CAM-B3LYP			3.92	0.2198	3.71	0.0000
	TD-ωB97XD			3.94	0.2544	3.74	0.0000
	Exptl.			3.63^h

---

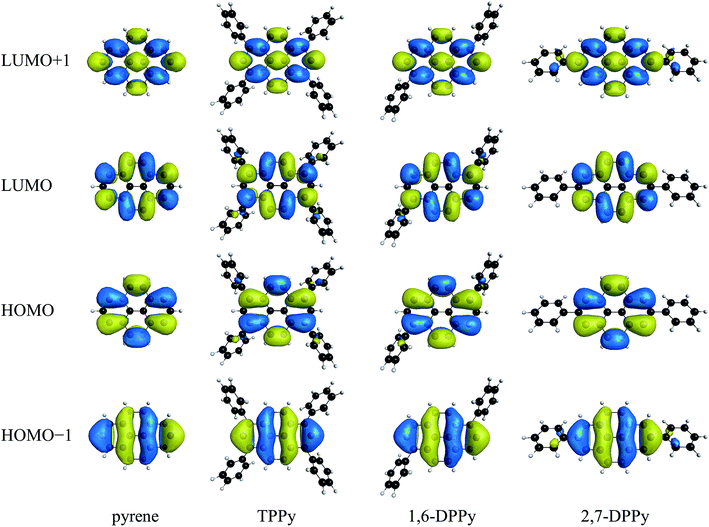Fig. 2 Natural orbitals of pyrene, TPPy, 1,6-DPPy, and 2,7-DPPy from the MCSCF wave functions with the MRX(4) configuration space.

3.1.1. Pyrene. The GMCQDPT-calculated excitation energies of pyrene exhibit systematic improvements with increasing n. The calculated ¹L_b excitation energy with MRX(2) is underestimated by approximately 0.2 eV; the deviation is suppressed with an increase of the n value; the ¹L_a and ¹L_b excitation energies calculated with MRX(3) and MRX(4) are both in good agreement with the experimental values. In contrast, the MCQDPT results largely fluctuate depending on the reference space. Both the ¹L_a and ¹L_b excitation energies with CAS(8πe, 8πo) are relatively close to the corresponding experimental values, whereas both values are significantly underestimated with CAS(4πe, 4πo). The ¹L_a excitation energy calculated with CAS(12πe, 12πo) is close to the experimental values; however, the ¹L_b excitation energy is overestimated by as much as ca. 0.6 eV, so that the predicted energetic ordering of these two states is contrary to the experimental results. The ¹L_b excitation energy is more sensitive to the reference space than the ¹L_a excitation energy, which suggests its considerable multi-configuration character. The EOM-CCSD calculation overestimates the excitation energies by approximately 0.5 eV for both ¹L_a and ¹L_b. The calculation results with the TDDFT method are similar to those reported in pioneering works.^{73,81,82,105,130,131} In the B3LYP results, the ¹L_a excitation energy is underestimated, whereas the ¹L_b excitation energy is overestimated. The predicted ordering of these states in energy is consequently inconsistent with the experimental ordering. Although the calculated ordering is marginally correct in the CAM-B3LYP and ωB97XD results, the excitation energies of the ¹L_a and ¹L_b states are quite close to each other due to serious overestimations of the ¹L_b energy level. Thus, reliable calculations of the ¹L_a and ¹L_b excitation energies could not be accomplished using the exchange-correlation functionals examined here. The calculated oscillator strengths of the ¹L_a state are much larger than those of the ¹L_b state in all cases, which is in agreement with the experimental observations.⁶⁶

3.1.2. TPPy. The excitation energies calculated for TPPy are generally decreased from those for pyrene. The GMCQDPT calculations suggest that the ¹L_a excitation energy decreases to a greater extent than the ¹L_b excitation energy from that of pyrene through tetraphenyl substitution. As a result, the ¹L_a energy level approaches ¹L_b in the results with MRX(2) and MRX(3). However, the ¹L_a state is still higher-lying than the ¹L_b state in these results. In contrast, the energetic ordering of ¹L_a and ¹L_b is inverted in the calculation results with MRX(4), and the ¹L_a state is determined to be the lowest singlet excited state.^68,69 In addition, the ¹L_a excitation energies calculated with GMCQDPT are close to the experimental value. The MCQDPT results largely vary depending on the reference space, similar to the calculations for pyrene. The results with CAS(4πe, 4πo) and CAS(8πe, 8πo) are similar to the GMCQDPT calculations with MRX(2) and MRX(3): the ¹L_a state approaches ¹L_b state in terms of energy; however, it is still higher-lying than the ¹L_b state and the ¹L_a–¹L_b inversion is not predicted. The calculations with CAS(12πe, 12πo) give confusing results: the incorrectly-predicted energetic ordering of ¹L_a and ¹L_b for pyrene is inverted, which results in another inconsistency with the experimentally-deduced scheme. The EOM-CCSD calculation fails to predict the ¹L_a–¹L_b inversion through tetraphenyl substitution and overestimates the ¹L_a excitation energy. Given the overestimations of the excitation energies in pyrene, the ¹L_b excitation energy of TPPy may also be overestimated. The TDDFT calculations predict that the ¹L_a state is lower-lying than the ¹L_b state in TPPy, which is similar to the GMCQDPT calculations with MRX(4). The ¹L_a excitation energy with B3LYP is in good agreement with the experimental value, whereas CAM-B3LYP and ωB97XD give overestimated values. The ¹L_b excitation energies are higher than that obtained using GMCQDPT with MRX(4) by 0.25 eV for B3LYP and by ca. 0.5 eV for the other two functionals.

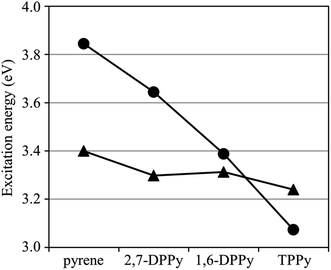
Overall, provided that the GMCQDPT method along with MRX(4) is adopted, the excitation energies of pyrene and TPPy can be accurately calculated, and the ¹L_a–¹L_b inversion through tetraphenyl substitution is predicted. The calculated oscillator strength of the ¹L_a state for TPPy is consistently larger than that of pyrene, whereas that of the ¹L_b state is still vanishingly small.

3.1.3. 1,6-DPPy. The calculations suggest that the excitation energies of the DPPy derivatives are generally lower than those of pyrene. Let us first examine the calculation results of 1,6-DPPy. In the calculation results of GMCQDPT with MRX(4), the ¹L_a energy level shifts largely downward from that of pyrene and approaches the ¹L_b energy level. Although the energetic ordering of the ¹L_a and ¹L_b states is unchanged, their energy levels are quite close to each other. The calculated ¹L_a oscillator strength of 1,6-DPPy is larger than that of pyrene, which results in the ordering of pyrene < 1,6-DPPy < TPPy.

The TDDFT calculations also predict a downward shift of the ¹L_a energy level without significant change of the ¹L_b energy level. However, in contrary to the GMCQDPT results, the TDDFT calculations suggest that the ¹L_a state is the lowest singlet excited state. As mentioned above, the ¹L_b excitation energy of pyrene is significantly overestimated by the TDDFT calculations. The ¹L_a energy level calculated using TD-B3LYP is estimated to be lower than the ¹L_b energy level even for non-substituted pyrene. The gap between ¹L_a and ¹L_b is extremely underestimated using TD-CAM-B3LYP and TD-ωB97XD; because of this imbalanced alignment of the ¹L_a and ¹L_b energy levels for non-substituted pyrene, the energetic ordering of the ¹L_a and ¹L_b states is easily inverted through the downward shift of the ¹L_a energy level. Meanwhile, the TDDFT calculations suggest an increase of the ¹L_a oscillator strength through the diphenyl substitution as well as the GMCQDPT calculations. The oscillator strengths of the ¹L_b state are much smaller than those of the ¹L_a state, as with the cases of pyrene and TPPy. Yet, 1,6-DPPy exhibits the largest ¹L_b oscillator strength among the molecules calculated here.

3.1.4. 2,7-DPPy. In the results of GMCQDPT with MRX(4), the excitation energies of 2,7-DPPy only slightly decrease from those of pyrene for both ¹L_a and ¹L_b. Consequently, the energy gap between the ¹L_a and ¹L_b states (0.34 eV) is only slightly decreased from the value in pyrene (0.44 eV). Contrary to the other two derivatives, 2,7-DPPy exhibits a decreased ¹L_a oscillator strength compared to pyrene. Thus, the influence of phenyl substituents is dependent not only on the excited state but also on the substitution position.

The results of TDDFT calculations show a different behavior from the GMCQDPT results; the ¹L_b energy level is more largely shifted downward without significant change of the ¹L_a energy level. The behavior is also in contrast to the case of 1,6-DPPy which exhibits a largely downward shift of the ¹L_a energy level without a major change in the ¹L_b energy level. Meanwhile, a decrease of the ¹L_a oscillator strength through diphenyl substitution is predicted using TDDFT, as with GMCQPDT.

3.2. Discussion

3.2.1. Dependence on the reference space. The excitation energies calculated using GMCQDPT with MRX(4) are plotted in Fig. 3 as a visualization of the energy level shifts of the ¹L_a and ¹L_b states through phenyl substitutions. The phenyl groups at 2,7-positions have less impact on the excitation energies. In contrast, the ¹L_a energy level shifts largely downward in 1,6-DPPy without a significant change of the ¹L_b energy level. The further downward shift of the ¹L_a energy level causes the energetic ordering of the ¹L_a and ¹L_b states in TPPy to be inverted from that in pyrene. Therefore, the ab initio calculation results corroborate the ¹L_a–¹L_b inversion that was hypothesized based on the experimentally-observed photophysical properties and supported by semi-empirical calculations.^68,69,72 The results indicate that the fluorescence emission of TPPy has an ¹L_a parentage, which is consistent with the high q_F and short τ of TPPy with respect to pyrene. Let us first discuss the dependence of the calculation results on the reference space.

Fig. 3 Excitation energies of the ¹L_a (●) and ¹L_b (▲) states calculated using GMCQDPT with MRX(4).

The accuracy of the MRPT calculation reveals a strong dependence on the reference configuration space. Therefore, the requirements for the reference space to achieve reliable calculations can be determined from these results. The excitation energies with MCQDPT are highly dependent on the reference CAS, whereas those with GMCQDPT vary only in a narrow range. Thus, the calculation accuracy is sensitive to the number of active orbitals. There is no guarantee that MRPT with less active orbitals will be successful, even though its reference space is the CAS. In contrast, the incorporation of multiply-excited configurations into the reference space leads to a systematic improvement within the framework of a full π valence reference space. RASPT2 calculations by Nenov et al. implied that the reference space with incorporation of up to quadruple excitations is necessary to compute the excitation energies of pyrene with high accuracy.¹⁰¹ It should be noted that involving quadruply-excited configurations is also critically important for prediction of the ¹L_a–¹L_b inversion.

The improvement of the calculation accuracy through the expansion of the reference space implies a significant multi-configuration character of these excited states. Therefore, the main configurations of the excited states in the MCSCF wave functions and their weights were analyzed (Table 2). The total weights of the main configurations for ¹L_a and ¹L_b, denoted by σ_a and σ_b, are also presented in Table 2. A smaller σ value indicates a greater contribution of the electron configurations other than the main configurations. Therefore, the σ value is correlated with the degree of the multi-configuration character of the excited state. The weights of the main configurations are relatively reduced as the contributions of more electron configurations are incorporated; therefore, the σ values are decreased with expansion of the reference space. Let us review the results obtained for pyrene with MRX(n); the σ_b values are generally smaller than the σ_a values and more largely varied depending on the reference space. Such behavior can be attributed to the significant multi-configuration character of ¹L_b compared to ¹L_a, which is consistent with a high dependence of the calculated ¹L_b excitation energy on the reference space (Table 1). The calculations with MRX(4) give the smallest σ values among the examined reference spaces for both L_a and L_b; this is expected to be more suitable to deal with the complexity of these excited states. Although the σ values with CAS have similar trends to that with MRX(n), their fluctuations with the reference space are more pronounced and the values are generally larger than those with MRX(4). These results suggest that multi-configuration character is only insufficiently incorporated with these CAS references, even at the maximum CAS(12πe, 12πo). The σ values and their trends for TPPy, 1,6-DPPy and 2,7-DPPy are quite similar to those of pyrene, which indicates a comparable degree of the multi-configuration character of their excited states.

Table 2 Main configurations of the excited states and their weights. HOMO and LUMO are denoted as H and L, respectively. The values are rounded off to four decimal places

Molecule	Method	Reference space	^1La			^1Lb
			H → L	H−1 → L+1	σa	H → L+1	H−1 → L	σb
Pyrene	GMCQDPT	MRX(2)	0.7295	0.1563	0.8858	0.4089	0.3971	0.8060
		MRX(3)	0.6808	0.1458	0.8265	0.3775	0.3594	0.7369
		MRX(4)	0.6577	0.1185	0.7762	0.3318	0.3267	0.6586
	MCQDPT	CAS(4πe, 4πo)	0.7906	0.2024	0.9930	0.5465	0.4451	0.9916
		CAS(8πe, 8πo)	0.7900	0.1163	0.9063	0.4259	0.3996	0.8255
		CAS(12πe, 12πo)	0.7370	0.0818	0.8188	0.3550	0.3605	0.7154
TPPy	GMCQDPT	MRX(2)	0.7699	0.1189	0.8888	0.4247	0.3829	0.8076
		MRX(3)	0.7250	0.1033	0.8283	0.3901	0.3487	0.7388
		MRX(4)	0.6923	0.0866	0.7789	0.3405	0.3195	0.6600
	MCQDPT	CAS(4πe, 4πo)	0.8638	0.1270	0.9907	0.5879	0.4040	0.9918
		CAS(8πe, 8πo)	0.8388	0.0680	0.9068	0.4377	0.3716	0.8093
		CAS(12πe, 12πo)	0.7730	0.0478	0.8208	0.3563	0.3415	0.6978
1,6-DPPy	GMCQDPT	MRX(4)	0.6330	0.0947	0.7277	0.3186	0.3040	0.6226
2,7-DPPy	GMCQDPT	MRX(4)	0.6238	0.1465	0.7703	0.3301	0.3285	0.6587

---

3.2.2. Effects of phenyl groups on the excitation energies. We move on to the discussion on the effects of phenyl substitutions. The σ values analyzed above indicate that the ¹L_a and ¹L_b excited states have considerable multi-configuration characters. Nevertheless, the main configurations of these states still have large weights (Table 2), suggesting that the effects of phenyl groups might be essentially understood based on the molecular orbitals which are relevant to the main configurations: HOMO−1, HOMO, LUMO and LUMO+1. In this regard, the correlation between these molecular orbitals and the calculation results is explored.

The GMCSCF wave function with MRX(n) was constructed in terms of a linear combination of electron configurations and the GMCSCF calculations were carried out with a state-averaging scheme. Consequently, the GMCSCF orbital energies do not have clear physical meanings. The orbital energies obtained using the DFT calculations are dependent on the exchange-correlation functionals. Therefore, we analyzed the Hartree–Fock orbital energies collected in Table 3 where the energy gap between the p and q orbitals is denoted by Δ_p/q; the energy shifts from the corresponding value of pyrene are shown in parentheses. The molecular orbitals obtained from the Hartree–Fock calculations are shown in Fig. S4.† In TPPy and 1,6-DPPy, the HOMO and LUMO energy levels are largely shifted compared to the HOMO−1 and LUMO+1 levels; the HOMO energy level is shifted upward, whereas the LUMO energy level is shifted downward. In 2,7-DPPy, in contrast, the HOMO−1 and LUMO+1 energy levels of 2,7-DPPy are largely shifted without significant changes of HOMO and LUMO energies. These variations of the orbital energies are consistent with the orbital distributions shown in Fig. 2 and S4.† The HOMO and LUMO of pyrene have large coefficients at positions 1, 3, 6, and 8; therefore, these orbitals are sensitive to phenyl substitution at these positions. In contrast, the HOMO−1 and LUMO+1 have large coefficients at positions 2 and 7; the phenyl substitution at positions 2 and 7 has a large impact on these orbitals. The electronic interactions between pyrene moieties and phenyl substituents can be also visually confirmed in the molecular orbitals of pyrene derivatives; the HOMO and LUMO of TPPy and 1,6-DPPy are partially extended to the phenyl substituents, whereas HOMO−1 and LUMO+1 are extended in 2,7-DPPy. The orbital extensions are more noticeable in the Hartree–Fock orbitals (Fig. S4†). As a result of the energetic changes of the orbitals, the Δ_HOMO/LUMO values are in the order of pyrene ≈ 2,7-DPPy > 1,6-DPPy > TPPy, which is in good agreement with that of the ¹L_a excitation energies obtained using GMCQDPT with MRX(4) (Table 1). Although the Δ_HOMO/LUMO value of 2,7-DPPy is almost the same as that with pyrene, Δ_{HOMO−1/LUMO+1} of 2,7-DPPy is much smaller than that of pyrene. The HOMO−1 → LUMO+1 single excitation is another main configuration of the ¹L_a states; therefore, a reduced Δ_{HOMO−1/LUMO+1} could be responsible for the slightly decreased ¹L_a excitation energy. A similar correlation between the Δ values and excitation energies can be also found for the TDDFT results (Table 1). Thus, as for ¹L_a, the calculated excitation energies are well correlated with the Δ values related to the main configurations.

Table 3 Molecular orbital energies calculated using the Hartree–Fock method (eV)^a

Orbital	Py	TPPy	1,6-DPPy	2,7-DPPy
a Values in parentheses are variations from the corresponding orbital energy of pyrene.
LUMO+1	+2.58	+2.45	+2.50	+1.93
		(−0.13)	(−0.08)	(−0.65)
LUMO	+1.62	+1.32	+1.46	+1.55
		(−0.30)	(−0.16)	(−0.07)
HOMO	−7.03	−6.64	−6.82	−7.12
		(+0.39)	(+0.21)	(−0.09)
HOMO−1	−8.07	−7.95	−8.04	−7.48
		(+0.12)	(+0.03)	(+0.59)
ΔHOMO/LUMO	+8.65	+7.96	+8.28	+8.67
		(−0.69)	(−0.37)	(+0.02)
ΔHOMO−1/LUMO+1	+10.65	+10.40	+10.54	+9.41
		(−0.25)	(−0.11)	(−1.24)
ΔHOMO/LUMO+1	+9.61	+9.09	+9.32	+9.05
		(−0.52)	(−0.29)	(−0.56)
ΔHOMO−1/LUMO	+9.69	+9.27	+9.50	+9.03
		(−0.42)	(−0.19)	(−0.66)

---

The calculated Δ_HOMO/LUMO+1 and Δ_{HOMO−1/LUMO} values of phenyl substituted derivatives are lower than those of pyrene, which is consistent with their lower ¹L_b excitation energies obtained using GMCQDPT with MRX(4). The fluctuations of the Δ_HOMO/LUMO+1 and Δ_{HOMO−1/LUMO} values are rather milder than those of the Δ_HOMO/LUMO and Δ_{HOMO−1/LUMO+1} values. This behavior is also consistent with the insensitivity of the ¹L_b excitation energies to phenyl substitution compared to the ¹L_a excitation energies, which results in a reduction of the ¹L_a–¹L_b gap in 1,6-DPPy and the ¹L_a–¹L_b inversion in TPPy (Fig. 3). However, the Δ_HOMO/LUMO+1 and Δ_{HOMO−1/LUMO} values are in the order of pyrene > 1,6-DPPy > TPPy > 2,7-DPPy, which is not in agreement with the ordering of the ¹L_b excitation energies with GMCQDPT: pyrene > 1,6-DPPy ≈ 2,7-DPPy > TPPy (Table 1). The ¹L_b state has significant multi-configuration character, as suggested from the less σ values (Table 2), which could be responsible for the weak correlation between the Δ values and the ¹L_b excitation energies, and also for smaller fluctuations of the ¹L_b excitation energies. In contrast to the GMCQDPT results, the ¹L_b excitation energies with TDDFT exhibit a stronger correlation with the Δ_HOMO/LUMO+1 and Δ_{HOMO−1/LUMO} values; these values are in the same order: pyrene > 1,6-DPPy > TPPy > 2,7-DPPy. Since TDDFT is a one-particle theory, the excitation energies obtained using TDDFT are susceptible to the energies of one-electron orbitals. Instead, the ¹L_b excitation energy tends to be overestimated because of insufficient incorporation of multi-configuration character.

3.2.3. Effects of phenyl groups on the oscillator strengths. The excitation energies are reasonably correlated with the Δ values, suggesting that the ¹L_a and ¹L_b states are primarily characterized by their main configurations. Therefore, the effects of phenyl substitution on the oscillator strength could be also understood based on the orbitals related to the main configurations. As for allowed transitions, spatial expansion of the relevant molecular orbitals generally leads to an increased oscillator strength through enlargement of the transition dipole moment. The HOMO and LUMO are spatially extended to four phenyl groups in TPPy and two phenyl groups in 1,6-DPPy (Fig. 2). Therefore, the calculated ¹L_a oscillator strengths are in the order of TPPy > 1,6-DPPy > pyrene. In contrast, the calculated ¹L_a oscillator strength of 2,7-DPPy is decreased from that of pyrene. The mechanism can also be understood based on the main configurations.^129,132 A linear combination of HOMO → LUMO and HOMO−1 → LUMO+1 singly excited configurations results in ¹L_a as a lower-energy component and ¹B_a as a higher-energy component.¹²⁹ The transition moments derived from these main configurations are counteracted with each other in ¹L_a, whereas they are reinforced in ¹B_a. The weights of these configurations are different; therefore, a transition moment still remains after their mutual cancellation, and the ¹L_a state can thus give a visible absorption band. The difference in weights between these main configurations of 2,7-DPPy is reduced from that of pyrene (Table 2). The weight of the HOMO−1 → LUMO+1 excited configuration of 2,7-DPPy is specifically increased from that of pyrene, while that of the HOMO → LUMO excited configuration is decreased. The origin of such behavior is a reduced Δ_{HOMO−1/LUMO+1} without a major change in Δ_HOMO/LUMO, so that the weight of the HOMO−1 → LUMO+1 excitation is relatively increased. In addition, the transition moment originated from the HOMO−1 → LUMO+1 single excitation is enlarged because these orbitals are partially extended to phenyl groups at positions 2 and 7. Therefore, the transition moments derived from these configurations are largely canceled by each other, which results in a decreased oscillator strength. Qiao et al. measured the UV/Vis absorption spectra of pyrene and its 2,7-substituted derivatives in dichloromethane.¹²¹ The results showed that 2,7-DPPy exhibited an absorption band with λ_max of 342 nm and this band is expected to have parentage from ¹L_a of pyrene. The molar extinction coefficient is slightly smaller than that of the pyrene ¹L_a absorption band. The present calculation results are consistent with the experimental observations. The linear combination of HOMO → LUMO+1 and HOMO−1 → LUMO singly excited configurations results in ¹L_b as a lower-energy component and ¹B_b as a higher-energy component.¹²⁹ Therefore, the transition moments derived from these main configurations are counteracted each other in ¹L_b, whereas they are reinforced in ¹B_b. These configurations have almost the same weights in ¹L_b (Table 2); therefore, the transition dipole moments are almost completely canceled, which results in its negligibly small oscillator strength. The cancellation is slightly suppressed in 1,6-DPPy because of its lower symmetry. Consequently, the ¹L_b oscillator strength of 1,6-DPPy is high when compared to pyrene and other derivatives with higher symmetries.

The results of the TDDFT calculations are similar to those obtained from the GMCQDPT calculations; the calculated ¹L_a oscillator strengths are in the order of TPPy > 1,6-DPPy > pyrene; the calculated ¹L_b oscillator strengths are nearly zero except for 1,6-DPPy. Overall, the effects of substituents on the ¹L_a excitation energy, the ¹L_a and ¹L_b oscillator strengths can be reasonably evaluated using TDDFT; however, the ¹L_b excitation energy cannot be accurately predicted; in the worse cases, even the energetic ordering is incorrectly predicted. Thus, a multi-reference treatment is essential for an accurate calculation of the ¹L_b excitation energy, the ordering of the ¹L_a and ¹L_b states, and the energy gap between these states.

4. Conclusion

The absorption and fluorescence emission behavior of pyrene derivatives is characterized by the low-lying excited states derived from ¹L_a and ¹L_b of pyrene. In this study, pyrene, TPPy, 1,6-DPPy, and 2,7-DPPy as typical examples were calculated using MRPT methods to explore a dependable computational scheme for these excited states. When all valence π and π* orbitals on the pyrene moiety were incorporated into the reference space, the calculated ¹L_a and ¹L_b excitation energies of pyrene were in good agreement with the experimental values. The fluorescence emission of TPPy was predicted to have pyrene ¹L_a parentage, which theoretically corroborates the experimental observations. A reference space involving singly, doubly, triply, and quadruply excited configurations was required to predict the ¹L_a–¹L_b inversion through tetraphenyl substitution. MRPT calculations with smaller reference spaces and single-reference theory calculations exhibit inconsistencies with these results, which suggests that adequate treatment of the multi-configuration character is essential. The effect of phenyl substitution was dependent not only on the excited state but also on the substitution position. The detailed mechanism was clarified by examination of the MCSCF wave functions. These calculations were successfully conducted at a tractable computational cost by the adoption of GMCQDPT to enable the handling of general types of reference configuration space.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

This work was partially supported by the Advanced Catalytic Transformation Program for Carbon Utilization (ACT-C) of the Japan Science and Technology Agency (JST) (Grant number: JPMJCR12Y1). The authors are grateful to Dr Norihiro Mizoshita and Mr Yoshifumi Maegawa at Toyota Central R&D Labs.; this study was motivated by their studies on mesoporous light-emitting materials. The authors are also grateful to Dr Yuri Yamada at Toyota Central R&D Labs. for technical help.

References

1. T. M. Figueira-Duarte and K. Müllen, Chem. Rev., 2011, 111, 7260–7314.
2. B.-C. Wang, J.-C. Chang, H.-C. Tso, H.-F. Hsu and C.-Y. Cheng, J. Mol. Struct.: THEOCHEM, 2003, 629, 11–20.
3. T. M. Figueira-Duarte, S. C. Simon, M. Wagner, S. I. Druzhinin, K. A. Zachariasse and K. Müllen, Angew. Chem., Int. Ed., 2008, 47, 10175–10178.
4. K. Fujimoto, H. Shimizu, M. Furusyo, S. Akiyama, M. Ishida, U. Furukawa, T. Yokoo and M. Inouye, Tetrahedron, 2009, 65, 9357–9361.
5. M. Sase, S. Yamaguchi, Y. Sagara, I. Yoshikawa, T. Mutai and K. Araki, J. Mater. Chem., 2011, 21, 8347–8354.
6. A. G. Crawford, A. D. Dwyer, Z. Liu, A. Steffen, A. Beeby, L.-O. Pålsson, D. J. Tozer and T. B. Marder, J. Am. Chem. Soc., 2011, 133, 13349–13362.
7. S.-S. Li, K.-J. Jiang, C.-C. Yu, J.-H. Huang, L.-M. Yang and Y.-L. Song, New J. Chem., 2014, 38, 4404–4408.
8. Y. Niko, S. Sasaki, K. Narushima, D. K. Sharma, M. Vacha and G.-i. Konishi, J. Org. Chem., 2015, 80, 10794–10805.
9. H. Örücü and N. Acar, Comput. Theor. Chem., 2015, 1056, 11–18.
10. R. Liu, H. Ran, Z. Zhao, X. Yang, J. Zhang, L. Chen, H. Sun and J.-Y. Hu, ACS Omega, 2018, 3, 5866–5875.
11. V. S. Vyas, S. V. Lindeman and R. Rathore, J. Photochem. Photobiol., A, 2019, 375, 209–218.
12. T. Oyamada, S. Akiyama, M. Yahiro, M. Saigou, M. Shiro, H. Sasabe and C. Adachi, Chem. Phys. Lett., 2006, 421, 295–299.
13. J. N. Moorthy, P. Natarajan, P. Venkatakrishnan, D.-F. Huang and T. J. Chow, Org. Lett., 2007, 9, 5215–5218.
14. N. Mizoshita, Y. Goto, Y. Maegawa, T. Tani and S. Inagaki, Chem. Mater., 2010, 22, 2548–2554.
15. S. Yamaguchi, I. Yoshikawa, T. Mutai and K. Araki, J. Mater. Chem., 2012, 22, 20065–20070.
16. Y. Maegawa, N. Mizoshita, T. Tani and S. Inagaki, Chem. Lett., 2012, 41, 316–318.
17. K. Sumi, Y. Niko, K. Tokumaru and G.-i. Konishi, Chem. Commun., 2013, 49, 3893–3895.
18. D. Chercka, S.-J. Yoo, M. Baumgarten, J.-J. Kim and K. Müllen, J. Mater. Chem. C, 2014, 2, 9083–9086.
19. T. H. El-Assaad, M. Auer, R. Castañeda, K. M. Hallal, F. M. Jradi, L. Mosca, R. S. Khnayzer, D. Patra, T. V. Timofeeva, J.-L. Brédas, E. J. W. List-Kratochvil, B. Wex and B. R. Kaafarani, J. Mater. Chem. C, 2016, 4, 3041–3058.
20. H. Ju, K. Wang, J. Zhang, H. Geng, Z. Liu, G. Zhang, Y. Zhao and D. Zhang, Chem. Mater., 2017, 29, 3580–3588.
21. D. H. Ahn, J. H. Jeong, J. Song, J. Y. Lee and J. H. Kwon, ACS Appl. Mater. Interfaces, 2018, 10, 10246–10253.
22. H. Jung, S. Kang, H. Lee, Y.-J. Yu, J. H. Jeong, J. Song, Y. Jeon and J. Park, ACS Appl. Mater. Interfaces, 2018, 10, 30022–30028.
23. H. Maeda, T. Suzuki and M. Segi, Photochem. Photobiol. Sci., 2018, 17, 781–792.
24. N. Mizoshita and S. Inagaki, Macromol. Chem. Phys., 2018, 219, 1700596.
25. J.-H. Lee, C.-H. Chen, P.-H. Lee, H.-Y. Lin, M.-k. Leung, T.-L. Chiu and C.-F. Lin, J. Mater. Chem. C, 2019, 7, 5874–5888.
26. F. M. Winnik, Chem. Rev., 1993, 93, 587–614.
27. T. Förster and K. Kasper, Z. Phys. Chem., 1954, 1, 275–277.
28. J. B. Birks, Rep. Prog. Phys., 1975, 38, 903–974.
29. T. Azumi and S. P. McGlynn, J. Chem. Phys., 1964, 41, 3131–3138.
30. J. Duhamel, Acc. Chem. Res., 2006, 39, 953–960.
31. M. Ingratta, J. Hollinger and J. Duhamel, J. Am. Chem. Soc., 2008, 130, 9420–9428.
32. S. J. Teertstra, W. Y. Lin, M. Gauthier, M. Ingratta and J. Duhamel, Polymer, 2009, 50, 5456–5466.
33. Z. Xu, N. J. Singh, J. Lim, J. Pan, H. N. Kim, S. Park, K. S. Kim and J. Yoon, J. Am. Chem. Soc., 2009, 131, 15528–15533.
34. M. Danko, P. Hrdlovič, M. Brzezinski, A. Duda and T. Biela, Polymer, 2018, 156, 76–84.
35. G. Bains, A. B. Patel and V. Narayanaswami, Molecules, 2011, 16, 7909–7935.
36. A. Fujii, Y. Sekiguchi, H. Matsumura, T. Inoue, W.-S. Chung, S. Hirota and T. Matsuo, Bioconjugate Chem., 2015, 26, 537–548.
37. A. A. Martí, S. Jockusch, N. Stevens, J. Ju and N. J. Turro, Acc. Chem. Res., 2007, 40, 402–409.
38. P. Conlon, C. J. Yang, Y. Wu, Y. Chen, K. Martinez, Y. Kim, N. Stevens, A. A. Marti, S. Jockusch, N. J. Turro and W. Tan, J. Am. Chem. Soc., 2008, 130, 336–342.
39. X. Su, X. Xiao, C. Zhang and M. Zhao, Appl. Spectrosc., 2012, 66, 1249–1261.
40. F. Wojciechowski, J. Lietard and C. J. Leumann, Org. Lett., 2012, 14, 5176–5179.
41. C. Wu, C. Wang, L. Yan and C. J. Yang, J. Biomed. Nanotechnol., 2009, 5, 495–504.
42. A. O. Krasheninina, S. D. Novopashina, K. E. Apartsin and G. A. Venyaminova, Molecules, 2017, 22, 2108.
43. S. K. Kim, S. H. Lee, J. Y. Lee, J. Y. Lee, R. A. Bartsch and J. S. Kim, J. Am. Chem. Soc., 2004, 126, 16499–16506.
44. X.-L. Ni, S. Wang, X. Zeng, Z. Tao and T. Yamato, Org. Lett., 2011, 13, 552–555.
45. S. Das, A. Sahana, A. Banerjee, S. Lohar, D. A. Safin, M. G. Babashkina, M. Bolte, Y. Garcia, I. Hauli, S. K. Mukhopadhyay and D. Das, Dalton Trans., 2013, 42, 4757–4763.
46. S. Sarkar, S. Roy, A. Sikdar, R. N. Saha and S. S. Panja, Analyst, 2013, 138, 7119–7126.
47. W. Cho, H. J. Lee, G. Choi, S. Choi and M. Oh, J. Am. Chem. Soc., 2014, 136, 12201–12204.
48. S. S. Razi, R. Ali, P. Srivastava and A. Misra, RSC Adv., 2015, 5, 79538–79547.
49. M. Shellaiah, Y. C. Rajan, P. Balu and A. Murugan, New J. Chem., 2015, 39, 2523–2531.
50. M. Zhao, X. Zhou, J. Tang, Z. Deng, X. Xu, Z. Chen, X. Li, L. Yang and L.-J. Ma, Spectrochim. Acta, Part A, 2017, 173, 235–240.
51. Y. Upadhyay, T. Anand, L. T. Babu, P. Paira, G. Crisponi, A. K. Sk, R. Kumar and S. K. Sahoo, Dalton Trans., 2018, 47, 742–749.
52. S. Zhang, L. Ding, F. Lü, T. Liu and Y. Fang, Spectrochim. Acta, Part A, 2012, 97, 31–37.
53. A. Ghosh, A. Sengupta, A. Chattopadhyay and D. Das, Chem. Commun., 2015, 51, 11455–11458.
54. S. Lohar, D. A. Safin, A. Sengupta, A. Chattopadhyay, J. S. Matalobos, M. G. Babashkina, K. Robeyns, M. P. Mitoraj, P. Kubisiak, Y. Garcia and D. Das, Chem. Commun., 2015, 51, 8536–8539.
55. K. Khownium, J. Romsaiyud, S. Borwornpinyo, P. Wongkrasant, P. Pongkorpsakol, C. Muanprasat, B. Boekfa, T. Vilaivan, S. Ruchirawat and J. Limtrakul, New J. Chem., 2019, 43, 7051–7056.
56. S. Shirai, S. Iwata, T. Tani and S. Inagaki, J. Phys. Chem. A, 2011, 115, 7687–7699.
57. S. Shirai, S. Iwata, Y. Maegawa, T. Tani and S. Inagaki, J. Phys. Chem. A, 2012, 116, 10194–10202.
58. S. Shirai, Y. Kurashige and T. Yanai, J. Chem. Theory Comput., 2016, 12, 2366–2372.
59. Y. Numata, Y. Suzuki and I. Suzuka, J. Photochem. Photobiol., A, 2012, 237, 49–52.
60. K. Yamazaki, N. Niitsu, K. Nakamura, M. Kanno and H. Kono, J. Phys. Chem. A, 2012, 116, 11441–11450.
61. B. Saed and R. Omidyan, J. Phys. Chem. A, 2013, 117, 2499–2507.
62. M. J. Bertocchi, A. Bajpai, J. N. Moorthy and R. G. Weiss, J. Phys. Chem. A, 2017, 121, 458–470.
63. J. Merz, J. Fink, A. Friedrich, I. Krummenacher, H. H. Al Mamari, S. Lorenzen, M. Haehnel, A. Eichhorn, M. Moos, M. Holzapfel, H. Braunschweig, C. Lambert, A. Steffen, L. Ji and T. B. Marder, Chem.–Eur. J., 2017, 23, 13164–13180.
64. F. Lu, N. Kitamura, T. Takaya, K. Iwata, T. Nakanishi and Y. Kurashige, Phys. Chem. Chem. Phys., 2018, 20, 3258–3264.
65. J. R. Platt, J. Chem. Phys., 1949, 17, 484–495.
66. J. Tanaka, Bull. Chem. Soc. Jpn., 1965, 38, 86–102.
67. M. Kasha, Discuss. Faraday Soc., 1950, 9, 14–19.
68. C. Rullière, E. C. Colson and P. C. Roberge, Can. J. Chem., 1975, 53, 3269–3275.
69. J. C. Rayez and C. Rulliere, Chem. Phys. Lett., 1979, 63, 289–292.
70. I. B. Berlman, J. Phys. Chem., 1970, 74, 3085–3093.
71. I. B. Berlman, in Handbook of Fluorescence Spectra of Aromatic Molecules, ed. I. B. Berlman, Academic Press, 2nd edn, 1971, pp. 107–415,  DOI:10.1016/B978-0-12-092656-5.50011-3.
72. W. Sotoyama, H. Sato, M. Kinoshita, T. Takahashi, A. Matsuura, J. Kodama, N. Sawatari and H. Inoue, SID Symposium Digest of Technical Papers, 2003, 34, 1294–1297.
73. I. S. K. Kerkines, I. D. Petsalakis, G. Theodorakopoulos and W. Klopper, J. Chem. Phys., 2009, 131, 224315.
74. E. Runge and E. K. U. Gross, Phys. Rev. Lett., 1984, 52, 997–1000.
75. E. K. U. Gross and W. Kohn, Adv. Quantum Chem., 1990, 21, 255–291.
76. C. Jamorski, M. E. Casida and D. R. Salahub, J. Chem. Phys., 1996, 104, 5134–5147.
77. M. Petersilka, U. J. Gossmann and E. K. U. Gross, Phys. Rev. Lett., 1996, 76, 1212–1215.
78. M. E. Casida, C. Jamorski, K. C. Casida and D. R. Salahub, J. Chem. Phys., 1998, 108, 4439–4449.
79. L. González, D. Escudero and L. Serrano-Andrés, ChemPhysChem, 2012, 13, 28–51.
80. A. D. Laurent, C. Adamo and D. Jacquemin, Phys. Chem. Chem. Phys., 2014, 16, 14334–14356.
81. Y. H. Park and B.-S. Cheong, Curr. Appl. Phys., 2006, 6, 700–705.
82. E. L. Graef and J. B. L. Martins, J. Mol. Model., 2019, 25, 183.
83. M. Parac and S. Grimme, Chem. Phys., 2003, 292, 11–21.
84. S. Grimme and M. Parac, ChemPhysChem, 2003, 4, 292–295.
85. Y.-L. Wang and G.-S. Wu, Int. J. Quantum Chem., 2008, 108, 430–439.
86. L. Goerigk and S. Grimme, J. Chem. Theory Comput., 2011, 7, 3272–3277.
87. N. Kuritz, T. Stein, R. Baer and L. Kronik, J. Chem. Theory Comput., 2011, 7, 2408–2415.
88. R. M. Richard and J. M. Herbert, J. Chem. Theory Comput., 2011, 7, 1296–1306.
89. M. Krykunov, S. Grimme and T. Ziegler, J. Chem. Theory Comput., 2012, 8, 4434–4440.
90. B. Moore, H. Sun, N. Govind, K. Kowalski and J. Autschbach, J. Chem. Theory Comput., 2015, 11, 3305–3320.
91. O. Christiansen, H. Koch and P. Jørgensen, Chem. Phys. Lett., 1995, 243, 409–418.
92. H. Lischka, D. Nachtigallová, A. J. A. Aquino, P. G. Szalay, F. Plasser, F. B. C. Machado and M. Barbatti, Chem. Rev., 2018, 118, 7293–7361.
93. Y. Bito, N. Shida and T. Toru, Chem. Phys. Lett., 2000, 328, 310–315.
94. C.-H. Chin and S. H. Lin, Phys. Chem. Chem. Phys., 2016, 18, 14569–14579.
95. H. Nakano, J. Chem. Phys., 1993, 99, 7983–7992.
96. K. Andersson, P. Å. Malmqvist and B. O. Roos, J. Chem. Phys., 1992, 96, 1218–1226.
97. B. O. Roos, Adv. Chem. Phys., 1987, 69, 399–445.
98. A. Y. Freidzon, R. R. Valiev and A. A. Berezhnoy, RSC Adv., 2014, 4, 42054–42065.
99. A. A. Granovsky, J. Chem. Phys., 2011, 134, 214113.
100. P.-Å. Malmqvist, A. Rendell and B. O. Roos, J. Phys. Chem., 1990, 94, 5477–5482.
101. A. Nenov, A. Giussani, B. P. Fingerhut, I. Rivalta, E. Dumont, S. Mukamel and M. Garavelli, Phys. Chem. Chem. Phys., 2015, 17, 30925–30936.
102. F. Aquilante, T. B. Pedersen and R. Lindh, J. Chem. Phys., 2007, 126, 194106.
103. F. Aquilante, P.-Å. Malmqvist, T. B. Pedersen, A. Ghosh and B. O. Roos, J. Chem. Theory Comput., 2008, 4, 694–702.
104. J. A. Noble, C. Aupetit, D. Descamps, S. Petit, A. Simon, J. Mascetti, N. Ben Amor and V. Blanchet, Phys. Chem. Chem. Phys., 2019, 21, 14111–14125.
105. B. Shi, D. Nachtigallová, A. J. A. Aquino, F. B. C. Machado and H. Lischka, J. Chem. Phys., 2019, 150, 124302.
106. S. Grimme and M. Waletzke, J. Chem. Phys., 1999, 111, 5645–5655.
107. B. Shi, D. Nachtigallová, A. J. A. Aquino, F. B. C. Machado and H. Lischka, Phys. Chem. Chem. Phys., 2019, 21, 9077–9088.
108. H. Nakano, R. Uchiyama and K. Hirao, J. Comput. Chem., 2002, 23, 1166–1175.
109. J. Ivanic, J. Chem. Phys., 2003, 119, 9364–9376.
110. J. Ivanic, J. Chem. Phys., 2003, 119, 9377–9385.
111. L. Roskop and M. S. Gordon, J. Chem. Phys., 2011, 135, 044101.
112. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
113. P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627.
114. H. Koch and P. Jørgensen, J. Chem. Phys., 1990, 93, 3333–3344.
115. J. F. Stanton and R. J. Bartlett, J. Chem. Phys., 1993, 98, 7029–7039.
116. T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57.
117. J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620.
118. T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023.
119. M. Baba, M. Saitoh, Y. Kowaka, K. Taguma, K. Yoshida, Y. Semba, S. Kasahara, T. Yamanaka, Y. Ohshima, Y.-C. Hsu and S. H. Lin, J. Chem. Phys., 2009, 131, 224318.
120. X. Feng, H. Tomiyasu, J.-Y. Hu, X. Wei, C. Redshaw, M. R. J. Elsegood, L. Horsburgh, S. J. Teat and T. Yamato, J. Org. Chem., 2015, 80, 10973–10978.
121. Y. L. Qiao, J. Zhang, W. Xu and D. B. Zhu, Tetrahedron, 2011, 67, 3395–3405.
122. M. W. Schmidt, K. K. Baldridge, J. A. Boatz, S. T. Elbert, M. S. Gordon, J. H. Jensen, S. Koseki, N. Matsunaga, K. A. Nguyen, S. Su, T. L. Windus, M. Dupuis and J. A. Montgomery Jr, J. Comput. Chem., 1993, 14, 1347–1363.
123. M. S. Gordon and M. W. Schmidt, in Theory and applications of computational chemistry, ed. C. E. Dykstra, G. Frenking, K. S. Kim and G. E. Scuseria, Elsevier, Amsterdam, 2005, pp. 1167–1189,  DOI:10.1016/B978-044451719-7/50084-6.
124. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford CT, 2016.
125. R. S. Becker, I. S. Singh and E. A. Jackson, J. Chem. Phys., 1963, 38, 2144–2171.
126. E. A. Mangle and M. R. Topp, J. Phys. Chem., 1986, 90, 802–807.
127. C. M. Jones and S. A. Asher, J. Chem. Phys., 1988, 89, 2649–2661.
128. V. de Halleux, J. P. Calbert, P. Brocorens, J. Cornil, J. P. Declercq, J. L. Bredas and Y. Geerts, Adv. Funct. Mater., 2004, 14, 649–659.
129. N. S. Ham and K. Ruedenberg, J. Chem. Phys., 1956, 25, 13–26.
130. M. K. Roos, S. Reiter and R. de Vivie-Riedle, Chem. Phys., 2018, 515, 586–595.
131. Y. Niko, S. Kawauchi, S. Otsu, K. Tokumaru and G.-i. Konishi, J. Org. Chem., 2013, 78, 3196–3207.
132. E. B. Guidez and C. M. Aikens, J. Phys. Chem. C, 2013, 117, 21466–21475.

---

Footnote

† Electronic supplementary information (ESI) available: Natural orbitals from MCSCF wave functions (Fig. S1–S3); total energies and MCSCF excitation energies (Table S1); Hartree–Fock orbitals (Fig. S4). See DOI: 10.1039/c9ra10483f

---