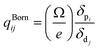Tellurium–oxygen group enhanced birefringence in tellurium phosphates: a first-principles investigation

Abstract

Phosphates possess a relatively large UV/DUV cutoff edge, but these compounds usually have very small birefringence. Recently the Te₂P₂O₉ crystal was synthesized and its birefringence was reported to be as large as 0.106 at 1013.98 nm. Herein, we investigated the electronic structure and optical properties of Te₂P₂O₉ using the first-principles method. The obtained results are in good agreement with the experimental values. The Born effective charges and SHG density of Te₂P₂O₉ show that the contribution to the birefringence and SHG response mainly originates from the TeO₅ group. The electronic structures and optical response of Ba₂TeO(PO₄)₂ and Te₃O₃(PO₄)₂ were also investigated for comparison. The results show that these two tellurium phosphates also possess a large birefringence similar to Te₂P₂O₉. Also, the birefringence originates from the TeO_x polyhedrons, which was confirmed by the real-space atom-cutting results and distortion indices.

---

1. Introduction

Nowadays, nonlinear optical (NLO) materials have attracted widespread attention because they can be used to obtain wide-band and tunable laser sources via the second order NLO effect.^1–5 During the past decades, numerous inorganic NLO materials have been obtained, including infrared, visible and ultraviolet (UV) materials.^6–10 Also, borates, phosphates and carbonates are thought to be good candidates for UV/deep-UV NLO compounds, such as BBO,^11,12 LiB₃O₅ (LBO),^13–15 CsLiB₆O₁₀ (CLBO),^16–18 CsB₃O₅ (CBO),^19,20 and KBe₂BO₃F₂ (KBBF).^21–24 It has been proven that the introduction of fluorine into borates is beneficial to obtain short UV cutoff edges and suitable birefringence and large NLO responses,^25,26 and new deep-UV fluorooxoborates with good performances were obtained such as Li₂B₆O₉F₂,²⁵ AB₄O₆F (A = NH₄, K, Rb, and Cs),^27,28 and SrB₅O₇F₃.²⁹

Recently, phosphates have been reported to be good candidates as UV and deep-UV NLO crystal materials because of their short UV cut-off edge,^30,31 including Rb₂Ba₃(P₂O₇)₃ (<200 nm),³² Ba₅P₆O₂₀ (about 167 nm),³³ and KLa(PO₃)₄ (162 nm).³⁴ However, phosphates also have drawbacks. Most of the reported phosphates have a relatively small birefringence, which has relationship with the regular tetrahedron of the PO₄ units. First principles investigations show that the anisotropic polarization of the regular PO₄ unit is relatively small. Thus, to overcome this inherent drawback, different types of d⁰ transition metal cations (Ti⁴⁺, Mo⁶⁺, etc.)³⁵ and lone pair electrons (Bi³⁺, Te⁴⁺, Pb²⁺, etc.) are introduced to phosphates. Wang et al. at Shandong University³⁶ obtained large-size Te₂P₂O₉ crystals via the Czochralski method. The crystals had the acentric polar space group Cc, and their basic building units were the PO₄ tetrahedron and TeO₅ square pyramid. Their linear and nonlinear optical properties were also investigated.³⁶ The SHG response and birefringence of Te₂P₂O₉ are relatively large, which is 1.3 × KDP, and 0.13786–0.10615 at 404.66–1013.98 nm, respectively. Curiously, how can it possess such a large birefringence in comparison with other phosphates? Also, what is the origination of this large birefringence in phosphates?

Herein, we calculated the electronic structure and optical properties of Te₂P₂O₉. The obtained refractive indices, birefringence and SHG tensor agree well with the experimental values. Utilizing its electronic structures, Born effective charges, and the SHG density method, the atomic contribution to the birefringence and SHG tensors of Te₂P₂O₉ are investigated. The results show that the TeO₅ polyhedrons give the main contribution to the optical anisotropic birefringence and SHG response. Furthermore the optical response of the other tellurium phosphates Ba₂TeO(PO₄)₂ (ref. 37) and Te₃O₃(PO₄)₂ (ref. 38) were also investigated for comparison. These two compounds possess similar basic building units as Te₂P₂O₉, which are an isolated PO₄ tetrahedron and TeO_x polyhedrons (more details can be found in Table S1 in the ESI†). These two compounds also have very large birefringence like Te₂P₂O₉. The large birefringence in these tellurium phosphates originate from the TeO_x polyhedrons, which was further confirmed by the real-space atom-cutting results and the distortion indices.

2. Computational details

To better understand the relationship between the structure and optical properties, the electronic structure and Born effective charges were investigated using the first-principles method implemented in the CASTEP package.^39,40 During the calculation, the exchange-correlation functional with the Perdew–Burke–Ernzerhof (PBE)^41,42 functional and the norm-conserving pseudopotentials (NCP) was adopted. The kinetic energy cutoffs were set as 830 eV for Te₂P₂O₉, 830 eV for Te₃O₃(PO₄)₂, and 830 eV for Ba₂TeO(PO₄)₂. The k-point mesh in the Monkhorst–Pack was set as 5 × 5 × 3 (Te₂P₂O₉), 2 × 3 × 3 (Te₃O₃(PO₄)₂), and 4 × 4 × 3 (Ba₂TeO(PO₄)₂). After the electronic structures were obtained, the refractive indices and the birefringence were further calculated via the OPTADOS code.^43,44 The nonlinear optical tensors of Te₂P₂O₉ were further investigated using the method described in ref. 45–47. For comparison, the electronic structures and optical properties of Te₂P₂O₉ were also investigated using the LDA(CA-PZ), GGA(PW91) and GGA(RPBE) functionals (shown in Table S2 in the ESI†). The results show that the GGA-PBE functional gives more reliable results in comparison with the experimental values. Hence, herein, we only discuss the GGA-PBE results.

3. Results and discussions

3.1 The electronic structures of Te₂P₂O₉

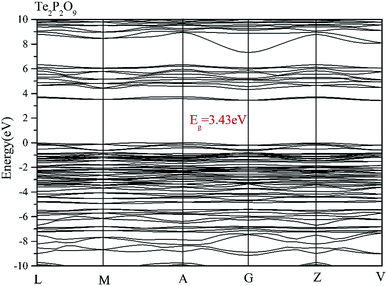
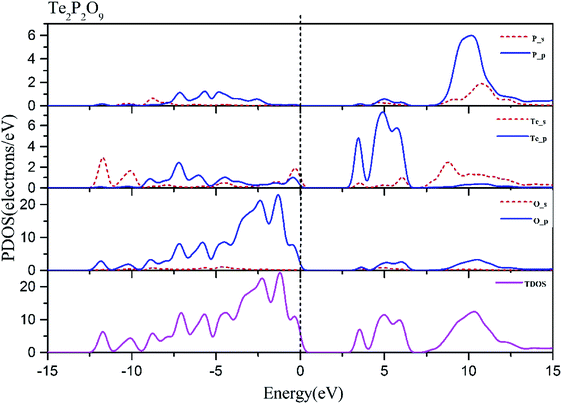
Using the method described above, the band structures and the projected density of states of Te₂P₂O₉ were obtained. It can be seen clearly from Fig. 1 that Te₂P₂O₉ is an indirect bandgap compound with the bandgap of 3.43 eV. The obtained bandgap is smaller than the experimental value (about 4.30 eV).³⁶ This underestimation of the bandgap may be related with the derivative discontinuity of the exchange-correlation energy.⁴⁸

Fig. 1 Obtained band structures of Te₂P₂O₉.

The projected density of states (PDOS) of Te₂P₂O₉ is shown in Fig. 2. For the Te₂P₂O₉ compound, the states of the valence bands (VB) from −10 eV to the Fermi level are mainly the Te sp, P sp and O sp states. The states at the bottom of the conduction bands (CB) from 3 eV to 6.5 eV are dominated by the Te 5p and O 2p orbitals. From the states at the valence band and the conduction band, the hybrid states of the P–O and Te–O chemical bonds can be determined. According to the revised model,^10,49–53 the lone pair states from the Te–O chemical bond can be deduced. The optical properties of the material are closely related to the electronic transition between the top of the valence band and the bottom of the conduction band. Hence, we believe that the Te–O and P–O chemical bonds play an important role in determining the optical properties of Te₂P₂O₉.

Fig. 2 Projected density of states (PDOS) of Te₂P₂O₉.

3.2 The refractive indices and Born effective charges of Te₂P₂O₉

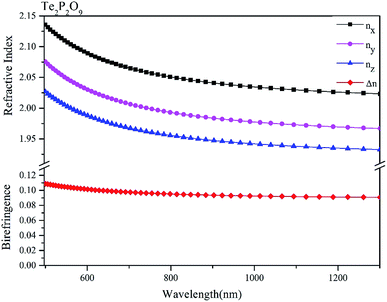
The obtained refractive indices and birefringence of Te₂P₂O₉ are shown in Fig. 3. From the data shown in Fig. 3, it can be determined that the calculated refractive indices follow the order of n_x > n_y > n_z. The calculated birefringence is 0.12496–0.09236 in the wavelength range of 404.65–1013.61 nm. It is interesting to note that the reported experimental birefringence of Te₂P₂O₉ is 0.13786–0.10615 in the wavelength range of 404.66–1013.98 nm. Thus, it is obvious that the calculated value matches well with the experimental value.

Fig. 3 Calculated refractive indices and birefringence of Te₂P₂O₉.

To better understand the atomic contribution to the optical anisotropic birefringence, the Born effective charges^54–56 were also investigated in this work. Because the optical anisotropic birefringence is closely related with the difference in the macroscopic polarizability along different optical axes, we focused on the anisotropic polarization.^57–59 The Born effective charges are defined as:

where δ_pi is the change in polarization along the displacement direction δ_dj. More details can be found elsewhere.^60,61 The obtained Born effective charges are shown in Table 1 and Table S3 in the ESI.† It is interesting to note that unlike ABCO₃F described in ref. 61, which has nondiagonal tensors of atomic Born effective charges of almost zero, nonzero nondiagonal tensors are found in Te₂P₂O₉. As described in ref. 61, the base unit of ABCO₃F compounds are CO₃ groups, and the CO₃ groups are all in a coplanar plane, which makes the nondiagonal tensors of the Born effective charges in these carbonates vanish. In contrast, for the Te₂P₂O₉ compound described herein, it crystallizes in a 3D structure with PO₄ tetrahedrons and a TeO₅ square pyramid connected by Te–O and P–O chemical bonds. This complicated 3D structure makes it possess nonzero Born effective charges (shown in Table S3 in ESI†). Specifically, when the Te₂P₂O₉ compound is exposed to an external electric field along the special direction, the electrons move everywhere, not only in the direction of the external electric field, but also the vertical direction. Hence, nonzero nondiagonal Born effective charges can be found in Te₂P₂O₉. Furthermore, we also performed a detailed investigation into the diagonal Born effective charges along the optic principal axis and calculated the difference in the Born effective charges. As described above, the refractive indices follow the sequence of n_x > n_y > n_z, thus the difference in the Born effective charges was obtained by the q_xx − q_zz. The obtained diagonal tensor of the atomic Born effective charges of Te₂P₂O₉ q^Born_ij is shown in Table 1. As shown in Table 1, a relatively large difference in the Born effective charge tensors was found in the Te and O atoms, while the P atoms possess a relative small difference in comparison, implying that the Te and O atoms make a relatively large atomic contribution to the anisotropic birefringence. We believe that the contribution to the birefringence is provided mainly by the TeO₅ group.

Table 1 Obtained diagonal tensor of the atomic Born effective charges of Te₂P₂O₉

Compound	Atom	qxx	qyy	qzz	Δq^(Born)
Te2P2O9	Te1	4.34265	4.65936	6.63644	−2.29379
	Te2	6.4218	5.38842	3.37218	3.04962
	Te3	4.34265	4.65936	6.63644	−2.29379
	Te4	6.4218	5.38842	3.37218	3.04962
	P1	4.40285	3.49299	4.36297	0.03988
	P2	4.70919	4.86415	3.77507	0.93412
	P3	4.40285	3.49299	4.36297	0.03988
	P4	4.70919	4.86415	3.77507	0.93412
	O1	−1.78151	−1.84853	−2.74356	0.96205
	O2	−3.2844	−2.12701	−1.33367	−1.95073
	O3	−2.85789	−1.94646	−1.32288	−1.53501
	O4	−1.40561	−0.89945	−3.71391	2.3083
	O5	−1.30274	−2.25599	−1.88828	0.58554
	O6	−1.56074	−3.25254	−1.86712	0.30638
	O7	−1.54143	−1.92023	−2.76231	1.22088
	O8	−3.00828	−2.10674	−1.13507	−1.87321
	O9	−3.13389	−2.04796	−1.37986	−1.75403
	O10	−1.78151	−1.84853	−2.74356	0.96205
	O11	−3.2844	−2.12701	−1.33367	−1.95073
	O12	−2.85789	−1.94646	−1.32288	−1.53501
	O13	−1.40561	−0.89945	−3.71391	2.3083
	O14	−1.30274	−2.25599	−1.88828	0.58554
	O15	−1.56074	−3.25254	−1.86712	0.30638
	O16	−1.54143	−1.92023	−2.76231	1.22088
	O17	−3.00828	−2.10674	−1.13507	−1.87321
	O18	−3.13389	−2.04796	−1.37986	−1.75403

---

3.3 The contribution from TeO_x polyhedrons in tellurium phosphate

To better understand the contribution from the TeO_x polyhedrons to the birefringence, the electronic structures and the optical response of the other tellurium phosphates Ba₂TeO(PO₄)₂ and Te₃O₃(PO₄)₂ were also investigated. The obtained band structures and projected density of states (PDOS) of Ba₂TeO(PO₄)₂ and Te₃O₃(PO₄)₂ are shown in Fig. S1–S4 in the ESI.† As shown in Fig. S1 and S3,† the obtained bandgap of Ba₂TeO(PO₄)₂ and Te₃O₃(PO₄)₂ are 4.11 and 3.63 eV, respectively. To overcome the underestimation of the bandgap, HSE06 calculations⁶² were performed using the PWmat code.^63,64 The obtained HSE06 bandgap of Ba₂TeO(PO₄)₂ and Te₃O₃(PO₄)₂ is 4.47, and 4.18 eV, respectively. As shown in Fig. S2 and S4,† the states at the top of the valence band and at the bottom of the conduction band are mainly the Te-sp states, O-sp states, and P-sp states. Also, the chemical bonds of Te–O and P–O can also be found at the top of the valence band. Hence, it can be deduced that the TeO_x polyhedron and PO₄ tetrahedron may play an important role in determining the optical response of these tellurite phosphates.

The refractive indices and birefringence of Ba₂TeO(PO₄)₂ and Te₃O₃(PO₄)₂ were also obtained using the method described above, and the results are shown in Fig. S5 and S6,† respectively, and Table 2. As shown in Fig. S5 and S6,† the Ba₂TeO(PO₄)₂ and Te₃O₃(PO₄)₂ possess a relatively large birefringence of 0.110 and 0.121 (at 1064 nm), respectively. The birefringence of these compounds follow the sequence of Δn(Te₃O₃(PO₄)₂) > Δn(Ba₂TeO(PO₄)₂) > Δn(Te₂P₂O₉).

Table 2 The obtained refractive indices and birefringence (at 1064 nm) of Te₂P₂O₉, Ba₂TeO(PO₄)₂, and Te₃O₃(PO₄)₂ after real-space atom-cutting was performed

Crystal	Contribution	nx	ny	nz	Δn
Te2P2O9	Cut-PO	1.484	1.458	1.405	0.079
	Cut-TeO	1.232	1.226	1.203	0.029
	Origin	2.031	1.974	1.939	0.092
Ba2TeO(PO4)2	Cut-BaO	1.408	1.332	1.323	0.085
	Cut-PO	1.555	1.486	1.475	0.080
	Cut-TeO	1.600	1.588	1.563	0.037
	Origin	1.877	1.860	1.767	0.110
Te3O3(PO4)2	Cut-PO	1.622	1.585	1.570	0.052
	Cut-TeO	1.243	1.229	1.211	0.032
	Origin	2.027	1.998	1.906	0.121

---

The contribution from different polyhedrons was further investigated using the real-space atom-cutting method.⁴⁵ During the calculation, the atom-cutting radius of O, P, Te, and Ba was set as 1.10, 0.95, 0.96, and 1.74 Å, respectively. After the real-space atom-cutting method was performed, the refractive indices and birefringence of Te₂P₂O₉, Ba₂TeO(PO₄)_2, and Te₃O₃(PO₄)₂ were obtained, which are shown in Table 2, and Fig. S7–S9 in the ESI,† respectively. As shown in Table 2, in comparison with the PO₄ tetrahedron and BaO_x polyhedrons, the TeO_x polyhedrons give the main contribution to the total birefringence. Taking Te₂P₂O₉ as example, the its birefringence is about 0.092 at 1064 nm. However, after the TeO₅ polyhedron was removed, the obtained birefringence of the other part (marked as cut-TeO) is only about 0.029, implying that the TeO₅ polyhedron may give a contribution of about (0.092 − 0.029 = 0.063) to the total birefringence of Te₂P₂O₉. Thus, in comparison with the PO₄ tetrahedron, the TeO₅ polyhedron gives main contribution to the total birefringence. A similar conclusion was also found for the other tellurium phosphates, Ba₂TeO(PO₄)₂ and Te₃O₃(PO₄)₂ (as shown in Table 2). It is interesting to note that the conclusion obtained from the real-space atom-cutting is consistent with the results obtained from the Born-effective charges analysis (as described above).

The optical anisotropic birefringence is related with the anisotropic optical response from the different polyhedrons. The relatively small anisotropic polarization of the regular PO₄ unit may be related with the relatively small distortion with the regular PO₄ unit. Herein, the distortion indices of the different polyhedrons in these tellurium phosphates were also investigated. The distortion indices, defined by Baur as 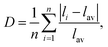⁶⁵ was calculated using the VESTA software.⁶⁶ The obtained distortion indices of the different polyhedrons in these tellurium phosphates are shown in Table 3. As described above, the TeO_x polyhedrons give the main contribution to the total birefringence, and hence was focused on the distortion indices of the TeO_x polyhedron. As shown in Table 3, the distortion indices of the TeO_x polyhedrons follow the sequence of D(Te₃O₃(PO₄)₂) > D(Ba₂TeO(PO₄)₂) > D(Te₂P₂O₉), which is consistent with the sequence of the birefringence of Δn(Te₃O₃(PO₄)₂) > Δn(Ba₂TeO(PO₄)₂) > Δn(Te₂P₂O₉).

Table 3 The obtained distortion indices of the different polyhedrons in Te₂P₂O₉, Ba₂TeO(PO₄)₂, and Te₃O₃(PO₄)₂

	Te2P2O9	Ba2TeO(PO4)2	Te3O3(PO4)2
PO4	0.005	0.020	0.013
TeOx	0.034	0.039	0.051
BaOx		0.034

---

3.4 The atomic contribution to the SHG response of Te₂P₂O₉

The SHG tensors of Te₂P₂O₉ were also obtained (shown in Table 4). For that crystallized in the Cc space group, there are six independent nonzero SHG tensors, d₁₁, d₁₂, d₁₃, d₁₅, d₂₄ and d₃₃. As shown in Table 4, for Te₂P₂O₉, the maximum is d₃₃ = 1.01 pm V⁻¹, which is about 2.6 times that of d₃₆(KDP). The obtained SHG tensors are comparable with the experimental powder second-harmonic generation (PSHG) intensity (about 1.3 × KDP). The experimental values agree well with the calculated values, indicating that the method selected in this work is appropriate. To deeply investigate the atomic contribution to the SHG tensors, the spatial distribution of the atomic SHG density was also calculated. The SHG density method is a normalized weighting coefficient via the use of the effective SHG response of each occupied and unoccupied band.^59,60 Using this method, the states irrelevant to the SHG response will not be shown, and the distribution of the SHG density represents the origin of the SHG response. Herein, we only show the SHG density obtained from the virtual electron process (labeled as veocc) and the virtual hole process (labeled as vhunocc). The obtained SHG density of Te₂P₂O₉ is shown in Fig. 4, where the color part and white–black part represent the SHG density of the veocc and vhunocc process, respectively. As shown in Fig. 4, there is no SHG distribution around the P atoms, implying that the P atoms give a relatively small contribution to the total SHG response. It is shown that the SHG density is distributed mainly on the Te and O atoms, indicating that the TeO₅ polyhedrons give the main contribution to the total SHG response.

Table 4 The calculated SHG tensors and experimental powder SHG (PSHG) intensity

Crystal	Space group	Calculated SHG tensors (pm V^−1)	PSHG intensity
Te2P2O9	Cc	d11 = −0.17, d15 = −0.53, d12 = 0.59, d13 = −0.56, d24 = −0.95, d33 = 1.01	1.3 × KDP

---

Fig. 4 The obtained SHG density of Te₂P₂O₉. Note that the brown, pink, and red atoms are Te, P, and O atoms; and the color and black–white clouds are the veocc and vhunocc SHG densities, respectively.

4. Conclusions

In this work, the refractive indices, birefringence, and the SHG coefficient of Te₂P₂O₉ were obtained using the first-principles method. The obtained results are in good agreement with the experimental values. The calculated birefringence of Te₂P₂O₉ is 0.12496–0.09236 in the wavelength range of 404.65–1013.61 nm. The maximum SHG tensor d₃₃ is 1.01 pm V⁻¹, which is about 2.6 times that of d₃₆ (KDP). The atomic contribution to the birefringence and SHG response was also investigated using the projected density of states, Born effective charges, and real-space SHG density method. The results show that the TeO₅ groups play an important role in determining the birefringence and SHG response of Te₂P₂O₉. The electronic structures and optical response of Ba₂TeO(PO₄)₂ and Te₃O₃(PO₄)₂ were also investigated for comparison. The results show these two tellurium phosphates also possess a large birefringence like Te₂P₂O₉. Also, the birefringence originates from the TeO_x polyhedrons, which was confirmed by the real-space atom-cutting results and distortion indices.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (No. 11664037, 11864040), the Natural Science Foundation of Xinjiang Uygur Autonomous Region of China (Grant No. 2018D01C079, 2018D01C072), the Science and Technology Research Program for Colleges and Universities in the Department of Education in Xinjiang Uygur Autonomous Region of China (Grant No. XJEDU2017M006). The author Haibin Cao acknowledges support from Foundation for High-level Talents in Shihezi University (RCZX201511), and Applied Basic Research Foundation of Science and Technology in Shihezi University (2015ZRKXYQ07).

References

1. C. T. Chen, G. L. Wang, X. Y. Wang and Z. Y. Xu, Deep-UV nonlinear optical crystal KBe₂BO₃F₂ – discovery, growth, optical properties and applications, Appl. Phys. B, 2009, 97, 9–25.
2. Y. Ning, C. Tu, X. Long and M. Hong, Recent Advances in Crystal Growth in China: Laser, Nonlinear Optical, and Ferroelectric Crystals, Cryst. Growth Des., 2010, 10, 4672–4681.
3. W. Zhang, H. Yu, H. Wu and P. S. Halasyamani, Phase-Matching in Nonlinear Optical Compounds: A Materials Perspective, Chem. Mater., 2017, 29, 2655–2668.
4. Z. Hu, T. Higashiyama, M. Yoshimura, Y. Yap, Y. Mori and T. Sasaki, A New Nonlinear Optical Borate Crystal K₂Al₂B₂O₇ (KAB), Jpn. J. Appl. Phys., 1998, 37, L1093–L1094.
5. H. P. Wu, H. W. Yu, Z. H. Yang, X. L. Hou, S. L. Pan, X. Su, K. R. Poeppelmeier and J. M. Rondinelli, Designing a deep ultraviolet nonlinear optical material with large second harmonic generation response, J. Am. Chem. Soc., 2013, 135, 4215–4219.
6. X. L. Chen, B. B. Zhang, F. F. Zhang, Y. Wang, M. Zhang, Z. H. Yang, K. R. Poeppelmeier and S. L. Pan, Designing an excellent deep-ultraviolet birefringent material for light polarization, J. Am. Chem. Soc., 2018, 140, 16311–16319.
7. Y. Wang, B. Zhang, Z. Yang and S. Pan, Cation-Tuned Synthesis of Fluorooxoborates: Approaching the Optimal Deep-Ultraviolet Nonlinear Optical Materials, Angew. Chem., Int. Ed., 2018, 57, 2150–2154.
8. G. Q. Shi, Y. Wang, F. F. Zhan, B. B. Zhang, R. H. Yang, X. L. Hou, S. L. Pan and K. R. Poeppelmeier, Finding the Next Deep-Ultraviolet Nonlinear Optical Material: NH₄B₄O₆F, J. Am. Chem. Soc., 2017, 139, 10645–10648.
9. B. H. Lei, Z. Yang and S. Pan, Enhancing optical anisotropy of crystals by optimizing bonding electron distribution in anionic groups, Chem. Commun., 2017, 53, 2818–2821.
10. X. Dong, Q. Jing, Y. Shi, Z. Yang, S. Pan, K. R. Poeppelmeier, J. Young and J. M. Rondinelli, Pb₂Ba₃(BO₃)₃Cl: A Material with Large SHG Enhancement Activated by Pb-Chelated BO₃Groups, J. Am. Chem. Soc., 2015, 46, 9417–9422.
11. G. Qu, Z. Hu, Y. Wang, Q. Yang and L. Tong, Synthesis of Optical-Quality Single-Crystal β-BaB₂O₄ Microwires and Nanowires, Adv. Funct. Mater., 2013, 23, 1232–1237.
12. Y. Xu, W. Y. Ching and R. H. French, Electronic structure and interatomic bonding of crystalline β-BaB₂O₄ with comparison to LiB₃O₅, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 17695–17702.
13. C. Chen, Y. Wu, A. Jiang, B. Wu, G. You, R. Li and S. Lin, New nonlinear-optical crystal: LiB₃O₅, J. Opt. Soc. Am. B, 1989, 6, 616–621.
14. A. Borsutzky, R. Brünger, C. Huang and R. Wallenstein, Harmonic and sum-frequency generation of pulsed laser radiation in BBO, LBO, and KD*P, Appl. Phys. B: Photophys. Laser Chem., 1991, 52, 55–62.
15. Q. H. Xue, Q. Zheng, Y. K. Bu, F. Q. Jia and L. S. Qian, High-power efficient diode-pumped Nd : YVO₄/LiB₃O₅ 457 nm blue laser with 4.6 W of output power, Opt. Lett., 2006, 31, 1070–1072.
16. J. Sakuma, Y. Asakawa and M. Obara, Generation of 5-W deep-UV continuous-wave radiation at 266 nm by an external cavity with a CsLiB₆O₁₀ crystal, Opt. Lett., 2004, 29, 92–94.
17. N. Umemura and K. Kato, Ultraviolet generation tunable to 0.185 microm in CsLiB₆O₁₀, Appl. Opt., 1997, 36, 6794–6796.
18. D. Xue, K. Betzler and H. Hesse, Chemical-bond analysis of the nonlinear optical properties of the borate crystals LiB₃O₅, CsLiB₆O₁₀, and CsB₃O₅, Appl. Phys. A: Mater. Sci. Process., 2002, 74, 779–782.
19. Y. Wu, et al., CsB₃O₅: A new nonlinear optical crystal, Appl. Phys. Lett., 1993, 62, 2614–2615.
20. H. Kitano, et al., Efficient 355-nm generation in CsB₃O₅ crystal, Opt. Lett., 2003, 28, 263–265.
21. C. Chen, Z. Xu, D. Deng, J. Zhang, G. Wong, B. Wu, N. Ye and D. Tang, The vacuum ultraviolet phase matching characteristics of nonlinear optical KBe₂BO₃F₂ crystal, Appl. Phys. Lett., 1998, 68, 2930–2932.
22. C. Chen, J. Lu, G. Wang, Z. Xu, J. Wang, C. Zhang and Y. Liu, Deep Ultraviolet Harmonic Generation with KBe₂BO₃F₂ Crystal, Chin. Phys. Lett., 2001, 18, 1081.
23. C. Chen, J. Lu, T. Togashi, T. Suganuma, T. Sekikawa, S. Watanabe, Z. Y. Xu and J. Wang, Second-harmonic generation from a KBe₂BO₃F₂ crystal in the deep ultraviolet, Opt. Lett., 2002, 27, 637–639.
24. T. Togashi, T. Kanai, T. Sekikawa, S. Watanabe, C. Chen, C. Zhang, Z. Xu and J. Wang, Generation of vacuum-ultraviolet light by an optically contacted, prism-coupled KBe₂BO₃F₂ crystal, Opt. Lett., 2003, 28, 254.
25. B. B. Zhang, G. Q. Shi, Z. H. Yang, F. F. Zhang and S. L. Pan, Fluorooxoborates: Beryllium-Free Deep-Ultraviolet Nonlinear Optical Materials without Layered Growth, Angew. Chem., Int. Ed., 2017, 56, 3916–3919.
26. Z. Yang, B.-H. Lei, W. Zhang and S. Pan, Module-Analysis-Assisted Design of Deep Ultraviolet Fluorooxoborates with Extremely Large Gap and High Structural Stability, Chem. Mater., 2019, 31, 2807–2813.
27. X. Wang, Y. Wang, B. Zhang, F. Zhang, Z. Yang and S. Pan, CsB₄O₆F: A Congruent-Melting Deep-Ultraviolet Nonlinear Optical Material by Combining Superior Functional Units, Angew. Chem., Int. Ed., 2017, 56, 14119–14123.
28. Z. Zhang, Y. Wang, B. Zhang, Z. Yang and S. Pan, Polar Fluorooxoborate, NaB₄O₆F: A Promising Material for Ionic Conduction and Nonlinear Optics, Angew. Chem., Int. Ed., 2018, 57, 6577–6581.
29. M. Mutailipu, M. Zhang, B. Zhang, L. Wang, Z. Yang, X. Zhou and S. Pan, SrB₅O₇F₃ Functionalized with [B₅O₉F₃]⁶⁻ Chromophores: Accelerating the Rational Design of Deep-ultraviolet Nonlinear Optical Materials, Angew. Chem., Int. Ed., 2018, 57, 6095–6099.
30. Y. Shen, S. Zhao, B. Zhao, C. Ji, L. Li, Z. Sun, M. Hong and J. Luo, Strong Nonlinear-Optical Response in the Pyrophosphate CsLiCdP₂O₇ with a Short Cutoff Edge, Inorg. Chem., 2016, 55, 11626–11629.
31. M. Abudoureheman, S. Han, B. Lei, Z. Yang, X. Long and S. Pan, KPb₂(PO₃)₅: a novel nonlinear optical lead polyphosphate with a short deep-UV cutoff edge, J. Mater. Chem. C, 2016, 4, 10630–10637.
32. S. Zhao, P. Gong, S. Luo, L. Bai, Z. Lin, C. Ji, T. Chen, M. Hong and J. Luo, Deep-Ultraviolet Transparent Phosphates RbBa₂(PO₃)₅ and Rb₂Ba₃(P₂O₇)₂ Show Nonlinear Optical Activity from Condensation of [PO₄]³⁻ Units, J. Am. Chem. Soc., 2014, 136, 8560–8563.
33. S. Zhao, P. Gong, S. Luo, L. Bai, Z. Lin, Y. Tang, Y. Zhou, M. Hong and J. Luo, Tailored Synthesis of a Nonlinear Optical Phosphate with a Short Absorption Edge, Angew. Chem., Int. Ed. Engl., 2015, 127, 4291–4295.
34. P. Shan, T. Sun, H. Chen, H. Liu, S. Chen, X. Liu, Y. Kong and J. Xu, Crystal growth and optical characteristics of beryllium-free polyphosphate, KLa(PO₃)₄, a possible deep-ultraviolet nonlinear optical crystal, Sci. Rep., 2016, 6, 25201.
35. V. G. Dmitriev, G. G. Gurzadyan and D. N. Nikogosyan, Properties of Nonlinear Optical Crystals, in Handbook of Nonlinear Optical Crystals. Springer Series in Optical Sciences, Springer, Berlin, Heidelberg, 1997, vol. 64.
36. W. Dong, Q. Yao, J. Zhang, L. Liu, J. Li and J. Wang, Czochralski Growth and Characterization of a Novel Nonlinear Optical Crystal Te₂P₂O₉, Cryst. Growth Des., 2018, 18, 5919–5926.
37. K. Min Ok and P. S. Halasyamani, Synthesis, structure, and characterization of a new one-dimensional tellurite phosphate, Ba₂TeO(PO₄)₂, ChemInform, 2006, 179(5), 1345–1350.
38. H. Mayer and M. Weil, Synthesis and crystal structure of Te₃O₃(PO₄)₂, a compound with 5-fold coordinate tellurium(IV), Cheminform, 2003, 629(6), 1068–1072.
39. M. Segall, P. Lindan, M. Probert, C. Pickard, P. Hasnip, S. Clark and M. Payne, First-principles simulation: ideas, illustrations and the CASTEP code, J. Phys.: Condens. Matter, 2002, 14, 2717–2744.
40. S. Clark, M. Segall, C. Pickard, P. Hasnip, M. Probert, K. Refson and M. Payne, First principles methods using CASTEP, Z. Kristallogr., 2005, 220, 567–570.
41. M. Ernzerhof and G. E. Scuseria, Assessment of the Perdew–Burke–Ernzerhof exchange-correlation functional, J. Chem. Phys., 1999, 110, 5029–5036.
42. B. Hammer, L. Hansen and J. Nørskov, Improved adsorption energetics within density-functional theory using revised Perdew-Burke-Ernzerhof functionals, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 7413–7421.
43. R. J. Nicholls, A. J. Morris, C. J. Pickard and J. R. Yates, OptaDOS - a new tool for EELS calculations, J. Phys.: Conf. Ser., 2012, 371, 012062.
44. A. J. Morris, R. J. Nicholls, C. J. Pickard and J. R. Yates, OptaDOS: A tool for obtaining density of states, core-level and optical spectra from electronic structure codes, Comput. Phys. Commun., 2014, 185, 1477–1485.
45. Z. Lin, Z. Wang, C. Chen, S. Chen and M. Lee, Mechanism for linear and nonlinear optical effects in crystals of the Sr₂Be₂B₂O₇ family, J. Appl. Phys., 2003, 93, 9717–9723.
46. B. Zhang, M. Lee, Z. Yang, Q. Jing, S. Pan, M. Zhang, H. Wu, X. Su and C. Li, Simulated pressure-induced blue-shift of phase-matching region and nonlinear optical mechanism for K₃B₆O₁₀X (X = Cl, Br), Appl. Phys. Lett., 2015, 106, 992.
47. Q. Jing, X. Dong, X. Chen, Z. Yang, S. Pan and C. Lei, The lone-pairs enhanced birefringence and SHG response: A DFT investigation on M₂B₅O₉Cl (M = Sr, Ba, and Pb), Chem. Phys., 2015, 453–454, 42–46.
48. J. Perdew and M. Levy, Physical Content of the Exact Kohn–Sham Orbital Energies: Band Gap and Derivative Discontinuities, Phys. Rev. Lett., 1983, 51, 1884–1887.
49. A. Walsh, D. J. Payne, R. G. Egdell and G. W. Watson, Stereochemistry of post-transition metal oxides: revision of the classical lone pair model, Chem. Soc. Rev., 2011, 40, 4455–4463.
50. A. Walsh and G. Watson, The origin of the stereochemically active Pb(II) lone pair : DFT calculations on PbO and PbS, J. Solid State Chem., 2005, 178, 1422–1428.
51. A. Walsh and G. W. Watson, Influence of the anion on lone pair formation in Sn(II) monochalcogenides: a DFT study, J. Phys. Chem. B, 2005, 109, 18868–18875.
52. J. Raulot, G. Baldinozzi, R. Seshadri and P. Cortona, An ab-initio Study of the Role of Ione Pairs in the Structure and Insulator-Metal Transition in SnO and PbO, Solid State Sci., 2002, 4, 467–474.
53. D. J. Payne, R. G. Egdell, A. Walsh, G. W. Watson, J. Guo, P. A. Glans, T. Learmonth and K. E. Smith, Electronic Origins of Structural Distortions in Post-Transition Metal Oxides: Experimental and Theoretical Evidence for a Revision of the Lone Pair Model, Phys. Rev. Lett., 2006, 96, 157403.
54. P. Hohenberg and W. Kohn, Inhomogeneous Electron Gas, Phys. Rev., 1964, 136, B864.
55. A. Filippetti and N. A. Spaldin, Strong-correlation effects in Born effective charges, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 045111.
56. A. Roy, R. Prasad, S. Auluck and A. Garg, First-Principles Calculation of Born Effective Charges and Spontaneous Polarization of Ferroelectric Bismuth Titanate, J. Phys.: Condens. Matter, 2010, 22, 165902.
57. R. Resta and D. Vanderbilt, Theory of Polarization: A Modern Approach, Top. Appl. Phys., 2007, 105, 31–68.
58. R. Resta, Modern theory of polarization in ferroelectrics, Ferroelectrics, 1994, 151, 49–58.
59. Q. Zhang, Q. Jing, H. Duan and H. Cao, The relationship between covalent bonds and the optical response in a nonpolar family ATeMoO₆ (A=Mg, Zn, Cd): A Berry-Phase investigation, J. Solid State Chem., 2018, 264, 22–28.
60. N. A. Spaldin, A beginner's guide to the modern theory of polarization, J. Solid State Chem., 2012, 195, 2–10.
61. Q. Jing, G. Yang, J. Hou, M. Sun and H. Cao, Positive and negative contribution to birefringence in a family of carbonates: A Born effective charges analysis, J. Solid State Chem., 2016, 244, 69–74.
62. A. V. Krukau, O. A. Vydrov, A. F. Izmaylov and G. E. Scuseria, Influence of the Exchange Screening Parameter on the Performance of Screened Hybrid Functionals, J. Chem. Phys., 2006, 125, 224106.
63. W. Jia, J. Fu and Z. Cao, et al., Fast plane wave density functional theory molecular dynamics calculations on multi-GPU machines, J. Comput. Phys., 2013, 251, 102–115.
64. W. Jia, Z. Cao and L. Wang, et al., The analysis of a plane wave pseudopotential density functional theory code on a GPU machine, Comput. Phys. Commun., 2013, 184, 9–18.
65. W. H. J. A. C. Baur, The geometry of polyhedral distortions. Predictive relationships for the phosphate group, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1974, 30(5), 1195–1215.
66. K. Momma and F. Izumi, VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data, J. Appl. Crystallogr., 2011, 44, 1272–1276.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c9ra10653g

---