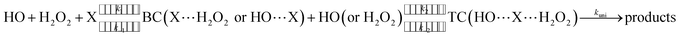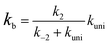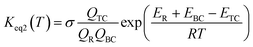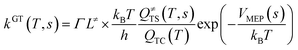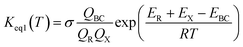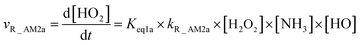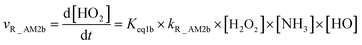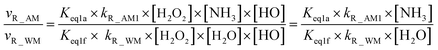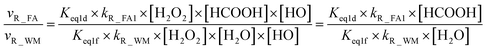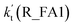DOI:
10.1039/D0RA00024H
(Paper)
RSC Adv., 2020,
10, 9093-9102
Effect of NH3 and HCOOH on the H2O2 + HO → HO2 + H2O reaction in the troposphere: competition between the one-step and stepwise mechanisms†
Received
2nd January 2020
, Accepted 13th February 2020
First published on 2nd March 2020
Abstract
The H2O2 + HO → HO2 + H2O reaction is an important reservoir for both radicals of HO and HO2 catalyzing the destruction of O3. Here, this reaction assisted by NH3 and HCOOH catalysts was explored using the CCSD(T)-F12a/cc-pVDZ-F12//M06-2X/aug-cc-pVTZ method and canonical variational transition state theory with small curvature tunneling. Two possible sets of mechanisms, (i) one-step routes and (ii) stepwise processes, are possible. Our results show that in the presence of both NH3 and HCOOH catalysts under relevant atmospheric temperature, mechanism (i) is favored both energetically and kinetically than the corresponding mechanism (ii). At 298 K, the relative rate for mechanism (i) in the presence of NH3 (10, 2900 ppbv) and HCOOH (10 ppbv) is respectively 3–5 and 2–4 orders of magnitude lower than that of the water-catalyzed reaction. This is due to a comparatively lower concentration of NH3 and HCOOH than H2O which indicates the positive water effect under atmospheric conditions. Although NH3 and HCOOH catalysts play a negligible role in the reservoir for both radicals of HO and HO2 catalyzing the destruction of O3, the current study provides a comprehensive example of how acidic and basic catalysts assisted the gas-phase reactions.
1. Introduction
Hydrogen peroxide (H2O2) is of great importance not only because it is involved in various biological and atmospheric processes,1 but it's also one of the major sources of hydroxyl (HO) and hydroperoxyl (HO2) radicals which play an important role in combustions and atmospheric chemical processes.1 Hydroxyl radical (HO) plays an important role in maintaining the balance of atmospheric composition and forming reactive peroxides.2,3 Also, from the standpoint of degradation ability,4,5 HO radicals can react with one ozone molecule to produce molecular oxygen and the HO2 radicals in the upper atmosphere. As an important reaction in HOx chemistry, the H2O2 + HO reaction shown in eqn (1) can determine the consumption of HO radicals in HOx chain reactions. Meanwhile, this reaction is also an important reservoir5,6 for both radicals of HO and HO2 catalyzing the destruction of ozone (O3).| | |
H2O2 + HO → HO2 + H2O
| (1) |
It is obvious from previous reports that the H2O2 + HO reaction has been extensively studied both experimentally7–12 and theoretically.10,13–15 In terms of experiments, for the gas-phase reaction of H2O2 + HO, Vakhtin et al.16 obtained its rate coefficient (1.78 ± 0.19) × 10−12 cm3 per molecule per s at 296 K through the laser-induced resonance fluorescence technology. Similar to the report of Vakhtin et al.,16 NASA/JPL17 evaluation suggested the rate coefficient for the H2O2 + HO reaction between 200 and 300 K was 1.8 × 10−12 cm3 per molecule per s. In addition, the results obtained by the experimental group18,19 revealed that the rate coefficients for the H2O2 + HO reaction have positive temperature dependence within different temperature ranges. From the theoretical point of view, Francisco's group20 has studied the mechanism of H2O2 + HO reaction at the CCSD(T)/CBS//MP2/aug-cc-pVDZ level, and their calculated rate coefficient was 1.56 × 10−12 cm3 per molecule per s at 298 K, which was in good agreement with the experimental results reported by Vaghjiani and coworkers.10 Then, a water-assisted H2O2 + HO reaction has been reported by Francisco's group. Their calculations show that the rate coefficient for the H2O2 + HO reaction with H2O was 4.09 × 10−12 cm3 per molecule per s at 298 K, which was 2.6 times larger than the value of the unassisted reaction. Subsequently, the reactions of H2O2⋯(H2O)n (n = 1–3) + HO and H2O2 + HO⋯(H2O)n (n = 1–3) have been investigated by our group,21 where the catalytic effect of (H2O)n (n = 1–3) is mainly taken from the contribution of H2O, and in H2O-assisted reaction, one-step process occurring through cage-like hydrogen bonding network complex and the transition state is kinetically favorable. However, this effort has focused only on the process of H2O2 + HO reaction without and with water. As far as we know, the effect of NH3 and HCOOH on H2O2 + HO → HO2 + H2O reaction has not been elucidated in the literature yet.
As the most abundant of all alkaline gases, the concentration of NH3 was found to be 10 ppm in dairy farms and 30 ppb in a polluted ambient atmosphere.22–25 Meanwhile, NH3 has similar efficiency as H2O in catalyzing many hydrogen abstraction reactions.26–30 Based on the fact that the possibility of the NH3-catalytic effect on the H2O2 + HO → HO2 + H2O reaction has been investigated theoretically in this work. Also, owing to the significant abundance of HCOOH in the atmosphere, HCOOH can also be an effective catalyst like H2O and NH3. It has been proved in previous investigations that HCOOH can decrease the energy significantly for several atmospheric hydrogen abstraction reactions.31–37 Thus, it is also necessary to study the possible catalytic effect of HCOOH on the H2O2 + HO reaction.
In the present work, the effect of NH3 and HCOOH on the H2O2 + HO → HO2 + H2O reaction has been investigated from both energetic and kinetic aspects, which was organized in two ways. Firstly, the roles of NH3 and HCOOH in the H2O2 + HO → HO2 + H2O reaction have been studied by both stepwise mechanism and one-step process. Then, the relative impacts of NH3 and HCOOH and their competition with H2O have been investigated by considering the dependence of rate coefficient on temperature and catalyst concentrations. Through our research, we expect to provide significant theoretical guidance for further revealing of the H2O2 + HO → HO2 + H2O reaction assisted by acidic, neutral and basic catalysts in the actual atmospheric environment.
2. Computational methods
2.1 Electronic structure calculation
The electronic structure calculations have been carried out by the Gaussian 09 program.38 Geometries of all the species including reactants, pre-reactive complexes, transition states, post-reactive complexes, and products were optimized at the M06-2X/aug-cc-pVTZ level. The corresponding frequencies of the optimized geometries were computed at the same level to prove the characteristics of the transition states with one imaginary frequency and the stationary points possess all real frequencies. The minimum energy paths (MEPs) were obtained by intrinsic reaction coordinate (IRC)39–41 calculations at the same level which confirms TSs, reactants, and products. IRC calculations also confirmed the presence of pre- and post-reactive complexes at the entry and exit site of reaction path.
To improve the accuracy of the energetics, using M06-2X/aug-cc-pVTZ optimized geometries, single-point energy was calculated using ORCA42 at the CCSD(T)-F12a/cc-pVDZ-F12 level,43–45 and the scaled ZPEs were added to them. The scaling factor employed to adjust the ZPEs was 0.9490.46 The reliability of CCSD(T)-F12a/cc-pVDZ-F12 method was further tested by the single point energies of H2O2 + HO → HO2 + H2O reaction at the W3X-L and W2X47 using MRCC48,49 program packages. It is noted that quantitative barrier heights47,50–53 for complex atmospheric reactions can be obtained using W3X-L, where the accuracy of W2X and W3X-L can respectively reach for the all-electron scalar-relativistic CCSD(T)/CBS and CCSD(Q)/CBS. Here, the calculated results showed that the unsigned error of CCSD(T)-F12a/cc-pVDZ-F12 is less than 0.5 kcal mol−1 (Table S1†), when compared with W3X-L results. Therefore, the affordable CCSD(T)-F12a/cc-pVDZ-F12 method is chosen to do single point energy calculations for the H2O2 + HO → HO2 + H2O reaction assisted by NH3 and HCOOH.
2.2 Chemical kinetics calculations
H2O2 + HO → HO2 + H2O reaction assisted by catalyst X (X = NH3 and HCOOH) can be regarded as a sequential bimolecular reaction shown in eqn (2).| |
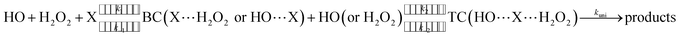 | (2) |
In eqn (2), the dimer H2O2⋯HO is assumed to be less important than H2O2⋯X and HO⋯X, due to the small concentration of H2O2 and HO radicals. So, the sequential bimolecular route would first occur through the formation of a bimolecular complex BC (X⋯H2O2 or HO⋯X), and then bimolecular complex combines with the other reactant (HO or H2O2) to form the trimolecular complex TC (HO⋯X⋯H2O2). Subsequently, the trimolecular complex undergoes a unimolecular reaction via the corresponding TS to form the products. Assuming a steady-state approximation, trimolecular complex TC is in equilibrium with bimolecular complex BC and reactant (H2O2 or HO), the bimolecular rate coefficient (kb) for the reaction between BC and reactant (H2O2 or HO) can be written as eqn (3) and calculated by employing Polyrate 8.2 program54 coupled with the steady-state approximation.| |
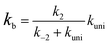 | (3) |
Here assuming k−2 is much larger than kuni, kb of eqn (3) can be simplified as eqn (4).
This kinetic model is reasonably correct at the high-pressure limit. In eqn (4), the equilibrium constant Keq2 can be written in eqn (5), while the rate coefficient constant (kuni) from trimolecular complex to the products can be minimized by varying the transition state dividing surface along the reaction coordinate to get the CVT rate coefficients given by eqn (6) and (7):55–58
| |
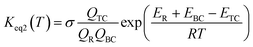 | (5) |
| |
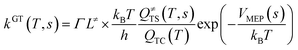 | (6) |
| | |
kCVT(T) = minskGT(T, 〈s〉) = kGT[T,sCVT(T)]
| (7) |
where
QTC,
QBC and
QR in
eqn (5) is respectively the total partition function of the trimolecular complex TC, bimolecular complex BC and reactant (HO or H
2O
2);
ETC,
EBC and
ER is respectively the energy of trimolecular complex TC, bimolecular complex BC and reactant (HO or H
2O
2).
kGT(
T,
s) in
eqn (6) and
kCVT(
T) in
eqn (7) is respectively the rate coefficient of generalized and canonical variational transition state theory.
Γ is the small curvature tunneling (SCT)
59,60 correction,
L≠ is the reaction path degeneracy,
h is the Planck's constant,
kB is the Boltzmann constant,
VMEP(
s) is the classical barrier height and
Q≠TS is the total partition functions for the transition state. It should be noted that
Keq2 calculated here has been successfully performed in calculating the complexes
61–65 of H
2O⋯VOC, H
2O⋯HCHO, H
2O⋯CH
3COCH
3, H
2O⋯CH
2NH, H
2O⋯HO
2, H
2O⋯SO
2, and H
2O⋯NO
2. In this work, we do not consider the effects of partial pressure on the formation of these complexes because there are no experimental data to show that the equilibrium constants of these complexes are determined by pressure.
The equilibrium constant for the formation of the bimolecular complex (Keq1) can also be calculated using corresponding partition functions and energies (obtained from electronic structure calculations) as eqn (8)
| |
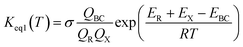 | (8) |
where
QBC and
QR are the total partition functions of the bimolecular complex and reactants, respectively;
EBC and
ER are the energies of bimolecular complex and reactants, respectively. From the above, the rate (
v) of the sequential bimolecular reaction can be written as:
| | |
v = Keq1 × Keq2 × kuni × [X] × [HO] × [H2O2]
| (9) |
Here,
v is considered as a measure of the relative efficiencies of the different catalysts under atmospheric conditions.
3. Results and discussions
3.1 Reactants
In the presence of catalyst X, the H2O2 + HO + X reaction going through a termolecular reaction has a much lower probability than the sequential bimolecular reaction. In this work, the sequential bimolecular reaction is that, initially, the H2O2 + HO + X reaction goes through a two-body complex between catalyst X and one of the two reactants (H2O2 or HO) and then the two-body complex will react with the other reactant. It should be noted that, because of the small concentration of H2O2 and HO radicals, the concentration of dimer H2O2⋯HO is much lower as compared to the dimers of H2O2⋯X and HO⋯X. Thus, H2O2⋯HO complex can be neglected and it is not taken into account here. Such investigations have been studied in similar investigations,52,66–70 where the dimer between the two reactants has not been involved in X assisted reactions. Above step is followed since it is very necessary to first identify the stable binary complexes of H2O2⋯X and HO⋯X. To achieve this aim, we performed a stable global minimum searching of geometrical configurations using Tsinghua Global Minimum (TGMin) program71,72 to search out variety geometrical configurations of H2O2⋯X and HO⋯X complexes firstly. Secondly initial structures obtained for these binary complexes were selected for geometry optimization using the M06-2X/6-31+G(d,p) level. Then, the structures within 5.0 kcal mol−1 of the global minimum were re-optimized by M06-2X/aug-cc-pVTZ level. The optimized structures for the most stable H2O2⋯X and HO⋯X complexes have been shown in Fig. 1. As displayed in Fig. 1, the stable binary H2O2⋯NH3 complex shows a five-membered ring with two hydrogen bonds (H4⋯N, 1.85 Å; H1⋯O2, 2.67 Å) involved. Its stabilization energy is 6.6 kcal mol−1 relative to the separate reactants of H2O2 and NH3, and is respectively stabilized by 1.1 and 6.6 kcal mol−1 than the other two binary complexes of HO⋯NH3 and NH3⋯HO. Binary complexes of H2O2⋯HCOOH and HO⋯HCOOH were formed with stabilization energies of 10.1 and 4.9 kcal mol−1, respectively. The energy difference between these two complexes can be explained in terms of ring size formed within their structures. The former complex is formed with a seven-membered ring structure, while the latter complex forms a six-membered ring structure.
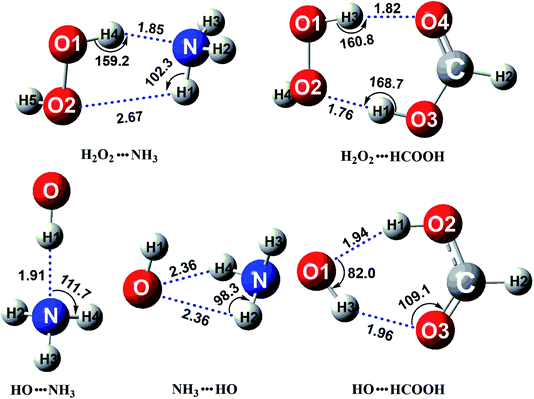 |
| | Fig. 1 The optimized structures for the most stable complex of H2O2 (or HO) with catalyst X (X = NH3 and HCOOH) at the CCSD(T)-F12a/cc-pVDZ-F12//M06-2X/aug-cc-pVTZ level. | |
3.2 Mechanism and kinetic for NH3-assisted reaction
Depending on the type of the binary complex discussed above, three different binary mechanisms, labelled as H2O2⋯NH3 + HO, HO⋯NH3 + H2O2, and NH3⋯HO + H2O2, were obtained (as illustrated in Fig. 2). Among the three NH3 assisted H2O2 + HO → HO2 + H2O reactions, one proceeds through both one-step and stepwise mechanisms and the other two occur-only through a one-step mechanism. The relative energies to the separate reactants in the presence of NH3 are given in Table S5.†
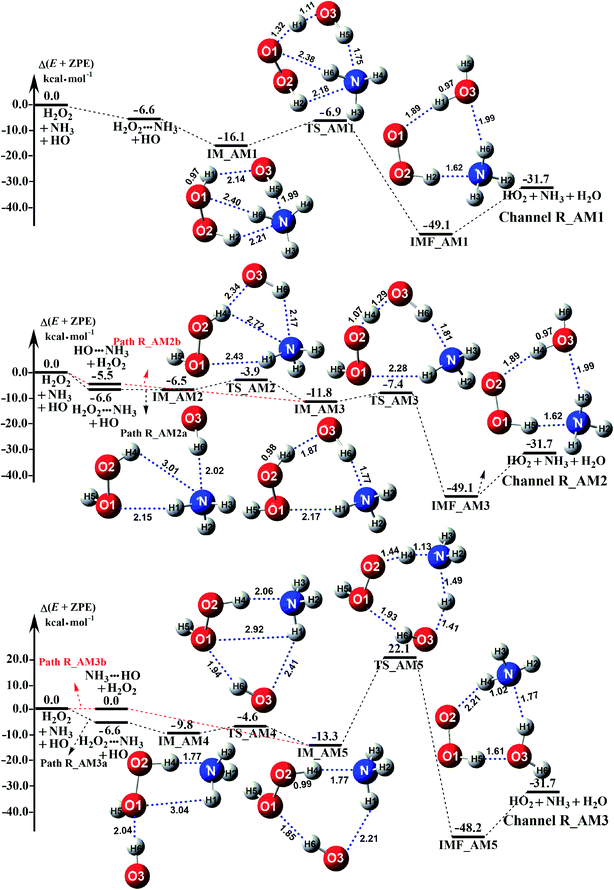 |
| | Fig. 2 Schematic potential energy diagrams for NH3 catalyzed H2O2 + HO → HO2 + H2O reaction at the CCSD(T)-F12a/cc-pVDZ-F12//M06-2X/aug-cc-pVTZ level. | |
As for Channel R_AM1, the reaction starting with H2O2⋯NH3 + HO reactants leads to a termolecular hydrogen bond complex IM_AM1 with a binding energy of 9.5 kcal mol−1 relatives to the separate H2O2⋯NH3 + HO reactants. Because of the geometry, additional two hydrogen bonds (N⋯H5, 1.99 Å; O3⋯H1, 2.14 Å) were formed in complex IM_AM1 as compared to H2O2⋯NH3 complex. This leads to complex IM_WM1 shows a quasi-planar cage-like hydrogen bonding network structure. Starting from complex IM_AM1, Channel R_AM1 proceeds through the transition state TS_AM1 where the O atom of HO radical extracts one H atom of H2O2 moiety in H2O2⋯NH3 complex. As illustrated in Fig. 2(a), TS_AM1 has a computed barrier of 9.2 kcal mol−1 relatives to complex IM_AM1. This barrier height is much lower than that for H2O2 + HO → HO2 + H2O reaction without catalyst X, which has an energy barrier of 14.1 kcal mol−1 as compared to corresponding pre-reactive complex IM1 (Table S5†). Similarity, compared with the reaction without X, the computed free energy barrier (ΔG, 298 K) of the transition state TS_AM1 to the complex IM_AM1 is reduced to 9.6 kcal mol−1 from 14.1 kcal mol−1. Differently from complex IM_AM1 and transition state TS_AM1, post-reactive complex IMF_AM1 shows a planar structure with its stabilization energy of 42.5 kcal mol−1 relatives to H2O2⋯NH3 + HO reactants.
As for Channel R_AM2, when NH3 has introduced into the H2O2 + HO → HO2 + H2O reaction, two kinds of entrance channels, H2O2⋯NH3 + HO (Path R_AM2a) and HO⋯NH3 + H2O2 (Path R_AM2b), have been displayed in Fig. 2(b). When binary complex H2O2⋯NH3 and HO play as reactants, the reaction occurs in stepwise route, which is similar to H2O catalyzed reactions21,28,62,73,74 of HO2 + HO, HO2 + HS, H2O2 + HO, HO2 + Cl, and HO2 + NH2, as well as NH3-catalyzed HO2 + Cl reaction.28 The first step begins with pre-reactive complex IM_AM2, which transforms into seven-membered ring complex IM_AM3 through transition state TS_AM2 by a ring enlargement. It is noted that complex IM_AM3 has a binding energy of 11.8 kcal mol−1, larger by 5.3 kcal mol−1 that of complex IM_AM2. At the same time, the barrier height of the ring enlargement is only 2.6 kcal mol−1, revealing that this elementary step can occur easily both thermodynamically and kinetically. In the second step, the IM_AM3 complex undergoes a direct hydrogen abstraction by the O atom of HO moiety abstracting one H atom of H2O2 moiety. This elementary step overcomes a barrier height of 4.4 kcal mol−1, which is higher by 1.8 kcal mol−1 than the corresponding barrier height for the step of ring enlargement. This reveals that the second step is the rate-determining step. When HO⋯NH3 and H2O2 act as reactants, the reaction occurs in one elementary step, which is similar to the H2O2 + HO → HO2 + H2O reaction in the absence of a catalyst. Starting from HO⋯NH3 + H2O2 reactants, Path R_AM2b starts with pre-reactive complex IM_AM3 and proceeds through the transition state TS_AM3 to from the post-reactive complex IMF_AM3, which has been discussed above. To check the competition between H2O2⋯NH3 + HO and HO⋯NH3 + H2O2 in Channel R_AM2, the rate via the routes of H2O2⋯NH3 + HO (Path R_AM2a) and HO⋯NH3 + H2O2 (Path R_AM2b) is respectively given in eqn (10) and (11).
| |
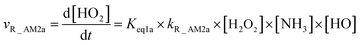 | (10) |
| |
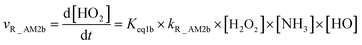 | (11) |
where
Keq1a and
Keq1b respectively denote the equilibrium constant for the formation of H
2O
2⋯NH
3 and HO⋯NH
3;
kR_AM2a and
kR_AM2b respectively denote the bimolecular rate constant of Path R_AM2a and Path R_AM2b. The calculated rate ratio for
vR_AM2a/
vR_AM2b reveals that the entrance of HO⋯NH
3 and H
2O
2 is more important than that of H
2O
2⋯NH
3 and HO with the ratio of
vR_AM2a/
vR_AM2b is 5.99 × 10
−6 to 2.36 × 10
−5 between 280 and 320 K (
Table 1). As a result, Channel R_AM2 occurs mainly through HO⋯NH
3 + H
2O
2 reactants. Similarity, the NH
3⋯HO + H
2O
2 reaction (Path R_AM3b) only has been taken into account in Channel R_AM3, and the reaction starting from H
2O
2⋯NH
3 + HO reactants (Path R_AM3a) has been neglected because the ratio of
vR_AM3a/
vR_AM3b listed in
Table 1 is 3.45 × 10
−3 to 7.24 × 10
−3 between 280 and 320 K.
Table 1 The bimolecular rate coefficients (cm3 per molecules per s) and rate ratio for NH3 catalyzed H2O2 + HO → HO2 + H2O reaction within the temperature range of 280–320 K
| T/K |
kR_AM1 |
kR_AM2a |
kR_AM2b |
vR_AM2a/vR_AM2b |
kR_AM3a |
kR_AM3b |
vR_AM3a/vR_AM3b |
vR_AM2b/vR_AM3b |
vR_AM1/vR_AM2b |
| 280 |
1.35 × 10−10 |
2.06 × 10−16 |
5.91 × 10−11 |
5.99 × 10−6 |
2.49 × 10−34 |
3.54 × 10−28 |
3.45 × 10−3 |
4.75 × 1020 |
3.95 |
| 290 |
1.13 × 10−10 |
2.54 × 10−16 |
4.68 × 10−11 |
8.77 × 10−6 |
4.98 × 10−34 |
3.92 × 10−28 |
4.24 × 10−3 |
2.46 × 1020 |
3.91 |
| 298 |
9.95 × 10−11 |
2.98 × 10−16 |
3.93 × 10−11 |
1.17 × 10−5 |
8.84 × 10−34 |
4.47 × 10−28 |
4.93 × 10−3 |
1.42 × 1020 |
3.92 |
| 300 |
9.64 × 10−11 |
3.09 × 10−16 |
3.75 × 10−11 |
1.25 × 10−5 |
1.02 × 10−33 |
4.63 × 10−28 |
5.14 × 10−3 |
1.24 × 1020 |
3.91 |
| 310 |
8.39 × 10−11 |
3.70 × 10−16 |
3.06 × 10−11 |
1.74 × 10−5 |
2.14 × 10−33 |
5.81 × 10−28 |
6.14 × 10−3 |
6.09 × 1019 |
3.94 |
| 320 |
7.43 × 10−11 |
4.38 × 10−16 |
2.55 × 10−11 |
2.36 × 10−5 |
4.58 × 10−33 |
7.69 × 10−28 |
7.24 × 10−3 |
2.93 × 1019 |
4.01 |
Regarding Channel R_AM3 starting from NH3⋯HO + H2O2 reactants, seven-membered ring complex IM_AM5 proceeded through transition state TS_AM5 to from post-reactive complex IMF_AM5 with the barrier height of 35.4 kcal mol−1. It is noted that the barrier height of Channel R_AM3 is 31.0 kcal mol−1 higher than the corresponding barrier height value involved in Channel R_AM2, while the computed free energy barrier (ΔG, 298 K) of Channel R_AM3 is higher by 32.9 kcal mol−1 than that of Channel R_AM2. Such energy difference between Channels R_AM2 and R_AM3 is possibly due to that Channel R_AM2 involves a direct hydrogen abstraction, whereas double hydrogen transfers were involved in Channel R_AM3. This mechanism discrepancy between Channels R_AM2 and R_AM3 is consistent with water-catalyzed H2O2 + HO → HO2 + H2O reaction.21 Hence, double hydrogen transfers mechanisms are considered to be much less probable than the direct hydrogen abstraction mechanism with the mechanism from the IM_AM5 complex being the most unlikely due to the high energy barrier. As a result, the double hydrogen transfer mechanism has not been involved in the HCOOH-catalyzed reaction below. Furthermore, the calculated rate ratio for vR_AM1/vR_AM2b reveals that Channel R_AM1 is more important than that of Channel R_AM2 with the ratio of vR_AM1/vR_AM2b is 3.95–4.01 between 280 and 320 K (Table 1).
3.3 Mechanism and kinetic for HCOOH-assisted reaction
The potential energy surfaces of the reaction channels in the presence of HCOOH for H2O2 + H2O formations occurring through Channels R_FA1 and R_FA2 have been displayed in Fig. 3. As for Channel R_FA1 starting from H2O2⋯HCOOH + HO reactants, the route begins with the formation of the complex IM_FA1. Complex IM_FA1 forms a hydrogen-bonded configuration with a binding energy of 5.9 kcal mol−1 as compared to H2O2⋯HCOOH + HO reactants. The structure of IM_FA1 resembles that of H2O2⋯HCOOH complex with additional two hydrogen bonds (H3⋯O5, 1.98 Å; O1⋯H4, 1.99 Å) formed between HO and H2O2⋯HCOOH complex. Starting from IM_FA1 complex, the O atom of HO radical directly abstracts the H4 of H2O2 moiety in H2O2⋯HCOOH complex, overcoming transition state TS_FA1 with an energy of 0.6 kcal mol−1 with respect to H2O2⋯HCOOH + HO reactants. The barrier height of Channel R_FA1 is 6.5 kcal mol−1, which is lower by 7.6 kcal mol−1 than the similar route in the absence of a catalyst. Meanwhile, the computed free energy barrier (ΔG, 298 K) is reduced to 7.2 kcal mol−1 from 14.1 kcal mol−1 in the bare H2O2 + HO reaction. This indicates that HCOOH in Channel R_FA1 plays a positive catalytic role in the H2O2 + HO → HO2 + H2O reaction by reducing the energy barrier.
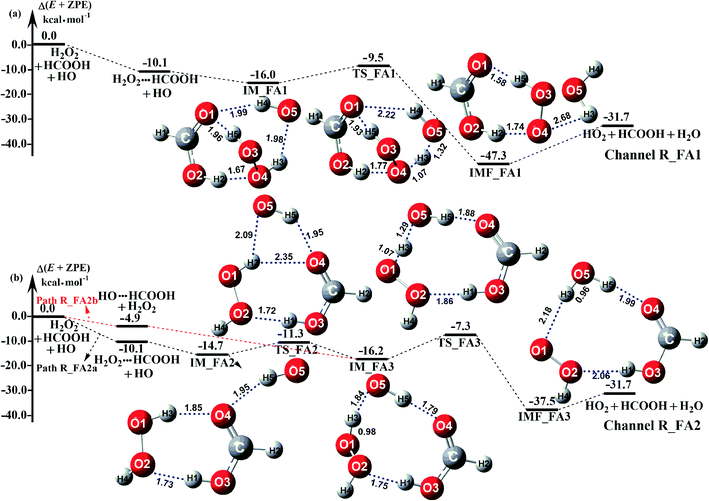 |
| | Fig. 3 Schematic potential energy diagrams for favorable channels of HCOOH catalyzed H2O2 + HO → HO2 + H2O reaction at the CCSD(T)-F12a/cc-pVDZ-F12//M06-2X/aug-cc-pVTZ level. | |
Because of relative energy, Channel R_FA2 occurring through the H2O2⋯HCOOH + HO reactants is more favorable than that starting from HO⋯HCOOH + H2O2 reactants. Given the relative concentration, the concentration of binary complex of H2O2⋯HCOOH (2.10 molecules per cm3) is much higher than that of the binary complex of HO⋯HCOOH (4.17 × 10−5 molecules per cm3). However, as listed in Table 2, the ratio (vR_FA2a/vR_FA2b) between H2O2⋯HCOOH + HO (Path R_FA2a) and HO⋯HCOOH + H2O2 reaction (Path R_FA2b) in Channel R_FA2 is 0.02–0.03 between 280 and 320 K. The above facts reveal that for Channel R_FA2, the interaction between HO⋯HCOOH + H2O2 would be more favorable than the action via H2O2⋯HCOOH + HO route. As for Path R_FA2b, beginning with the HO⋯HCOOH + H2O2 reactants, the reaction involves the formation of pre-reactive complex IM_FA3 with the binding energy of 11.3 kcal mol−1 as compared to HO⋯HCOOH + H2O2 reactants. In the viewpoint of geometrical structure, IM_FA3 shows a nine-membered ring with three hydrogen bonds (H3⋯O5, 1.84 Å; O4⋯H5, 1.79 Å; O2⋯H1, 1.75 Å) involved. After complex IM_FA3, Path R_FA2 occurs through transition state TS_FA3 where the O atom of HO radical abstracts the H atom of H2O2 followed by the elongation of the H5⋯O4 and H1⋯O2 bonds respectively by 0.09 Å and 0.11 Å. TS_FA3, as illustrated in Fig. 3, has a computed energy barrier of 8.9 kcal mol−1 relatives to complex IM_FA3, lying at 7.3 kcal mol−1 below the separate reactants of H2O2 + HO + HCOOH. This barrier height is much lower than the H2O2 + HO → HO2 + H2O reaction, whose energy barrier is determined to be 14.1 kcal mol−1. Similarity, the computed free energy barrier (ΔG, 298 K) is reduced to 8.9 kcal mol−1 from 14.1 kcal mol−1 in the bare H2O2 + HO reaction. This indicates that HCOOH in Channel R_FA2 also plays a positive catalytic role in reducing the energy barrier of the H2O2 + HO → HO2 + H2O reaction.
Table 2 The bimolecular rate coefficients (cm3 per molecules per s) and rate ratio for HCOOH catalyzed H2O2 + HO → HO2 + H2O reaction within the temperature range of 280–320 K
| T/K |
kR_FA1 |
kR_FA2a |
kR_FA2b |
vR_FA2a/vR_FA2b |
vR_FA1/vR_FA2b |
| 280 |
9.50 × 10−11 |
3.95 × 10−13 |
1.86 × 10−8 |
0.02 |
5.24 |
| 290 |
7.32 × 10−11 |
3.87 × 10−13 |
1.09 × 10−8 |
0.02 |
4.64 |
| 298 |
6.07 × 10−11 |
3.82 × 10−13 |
7.29 × 10−9 |
0.03 |
4.19 |
| 300 |
5.81 × 10−11 |
3.81 × 10−13 |
6.64 × 10−9 |
0.03 |
4.10 |
| 310 |
4.67 × 10−11 |
3.78 × 10−13 |
4.20 × 10−9 |
0.03 |
3.65 |
| 320 |
3.83 × 10−11 |
3.79 × 10−13 |
2.76 × 10−9 |
0.03 |
3.30 |
As a result of the above, HCOOH-assisted H2O2 + HO → HO2 + H2O reaction mainly occurs through H2O2⋯HCOOH + HO reaction (Path R_FA1) and HO⋯HCOOH + H2O2 reaction (Path R_FA2b) by one-step route. Moreover, one-step route occurring through HO⋯HCOOH + H2O2 reaction is more competitive than H2O2⋯HCOOH + HO reaction with the ratio of vR_FA1/vR_FA2b is 5.24–3.30 between 280 and 320 K (Table 2).
3.4 Relative impact of NH3 and HCOOH in troposphere
From the mechanism and kinetic discussed above, X-assisted H2O2 + HO → HO2 + H2O reaction mainly proceeds through the H2O2⋯X + HO reaction by one-step mechanism. Here, the relative rates for NH3 and HCOOH to H2O have been calculated to get a realistic diagram of the relative impact of the NH3 and HCOOH in the troposphere. To achieve this aim, one-step reaction mechanism of H2O2 + HO → HO2 + H2O reaction assisted by H2O at the CCSD(T)-F12a/cc-pVDZ-F12//M06-2X/aug-cc-pVTZ level has been shown in Fig. S1,† while its rate coefficient within the temperature range of 213–320 K is listed in Table S6.† Thus, the relative rate for NH3 to H2O as well as the relative rate for HCOOH as compared to H2O is respectively given in eqn (12) and (13).| |
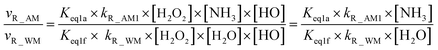 | (12) |
| |
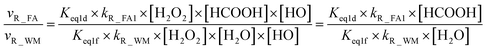 | (13) |
where Keq1a, Keq1d, and Keq1f respectively denote the equilibrium constant for the formation of H2O2⋯NH3, H2O2⋯HCOOH and H2O2⋯H2O; kR_AM1, kR_FA1 and kR_WM respectively denote the bimolecular rate coefficient for the favorable one-step mechanism in H2O2 + HO → HO2 + H2O reaction assisted by NH3, HCOOH and H2O. [NH3], [HCOOH] and [H2O] are the concentration of NH3, HCOOH and H2O, which was obtained from previous report values.55,64,65,70,75
The relative rates for vR_AM1/vR_WM and vR_FA1/vR_WM within the temperature range of 280–320 K are given in Table 3. As seen in Table 3, when the concentrations of H2O at 100% (2.60 × 1017 molecule per cm3 to 2.30 × 1018 molecule per cm3)76 RH and NH3 at 10 ppbv (2.60 × 1011 molecule per cm3 to 2.30 × 1011 molecule per cm3),22–24 the calculated vR_AM1/vR_WM value is below 2.47 × 10−3 to 9.40 × 10−5 within the temperature range of 280–320 K. Moreover, when the concentration of NH3 at 2900 ppbv (7.60 × 1013 molecule per cm3 to 6.70 × 1013 molecule per cm3),25 the calculated vR_AM1/vR_WM is still below 0.72–2.74 × 10−2. This reveals that the H2O2 + HO → HO2 + H2O reaction with NH3 cannot compete with the reaction in the presence of H2O. Similarity, when the concentration of HCOOH at 2.60 × 1011 molecule per cm3 to 2.30 × 1011 molecule per cm3,77 the calculated vR_FA1/vR_WM value is 2.44 × 10−2 to 3.05 × 10−4 within the temperature range of 280–320 K, indicating that the H2O2 + HO → HO2 + H2O reaction with HCOOH also cannot compete with the corresponding reaction in the presence of H2O.
Table 3 The pseudo-first-order rate coefficients (cm3 per molecules per s) for H2O, NH3 and HCOOH catalyzed H2O2 + HO → HO2 + H2O reaction within the temperature range of 280–320 K
| T/K |
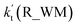
(100% RH) |
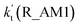
(10 ppbv) |
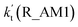
(2900 ppbv) |
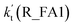
(high 10 ppbv) |
| 280 |
2.13 × 10−17 |
5.25 × 10−20 |
1.53 × 10−17 |
5.19 × 10−19 |
| 290 |
3.29 × 10−17 |
3.20 × 10−20 |
9.35 × 10−18 |
2.34 × 10−19 |
| 298 |
4.63 × 10−17 |
2.29 × 10−20 |
6.50 × 10−18 |
1.27 × 10−19 |
| 300 |
5.01 × 10−17 |
2.02 × 10−20 |
5.99 × 10−18 |
1.12 × 10−19 |
| 310 |
7.54 × 10−17 |
1.39 × 10−20 |
3.99 × 10−18 |
5.82 × 10−20 |
| 320 |
1.01 × 10−16 |
9.49 × 10−21 |
2.76 × 10−18 |
3.07 × 10−20 |
| T/K |
vR_AM1 (10 ppbv)/vR_WM (100% RH) |
vR_AM1 (2900 ppbv)/vR_WM (100% RH) |
vR_FA1 (high)/vR_WM (100% RH) |
| 280 |
2.47 × 10−3 |
0.72 |
2.44 × 10−2 |
| 290 |
9.73 × 10−4 |
0.28 |
7.13 × 10−3 |
| 298 |
4.94 × 10−4 |
0.14 |
2.75 × 10−3 |
| 300 |
4.04 × 10−4 |
0.12 |
2.23 × 10−3 |
| 310 |
1.84 × 10−4 |
5.29 × 10−2 |
7.72 × 10−4 |
| 320 |
9.40 × 10−5 |
2.74 × 10−2 |
3.05 × 10−4 |
4. Summary and conclusions
The effect of catalyst X (X = NH3 and HCOOH) on the H2O2 + HO → HO2 + H2O reaction was investigated by using quantum chemical calculations and canonical variational transition state theory with small curvature tunneling correction. Two kinds of acid–base catalyzed mechanism, namely one-step route and stepwise processes, were found in the reaction assisted by catalyst X. As for the one-step route, the reaction proceeded through similar direct hydrogen abstraction with the reaction without catalyst X. We found one-step mechanism that is promoted by a low energy barrier, was respectively predicted to take place at a bimolecular rate coefficient of 9.95 × 10−11 cm3 per molecule per s (NH3-assisted reaction) and 6.07 × 10−11 cm3 per molecule per s (HCOOH-assisted reaction) at 298 K, and is very closed to the rate coefficient for the reaction without catalyst X. Stepwise processes here were explored by direct hydrogen abstraction and double hydrogen abstraction transfer mechanism, and were found to be kinetically more favorable via direct hydrogen abstraction. However, this hydrogen abstraction in a stepwise route is essentially less important than the hydrogen abstraction in a one-step mechanism.
Within the temperature ranging from 280 K to 320 K, the pseudo-first-order rate coefficient for one-step mechanism in the presence of NH3 (10 ppbv) and HCOOH (10 ppbv) is only 5.25 × 10−20 to 9.49 × 10−21 cm3 per molecule per s and 5.19 × 10−19 to 3.07 × 10−20 cm3 per molecule per s, respectively. This was largely decreased by 3–5 and 2–4 orders of magnitude than the reaction assisted by H2O in which the positive water effect is significant under atmospheric conditions. This catalytic difference between catalyst X and H2O is possibly due to a much lower concentration of NH3 and HCOOH relative to H2O. Despite the fact that H2O2 + HO → HO2 + H2O reaction with catalyst X is not so efficient to shift the overall HO2 + H2O formation rate, the present study provides a comprehensive model of how acidic and basic catalysts assisted the gas-phase reactions.
Conflicts of interest
The authors declare no competing financial interest.
Acknowledgements
This work was supported by the National Natural Science Foundation of China (No: 21603132), the Shaanxi Provincial Natural Science Foundation (No: 2019JM-336 and 2019JQ-880), the Shaanxi Provincial Department of Education Project (18JK0147 and 18JS022), Shanghai Science and Technology Committee (16DZ2270100).
References
- T. P. Marcy, D. W. Fahey, R. S. Gao, P. J. Popp, E. C. Richard, T. L. Thompson, K. H. Rosenlof, E. A. Ray, R. J. Salawitch, C. S. Atherton, D. J. Bergmann, B. A. Ridley, A. J. Weinheimer, M. Loewenstein, E. M. Weinstock and M. J. Mahoney, Science, 2004, 304, 261–265 CrossRef CAS PubMed.
- P. A. Ariya, R. Sander and P. J. Crutzen, J. Geophys. Res.: Atmos., 2000, 105, 17721–17738 CrossRef CAS.
- Y. Elshorbany, I. Barnes, K. H. Becker, J. Kleffmann and P. Wiesen, Z. Physiol. Chem., 2010, 224, 967–987 CrossRef CAS.
- A. Mansergas and J. M. Anglada, ChemPhysChem, 2007, 8, 1534–1539 CrossRef CAS PubMed.
- S. A. Nizkorodov, W. W. Harper, B. W. Blackmon and D. J. Nesbitt, J. Phys. Chem. A, 2000, 104, 3964–3973 CrossRef CAS.
- T. J. Wallington, K. W. Jucks and G. S. Tyndall, Int. J. Chem. Kinet., 1998, 30, 707–709 CrossRef CAS.
- E. Jiménez, T. Gierczak, H. Stark, J. B. Burkholder and A. R. Ravishankara, J. Phys. Chem. A, 2004, 108, 1139–1149 CrossRef.
- A. A. Turnipseed, G. L. Vaghjiani, T. Gierczak, J. E. Thompson and A. R. Ravishankara, J. Chem. Phys., 1991, 95, 3244–3251 CrossRef CAS.
- G. L. Vaghjiani and A. R. Ravishankara, J. Chem. Phys., 1990, 92, 996–1003 CrossRef CAS.
- G. L. Vaghjiani, A. R. Ravishankara and N. Cohen, J. Phys. Chem., 1989, 93, 7833–7837 CrossRef CAS.
- F. Temps and H. Gg. Wagner, Bunsen-Ges. Phys. Chem., Ber., 1982, 86, 119–125 CrossRef CAS.
- W. J. Marinelli and H. S. Johnston, J. Chem. Phys., 1982, 77, 1225–1234 CrossRef CAS.
- F. Atadinc, H. Günaydin, A. S. Özen and V. Aviyente, Int. J. Chem. Kinet., 2005, 37, 502–514 CrossRef CAS.
- R. R. Baldwin and R. W. Walker, J. Chem. Soc., Faraday Trans., 1979, 75, 140–154 RSC.
- P. H. Wine, D. H. Semmes and A. R. Ravishankara, J. Chem. Phys., 1981, 75, 4390–4395 CrossRef CAS.
- A. B. Vakhtin, D. C. McCabe, A. R. Ravishankara and S. R. Leone, J. Phys. Chem. A, 2003, 107, 10642–10647 CrossRef CAS.
- S. P. Sander, D. M. Golden, M. J. Kurylo, G. K. Moortgat, P. H. Wine, A. R. Ravishankara, C. E. Kolb, M. J. Molina, B. J. Finlayson-Pitts and R. E. Huie, Chemical kinetics and photochemical data for use in atmospheric studies evaluation number 15, 2006 Search PubMed.
- E. Vöhringer-Martinez, B. Hansmann, H. Hernandez-Soto, J. S. Francisco, J. Troe and B. Abel, Science, 2007, 315, 497–501 CrossRef PubMed.
- Z. K. Hong, R. D. Cook, D. F. Davidson and R. K. Hanson, J. Phys. Chem. A, 2010, 114, 5718–5727 CrossRef CAS PubMed.
- R. J. Buszek, M. Torrent-Sucarrat, J. M. Anglada and J. S. Francisco, J. Phys. Chem. A, 2012, 116, 5821–5829 CrossRef CAS PubMed.
- T. L. Zhang, X. G. Lan, Y. H. Zhang, R. Wang, Y. Q. Zhang, Z. Y. Qiao and N. Li, Mol. Phys., 2019, 117, 516–530 CrossRef CAS.
- J. J. Orlando, G. S. Tyndall and G. P. Brasseur, Atmospheric chemistry and global change, Oxford University Press, 1999 Search PubMed.
- V. P. Aneja, D. R. Nelson, P. A. Roelle, J. T. Walker and W. Battye, J. Geophys. Res.: Atmos., 2003, 108(D4), 4152 CrossRef.
- J. X. Warner, Z. Wei, L. L. Strow, R. R. Dickerson and J. B. Nowak, Atmos. Chem. Phys. Discuss., 2015, 15, 35823–35856 CrossRef.
- N. Hiranuma, S. D. Brooks, D. C. O. Thornton and B. W. Auvermann, J. Air Waste Manage. Assoc., 2010, 60, 210–218 CrossRef CAS PubMed.
- B. Bandyopadhyay, P. Biswas and P. Kumar, Phys. Chem. Chem. Phys., 2016, 18, 15995–16004 RSC.
- B. Bandyopadhyay, P. Kumar and P. Biswas, J. Phys. Chem. A, 2017, 121, 3101–3108 CrossRef CAS PubMed.
- T. L. Zhang, Y. Q. Zhang, M. J. Wen, Z. Tang, B. Long, X. H. Yu, C. B. Zhao and W. L. Wang, RSC Adv., 2019, 9, 21544–21556 RSC.
- B. Long, X. F. Tan, Y. B. Wang, J. Li, D. S. Ren and W. J. Zhang, ChemistrySelect, 2016, 1, 1421–1430 CrossRef CAS.
- M. L. Wei, X. F. Tan, Z. W. Long and B. Long, RSC Adv., 2017, 7, 56211–56219 RSC.
- S. Mallick, S. Sarkar, P. Kumar and B. Bandyopadhyay, J. Phys. Chem. A, 2017, 122, 350–363 CrossRef PubMed.
- S. Ghoshal and M. K. Hazra, RSC Adv., 2015, 5, 17623–17635 RSC.
- R. J. Buszek, A. Sinha and J. S. Francisco, J. Am. Chem. Soc., 2011, 133, 2013–2015 CrossRef CAS PubMed.
- M. K. Hazra and T. Chakraborty, J. Phys. Chem. A, 2006, 110, 9130–9136 CrossRef CAS PubMed.
- G. D. Silva, Angew. Chem., Int. Ed., 2010, 49, 7523–7525 CrossRef PubMed.
- M. K. Hazra and T. Chakraborty, J. Phys. Chem. A, 2005, 109, 7621–7625 CrossRef CAS PubMed.
- B. Long, Z. Long, Y. Wang, X. Tan, Y. Han, C. Long, S. Qin and W. Zhang, ChemPhysChem, 2012, 13, 323–329 CrossRef CAS PubMed.
- M. J. Frisch, G. Trucks, J. A. pople, et al., Gaussian 09, Revision A.01, Gaussian Inc, Pittsburgh, PA, 2009 Search PubMed.
- K. Fukui, Acc. Chem. Res., 1981, 14, 363–368 CrossRef CAS.
- C. Gonzalez and H. B. Schlegel, J. Chem. Phys., 1989, 90, 2154–2161 CrossRef CAS.
- M. page and J. W. McIver Jr, J. Chem. Phys., 1988, 88, 922–935 CrossRef CAS.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78 CAS.
- N. Bork, J. Elm, T. Olenius and H. Vehkamäki, Atmos. Chem. Phys., 2014, 14, 12023–12030 CrossRef.
- N. Myllys, J. Elm, R. Halonen, T. Kurtén and H. Vehkamäki, J. Phys. Chem. A, 2016, 120, 621–630 CrossRef CAS PubMed.
- J. Elm and K. Kristensen, Phys. Chem. Chem. Phys., 2017, 19, 1122–1133 RSC.
- D. Kashinski, G. Chase, R. Nelson, O. Di Nallo, A. Scales, D. VanderLey and E. F. C. Byrd, J. Phys. Chem. A, 2017, 121, 2265–2273 CrossRef CAS PubMed.
- B. Chan and L. Radom, J. Chem. Theory Comput., 2015, 11, 2109–2119 CrossRef CAS PubMed.
- Z. Rolik, L. Szegedy, I. Ladjánszki, B. Ladóczki and M. Kállay, J. Chem. Phys., 2013, 139, 094105 CrossRef PubMed.
- M. Kállay, Z. Rolik, I. Ladjánszki, L. Szegedy, B. Ladóczki, J. Csontos and B. Kornis, MRCC, A Quantum Chemical Program Suite, 2015, see www.mrcc.hu, 2019 Search PubMed.
- B. Long, J. L. Bao and D. G. Truhlar, Unimolecular reaction of acetone oxide and its reaction with water in the atmosphere, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 6135–6140 CrossRef CAS PubMed.
- B. Long, J. L. Bao and D. G. Truhlar, Phys. Chem. Chem. Phys., 2017, 19, 8091–8100 RSC.
- B. Long, J. L. Bao and D. G. Truhlar, J. Am. Chem. Soc., 2016, 138, 14409–14422 CrossRef CAS PubMed.
- B. Long, J. L. Bao and D. G. Truhlar, J. Am. Chem. Soc., 2018, 141, 611–617 CrossRef PubMed.
- Y. Chuang, J. Corchado, P. Fast, J. Villà, E. Coitino, W. Hu, Y. Liu, G. Lynch, K. Nguyen and C. Jackels, POLYRATE, Version 8.2, Department of Chemistry and Supercomputer Institute, University of Minnesota, Minnesota, CP, 1999 Search PubMed.
- J. L. Bao and D. G. Truhlar, Chem. Soc. Rev., 2017, 46, 7548–7596 RSC.
- B. C. Garrett and D. G. Truhlar, J. Chem. Phys., 1979, 70, 1593–1598 CrossRef CAS.
- B. C. Garrett and D. G. Truhlar, J. Am. Chem. Soc., 1979, 101, 4534–4548 CrossRef CAS.
- B. C. Garrett, D. G. Truhlar, R. S. Grev and A. W. Magnuson, J. Phys. Chem., 1980, 84, 1730–1748 CrossRef CAS.
- Y. P. Liu, G. C. Lynch, T. N. Truong, D. H. Lu, D. G. Truhlar and B. C. Garrett, J. Am. Chem. Soc., 1993, 115, 2408–2415 CrossRef CAS.
- D. H. Lu, T. N. Truong, V. S. Melissas, G. C. Lynch, Y. P. Liu, B. C. Garrett, R. Steckler, A. D. Isaacson, S. N. Rai, G. C. Hancock, J. G. Lauderdale, T. Joseph and D. G. Truhlar, Comput. Phys. Commun., 1992, 71, 235–262 CrossRef CAS.
- T. L. Zhang, R. Wang, H. Chen, S. T. Min, Z. Y. Wang, C. B. Zhao, Q. Xu, L. X. Jin, W. L. Wang and Z. Q. Wang, Phys. Chem. Chem. Phys., 2015, 17, 15046–15055 RSC.
- T. L. Zhang, X. G. Lan, Z. Y. Qiao, R. Wang, X. H. Yu, Q. Xu, Z. Y. Wang, L. X. Jin and Z. Q. Wang, Phys. Chem. Chem. Phys., 2018, 20, 8152–8165 RSC.
- C. Iuga, J. R. Alvarez-Idaboy and A. Vivier-Bunge, Theor. Chem. Acc., 2011, 129, 209–217 Search PubMed.
- M. A. Ali, M. Balaganesh and K. C. Lin, Phys. Chem. Chem. Phys., 2018, 20, 4297–4307 RSC.
- R. Wang, Q. Y. Yao, M. J. Wen, S. B. Tian, Y. Wang, Z. Y. Wang, X. H. Yu, X. Z. Shao and L. Chen, RSC Adv., 2019, 9, 16195–16207 RSC.
- M. A. Ali, M. Balaganesh and S. Jang, Atmos. Environ., 2019, 207, 82–92 CrossRef CAS.
- Z. G. Dong, F. Xu and B. Long, Comput. Theor. Chem., 2018, 1140, 7–13 CrossRef CAS.
- F. Y. Liu, X. F. Tan, Z. W. Long, B. Long and W. J. Zhang, RSC Adv., 2015, 5, 32941–32949 RSC.
- X. F. Tan, B. Long, D. S. Ren, W. J. Zhang, Z. W. Long and E. Mitchell, Phys. Chem. Chem. Phys., 2018, 20, 7701–7709 RSC.
- S. Sarkar, B. K. Oram and B. Bandyopadhyay, J. Phys. Chem. A, 2019, 123, 3131–3141 CrossRef CAS PubMed.
- X. Chen, Y. F. Zhao, L. S. Wang and J. Li, Comput. Theor. Chem., 2017, 1107, 57–65 CrossRef CAS.
- Y. F. Zhao, X. Chen and J. Li, Nano Res., 2017, 10, 3407–3420 CrossRef CAS.
- T. L. Zhang, C. Yang, X. K. Feng, J. X. Kang, L. Song, Y. S. Lu, Z. Y. Wang, Q. Xu, W. L. Wang and Z. Q. Wang, Phys. Chem. Chem. Phys., 2016, 18, 17414–17427 RSC.
- T. L. Zhang, K. Wang, Z. Y. Qiao, Y. Q. Zhang, L. Geng, R. Wang, Z. Y. Wang, C. B. Zhao and L. X. Jin, RSC Adv., 2018, 8, 37105–37116 RSC.
- B. Du and W. C. Zhang, J. Phys. Chem. A, 2013, 117, 6883–6892 CrossRef CAS PubMed.
- S. Sarkar, S. Mallick, D. Kaushik, P. Kumar and B. Bandyopadhyay, Phys. Chem. Chem. Phys., 2017, 19, 27848–27858 RSC.
- T. Stavrakou, J. Müller, J. Peeters, A. Razavi, L. Clarisse, C. Clerbaux, P. F. Coheur, D. Hurtmans, M. De Mazière, C. Vigouroux, N. M. Deutscher, D. W. T. Griffith, N. Jones and C. Paton-Walsh, Nat. Geosci., 2012, 5, 26–30 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ra00024h |
| ‡ Mingjie Wen, Zhaopeng Zeng, Yousong Lu and Yan Wang are contributed equally to this work. |
|
| This journal is © The Royal Society of Chemistry 2020 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *ac,
Mingjie Wen‡
ac,
Zhaopeng Zeng‡a,
Yousong Lu‡b,
Yan Wang‡a,
Wei Wang
*ac,
Mingjie Wen‡
ac,
Zhaopeng Zeng‡a,
Yousong Lu‡b,
Yan Wang‡a,
Wei Wang a,
Xianzhao Shao*a,
Zhiyin Wanga and
Lily Makroni*b
a,
Xianzhao Shao*a,
Zhiyin Wanga and
Lily Makroni*b