Theoretical study of the mechanical properties of CrFeCoNiMo_x (0.1 ≤ x ≤ 0.3) alloys

Abstract

Based on exact muffin-tin orbitals (EMTO) and coherent potential approximation (CPA), we investigate the effects of Mo content on the mechanical properties of CrFeCoNiMo_x (0.1 ≤ x ≤ 0.3) high-entropy alloys (HEAs) with a face-centered-cubic (fcc) crystal structure; relevant physical parameters are calculated as a function of Mo content. The results indicate that the theoretical predictions of lattice constant, elastic constants, shear modulus, and Young's modulus are in good agreement with the available experimental data, which proves the validity of the applied approach. CrFeCoNiMo_0.26 HEA has better ductility and plasticity with respect to other HEAs with different Mo contents because it has the minimum elastic moduli and Vickers hardness, and has the maximum Pugh's ratio and anisotropy factors, etc. CrFeCoNiMo_0.2 HEA has better plasticity compared with CrFeCoNiMo_0.1 and CrFeCoNiMo_0.3 HEAs due to its minimum energy factor and maximum dislocation width. Screw dislocation is more likely to nucleate in CrFeCoNiMo_x (0.1 ≤ x ≤ 0.3) HEAs than edge dislocation. The present studies are helpful to explore the excellent mechanical properties of CrFeCoNiMo_x (0.1 ≤ x ≤ 0.3) HEAs during experiments.

---

1 Introduction

In 2004, high-entropy alloys (HEAs) were first introduced by Yeh et al. and Cantor et al.,^1–3 and are different from traditional alloys with only one principal element, consisting of multiple components in equiatomic or nearly equiatomic ratios.^4,5 The high-entropy effect makes the alloy form a simple cubic crystal structure rather than a complex structure with multi-phases and intermetallic compounds. For example, CoCrFeNiAl,⁶ CoCuMnNi,⁷ FeMnCoCr,⁸ VCrFeCoNi,⁹ AlCrMoNbZrN,¹⁰ and CrMnFeCoNi¹¹ form a face-centered-cubic (fcc) solid solution structure, TiNbMoTaW,¹² TaNbHfZrTi,¹³ NbMoTaW and VNbMoTaW,¹⁴ AlTiVCrMnFeCoNiCu,¹⁵ TiZrNbTaMo,¹⁶ and CuCrFeMoTi¹⁷ crystallize into a body-centered-cubic (bcc) phase. Therefore, these special mixtures have many excellent properties, such as high strength,^7,9 high hardness,¹² good ductility,¹³ corrosion and oxidation resistance,^18,19 magnetism,²⁰ and so on. Jo et al.⁹ conducted tensile and fracture toughness tests on the non-equiatomic V₁₀Cr₁₀Fe₄₅Co₂₀Ni₁₅ HEA, and the results showed that the present alloy had good damage tolerance with a tensile strength of 1 GPa and elongation of 60%. Effects of Ti additions on mechanical properties of NbMoTaV and VNbMoTaW refractory HEAs were investigated by Han.¹² In his study, an interesting phenomenon was found that the structure relaxation of as-cast HEAs resulted by annealing did not cause softening, the hardness value of TiNbMoTaV alloy changed from 498.7 ± 8.3 HV to 510.9 ± 5.7 HV after annealing at 1200 °C for 24 h, and that of TiVNbMoTaW alloy increased from 510.3 ± 6.0 HV to 522.3 ± 11.2 HV. Chou et al.¹⁸ studied the electrochemical properties of Co_1.5CrFeNi_1.5Ti_0.5Mo_x (x = 0, 0.1, 0.5, 0.8) HEAs in acidic, marine, and basic environments at ambient temperature 25 °C, and clearly revealed that the corrosion resistance of the Mo-free alloy was superior to that of the Mo-containing alloys. Hsieh et al.²¹ prepared HEA (AlCrNbSiTiV)N nitride films on stainless steel and glass substrates using direct current reactive magnetron sputtering, and found that the films were homogeneous, very compact and adhere perfectly to the substrate. Meanwhile, more studies on HEAs were conducted by researchers.^22–24

In addition to the above experimental studies, theoretical analyses are also important methods to research the characteristics of HEAs. Sun et al.²⁵ used the ab initio theory to investigate the phase selection rule of paramagnetic Al_xCrMnFeCoNi (0 ≤ x ≤ 5) HEAs, and found that the crystal structure of alloys transformed from fcc phase to bcc phase in the range of 0.482–1.361, which was consistent with experimental measurements. Combined with the special quasi-random structure (SQS) method, Yang et al.²⁶ comparatively analyzed the thermodynamic properties of (TaNbHfTiZr)C and (TaNbHfTiZr)N HEAs by first-principles calculations in conjunction with quasi-harmonic Debye–Grüneisen model. They found that the (TaNbHfTiZr)N alloy was more stable at high temperature because its entropy increased significantly with increasing temperature. With the deepening of theoretical research, Vitos (2007) proposed a feasible approach, the exact muffin-tin orbitals (EMTO), for the determination of energy changes due to anisotropic lattice distortions in ordered systems, in alloys with chemical disorder as well as those with both chemical and magnetic disorder,²⁷ and then combined with the coherent potential approximation (CPA)^28–30 to study the properties of multicomponent alloys. Based on the EMTO-CPA method, many works have been done on HEAs.^31–36 Huang et al.³¹ studied the thermal expansion, elastic, and magnetic properties of FeCoNiCu-based HEAs by using the EMTO-CPA method, the calculated results were in line with the available experimental and theoretical data. Ge et al.³² applied this approach to research the elastic and thermal properties of single-phase ternary and quaternary AlTiCrNbMo refractory HEAs, and Li investigated the third-order elastic constants and related elastic anharmonic properties of three fcc paramagnetic HEAs by means of the EMTO-CPA method.³³ Consequently, the EMTO-CPA method is a valid theoretical analysis method to study the properties of HEAs.

The CrFeCoNi-based HEAs are frequently studied during the theoretical analysis of the properties of HEAs, including VCrFeCoNi,⁹ AlCrMnFeCoNi,²⁵ FeCoNiCuCr,³¹ CrMnFeCoNi,³³ etc., and the calculated results are in line with the available experimental data. To the best of our knowledge, however, there is no theoretical study on the mechanical properties of CrFeCoNi-based HEAs with different Mo contents, but only a few experimental analyses.^37–40 Hence, the aim of this paper is to study the effects of Mo content on mechanical properties of CrFeCoNiMo_x (0.1 ≤ x ≤ 0.3) HEAs with fcc crystal structure via first-principles calculations in conjunction with the EMTO-CPA method, where the related physical parameters, e.g., total energy, lattice constant, elastic constants, and elastic moduli, are calculated as a function of Mo content. And then the dependencies of these physical parameters are presented and discussed on Mo contents in the CrFeCoNiMo_x (0.1 ≤ x ≤ 0.3) HEAs. The results show that this work provides a valuable insight for further theoretical and experimental studies of CrFeCoNiMo_x (0.1 ≤ x ≤ 0.3) HEAs.

2 Theoretical methodology

The first-principles calculations of CrFeCoNiMo_x (0.1 ≤ x ≤ 0.3) HEAs is realized by the EMTO-CPA method based on the density functional theory (DFT). The generalized gradient approximation (GGA) within the Perdew–Burke–Ernzerhof (PBE) is selected as the concrete formalism of exchange–correlation functional.⁴¹ The disordered local moment model is employed to describe the paramagnetic state calculations.⁴² Calculating total energy with full charge-density technique,²⁷ and adopting the single-site CPA method to resolve the substitutional and magnetic disorders.^28–30 The scalar-relativistic approximation and soft-core scheme are applied to solve the Kohn–Sham equations of single electron. The local lattice relaxation effects and atomic short-range order are completely ignored because the CPA method is a single-site mean-field approximation. The electronic states of s, p, d, and f orbitals are included in the basis set. The Green's functions of 16 complex energy points on a semicircular including valence states below the Fermi level are calculated. To guarantee the convergence accuracy of all energies, we used 29 × 29 × 29 inequivalent k-points for integration calculations in the Brillouin zone. The equilibrium volume and equilibrium lattice constant are obtained from the equation of state obtained by fitting the calculated energy-volume data by the Morse-type function.⁴³

3 Results and discussions

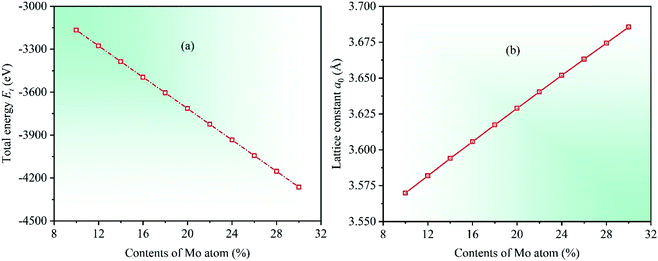
Under the known parameters, two basic parameters of the unit cell of CrFeCoNiMo_x (0.1 ≤ x ≤ 0.3) HEAs, total energy E_t and equilibrium lattice constant a₀, are calculated firstly, and the theoretical predictions as a function of Mo content are shown in Fig. 1. In the light of the calculated results, it can be found that the value of total energy E_t decreases linearly with increasing Mo content from 0.1 to 0.3, while the lattice constant a₀ is opposite, indicating that Mo atom addition to CrFeCoNi-based HEAs causes a dilation of the lattice, which increases the interatomic distance and reduces the electron interactions, thereby decreasing the total energy of unit cell. To prove the validity of theoretical analysis, we present the calculated lattice constant a₀ along with available experimental data for equiatomic CrFeCoNiMo_0.2 HEA and non-equiatomic CrFeCoNiMo_0.23 HEA, as listed in Table 1, in which we did an extra calculation on the median value x = 0.23. By comparison, it can be seen that the calculated lattice constants of CrFeCoNiMo_0.2 and CrFeCoNiMo_0.23 HEAs are 3.629 and 3.646 Å, respectively, which are in good agreement with the experimental data,^38–40,44 indicating that the theoretical analysis is feasible.

Fig. 1 Dependencies of (a) total energy E_t and (b) lattice constant a₀ on Mo contents in CrFeCoNiMo_x (0.1 ≤ x ≤ 0.3) HEAs. Mo atom addition to CrFeCoNi-based HEAs will decrease the total energy E_t and increase the lattice constant a₀.

Table 1 Comparisons of theoretical predictions with available experimental data for CrFeCoNiMo_0.2 and CrFeCoNiMo_0.23 HEAs

HEAs	Present	Experimental data
CrFeCoNiMo0.2
a0	3.629	3.585,^38 3.595,^40 3.608 (ref. 44)
G	92.40	85 (ref. 40)
CrFeCoNiMo0.23
a0	3.646	3.604 (ref. 39)
C11	270.6	216 (ref. 39)
C12	213.2	175 (ref. 39)
C44	177.7	189 (ref. 39)
E	234.2	274 (ref. 39)

---

To investigate the effects of Mo content on mechanical properties of CrFeCoNiMo_x (0.1 ≤ x ≤ 0.3) HEAs, elastic constants need to be calculated to determine the stability of crystal structure and to derive other physical parameters. The mechanical stability of materials can be described by elastic constants C₁₁, C₁₂, and C₄₄ for the cubic crystal structure, and they must satisfy the stability criterion C₁₁ > 0, C₄₄ > 0, C₁₁ − C₁₂ > 0, and C₁₁ + 2C₁₂ > 0.⁴⁵ Through calculation, the dependencies of theoretical elastic constants on Mo contents in CrFeCoNiMo_x (0.1 ≤ x ≤ 0.3) HEAs are displayed in Fig. 2. It can be found that the values of elastic constants C₁₁, C₁₂, and C₄₄ always meet the stability criterion of cubic crystal at different Mo contents, indicating that the crystal structure of CrFeCoNiMo_x (0.1 ≤ x ≤ 0.3) HEAs can maintain mechanical stability. Obviously, the total varying trend of each curve is gradually decreasing with the increase of Mo content, the reason is that the lattice constant a₀ increases linearly with increasing Mo content, which increases the distance between atoms, thus weakening the strength of the bonding force between atoms, thereby elastic constants decrease with the increase of Mo content. And there is a dramatic change of the values of elastic constants C₁₁ and C₁₂ as Mo content increases from 0.26 to 0.28, indicating that the deformation resistance of materials has a significant change, where the dramatic decline may be attributed to the structural phase transition caused by severe lattice distortion in HEAs, but the current EMTO-CPA method cannot explain the reason. Meanwhile, these obvious changes of the elastic constants will cause the change of relevant physical parameters. In Table 1, we list the calculated elastic constants along with available experimental data³⁹ for CrFeCoNiMo_0.23 HEA, it can be seen that the theoretical predictions and experimental results are generally consistent with each other.

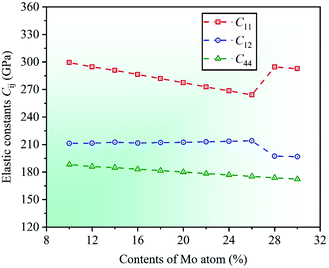Fig. 2 Dependencies of elastic constants C_ij on Mo contents in CrFeCoNiMo_x (0.1 ≤ x ≤ 0.3) HEAs. The deformation resistance of CrFeCoNiMo_x (0.26 ≤ x ≤ 0.28) HEAs has a significant change.

As is known to all, HEAs have various excellent mechanical properties, including high strength, high hardness, good ductility, and so on. These performances are usually related to the elastic moduli of materials, such as Young's modulus E, shear modulus G, and bulk modulus B, and the larger value indicates the stronger deformation resistance of materials.^46,47 The material moduli with respect to elastic constants C_ij can be written as B = (C₁₁ + 2C₁₂)/3, G = (G_V + G_R)/2, and E = 9BG/(3B + G), where G_V = (C₁₁ − C₁₂ + C₄₄)/5 is Voigt shear modulus, and G_R = 5(C₁₁ − C₁₂)C₄₄/[4C₄₄ + 3(C₁₁ − C₁₂)] represents Reuss shear modulus.⁴⁸

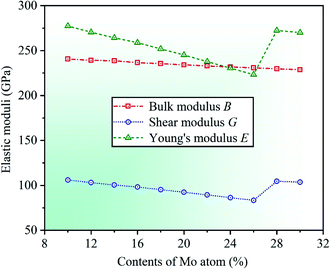
By calculation, we present the theoretical elastic moduli E, G, and B for CrFeCoNiMo_x (0.1 ≤ x ≤ 0.3) HEAs as a function of Mo content, as shown in Fig. 3. It can be found that the bulk modulus B decreases gradually with increasing Mo content, and the trend of Young's modulus E is similar to that of the shear modulus G that the value of elastic modulus decreases at first, then increases, and then decreases with the increase of Mo content, and both of them increase dramatically as Mo content increases from 0.26 to 0.28. Herein, the decrease of elastic moduli indicates that the deformation resistance of HEAs decline, and the significant increase of elastic moduli demonstrates that the capability of alloys to resist elastic and shear deformation enhance remarkably. When Mo content is 26%, Young's modulus E and shear modulus G get the minimum values, suggesting that CrFeCoNiMo_0.26 HEA has the worst resistance to elastic and shear deformation compared with other HEAs with different Mo contents. As the same time, the reliability of the theoretical analysis is verified by comparing the calculated elastic modulus with available experimental results for CrFeCoNiMo_0.2 and CrFeCoNiMo_0.23 HEAs, as listed in Table 1. It can be seen that the theoretical predictions of shear modulus G is 92.4 GPa for CrFeCoNiMo_0.2 HEA and Young's modulus E is 234.2 GPa for CrFeCoNiMo_0.23 HEA, which are generally agreement with the available experimental data G = 85 GPa and E = 274 GPa, respectively.^39,40

Fig. 3 Dependencies of elastic moduli on Mo contents in CrFeCoNiMo_x (0.1 ≤ x ≤ 0.3) HEAs. CrFeCoNiMo_0.26 HEA has the worst resistance to elastic and shear deformation compared with other HEAs with different Mo contents because the corresponding Young's modulus and shear modulus get the minimum values.

Meanwhile, another important material modulus, G_(110)[11̄0], is calculated to further investigate the deformation resistance of CrFeCoNiMo_x (0.1 ≤ x ≤ 0.3) HEAs. 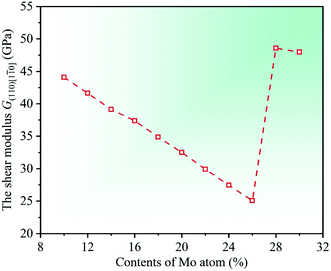Herein, G_(110)[11̄0] is a shear modulus which can be used to represent the shear deformation resistance in the (110)[11̄0] crystallographic direction.^49,50 The shear modulus can be derived from the elastic constants C_ij by G_(110)[11̄0] = (C₁₁ − C₁₂)/2. By calculation, the dependencies of the shear modulus G_(110)[11̄0] on Mo contents in CrFeCoNiMo_x (0.1 ≤ x ≤ 0.3) HEAs are obtained and displayed in Fig. 4. It can be seen that the value of modulus G_(110)[11̄0] decreases first, then increases, and then decreases with the increase in contents of Mo atom, in which the decrease of material modulus indicates that the shear deformation resistance of HEAs decline. Clearly, the shear modulus G_(110)[11̄0] take the minimum value when Mo content is 26%, indicating that the resistance to shear deformation of CrFeCoNiMo_0.26 HEA is the worst. And there is a rapidly increase for the shear modulus G_(110)[11̄0] when Mo contents are in the range of 26% and 28%. The variation trend is attributed to the reason that Mo content of 28% greatly increases the shear modulus in the (110)[11̄0] direction, thus, the resistance to shear deformation of CrFeCoNiMo_x (0.26 ≤ x ≤ 0.28) HEAs is greatly improved in the (110)[11̄0] crystallographic direction, which fits well with the results of Fig. 3.

Fig. 4 Dependencies of shear modulus G_(110)[11̄0] on Mo contents in CrFeCoNiMo_x (0.1 ≤ x ≤ 0.3) HEAs. The shear deformation resistance t of CrFeCoNiMo_0.26 HEA is the least because it has the minimum shear modulus G_(110)[11̄0].

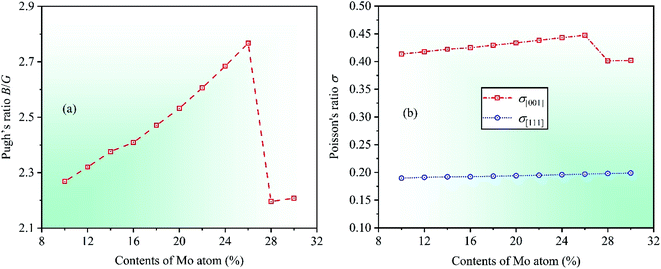
Ductile-brittle transition can also influence the mechanical properties of materials. In 1954, Pugh summed up a vital conclusion that the ductile–brittle transition was related to the ratio between bulk modulus B and shear modulus G for multicomponent alloys.⁴⁶ The critical value of the ratio B/G is about 1.75, indicating that materials with B/G > 1.75 are ductile whereas those with B/G < 1.75 brittle. By calculation, the dependencies of theoretical Pugh's ratio B/G on Mo contents in CrFeCoNiMo_x (0.1 ≤ x ≤ 0.3) HEAs is depicted in Fig. 5a. With the increase in contents of Mo atom, it can be seen that the value of Pugh's ratio B/G is always greater than 1.75 indicating that CrFeCoNiMo_x (0.1 ≤ x ≤ 0.3) HEAs present good ductility in nature. Clearly, Pugh's ratio B/G gets the maximum value as Mo content is 26%, which implies that CrFeCoNiMo_0.26 HEA has the best ductility. When Mo contents are in the range of 26% and 28%, the dramatic decline of theoretical value indicates that the ductility of CrFeCoNiMo_x (0.26 ≤ x ≤ 0.28) HEAs decrease significantly, and the result also shows that the deformation resistance of HEAs enhance, which agrees well with the results of Fig. 3.

Fig. 5 Dependencies of (a) Pugh's ratio B/G and (b) Poisson's ratio σ on Mo contents in CrFeCoNiMo_x (0.1 ≤ x ≤ 0.3) HEAs. CrFeCoNiMo_x (0.1 ≤ x ≤ 0.3) HEAs has good ductility because Pugh's ratio B/G is always greater than 1.75, and the Poisson's ratios σ_[001] gets the maximum value when Mo content is 26% indicating CrFeCoNiMo_0.26 HEA has the best plasticity.

Poisson's ratio σ is an important parameter to reflect the plasticity of alloys, the larger ratio indicates the better plastic property of materials, and the range is generally 0 to 0.5. Poisson's ratio of fcc crystal structure could be expressed by σ_[001] and σ_[111] in the [001] and [111] crystallographic directions, the specific expressions are σ_[001] = C₁₂/(C₁₁ + C₁₂) and σ_[111] = (C₁₁ + 2C₁₂ − 2C₄₄)/2(C₁₁ + 2C₁₂ + C₄₄).⁴⁷ Through calculation, the dependencies of Poisson's ratios σ_[001] and σ_[111] on Mo contents are shown in Fig. 5b. With increasing Mo content, it can be found that the Poisson's ration σ_[001] increases first and then decreases, while the Poisson's ratio σ_[111] increases slowly, but this change is hard to detect intuitively, where the increase of Poisson's ratios σ_[001] and σ_[111] demonstrates that the plasticity of alloys enhance in the [001] and [111] directions, respectively. Obviously, when Mo content is 26%, the Poisson's ratios σ_[001] gets the maximum value indicating that CrFeCoNiMo_0.26 HEA has the best plasticity compared with other HEAs with different Mo contents. There is a significant decreasing for the value of Poisson's ratio σ_[001] when Mo contents are in the range of 26% and 28%, suggesting that the plasticity of CrFeCoNiMo_x (0.26 ≤ x ≤ 0.28) HEAs decreases remarkably in the [001] direction.

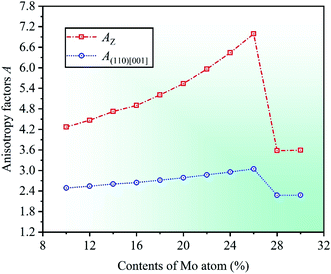
Severe lattice distortion is the essential characteristic of HEAs, which significantly breaks the structural symmetry of crystal cell, and then the material exhibits anisotropy. Therefore, elastic anisotropy is an important parameter to study the mechanical properties of materials, and it can be quantified by anisotropy factor A.^51,52 Anisotropy factor A = 1 corresponds to the isotropic materials, otherwise anisotropic. A comprehensive study on the elastic anisotropy was made by Yoo.⁵³ In his study, a cross-slip-pinning model was proposed to study the cross slip of screw dislocations, and the results showed that the larger the anisotropy factor A, the greater the driving force, and the easier it was to promote the cross slip of screw dislocations. The elastic anisotropy of cubic crystal can be expressed by anisotropy factors A_Z and A_(110)[001], which are related to elastic constants. The calculation formulas are A_Z = 2C₄₄/(C₁₁ − C₁₂) and A_(110)[001] = C₄₄(D₁ + 2C₁₂ + C₁₁)/(C₁₁D₁ − C₁₂²),^54,55 where A_Z is Zener ratio which can be used to represent the ratio of shear moduli between the (100) and (110) crystal planes, and also to describe the degree of elastic anisotropy in cubic crystal. A_(110)[001] represents the anisotropy factor in the (110)[001] crystallographic direction, and D₁ = C₄₄ + (C₁₁ + C₁₂)/2.

By calculation, the anisotropy factors A_Z and A_(110)[001] with respect to different Mo contents in CrFeCoNiMo_x (0.1 ≤ x ≤ 0.3) HEAs are obtained, as shown in Fig. 6. Obviously, the values of anisotropy factors are greater than unity at different Mo contents suggesting that the cubic crystal structure in CrFeCoNiMo_x (0.1 ≤ x ≤ 0.3) HEAs is anisotropic. Meanwhile, the overall trend of both anisotropy factors is gradually increasing as the Mo content increases from 0.1 to 0.26, which denotes that the anisotropy of CrFeCoNiMo_x (0.1 ≤ x ≤ 0.26) HEAs is improved between the (100) and (110) crystal planes, as well as the (110)[001] crystallographic direction. And they get the maximum values when Mo content is 26%, indicating that the cross-slip of screw dislocations is most likely to occur in CrFeCoNiMo_0.26 HEA, thereby it has better plasticity. Then, the values of anisotropy factors decrease dramatically when Mo contents are in the range of 26% and 28%, which shows that the driving force for the cross-slip of screw dislocations in crystal structure decline significantly, thereby enhancing the strength of materials, it fits well with the results of Fig. 3.

Fig. 6 Dependencies of anisotropy factors A on Mo contents in CrFeCoNiMo_x (0.1 ≤ x ≤ 0.3) HEAs. Anisotropy factors get the maximum values when Mo content is 26%, indicating that the cross-slip of screw dislocations is most likely to occur in CrFeCoNiMo_0.26 HEA.

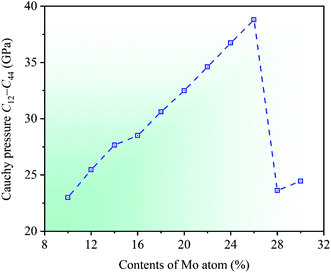
Cauchy pressure C₁₂ − C₄₄ is an important physical parameter to describe the atomic bonding characteristics of materials, which reflects the nature of bonding at the atomic level.⁵⁶ Researches show that the atomic bonding has metallic characteristic for C₁₂ − C₄₄ > 0, whereas those has directional characteristic for C₁₂ − C₄₄ < 0, and the larger absolute value indicates the stronger metallic or directional characteristic of materials.^52,57 In the light of the calculated elastic constants, the dependencies of Cauchy pressure C₁₂ − C₄₄ on Mo contents in CrFeCoNiMo_x (0.1 ≤ x ≤ 0.3) HEAs are shown in Fig. 7. It can be seen that the value of Cauchy pressure C₁₂ − C₄₄ is always positive at different Mo contents, thereby the atomic bonding of CrFeCoNiMo_x (0.1 ≤ x ≤ 0.3) HEAs mainly exhibits metallic characteristic. Obviously, the Cauchy pressure C₁₂ − C₄₄ gets the maximum value when Mo content is 26%, indicating that the atomic bonding of CrFeCoNiMo_0.26 HEA has the strongest metallic characteristic. Then, the value of Cauchy pressure C₁₂ − C₄₄ decreases dramatically when Mo contents are in the range of 26% and 28%, which shows that the metallic characteristic of atomic bonding decline remarkably.

Fig. 7 Dependencies of Cauchy pressure C₁₂ − C₄₄ on Mo contents in CrFeCoNiMo_x (0.1 ≤ x ≤ 0.3) HEAs. Cauchy pressure C₁₂ − C₄₄ get the maximum values when Mo content is 26%, indicating that the atomic bonding of CrFeCoNiMo_0.26 HEA has the strongest metallic characteristic.

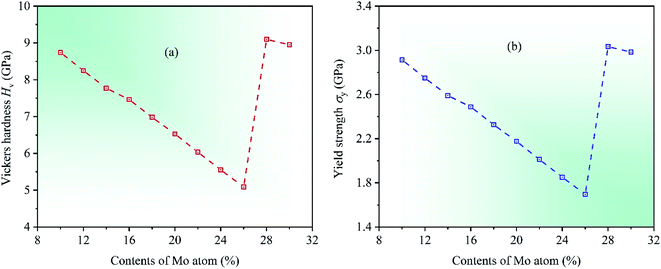
In order to further investigate the mechanical properties of CrFeCoNiMo_x (0.1 ≤ x ≤ 0.3) HEAs, we calculate the hardness and yield strength of materials. Hardness is the intrinsic resistance to deformation of materials when a force is applied, and yield strength refers to the ability to resist plastic deformation.⁵⁸ In 2011, a comprehensive study on the hardness of polycrystalline materials was made by Chen et al.,⁵⁹ they found that there was a relationship between hardness and elasticity of materials, which could be used to predict the hardness of crystalline materials, and a computational model was proposed to estimate the Vickers hardness H_v of polycrystalline materials, the corresponding expression is H_v = 2(k²G)^0.585 − 3, where k = G/B. Meanwhile, yield strength can be expressed as σ_y = H_v/3.⁶⁰ Through calculation, the dependencies of two physical parameters on Mo contents in CrFeCoNiMo_x (0.1 ≤ x ≤ 0.3) HEAs are depicted in Fig. 8. Obviously, the values of Vickers hardness H_v and yield strength σ_y decrease first, then increase, and then decrease with increasing of Mo content, where the reduction of numerical values indicates that the deformation resistance of HEAs declines. When Mo content is 26%, the Vickers hardness H_v and yield strength σ_y take the minimum values, indicating that the deformation resistance of CrFeCoNiMo_0.26 HEA is minimal, which fits well with the results of Fig. 3.

Fig. 8 Dependencies of (a) Vickers hardness H_v and (b) yield strength σ_y on Mo contents in CrFeCoNiMo_x (0.1 ≤ x ≤ 0.3) HEAs. Vickers hardness H_v and yield strength σ_y take the minimum values when Mo content is 26%, indicating that the CrFeCoNiMo_0.26 HEA has the least resistance to deformation.

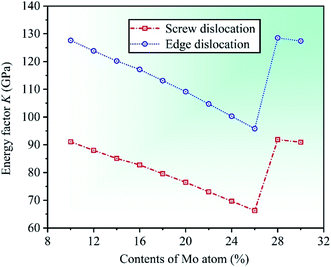
The plasticity of crystalline materials is also related to their dislocation nucleation ability, which can be estimated by energy factor K, the smaller value indicates that dislocation is more likely to nucleate in alloys. According to the works of Foreman and Savin et al.,^61,62 energy factor K of the screw and edge dislocations could be expressed by elastic constants C_ij, the specific expressions are 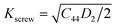and 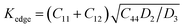, in which D₂ = C₁₁ − C₁₂, D₃ = C₁₁(C₁₁ + C₁₂ + 2C₄₄). Through calculation, we present the theoretical energy factors K_screw and K_edge for CrFeCoNiMo_x (0.1 ≤ x ≤ 0.3) HEAs as a function of Mo content, as shown in Fig. 9. Obviously, these two energy factors have the similar varying trend that their values decrease first, then increase, and then decrease with increasing of Mo content. When Mo content is 26%, both of them get the minimum values indicating that screw and edge dislocations are most likely to nucleate in CrFeCoNiMo_0.26 HEA, thereby the alloy has better plasticity, which is in a good agreement with the results of Fig. 5b. Meanwhile, the energy factor of screw dislocation is smaller than that of the edge dislocation, suggesting that the nucleation of screw dislocation is easier to occur in CrFeCoNiMo_x (0.1 ≤ x ≤ 0.3) HEAs.

Fig. 9 Dependencies of energy factor K on Mo contents in CrFeCoNiMo_x (0.1 ≤ x ≤ 0.3) HEAs. Energy factors K_screw and K_edge get the minimum values when Mo content is 26%, indicating that screw and edge dislocations are most likely to nucleate in CrFeCoNiMo_0.26 HEA, thereby the alloy has better plasticity.

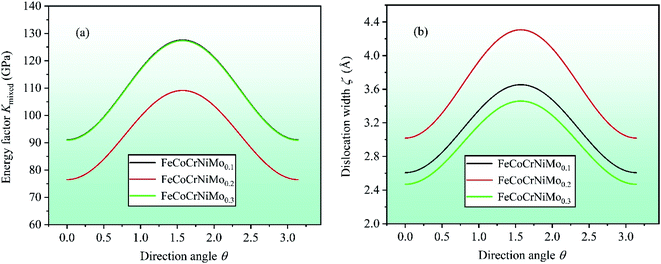
Lastly, energy factor K_mixed of mixed dislocation is calculated to study the mechanical properties of CrFeCoNiMo_x (0.1 ≤ x ≤ 0.3) HEAs, which is a function of the direction angle θ (0 ≤ θ ≤ π) between Burgers vector and dislocation line, and the corresponding expression is K_mixed = K_edge sin² θ + K_screw cos² θ.^61,63 In order to further investigate the dislocation properties of CrFeCoNiMo_x (0.1 ≤ x ≤ 0.3) HEAs, dislocation width is calculated as ζ = K_mixedd/(C₁₁ − C₁₂), in which d represents the spacing between glide phases. By calculation, the dependencies of energy factor K_mixed and dislocation width ζ on the direction angle θ (0 ≤ θ ≤ π) are displayed in Fig. 10, where θ = 0 corresponds to the screw dislocation and θ = π/2 is the edge dislocation. In Fig. 10a, it can be found that CrFeCoNiMo_0.2 HEA has the smallest energy factor for screw (θ = 0) and edge (θ = π/2) dislocations with respect to CrFeCoNiMo_0.1 and CrFeCoNiMo_0.3 HEAs, indicating that mixed dislocation is more likely to nucleate in CrFeCoNiMo_0.2 HEA, thereby the alloy has better plasticity. And the energy factor of screw dislocation is smaller than that of the edge dislocation suggesting that the screw dislocation is more likely to occur in CrFeCoNiMo_x (x = 0.1, 0.2, 0.3) HEAs. In Fig. 10b, CrFeCoNiMo_0.2 HEA has the maximum dislocation width compared with CrFeCoNiMo_0.1 and CrFeCoNiMo_0.3 HEAs, indicating that CrFeCoNiMo_0.2 HEA has the minimum stacking-fault energy to promote twinning deformation, thereby improving the plasticity of alloy.

Fig. 10 The dependencies of (a) energy factor K_mixed of mixed dislocation and (b) dislocation width ζ on direction angle θ (0 ≤ θ ≤ π) between Burgers vector and dislocation line. CrFeCoNiMo_0.2 HEA has the minimum energy factor and the maximum dislocation width compared with CrFeCoNiMo_0.1 and CrFeCoNiMo_0.3 HEAs, thereby the alloy has better plasticity.

4 Conclusions

In this work, EMTO-CPA method is used to study the mechanical properties of CrFeCoNiMo_x (0.1 ≤ x ≤ 0.3) HEAs with fcc crystal structure. Results show that the theoretical values of lattice constant, elastic constants, shear modulus, and Young's modulus fit well with the available experimental data. In the light of the stability criterion, the calculated elastic constants indicate that CrFeCoNiMo_x (0.1 ≤ x ≤ 0.3) HEAs can maintain mechanical stability. Atomic bonding of alloys mainly exhibits metallic characteristic since the value of Cauchy pressure is always positive at different Mo contents. When Mo contents are in the range of 26% and 28%, several physical parameters have a remarkable change, including elastic moduli, Pugh's ratio, Cauchy pressure, yield strength, and so on. The results reveal that the CrFeCoNiMo_0.26 HEA exhibits better ductility and plasticity with respect to other alloys with different Mo contents, because it has the maximum Pugh's ratio and anisotropy factors, and has the minimum Vickers hardness and yield strength, etc. CrFeCoNiMo_0.2 HEA has the minimum energy factor and the maximum dislocation width compared with CrFeCoNiMo_0.1 and CrFeCoNiMo_0.3 HEAs, indicating that the dislocation is easily inclined to nucleate in CrFeCoNiMo_0.2 HEA, and the minimum stacking-fault energy in CrFeCoNiMo_0.2 HEA may promote twining deformation, thereby enhancing the plasticity. The present results provide a theoretical prediction for exploring the excellent mechanical properties of CrFeCoNiMo_x (0.1 ≤ x ≤ 0.3) HEAs.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We greatly appreciate the support of National Natural Science Foundation of China (51971091), the Key Laboratory of Guangdong Regular Higher Education (2017KSYS012), Foshan Key Technology Project (1920001000409), Guangzhou Technical Project (201704030113), and Prof. Levente Vitos for his developed codes of EMTO-CPA method. This work is implemented in National Supercomputer Centers in Changsha, China.

References

1. J. W. Yeh, S. K. Chen, S. J. Lin, J. Y. Gan, T. S. Chin, T. T. Shun, C. H. Tsau and S. Y. Chang, Adv. Eng. Mater., 2004, 6, 299–303.
2. J. W. Yeh, S. J. Lin, T. S. Chin, J. Y. Gan, S. K. Chen, T. T. Shun, C. H. Tsau and S. Y. Chou, Metall. Mater. Trans. A, 2004, 35, 2533–2536.
3. B. Cantor, I. T. H. Chang, P. Knight and A. J. B. Vincent, Mater. Sci. Eng., A, 2004, 375–377, 213–218.
4. J. Y. He, W. H. Liu, H. Wang, Y. Wu, X. J. Liu, T. G. Nieh and Z. P. Lu, Acta Mater., 2014, 62, 105–113.
5. Z. P. Wang, Q. H. Fang, J. Li, B. Liu and Y. Liu, Mater. Sci. Technol., 2018, 34, 349–354.
6. T. T. Shun, C. H. Hung and C. F. Lee, J. Alloys Compd., 2010, 493, 105–109.
7. D. G. Kim, Y. H. Jo, J. M. Park, W. M. Choi, H. S. Kim, B. J. Lee, S. S. Sohn and S. Lee, J. Alloys Compd., 2020, 812, 1–9.
8. X. Y. Liu, S. Q. Zhou and Y. Xu, Mater. Lett., 2018, 233, 142–145.
9. Y. H. Jo, K. Y. Doh, D. G. Kim, K. Lee, D. W. Kim, H. Sung, S. S. Sohn, D. Lee, H. S. Kim, B. J. Lee and S. Lee, J. Alloys Compd., 2019, 809, 1–9.
10. W. Zhang, R. Tang, Z. B. Yang, C. H. Liu, H. Chang, J. J. Yang, J. L. Liao, Y. Y. Yang and N. Liu, J. Nucl. Mater., 2018, 512, 15–24.
11. B. Gludovatz, A. Hohenwarter, D. Catoor, E. H. Chang, E. P. George and R. O. Ritchie, Science, 2014, 345, 1153–1158.
12. Z. D. Han, N. Chen, S. F. Zhao, L. W. Fan, G. N. Yang, Y. Shao and K. F. Yao, Intermetallics, 2017, 84, 153–157.
13. O. N. Senkov, J. M. Scott, S. V. Senkova, D. B. Miracle and C. F. Woodward, J. Alloys Compd., 2011, 509, 6043–6048.
14. O. N. Senkov, G. B. Wilks, J. M. Scott and D. B. Miracle, Intermetallics, 2011, 19, 698–706.
15. Y. J. Zhou, Y. Zhang, Y. L. Wang and G. L. Chen, Mater. Sci. Eng., A, 2007, 454–455, 260–265.
16. S. P. Wang, E. Ma and J. Xu, Intermetallics, 2018, 103, 78–87.
17. M. Dias, A. Ruza, F. Guerreiro, R. C. Silva, A. P. Goncalves, U. V. Mardolcar and E. Alves, Mater. Sci. Eng., B, 2018, 238–239, 18–25.
18. Y. L. Chou, J. W. Yeh and H. C. Shih, Corros. Sci., 2010, 52, 2571–2581.
19. M. H. Chuang, M. H. Tsai, W. R. Wang, S. J. Lin and J. W. Yeh, Acta Mater., 2011, 59, 6308–6317.
20. P. F. Yu, L. J. Zhang, H. Cheng, H. Zhang, M. Z. Ma, Y. C. Li, G. Li, P. K. Liaw and R. P. Liu, Intermetallics, 2016, 70, 82–87.
21. T. H. Hsieh, C. H. Hsu, C. Y. Wu, J. Y. Kao and C. Y. Hsu, Curr. Appl. Phys., 2018, 18, 512–518.
22. Z. Wu, C. M. Parish and H. Bei, J. Alloys Compd., 2015, 647, 815–822.
23. H. Luo, Z. M. Li and D. Raabe, Nature, 2017, 7, 1–7.
24. Q. Q. Wei, L. Q. Wang, Y. F. Fu, J. N. Qin, W. J. Lu and D. Zhang, Mater. Des., 2011, 32, 2934–2939.
25. X. Sun, H. L. Zhang, S. Lu, X. D. Ding, Y. Z. Wang and L. Vitos, Acta Mater., 2017, 140, 366–374.
26. Y. Yang, L. Ma, G. Y. Gan, W. Wang and B. Y. Tang, J. Alloys Compd., 2019, 788, 1076–1083.
27. L. Vitos, Computational quantum mechanics for materials engineers: the EMTO method and applications, Springer, London, 2007.
28. P. Soven, Phys. Rev., 1967, 156, 809–813.
29. D. W. Taylor, Phys. Rev., 1967, 156, 1017–1029.
30. B. L. Gyorffy, Phys. Rev. B: Solid State, 1972, 5, 2382–2384.
31. S. Huang, A. Vida, A. Heczel, E. Holmstrom and L. Vitos, JOM, 2017, 69, 2107–2112.
32. H. J. Ge, F. Y. Tian and Y. Wang, Comput. Mater. Sci., 2017, 128, 185–190.
33. X. Q. Li, J. Alloys Compd., 2018, 764, 906–912.
34. F. Y. Tian, L. K. Varga, J. Shen and L. Vitos, Comput. Mater. Sci., 2016, 111, 350–358.
35. P. Y. Cao, X. D. Ni, F. Y. Tian, L. K. Varga and L. Vitos, J. Phys.: Condens. Matter, 2015, 27, 1–6.
36. L. Y. Tian, G. S. Wang, J. S. Harris, D. L. Irving, J. J. Zhao and L. Vitos, Mater. Des., 2017, 114, 243–252.
37. J. W. Wang, Y. Liu, B. Liu, Y. Wang, Y. K. Cao, T. C. Li and R. Zhou, Mater. Sci. Eng., A, 2017, 689, 233–242.
38. W. H. Liu, Z. P. Lu, J. Y. He, J. H. Luan, Z. J. Wang, B. Liu, Y. Liu, M. W. Chen and C. T. Liu, Acta Mater., 2016, 116, 332–342.
39. B. Cai, B. Liu, S. Kabra, Y. Q. Wang, K. Yan, P. D. Lee and Y. Liu, Acta Mater., 2017, 127, 471–480.
40. L. Tang, K. Yan, B. Cai, Y. Q. Wang, B. Liu, S. Kabra, M. M. Attallah and Y. Liu, Scr. Mater., 2020, 178, 166–170.
41. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
42. B. L. Gyorffy, A. J. Pindor, J. Staunton, G. M. Stocks and H. Winter, J. Phys. F: Met. Phys., 1985, 15, 1337–1386.
43. L. A. Girifalco and V. G. Weizer, Phys. Rev., 1959, 114, 687–690.
44. P. H. Wu, N. Liu, W. Yang, Z. X. Zhu, Y. P. Lu and X. J. Wang, Mater. Sci. Eng., A, 2015, 642, 142–149.
45. J. F. Nye, Physical properties of crystals: their representation by tensors and matrices, Oxford University Press, Oxford, 1985.
46. S. F. Pugh, Philos. Mag., 1954, 45, 823–843.
47. Z. P. Wang, Q. H. Fang, J. Li and B. Liu, Superlattices Microstruct., 2018, 116, 141–150.
48. O. L. Anderson, J. Phys. Chem. Solids, 1963, 24, 909–917.
49. H. Z. Fu, W. M. Peng and T. Gao, Mater. Chem. Phys., 2009, 115, 789–794.
50. H. Z. Fu, D. H. Li, F. Peng, T. Gao and X. L. Cheng, Comput. Mater. Sci., 2008, 44, 774–778.
51. M. Mattesini, R. Ahuja and B. Johansson, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 1–5.
52. H. Z. Fu, Z. G. Zhao, W. F. Liu, F. Peng, T. Gao and X. L. Cheng, Intermetallics, 2010, 18, 761–766.
53. M. H. Yoo, Scr. Metall., 1986, 20, 915–920.
54. K. Lau and A. K. Mccurdy, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 8980–8984.
55. H. Z. Fu, X. F. Li, W. F. Liu, Y. M. Ma, T. Gao and X. H. Hong, Intermetallics, 2011, 19, 1959–1967.
56. D. G. Pettifor, Mater. Sci. Technol., 2013, 8, 345–349.
57. R. A. Johnson, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 3924–3931.
58. J. S. Tse, J. Superhard Mater., 2010, 32, 177–191.
59. X. Q. Chen, H. Y. Niu, D. Z. Li and Y. Y. Li, Intermetallics, 2011, 19, 1275–1281.
60. A. J. Zaddach, C. Niu, C. C. Koch and D. L. Irving, JOM, 2013, 65, 1780–1789.
61. A. J. E. Foreman, Acta Metall., 1955, 3, 322–330.
62. M. M. Savin, V. M. Chernov and A. M. Strokova, Phys. Status Solidi A, 1976, 35, 747–754.
63. C. N. Reid, Acta Metall., 1966, 14, 13–16.

---