Featured properties of Li⁺-based battery anode: Li₄Ti₅O₁₂

Abstract

3D ternary Li₄Ti₅O₁₂, a Li⁺-based battery anode, presents an unusual lattice symmetry (triclinic crystal), band structure, charge density, and density of states under first-principles calculations. It is a large direct-gap semiconductor with E^d_g ∼ 2.98 eV. The atom-dominated valence and conduction bands, the spatial charge distribution and the atom- and orbital-decomposed van Hove singularities are available for delicate identifications of multi-orbital hybridizations in Li–O and Ti–O bonds. The extremely non-uniform chemical environment, which induces very complicated hopping integrals, directly arises from the large bonding fluctuations and the highly anisotropic configurations. Also, the developed theoretical framework is very useful for fully understanding cathodes and electrolytes of oxide compounds.

---

1 Introduction

Commercialized lithium-ion batteries (LIBs) principally consist of a cathode (positive electrode), an anode (negative electrode) and an electrolyte, in which the third component is closely related to the unusual transport of positive lithium ions (Li⁺) between the two electrodes.^1–5 Experimental progress covers two main types of negative electrode in LIBs, graphite and lithium titanium oxide. From an industrial point of view, graphite-based anode material for LIBs is very easy to produce, which leads to a lower cost. However, this system has a serious disadvantage in terms of volume expansion over many rapid charging and discharging processes.^6,7 When lithium titanium oxide serves as the negative electrode, it is able to provide a long life, rapid charging, high input/output power performance, excellent low-temperature operation, and a wide effective state of charge range. On the other hand, this compound can overcome the drastic volume changes in the graphitic materials⁷ and is known as a zero-strain material. Moreover, lithium titanium oxide has a high reaction potential plateau at 1.55 V vs. Li/Li⁺,⁸ which will prevent the occurrence of lithium dendrites and whiskers, sometimes causing a short circuit, failure, or even a fire, so this enhances the safety issue of lithium-ion batteries.^9–12 On the theoretical side, the graphite intercalation compounds of Li⁺ ions/Li atoms are predicted to present AA or AB stacking configurations¹³ when the adion/adatom concentration is sufficiently high or low. Furthermore, semi-metallic/metallic behaviors, which are determined by the band overlap/the Fermi level at the conduction bands, come into existence in the case of Li⁺/Li intercalation.^13,14 There are only a few first-principles studies^15–18 on LiTiO-related materials with unusual superconducting properties.^15–18 Thorough theoretical studies of their essential properties are absent, even pure numerical calculations,^15–19 e.g. the absence of significant orbital hybridizations in different chemical bonds. The critical physical/chemical/material pictures are one of the main focuses of this paper.

Previous simulation methods²⁰ based on first-principles calculations can provide rich and unique phenomena, especially for emergent 2D layered materials. For example, systematic studies have been conducted on the essential properties of few-layer graphene systems,²¹ 1D graphene nanoribbons,²² and silicene-related materials,²³ with chemical absorptions^24,25 and substitutions.²⁶ Such investigations clearly illustrate that the quasiparticle charges/orbitals and spins dominate all the diversified phenomena. The delicate VASP results and thorough analyses are capable of proposing significant mechanisms/pictures to fully understand the geometric, electronic and magnetic properties. The important multi-/single-orbital hybridizations in various chemical bonds are obtained from the optimal lattice symmetry, the atom-dominated band structures, the spatial charge densities & their variations after chemical modifications, and the atom- & orbital-decomposed density of states. Furthermore, the spin distribution configurations (non-, ferro- & antiferromagnetic configurations) associated with the host and/or guest atoms are accurately identified from the spin-split/spin-degenerate energy bands, the spin density distributions, the net magnetic moments, and the spin-projected van Hove singularities. This developed framework, which is successfully conducted on silicene- and graphene-related systems, could be generalized to other emergent materials, or needs to be thoroughly tested in further investigations. It is thus expected to be very suitable for studying the rather complicated geometric and electronic properties of mainstream Li⁺-based batteries,²⁷ mainly including cathode,²⁷ anode²⁷ and electrolyte materials.²⁸ In addition, the direct combination of numerical simulations with phenomenological models would be very useful to thoroughly understand the unusual and diverse properties, e.g. the linking of VASP calculations^21,22,44 and generalized tight-binding models²⁹ for rich magnetic quantization.³⁰

This paper is mainly focused on the geometric structure and electronic properties of the Li₄Ti₅O₁₂-related anode material in Li⁺-based batteries.^31,32 The first-principles calculated results cover the total ground state energy, lattice symmetry, various Li–O and Ti–O, the atom-dominated band structure, the spatial charge density distribution, and the atom- & orbital-projected van Hove singularities. The spin-dependent behaviors, the spin-split electronic states, the net magnetic moment and the spin density distributions will be fully tested to investigate whether or not they could survive in the ternary transition-metal atom compound. Such physical properties will play important roles in achieving critical multi-orbital hybridizations in three kinds of chemical bonds. The difficulties of analysis lie in the very complicated orbital-decomposed density of states, which is supported by the electronic energy spectrum and carrier density. The theoretical predictions, which are conducted on the optimal geometry, the occupied valence state and the energy gap & whole energy spectrum, could be verified by high-resolution measurements of X-ray diffraction/low-energy electron diffraction (LEED),³³ angle-resolved photoemission spectroscopy (ARPES),³⁴ and scanning tunneling microscopy (STM).³⁵

2 Theoretical simulation methods

The rich and unique geometric structures and electronic properties of the three-dimensional Li₄Ti₅O₁₂ compound are thoroughly investigated by density functional theory (DFT)³⁶ implemented by the Vienna ab initio simulation package (VASP).³⁷ The many-particle exchange and correlation energies, which mainly arise from the electron–electron Coulomb interactions, are calculated from the Perdew–Burke–Ernzerhof (PBE)³⁸ functional under the generalized gradient approximation. Furthermore, the projector-augmented wave (PAW)^39,40 pseudopotentials are able to characterize the electron–ion interactions. It is well known that these two kinds of intrinsic interactions have no exact formulas,⁴¹ i.e. it is very difficult to express the single- and many-particle Hamiltonian in an analytic form.⁴¹ In general, plane waves with a kinetic energy cutoff of 520 eV are chosen as a complete set;⁴¹ therefore, they are very reliable and suitable for evaluating Bloch wave functions and electronic energy spectra. The first Brillouin zone is sampled by 3 × 3 × 3 and 12 × 12 × 12 k-point meshes within the Monkhorst–Pack scheme for geometric optimizations and electronic structures, respectively. Such points are sufficient for obtaining the reliable orbital-projected density of states, spatial charge distributions, and spin density configurations. The convergence of the ground-state energy is 10⁻⁵ eV between two consecutive simulation steps, and the maximum Hellmann–Feynman force acting on each atom is less than 0.01 eV Å⁻¹ during the ionic relaxations.

The delicate VASP calculations and detailed analyses are conducted on certain physical quantities,³⁷ such as the atom-dominated band structures, the spatial charge densities, the atom- & orbital-decomposed van Hove singularities, the spin distribution configurations, the spin-split or spin-degenerate energy bands, and the net magnetic moments. As a result, the critical pictures, the multi- and/or single-orbital hybridizations in chemical bonds and the spin configurations due to different atoms could be attained using the concise scheme. Such viewpoints will be very useful in fully comprehending the diversified physical/chemical/material phenomena. The theoretical framework has been successful in the systematic investigation of the geometric, electronic and magnetic properties of few-layer 2D graphene systems,⁴² 1D graphene nanoribbons⁴³ and 2D silicene-related materials. Very interestingly, chemical modifications through adatom chemisorptions and guest-atom substitutions can greatly diversify various fundamental properties.⁴⁴ Apparently, the developed viewpoints are available in other condensed-matter systems. For example, they should be suitable for thoroughly exploring the diverse phenomena of Li⁺-based battery anode/cathode/electrolyte materials.^1–3

Numerical simulations might be available in combination with phenomenological models. For example, the first-principles calculations for band structures could be fitted by the tight-binding model/the effective-mass approximation if the electronic energy spectra across the Fermi level are not so complicated.⁴⁴ This viewpoint has been very successful in fully examining the diversified essential properties of few-layer graphene systems, e.g. the diverse magnetic quantization of AA-,^45–47 AB-,^47,48 ABC-⁴⁹ and AAB-stacked graphenes under the generalized tight-binding model with any external fields. Such a model is closely related to the parameterized Hamiltonian; that is, the various hopping integrals, due to the different orbital hybridizations, need to be taken into account for its diagonalization. Apparently, they play critical roles in expressing the suitable and reliable Hamiltonian. Specifically, the current Li₄Ti₅O₁₂ material presents an extremely non-uniform chemical environment in a primitive unit cell (discussed in Fig. 1); therefore, it might be very difficult to achieve a reliable tight-binding model with the various chemical bonds.

Fig. 1 The optimal geometry of Li₄Ti₅O₁₂, with triclinic symmetry, where a primitive unit cell has 42 atoms. Lattice constants: a = 5.288 Å, b = 9.532 Å, and c = 9.932 Å; tilted angles: α = 73.122°, β = 78.042°, and γ = 78.913°.

3 Rich geometric symmetries of 3D Li₄Ti₅O₁₂ compound

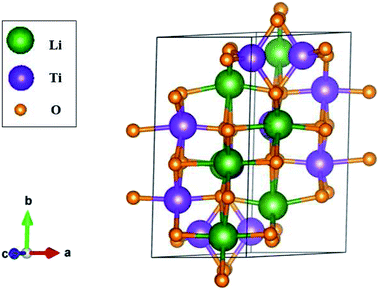
The three-dimensional Li₄Ti₅O₁₂ compound exhibits unusual geometric symmetries. One of the meta-stable configurations that possesses the smallest unit cell is chosen for a model study. This corresponds to a triclinic structure, as clearly illustrated in Fig. 1. 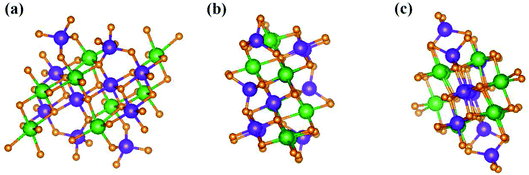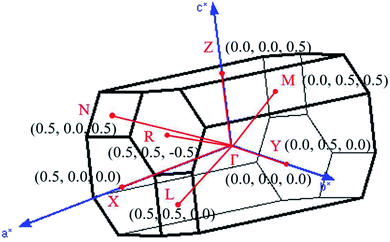A primitive unit cell has 42 atoms (8 Li, 10 Ti and 24 O atoms), lattice constants of a = 5.288 Å, b = 9.532 Å, and c = 9.932 Å, and tilted angles of α = 73.122°, β = 78.042°, and γ = 78.913° about x̂, ŷ, and ẑ, respectively. The space-group symmetries belong to Hermann–Mauguin (P1), Hall (−P1), and point group 1̄. Apparently, a highly anisotropic and extremely non-uniform chemical environment exists. The projections of this 3D material on different planes present diverse atom arrangements, such as those of (a) (100), (b) (010), (c) (001) (Fig. 2(a)–(c)), where Li, Ti, and O atoms are respectively represented by green, violet, and orange balls. The real-space lattice is available to get the reciprocal lattice, where the band structure is obtained along the paths of high-symmetry points X–Γ–Y|L–Γ–Z|N–Γ–M|R–Γ (defined in Fig. 3).

Fig. 2 The geometric structure of Li₄Ti₅O₁₂ along different projections: (a) (100), (b) (010), (c) (001), in which Li, Ti, and O atoms are represented by green, violet, and orange balls, respectively.

Fig. 3 The first Brillouin zone with the paths of high-symmetry points.

The unique chemical bonds that survive in a primitive unit cell will determine the fundamental properties. They include Li–O and Ti–O bonds, for which the total numbers are 48 and 52, respectively. According to the delicate first-principles calculations in Table 1, their bond lengths might lie in a wide range of ∼1.988–2.479 Å and 1.757–2.210 Å. This diversified phenomenon will be directly reflected in the distribution width of the spatial charge density (Fig. 5). Both Li–O and Ti–O bonds exhibit sufficiently large modulations, clearly indicating non-uniform bonding strengths. This might lead to the easy intercalation of Li⁺ ions and thus the structural transformation to another meta-stable geometric configuration. Furthermore, all the chemical bonds are generated by multi-orbital hybridizations (discussed in the orbital-dependent density of states in Fig. 6). A variety of orbital hybridizations come into existence in this anode material, and so do the hopping integrals in the tight-binding model.⁵⁰

Table 1 The various chemical bond lengths in Li₄Ti₅O₁₂, in which the total number of Li–O and Ti–O bonds is 100

No. of bonds	Atom–atom	Bond length (Å)
48	Li–O	1.988–2.479
52	Ti–O	1.757–2.210

---

Fig. 4 (a) Electronic energy spectrum for Li₄Ti₅O₁₂ along the high-symmetry points in the first Brillouin zone within the range of −6.0 eV ≤ E^c,v ≤ 4.0 eV; for the specific (b) lithium, (c) titanium and (d) oxygen dominances (green, violet and orange balls, respectively).

Fig. 5 (a) The different Li–O & Ti–O chemical bonds (LiO₆, TiO₄, TiO₆), in which diversified spatial charge density distributions under the longest/middle/shortest Li–O for (b)/(c)/(d) and Ti–O for (e)/(f)/(g), respectively; (h) shows those of the isolated atoms.

Fig. 6 The atom- and orbital-decomposed density of states due to (a) Li, Ti, and O atoms (green, violet, and orange curves); (b) Li-2s orbital (green curve); (c) Ti-(4s, 3d_x²−y², 3d_xy, 3d_yz, 3d_xz, 3d_z²) orbitals (purple, light blue, dark blue, red, light green, yellow curves); and (d) O-(2s, 2p_x, 2p_y, 2p_z) orbitals (blue, purple, green, pink-orange curves).

The theoretical predictions for the optimal geometric structures could be verified by experimental investigations. Both X-ray diffraction⁵¹ and low-energy electron diffraction (LEED)^33,52 are suitable for measuring the 3D lattice symmetries, but not scanning tunneling microscopy (STM)⁵³ and tunneling electron microscopy (TEM)^35,53 for the nanoscale top- and side-view structures, respectively. For the 3D Li₄Ti₅O₁₂ material, they could be utilized to thoroughly explore the diversified lengths of the Li–O and Ti–O bonds. This will be very useful in indirectly identifying the complicated multi-orbital hybridizations in all chemical bonds.

4 Rich and unique electronic properties

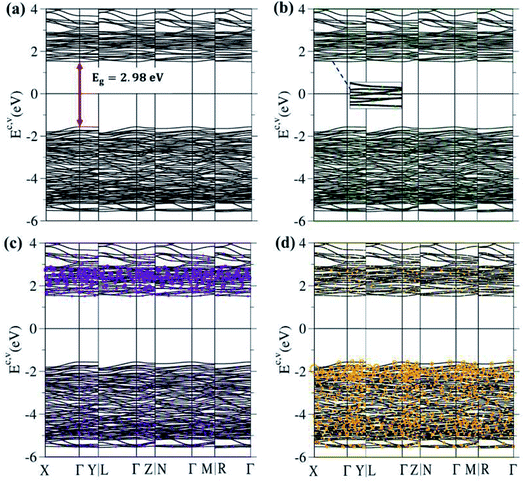
The 3D ternary compound Li₄Ti₅O₁₂ exhibits unusual electronic states. The first-principles band structure, as indicated in Fig. 4(a), is very sensitive to changes of the wave vector. Consequently, it is highly anisotropic. Apparently, the occupied electron energy spectrum is asymmetric to the unoccupied hole spectrum about the Fermi level (E_F − 0), mainly due to the different multi-orbital hybridizations in the non-uniform chemical bonds (Fig. 1). The highest occupied valence-band state and the lowest unoccupied conduction-band state determine an energy gap of E^d_g ∼ 2.98 eV (red perpendicular arrow in Fig. 4(a)); furthermore, they emerge at the same wave vector, leading to a direct-gap semiconductor. This band gap is equal to the optical threshold absorption frequency; that is, the optical spectroscopies⁵⁴ are very suitable for examining the theoretical prediction of E^d_g. E_g is too wide to generate the spin-split electronic states across the Fermi level, where this phenomenon is supported by the spin-degenerate valence and conduction bands below and above E_F, respectively, with sufficiently great energy spacing. As a result, the net magnetic moment is zero and the spin-dependent interactions could be ignored in this ternary compound. This band gap is close to the values of the theoretical results, which are 3.015 eV⁵⁶ and 2.52 eV,¹⁶ and to the experimental result of 2.95 eV.⁵⁷ Plenty of valence and conduction energy subbands exist because of the many atoms and outer orbitals in a large unit cell. Generally speaking, the energy dispersions are weak but significant. Their widths might lie in the range of ∼0.08–0.31 eV. The different energy subbands present non-crossing, crossing and anti-crossing behaviors. It should be noted that the latter phenomenon will appear when two neighboring subbands possess comparable independent components within the anti-crossing region,⁵⁵ e.g. the almost competitive amplitude of the same model in two anti-crossing Landau levels.⁵⁵

The atom dominances, which are represented by the ball radii, are very useful in understanding the critical roles of chemical bonds in the rich electronic states, such as the contributions to the electronic states of lithium, titanium and oxygen atoms through green, violet and orange balls, respectively. It is very difficult to observe the obvious contributions of the Li atoms, in which only small green circles are revealed in the whole range of valence and conduction subbands (Fig. 4(b)). This unique result clearly illustrates that the chemical bonding strengths (the hopping integrals of neighboring atoms)^29,63 of the 48 Li–O bonds (Fig. 2 and 3) should present a very wide range because of the large fluctuation of their lengths; furthermore, each Li atom only makes a single-orbital contribution of 2s. On the other hand, the Ti contributions are observable and very important within the valence- and conduction-band ranges of −5.50 eV ≤ E^v ≤ −1.49 eV and 1.49 eV ≤ E^c ≤ 4.0 eV, respectively, especially for the latter. Apparently, the unoccupied electronic states are dominated by titanium atoms, but not oxygen atoms. The opposite is true for the oxygen contributions. Such a phenomenon might be associated with the simultaneous existence of many O-related chemical bonds (100), with deeper (2s, 2p_x, 2p_y, 2p_z)-orbital energies. In short, atom-dominated electronic structures could provide partial information about critical multi-orbital hybridizations.

The theoretical predictions, which are conducted on the wave-vector-dependent band structures below E_F, could be verified by high-resolution ARPES.³⁴ Many previous measurements have clearly identified the low-energy valence bands of layered graphene systems as being only initiated from the K/K′ valleys,⁵⁸ such as the linear Dirac-cone structure in twisted bilayer graphene (Moire superlattices with very large unit cells)⁵⁹ & monolayer graphene,⁶⁰ the parabolic/parabolic and linear dispersions in bilayer/tri-layer AB stackings,^60,61 the linear, partially flat and Sombrero-shaped bands in tri-layer ABC stacking,^61,62 and the semi-metallic property of bulk Bernal graphite.⁶¹ These diversified electronic energy spectra are identified to only arise from the pure and unique interlayer 2p_z–2p_z orbital hybridizations in normal/enlarged honeycomb lattices, according to consistency between the first-principles method⁶³ and the tight-binding model.^29,63 Similar experimental measurements are available in examining the main features of the 3D ternary compound Li₄Ti₅O₁₂, such as the sensitive dependence on the wave vector, the large band gap, the highly asymmetric electron and hole energy spectra, the weak but significant energy dispersions, and the frequent non-crossing/crossing/anti-crossing behaviors. Their verifications are very helpful in solving the critical orbital hybridizations of chemical bonds.

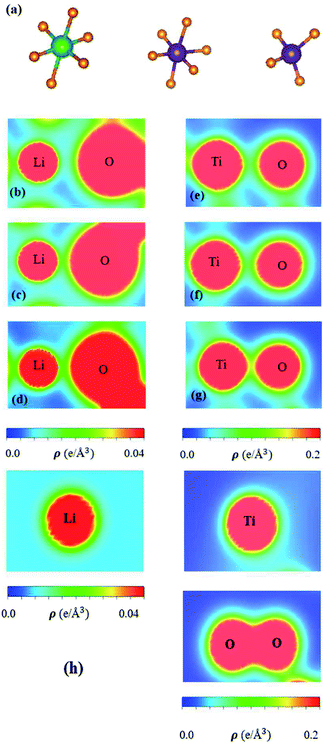
The spatial charge distributions on different chemical bonds, as clearly indicated in Fig. 5(a)–(h), are capable of providing the first-step orbital hybridizations for further examination by the delicate atom- and orbital-decomposed van Hove singularities (discussed in Fig. 6). The optimal geometry, with a triclinic unit cell (Fig. 2), shows the LiO₆, TiO₄ and TiO₆ chemical bonds, illustrating the highly non-uniform chemical environment. Their distinct bond lengths (Table 1) only direct the diversified chemical bonding strengths (the diverse charge density distributions). That is to say that the spatial carrier densities, being closely related to the electron orbitals of each atom, are very sensitive to changes of the nearest-neighbor distances. As for the shortest Li–O bonds (1.988 Å in Fig. 5(d)), only the 2s-orbital provides a dilute charge density around the lithium atom, in which the effective distribution range is about 0.52 Å as measured from the deep blue region of the Li⁺-ion core to the light region of the extended 2s-orbital. Apparently, the two 1s orbitals are independent of critical orbital hybridizations in the Li–O bonds. An obvious overlap of distinct orbital charges exists in the range of 1.20–1.60 Å distance from the O-core. Furthermore, the significant O-orbitals, indicated by the light green and yellow colors, are deduced to arise from the (2p_x, 2p_y, 2p_z) orbitals. However, the O-dependent 2s orbitals are far away from that of the lithium atom; therefore, their contributions to the chemical bonds are almost negligible. With the decrease in Li–O length (2.479 Å and 2.249 Å in Fig. 6(b) and (c), respectively), the charge overlap behavior between Li and O atoms is obviously increased. Very interestingly, the multi-orbital hybridizations of 2s–(2p_x, 2p_y, 2p_z) in Li–O bonds present diverse hopping integrals.⁶³

There are more Ti–O chemical bonds and quite strong bonding strengths (Fig. 5(e)–(g)), compared with Li–O bonds. The effective distribution range of the Ti atom is somewhat higher than that of the O atom because of the large atomic number. Most importantly, it could be classified into dark red, light red, and yellow-green regions, which, respectively, correspond to (3s, 3p_x, 3p_y, 3p_z), 4s, and (3d_x²−y², 3d_xy, 3d_yz, 3d_xz, 3d_z²). Apparently, the former orbitals do not take part in the important multi-orbital hybridizations in the Ti–O bonds. The deformed carrier distributions between the Ti and O atoms, as shown in the distinct bond length cases, clearly illustrate the diversified charge transfers from the former to the latter. The extremely non-uniform chemical bonds, even for similar bonds, will induce high barriers in generating suitable hopping integrals for the phenomenological models, e.g. reliable parameters in the tight-binding model.^63,64

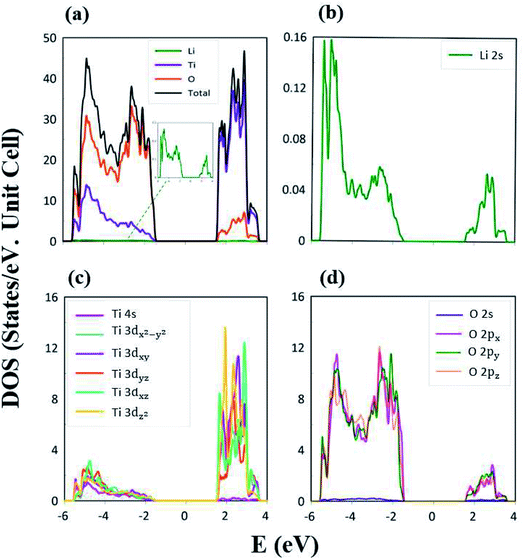
The atom- and orbital-projected density of states, as clearly indicated in Fig. 6(a)–(d), are able to provide full information on the significant multi-orbital hybridizations of the Li–O and Ti–O chemical bonds. Apparently, the density of states per unit cell vanishes with a large band gap of E^d_g ∼ 2.98 eV (Fig. 4(a)–(d)), and its valence and conduction spectra are highly asymmetric to each other. Whether a very wide gap will induce difficulties in experimental observations could be tested by further STS measurements (discussed later).^65,66 A lot of shoulders and asymmetric/symmetric peaks exist. Such van Hove singularities principally originate from the band-edge states of energy subbands, with the local minimum, maximum, saddle and almost dispersionless points in the energy wave-vector spaces. They might appear in between the high-symmetry points. It is well known that 3D parabolic energy dispersions can create square-root dependences.⁶⁷ Generally speaking, the titanium and oxygen atoms, respectively, dominate the density of states in the energy range of −5.50 eV ≤ E^v ≤ −1.49 eV and 1.49 eV ≤ E^c ≤ 4.0 eV (violet and orange curves). Furthermore, the lithium atoms only make minor contributions to the whole valence and conduction energy spectra (green curve in Fig. 6(b)) through only the 2s orbital, but not two core-level 1s orbitals.

The important contributions of various orbitals, which mainly come from (I) Li-2s orbital (green curve in Fig. 6(b)), (II) Ti-(4s, 3d_x²−y², 3d_xy, 3d_yz, 3d_xz, 3d_z²) orbitals (purple, light blue, dark blue, red, light green, yellow curves in Fig. 6(c)), and (III) O-(2s, 2p_x, 2p_y, 2p_z) orbitals (blue, purple, green, pink curves in Fig. 6(d)), are worthy of closer examination. The enlarged spectral scale for lithium atoms is able to provide clear van Hove singularities, i.e. their number, energies, intensities and forms are clearly illustrated in Fig. 6(b). These main features are similar to those of the (2p_x, 2p_y, 2p_z)-decomposed density of states for oxygen atoms (Fig. 6(d)). The similarities, which cover the whole energy spectrum (i.e. −6.0 eV ≤ E ≤ 4.0 eV), only reflect the very important 48 Li–O chemical bonds with multi-orbital hybridizations (Fig. 1 and 2). It should be noted that the O-2s orbitals make almost zero contribution to the specific energy range. The principal reason might be that they belong to the fully occupied states in the spin-up and spin-down configurations; therefore, any dangling bonds/chemical bonds are forbidden. The effective width of the energy spectrum, being closely related to the Li–O chemical bonds, is more than 10.0 eV. This unusual characteristic is attributed to the complicated 2s-(2p_x, 2p_y, 2p_z) chemical bonding (multi-orbital hopping integrals and on-site Coulomb potentials)⁶³ and the large bond-length modulations (1.988–2.479 Å; easily modulated hopping integrals).

In addition to the Li–O bonds, the oxygen atoms also make significant contributions to the Ti–O bonds, especially for the valence-state energy spectrum. Obvious evidence is revealed by the similar van Hove singularities in terms of the orbital-decomposed special forms, energies and numbers. Concerning the transition-metal titanium atoms, six unique orbitals exist (4s, 3d_x²−y², 3d_xy, 3d_yz, 3d_xz, 3d_z²), which take part in the chemical bonding of oxide compounds, as clearly illustrated in Fig. 6(c). The orbital-dependent contributions are almost comparable across the whole energy spectrum, except for the small 4s-orbital density of states in the conduction-band range (the purple curve). Very interestingly, the initial conduction-/valence-state energy spectrum is mainly determined by the titanium and oxygen atoms. In short, the Li–O and Ti–O chemical bonds are deduced to have multi-orbital hybridizations of 2s–(2p_x, 2p_y, 2p_z) and (4s, 3d_x²−y², 3d_xy, 3d_yz, 3d_xz, 3d_z²)–(2p_x, 2p_y, 2p_z), respectively.

High-resolution STS measurement is the most efficient technique for examining the various van Hove singularities due to the band-edge states. To date, a rather weak tunneling quantum current could be measured in a very accurate way; furthermore, its differential conductance of dI/dV is deduced to be approximately proportional to the density of states. For example, such experiments have been successful in identifying significant coupling effects in few-layer graphene systems, e.g. an almost symmetric V-shape structure vanishing at the Fermi level for a monolayer (a zero-gap semiconductor),⁶⁸ the logarithmically symmetric peaks in twisted bilayer graphene,⁶⁹ a gate-voltage-induced energy gap for bilayer AB and tri-layer ABC stacking,^61,69 a delta-function-like peak centered about E_F in tri-layer and penta-layer ABC stackings,^70,71 and a sharp dip structure near E_F combined with a pair of square-root peaks under tri-layer AAB stacking (a narrow-gap semiconductor with constant-energy loops).⁷² Further experimental investigations that are suitable for the 3D ternary compound Li₄Ti₅O₁₂ are required to detect a large band gap of E^d_g ∼ 2.98 eV, a lot of asymmetric/symmetric peaks & broadening shoulders, the high asymmetry of electron & hole energy spectra, and their different widths. The measured results, combined with the theoretical predictions of van Hove singularities, might be very useful in comprehending the complicated multi-orbital hybridizations of Li–O and Ti–O.

The first-principles results could be utilized to establish a phenomenological model, the tight-binding model discussed in Section 2. However, for the 3D Li₄Ti₅O₁₂ compound,⁶³ a lot of different chemical bonds exist in a primitive unit cell (100 Li–O and Ti–O bonds; Fig. 1 and 2), and there are very complicated valence and conduction subbands with a large band gap of E_g = 2.98 eV (Fig. 4(a)–(d)), non-homogeneous spatial charge densities in diverse chemical bonds (Fig. 5(a)–(g)), and three kinds of multi-orbital hybridizations in van Hove singularities (Fig. 6(a)–(d)). Such critical factors are almost impossible to include in the parameterized tight-binding model. That is to say that the extremely non-uniform hopping integrals that are associated with various orbital hybridizations are rather difficult to achieve in order to fit the main features of the first-principles band structure. It seems that obtaining a reliable tight-binding model in Li⁺-based anode,⁷³ cathode⁷³ and electrolyte materials⁷³ will become an open issue, since it is relatively easy to understand the essential physical/material/chemical properties⁷⁴ from the concise pictures.

5 Concluding remarks

A theoretical framework based on first-principles calculations⁴⁴ is developed for the essential properties of the 3D ternary compound Li₄Ti₅O₁₂. The critical multi-orbital hybridizations in Li–O and Ti–O chemical bonds are delicately identified from the atom-dominated valence and conduction bands, the spatial charge density, and the atom- and orbital-decomposed density of states. Their highly anisotropic and non-uniform characteristics in a large unit cell clearly indicate that a reliable tight-binding model, with various hopping integrals and on-site Coulomb potentials, is almost impossible to achieve for the simulation of the VASP band structure. Similar developments could be generalized to Li⁺-based battery cathode,⁷⁵ anode⁷⁶ and electrolyte materials.⁷⁷ In particular, rich oxide compounds are worthy of systematic investigations of diversified physical/chemical/materials science phenomena. The current anode material, with the smallest unit cell of 42 atoms, is a triclinic structure in the tilted three axes. There exist 100 chemical bonds, in which the very strong covalent bonding makes this system present a large direct gap of E^d_g ∼ 2.98 eV, equal to the optical threshold absorption frequency. High-resolution optical spectroscopy measurements⁷⁸ are expected to be very efficient in examining the semiconducting behavior. Many valence and conduction bands are highly asymmetric to each other about the Fermi level, in which their energy dispersions are weak along any direction. Generally speaking, the whole band structure, which is related to the critical chemical bonding, lies in the range of −6.0 eV ≤ E^c,v ≤ 4.0 eV. It also reveals frequent subband non-crossing, crossing and anti-crossing.⁵⁵ Moreover, the band-edge states, the critical points in the energy-wave-vector spaces, appear as van Hove singularities in the density of states. The atom- and orbital-dependent special structures, the asymmetric/symmetric peaks and broadening shoulders, are successful in identifying the important multi-orbital hybridizations, such as 2s–(2p_x, 2p_y, 2p_z) and (4s, 3d_x²−y², 3d_xy, 3d_yz, 3d_xz, 3d_z²)–(2p_x, 2p_y, 2p_z) in Li–O and Ti–O bonds, respectively. The critical mechanisms are also supported by the spatial charge density distribution, while the diverse covalent bonding is partially supported by the atom-created energy bands and charge density distributions. Very interestingly, in addition to the Li₄Ti₅O₁₂ compound, other 3D LiTiO-related ternary materials exist, e.g. LiTi₂O₄,⁷⁹ Li₂Ti₂O₄,⁸⁰ and Li₇Ti₅O₁₂.⁸⁰ Such unusual condensed-matter systems are found to have diverse geometric symmetries^16,80 and thus exhibit quite different electronic,⁸⁰ optical,⁸⁰ and superconducting properties. The current study clearly shows the very large variations of chemical bond lengths. Relatively easy modulations of chemical bonds might be helpful in solving the open issue: the structural transformation between two meta-stable configurations during the charging or discharging processes of Li⁺-based batteries.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the Hi-GEM Research Center and the Taiwan Ministry of Science and Technology (Grant number MOST 108-3017-F-006-003).

References

1. M. Li, J. Lu, Z. Chen and K. Amine, Adv. Mater., 2018, 30, 1800561.
2. G. Pistoia, Lithium-Ion Batteries: Advances and Applications, Elsevier, 2014.
3. D. Deng, Energy Sci. Eng., 2015, 3, 385.
4. N. Nitta, F. Wu, J. T. Lee and G. Yushin, Mater. Today, 2015, 18, 252.
5. D. Ouyang, M. Chen, J. Liu, R. Wei, J. Weng and J. Wang, RSC Adv., 2018, 8, 33414.
6. X. Wang, Y. Sone, G. Segami, H. Naito, C. Yamada and K. J. Kibe, J. Electrochem. Soc., 2007, 154, A14.
7. S. Schweidler, L. D. Biasi, A. Schiele, P. Hartmann, T. Brezesinski and J. Janek, J. Phys. Chem. C, 2018, 122, 8829.
8. Y. Wang, Y.-X. Zhang, W.-J. Yang, S. Jiang, X.-W. Hou, R. Guo, W. Liu, P. Huang, J. Lu, H.-T. Gu and J.-Y. Xie, J. Electrochem. Soc., 2019, 166, A5014.
9. J. Lu, C. Nan, Q. Peng and Y. Li, J. Power Sources, 2012, 202, 246.
10. Z. Liu, N. Zhang and K. Sun, J. Mater. Chem., 2012, 22, 11688.
11. C. Cheng, H. Liu, J. Li, X. Xue, H. Cao and D. Wang, J. Power Sources, 2015, 283, 237.
12. H. Chiu, X. Lu, J. Zhou, L. Gu, J. Reid and R. Gauvin, Adv. Energy Mater., 2017, 7, 1601825.
13. S.-Y. Lin, W. B. Li, N. T. T. Tran, A. Schiele, P. Hartmann, T. Brezesinski and J. Janek, 2018, arXiv:1810.11166.
14. K. Ji, J. Han, A. Hirata, T. Fujita, Y. Shen, S. Ning, P. Liu, H. Kashani, Y. Tian, Y. Ito, J. Fujita and Y. Oyama, Nat. Commun., 2019, 10, 275.
15. Y. Tanaka, M. Ikeda, M. Sumita, T. Ohno and K. Takada, Phys. Chem. Chem. Phys., 2016, 18, 23383.
16. Y. Liu, J. Lian, Z. Sun, M. Zhao, Y. Shi and H. Song, Chem. Phys. Lett., 2017, 677, 114.
17. K. Tada, M. Kitta, H. Ozaki and S. Tanaka, Chem. Phys. Lett., 2019, 731, 136598.
18. M. Li, T. Gould, Z. Su, S. Li, F. Pan and S. Zhang, Appl. Phys. Lett., 2019, 115, 073902.
19. S. Zahn, J. Janek and D. Mollenhauer, J. Electrochem. Soc., 2017, 164, A221.
20. T. Ohta, A. Bostwick, T. Seyller, K. Horn and E. Rotenberg, Science, 2006, 313, 951.
21. H. J. Park, J. Meyer, S. Roth and V. Skákalová, Carbon, 2010, 48, 1088.
22. A. Celis, M. N. Nair, A. Taleb-Ibrahimi, E. H. Conrad, C. Berger, W. de Heer and A. Tejeda, J. Phys. D: Appl. Phys., 2016, 49, 143001.
23. D. Jose and A. Datta, Phys. Chem. Chem. Phys., 2011, 13, 7304.
24. D. K. Nguyen, N. T. T. Tran, Y.-H. Chiu and M.-F. Lin, Sci. Rep., 2019, 9, 13746.
25. J. Sivek, H. Sahin, B. Partoens and F. M. Peeters, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 085444.
26. T. TeshomeAyan and D. Orcid, J. Phys. Chem. C, 2017, 121, 15169.
27. M. D. Bhatt and C. O’Dwyer, Phys. Chem. Chem. Phys., 2015, 17, 4799.
28. X. Wu, K. Pan, M. Jia, Y. Ren, H. He, L. Zhang and S. Zhang, Green Energy Environ., 2015, 3, 385.
29. E. Nielsen, R. Rahman and R. P. Muller, J. Appl. Phys., 2012, 112, 114304.
30. Y.-K. Huang, S.-C. Chen, Y.-H. Ho, C.-Y. Lin and M.-F. Lin, Sci. Rep., 2015, 4, 7509.
31. H. Gwon, J. Hong, H. Kim, D.-H. Seo, S. Jeon and K. Kang, Energy Environ. Sci., 2014, 7, 538.
32. G. Zhou, F. Li and H.-M. Cheng, Energy Environ. Sci., 2014, 7, 1307.
33. F. Jona, J. A. Strozier and W. S. Yang, Rep. Prog. Phys., 1982, 45, 527.
34. B. Lv, T. Qian and H. Ding, Nat. Phys., 2019, 1, 609.
35. G. Binnig and H. Rohrer, Surf. Sci., 1985, 152–153, 17.
36. N. Argaman and G. Makov, Am. J. Phys., 2000, 68, 69.
37. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15.
38. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
39. P. E. Blochl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953.
40. T. Rangel, D. Caliste, L. Genovese and M. Torrent, Comput. Phys. Commun., 2016, 208, 1.
41. G. H. Booth, T. Tsatsoulis, G. K.-L. Chan and A. Grüneis, J. Chem. Phys., 2016, 145, 084111.
42. J. H. Warner, M. H. Rümmeli, T. Gemming, B. Büchner and G. A. D. Briggs, Nano Lett., 2009, 9, 102.
43. S.-Y. Lin, N. T. T. Tran, S. L. Chang, W. P. Su and M.-F. Lin, Structure- and Adatom-Enriched Essential Properties of Graphene Nanoribbons, CRC press, 2018.
44. S.-Y. Lin, S. L. Chang, H. H. Chen, S. H. Su, J.-C. Huang and M.-F. Lin, Phys. Chem. Chem. Phys., 2016, 18, 18978.
45. Y.-H. Ho, J.-Y. Wu, R.-B. Chen, Y.-H. Chiu and M.-F. Lin, Appl. Phys. Lett., 2010, 97, 101905.
46. J. K. Lee, S. C. Lee, J. P. Ahn, S. C. Kim, J. I. Wilson and P. John, J. Chem. Phys., 2008, 129, 234709.
47. A. V. Rozhkova, A. O. Sboychakova, A. L. Rakhmanova and F. Noria, Phys. Chem. Chem. Phys., 2015, 17, 4799.
48. C. L. Lu, C. P. Chang, Y. C. Huang, R. B. Chen and M.-L. Lin, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 144427.
49. M. Yankowitz, I. Joel, J. Wang, A. G. Birdwell, Y.-A. Chen, K. Watanabe, T. Taniguchi, P. Jacquod, P. San-Jose and P. Jarillo-Herrero, Nat. Mater., 2014, 13, 786.
50. C.-Z. Wang, W.-C. Lu, Y.-X. Yao, J. Li, S. Yip and K.-M. Ho, Sci. Model. Simul., 2008, 15, 81.
51. S. Ravi, D. P. Bisen, S. Usha and B. G. Sharma, Recent Res. Sci. Technol., 2012, 4, 77.
52. L. J. Clarke, Surface crystallography: an introduction to low energy electron diffraction, John Wiley & Sons Ltd, 1985.
53. P. Lauffer, K. V. Emtsev, R. Graupner, T. Seyller, L. Ley, S. A. Reshanov and H. B. Weber, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 155426.
54. T. Y. Jeong, H. Kim, S.-J. Choi, K. Watanabe, T. Taniguchi, K. J. Yee, Y. S. Kim and S. Jung, Nat. Commun., 2019, 10(1), 3825.
55. X. C. Zhang, I. Martin and H. W. Jiang, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 073301.
56. A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, APL Mater., 2013, 1, 011002.
57. S. Özen and V. Şenay, J. Phys. D: Appl. Phys., 2016, 49, 105303.
58. M. Koshino and E. McCann, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 115315.
59. Y. K. Ryu Cho, R. Frisenda and A. Castellanos-Gomez, Chem. Commun., 2019, 55, 11498.
60. A. H. Castro Neto, F. Guinea, N. M. R. Peres, K. S. Novoselov and A. K. Geim, Rev. Mod. Phys., 2009, 81, 109.
61. C. Coletti, S. Forti, A. Principi, K. V. Emtsev, A. A. Zakharov, K. M. Daniels, B. K. Daas, M. V. S. Chandrashekhar, T. Ouisse, D. Chaussende, A. H. MacDonald, M. Polini and U. Starke, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 155439.
62. S. Hattendorf, A. Georgi, M. Liebmann and M. Morgenstern, Surf. Sci., 2013, 610, 53.
63. V. Zólyomi, J. R. Wallbank and V. I. Fal’ko, 2D Mater., 2014, 1, 011005.
64. P. Koskinen and V. Mäkinen, Comput. Mater. Sci., 2009, 47, 237.
65. S. Kano, T. Tadaa and Y. Majima, Chem. Soc. Rev., 2015, 44, 970.
66. G. Li, A. Luican and E. Y. Andrei, Phys. Rev. Lett., 2009, 102, 176804.
67. S. Tang and M. S. Dresselhaus, Appl. Phys. Lett., 2014, 105, 033907.
68. H. C. Chung, C. P. Chang, C. Y. Lin and M. F. Lin, Phys. Chem. Chem. Phys., 2016, 18, 7573.
69. Z. F. Wang, F. Liu and M. Y. Chou, Nano Lett., 2012, 12, 3833.
70. C. H. Ho, S. J. Tsai, R. B. Chen, Y. H. Chiu and M.-F. Lin, J. Nanosci. Nanotechnol., 2011, 11, 4938.
71. Y. Que, W. Xiao, H. Chen, D. Wang, S. Du and H.-J. Gao, Appl. Phys. Lett., 2015, 107, 263101.
72. C.-Y. Lin, B.-L. Huang, C.-H. Ho, G. Gumbs and M.-F. Lin, Phys. Rev. B, 2018, 98, 195442.
73. C.-P. Chou, A. W. Sakti, Y. Nishimura and H. Nakai, Chem. Rec., 2018, 18, 1.
74. M. H. Lee, H. C. Chung, J. M. Lu, C. P. Chang and M.-F. Lin, Mater. Sci., 2015, 95, 2717.
75. G. E. Blomgren, J. Electrochem. Soc., 2017, 164, A5019.
76. J. Lu, Z. Chen, F. Pan, Y. Cui and K. Amine, Electrochem. Energy Rev., 2018, 1, 35.
77. Y. Yamada, J. Wang, S. Ko, E. Watanabe and A. Yamada, Nat. Energy, 2019, 4, 269.
78. N. H. Wan, F. Meng, T. Schröder, R.-J. Shiue, E. H. Chen and D. Englund, Nat. Commun., 2015, 6, 7762.
79. K. Yoshimatsu, M. Niwa, H. Mashiko, T. Oshima and A. Ohtomo’, Sci. Rep., 2015, 5, 16325.
80. Y. Liu, J. Lian, Z. Sun, M. Zhao, Y. Shi and H. Song, Chem. Phys. Lett., 2017, 677, 114.

---