Open Access Article
Open Access ArticleSalt doping to improve thermoelectric power factor of organic nanocomposite thin films†
Daniel L. Stevensa,
Geethal Amila Gamage b,
Zhifeng Ren
b,
Zhifeng Ren b and
Jaime C. Grunlan
b and
Jaime C. Grunlan *acd
*acd
aDepartment of Chemistry, Texas A&M University, 3255 TAMU, College Station, Texas 77843, USA. E-mail: jgrunlan@tamu.edu; Fax: +1-979-845-2081; Tel: +1-979-845-3027
bDepartment of Physics and Texas Center for Superconductivity at the University of Houston (TcSUH), University of Houston, Houston, Texas 77204, USA
cDepartment of Materials Science and Engineering, Texas A&M University, 3003 TAMU, College Station, Texas 77843, USA
dDepartment of Mechanical Engineering, Texas A&M University, 3123 TAMU, College Station, 77843, USA
First published on 23rd March 2020
Abstract
Thermoelectric materials with a large Seebeck coefficient (S) and electrical conductivity (σ) are required to efficiently convert waste heat into electricity, but their interdependence makes simultaneously improving these variables immensely challenging. To address this problem, bilayers (BL) of poly(diallyldimethylammonium chloride) (PDDA) and double-walled carbon nanotubes (DWNT), stabilized by KBr-doped poly(3,4-ethylenedioxythiophene):poly(styrene sulfonate) (PEDOT:PSS) were deposited using layer-by-layer (LbL) assembly. Doping PEDOT:PSS with KBr, prior to DWNT dispersion and LbL assembly, results in a six-fold improvement in electrical conductivity with little change in the Seebeck coefficient. A maximum power factor (PF = S2σ) of 626 ± 39 μW m−1 K−2 is obtained from a 20 BL PDDA/PEDOT:PSS–DWNT film (∼46 nm thick), where PEDOT:PSS was doped with 3 mmol KBr. This large PF is due to the formation of a denser film containing a greater proportion of DWNT, which was influenced by the charge-screening effects imparted by the salt dopant that separates PSS from PEDOT. This study demonstrates a relatively simple strategy to significantly increase the thermoelectric performance of fully organic nanocomposites that are useful for low temperature thermoelectric devices.
1. Introduction
The large amount of waste heat associated with energy production presents a tremendous opportunity for thermoelectric materials.1,2 Thermoelectric energy generation, the means of converting thermal energy into electrical energy with no moving parts, is a waste heat recycling technology. The thermoelectric performance of a material is typically evaluated using a dimensionless figure of merit: ZT = (S2σT/κ), where S, σ, κ, and T, are the Seebeck coefficient (μV K−1), electrical conductivity (S m−1), thermal conductivity (W m−1 K−1), and the absolute temperature (K), respectively. S2σ is commonly referred to as the power factor (PF), which is reliable means of comparison for organic thermoelectric materials due to their inherently low thermal conductivities.3 While the ideal thermoelectric material would have a high S, high σ, and low κ, their interdependencies make improving ZT challenging.4,5Creating nanoscale domains in a thermoelectric material has been shown to increase the thermoelectric figure of merit by creating more sites for phonon scattering, thereby reducing κ, without hampering S or σ. This strategy further reduces material dimensions to the nanoscale, which allows for finer control over the electronic density of states that are more conducive to thermoelectric behavior.5,6 Nanostructuring has been demonstrated for traditional inorganic semiconductors, which have historically been plagued by toxicity, rigidity, and scarcity concerns.7,8 Flexible inorganic thermoelectric modules have been developed, but these materials have much lower power factor relative to their ingots.9–11 Thermoelectric composites comprised solely of organic materials have also received significant research attention. Many of these composites have power factors that are on par with flexible inorganic-filled materials at similar temperatures.12–14
Of the various organic thermoelectric materials studied, composites prepared using layer-by-layer (LbL) assembly have yielded much larger power factors compared to nanocomposites prepared by traditional mixing methods due to the greater interconnection amongst nanostructures.15–17 LbL assembly involves the cyclical exposure to aqueous solution of materials with attractive interactions (i.e. electrostatic, hydrogen bonding, π–π stacking, etc.),18–20 which offers nanoscale control over the film architecture during deposition. Polyelectrolytes, nanoparticles, conjugated polymers, and clays have all been assembled on a variety of substrates.21–24 In addition to changing chemical compounds, many variables such as ionic strength, temperature, and pH can be used to create a film of a particular thickness and function.25,26 Thermoelectric films comprised of double-walled carbon nanotubes (DWNT) and graphene, stabilized by polymeric surfactants (e.g. poly(3,4,-ethylenedioxythiophene):poly(styrene sulfonate) (PEDOT:PSS)) have power factors comparable to commercial bismuth telluride Bi2Te3 near room temperature.15,16,27 These materials exhibit a simultaneous increase in the Seebeck coefficient and electrical conductivity as a function of deposition cycles due to an increase in charge carrier mobility.
Strategies that improve the thermoelectric performance of PEDOT:PSS films involve the segregation of PEDOT and PSS to create a longer electron conduction pathway. PEDOT:PSS is a water soluble, intrinsically conductive polymer complex has been used extensively as a p-type organic thermoelectric material that can be prepared by polymerizing EDOT in the presence of PSS.28,29 Water solubility is due to the ionic stabilization PSS imparts to the conductive and hydrophobic PEDOT, which adopts a coiled conformation in water with a PSS shell encapsulating a PEDOT core.30 This core–shell material results in very poor thermoelectric performance when deposited onto a glass substrate.31,32 Separating the PSS from PEDOT decreases the distance between the electrically conductive chains. For example, adding polar solvents, such as ethylene glycol and DMSO, can dissociate PSS from PEDOT, resulting in an increase in electrical conductivity.33–35 In addition to improving the film morphology, the amount of anionic sulfonate groups (i.e. extent of oxidation) on PSS can be tuned to influence the ionic interactions between these molecules. For example, Fan et al. were able to improve the thermoelectric properties of spin-coated PEDOT:PSS films five-fold after exposing them to NaOH after three treatments in H2SO4(aq).36
One strategy to improve the thermoelectric performance of spin-coated PEDOT:PSS films is to expose them to common inorganic salts (e.g. CuCl2, ZnCl2, etc.) solvated in a polar organic solvent (e.g. DMF). The addition of salt increases the level of the polymer segregation, which was shown to simultaneously improve the Seebeck coefficient and electrical conductivity.37 Softer, more polarizable cations were found to be more effective at simultaneously increasing the Seebeck coefficient and electrical conductivity of PEDOT:PSS films due to their ability to remove PSS more efficiently from the film through charge screening effects.37–39 Dissociated salt ions are known to shield oppositely charged repeat units on polyelectrolytes, preventing strong electrostatic interactions between them. In the case of LbL-assembled films, thicker growth occurs with salt due to more polymer being required to electrostatically compensate the surface charge formed from the previous deposition step.25
In the present study, salt was used to separate PEDOT and PSS prior to LbL deposition to prepare polymer nanocomposite thin films. KBr was added to a PEDOT:PSS solution to weaken the interactions between the two components, followed by DWNT dispersion by means of ultra-sonication. The thermoelectric properties of a 20 bilayer (BL) thin film were analyzed as a function of the concentration of KBr dopant. A 20 BL PDDA/PEDOT:PSS–DWNT film doped with 3 mmol of KBr (∼46 nm thick) exhibits an electrical conductivity of 1479 S cm−1 and a Seebeck coefficient of 65.1 μV K−1, which results in a power factor of 626 μW m−1 K−2. This power factor is six times larger than the undoped control, and is attributed to an increase in electrical conductivity without a decrease in the Seebeck coefficient from the greater proportion of DWNT that is deposited as a result of doping. This work demonstrates the ability of salt to improve the PF of multilayer polyelectrolyte nanocomposites, which can be utilized for low temperature thermoelectric power generation applications.
2. Experimental
2.1 Materials
Poly(diallyldimethylammonium chloride) (PDDA) (Mw = 200![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000–350
000–350![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 g mol−1, 20 wt% aqueous solution) and KBr (>99%) were purchased from Millipore-Sigma (Milwaukee, WI). Poly(3,4-ethylenedioxythiophene):poly(styrenesulfonate) (PEDOT:PSS) was purchased from Heraeus Precious Metals (Clevios PH 1000, Hanau, Germany). Double-walled carbon nanotubes (DWNT) were purchased from Continental Carbon Nanotechnologies Inc. (XB type, 1 μm length and 2 nm diameter, Houston, TX). Each chemical was used as received and all solutions were prepared using 18 MΩ deionized (DI) water. Silicon wafers (p-type, 100, University Wafer, Boston, MA) and 179 μm poly(ethylene terephthalate) (PET) (ST 505, Tekra Crop., New Berlin, WI) were used as the substrates in this study.
000 g mol−1, 20 wt% aqueous solution) and KBr (>99%) were purchased from Millipore-Sigma (Milwaukee, WI). Poly(3,4-ethylenedioxythiophene):poly(styrenesulfonate) (PEDOT:PSS) was purchased from Heraeus Precious Metals (Clevios PH 1000, Hanau, Germany). Double-walled carbon nanotubes (DWNT) were purchased from Continental Carbon Nanotechnologies Inc. (XB type, 1 μm length and 2 nm diameter, Houston, TX). Each chemical was used as received and all solutions were prepared using 18 MΩ deionized (DI) water. Silicon wafers (p-type, 100, University Wafer, Boston, MA) and 179 μm poly(ethylene terephthalate) (PET) (ST 505, Tekra Crop., New Berlin, WI) were used as the substrates in this study.
2.2 Preparation of PEDOT:PSS (KBr)–DWNT suspensions
KBr (1–4 mmol) was added to 5 g of Clevios PH 1000, similar to a previous report.40 After doping PEDOT:PSS with KBr, 0.05 g of DWNT was suspended in the KBr-PEDOT:PSS solution using a mortar and pestle. DI water was added to adjust the concentration of PEDOT:PSS and DWNT to 0.06 wt% and 0.05 wt%, respectively. These DWNT suspensions were bath sonicated for 30 minutes, followed by tip sonication in an ice bath for 30 minutes at 15 W. This sonication cycle was repeated to ensure the suspensions were completely homogenized. The PEDOT:PSS (KBr)–DWNT solutions were centrifuged at 4000 rpm for 20 minutes. The supernatant was separated from the gelatinous precipitate using a pipette and used for coating.2.3 Layer-by-layer assembly
All substrates were cleaned using a sequence of rinses (DI water, methanol, DI water), and then dried with compressed air. Silicon wafers and PET substrates were subsequently cleaned in a plasma chamber (Atto Plasma System, Thierry, Royal Oak, MI) or by corona treatment (BD-20C, Electro-Technic Products Inc., Chicago, IL), respectively, to impart a negative surface charge before film deposition. LbL assembly was conducted using an automated coating system.41 The substrate was initially submerged in a 0.25 wt% PDDA solution for five minutes, followed by rinsing with DI water and drying with compressed air. This initial deposition procedure was followed identically for the PEDOT:PSS (KBr)–DWNT solution. The end of this sequence results in one PDDA/PEDOT:PSS (KBr)–DWNT bilayer (BL). For subsequent cycles, all depositions times were one minute and the pH of both solutions were unadjusted. This coating procedure was followed identically for all substrates used in this study.2.4 Film characterization
Thickness and refractive index of films deposited on Si wafers were measured using an α-SE ellipsometer (J.A. Woolam Co. Lincoln, NE), with a 632.8 nm laser held at a 70° angle. Raman spectra on 20 BL films deposited on silicon wafers were collected using a Jobin-Yvon Horiba Labram HR instrument (Piscataway, NJ), equipped with a 514.5 Ar-ion laser and paired with an Olympus BX41 optical microscope (Waltham, MA). Topology of 20 BL films deposited on a silicon wafer were collected using a Dimension Icon atomic force microscope (AFM) (Bruker, Billerica, MA). AFM probes (HQ:NSC35/Al BS, Micromasch USA Watsonville, CA) had a force constant of 5.5–16 N m−1 and a tip radius of ∼8 nm. Topographic AFM images were collected over a 5 × 5 μm area, with a scan speed of 0.5 Hz and 512 scans per line. XPS spectra of 20 BL films deposited on Si wafers were taken with an Omicron XPS/UPS system (Denver, CO), using a monochromatic DAR Mg X-ray source at 1253.6 eV, with an energy resolution of 0.8 eV. Reported XPS peaks were calibrated to the adventitious carbon peak in the C 1s region at 284.8 eV.2.5 Thermoelectric measurements
Film resistance of 8 × 12 mm nanocomposite thin films, deposited on PET, were measured using a Signatone Pro 4 four-point probe (Gilroy, CA) connected using a SCB-68 I/O connector block (National Instruments, Austin, TX) to a E3644A DC Power Supply and a 2400 Keithley multimeter (Cleveland, OH) at an operating voltage of 10 V. The probe tips were 0.4 mm in diameter with a separation of 1.0 mm between the tips. The sheet resistance was calculated using Rs = 4.23(V/I), where 4.23 is the correction factor based on the dimensions of the substrate relative to the spacing between the probes.42 Electrical conductivity was found by taking the inverse of the product of the thickness and the sheet resistance. Temperature-dependent resistance data were acquired using a commercial Dynacool Physical Property Measurement System (PPMS) (Quantum Design, San Diego, CA) using a four-point probe setup. The resistivity was calculated by multiplying the measured resistance by the ratio of the area divided by the length of the sample. The inverse of the resistivity is the electrical conductivity of the sample. Temperature-dependent carrier densities were acquired by Hall effect measurements in a van der Pauw geometry using the same PPMS Dynacool instrument, with a magnetic field of ±3 T and an electrical current of 500 μA. Carrier mobility values were acquired by using: σ = neμ, where σ is the electrical conductivity (S cm−1), n is the carrier concentration (cm−3), e is the elementary charge (C), and μ is the carrier mobility (cm2 V−1 s−1). The Seebeck coefficient was measured with a home-built setup using a previously reported method.15,43 The thermoelectric voltage across the film was measured at eight different temperature differentials between 0 and 10 K. Reported Seebeck coefficients came from the slope of the linear fit to the voltage vs. temperature gradient across the film, with its y-intercept fixed at 0 V. The correlation coefficient for each linear fit was at least 0.99.3. Results and discussion
Fig. 1a shows the layer-by-layer deposition process used in this study, as well as an illustration of the resulting multilayer film. Fig. 1b shows the chemical structures of the ingredients used to prepare these films. LbL films comprised of PDDA and PEDOT:PSS–DWNT were used as a model system that has exhibited excellent thermoelectric behavior.15,16,44 PEDOT:PSS was used as a conductive constituent and anionic polymer surfactant to effectively disperse DWNT in water. KBr was chosen as a dopant for this system due to its prevalence in polyelectrolyte multilayer, its study in LbL-assembled films, and its larger atomic size of K+ relative to Na+.26,37 Larger salt ions have a larger doping efficiency on polyelectrolyte multilayers due to their effects on the surrounding water structure.25,26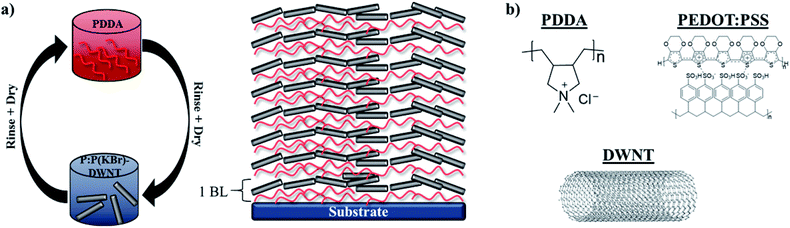 | ||
| Fig. 1 (a) Schematic of layer-by-layer deposition and (b) chemical structures of each major film component. | ||
The influence of KBr concentration on the growth of PDDA/PEDOT:PSS (KBr)–DWNT films is shown in Fig. 2a. Doping PEDOT:PSS with KBr results in thicker films as compared to the undoped control due to salt-induced charge screening. In the preparation of polyelectrolyte multilayers, salt is used to screen charged repeat units, which requires more polymer to overcompensate the surface charge of the previously deposited layer and results in thicker films.25,26,45 Interestingly, adding more KBr to the PEDOT:PSS–DWNT solution decreases film thickness, which may be due to PSS being removed from solution after centrifuging. Previous reports have shown that when PEDOT:PSS films are treated with a salt or ionic liquid, PEDOT and PSS disassociate from one another due to an ion exchange reaction (KBr + PEDOT:PSS → K:PSS + PEDOT:Br), which results in PSS removal.37,38,46 Furthermore, increasing the amount of KBr results in larger refractive indices (Fig. 2b). The decreased film thickness coupled with a larger refractive index, with increasing the amount of KBr, suggest greater film density.47
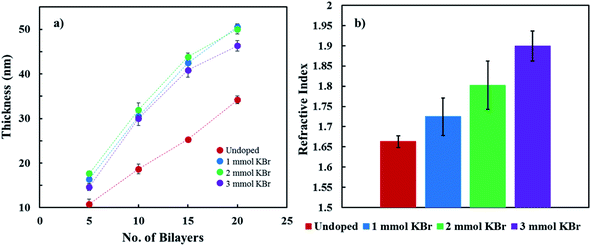 | ||
| Fig. 2 (a) Film thickness as a function of bilayers deposited, with varying KBr concentration. (b) Refractive index of 20 BL films as a function of KBr concentration. | ||
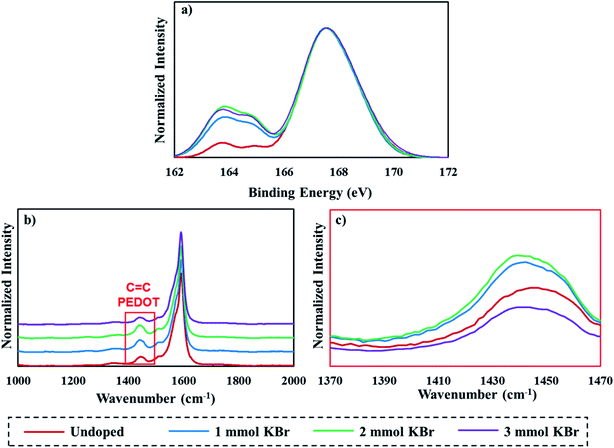
Raman and XPS S 2p spectra were collected to probe any variations in film composition. XPS measurements conducted on PEDOT:PSS result in two peaks that correspond to the different local bonding environments of sulfur (the thiophene ring in PEDOT (∼163.9 eV) and the sulfonate group in PSS (∼167.6 eV)).48–50 Normalized XPS spectra of 20 BL films show that an increase in the PEDOT:PSS ratio is achieved with the addition of KBr (Fig. 3a). Some PSS is being removed during centrifugation due to the ion exchange reaction between PEDOT:PSS and KBr. This observation is consistent with the thickness data, and may account for the steadily decreasing thickness as a function of KBr concentration. The maximum PEDOT:PSS ratio is achieved with 2 mmol KBr. Adding 3 mmol KBr does not substantially change the PEDOT:PSS ratio in the film, which suggests the changes in film thickness and density are due to a different amount of DWNT.
Raman spectra normalized to the G band (∼1590 cm−1) of DWNT gathered on 20 BL films are shown in Fig. 3b. The peak near 1430 cm−1 corresponds to the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C symmetric stretch in PEDOT, so these spectra compare the relative amounts of DWNT to PEDOT.51 The amount of PEDOT relative to DWNT gradually increases and reaches a maximum proportion at 2 mmol KBr, but then drastically decreases when comparing the 2 mmol to 3 mmol KBr-doped samples, indicating that a greater proportion of DWNT is deposited relative to PEDOT:PSS in tandem with an increase in film density (Fig. 2b, 3b and c). It is noteworthy that increasing the KBr concentration from 3 mmol to 4 mmol KBr results in a lower PEDOT:PSS ratio, but a higher amount of DWNT relative to PEDOT (Fig. S1†), which suggests that much less PEDOT:PSS is incorporated in the film than the other KBr-doped films.
C symmetric stretch in PEDOT, so these spectra compare the relative amounts of DWNT to PEDOT.51 The amount of PEDOT relative to DWNT gradually increases and reaches a maximum proportion at 2 mmol KBr, but then drastically decreases when comparing the 2 mmol to 3 mmol KBr-doped samples, indicating that a greater proportion of DWNT is deposited relative to PEDOT:PSS in tandem with an increase in film density (Fig. 2b, 3b and c). It is noteworthy that increasing the KBr concentration from 3 mmol to 4 mmol KBr results in a lower PEDOT:PSS ratio, but a higher amount of DWNT relative to PEDOT (Fig. S1†), which suggests that much less PEDOT:PSS is incorporated in the film than the other KBr-doped films.
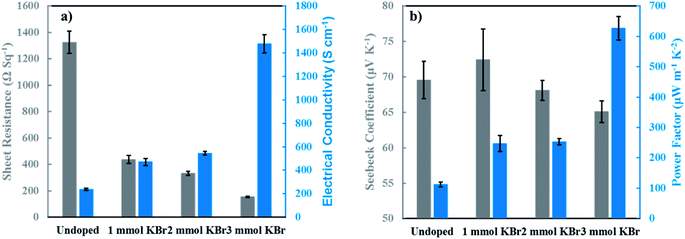
Thermoelectric properties were evaluated as a function of KBr concentration to investigate how the amount of dopant affects thermoelectric performance. Fig. 4a shows the sheet resistance and electrical conductivity acquired at room temperature. The electrical conductivity of the undoped sample increases from 238 ± 10 S cm−1 to 471 ± 30 S cm−1 after adding 1 mmol KBr. The conductivity at 2 mmol KBr increases modestly to 544 ± 15 S cm−1. The maximum conductivity of 1479 ± 78 S cm−1 is achieved with 3 mmol KBr, which is ∼6× larger than the undoped control. This improvement is attributed to a large increase in the carrier density (Fig. S2.†). It should be noted that adding 4 mmol KBr results in a lower electrical conductivity value of 1068 ± 28 S cm−1, which is likely due to the lower amount of PEDOT and PSS in solution to effectively disperse DWNT (Fig, S1, Table S1†). Insufficient PSS in the DWNT solution may lead to excessive bundling, resulting in a lower electrical conductivity.
The Seebeck coefficient and power factor as a function of KBr concentration is shown in Fig. 4b. Interestingly, the maximum Seebeck coefficient of 72 ± 4.4 μV K−1 is achieved at 1 mmol KBr. The value of the Seebeck coefficient steadily decreases at 2 and 3 mmol KBr (68.1 ± 1.4 μV K−1 and 65.1 ± 1.5 μV K−1, respectively). Relatively large Seebeck coefficients for LbL-assembled thermoelectric nanocomposites containing DWNT and graphene have been attributed to increased carrier mobility, but these films used polyaniline as the polycationic component.15,16 Recently, a thermoelectric film using PDDA exhibited an improved Seebeck coefficient due to a greater instantaneous rate of change of the energy-dependent conductivity near EF, even with a slightly lower carrier mobility.43 This observation also resulted in a greater asymmetry in the density of states near EF, which is another established method of increasing the Seebeck coefficient.5 Previous reports for PEDOT:PSS films show an increase in the Seebeck coefficient with the removal of insulating PSS, which has been attributed to an increase in carrier mobility with the decreased π–π stacking distances between PEDOT chains. PSS removal is accompanied by a large increase in carrier density, so the similar Seebeck coefficients observed as a function of KBr concentration may be a result of the increasing energy-dependent electrical conductivity near EF and the increasing carrier density canceling each other out. Increased power factors were observed as a function of KBr concentration due to the improvement in the electrical conductivity. The maximum power factor of 626 ± 39 μW m−1 K−2 is achieved using 3 mmol KBr, which is 6× larger than the undoped control. It is noteworthy that the electrical conductivity improves six-fold with minimal decrease in the Seebeck coefficient, suggesting that this salt doping strategy decouples these parameters.
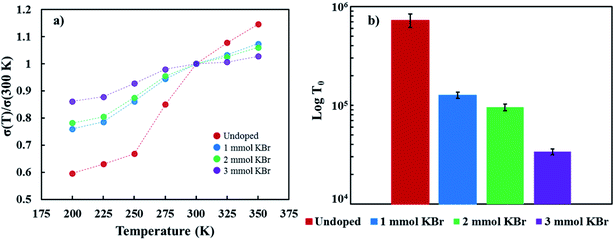
Temperature-dependent electrical conductivity of the KBr-doped samples normalized to the electrical conductivity at 300 K show it increases as temperature increases, indicating a thermally-activated conductivity mechanism (Fig. 5a). Disordered semiconductors containing carbon nanotubes typically follow a 3D variable range hopping (3D VRH) conduction model, where thermal energy assists charge carriers hopping to and from conduction sites.52,53 The 3D VRH model is 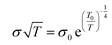 , where σ is the electrical conductivity, T is the absolute temperature, σ0 is a pre-exponential factor, and T0 is the characteristic Mott temperature. T0 directly correlates to the energy barrier for the hopping conduction to occur, where a lower value indicates a lower barrier for electron transport.54,55 Fig. 5a shows that T(σ) exhibits less variation with an increasing KBr concentration. The influence of temperature on electrical conductivity progressively weakens as a function of added KBr dopant. This change in T(σ) is likely due to the greater proportion of DWNT incorporated in the films, as shown in Fig. 3, which is consistent with the gradual increase in carrier density as a function of KBr concentration. The T0 values were calculated from the regression data found from a plot of ln(σ√T) vs. K−0.25 (Fig. S3.†) As more KBr is added, the characteristic Mott temperature gets smaller, likely due to a greater amount of metallic conduction as a result of more DWNT being deposited (Fig. 5b).52
, where σ is the electrical conductivity, T is the absolute temperature, σ0 is a pre-exponential factor, and T0 is the characteristic Mott temperature. T0 directly correlates to the energy barrier for the hopping conduction to occur, where a lower value indicates a lower barrier for electron transport.54,55 Fig. 5a shows that T(σ) exhibits less variation with an increasing KBr concentration. The influence of temperature on electrical conductivity progressively weakens as a function of added KBr dopant. This change in T(σ) is likely due to the greater proportion of DWNT incorporated in the films, as shown in Fig. 3, which is consistent with the gradual increase in carrier density as a function of KBr concentration. The T0 values were calculated from the regression data found from a plot of ln(σ√T) vs. K−0.25 (Fig. S3.†) As more KBr is added, the characteristic Mott temperature gets smaller, likely due to a greater amount of metallic conduction as a result of more DWNT being deposited (Fig. 5b).52
There are additional reasons why varying the proportions of PEDOT, PSS, and DWNT improve thermoelectric behavior. In addition to improving electrical conductivity, KBr addition increases carrier density due to the removal of insulating material (i.e. PSS) in the multilayer film.43 Another contribution to improved thermoelectric performance may be due to the presence of residual Br− as a result of PSS removal in the film that provides additional p-type doping.56 It is also possible that K+ resides closer to carbon nanotubes than Na+, which may provide more potent p-type doping (i.e. greater increase in carrier density) by bringing more oxygen molecules in water closer to the wall of the carbon nanotubes.57 To investigate this notion further, films doped with 3 mmol NaBr were prepared and the TE properties were measured (Fig. S4†). The 20 BL film doped with 3 mmol KBr yields a Seebeck coefficient and an electrical conductivity of 65.1 ± 1.5 μV K−1 and 1479 ± 78 S cm−1, while the same film doped with 3 mmol NaBr yields values of 67.2 ± 1.7 μV K−1 and 464 ± 14 S cm−1. The larger electrical conductivity and slightly lower Seebeck coefficient for the KBr-doped film suggests a greater carrier density relative to the NaBr-doped film.
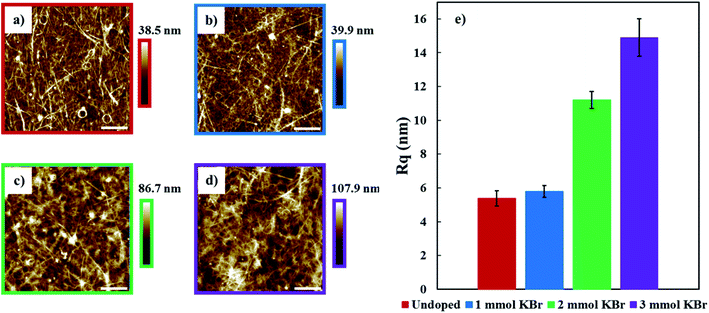
The surface morphology of 20 BL films was measured using AFM in tapping mode (Fig. 6a–d). All of these images show many carbon nanotube bundles that facilitate electron transport. As more KBr is added to these solutions, films with progressively greater surface roughness values are formed. Doping with 1 mmol KBr increases the surface roughness from 5.4 ± 0.5 to 5.8 ± 0.4 nm, relative to the undoped film. Increasing the concentration of KBr to 2 and 3 mmol results in a further increase in surface roughness to 11.2 ± 0.5 and 14.9 ± 1.1 nm, respectively. These rougher surfaces are due to larger DWNT bundles that are the result of having less PSS available to stabilize/disperse the nanotubes in solution. These bundles may contribute to increased electrical conductivity due to the decreased distance between DWNT junctions that facilitates better electron transport, which is suggested by the lower T0 obtained from the 3D VRH model.58
4. Conclusions
Doping PEDOT:PSS with KBr prior to dispersing DWNT, when depositing thin films using layer-by-layer assembly, was investigated. Thermoelectric properties were measured as a function of KBr concentration. A 20 BL PDDA/PEDOT:PSS–DWNT doped with 3 mmol KBr has an electrical conductivity of 1479 ± 78 S cm−1 and a Seebeck coefficient of 65.1 ± 1.5 μV K−1, which translates to a power factor of 626 ± 39 μW m−1 K−2. This is a six-fold improvement in PF relative to the undoped control due to the greater proportion of DWNT that is deposited during film deposition. DWNT content in the film coincides with a reduction in PSS, which also serves to promote greater connectivity amongst PEDOT chains. KBr weakens the strength of interaction between PEDOT and PSS, which allows for a greater amount of conductive PEDOT and DWNT to be deposited. This study demonstrates that salt can be used to tailor the amount of carbon nanotubes that are deposited during LbL assembly, resulting in a larger electrical conductivity without altering the Seebeck coefficient (i.e. these values are decoupled). Future work includes investigating how the size of the alkali metal in the salt dopant affects the thermoelectric properties of this system. This strategy demonstrates another tool for multilayer polymer nanocomposite preparation can be used to prepare high performance, low temperature thermoelectric materials.Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
The authors acknowledge the Texas A&M Engineering Experiment Station, and the Materials Characterization Facility for infrastructural support of this work.References
- W. Liu, X. Yan, G. Chen and Z. Ren, Nano Energy, 2012, 1, 42–56 CrossRef CAS.
- A. B. Little and S. Garimella, Energy, 2011, 36, 4492–4504 CrossRef CAS.
- B. Russ, A. Glaudell, J. J. Urban, M. L. Chabinyc and R. A. Segalman, Nat. Rev. Mater., 2016, 1, 16050 CrossRef CAS.
- J. L. Blackburn, A. J. Ferguson, C. Cho and J. C. Grunlan, Adv. Mater., 2018, 30, 1704386 CrossRef PubMed.
- M. S. Dresselhaus, G. Chen, M. Y. Tang, R. Yang, H. Lee, D. Wang, Z. Ren, J. P. Fleurial and P. Gogna, Adv. Mater., 2007, 19, 1043–1053 CrossRef CAS.
- J. Mao, Z. Liu and Z. Ren, npj Quantum Mater., 2016, 1, 1–9 Search PubMed.
- B. Poudel, Q. Hao, Y. Ma, Y. Lan, A. Minnich, B. Yu, X. Yan, D. Wang, A. Muto, D. Vashaee, X. Chen, J. Liu, M. S. Dresselhaus, G. Chen and Z. Ren, Science, 2008, 320, 634–638 CrossRef CAS PubMed.
- H. Sun, L.-D. Zhao, M. G. Kanatzidis, C. Wolverton, C. Uher, G. Tan, S.-H. Lo, V. P. Dravid and Y. Zhang, Nature, 2014, 508, 373–377 CrossRef PubMed.
- B. Paul, V. Khranovskyy, R. Yakimova and P. Eklund, Mater. Res. Lett., 2019, 7, 239–243 CrossRef CAS.
- B. Paul, J. Lu and P. Eklund, ACS Appl. Mater. Interfaces, 2017, 9, 25308–25316 CrossRef CAS PubMed.
- J. Feng, W. Zhu, Y. Deng, Q. Song and Q. Zhang, ACS Appl. Energy Mater., 2019, 2, 2828–2836 CrossRef CAS.
- C. Bounioux, P. Díaz-Chao, M. Campoy-Quiles, M. S. Martín-González, A. R. Goñi, R. Yerushalmi-Rozen and C. Müller, Energy Environ. Sci., 2013, 6, 918–925 RSC.
- X. C. Qin Yao, L. Chen, W. Zhang and S. Liufu, ACS Nano, 2010, 4, 2445–2451 CrossRef PubMed.
- H. Wang, S. I. Yi, X. Pu and C. Yu, ACS Appl. Mater. Interfaces, 2015, 7, 9589–9597 CrossRef CAS PubMed.
- C. Cho, B. Stevens, J. H. Hsu, R. Bureau, D. A. Hagen, O. Regev, C. Yu and J. C. Grunlan, Adv. Mater., 2015, 27, 2996–3001 CrossRef CAS PubMed.
- C. Cho, K. L. Wallace, P. Tzeng, J. H. Hsu, C. Yu and J. C. Grunlan, Adv. Energy Mater., 2016, 6, 1502168 CrossRef.
- K. Zhang, Y. Zhang and S. Wang, Sci. Rep., 2013, 3, 3448 CrossRef PubMed.
- J. C. G. F. Xiang, S. M. Ward and T. M. Givens, Soft Matter, 2015, 11, 1001–1007 RSC.
- D. E. Bergbreiter and B. S. Chance, Macromolecules, 2007, 40, 5337–5343 CrossRef CAS.
- Y. T. Park, A. Y. Ham and J. C. Grunlan, J. Phys. Chem. C, 2010, 114, 6325–6333 CrossRef CAS.
- E. M. Saurer, R. M. Flessner, S. P. Sullivan, M. R. Prausnitz and D. M. Lynn, Biomacromolecules, 2010, 11, 3136–3143 CrossRef CAS PubMed.
- G. Decher, Science, 1997, 277, 1232–1237 CrossRef CAS.
- Y. H. Yang, L. Bolling, M. A. Priolo and J. C. Grunlan, Adv. Mater., 2013, 25, 503–508 CrossRef CAS PubMed.
- N. Sakai, G. K. Prasad, Y. Ebina, K. Takada and T. Sasaki, Chem. Mater., 2006, 18, 3596–3598 CrossRef CAS.
- S. T. Dubas and J. B. Schlenoff, Macromolecules, 1999, 32, 8153–8160 CrossRef CAS.
- J. Borges and J. F. Mano, Chem. Rev., 2014, 114, 8883–8942 CrossRef CAS PubMed.
- C. Cho, M. Culebras, K. L. Wallace, Y. Song, K. Holder, J. H. Hsu, C. Yu and J. C. Grunlan, Nano Energy, 2016, 28, 426–432 CrossRef CAS.
- O. Bubnova, Z. U. Khan, H. Wang, S. Braun, D. R. Evans, M. Fabretto, P. Hojati-Talemi, D. Dagnelund, J. B. Arlin, Y. H. Geerts, S. Desbief, D. W. Breiby, J. W. Andreasen, R. Lazzaroni, W. M. Chen, I. Zozoulenko, M. Fahlman, P. J. Murphy, M. Berggren and X. Crispin, Nat. Mater., 2014, 13, 190–194 CrossRef CAS PubMed.
- K. Choi, S. L. Kim, S. I. Yi, J. H. Hsu and C. Yu, ACS Appl. Mater. Interfaces, 2018, 10, 23891–23899 CrossRef CAS PubMed.
- R. Piramuthu Raja Ashok, M. S. Thomas and S. Varughese, Soft Matter, 2015, 11, 8441–8451 RSC.
- J. Luo, D. Billep, T. Blaudeck, E. Sheremet, R. D. Rodriguez, D. R. T. Zahn, M. Toader, M. Hietschold, T. Otto and T. Gessner, J. Appl. Phys., 2014, 115, 054908 CrossRef.
- S. Liu, H. Deng, Y. Zhao, S. Ren and Q. Fu, RSC Adv., 2015, 5, 1910–1917 RSC.
- A. M. Nardes, M. Kemerink, R. A. J. Janssen, J. A. M. Bastiaansen, N. M. M. Kiggen, B. M. W. Langeveld, A. J. J. M. Van Breemen and M. M. De Kok, Adv. Mater., 2007, 19, 1196–1200 CrossRef CAS.
- G. H. Kim, L. Shao, K. Zhang and K. P. Pipe, Nat. Mater., 2013, 12, 719–723 CrossRef CAS PubMed.
- J. Luo, D. Billep, T. Waechtler, T. Otto, M. Toader, O. Gordan, E. Sheremet, J. Martin, M. Hietschold, D. R. T. Zahn and T. Gessner, J. Mater. Chem. A, 2013, 1, 7576–7583 RSC.
- Z. Fan, P. Li, D. Du and J. Ouyang, Adv. Energy Mater., 2017, 7, 1602116 CrossRef.
- Z. Fan, D. Du, Z. Yu, P. Li, Y. Xia and J. Ouyang, ACS Appl. Mater. Interfaces, 2016, 8, 23204–23211 CrossRef CAS PubMed.
- Y. Xia and J. Ouyang, Macromolecules, 2009, 42, 4141–4147 CrossRef CAS.
- Y. Marcus, Thermochim. Acta, 1986, 104, 389–394 CrossRef CAS.
- S. Kee, N. Kim, B. S. Kim, S. Park, Y. H. Jang, S. H. Lee, J. Kim, J. Kim, S. Kwon and K. Lee, Adv. Mater., 2016, 28, 8625–8631 CrossRef CAS PubMed.
- D. Gamboa, M. A. Priolo, A. Ham and J. C. Grunlan, Rev. Sci. Instrum., 2010, 81, 036103 CrossRef PubMed.
- F. M. Smits, Bell Syst. Tech. J., 1958, 37, 711–718 CrossRef.
- D. L. Stevens, A. Parra and J. C. Grunlan, ACS Appl. Energy Mater., 2019, 2, 5975–5982 CrossRef CAS.
- Y. T. Park, A. Y. Ham, Y. H. Yang and J. C. Grunlan, RSC Adv., 2011, 1, 662–671 RSC.
- G. Decher and J. B. Schlenoff, Multilayer Thin Films: Sequential Assembly of Nanocomposite Materials, 2nd edn, 2012 Search PubMed.
- A. Mazaheripour, S. Majumdar, D. Hanemann-Rawlings, E. M. Thomas, C. McGuiness, L. D'Alencon, M. L. Chabinyc and R. A. Segalman, Chem. Mater., 2018, 30, 4816–4822 CrossRef CAS.
- Y. Gu, X. Huang, C. G. Wiener, B. D. Vogt and N. S. Zacharia, ACS Appl. Mater. Interfaces, 2015, 7, 1848–1858 CrossRef CAS PubMed.
- E. Jin Bae, Y. Hun Kang, K. S. Jang and S. Yun Cho, Sci. Rep., 2016, 6, 18805 CrossRef PubMed.
- M. Van der Auweraer, P. Andersson, A. Volodin, C. van Haesendonck, M. Berggren, X. Crispin, A. Crispin, W. R. Salaneck, P. C. M. Grim and F. L. E. Jakobsson, Chem. Mater., 2006, 18, 4354–4360 CrossRef.
- X. Crispin, S. Marciniak, W. Osikowicz, G. Zotti, A. W. D. van der Gon, F. Louwet, M. Fahlman, L. Groenendaal, F. D. E. Schryver and W. R. Salaneck, J. Polym. Sci., Part B: Polym. Phys., 2003, 41, 2561–2583 CrossRef CAS.
- S. H. Lee, H. Park, S. Kim, W. Son, I. W. Cheong and J. H. Kim, J. Mater. Chem. A, 2014, 2, 7288–7294 RSC.
- S. Luo, T. Liu, S. M. Benjamin and J. S. Brooks, Langmuir, 2013, 29, 8694–8702 CrossRef CAS PubMed.
- G. Paasch, T. Lindner and S. Scheinert, Synth. Met., 2002, 132, 97–104 CrossRef CAS.
- N. F. Mott and E. A. Davis, Electronic Processes in Non-Crystalline Materials, Clarendon, Oxford, UK, 2nd edn, 1979 Search PubMed.
- P. Nagels, in Amorphous Semiconductors, ed. M. H. Brodsky, Springer Berlin Heidelberg, Berlin, Heidelberg, 1985, pp. 113–158 Search PubMed.
- S. M. Kim, K. K. Kim, Y. W. Jo, M. H. Park, S. J. Chae, D. L. Duong, C. W. Yang, J. Kong and Y. H. Lee, ACS Nano, 2011, 5, 1236–1242 CrossRef CAS PubMed.
- T. A. Pham, S. M. G. Mortuza, B. C. Wood, E. Y. Lau, T. Ogitsu, S. F. Buchsbaum, Z. S. Siwy, F. Fornasiero and E. Schwegler, J. Phys. Chem. C, 2016, 120, 7332–7338 CrossRef CAS.
- J. L. Blackburn, S. D. Kang, M. J. Roos, B. Norton-Baker, E. M. Miller and A. J. Ferguson, Adv. Electron. Mater., 2019, 5, 1800910 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ra00763c |
| This journal is © The Royal Society of Chemistry 2020 |