Open Access Article
Open Access ArticleFast diffusion mechanism in Li4P2S6 via a concerted process of interstitial Li ions†
Andreas R. Stamminger *ab,
Benedikt Ziebartha,
Matous Mrovec
*ab,
Benedikt Ziebartha,
Matous Mrovec b,
Thomas Hammerschmidt
b,
Thomas Hammerschmidt b and
Ralf Drautz
b and
Ralf Drautz b
b
aRobert Bosch GmbH, Corporate Research, 71272, Renningen, Germany. E-mail: andreas.stamminger@de.bosch.com
bRuhr-Universität Bochum, Interdisciplinary Centre for Advanced Materials Simulation, Universitätsstraβe 150, 44801, Bochum, Germany
First published on 13th March 2020
Abstract
The synthesis of Li superionic conductor Li7P3S11 may be accompanied by the formation of a detrimental Li4P2S6 phase due to a high mixing sensitivity of precursor materials. This phase exhibits a poor ionic conductivity whose origins are not fully understood. Recently Dietrich et al. investigated the energetics of Li ion migration in Li4P2S6 with nudged elastic band (NEB) calculations. The observed large migration barrier of 0.51 eV for purely interstitial diffusion leads to an interpretation of the low ionic conductivity by kinetic limitations. Based on ab initio molecular dynamics simulations (AIMD) we propose a new and energetically much more favorable diffusion path available to interstitial Li ion charge carriers that has not been considered so far. It consists of a concerted process in which a second lithium atom is pushed out from its equilibrium lattice position by the diffusing lithium ion. A detailed analysis with NEB calculations shows that the energy barrier for this concerted diffusion is only 0.08 eV, i.e. an order of magnitude lower than the previously reported value for purely interstitial diffusion. Therefore, the observed low ionic conductivity of Li4P2S6 is likely not originating from kinetic limitations due to high diffusion barriers but rather from thermodynamic reasons associated with a low concentration of free charge carriers. We therefore expect that increasing the charge carrier concentration by doping is a viable design route to optimize the ionic conductivity of this material.
1 Introduction
All-solid-state lithium batteries promise to outperform conventional batteries with liquid electrolytes, offering higher power and energy densities while maintaining a high level of safety.2–5 The major task that needs to be accomplished to enable this new technology is a successful development of a suitable solid-state electrolyte (SSE) with a high ionic conductivity.3,6Recently, chalcogenide-based compounds,7–9 such as Li7P3S11, have been identified as the most promising SSE candidate materials.10 A glass-ceramic phase of Li7P3S11 was found to exhibit a remarkably high ionic conductivity of up to 10−3 S cm−1 at room temperature.4,11–14 This glass-ceramic phase can be prepared by a careful heat treatment from a mixture of Li2S and P2S5 precursor materials with a ratio of 70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30.15–17 Moreover, small deviations from this optimal composition lead to a dramatic decrease of ionic conductivity in the resulting materials. For instance, a slightly altered ratio of 67
30.15–17 Moreover, small deviations from this optimal composition lead to a dramatic decrease of ionic conductivity in the resulting materials. For instance, a slightly altered ratio of 67![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 33 leads to the formation of glass-type Li4P2S7. Although synthesized from the same precursors this material shows ionic conductivities of only up to 10−5 S cm−1, i.e., two orders of magnitude below the conductivities reported for Li7P3S11.1,4 An even lower ionic conductivity of about 10−7 S cm−1 at room temperature has been found for the thermodynamically stable Li4P2S6 phase that crystallizes readily from the Li4P2S7 glass phase at elevated temperatures and is associated with a decrease of the sulfur content.4,14,17–21
33 leads to the formation of glass-type Li4P2S7. Although synthesized from the same precursors this material shows ionic conductivities of only up to 10−5 S cm−1, i.e., two orders of magnitude below the conductivities reported for Li7P3S11.1,4 An even lower ionic conductivity of about 10−7 S cm−1 at room temperature has been found for the thermodynamically stable Li4P2S6 phase that crystallizes readily from the Li4P2S7 glass phase at elevated temperatures and is associated with a decrease of the sulfur content.4,14,17–21
As the formation of these detrimental phases is unavoidable during large-scale production (e.g., due to local inhomogeneities in the composition or temperature fluctuations), it is important to understand the origins of their low ionic conductivities. Recent studies showed that the ionic conductivity in several electrolyte materials is primarily determined by the correlated motion of charge carriers. For instance, He et al.22 showed that the diffusion of lithium ions in the high-conducting Li7La3Zr2O12 (LLZO), Li1.3Al0.3Ti1.7(PO4)3 (LATP) and Li10GeP2S12 (LGPS) is mitigated by a complex migration process. They showed that the occupation of high-energy sites by mobile charge carriers induces concerted migration processes with significantly lower migration barriers than direct diffusion between interstitial sites. Similar results for Li2CO3 (ref. 23) and β-Li3PS4 (ref. 24–26) showed that the observed high lithium ion conductivity in these materials can be explained by the simultaneous movement of lithium ions. Likewise, Zhang et al.27 reported a cooperative diffusion mechanism for Na+ ions in Na3Zr2Si2PO12 (NaSICON). Despite these findings of the paramount role of concerted migration in several electrolyte materials, surprisingly, up to now only purely interstitial diffusion processes have been considered in the estimation of migration barriers for Li4P2S6. Only Hood et al.18 already suggested the possible importance of more complex migration paths in this material, involving both interstitial and host lattice ions.
Inspired by this gap in literature and the recent reports on low migration barriers for concerted diffusion in other superionic conductor materials, we investigate the possibility of concerted diffusion of Li ions in the most detrimental, crystalline Li4P2S6 phase. Our theoretical investigation employs extensive first-principles calculations based on density functional theory. We combine ab initio molecular dynamics (AIMD) and the nudged elastic band (NEB) method to obtain an in-depth insight into Li diffusion. While AIMD simulations enable the sampling of a large number of Li migration trajectories in an unbiased way, the NEB calculations provide a detailed and quantitative analysis of minimum energy paths. This combined approach allowed us to identify an additional migration process in Li4P2S6 that cannot be described by independent jumps of a single interstitial or vacancy but rather by concerted interaction of two Li ions.22,28,29 Moreover, the identified process is found to create a two dimensional diffusion network with a low energy barrier, available for all present charge carriers. This finding reveals a high mobility for interstitial lithium ions, in addition to the high mobility found for vacancies by Dietrich et al.,1 ruling out kinetic limitations as reason for the observed low ionic conductivity of Li4P2S6.
The paper is organized as follows. A detailed discussion of the computational methods and parameters is provided in Section 2. The results obtained from our simulations are presented in Section 3 followed by a detailed discussion of the results in Section 4. Finally, we conclude in the last Section 5.
2 Computational methods
2.1 Density functional theory
Our AIMD simulations and NEB calculations were carried out within the framework of density functional theory (DFT)30,31 and managed by the Automated Interactive Infrastructure and Database (AiiDA).32 All DFT simulations were based on the projector augmented wave method (PAW) and performed with the Vienna Ab initio Simulation Package (VASP)33–36 using the supplied PAW potentials.37 To approximate the exchange-correlation functional the Perdew–Burke–Ernzerhof functional38 within the generalized gradient approximation has been chosen.To ensure the validity of our results for the investigated Li4P2S6 structure, we first performed static calculations to converge the total energy of the structure with respect to the plane-wave energy cutoff and the k-point sampling of the Brillouin zone. For a primitive unit cell containing a total of 12 atoms, an energy cutoff of Ecut = 420 eV and a (3 × 3 × 2) k-point mesh are sufficient to converge the total energy to within 0.001 eV per atom. Using the determined cutoff and k-point parameters both the volume and atomic positions of the initial structure were relaxed to obtain an equilibrated configuration for the subsequent NEB and AIMD simulations. To achieve a well relaxed unit cell, tight convergence thresholds of 10−9 eV and 10−4 eV Å−1 have been used for the self-consistency cycle and the forces, respectively.
For the AIMD simulations, the convergence criterion for the total energy was set to 0.01 eV per atom for the sake of computational efficiency. From convergence tests we verified that for a supercell containing 96 atoms, used in our AIMD simulations, a Γ-point only calculation with a plane-wave cutoff of Ecut = 300 eV suffices to fulfill this criterion.
Apart from the validation of the plane-wave cutoff and the k-point sampling, we also used our NEB calculations to test the performance of the available Li/Li_sv pseudo potentials treating 1s-electrons either as core (Li) or valence (Li_sv) electrons. From this benchmark we found that both potentials yield the same results and hence, the computationally less demanding Li pseudo potential was employed in all our calculations.
2.2 Structural properties
The initial crystal structure of Li4P2S6 was constructed based on the P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) 1m space group (cf. Table 1). The resulting structure, shown in Fig. 1, corresponds to a planar arrangement proposed by Dietrich et al.1 based on X-ray diffraction analysis and subsequent Rietveld refinement. After structural optimization of the initial structure, we obtained the lattice constants a = b = 6.108 Å and c = 6.602 Å that agree well with the experimentally obtained lattice constants of a = b =(6.0773 ± 0.0005) Å and c =(6.5985 ± 0.0006) Å.1 Dietrich et al. have identified three possible interstitial sites for Li ions in this structure type, among which the ‘1b’ Wyckoff position (see Fig. 1) was found to be energetically most favorable. Based on this analysis, we therefore assumed the ‘1b’ Wyckoff sites to be the most sensible initial position for additional Li ions in our AIMD and NEB simulations of interstitial Li migration.
1m space group (cf. Table 1). The resulting structure, shown in Fig. 1, corresponds to a planar arrangement proposed by Dietrich et al.1 based on X-ray diffraction analysis and subsequent Rietveld refinement. After structural optimization of the initial structure, we obtained the lattice constants a = b = 6.108 Å and c = 6.602 Å that agree well with the experimentally obtained lattice constants of a = b =(6.0773 ± 0.0005) Å and c =(6.5985 ± 0.0006) Å.1 Dietrich et al. have identified three possible interstitial sites for Li ions in this structure type, among which the ‘1b’ Wyckoff position (see Fig. 1) was found to be energetically most favorable. Based on this analysis, we therefore assumed the ‘1b’ Wyckoff sites to be the most sensible initial position for additional Li ions in our AIMD and NEB simulations of interstitial Li migration.
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) 1m space group. The internal coordinates x, y and z are given in units of the lattice constants
1m space group. The internal coordinates x, y and z are given in units of the lattice constants
| Species | Wyckoff | x | y | z |
|---|---|---|---|---|
| Li1 | 2c | 0.3333 | 0.6667 | 0.0 |
| Li2 | 2d | 0.6667 | 0.3333 | 0.5 |
| P | 2e | 0.0 | 0.0 | 0.1715 |
| S | 6k | 0.3237 | 0.0 | 0.25 |
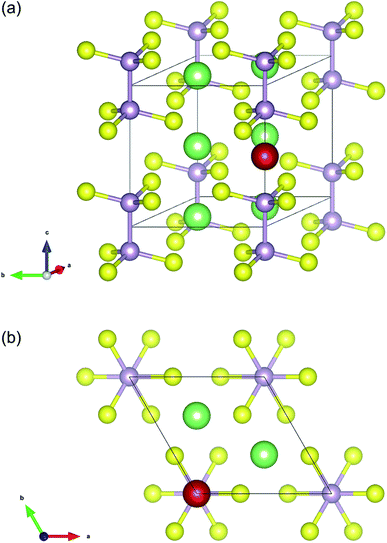 | ||
| Fig. 1 Unit cell structure of Li4P2S6 with constituent atoms placed according to the Wyckoff positions defined in Table 1 (P: light purple, S: yellow, Li: green). Additionally, a single Li atom (marked in red) was placed at the interstitial ‘1b’ Wyckoff position used as initial position for AIMD and NEB calculations of Li migration. | ||
2.3 Ab initio molecular dynamics calculations
The AIMD simulations were performed in the canonical ensemble (NVT) for a total period of 100 ps or 300 ps (see below) with a step size of 2.0 fs per iteration. To control the temperature of the system, a Nosé–Hoover thermostat39,40 was used, with a temperature rescaling in every 10th iteration step. To decrease spurious interactions between periodic images, all AIMD simulations were carried out using a (2 × 2 × 2) supercell containing 96 atoms that was created from the relaxed, primitive unit cell. In addition, a single lithium ion was added to the supercell at the interstitial ‘1b’ Wyckoff site (see Fig. 1) to initiate the interstitial diffusion process. An excess charge due to the positively charged interstitial Li ion was compensated by adding a constant background charge to the supercell.2.4 Nudged elastic band calculations
The NEB calculations were performed using the same supercell size as that in the AIMD simulations. The initial NEB configurations were constructed based on Li migration paths observed in the AIMD simulations (see below). Again, a constant background charge was added to each image to balance the excess charge of the interstitial Li ion. Energy barriers along the migration paths were calculated using the NEB climbing image method implemented in the VASP Transition State Tools package.41,42 All NEB calculations were done for a fixed cell shape and volume. Punctual tests with full relaxation of the cell showed only small differences for the diffusion barriers of the order of 10 meV. These constraints together with a collective NEB relaxation (equidistant spacing between images) significantly slow down the convergence of forces. To counter this slowdown we performed NEB calculations using a reduced force-convergence threshold of 0.02 eV Å−1. To verify our settings we repeated the NEB calculations for the pure interstitial and vacancy diffusion paths of Dietrich et al.1 We find excellent agreement with the published results as shown in the ESI Fig. S2 and S3.†3 Results
The AIMD simulations were carried out for temperatures ranging from 300 K up to 1000 K using the setup discussed in Section 2. To evaluate the diffusion, the mean squared displacement MSD(Li)(t) of lithium atoms was calculated. The diffusion coefficient D may then be estimated from the slope of MSD(Li)(t)
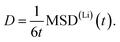 | (1) |
The mean squared displacements obtained from 100 ps AIMD simulations at temperatures between 400 K and 500 K, shown in Fig. 2, exhibit several discontinuities corresponding to Li migration events. Such a step-like behavior adds a large uncertainty to the evaluation of the average MSD(Li)(t) values. To obtain more reliable results we increased the number of migration events recorded in the AIMD trajectories. To this end, we performed AIMD simulations at elevated temperatures ranging from 800 K to 1000 K to sample a larger number of migration events in our trajectories. To reduce statistical noise, the total simulation time was increased to 300 ps for the calculations. However, despite the larger temperatures and the simulation time being tripled, the recorded MSD(Li)(t) dependencies still show sizable fluctuations (see ESI Fig. S1†).
 | ||
| Fig. 2 Mean squared displacements obtained from AIMD simulations between 400 K and 500 K. Only few migration events corresponding to the discontinuities are observed. | ||
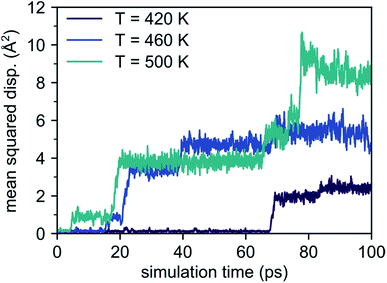
The reason for this behavior is found from analyzing the MSD components along the directions of the crystal axes. From this analysis, we obtain information about the anisotropy of Li migration, which is shown in Fig. 3 for the AIMD simulation at 1000 K. This decomposition reveals that there is no diffusion component in the [001]-direction, i.e. the Li diffusion is purely two-dimensional and confined to the {001} planes only. This strong anisotropy greatly reduces the number of migrating lithium ions only to those located in the {002} planes, where also the additional Li atom was added (cf. Fig. 1). As a consequence, only 9 out of the total of 33 Li ions in the supercell contribute to the MSD, enhancing statistical noise.
 | ||
| Fig. 3 MSD components along the [100], [010] and [001] lattice directions (cf. Fig. 1) obtained from an AIMD simulation at 1000 K. | ||
 | ||
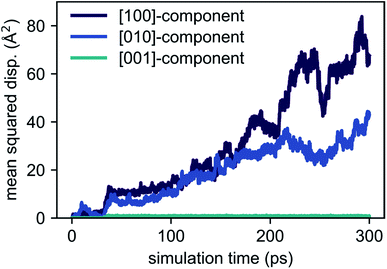
| Fig. 4 Temperature dependence of Li diffusivity in Li4P2S6 obtained from AIMD simulation data following eqn (1). Linear regression gives a low activation energy of about 200 meV for lithium migration. | ||
To get a rough estimate for the activation barrier from the MSD data we assume an equilibration time of 10 ps. For a better statistical significance we split the remaining total MSD evaluation into 10 sub-samples MSD(Li)i(τ) with a length of τ = 29 ps for each sample. Diffusivities for the mobile lithium ions are then obtained from linear regression to the averaged MSD dependence
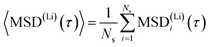 | (2) |
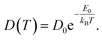 | (3) |
Based on our simulation results, we estimate the corresponding activation barrier for Li interstitial diffusion in Li4P2S6 to be EAIMDa = (200 ± 50) meV, with prefactor D0 = 6.1 × 10−5 cm2 s−1.
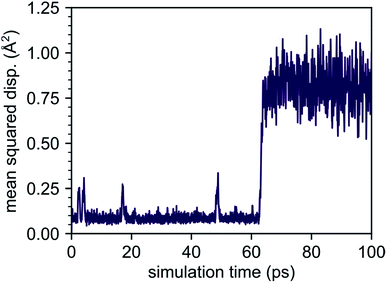
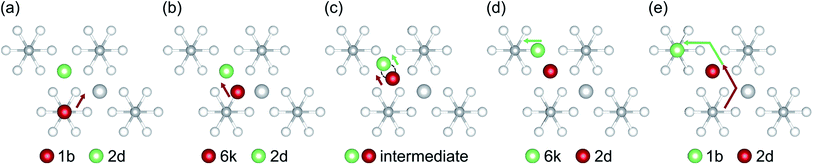
Although our AIMD simulations at lower temperatures are not reliable for extraction of diffusion data, the small number of migration events makes these AIMD trajectories valuable for tracking and in-depth analysis of the underlying migration paths. To this end, we further analyzed the MSD dependence recorded at 310 K, shown in Fig. 5. In this AIMD simulation, only a single jump event occurred during the 100 ps run, greatly simplifying the task of identifying the underlying processes and tracking the corresponding migration path. Our analysis reveals a migration of the interstitial Li ion between two ‘1b’ Wyckoff positions, that cannot be described entirely by independent migration events of a single Li ion. Instead, the complete process is composed of several subsequent steps. In the first step, an interstitial Li ion migrates from its initial ‘1b’ Wyckoff position to an intermediate ‘6k’ Wyckoff position. This is followed by the knock-out of a bound lithium atom from its ‘2d’ Wyckoff position (Li2, cf. Table 1) to another ‘6k’ site (shown schematically in Fig. 6), and the incorporation of the migrating ion into the vacated ‘2d’ site. In the last step, the released lithium ion migrates to a nearest interstitial ‘1b’ Wyckoff position that is energetically most favorable.
To explore the energetics of this migration mechanism, we analyzed the whole pathway using the NEB method. For the NEB calculation, the complete migration process was divided into three segments. The first segment corresponds to the migration of the interstitial Li ion from its initial ‘1b’ Wyckoff site to a neighboring ‘6k’ Wyckoff site as shown in Fig. 6a and b. The second segment deals with the actual concerted process displayed in Fig. 6b–d. The final migration of the displaced lattice ion to the next ‘1b’ Wyckoff position corresponds to Fig. 6d and e. The computed minimum energy path (MEP) is shown in Fig. 7. It is symmetric, as expected from the geometry of the Li4P2S6 crystal structure, and contains two local minima corresponding to configurations where the diffusing Li ion occupies the ‘6k’ Wyckoff sites. The migration barrier for the forward and backward jumps between the ‘1b’ Wyckoff site and the metastable ‘6k’ Wyckoff site is about 80 meV and 40 meV, respectively. The barrier associated with the concerted process is symmetric with a height of about ENEBconcerted = 80 meV. The overall barrier for the complete migration process equals to ENEBa = 120 meV and is significantly lower compared to previously reported barriers for purely interstitial diffusion (see Fig. 8 for a direct comparison).
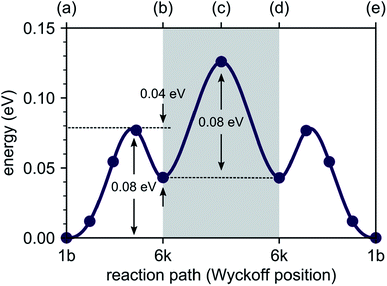 | ||
| Fig. 7 Energy profile of an interstitial lithium ion migrating between the most stable interstitial positions at the ‘1b’ Wyckoff sites via the ‘6k’ Wyckoff sites. The energy barrier necessary to trigger the concerted process, allowing for migration between different P2S6 structures, is shown within the gray box (data points annotated by (a), (b), (c), (d) and (e) correspond to the intermediate structures shown in Fig. 6). | ||
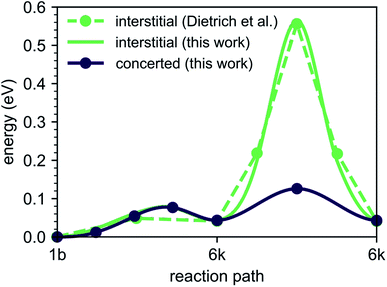 | ||
| Fig. 8 Energy barriers for the diffusion path ‘1b’–‘6k’–‘6k’ with and without the concerted process calculated in this work compared to available literature results for purely interstitial diffusion. | ||
4 Discussion
Our AIMD simulations revealed a concerted migration mechanism for interstitial Li ions in the {001} plane of crystalline Li4P2S6. This mechanism can be divided into three subsequent steps: the first step is characterized by local jumps of an interstitial Li ion from its most stable ‘1b’ Wyckoff position to one of the surrounding, metastable ‘6k’ Wyckoff sites. In the second step, the migrating interstitial ion knocks out a Li atom from a neighboring ‘2d’ Wyckoff lattice site and takes its position. Finally, in the third step, the ejected Li ion migrates from the metastable ‘6k’ to the most stable ‘1b’ Wyckoff position. Hence, the complete concerted process results in a 2D diffusion of Li interstitials in between the stacked P2S6 structural units of Li4P2S6.By analyzing the process using NEB calculations, we found similar activation barriers of about ENEB1b–6k = ENEBconcerted = 80 meV for the forward ‘1b’ → ‘6k’ interstitial jump and the ‘6k’ → ‘2d’ concerted process. However, since the ‘6k’ interstitial site is energetically less favorable than the ‘1b’ site, the migration barrier for the first jump is not symmetric (cf. Fig. 7). As the backward ‘6k’ → ‘1b’ jump is associated with a barrier of only 40 meV, i.e., about half of that for the forward jump, the probability for backward jumps significantly exceeds that of the forward jumps. It is therefore likely that a single concerted migration event will include a large number of preceding back and fourth jumps between the ‘1b’ and ‘6k’ sites. This presumption is fully consistent with our AIMD simulations. In Fig. 5 four smaller peaks, corresponding to the jumps between ‘1b’ and ‘6k’ Wyckoff sites, are visible between 0.0 and 60.0 ps before a concerted process happens at about 62.0 ps.
Our predicted activation barrier of ENEB1b–6k = 80 meV for the ‘1b’ → ‘6k’ migration is in excellent agreement with the result found by Dietrich et al.1 However, the energy barrier for the complete process of concerted diffusion (see Fig. 6) of about ENEBa = 120 meV is much lower than the energy barrier of about 500 meV for the in-plane Li migration found in their work.1 This difference can be attributed to the two distinct migration mechanisms. The barrier investigated by Dietrich et al. corresponds to a direct interstitial jump between two ‘6k’ sites, where the migrating Li ion has to pass between two closely-spaced Li atoms occupying the ‘2d’ lattice sites. Due to strong steric and Coulombic interactions the corresponding barrier is significantly higher than the barrier associated with the concerted mechanism investigated in this work. The low energy barrier of the concerted process is consistent with the low estimated activation energy of EAIMDa = (200 ± 50) meV derived directly from our AIMD simulations (cf. Fig. 4).
Our study illustrates limitations in predicting diffusion properties based solely on NEB calculations since these are usually restricted to anticipated migration mechanisms. Based on AIMD simulations, we were able to show that Li4P2S6 features concerted interstitial migration leading to a low energy barrier compared to purely interstitial migration.
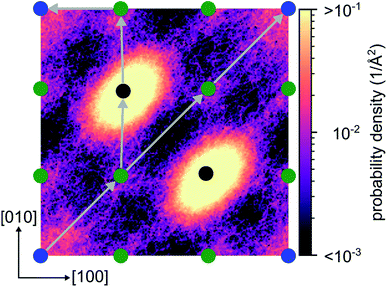
From the energy barriers obtained by our NEB calculations, we assume that migration paths enabling long range 2D diffusion with low activation barriers exist in crystalline Li4P2S6. To support this assumption we analyze the lithium probability density calculated from the AIMD simulation at 1000 K. The calculated distribution of lithium ions shows a 2D diffusion network of adjacent Wyckoff ‘1b’ sites connected by the concerted migration process. Furthermore, a negligible probability is found for the passage of an interstitial lithium ion through two neighboring Wyckoff ‘2d’ positions (see diagonal path in Fig. 9). This confirms that the correlated jumps, described in this work, are the dominant migration process while purely interstitial migration remains inactive even at elevated temperatures due to their associated large activation barriers.
Assuming an Arrhenius behavior over the whole temperature range, we estimate the room temperature diffusivity to D(300 K) ≈ 3.2 × 10−8 cm2 s−1. If we consider the interstitial Li ions to be the only active charge carriers, the theoretical room temperature conductivity amounts to σ(300 K) ≈ 1.2 × 10−4 S cm−1. This value is only one order of magnitude less than the experimentally determined room temperature conductivity of the super-ionic conductor Li7P3S11 (σexp0(300 K) ≈ 3.2 × 10−3 S cm−1 corresponding to an activation barrier of about Eexpa ≈ 0.19 eV (ref. 12 and 17)). However, this is in sharp contrast to the low conductivities measured for crystalline Li4P2S6.1,4,18 This large discrepancy may have several reasons. As mentioned above, the fast diffusion channels are limited to the {001} planes only forming a 2D diffusion network. In addition, the estimated theoretical conductivity implies a large charge carrier concentration of about 9.7 × 10−4 mol cm−3. However, this required charge carrier concentration cannot be reached naturally due to the large formation energy of about 1.0 eV for Frenkel defects in Li4P2S6 (ref. 1 and 44) suppressing an efficient formation of free charge carriers. Hence, even though migration paths with low activation barrier exist in crystalline Li4P2S6, its ionic conductivity is ultimately controlled by thermodynamics leading to an intrinsically small charge carrier concentration. A possible remedy to this problem could be to increase the amount of interstitial Li ions artificially by aliovalent doping of Li4P2S6, which may be subject of a future work. This would bypass the problem of the intrinsically low defect concentration and would allow to exploit the discovered low energy migration path to increase the ionic conductivity of the material.
5 Conclusion
In this work, we investigated the diffusion properties of interstitial Li ions in crystalline Li4P2S6 which occurs as a secondary phase in sulfidic solid-state electrolytes of all-solid-state batteries. Using combined AIMD and NEB simulations we identified a concerted migration mechanism that is associated with a small energy barrier of about 0.12 eV. Our findings show that interstitial diffusion via concerted migration is the most probable diffusion path in this material. With this finding, we attribute the experimentally observed low ionic conductivity of Li4P2S6 to thermodynamic origins rather than kinetic limitations of diffusion. Therefore, bypassing the large defect formation enthalpy in Li4P2S6 by engineering the concentration of interstitial Li ions, this mechanism has the potential to greatly improve the ionic conductivity of this material.Conflicts of interest
There are no conflicts to declare.References
- C. Dietrich, M. Sadowski, S. Sicolo, D. A. Weber, S. J. Sedlmaier, K. S. Weldert, S. Indris, K. Albe, J. Janek and W. G. Zeier, Local Structural Investigations, Defect Formation, and Ionic Conductivity of the Lithium Ionic Conductor Li4P2S6, Chem. Mater., 2016, 28, 8764–8773 CrossRef CAS.
- J. Janek and W. Zeier, A solid future for battery development, Nat. Energy, 2016, 1, 16141 CrossRef.
- A. Sakuda, A. Hayashi and M. Tatsumisago, Sulfide solid electrolyte with favorable mechanical property for all-solid-state lithium battery, Sci. Rep., 2013, 3, 2261 CrossRef PubMed.
- M. Tatsumisago, F. Mizuno and A. Hayashi, All-solid-state lithium secondary batteries using sulfide-based glass-ceramic electrolytes, J. Power Sources, 2006, 159, 193–199 CrossRef CAS.
- Y. Kato, S. Hori, T. Saito, K. Suzuki, M. Hirayama, A. Mitsui, M. Yonemura, H. Iba and R. Kanno, High-power all-solid-state batteries using sulfide superionic conductors, Nat. Energy, 2016, 1, 16030 CrossRef CAS.
- K. Takada, Progress and prospective of solid-state lithium batteries, Acta Mater., 2013, 61, 759–770 CrossRef CAS.
- A. Hayashi, S. Kama, F. Mizuno, K. Tadanaga, T. Minami and M. Tatsumisago, Characterization of Li2S-P2S5 glass-ceramics as a solid electrolyte for lithium secondary batteries, Solid State Ionics, 2004, 175, 683–686 CrossRef CAS.
- S. Ujiie, A. Hayashi and M. Tatsumisago, Structure, ionic conductivity and electrochemical stability of Li2S-P2S5-LiI glass and glass-ceramic electrolytes, Solid State Ionics, 2012, 211, 42–45 CrossRef CAS.
- D. Liu, W. Zhu, Z. Feng, A. Guerfi, A. Vijh and K. Zaghib, Recent progress in sulfide-based solid electrolytes for Li-ion batteries, Mater. Sci. Eng., B, 2016, 213, 169–176 CrossRef CAS.
- M. Tatsumisago and A. Hayashi, Sulfide Glass-Ceramic Electrolytes for All-Solid-State Lithium and Sodium Batteries, Int. J. Appl. Glass Sci., 2014, 5, 226–235 CrossRef CAS.
- K. Mori, K. Enjuji, S. Murata, K. Shibata, Y. Kawakita, M. Yonemura, Y. Onodera and T. Fukunaga, Direct observation of fast lithium-ion diffusion in a superionic conductor: Li7P3S11 metastable crystal, Phys. Rev. Appl., 2015, 4, 54008 CrossRef.
- F. Mizuno, A. Hayashi, K. Tadanaga and M. Tatsumisago, New, highly ion-conductive crystals precipitated from Li2S-P2S5 glasses, Adv. Mater., 2005, 17, 918–921 CrossRef CAS.
- F. Mizuno, A. Hayashi, K. Tadanaga and M. Tatsumisago, New lithium-ion conducting crystal obtained by crystallization of the Li2S-P2S5 glasses, Electrochem. Solid-State Lett., 2005, 8, A603–A606 CrossRef CAS.
- K. Minami, A. Hayashi and M. Tatsumisago, Preparation and characterization of superionic conducting Li7P3S11 crystal from glassy liquids, J. Ceram. Soc. Jpn., 2010, 118, 305–308 CrossRef CAS.
- Y. Seino, M. Nakagawa, M. Senga, H. Higuchi, K. Takada and T. Sasaki, Analysis of the structure and degree of crystallisation of 70Li2S-30P2S5 glass ceramic, J. Mater. Chem. A, 2015, 3, 2756–2761 RSC.
- Y. Seino, T. Ota, K. Takada, A. Hayashi and M. Tatsumisago, A sulphide lithium super ion conductor is superior to liquid ion conductors for use in rechargeable batteries, Energy Environ. Sci., 2014, 7, 627–631 RSC.
- F. Mizuno, A. Hayashi, K. Tadanaga and M. Tatsumisago, High lithium ion conducting glass-ceramics in the system Li2S-P2S5, Solid State Ionics, 2006, 177, 2721–2725 CrossRef CAS.
- Z. D. Hood, C. Kates, M. Kirkham, S. Adhikari, C. Liang and N. Holzwarth, Structural and electrolyte properties of Li4P2S6, Solid State Ionics, 2016, 284, 61–70 CrossRef CAS.
- H. Eckert, Z. Zhang and J. Kennedy, Structural Transformation of Non-Oxide Chalcogenide Glasses. The Short-Range Order of Li2S-P2S5 Glasses Studied by Quantitative 31P and 6, 7Li High-Resolution Solid-State NMR, Chem. Mater., 1990, 2, 273–279 CrossRef CAS.
- A. Hayashi, K. Minami and M. Tatsumisago, Development of sulfide glass-ceramic electrolytes for all-solid-state lithium rechargeable batteries, J. Solid State Electrochem., 2010, 14, 1761–1767 CrossRef CAS.
- R. Mercier, J. Malugani, B. Fahys, J. Douglande and G. Robert, Synthese, structure cristalline et analyse vibrationnelle de l'hexathiohypodiphosphate de lithium Li4P2S6, J. Solid State Chem., 1982, 43, 151–162 CrossRef CAS.
- X. He, Y. Zhu and Y. Mo, Origin of fast ion diffusion in super-ionic conductors, Nat. Commun., 2017, 8, 15893 CrossRef CAS PubMed.
- Y. Yang, Q. Wu, Y. Cui, Y. Chen, S. Shi, R.-Z. Wang and H. Yan, Elastic Properties, Defect Thermodynamics, Electrochemical Window, Phase Stability, and Li+ Mobility of Li3PS4: Insights from First-Principles Calculations, ACS Appl. Mater. Interfaces, 2016, 8, 25229–25242 CrossRef CAS PubMed.
- S. Shi, P. Lu, Z. Liu, Y. Qi, L. G. Hector, H. Li and S. J. Harris, Direct Calculation of Li-Ion Transport in the Solid Electrolyte Interphase, J. Am. Chem. Soc., 2012, 134, 15476–15487 CrossRef CAS PubMed.
- S. Shi, Y. Qi, H. Li and L. G. Hector, Defect Thermodynamics and Diffusion Mechanisms in Li2CO3 and Implications for the Solid Electrolyte Interphase in Li-Ion Batteries, J. Phys. Chem. C, 2013, 117, 8579–8593 CrossRef CAS.
- S. Shi, J. Gao, Y. Liu, Y. Zhao, Q. Wu, W. Ju, C. Ouyang and R. Xiao, Multi-scale computation methods: their applications in lithium-ion battery research and development, Chin. Phys. B, 2015, 25, 18212 CrossRef.
- Z. Zhang, Z. Zou, K. Kaup, R. Xiao, S. Shi, M. Avdeev, Y. Hu, D. Wang, B. He, H. Li, X. Huang, L. F. Nazar and L. Chen, Correlated Migration Invokes Higher Na+-Ion Conductivity in NaSICON-Type Solid Electrolytes, Adv. Energy Mater., 2019, 9, 1902373 CrossRef CAS.
- W. Richards, Y. Wang, L. Miara, J. Kim and G. Ceder, Design of Li1+2xZn1–xPS4, a new lithium ion conductor, Energy Environ. Sci., 2016, 9, 3272–3278 RSC.
- B. Lang, B. Ziebarth and C. Elsässer, Lithium Ion Conduction in LiTi2(PO4)3 and Related Compounds Based on the NASICON Structure: A First-Principles Study, Chem. Mater., 2015, 27, 5040–5048 CrossRef CAS.
- P. Hohenberg and W. Kohn, Inhomogeneous electron gas, Phys. Rev., 1964, 136, B864–B871 CrossRef.
- W. Kohn and L. Sham, Self-consistent equations including exchange and correlation effects, Phys. Rev., 1965, 140, A1133–A1138 CrossRef.
- G. Pizzi, A. Cepellotti, R. Sabatini, N. Marzari and B. Kozinsky, AiiDA: automated interactive infrastructure and database for computational science, Comput. Mater. Sci., 2016, 111, 218–230 CrossRef.
- G. Kresse and J. Hafner, Ab initio molecular dynamics for liquid metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS PubMed.
- G. Kresse and J. Hafner, Ab initio molecular-dynamics simulation of the liquid-metal-amorphous-semiconductor transition in germanium, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251–14269 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Efficiency of ab initio total energy calculations for metals and semiconductors using a plane-wave basis set, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- G. Kresse and D. Joubert, From ultrasoft pseudopotentials to the projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- J. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- S. Nosé, A unified formulation of the constant temperature molecular dynamics methods, J. Chem. Phys., 1984, 81, 511–519 CrossRef.
- W. Hoover, Canonical dynamics: equilibrium phase-space distributions, Phys. Rev. A, 1985, 31, 1695–1697 CrossRef PubMed.
- G. Henkelman, B. Uberuaga and H. Jónsson, Climbing image nudged elastic band method for finding saddle points and minimum energy paths, J. Chem. Phys., 2000, 113, 9901–9904 CrossRef CAS.
- G. Henkelman and H. Jónsson, Improved tangent estimate in the nudged elastic band method for finding minimum energy paths and saddle points, J. Chem. Phys., 2000, 113, 9978–9985 CrossRef CAS.
- X. He, Y. Zhu, A. Epstein and Y. Mo, Statistical variances of diffusional properties from ab initio molecular dynamics simulations, npj Comput. Mater., 2018, 4, 18 CrossRef.
- M. Sadowski, S. Sicolo and K. Albe, Defect thermodynamics and interfacial instability of crystalline Li4P2S6, Solid State Ionics, 2018, 319, 53–60 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ra00932f |
| This journal is © The Royal Society of Chemistry 2020 |