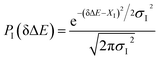Open Access Article
Open Access ArticleTo unravel the connection between the non-equilibrium and equilibrium solvation dynamics of tryptophan: success and failure of the linear response theory of fluorescence Stokes shift†
Xiaofang Wanga,
Jirui Guoa,
Tanping Li *a and
Zhiyi Weib
*a and
Zhiyi Weib
aSchool of Physics and Optoelectronic Engineering, Xidian University, Xi'an, 710071, People's Republic of China. E-mail: tpli@xidian.edu.cn
bBeijing National Laboratory for Condensed Matter Physics, Institute of Physics, Chinese Academy of Sciences, Beijing 100190, China
First published on 13th May 2020
Abstract
The connections between the non-equilibrium solvation dynamics upon optical transitions and the system's equilibrium fluctuations are explored in aqueous liquid. Linear response theory correlates time-dependent fluorescence with the equilibrium time correlation functions. In the previous work [T. Li, J. Chem. Theory Comput., 2017, 13, 1867], Stokes shift was explicitly decomposed into the contributions of various order time correlation functions on the excited state surface. Gaussian fluctuations of the solute–solvent interactions validate linear response theory. Correspondingly, the deviation of the Gaussian statistics causes the inefficiency of linear response evaluation. The above mechanism is thoroughly tested in this study. By employing molecular simulations, multiple non-equilibrium processes, not necessarily initiated from the ground state equilibrium minimum, were examined for tryptophan. Both the success and failure of linear response theory are found for this simple system and the mechanism is analyzed. These observations, assisted by the width dynamics, the initial state linear response approach, and the variation of the solvation structures, integrally verify the virtue of the excited state Gaussian statistics on the dynamics of Stokes shift.
Introduction
Fluorescence Stokes shift is applied extensively to probe solvation dynamics and chemical reactions in aqueous medium.1–6 Photon excitation of a chromophore solute enables charge redistribution from its electronic ground state to the excited state, leading to rotation/diffusional motions of the environmental solvent molecules. The chromophore returns to the ground state emitting fluorescence. The analysis of spectroscopic data reveals the relaxation process of the solvent.7–11 Linear response theory correlates the non-equilibrium dynamics of the system with its equilibrium fluctuations,12 in which the Stokes shift is evaluated by the equilibrium time correlation function of the solute–solvent interactions on the ground or the excited state surface.13–17 Correspondingly, spectroscopic measurements of the Stokes shift enable the assessment of equilibrium solvation dynamics, which is usually difficult by direct experimental observations.The application of linear response theory on Stokes shift has achieved remarkable success.9,13–15,17–22 Nevertheless, the validity of linear response theory is interpreted differently in literatures.23–29 Using the equilibrium properties of the unperturbed surface, the ground state linear response approach is employed in numerous systems.13,15,16,30 This treatment, originating from the perturbation theory,12 assumes the perturbation to be much less than the Boltzmann energy kBT and is often inapplicable for the Stokes shift. Gaussian statistics on the excited state surface ensures the rigorous validity of linear response theory, even though the initial configurations of the non-equilibrium process are far from the equilibrium minimum.25,31 This argument in favour of the excited-state linear response theory has been well-supported by a number of studies. For example, Li's theoretical investigations show the consistent dynamics between the Stokes shift and excited state equilibrium fluctuations for the protein Staphylococcus nuclease, which are clearly different from the ground state equilibrium ones.26,32 Heid et al. have thoroughly tested the ground and excited state linear response theory for different benzene-like solutes and concluded that the ground state linear response approach is not recommended.27,33
Laird and Thompson have previously shown that linear response theory is validated due to the factorizing of the high order time correlation functions into the lower ones.25,31,34 Li and co-workers further explicitly decomposed the total energy shift into the summation of all the time correlation functions.26,35 Whether those orders with the dominant contributions obey the same dynamics as the linear one, as characterized by Gaussian statistics, sets the validity of linear response theory. This mechanism is supported by investigations in the protein.26 In this context, we further examined the linear response for a single tryptophan in aqueous solution using molecular simulations (MD). The fluorescence Stokes shift experiments of tryptophan have been performed extensively.8,36–40 The internal conversion between the two excited state singlets of the tryptophan indole occurs within sub-picoseconds. The lifetime of the chromophore is longer than 500 picoseconds.36 These properties enable tryptophan to be an ideal optical probe to study the hydration dynamics in bulk water and proteins. Molecular dynamics simulations of tryptophan in bulk water were performed owing to the following merits. Firstly, the simulation results can be compared with the experimental results. Furthermore, it is feasible to acquire sufficient sampling data on the configurational space for such a simple system, which is always a bottleneck in the complex proteins. The multiple non-equilibrium MD simulations were designed to propagate on the excited state surface with the initial configurations not necessarily sampled from the ground state equilibrium minimum. The connections with the system's equilibrium statistics were examined to analyze the origin of linear response theory. The remainder of this paper is organized as follows. The descriptions of the theory and the simulation details are firstly presented. The simulation results are shown in the discussions. Finally, the results are summarized in the conclusion session.
Theory and simulation details
In fluorescence experiments, Stokes shift depicts the non-equilibrium ensemble average of the solute–solvent interaction by ΔES(t) = 〈δΔE(t)〉 propagating on the excited state surface, where the initial configurations are sampled over the ground state equilibrium minimum. For each configuration, the solute–solvent interaction is defined as δΔE = β(ΔE(t) − 〈ΔE〉e), where ΔE is the energy difference of the system between the excited and ground state surface, and the bracket 〈⋯〉e represents the average over the excited state equilibrium. The scaling factor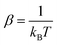 is introduced to enable the interaction δΔE of a dimensionless variable. Due to the equality δΔE(∝) = 0 in the long time limit, the normalized solvation time correlation function is evaluated by
is introduced to enable the interaction δΔE of a dimensionless variable. Due to the equality δΔE(∝) = 0 in the long time limit, the normalized solvation time correlation function is evaluated by 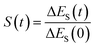 to depict the dynamics of the non-equilibrium relaxation.
to depict the dynamics of the non-equilibrium relaxation.
In literature, Stokes shift is also evaluated by 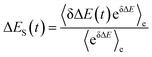 .5,25 By applying Taylor expansion on eδΔE, ΔES(t) is correlated with the various order equilibrium time correlation 〈δΔE(t)δΔE(0)n〉e on the excited state surface. Our previous work further rearranges the time correlation function into26
.5,25 By applying Taylor expansion on eδΔE, ΔES(t) is correlated with the various order equilibrium time correlation 〈δΔE(t)δΔE(0)n〉e on the excited state surface. Our previous work further rearranges the time correlation function into26
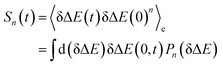 | (1) |
The accumulation 〈δΔE(t)δΔE(0)n〉e is thus converted into an integration over δΔE. δΔE(0,t) is interpreted as follows. For a given value of δΔE, the related configurations are sampled over the excited state equilibrium fluctuations. Upon the evolution of the time interval t, each configuration results in a solute–solvent interaction. δΔE(0,t) is referred to as the average of the above propagated energies. Therefore, δΔE(0,t) relies on both δΔE and time t. The value of δΔE(0,0) at time zero is naturally δΔE itself. Pn(δΔE) = δΔEnPe(δΔE) is the weight function and Pe(δΔE) is the excited state equilibrium distribution. Sn(t) is thus pictured as the ensemble summation over a branch of δΔE(0,t) weighted with the weight function Pn(δΔE). Sn(t) relaxes and decays to zero in the long time limit. The decay rate is characterized by 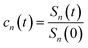 . Obviously, those δΔE, like the stationary points on the weight function Pn(δΔE), take the most significant contributions over the summation and dominantly control the dynamics of Sn(t). It is noted that Sn(0) = ∫d(δΔE)δΔEPn(δΔE) can be calculated for a given distribution Pe(δΔE) and the associated weight function Pn(δΔE).
. Obviously, those δΔE, like the stationary points on the weight function Pn(δΔE), take the most significant contributions over the summation and dominantly control the dynamics of Sn(t). It is noted that Sn(0) = ∫d(δΔE)δΔEPn(δΔE) can be calculated for a given distribution Pe(δΔE) and the associated weight function Pn(δΔE).
Dynamic Stokes shift is correlated with all the time correlation functions Sn(t).25,31 The explicit decomposition can be found in our previous work,26 and here is a concise presentation. For the non-equilibrium relaxation propagating on the excited state surface, the initial distribution of the solute–solvent interactions is represented as the summation of all the weight functions by
| PI(δΔE) = ∑fnPn(δΔE) | (2) |
| ΔES(t) = ∑fnSn(t) = ∑fnSn(0)cn(t) | (3) |
The n-th order contributes fnSn(0) to the total Stokes shift with the dynamics characterized by cn(t). Giving Gaussian statistics of the solute–solvent interaction on the excited state surface, Wick's theorem enables the even order S2n(t) to disappear, and all the odd S2n+1(t) to exhibit the same decay rates by25,41
| c2n+1(t) = c1(t) | (4) |
Therefore, the Stokes shift merely arises from the odd order time correlation function with the contribution f2n+1S2n+1(0) from the order 2n + 1. Both f2n+1 and S2n+1(0) can be evaluated by the Gaussian type weight function 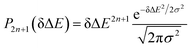 , in which
, in which 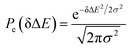 is the excited state Gaussian distribution with the width σ. According to eqn (4), the solvation time correlation function remains consistent with the odd order time correlation functions, namely the linear one by
is the excited state Gaussian distribution with the width σ. According to eqn (4), the solvation time correlation function remains consistent with the odd order time correlation functions, namely the linear one by
| S(t) = c1(t) | (5) |
The above derivations validate the linear response theory of Stokes shift with the excited state Gaussian fluctuations.
MD simulations
Molecular dynamics simulations were conducted using the GROMACS program package42 combined with the SPC/E water model. GROMOS96 force field43 was applied for the ground state tryptophan. The charges of the excited state indole was taken from the reference,44 and the charges of the reference states are shown in ESI.† The temperature was set at 298 K for the MD simulations, and it was set at 353 K for the equilibrium simulation of the state gT1.Results and discussion
Excited state equilibrium properties
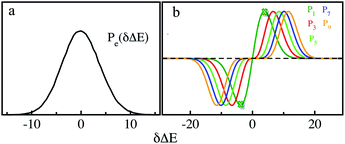
MD simulations on the excited state surface were firstly employed to probe the equilibrium properties of tryptophan in aqueous solution. As exhibited in the methodology section, the solute–solvent interaction δΔE is the central quantity for the evaluation of linear response theory. The equilibrium distribution of δΔE is displayed in Fig. 1a, showing the Gaussian profile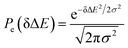 with σ of 3.8. Correspondingly, the free energy surface of δΔE (not presented) exhibits a parabolic curve. The resulting weight functions
with σ of 3.8. Correspondingly, the free energy surface of δΔE (not presented) exhibits a parabolic curve. The resulting weight functions 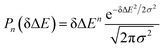 were also plotted for the odd orders 1, 3, 5, 7 and 9 (Fig. 1b). All the curves show the anti-symmetric structure, in which two stationary points locate at ±3.8, ±6.6, ±8.5, ±10.1 and ±11.4, respectively, for the above orders. These values of δΔE play a critical role in the dynamics of Sn(t) due to their prevailing weight for the ensemble summation in eqn (1). It is noted that the higher the order, the farther the separation of their stationary points from the origin.
were also plotted for the odd orders 1, 3, 5, 7 and 9 (Fig. 1b). All the curves show the anti-symmetric structure, in which two stationary points locate at ±3.8, ±6.6, ±8.5, ±10.1 and ±11.4, respectively, for the above orders. These values of δΔE play a critical role in the dynamics of Sn(t) due to their prevailing weight for the ensemble summation in eqn (1). It is noted that the higher the order, the farther the separation of their stationary points from the origin.
We further examined the decay rates of the odd order S2n+1(t). By equivalently accumulating 〈δΔE(t)δΔE(0)2n+1〉e over the excited state equilibrium, S2n+1(t) was derived for the orders 1, 3, 5, 7 and 9. Ideally, one would like to acquire various order time correlation functions, as many as possible, to examine the dynamics of the spontaneous fluctuations. However, the accurate evaluation of S2n+1(t) requests abundant samplings on those δΔE at and around the stationary points of the weight function, which is obviously difficult for the higher orders. Hence, we merely calculated the time correlation functions up to the 9-th order. The normalized form c2n+1(t) was calculated and is displayed in Fig. 2. All the curves surprisingly exhibit almost the same decay rates. The relaxation processes are characterized by an inertial decay on the femtosecond time scale, and the dynamics on a few picoseconds correlated to the rotational/diffusional motion of the water molecules. The identical relaxation processes of these orders verify the Gaussian statistics of the energy fluctuations on the excited state surface. Its critical role in the non-equilibrium relaxations was further examined in the following context.
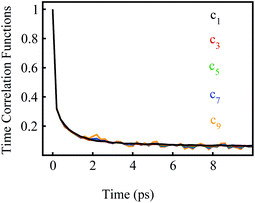 | ||
| Fig. 2 Normalized time correlation functions c2n+1(t) of the odd orders. The decay rates are the same up to the 9-th order. | ||
Non-equilibrium relaxations versus equilibrium fluctuations
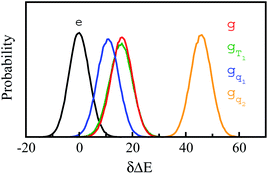
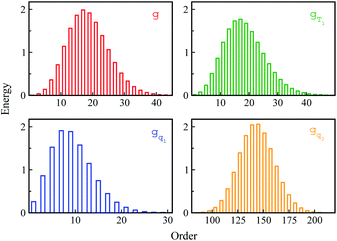
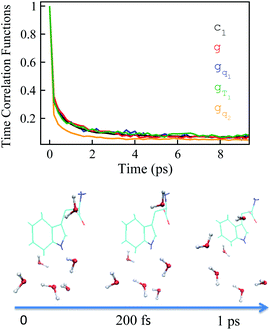
Stokes shift depicts the ensemble average of the solute–solvent interactions, in which the non-equilibrium trajectories propagate on the excited state (e) surface with the initial configurations sampled from the ground state (g) equilibrium. To unravel the connection between the non-equilibrium and equilibrium processes, we specifically designed the non-equilibrium trajectories propagating on the excited state surface, whereas the sampling of the initial configurations were tuned not necessarily from the ground state minimum. To serve the initial configuration sampling, several additional equilibrium simulations were performed by modulating either the simulation temperature or the potential parameters (SI). Compared with the ground state simulation, a high temperature of 353 K was set for a broader visit over the configuration space, providing the equilibrium state termed as gT1. Similarly, the partial charges on indole were tuned to enable the configuration sampling deviating from the ground state equilibrium, referred to as the state gq1 and gq2. For all the states g, gT1, gq1 and gq2, the equilibrium distributions PI(δΔE) of the solute–solvent interaction were firstly derived (Fig. 3). All the curves show the shifted Gaussian forms. The profiles of the states gT1 and g take the same center, but with a larger width for the former. For the states gq1 and gq2, the energy distributions obviously deviate from the ground state profile.Non-equilibrium simulations were performed by propagating trajectories on the excited-state surface with the initial configurations sampled from the equilibrium fluctuations of the states g, gT1, gq1 and gq2. We firstly inspected the total energy shifts by applying ΔES(0) = ∫d(δΔE)δΔEPI(δΔE), which are 16.0, 16.0, 10.8 and 46 for the above non-equilibrium processes, respectively. By further projecting the initial distribution PI(δΔE) into the Gaussian type weight functions (eqn (2)), ΔES(0) was decomposed into the contributions of the odd order time correlation functions by f2n+1S2n+1(0) (Fig. 4). The peak energy of PI(δΔE), namely the center of the profile, notifies the order of the weight function making the maximum contribution. For example, the center of PI(δΔE) is 10.8 for the state gq1, residing closely to the stationary point (10.1) of the 7-th weight function. Correspondingly, f7S7(0) of the 7th order contributes maximally among all the time correlation functions. The same correspondences are observed for the states g, gT1, and gq2. For both the states g and gT1, the maximum contribution to the energy decomposition arises from the 17-th order, which is attributed to the close residence between the center (16.0) of their PI(δΔE) and the stationary point (15.7) of the 17-th weight function. However, about 80% of the contributions to ΔES(0) arise from the order 9–25 for the state g, and from the order 7–29 for the state gT1. The broader distribution PI(δΔE) of the latter enables it to correlate with more weight functions than the ground state ones. For the state gq2, the orders of 121–163 contribute 82% to the total energy shift. The maximum contribution is from the 145-th order. The associated stationary point (45.8) is close to the center (46.0) of the initial distribution PI(δΔE).
The time relaxations of ΔES(t) were obtained for the non-equilibrium processes, in which the inital configurations were sampled from the states g, gq1, gT1 and gq2 respectively (Fig. 5). The normalized solvation time correlation functions S(t) were compared with the excited state time correlation functions c1(t) to check the validity of linear response theory. As a result of Gaussian statistics, Stokes shift is represented as the summation of all the odd order time correlation functions by
| ΔES(t) = f2n+1S2n+1(0)c2n+1(t) | (6) |
The energy allocations of the total decay ΔES(0) are shown in Fig. 4. For the states g, gq1, gT1, those orders taking the most dominant contributions are the lower ones. Their equilibrium time correlation functions c2n+1(t) obey the same dynamics as the linear one c1(t) owing to Gaussian statistics of the energy variable δΔE. Therefore, the non-equilibrium solvation time correlation S(t) remains consistent with c1(t) as expected by linear response theory. In contrast, the non-equilibrium dynamics of the state gq2 are evidently different from c1(t). In this case, most of the energy contributions are from the higher orders. For example, the maximum contribution is from the 145-th order. For those very high orders, the equilibrium time correlation functions of c2n+1(t) can hardly be accumulated due to sampling difficulties. We speculate that their dynamics are different from the linear order c1(t) due to the deviation of the Gaussian statistics, causing discrepancy between the non-equilibrium dynamics and the linear response expectation. Therefore, both the success and failure of linear response theory were observed and the mechanisms were interpreted. We also compared the simulation with the experimental results, in which the relaxation ΔES(t) of the state g corresponds to the experimental measurements of Stokes shift. The simulated solvation time correlation function of the state g is fitted with the function 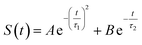 , leading to the inertial decay τ1 of 170 femtosecond and τ2 of 1.0 picosecond. The simulation results are in good agreement with the experimental measurements, which shows the dynamics of 1.6 picoseconds upon the initial ultrafast decay for the tryptophan solution.45 The molecular mechanism for the biphasic relaxation is shown in Fig. 5 (bottom panel). The time scale τ1 is mostly attributed to the reorientation motion of the neighboring water molecules of indole, and τ2 is linked with the rotational and diffusional motions of water.
, leading to the inertial decay τ1 of 170 femtosecond and τ2 of 1.0 picosecond. The simulation results are in good agreement with the experimental measurements, which shows the dynamics of 1.6 picoseconds upon the initial ultrafast decay for the tryptophan solution.45 The molecular mechanism for the biphasic relaxation is shown in Fig. 5 (bottom panel). The time scale τ1 is mostly attributed to the reorientation motion of the neighboring water molecules of indole, and τ2 is linked with the rotational and diffusional motions of water.
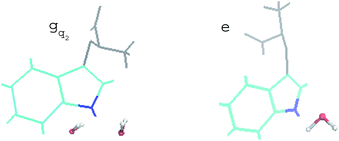
For the non-equilibrium solvation time correlation function S(t) of the state gq2, we further probed the molecular origin for the failure of linear response theory. The solvation structures in the proximity of indole were examined for gq2 and the excited state, which provided the most relevant information on the initial and final configuration over the non-equilibrium process. The artificial charge modulation on the state gq2 makes a significant change in its dipole moment compared with the excited state, which is 9.7 D and 5.1 D, respectively, with an angle flip of 137° (Fig. S2 in ESI†). As a result, the solvation structure in proximity to indole was significantly rearranged. Fig. 6 displays the typical snapshots for the two states. The average number of water molecules within 3 Å of the nitrogen atom is 2.3 and 1.1 for the state gq2 and the excited state, respectively. Therefore, the H-bond structure between the solute and the solvents vary significantly over non-equilibrium relaxation. This gross change in the solvation structure, as reported in literatures,24,46,47 correlates with the discrepancy between the non-equilibrium and equilibrium dynamics and accounts for the breakdown of linear response theory.
Equilibrium time correlation functions of initial states
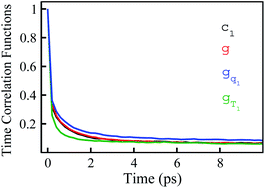
In numerous studies, linear response theory of Stokes shift has been evaluated by applying the ground state equilibrium time correlation functions.13,15 From the previous discussions, the dynamics of S(t) are almost the same for the non-equilibrium relaxations initiated of the states g, gq1 and gT1, which are well characterized by the excited state linear response approach c1(t). It is worth probing the equilibrium dynamics for these unperturbed states. The normalized linear order time correlation function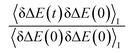 is accumulated over the equilibrium fluctuations of the states g, gq1 and gT1 (Fig. 7). Here, the bracket 〈⋯〉I represents the average over the initial state equilibrium. All the curves show obviously different decay rates. Compared with the excited state c1(t), only the state g shows similar dynamics. The dynamics are slightly slower for the state gq1 and faster for the state gT1 due to the artificial setting of a higher temperature. Therefore, the decay rates of ΔES(t) for these nonequilibrium processes directly correlate with the final state Gaussian fluctuations, despite the distinct equilibrium dynamics of their initial states. Consequently, the excited state linear response approach is recommended to characterize the relaxation of Stokes shift. On the other hand, it is also noted that the time correlation function of the state g is similar to that of the excited state c1(t). This similarity indicates that the ground state linear response theory may provide a reasonable evaluation on Stokes shift, once the associated equilibrium dynamics agree with the excited state ones. This observation is consistent with the literature results, wherein numerous systems show the accuracy of the ground state linear response theory.13,15
is accumulated over the equilibrium fluctuations of the states g, gq1 and gT1 (Fig. 7). Here, the bracket 〈⋯〉I represents the average over the initial state equilibrium. All the curves show obviously different decay rates. Compared with the excited state c1(t), only the state g shows similar dynamics. The dynamics are slightly slower for the state gq1 and faster for the state gT1 due to the artificial setting of a higher temperature. Therefore, the decay rates of ΔES(t) for these nonequilibrium processes directly correlate with the final state Gaussian fluctuations, despite the distinct equilibrium dynamics of their initial states. Consequently, the excited state linear response approach is recommended to characterize the relaxation of Stokes shift. On the other hand, it is also noted that the time correlation function of the state g is similar to that of the excited state c1(t). This similarity indicates that the ground state linear response theory may provide a reasonable evaluation on Stokes shift, once the associated equilibrium dynamics agree with the excited state ones. This observation is consistent with the literature results, wherein numerous systems show the accuracy of the ground state linear response theory.13,15
Width dynamics
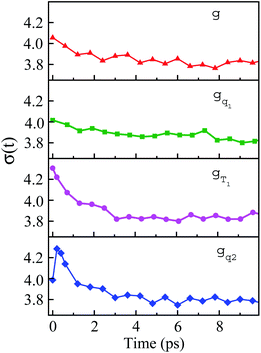
The non-stationarity of Gaussian statistics is linked with the inefficiency of linear response theory in literatures.23,31,33 At a specific time t upon the perturbation during the non-equilibrium process, the probability distribution of the solute–solvent interactions is depicted by the Gaussian function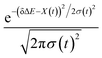 , in which the profile center X(t) and width σ(t) are obtained by X(t) = 〈δΔE〉t and σ(t)2 = 〈δΔE2〉t − 〈δΔE〉t2, respectively. The bracket 〈⋯〉t represents the average over the energy ensemble at the time t. The time evolutions of the width σ(t) are derived over the non-equilibrium processes to depict the stationarity of the Gaussian statistics (Fig. 8). The width decreases slightly for the states g, gq1 and obviously narrows for the state gT1. Linear response theory successfully depicts the non-equilibrium dynamics of ΔES(t) for all these three states (in Fig. 5). For the state gq2, the width dynamics show a large intermediate broadening right on perturbation. Meanwhile, linear response evaluation fails to describe the non-equilibrium event. Our integrated observations thus do not show the explicit correlation between the non-stationarity of Gaussian statistics and the validity of linear response theory.
, in which the profile center X(t) and width σ(t) are obtained by X(t) = 〈δΔE〉t and σ(t)2 = 〈δΔE2〉t − 〈δΔE〉t2, respectively. The bracket 〈⋯〉t represents the average over the energy ensemble at the time t. The time evolutions of the width σ(t) are derived over the non-equilibrium processes to depict the stationarity of the Gaussian statistics (Fig. 8). The width decreases slightly for the states g, gq1 and obviously narrows for the state gT1. Linear response theory successfully depicts the non-equilibrium dynamics of ΔES(t) for all these three states (in Fig. 5). For the state gq2, the width dynamics show a large intermediate broadening right on perturbation. Meanwhile, linear response evaluation fails to describe the non-equilibrium event. Our integrated observations thus do not show the explicit correlation between the non-stationarity of Gaussian statistics and the validity of linear response theory.
Conclusion
We systematically examined linear response theory for tryptophan in aqueous solution. For multiple non-equilibrium relaxations not necessarily initiated from the ground state minimum, the excited state Gaussian statistics were assigned to account for the validity of linear response theory. On the other hand, the breakdown of linear response theory was also observed for a non-equilibrium process driven far from the equilibrium minimum. Parabolic curvature of the free energy surface could distort and Gaussian statistics deviate, leading to the failure of linear response theory. Our results, therefore, verify the connection between the excited state Gaussian fluctuations and the dynamics of the non-equilibrium relaxations.The mechanism of linear response theory has been carefully examined in literature. Heid and co-workers found that a large intermediate broadening for the width of the energy distribution correlates with a failure of the time correlation function to describe the non-equilibrium event.27 Our observations coincide with their conclusion. Among the non-equilibrium processes, the only case with the failure of linear response theory shows the strong peculiarity of width dynamics, namely intermediate broadening, and all the others with the success of linear response theory show either relatively stable or gradual narrowing of width. Therefore, the abrupt change, and not the absolute change, of the width links to the failure of linear response theory. How this specificity of the width dynamics inherently correlates with the non-Gaussian statistics, as assigned to be the origin of nonlinear behavior in this study, needs further investigations and illumination.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The work was supported by the National Natural Science Foundation of China (Grant No. 11974267), Natural Science Foundation of Shaanxi Provincial Department of Education (Grant No. 2019JM-556) and 111 Project under Grant B17035.References
- E. W. Castner, M. Maroncelli and G. R. Fleming, J. Chem. Phys., 1987, 86, 1090 CrossRef CAS.
- M. Maroncelli and G. R. Fleming, J. Chem. Phys., 1987, 86, 6221 CrossRef CAS.
- V. Nagarajan, A. M. Brearley, T. J. Kang and P. F. Barbara, J. Chem. Phys., 1987, 86, 3183 CrossRef CAS.
- M. Maroncelli, J. Chem. Phys., 1991, 94, 2084 CrossRef CAS.
- E. A. Carter and J. T. Hynes, J. Chem. Phys., 1991, 94, 5961 CrossRef CAS.
- B. Biman and J. Biman, Chem. Soc. Rev., 2010, 39, 1936 RSC.
- P. Samir Kumar and A. H. Zewail, Chem. Rev., 2004, 104, 2099 CrossRef PubMed.
- L. Zhang, L. Wang, Y. T. Kao, W. Qiu, Y. Yang, O. Okobiah and D. Zhong, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 18461 CrossRef CAS PubMed.
- K. E. Furse and S. A. Corcelli, J. Am. Chem. Soc., 2008, 130, 13103 CrossRef CAS PubMed.
- Y. Qin, L. Wang and D. Zhong, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 201602916 CrossRef PubMed.
- J. Yang, Y. Wang, L. Wang and D. Zhong, J. Am. Chem. Soc., 2017, 139, 4399 CrossRef CAS PubMed.
- D. Chandler, Introduction to Modern Statistical Mechanics, Oxford Univ. Press, New York, 1987 Search PubMed.
- L. Nilsson and B. Halle, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 13867 CrossRef CAS PubMed.
- A. A. Golosov and M. Karplus, J. Phys. Chem. B, 2007, 111, 1482 CrossRef CAS PubMed.
- T. Li, A. A. Hassanali, Y. T. kao, D. Zhong and S. J. Singer, J. Am. Chem. Soc., 2007, 129, 3376 CrossRef CAS PubMed.
- K. E. Furse, B. A. Lindquist and S. A. Corcelli, J. Phys. Chem. B, 2008, 112, 3231 CrossRef CAS PubMed.
- K. E. Furse and S. A. Corcelli, J. Phys. Chem. Lett., 2010, 1, 1813 CrossRef CAS.
- M. Maroncelli and G. R. Fleming, J. Chem. Phys., 1988, 89, 5044 CrossRef CAS.
- B. J. Schwartz and P. J. Rossky, J. Chem. Phys., 1994, 101, 6902 CrossRef.
- B. M. Ladanyi and B. C. Perng, J. Phys. Chem. A, 2002, 106, 6922 CrossRef CAS.
- Y. Shim, M. Y. Choi and H. J. Kim, J. Chem. Phys., 2005, 122, 044510 CrossRef CAS PubMed.
- Z. L. Terranova and S. A. Corcelli, J. Phys. Chem. B, 2018, 122, 6823 CrossRef CAS PubMed.
- P. L. Geissler and D. Chandler, J. Chem. Phys., 2000, 113, 9759 CrossRef CAS.
- T. Guohua and R. M. Stratt, J. Chem. Phys., 2006, 125, 12981 Search PubMed.
- B. B. Laird and W. H. Thompson, J. Chem. Phys., 2007, 126, 211104 CrossRef PubMed.
- T. Li, J. Chem. Theory Comput., 2017, 13, 1867 CrossRef CAS PubMed.
- E. Heid, W. Moser and C. Schröder, Phys. Chem. Chem. Phys., 2017, 19, 10940 RSC.
- D. Roy and M. Maroncelli, J. Phys. Chem. B, 2012, 116, 5951 CrossRef CAS PubMed.
- E. Heid and C. Schröder, Phys. Chem. Chem. Phys., 2019, 21, 2013 Search PubMed.
- N. Pal, H. Shweta, M. K. Singh, S. D. Verma and S. Sen, J. Phys. Chem. Lett., 2015, 6, 1754 CrossRef CAS PubMed.
- A. J. Schile and W. H. Thompson, J. Chem. Phys., 2017, 146, 154109 CrossRef PubMed.
- T. Li and R. Kumar, J. Chem. Phys., 2015, 143, 174501 CrossRef PubMed.
- E. Heid and C. Schröder, Phys. Chem. Chem. Phys., 2018, 20, 5246 RSC.
- B. B. Laird and W. H. Thompson, J. Chem. Phys., 2011, 135, 084511 CrossRef PubMed.
- T. Li and X. Wang, J. Chem. Theory Comput., 2019, 15, 471 CrossRef CAS PubMed.
- W. Lu, J. Kim, W. Qiu and D. Zhong, Chem. Phys. Lett., 2004, 388, 120 CrossRef CAS.
- A. A. Hassanali, L. Tanping, Z. Dongping and S. J. Singer, J. Phys. Chem. B, 2006, 110, 10497 CrossRef CAS PubMed.
- W. Qiu, Y. T. Kao, L. Zhang, Y. Yang, L. Wang, W. E. Stites, D. Zhong and A. H. Zewail, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 13979 CrossRef CAS PubMed.
- Z. Chen, J. A. Stevens, J. J. Link, G. Lijun, W. Lijuan and Z. Dongping, J. Am. Chem. Soc., 2009, 131, 2846 CrossRef PubMed.
- S. J Nathan and P. R. Callis, J. Phys. Chem. B, 2013, 117, 9598 CrossRef PubMed.
- G. C. Wick, Phys. Rev., 1950, 80, 268 CrossRef.
- E. Lindahl, B. Hess and D. V. D. Spoel, Molecular Modeling Annual, 2001, 7, 306 CrossRef CAS.
- W. R. P. Scott, P. H. Hünenberger, I. G. Tironi, A. E. Mark, S. R. Billeter, J. Fennen, A. E. Torda, T. Huber, A. Peter Krüger and W. F. V. Gunsteren, J. Phys. Chem. A, 1999, 103, 3596 CrossRef CAS.
- T. Li, A. A. Hassanali and S. J. Singer, J. Phys. Chem. B, 2008, 112, 16121 CrossRef CAS PubMed.
- W. Lu, J. Kim, W. Qiu and D. Zhong, Chem. Phys. Lett., 2004, 388, 120 CrossRef CAS.
- L. Turi, P. Mináry and P. J. Rossky, Chem. Phys. Lett., 2000, 316, 465 CrossRef CAS.
- A. E. Bragg, M. C. Cavanagh and B. J. Schwartz, Science, 2008, 321, 1817 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ra01227k |
| This journal is © The Royal Society of Chemistry 2020 |