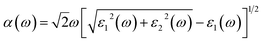Open Access Article
Open Access ArticleSynergistic effects of dopant (Ti or Sn) and oxygen vacancy on the electronic properties of hematite: a DFT investigation†
Haijun Pan *ab,
Dongbiao Aoa and
Gaowu Qinc
*ab,
Dongbiao Aoa and
Gaowu Qinc
aSchool of Resources and Materials, Northeastern University at Qinhuangdao, Qinhuangdao 066004, People's Republic of China. E-mail: panhaijun@neuq.edu.cn
bKey Laboratory of Dielectric and Electrolyte Functional Materials Hebei Province, Qinhuangdao 066004, People's Republic of China
cKey Laboratory for Anisotropy and Texture of Materials, Northeastern University, Shenyang 110819, People's Republic of China
First published on 17th June 2020
Abstract
Hematite has been widely studied as one of the most promising photoanodes in the photoelectrochemical decomposition of water. At present, a prevailing strategy of coupling dopant (Ti or Sn) with oxygen vacancies has been proposed by experiment, and effectively improves the photocatalytic activity. In order to clarify the intrinsic reasons for the improvement of the photochemical activity, density functional theory is adopted to calculate the formation mechanism and electronic properties of hematite with doping ions and oxygen vacancies. The result shows that the doped atom is beneficial to the formation of oxygen vacancies in hematite, thus forming a stable structure containing doping ions and oxygen vacancies. Due to the synergistic effects of dopant and oxygen vacancies, the bandgap of hematite decreases, and donor levels are introduced into the bandgap, which lead to the increase of carrier concentration. In the system with doped Ti and oxygen vacancies, donor levels are introduced at 1.47 eV and 1.73 eV below the bottom of the conduction band, respectively. For the case containing Sn and oxygen vacancies, the donor level is introduced at 1.75 eV from the conduction band minimum. Our results elaborate the reasons for the enhancement of carrier densities in terms of electronic structure, and provide some guidance for the future modification of photocatalysts.
Introduction
Since Fujishima used TiO2 to split water into H2 under ultraviolet light, photoelectrochemical (PEC) systems have long been considered as methods to produce clean hydrogen by solar energy harvesting, gradually becoming the focus of world attention.1 Among various oxide semiconductor photocatalysts, hematite (α-Fe2O3) has been capturing considerable research attention by serving as a water oxidation photoanode. Hematite is abundant in minerals, non-toxic and chemically stable in aqueous solution. In addition, hematite has a favorable bandgap (∼2.2 eV), which corresponds to the major part of the solar spectrum.2,3 What is more, its valence band locates below the oxidation potential of water, possessing strong oxidation ability.4 Theoretically, the solar to hydrogen (STH) efficiency of Fe2O3 can reach as high as 12.9%, with a photocurrent density of 12.6 mA cm−2.5 However, the reported efficiency of hematite is much less than the theoretical value. Generally, the reason for this inconsistency lies in the short hole-diffusion length (2–4 nm),6 the short lifetimes of the excited electrons (<10 ps),7 and low electron mobility in hematite.8Doping has been employed as one of the important methods in improving the photocatalytic performance of Fe2O3. Among numerous doped ions, Sn4+ doping9–13 and Ti4+ doping14–17 can greatly enhance the photocatalytic activity and photocurrent of Fe2O3. The experimental and theoretical analysis show that enhancement of its photocatalytic activity is mainly due to the increase of carrier concentration, the reduction of electron–hole recombination rate and the decrease of optical bandgap. Also, doping can alert the interfacial properties between catalyst and electrolyte, such as electric field across the space charge layer and charge transfer kinetics.
Preparation of oxygen vacancy (VO) in Fe2O3 has been proved to be another effective method to improve its photocatalytic activity. Experimentally, Ling et al. decomposed the β-FeOOH nanowires at 550 °C in an oxygen-deficient condition to obtain hematite nanowires containing oxygen vacancies, which yielded a substantially enhanced photocurrent density.18 Li et al. present the preparation of H2-treated hematite nanostructures by a pyrolysis of NaBH4 in a crucible.19 The H2-treated hematite photoelectrode displays a photocurrent of 2.28 mA cm−2 at 1.23 V vs. RHE, which is over 2.5 times higher than that of pristine hematite. Rioult et al. prepare the single crystalline film of hematite through atomic oxygen assisted molecular beam epitaxy, and adjust the concentration of oxygen vacancy through annealing in UHV.20 For the optimal oxygen vacancy concentration, the sample shows a 50% photocurrent gain and reduction for the onset potential by 0.2 V with respect to stoichiometric hematite. In terms of electronic properties, the formation of oxygen vacancies is supposed to lead to an increase in donor concentration in Fe2O3.
From a design perspective, synergistic effect of ion doping and oxygen vacancy can produce a cumulative effect on electronic properties, which is necessary to achieve sufficiently higher photocatalytic efficiency. Experimentally, many researchers have found that the presence of oxygen vacancy can further enhance the photocatalytic performance of doped Fe2O3. Through control of the oxygen partial pressure, Sn doped hematite with VO can exhibit a higher photocurrent than that of normally prepared hematite. This enhancement can be attributed to the improvement of electrical conductivity due to carrier generation from defects.21 The results obtained by Pu et al. suggest that oxygen vacancies in Ti doped hematite mainly affect the performance by improving the donor densities with lower oxidation state of Fe, while Ti-doping might affect the performance of hematite by surface catalytic effects or more active sites for water oxidation.22 Wang et al. conclude that the presence of VO can not only promote surface electrocatalytic oxygen evolution reaction (OER) processes, but also increase the carrier concentration.23 Zhou et al. annealed Sn doped Fe2O3 in a reducing atmosphere created by partial oxidation of graphite to produce oxygen vacancies. The donor density increases by 73% in Sn-doped Fe2O3 annealed on graphite at 770 °C for 20 min, and ∼70% enhancement in photocurrent density is observed.24 Other experiments also indicate that carrier densities or conductivity enhancement is one of key reasons for the enhanced photoactivity.25,26 Actually, the existence of oxygen vacancies and doped ions in Fe2O3 is very complex, and synergistic effects of them on the electronic properties of hematite are still not clear.
This paper mainly focus on the interaction between oxygen vacancy and doped ion in Fe2O3, and the corresponding electronic properties in order to reveal the fundamental reasons for the improvement of photocatalytic performance. The results indicate that the doped atom (Sn or Ti) is beneficial to the formation of oxygen vacancy in hematite. In addition to reducing the bandgap width, the synergistic effects of oxygen vacancy and doping can introduce donor levels into the bandgap, which is responsible for improvement of electrical conductivity.
Computational methods
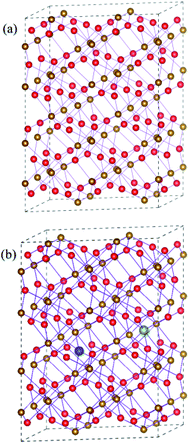
Hematite has a hexagonal close-packed crystal structure with the space group of R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) 2/C (no. 167), and one unit cell contains 12 Fe and 18 O atoms. Here, we construct a 120-atom 2 × 2 × 1 supercell in order to understand synergistic effects of doping and oxygen vacancy on the electronic properties of hematite, which are shown in Fig. 1(a). For metal atom doping, we use one metal atom (Ti or Sn) to replace one Fe atom in the supercell. As for oxygen vacancy, one of equivalent O atoms is artificially removed. As can be seen in Fig. 1(b), the supercell containing doped atom and oxygen vacancy is modelled by replacing a Fe atom with a metal atom around the oxygen vacancy. In addition to the most stable model mentioned above, other possible models have been carefully examined, which are provided in Fig. S1 and Table S1 in the ESI.†
2/C (no. 167), and one unit cell contains 12 Fe and 18 O atoms. Here, we construct a 120-atom 2 × 2 × 1 supercell in order to understand synergistic effects of doping and oxygen vacancy on the electronic properties of hematite, which are shown in Fig. 1(a). For metal atom doping, we use one metal atom (Ti or Sn) to replace one Fe atom in the supercell. As for oxygen vacancy, one of equivalent O atoms is artificially removed. As can be seen in Fig. 1(b), the supercell containing doped atom and oxygen vacancy is modelled by replacing a Fe atom with a metal atom around the oxygen vacancy. In addition to the most stable model mentioned above, other possible models have been carefully examined, which are provided in Fig. S1 and Table S1 in the ESI.†
All calculations are performed in the framework of the spin-polarized density functional theory with Vienna ab initio simulation package (VASP) code.27 The valence electron and ion core interactions are described by the projector augmented wave (PAW) potential.28 The exchange–correlation potential is described by generalized gradient approximation (GGA) with the Perdew–Burke–Ernzerhof (PBE) scheme.29 The cutoff energy for electronic wave functions is 500 eV, which is high enough for energy convergence. The Brillouin-zone integration is performed using Monkhorst–Pack grids of 3 × 3 × 1.30 The lattice parameters and atomic positions of pure and doped hematite are fully relaxed using a conjugate gradient minimization algorithm until force convergence of 1 meV Å−1 and energy convergence of 10−5 eV are reached. The framework of GGA + U invented by Dudarev et al. is selected in this simulation.31 The value of U–J is set to 4.3 eV, which is symmetrically picked out by Mosey et al.32
Results and discussion
The formation energy
The formation energies of various defects in Fe2O3 are investigated in order to know the growth mechanism and relative stability of new systems. With respect to neutral defects in Fe2O3, the formation energies can be calculated as follows:33| E(VO)f = E(VO) − E(pure) + μO |
| E(MFe)f = E(MFe) − E(pure) − μM + μFe |
| E(MFe + VO)f = E(MFe + VO) − E(pure) − μM + μFe + μO |
E(pure) is the total energy of the hematite 2 × 2 × 1 supercell. E(VO), E(MFe) and E(MFe + VO) are the total energy of the systems containing VO, MFe = TiFe or SnFe, and (MFe + VO), respectively. μM, μFe and μO represent the chemical potential of M, Fe, and O, respectively.
As is well known, the chemical potential is closely related to the sample growth condition, which could be very different from O-rich to Fe-rich conditions. Under Fe-rich growth condition, the chemical potential μFe is calculated from the energy of one bulk Fe atom, and the corresponding μO can be obtained from μFe2O3 = 2μFe + 3μO. Under O-rich condition, the chemical potential μO is determined by half of the energy of an O2 molecule, and the μFe can be calculated from the formula above. The formation energy as a function of oxygen chemical potential is plotted in Fig. 2. Regardless of the preparation conditions, the formation energy of oxygen vacancy is always positive, indicating that the formation of oxygen vacancy will be inhibited during the growth of Fe2O3. Relatively small formation energy of TiFe (SnFe) over the entire range of μO illustrates that Ti (Sn) substitution for Fe can be easily achieved, which has been confirmed by experimental results. More interestingly, the formation energy of TiFe (or SnFe) and oxygen vacancy is much lower than that of oxygen vacancy in Fe2O3. This result shows that the introduction of doped ions would promote the occurrence of oxygen vacancy. In experiment, Pu et al. verifies the production of oxygen vacancy in Ti-doped hematite could be easier compared to that in undoped hematite under a moderate partial oxygen pressure range.22
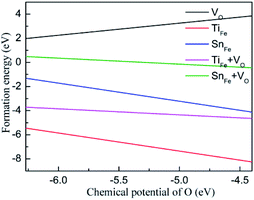 | ||
| Fig. 2 The formation energy of VO, TiFe, SnFe, TiFe + VO or SnFe + VO as a function of the chemical potential of O. | ||
Electronic structures
In this section, we first analyze the electronic structure and charge distribution of Fe2O3 with low concentration dopant. Furthermore, we discuss the changes of them caused by the interaction between oxygen vacancy and doped ions, so as to explain the nature of the enhancement of photocatalytic properties observed in experiments.In Fig. 3(a1), it can be found that the Fe 3d states are the main component of conduction band minimum, and the valence band maximum is composed of Fe 3d and O 2p states. It is reported that the hematite possess a stable antiferromagnetic (AFM) ground state below −10 °C, in which the magnetic moment direction of Fe atom is along the [0001]. In Fig. 3(a2) and (a3), density of states of a single atom is plotted. It shows that Fe 3d electrons have weak interaction with O 2p electrons in the range of −8–−4 eV, which leads to the emergence of unpaired spin electrons. Thus, the magnetic moment on the Fe atom mainly originates from these unpaired Fe 3d electrons in this energy range. The calculated magnetic moment around iron atoms is 4.15 μB, which is consistent with the experimental results in the literature.34,35 The bandgap is predicted to be 2.20 eV. The electronic structure of pristine Fe2O3 is consistent with previous computational observations.14 For charge transfer in Fe2O3, Bader charge analysis (Fig. S2a†) points out that the Fe atom loses 1.72e to surrounding O atoms, and O atom obtains 1.15e from nearby Fe atoms. Correspondingly, the XPS result in the experiment indicates that the Fe and O atom convert to Fe3+ and O2− state after the formation of Fe2O3, respectively.36
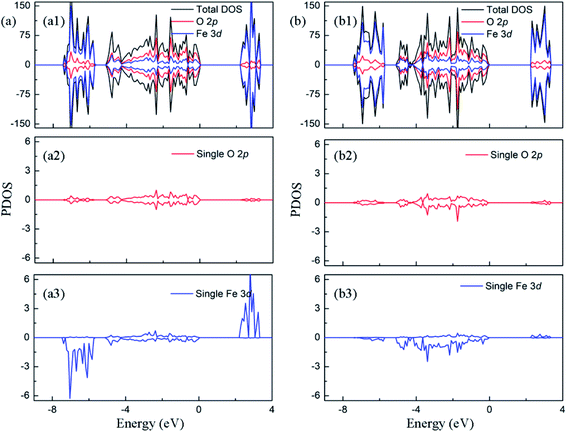 | ||
| Fig. 3 The projected density of states of (a) perfect Fe2O3 and (b) Fe2O3 containing VO. The Fermi level is set to zero. | ||
The introduction of oxygen vacancy changes local atomic structure and the interaction between O and Fe atoms, leading to a significant change in the electronic structure of Fe2O3. Fig. 3(b2) and (b3) shows the electronic density of states of typical O and Fe atoms near the oxygen vacancy. Compared with pristine Fe2O3, it can be seen that there is a stronger interaction between the Fe 3d orbital electrons and the surrounding O 2p electrons in −6–0 eV. Therefore, the number of spin unpaired electrons in Fe 3d orbital decreases, and magnetic moment of Fe atom reduces to 3.69 μB. Due to the presence of oxygen vacancy, only 1.33 charges are supplied to the lattice by the surrounding iron atoms.
For Ti doping at low concentration, electronic structure (Fig. 4(a4)) shows that hybrid orbits are first formed by 3d and 4s orbitals of Ti atom, and then interact with O 2p orbitals. In Fig. S3c,† the Bader charge analysis indicates that the doped Ti atom will lose 1.94e to the Fe2O3 lattice. Although Ti atom has one more valence electron than Fe atom, the charge on oxygen atoms surrounding Ti atom does not increase compared to undoped Fe2O3. The reason for this phenomenon is that the introduction of Ti atoms weakens the interaction between the surrounding O atoms and Fe atoms, which reduces the charge transfer between Fe and O atoms. At the same time, the charge on the Fe atoms will increase. The electronic property of the Fe atom closest to the Ti atom in the adjacent atomic layer is the most sensitive to this lattice distortion. Fig. 4(a2) and (a3) state that Fe 3d electrons have a strong hybridization with O 2p electrons in the range of −6–0 eV. On this typical Fe atom, the magnetic moment is changed into 3.60 μB.
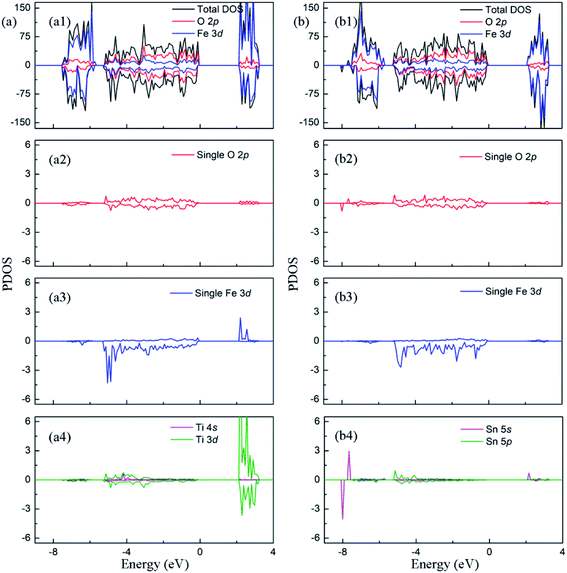 | ||
| Fig. 4 The projected density of states of (a)Ti doped Fe2O3 and (b) Sn doped Fe2O3. The Fermi level is set to zero. | ||
For Sn doping at low concentration, electronic structure (Fig. 4(b4)) shows that hybrid orbits are first formed by 5s and 5p orbitals of Sn atom, and then interact with O 2p orbitals. In this process, Sn atom will provide 2.28e to the crystal lattice, displaying a stronger degree of ionization than Fe atom, while the surrounding oxygen atoms get 1.17e. The experimental results show that Sn atom possesses 4+ state in Sn doped Fe2O3. Compared to pure hematite, an extra electron would be introduced by Sn4+ and hope between Fe3+ ions. The calculation result shows that the extra electron mainly distributes over oxygen atoms, and needs to be excited from O 2p to Fe 3d before transfer across the Fe3+ ions.9 As with Ti doping, Sn doping can also change the bonding mode between Fe and O atoms(shown in Fig. 4(b)). The magnetic moment on the typical Fe atom becomes to 3.62 μB.
In order to clarify the enhancement of photocatalytic activity observed by experiments, the change of electronic properties caused by the presence of doped ion and oxygen vacancy are calculated. The density of states of (TiFe + VO)–Fe2O3 is plotted in Fig. 5(a). The spin-up and -down donor states are introduced at 1.47 eV and 1.73 eV from the bottom of the conduction band minimum, respectively. As shown in Fig. 5(a2) and (a3), the interaction between Fe 3d and O 2p electrons in the range of −1–−6 eV reduces the number of unpaired electrons in 3d orbit, which leads to the reduction of the magnetic moment on Fe atom (3.60 μB). Besides, it also contributes to the local donor levels, which indicates the emergence of Fe2+ ion.37 In order to explain the formation of donor levels, the average changes of Fe–O bond length around oxygen vacancy are compared when various defects appear. In Fe2O3 containing O vacancy, the bond length of the Fe–O bond around the oxygen vacancy decreases by about 0.026 Å on average, indicating that the five coordinated Fe atom has stronger interaction with the surrounding O atom. Thus, there are no mid-gap levels in Fig. 3(b). In (TiFe + VO)–Fe2O3, the average increase of Fe–O bond length is about 0.008 Å for the five coordinated Fe atom. By comparing the change of bond length, it is pointed out that the additional nonlocal electrons brought by Ti will weaken the bonding strength between the Fe and O atoms near the O vacancy, which cause the increase of the unbonded electrons in Fe atoms. Therefore, the properties of the donor states mainly possess the electronic properties of Fe 3d and O 2p. The Bader charge analysis shows that there are 6.68e on each Fe atom adjacent to O vacancy, which is 0.5e more than that in the perfect Fe2O3. The partial charge density of the intermediate state is plotted in Fig. S3.† It points out that the partial charge density of donor states is mainly distributed on the Fe atom around the O vacancy than others. In addition, the bandgap width decreased to 2.07 eV due to the downward movement of the conduction band. The density of states of (SnFe + VO)–Fe2O3 is plotted in Fig. 5(b). The donor level is introduced at 1.75 eV from the conduction band minimum in the system with doped Sn ions and oxygen vacancy. As shown in Fig. 5(b2) and (b3), Fe 3d have obvious hybridization with O 2p in the range of −1–−6 eV, and the occupied energy level is introduced into the bandgap. The magnetic moment of Fe atom changes to 3.63 μB due to the change of electron configuration in 3d orbital. In (SnFe + VO)–Fe2O3, the average increase of Fe–O bond length is about 0.018 Å for the five coordinated Fe atom. By comparing the change of bond length, we conclude that the additional nonlocal electrons brought by Sn can also weaken the bonding strength between the Fe and O atoms around the O vacancy, causing the increase of the unbonded electrons in Fe atoms. Therefore, the properties of the donor states possess the electronic properties of Fe 3d and O 2p. The Bader charge analysis indicates that the Fe atom adjacent to O vacancy has 0.5e more than that in Fe2O3, which leads to local donor levels as mentioned above. The partial charge density plotted in Fig. S3† mainly distribute on the atoms around O vacancy. The co-existence of oxygen vacancy and Sn doping also reduce the bandgap width of hematite to 2.09 eV. From the analysis of electronic properties, synergistic effects of oxygen vacancy and doping make the band gap width decrease, and donor levels appear, which are beneficial to the absorption of photons and the increase of carrier concentration observed in experiment.
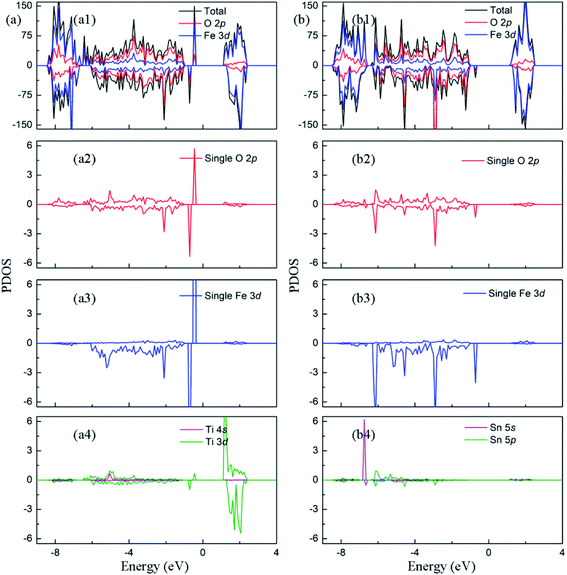 | ||
| Fig. 5 The projected density of states of (a) (TiFe + VO)–Fe2O3 (b) (SnFe + VO)–Fe2O3. The Fermi level is set to zero. | ||
The prediction of optical properties helps us to understand optical photons interacting with the electrons in the pure and impurity-contained hematite. The absorption coefficient α(ω) can be derived from the real and imaginary parts of the dielectric function as follow:
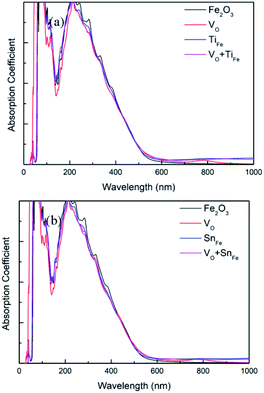
As is shown in Fig. 6, the absorption edge of perfect Fe2O3 in the visible light region is about 560 nm, which is in agreement with experimental measurements. The optical absorption edge is about 600 nm (or 590 nm) for Fe2O3 containing O vacancy and Ti atom (or Sn), which is attributed to the bandgap reduction. Besides, it can be seen that low-energy photons (<bandgap) can still be absorbed for the two investigated systems. The reason for the improvement of light absorption ability lies in the deep donor levels, which act as ‘steps’ in electronic transition from valence band to conduction band. For (TiFe + VO)–Fe2O3 system, the wavelength of the absorbed photons can reach 3600 nm, which corresponds to excite electrons in the valence band to the donor energy level. For the case of (SnFe + VO)–Fe2O3, this value is 3650 nm.
Conclusions
In brief, this paper investigates the formation mechanisms and the electronic structures of Fe2O3 with doped atom and oxygen vacancy by first principles calculation. Our results demonstrate that: (1) the oxygen vacancy is easier to be created due to the introduction of doped atom Ti or Sn. (2) The interaction of oxygen vacancy and doping has obvious effects on the electronic structure around the bandgap of hematite. The oxygen vacancy and doped Ti make the bandgap decrease from 2.20 eV to 2.07 eV. Meanwhile, two donor levels are generated at 1.47 eV and 1.73 eV under the bottom of the conduction band, respectively. For the system with oxygen vacancy and doped Sn ions, the bandgap width shrinks to 2.09 eV, and the donor level is introduced at 1.75 eV from the conduction band minimum. (3) The interaction of doping and oxygen vacancy can enlarge visible light absorption edge and improve utilization of low energy photons due to intermediate bands within bandgap.Conflicts of interest
There are no conflicts to declare.Notes and references
- A. Fujishima and K. Honda, Nature, 1972, 238, 37 CrossRef CAS PubMed.
- T. Bak, J. Nowotny, M. Rekas and C. C. Sorrell, Int. J. Hydrogen Energy, 2002, 27, 991–1002 CrossRef CAS.
- P. Merchant, R. Collins, R. Kershaw, K. Dwight and A. Wold, J. Solid State Chem., 1979, 27, 307–315 CrossRef CAS.
- A. Kay, I. Cesar and M. Grätzel, J. Am. Chem. Soc., 2006, 128, 15714–15721 CrossRef CAS PubMed.
- A. B. Murphy, P. R. F. Barnes, L. K. Randeniya, I. C. Plumb, I. E. Grey, M. D. Horne and J. A. Glasscock, Int. J. Hydrogen Energy, 2006, 31, 1999 CrossRef CAS.
- H. J. Ahn, M. J. Kwak, J. S. Lee, K. Y. Yoon and J. H. Jang, J. Mater. Chem. A, 2014, 2, 19999–20003 RSC.
- N. J. Cherepy, D. B. Liston, J. A. Lovejoy, H. M. Deng and J. Z. Zhang, J. Phys. Chem. B, 1998, 102, 770 CrossRef CAS.
- Y. Zhang, S. Jiang, W. Song, P. Zhou, H. Ji, W. Ma, W. Hao, C. Chen and J. Zhao, Energy Environ. Sci., 2015, 8, 1231–1236 RSC.
- S. Song, J. Kim, D. Lee, J. Lee, T. Min, J. A. Chae, J. S. Bae, J. Lee, J. S. Lee and S. Park, J. Am. Ceram. Soc., 2017, 100, 3928–3934 CrossRef CAS.
- X. Meng, G. Qin, W. A. Goddard III, S. Li, H. Pan, X. Wen, Y. Qin and L. Zuo, J. Phys. Chem. C, 2013, 117, 3779–3784 CrossRef CAS.
- K. Sivula, R. Zboril, F. Le Formal, R. Robert, A. Weidenkaff, J. Tucek, J. Frydrych and M. Grätzel, J. Am. Chem. Soc., 2010, 132, 7436 CrossRef CAS PubMed.
- G. Wang, Y. Ling, H. Wang, L. Xihong and Y. Li, J. Photochem. Photobiol. C Photochem. Rev., 2014, 19, 35 CrossRef CAS.
- Y. Ling, G. Wang, D. A. Wheeler, J. Z. Zhang and Y. Li, Nano Lett., 2011, 11, 2119–2125 CrossRef CAS PubMed.
- M. N. Huda, A. Walsh, Y. Yan, S. H. Wei and M. M. Al-Jassim, J. Appl. Phys., 2010, 107, 123712 CrossRef.
- J. A. Glasscock, P. R. F. Barnes, I. C. Plumb and N. Savvides, J. Phys. Chem. C, 2007, 111, 44 CrossRef.
- M. Zhang, W. Luo, Z. Li, T. Yu and Z. Zou, Appl. Phys. Lett., 2010, 97, 042105 CrossRef.
- J. Deng, J. Zhong, A. Pu, D. Zhang, M. Li, X. Sun and S. T. Lee, J. Appl. Phys., 2012, 112, 084312 CrossRef.
- Y. Ling, G. Wang, J. Reddy, C. Wang, J. Z. Zhang and Y. Li, Angew. Chem., Int. Ed., 2012, 51, 4074–4079 CrossRef CAS PubMed.
- M. Li, J. Deng, A. Pu, P. Zhang, H. Zhang, J. Gao, Y. Hao, J. Zhong and X. Sun, J. Mater. Chem. A, 2014, 2, 6727–6733 RSC.
- M. Rioult, D. Stanescu, E. Fonda, A. Barbier and H. Magnan, J. Phys. Chem. C, 2016, 120, 7482–7490 CrossRef CAS.
- T. Y. Yang, H. Y. Kang, U. Sim, Y. J. Lee, J. H. Lee, B. Koo, K. T. Nam and Y. C. Joo, Phys. Chem. Chem. Phys., 2013, 15, 2117–2124 RSC.
- A. Pu, J. Deng, M. Li, J. Gao, H. Zhang, Y. Hao, J. Zhong and X. Sun, J. Mater. Chem. A, 2014, 2, 2491–2497 RSC.
- Z. Wang, X. Mao, P. Chen, M. Xiao, S. Monny, S. Wang, M. Konarova, A. Du and L. Wang, Angew. Chem., 2019, 131(4), 1042–1046 CrossRef.
- Y. Zhou, M. Yan, J. Hou, Y. Niu, D. Ni, H. Shen, P. Niu and Y. Ma, Sol. Energy, 2019, 179, 99–105 CrossRef CAS.
- Z. Zhou, S. Wu, L. Qin, L. Li, L. Li and X. Li, J. Mater. Chem. A, 2018, 6, 15593–15602 RSC.
- J. Wang, N. H. Perry, L. Guo, L. Vayssieres and H. L. Tuller, ACS Appl. Mater. Interfaces, 2018, 11(2), 2031–2041 CrossRef PubMed.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758 CrossRef CAS.
- J. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188 CrossRef.
- S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505 CrossRef CAS.
- N. J. Mosey, P. Liao and E. A. Carter, J. Chem. Phys., 2008, 129, 014103 CrossRef PubMed.
- M. Tang, J. X. Shang and Y. Zhang, RSC Adv., 2018, 8, 640 RSC.
- L. W. Finger and R. M. Hazen, J. Appl. Phys., 1980, 51, 5362 CrossRef CAS.
- Y. Sato and S.-I. Akimoto, J. Appl. Phys., 1979, 50, 5285 CrossRef CAS.
- P. Kumar, P. Sharma, R. Shrivastav, S. Dass and V. R. Satsangi, Int. J. Hydrogen Energy, 2011, 36, 2777 CrossRef CAS.
- J. H. Seo, K. Choi, J. Nam, H. Lee and J. H. Lee, Appl. Catal., B, 2020, 260, 118186 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ra01450h |
| This journal is © The Royal Society of Chemistry 2020 |