DOI:
10.1039/D0RA01661F
(Paper)
RSC Adv., 2020,
10, 16527-16536
Structural investigation of ternary PdRuM (M = Pt, Rh, or Ir) nanoparticles using first-principles calculations†
Received
21st February 2020
, Accepted 5th April 2020
First published on 27th April 2020
Abstract
We perform first-principles calculations and Monte Carlo sampling to investigate the structures of ternary PdRuM (M = Pt, Rh, or Ir) nanoparticles (NPs) with respect to three different spherical shapes. The morphologies include hexagonal close-packed (hcp), truncated-octahedral (fcc), and icosahedral (Ih, fcc) shapes with 57, 55, and 55 atoms, respectively. The calculations show that the atomic position is dominant in determining the stability of the ternary NPs. For bare ternary NPs, Pd and Ru atoms favor a location on the vertex sites and the core, respectively, which can be understood by the surface energy of the corresponding slab models. For single-crystalline NPs, the binary shell could be either a solid solution or a segregation alloy depending on composition and morphology. However, polycrystalline Ih NPs only form segregated binary shells surrounding the Ru core. Such configurations tend to minimize the surface lattice to gain more energy from the d orbital of the transition metals. In addition to the bare NPs, we study the oxidized ternary NPs. The results show that the Ru atoms penetrate outwards from the core to the surface reducing the oxidation formation energy. Furthermore, oxygen adsorption facilitates Pt, Pd, and Pd penetration into the PdRuPt, PdRuRh, and PdRuIr NPs, respectively. Most of the oxide shells are a solid solution, except for the PdRuRh NP with an Ih shape, which is found to be in a segregation shell. The free energy calculation reveals that the pure hcp NPs are thermodynamically unstable under oxygen-rich conditions. This work clearly demonstrates the structural trends of small ternary NPs and their oxidation, unveiling that the structural trends can be understood by the surface formation energy and the interplay between adsorbent and adsorbing oxygen atoms.
1 Introduction
Metallic nanoparticles (NPs) are promising functional materials in many fields such as: energy conservation, catalysis, chemosensing and element storage.1–4 In order to achieve better performance of particular functions, many experiments aim to synthesize modified NPs to adjust their properties physically and chemically. For example, experimental and theoretical investigations have reported that a TiPt alloy provides a better oxygen reduction reaction (ORR) than pure Ti NPs in fuel cell applications.5–7 There are many different shapes of metallic NPs which have been observed in experiments, such as icosahedron, decahedron, octahedron, and their variants. The stability of NPs depends on the number of atoms and the atomic composition.8 Nevertheless, recent work has demonstrated that the morphology of NPs can reversibly transform the exposed facets under different solvent conditions to minimize the surface energy.9,10 Apart from the morphology change of pure NPs induced by the environment, the different composition of multinary NPs can lead to different exposed facets with various atomic composition. For example, a recent experiment observed that the core–shell structure of bimetallic AuAg NPs is determined by the composition ratio of Au and Ag atoms. The species with greater concentration in the binary alloy occupies the shell sites of the NPs.11 Thus, besides this intrinsic property influencing the configuration, there are many factors significantly influencing the structure of NPs.12 In order to provide deeper insight into the structural properties of NPs, the configuration of many NPs have been investigated with different levels of theoretical methods. The theoretical calculations imply that the core–shell structure is not a necessary configuration for stable bimetallic NPs, and it might be possible to consider an onion structure and solid solution as alternative options.13 In addition, for bimetallic TiPt NPs used in fuel cells it has been found that their oxidation can facilitate the formation of multiple core and shell NPs.14
Bimetallic PdRu NPs have been reported to provide more efficient catalytic reactions – such as COx conversion, NOx conversion, and hydrogenation reactions – than their parent metallic NPs.15–18 HAADF-STEM images clarified the Pd and Ru atoms are homogeneously distributed in the synthesized NPs at room temperature.15 By heating up to 550 K, in situ XRD experimentally observed that the PdRu NPs segregate into fcc Pd and hexagonal close-packed (hcp) Ru phases.19 Besides, X-ray absorption spectroscopy observed that the Ru atoms enrich the PdRu NPs surface region under ORR activity with Ru–O formation.20 Further, TEM images clearly show that the hcp Ru monolayer can be deposited on fcc Pd NPs along the [111] direction via a random hcp (rhcp) structure, whose structure is similar to that of stacking faults and is usually observed in hexagonal lattices.17,21,22 Apart from the structural study, it is worth noting that PdRu NPs suffer from the loss of metal elements during catalytic cycles.23 In order to overcome this drawback and explore higher catalytic activity materials, PdRu-based NPs or alloys have been studied. A recent work reported the synthesis of ternary NPs with controlled composition and selectivity.24 PdRuPt NPs exhibit higher catalytic activity and durability in fuel cells compared to commercial Pt/C and PtRu/C catalysts.25 In addition, Rh and Ir additives are suggested for as-prepared PdRu NPs due to their promising ability in NO reactions.26,27 PdRu-based ternary NPs therefore are one of the promising catalytic materials for the next generation. There are only a few theoretical calculations of ternary NPs, but ternary slab or bulk calculations can still provide constructive information for the following research. The density functional theory (DFT) calculations demonstrate that the Pd atoms should segregate into two surfaces for PdRuRh ternary slab, and Ru and Rh atoms form a binary bulk as a solid solution.28 Besides, the MD and DFT calculations have shown that the ternary NPs may have structural variations even at lower temperature.29
There is a lot of research which has investigated oxygen adsorption on Pd, Ru, Pt, Rh, and Ir surfaces, subsurfaces or in the bulk using electron energy loss spectroscopy (EELS), low energy electron diffraction (LEED), and thermal desorption spectroscopy (TDS).30–32 The most common adsorbent surfaces are fcc (111) and hcp (0001). A (2 × 2) diffraction pattern of lower monolayer (ML) coverage has been usually observed in the LEED experiments.33 In addition, the increased coverage decreases the binding energy of oxygen adsorption, revealing the lateral O–O repulsion. Theoretical investigations also compute the oxygen adsorption energy depending upon the oxygen coverage and the oxygen adsorption sites, namely, four common sites: 3-fold fcc, 3-fold hcp, bridge, and top sites.34–38 In addition, the vibrational frequency of peroxide or superoxide have been observed, indicating O2 molecules can molecularly adsorbs on cleaved surfaces.30,39 There are many theoretical studies which provide useful information on the oxidized NPs. A recent theoretical work demonstrates that the oxygen adsorption on 3-fold hollow sites, and the linear O–metal–O configuration can minimize the adsorption energy.40 The expansion of the calculated surface lattice as the oxygen coverage increases implies the increase of surface strain of NPs under the oxidization process.40 The variance of the surface lattice significantly influences not only the selectivity of oxygen adsorption, but also the oxygen penetration into the NPs.40,41 Apart from the properties of NPs, the chosen substrates can provide different oxygen adsorption and catalytic performance. Recent work demonstrates that the Pt NPs supported on the defective graphene can increase the adsorption energy by 1.62 eV per pair (pair means O2 molecule) further enhancing the catalytic activity.42 Furthermore, the Mars–van Krevelen mechanism also involves molecule adsorption on defective substrates to reinforce catalytic performance.
Although there are many experimental investigations which have studied ternary PdRuM (M = Pt, Rh, or Ir) NPs and their catalytic reaction, atomistic insight into the ternary PdRuM NPs and oxygen adsorption on hcp (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1) surfaces (or facets) is missing. Therefore, we study the structure of bare ternary NPs, hcp surface oxidation, and the oxidized NPs to extend the ternary NPs research. The paper is organized as follows: Section 2 describes the methodology employed in our calculations. The results are presented in Section 3. Finally, Section 4 discusses the interplay of physical mechanisms governing the structural trend of the ternary NPs, and a summary is provided as the conclusion.
1) surfaces (or facets) is missing. Therefore, we study the structure of bare ternary NPs, hcp surface oxidation, and the oxidized NPs to extend the ternary NPs research. The paper is organized as follows: Section 2 describes the methodology employed in our calculations. The results are presented in Section 3. Finally, Section 4 discusses the interplay of physical mechanisms governing the structural trend of the ternary NPs, and a summary is provided as the conclusion.
2 Method
First-principles DFT calculations are performed using the Perdew, Burke, and Ernzerhof (PBE) exchange–correlation functional and pseudo-atomic localized basis function as implemented in the OpenMX (Open source package for Material eXplorer) software package.43–45 For transition metal (Pd, Ru, Pt, Rh, and Ir) and oxygen atoms, the basis functions TM7.0-s2p2d2f1 and O7.0-s3p3d2f1 are employed in the calculations, respectively, which were generated by the confinement scheme, and optimized by a variational optimization method.43 The pseudopotentials of Pd, Ru, Pt, Rh, Ir, and O atoms include 16, 14, 16, 15, 15, and 6 valence electrons, respectively. The accuracy of the basis functions and pseudopotentials we used were carefully benchmarked by the delta gauge method.46 Real space grid techniques are used for the numerical integrations and the solution of the Poisson equation using FFT with the energy cutoff of 300 Ryd.45 The Γ-point is used for the k-point sampling of all NP calculations, and 13 × 13 × 13 as the k-point sampling for bulk calculations. Following the above approach, the optimized lattice constants (a) for Pd, Pt, Rh, and Ir fcc structures are 3.95, 3.97, 3.84, and 3.88 Å, respectively as shown in Table 1. In addition, the lattice constant a and c/a ratio of the Ru hcp structure are 2.73 Å and 1.56, respectively. These structural parameters compare well with both experimental and other theoretical results. Moreover, the bond length of the optimized molecular oxygen is 1.24 Å in a supercell with 10 × 10 × 10 Å3 cubic dimensions. The energy tolerance for self-consistent field optimization is 1 ×10−6 hartree, the force tolerance per atom for geometry optimization is less than 5 ×10−4 hartree bohr−1.
Table 1 Optimised lattice constant (a) for five elements in fcc and hcp structures. ΔE represents the energy difference between the bulk fcc and hcp structures (Efcc − Ehcp)
| |
fcc |
hcp |
ΔE (eV) |
| a (Å) |
a (Å) |
c/a |
| Pd |
3.95 |
2.79 |
1.67 |
−0.045 |
| Ru |
3.82 |
2.73 |
1.56 |
0.116 |
| Pt |
3.97 |
2.81 |
1.70 |
−0.020 |
| Rh |
3.84 |
2.71 |
1.63 |
−0.040 |
| Ir |
3.88 |
2.74 |
1.64 |
−0.600 |
Monte Carlo (MC) sampling is utilized to decide the atomic arrangement randomly. The procedure of the selection process is as follows. Firstly, we construct the atomic coordinate for hcp, truncated-octahedral (tOh), and icosahedral (Ih) NPs with 57, 55, and 55 atoms in total, respectively. Hereafter, the above NPs are abbreviated as hcp57, tOh55, and Ih55. The hcp NP includes two (0001) and twelve (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1) facets (pyramidal slip plane).47–49 For fcc NPs, the tOh NP involves six (001) and eight (111) facets, while the Ih NP includes only twenty (111) facets. By considering the crystalline structure, these morphologies are categorized into single crystalline (hcp and tOh shapes) and polycrystalline (Ih shape) NPs. After the construction of NPs, the MC sampling assigns the atomic species to individual atoms for respective NPs. The ratio of Pd
1) facets (pyramidal slip plane).47–49 For fcc NPs, the tOh NP involves six (001) and eight (111) facets, while the Ih NP includes only twenty (111) facets. By considering the crystalline structure, these morphologies are categorized into single crystalline (hcp and tOh shapes) and polycrystalline (Ih shape) NPs. After the construction of NPs, the MC sampling assigns the atomic species to individual atoms for respective NPs. The ratio of Pd![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ru
Ru![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) M elements is approximately 1
M elements is approximately 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. In the bare NPs investigation, 30 MC samples are applied to each combination of ternary NPs (both element composition and morphology). Therefore, there are 270 ternary NPs to be optimized at this stage of bare NPs calculation. In order to compare the stability among the NPs, we calculate the formation energy
1. In the bare NPs investigation, 30 MC samples are applied to each combination of ternary NPs (both element composition and morphology). Therefore, there are 270 ternary NPs to be optimized at this stage of bare NPs calculation. In order to compare the stability among the NPs, we calculate the formation energy
| |
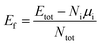 | (1) |
where
Etot represents the total energy of ternary NPs,
Ni and
Ntot mean the number of atoms in particular species, i, and in total, respectively.
μi is the bulk energy of a particular element per atom. To further understand the stability regarding the atomic arrangements, we compute the average displacement of each species taken from the center of NPs to determine their positions
| | |
Δrs = ∑|rs,i − rc|/Ns
| (2) |
where
rs,i and
rc represent the coordinate of species s of atom i, and the central positions of the NPs, respectively.
Ns is the total number of the element s, and the subscript i represents the atom index. To assess the structural trends revealed by the MC sampling, we also calculate the surface energies of the slab models defined by
| |
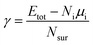 | (3) |
where
Etot and
μi indicate the total energy of the slab system and the bulk energy of species i per atom, respectively.
Ni and
Nsur imply the number of atoms of the slab and on the surface sites, respectively. To quantify the stability of oxygen adsorption, the adsorption energy is calculated as
| |
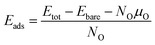 | (4) |
where
Etot and
Ebare represent the total energy of the optimized system with oxygen adsorption and without, respectively.
NO and
μO are the number of adsorbed oxygen atoms and chemical potential of oxygen, respectively. The chemical potential of oxygen is equal to the half energy of oxygen molecules,
μO = ½
EO2, under O K temperature.
3 Results
3.1 Stability of ternary NPs
We utilise the Monte Carlo sampling to allocate the species for each atom of the ternary NPs to obtain the different possible atomic configurations in an unbiased way. Note that the details are described in the method section. In order to understand the structural trend of the ternary NPs, we calculate the average displacement (eqn (2)) of each element in each NP. Fig. 1 shows the displacement variation versus the formation energy of the NPs. The red-dashed rectangles indicate the most energetically stable structures in the calculations of MC sampling. Thus, the general trends of atomic position in stable atomic configurations can be summarized as shown in Table 2, implying which are the favorable atoms from the core to the surface (especially vertex) regions. Pt, Pd, and Ru should be organized into the surface, subsurface, and core of the PdRuPt NPs, respectively. For PdRuRh NPs, Pd, Rh, and Ru follow the order of surface, subsurface, and core sites, respectively. The atomic ordering of PdRuIr NPs depends upon the fcc or hcp crystalline NPs. For fcc PdRuIr NPs, Pd, Ir, and Ru atoms should appear at surface, subsurface, and core, respectively. However, Ru and Ir atoms reverse their atomic ordering in the hcp PdRuIr NPs. To interpret these particular orderings, we calculated the surface formation energy for the respective cleaved surfaces, including fcc (111) and hcp (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1) as summarized in Table 3. The predicted orderings of MC sampling show good agreement with the surface formation energy, i.e., the element with the smaller surface formation energy tends to locate at the surface region.
1) as summarized in Table 3. The predicted orderings of MC sampling show good agreement with the surface formation energy, i.e., the element with the smaller surface formation energy tends to locate at the surface region.
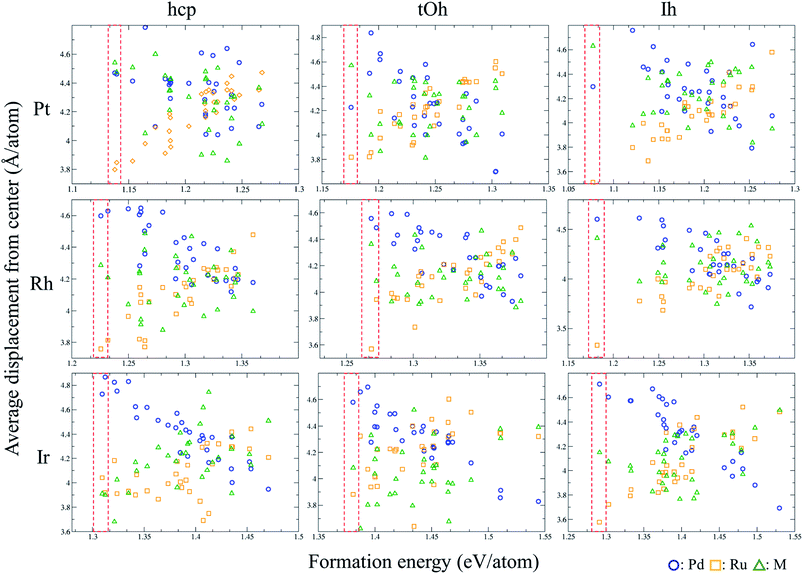 |
| | Fig. 1 Variation of the average displacement from the centre of the PdRuM NPs versus the formation energy per atom. The arrangements of these ternary NPs are generated using the MC sampling. | |
Table 2 Atomic arrangements (a) predicted using the MC sampling, and (b) the most stable structures in the calculation. The “Core” indicates that the specific element favors a location in the center of the NPs, while “Surface” implies that the element prefers to adsorb on the surface, especially the vertex sites
| |
fcc NPs |
hcp NPs |
| PdRuPt |
PdRuRh |
PdRuIr |
PdRuPt |
PdRuRh |
PdRuIr |
| (a) Prediction using Monte Carlo sampling |
| Surface |
Pt |
Pd |
Pd |
Pt |
Pd |
Pd |
| ↑ |
Pd |
Rh |
Ir |
Pd |
Rh |
Ru |
| Core |
Ru |
Ru |
Ru |
Ru |
Ru |
Ir |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
| (b) Most stable structure in the calculations |
| Surface |
Pd |
Pd |
Pd |
Pd |
Pd |
Pd |
| ↑ |
Pt |
Rh |
Ir |
Pt |
Rh |
Ir |
| Core |
Ru |
Ru |
Ru |
Ru |
Ru |
Ru |
Table 3 Surface formation energies with respect to five elements in the fcc and hcp structures. The fcc (001) and hcp (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1) contain 8 layers, fcc (111) and hcp (0001) involve 6 layers. For the in-plane lattice constants, a, of these structures refer to Table 1
1) contain 8 layers, fcc (111) and hcp (0001) involve 6 layers. For the in-plane lattice constants, a, of these structures refer to Table 1
| |
fcc |
hcp |
| γ (eV per atom) |
γ (eV per atom) |
| (001) |
(111) |
(0001) |
(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1) 1) |
| Pd |
0.88 |
0.68 |
0.74 |
0.91 |
| Ru |
1.84 |
1.31 |
1.09 |
1.25 |
| Pt |
0.88 |
0.62 |
0.74 |
0.97 |
| Rh |
1.17 |
0.87 |
0.96 |
1.11 |
| Ir |
1.37 |
0.97 |
1.11 |
1.33 |
By following the trend shown in Table 2(a), we manually created several ternary NPs to find the most stable configuration. Fig. 2 shows the most stable structures found in our structural survey and Table 2(b) summarizes the atomic orderings of the most stable ternary NPs. For all the bare ternary NPs, the Ru atoms form a core surrounded by the binary shell, and the Pd atoms prefer to locate on the vertex sites in most cases. The most stable configurations of the shell structures are categorized into two groups. One is where Pd and M atoms are homogeneously mixed as a solid solution alloy, and the other is where the Pd and M atoms segregate from each other forming two semi-spheres as shown in Fig. 2. The former configuration is the most stable for all the single crystalline ternary NPs except for the PdRuIr NP in the tOh shape. Meanwhile, the PdRuIr NP in the tOh shape and all the ternary Ih NPs favor the formation of a segregation configuration. The ternary NPs shown in Fig. 2 are more stable by 0.1 to 0.2 eV per atom than the ones obtained from the MC sampling. There are two contradictions between the orderings predicted by the MC sampling and the one of the most stable structures shown in Table 2. The first one is the exchange between Ru and Ir atoms in hcp-PdRuIr NPs. This is due to the fact that the larger bond length of the Ir atoms, compared to the Ru atoms, expands the surface lattice by 1% when Ir atoms form a core in the NPs. The surface expansion increases the surface energy destabilizing the ternary NPs. The second contradiction is the exchange between Pd and Pt atoms for all PdRuPt NPs. According to the surface formation energy, the Pd and Pt surfaces should be comparable. However, the formation energy of the pure Pd NPs is more stable by 0.15 eV per atom than the pure Pt NPs (see Table S1 in the ESI†). Thus, Pd atoms should be allocated at the surface sites rather than Pt atoms. The variance of the formation energy of different pure NPs can be understood by the Friedel model, which demonstrates that transition metals with different filled d orbitals possess changed cohesive energy, and the cohesive energy becomes greater from 3d, 4d to 5d.50 Thus, a transition metal with larger cohesive energy indicates their increased instability in the formed NPs.
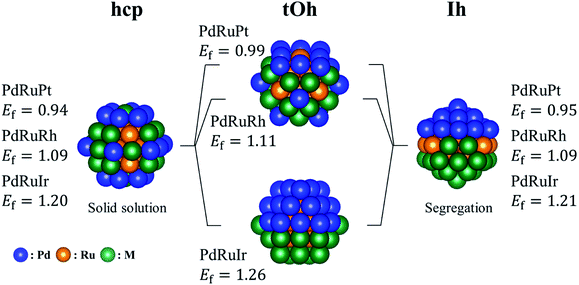 |
| | Fig. 2 The most energetically stable ternary PdRuM NPs in the calculations. The blue, orange, and green spheres represent the Pd, Ru, and M (M = Pt, Rh, or Ir) atoms, respectively. The listed formation energies (Ef) are in eV per atom unit. | |
There are two main factors we have found that dominate the stability of bare ternary NPs. The first factor has been shown above, i.e., Pd and Ru atoms should respectively occupy the vertex sites and in the core region in order to increase the stability. The other one is on the surface lattice of ternary NPs: in the calculations, we found that these particular configurations all tend to maximally minimize their surface lattice compared to the bond length of 3.79 Å. Because the ternary NPs are Pd based and the Pd lattice constant is greater than that of the Ru atom, thus we specify the bond length of 3.79 Å in fcc Pd as the reference for bond length. For the NPs with a solid solution shell, the Pd–M bond length decreases by 3.8% on average. Meanwhile, the bond reduction of 3.0% on average, has been found for the configurations with a segregation shell. In addition, the Ir–Ir bond length shows a significant reduction of 6.2%. Fig. 3 demonstrates the strain effect using an fcc (111) monolayer structure to model the monolayer shell. Fig. 3(a) shows the strain effect of the solid solution alloys and Fig. 3(b) demonstrates the influence on the pure monolayers. In this simple model, the reduction of 1%, from 2.79 Å, in Pd–Pt, Pd–Rh and Pd–Ir surface bond lengths can lead to 0.09, 0.10, and 0.13 eV per Pd–M pair (hereafter pair) energy gain, respectively. Furthermore, the reduction of 1% in Pd–Pd, Pt–Pt, Rh–Rh, and Ir–Ir bond length respectively decreases by 0.07, 0.13, 0.14, and 0.19 eV per pair. The energy gains of the solid solution surface (2ΔEPd–M) and segregation surface (ΔEPd–Pd + ΔEM–M) are almost comparable, but the configurations with Pd atoms at the vertex sites provide better stability for NPs formation. Thus, in most cases the solid solution alloys dominate the shell configurations. However, due to the greater bond reduction of Ir–Ir on ternary NPs, we suggest the segregation shell should dominate the PdRuIr NPs without considering the Pd vertex influence. Apart from the single crystalline, the solid solution shell seems to be energetically too unstable to deal with the Ih NPs. We believe the interior boundaries in Ih NPs are unfavourable for the formation of a shell with solid solution alloy, therefore the segregation configuration takes over the shell structure of Ih NPs. Obviously, we analyze only the configuration on the binary shell since Ru atoms already form a bulk-like core. We assume its influence on the formation energy can be ignored as long as the core exists. The result shows that the surface strain has a dominant effect on the surface energy, leading to the specific configurations of solid solution and segregation shells. In addition, the element on the low coordination sites plays an important role for the ternary NPs at this scale. Once the NP scale increases, the influence of low coordination sites should lose its dominant stability effect.
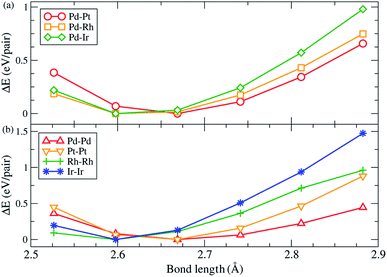 |
| | Fig. 3 The variation of total energy as a function of different bond lengths. The monolayer hexagonal structure is modelled by the monolayer shell of the ternary NPs. (a) is for Pd–M alloy surfaces, while (b) shows the same species surfaces of pure Pd, Pt, Rh, and Ir atoms. | |
Apart from the structural analysis, Bader analysis shows that the bare ternary NPs have a negatively charged shell and a positively charged core. In other words, the Ru atom transfers 0.2 electrons to the M atoms on average, while the Pd atoms stay neutral. However, the Pd atoms receive a half charge transferred from the Ru atoms in the PdRuRh and PdRuIr NPs with an Ih shape. This kind of charge transfer is not unique solely for core(Ru)–shell(Pd and M) configurations, but also for the structures from the calculations by the MC sampling.
3.2 Oxygen adsorption on hcp (10![[1 with combining macron]](https://www.rsc.org/images/entities/h3_char_0031_0304.gif) 1) surfaces
1) surfaces
Oxygen adsorption and diffusion on fcc (111), fcc (001), and hcp (0001) surfaces has been studied in many elements and different phases (such as bulk, surface, and NP).38,51–56 However, oxygen adsorption on the hcp (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1) surface has limited research. Thus, we provide the adsorption energy of an oxygen atom on Pd, Ru, Pt, Rh, and Ir hcp (10
1) surface has limited research. Thus, we provide the adsorption energy of an oxygen atom on Pd, Ru, Pt, Rh, and Ir hcp (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1) surfaces as summarized in Table 4. The Pd, Ru, Rh, and Ir slabs consist of 4 layers of hcp (10
1) surfaces as summarized in Table 4. The Pd, Ru, Rh, and Ir slabs consist of 4 layers of hcp (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1) surfaces, while the Pt slab involves 8 layers of hcp (10
1) surfaces, while the Pt slab involves 8 layers of hcp (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1) surfaces. There are four different adsorption sites for an oxygen atom on the hcp (10
1) surfaces. There are four different adsorption sites for an oxygen atom on the hcp (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1) surface, i.e., a 4-fold hollow site, 3-fold fcc site, 3-fold hcp site, and a bridge site. The on-top site adsorption is not thermodynamically stable, and the geometry optimization leads to the oxygen falling into the adjacent hollow site instead of adsorbing on the on-top site. The difference between the 3-fold fcc and 3-fold hcp site is the number of second-nearest neighbors on the subsurface. The former site has 3 on the subsurface while the latter only possesses 1 directly below the adsorbing oxygen atom.40 The bond length (metal–oxygen) of the bridged site is the shortest, at less than 2.0 Å, and the longest one is the oxygen adsorption on the 4-fold hollow site, which is around 2.1 Å. This result indicates that the oxygen adsorption on the 3-fold fcc site is the most stable compared to the other three sites and the preference of oxygen adsorption is found to be Ru → Rh → Ir → Pd ≈ Pt. The adsorption energy of oxygen atom is comparable to the calculated oxygen adsorption on the fcc (111) surfaces, which has been summarized in Table S2† for comparison.
1) surface, i.e., a 4-fold hollow site, 3-fold fcc site, 3-fold hcp site, and a bridge site. The on-top site adsorption is not thermodynamically stable, and the geometry optimization leads to the oxygen falling into the adjacent hollow site instead of adsorbing on the on-top site. The difference between the 3-fold fcc and 3-fold hcp site is the number of second-nearest neighbors on the subsurface. The former site has 3 on the subsurface while the latter only possesses 1 directly below the adsorbing oxygen atom.40 The bond length (metal–oxygen) of the bridged site is the shortest, at less than 2.0 Å, and the longest one is the oxygen adsorption on the 4-fold hollow site, which is around 2.1 Å. This result indicates that the oxygen adsorption on the 3-fold fcc site is the most stable compared to the other three sites and the preference of oxygen adsorption is found to be Ru → Rh → Ir → Pd ≈ Pt. The adsorption energy of oxygen atom is comparable to the calculated oxygen adsorption on the fcc (111) surfaces, which has been summarized in Table S2† for comparison.
Table 4 Single oxygen atom adsorption on hcp (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1) surfaces of Pd, Ru, Pt, Rh, and Ir hcp crystalline structures. The four fold hollow site adsorption energy of the Ir surface is missing, because the oxygen is too unstable to adsorb on this site. The oxygen atom preferentially adsorbs on the bridge site of the Ir surface instead of the 4-fold hollow site
1) surfaces of Pd, Ru, Pt, Rh, and Ir hcp crystalline structures. The four fold hollow site adsorption energy of the Ir surface is missing, because the oxygen is too unstable to adsorb on this site. The oxygen atom preferentially adsorbs on the bridge site of the Ir surface instead of the 4-fold hollow site
| |
Eads (eV per atom) |
| 4-fold hollow site |
3-fold fcc site |
3-fold hcp site |
Bridge site |
| Pd |
−1.84 |
−2.06 |
−1.97 |
−1.59 |
| Ru |
−3.41 |
−3.65 |
−3.39 |
−3.10 |
| Pt |
−1.21 |
−1.84 |
−1.50 |
−1.35 |
| Rh |
−2.41 |
−2.78 |
−2.59 |
−2.40 |
| Ir |
— |
−2.47 |
−2.30 |
−2.43 |
3.3 Oxygen adsorption on pure NPs
Since Section 3.2 demonstrates the oxygen adsorption on hcp (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1) surfaces, the continuation of the work is to reveal the configurations of a pair of oxygen atoms adsorbing on hcp NPs. In this section, we consider a pure Pd hcp57 NP to demonstrate the oxygen adsorption. Fig. 4 shows four possible configurations of oxygen adsorption on hcp57 NPs with the O–O bond length less than 5 Å. In this section, two oxygen atoms both adsorbing on hcp (0001) facets is not considered due to its similarity to oxygen atom adsorption on the fcc (111) facet. The oxygen adsorption of types (A) to (D) are described as follows: (A) two oxygen atoms adsorb on the same hcp (10
1) surfaces, the continuation of the work is to reveal the configurations of a pair of oxygen atoms adsorbing on hcp NPs. In this section, we consider a pure Pd hcp57 NP to demonstrate the oxygen adsorption. Fig. 4 shows four possible configurations of oxygen adsorption on hcp57 NPs with the O–O bond length less than 5 Å. In this section, two oxygen atoms both adsorbing on hcp (0001) facets is not considered due to its similarity to oxygen atom adsorption on the fcc (111) facet. The oxygen adsorption of types (A) to (D) are described as follows: (A) two oxygen atoms adsorb on the same hcp (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1) facets, one adsorbs on the 3-fold hollow site and the other adsorbs on the bridge site at the edge; (B) two oxygen atoms adsorb on the same hcp (10
1) facets, one adsorbs on the 3-fold hollow site and the other adsorbs on the bridge site at the edge; (B) two oxygen atoms adsorb on the same hcp (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1) facet, the oxygen atoms initially adsorb on the 3-fold and 4-fold hollow sites. However, after optimization, the 4-fold site is reconstructed into a 3-fold site; (C) two oxygen atoms both adsorb on adjacent 3-fold hollow sites, but one adsorbs on the hcp (0001) facet and the other adsorbs on the hcp (10
1) facet, the oxygen atoms initially adsorb on the 3-fold and 4-fold hollow sites. However, after optimization, the 4-fold site is reconstructed into a 3-fold site; (C) two oxygen atoms both adsorb on adjacent 3-fold hollow sites, but one adsorbs on the hcp (0001) facet and the other adsorbs on the hcp (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1) facet; (D) two oxygen atoms adsorb on the adjacent hcp (10
1) facet; (D) two oxygen atoms adsorb on the adjacent hcp (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1) facets, both originally adsorb on the 4-fold hollow sites. After geometry optimization, the two facets locally transform into fcc (111)-like facets, thus the oxygen atoms adsorb on the 3-fold hollow sites. The local transformation occurring in the types B and D lead to a larger distortion energy (Ed ≈ 0.5 eV per NP) compared to the type A and C (Ed ≈ 0.2 eV per NP). The repulsion between the oxygen atoms dominates the adsorption energy of the oxygen adsorption, and the adsorption on the 4-fold hollow site may lead to a locally structural transformation.
1) facets, both originally adsorb on the 4-fold hollow sites. After geometry optimization, the two facets locally transform into fcc (111)-like facets, thus the oxygen atoms adsorb on the 3-fold hollow sites. The local transformation occurring in the types B and D lead to a larger distortion energy (Ed ≈ 0.5 eV per NP) compared to the type A and C (Ed ≈ 0.2 eV per NP). The repulsion between the oxygen atoms dominates the adsorption energy of the oxygen adsorption, and the adsorption on the 4-fold hollow site may lead to a locally structural transformation.
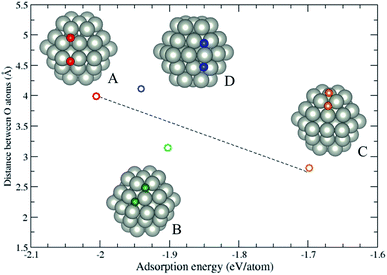 |
| | Fig. 4 The variation of adsorption energy of a pair of oxygen atoms versus the distance between the oxygen atoms. The color of the circles corresponds to the colored oxygen atoms and the dashed line is a guide for the eye. | |
Besides the oxygen adsorption on pure surfaces in Section 3.2, we calculated the adsorption energy for oxidized hcp57, tOh55, and Ih55 NPs as well. Pure hcp, tOh, and Ih NPs are adsorbed with 42, 48, and 60 oxygen atoms on the surfaces, respectively. The oxygen adsorption on fcc NPs is based on recent theoretical calculations,40 while the prediction of the oxidized hcp NPs is in accordance with the pair oxidation study in Fig. 4. The adsorption energy is summarized in Table 5 and the configurations of the oxygen atoms is similar to that shown in Fig. 5. In general, oxygen atoms prefer to adsorb on 3-fold hollow sites, which can maximize the coverage of oxygen adsorption. The adsorption energies of oxygen atoms on the NPs are in good agreement with the one on the surfaces shown in Table 4, but only Pt NPs show better stability of oxygen adsorption than Pd NPs. Thus, following the result above, Table 6 summarizes the suggested atomic ordering from core to surface (vertex) with respect to the oxidized ternary NPs. Although oxygen atoms preferentially adsorb on Pt NPs rather than Pd NPs, we still suggest Pd on subsurface sites of oxidized NPs would provide better stability for the NPs. In order to ensure the result is accurate, we will examine the situation of Pt on the surface for PdRuPt NPs in the next section.
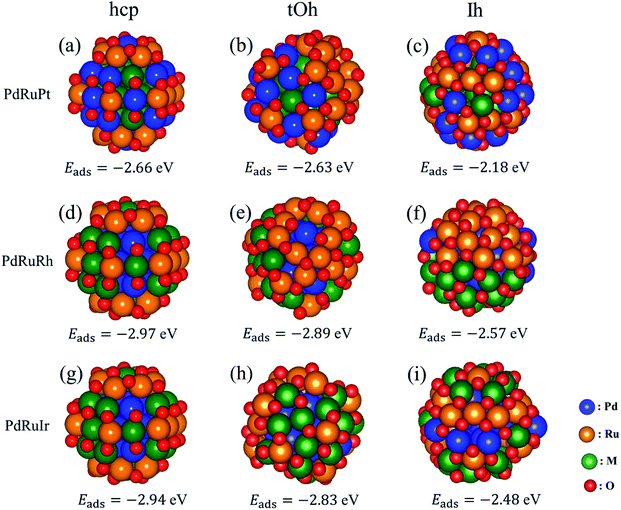 |
| | Fig. 5 The most energetically stable structures of high oxygen coverage on hcp, tOh, and Ih ternary NPs. The number of oxygen atoms adsorbing on hcp, tOh, and Ih NPs is 42, 48, and 60, respectively. The first, second, and third columns represent the NPs in hcp, tOh, and Ih shapes, respectively. The first, second, and third rows indicate the PdRuPt, PtRuRh, and PdRuIr systems, respectively. The listed adsorption energies are in eV per atom. | |
Table 5 Adsorption energy of oxygen atoms on pure Pd, Ru, Pt, Rh, and Ir NPs with hcp, tOh, and Ih shapes. There are 42, 48, and 60 oxygen atoms adsorbing on hcp57, tOh55, and Ih55 NPs, respectively
| |
Eads (eV per atom) |
| hcp |
tOh |
Ih |
| Pd |
−1.57 |
−1.65 |
−1.47 |
| Ru |
−3.15 |
−3.09 |
−2.78 |
| Pt |
−1.72 |
−1.70 |
−1.64 |
| Rh |
−2.44 |
−2.44 |
−2.14 |
| Ir |
−2.48 |
−2.43 |
−2.16 |
Table 6 Atomic arrangements of oxidized ternary NPs predicted using the oxidation formation energy. The “Core” indicates that the specific element favors locating in the center of the NPs, while “Surface” implies that the particular atom prefers to adsorb on the surface, especially the vertex sites
| Suggested oxidized ternary NPs |
| |
PdRuPt |
PdRuRh |
PdRuIr |
| Surface |
Ru |
Ru |
Ru |
| ↑ |
Pd |
Rh |
Ir |
| Core |
Pt |
Pd |
Pd |
3.4 Oxygen adsorption on ternary NPs
In order to understand the atomic arrangement of ternary NPs under an oxygen-rich catalytic environment (such as for NOx and SOx), we investigate the oxidized ternary NPs. When hcp NPs undergo lower oxygen adsorption as shown in Fig. 4, the local crystalline transformation makes it difficult to increase the oxygen coverage with high symmetry configurations step by step. We therefore only consider the highest oxygen coverage that we can achieve on the surface for investigating the oxidized ternary NPs. The prediction of atomic ordering, Table 6, of oxidized ternary NPs shows that the Ru atoms should locate on the surface (especially the vertex sites) to minimize the adsorption energy. To confirm this prediction, we consider four types of atomic arrangement of the ternary NPs, including solid solution shell, segregation shell, random arrangement for the whole NPs, and Ru-core configurations. The first two configurations include a Pd or Pt core depending on the ternary NPs. Meanwhile, the solid solution configurations mean that Ru atoms locating at the vertex sites and mixing with Pd, Rh, and Ir atoms act as binary shells for PdRuPt, PdRhRh, and PdRuIr NPs, respectively. The segregation configurations involve two semi-sphere shells with different elements and the same core structures as in the solid solution configurations. The random configurations are the most stable structures generated using the MC sampling in Section 3.1, and the Ru-core configurations are the most stable structures we found for bare ternary NPs as shown in Fig. 2. In addition, we reverse the position of the Pd and Pt atoms to confirm the atomic ordering of PdRuPt NPs. Therefore, there are 46 oxidized ternary NPs in total for examination. Fig. 5 shows the most energetically stable configurations for the oxidized ternary NPs. The result indicates that the configurations with a binary solid solution shell are the most favorable structures with high symmetry oxygen coverage, except for the oxidized PdRuRh NPs in an Ih shape. The exception has the most stable structure with a segregation shell, which is due to the similar bond length and electronic structures between Ru and Rh atoms. The listed adsorption energies of hcp and tOh NPs are lower than the one of Ih NPs, indicating that the lower coordination facets (such as hcp (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1) and fcc (001)) provide better ability to capture oxygen atoms. Besides, we also exchange the Pd and Pt positions for the PdRuPt NPs calculations in order to ensure the predicted atomic ordering. The exchange does not benefit the stability to the oxidized ternary PdRuPt NPs. Therefore, it is confirmed that the predicted arrangement summarized in Table 6 is valid for this scale of NP. The result shows the oxidation on facets facilitates the Ru penetration outwards to the surface of the NPs, while Pt, Pd, and Pd atoms penetrate inwardly into the PdRuPt, PdRuRh, and PdRuIr NPs, respectively. In addition, the bridge sites of the NPs provide better adsorption ability compared to the 3-fold hollow sites.
1) and fcc (001)) provide better ability to capture oxygen atoms. Besides, we also exchange the Pd and Pt positions for the PdRuPt NPs calculations in order to ensure the predicted atomic ordering. The exchange does not benefit the stability to the oxidized ternary PdRuPt NPs. Therefore, it is confirmed that the predicted arrangement summarized in Table 6 is valid for this scale of NP. The result shows the oxidation on facets facilitates the Ru penetration outwards to the surface of the NPs, while Pt, Pd, and Pd atoms penetrate inwardly into the PdRuPt, PdRuRh, and PdRuIr NPs, respectively. In addition, the bridge sites of the NPs provide better adsorption ability compared to the 3-fold hollow sites.
The calculated average O–O bond length for ternary hcp, tOh, and Ih NPs is approximately 3.7, 3.5, and 3.5 Å, respectively. The slightly larger O–O distance of hcp NPs indicates the lower oxygen coverage density on hcp NPs. In addition, the bond analysis (histogram shown in Fig. S1†) demonstrates that the O–O bond distribution of the PdRuPt NPs partly differs to the other two ternary NPs. The PdRuPt NPs provide dramatically increased O–O bond lengths of 2.4 and 4.0 Å by an additional 8 and 10%, respectively, compared to the ones of the PdRuRh and PdRuIr NPs. The particular bond lengths refer to the oxidized Pd atoms on the surface, the PdO is a quasi one-dimensional structure and exhibits four oxygen atoms adsorbing on a Pd atom. The bond lengths of 2.4 and 4.0 Å belong to the distances of two adjacent (short side) and two diagonal oxygen atoms. The rest of the O–O bond length distribution of PdRuPt NPs are consistent with the other two oxidized NPs. Table 7 summarizes the average Ru–O bond length for the respective ternary NPs. The oxidized hcp NPs show relatively small Ru–O bond lengths (1.89 to 1.95 Å) compared to fcc NPs. The bond analysis demonstrates that the shorter Ru–O bond is the attribute of the bridge site adsorption. The larger number of bridge site adsorptions of hcp NPs causes a decrease of the Ru–O bond length by 2.5%. Therefore, the morphology of ternary NPs might be possible to clarify using the vibrational frequency of the Ru–O signal without visual observation. Bader analysis shows that the ternary NPs transfer an average of 0.75 electrons to each oxygen atom, but it is hard to find any strong correlation between the charge transfer and the adsorption sites (or adsorbed elements) in the present investigation.
Table 7 The average Ru–O bond length with respect to different oxidized ternary NPs
| Average Ru–O bond length (Å) |
| |
PdRuPt |
PdRuRh |
PdRuIr |
| hcp57 |
1.89 |
1.92 |
1.95 |
| tOh55 |
1.94 |
1.97 |
2.00 |
| Ih55 |
2.02 |
1.97 |
2.00 |
In order to access the thermodynamic stability of oxidized NPs, the free energy per metal atom is calculated by
| |
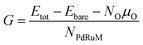 | (5) |
where
Etot and
Ebare respectively represent the total energy of the oxidized and bare NPs.
NO and
NPdRuM are the number of oxygen and metal atoms, respectively.
μO indicates the chemical potential of the oxygen atom corresponding to various conditions, which can be formulated as
μi(
T,
pi) =
μ0(
T,
p0) + ½
kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
ln(
pi/
p0), where subscript i represents the state of the oxygen atom, and superscript “0” means the ground state.
kB,
T, and
p represent the Boltzmann constant, temperature, and pressure, respectively. In
eqn (5), the total energy of bare ternary NPs has been subtracted in order to eliminate the effect from the bare Ru-out configurations, focusing on the energy gain by oxidation.
Fig. 6 demonstrates the free energy for respective ternary NPs as a function of oxygen chemical potential. The reference of
μO = 0 in
Fig. 6 refers to the half energy of the oxygen molecule.
57 The reduction limit (turning point) of each free energy plot, summarized in
Table 8, indicates the chemical potential of the first oxygen atom adsorbing on the NPs. The hcp and tOh NPs present the lower
μO of reduction limit demonstrating that the oxygen atoms prefer to adsorb on the NPs with lower coordination facets. The free energy shows that the tOh and Ih NPs are almost the dominant morphologies of the oxidized ternary NPs. Pure hcp NPs are only thermodynamically stable when
μO < −4.91, < −5.01, and < −4.45 eV for PdRuPt, PdRuRh, and PdRuIr NPs, respectively. However, according to the chemical table of oxygen atoms,
μO < −4.0 eV is an extreme oxygen-poor condition.
57 Thus, we suggest that the pure hcp NPs cannot survive under oxygen-rich conditions. The result indicates that the binary shell of the oxidized NPs is a solid solution alloy in most cases, and the fcc NPs are thermodynamically stable under an oxygen-rich condition instead of pure hcp NPs. In addition, we note that the chemical potential at which the ternary NPs start to be oxidized is lower than that in the surface reduction limit, indicating the NPs are more easily oxidized than those of the surface (Pd, Ru, Pt, Rh, and Ir).
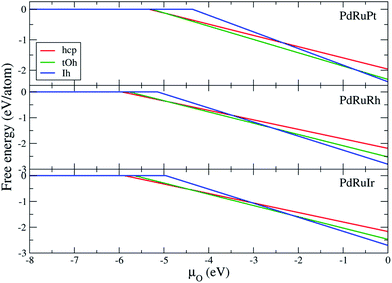 |
| | Fig. 6 Free energy of ternary NPs with hcp, tOh, and Ih morphologies as a function of oxygen chemical potential. μO = 0 eV represents oxygen molecule as an ideal-gas-like reservoir (T = 0 K, p = 1 atm). | |
Table 8 Oxygen chemical potential μO at which oxidation ternary NPs occur. The value can correspond to the turning points with respect to the different ternary NPs in Fig. 6
| |
μO (eV) |
| PdRuPt |
PdRuRh |
PdRuIr |
| hcp |
−5.33 |
−5.94 |
−5.88 |
| tOh |
−5.27 |
−5.78 |
−5.66 |
| Ih |
−4.36 |
−5.14 |
−4.96 |
4 Conclusion and discussion
In summary, we have investigated the structures of bare and oxidized ternary NPs with hcp, tOh, and Ih shapes. The study indicates that the Ru atoms should form a core in the NPs surrounded by a binary shell mixed with Pd and M atoms. The shell is categorized into solid solution and segregation configurations depending upon the element composition and crystalline structure. Generally, single crystalline NPs involve solid solution shells, and polycrystalline NPs provide segregation shells. Our analysis shows that these particular configurations tend to optimize the surface lattice to minimize the formation energy of bare ternary NPs. The oxidation calculations demonstrate that the oxygen adsorption facilitates the atomic penetration between the surface and core, the RuO shell significantly reduces the formation energy. In addition, the result shows that the hcp NPs provide higher stability for oxygen adsorption, but the less adsorbed sites make oxidized hcp NPs thermodynamically unstable in the free energy calculation in most of the chemical potential range. Finally, We have also examined the spin-polarization calculations on both bare ternary NPs and oxidized NPs. The result demonstrates that the ternary NPs in this scale are non-magnetic.
The result of the ternary NPs investigation, summarized above, demonstrates that the atomic position governs the stability of the ternary NPs. However, since the studied NPs are of small size, the investigation may miss some factors influencing the configuration of real scale ternary NPs. For example, the stacking fault of fcc structure in a multinary alloy may increase the formation energy.58 In addition, the larger number of layers of shell on larger NPs could make strain play a different role on the ternary NPs. Finally, we suggest that the real scale NPs are the core–shell system with Ru core and Pd–M solid solution shell. The number of Ru cores depend upon the size of the ternary NPs.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
This work was supported by Priority Issue (creation of new functional devices and high-performance materials to support next-generation industries) to be tackled using Post “K” Computer, Ministry of Education, Culture, Sports, Science and Technology (MEXT), Japan. HA and OY were financially supported by JST ACCEL Grant Number JPJPMJAC1501, Japan.
References
- K.-W. Park, J.-H. Choi, S.-A. Lee, C. Pak, H. Chang and Y.-E. Sung, J. Catal., 2004, 224, 236–242 CrossRef CAS.
- R. Narayanan and M. A. El-Sayed, J. Am. Chem. Soc., 2003, 125, 8340–8347 CrossRef CAS PubMed.
- E. Oliveira, C. Nunez, H. M. Santos, J. Fernandez-Lodeiro, A. Fernandez-Lodeiro, J. L. Capelo and C. Lodeiro, Sens. Actuators, B, 2015, 212, 297–328 CrossRef CAS.
- K.-J. Jeon, H. R. Moon, A. M. Ruminski, B. Jiang, C. Kisielowski, R. Bardhan and J. J. Urban, Nat. Mater., 2011, 10, 286 CrossRef CAS PubMed.
- H. Duan, Q. Hao and C. Xu, J. Power Sources, 2015, 280, 483–490 CrossRef CAS.
- P. C. Jennings, H. A. Aleksandrov, K. M. Neyman and R. L. Johnston, J. Phys. Chem. C, 2015, 119, 11031–11041 CrossRef CAS.
- P. C. Jennings, B. G. Pollet and R. L. Johnston, Phys. Chem. Chem. Phys., 2012, 14, 3134–3139 RSC.
- F. Baletto and R. Ferrando, Rev. Mod. Phys., 2005, 77, 371 CrossRef CAS.
- P. Geysermans, F. Finocchi, J. Goniakowski, R. Hacquart and J. Jupille, Phys. Chem. Chem. Phys., 2009, 11, 2228–2233 RSC.
- Y. Zhou, Y. Zhu, Z.-Q. Wang, S. Zou, G. Ma, M. Xia, X. Kong, L. Xiao, X.-Q. Gong and J. Fan, J. Am. Chem. Soc., 2017, 139, 13740–13748 CrossRef CAS PubMed.
- T.-W. Liao, A. Yadav, K.-J. Hu, J. van der Tol, S. Cosentino, F. D’Acapito, R. E. Palmer, C. Lenardi, R. Ferrando and D. Grandjean, et al., Nanoscale, 2018, 10, 6684–6694 RSC.
- I. Lee, M. A. Albiter, Q. Zhang, J. Ge, Y. Yin and F. Zaera, Phys. Chem. Chem. Phys., 2011, 13, 2449–2456 RSC.
- H. Liu, G. Canizal, P. Schabes-Retchkiman and J. Ascencio, J. Phys. Chem. B, 2006, 110, 12333–12339 CrossRef CAS PubMed.
- S. Gholhaki, S.-H. Hung, D. J. Cant, C. E. Blackmore, A. G. Shard, Q. Guo, K. P. McKenna and R. E. Palmer, RSC Adv., 2018, 8, 27276–27282 RSC.
- K. Kusada, H. Kobayashi, R. Ikeda, Y. Kubota, M. Takata, S. Toh, T. Yamamoto, S. Matsumura, N. Sumi and K. Sato, et al., J. Am. Chem. Soc., 2014, 136, 1864–1871 CrossRef CAS PubMed.
- C. Huang, X. Yang, H. Yang, P. Huang, H. Song and S. Liao, Appl. Surf. Sci., 2014, 315, 138–143 CrossRef CAS.
- D. Wu, K. Kusada and H. Kitagawa, Sci. Technol. Adv. Mater., 2016, 17, 583–596 CrossRef CAS PubMed.
- K. Sato, H. Tomonaga, T. Yamamoto, S. Matsumura, N. D. B. Zulkifli, T. Ishimoto, M. Koyama, K. Kusada, H. Kobayashi and H. Kitagawa, et al., Sci. Rep., 2016, 6, 28265 CrossRef CAS PubMed.
- J. Fisher, N. Cabello-Moreno, E. Christian and D. Thompsett, Electrochem. Solid-State Lett., 2009, 12, B77–B81 CrossRef CAS.
- Y. Sun, Y.-C. Hsieh, L.-C. Chang, P.-W. Wu and J.-F. Lee, J. Power Sources, 2015, 277, 116–123 CrossRef CAS.
- X. Huang, H. Li, S. Li, S. Wu, F. Boey, J. Ma and H. Zhang, Angew. Chem., Int. Ed., 2011, 50, 12245–12248 CrossRef CAS PubMed.
- J. Ge, D. He, L. Bai, R. You, H. Lu, Y. Lin, C. Tan, Y.-B. Kang, B. Xiao and Y. Wu, et al., J. Am. Chem. Soc., 2015, 137, 14566–14569 CrossRef CAS PubMed.
- D. Wu, Z. Zheng, S. Gao, M. Cao and R. Cao, Phys. Chem. Chem. Phys., 2012, 14, 8051–8057 RSC.
- M. S. I. Sarker, T. Nakamura and S. Sato, J. Mater. Res., 2014, 29, 856–864 CrossRef.
- C. Shang, Y. Guo and E. Wang, Nano Res., 2018, 11, 4348–4355 CrossRef CAS.
- R. Voorhoeve and L. Trimble, J. Catal., 1978, 54, 269–280 CrossRef CAS.
- K. Almusaiteer, R. Krishnamurthy and S. Chuang, Catal. Today, 2000, 55, 291–299 CrossRef CAS.
- S. M. Aspera, R. L. Arevalo, H. Nakanishi and H. Kasai, Surf. Sci., 2018, 671, 51–59 CrossRef CAS.
- S. Erkoç and H. Oymak, J. Phys. Chem. B, 2003, 107, 12118–12125 CrossRef.
- X. Guo, A. Hoffman and J. T. Yates Jr, J. Chem. Phys., 1989, 90, 5787–5792 CrossRef CAS.
- J. L. Gland, B. A. Sexton and G. B. Fisher, Surf. Sci., 1980, 95, 587–602 CrossRef CAS.
- A. Böttcher and H. Niehus, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 60, 14396–14404 CrossRef.
- D. H. Parker, M. E. Bartram and B. E. Koel, Sur. Sci., 1989, 217, 489–510 CrossRef CAS.
- M. Todorova, K. Reuter and M. Scheffler, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 195403 CrossRef.
- M. P. Hyman and J. W. Medlin, J. Phys. Chem. B, 2006, 110, 15338–15344 CrossRef CAS PubMed.
- C. Stampfl, S. Schwegmann, H. Over, M. Scheffler and G. Ertl, Phys. Rev. Lett., 1996, 77, 3371 CrossRef CAS PubMed.
- M. V. Ganduglia-Pirovano and M. Scheffler, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 15533 CrossRef CAS.
- Y. Xu and M. Mavrikakis, J. Chem. Phys., 2002, 116, 10846–10853 CrossRef CAS.
- P. Jakob, A. Schlapka and P. Gazdzicki, J. Chem. Phys., 2011, 134, 224707 CrossRef PubMed.
- S.-H. Hung and K. P. McKenna, J. Phys. Chem. C, 2018, 122, 3107–3114 CrossRef CAS.
- L. Wang, A. Roudgar and M. Eikerling, J. Phys. Chem. C, 2009, 113, 17989–17996 CrossRef CAS.
- D.-H. Lim and J. Wilcox, J. Phys. Chem. C, 2011, 115, 22742–22747 CrossRef CAS.
- T. Ozaki, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 155108 CrossRef.
- T. Ozaki and H. Kino, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 195113 CrossRef.
- T. Ozaki and H. Kino, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 045121 CrossRef.
- K. Lejaeghere, G. Bihlmayer, T. Björkman, P. Blaha, S. Blügel, V. Blum, D. Caliste, I. E. Castelli, S. J. Clark and A. Dal Corso, et al., Sci, 2016, 351, aad3000 CrossRef PubMed.
- G. Wang, M. Van Hove, P. Ross and M. Baskes, J. Chem. Phys., 2004, 121, 5410–5422 CrossRef CAS PubMed.
- Y. Nanba, T. Ishimoto and M. Koyama, J. Phys. Chem. C, 2017, 121, 27445–27452 CrossRef CAS.
- T. Britton, F. Dunne and A. Wilkinson, Proc. R. Soc. A, 2015, 471, 20140881 CrossRef.
- J. Friedel, Proc. Int. School in Physics “Enrico Fermi”, Course XXXVII, ed. W. Marshall, Academic Press, New York, 1967, pp. 283–318 Search PubMed.
- M. Todorova, K. Reuter and M. Scheffler, J. Phys. Chem. B, 2004, 108, 14477–14483 CrossRef CAS.
- C. Stampfl, S. Schwegmann, H. Over, M. Scheffler and G. Ertl, Phys. Rev. Lett., 1996, 77, 3371–3374 CrossRef CAS PubMed.
- O. R. Inderwildi, D. Lebiedz, O. Deutschmann and J. Warnatz, J. Chem. Phys., 2005, 122, 034710 CrossRef PubMed.
- H. Tang, A. Van der Ven and B. L. Trout, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 045420 CrossRef.
- M. Todorova, K. Reuter and M. Scheffler, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 195403 CrossRef.
- M. Lynch and P. Hu, Surf. Sci., 2000, 458, 1–14 CrossRef CAS.
- R. Karsten and S. Matthias, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 65, 035406 CrossRef.
- L.-Y. Tian, R. Lizárraga, H. Larsson, E. Holmström and L. Vitos, Acta Mater., 2017, 136, 215–223 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ra01661f |
|
| This journal is © The Royal Society of Chemistry 2020 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article ,
Hiroshi Akiba,
Osamu Yamamuro and
Taisuke Ozaki*
,
Hiroshi Akiba,
Osamu Yamamuro and
Taisuke Ozaki*
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1) surfaces (or facets) is missing. Therefore, we study the structure of bare ternary NPs, hcp surface oxidation, and the oxidized NPs to extend the ternary NPs research. The paper is organized as follows: Section 2 describes the methodology employed in our calculations. The results are presented in Section 3. Finally, Section 4 discusses the interplay of physical mechanisms governing the structural trend of the ternary NPs, and a summary is provided as the conclusion.
1) surfaces (or facets) is missing. Therefore, we study the structure of bare ternary NPs, hcp surface oxidation, and the oxidized NPs to extend the ternary NPs research. The paper is organized as follows: Section 2 describes the methodology employed in our calculations. The results are presented in Section 3. Finally, Section 4 discusses the interplay of physical mechanisms governing the structural trend of the ternary NPs, and a summary is provided as the conclusion.![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1) facets (pyramidal slip plane).47–49 For fcc NPs, the tOh NP involves six (001) and eight (111) facets, while the Ih NP includes only twenty (111) facets. By considering the crystalline structure, these morphologies are categorized into single crystalline (hcp and tOh shapes) and polycrystalline (Ih shape) NPs. After the construction of NPs, the MC sampling assigns the atomic species to individual atoms for respective NPs. The ratio of Pd
1) facets (pyramidal slip plane).47–49 For fcc NPs, the tOh NP involves six (001) and eight (111) facets, while the Ih NP includes only twenty (111) facets. By considering the crystalline structure, these morphologies are categorized into single crystalline (hcp and tOh shapes) and polycrystalline (Ih shape) NPs. After the construction of NPs, the MC sampling assigns the atomic species to individual atoms for respective NPs. The ratio of Pd![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ru
Ru![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) M elements is approximately 1
M elements is approximately 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. In the bare NPs investigation, 30 MC samples are applied to each combination of ternary NPs (both element composition and morphology). Therefore, there are 270 ternary NPs to be optimized at this stage of bare NPs calculation. In order to compare the stability among the NPs, we calculate the formation energy
1. In the bare NPs investigation, 30 MC samples are applied to each combination of ternary NPs (both element composition and morphology). Therefore, there are 270 ternary NPs to be optimized at this stage of bare NPs calculation. In order to compare the stability among the NPs, we calculate the formation energy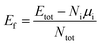
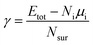
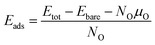
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1) as summarized in Table 3. The predicted orderings of MC sampling show good agreement with the surface formation energy, i.e., the element with the smaller surface formation energy tends to locate at the surface region.
1) as summarized in Table 3. The predicted orderings of MC sampling show good agreement with the surface formation energy, i.e., the element with the smaller surface formation energy tends to locate at the surface region.

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1) contain 8 layers, fcc (111) and hcp (0001) involve 6 layers. For the in-plane lattice constants, a, of these structures refer to Table 1
1) contain 8 layers, fcc (111) and hcp (0001) involve 6 layers. For the in-plane lattice constants, a, of these structures refer to Table 1
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1)
1)![[1 with combining macron]](https://www.rsc.org/images/entities/h3_char_0031_0304.gif) 1) surfaces
1) surfaces![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1) surface has limited research. Thus, we provide the adsorption energy of an oxygen atom on Pd, Ru, Pt, Rh, and Ir hcp (10
1) surface has limited research. Thus, we provide the adsorption energy of an oxygen atom on Pd, Ru, Pt, Rh, and Ir hcp (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1) surfaces as summarized in Table 4. The Pd, Ru, Rh, and Ir slabs consist of 4 layers of hcp (10
1) surfaces as summarized in Table 4. The Pd, Ru, Rh, and Ir slabs consist of 4 layers of hcp (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1) surfaces, while the Pt slab involves 8 layers of hcp (10
1) surfaces, while the Pt slab involves 8 layers of hcp (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1) surfaces. There are four different adsorption sites for an oxygen atom on the hcp (10
1) surfaces. There are four different adsorption sites for an oxygen atom on the hcp (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1) surface, i.e., a 4-fold hollow site, 3-fold fcc site, 3-fold hcp site, and a bridge site. The on-top site adsorption is not thermodynamically stable, and the geometry optimization leads to the oxygen falling into the adjacent hollow site instead of adsorbing on the on-top site. The difference between the 3-fold fcc and 3-fold hcp site is the number of second-nearest neighbors on the subsurface. The former site has 3 on the subsurface while the latter only possesses 1 directly below the adsorbing oxygen atom.40 The bond length (metal–oxygen) of the bridged site is the shortest, at less than 2.0 Å, and the longest one is the oxygen adsorption on the 4-fold hollow site, which is around 2.1 Å. This result indicates that the oxygen adsorption on the 3-fold fcc site is the most stable compared to the other three sites and the preference of oxygen adsorption is found to be Ru → Rh → Ir → Pd ≈ Pt. The adsorption energy of oxygen atom is comparable to the calculated oxygen adsorption on the fcc (111) surfaces, which has been summarized in Table S2† for comparison.
1) surface, i.e., a 4-fold hollow site, 3-fold fcc site, 3-fold hcp site, and a bridge site. The on-top site adsorption is not thermodynamically stable, and the geometry optimization leads to the oxygen falling into the adjacent hollow site instead of adsorbing on the on-top site. The difference between the 3-fold fcc and 3-fold hcp site is the number of second-nearest neighbors on the subsurface. The former site has 3 on the subsurface while the latter only possesses 1 directly below the adsorbing oxygen atom.40 The bond length (metal–oxygen) of the bridged site is the shortest, at less than 2.0 Å, and the longest one is the oxygen adsorption on the 4-fold hollow site, which is around 2.1 Å. This result indicates that the oxygen adsorption on the 3-fold fcc site is the most stable compared to the other three sites and the preference of oxygen adsorption is found to be Ru → Rh → Ir → Pd ≈ Pt. The adsorption energy of oxygen atom is comparable to the calculated oxygen adsorption on the fcc (111) surfaces, which has been summarized in Table S2† for comparison.
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1) surfaces of Pd, Ru, Pt, Rh, and Ir hcp crystalline structures. The four fold hollow site adsorption energy of the Ir surface is missing, because the oxygen is too unstable to adsorb on this site. The oxygen atom preferentially adsorbs on the bridge site of the Ir surface instead of the 4-fold hollow site
1) surfaces of Pd, Ru, Pt, Rh, and Ir hcp crystalline structures. The four fold hollow site adsorption energy of the Ir surface is missing, because the oxygen is too unstable to adsorb on this site. The oxygen atom preferentially adsorbs on the bridge site of the Ir surface instead of the 4-fold hollow site
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1) surfaces, the continuation of the work is to reveal the configurations of a pair of oxygen atoms adsorbing on hcp NPs. In this section, we consider a pure Pd hcp57 NP to demonstrate the oxygen adsorption. Fig. 4 shows four possible configurations of oxygen adsorption on hcp57 NPs with the O–O bond length less than 5 Å. In this section, two oxygen atoms both adsorbing on hcp (0001) facets is not considered due to its similarity to oxygen atom adsorption on the fcc (111) facet. The oxygen adsorption of types (A) to (D) are described as follows: (A) two oxygen atoms adsorb on the same hcp (10
1) surfaces, the continuation of the work is to reveal the configurations of a pair of oxygen atoms adsorbing on hcp NPs. In this section, we consider a pure Pd hcp57 NP to demonstrate the oxygen adsorption. Fig. 4 shows four possible configurations of oxygen adsorption on hcp57 NPs with the O–O bond length less than 5 Å. In this section, two oxygen atoms both adsorbing on hcp (0001) facets is not considered due to its similarity to oxygen atom adsorption on the fcc (111) facet. The oxygen adsorption of types (A) to (D) are described as follows: (A) two oxygen atoms adsorb on the same hcp (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1) facets, one adsorbs on the 3-fold hollow site and the other adsorbs on the bridge site at the edge; (B) two oxygen atoms adsorb on the same hcp (10
1) facets, one adsorbs on the 3-fold hollow site and the other adsorbs on the bridge site at the edge; (B) two oxygen atoms adsorb on the same hcp (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1) facet, the oxygen atoms initially adsorb on the 3-fold and 4-fold hollow sites. However, after optimization, the 4-fold site is reconstructed into a 3-fold site; (C) two oxygen atoms both adsorb on adjacent 3-fold hollow sites, but one adsorbs on the hcp (0001) facet and the other adsorbs on the hcp (10
1) facet, the oxygen atoms initially adsorb on the 3-fold and 4-fold hollow sites. However, after optimization, the 4-fold site is reconstructed into a 3-fold site; (C) two oxygen atoms both adsorb on adjacent 3-fold hollow sites, but one adsorbs on the hcp (0001) facet and the other adsorbs on the hcp (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1) facet; (D) two oxygen atoms adsorb on the adjacent hcp (10
1) facet; (D) two oxygen atoms adsorb on the adjacent hcp (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1) facets, both originally adsorb on the 4-fold hollow sites. After geometry optimization, the two facets locally transform into fcc (111)-like facets, thus the oxygen atoms adsorb on the 3-fold hollow sites. The local transformation occurring in the types B and D lead to a larger distortion energy (Ed ≈ 0.5 eV per NP) compared to the type A and C (Ed ≈ 0.2 eV per NP). The repulsion between the oxygen atoms dominates the adsorption energy of the oxygen adsorption, and the adsorption on the 4-fold hollow site may lead to a locally structural transformation.
1) facets, both originally adsorb on the 4-fold hollow sites. After geometry optimization, the two facets locally transform into fcc (111)-like facets, thus the oxygen atoms adsorb on the 3-fold hollow sites. The local transformation occurring in the types B and D lead to a larger distortion energy (Ed ≈ 0.5 eV per NP) compared to the type A and C (Ed ≈ 0.2 eV per NP). The repulsion between the oxygen atoms dominates the adsorption energy of the oxygen adsorption, and the adsorption on the 4-fold hollow site may lead to a locally structural transformation.
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1) and fcc (001)) provide better ability to capture oxygen atoms. Besides, we also exchange the Pd and Pt positions for the PdRuPt NPs calculations in order to ensure the predicted atomic ordering. The exchange does not benefit the stability to the oxidized ternary PdRuPt NPs. Therefore, it is confirmed that the predicted arrangement summarized in Table 6 is valid for this scale of NP. The result shows the oxidation on facets facilitates the Ru penetration outwards to the surface of the NPs, while Pt, Pd, and Pd atoms penetrate inwardly into the PdRuPt, PdRuRh, and PdRuIr NPs, respectively. In addition, the bridge sites of the NPs provide better adsorption ability compared to the 3-fold hollow sites.
1) and fcc (001)) provide better ability to capture oxygen atoms. Besides, we also exchange the Pd and Pt positions for the PdRuPt NPs calculations in order to ensure the predicted atomic ordering. The exchange does not benefit the stability to the oxidized ternary PdRuPt NPs. Therefore, it is confirmed that the predicted arrangement summarized in Table 6 is valid for this scale of NP. The result shows the oxidation on facets facilitates the Ru penetration outwards to the surface of the NPs, while Pt, Pd, and Pd atoms penetrate inwardly into the PdRuPt, PdRuRh, and PdRuIr NPs, respectively. In addition, the bridge sites of the NPs provide better adsorption ability compared to the 3-fold hollow sites.
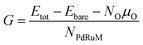
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(pi/p0), where subscript i represents the state of the oxygen atom, and superscript “0” means the ground state. kB, T, and p represent the Boltzmann constant, temperature, and pressure, respectively. In eqn (5), the total energy of bare ternary NPs has been subtracted in order to eliminate the effect from the bare Ru-out configurations, focusing on the energy gain by oxidation. Fig. 6 demonstrates the free energy for respective ternary NPs as a function of oxygen chemical potential. The reference of μO = 0 in Fig. 6 refers to the half energy of the oxygen molecule.57 The reduction limit (turning point) of each free energy plot, summarized in Table 8, indicates the chemical potential of the first oxygen atom adsorbing on the NPs. The hcp and tOh NPs present the lower μO of reduction limit demonstrating that the oxygen atoms prefer to adsorb on the NPs with lower coordination facets. The free energy shows that the tOh and Ih NPs are almost the dominant morphologies of the oxidized ternary NPs. Pure hcp NPs are only thermodynamically stable when μO < −4.91, < −5.01, and < −4.45 eV for PdRuPt, PdRuRh, and PdRuIr NPs, respectively. However, according to the chemical table of oxygen atoms, μO < −4.0 eV is an extreme oxygen-poor condition.57 Thus, we suggest that the pure hcp NPs cannot survive under oxygen-rich conditions. The result indicates that the binary shell of the oxidized NPs is a solid solution alloy in most cases, and the fcc NPs are thermodynamically stable under an oxygen-rich condition instead of pure hcp NPs. In addition, we note that the chemical potential at which the ternary NPs start to be oxidized is lower than that in the surface reduction limit, indicating the NPs are more easily oxidized than those of the surface (Pd, Ru, Pt, Rh, and Ir).
ln(pi/p0), where subscript i represents the state of the oxygen atom, and superscript “0” means the ground state. kB, T, and p represent the Boltzmann constant, temperature, and pressure, respectively. In eqn (5), the total energy of bare ternary NPs has been subtracted in order to eliminate the effect from the bare Ru-out configurations, focusing on the energy gain by oxidation. Fig. 6 demonstrates the free energy for respective ternary NPs as a function of oxygen chemical potential. The reference of μO = 0 in Fig. 6 refers to the half energy of the oxygen molecule.57 The reduction limit (turning point) of each free energy plot, summarized in Table 8, indicates the chemical potential of the first oxygen atom adsorbing on the NPs. The hcp and tOh NPs present the lower μO of reduction limit demonstrating that the oxygen atoms prefer to adsorb on the NPs with lower coordination facets. The free energy shows that the tOh and Ih NPs are almost the dominant morphologies of the oxidized ternary NPs. Pure hcp NPs are only thermodynamically stable when μO < −4.91, < −5.01, and < −4.45 eV for PdRuPt, PdRuRh, and PdRuIr NPs, respectively. However, according to the chemical table of oxygen atoms, μO < −4.0 eV is an extreme oxygen-poor condition.57 Thus, we suggest that the pure hcp NPs cannot survive under oxygen-rich conditions. The result indicates that the binary shell of the oxidized NPs is a solid solution alloy in most cases, and the fcc NPs are thermodynamically stable under an oxygen-rich condition instead of pure hcp NPs. In addition, we note that the chemical potential at which the ternary NPs start to be oxidized is lower than that in the surface reduction limit, indicating the NPs are more easily oxidized than those of the surface (Pd, Ru, Pt, Rh, and Ir).





