Bandgap engineering of few-layered MoS₂ with low concentrations of S vacancies

Abstract

Band-gap engineering of molybdenum disulfide (MoS₂) by introducing vacancies is of particular interest owing to the potential optoelectronic applications. In this work, systematic density functional theory (DFT) calculations were carried out for few-layered 3R-MoS₂ with different concentrations of S vacancies. All results revealed that the defect energy levels introduced on both sides of the Fermi level formed an intermediate band in the band gap. Both the edges of the intrinsic and intermediate bands of the structures with the same type of vacancies were generally closer to the Fermi level, and the gaps decreased as the number of layers increased from 2 to 4. The preferentially formed S vacancies at the top layer and the transition of defect types from point to line led to similar indirect band gaps for 2- and 4-layered 3R-MoS₂ with a low bulk concentration (around 5%) of S vacancies. This is different from most reported results about transition metal dichalcogenide (TMD) materials that the indirect band gap decreases as the number of layers increases and the low concentrations of vacancies show negligible influence on the band gap value.

---

1 Introduction

Since the discovery of graphene, numerous two-dimensional (2D) materials have been synthesized and investigated. Molybdenum disulfide (MoS₂), a transition metal dichalcogenide (TMD) existing mainly in 1T (tetragonal, AA stacking), 2H (hexagonal, ABAB stacking), and 3R (rhombohedral, ABCABC stacking) polymorphs, is one of the most prominent 2D materials owing to its wide potential optoelectronic applications, such as phototransistors,¹ solar cells,² light-emitting devices³ and catalysis.^4–6

Many experiments show that monolayer MoS₂ is a direct band gap semiconductor with an optical gap of 1.9 eV³ and strong photoluminescence (PL), while multilayers exhibit much weaker PL due to their indirect band gap.⁷ The band gap of MoS₂ decreases as the number of layers increases.^7–9 The properties of MoS₂ are commonly optimized by strain, doping and defect engineering.^10–15 For example, both doping and defects have been reported as effective ways for the band-gap engineering of MoS₂ to significantly strengthen the optical absorption.^16–22 It has also been shown that low concentrations of vacancies may induce shallow and deep energy levels with negligible influence on the band gap value.^23,24

Theoretically, the direct band gap is calculated to be 1.68 eV for monolayered MoS₂.²⁵ It becomes indirect and decreases as the number of layers increases.^9,26,27 The optical direct band gap (at the K point) stays almost unchanged and is close to the value of the optical direct band gap of a bulk system.²⁸ Dopants and defects can not only modulate the band gap and energy level, but also modify the compositions of the band edges.^29–35 For example, point and line S vacancies can form deep or shallow gaps, induce a reduction in the band gap and even alter the electronic properties from semiconductors to metals.^10,19,36

Different from the unit cell of the 1T and 2H phases, the unit cell of the 3R phase comprises triple-layer (ABC) stacking. In this way, the periodic symmetry is broken for structures with incomplete ABC stacking such as AB, ABCA, and ABCAB.³⁷ Therefore, it is expected that 3R-type few-layered MoS₂ should have different properties from the other types of MoS₂.^38,39 Here, considering the different distributions and concentrations of S vacancies, systemic density functional theory (DFT) calculations were carried out to study the band structure engineering of few-layered (2 to 4) 3R MoS₂.

2 Computational details

All DFT calculations were performed within the generalized gradient approximation of the Perdew–Burke–Ernzerhof (PBE) functional using the Vienna ab initio simulation package (VASP).^40,41 van der Waals corrections were considered for all calculations.⁴² An energy cut off of 500 eV for the plane-wave expansion was used and the force on the relaxed atoms was less than 0.01 eV Å⁻¹. In the supercell, the vacuum region of 15 Å was contained in the z-direction. In the band structure calculations, the Brillouin zone was sampled using a (18 × 18 × 1) Γ-centered mesh for the unit cell,³⁷ which has been proved to be useful in describing layered structures. The calculated values of the lattice constants for 3R bulk MoS₂ were a = 3.191 Å and c = 18.530 Å, close to the experimental values (3.163 Å and 18.370 Å, respectively).⁴³ The calculated band gap of pristine bulk 3R MoS₂ was 0.80 eV, and those for 1-, 2-, 3- and 4-layered (ABCA) structures were 1.81, 1.33, 0.97 and 0.91 eV, respectively; these were in agreement with the reported experimental (1.96 and 1.55 eV for 1- and 2-layered structures, respectively)⁴⁴ and calculated (1.68, 1.11, 0.93, and 0.88 eV for 1-, 2-, 3- and 4-layered structures, respectively)^25,37 results. Band structure calculations with and without spin polarization were carried out for 3R MoS₂ with S point vacancies, which revealed that the spin polarization had a negligible influence on the band structures. Thus, the spin polarization was not considered in this study.

3 Results and discussion

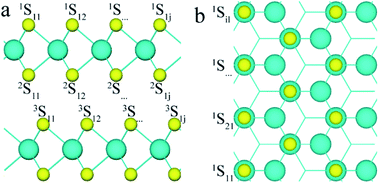
To analyse the structure of 3R MoS₂, the first, second and third layers of S atoms were denoted with superscripts 1, 2, and 3, and the row and column of the S atoms were denoted with subscripts i and j, respectively, as shown in Fig. 1 (e.g., ⁿS_ij represents the S atom at i row and j column on the n^th S layer). To study the effect of defects on the band structure of 3R MoS₂, the formation energies of neutral and charged S point vacancies were calculated based on the following functions:

E_f[S] = E_tot[S] − E_tot[pure] − ∑nμ (1)

E_f[S^q] = E_tot[S^q] − E_tot[pure] − ∑nμ + q[E_F + E_υ + ΔV] (2)

Here, E_f[S] represents the formation energy of S vacancies, E_tot[S] and E_tot[pure] represent the energies of the structure with and without S vacancies, and n and μ are the number and chemical potential of the S atoms in the S₈ ring, respectively. E_F is the Fermi level referenced to the valence band maximum of pure MoS₂. E_υ is the energy of the valence band maximum of pure MoS₂. ΔV represents a correction term to align the electrostatic potential in the defect supercell with that in pure MoS₂.⁴⁵

Fig. 1 The (a) side and (b) top views of the 2-layered 3R MoS₂ (the number of superscripts represents the layer of S atoms, and the first and second subscripts represent the row and column of S atoms, respectively).

The formation energy of one S point defect was calculated by adopting a (6 × 6) supercell, which was large enough to avoid the influence of adjacent periodicity (d_S–S = 19.15 Å), and the result (2.89 eV per S vacancy) was consistent with the reported value (2.57 eV).⁴⁶ The formation energies of the negatively charged (−0.3, −1, −2e) S vacancies were calculated for 2-layered structures by the second formula. The results showed that the formation energies of the charged vacancies became larger (by 0.15, 0.64, and 1.61 eV) than that of the neutral ones and increased with the charge carried by the S vacancies; thus, they were not considered here. It should be noted that a constant chemical potential was adopted here,^47,48 and the case may be different when the chemical potentials corresponding to the S (or Mo)-rich conditions were changed.^49–51

For simplicity, two S point vacancies with different combinations were considered to understand the influence of the interval of S point vacancies. All models can be classified into two groups: (i) two S vacancies at the same S layer (labeled as ¹S₁₁/¹S_ij or ²S₁₁/²S_ij); (ii) two S vacancies at different S layers (labeled as ¹S₁₁/²S_ij or ²S₁₁/³S_ij). Here, ¹S₁₁ and ²S_ij were at the same Mo layer, while ²S₁₁ and ³S_ij were within different Mo layers. Different cases were considered for each group; for example, for the group (i), the ¹S₁₁ atom was combined with other ¹S_ij atoms in the same layer (see Fig. 1). Also, a smaller (4 × 3) (AB)-layered supercell was built to compare the tendency of the formation energies of S point vacancies in different concentrations. The formation energies are shown in Table 1.

Table 1 The formation energies of two S vacancies in (6 × 6) and (4 × 3) (in italics) supercells

	^1S11/^1Sij (^2S11/^2Sij)					^1S11/^2Sij			^2S11/^3Sij
Distance (Å)	3.191	5.527	6.382	8.882	9.573	3.115	4.457	6.343	3.576	4.793	5.578	8.595
Eform (eV)	5.75	5.80	5.83	5.81	5.81	5.75	5.88	5.82	5.85	5.87	5.87	5.87
	5.85	5.91	5.93 (6.00)			5.88	5.94	5.88	5.90	5.91	5.92	5.92

---

It was clear that the formation energy of two S point vacancies at the top layer was smaller than that for the ones with a similar distance at inner layers (5.78 vs. 5.84 eV; 5.93 vs. 6.00 eV), indicating that the structure with vacancies at the surface was more stable in energy. This was consistent with the reported results.^49,50 When two vacancies were at the top layer and interacted with each other, the formation energy increased with the S–S distance (5.75 and 5.83 eV for ¹S₁₁/¹S₁₂ and ¹S₁₁/¹S₁₃, respectively), implying that the structure with the second S point vacancy closer to the first S point vacancy was more stable. When two S point vacancies were located at both sides of the Mo layer, the formation energy was regulated by their distance and sites. We noted that the formation of S point vacancies from the pristine structure inside the layers should be difficult because the S atoms needed much higher energy to get rid of the other atoms to reach the surface. However, to investigate the influence of S vacancies on the band structure of 3R MoS₂ systemically, all cases were considered here.

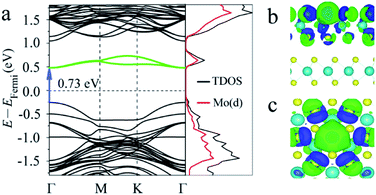
First, the band structures of MoS₂ with one S point vacancy were studied. The (3 × 3) supercell models with one S point vacancy were built for 2-, 3- and 4-layered MoS₂ by removing one S atom from the model, and the point vacancies at different layers were considered. Compared with the band structure of pristine 2-layered MoS₂ with an indirect band gap of 1.33 eV, the S point vacancy has a slight influence on the intrinsic band gap, while some states are introduced into the forbidden band region as the S atom is removed (see Fig. 2a). They are located on both sides of the Fermi level. One shallow occupied state around VBM and two deep unoccupied states located below CB led to an intermediate band with a gap (E_g) of 0.73 eV in the band gap. Our tests showed that S point vacancies at different layers had a slight influence on the results.

Fig. 2 (a) Band structure, partial density of states (PDOS) and (b and c) charge-density difference for 2-layered MoS₂ with one S point defect at the top S layer (side and top views). The charge density difference was calculated according to Δρ_diff = ρ_[MoS2] − ρ_{[MoS2_defect]} − ρ_[S]. The isosurfaces were calculated at 0.005 e Å⁻³. The blue and green isosurfaces represent charge depletion and accumulation regions, respectively.

To obtain more insights into the influence of vacancies on the band structure of MoS₂, we also calculated the partial density of states (PDOS) and charge density difference. The results showed that the states introduced into the forbidden region of the band structure were mainly contributed from the d orbitals of its neighboring Mo atoms (Fig. 2a). The charge density difference (see Fig. 2b and c) showed that charge redistributed over the whole layer with S vacancies, especially over the atoms adjacent to the defects. The free electrons provided by the S vacancies were trapped by the surrounding Mo atoms, indicating that the defect levels were spatially localized at the defect sites.

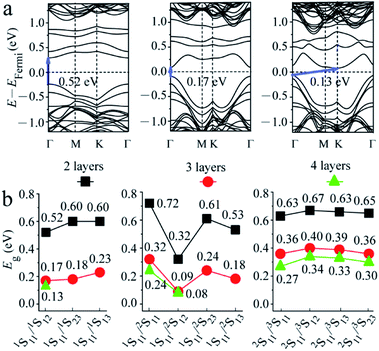
The band structure of 2-layered MoS₂ with two S point vacancies was then considered. A (4 × 3) supercell was used to consider two S vacancies with different distances. The band structures for some special structures (¹S₁₁/¹S₁₂, ¹S₁₁/²S₁₁, ¹S₁₁/²S₁₂, and ²S₁₁/³S₁₁) are shown in Fig. 3a and S1.† The results were similar to that obtained with one S point vacancy. The values of the intrinsic band gaps of MoS₂ showed little disturbance after the introduction of two S point vacancies, while an intermediate band with a smaller intermediate gap was introduced in the band gap.

Fig. 3 (a) Band structures for 2-, 3-, and 4-layered MoS₂ with ¹S₁₁/¹S₁₂ combinational vacancies as an example and (b) the gaps of the intermediate band in the band gap (E_g) for 2-, 3-, and 4-layered MoS₂ with two S vacancies at 4% bulk concentrations.

The gaps of the intermediate band in the band gap for all structures are shown in Fig. 3b. It was seen that when two S atoms were removed from the top S layer of 2-layered structures, E_g increased with the S–S distance, i.e., 0.52 < 0.60 = 0.60 eV, corresponding to the distances of 3.191 (¹S₁₁/¹S₁₂), 5.527 (¹S₁₁/¹S₂₃) and 6.382 (¹S₁₁/¹S₁₃) Å. It was noted that the distance from ¹S₁₃ to ¹S₁₁ was the same as that inferred from the image of ¹S₁₁ in adjacent periodicity, i.e., the defects of ¹S₁₁/¹S₁₃ were equally distributed along one line. In summary, the smaller gap of the intermediate band in the band gap can be obtained by introducing defect levels. When the interval of two S vacancies was larger than 9.489 Å (corresponding to the 3 × 3 supercells with one S vacancy, as mentioned above), the defect levels introduced by the two S vacancies were almost at the same position. We proposed that the defect levels could be introduced at special energy positions by adjusting the distribution of vacancies.

The case becomes complicated when two S atoms are removed from the first and second S layers. There are the largest (0.72 eV (¹S₁₁/²S₁₁)) and the smallest (0.32 eV (¹S₁₁/²S₁₂)) (Fig. S1†) gaps of the intermediate band in 2-layered structures, corresponding to the model with two adjacent and diagonal S atoms removed from the same Mo atom. The E_g values for the model with the larger distances of 6.343 Å (¹S₁₁/²S₂₃) and 7.100 Å (¹S₁₁/²S₁₃) were 0.61 and 0.53 eV, respectively. It was noted that the ¹S₁₁/²S₁₃ vacancies were evenly distributed along the a direction. In comparison, E_g for the structures with two S point vacancies at the second and third S layers showed a slight difference in values.

3- and 4-layered MoS₂ materials with two S point vacancies at the same concentration were also considered for comparison by using (4 × 2) and (3 × 2) supercell models, respectively. The results (Fig. 3 and S1†) were similar to that observed for one S point defect. The intrinsic band gap of MoS₂ showed little disturbance after the introduction of two S vacancies, while a smaller gap of the intermediate band in the band gap was introduced. Both gaps of the intrinsic and intermediate bands became smaller as the number of layers increased from 2 to 4 owing to the downward shift in the unoccupied energy levels and the upward shift in the occupied energy levels. However, the difference between the 3- and 4-layered structures was much smaller than that between the 2- and 3-layered structures due to the different stacking sequences (AB, ABC, and ABCA), which was similar to the tendency of pristine structures.³⁷

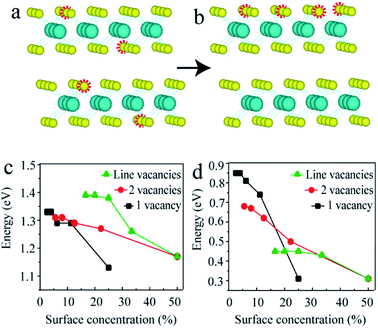
As mentioned above, the point vacancies preferred to form at the top S layer and accumulated along one line, which indicated that in the experiment, the distribution of S vacancies was not homogeneous, i.e., the surface concentration of the S vacancies was much higher than that in the inner layer. Since the data obtained from experiments are generally average densities, the schematics for 2-layered MoS₂ with 4S vacancies on average and at the top layer are shown in Fig. 4a and b, respectively. In this case, the surface concentration of the S vacancies was much larger (4 times). Here, we constructed n × n (n = 2, 3, …, 6) supercells for 2-layered MoS₂ with one and two adjacent point vacancies and line vacancies at the top layer to investigate the effect of S vacancies on the band structures on increasing the surface concentration (0 to 50%, corresponding to the concentration from 0 to 12.5%).

Fig. 4 (a) Schematic diagram of vacancies on average. (b) Schematic diagram of vacancies on the top S layer. (c) The gaps of intrinsic and (d) intermediate bands in the band gaps for n × n (n = 2, 3, …, 6) supercells with one (black) and two (red) adjacent point vacancies and line (green) vacancies.

The black, red and green lines in Fig. 4c and d represent the gaps of the intrinsic and intermediate bands for the models with one, two point and line vacancies, respectively. It is clear that the slopes of black, red and green lines are different, indicating that the vacancy type has a substantial influence on the band gap on increasing the vacancy concentrations. This means that the band gap decreases as the number of layers increases for few-layered structures and the difference in the structures with n and n + 1 layers becomes smaller. The phenomenon observed in our recent experiments supported this conclusion: the band gap for a 4-layered structure is equal to the value of a 2-layered structure and larger than that of a 3-layered structure.⁵² In addition, these results offer a variety of benefits for MoS₂ material design with a tunable band gap in almost the full range between 0.08 eV and 1.8 eV.

4 Conclusions

As a typical 2D material, MoS₂ has attracted significant attention due to its potential applications in electronic and optoelectronic devices. It is of particular interest that vacancies usually play an important role in tuning and modifying its various properties. In this work, we revealed the regulation of the gaps of the intrinsic and intermediate bands for 3R MoS₂ with different concentrations of S point vacancies. All results showed that the gaps of both intrinsic and intermediate bands in the band gap of MoS₂ decreased as the number of layers increased, while the difference for the 3- and 4-layered structures was much smaller than that for the 2- and 3-layered structures due to the different stacking sequences, which was consistent with the results for the pristine ones. For the structures with the same type and concentration of S vacancies, the band gap increased with the distance of S vacancies. As the concentration of the surface vacancies increased, the type of vacancy defects changed from point to line accordingly. These regulations of the gaps of the intrinsic and intermediate bands by S point vacancies reveal an effective way for the band-gap engineering of MoS₂, opening up a direction for modulating band gaps for 2D material applications.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors acknowledge the financial support from the National Science Foundation of Beijing (2184130) and the National Natural Science Foundation of China (11672079, 11975045).

Notes and references

1. Z. Yin, H. Li, H. Li, L. Jiang, Y. Shi, Y. Sun and G. Lu, ACS Nano, 2012, 6, 74–80.
2. J. Feng, X. F. Qian, C.-W. Huang and J. Li, Nat. Photonics, 2012, 6, 865–871.
3. R. S. Sundaram, M. Engel, A. Lombardo, R. Krupke, A. C. Ferrari, P. Avouris and M. Steiner, Nano Lett., 2013, 13, 1416–1421.
4. J. Xie, H. Zhang, S. Li, R. Wang, X. Sun, M. Zhou, J. Zhou, X. W. Lou and Y. Xie, Adv. Mater., 2013, 25, 02685.
5. Y. Li, Y.-L. Li, C. M. Araujo, W. Luo and R. Ahuja, Catal. Sci. Technol., 2013, 3, 2214–2220.
6. J. Deng, H. Li, J. Xiao, Y. Tu, D. Deng, H. Yang, H. Tian, J. Li, P. Ren and X. Bao, Energy Environ. Sci., 2015, 8, 1594–1601.
7. H. S. Lee, S. W. Min, Y. G. Chang, M. K. Park, T. Nam, H. Kim, J. H. Kim, S. Ryu and S. Im, Nano Lett., 2012, 12, 3695–3700.
8. K. F. Mak, C. Lee, J. Hone, J. Shan and T. F. Heinz, Phys. Rev. Lett., 2010, 105, 136805.
9. T. Heine, Acc. Chem. Res., 2015, 48, 65–72.
10. A. N. Enyashin, M. Bar-Sadan, L. Houben and G. Seifert, J. Phys. Chem. C, 2013, 117, 10842–10848.
11. S. B. Desai, G. Seol, J. S. Kang, H. Fang, C. Battaglia, R. Kapadia, J. W. Ager, J. Guo and A. Javey, Nano Lett., 2014, 14, 4592–4597.
12. A. P. Nayak, T. Pandey, D. Voiry, J. Liu, S. T. Moran, A. Sharma, C. Tan, C. H. Chen, L. J. Li, M. Chhowalla, J. F. Lin, A. K. Singh and D. Akinwande, Nano Lett., 2015, 15, 346–353.
13. E. Aydin, M. D. Bastiani and S. D. Wolf, Adv. Mater., 2019, 31, 1900428.
14. O.-M. Josue, Z. Wang, C.-S. Rodolfo, M.-G. Aaron, F. Wang, X. Yao, M. Terrones and M. Endo, Adv. Mater., 2019, 31, 1805717.
15. S. B. Ogale, Adv. Mater., 2010, 22, 3125–3155.
16. W. Zhou, X. Zou, S. Najmaei, Z. Liu, Y. Shi, J. Kong, J. Lou, P. M. Ajayan, B. I. Yakobson and J. C. Idrobo, Nano Lett., 2013, 13, 2615.
17. D. M. Sim, M. Kim, S. Yim, M.-J. Choi, J. Choi, S. Yoo and Y. S. Jung, ACS Nano, 2015, 9, 12115–12123.
18. H. Shu, Y. Li, X. Niu and J. Wang, ACS Appl. Mater. Interfaces, 2016, 8, 13150–13156.
19. S. Wang, G. D. Lee, S. Lee, E. Yoon and J. H. Warner, ACS Nano, 2016, 10, 5419–5430.
20. J. Lin, S. T. Pantelides and W. Zhou, ACS Nano, 2019, 9, 5189–5197.
21. Y. Chen, S. Huang, X. Ji, K. Adepalli, K. Yin, X. Ling, X. Wang, J. Xue, M. Dresselhaus, J. Kong and B. Yildiz, ACS Nano, 2018, 12, 2569–2579.
22. C. Kastl, R. J. Koch, C. T. Chen, J. Eichhorn, S. Ulstrup, A. Bostwick, C. Jozwiak, T. R. Kuykendall, N. J. Borys, F. M. Toma, S. Aloni, W.-B. Alexander, R. Eli and M. S. Adam, ACS Nano, 2019, 13, 1284–1291.
23. J. Jiang, C. Ling, T. Xu, W. Wang, X. Niu, A. Zafar, Z. Yan, X. Wang, Y. You, L. Sun, J. Lu, J. Wang and Z. Ni, Adv. Mater., 2018, 30, 1804332.
24. H. Xu, X. Han, X. Dai, W. Liu, J. Wu, J. Zhu, D. Kim, G. Zou, K. A. Sablon, A. Sergeev, Z. Guo and H. Liu, Adv. Mater., 2018, 30, 1706561.
25. P. Johari and V. B. Shenoy, ACS Nano, 2012, 6, 5449–5456.
26. J. K. Ellis, M. J. Lucero and G. E. Scuseria, Appl. Phys. Lett., 2011, 99, 261908.
27. M.-S. Alejandro, K. Hummer and L. Wirtz, Surf. Sci. Rep., 2015, 70, 554–586.
28. A. Kuc, N. Zibouche and T. Heine, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 245213.
29. L.-p. Feng, J. Su and Z.-t. Liu, J. Alloys Compd., 2014, 613, 122–127.
30. V. Wang, Y. Kawazoe and W. T. Geng, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 045433.
31. M. Pandey, F. A. Rasmussen, K. Kuhar, T. Olsen, K. W. Jacobsen and K. S. Thygesen, Nano Lett., 2016, 16, 2234.
32. D. Wang, W. Ju, T. Li, Q. Zhou, Z. Gao, Y. Zhang and H. Li, J. Phys. Chem. Solids, 2019, 131, 119–124.
33. S. Chen, P. Narang, H. A. Atwater and L. Wang, Adv. Mater., 2014, 26, 311–315.
34. S. Haldar, H. Vovusha, M. K. Yadav, O. Eriksson and B. Sanyal, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 235408.
35. L. Ao, H. Y. Xiao, X. Xiang, S. Li, K. Z. Liu, H. Huang and X. T. Zu, Phys. Chem. Chem. Phys., 2015, 17, 10737.
36. Y. Han, T. Hu, R. Li, J. Zhou and J. Dong, Phys. Chem. Chem. Phys., 2015, 17, 3813–3819.
37. X. Fan, W. T. Zheng, J. L. Kuo, D. J. Singh, C. Q. Sun and W. Zhu, Sci. Rep., 2016, 6, 24140–24148.
38. T. Cusati, A. Fortunelli, G. Fiori and G. Iannaccone, Phys. Rev. B, 2018, 98, 115403.
39. J. Park, I. W. Yeu, G. Han, C. Jang, J. Y. Kwak, C. S. Hwang and J. H. Choi, J. Phys.: Condens. Matter, 2019, 31, 315502.
40. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
41. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
42. S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799.
43. B. B. Schonfeld, J. J. Huangt and S. C. Moss, Acta Crystallogr., Sect. B: Struct. Sci., 1983, 39, 404–407.
44. K. He, C. Poole, K. F. Mak and J. Shan, Nano Lett., 2013, 13, 2931.
45. C. G. Van de Walle and J. Neugebauer, J. Appl. Phys., 2004, 2004(95), 3851–3879.
46. S. KC, R. C. Longo, R. Addou, R. M. Wallace and K. Cho, Nanotechnology, 2014, 25, 375703.
47. Y. Liu, K. Palotas, X. Yuan, T. j. Hou, H. p. Lin, Y. y. Li and S.-T. Lee, ACS Nano, 2017, 11, 2060–2065.
48. K. Yang, Y. Dai, B. Huang and M.-H. Whangbo, Chem. Mater., 2008, 20, 6528–6534.
49. S. Urasaki and H. Kageshima, Jpn. J. Appl. Phys., 2018, 57, 125202.
50. L. Feng, J. Su, S. Chen and Z. Liu, Mater. Chem. Phys., 2014, 148, 5–9.
51. N. Kodama, T. Hasegawa, Y. Okawa, T. Tsuruoka, C. Joachim and M. Aono, Jpn. J. Appl. Phys., 2010, 49, 08LB01.
52. J. Shi and X. Liu, unpublished work.

---

Footnote

† Electronic supplementary information (ESI) available: Band structures for different layered MoS₂ with combinational vacancies. See DOI: 10.1039/d0ra01676d

---