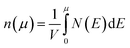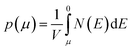Ternary selenides A₂Sb₄Se₈ (A = K, Rb and Cs) as an n-type thermoelectric material with high power factor and low lattice thermal conductivity: importance of the conformationally flexible Sb–Se–Se–Sb bridges

Abstract

We investigated the thermoelectric properties of the layered ternary selenides A₂Sb₄Se₈ (A = K, Rb and Cs) and the lattice thermal conductivity of K₂Sb₄Se₈ on the basis of DFT calculations, to find that these selenides are a high-performance n-type thermoelectric material. The Seebeck coefficients and power factors calculated for the electron carriers of A₂Sb₄Se₈ (A = K, Rb and Cs) are greater than those of the well-known thermoelectric materials Bi₂Te₃ and PbTe. The lattice thermal conductivity κ_latt of K₂Sb₄Se₈ is comparable to that of PbTe, well-known for its low lattice thermal conductivity. In terms of both electronic and phonon structures, the structural parts of the A₂Sb₄Se₈ (A = K, Rb and Cs) phases crucial for their thermoelectric properties are the conformationally-flexible Sb–Se–Se–Sb bridges that interlink between their structurally rigid units.

---

Introduction

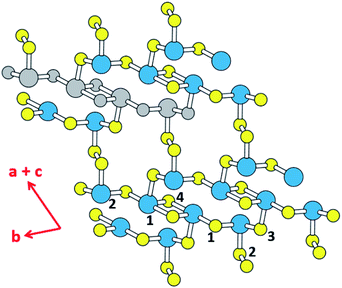
Thermoelectricity enables a direct conversion between thermal and electrical energies, so materials exhibiting thermoelectricity have received much attention for power generation and cooling.^1,2 In particular, thermoelectric power generation is potentially important for waste heat collection and efficient energy utilization, although its application is limited due to the low efficiency of thermoelectric devices. The efficiency of a thermoelectric material at a given temperature T depends on the figure of merit, ZT = S²σT/κ, where σ, κ and S are the electrical conductivity, the thermal conductivity and the Seebeck coefficient, respectively.³ The amount of power generated by a thermoelectric material is related to the power factor, S²σ, which is the major element governing the magnitude of ZT.⁴ Another element raising the ZT is a low thermal conductivity κ, which is composed of the electric thermal conductivity (κ_el) and the lattice thermal conductivity (κ_latt), that is, κ = κ_el + κ_latt. κ_el is directly proportional to the carrier concentration, n, because κ_el ∝ σ via the Wiedemann–Franz law, κ_el = LσT,⁵ where L is Lorenz number, and because σ ∝ n. In general, a high figure of merit ZT requires a compromise between the carrier concentration and the thermal conductivity.^6,7 In terms of the carrier densities affecting the thermoelectric properties of a material, the electronic states lying close to its conduction band minimum (CBM) and valence band maximum (VBM) (i.e., those typically within ∼0.5 eV of the CBM or the VBM) are found to be crucial.⁸ From the viewpoint of understanding the structure–property relationship governing the thermoelectric properties of a material, it is important to find which structural part of the material is largely responsible for those states close to the CBM and VBM.

The binary tellurides Bi₂Te₃ (ref. 9a) and PbTe^9b are well-known efficient thermoelectric materials. It is of interest and importance to search for a potential high-performance thermoelectric material that can be as efficient as Bi₂Te₃ and PbTe. In the present work we carry out DFT calculations to explore the thermoelectric properties of the layered ternary selenide K₂Sb₄Se₈ (ref. 10) as well as its isostructural phases Rb₂Sb₄Se₈ (ref. 11a) and Cs₂Sb₄Se₈.^11b As depicted in Fig. 1, K₂Sb₄Se₈ consists of Sb₄Se₈ layers separated by K⁺, and each layer is made up of Sb(1)Se₄ seesaw units, Sb(2)Se₃ pyramids, and Se₂ dimers. There are two types of cross-linked rings in each Sb₄Se₈ layer; one is the 12-membered ring made up of two Sb(1)₂Se₆ and two Sb(2)Se₃ units, and the other is the 14-membered ring made up of four Sb(2)Se₃, two Se(2)₂ and two Sb(1)Se₄ seesaw units. From the viewpoint of understanding the lattice thermal conductivity of K₂Sb₄Se₈, it is more convenient to consider each Sb₄Se₈ layer in terms of the “Sb₄Se₆” chains made up of cross-linked 12-membered rings, which run along the b-direction. For clarity, one Sb₄Se₆ repeat unit of this chain is colored in grey in Fig. 1. When these Sb₄Se₆ chains are bridged by the Se(2)₂ dimers to form 14-membered rings between the Sb₄Se₆ chains, we obtain the Sb₄Se₈ layer.

Fig. 1 Schematic diagram showing the structure of the Sb₄Se₈ layer of K₂Sb₄Se₈. The large and small circles represent the Sb and Se atoms, respectively. The Sb(1) and Sb(2) atoms are represented by blue circles, and Se(1)–Se(4) atoms by yellow circles, except for one Sb₄Se₆ unit. The latter is indicated by grey circles for both Sb and Se, for clarity. The Sb₄Se₈ layer is composed of 12- and 14-membered rings that are cross-linked. The cross-linked 12-membered rings form the Sb₄Se₆ chains running along the b-direction. The Sb₄Se₆ chains are linked by Se₂ dimers to form 14-membered rings that are cross-linked. It should be noted that the b- and (a + c)-crystallographic directions of K₂Sb₄Se₈ are the same as those of Rb₂Sb₄Se₈, but correspond to the a- and (b–c)-directions of Cs₂Sb₄Se₈, respectively.

Since the Sb–Se(2)–Se(2)–Sb bridges have a high conformational flexibility (namely, a soft potential energy curve with respect to a small variation in the dihedral angle ∠Sb–Se(2)–Se(2)–Sb), it is expected that the Sb₄Se₈ layer is more rigid along the Sb₄Se₆ chain direction (i.e., along the b-direction for K₂Sb₄Se₈) than along the interchain direction [i.e., along the (a + c)-direction for K₂Sb₄Se₈]. In addition, the K₂Sb₄Se₈ crystal should be least rigid along the interlayer direction because there is no covalent bonding between adjacent Sb₄Se₈ layers. In this low-dimensional structure of K₂Sb₄Se₈ as determined by X-ray diffraction, the unit cell parameters are large so that the lattice thermal conductivity would be low with short mean path for acoustic phonons.¹² Thus, it is worthwhile investigate the possibility that K₂Sb₄Se₈ as well as its two isostructural selenides, Rb₂Sb₄Se₈ and Cs₂Sb₄Se₈, are a high-performance thermoelectric material. In the present work, we examine the Seebeck coefficients and power factors of A₂Sb₄Se₈ (A = K, Rb, Cs) and the lattice thermal conductivity of K₂Sb₄Se₈ on the basis of DFT calculations, to predict that the ternary selenides A₂Sb₄Se₈ (A = K, Rb, Cs) are a high-performance thermoelectric material comparable in efficiency to, or better than, the well-known thermoelectric materials Bi₂Te₃ and PbTe.

Details of calculations

Our DFT calculations employed the frozen-core projector augmented wave (PAW) method¹³ encoded in the Vienna ab initio simulation package (VASP),¹⁴ with the generalized-gradient approximation (GGA)¹⁵ of Perdew, Burke and Ernzerhof (PBE) for the exchange–correlation functional and the plane-wave-cut-off energy of 450 eV. The BoltzTrap code¹⁶ was used to calculate the thermoelectric properties of all K₂Sb₄Se₈ systems, which solves the semi-classical Boltzmann equation using the rigid band approach.^17,18 This method has been successful in calculating the transport properties and predicting the optimal doping levels for thermoelectric materials.^17–20 To ensure the convergence of the calculated thermoelectric properties, the irreducible Brillouin zone was sampled by a set of 2000 k-points. The BoltzTrap code allows one to calculate the electrical conductivity σ, the Seebeck coefficient S, and the power factor S²σ/τ under the assumption that the electron momentum relaxation time τ is independent of energy. We employ the latter assumption, because there is currently no information about the τ of A₂Sb₄Se₈. The power factors calculated under this assumption are greater than the experimental values,²¹ but this overestimation arises in part from the fact that the band gaps are under estimated by DFT calculations. We note that the thermoelectric properties of numerous systems have been explained by using this assumption.²² We simulate the phonon behavior of K₂Sb₄Se₈ by using the frozen phonon method implemented in Phono3py²³ to investigate the lattice thermal conductivity.

Electronic structures

The electronic structure calculated for K₂Sb₄Se₈ is presented in terms of the total density of states (DOS) in Fig. 2a, and in terms of band dispersion relations in Fig. 2b along several wave vector directions of the first Brillouin zone (Fig. 2c). K₂Sb₄Se₈ has a band gap of ∼1.0 eV. The projected DOS (PDOS) calculated for the Sb and Se atoms of K₂Sb₄Se₈ are presented in Fig. 3. The PDOS plots for the Se(1), Se(3) and Se(4) are very similar but differ considerably from that for Se(2). In the occupied states of the PDOS, the Se(1), Se(3), and Se(4) each show two band blocks, which represent the bonding states between Sb and Se and the nonbonding states of Se. In contrast, the Se(2) shows roughly three band blocks, which arise from the Se(2)–Se(2) bonding states in addition to the Se–Sb bonding and the Se nonbonding states.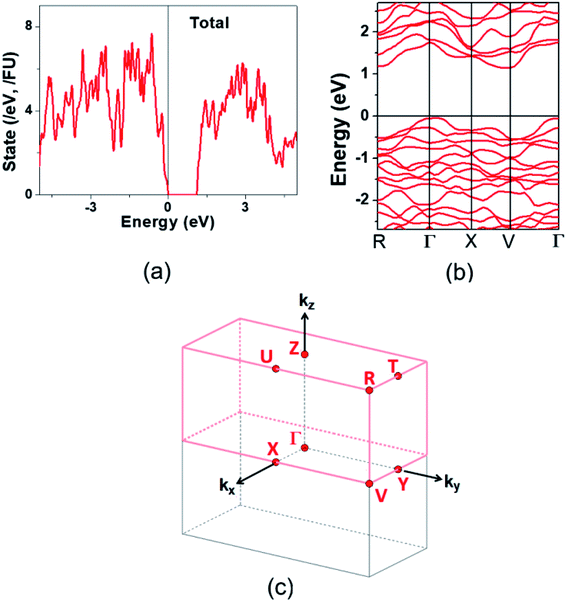

Fig. 2 Electronic structure calculated for K₂Sb₄Se₈: (a) Total DOS plot. (b) Band dispersion relations. (c) First Brillouin zone associated with a crystal lattice of space group P1̄.

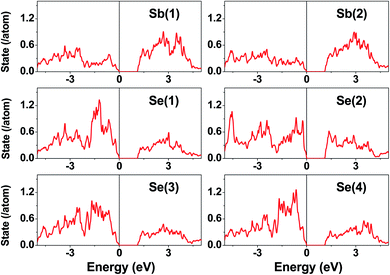Fig. 3 PDOS plots calculated for the Sb(1), Sb(2), Se(1), Se(2), Se(3), and Se(4) atoms of K₂Sb₄Se₈.

This reflects that the formal oxidation state of Se(1), Se(3), and Se(4) atoms is −2 whereas that of the Se(2) is −1. At the CBM and VBM, the Se(2) contributes more strongly than does the Se(1), Se(3) or Se(4) atom, and than does the Sb(1) or Sb(2) atom. Since the thermoelectric properties of a material are mainly influenced by the electronic states lying very close to its CBM and VBM (i.e., typically those within ∼0.5 eV from the VBM and CBM),⁸ the thermoelectric properties of K₂Sb₄Se₈ should be strongly influenced by the electronic structures associated with the Se(2)₂ dimer units. The total DOS plots of Rb₂Sb₄Se₈ and Cs₂Sb₄Se₈, presented in Fig. S1 in the ESI,† are very similar to that of K₂Sb₄Se₈ presented in Fig. 2.

Thermoelectric properties

We calculate the Seebeck coefficients of A₂Sb₄Se₈ (A = K, Rb, Cs) at 300 K as a function of the chemical potential μ. In terms of the rigid band approximation, the electron density can be introduced into A₂Sb₄Se₈ by raising the Fermi level E_f from the CBM, so the chemical potential μ defined as μ = E_f − CBM, with the electron density n(μ) given by
where V is the unit cell volume, and N(E) the total DOS at energy E. Similarly, the hole density can be introduced into A₂Sb₄Se₈ by lowering the Fermi level E_f from the VBM, so the chemical potential μ is defined as μ = VBM − E_f, with the hole density p(μ) given by

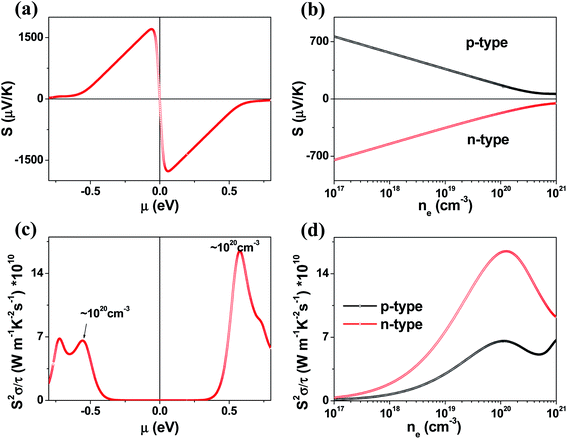
The μ-dependence of the Seebeck coefficients S calculated for K₂Sb₄Se₈ (Fig. 4a) shows two peaks at μ ≈ ±0.061 eV with S ≈ ±1700 μV K⁻¹. These values are considerably greater than those of the well-known thermoelectric materials Bi₂Te₃ (the calculated S ≈ ±250 μV K⁻¹)¹⁶ and PbTe (the calculated S ≈ ±350 μV K⁻¹).²⁰ The dependence of S on the electron density and that on the hole density (Fig. 4b) reveals that the S decreases in magnitude steadily with increasing either the electron or the hole density. Under the assumption that the relaxation times τ is energy-independent, we calculate the power factor S²σ/τ. The calculated S²σ/τ is presented as a function of μ (Fig. 4c) and as a function of the carrier density (Fig. 4d). The power factor for the electron carriers is considerably greater than that for the hole carriers (e.g., the n-type S²σ/τ is larger than the p-type S²σ/τ by a factor of ∼2). This reflects that the electrical conductivity for the electron carriers is much greater than that for the hole carriers. The Seebeck coefficients and the power factors calculated for Rb₂Sb₄Se₈ and Cs₂Sb₄Se₈ are summarized in Fig. S2, S3, and S5 in the ESI,† respectively. They are very similar to those described for K₂Sb₄Se₈ described above.

Fig. 4 Thermodynamic properties of K₂Sb₄Se₈ calculated at 300 K: (a) Seebeck coefficient S as function of the chemical potential μ. (b) Seebeck coefficient S as function of the carrier density n. (c) Power factor S²σ/τ as function of the chemical potential μ. (d) Power factor S²σ/τ as function of the carrier density n.

We also investigated the temperature dependence of the Seebeck coefficients S and the power factor S²σ/τ for A₂Sb₄Se₈ for A = K, Rb and Cs (Fig. S5 in the ESI†). In comparing these values of the three compounds, it is necessary to consider the possible uncertainties in their carrier densities. Thus, we calculate the Seebeck coefficients S and the power factor S²σ/τ for different carrier densities within the range between 1 × 10¹⁹ to 5 × 10²⁰ cm⁻³. Fig. S5† reveals that, for both electron and hole carriers, the Seebeck coefficients S and the power factor S²σ/τ (in the upper and down panels, respectively) gradually increases with temperature. This is due to the increase in thermal energy. The power factor for the electron carriers is considerably greater than that for the hole carriers reflecting that the electrical conductivity for the electron carriers is much greater than that for the hole carriers.

The band dispersion relations calculated for K₂Sb₄Se₈ (Fig. 2b) show that K₂Sb₄Se₈ has an indirect band gap with the CBM at the M point and the VBM at the Γ point. The VBM has a hole valley at Γ, while the CBM has an electron valley and pseudo electron valley at M and R, respectively. The presence of flat band dispersion relations enhances the DOS and hence the carrier density. Since the CBM has more valleys than does the VBM, the carrier concentration should be enhanced near the CBM,²⁴ so that the electrical conductivity is higher for the electrons than for the holes. This explains why the n-type power factor is considerably higher than the p-type power factor despite that the calculated Seebeck coefficients for the hole and electron carriers are similar. The band dispersion relations of Rb₂Sb₄Se₈ and Cs₂Sb₄Se₈, presented in Fig. S4 in the ESI,† are very similar to that of K₂Sb₄Se₈ described above.

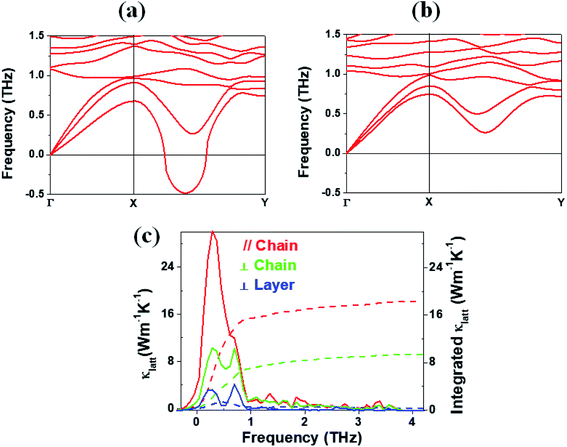
Lattice thermal conductivity

In general, a low lattice thermal conductivity κ_latt is found for a low dimensional material with heavy elements and large unit cell parameters. K₂Sb₄Se₈ is such a material. As already discussed (see Fig. 1), each Sb₄Se₈ layer of K₂Sb₄Se₈ is more rigid along the Sb₄Se₆ chain direction (i.e., the b-direction for K₂Sb₄Se₈) than along the interchain direction within a Sb₄Se₈ layer [i.e., the (a + c)-direction for K₂Sb₄Se₈]. Thus, the thermal transport of K₂Sb₄Se₈ should occur largely along the b-direction, and that along the (a + c)-direction should be weak, and so should be that along the (a–c)-direction (i.e., the interlayer direction). We examine the phonon properties and the lattice thermal conductivity of K₂Sb₄Se₈ using the Phono3py²³ code combined with DFT calculations. The phonon dispersion relations calculated for K₂Sb₄Se₈ using the experimental structure, shown in Fig. 5a, reveal the presence of an imaginary vibrational frequency. This indicates that the crystal structure as determined by X-ray diffraction measurements has a structural instability, suggesting the possibility that the real crystal structure has structural defects such as the charge density wave, local kinks, and fluctuations that are not detected by X-ray diffraction.²⁵ This imaginary frequency disappears when the phonon dispersion relations are calculated for the structure of K₂Sb₄Se₈ optimized by DFT calculations (Fig. 5b). Nevertheless, there exist low-frequency phonons, indicating the presence of a soft potential, which is associated most likely with the conformationally-flexible Sb–Se–Se–Sb bridges.

Fig. 5 Phonon dispersion relations calculated for (a) the experimental and (b) optimized structures of K₂Sb₄Se₈. (c) Lattice thermal conductivities κ_latt along the Sb₄Se₆ chain, along the interchain within the Sb₄Se₈ layer, and along the interlayer directions as a function of the frequency (solid lines). The integrated lattice thermal conductivities along the three directions are also shown (dashed lines).

We calculate the lattice thermal conductivities by solving the linearized phonon Boltzmann equation with the single-mode relaxation time approximation, results of which are presented in Fig. 5c. As expected from the crystal structure of K₂Sb₄Se₈, the thermal conductivities decrease in the order, the Sb₄Se₆ chain direction > the interchain direction of the Sb₄Se₈ layer > the interlayer direction. The lattice thermal conductivity κ_latt of K₂Sb₄Se₈ is estimated to be 5.32 W mK⁻¹, which is comparable to that of PbTe (with calculated κ_latt ≈ 2 W mK⁻¹),²⁶ a well-known material for low lattice conductivity. The low lattice thermal conductivity of K₂Sb₄Se₈ is attributed to a decreased mean free path resulting from the large unit cell parameters, the low dimensional structure, and the structural instability arising from the conformationally flexible Sb–Se(2)–Se(2)–Sb bridges. For each b–Se(2)–Se(2)–Sb bridge, the potential energy curve with respect to a small change in the ∠Sb–Se(2)–Se(2)–Sb dihedral angle should be soft. It is most likely that the soft motions of the crystal lattice involve the slipping of each Sb₄Se₆ chain against its neighboring Sb₄Se₆ chains within each Sb₄Se₈ layer. The Sb–Se(2)–Se(2)–Sb bridges would act as phonon scattering centers rather than phonon transmittance paths due to their conformational flexibility. The lattice thermal conductivities of Rb₂Sb₄Se₈ and Cs₂Sb₄Se₈ should be similar to that of K₂Sb₄Se₈ because Rb₂Sb₄Se₈ and Cs₂Sb₄Se₈ are very similar to K₂Sb₄Se₈ in atomic and electronic structures.

Discussion

Our calculations suggest that the ternary selenides A₂Sb₄Se₈ (A = K, Rb, Cs) have high Seebeck coefficients, high power factors for the electron carriers, and low thermal conductivities. We estimate the ZT value of K₂Sb₄Se₈ at T = 300 K by using the calculated lattice thermal conductivity κ_latt of 5.32 W mK⁻¹ and the relaxation time τ ≈ 2 × 10⁻¹⁴ s. In general, the relaxation time τ of conventional semiconductors is of the order of 10⁻¹⁴ s.²⁷ For example, the relaxation times τ ≈ 2 × 10⁻¹⁴ and 3 × 10⁻¹⁴ s reproduce the experimental resistivities of Bi₂Te₃ and PbTe, respectively.^27,28 The ZT values of K₂Sb₄Se₈ estimated by using τ ≈ 2 × 10⁻¹⁴ s are presented in Fig. 6. The μ-dependence of the ZT (Fig. 6a) shows a peak at μ ≈ 0.56 eV with ZT ≈ 0.27, and another peak at μ ≈ −0.54 eV with ZT ≈ 0.14. The dependence of ZT on the carrier densities (Fig. 6b) reveals a peak at the electron carrier density of ∼10²⁰ cm⁻³, which corresponds to the chemical potential μ ≈ 0.56 eV, and another peak at the hole carrier density of ∼7 × 10¹⁹ cm⁻³, which corresponds to the chemical potential μ ≈ −0.54 eV. The ZT of K₂Sb₄Se₈ is greater for the electron carriers than for the hole carriers by a factor of ∼2. The calculated ZT values of K₂Sb₄Se₈ are comparable to those estimated for Bi₂Te₃.^27c,29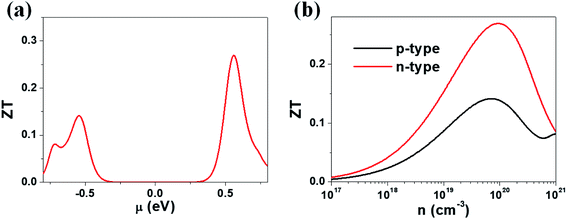

Fig. 6 ZT values calculated for K₂Sb₄Se₈ with τ ≈ 2 × 10⁻¹⁴ s: (a) the μ-dependence of the ZT using κ_latt = 5.32 W mK⁻¹. (b) The carrier density dependence of the ZT using κ_latt = 5.32 W mK⁻¹.

We note that the electronic states crucial for determining the n-type (p-type) Seebeck coefficients are those lying mainly within ∼0.5 eV from the CBM (VBM).⁸ Such states of A₂Sb₄Se₈ (A = K, Rb, Cs) are represented largely by the Se(2) atoms forming the Sb–Se(2)–Se(2)–Sb bridges between two adjacent Sb₄Se₆ chains in each Sb₄Se₈ layer. Furthermore, the lattice thermal conductivity of A₂Sb₄Se₈ (A = K, Rb, Cs) is expected to be lowered by the Sb–Se(2)–Se(2)–Sb bridges because they are conformational flexible as mentioned above. Thus, in terms of both electronic and vibrational factors, the Sb–Se(2)–Se(2)–Sb bridges play a crucial role in enhancing the thermoelectric properties of A₂Sb₄Se₈ (A = K, Rb, Cs).

Concluding remarks

Our work suggests that the layered ternary selenides A₂Sb₄Se₈ (A = K, Rb, Cs) are a promising thermoelectric material comparable in efficiency to, or better than, the well-known thermoelectric materials such as Bi₂Te₃ and PbTe. The power factor and ZT values estimated for the electron carriers are considerably greater than those for the hole carriers by a factor of ∼2. Thus, the ternary selenides A₂Sb₄Se₈ (A = K, Rb, Cs) are predicted to be a high-performance n-type thermoelectric material. The electronic and phonon structures associated with the Se(2)₂ dimer units of the conformationally-flexible Sb–Se(2)–Se(2)–Sb bridges are crucial in determining the thermoelectric properties of A₂Sb₄Se₈ (A = K, Rb, Cs).

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This research was supported by Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education (NRF-2017R1D1A1B03036257), Supercomputing Center/Korea Institute of Science and Technology Information with supercomputing resources including technical support (KSC-2018-CHA-0019).

Notes and references

1. G. S. Nolas, J. Sharp and H. Goldsmid, Thermoelectrics: Basic Principles and New Materials Developments, Springer, New York, 2001.
2. D. M. Rowe, Thermoelectrics Handbook: Macro to Nano, CRC Press, Boca Raton, 2006.
3. A. J. Minnich, M. S. Dresselhaus, G. F. Ren and G. Chen, Energy Environ. Sci., 2009, 2, 466–479.
4. L. L. Baranowski, G. J. Snyder and E. S. Toberer, J. Appl. Phys., 2013, 115, 126102.
5. R. Franz and G. Wiedemann, Ann. Phys., 1853, 165, 497–531.
6. J. Q. He, M. G. Kanatzidis and V. P. Dravid, Mater. Today, 2013, 16, 166–176.
7. L. D. Zhao, V. P. Dravid and M. G. Kanatzidis, Energy Environ. Sci., 2014, 7, 251–268.
8. (a) C. Lee, J. H. Shim and M.-H. Whangbo, Inorg. Chem., 2018, 57, 11895–11900; (b) C. Lee, J. N. Kim, J.-Y. Tak, H. K. Cho, J. H. Shim, Y. S. Lim and M.-H. Whangbo, AIP Adv., 2018, 8, 115213; (c) C. Lee, T.-H. An, E. E. Gordon, H. S. Ji, C. Park, J. H. Shim, Y. S. Lim and M.-H. Whangbo, Chem. Mater., 2017, 29, 2348–2354.
9. (a) S. Nakajima, J. Phys. Chem. Solids, 1963, 24, 479–485; (b) N. Bouad, L. Chapon, R.-M. Marin-Ayral, F. Bouree-Vigneron and J. C. Tedenac, J. Solid State Chem., 2003, 173, 189–195.
10. W. S. Sheldrick and M. Wachhold, Z. Kristallogr. NCS, 1998, 213, 25.
11. (a) W. S. Sheldrick and M. Wachhold, Z. Kristallogr. NCS, 1998, 213, 24; (b) W. S. Sheldrick and J. Kaub, Z. Anorg. Allg. Chem., 1986, 536, 114–118.
12. J. R. Sootsman, D. Y. Chung and M. G. Kanatzidis, Angew. Chem., Int. Ed., 2009, 48, 8616–8639.
13. (a) P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979; (b) G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
14. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
15. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
16. G. K. H. Madsen and D. Singh, Comput. Phys. Commun., 2006, 175, 67–71.
17. G. K. H. Madsen, J. Am. Chem. Soc., 2006, 128, 12140–12146.
18. T. J. Scheidemante, C. Ambrosch-Draxl, T. Thonhauser, J. V. Badding and J. O. Sofo, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 125210.
19. (a) L. Chaput, P. Pécheur, J. Tobola and H. Scherrer, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 085126; (b) X. Gao, K. Uehara, D. D. Klug, S. Patchkovskii, J. S. Tse and T. M. Tritt, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 125202.
20. D. J. Singh, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 195217.
21. W. Chen, J.-H. Pöhls, G. Hautier, D. Broberg, S. Bajaj, U. Aydemir, G. M. Gibbs, H. Zhu, M. Asta, G. J. Snyder, B. Meredig, M. A. White, K. Perssonae and A. Jain, J. Mater. Chem. C, 2016, 4, 4414–4426.
22. (a) C. Lee, J. Hong, M.-H. Whangbo and J. H. Shim, Chem. Mater., 2013, 25, 3745–3752; (b) C. Lee, J. Hong, W. R. Lee, D. Y. Kim and J. H. Shim, J. Solid State Chem., 2014, 211, 113–119.
23. A. Togo, L. Chaput and I. Tanaka, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 094306.
24. (a) J. Hong, C. Lee, J.-S. Park and J. H. Shim, Phys. Rev. B: Condens. Matter Mater. Phys., 2016, 93, 035445; (b) J. Xin, Y. Tang, Y. Liu, X. Zhao, H. Pan and T. Zhu, npj Quantum Mater., 2018, 3, 9; (c) Y. Tang, Z. M. Gibbs, L. A. Agapito, G. Li, H.-S. Kim, M. B. Nardelli, S. Curtarolo and G. J. Snyder, Nat. Mater., 2015, 14, 1223–1228; (d) R. Hanus, X. Guo, Y. Tang, G. Li, G. J. Snyder and W. G. Zeier, Chem. Mater., 2017, 29, 1156–1164.
25. (a) H. B. Nielsen and M. Ninomiya, Prog. Theor. Phys., 2005, 113, 603–624; (b) H. Kim, C.-J. Kang, K. Kim, J. H. Shim and B. I. Min, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 165130.
26. (a) Z. Tian, J. Garg, K. Esfarjani, T. Shiga, J. Shiomi and G. Chen, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 184303; (b) J. M. Skelton, S. C. Parker, A. Togo, I. Tanaka and A. Walsh, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 205203; (c) T. Shiga, J. Shiomi, J. Ma, O. Delaire, T. Radzynski, A. Lusakowski, K. Esfarjani and G. Chen, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 155203.
27. (a) H.-W. Jeon, H.-P. Ha, D.-B. Hyun and J.-D. Shim, J. Phys. Chem. Solids, 1991, 52, 579–585; (b) T. J. Scheidemantel, C. Ambrosch-Draxl, T. Thonhauser, J. V. Badding and J. O. Sofo, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 125210; (c) B.-L. Huang and M. Kaviany, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 125209.
28. S. Ahmad and S. D. Mahanti, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 165203.
29. (a) I. T. Witting, T. C. Chasapis, F. Ricci, M. Peters, N. A. Heinz, G. Hautier and G. J. Snyder, Adv. Electron. Mater., 2019, 5, 1800904; (b) J. N. Kim, M. Kaviany and J.-H. Shim, Phys. Rev. B, 2016, 93, 075119; (c) M.-Y. Han, Y. Jin, D.-H. Lee and S.-J. Kim, Mater, 2017, 10, 1235.

---

Footnotes

† Electronic supplementary information (ESI) available: Fig. S1 (the PDOS plots calculated for Rb₂Sb₄Se₈ and Cs₂Sb₄Se₈), Fig. S2 (the thermoelectric properties of Rb₂Sb₄Se₈ calculated as a function of the chemical potential and the carrier density), Fig. S3 (the thermoelectric properties of Cs₂Sb₄Se₈ calculated as a function of the chemical potential and the carrier density), Fig. S4 (the band dispersion relations calculated for Rb₂Sb₄Se₈ and Cs₂Sb₄Se₈), and Fig. S5 (the temperature dependence of the Seebeck coefficients S (upper panels) and the power factor S²σ/τ (down panels) plots calculated for K₂Sb₄Se₈, Rb₂Sb₄Se₈, and Cs₂Sb₄Se₈). See DOI: 10.1039/d0ra01751e

‡ First two authors contributed equally to this work and should be considered co-first authors.

---