Open Access Article
Open Access ArticleAn indication of spin-transition accompanied by an order-disorder structural transformation in [Ni(phpyNO)2(NCS)2] (phpyNO = tert-butyl 5-phenyl-2-pyridyl nitroxide)†
Yukiya Kyoden and
Takayuki Ishida *
*
Department of Engineering Science, The University of Electro-Communications, Chofu, Tokyo 182-8585, Japan. E-mail: takayuki.ishida@uec.ac.jp
First published on 23rd April 2020
Abstract
Reaction of nickel(II) thiocyanate and tert-butyl 5-phenyl-2-pyridyl nitroxide (phpyNO) afforded a 2p–3d–2p heterospin triad [Ni(phpyNO)2(NCS)2]. The compound crystallizes in the orthorhombic Pbcn space group. The whole molecule is crystallographically independent. The torsion angles around Ni–O–N–C2py are 26.8(4) and 27.3(4)° at 400 K, indicating appreciable orbital overlaps of the radical π* and nickel(II) 3dx2−y2/3dz2 orbitals. In a low-temperature region, the torsion was enhanced, and the space group changed to monoclinic P21/c with a doubled asymmetric unit volume. The χmT value was practically null below ca. 140 K and, on heating to 400 K, gradually increased and reached 1.30 cm3 K mol−1. A van't Hoff analysis suggests a spin transition at T1/2 = 530(20) K. Density functional theory calculation reproduced ground Stotal = 0 with singlet-triplet gaps of 910 and 1263 K for the 140 K structure, and the gap was reduced to 297 K at 400 K. Consequently, the present compound can be considered as an incomplete spin-crossover material, as a result of T1/2 located above the experimental temperature window.
Introduction
Persistent organic free radicals are potential building blocks for molecule-based materials showing magnetic, chromic, conducting, and related functions, and they attract much attention from materials chemists.1,2 The wide diversity of paramagnetic centres and mutual spatial arrangements are available in heterospin systems, in the context of frontier orbital engineering. Gatteschi et al. have proposed the versatile “metal–radical approach”, where strong magnetic exchange coupling is operative in direct coordination bonds between paramagnetic metal ion and organic radical chromophores.3The exchange coupling in 3d9-copper(II)- and 3d8-nickel(II)-radical complexes is the best described in 3d–2p compounds.3–5 The magnetic (singly-occupied) orbitals are well defined as metal dσ (3dx2−y2 for copper(II), 3dx2−y2 and 3dz2 for nickel(II)) and radical π* orbitals. Ferromagnetic coupling occurs when magnetic orbitals are arranged in a σ–π* orthogonal manner. On the other hand, an orbital overlap between them given by breakdown of the orthogonal arrangement (a metal ion lifted above the ligand π-conjugation nodal plane for example) leads to antiferromagnetic interaction.6 The exchange interaction is sensitive to the coordination geometry, and the magnitude sometimes exceeds a thermal energy of 300 K, whether ferro- or antiferromagnetic.
Among spin-crossover (SCO) materials, switching between S = 0 and S = 2 states is the most popularly examined in 3d6 iron(II) complexes.7,8 When SCO occurs between dia- and paramagnetic states, concomitant alteration of physical properties would be dramatic. A number of ligands having a tert-butyl nitroxide (aminoxyl) group have been developed for building blocks in 2p–3d heterospin5,9 as well as 2p–4f heterospin10 compounds. There have been only two examples reported at present on the spin transition between Stotal = 0 ⇄ 2,11,12 where two S = 1/2 paramagnetic ligands and an S = 1 nickel(II) centre are involved. What “spin crossover” covers may be extended to multi-centred systems showing an essentially similar spin-multiplicity switch at their ground state.11–13 The spin state is regulated by ferro-/antiferromagnetic balance continuum in multi-centred systems,11 in place of the Hund/aufbau principles, or potential/kinetic exchange interactions, in one-centred systems.
According to the mechanism of entropy-driven SCO, a high-spin state is low-lying in a high-temperature phase because of an enhanced entropy term in G = H − TS. Entropy as a temperature coefficient becomes larger when a higher spin multiplicity is realized. The critical temperature Tc is defined where the level crossing of the energies of high-spin (HS) and low-spin (LS) states takes place, as depicted in Fig. 1. As for copper(II)- and nickel(II)-radical chelates, the experiments revealed non-planar chelate rings found in the LS phase while highly planar chelate rings in the HS phase. This scenario has been established for [Ni(phpyNO)2X2] with X = Cl11 and Br12 (phpyNO = tert-butyl 5-phenyl-2-pyridyl nitroxide;6a Fig. 2). The purpose of this paper is to describe what happens in the X = NCS case.
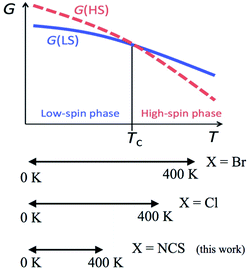 | ||
| Fig. 1 A schematic Gibbs energy diagram for spin-transition materials. The experimental temperature windows of [Ni(phpyNO)2X2] are also shown in a lower panel. | ||
Results
Molecular design and preparation
The previous reports on [Ni(phpyNO)2X2] with X = Cl,11 Br12 gave a hint to a molecular design using pseudohalogen coligands. A steric effect may modulate SCO phenomenon. Complex [Ni(phpyNO)2(NCS)2] was facilely prepared by mixing solutions of the paramagnetic ligand and commercially available Ni(NCS)2 in an established manner.11,12 The complex was characterized by means of IR spectroscopic, elemental, and X-ray crystallographic analyses, clarifying the absence of solvent molecules.Structural study
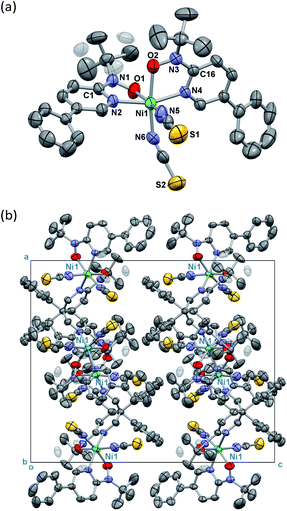
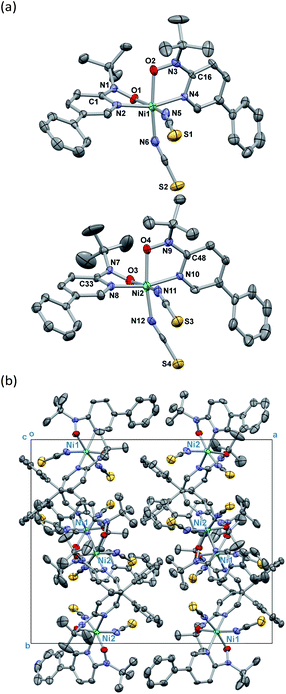
Single-crystal X-ray diffraction on [Ni(phpyNO)2(NCS)2] was performed at several temperatures, and the molecular structures at 140 and 400 K are shown in Fig. 3 and 4, respectively. Selected crystallographic data and geometrical parameters are summarized in Tables 1 and 2, respectively. The crystal consists of discrete molecules. A heterospin triad 2p–3d–2p was constructed, with five-membered chelate rings involving a direct nickel-nitroxide bond. The coligand NCS− is coordinated at a nitrogen atom. The coordination geometry of the nickel(II) ion is approximately octahedral, indicating SNi2+ = 1. No meaningful residual electron density due to solvent molecules was found. Interestingly, the variable temperature analysis clarified that the present compound underwent an order–disorder structural transition. The transition occurred in a single-crystal-to-single-crystal manner, but the residual R factors were relatively unsatisfactory, owing to deterioration of the single crystal on varying temperature.| a R = Σ[|Fo| − |Fc|]/Σ|Fo|.b wR = [Σw(Fo2 − Fc2)/ΣwFo4]1/2. | ||
|---|---|---|
| Formula | C32H34N6NiO2S2 | |
| Formula weight | 657.48 | |
| T/K | 140 | 400 |
| Crystal system | Monoclinic | Orthorhombic |
| Space group | P21/c | Pbca |
| a/Å | 19.990(4) | 17.0732(19) |
| b/Å | 16.865(3) | 19.194(3) |
| c/Å | 18.965(3) | 20.667(3) |
| β/deg | 90.338(10) | 90 |
| V/Å3 | 6394(2) | 6772.7(16) |
| Z | 8 | 8 |
| dcalcd/g cm−3 | 1.366 | 1.290 |
| μ(MoKα)/mm−1 | 0.777 | 0.733 |
| Number of total reflections | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 745 745 |
7078 |
| R(F) (I > 2σ(I))a, wR(F2) (all refls)b | 0.0997, 0.2298 | 0.0698, 0.1563 |
| Goodness-of-fit parameter | 1.038 | 1.015 |
| T/K | 140 | 400a |
|---|---|---|
| a The Ni2 molecule is identical to the Ni1 molecule. | ||
| Ni1–O1, Ni2–O3 | 2.053(6), 2.049(6) | 2.043(3) |
| Ni1–O2, Ni2–O4 | 2.046(6), 2.052(6) | 2.066(3) |
| Ni1–N2, Ni2–N8 | 2.042(7), 2.034(7) | 2.059(3) |
| Ni1–N4, Ni2–N10 | 2.039(6), 2.039(7) | 2.049(3) |
| Ni1–N5, Ni2–N11 | 2.012(8), 2.019(9) | 1.997(4) |
| Ni1–N6, Ni2–N12 | 2.030(8), 2.020(8) | 2.030(4) |
| O1–N1, O3–N7 | 1.278(8), 1.312(8) | 1.287(4) |
| O2–N3, O4–N9 | 1.309(8), 1.302(8) | 1.292(4) |
| O1⋯N2, O3⋯N4 | 2.872(8), 2.847(8) | 2.867(5) |
| O1–Ni1–N2, O3–Ni2–N8 | 75.2(3), 76.5(3) | 75.90(13) |
| O2–Ni1–N4, O4–Ni2–N10 | 77.1(2), 75.5(3) | 75.56(14) |
| O1–Ni1–N5, O3–Ni2–N11 | 171.9(3), 171.8(3) | 171.77(15) |
| O2–Ni1–N6, O4–Ni2–N12 | 171.2(3), 169.0(3) | 170.56(14) |
| Ni1–O1–N1–C1, Ni2–O3–N7–C33 | −33.7(8), −38.2(8) | −26.8(4) |
| Ni1–O2–N3–C16, Ni2–O4–N9–C48 | 35.8(8), 38.2(7) | 27.3(4) |
The compound crystallizes in an orthorhombic Pbcn space group. A whole molecule corresponds to a crystallographically independent unit. A disorder was observed in a tert-butyl group, and the occupancy factor was refined to be 0.61(2)/0.39(2) at 400 K (Fig. 3a). According to the magneto-structure relationship,6,12 the torsion angle M–O–N–C2py ϕ is a convenient index to evaluate the atomic displacement from the ligand π-conjugation plane. In the present compound, the torsion angles around Ni–O–N–C2py are 26.8(4) and 27.3(4)° at 400 K, indicating appreciable orbital overlaps of the magnetic radical and nickel orbitals. A non-bonded O1⋯O2 distance is relatively short (2.867(5) Å) but slightly longer than the sum of the van der Waals radii (2.8 Å for O/O).14
On the other hand, the disordered tert-butyl portion became ordered at 140 K. Namely, the molecule is differentiated into two independent molecules, called Ni1 and Ni2 molecules, each of which has an ordered tert-butyl conformation (Fig. 4a). The symmetry elements were reduced, giving a monoclinic unit cell with β = 90.338(10)°. The space group changed to P21/c. It is a normal trend that the low-temperature phase has a lower symmetry.15,16 The chelate plane is further deformed, as indicated with the Ni–O–N–C2py torsion angles of 33.7(8), 35.8(8), 38.2(8), and 38.2(7)° at 140 K. Despite such molecular transformation, the crystal packing motif is practically unchanged across the structural transformation (Fig. 3b and 4b).
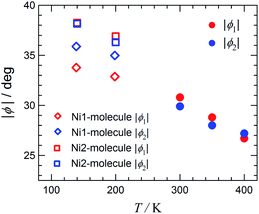
Fig. 5 displays the plot of the torsion angles against temperature for [Ni(phpyNO)2(NCS)2], where structures at 300, 350, and 400 K were solved in an orthorhombic unit cell while those at 140 and 200 K in a monoclinic cell. The torsion angle monotonically increases on cooling. The oxygen atoms are located under the control of the conformational potential surface, regulated by the tert-butyl angular positions. As a result, the separation of ϕ′s is distinct. In other words, the ordering of tert-butyl conformation is proven to be substantial in Fig. 5.
One may wonder whether the determined structure is an identical geometry or an average in time or in space.17 As Fig. 5 shows, the 400 K structure is a transient structure, as indicated with a considerable slope of ϕ against T at 400 K, but the thermal ellipsoids of the oxygen atoms are normal (Fig. 3). Furthermore, an energy level-crossing could occur between the continuous functions of T (Fig. 1). Therefore, in the present case, every structure has an identical geometry with an identical HS-LS energy gap, but magnetic properties are averaged over contributions from each level having thermal population.
Magnetic study
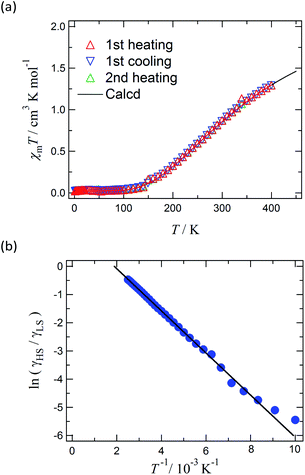
Magnetic susceptibility of [Ni(phpyNO)2(NCS)2] was measured from 1.8 to 400 K at 0.5 T (Fig. 6a). The χmT value was 1.30 cm3 K mol−1 at 400 K, being much smaller than the theoretical spin-only value, 1.75 cm3 K mol−1. A considerable positive slope remained at 400 K. Upon cooling from 400 to 1.8 K, the χmT value approaches null. The presence of strong antiferromagnetic interaction is indicated, and the coupling must be attributed to the intramolecular 2p–3d relations from the structural study. In the low temperature phase the magnetic properties are given as an average from those of two independent molecules (see above). The antiferromagnetic couplings totally agree with the prediction from the coordination structure. According to Okazawa's formalism,18 the critical angle ϕc is 21(1)°. All of the ϕ values recorded here fell in the antiferromagnetic region.As described above, the molecular structure is changed (Fig. 3 and 4), and the exchange interaction is sensitive to the structure. Therefore the van Vleck analysis using constant exchange coupling is inappropriate. Instead, the magnetic data of [Ni(phpyNO)2(NCS)2] were assumed to obey the van't Hoff equation (eqn (1)). Such an equilibrium model has often been applied to analyse spin-transition behaviour.19,20
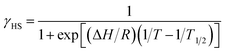 | (1) |
| χmT = C0 γHS + C1 | (2) |
The experimental χmT value was reduced to the molar fraction of the HS molecules (γHS) (eqn (2)), where C0 and C1 imply the Curie constants for the HS state and the paramagnetic impurity bias, respectively. A satisfactory linear fit appeared in the van't Hoff plot (Fig. 6b) with the parameters optimized, as follows: C0 = 3.29(12) cm3 K mol−1, C1 = 0.0246(7) cm3 K mol−1, T1/2 = 530(20) K, and the enthalpy change ΔH = 6.21(7) kJ mol−1. The C0 value is reasonably acceptable in comparison with the theoretical spin-only S = 2 value (3.0 cm3 K mol−1). The very small C1 indicates the high purity of the sample. The relatively large statistic error of T1/2 is unavoidable from the fitting analysis on the onset data. The entropy change was estimated as ΔS = 12(1) J K−1 mol−1 from the relation T1/2 ΔS = ΔH, because ΔG vanishes at equilibrium. In short, the present compound exhibited thermally induced spin transition, but the thermal energy is insufficient even at 400 K. The domain model20 indicates an almost uncooperative system from the very gradual spin-transition profile.
Symmetry-breaking transition,15 order-disorder transition in particular,16 often has connection with multi-step and/or hysteretic SCO. It seems to be a rare case;21 though the space group and crystal system have been changed, the SCO profile keeps one-step and nonhysteretic.
DFT calculation study
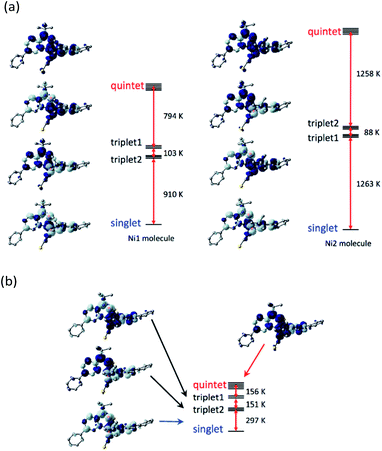
To check the exchange coupling change depending on the structure, the density functional theory (DFT) calculation22 was performed to the determined structure of [Ni(phpyNO)2(NCS)2]. The self-consistent field (SCF) energies on the 140 and 400 K structures were calculated on the UB3LYP/6-311+G(2d,p) level. At 140 K (Fig. 7a), the lowest state was singlet, drawn as ↓-↑↑-↓ for the spin structure in N1O1–Ni–O2N3. The highest one was quintet, ↑-↑↑-↑. Two triplet states, ↑-↑↑-↓ and ↓-↑↑-↑, intervene them. The energy gaps between the ground and the first excited states are 910 and 1263 K for the Ni1 and Ni2 molecules, respectively, which are much larger than the thermal energy of a conventional experimental temperature range.The ground state remained singlet at 400 K (Fig. 7b), indicating that the exchange couplings are both antiferromagnetic in the entire temperature range here. However, we have to pay attention to the fact that the energy gap between the ground and the first excited states became as narrow as 297 K, which is comparable to the temperatures where the magnetic properties were measured.
Quantification of the exchange coupling parameter J in the spin Hamiltonian Ĥ = –2J(S1·S2 + S2·S3) does not give high reliability solely from this calculation. The problem resides in the accidentally short intramolecular radical–radical distance.12
Discussion
Now let us overview the results on the derivatives with X = Cl,11 Br,12 and NCS (this study). The T1/2 order is as follows: T1/2(Br) < T1/2(Cl) < T1/2(NCS) (Table 3). This situation is illustrated in the bottom of Fig. 1. The present compound can be considered as an incomplete spin-crossover (or pseudo spin-transition23) material, as a result of T1/2 located far above the experimental temperature window.The ligand field splitting is not important in the present SCO scenario, because the HS/LS states are regulated by 3d–2p ferro-/antiferromagnetic exchange interactions. The crystallographic analysis clarified that the coligands occupied the trans positions of the radical oxygen atoms. The trans-influence order is known to be Cl− < Br− < NCS−,24 suggesting that the stronger ligand would bring about the weaker trans bond. As summarized in Table 3, unexpectedly, the shortest Ni–O bond lengths were characterized in the NCS derivative. The bond strength is supposed to have relation to a covalent character due to the strong 3d–2p antiferromagnetic coupling.
Steric effects from the coligands seem to be key, because the order of the van der Waals radii and covalent radii is r(N) < r(Cl) < r(Br),14 which coincides with the T1/2 order. The following is one of possible explanations. Sterically bulky coligands suppress out-of-plane distortion of the chelate rings, while smaller coligands can accommodate atomic displacement out of the chelate plane in a nickel(II) coordination sphere. Thus, bulkiness stabilizes the HS state and causes a low-temperature shift of T1/2.
The entropy change of SCO can be interpreted as a sum of electronic, vibrational, and conformational terms. The electronic contribution is given with the degeneracy of each state.25 In the case where singlet and quintet states are involved, the electronic contribution is given as ΔSelec = R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln{(2SHS + 1)/(2SLS + 1)} = R
ln{(2SHS + 1)/(2SLS + 1)} = R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 = 13.38 J K−1 mol−1. We have to assume the conformational contribution ΔSconf = R
5 = 13.38 J K−1 mol−1. We have to assume the conformational contribution ΔSconf = R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 = 5.76 J K−1 mol−1 from the order-disorder structural transition. In addition, vibrational contribution ΔSvib is present as well in total ΔS. The previous works on the [Ni(phpyNO)2X2] reported reasonable ΔS = 26.3(1) and 24.0(7) J K−1 mol−1 for X = Cl11 and Br,12 respectively. It should be noted that comparably small ΔS = 12(2) J K−1 mol−1 was obtained here.
2 = 5.76 J K−1 mol−1 from the order-disorder structural transition. In addition, vibrational contribution ΔSvib is present as well in total ΔS. The previous works on the [Ni(phpyNO)2X2] reported reasonable ΔS = 26.3(1) and 24.0(7) J K−1 mol−1 for X = Cl11 and Br,12 respectively. It should be noted that comparably small ΔS = 12(2) J K−1 mol−1 was obtained here.
However, the small ΔS does not necessarily imply the lower spin multiplicity at the high-temperature phase. The following notices strongly suggest that the ground state should be HS in the high-temperature phase: (1) the driving force is required for structural modification toward a planar chelate on both wings when heated. (2) Order–disorder-type structural transition is often accompanied by spin transition. (3) The Curie constant of the high-temperature phase is C0 = 3.29(12) cm3 K mol−1, being quite compatible with theoretical one for the quintet species. It is inevitable that the ground state is depopulated under high-temperature conditions, and effective ΔS from the experimental data may be short accordingly.
Conclusions
The present compound, doubly chelated [Ni(phpyNO)2(NCS)2], has been synthesized as a 2p–3d–2p heterospin triad. The exchange coupling is strongly antiferromagnetic in a low-temperature structure whilst moderately antiferromagnetic in a high-temperature structure. The T1/2 value is estimated to be 530(20) K. This compound can be considered as an incomplete spin-crossover material because the molecular structure at 400 K still is an intermediate toward the HS structure. Even if temperature is raised sufficiently above T1/2, the susceptibility could not reach the theoretical HS value owing to a thermal depopulation effect.We have to stress that the exchange parameter J is a function of temperature. Detailed structural study is needed to reveal a gradual structural transformation. In comparison among the Cl, Br, and NCS derivatives, the order is shown as T1/2(Br) < T1/2(Cl) < T1/2(NCS). The unconventional scenario of the multi-centred spin crossover seems to be plausible after the coligand dependence on T1/2 is overviewed.
Experimental section
Preparation and characterization
After combining a dichloromethane solution (0.65 mL) containing phpyNO6a (72.5 mg; 0.301 mmol) and a methanol solution (0.90 mL) containing Ni(NCS)2 (26.8 mg; 0.153 mmol) at room temperature, the mixture was allowed to stand a few h. Dark red needles of [Ni(phpyNO)2(NCS)2] were precipitated, collected on a filter, and air-dried. The yield was 24.9 mg (0.0378 mmol; 25%). Mp. 191 °C (dec.). IR (attenuated total reflection (ATR)) 2983, 2061, 1450, 1256, 1176, 1011, 760, 689, 554 cm−1. Anal. Calcd. for C32H34N6NiO2S2: C, 58.46; H, 5.21; N, 12.78; S, 9.75%. Found: C, 58.20; H, 5.52; N, 12.82; S, 9.62%. A polymorphic non-SCO byproduct was obtained as hexagonal-shaped dark red plates in another run. IR (ATR): 2988, 2092, 2071, 1451, 1258, 1178, 1010, 764, 697, 555 cm−1. Anal. Calcd. for C32H34N6NiO2S2: C, 58.46; H, 5.21; N, 12.78; S, 9.75%. Found: C, 58.19; H, 5.35; N, 12.78; S, 9.50%. This byproduct crystallized in a monoclinic P2/c space group with a = 17.843(4), b = 11.274(3), c = 17.612(5) Å, β = 112.001(11)°.Crystallographic analysis
X-Ray diffraction data of a single crystal of [Ni(phpyNO)2(NCS)2] were acquired on a Rigaku Saturn70 diffractometer with a CCD detector and graphite monochromated Mo Kα radiation (λ = 0.71073 Å). The structures were solved in the CRYSTALSTRUCTURE program,26 and the parameters were refined in the Shelxl program.27 Selected crystal data are summarized in Table 1, and important geometrical parameters are listed in Table 2.Magnetic analysis
Magnetic susceptibilities of polycrystalline [Ni(phpyNO)2(NCS)2] were acquired on a Quantum Design MPMS XL-7 SQUID magnetometer. The magnetic response was corrected with diamagnetic blank from the sample holder measured separately. The diamagnetism of the sample itself was estimated from Pascal's constant.DFT calculation
Density functional theory (DFT) calculations were performed with the Gaussian03 rev. C.02.22 A single-point calculation was applied to the geometry of [Ni(phpyNO)2(NCS)2] from the X-ray crystallography. The self-consistent field energy was converged to 10−7 a.u. on the UB3LYP28/6-311+G(2d,p) level. The broken symmetry method29 was utilized.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was financially supported with Izumi Science and Technology Foundation (Grant number 2019-J-033).Notes and references
- (a) Stable Radicals: Fundamentals and Applied Aspects of Odd-Electron Compounds, ed. R. G. Hicks, Wiley, Chichester, UK, 2010 Search PubMed; (b) H. Iwamura, Polyhedron, 2013, 66, 3 CrossRef CAS; (c) I. Ratera and J. Veciana, Chem. Soc. Rev., 2012, 41, 303 RSC; (d) Nitroxides. Brief History, Fundamentals, and Recent Developments, ed. G. I. Likhtenshtein, Springer, Switzerland, 2020 Search PubMed.
- (a) B. K. Rugg, B. T. Phelan, N. E. Horwitz, R. M. Young, M. D. Krzyaniak, M. A. Ratner and M. R. Wasielewski, J. Am. Chem. Soc., 2017, 139, 15660 CrossRef CAS PubMed; (b) X. Ai, Y. Chen, Y. Feng and F. Li, Angew. Chem., Int. Ed., 2018, 57, 2869 CrossRef CAS PubMed; (c) K.-A. Hansen and J. P. Blinco, Polym. Chem., 2018, 9, 1479 RSC.
- (a) A. Caneschi, D. Gatteschi, R. Sessoli and P. Rey, Acc. Chem. Res., 1989, 22, 392–398 CrossRef CAS; (b) X. Meng, W. Shi and P. Cheng, Coord. Chem. Rev., 2019, 378, 134 CrossRef CAS.
- (a) D. Luneau, P. Rey, J. Laugir, P. Fries, A. Caneschi, D. Gatteschi and R. Sessoli, J. Am. Chem. Soc., 1991, 113, 1245 CrossRef CAS; (b) A. Ali, D. Dhar, S. K. Barman, F. Lloret and R. Mukherjee, Inorg. Chem., 2016, 55, 5759 CrossRef CAS PubMed; (c) M. S. de Souza, M. Briganti, S. G. Reis, D. Stinghen, C. S. Bortolot, R. A. Cassaro, G. P. Guedes, F. C. da Silva, V. F. Ferreira, M. A. Novak, S. Soriano, F. Totti and M. G. F. Vaz, Inorg. Chem., 2019, 58, 1976 CrossRef CAS PubMed.
- (a) A. Okazawa, T. Nogami and T. Ishida, Chem. Mater., 2007, 19, 2733 CrossRef CAS; (b) K. Osanai, A. Okazawa, T. Nogami and T. Ishida, J. Am. Chem. Soc., 2006, 128, 14008 CrossRef CAS PubMed; (c) C. Aoki, T. Ishida and T. Nogami, Inorg. Chem., 2003, 42, 7616 CrossRef CAS PubMed.
- (a) A. Okazawa, Y. Nagaichi, T. Nogami and T. Ishida, Inorg. Chem., 2008, 47, 8859 CrossRef CAS PubMed; (b) A. Okazawa, T. Nogami and T. Ishida, Polyhedron, 2009, 28, 1917 CrossRef CAS.
- M. A. Halcrow, Spin-Crossover Materials: Properties and Applications, John Wiley & Sons, Ltd., Oxford, UK, 2013 Search PubMed.
- (a) G. Aromí and J. A. Real, Special Issue “Spin Crossover (SCO) Research”, Magnetochemistry, 2016, 2, 28 CrossRef; (b) K. Takahashi, Special Issue “Spin-Crossover Complexes”, Inorganics, 2018, 6, 32 CrossRef; (c) T. Kitazawa, Special Issue “Synthesis and Applications of New Spin Crossover Compounds”, Crystals, 2019, 9, 382 CrossRef CAS; (d) S. Hayami, S. M. Holmes and M. A. Halcrow, Themed Issue “Spin-State Switches in Molecular Materials Chemistry”, J. Mater. Chem. C, 2015, 3, 7767 RSC.
- (a) A. Okazawa, D. Hashizume and T. Ishida, J. Am. Chem. Soc., 2010, 132, 11516 CrossRef CAS; (b) A. Okazawa and T. Ishida, Inorg. Chem., 2010, 49, 10144 CrossRef CAS.
- (a) T. Kanetomo, T. Kihara, A. Miyake, A. Matsuo, M. Tokunaga, K. Kindo, H. Nojiri and T. Ishida, Inorg. Chem., 2017, 56, 3310 CrossRef CAS PubMed; (b) T. Kanetomo, T. Yoshitake and T. Ishida, Inorg. Chem., 2016, 55, 8140 CrossRef CAS PubMed; (c) T. Ishida, R. Murakami, T. Kanetomo and H. Nojiri, Polyhedron, 2013, 66, 183–187 CrossRef CAS.
- Y. Homma and T. Ishida, Chem. Mater., 2018, 30, 1835 CrossRef CAS.
- Y. Kyoden, Y. Homma and T. Ishida, Inorg. Chem., 2019, 58, 10743 CrossRef CAS PubMed.
- V. Ovcharenko, S. Fokin, E. Chubakova, G. Romanenko, A. Bogomyakov, Z. Dobrokhotova, N. Lukzen, V. Morozov, M. Petrova, M. Petrova, E. Zueva, I. Rozentsvelg, E. Rudyakova, G. Levkovskaya and R. Sagdeev, Inorg. Chem., 2016, 55, 5853 CrossRef CAS.
- (a) A. Bondi, J. Phys. Chem., 1964, 68, 441 CrossRef CAS; (b) P. Pyykko and M. Atsumi, Chem. – Eur. J., 2009, 15, 186 CrossRef PubMed.
- N. Ortega-Villar, M. C. Munoz and J. A. Real, Magnetochemistry, 2016, 2, 16 CrossRef.
- (a) M. Griffin, S. Shakespeare, H. J. Shepherd, C. J. Harding, J. –F. Létard, C. Desplanches, A. E. Goeta, J. A. K. Howard, A. K. Powell, V. Mereacre, Y. Garcia, A. D. Naik, H. Muller-Bunz and G. G. Morgan, Angew. Chem., Int. Ed., 2011, 50, 896 CrossRef CAS PubMed; (b) C. F. Sheu, S. Pillet, Y. C. Lin, S. M. Chen, I. J. Hsu, C. Lecomte and Y. Wang, Inorg. Chem., 2008, 47, 10866 CrossRef CAS PubMed.
- R. Sanchez-de-Armas, N. C. Hernandez and C. J. Calzado, Inorg. Chem. Front., 2019, 6, 1228 RSC.
- A. Okazawa, IOP Conf. Ser.: Mater. Sci. Eng., 2017, 202, 012002 CrossRef.
- O. Kahn, Molecular Magnetism, VCH, New York, 1993, ch. 4 Search PubMed.
- R. Boca, Theoretical Foundations of Molecular Magnetism: Current Methods in Inorganic Chemistry, Elsevier, Amsterdam, 1999, vol. 1 Search PubMed.
- A. Kashiro, K. Some, Y. Kobayashi and T. Ishida, Inorg. Chem., 2019, 58, 7672 CrossRef PubMed.
- M. J. Frisch, et al., Gaussian 03 revision C.02, Gaussian Inc., Wallingford, USA, 2004 Search PubMed.
- F. Lanfranc de Panthou, E. Belorizky, R. Calemczuk, D. Luneau, C. Marcenat, E. Ressouche, P. Turek and P. Rey, J. Am. Chem. Soc., 1995, 117, 11247 CrossRef CAS.
- (a) T. G. Appleton, H. C. Clark and L. E. Manzer, Coord. Chem. Rev., 1973, 10, 335 CrossRef CAS; (b) D. F. Shriver and P. W. Atkins, Inorganic Chemistry, Oxford Univ. Press, Oxford, 4th edn., 1999, ch. 20 Search PubMed.
- (a) G. Molnar, M. Mikolasek, K. Ridier, A. Fahs, W. Nicolazzi and A. Bousseksou, Ann. Phys., 2019, 531, 1900076 CrossRef CAS; (b) J. Cirera, M. Via-Nadal and E. Ruiz, Inorg. Chem., 2018, 57, 14097 CrossRef CAS PubMed; (c) M. Valtiner, H. Paulsen, P. Weinberger and W. Linert, MATCH, 2007, 57, 749 CAS.
- CRYSTALSTRUCTURE, version 4.2, Rigaku/MSC, The Woodlands, TX, 2010–2015 Search PubMed.
- G. M. Sheldrick, SHELXL-2016/6, Acta Crystallogr., Sect. C: Struct. Chem., 2015, 71, 3 Search PubMed.
- (a) A. D. Becke, J. Chem. Phys., 1993, 98, 5648 CrossRef CAS; (b) C. Lee, W. Yang and R. G. Parr, Phys. Rev. B, 1988, 37, 785 CrossRef CAS PubMed.
- K. Yamaguchi, Y. Takahara and T. Fueno, in Applied Quantum Chemistry, ed J. V. H. Smith, H. F. Schaefer and K. Morokuma, Reidel, Dordrecht, 1986, pp. 155–184 Search PubMed.
Footnote |
| † CCDC numbers 1983989 and 1983990 for the structures of [Ni(phpyNO)2(NCS)2] measured at 140 K and 400 K, respectively. For crystallographic data in CIF or other electronic format see DOI: 10.1039/d0ra02041a |
| This journal is © The Royal Society of Chemistry 2020 |