Open Access Article
Open Access ArticleConformational dynamics of superoxide dismutase (SOD1) in osmolytes: a molecular dynamics simulation study†
Ishrat Jahan and
Shahid M. Nayeem *
*
Department of Chemistry, Aligarh Muslim University, Aligarh-202002, U.P., India. E-mail: jishrat17@gmail.com; msnayeem.ch@amu.ac.in; Tel: +91-9412527078
First published on 30th July 2020
Abstract
Amyotrophic lateral sclerosis (ALS) is a progressive neurodegenerative disease caused by the misfolding of Cu, Zn superoxide dismutase (SOD1). Several earlier studies have shown that monomeric apo SOD1 undergoes significant local unfolding dynamics and is the predecessor for aggregation. Here, we have employed atomistic molecular dynamics (MD) simulations to study the structure and dynamics of monomeric apo and holo SOD1 in water, aqueous urea and aqueous urea–TMAO (trimethylamine oxide) solutions. Loop IV (zinc-binding loop) and loop VII (electrostatic loop) of holo SOD1 are considered as functionally important loops as they are responsible for the structural stability of holo SOD1. We found larger local unfolding of loop IV and VII of apo SOD1 as compared to holo SOD1 in water. Urea induced more unfolding in holo SOD1 than apo SOD1, whereas the stabilization of both the form of SOD1 was observed in ternary solution (i.e. water/urea/TMAO solution) but the extent of stabilization was higher in holo SOD1 than apo SOD1. The partially unfolded structures of apo SOD1 in water, urea and holo SOD1 in urea were identified by the exposure of the hydrophobic cores, which are highly dynamic and these may be the initial events of aggregation in SOD1. Our simulation studies support the formation of aggregates by means of the local unfolding of monomeric apo SOD1 as compared to holo SOD1 in water.
Introduction
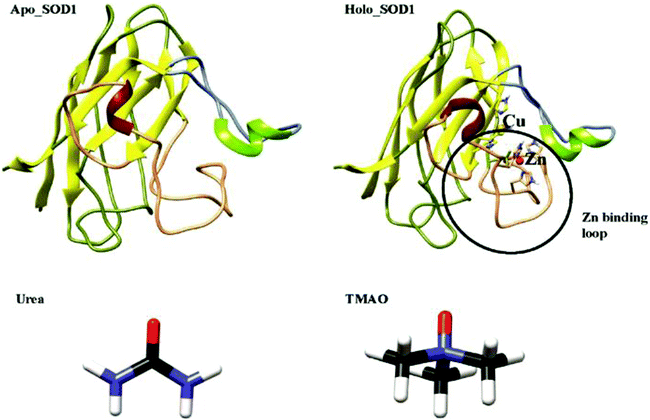
Amyotrophic lateral sclerosis (ALS), also known as motor neuron disease (MND), is a fatal neurodegenerative disorder that affects the nerve cells in the brainstem and spinal cord, which causes gradual paralysis and ultimately leads to patient death. ALS is of two types-sporadic and familial. About 90–95% of ALS cases are due to unknown causes and are termed as sporadic (sALS), and the remaining ALS cases are due to familial inheritance (fALS) and are associated with mutations in the SOD1 genes in a dominant manner.1,2 The key pathological hallmark of ALS is the misfolding and aggregation of SOD1;3–5 nonetheless the structural events provoking the misfolding of SOD1 remains controversial. So far, more than 180 mutations have been reported in SOD1, which have been associated with ALS and these mutations are located throughout the polypeptide chain.6 The formation of protein aggregates in the motor neurons of fALS patients and transgenic mice is the main element of ALS.7,8 It has been proposed that disulphide bond reduction or metal loss from SOD1 causes the misfolding of SOD1, which may form insoluble aggregates and by that, increase the intracellular fractions of the apo or disulphide reduced state.9,10 In solution, SOD1 protein forms stable homo-dimers where each SOD1 unit contains 153 amino acids, binds to 1 copper and 1 zinc ion and has a conserved intra-monomer disulphide bond (Cys57–Cys146). Each monomeric subunit of SOD1 has eight antiparallel immunoglobulin-like β-strands with N-terminal strands (strands 1, 2, 3, and 6) and C-terminal strands (strands 4, 5, 7, and 8). It has seven loops, where two of the loops are long and functionally very important as they are connecting the eight strands of SOD1 (Fig. 1). The structurally important zinc ion is bound by the zinc-binding loop (residues 49–83) and the electrostatic loop (residues 121–142) plays an important role in accompanying the superoxide anion to the active site.11,12 The zinc-binding loop is important as it is responsible for the structure and function of the copper active site.Many studies have proposed that the main reason for the SOD1 aggregation is a monomeric species where sticky sequence regions of SOD1 have been exposed through the local unfolding of the central β-sheets13,14 by the reduction/loss of the intramolecular disulphide bond,15 cross-linked oxidatively via the cysteine,16 oligomerized through the active site loops,11,17 or by a combination of mechanisms.18 Moreover, it has also been found that the disulphide-reduced apo SOD1 monomer is slightly stable at physiological temperature,19,20 which suggests that the partial unfolding of β-sheets will serve as a starting point for aggregation. Nonetheless, several studies have also proved that the overall unfolding of SOD1 is the disease precursor in vivo.19,21,22
Computational studies provide an additional understanding of the structural properties of SOD1. A few groups have used MD simulations to study the structure and dynamics of wild-type apo SOD1 and its mutants in water.23–27 They found that the loss of the metal ion and disulphide bond increases the propensity of apo SOD1 to unfold and form aggregates. Mutants of apo SOD1 undergo distinct unfolding patterns and thus favour the aggregation. In contrast, we have performed atomistic MD simulations of both these forms of SOD1, i.e., apo and holo SOD1 in water and in osmolytes (urea and TMAO) to study the structure and dynamics of apo and holo SOD1. The all-atom Monte Carlo method has been employed by Bille et al.28 to investigate the local unfolding and dynamics of the β-sheet of the SOD1 monomer. Das and Plotkin29 performed simulations of SOD1 where a local measure of force resistance was computed and analysed. Their results provide insights into the internal stress of the native structure of SOD1. These studies provide an abundance of information about the properties of SOD1, which is important in understanding their role in protein folding and aggregation at the molecular level. It has been reported earlier that the monomeric apo SOD1 species is responsible for the formation of aggregates.13 Urea is a naturally occurring osmolyte that causes the denaturation of proteins. Most of the studies reported earlier show urea-induced protein denaturation. It has now been accepted that urea induces protein denaturation via a direct mechanism, i.e., by binding to the protein side-chains and backbone with less disorder of the water structure (i.e., less distortion of the tetrahedral order parameter of water molecules).30–36 TMAO is also a naturally occurring protein-protective osmolyte present in living organisms, mainly in marine animals such as sharks, rays and cartilaginous fishes and it counteracts the effect of urea-induced protein denaturation.37,38 The exact mechanism of TMAO action on protein by which it stabilizes the protein remains arguable. Many computational and experimental studies reported earlier proposed that TMAO forms a complex with 2–3 water molecules39 and results in the depletion of TMAO molecules from protein surfaces or causes the unfavourable interaction of TMAO with the protein backbone.35,40–43 Most of the efforts in the past decades have been invested in studying the individual action of urea and TMAO on the protein structure. In our present study, we have tried to explore the conformational dynamics of monomeric apo and holo SOD1 in water, urea and urea–TMAO solution through standard molecular dynamics simulations since the structural dynamics of SOD1 are associated with the early stages of aggregation, which cause ALS disease. Here, we have also demonstrated how TMAO counteracts the urea denaturation and its interactions, which shows its protein-protective nature in the presence of urea. We have also explored the relative conformational fluctuations of apo and holo forms of SOD1 in different environments.
Methods
MD simulations were carried out on the monomers of the apo and holo forms of the SOD1 protein with PDB ID-2C9V obtained from the RCSB protein data bank. The apo form of SOD1 was obtained by removing all the metal ions and heteroatoms from the structure. The all-atom MD simulations were carried out by Gromacs v5.1.4 (ref. 44) using GROMOS53a5 force fields.45 To solvate each of the proteins with water, urea/water and urea/TMAO/water mixture in a cubic simulation box of side 60 Å, the SPC/E water model was used.46 The parameters for urea and TMAO molecules were built from an automated topology builder (ATB)47 and are provided in the ESI.† The ATB generated parameters were found to be reliable and have been widely used in several current studies.48–53 However, the effectiveness of ATB parameters was also justified by calculating the transport properties (i.e. self-diffusion coefficient), structural properties (RDF and number of hydrogen bonds) and thermodynamic properties (density) of the TMAO box, and the results were compared with the Shea force field54 and the united atom force field (generated from ATB) of TMAO as a benchmark test;55 these are reported in the ESI.† The numbers of osmolytes and water molecules that were used to prepare an aqueous mixture of 4 M urea and 2 M TMAO in a cubic simulation box of side 60 Å have been provided in the ESI (Table S1).† Protein was placed in the centre of the equilibrated box and overlapping water molecules were deleted. Position restraints were applied to the metal ions and on the residues involved in the interaction in the case of holo SOD1. Ions were added to neutralize the system.Energy minimization was done on each system using the steepest descent algorithm for 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps followed by equilibration. A total of six standard MD simulations (1.2 μs) was performed and, for each of the six systems, a 200 ns production run was carried out with an integration time step of 2 fs at 300 K using the NPT ensemble. The Berendsen weak coupling algorithm was used in both cases, i.e., for pressure at 1 bar with a coupling constant of 0.5 ps and for temperature with coupling constant of 0.1 ps.56 The coordinates and trajectory were saved at every 10 ps. A similar simulation protocol was used to that described earlier.57
000 steps followed by equilibration. A total of six standard MD simulations (1.2 μs) was performed and, for each of the six systems, a 200 ns production run was carried out with an integration time step of 2 fs at 300 K using the NPT ensemble. The Berendsen weak coupling algorithm was used in both cases, i.e., for pressure at 1 bar with a coupling constant of 0.5 ps and for temperature with coupling constant of 0.1 ps.56 The coordinates and trajectory were saved at every 10 ps. A similar simulation protocol was used to that described earlier.57
Analyses of the MD trajectories obtained after the production run were conducted using Gromacs utilities. To determine whether the system reached equilibrium, thermodynamic parameters, potential energy and density of the system were calculated and were found to be uniform throughout the simulation, which showed that the system had reached equilibrium (Fig. S1 and S2†). To define the conformational changes of each holo and apo SOD1 in water, urea/water and urea/TMAO/water during the simulation, the RMSD (root mean square deviations) were calculated. Nc (fraction of native contacts), residual hydrophobic contact map and the SASA (solvent accessible surface area) were calculated to determine the changes in holo and apo SOD1 variants in water, urea–water and urea–TMAO–water solution. Configurational entropies and the number of intermolecular hydrogen bonds were also calculated to monitor the extent of unfolding in both holo and apo SOD1 in all three systems. Essential dynamics analysis and DSSP analyses were also performed using Gromacs utilities. The Delphi program58 has been used to calculate the surface potential of the apo and holo SOD1 exposed in different osmolytes. The surface potential was calculated for the initial structure and the structure obtained after 200 ns MD. The PDB of apo and holo SOD1 were written at 200 ns of the MD simulations using the Gromacs44 gmx trjconv command. The parameters used for Delphi calculations are as follows: grid size of 80, percent fill 80, probe radius 1.4, internal dielectrics 2.0, and external dielectric 80. Ionic strength was kept at 0 for all the calculations. The distributions of water and osmolyte molecules around SOD1 were also calculated in terms of the radial distribution function (RDF) and it was defined as the probability of finding the molecules at a distance ‘r’ from another tagged molecule. This was denoted as g(r) and was calculated using the gmx RDF command of Gromacs utilities. The three-dimensional arrangement of water and osmolyte molecules around SOD1 were calculated in terms of the spatial distribution function (SDF). SDF of the oxygens of water (OW), oxygens of urea (OU) and nitrogens of TMAO (NT) were calculated using the gmx spatial command of Gromacs utilities in all the systems of apo and holo SOD1. Visualization of the results was done using the VMD59 software.
Essential dynamics analysis
The collective motion of apo and holo SOD1 in water, urea and urea–TMAO solution during the course of the simulation can be studied in terms of essential dynamics,60 which were performed using GROMACS utilities. The covariance matrix was built by taking the atomic co-ordinates obtained from MD trajectories and the collective motions of apo and holo SOD1 were saved as eigenvalues and eigenvectors, which provide the magnitude of their motion. Each eigenvector shows the motion of atoms, which in turn displays the direction of the motion of the protein. Here, the first two eigenvectors were considered as they make the greatest contribution to the magnitude of motion of apo and holo SOD1 throughout the trajectory.Free energy landscape (FEL) plots61 were also plotted by considering the first two eigenvectors (PC1 and PC2).
Results and discussion
Structural dynamics of apo and holo SOD1 variants
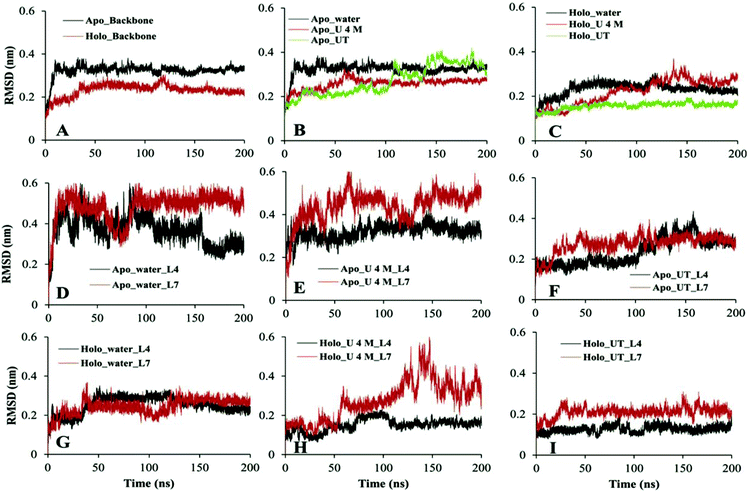
Evaluation of the RMSD is a routine check to analyse the structural stability of the protein. The RMSD of the backbone atoms of apo and holo SOD1 in water, along with the urea and urea–TMAO solution, were computed with respect to the initial native structure to quantify the extent of structural changes (Fig. 2). We first compared the behaviour of apo and holo SOD1 in water and then we analysed the behaviour of apo and holo SOD1 in the presence of osmolytes with respect to the system with no osmolyte. The RMSD of apo and holo SOD1 in water reached a stable conformation at 0.34 nm and 0.23 nm within 50 ns of the simulation and remained stable throughout the simulation. However, a little fluctuation in the RMSD of holo SOD1 was observed near 120 ns of the simulation and after that, it remained stable. The RMSD of the backbone atoms of apo SOD1 in urea was lower than that in water, which indicates that apo SOD1 underwent fewer structural changes in urea than in water. In the urea–TMAO ternary solution, the RMSD showed fluctuations near 150–170 ns and after that, it decreased from 0.38 nm to 0.3 nm (Fig. 2B). The RMSD of holo SOD1 in urea showed a large fluctuation and it increased from 0.1 nm to 0.3 nm, suggesting the unfolding of the protein, which was as expected since urea leads to the extended conformation of the protein.61 However, the RMSD of holo SOD1 in the urea–TMAO solution remained constant throughout the simulation and was even less than that in water, which might be due to the stabilizing nature of TMAO (Fig. 2C). The larger fluctuation in the RMSD of apo SOD1 was assumed to be the cause of aggregation as compared to holo SOD1. We also calculated the RMSD of metal-binding (loop IV) and electrostatic loops (loop VII) since they are believed to be highly responsible for the structural stability of protein.26,62,63 The removal of metal ions from their active sites caused the loops loosen and become more dynamic, which may have increased the propensity to form aggregates; this can be validated from the RMSF (root mean square fluctuation) and the hydrophobic SASA of residues (H46, H48, H63, H71, H80, D83, H120) interacting with metal ions in both forms of SOD1 in water (Fig. S3†). The RMSF and hydrophobic SASA of residues of apo SOD1 showed larger values than holo, which indicated that the loss of metal ions from their active sites might be the reason for the higher aggregation propensity of apo SOD1 than holo SOD1. The RMSD of loops IV and VII of apo SOD1 showed larger fluctuations in water as compared to holo SOD1, which indicated the greater propensity for apo SOD1 to aggregate in water as compared to holo SOD1. However, the RMSD of loop IV of holo SOD1 in urea showed less fluctuation and loop VII showed more fluctuation than apo in urea. It was observed that the RMSD of loop VII showed a larger fluctuation than loop IV in both forms of the protein, which indicated that the large unfolding in the protein arose because of loop VII. In the ternary system, both loops were stabilized but the extent of stabilization was higher in holo SOD1 (Fig. 2F and I).Another important parameter for monitoring the compactness of the protein is the radius of gyration, Rg. The probability distribution of Rg of apo and holo SOD1 in water, urea and urea–TMAO solution has been plotted (Fig. 3). Apo SOD1 in water showed a broader peak whose Rg value ranged from 1.43 to 1.46 nm, whereas holo SOD1 in water showed a sharp peak at 1.45 nm, which showed the compactness of holo SOD1 (Fig. 3). The larger value of Rg in apo SOD1 indicated a decrease in the compactness of the protein, which might be due to the deficiency of the metal ions since they are responsible for the high stability of the protein when it is in its fully functional form.64 The Rg value of apo SOD1 in urea was larger than that in water and it decreased in the urea–TMAO solution. The large value of Rg of apo SOD1 in urea may be attributed to more fluctuations in loop VII of apo SOD1, which decreased the compactness of the protein; this was also seen from the RMSD of loop VII of apo SOD1 in urea (Fig. 2E). However, Rg of holo SOD1 in urea showed a broader peak with Rg value ranging from 1.47 to 1.49 nm, which was larger than holo SOD1 in water. In ternary solution, both proteins were stabilised but the probability of the Rg value of 1.45 nm was higher in holo SOD1 than in apo SOD1. Hence, holo SOD1with metal was less prone to aggregation than the apo form.13,14
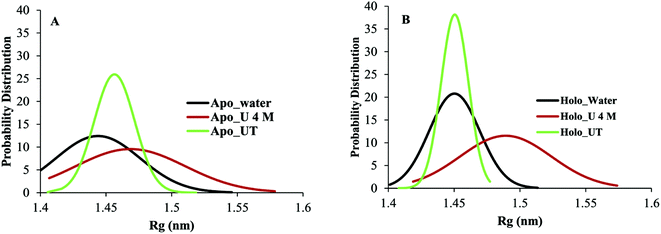 | ||
| Fig. 3 Probability distribution of the radius of gyration (Rg) of apo and holo SOD1 in water, urea and urea–TMAO solution. | ||
One of the essential processes in the protein folding/unfolding study is the breakage or formation of specific contacts between the two residues of the protein chain. Here, we calculated the fraction of native contacts (Nc) of apo and holo SOD1 in water and in osmolytes as a function of time during the last 50 ns of the simulation (Fig. 4) (we discarded the first 150 ns of the simulation as an equilibration time based on the RMSD). The fraction of native contacts in apo SOD1 was considerably smaller than that of holo SOD1 in water, indicating the relatively lower stability of apo SOD1 as compared to the holo form (Fig. 4A). However, in apo SOD1, a significant increase in native contacts was found in 4 M urea at the end of the simulation, which was closer to that of holo SOD1 in 4 M urea (Fig. 4B). The partial unfolding and destabilization of holo SOD1 were observed in 4 M urea as the fraction of native contacts decreased as compared to that in water. In the ternary system, the value of Nc was restored in both apo and holo forms but this increase was higher in holo than in apo SOD1, which illustrates that the unfolding of the protein is smaller and it might remain in its native conformation (Fig. 4C).
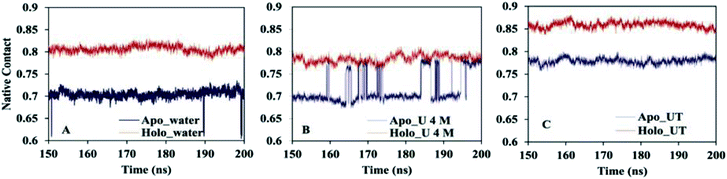 | ||
| Fig. 4 Fractions of the native contact of apo and holo SOD1 in (A) water, (B) urea and (C) urea–TMAO solution. | ||
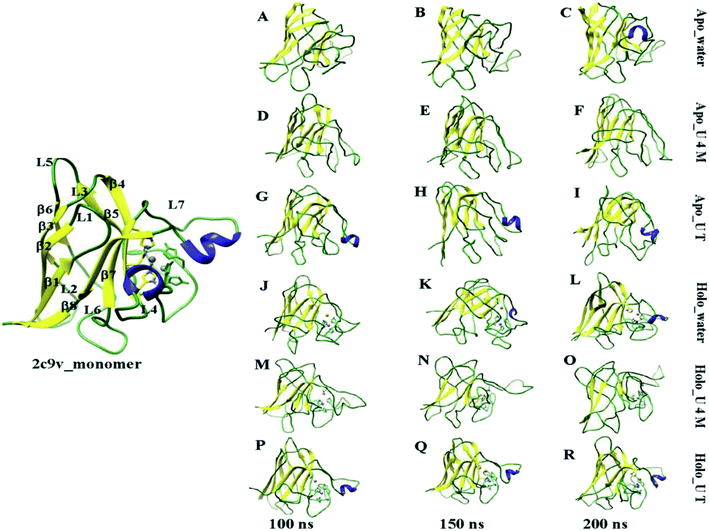
To visually demonstrate the extent of the unfolding of apo and holo SOD1 in water and in osmolytes, several configurations of the protein at different time intervals (i.e. 100 ns, 150 ns and 200 ns), in water and in osmolytes are displayed (Fig. 5). As a reference, the monomeric holo SOD1 structure obtained from the RCSB protein data bank is also provided in Fig. 5, highlighting the secondary structural segment. It is clear from the figure that in apo SOD1, the α-helix present in loop IV and loop VII diminished at the end of the simulation in urea and remained 1% in water. The gain in the α-helical content (up to 3%) was observed in the urea–TMAO solution, which showed the dominant stabilizing nature of TMAO as it counteracted the effect of urea on protein.65 On the other hand, the loss of the secondary structure of holo SOD1 was lower in comparison to apo SOD1 in water (Fig. 5A–C and J–L). However, in urea, loops IV & VII of holo SOD1 were completely loosened and also the α-helix content was completely converted into a flexible coil-like structure with the convincing loss of the secondary structure as evident from Fig. 5M–O. In the ternary system, the distortion of the secondary structure was less since the loss of the α-helical content was smaller than in urea, which showed that TMAO counteracted the effect of urea (Fig. 5P–R). The large expansion of loops IV & VII of apo SOD1 in water and urea, and of holo SOD1 in urea, is one of the reasons for the formation of aggregates since it leads to the separation of the segments corresponding to β4, β5, β7, and β8. These snapshots of apo and holo SOD1 conformations are consistent with our earlier results stated above.
Inconsistency in the secondary structure
The percentages of the secondary structure contents of apo and holo SOD1 under all conditions, i.e., in water, urea and urea–TMAO solutions, were calculated using the DSSP program (Table 1). Remarkable changes in the secondary structure contents of apo and holo SOD1 were observed during the last 50 ns of the simulation as compared with the holo SOD1 at 0 ns of the simulation time. During the start of the simulation, the percentages of α-helix, β-sheet, turns and coil contents of holo SOD1 were 3%, 32%, 12% and 29%, respectively. The percentage of the β-sheet content of apo SOD1 did not show any significant changes under all the conditions; however, notable changes in the coils, turns and helix percentages were observed. The percentages of α-helical content of apo SOD1 in water, urea and urea–TMAO were 1%, 1%, and 3%. The α-helical content decreased in water and urea, whereas in urea–TMAO solution, it remained constant. The α-helix is present in loops IV & VII of SOD1 and is considered as a functionally important loop. A decrease in the α-helical content caused the extension of loops IV & VII, and in turn destabilised the protein, which made the protein aggregation-prone. The α-helical contents of holo SOD1 in water, urea and urea–TMAO solutions were 2%, 0% and 3%. The larger unfolding of holo SOD1 was observed in urea; however, the distortion of the secondary structure was smaller in ternary solution. Thus, holo SOD1 was more stable and retained most of its secondary structure in water and urea–TMAO solution.| System | Helix | β-sheet | Coil | Turn |
|---|---|---|---|---|
| Apo_water | 1 | 30 | 36 | 3 |
| Apo_U 4 M | 1 | 31 | 39 | 6 |
| Apo_UT | 3 | 31 | 38 | 5 |
| Holo_water | 2 | 34 | 29 | 7 |
| Holo_U 4 M | 0 | 23 | 44 | 5 |
| Holo_UT | 3 | 34 | 31 | 5 |
Solvent accessible surface area (SASA)
A decrease in the native contact (Nc) value leads to protein expansion, which consequently increases the solvent accessible surface area of the protein. To further examine the behaviour of apo and holo proteins in the presence of osmolyte, we plotted the residue-wise SASA changes in osmolytes with respect to the corresponding apo and holo SOD1 systems in water only (Fig. 6). In 4 M urea, the positive value of the SASA indicates that unfolding occurs in both forms of SOD1, which leads to an increase in the solvent-accessible surface area of the protein. β2 of apo SOD1 underwent more unfolding than holo SOD1 as observed from the increased value of the SASA, whereas the extent of unfolding in β3, loop IV, β5, β6 and loop VII of holo SOD1 was found to be a little larger than in apo SOD1 in the presence of urea (Fig. 6A). The increases in the SASA value of the β5 and β6 strands are consistent with the findings that show the involvement of these strands in aggregate formation.17,23 In ternary systems, the ΔSASA value decreases in both cases but this decrease was higher in holo SOD1 (mainly in loop IV & VII, β2, β3, β5 and β6), which depicts the larger stability of holo SOD1 in the urea–TMAO solution than apo SOD1, which is in agreement with the native contacts (Fig. 4) and DSSP (Table 1) results.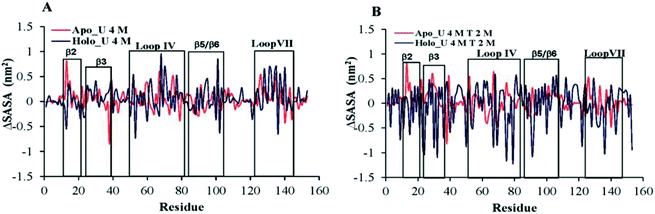 | ||
| Fig. 6 The difference between the SASA per residue of apo and holo SOD1 containing (A) urea and (B) urea–TMAO w.r.t apo and holo SOD1 in water, respectively. | ||
Changes in the conformational stability of the β-strand
Another important preserving element that sustains the folded structure of SOD1 is the β-barrel plug and it consists of loop III (residue 37–40) and loop V (residue 90–94).66,67 Loop V is considered as an aggregation site in SOD1 and it connects the edge strands β5 and β6.68 The probability distribution of the SASA of loop V of apo and holo SOD1 in water, urea and urea–TMAO solutions were plotted. We observed the shift in the dynamics of loop V in apo and holo SOD1 in water and in 4 M urea solution (Fig. 7A and B). The probability of loop V having a SASA value of 7.9 nm2 is higher in apo SOD1 than loop V of holo SOD1 in water (Fig. 7A). This change in dynamics destabilizes the β-strand, which then causes the β5 and β6 strand to move apart and in turns leads to the opening of the β-strand and causes aggregation. However, in the presence of urea, the loop V of holo SOD1 has a higher probability with a SASA value of 7.5 nm2 than apo SOD1, which shows larger unfolding in holo than apo SOD1 (Fig. 7B). In the presence of urea–TMAO solution, the probability of loop V having a SASA value of 7.5 nm2 decreases in both forms but this decrease is higher in holo SOD1 (Fig. 7C), which shows the lower flexibility of the β-plug region in both forms, indicating that SOD1 is less prone to aggregation. These results suggest that apo SOD1 in water, urea and holo SOD1 in urea are more prone to aggregation as the opening of the β-strand occurs, which in turn exposes the hydrophobic core of the protein (Fig. 8) and therefore causes aggregation.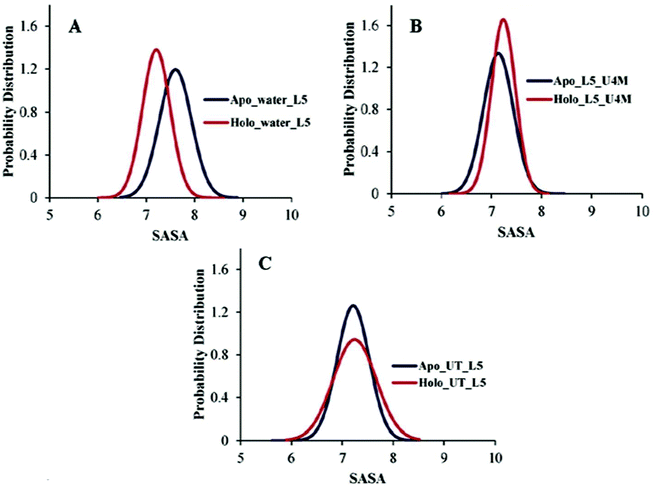 | ||
| Fig. 7 Probability distribution of the SASA of loop V of apo and holo SOD1 in (A) water, (B) urea and (C) urea–TMAO solutions. | ||
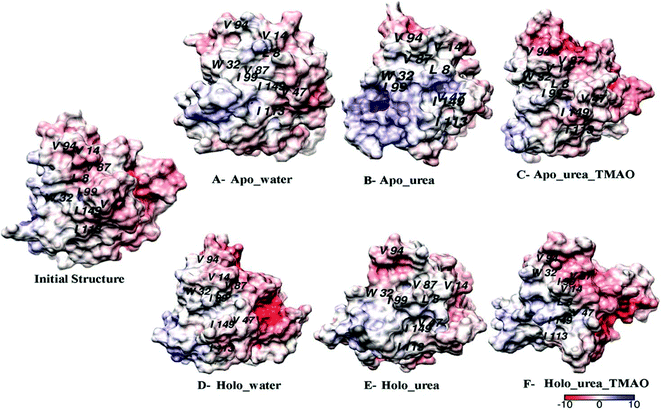
To see the hydrophobic surfaces of apo and holo SOD1 exposed in different solvents, the Delphi program58 was used to calculate the surface potential of apo and holo SOD1. It was observed that the hydrophobic residues (viz. L8, V14, W32, V47, V87, I99, I113, and I149) were buried in the initial structure of SOD1. In the presence of water, most of the hydrophobic residues (viz. V14, W32, V94, I99, I113, and I149) of apo SOD1 were exposed and in the presence of urea, the exposed hydrophobic residues were L8, V14, W32, V87, V94, and I149 at the end of the simulation (Fig. 8A and B). In ternary solution, some of the hydrophobic residues of apo SOD1 (viz. V14, W32, V47, V87, V94, I113, and I149) remained buried (Fig. 8C). However, most of the hydrophobic residues (L8, V14, W32, V47, V87, I99, I113, and I149) of holo SOD1 in urea were exposed except for the V94 at the end of the simulation (Fig. 8E) in comparison to the initial structure of holo SOD1. In the presence of water and urea–TMAO solution, the hydrophobic residues remained buried (Fig. 8D and F) at the end of the simulation, which showed the compactness of holo SOD1 as compared to apo SOD1, also in agreement with the above results.
The further stability of SOD1 was examined by calculating the pairwise distance distribution of the β-strand region residues G37 and G93 (Table 2). We found that the distance between these residues was larger in apo SOD1 as compared to holo SOD1 in water. Furthermore, this distance decreased in 4 M urea in apo SOD1 and further decreased in ternary solution. However, in holo SOD1, the distance between these residues increased in urea and then decreased in urea–TMAO solution, suggesting the destabilization and then stabilization of the β-plug regions of holo SOD1.
| SOD1 | G37–G93 | G73–L126 | N86–L126 | A4–I99 | A4–I149 |
|---|---|---|---|---|---|
| Apo_water | 0.22 ± 0.06 | 1.08 ± 0.08 | 0.38 ± 0.14 | 1.05 ± 0.05 | 0.43 ± 0.03 |
| Apo_U 4 M | 0.21 ± 0.03 | 0.49 ± 0.09 | 0.34 ± 0.03 | 0.95 ± 0.06 | 0.39 ± 0.03 |
| Apo_UT | 0.18 ± 0.04 | 0.40 ± 0.12 | 0.20 ± 0.08 | 0.77 ± 0.06 | 0.40 ± 0.03 |
| Holo _water | 0.20 ± 0.03 | 0.50 ± 0.06 | 0.43 ± 0.10 | 1.00 ± 0.09 | 0.39 ± 0.03 |
| Holo_U 4 M | 0.73 ± 0.13 | 0.54 ± 0.04 | 1.28 ± 0.12 | 1.11 ± 0.06 | 0.38 ± 0.02 |
| Holo_UT | 0.40 ± 0.10 | 0.36 ± 0.04 | 0.34 ± 0.05 | 1.00 ± 0.04 | 0.40 ± 0.03 |
The variation in the distance between loops IV & VII residues (i.e. G73–L126 and N86–L126) was also analysed (Table 2). As seen from Table 2, the distance between these residues of apo SOD1 was higher in water and decreased in urea and further decreased in the urea–TMAO solution. However, in holo SOD1, the distance was higher in urea and smaller in water and urea–TMAO solution, which indicated that the β-plug regions were more compact in water and ternary solution than in urea. These results suggest that apo SOD1 in water and holo SOD1 in urea are more prone to aggregation, which is in agreement with the SASA of loop V.
Hydrophobic contact map
Distinctive solvent exposure of apo and holo SOD1 proteins may disturb the hydrophobic contacts of the protein; therefore, hydrophobic contact map analysis was performed in water, urea and urea–TMAO solutions (Fig. 9). After inspecting the results more closely, it was observed that the tertiary structure of the apo SOD1 underwent greater destruction than holo SOD1, with the loss of the long-range hydrophobic contacts in water being marked by the removal of points farther (10–21, 21–10) in apo than holo SOD1 (Fig. 9A and D). This shows that the β4 and β8 strands of apo SOD1 underwent more conformational changes than holo SOD1 in water. In the presence of urea, the loss of long-range hydrophobic contacts was observed more in holo SOD1 than in apo SOD1, marked by the points (1–13, 7–21, 10–21, 13–1 and 21–10) (Fig. 9E). This signifies the considerable unfolding of β1, β3, β4, β5, β7 and β8 strands of holo SOD1 in urea, also in agreement with the experimental results reported by Furukawa et al., which showed the three major regions, namely, the N-terminal β-sheet, i.e., strands 1, 2 and 3; the middle region, i.e., strand 6; and C-terminal strand 8, which is responsible for the formation of aggregates.69 In 4 M urea, some new long-range hydrophobic contacts were formed in apo SOD1 (5–13, 6–18, 7–18 and 13–5) (Fig. 9B). In the ternary solution, the formation of some new contacts took place along with the reappearance of those long-range hydrophobic contacts in both apo and holo SOD1 (Fig. 9C and F). In apo SOD1, some new short-range contacts were also formed. This indicates that the loss of the native-like compact conformation of SOD1 was smaller in the ternary solution in both forms. The overall result suggests that β1, β3, β4, β5, β7 and β8 strands of holo SOD1 displayed noticeable loss and unfolding of protein in 4 M urea as compared to apo SOD1 with the expulsion of long-range contacts involving β1–β5, β3–β8, β4–β7 and β4–β8. However, breakage of these long-range contacts was smaller in ternary solution in both apo and holo SOD1.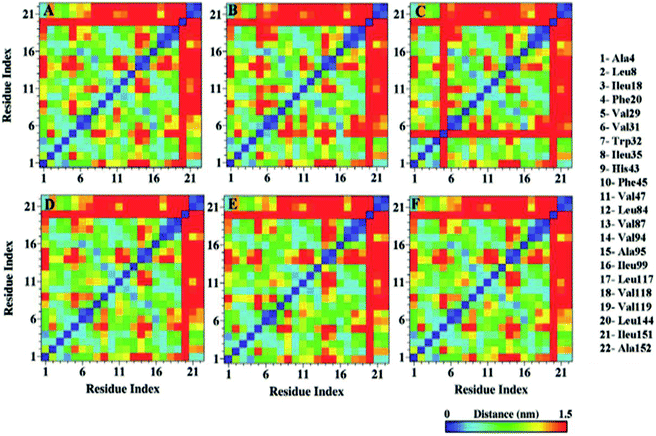 | ||
| Fig. 9 Hydrophobic contact map of apo and holo SOD1 barrels in water (A & D), urea (B & E) and in urea–TMAO solution (C & F). | ||
In addition, the disruption of the tertiary structure, as well as the dynamics of unfolding, can also be validated by the calculation of the pair-wise distance of long-range contacts between edge strands, i.e., Ala4 (β1)–Ile99 (β6) and Ala4 (β1)–Ile149 (β8) of apo and holo SOD1 in all conditions (Table 2). We found that in water, the pair-wise distance between these strands was larger in apo than holo SOD1, which may cause the tertiary contacts of apo SOD1 to vanish. In the presence of urea, the pair-wise distance in the Ala4 (β1)–Ile99 (β6) strand of holo SOD1 was larger than apo SOD1, whereas it remained almost constant in Ala4 (β1)–Ile149 (β8) in both forms of protein, which indicates that the extent of unfolding was greater in the β1–β6 strand of holo than in apo SOD1. In the presence of urea–TMAO, the hydrophobic contacts started reappearing in both apo and holo SOD1 as the pairwise distance between Ala4 (β1)–Ile99 (β6) in both apo and holo SOD1 decreased (Table 2), which is in agreement with all the above results.
Configurational entropies of apo and holo SOD1
An increase in the configurational entropy of protein indicates an increased conformational fluctuation/disorder of a protein.70 Such conformational disorder in apo and holo SOD1 can be different along different unfolding pathways in water and in osmolytes as discussed above (Fig. 5). We have further seen that loops IV & VII of apo SOD1 in the given conditions showed different unfolding behaviour than holo SOD1. The differential unfolding behaviours of apo and holo SOD1 in different conditions led to the gain or loss of entropy, which has been explored in this section.The configurational entropy of protein can be measured by using the method proposed by Schlitter.71 The method proposed by Schlitter is proficient for directly calculating the absolute entropies of large macromolecules from their Cartesian coordinates and is based on one-dimensional quantum mechanical harmonic oscillator approximation. In this method, the absolute entropy (Sabs) can be estimated as
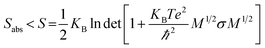 | (1) |
| σij = 〈(xi − 〈xi〉)(xj − 〈xj〉)〉 | (2) |
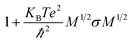 . One of the specific upper hands of this method is that it can be used for calculating the entropy contribution of a particular subset of atoms forming a segment of macromolecules like proteins, which otherwise cannot be calculated from other available methods.
. One of the specific upper hands of this method is that it can be used for calculating the entropy contribution of a particular subset of atoms forming a segment of macromolecules like proteins, which otherwise cannot be calculated from other available methods.
The cumulative configurational entropies (S) of apo and holo SOD1 in water, urea and urea–TMAO solutions at 300 K were calculated throughout the simulation trajectories. The entropy contributions obtained from backbone atoms and the non-hydrogen side-chain atoms are shown in Fig. 10. The entropy values were normalised by dividing by the number of atoms to avoid the difference in the number of backbone and side-chain atoms. As evident from the figure, the gain in entropy was larger in the side chain of SOD1 than in the backbone, which indicates that the large conformational changes in the protein arise due to the disturbance in the sidechain of SOD1. Apo SOD1 in water contributed more to the protein's entropy than the holo SOD1; i.e., the gain in the entropy of apo SOD1 in water was higher than holo SOD1, which indicates the larger conformational change of apo SOD1. In the presence of urea, the entropy gain in apo SOD1 was a little less than that in water (both in backbone and sidechain atoms) (Fig. 10A and C), which showed that apo SOD1 underwent less conformational changes in the presence of urea, whereas in holo SOD1, the entropy of the backbone atoms continued increasing in the presence of urea (Fig. 10B), which indicated that the unfolding occurred in both forms. In the ternary system, the entropy contribution of backbone atoms in both forms of SOD1 was reduced, which indicates the stabilisation of protein where stabilization is greater in holo than in apo SOD1. A similar pattern was also observed for the side chains of SOD1 in both forms for all the conditions. Since loops IV & VII are considered as the important functional loops since they are responsible for the stability of the SOD1 protein,73 we also calculated the configurational entropies of the backbone and side-chain atoms of these loops over the last 50 ns of the simulations under all conditions. Time evolution entropies of backbone and sidechain atoms of loops IV & VII of apo and holo SOD1 under all conditions are shown in the ESI (Fig. S4 and S5).† The backbone atoms of loop 4 of holo SOD1 underwent less conformational changes than apo SOD1. However, in the case of apo SOD1, the backbone and sidechain atoms of loop 4 had minor differences in their entropies in all the conditions. The sidechain atoms of loop 4 of holo SOD1 showed a decrease in the entropy in the ternary system, which indicates that holo SOD1 was more stabilised than apo SOD1. The backbone and sidechain atoms of loop 7 of holo SOD1 underwent a noticeable conformational transformation in urea and hence, a gain in entropy was observed. The entropy gained by loops IV & VII of apo SOD1 in water was consistent with the unfolding and breaking of secondary structures of the whole protein as compared to holo SOD1 as discussed in the above results.
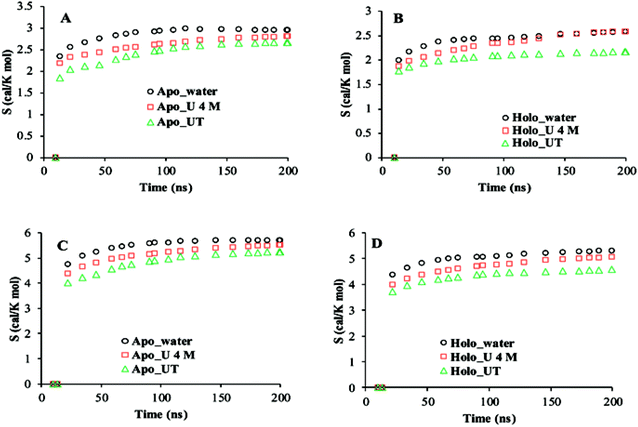 | ||
| Fig. 10 Cumulative configuration entropies (per atom) of the backbone (A and B) and sidechain (C and D) of apo and holo SOD1 in water, urea and urea–TMAO solutions, respectively. | ||
Hydrogen bond analysis
The extent of the unfolding of apo and holo SOD1 was further studied in terms of the number of intermolecular hydrogen bonds present in apo and holo proteins in water, urea and urea–TMAO solutions. We calculated the probability distribution of the number of hydrogen bonds present in apo and holo SOD1 under all conditions and it was observed that the probability of finding more hydrogen bonds (105 hydrogen bonds) was higher in holo SOD1 than in apo SOD1 in water (Fig. 11A). In the presence of 4 M urea, the probability of finding 85 hydrogen bonds was higher in apo SOD1 than in holo (Fig. 11B) and in the presence of the urea–TMAO solution, the probability of finding 100 hydrogen bonds increased in the holo as compared to apo SOD1. The overall results suggested that the extent of unfolding was smaller in holo SOD1 in water and in urea–TMAO solution, and thus less prone to aggregation than apo SOD1. However, in the presence of urea, the extent of unfolding was greater in holo than in apo; i.e., the holo form became less stable than apo since the intermolecular interactions in holo SOD1 were reduced and its stability was less affected in the presence of the urea–TMAO solution, where intermolecular interactions in protein increased. Although both forms of SOD1 were stabilised in the presence of urea–TMAO, the extent of the loss of hydrogen bonds was higher in apo than in holo (Fig. 11C), which is in agreement with the secondary structure content results.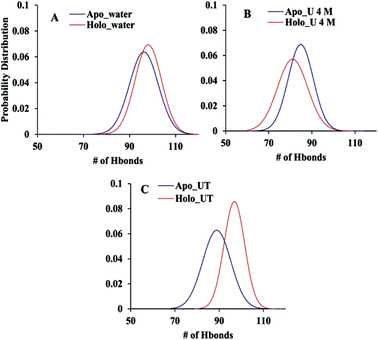 | ||
| Fig. 11 Probability distribution of the number of intramolecular hydrogen bonds present in apo and holo SOD1 in (A) water, (B) urea and (C) TMAO. | ||
Essential dynamics analysis
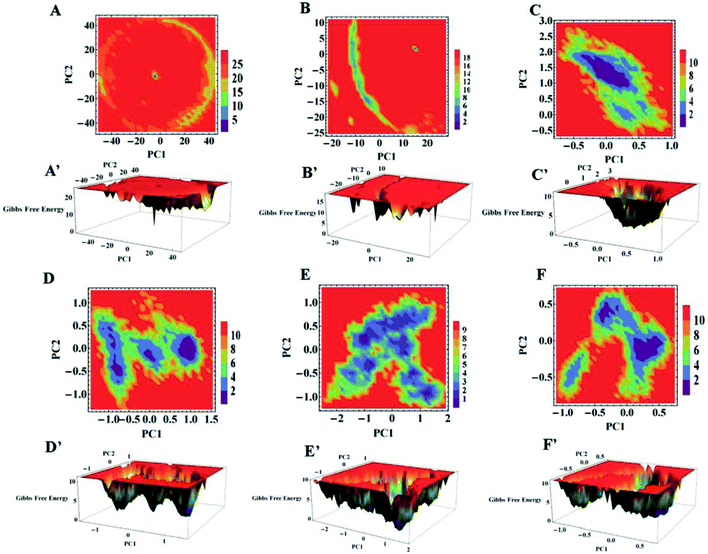
To further explore the conformational dynamics of apo and holo SDO1 proteins in water, urea and urea–TMAO solutions, essential dynamics (ED) was performed on the protein backbone. The first two principal components (PC1 and PC2) from ED were used in constructing the free energy surface. These two components correspond to large-scale collective motions, which were used to determine the feasible conformational changes in the protein. The 2D and 3D constructed free energy landscape (FEL) projected onto the first two principal components of apo and holo SOD1 in water, urea and urea–TMAO solutions are represented in Fig. 12, with the Gibbs free energy ranging from 1 to 5 kJ mol−1. The 3D free energy landscape of proteins shows the stability of the protein based on the shape and size of the funnel with a global minimum energy area. The more concentrated the blue region of the FEL is an indicator of the higher stability of the protein.74 A 2D-FEL plot of apo SOD1 in water and urea shows that apo SOD1 samples smaller basins of conformations with very low population density of particular conformations (Fig. 12A and B), as also seen from the 3D-FEL plot (Fig. 12A′ and B′). This suggests that very few conformations of apo SOD1 have stable energy and all the other conformations are unstable, which indicates the unfolding of proteins in water and urea (Fig. 12A and B). In the presence of the urea–TMAO solution, the apo SOD1 samples wider basins of conformation with a higher population density of particular conformations, indicating that a stable conformation was attained by most of the conformations in ternary solution (Fig. 12C). The 3D-plot also shows single minima with more concentrated blue zones indicating the greater stability of apo SOD1 in ternary solution (Fig. 12C′). Holo SOD1 in water and urea–TMAO solutions sample wider basins of conformations with higher population densities of a particular conformation (Fig. 12D, D′, F and F′). However, holo SOD1 in urea also samples wider basins of conformations but with lower population density and multiple minima as evident from the 3D plot, which shows the unfolding of the protein (Fig. 12E and E′). Holo SOD1 in water exhibits four different conformations having global minimum energy and in urea–TMAO solution, it exhibits two minima with higher population density, which shows the stabilization of SOD1 in ternary solution in comparison to holo SOD1 in urea where multiple minima are observed (Fig. 12E′). This result is also in agreement with the above-stated results.The overall conclusion from our static and dynamic results revealed that absolute changes in the conformational structure of apo SOD1 in water, urea and holo SOD1 in urea were observed, as any change in the conformations of SOD1 from its native structure causes protein unfolding and aggregation, thus enhancing the pathogenicity of the disease.
Water and osmolyte properties around loops IV & VII
So far, we have studied apo and holo SOD1 conformation changes in water, urea and urea–TMAO solutions during MD simulations. It was found that apo SOD1 underwent partial unfolding in water as compared to holo SOD1; in urea, partial unfolding was larger in holo than apo SOD1. The extent of unfolding is reduced in ternary solution in both forms of SOD1. Since loops IV & VII are considered biologically functional loops of SOD1, any unfolding in these loops may disturb the biological function of the whole protein. Because of the different unfolding patterns of apo and holo SOD1 under different conditions, it could influence the water and osmolyte properties at the interface. In this section, we explored the effects of apo and holo SOD1 on water and osmolyte properties around loops IV & VII under different conditions. The structural arrangements of water, urea and TMAO molecules around loops IV & VII of apo and holo SOD1 were studied through the radial distribution function (RDF) ‘g(r)’ of the oxygens of water (OW), oxygens of urea (OU) and nitrogens of TMAO (NT) molecules around loops IV & VII. No major changes in the RDF of OW around loops IV & VII of apo and holo SOD1 were observed (Fig. S6†). However, a slight decrease in the RDF of OW around loops IV & VII of apo and holo SOD1 was observed in the presence of urea and urea–TMAO solutions in comparison to apo and holo SOD1 in water (Fig. S6A and D†). In the presence of urea, the distribution of OU around loops IV & VII of holo SOD1 was higher in the first and second solvation shells than apo SOD1, whereas in ternary solution, the distribution of OU around loops IV & VII of holo SOD1 decreased in comparison to apo SOD1 (Fig. 13). These results suggest that holo SOD1 was more solvent-exposed in the presence of urea than apo SOD1, which is in agreement with the SASA results (Fig. 6). In ternary solution, the RDF of NT around loops IV & VII of both forms of SOD1 in the first solvation shell was found to be smaller than urea, which indicated fewer interactions of TMAO molecules in comparison to urea (Fig. 13B, D and S7†). Similar TMAO behaviour was also observed,75,76 where the exclusion of TMAO from the first solvation shell took place, which showed the “osmophobic effect” of TMAO in protecting the protein from denaturation in the urea–TMAO solution. We also calculated the RDF of OW, OU and NT around the full apo and holo SOD1 in water and in osmolytes. A similar pattern was observed to the case of loops IV & VII (Fig. S8†), which indicated that small disturbances in loops IV & VII of SOD1 will affect the whole protein.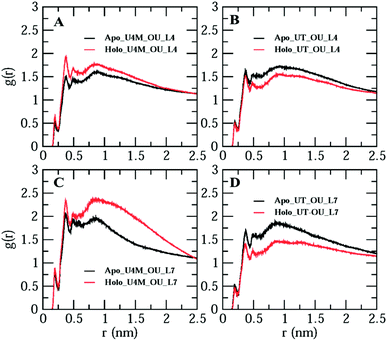 | ||
| Fig. 13 Radial distribution function of the oxygens of urea (OU) around loops IV & VII of apo and holo SOD1 in urea (A &C) and in urea–TMAO (B & D) solutions. | ||
Spatial distribution function (SDF)
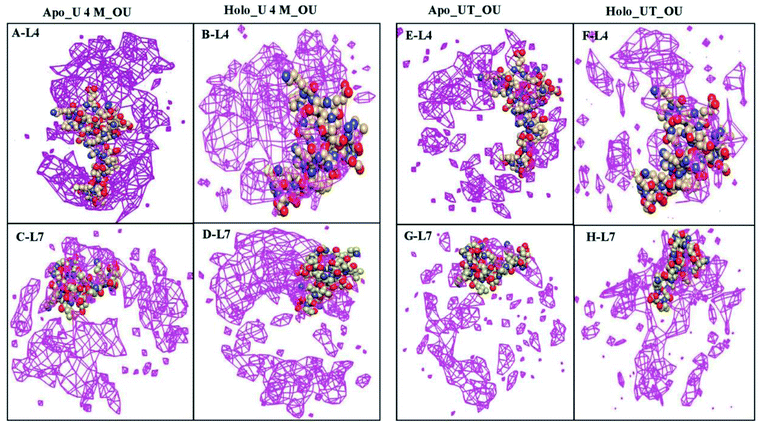
To further determine the spatial three-dimensional arrangement of the oxygens of urea (OU) molecules around particular loops, i.e., loops IV & VII (L4 & L7) of apo and holo SOD1 in urea and in urea–TMAO solutions, the spatial distribution function was calculated using the gmx spatial command of the Gromacs utilities. Since it was difficult to view the variation of SDF (i.e. three-dimensional data in general) over the entire local space, we were left with two basic approaches. One was to view the variation in terms of two-dimensional “slices” by using the full three-dimensional data set or to see the variation in terms of iso-surfaces (or contours) at particular threshold values. Herein, we have represented the SDF in terms of “iso-surfaces” (Fig. 14) as it gives a better sense of the three-dimensional structure present and the slice form shows the actual variation in the data, which indicates the specificity of the structural features.77,78 SDF of OU is shown in purple in the first solvation shell corresponding to the RDF plot (Fig. 13). The SDF of OU around L4 and L7 was found to be higher in holo SOD1 than in apo-SOD1 in urea, whereas in the case of the ternary solution, the SDF of OU around both loops in both apo and holo-SOD1 decreased but the decrease was higher in holo than in apo-SOD1 (Fig. 14), which is in agreement with the RDF results (Fig. 13). We also calculated the SDF of the oxygens of water (OW) molecules around L4 and L7 of apo and holo SOD1 in water, urea and urea–TMAO solutions (Fig. S9†). A slight decrease in the SDF of OW around L4 and L7 of the apo and holo SOD1 was observed in urea in comparison to apo and holo SOD1 in water. However, in ternary solution, a very slight change in SDF of OW around L4 and L7 of apo and holo SOD1 was observed with respect to apo and holo SOD1 in water. No major differences in the SDF of the nitrogens of TMAO (NT) around L4 and L7 of apo and holo SOD1 were observed in ternary solution (Fig. S10†). Similar results were obtained from the RDF plot (Fig. 13).The average numbers of hydrogen bonds formed between water and osmolytes with loops IV & VII of apo and holo SOD1 were also calculated and are listed in Table 3. In water, the number of hydrogen bonds formed with loops IV & VII of apo SOD1 with water is larger than that of holo SOD1 as more unfolding was observed in apo SOD1 in water. In the presence of the water–urea binary solution, the number of hydrogen bonds formed between urea and loop IV of holo SOD1 was larger than that in apo SOD1, whereas this number is larger with loop VII of apo SOD1.
| SOD1 system | Loop IV | Loop VII | |
|---|---|---|---|
| Apo_water | 73.5 | 65.2 | |
| Apo_U 4 M | Water | 37.0 | 32.0 |
| Urea | 57.7 | 53.0 | |
| Apo_UT | Water | 35.2 | 22.5 |
| Urea | 52.0 | 37.6 | |
| TMAO | 2.8 | 2.7 | |
| Holo_water | 69.8 | 57.3 | |
| Holo_U 4 M | Water | 34.5 | 27.9 |
| Urea | 61.3 | 49.0 | |
| Holo_UT | Water | 29.5 | 29.5 |
| Urea | 51.6 | 28.7 | |
| TMAO | 5.7 | 3.1 |
The greater the number of hydrogen bonds formed between urea and loops of SOD1, the greater will be the unfolding. Since the number of hydrogen bonds formed between urea and loops of holo SOD1 was larger as compared to apo SOD1, it caused the greater unfolding of holo SOD1 in the presence of urea, which is also in agreement with the earlier explained DSSP results. In ternary solution, the number of hydrogen bonds formed with urea and loops IV & VII of SOD1 decreased in both forms but this decrease was higher in holo SOD1 than in apo, i.e., the extent of unfolding decreased in both forms of SOD1 in ternary solution. This showed the stabilizing nature of TMAO as it counteracted the effect of urea by removing the urea molecules from the protein surface, as the number of hydrogen bonds formed between urea and loops decreased in ternary solution as compared to the binary solution (Table 3). Similar behaviour was shown by TMAO in ternary solution (urea–TMAO–water), where the stabilisation of SNase protein took place in ternary solution as TMAO counteracted the effects of urea.75
Conclusion
We performed multi-scale molecular dynamics simulations of apo and holo SOD1 in the presence of water, urea/water and urea/TMAO/water solutions to study the conformational dynamics of SOD1, which causes aggregation. Our simulation results suggested that apo SOD1 is more prone to aggregation than holo SOD1 in water, which was also reported experimentally, but no simulation of SOD1 had been reported in urea and urea/TMAO solutions. The overall results suggest that urea induces large conformational dynamics in holo SOD1 as compared to apo SOD1, and results in different local unfolding of β-strands, which then undergo an overall unfolding and may cause aggregation. The results provided by our simulation indicate that along with the distortion of the hydrophobic cores of SOD1 protein, the β-strands that underwent more destruction include β2, β3, β5 and β6, which might be responsible for the formation of aggregates. This was also reported experimentally since they were more solvent-exposed as explained by the SASA and Delphi surface potential results. Less unfolding was observed in holo SOD1 in the presence of water and water/urea/TMAO solutions. Apo SOD1 underwent less unfolding in the presence of 4 M urea solution as compared to holo SOD1 in urea and was stabilized in the presence of urea–TMAO solution. Apo SOD1 was more prone to aggregation than holo SOD1 in water.The results indicate that by changing the nature of the solvents, the conformational dynamics of SOD1 proteins can be naturally modified, which consequently helps in controlling the pathological misfolding and aggregation of proteins.
Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
We acknowledge the support provided by the NPSF-PARAM YUVA-II and BRAF at C-DAC, Pune, India, for providing the supercomputer facility in carrying out MD simulations. We are also thankful to DST for providing financial support as INSPIRE Fellowship and DRS-II SAP to the Department of Chemistry A. M. U. in carrying out above research work.References
- D. R. Rosen, T. Siddique, D. Patterson, D. A. Figlewicz, P. Sapp, A. Hentati, D. Donaldson, J. Goto, J. P. O'Regan and H. X. Deng, et al., Mutations in Cu/Zn superoxide dismutase gene are associated with familial amyotrophic lateral sclerosis, Nature, 1993, 362(6415), 59–62 CrossRef CAS PubMed.
- J. S. Valentine, P. A. Doucette and S. Zittin Potter, Copper-zinc superoxide dismutase and amyotrophic lateral sclerosis, Annu. Rev. Biochem., 2005, 74, 563–593 CrossRef CAS PubMed.
- L. I. Bruijn, M. K. Houseweart, S. Kato, K. L. Anderson, S. D. Anderson, E. Ohama, A. G. Reaume, R. W. Scott and D. W. Cleveland, Aggregation and motor neuron toxicity of an ALS-linked SOD1 mutant independent from wild-type SOD1, Science, 1998, 281(5384), 1851–1854 CrossRef CAS PubMed.
- J. Liu, C. Lillo, P. A. Jonsson, C. Vande Velde, C. M. Ward, T. M. Miller, J. R. Subramaniam, J. D. Rothstein, S. Marklund, P. M. Andersen, T. Brannstrom, O. Gredal, P. C. Wong, D. S. Williams and D. W. Cleveland, Toxicity of familial ALS-linked SOD1 mutants from selective recruitment to spinal mitochondria, Neuron, 2004, 43(1), 5–17 CrossRef CAS PubMed.
- J. Wang, G. Xu and D. R. Borchelt, Mapping superoxide dismutase 1 domains of non-native interaction: roles of intra- and intermolecular disulfide bonding in aggregation, J. Neurochem., 2006, 96(5), 1277–1288 CrossRef CAS PubMed.
- R. Wroe, A. Wai-Ling Butler, P. M. Andersen, J. F. Powell and A. Al-Chalabi, ALSOD: the Amyotrophic Lateral Sclerosis Online Database, Amyotrophic Lateral Scler., 2008, 9(4), 249–250 CrossRef CAS PubMed.
- P. Pasinelli, M. E. Belford, N. Lennon, B. J. Bacskai, B. T. Hyman, D. Trotti and R. H. Brown Jr, Amyotrophic lateral sclerosis-associated SOD1 mutant proteins bind and aggregate with Bcl-2 in spinal cord mitochondria, Neuron, 2004, 43(1), 19–30 CrossRef CAS PubMed.
- L. I. Bruijn, T. M. Miller and D. W. Cleveland, Unraveling the mechanisms involved in motor neuron degeneration in ALS, Annu. Rev. Neurosci., 2004, 27, 723–749 CrossRef CAS PubMed.
- Y. Furukawa and T. V. O'Halloran, Amyotrophic lateral sclerosis mutations have the greatest destabilizing effect on the apo- and reduced form of SOD1, leading to unfolding and oxidative aggregation, J. Biol. Chem., 2005, 280(17), 17266–17274 CrossRef CAS PubMed.
- S. V. Seetharaman, M. Prudencio, C. Karch, S. P. Holloway, D. R. Borchelt and P. J. Hart, Immature copper-zinc superoxide dismutase and familial amyotrophic lateral sclerosis, Exp. Biol. Med., 2009, 234(10), 1140–1154 CrossRef CAS PubMed.
- A. Nordlund, L. Leinartaite, K. Saraboji, C. Aisenbrey, G. Grobner, P. Zetterstrom, J. Danielsson, D. T. Logan and M. Oliveberg, Functional features cause misfolding of the ALS-provoking enzyme SOD1, Proc. Natl. Acad. Sci. U. S. A., 2009, 106(24), 9667–9672 CrossRef CAS PubMed.
- A. Hornberg, D. T. Logan, S. L. Marklund and M. Oliveberg, The coupling between disulphide status, metallation and dimer interface strength in Cu/Zn superoxide dismutase, J. Mol. Biol., 2007, 365(2), 333–342 CrossRef PubMed.
- Y. Furukawa, K. Kaneko, K. Yamanaka and N. Nukina, Mutation-dependent polymorphism of Cu,Zn-superoxide dismutase aggregates in the familial form of amyotrophic lateral sclerosis, J. Biol. Chem., 2010, 285(29), 22221–22231 CrossRef CAS PubMed.
- A. Nordlund and M. Oliveberg, Folding of Cu/Zn superoxide dismutase suggests structural hotspots for gain of neurotoxic function in ALS: parallels to precursors in amyloid disease, Proc. Natl. Acad. Sci. U. S. A., 2006, 103(27), 10218–10223 CrossRef CAS PubMed.
- Y. Furukawa, I. Anzai, S. Akiyama, M. Imai, F. J. Cruz, T. Saio, K. Nagasawa, T. Nomura and K. Ishimori, Conformational Disorder of the Most Immature Cu, Zn-Superoxide Dismutase Leading to Amyotrophic Lateral Sclerosis, J. Biol. Chem., 2016, 291(8), 4144–4155 CrossRef CAS PubMed.
- L. Banci, I. Bertini, A. Durazo, S. Girotto, E. B. Gralla, M. Martinelli, J. S. Valentine, M. Vieru and J. P. Whitelegge, Metal-free superoxide dismutase forms soluble oligomers under physiological conditions: a possible general mechanism for familial ALS, Proc. Natl. Acad. Sci. U. S. A., 2007, 104(27), 11263–11267 CrossRef CAS PubMed.
- J. S. Elam, A. B. Taylor, R. Strange, S. Antonyuk, P. A. Doucette, J. A. Rodriguez, S. S. Hasnain, L. J. Hayward, J. S. Valentine, T. O. Yeates and P. J. Hart, Amyloid-like filaments and water-filled nanotubes formed by SOD1 mutant proteins linked to familial ALS, Nat. Struct. Biol., 2003, 10(6), 461–467 CrossRef CAS PubMed.
- Y. M. Hwang, P. B. Stathopulos, K. Dimmick, H. Yang, H. R. Badiei, M. S. Tong, J. A. Rumfeldt, P. Chen, V. Karanassios and E. M. Meiering, Nonamyloid aggregates arising from mature copper/zinc superoxide dismutases resemble those observed in amyotrophic lateral sclerosis, J. Biol. Chem., 2010, 285(53), 41701–41711 CrossRef CAS PubMed.
- C. Kayatekin, J. A. Zitzewitz and C. R. Matthews, Disulfide-reduced ALS variants of Cu, Zn superoxide dismutase exhibit increased populations of unfolded species, J. Mol. Biol., 2010, 398(2), 320–331 CrossRef CAS PubMed.
- K. A. Vassall, H. R. Stubbs, H. A. Primmer, M. S. Tong, S. M. Sullivan, R. Sobering, S. Srinivasan, L. A. Briere, S. D. Dunn, W. Colon and E. M. Meiering, Decreased stability and increased formation of soluble aggregates by immature superoxide dismutase do not account for disease severity in ALS, Proc. Natl. Acad. Sci. U. S. A., 2011, 108(6), 2210–2215 CrossRef CAS PubMed.
- L. Lang, M. Kurnik, J. Danielsson and M. Oliveberg, Fibrillation precursor of superoxide dismutase 1 revealed by gradual tuning of the protein-folding equilibrium, Proc. Natl. Acad. Sci. U. S. A., 2012, 109(44), 17868–17873 CrossRef CAS PubMed.
- H. Wang, L. Lang, D. T. Logan, J. Danielsson and M. Oliveberg, Tricking a Protein To Swap Strands, J. Am. Chem. Soc., 2016, 138(48), 15571–15579 CrossRef CAS PubMed.
- S. D. Khare and N. V. Dokholyan, Common dynamical signatures of familial amyotrophic lateral sclerosis-associated structurally diverse Cu, Zn superoxide dismutase mutants, Proc. Natl. Acad. Sci. U. S. A., 2006, 103(9), 3147–3152 CrossRef CAS PubMed.
- R. W. Strange, C. W. Yong, W. Smith and S. S. Hasnain, Molecular dynamics using atomic-resolution structure reveal structural fluctuations that may lead to polymerization of human Cu-Zn superoxide dismutase, Proc. Natl. Acad. Sci. U. S. A., 2007, 104(24), 10040–10044 CrossRef CAS PubMed.
- T. Schmidlin, B. K. Kennedy and V. Daggett, Structural changes to monomeric CuZn superoxide dismutase caused by the familial amyotrophic lateral sclerosis-associated mutation A4V, Biophys. J., 2009, 97(6), 1709–1718 CrossRef CAS PubMed.
- F. Ding and N. V. Dokholyan, Dynamical roles of metal ions and the disulfide bond in Cu, Zn superoxide dismutase folding and aggregation, Proc. Natl. Acad. Sci. U. S. A., 2008, 105(50), 19696–19701 CrossRef CAS PubMed.
- F. Ding, Y. Furukawa, N. Nukina and N. V. Dokholyan, Local unfolding of Cu, Zn superoxide dismutase monomer determines the morphology of fibrillar aggregates, J. Mol. Biol., 2012, 421(4–5), 548–560 CrossRef CAS PubMed.
- A. Bille, S. A. E. Jonsson, M. Akke and A. Irback, Local unfolding and aggregation mechanisms of SOD1: a Monte Carlo exploration, J. Phys. Chem. B, 2013, 117(31), 9194–9202 CrossRef CAS PubMed.
- A. Das and S. S. Plotkin, SOD1 exhibits allosteric frustration to facilitate metal binding affinity, Proc. Natl. Acad. Sci. U. S. A., 2013, 110(10), 3871–3876 CrossRef CAS PubMed.
- A. Wang and D. W. Bolen, A naturally occurring protective system in urea-rich cells: mechanism of osmolyte protection of proteins against urea denaturation, Biochemistry, 1997, 36(30), 9101–9108 CrossRef CAS PubMed.
- M. Auton, L. M. Holthauzen and D. W. Bolen, Anatomy of energetic changes accompanying urea-induced protein denaturation, Proc. Natl. Acad. Sci. U. S. A., 2007, 104(39), 15317–15322 CrossRef CAS PubMed.
- P. J. Rossky, Protein denaturation by urea: slash and bond, Proc. Natl. Acad. Sci. U. S. A., 2008, 105(44), 16825–16826 CrossRef CAS PubMed.
- L. Hua, R. Zhou, D. Thirumalai and B. J. Berne, Urea denaturation by stronger dispersion interactions with proteins than water implies a 2-stage unfolding, Proc. Natl. Acad. Sci. U. S. A., 2008, 105(44), 16928–16933 CrossRef CAS PubMed.
- D. R. Canchi, D. Paschek and A. E. Garcia, Equilibrium study of protein denaturation by urea, J. Am. Chem. Soc., 2010, 132(7), 2338–2344 CrossRef CAS PubMed.
- E. J. Guinn, L. M. Pegram, M. W. Capp, M. N. Pollock and M. T. Record Jr, Quantifying why urea is a protein denaturant, whereas glycine betaine is a protein stabilizer, Proc. Natl. Acad. Sci. U. S. A., 2011, 108(41), 16932–16937 CrossRef CAS PubMed.
- B. Moeser and D. Horinek, Unified description of urea denaturation: backbone and side chains contribute equally in the transfer model, J. Phys. Chem. B, 2014, 118(1), 107–114 CrossRef CAS PubMed.
- P. H. Yancey and G. N. Somero, Counteraction of urea destabilization of protein structure by methylamine osmoregulatory compounds of elasmobranch fishes, Biochem. J., 1979, 183(2), 317–323 CrossRef CAS PubMed.
- P. H. Yancey, M. E. Clark, S. C. Hand, R. D. Bowlus and G. N. Somero, Living with water stress: evolution of osmolyte systems, Science, 1982, 217(4566), 1214–1222 CrossRef CAS PubMed.
- J. Hunger, N. Ottosson, K. Mazur, M. Bonn and H. J. Bakker, Water-mediated interactions between trimethylamine-N-oxide and urea, Phys. Chem. Chem. Phys., 2015, 17(1), 298–306 RSC.
- G. D. Rose, P. J. Fleming, J. R. Banavar and A. Maritan, A backbone-based theory of protein folding, Proc. Natl. Acad. Sci. U. S. A., 2006, 103(45), 16623–16633 CrossRef CAS PubMed.
- D. W. Bolen and G. D. Rose, Structure and energetics of the hydrogen-bonded backbone in protein folding, Annu. Rev. Biochem., 2008, 77, 339–362 CrossRef CAS PubMed.
- D. R. Canchi, P. Jayasimha, D. C. Rau, G. I. Makhatadze and A. E. Garcia, Molecular mechanism for the preferential exclusion of TMAO from protein surfaces, J. Phys. Chem. B, 2012, 116(40), 12095–12104 CrossRef CAS PubMed.
- D. R. Canchi and A. E. Garcia, Cosolvent effects on protein stability, Annu. Rev. Phys. Chem., 2013, 64, 273–293 CrossRef CAS PubMed.
- D. Van Der Spoel, E. Lindahl, B. Hess, G. Groenhof, A. E. Mark and H. J. C. Berendsen, GROMACS: fast, flexible, and free, J. Comput. Chem., 2005, 26(16), 1701–1718 CrossRef CAS PubMed.
- C. Oostenbrink, A. Villa, A. E. Mark and W. F. van Gunsteren, A biomolecular force field based on the free enthalpy of hydration and solvation: the GROMOS force-field parameter sets 53A5 and 53A6, J. Comput. Chem., 2004, 25(13), 1656–1676 CrossRef CAS PubMed.
- H. J. C. Berendsen, J. R. Grigera and T. P. Straatsma, The missing term in effective pair potentials, J. Phys. Chem., 1987, 91(24), 6269–6271 CrossRef CAS.
- A. K. Malde, L. Zuo, M. Breeze, M. Stroet, D. Poger, P. C. Nair, C. Oostenbrink and A. E. Mark, An Automated Force Field Topology Builder (ATB) and Repository: Version 1.0, J. Chem. Theory Comput., 2011, 7(12), 4026–4037 CrossRef CAS PubMed.
- S. Dalal, A. Mhashal, N. Kadoo and S. M. Gaikwad, Functional stability and structural transitions of Kallikrein: spectroscopic and molecular dynamics studies, J. Biomol. Struct. Dyn., 2017, 35(2), 330–342 CrossRef CAS PubMed.
- E. S. dos Santos, D. H. S. Gritta and J. S. de Almeida, Analysis of interactions between potent inhibitors of ATP sulfurylase via molecular dynamics, Mol. Simul., 2015, 42(8), 605–610 CrossRef.
- M. Hajnic, J. I. Osorio and B. Zagrovic, Interaction preferences between nucleobase mimetics and amino acids in aqueous solutions, Phys. Chem. Chem. Phys., 2015, 17(33), 21414–21422 RSC.
- W. Plazinski, A. Plazinska and M. Drach, Acyclic forms of aldohexoses and ketohexoses in aqueous and DMSO solutions: conformational features studied using molecular dynamics simulations, Phys. Chem. Chem. Phys., 2016, 18(14), 9626–9635 RSC.
- Y. Wei, H. Wang, G. Liu, Z. Wang and S. Yuan, A molecular dynamics study on two promising green surfactant micelles of choline dodecyl sulfate and laurate, RSC Adv., 2016, 6(87), 84090–84097 RSC.
- G. Qu, C. Xue, M. Zhang, S. Liang, Y. Han and W. Ding, Molecular Dynamics Simulation of Sulfobetaine-Type Zwitterionic Surfactants at the Decane/Water Interface: Structure, Interfacial Properties, J. Dispersion Sci. Technol., 2016, 37(12), 1710–1717 CrossRef CAS.
- L. Larini and J. E. Shea, Double resolution model for studying TMAO/water effective interactions, J. Phys. Chem. B, 2013, 117(42), 13268–13277 CrossRef CAS PubMed.
- D. Markthaler, J. Zeman, J. Baz, J. Smiatek and N. Hansen, Validation of Trimethylamine-N-oxide (TMAO) Force Fields Based on Thermophysical Properties of Aqueous TMAO Solutions, J. Phys. Chem. B, 2017, 121(47), 10674–10688 CrossRef CAS PubMed.
- H. J. C. Berendsen, J. P. M. Postma, W. F. v. Gunsteren, A. DiNola and J. R. Haak, Molecular dynamics with coupling to an external bath, J. Chem. Phys., 1984, 81(8), 3684–3690 CrossRef CAS.
- I. Jahan and S. M. Nayeem, Effect of Urea, Arginine, and Ethanol Concentration on Aggregation of 179CVNITV184 Fragment of Sheep Prion Protein, ACS Omega, 2018, 3(9), 11727–11741 CrossRef CAS PubMed.
- L. Li, C. Li, S. Sarkar, J. Zhang, S. Witham, Z. Zhang, L. Wang, N. Smith, M. Petukh and E. Alexov, DelPhi: a comprehensive suite for DelPhi software and associated resources, BMC Biophys., 2012, 5, 9 CrossRef PubMed.
- W. Humphrey, A. Dalke and K. Schulten, VMD: visual molecular dynamics, J. Mol. Graphics, 1996, 14(1), 33–38 CrossRef CAS PubMed.
- A. Amadei, A. B. M. Linssen and H. J. C. Berendsen, Essential dynamics of proteins, Proteins: Struct., Funct., Bioinf., 1993, 17(4), 412–425 CrossRef CAS PubMed.
- I. Jahan and S. M. Nayeem, Effect of Osmolytes on Conformational Behavior of Intrinsically Disordered Protein alpha-Synuclein, Biophys. J., 2019, 117(10), 1922–1934 CrossRef CAS PubMed.
- L. Banci, I. Bertini, M. Boca, V. Calderone, F. Cantini, S. Girotto and M. Vieru, Structural and dynamic aspects related to oligomerization of apo SOD1 and its mutants, Proc. Natl. Acad. Sci. U. S. A., 2009, 106(17), 6980–6985 CrossRef CAS PubMed.
- K. Teilum, M. H. Smith, E. Schulz, L. C. Christensen, G. Solomentsev, M. Oliveberg and M. Akke, Transient structural distortion of metal-free Cu/Zn superoxide dismutase triggers aberrant oligomerization, Proc. Natl. Acad. Sci. U. S. A., 2009, 106(43), 18273–18278 CrossRef CAS PubMed.
- Y. Sheng, M. Chattopadhyay, J. Whitelegge and J. S. Valentine, SOD1 aggregation and ALS: role of metallation states and disulfide status, Curr. Top. Med. Chem., 2012, 12(22), 2560–2572 CrossRef CAS PubMed.
- P. Ganguly, P. Boserman, N. F. A. van der Vegt and J.-E. Shea, Trimethylamine N-oxide Counteracts Urea Denaturation by Inhibiting Protein-Urea Preferential Interaction, J. Am. Chem. Soc., 2018, 140(1), 483–492 CrossRef CAS PubMed.
- J. A. Rumfeldt, P. B. Stathopulos, A. Chakrabarrty, J. R. Lepock and E. M. Meiering, Mechanism and thermodynamics of guanidinium chloride-induced denaturation of ALS-associated mutant Cu,Zn superoxide dismutases, J. Mol. Biol., 2006, 355(1), 106–123 CrossRef CAS PubMed.
- J. A. Tainer, E. D. Getzoff, K. M. Beem, J. S. Richardson and D. C. Richardson, Determination and analysis of the 2 A-structure of copper, zinc superoxide dismutase, J. Mol. Biol., 1982, 160(2), 181–217 CrossRef CAS PubMed.
- J. S. Richardson and D. C. Richardson, Natural beta-sheet proteins use negative design to avoid edge-to-edge aggregation, Proc. Natl. Acad. Sci. U. S. A., 2002, 99(5), 2754–2759 CrossRef CAS PubMed.
- Y. Furukawa, K. Kaneko, K. Yamanaka, T. V. O'Halloran and N. Nukina, Complete loss of post-translational modifications triggers fibrillar aggregation of SOD1 in the familial form of amyotrophic lateral sclerosis, J. Biol. Chem., 2008, 283(35), 24167–24176 CrossRef CAS PubMed.
- D. L. Nelson and M. M. Cox, Lehninger, principles of biochemistry, Worth Publishing, New York, 2000 Search PubMed.
- J. Schlitter, Estimation of absolute and relative entropies of macromolecules using the covariance matrix, Chem. Phys. Lett., 1993, 215, 617–621 CrossRef CAS.
- A. Ioan and K. Martin, On the calculation of entropy from covariance matrices of the atomic fluctuations, J. Chem. Phys., 2001, 115(14), 6289–6292 CrossRef.
- Y. Sheng, M. Chattopadhyay, J. Whitelegge and J. S. Valentine, SOD1 aggregation and ALS: role of metallation states and disulfide status, Curr. Top. Med. Chem., 2012, 12(22), 2560–2572 CrossRef CAS PubMed.
- L. Wang, R. Zeng, X. Pang, Q. Gu and W. Tan, The mechanisms of flavonoids inhibiting conformational transition of amyloid-b42 monomer: a comparative molecular dynamics simulation study, RSC Adv., 2015, 5(81), 66391–66402 RSC.
- N. Smolin, V. P. Voloshin, A. V. Anikeenko, A. Geiger, R. Winter and N. N. Medvedev, TMAO and urea in the hydration shell of the protein SNase, Phys. Chem. Chem. Phys., 2017, 19(9), 6345–6357 RSC.
- Q. Zou, B. J. Bennion, V. Daggett and K. P. Murphy, The Molecular Mechanism of Stabilization of Proteins by TMAO and Its Ability to Counteract the Effects of Urea, J. Am. Chem. Soc., 2002, 124(7), 1192–1202 CrossRef CAS PubMed.
- P. G. Kusalik, A. Laaksonen and I. M. Svishchev, Spatial structure in molecular liquids, Molecular Dynamics: From Classical to Quantum Methods, ed. P. B. Balbuena and J. M. Seminario, Elsevier, 1999, pp. 61–97 Search PubMed.
- A. Vishnyakov, A. P. Lyubartsev and A. Laaksonen, Molecular Dynamics Simulations of Dimethyl Sulfoxide and Dimethyl Sulfoxide-Water Mixture, J. Phys. Chem. A, 2001, 105(10), 1702–1710 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Force field parameter for urea and TMAO, Table S1: number of osmolytes and water molecules used during the simulations. Fig. S1–S10 show the potential energy, density of the six systems, RMSF and hydrophobic SASA of residues interacted with metal ions, configurational entropy of backbone and sidechain atom of loop IV & VII of apo and holo SOD1 in water and in osmolytes, RDF of OW of water molecules, RDF of NT of TMAO molecules around loops IV & VII of both forms of SOD1, RDF of OW (water), OU (urea) and NT (TMAO) around full apo and holo SOD1 in water and in osmolytes. SDF of OW of water molecules in binary and ternary solutions around loops IV & VII of both forms of SOD1, SDF of NT of TMAO molecules in ternary solution around loops IV & VII of both forms of SOD1. See DOI: 10.1039/d0ra02151b |
| This journal is © The Royal Society of Chemistry 2020 |