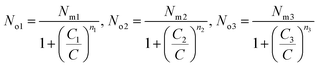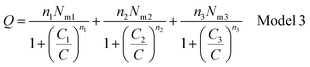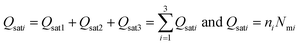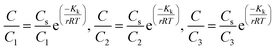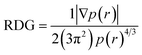Open Access Article
Open Access ArticleA microscopic and macroscopic investigation of the adsorption of N719 dye on ZnO nanopowders (ZNP) and ZnO nanorods (ZNR) for dye sensitized solar cells using statistical physics treatment and DFT simulation
Marwa Ben Manaa *a,
Noureddine Issaouia,
Youssef O. Al-Ghamdib,
Hafedh Belmabrouk
*a,
Noureddine Issaouia,
Youssef O. Al-Ghamdib,
Hafedh Belmabrouk cd and
Abdelmottaleb Ben Laminea
cd and
Abdelmottaleb Ben Laminea
aLaboratory of Quantum and Statistical Physics, LR18ES18, University of Monastir, Faculty of Sciences, Monastir 5079, Tunisia. E-mail: ben.manaa.marwa@gmail.com
bDepartment of Chemistry, College of Science at Zulfi, MajmaahUniversity, Al Majmaah 11952, Saudi Arabia
cDepartment of Physics, College of Science at Zulfi, MajmaahUniversity, Saudi Arabia
dLaboratory of Electronics and Microelectronics, Faculty of Science of Monastir, University of Monastir, Tunisia
First published on 23rd July 2020
Abstract
In this paper, three adsorption isotherms of N719 dye on two different adsorbents, ZnO nanopowder and ZnO nanorods, at three different thicknesses have been fitted using a monolayer model with three types of receptor sites treated by statistical physics. The model involved parameters are: three coefficients (n1, n2 and n3) indicating the numbers of adsorbed dye molecules per site, three parameters (Nm1, Nm2 and Nm3) indicating the receptor site densities and three adsorption energies ((−ε1), (−ε2) and (−ε3)). The evolution of these parameters in relation with thickness of ZnO was discussed. The pore size distribution (PSD) of ZnO nanopowder and ZnO nanorods as a function of the thickness has been studied using the chosen adequate model. The molecular electrostatic potential (MEP) has been investigated to optimize the different adsorbed geometries of the complex N719 dye@ZnO. The intermolecular interactions between the N719 dye and the ZnO surface have been studied by using the quantum theory of atoms in molecules (AIM) and reduced density gradient RDG. The results of the MEP, topological AIM and RDG are in agreement with the results of statistical physics
1. Introduction
Dye-sensitized solar cells (DSSCs) are attracting widespread research areas and commercial interest due to the low-cost harvest of solar energy using sustainable and environmentally friendly materials.1 DSSCs consist of a TiO2 electrode adsorbed dye, an electrolyte solution, and a platinum counter electrode. In this class of cells, the TiO2 electrode plays a main role in relation to the loading dye and in separating and transporting electrons.2,3 In the assembly of DSSCs, the dye plays a key role in absorbing sunlight and converting solar energy to electrical energy with the aid of a semiconducting photoanode.4,5 Therefore, the cell performance is mainly dependent on the type of dye used as a sensitizer.6 Numerous metal complexes and organic dyes4,5 have been synthesized and used as sensitizers. Ruthenium-based complexes are considered as good sensitizers for DSSCs because of their intense charge transfer absorption over the entire visible range and highly efficient metal to ligand charge transfer.7 TiO2 has been one of the most widely studied semiconducting materials and it has been used for DSSCs due to not only its photochemical and photoelectrochemical properties but also to its low-cost, its availability, and its non-toxic nature.8,9 Besides TiO2 and ZnO have been also investigated as an electron conducting material (electrode) in DSCs. It has a band gap energy and a conduction band that are similar to TiO2.9 It should be also noted that films of ZnO have been shown to have 2 orders of magnitude higher electron mobility than TiO2, (110 cm2 V−1 s−1 comparing to 0.01–1 cm2 V−1 s−1) an important factor in DSSC performance.10,11 Based on these characteristics, ZnO should be a promising photoelectrode material in DSC applications. Among the different techniques used to grow ZnO thin films, such as magnetron and RF magnetron sputtering, pulsed laser deposition and metal–organic chemical vapor deposition, electrophoretic deposition (EPD) are gaining increasing interest, due to its versatility and high potential for scaling up to large volumes.12,13Moreover, the electrophoretic deposition (EPD) method is a well known technique for obtaining highly uniform films with thickness from the nanometer to micrometer scale by changing the applied voltage and deposition time14,15 which has been used for coating a variety of materials.16 Hence, this technique is suitable for fabricating thin-films for DSSCs because it allows to control the film thickness of photoelectrode which is critical to cell efficiency.
In addition, previous studies have shown that, in the dye sensitized solar cells, only chemisorbed dye molecules can inject electrons into the electrode material indicating just only the first layer of dye molecules is effective.17,18 However, multi-layers of dye can absorb incident light but cannot inject the electrons to the photoelectrode. Therefore, it would be better to optimize the adsorbed dye for further improving performance. A more accurate way for determining whether dye monolayers or multilayers are formed is by employing direct methods. There are few experimental techniques that offer direct information about the ZnO interface structure and the N719 ruthenium-based dye such as using the photoelectron spectroscopy (PES) technique,19 this method has been performed also on dye-sensitized ZnO electrodes to study the N719 and Z-907 dyes coverage and the anchoring to the ZnO surface. This technique has indicated that the adsorbed N719 dye on ZnO film is a multilayer process in a specific experimental conditions.19 In addition, Neutral Impact Collision Ion Scattering Spectroscopy (NICISS) is also an experimental direct technique which has been used with the standard indirect solution depletion method to investigate the adsorbed layer of N719 dye on titanium oxide.20 Previously, the combination of both direct experimental techniques AFM and Neutral Impact Collision Ion Scattering Spectroscopy (NICISS) allowed conclusions to be drawn about the thickness and homogeneity of the adsorbed dye layer.21 Various theoretical method based on quantum chemistry calculation has provided the valuable reference for predicting the relationship between the structure and photoelectrical properties of molecules for dye sensitized solar cells.22,23 Ben Lamine et al.24 have developed a statistical physics treatment based on quantum physics theory which is useful to interpret various adsorption systems.25,26 Marwa et al.27–31 have improved this theory and developed new statistical physics models for modeling adsorption isotherms of dyes for DSSCs applications. Recently, to investigate the optical properties of DSSCs, theoretical methods as computational simulations rooted in density functional theory (DFT) and time-dependent DFT (TDDFT) have become a crucial tool to understand the detailed atomistic and the interatomic interactions that are more necessary to the complex dye/semiconductor interaction.32,33 Therefore, it is necessary to combine the statistical physics and DFT approaches to be used as an efficient predictive tool in studies of DSSCs optimization. In this context, studies on dye-sensitized ZnO models are however scarce (see, for example, ref. 34 and 35) and to the best of our knowledge, the interaction of the prototypical N719 Ru(II) dye with ZnO has never been reported using these both approaches. In order to fill this void, we present here a statistical physics formalism to describe in the macroscopic level the adsorption process of the N719 dye into the ZnO surface. The analytical expressions have been developed by the statistical physics theory to model the adsorption isotherms of N719 dye into ZnO nanopowders (ZNP) and ZnO nanorods (ZNR) at different thickness of EPD films. These films ZNP and ZNR were fabricated by an electrophoretic deposition technique (EPD) at three deposition time t1 = 1 min, t2 = 3 min and t3 = 5 min. The variation of adsorbent thickness represents an important parameter which has a strong influence on the evolution of the adsorption process. The statistical physics modeling gives physico–chemical parameters that are involved in these analytical expressions. With these parameters (adsorption energy, stoichiomtric coefficients, number of layers and receptor sites density), the adsorption process description is becoming very significant. While the DFT simulation has been used to study the interatomic interaction between the prototypical N719 dye and the ZnO nanostructure. We pay particular attention to the adsorption modes, geometries and energies. At the first time, the optimization of adsorbed geometries of the complex N719 dye@ZnO have been carried out by a molecular electrostatic potential (MEP) to predict reactive sites for electrophilic and nucleophilic attack and the interaction energies have been investigated by using the topological AIM and reduced density gradient RDG.
2. Material and methods
2.1 Adsorbate
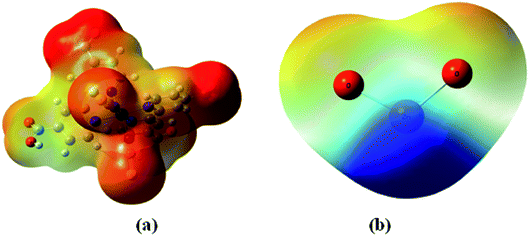
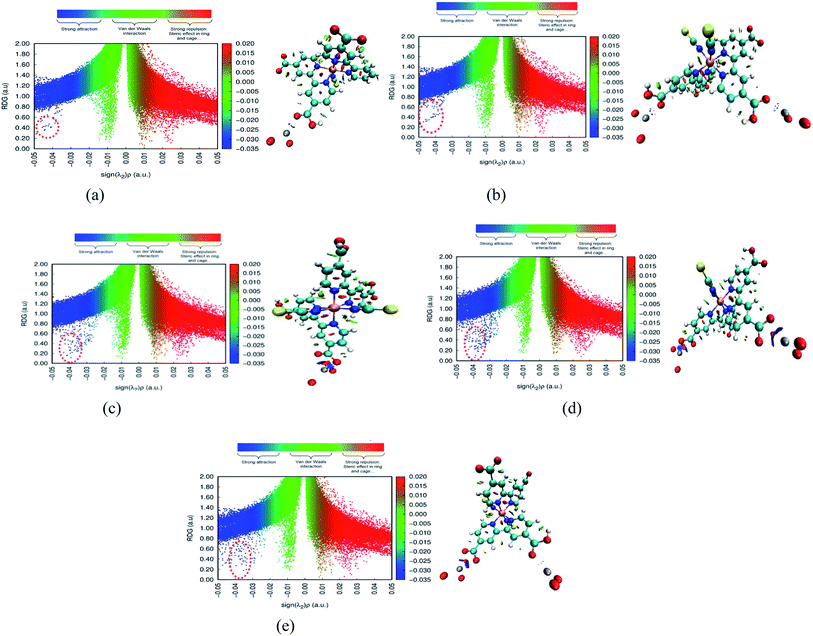
The adsorbate is a N719 dye (Ruthenizer 535-bisTBA) was purchased from Solaronix.36The chemical structures of the N719 dye are illustrated in Fig. 1
 | ||
| Fig. 1 Chemical structure of N719 dye (a) and (b) the optimized structure of N719 dye determined by the DFT simulation. | ||
2.2 Adsorbent
ZnO nanopowders (Sigma-Aldrich, hereafter denoted ZNP) were purchased and used without further purification. ZnO nanorods (hereafter denoted ZNR) were fabricated from 0.3 M ZnO sols treated by solvothermal synthesis (150 °C for 5 days).35,362.3 Adsorption isotherms
The fabricated ZnO films whose area was 0.5 cm2 (photoelectrodes; PE) were soaked in 0.05, 0.15, 0.2, 0.3, and 1.0 mM of an ethanolic N719 (Solaronix) dye solution for 30 min, followed by rinsing with dry EtOH (C2H5OH, clear leader) and letting them dry. The UV-Vis spectroscopy (UV-2401, Shimadzu) has been used to determine the amount of dye loaded onto the films.36 Then, the films loaded with dye where then soaked in 0.1 M NaOH mix solution of water/ethanol (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, v/v) to desorb the dye, and the absorption of spectrum of samples has been measured.
1, v/v) to desorb the dye, and the absorption of spectrum of samples has been measured.
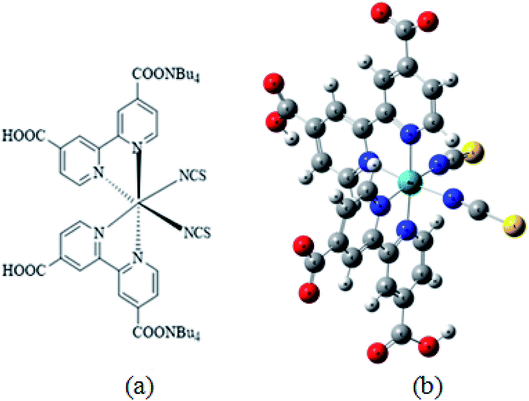
The adsorption isotherms of N719 dye on ZnO nanopowders (ZNP) and ZnO nanorods (ZNR) at different thickness of EPD films are illustrated in Fig. 2.36
 | ||
| Fig. 2 Adsorption isotherms of N719 dye on ZNP and ZNR materials at different thickness of EPD films.36 | ||
3. Theory of statistical physics treatment
Adsorption process involves an exchange of particles from the dissolved free state to the adsorbed state. Its investigation by statistical physics formalism cannot be performed without employing the grand canonical ensemble to take account of the particle number variation through the introduction of the chemical potential variable in the adsorption process.24,37 Theoretical modeling of adsorption isotherms in gas or liquid phase based on statistical physics development is a powerful technique used for surface characterization. One of the advantages of applying this theory is to give a physicochemical meaning to the parameters involved in the model and then to provide new interpretations of the adsorption process at molecular level. In order to treat the adsorption process by using the statistical physics methods, certain hypotheses were considered as a basis of the corresponding treatment and applied to facilitate the calculations as well as interpretations. At a first approximation, the interaction between the dye molecules was neglected, the internal degrees of freedom of the studied molecules are also neglected and we except the translation freedom degrees. Indeed, the electronic degrees of freedom cannot be thermally excited. The rotational freedom degrees could be considered as are frozen in the solution. Finally, the vibrationel freedom degrees can be neglected at first approximation at room temperature.According to these assumptions, in the liquid phase, the adsorption reaction of a dye molecule (D) onto a receptor site (S) should include a stoichiometric coefficient n as expressed in the following equation:
| nD + R ⇆ DnR | (1) |
In this treatment, the starting point, is the use of the grand canonical partition function which describes the system microscopic states in the adsorption process.
The grand canonical partition function of one receptor site can be expressed as:
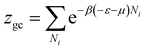 | (2) |
The total grand canonical partition function related to Nm receptor sites per unit mass is written as follows:
| Zt = (zgc)Nm | (3) |
The average site occupation number No can be derived from the total grand canonical partition function:24,37
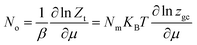 | (4) |
| Q = nNo | (5) |
The analytical expression Q is calculated by considering a given starting a given staring partition function. Now we have to choose plausible model analytical expressions from the literature which susceptible to best fit the experimental adsorptions isotherms curves. Taking account of the isotherms forms, the experimental curves have been fitted with the conventional model Langmuir and with the six proposed statistical physics models: a monolayer model with one energy (Model 1), a monolayer model with two energies (Model 2), monolayer model with three energies (Model 3), a monolayer model with four energies (Model 4), a double layer with one energy (Model 5) and a double layer with two energies (Model 6). We established analytical expressions corresponding to the adsorption isotherms N719 on ZNP and ZNR materials on the basis of statistical physics treatment. In the next section, we developed with details the adequate grand canonical partition function, and afterward the analytical expression of the best fitting model.
All the expressions of the others treated models are given in the Appendix.
3.1 Development of the best fitting model: the monolayer model with three types of sites
This model is an extended Hill model but with three different types of receptor sites taking into account of the heterogeneity of ZNP and ZNR surfaces. To develop this model by using the grand canonical ensemble in statistical physics, we supposed that the adsorption process occurs onto three types of sites characterized by three different adsorption energies (−ε1, −ε2 and −ε3). The value of the adsorption energy is characteristic of the receptor site with a density of receptor sites noticed Nm1, Nm2 and Nm3. One receptor site is supposed to be empty or occupied by one or more dye molecules.The first step to establish this model is to express the grand canonical partition function of one receptor site describing the microscopic states of the adsorbing system. Therefore, the grand canonical partition functions of one site of the three types are expressed by the following relations:
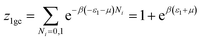 | (6) |
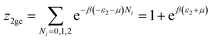 | (7) |
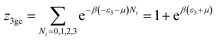 | (8) |
Therefore, the total partition function of the monolayer model of three receptor sites is:
| Zt = (z1gc)Nm1(z2gc)Nm2(z3gc)Nm3 | (9) |
Using the previous definition of occupation number, the each average number of occupied sites is:
| Q = n1No1 + n2No2 + n3No3 | (10) |
Finally, Q is the number of adsorbed molecules of dye versus the concentration C is:
4. Results and discussion
4.1. Best fitting model choice
Experimental data were analyzed by non-linear curve fitting analysis, using Microcal Origin Lab software (Origin Lab, Northampton, MA), to fit our adsorption isotherm with the different statistical physics models presented in the previous sections. The fitting goodness of each model was discussed in terms of different error functions. The best fitting adsorption isotherm was determined by the well-known correlation coefficient R2 and the analysis of the residual root mean square error (RMSE) called as the estimated standard error of the regression. They are the most popular used method to determine the optimum isotherm.The correlation coefficient R2 was calculated using the following equation:
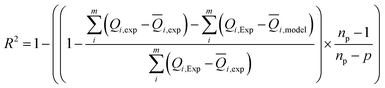 | (11) |
For a number p of adjustable parameters, the estimated standard error is given by the following relation.38
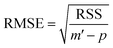 | (12) |
In Table 1 we present the adjustment correlation coefficient of the seven treated model at three different thicknesses.
| R2 | ||||||||
|---|---|---|---|---|---|---|---|---|
| Studied system | Th (μm) | Langmuir | Monolayer with one energy | Monolayer model with two energies | Monolayer model with three energies | Monolayer model with four energies | Double layer with one energy | Double layer with two energies |
| ZNP | 1.5 | 0.95 | 0.987 | 0.998 | 0.999 | 0.978 | 0.877 | 0.756 |
| 3 | 0.97 | 0.898 | 0.978 | 0.998 | 0.897 | 0.885 | 0.873 | |
| 5 | 0.96 | 0.856 | 0.988 | 0.989 | 0.987 | 0.897 | 0.876 | |
| ZNR | 2 | 0.89 | 0.78 | 0.69 | 0.999 | 0.87 | 0.676 | 0.765 |
| 6 | 0.76 | 0.88 | 0.87 | 0.989 | 0.889 | 0.778 | 0.887 | |
| 7.7 | 0.77 | 0.87 | 0.89 | 0.999 | 0.899 | 0.855 | 0.654 | |
| RMSE | ||||||||
|---|---|---|---|---|---|---|---|---|
| Studied system | Th (μm) | Langmuir | Model 1 | Model 2 | Model 3 | Model 4 | Model 5 | Model 6 |
| ZNP | 1.5 | 0.41 | 0.01 | 0.03 | 0.003 | 0.022 | 0.341 | 0.231 |
| 3 | 0.31 | 0.42 | 0.071 | 0.006 | 0.03 | 0.111 | 0.453 | |
| 5 | 0.62 | 0.8 | 0.05 | 0.009 | 0.053 | 0.134 | 0.521 | |
| ZNR | 2 | 0.03 | 0.32 | 0.232 | 0.001 | 0.04 | 0.120 | 0.211 |
| 6 | 0.52 | 0.66 | 0.211 | 0.003 | 0.023 | 0.452 | 0.143 | |
| 7.7 | 0.83 | 0.543 | 0.273 | 0.002 | 0.034 | 0.321 | 0.121 | |
The Table 1 shows that the coefficient correlation R2 of the model 3 are close to the unity and its values of RMSE are close to zero in comparison of the other tested models. Indeed, the monolayer model with three energies is considered as the adequate model to describe the adsorption process of N719 dye on the two materials ZNP and ZNR. In addition, to R2 and RMSE coefficients criteria, our choice has also taken into account the physics justification in model selection. If the monolayer model of three energies is chosen as the best fitting model, it would provide the best description of the adsorption data of N719 dye on ZNP and ZNR materials. All its adjusting parameters are reported in Table 2.
| Adsorbent | Th (μm) | n1 | n2 | n3 | Nm1 (mmol cm−2) | Nm2 (mmol cm−2) | Nm3 (mmol cm−2) | Qsat1 (mmol cm2) | Qsat2 (mmol cm−2) | Qsat3 (mmol cm−2) |
|---|---|---|---|---|---|---|---|---|---|---|
| ZNP | 1.5 | 0.4 | 1.4 | 2.7 | 0.4 | 1.5 | 2 | 0.16 | 2.1 | 5.4 |
| 3 | 0.9 | 1.9 | 3.2 | 0.8 | 2 | 2.4 | 0.72 | 3.8 | 7.68 | |
| 6 | 1.2 | 2.4 | 3.7 | 1.2 | 2.4 | 3 | 1.44 | 5.76 | 11.1 | |
| ZNR | 2 | 0.6 | 3.2 | 6.4 | 0.8 | 2.5 | 4 | 0.48 | 8 | 25.6 |
| 5 | 1.4 | 4.3 | 7.3 | 1.5 | 3 | 4.2 | 2.1 | 12.9 | 30.66 | |
| 7.7 | 2.5 | 5 | 8.4 | 2.2 | 3.2 | 4.6 | 5.5 | 16 | 38.64 |
The adsorption equilibrium data for N719 dye on ZNP and ZNR fitted by the adequate model are reported in Fig. 3.
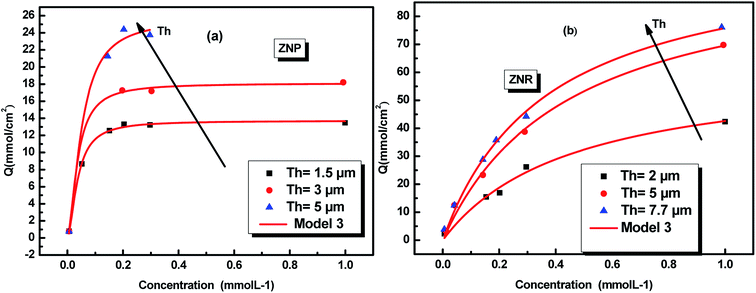 | ||
| Fig. 3 Fitted adsorption isotherms of N719 dye on ZnO nanopowder (ZNP) (a) and on ZnO nanorods (ZNR) (b) at different thickness of (EPD) film: the squares, circles and triangles are the experimental data36 and the continuous red lines are the simulated data. | ||
The physicochemical model parameters have a main role to describe with detail the adsorption process at a molecular level. They give more details of the adsorption process allowing a careful description of the dynamic and the steps of the absorption process.
The different fitted parameters are classified in two categories: stereographic and energetic parameters. The stereographic parameters are the numbers of adsorbed dye molecules per site n1, n2 and n3. These numbers represent the stoichiometric parameters. They give also the geometric properties of the studied aggregates, such as their orientation and their sizes. The densities Nmi are also geometric indication of the sites repartition. The second category of parameters is energetic. They represent the halves-saturation concentrations C1, C2 and C3 which allow to calculate the adsorption energies in order to identify the kind of the anchorage of N719 dye on the ZNP and ZNR materials.
4.2. Stereographic interpretations
The reaction eqn (1) can be replaced using model 3 by three reactions eqn (13), (14) and (15).
The reaction in the first site is written as:
| n1D + R ⇆ Dn1R | (13) |
The reaction in the second site is written as:
| n2D + R ⇆ Dn2R | (14) |
The reaction in the third site is written as:
| n3D + R ⇆ Dn3R | (15) |
This parameter can also give information on the positions of the adsorbed molecule at the adsorbent surface sites. In fact, a molecule has several manners to be anchored on the receptor site according to its geometry and its angle of incidence with the adsorbent surface.
In general, the n parameter plays two main roles: one hand, it describes geometrically the adsorption position of dye on the adsorbent surface as function of their values determined by numerical simulation. Other hand, describes the aggregation phenomena and their degree of the adsorbate molecules in solution.37 According to the adsorption position of the dye, it can be distinguished two possible configurations relative to the surface: in the first case, if this value is superior to 1, it represents the number of docked molecules which interact with one receptor site describing a multi-molecular process. This describes the case that the dye molecules are anchored by a gathered n dye molecules on the adsorbent surface as an aggregate or a linear polymer. In the second case, if this value is inferior to 1, it would represent “the fraction of the dye per site”, leading to a horizontal docking37,38 on the adsorbent surface and showing that the adsorption is multi-docking process.37,38 Then n′ = 1/n represents the anchorage number of one dye molecule on an average number of receptor sites.37,38 Referring to the values of this parameter (Table 2), we noticed that there are values superior to the unity and others are inferior at a time.
In order to simplify the description, let's consider an example in the case of adsorption of N719 dye on ZNP film a value of n which is superior to the unit: n2 = 1.4 at applied thickness of (EPD) = 1.5 μm. We can write 1.4 = 1 × x + (1 − x) × 2. A rate of 60% receptor sites are docked by one molecule and 40% of receptor sites are occupied by two molecules of N719 dye with a non parallel position. However, in the case of adsorption of N719 dye on ZNR film, we noticed different behaviors with n1 ˃ 1 and n1 < 1. For n1 < 1 let's take this case when n1 = 0.6. The dye N719 is anchored on the surface of ZNR with at least two different manners. This value can be considered as an average between 1/2 and 1. Therefore, we can describe it by this relation 0.6 = x × 1 + (1 − x) × 1/2 enables to calculate the percentage values of single docked molecule (x = 40%) and double docked one (1 − x = 60%). Moreover, from the Table 2, we noticed that the different thickness of EPD films has a noticed influence on the stereography of the adsorption process or on the variation of the number of adsorbed dye molecules on the ZNP and ZNR films. Indeed, we reported in Fig. 4 the evolution of the numbers of dye molecules per site calculated with model 3 as function of the thickness of EPD films.
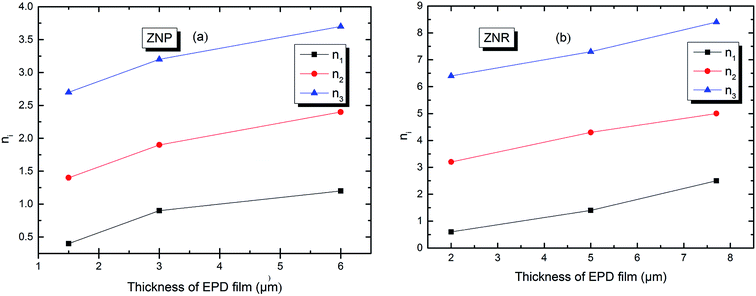 | ||
| Fig. 4 Numbers of adsorbed dye molecules per sites n versus the thickness of EPD films: (a) ZNP and (b) ZNR. | ||
The Fig. 4 shows first of all, that the numbers of adsorbed dye molecules ni increase with the increase of the thickness of (EPD) for a given fixed type of sites. This can be explained that the increase in thickness leads to an increase of the attraction to the dye molecule. This can be expressed by an increase of an attraction mean field, synonym of an increase of the adsorption energy (Fig. 7 and Table 3) and consequently an increase of chemical potential through the increase of ni. The Fig. 4 shows also, that for a given thickness, the ni is increased conventionally from the first type of sites till the last type or the third type of sites. But in reality, the more energetic site will be the first to be kinetically occupied. So the third type of sites will be the first occupied, followed by the second and so on. We see from the Fig. 4 that the third and the second types are multimolecular adsorption process or dye aggregation adsorption process. The first type or the last occupied or the less energetic, becomes a multianchorage adsorption process n1 ≤ 1. Finally, comparing Fig. 4(a) and (b) we notice that the features of the adsorption process in ZNP and ZNR are similar. However, due to the energetic aspect and so to the aggregation parameter ni which are better in ZNR then ZNP leading to the an amelioration of the adsorption capacity defined by the following relation
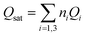 | (16) |
| Studied system | Thickness of EPD film (μm) | C1 mol L−1 | C2 mol L−1 | C3 mol L−1 | −ε1 kJ mol−1 | −ε2 kJ mol−1 | −ε3 kJ mol−1 |
|---|---|---|---|---|---|---|---|
| ZnO (ZNP) | 1.5 | 5 × 10−11 | 8 × 10−11 | 0.2 × 10−11 | 58.76 | 57.60 | 66.740 |
| 3 | 6 × 10−13 | 2 × 10−13 | 0.5 × 10−13 | 69.72 | 72.44 | 79.86 | |
| 6 | 5 × 10−14 | 2 × 10−14 | 1 × 10−14 | 75.87 | 78.15 | 85.56 | |
| ZnO (ZNR) | 2 | 0.5 × 10−7 | 4 × 10−8 | 2 × 10−8 | 41.64 | 42.19 | 43.91 |
| 5 | 0.8 × 10−9 | 0.2 × 10−9 | 0.5 × 10−10 | 52 | 55.33 | 58.76 | |
| 7.7 | 2 × 10−11 | 0.9 × 10−11 | 0.4 × 10−11 | 61.03 | 63.01 | 65.02 |
The variation of the receptor sites densities Nmi versus the thickness of EPD films is reported in Fig. 5.
 | ||
| Fig. 5 The evolution of the densities of receptor site versus the thickness of EPD films. (a) ZNP and (b) ZNR. | ||
The Fig. 5 shows that the densities Nmi increase with an increase of (EPD) films thickness. This is probably related to the increase in the adsorption energy caused by an increase of the thickness. This thickness gives a medium confinement leading to a reinforcement of the aggregation process in one hand, but also to a reinforcement of the accessibility of additional adsorption receptor sites for the N719 dye molecules in another hand. Therefore the N719 dye molecules can be easily fixed onto the adsorbent surface.
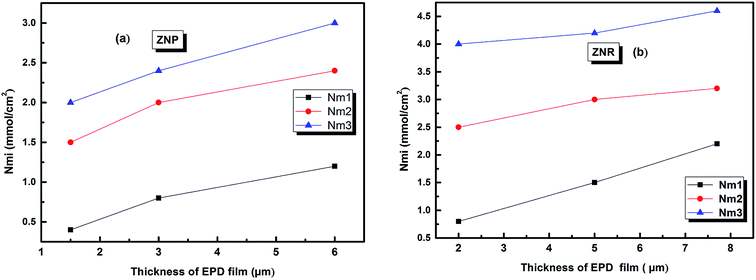
The evolution of this parameter as a function of the thickness of EPD films is reported in Fig. 6
 | ||
| Fig. 6 The evolution of the amount of adsorbed molecules versus the thickness of (EPD) films. (a) ZNP and (b) ZNR. | ||
From (Fig. 6a and b), we noticed that the values of Qsati increased with the increase of thickness of (EPD) films both on ZNR and ZNP materials. These behaviours are consequently attributed to the two increases of the densities of receptor sites Nmi and to the molecules numbers ni per site cited in the Table 2. Moreover, the amount of adsorbed dye increased with film thickness due to the same reasons. However, the higher saturated adsorbed quantity per unit of surface onto films of ZNR can be attributed to the higher values of ni (Fig. 4(a)), and Nmi (Fig. 5(a))
5. Adsorption energies
In order to investigate the type of interaction between the N719 dye molecule and ZNP and ZNR materials, we calculated the adsorption energies of the dye molecule using the following expressions:
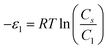 | (17) |
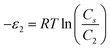 | (18) |
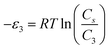 | (19) |
From the Table 3, we deduce that the value of adsorption energies (−ε1), (−ε2) and (−ε3) of the dye molecules adsorbed chemically on the ZNP surface and ZNR surface since the obtained values were superior than 40 KJ mol−1.39 Therefore, these values mean that the carboxylic group of N719 dye is chemically bond on the ZNP and the ZNR materials.
Indeed, the carboxylate groups provide a strong adsorption of the dye on the ZNR and the ZNR surface, thus fully justifying by involving valency forces through the exchange of electrons between dye molecules and ZnO nanorods ZNP and ZnO nanorods ZNR as covalent forces. We reported in Fig. 7 the evolution of energies of all receptor sites as a function of the different thicknesses of EPD films.
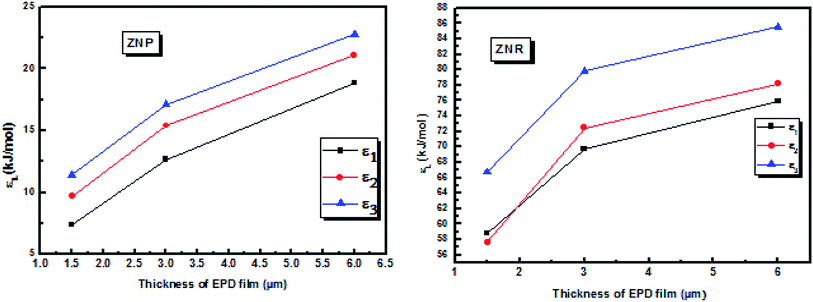 | ||
| Fig. 7 Evolution of the energies of the three receptor sites as a function of thickness of EPD films. | ||
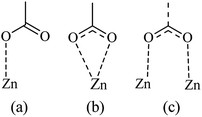
From the Fig. 7, we noticed that the value of energies increases with the increases of depositions times of ZNP and ZNR materials. This increase attributed to the increase of thickness of the adsorbents, can be easily attributed to the anchorage of N719 dye via carboxylic groups. According to the our previous results about the adsorption of the different models of N719 on nanoporous TiO2 (ref. 27) in the case of the adsorption N719 dye on ZNP and ZNR, we figure out three possible configurations in Fig. 8: three models for chemisorptions of the N719 dye carboxylate group on ZNR and on ZNP materials.
According to the obtained values of number of adsorbed dye molecules (Table 2), we illustrate in Fig. 9 an example of chemisorption anchorage of N719 dye via carboxylic group on the ZNP and ZNR respectively with hexagonal (Wurtzite) structure.40
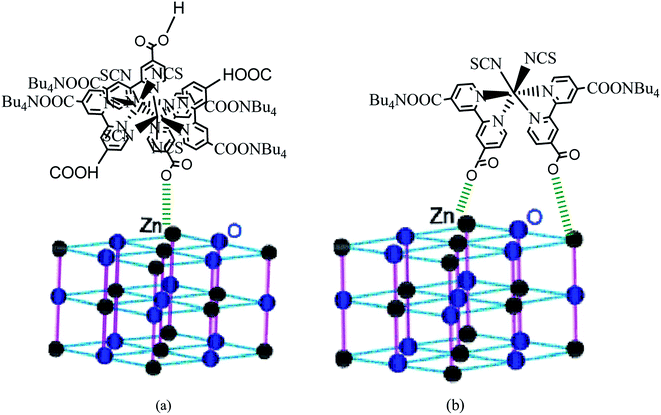 | ||
| Fig. 9 An example of the carboxylic group of N719 dye: (a) adsorbed chemically on the ZNP material via one carboxylic group according to the Table (n = 1.4 ˃ 1) and (b) adsorbed chemically on the ZNR surface via two carboxylic groups according to the Table 2 (n = 0.6 < 1) via one two carboxylic groups by bidentate chelate mode. | ||
6. Pore size distribution (PSD) determined by the adequate model
In this section, we characterized the adsorbent morphology by means of the PSD which describes the geometric heterogeneity of the N719 dye on ZNP and ZNR materials at different thicknesses during the adsorption process. In general, the Barrett–Joyner–Halenda (BJH) method, the most common method available in literature has been used to determine the pore size distribution of different porous materials, though, in our work, we estimated the PSD by a new Kelvin's law relating between the pore radius r and the dye concentration C and the concentration at saturation Cs developed by Patrick et al.41,42 that we previously used in (ref. 28 and 29).The Kelvin's law is given by the following equation:
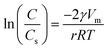 | (20) |
So we can write eqn (20) in the following relation:
 | (21) |
Substituting into eqn (9) the four relations:
we obtain an equation which relates the adsorbed quantity Q with the pore radius.
Therefore, the derivative of the adsorbed amount Q relative to the radius gives the pore size distribution of the adsorbent:27,28
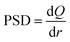 | (22) |
The variation of this distribution for different values of the temperature is illustrated in Fig. 10
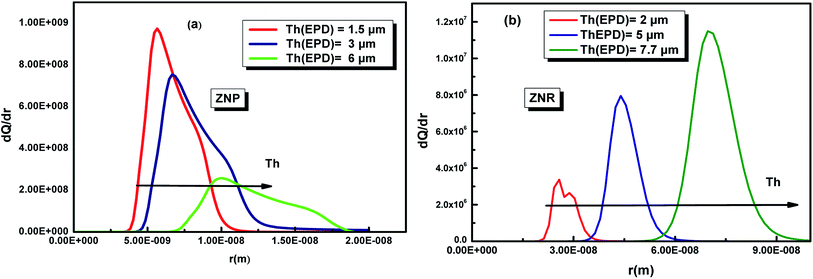 | ||
| Fig. 10 Pore size distribution of the ZNP (a) and ZNR (b) materials at different thicknesses Th of EPD films. | ||
First of all, the Fig. 10 shows that both ZNP and ZNR are mesoporous. The Fig. 10(a), shows also that the pore size distribution of ZNP exhibits particularly that the adsorbent is a mesoporous material with a pore radius about few nm (5 nm < r < 20 nm). However, the Fig. 10(b) shows that the adsorbent ZNR is also mesoporous material but with a large pore radius (20 nm < r < 90 nm) at applied thickness Th = 2 μm and Th = 5 μm and Th = 7.7 = μm. It is noticed that the thickness of EPD has a significant effect on the variation of the PSD of the two adsorbent materials ZNP and ZNR. The increase in thickness leads to a translation of PSD of the two materials to the higher pores.
In the next section, the DFT simulation has been used to complete the statistical physics to understand with details the molecular interaction between the N719 dye and the ZnO material.
7. DFT simulation: study of the interaction surface between the N719 dye and the ZnO
7.1 Computational details
The molecular geometry optimization of the dye sensitizer N719 was performed by using the B3LYP methods by means of the exchange–correlation functional and a 311++G(d,p) basis set with the Gaussian09 (G09) program package and the GaussView molecular visualization program.43–45 The B3LYP functional has been broadly used for calculations of various organic compounds, which justifies its use for the given system.46–48 The computational results showed the formation of hydrogen bonding and electrostatic interactions that suggest the increased reactivity and potential adsorption activity of these complexes. In order to estimate the different possible optimized geometries of the N719 dye adsorbed on the ZnO nanoparticle, first of all, we are interested in studying the molecular electrostatic potential to estimate the different active sites deduced from the electrophilic attack and nucleophilic reaction.7.2 Molecular electrostatic potential (MEP)
The molecular electrostatic potential surface (MEP) displays electrostatic potential distribution (electron and nuclei), size, dipole moments and shape of the molecule where the relative polarity can easily be visualized.49 It is very useful to predict reactive sites for electrophilic attack and nucleophilic reactions as well as hydrogen-bonding interactions.50,51 MEP maps can be obtained by mapping electrostatic potential onto the total electron density with color code. There are three important colors; blue, red and green used to indicate the value of the electrostatic potential. The surfaces with blue and red colors show the positive and negative values of the potential respectively. The surfaces with green colors indicate zero potential. In this study, the red, blue and green colors are used to identify the electrophilic, nucleophilic and neutral sites of N719 dye and ZnO material.The MEP surfaces mapped for the N719 dye and ZnO structure by using B3LYP/6- 311++G (d,p) level are shown in Fig. 11.
From the Fig. 11 the blue color reveals the strongest attraction whereas the red color indicates the strongest repulsion. The examination of this figure shows that there is an excess in electrons in the areas of negative potentials which is associated to the four carboxylic groups of N719 dye while the region of the positive potential (deficient in electrons) is associated to the Zn atom. This confirms the existence of five active sites between the adsorbate and the adsorbent. Indeed, these electrophilic and nucleophilic sites explain the formation of the O-bonds between the Zn atom and the carboxylic groups. The presence of this binding predicts a good stability of our system.
7.3 Adsorption modes: geometric optimization
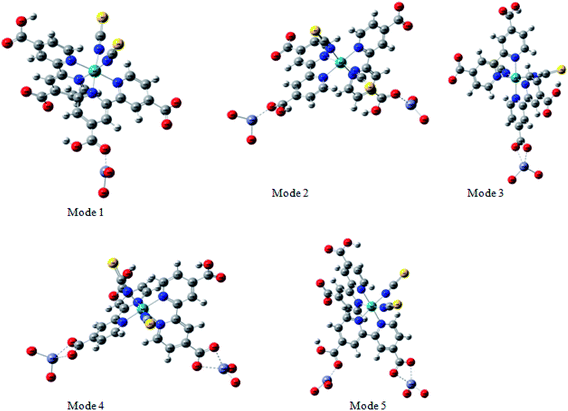
The adsorption of the dye on the semiconductor surface is known to play a main role on the dye sensitized solar cells DSSCs.46 Indeed, the strength of the dye/semiconductor interaction determines the stability of the nanocomposite lying at the heart of the solar cell.In order to study much better the interatomic interactions between the N719 dye and on the ZnO surface, a DFT simulation has been used to optimize the different adsorption geometries of the adsorbed N719 dye on ZnO surface. A correct prediction of the adsorption geometries is an essential prerequisite to properly capture the intricate electronic structure of the dye@ZnO nanocomposites. Therefore, different adsorption modes have been investigated for the interacting system (Fig. 12).
According to the molecular electrostatic potential (MEP), five possible optimized geometries for adsorption N719 dye on ZnO surface were selected to understand the molecular interaction during the adsorption process.
In the monodentate linkage form of the Mode 1, one oxygen atom O32 in the carboxylic group binds to a Zn atom, in the bidentate bridging linkage form of the Mode 2, the O34 atom in the one carboxylic group binds to a Zn58 atom and the oxygen atom O34 in the other carboxylic group binds to a Zn61 atom, whereas in the bidentate chelate linkage form of Mode 3, both oxygen atoms O36 and O37 of carboxylate ion group –COO– bind to a Zn58 atom,besides, in the bidentate bridging linkage form Mode 4, the both oxygen atoms O36 and O37 in the one carboxylate ion group –COO– bind to a Zn58 atom, and the linkage also between the both oxygen atoms O38 and O39 in the one carboxylate ion group –COO– bind to the Zn61 atom and concerning the Mode 5, both oxygen atoms O38 and O39 in the carboxylate ion group –COO– bind to the Zn58 atom and the oxygen atom O36 in the carboxylic group binds to a Zn61 atom.
Among these five modes, the Mode 1 and the Mode 2 are in coincidence with the two optimized geometries modes of the adsorbed N719 dye on the ZnO surface which recently determined by the group of De Angelis et al. by taking the CP method for geometry optimizations.52 However, the other modes are attributed to the our efficient MEP method which gives more possible optimized geometries of the complex N179 dye@ZnO.
Indeed, the MEP method could be used as an efficient predictive tool to help the optimization of dye-sensitized solar cells. Through the DFT simulation, we deduced that the three optimized modes: Mode 1, Mode 2 and Mode 3 determined by the DFT simulation are agreement with the three suggested models obtained by our statistical physics models (Fig. 8(a–c)). While in this work, the DFT simulation has been determined two another possible models like Mode 4 and Mode 5 involved in the carboxylic group and the carboxylate ion groups respectively: two possible carboxylate ions groups bind onto the ZnO surface (Mode 4) and one of the carboxylic group associated with the carboxylate ion group to bind on the ZnO surface (Mode 5). Indeed, the DFT simulation has been completed the statistical physics modeling to determine the possible adsorption modes that could be occurred on the ZnO surface. The results of DFT simulation are in coincidence with the previously result determined by the resonant Raman scattering and infrared absorption spectroscopy which suggested that the carboxylate ion groups of the N719 dye molecules bind to TiO2 surface either through bidentate chelate or bidentate bridging linkages at all stages of adsorptions.53
7.4 AIM approach: topological parameters
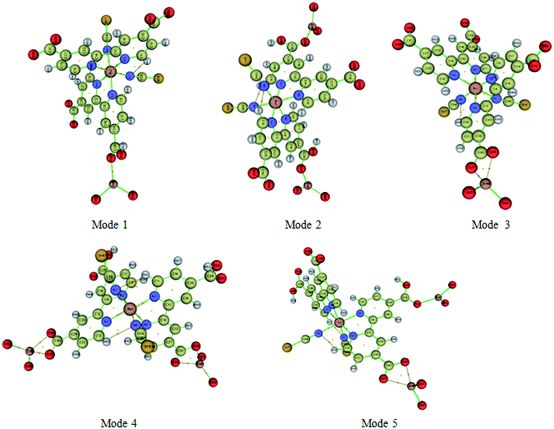
Atoms-In-Molecule (AIM) method provides an effective means of mapping topological properties of the electron density to Lewis structure representation of molecules. It is the one of the most useful tools to characterize atomic and molecular interactions, particularly hydrogen bonding, is the topological analysis using the Bader theory of ‘Atoms in molecules’ (AIM).54 According to AIM theory each chemical bond presents a critical point of binding denoted BCP and ring critical point RCP. The point BCP is defined as being a minimum of electronic density along the connecting path and a maximum in the other two perpendicular directions and the ring critical point RCP is represented the cyclic character of an atomic chain. Thought the location of the BCP several energetic and topological parameters can be calculated at their position in space. The calculated topological parameters are the following: the electron density r (r), the potential energy density and the interaction energy. These parameters were used to estimate the properties of the bonds in compounds and more particularly the hydrogen bonds.55Molecular graphs of the N719 dye and the ZnO using AIM2000 program are shown in Fig. 13 and the topological parameters are represented in the Table 4
| Modes | Types | Electron density | Potential energy density V(r) | Eint(kJ mol−1) | Average value of the interaction energy Eavg(kJ mol−1) | |
|---|---|---|---|---|---|---|
| Mode1 | BCPs | O32⋯Zn58 | 0.05644 | −0.07927 | −103.05 | −103.05 |
| Mode2 | BCPs | O34⋯Zn58 | 0.05639 | −0.07980 | −103.74 | −103.25 |
| O32⋯Zn61 | 0.05611 | −0.07904 | −102.76 | |||
| Mode3 | BCPs | O37⋯Zn58 | 0.03991 | −0.04944 | −64.27 | −66.98 |
| O36⋯Zn58 | 0.04260 | −0.05360 | −69.68 | |||
| NRCPs | R1 | 0.02727 | −0.03198 | |||
| Mode4 | BCPs | O37⋯Zn58 | 0.04260 | −0.05367 | −69.77 | −66.10 |
| O36⋯Zn58 | 0.03908 | −0.04822 | −62.69 | |||
| O38⋯Zn61 | 0.04249 | −0.05352 | −69.57 | |||
| O39⋯Zn61 | 0.03892 | −0.04798 | −62.38 | |||
| NRCPs | R1 | 0.02704 | −0.03166 | — | ||
| R2 | 0.02697 | −0.03155 | ||||
| Mode5 | BCPs | O37⋯Zn58 | 0.04616 | −0.05917 | −76.92 | −78.85 |
| O37⋯Zn58 | 0.03552 | −0.04284 | −55.69 | |||
| O37⋯Zn61 | 0.05688 | −0.07994 | −103.93 | |||
| NRCPs | R1 | 0.02671 | −0.03107 | — |
From the Table 4, it seems that the values of interaction energies are ranged from −55.69 kJ mol−1 to −215.26 kJ mol−1. The average values of interaction energies of the Mode 1, Mode 2, Mode 3, Mode 4 and Mode 5 are respectively −103.05 kJ mol−1, −103.25 kJ mol−1, −66.98 kJ mol−1, −66.10 kJ mol−1 and −78.85 kJ mol−1; through, this all values we noticed that the value of interaction energy of the Mode 1 is the highest value than the another values of interactions energies given by the rest of modes. According to the adsorption energies values determined by the statistical physics models, it seems that the values of interaction energies obtained by the DFT simulation are confirmed the chemisorption process of the adsorption N719 dye on the ZnO by means the different possible five modes. Therefore, the higher values of interaction energies obtained particularly by the Mode 1 and the Mode 2 are attributed to the group carboxylic groups which provides a strong adsorption process of the N719 dye on ZnO surface. From the Mode 2, it seems that the N719 dye adsorbs better on the ZnO surface when two carboxylic groups are exploited than when only one is involved. Therefore, the anchorage via the both carboxylic group is preferred to be the best adsorption mode which can make a good stability of the system. This later is agreement with previous result that proved that the N719 dye anchored chemically on the metal–oxide via two carboxylic groups and produced a good performance for dye sensitized solar cells.27,56 De Angelis et al.52 are reported that the N719 dye is predicted to be strongly interact with the ZnO surface via the bidentate bridging mode. This result is in coincidence with the bidentate bridging Mode 2 obtained by the DFT simulation which reported that the N719 dye anchored strongly on the ZnO surface via two carboxylic groups with a higher value of interaction energy 103.74 kJ mol−1 (Table 4).
Moreover, various theoretical and experimental researches have been reported that the ruthenium complexes dyes such as N719 and N3 dyes are chemically bind by means the bidentate chelate or bridging coordination into the oxide metal surface via two carboxylic groups.57,58 Furthermore, the ruthenium(II) polypyridyl complexes are among the most popular light harvesters within the solar cell community. In particular, the prototype [cis-(dithiocyanato)-Ru-bis(2,2′-bipyridine-4,4′-dicarboxylate)] complex (N3) and its doubly protonated (N719) dye have maintained a clear lead due to their efficiency.32,59 In this kind of compounds dyes, the bipyridine ligands ensure stable anchoring to the semiconductor surface through the carboxylic groups. In addition, the Table 4 shows also different bond and ring critical points of the five modes. The topological analysis of the five modes shows five binding critical points BCPs and three ring critical point RCPs: five BCPs (O32⋯Zn58), (O34⋯Zn58, O32⋯Zn61), (O37⋯Zn58, O36⋯Zn58), (O37⋯Zn58, O36⋯Zn58, O38⋯Zn61, O39⋯Zn61) and (O37⋯Zn58, O37⋯Zn58, O37⋯Zn561) are associated respectively to the Mode 1 the Mode 2, Mode 3, Mode 4, Mode 5, however, three RCPs are associated to the Mode 3, Mode 4 and Mode 5. Therefore, the presence of these critical points of binding BCPs were estimated the kind of binding between the adsorbate and the adsorbent by means of the value of electron density (Table 4), while, the presence of a new ring critical point RCP not only proved the stability of the system but also confirmed the cyclic character of an atomic chain. As shown in Fig. 13, the interactions between the oxygen atom of the N719 dye and the oxygen atom of the ZnO material via both carboxylates ion groups give rise to the both rings NRCP1 and NRCP2. Indeed, the combination of theses both rings NRCP1 and NRCP2 have been indicated more stability to the adsorption system. Moreover, it can be also observed that the Mode 5 gives rise to a significant NRCP1 which makes a good stability to the system compared to the new ring critical point RCP of the Mode 3 and Mode 4. The existence of one and two rings NRCP produced by the carboxylate ion groups during the adsorption process of N719 dye on ZnO surface is agreement with the previous result determined by the resonant Raman scattering and infrared absorption spectroscopy which reported that the N719 dye are anchored to the TiO2 surface through stable bidentate chelate or bidentate bridging linkages.52
7.5 Reduced density gradient (RDG)
In order to validate the results of the strong interaction of the N719 dye on the ZnO surface obatained by the statistical physics models and the DFT simulation, the existing of intermolecular interaction was also was carried out by a RDG plot analysis and isosurface of interactions by using the multi-wave function analysis. The results were performed and plotted respectively by the use of Multiwfn and VMD programs.60,61 The RDG approach is a dimensionless elementary amount obtained from the density and its first derivative developed by Johnson et al.62 The RDG is defined as:Based on the density r(r) against sign λ we have tried to understand and indicate the nature of strength of the different interactions between the N719 dye and the ZnO structure:
- If λ < 0: Attractive and binding interactions (strong interaction).
- If λ > 0: repulsive and non-binding interactions (steric effect inring and cage).
- Values close to zero indicating van der Waals interactions
The diagram RDG represents three regions of interactions: the interactions appear in the form of green plates are attributed to Van der Waals interactions; the red plates is related to the repulsive interactions which show a strong steric effect and the blue pates is attributed to the strong interaction. The results were collected in Fig. 14.
Therefore, the result shows that the diagrams RDG of the all modes exhibits the blue color of plates which proved the existence of the strong interaction intermolecular between the N719 dye and the ZnO material. These strong interactions appear as zones marked by red circles in each mode. From Fig. 14, a clear blue spots have been checked particularly in the bidentate chelate linkage of carboxylate ion group –COO– involved in Mode 3, Mode 4 and Mode 5 (Fig. 14(c)–(e)). These modes show a significant strong attractive interaction compared to the Mode 1 and the Mode 2 which attributed to the bidentate chelate linkage modes. Moreover, the result of RDG is agreement with the result of the MEP in its identification of the geometric optimization and the AIM topological. It confirmed also the existence of strong intermolecular interaction between the N719 dye and the ZnO surface via the carboxylic group which determined by the statistical physics models.
8. Conclusion
In this work we have applied two computational approaches which combine statistical physics theory and the DFT theory to study the adsorption process of N719 dye on ZnO nanopowders and ZnO nanorods at three different deposition times of (EPD) for dye sensitized solar cells. The statistical physics models has been used to model the adsorption isotherms of N719 dye on ZNP and ZNP materials by means of statistical physics treatment. Five models were used for fitting the experimental isotherms data of adsorption. The adsorption isotherms were well described by a monolayer model with three types of sites. The energetic parameters showed that the N719 dye molecules anchored chemically on the ZNP and ZNR surface via the carboxylic groups. The DFT simulation has been used to predict reactive sites for electrophilic and nucleophilic attack for the complex N719@ZnO by using the molecular electrostatic potential (MEP) at the B3LYP/6-311++G(d,p). The calculations of MEP reveal five possible optimized geometric of the adsorbed N719 dye on ZnO surface. The intermolecular interactions between the N719 dye and the ZnO surface has been studied by using the topological AIM and reduced density gradient RDG. The result of the MEP, topological AIM and RDG are in agreement with the result of statistical physics and confirmed that the N719 dye is chemically bonding on the ZnO surface with strengthened interaction energy via two carboxylic groups of bidentate bridging configuration. The excellent agreement of the computational approach DFT with a statistical physics theory indicates that the both approaches of this work could be used as an efficient predictive tool to help the optimization of dye-sensitized solar cells.Conflicts of interest
There are no conflicts to declare.Appendix A
Nomenclature
| zgc | Grand canonical partition function of one site |
| Zgc | Total grand canonical partition function of Nm sites |
| β | Boltzmann factor |
| μ | Chemical potential of the adsorbate state |
| h | Plancks constant |
| KB | Boltzmann constant |
| T | Temperature in K |
| Cs | The saturation dye concentration |
| C | The concentration of dye molecules |
| C1/2 | The concentration at half saturation |
| C1 | The concentration at half saturation for the first receptor site |
| C2 | The concentration at half saturation for the second receptor site |
| C3 | The concentration at half saturation for the third receptor site |
| No | The average number of occupied sites |
| Ni | The state of occupation number |
| Ztr | The translation partition function per unit of volume |
| −ε1 | The adsorption energy of first receptor site |
| −ε2 | The adsorption energy of second receptor site |
| −ε3 | The adsorption energy of third receptor site |
| n1 | The number of molecules per site of first site |
| n2 | The number of molecules per site of second site |
| n3 | The number of molecules per site of third site |
| Nm1 | Density of first receptor sites |
| Nm2 | Density of second receptor site |
| Nm3 | Density of third receptor site |
| J | Grand potential |
| Q | The adsorbed quantity |
Appendix B
Treatment of model analytical expressions used to fitting
Particular model: identical sites model (homogenous and monolayer process or Hill model).In the following we suppose that all the receptor sites are identical which corresponds to a homogenous adsorption process.
The grand canonical partition function in this case, for only one site, has the form
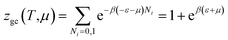 | (A1) |
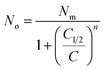 | (A2) |
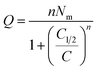 | (A3) |
The Langmuir model is a particular case of the Hill model, n takes the value of the unit
So its expression is:
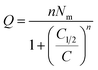 | (A4) |
Monolayer model with two energies
We suppose that the adsorption onto the first type is carried out with an energy (−ε1) and onto the second type with an energy (−ε2). In this case, the total grand canonical partition function can be written as follows if we consider the two sites are independent:| Ztotal = (z1gc)Nm1(z2gc)Nm2 | (A5) |
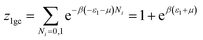 | (A6) |
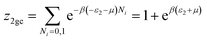 | (A7) |
Using the previous definition of occupation number, the total number of occupied sites is:
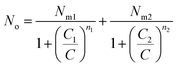 | (A8) |
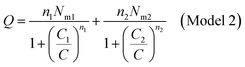 | (A9) |
Monolayer model with four energies
We developed this model by applying the same method.The partition functions of the four types of the site are expressed by the following relations:
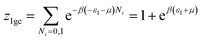 | (A10) |
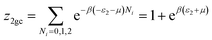 | (A11) |
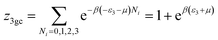 | (A12) |
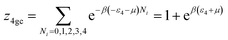 | (A13) |
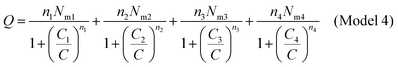 | (A14) |
Double layer with one energy
The partition function of the double layer with one energy is expressed by the following relation:
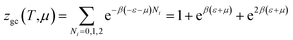 | (A15) |
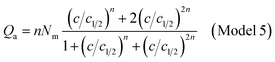 | (A16) |
Double layer with two energies
The partition function of the double layer with two energies is expressed by the following relation:
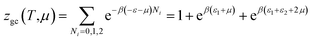 | (A17) |
The adsorbed quantity of dye versus the concentration is represented as follows
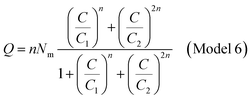 | (A18) |
References
- Y. M. Meng, Y. Lin and J. Y. Yang, Appl. Surf. Sci., 2013, 268, 561 CrossRef CAS.
- X. Fang, M. Li, K. Guo, Y. Zhu, Z. Hu and X. Liu, Electrochim. Acta, 2012, 65, 174 CrossRef CAS.
- P. G. Antonio, D. M. Hans, S. Helmut and S. Wilhelm, Br. J. Nutr., 2003, 89, 787 CrossRef PubMed.
- H.-J. Kim, Y.-T. Bin, S. N. Karthick, K. V. Hemalatha, C. Justin Raj, S. Venkatesan, S. Park and G. Vijayakumar, Natural dye extracted from Rhododendron species flowers as a photosensitizer in dye sensitized solar cell, Int. J. Electrochem. Sci., 2013, 8, 6734–6743 CAS.
- G. G. G. M. N. Hemamali and G. R. A. Kumara, Dye-sensitized solid state solar cells sensitized with natural pigment extracted from the grapes, Int. J. Sci. Res., 2013, 3, 1 e3 Search PubMed.
- Y. Chiba, A. Islam, Y. Watanab, R. Komiya, N. Koide and L. Han, Dye-sensitized solar cells with conversion efficiency of 11.1%, Jpn. J. Appl. Phys., 2006, 45, l638–l640 CrossRef CAS.
- S. Hao, J. Wu, Y. Huang and J. Lin, Natural dyes as photosensitizers for dye- sensitized solar cell, Sol. Energy, 2006, 80(2), 209e214 CrossRef.
- M. Gratzel, J. Photochem. Photobiol. C Photochem. Rev., 2003, 4, 145 CrossRef CAS.
- O. Carp, C. L. Huisman and A. Reller, Prog. Solid State Chem., 2004, 32, 33 CrossRef CAS.
- E. Hendry, M. Koeberg, B. O'Regan and M. Bonn, Nano Lett., 2006, 6, 755 CrossRef CAS PubMed.
- J. B. Baxter and C. A. Schmuttenmaer, J. Phys. Chem. B, 2006, 110, 25229 CrossRef CAS PubMed.
- I. Corni, M. P. Ryan and A. R. Boccaccini, J. Eur. Ceram. Soc., 2008, 28, 1353–1367 CrossRef CAS.
- A. R Boccaccini, J. A. Roether, B. J. C. Thomas, M. S. P. Shaffer, E. Chavez, E. Stoll and E. J. Minay, J. Ceram. Soc. Jpn., 2006, 114, 1–14 CrossRef.
- W. Sugimoto, O. Terabayashi, Y. Murakami and Y. Takasu, J. Mater. Chem., 2002, 12, 3814–3818 RSC.
- X. Zhang and W. Yang, Chem. Lett., 2007, 36, 1228–1229 CrossRef CAS.
- O. Van der Biest and L. Vandeperre, Annu. Rev. Mater. Sci., 1999, 29, 327–352 CrossRef CAS.
- F. Hirose, K. Kuribayashi, T. Suzuki, Y. Narita, Y. Kimura and M. Niwano, Electrochem. Solid State Lett., 2008, 11, 109 CrossRef.
- F. Hirose, K. Kuribayashi, M. Shikaku, Y. Narita, Y. Takahashi, Y. Kimura and M. Niwano, J. Electrochem. Soc., 2009, 156–987 Search PubMed.
- P. Marquet, G. Andersson, A. Snedden, L. Kloo and R. Atkin, Langmuir, 2010, 26, 9612–9616 CrossRef CAS PubMed.
- R. Sch€olin, M. Quintana, E. M. J. Johansson, M. Hahlin, T. Marinado, A. Hagfeldt and H. Rensmo, J. Phys. Chem. C, 2011, 115, 19274–19279 CrossRef.
- L. Ellis-Gibbings, V. Johansson, R. B. Walsh, L. Kloo, J. S. Quinton and G. G. Andersson, Langmuir, 2012, 28, 9431–9439 CrossRef CAS PubMed.
- P. Song, Y. Z. . Li, F. C. . Ma and M. T. . Sun, J. Mater. Chem. C, 2015, 3, 4810–4819 RSC.
- S. Ranjitha, G. Rajarajan, T. S. Gnanendra, P. M. Anbarasan and V. Aroulmoji, Spectrochim. Acta Mol. Biomol. Spectrosc., 2015, 149, 997–1008 CrossRef CAS PubMed.
- A. Ben Lamine and Y. Bouazra, Chem, 1997, 22, 67–65 CAS.
- N. Bouaziz, M. Ben Manaa and A. Ben Lamine, Phys. B, 2017, 525, 46–59 CrossRef CAS.
- N. Bouaziz, M. Ben Manaa and A. Ben Lamine, Results Phys., 2018, 9, 1323–1334 CrossRef.
- M. Ben Manaa, B. Schmaltz, M. Bouaicha, F. Tran Van and A. B. . Lamine, Sol. Energy, 2016, 135, 177–187 CrossRef.
- M. Ben Manaa, B. Schmaltz, N. Bouaziz, F. Tran Van and A. B. . Lamine, J. Alloys Compd., 2018, 765, 385–395 CrossRef CAS.
- M. Ben Manaa, N. Bouaziz, B. Schmaltz, F. Tran and A. Ben Lamine, Microporous Mesoporous Mater., 2018, 270, 82–92 CrossRef CAS.
- M. Ben Manaa, N. Issaoui, N. Bouaziz and A. Ben Lamine, J. Mater. Res. Technol., 2020, 9, 1175–1188 CrossRef.
- N. Bouaziz, M. Ben Manaa, F. Aouaini and A. Ben Lamine, Mater. Chem. Phys., 2019, 225, 111–121 CrossRef CAS.
- M. K. Nazeeruddin, F. De Angelis, S. Fantacci, A. Selloni, G. Viscardi, P. Liska, S. Ito, B. Takeru and M. Gratzel, J. Am. Chem. Soc., 2005, 127, 16835–16847 CrossRef CAS.
- M. K. Nazeeruddin, A. Kay, I. J. Rodicio, R. Humphry-Baker, E. Mueller, P. Liska, N. Vlachopoulos and M. Gratzel, J. Am. Chem. Soc., 1993, 115, 6382–6390 CrossRef CAS.
- A. Amat and F. De Angelis, Phys. Chem. Chem. Phys., 2012, 14, 10662–10668 RSC.
- M. M. Hedrick, M. L. Mayo, E. Badaeva and S. Kilina, J. Phys. Chem. C, 2013, 117, 18216–18224 CrossRef CAS.
- Y. Hara, M. T. Tejedor, K. Lara, D. Lubin, L. J. Brzozowski, D. J. Severseike and M. A. Anderson, Int. J. Electrochem. Sci., 2013, 8, 6734–6743 Search PubMed.
- S. Knani, M. Mathlouthi and A. Ben Lamine, Food Biophys., 2007, 2, 183–192 CrossRef.
- N. Bouaziz, M. Ben Manaa, B. Mohamed and A. Ben Lamine, Mol. Phys., 2020, 118, 1362–3028 CrossRef.
- N. Bouaziz, M. Ben Manaa and A. Ben Lamine, Results Phys., 2018, 9, 1323–1334 CrossRef.
- N. Faal Hamedani and F. Farzaneh, J. Sci. Islam. Repub. Iran, 2006, 9, 231–234 Search PubMed.
- W. A. Patrick and N. F. Eberman, J. Phys. Chem., 1925, 29, 220–228 CrossRef.
- W. A. Patrick and D. C. Jones, J. Phys. Chem., 1925, 29, 1–10 CrossRef CAS.
- F. J. Luque, J. M. . Lopez and M. Orozco, Theor. Chem. Acc., 2000, 103, 343–345 Search PubMed.
- R. I. Dennington, T. Keith and J. Millam, GaussView, Version 5.0.8, Semichem. Inc, Shawnee Mission, KS., 2008, vol.12, pp. 34–36 Search PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, and D. J. Fox, GAUSSIAN 09, Revision A.02, Gaussian, Inc., Wallingford, CT, 2009, vol.10, pp. 122–123 Search PubMed.
- N. Issaoui, H. Ghalla, S. Muthu, H. T. Flakus and B. Oujia, J. Mol. Struct., 2017, 1135, 209–221 CrossRef CAS.
- N. Issaoui, H. Ghalla, S. Muthu, H. T. Flakus and B. Oujia, Spectrochim. Acta, Part A, 2015, 136, 1227–1242 CrossRef CAS PubMed.
- F. De Angelis, F. Fantacci, S. Selloni, M. K. Nazeeruddin and M. Gratzel, J. Am. Chem. Soc., 2007, 129, 14156–14157 CrossRef CAS PubMed.
- B. Von Oepen, W. Kördel and W. Klein, Chemosphere, 1991, 22, 285–304 CrossRef CAS.
- N. Okulik and A. H. Jubert, Internet Electron. J. Mol. Des., 2005, 4, 17–30 CAS.
- E. Scrocco and J. Tomasi, Adv. Quantum Chem., 1978, 11, 115–121 CrossRef CAS.
- J. M. Azpiroz and F. De Angelis, J. Phys. Chem. A, 2014, 118, 5885–5893 CrossRef CAS PubMed.
- K. Suto, A. Konno, Y. Kawata, S. Tasaka and A. Sugita, Chem. Phys. Lett., 2012, 536, 45–49 CrossRef CAS.
- F. Biegler-Koning, J. Schonbohm and D. Bayles, AIM2000, J. Comput. Chem., 2001, 22, 545 CrossRef.
- U. Koch and P. Popelier, J. Phys. Chem. A, 1995, 99, 9747 CrossRef CAS.
- J. Wang and Z. Li, Chem. Mater., 2010, 22, 579–584 CrossRef CAS.
- M. Fujihira, N. Ohishi and T. Osa, Nature, 1977, 268, 226–228 CrossRef CAS.
- C. P. León, L. Lador, B. Reng and M. Thelalkat, J. Phys. Chem. B, 2006, 110, 8723–8730 CrossRef PubMed.
- M. K. Nazeeruddin, A. Kay, I. Rodicio, R. Humphry-Baker, E. Mueller, P. Liska, N. Vlachopoulos and M. Gratzel, J. Am. Chem. Soc., 1993, 115, 6382–6390 CrossRef CAS.
- T. Lu and F. W. Chen, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed.
- B. F. Minaev, G. V. Baryshnikov and V. A. Minaeva, Dyes Pigm., 2012, 92, 531–536 CrossRef CAS.
- E. R. Johnson, S. Keinan, P. Mori-Sanchez, J. Contreras-García, A. J. Cohen and W. Yang, J. Am. Chem. Soc., 2010, 132, 6498–6506 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2020 |