Multi-step hydration/dehydration mechanisms of rhombohedral Y₂(SO₄)₃: a candidate material for low-temperature thermochemical heat storage

Abstract

To evaluate rhombohedral Y₂(SO₄)₃ as a new potential material for low-temperature thermochemical energy storage, its thermal behavior, phase changes, and hydration/dehydration reaction mechanisms are investigated. Rhombohedral Y₂(SO₄)₃ exhibits reversible hydration/dehydration below 130 °C with relatively small thermal hysteresis (less than 50 °C). The reactions proceed via two reaction steps in approximately 0.02 atm of water vapor pressure, i.e. “high-temperature reaction” at 80–130 °C and “low-temperature reaction” at 30–100 °C. The high-temperature reaction proceeds by water insertion into the rhombohedral Y₂(SO₄)₃ host structure to form rhombohedral Y₂(SO₄)₃·xH₂O (x = ∼1). For the low-temperature reaction, rhombohedral Y₂(SO₄)₃·xH₂O accommodates additional water molecules (x > 1) and is eventually hydrated to Y₂(SO₄)₃·8H₂O (monoclinic) with changes in the host structure. At a water vapor pressure above 0.08 atm, intermediate Y₂(SO₄)₃·3H₂O appears. A phase stability diagram of the hydrates is constructed and the potential usage of Y₂(SO₄)₃ for thermal energy upgrades is assessed. The high-temperature reaction may act similarly to an existing candidate, CaSO₄·0.5H₂O, in terms of reaction temperature and water vapor pressure. Additionally, the hydration of rhombohedral Y₂(SO₄)₃·xH₂O to Y₂(SO₄)₃·3H₂O should exhibit a larger heat storage capacity. With respect to the reaction kinetics, the initial dehydration of Y₂(SO₄)₃·8H₂O to rhombohedral Y₂(SO₄)₃ introduces a microstructure with pores on the micron order, which might enhance the reaction rate.

---

1. Introduction

Thermal energy storage based on chemical reactions (TCHS: thermochemical heat storage) is a prospective technology for the reduction of fossil-fuel consumption by storing waste heat.^1,2 One of the expected roles of TCHS is storing and utilizing heat below 250 °C, where abundant low-grade waste heat and solar energy might be available. For widespread application, a critical challenge is to identify appropriate reversible dehydration/hydration reaction systems satisfying following criteria: suitable reaction temperature, enabling high heat storage capacity, fast enough reaction rate and heat output rate, long-term stability of thermophysical and mechanical properties including, for example, no liquefaction due to melting or deliquescence, non-toxicity of materials themselves and reaction products, the low cost of materials, etc.³ Solid–gas reactions using water vapor as a reactive gas (dehydration/hydration reactions) are favorable because water is safe and easily stored via condensation. To date, various salt hydrates, whose dehydration/hydration reactions can be operated below 250 °C, have been proposed, for example, MgSO₄·nH₂O (n = 0–7),^4–6 CaCl₂·nH₂O (n = 0–6),⁷ LiOH·H₂O,^8–10 Na₂S·5H₂O,^11,12 and CaSO₄·0.5H₂O.^13,14 However, these salt hydrates suffer from some undesirable behaviors related to hydration kinetics and cycle performance.‡ Despite numerous efforts related to the modification of material properties such as developing composite materials based on these salt hydrates, no materials have been widely used yet.

Recently, we reported the dehydration/hydration of β-La₂(SO₄)₃·H₂O as a new candidate reaction for TCHS below 250 °C.^15–17 The reactions proceed by insertion/deinsertion of the H₂O guest molecules into β-La₂(SO₄)₃ host lattices,§ which leads the rapid and reversible dehydration/hydration reaction even at low-temperature below 250 °C. Furthermore, β-La₂(SO₄)₃ is non-toxic and does not show melting and deliquescence. However, the heat storage capacity is insufficient due to the small changes in the hydration water content (β-La₂(SO₄)₃·H₂O: 3.2 mass% anhydrous basis). There is still a need to find other materials.

In this study, we focused on Y₂(SO₄)₃ as a new candidate material for the low-temperature TCHS system. Y₂(SO₄)₃ is another trivalent-rare-earth sulfate with a chemical formula analogous to that of β-La₂(SO₄)₃ but it has a crystal structure belonging to the rhombohedral system (space group: No. 148).¹⁹ Due to the differences of rare-earth elements and crystal structures, the hydration/dehydration behavior of rhombohedral Y₂(SO₄)₃ should differ from that of β-La₂(SO₄)₃ (monoclinic system, space group: 15). Thus it is worthwhile to investigate if rhombohedral Y₂(SO₄)₃ shows favorable hydration/dehydration behaviors. See ESI-1† for their crystal structures. Though there are a few studies associated with the phase changes, reaction temperature, and enthalpy changes on dehydration of Y₂(SO₄)₃·8H₂O,^20–22 the backward hydration reaction behaviors have not been reported. In addition, Y₂O_3, the raw material of Y₂(SO₄)₃, is oversupplied, so the cost is not expensive at this time, 3 USD kg⁻¹ in 2018.²³ Therefore, Y₂(SO₄)₃ might be a low-cost candidate for TCHS.

In this work, thermogravimetry (TG) studies of the hydration/dehydration reaction were conducted. High-temperature X-ray diffraction (XRD) investigated the crystal structure changes in the dehydration reaction. Then, we systematically investigated the phases formed in the hydration process under various conditions of temperatures and water vapor pressure p_H2O and discussed the available reactions for TCHS system. In addition, we examined the microstructures of Y₂(SO₄)₃ and Y₂(SO₄)₃·8H₂O by nitrogen gas adsorption (N₂ adsorption), optical microscopy, and transmission electron microscopy (TEM) because the microstructures should influence the dehydration/hydration reaction rates.¹⁷

2. Experimental

2.1 Materials

In this paper, a-few-hundreds-μm-large particles of Y₂(SO₄)₃·8H₂O (Strem Chemical, 99.9%) were used as the starting material for the syntheses of rhombohedral Y₂(SO₄)₃ by heating Y₂(SO₄)₃·8H₂O. The heating processes were either conducted at the time of thermogravimetry, high-temperature XRD and N₂ adsorption measurements in the respective apparatus or pre-conducted in a stand-alone furnace.

2.2 Thermogravimetry (TG)

To investigate the dehydration/hydration reaction behavior of rhombohedral Y₂(SO₄)₃, TG was conducted using a Rigaku Thermo plus TG 8120. Y₂(SO₄)₃·8H₂O was heated to about 400 °C, which is the temperature where dehydration to the anhydrate should be completed, and subsequently cooled to about 30 °C in the TG apparatus (“first heating–cooling cycle”) under a humidified argon gas (water vapor pressure p_H2O = 0.02 atm) flow. At this point, Y₂(SO₄)₃·xH₂O was obtained as a rehydrated phase of anhydrate Y₂(SO₄)₃. On the subsequent “second heating–cooling cycle” between 30–160 °C, the dehydration/hydration reaction behaviors of Y₂(SO₄)₃·xH₂O were investigated. Isothermal TG measurements at various temperatures in humidified argon (p_H2O = 0.023 atm) were conducted on the hydration of rhombohedral Y₂(SO₄)₃. For isothermal TG measurements, Y₂(SO₄)₃·8H₂O was used as the starting material and it was dehydrated to rhombohedral Y₂(SO₄)₃ upon heating to 320 °C in dry argon by TG. Subsequently, it was cooled to arbitrary temperatures and the isothermal hydration reaction started by switching flowing gas from dry argon to humidified argon.

In all the TG measurements, the sample material was put in a platinum cylindrical crucible with a diameter of 5 mm and a height of 5 mm and the same empty crucible was used as the reference.

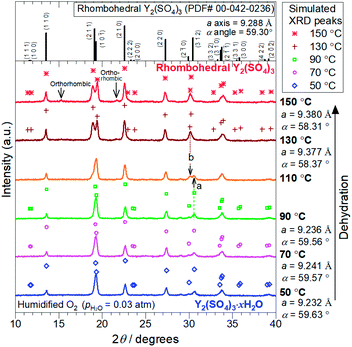
2.3 X-ray diffraction (XRD)

XRD measurements were conducted on a PANalytical X'Pert-Pro MPD using Cu Kα radiation. High-temperature data collection was achieved using an Anton Paar HTK1200N high-temperature oven-chamber under humidified oxygen. For the high-temperature XRD experiments, Y₂(SO₄)₃·8H₂O (Strem Chemical, 99.9%) was heated to 300 °C to form rhombohedral Y₂(SO₄)₃ and subsequently, it was cooled to 50 °C to form the hydrated phase Y₂(SO₄)₃·xH₂O. The XRD patterns during dehydration of Y₂(SO₄)₃·xH₂O were collected on the second heating process from 50 °C to 150 °C. All heating/cooling processes for in situ XRD measurements were conducted under 0.03 atm of p_H2O. Rietveld refinement analyses were performed with the help of a commercial software X'Pert HighScorePlus (PANalytical) on the in situ XRD patterns to identify the phase and the lattice parameters of the samples.

2.4 Isothermal hydration treatments of Y₂(SO₄)₃ under various temperature and p_H2O

The phases formed by the hydration of Y₂(SO₄)₃ under arbitrary temperatures (37–84 °C) and p_H2O (0.03–0.4 atm) were investigated by isothermal hydration treatments using two electric furnaces. Rhombohedral Y₂(SO₄)₃ was prepared by dehydration of Y₂(SO₄)₃·8H₂O at 200 °C for 1 hour in air. Rhombohedral Y₂(SO₄)₃ (0.1 g) was placed in an approximately 60 mL closed vessel. The vessel and a tank with water were put in separate furnaces and they were connected by the gas line across the furnaces. The vessel was maintained at a constant temperature for 3 hours while the p_H2O control was performed by flowing humidified argon gas at a rate of 200 mL min⁻¹ bubbled through water kept at a constant temperature. A ribbon heater was wrapped around the gas line outside the furnaces and kept over 80 °C to prevent condensation of water vapor in humidified argon gas.

The phases of the sample after the hydration treatments were identified by XRD. Fourteen batches under different conditions of temperature and p_H2O were examined. Based on the results of the isothermal TG and hydration treatments, the phase stability diagram of Y₂(SO₄)₃ with temperature and water vapor pressure axes (T–p_H2O map) was constructed.

2.5 Nitrogen gas adsorption measurements (N₂ adsorption)

The specific surface areas of the samples were evaluated by N₂ adsorption measurements at the liquid nitrogen temperature (77 K) using a BEL JAPAN BELSORP-max. Y₂(SO₄)₃·8H₂O (5.758 g) and rhombohedral Y₂(SO₄)₃ (1.321 g), which was prepared by heating Y₂(SO₄)₃·8H₂O at 200 °C for 1 hour in air, were placed in a Pyrex glass tube and subjected to a vacuum heating pretreatment. Afterward, N₂ adsorption measurements were conducted.

2.6 Optical microscope and TEM observations

Change in the morphology of the particles during the dehydration process of Y₂(SO₄)₃·8H₂O to rhombohedral Y₂(SO₄)₃ was analyzed by optical microscopy using a Nikon L150 L-150II-TI-DIC-A. Y₂(SO₄)₃·8H₂O was observed by the optical microscope as it is. Rhombohedral Y₂(SO₄)₃ made by heating Y₂(SO₄)₃·8H₂O at 270 °C for 2 hours in air and was observed by the optical microscope.

The microstructure inside the rhombohedral Y₂(SO₄)₃ particle was observed by TEM using a JEOL JEM-2100F. The rhombohedral Y₂(SO₄)₃ specimen for the TEM observation was cut out from the particle by a focused ion beam (FIB) using a JEOL JIB-4600F.

3. Results

3.1 Hydration/dehydration reaction behaviors of rhombohedral Y₂(SO₄)₃

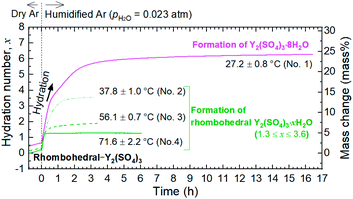
Fig. 1 shows a TG curve of rhombohedral Y₂(SO₄)₃ upon cooling/heating in humidified argon. Rhombohedral Y₂(SO₄)₃ can hydrate/dehydrate below 130 °C with relatively small thermal hysteresis (below 50 °C). The change in the hydration number x is greater than 1 and the total mass change in the hydration water content is larger than 10 mass% anhydrous basis. This value is larger than that of La₂(SO₄)₃ (3 mass%) and CaSO₄ (6 mass%) and a higher heat storage capacity is expected. Therefore, it may be a suitable material for the temperature range.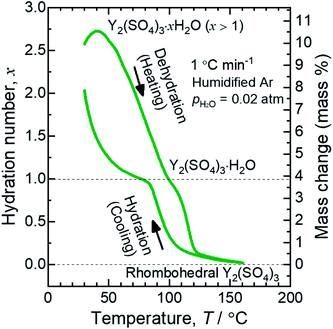

Fig. 1 TG curve of rhombohedral Y₂(SO₄)₃ undergoing hydration/dehydration reactions upon cooling/heating. Vertical axis in right side shows the mass changes of the sample. Vertical axis in left side shows apparent hydration number x calculated from the mass change. (Note: This data was presented at IMPRES2019.²⁴)

The TG curve (Fig. 1) suggests that the dehydration/hydration reactions proceed via two reaction steps. The temperature ranges of these two reaction steps are overlapping, preventing them from being clearly distinguished. Between 80–130 °C, apparent hydration number x varies steeply from 0 to approximately 1 (“high-temperature dehydration/hydration reaction”). Below 80 °C, Y₂(SO₄)₃·H₂O forms a hydrate with a larger hydration number in the cooling process. The dehydration/hydration reaction proceeds at 30–100 °C (“low-temperature dehydration/hydration reaction”). Both the high-temperature reaction and the low-temperature reaction may be useful for TCHS system. On the other hand, the phase changes in each reaction step are not established. Rosso et al. already reported the relationship between the reaction temperatures and formed hydrate phases of Y₂(SO₄)₃. Y₂(SO₄)₃·4H₂O is generated as an intermediate phase in the dehydration process of Y₂(SO₄)₃·8H₂O to Y₂(SO₄)₃.²¹ In contrast, our TG curve (Fig. 1) of rhombohedral Y₂(SO₄)₃ suggest another hydrate phase Y₂(SO₄)₃·H₂O. Here, we further investigate in detail the high-temperature and the low-temperature dehydration/hydration reactions.

3.1.1 High-temperature dehydration/hydration reaction. The crystal structure changes from Y₂(SO₄)₃·xH₂O to rhombohedral Y₂(SO₄)₃ during the dehydration reaction were investigated by high-temperature XRD. Fig. 2 shows XRD patterns during dehydration upon heating from 50 °C to 150 °C under humidified oxygen (p_H2O = 0.03 atm) and the reported diffraction peak positions of rhombohedral Y₂(SO₄)₃ (PDF#00-042-0236). Based on TG curves (Fig. 1), the XRD patterns below 110 °C (50, 70, and 90 °C) represent Y₂(SO₄)₃·xH₂O (x ≥ 1, depending on temperature), while those at higher temperatures (130 and 150 °C) represent rhombohedral Y₂(SO₄)₃. The marks shown above each XRD pattern except one at 110 °C represent the simulated XRD peaks based on the crystal structure of rhombohedral Y₂(SO₄)₃ with modified lattice parameters (a axial length, α angle) derived by Rietveld refinement. As can be seen in Fig. 2, the simulated and measured XRD peaks agree well at every temperature. Since the XRD patterns at each temperature are interpreted as rhombohedral Y₂(SO₄)₃ structure with the changed lattice parameters, the hydration reaction of rhombohedral Y₂(SO₄)₃ should proceed by water insertion into the host lattice. In particular, the overlapping patterns of the Y₂(SO₄)₃·xH₂O and rhombohedral Y₂(SO₄)₃ observed only at 110 °C, represented by the co-existing of “peak a” and “peak b” derived from the hydrate and anhydrate phases respectively. This should account for the steep high-temperature dehydration reaction of Y₂(SO₄)₃·xH₂O to rhombohedral Y₂(SO₄)₃.

Fig. 2 High-temperature XRD patterns collected during the dehydration reaction of Y₂(SO₄)₃·xH₂O to rhombohedral Y₂(SO₄)₃ in the heating process under humidified oxygen (p_H2O = 0.03 atm). Topmost chart shows the reported XRD pattern of rhombohedral Y₂(SO₄)₃, which is cited from ICDD (PDF#00-042-0236). The other part shows the measured XRD patterns and the simulated XRD peaks at each temperature. Marks shown above XRD patterns denote simulated XRD peaks obtained by Rietveld refinement using rhombohedral Y₂(SO₄)₃ (PDF#00-042-0236) as the initial crystal structure. The diffraction angles of simulated XRD peaks are determined by the results of lattice parameter refinements shown on the right side of the figure below each measurement temperature. Note that the intensities of simulated XRD peaks are assumed to be the same as the reported pattern (PDF#00-042-0236). Peak a and peak b in the XRD pattern at 110 °C, indicated by black arrows, are attributed to Y₂(SO₄)₃·xH₂O and rhombohedral Y₂(SO₄)₃ respectively. Two weak peaks, indicated as “orthorhombic”, in XRD pattern at 150 °C represent the slight formation of orthorhombic Y₂(SO₄)₃. The peaks are identified by the reported pattern of orthorhombic Y₂(SO₄)₃ (ICDD, PDF#04-009-9561).

Hereinafter we refer to the low-temperature hydrate phase below 110 °C as “rhombohedral Y₂(SO₄)₃·xH₂O (x ≥ 1)” and the reaction formula of the high-temperature reaction is written as follows:

Rhombohedral Y₂(SO₄)₃ (s) + H₂O (g) ⇄ Rhombohedral Y₂(SO₄)₃·H₂O (s)

At the lower temperatures (between 50–90 °C), the XRD patterns do not exhibit marked changes, but the hydration number x changes with temperature (see Fig. 1), suggesting that rhombohedral Y₂(SO₄)₃·xH₂O (x ≥ 1) has a nonstoichiometric hydration number.

3.1.2 Low-temperature dehydration/hydration reaction. To elucidate the phase changes and the reaction behaviors in the low-temperature hydration reaction, we conducted isothermal TG measurements and isothermal hydration treatments (IH). Table 1 shows the hydration conditions, formed phases, and the largest hydration numbers reached in each isothermal TG measurement and isothermal hydration treatment (IH No. 1–14). Fig. 3 shows the isothermal TG curves obtained by the above measurements. Fig. 4 and 5 show the XRD patterns of the samples after the isothermal TG measurements and isothermal hydration treatments. The results in Fig. 3, 4 and 5 are summarized in Table 1.

Table 1 Summary of the results of the isothermal TG measurements and the isothermal hydration (IH) treatments

Expt. #	Temp. (°C)	pH2O (atm)	Time (h)	x^b	Detected hydrated phases^c
					Y2(SO4)3·8H2O	Y2(SO4)3·3H2O	Rhombo-hedral^d	Unknown A	Unknown B
a “Time” for TG measurements represents the time required for a 90% mass increase relative to the final achieved mass at the end of the measurement.b x: hydration number.c Detected hydrated phases: hydrated phases detected by XRD measurements in the samples after the isothermal TG measurements and the isothermal hydration treatments (No. 1–14). “Strong” and “weak” represent the relative intensity of the XRD peaks derived from each phase. The phase with “strong” corresponds to the main phase formed in the hydration treatments (TG 1–4, IH 1–14) whereas the phase with “weak” corresponds to the secondary phases.d Rhombohedral: Rhombohedral Y2(SO4)3·xH2O
TG 1	27.2	0.023	3^a	6.3	Strong	—	Weak	—	—
TG 2	37.8	0.023	1^a	3.6	Weak	—	Strong	—	—
TG 3	56.1	0.023	1^a	1.9	Not measured by XRD
TG 4	71.6	0.023	0.2^a	1.3	Not measured by XRD
IH 1	38	0.043	3	—	Weak	—	Strong	—	—
IH 2	37	0.030	3	—	—	—	Strong	—	—
IH 3	55	0.13	3	—	Strong	Weak	—	—	—
IH 4	56	0.10	4	—	Strong	Weak	—	—	—
IH 5	55	0.088	3	—	—	—	Strong	—	—
IH 6	55	0.079	3	—	—	—	Strong	—	—
IH 7	69	0.24	3	—	Weak	Weak	—	Strong	—
IH 8	69	0.14	3	—	—	—	Strong	—	Weak
IH 9	79	0.40	4	—	Weak	Weak	—	Strong	—
IH 10	79	0.36	3	—	—	Strong	—	Weak	—
IH 11	79	0.32	3	—	—	Strong	—	—	—
IH 12	78	0.18	3	—	—	Weak	Strong	—	Weak
IH 13	78	0.14	3	—	—	—	Strong	—	Weak
IH 14	84	0.44	3	—	—	Strong	—	Weak	—

---

Fig. 3 TG curves of rhombohedral Y₂(SO₄)₃ of the isothermal hydration reaction at four different temperatures: 27.2 °C (No. 1), 37.8 °C (No. 2), 56.1 °C (No. 3), and 71.6 °C (No. 4). Temperature during the measurements fluctuated up to 2.2 °C. For these measurements, Y₂(SO₄)₃·8H₂O was used as the starting material. It was dehydrated to rhombohedral Y₂(SO₄)₃ at 320 °C in TG under dry argon. Then it was cooled to a predetermined temperature. The sample mass of rhombohedral Y₂(SO₄)₃ at around 320 °C, used for the basis of mass change, are as follows: 14.17 mg (No. 1), 14.34 mg (No. 2), 13.75 mg (No. 3), 13.54 mg (No. 4). While maintaining a constant temperature, the isothermal hydration reaction started by switching the flowing gas from dry argon to humidified argon (p_H2O = 0.023 atm) to examine the hydration process. Horizontal axis shows the elapsed time since the initiation of the hydration reaction by switching the flowing gas from dry argon to humidified argon.

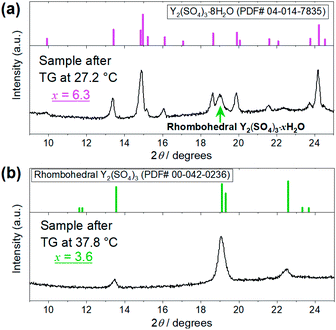Fig. 4 XRD patterns of the Y₂(SO₄)₃·nH₂O samples after the TG measurements at (a) 27.2 °C and (b) 37.8 °C shown in Fig. 3. (a) Top figure represents the reference pattern of Y₂(SO₄)₃·8H₂O (ICDD (PDF#04-014-7835)). In the bottom figure, there is an XRD peak attributed to the residual rhombohedral Y₂(SO₄)₃·xH₂O around 19°. (b) Top figure represents the reference pattern of rhombohedral Y₂(SO₄)₃ (ICDD (PDF#00-042-0236)).

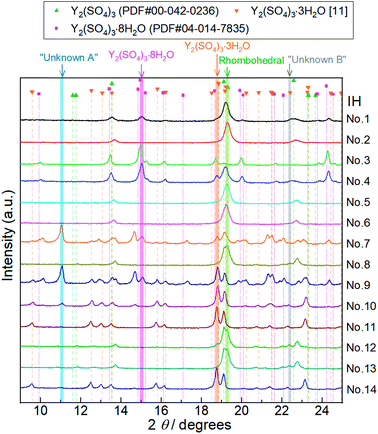Fig. 5 XRD patterns of Y₂(SO₄)₃ hydrate samples after 14 batches of isothermal hydration treatments (IH No. 1–14). Characteristic diffraction angles where distinctive peaks of Y₂(SO₄)₃·8H₂O, Y₂(SO₄)₃·3H₂O,²⁵ rhombohedral Y₂(SO₄)₃·xH₂O (Rhombohedral), Unknown A, and Unknown B exist are highlighted by pink, orange, green, blue, and gray, respectively. Peaks at 11.1° highlighted by a blue belt (No. 7, 9, 10, and 14) do not match any of the reported reference pattern peaks. These peaks are attributed to an unknown hydrated phase Unknown A. Similarly, we assumed that the peak at 22.4° highlighted by gray (No. 8, 12, and 13) is attributed to Unknown B. Doublet peaks around 19° are also attributed to Unknown B.

Depending on the hydration conditions, one or more of three known phases Y₂(SO₄)₃·8H₂O (monoclinic), Y₂(SO₄)₃·3H₂O (orthorhombic),^25,¶ and rhombohedral Y₂(SO₄)₃·xH₂O as well as two unknown phases (“Unknown A” and “Unknown B”) are present. Based on the isothermal TG results in Fig. 3, rhombohedral Y₂(SO₄)₃·H₂O, which is formed by the high-temperature hydration reaction, further is hydrated to rhombohedral Y₂(SO₄)₃·xH₂O (x > 1) and becomes Y₂(SO₄)₃·8H₂O (monoclinic) at lower temperatures. Isothermal hydration treatments under relatively high p_H2O (>0.08 atm) reveal that another intermediate hydrate Y₂(SO₄)₃·3H₂O appears at intermediate temperature.

The isothermal TG measurements indicate that rhombohedral Y₂(SO₄)₃·xH₂O has a nonstoichiometric hydration number x (>1). Fig. 3 shows the isothermal TG curves (TG No. 1–4) in the hydration reaction of rhombohedral Y₂(SO₄)₃ at a constant temperature of 27.2 (No. 1), 37.8 (No. 2), 56.1 (No. 3), and 71.6 °C (No. 4) under 0.023 atm of p_H2O. The apparent increase in the hydration number x becomes larger as the holding temperature is lowered: x = 1.3 (at 71.6 °C), 1.9 (at 56.1 °C), 3.6 (at 37.8 °C), and 6.3 (at 27.2 °C). Fig. 4(a) and (b) show the XRD patterns of the samples after the isothermal TG measurements at 27.2 °C and 37.8 °C. The pattern of the 6.3 hydrate-equivalent sample confirms the partial formation of Y₂(SO₄)₃·8H₂O (monoclinic), while the pattern of the 3.6 hydrate-equivalent sample indicates a single-phasic pattern quite similar to that of rhombohedral Y₂(SO₄)₃·xH₂O shown in Fig. 2. Therefore, rhombohedral Y₂(SO₄)₃·xH₂O may have a nonstoichiometric hydration number x and accommodate water molecules form x = 1 to at least x = 3.6. Such non-stoichiometry of hydrates has also been reported for MgSO₄ – H₂O system.⁴

In the 6.3 hydrate-equivalent sample, the rhombohedral Y₂(SO₄)₃·xH₂O phase still remains even after the isothermal TG curve (No. 1) reaches a plateau. This suggests that the hydration reaction of rhombohedral Y₂(SO₄)₃·xH₂O to Y₂(SO₄)₃·8H₂O was significantly slowed down in the middle of the reaction but the cause is unclear at this time. Based on Gibbs' phase rule, the equilibrium solid phase in the hydration reaction should be a single-phase. Thus Y₂(SO₄)₃·8H₂O is regarded as the equilibrium phase in the conditions (27.2 °C, p_H2O = 0.023 atm).||

According to the isothermal TG curves, the hydration reactions are almost complete in 3 hours. Therefore, it is reasonable that the equilibrium phases are contained in the detected phases in each batch (No. 1–14) and we can assume that the phase with the largest hydration number is the equilibrium hydrate for each condition. Based on this assumption, we constructed the phase stability diagram of Y₂(SO₄)₃ hydrates with temperature and water vapor pressure (T–p_H2O map) shown in Fig. 6. Only Y₂(SO₄)₃·8H₂O (monoclinic), Y₂(SO₄)₃·3H₂O (orthorhombic), and rhombohedral Y₂(SO₄)₃·xH₂O are considered.

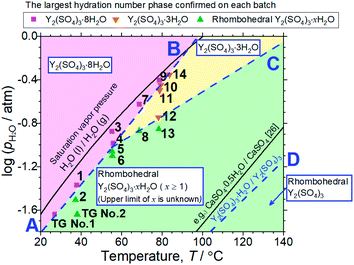Fig. 6 T–p_H2O map derived from 14 batches of hydration treatments that expose rhombohedral Y₂(SO₄)₃ under various temperatures and p_H2O for 3 hours. Here, only batches No. 4 and 9 are held for 4 hours. Additionally, the results of the isothermal TG measurements (Fig. 3) and the XRD (Fig. 4) are also represented by “TG No. 1” and “TG No. 2”. Pink squares represent batches where Y₂(SO₄)₃·8H₂O is formed. Orange inverted triangles represent batches where Y₂(SO₄)₃·3H₂O is formed but Y₂(SO₄)₃·8H₂O is not. Green triangles represent batches where neither Y₂(SO₄)₃·3H₂O and Y₂(SO₄)₃·8H₂O are formed. Two-phase equilibria are represented by broken lines. Broken lines A and B show the minimum p_H2O and maximum temperature required to form Y₂(SO₄)₃·8H₂O. Broken line C also shows those required to form Y₂(SO₄)₃·3H₂O. Broken line D represents the equilibrium between rhombohedral Y₂(SO₄)₃ and rhombohedral Y₂(SO₄)₃·H₂O. It is drawn using the estimated enthalpy and entropy changes of the dehydration/hydration reaction, determined by TG measurements under four different p_H2O. See ESI-2† for the TG curves. Temperature dependences of the saturation vapor pressure of liquid water and the equilibrium between CaSO₄ and CaSO₄·0.5H₂O are also shown.²⁶

Both Unknown A and Unknown B are not considered in constructing the T–p_H2O map for the following reasons. Unknown A and Unknown B are some hydrate phases of Y₂(SO₄)₃. Based on the detected conditions for them, the estimated hydration number of Unknown A is between 3 to 8 and that of Unknown B is between 1 to 3. Unknown A and Unknown B might have stable T–p_H2O regions near the broken lines B and C respectively but the regions should not be wide because they are always accompanied by rhombohedral Y₂(SO₄)₃·xH₂O, Y₂(SO₄)₃·3H₂O, or Y₂(SO₄)₃·8H₂O (see Table 1). As Unknown A and Unknown B are intermediate hydrate phases between the considered phases, even though they are omitted in Fig. 6, it should be sufficient to know the outline of the relationship between the hydration conditions and hydration number changes.

3.2 Microstructures of rhombohedral Y₂(SO₄)₃

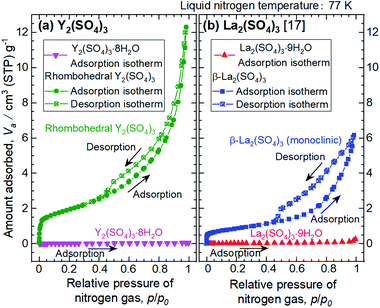
The microstructures of rhombohedral Y₂(SO₄)₃ obtained by dehydration of Y₂(SO₄)₃·8H₂O were investigated. Fig. 7(a) shows the N₂ adsorption isotherms of Y₂(SO₄)₃·8H₂O and rhombohedral Y₂(SO₄)₃. The specific surface area of rhombohedral Y₂(SO₄)₃ by the BET method (7 m² g⁻¹) is more than a hundredfold larger than that of the Y₂(SO₄)₃·8H₂O (0.05 m² g⁻¹). ESI-3† shows the BET plots. Fig. 8 shows photographs of (a) Y₂(SO₄)₃·8H₂O and (b) rhombohedral Y₂(SO₄)₃·xH₂O particles observed by optical microscopy. Note that the hydration number x of the rhombohedral phase was not known unclear accurately because rhombohedral Y₂(SO₄)₃ hydrates to some extent in air. Y₂(SO₄)₃·8H₂O particles show facet planes and high transparency, and they are likely a-few-hundreds-μm-large single crystals. On the other hand, rhombohedral Y₂(SO₄)₃·xH₂O particles are less transparent representing the polycrystalline nature. Correspondingly, a dark-field TEM image of rhombohedral Y₂(SO₄)₃ in Fig. 9 reveals crevices and voids at a-few-micrometer intervals.** A similar microstructure formation is observed in the case of dehydration of La₂(SO₄)₃·9H₂O to β-La₂(SO₄)₃ (Fig. 7(b)), which is known to improve the kinetics of hydration/dehydration reaction of β-La₂(SO₄)₃.¹⁷ The microstructure of rhombohedral Y₂(SO₄)₃ is also expected to promote the hydration/dehydration reaction rates by extending the surface area and shortening the diffusion length of water in the crystals although it was not confirmed yet.

Fig. 7 Adsorption/desorption isotherms obtained by N₂ adsorption measurements on (a) Y₂(SO₄)₃ and (b) La₂(SO₄)₃ for comparison. Pink inverted triangles show the isotherms of Y₂(SO₄)₃·8H₂O. Green circles denote the isotherms of rhombohedral Y₂(SO₄)₃ prepared by heating Y₂(SO₄)₃·8H₂O at 200 °C for 1 hour in air. Both samples are measured after a vacuum pretreatment for 1000 minutes at room temperature. Phase of both samples unchanged after N₂ adsorption measurements, which is confirmed by XRD. Vertical axis represents V_a, which means the volume of adsorbed nitrogen gas under standard temperature and pressure (STP). Here, the temperature is 273.15 K and the gas pressure is 101.325 kPa. Horizontal axis shows the relative pressure p/p₀ where p is the equilibrium pressure and p₀ is the saturation nitrogen gas pressure over liquid nitrogen at 77 K.

Fig. 8 Optical microscope images of (a) Y₂(SO₄)₃·8H₂O and (b) rhombohedral Y₂(SO₄)₃·xH₂O particles. Rhombohedral Y₂(SO₄)₃ made from Y₂(SO₄)₃·8H₂O by heating at 270 °C for 2 hour in air. Both particles look yellowish due to the light source of the optical microscope. Actually, Y₂(SO₄)₃·8H₂O is colorless and rhombohedral Y₂(SO₄)₃ is white under white light.

Fig. 9 Dark-field TEM image of the rhombohedral Y₂(SO₄)₃ specimen cut out from the rhombohedral Y₂(SO₄)₃ particle by FIB processing. Rhombohedral Y₂(SO₄)₃ made from Y₂(SO₄)₃·8H₂O by heating at 200 °C for 1 hour in air. Vertical black few-hundred-nm-thick layer at the right edge of the sample indicated by the red arrow is deposited carbon for FIB processing following the same procedure used in ref. 17.

4. Discussion

4.1 Relationships between water insertion mechanisms and reaction temperature ranges: comparison of rhombohedral Y₂(SO₄)₃ and β-La₂(SO₄)₃

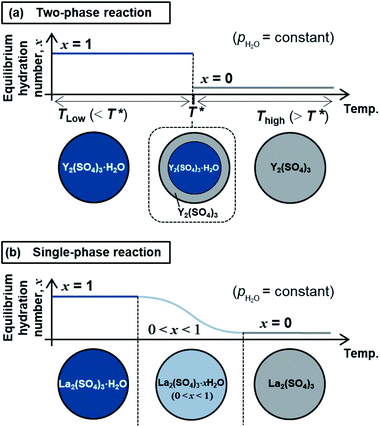
The high-temperature hydration reaction of rhombohedral Y₂(SO₄)₃·xH₂O (x = 0 or ∼1) likely proceeds by water insertion into the crystal lattice (see Section 3.1.1). This reaction is similar to the hydration reaction of β-La₂(SO₄)₃·xH₂O (0 ≤ x ≤ 1) (monoclinic).¹⁵ However, their water insertion mechanisms differ. Regarding β-La₂(SO₄)₃·xH₂O, the hydration number x changes continuously with maintaining a single-phase nature during the dehydration/hydration reactions. In contrast, the high-temperature hydration reaction of rhombohedral Y₂(SO₄)₃ is a “two-phase reaction” because two different phases (rhombohedral Y₂(SO₄)₃ and rhombohedral Y₂(SO₄)₃·H₂O) co-exist during the dehydration at 110 °C (see Section 3.1.1 and Fig. 2). Fig. 10 schematically depicts the dehydration processes of (a) the two-phase reaction and (b) the “single-phase reaction”. The two-phase reaction proceeds as the ratio of hydrated and dehydrated phases changes, while the single-phase reaction proceeds as the hydration number of the single solid phase continuously decreases. A two-phase reaction proceeds at a single equilibrium temperature in principle. Thus, the two-phase reaction with a sufficiently fast reaction rate can complete reversible reactions in a narrow temperature range (e.g., rhombohedral Y₂(SO₄)₃·xH₂O (x = 0 ⇄ ∼1): 80–130 °C at a rate of 1 °C min⁻¹). On the other hand, a single-phase reaction advances with changing the hydration number and the equilibrium temperature continuously in principle. Even if the reaction rate is fast enough, the reaction temperature range broadens (e.g., β-La₂(SO₄)₃·xH₂O: 80–250 °C at a rate of 1 °C min⁻¹ (ref. 15)). Therefore, the two-phase reaction with a sufficiently fast reaction rate is preferred for the TCHS system as the required temperature range for reaction completion narrows.

Fig. 10 Schematic diagrams of the dehydration processes for (a) the two-phase reaction of rhombohedral Y₂(SO₄)₃ and (b) the single-phase reaction of β-La₂(SO₄)₃. (a) Top figure is the schematic graph showing the change of equilibrium hydration number x with temperature increase. Here, T* represents the equilibrium temperature of the two-phase reaction between rhombohedral Y₂(SO₄)₃ and rhombohedral Y₂(SO₄)₃·H₂O. The schematic diagram under the graph shows the schematic of hydration number distribution of rhombohedral Y₂(SO₄)₃·H₂O spherical particle during heating. When the temperature is below T*, the equilibrium phase is rhombohedral Y₂(SO₄)₃·H₂O. At the equilibrium temperature T*, both phases are co-existing until the dehydration reaction finishes. Then rhombohedral Y₂(SO₄)₃ is the equilibrium phase when the temperature is upon T*. (b) The schematic graph showing the continuous change of equilibrium hydration number of β-La₂(SO₄)₃·xH₂O with temperature increase. The schematic diagram under the graph shows the schematic of hydration number distribution of β-La₂(SO₄)₃·xH₂O spherical particle during the dehydration reaction based on the single-phase reaction.

4.2 Applicability of rhombohedral Y₂(SO₄)₃ as a TCHS material

Based on the T–p_H2O map (Fig. 6), we consider an application of several reactions of rhombohedral Y₂(SO₄)₃ to chemical heat pumps to upgrade thermal energy. The application employs an apparatus consisting of a reactor containing rhombohedral Y₂(SO₄)₃ and an evaporator containing water. In the heat releasing step, saturated water vapor is transported from the evaporator to the reactor and rhombohedral Y₂(SO₄)₃ is hydrated. Here, the temperature lift (the temperature difference between the evaporator and the reactor) should ideally be equal to the difference between the dew point of water and the equilibrium temperature of the hydration reaction at a constant p_H2O. The equilibrium temperatures, the temperature lifts attained by reactions A, B, C, and D shown in Fig. 6 are represented by the temperature differences between the saturation vapor pressure line and the broken lines A, B, C, and D at a constant p_H2O (Fig. 6). As can be seen, reaction D (high-temperature reaction: Y₂(SO₄)₃/Y₂(SO₄)₃·H₂O) works similarly to the hydration reaction of CaSO₄ in terms of the temperature lift. Reaction C (Y₂(SO₄)₃·xH₂O/Y₂(SO₄)₃·3H₂O) may also be utilized under high p_H2O (> ∼0.08 atm). On the other hand, using the two-step reaction of C and D is disadvantageous in that they output heat at different temperatures which leads to a large temperature drop against stored heat. The reactions A (Y₂(SO₄)₃·xH₂O/Y₂(SO₄)₃·8H₂O) and B (Y₂(SO₄)₃·3H₂O/Y₂(SO₄)₃·8H₂O) may not be suitable for practical applications due to the small temperature lift (approximately 10 °C).

We also discuss in terms of heat storage density. The standard enthalpy change of the high-temperature dehydration reaction of rhombohedral Y₂(SO₄)₃·H₂O (reaction D) was estimated by a van't Hoff plot. The relationship between p_H2O and the equilibrium temperature of the reaction was assessed by TG measurements on rhombohedral Y₂(SO₄)₃·H₂O under four different p_H2O (ESI-2†). Fig. 11 shows the van't Hoff plot constructed from the equilibrium temperatures and p_H2O. From the slope of the approximated straight line, the estimated standard enthalpy change ΔH° of rhombohedral Y₂(SO₄)₃·H₂O is 46 kJ (mol-H₂O)⁻¹ or 99 kJ (kg-hydrate)⁻¹. The small gravimetric standard enthalpy change is attributed to the small hydration water content, i.e. the mass change with reaction D, equal to 3.72 mass%.

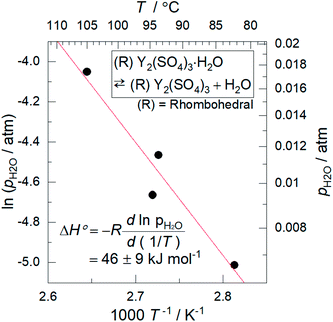Fig. 11 Van't Hoff plot for the high-temperature reaction of rhombohedral Y₂(SO₄)₃·H₂O. The equilibrium temperatures T are the estimated values from the TG measurements under four different p_H2O (ESI-2†). Because rhombohedral Y₂(SO₄)₃·H₂O dehydrates/hydrates via a two-phase reaction, the equilibrium temperature of the reaction (high-temperature reaction) should be a single temperature at each p_H2O.

However, if the additional hydration reaction C with 10.3 mass% of mass change is utilized, a larger heat storage capacity is expected although the ΔH°/kJ (kg-hydrate)⁻¹ of Y₂(SO₄)₃·3H₂O is not measured. Note that, among the dehydration/hydration reaction systems having similar equilibrium temperatures, the magnitude of ΔH°/kJ (kg-hydrate)⁻¹ dominantly depends on the mass change. This is because the ΔH°/kJ (mol-H₂O)⁻¹ of dehydration reaction is approximately proportional to the equilibrium temperature.²⁷ See (ESI-4)† for the relationship between the ΔH° and the equilibrium temperature. Thus, the mass change with the dehydration/hydration reaction is an indicator to simply evaluate the magnitude of the ΔH°/kJ (kg-hydrate)⁻¹.

Here, the gravimetric energy densities of Y₂(SO₄)₃·3H₂O and Y₂(SO₄)₃·H₂O are compared with other materials. The ΔH° or mass change of Y₂(SO₄)₃·3H₂O (10.4 mass%) and Y₂(SO₄)₃·H₂O (99 kJ (kg-hydrate)⁻¹, 3.72 mass%) is significantly lower than other salt hydrates with larger hydration numbers or with lower mass, for example, MgSO₄·6H₂O (1395 kJ (kg-hydrate)⁻¹, 47.3 mass%),⁵ CaCl₂·6H₂O (1649 kJ (kg-hydrate)⁻¹, 49.3 mass%),²⁸ Na₂S·5H₂O (1784 kJ (kg-hydrate)⁻¹, 53.6 mass%),¹¹ and LiOH·H₂O (1440 kJ (kg-hydrate)⁻¹, 42.9 mass%).²⁰ Compared with these salt hydrates, an advantage of Y₂(SO₄)₃ system is the ease of handling since neither of aggregation due to the melting or deliquescence or skin formation covering the bulk particles has been confirmed in the hydration/dehydration reaction process. Therefore, Y₂(SO₄)₃ system may be available for TCHS usage without developing composite materials with porous matrix and, in this respect, similar to CaSO₄·0.5H₂O and β-La₂(SO₄)₃·H₂O. The values of ΔH° and the mass change of Y₂(SO₄)₃·3H₂O or Y₂(SO₄)₃·H₂O are comparable to those of CaSO₄·0.5H₂O (240 kJ (kg-hydrate)⁻¹ (ref. 26) and 6.21 mass%) and those of β-La₂(SO₄)₃·H₂O (156 kJ (kg-hydrate)⁻¹ (ref. 15) and 3.08 mass%).

For TCHS application, heat output rate is also important but the performance of rhombohedral Y₂(SO₄)₃ has never been evaluated yet. Regarding the hydration reaction rate shown in Fig. 3, the hydration reaction with hydration number change x of 1–3 completed within tens of minutes and that with x = ∼6 completed within 3 hours. These hydration reaction rates are comparable to those reported in the hydration of other salts, i.e. MgSO₄,⁵ Na₂S,¹¹ β-La₂(SO₄)₃,¹⁷ and CaCl₂.²⁸

5. Conclusion

We examine the hydration/dehydration of rhombohedral Y₂(SO₄)₃ and their potential as a TCHS material by cyclic TG, high-temperature XRD, isothermal TG, isothermal hydration treatments, nitrogen gas adsorption, optical microscope observations, and TEM observations. TG measurements revealed that rhombohedral Y₂(SO₄)₃ can hydrate/dehydrate reversibly below 130 °C with relatively small thermal hysteresis (less than 50 °C) and large change in hydration water content (above 10 mass%). Rhombohedral Y₂(SO₄)₃ was found to be a favorable material in terms of the reaction temperature and the reaction behavior. The hydration reaction of rhombohedral Y₂(SO₄)₃ proceeds via at least two steps: the high-temperature reaction at 80–130 °C and the low-temperature reaction at 30–100 °C in 0.02 atm of p_H2O. The high-temperature hydration reaction proceeds by water insertion into rhombohedral Y₂(SO₄)₃ to form rhombohedral Y₂(SO₄)₃·H₂O with only minor changes in the host crystal structure. In the low-temperature hydration reaction, rhombohedral Y₂(SO₄)₃·H₂O further hydrates to rhombohedral Y₂(SO₄)₃·xH₂O (x > 1) while maintaining the host structure. There is a possibility that rhombohedral Y₂(SO₄)₃·xH₂O has a nonstoichiometric hydration number x. At lower temperature (at most 27 °C in 0.02 atm of p_H2O), it finally hydrates to Y₂(SO₄)₃·8H₂O which has a different crystal structure. Furthermore, another intermediate hydrate Y₂(SO₄)₃·3H₂O is formed in the hydration reaction under relatively high p_H2O (>0.08 atm) and intermediate temperature.

Regarding the application of rhombohedral Y₂(SO₄)₃ to thermochemical heat pumps for energy upgrades, the hydration of rhombohedral Y₂(SO₄)₃ to rhombohedral Y₂(SO₄)₃·H₂O can be used in the same manner as an existing candidate material CaSO₄·0.5H₂O in terms of reaction temperature and p_H2O. However, the standard enthalpy change ΔH° of the dehydration of rhombohedral Y₂(SO₄)₃·H₂O (46 kJ mol⁻¹) is not sufficient. The hydration of rhombohedral Y₂(SO₄)₃·xH₂O to Y₂(SO₄)₃·3H₂O (hydration water content: 11.6 mass% anhydrous basis) or Y₂(SO₄)₃·8H₂O (hydration water content: 30.9 mass% anhydrous basis) enables a larger change in the hydration number and thereby heat storage density, which is characteristic of this reaction system. Concerning the magnitude of the temperature lift on the practical use, the hydration to form Y₂(SO₄)₃·3H₂O may be available but that to form Y₂(SO₄)₃·8H₂O is not suitable since the temperature lift is as small as approximately 10 °C.

Finally, microstructure formed during the dehydration reaction from Y₂(SO₄)₃·8H₂O to rhombohedral Y₂(SO₄)₃ was investigated. The estimated surface area of rhombohedral Y₂(SO₄)₃ is 7 m² g⁻¹ while that of the original Y₂(SO₄)₃·8H₂O is significantly smaller (0.05 m² g⁻¹). Correspondingly, rhombohedral Y₂(SO₄)₃ has a fine microstructure with crevices and voids at intervals of a-few-micrometers. Such a fine microstructure is formed by initial dehydration reaction from Y₂(SO₄)₃·8H₂O and expected to enhance the dehydration/hydration reaction rates. If the microstructure size can be further improved in the synthesis of rhombohedral Y₂(SO₄)₃, a much faster hydration rate is expected.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We are grateful to Kenji Kazumi for the FIB processing, TEM observations, and discussion. We would also like to thank Kazuaki Toyoura for valuable discussion. This work was supported by a JSPS Grant-in-Aid for Young Scientists (B) Grant Number 17K17821 and Grant-in-Aid for JSPS Fellows Grant Number 19J15085.

Notes and references

1. P. Pardo, A. Deydier, Z. Anxionnaz-Minvielle, S. Rougé, M. Cabassud and P. Cognet, Renewable Sustainable Energy Rev., 2014, 32, 591–610.
2. T. Yan, R. Z. Wang, T. X. Li, L. W. Wang and I. T. Fred, Renewable Sustainable Energy Rev., 2015, 43, 13–31.
3. L. André, S. Abanades and G. Flamant, Renewable Sustainable Energy Rev., 2016, 64, 703–715.
4. L. Okhrimenko, L. Favergeon, K. Johannes, F. Kuznik and M. Pijolat, Thermochim. Acta, 2017, 656, 135–143.
5. V. Essen, H. Zondag, J. Gores, L. Bleijendaal, M. Bakker, R. Schuitema, W. Helden, Z. He and C. Rindt, J. Sol. Energy Eng., 2009, 131, 041014.
6. S. Hongois, F. Kuznik, P. Stevens and J.-J. Roux, Sol. Energy Mater. Sol. Cells, 2011, 95, 1831–1837.
7. K. N'Tsoukpoe, H. Rammelberg, A. Lele, K. Korhammer, B. Watts, T. Schmidt and W. Ruck, Appl. Therm. Eng., 2015, 75, 513–531.
8. M. Kubota, S. Matsumoto, H. Matsuda, H. Huang, Z. He and X. Yang, Adv. Mater. Res., 2014, 953, 757–760.
9. S. Li, H. Huang, X. Yang, Y. Bai, J. Li, N. Kobayashi and M. Kubota, Appl. Therm. Eng., 2018, 128, 706–711.
10. M. Kubota, S. Matsumoto and H. Matsuda, Appl. Therm. Eng., 2019, 150, 858–863.
11. R. Boer, W. Haije and J. Veldhuis, Thermochim. Acta, 2003, 395, 3–19.
12. A. Jong, F. Trausel, C. Finck, L. Vliet and R. Cuypers, Energy Procedia, 2014, 48, 309–319.
13. J.-H. Lee, H. Ogura and S. Sato, Appl. Therm. Eng., 2014, 63, 192–199.
14. Y. Shiren, M. Masuzawa and N. Kobayashi, WASET. International Journal of Environmental, Chemical, Ecological, Geological and Geophysical Engineering, 2015, vol. 9, pp. 803–807.
15. N. Hatada, K. Shizume and T. Uda, Adv. Mater., 2017, 29, 1606569/1–1606569/6.
16. K. Toyoura, H. Tai, N. Hatada, K. Shizume and T. Uda, J. Mater. Chem. A, 2017, 5, 20188–20194.
17. K. Shizume, N. Hatada, K. Toyoura and T. Uda, J. Mater. Chem. A, 2018, 6, 24956–24964.
18. H. Voigtländer, B. Winkler, W. Depmeier, K. Knorr and L. Ehm, in Host–Guest Systems Based on Nanoporous Crystals, ed. F. Laeri, F. Schüth, U. Simon and M. Wark, John Wiley & Sons, New Jersey, 1st edn, 2006, ch. 3, pp. 280–305.
19. R. Perret, B. Rosso and J. Loriers, Bull. Soc. Chim. Fr., 1968, 7, 2698–2699.
20. M. Kubota, S. Matsumoto and H. Matsuda, Appl. Therm. Eng., 2019, 150, 858–863.
21. B. Rosso, R. Perret and J. Lories, C. R. Hebd. Seances Acad. Sci., 1968, 267, 379–382.
22. W. Wendlandt, J. Inorg. Nucl. Chem., 1958, 7, 51.
23. D. Bernhardt, I. Reilly and J. Mineral, Commodity Summaries 2019, Department of the Interior (DOI), U.S. Geological Survey (USGS), Reston, VA, USA, 2019.
24. K. Shizume, N. Hatada, K. Toyoura, H. Tai, S. Yasui and T. Uda, Presented in part at the IMPRES2019, Kanazawa, October, 2019.
25. S. Mills, V. Petrříčicek, A. R. Kampf, R. Herbst-Imer and M. Raudsepp, J. Solid State Chem., 2011, 184, 2322–2328.
26. S. Lee, H. Matsuda and M. Hasatani, Kagaku Kogaku Ronbunshu, 1986, 12, 75–82.
27. S. Kiyabu, J. Lowe, A. Ahmed and D. Siegel, Chem. Mater., 2018, 30, 2006–2017.
28. F. Trausel, A.-J. Jong and R. Cuypers, Energy Procedia, 2014, 48, 447–452.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ra02566f

‡ The major problems of these salt hydrates are described below. MgSO₄·nH₂O (n = 0–7): shape instability due to the melting of the salt which occurs during dehydration of MgSO₄·7H₂O to MgSO₄·6H₂O.⁵ In addition, the fine powder rapidly forms a skin of the hydrated salt on the surface when it reacts with humid air, which decreases the reaction rate.⁶ CaCl₂·nH₂O (n = 0–6): agglomeration of the salt due to partial melting of the salt during the dehydration or a partial formation of a solution of the salt attributed to the hygroscopicity during rehydration, which decreases the reaction rate.⁷ LiOH·H₂O: the low hydration reaction rate of pure LiOH which limits the performance of low-temperature TCHS systems.^9,10 Na₂S·5H₂O: generation of toxic by-product H₂S gas by contacting with water.¹² CaSO₄·0.5H₂O: degradation due to phase transformation from CaSO₄ (III) to the low-hydration-reactive phase CaSO₄ (II) during repetitive dehydration/hydration reaction.^13,14

§ CaSO₄·0.5H₂O is also known to dehydrate and rehydrate by deinsertion and insertion of H₂O guest molecules into the sulfate host lattice.¹⁸

¶ The crystal structure of Y₂(SO₄)₃·3H₂O is considered to be the same as that of Yb₂(SO₄)₃·3H₂O reported by Mills et al.²⁵ The XRD pattern of Y₂(SO₄)₃·3H₂O shown in Fig. 5 as orange inverted triangles was estimated by adjusting only the diffraction angles of XRD peaks of Yb₂(SO₄)₃·3H₂O while the peak intensities were left as is.

|| Focusing only on condensed phases in the Y₂(SO₄)₃–H₂O pseudo-binary system, the degree of freedom F is represented as follows: F = C − P + 2 = 4 − P, where C is the number of independent components and P is the number of condensed phases. In the case of the isothermal hydration reaction of Y₂(SO₄)₃, the temperature and the total pressure are fixed and the chemical potential of H₂O is determined by the water vapor pressure of gas phase equilibrated with the Y₂(SO₄)₃–H₂O system. Then the degree of freedom becomes F = 1 − P. Because the F should be larger than zero, the number of the solid phase should be 1 at most.

** We did not conduct TEM observations on Y₂(SO₄)₃·8H₂O due to the difficulty with sample preparation. The dehydration reaction of Y₂(SO₄)₃·8H₂O proceeded even under a vacuum at room temperature on FIB processing for sample preparation.

---