Open Access Article
Open Access ArticleEnergetics and optical properties of carbon impurities in rutile TiO2†
Supparat Charoenphona,
Adisak Boonchunab,
Daungruthai Jarukanonta,
Jiraroj T-Thienprasert ab and
Pakpoom Reunchan
ab and
Pakpoom Reunchan *ab
*ab
aDepartment of Physics, Faculty of Science, Kasetsart University, Bangkok 10900, Thailand. E-mail: pakpoom.r@ku.ac.th
bThailand Center of Excellence in Physics, Ministry of Higher Education, Science, Research and Innovation, 328 Si Ayutthaya Road, Bangkok 10400, Thailand
First published on 26th May 2020
Abstract
Titanium dioxide is one of the most promising materials for many applications such as photovoltaics and photocatalysis. Non-metal doping of TiO2 is widely used to improve the photoconversion efficiency by shifting the absorption edge from the UV to visible-light region. Here, we employ hybrid density-functional calculations to investigate the energetics and optical properties of carbon (C) impurities in rutile TiO2. The predominant configurations of the C impurities are identified through the calculated formation energies under O-poor and O-rich growth conditions. Under the O-poor condition, we find that C occupying the oxygen site (CO) is energetically favorable for Fermi-level values near the conduction band minimum (n-type TiO2), and acts as a double acceptor. Under the O-rich condition, the Ci–VTi complex is energetically favorable, and is exclusively stable in the neutral charge state. We also find that interstitial hydrogen (Hi) can bind to CO, forming a CO–Hi complex. Our results suggest that CO and CO–Hi are a cause of visible-light absorption under oxygen deficient growth conditions.
1 Introduction
TiO2 is a material of great interest in electronics and optoelectronics, especially in photocatalysis.1 It is also a promising material for photovoltaic solar cells, especially for dye-sensitized solar cells.2,3 TiO2 exists as three polymorphs: rutile, anatase, and brookite. Both rutile and anatase TiO2 have been extensively explored for photocatalytic applications and different photocatalytic activities have been reported for both polymorphs.4,5 Besides, TiO2 can be synthesized as coexisting polymorphs by various growth processes,6,7 yielding better photocatalytic performance than that of an individual polymorph. In general, rutile TiO2 has a large band gap of 3.0 eV (ref. 8 and 9) that can only be activated under UV light irradiation, a major drawback for photocatalysis applications. Therefore, it is of great interest to find ways to extend the absorption wavelength range of TiO2 into the visible region without decreasing the photocatalytic activity. Various experimental techniques including dye sensitization10,11 and transition metal doping12–14 enable photocatalysts to operate under visible light irradiation. Recently, it has been reported that doping TiO2 with non-metals such as N, S or C extends the absorption edge from the UV to visible region.15–17The intentional and controlled incorporation of C impurities into the TiO2 lattice is an efficient method to enhance visible light photocatalytic activity.18–26 Carbon-doped TiO2 has been prepared using different synthetic methods21,26 and the favorable configuration of carbon impurities in the TiO2 lattice has been interpreted differently. In experiments, C dopants were often assumed to incorporate either as C substitutional on an O site (CO)18–21 or as C occupying an interstitial site (Ci).22–25 In addition, the mechanism underlying visible-light absorption is still ambiguous.
First-principles calculations based on density-functional theory (DFT) have been established as an important tool for understanding and acquiring knowledge of the behavior of defects and impurities in materials. Valentin et al.27 performed DFT calculations within the generalized gradient approximation (GGA)28 to study various possible C doping species in both anatase and rutile TiO2. In rutile, they found that carbon atoms energetically prefer to occupy an interstitial site next to an oxygen vacancy, Ci–VO, under oxygen-poor conditions, whereas carbon atoms prefer to occupy the titanium site (CTi) under oxygen-rich conditions. Generally, standard DFT methods grossly underestimate band gaps. In their GGA calculations, the calculated band gap of rutile TiO2 was 1.81 eV,27 much lower than the experimental value, partly because of self-interaction errors in DFT.29,30
Most defects and impurities can introduce levels in the band gap, in which electrons can be exchanged with the Fermi-level. This causes impurities, including C in TiO2 occurring in multiple charge states. In their previous study, Valentin et al.27 considered only the neutral charge state for all carbon impurities. Moreover, their calculated band gap of rutile TiO2 was underestimated; this might lead to an incomplete conclusion.
In the present work, we investigate the energetics and optical properties of plausible C impurities in rutile TiO2 in their stable charge states, including CO, CTi, Ci, Ci–VO and Ci–VTi complexes, through DFT calculations within the Heyd–Scuseria–Ernzerhof (HSE) hybrid functional for exchange and correlation. The HSE hybrid functional has been proven to yield not only a better description of the band gap, but also accurate defect levels and formation energies.31,32 The energetically favorable configurations of carbon impurities for certain Fermi levels and growth conditions are determined based on formation energies. The optical transitions are estimated using configuration coordinate diagrams. We find that under the O-poor condition, CO is energetically favorable in n-type TiO2, where the Fermi-level position is near the conduction band. We find that the localized states above the valence band produced by CO give rise to visible-light absorption. In addition, the effect of H impurities, which are ubiquitous and can unintentionally be incorporated in the material synthesis process, is considered. Our calculations indicate that interstitial H attracts CO, forming a CO–Hi complex. This complex could also be a cause of the visible-light absorption, unlike NO–Hi, which eliminates the visible-light absorption effects of NO in TiO2.33
2 Computational method
Our DFT calculations were employed within the HSE hybrid-functional34 and the projector-augmented wave (PAW) method35 as implemented in the VASP code.36 We used a well-converged energy cut-off of 420 eV for the projector-augmented plane waves. In this study, Ti 3s23p64s23d2 states were treated as valence states. For the calculations of lattice parameters, band gaps, and formation enthalpies, we employed a 6-atom conventional unit cell with 5 × 5 × 7 Monkhorst–Pack (MP) meshes for the Brillouin zone integrations.In the HSE approach, the Coulombic potential in the exchange energy is divided into short-range and long-range parts with a screening length of 10 Å. In the short-range part, the non-local Hartree–Fock (HF) exchange is mixed with the Perdew, Burke and Ernzerhof (PBE) GGA exchange energy.28 The long-range part and the correlation potential are represented by the PBE functional. We used the standard HF mixing α = 0.25, which is suitable for satisfaction of the generalized Koopmans’ theorem37 in both anatase and rutile TiO2.38 Geometry relaxations were performed for the cell volume and shape, as well as for the atomic positions of the conventional cell until the residual force was less than 0.02 eV Å−1.
For the calculations of C impurities, we extended the conventional cell by 2 × 2 × 3 to produce a 72-atom supercell and introduced a defect in the supercell. For the Brillouin zone integrations of the supercell, the k-points were sampled at a non-Γ-centered MP 2 × 2 × 2 mesh in which the Fock-exchange part39 was reduced by a factor of 2. All atoms were allowed to relax with a fixed cell volume until the residual forces are less than 0.02 eV Å−1.
The likelihood of incorporating an impurity in TiO2 is determined by its formation energy, which depends on the O (![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) O), Ti (
O), Ti (![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) Ti) and C (
Ti) and C (![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) C) chemical potentials. For example, the formation energy of CO in charge state q is defined as
C) chemical potentials. For example, the formation energy of CO in charge state q is defined as
| Ef(CO) = Etot(CO) − Etot(TiO2) − μC + μO + q(εF + EV) + Ecor, | (1) |
![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) Ti + Etot[Tibulk]). These reference energies are given by our DFT calculations for the total energy of bulk Ti per formula unit (−9.46 eV) and half the total energy of an isolated O2 molecule (−8.55 eV).
Ti + Etot[Tibulk]). These reference energies are given by our DFT calculations for the total energy of bulk Ti per formula unit (−9.46 eV) and half the total energy of an isolated O2 molecule (−8.55 eV).
The final term, Ecor, is the image charge correction term, which corrects for the Madelung energy of the defect point charge in the uniform background. The Coulomb image-charge corrections can be written as
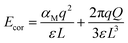 | (2) |
The chemical potentials ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) Ti and
Ti and ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) O are variables but must satisfy the stability condition
O are variables but must satisfy the stability condition ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) Ti +
Ti + ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) O = ΔHf(TiO2), where ΔHf(TiO2) is the formation enthalpy of TiO2. In principle,
O = ΔHf(TiO2), where ΔHf(TiO2) is the formation enthalpy of TiO2. In principle, ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) O can vary over a wide range from O-rich (
O can vary over a wide range from O-rich (![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) O = 0) to O-poor (
O = 0) to O-poor (![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) O = (ΔHf(TiO2) −
O = (ΔHf(TiO2) − ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) Ti)/2). At the O-rich limit, the chemical potential of Ti is given by
Ti)/2). At the O-rich limit, the chemical potential of Ti is given by ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) Ti = ΔHf(TiO2), while at the Ti-rich limit,
Ti = ΔHf(TiO2), while at the Ti-rich limit, ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) Ti is bound by the formation of Ti2O3, 2
Ti is bound by the formation of Ti2O3, 2![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) Ti + 3
Ti + 3![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) O < ΔHf(Ti2O3). The calculated ΔHf(TiO2) and ΔHf(Ti2O3) using the HSE approach are −9.93 eV and −15.94 eV, which are in good agreement with the experimental values of −9.78 eV42 and −15.74 eV,42 respectively.
O < ΔHf(Ti2O3). The calculated ΔHf(TiO2) and ΔHf(Ti2O3) using the HSE approach are −9.93 eV and −15.94 eV, which are in good agreement with the experimental values of −9.78 eV42 and −15.74 eV,42 respectively.
Since the Ti-to-O ratio is higher in Ti2O3 than in TiO2, we expect the growth of these alternate phases to be favorable under Ti-rich growth conditions. The stable thermodynamic condition of TiO2 is represented in the phase diagram illustrated in Fig. S1 (see ESI†). In this article, we present results of the formation energies for O-poor and O-rich conditions. Our analysis gives the chemical potential settings (![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) Ti,
Ti, ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) O) corresponding to Ti-rich (O-poor) and O-rich (Ti-poor) as (−2.10, −3.95) and (−9.93, 0) in eV, respectively. Under the O-rich growth condition,
O) corresponding to Ti-rich (O-poor) and O-rich (Ti-poor) as (−2.10, −3.95) and (−9.93, 0) in eV, respectively. Under the O-rich growth condition, ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) C is limited by the formation of the CO2 molecule, i.e.
C is limited by the formation of the CO2 molecule, i.e. ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) C = ΔHf(CO2) − 2
C = ΔHf(CO2) − 2![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) O, whereas under the O-poor (Ti-rich) growth condition,
O, whereas under the O-poor (Ti-rich) growth condition, ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) C is limited by the formation of TiC, i.e.
C is limited by the formation of TiC, i.e. ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) C = ΔHf(TiC) −
C = ΔHf(TiC) − ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) Ti.
Ti.
The thermodynamic transition levels are given by the Fermi energy at which the formation energies of the two charged states are equal:
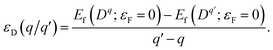 | (3) |
The thermodynamic transitions are represented by kinks in the plots of formation energy as a function of Fermi energy. Note that εF ranges over the band gap and is referenced to the VBM. Optical transitions were determined based on configuration coordinate diagrams following the standard procedure described in ref. 43.
3 Results
3.1 Fundamental properties of rutile TiO2
Rutile TiO2 can be described by a six-atom primitive cell with lattice parameters a and c, and an internal parameter u that defines the distance between Ti and O atoms in the plane perpendicular to the c direction, as shown in Fig. S2(a) in the ESI.† The lattice parameters calculated by HSE (using 25% HF exchange), band gap at Γ and formation enthalpy (ΔHf) are listed in Table 1. The calculated lattice parameters are in very good agreement with the experimental values. The calculated electronic band structure and the Brillouin zone are presented in Fig. S2 (see ESI†). Our calculated band gap is 3.34 eV, slightly higher than the experimental value of 3.03 eV.83.2 Model structure of carbon doping
In principle, there are three possible ways to include C atoms in the lattice. The first one is the substitution of an O by a C atom (CO); the second is the substitution of a Ti atom by a C atom (CTi). The third possibility is that a C atom is stabilized at an interstitial position (Ci). These three models of C impurities are shown in Fig. 1(a)–(c). We denote CO and CTi as on-site configurations since the C atoms remain at their respective lattice sites, constrained by the crystal symmetry.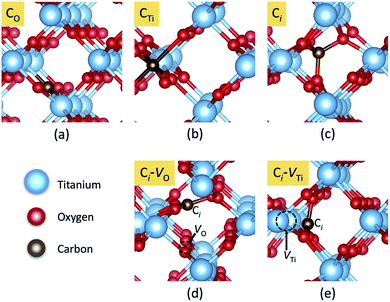 | ||
| Fig. 1 Local atomic structures of carbon impurities: (a) CO, (b) CTi, (c) Ci, (d) Ci–VO and (e) Ci–VTi in rutile TiO2. The red, blue, and brown spheres represent O, Ti, and C atoms, respectively. | ||
However, in the case of CO and CTi, the carbon atoms can significantly shift from the ideal lattice positions toward three nearby O atoms, stabilizing the low-symmetry (off-site) configurations. For CO, the off-site configuration can be represented as a complex between interstitial C and an oxygen vacancy (Ci–VO), while for CTi, the off-site configuration can be represented as interstitial C and a nearby titanium vacancy (Ci–VTi). The most energetically favorable low-symmetry (off-site) configurations of CO and CTi are shown in Fig. 1(d) and (e), respectively.
3.3 Carbon doped TiO2: formation energies
In our calculations, we vary the charge states of the defects to identify the most stable charge state. The formation energies of CO, CTi, Ci, Ci–VO and Ci–VTi as a function of the Fermi level are shown in Fig. 2. The vertical dashed line indicates the experimental band gap of 3.03 eV.8 Only the formation energy associated with the lowest-energy charge state of each defect is shown for the corresponding Fermi-level position.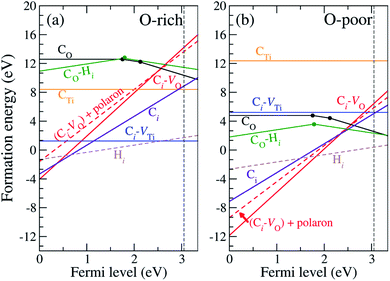 | ||
| Fig. 2 Defect formation energies as a function of Fermi energy under (a) O-rich and (b) O-poor conditions. The vertical dashed line indicates the experimental band gap.8 | ||
Since C has two fewer electrons than O, CO is likely to be negatively charged and acts as an acceptor. Fig. 2 shows that CO is stable in the neutral, − and 2− charge states with thermodynamic transition levels ε(0/−) and ε(−/2−) located at 1.77 and 2.12 eV above the VBM, indicating that CO is a deep acceptor with positive-U behavior. We find that CO is the prevalent defect under the O-poor limit for Fermi-level positions near the conduction band minimum (CBM). Deep transition levels of CO indicate that it induces impurity states in the band gap, which likely gives rise to optical transitions with lower energy than the band gap. The calculated density of states for CO is illustrated in Fig. S3 (see ESI†).
For Ci, we find that the C atom binds to four O atoms with an average C–O bond length of 1.40 Å. Since O has a much higher electronegativity than C, the C atom tends to donate its four valence electrons to the surrounding O atoms. Thus Ci is exclusively stable in the 4+ charge state, acting as a quadruple donor. Since the oxygen vacancy, VO, in rutile TiO2 is stable in the 2+ charge state44 and Ci is stable in the 4+ charge state, the Ci–VO complex is reasonably expected to occur in the 6+ charge state. Our calculations show that the Ci–VO complex is stable in the 6+ charge state and is prevalent under O-poor growth conditions for Fermi-level positions from 0 to 2.46 eV above the VBM. In addition, this complex can trap an additional electron in the form of a small polaron. The formation energy of (Ci–VO) + 1 polaron is included in Fig. 2, indicating that it becomes more stable than (Ci–VO) for Fermi-level positions higher than 2.46 eV. In Ci–VO, the C atom binds with three neighboring oxygen atoms, forming a carbonate ion-like structure, CO32−, as shown in Fig. 1(d). The average planar C–O bond length is 1.28 Å, which is very close to the calculated C–O bond length in CaCO3 of 1.29 Å.
Since Ti and C are isovalent, the substitution of Ti by a C atom does not create an extra electron or hole and is expected to occur in the neutral charge state. Our calculations show that CTi does not create defect levels in the band gap and thus is stable in the neutral charge state for the whole range of Fermi levels. We also find that a C atom is likely to be displaced from the Ti site and bind with three nearby O atoms in the form of a Ci–VTi complex (see Fig. 1(e)), which is 6 eV lower in energy than CTi. The average planar and apical C–O bond lengths of CTi are 1.55 Å and 2.10 Å, respectively. In Ci–VTi, the interstitial carbon atom also binds with three neighboring oxygen atoms, forming a carbonate ion-like structure, CO32−, as shown in Fig. 1(e), with an average C–O bond length of 1.29 Å. Much shorter C–O bond lengths in Ci–VTi compared to those in CTi reflect much stronger C–O bonds, resulting in a significantly lower formation energy. Under the O-rich limit, the Ci–VTi complex is a predominant defect for Fermi-level values higher than 1.13 eV above the VBM. When the Fermi level decreases toward the VBM, the donor-type defects Ci and (Ci–VO) become more stable. However, it is unlikely for TiO2 to have that relatively low Fermi level.
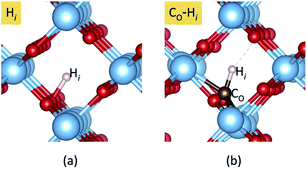
In addition, we consider the effects of hydrogen, which is ubiquitous and could be unintentionally incorporated during the growth process. Hydrogen has been reported to play an important role in the electrical properties of many oxides and affects the optical absorption of N impurities in TiO233 and SrTiO3.46 First, interstitial H (Hi) is found to prefer to bind with a host O atom without introducing any state in the band gap. Our calculations show that Hi is stable in the 1+ charge state, acting as a shallow donor. In addition, we find that an extra electron can be trapped at a Ti site in association with the presence of H+i. This result is in agreement with the DFT+U calculations.47 However, we do not consider this electron trapping here because the calculations could be very complicated and beyond the scope of the present work. Besides, the migration barrier of H+i in TiO2 has been reported to be 0.59 eV parallel and 1.28 eV perpendicular to the tetragonal c-axis,48 indicating that it is highly mobile at low temperature unless it is trapped by other defects or impurities. H+i can be trapped by CO acceptors via coulombic attraction.
Our calculated formation energies show that the CO–Hi complex is stable in + and − charge states with the transition level ε(+/−) located at 1.78 eV above the VBM. This characteristic of the complex is unlike NO–Hi in TiO2,33 which is stable only in the neutral charge state. For N−O in TiO2, the in-gap localized states of N−O are completely passivated by Hi. For C2−O, Hi partially passivates one of the localized in-gap states, leaving the other C-related states in the band gap. The average C–H bond length in the CO–Hi complex is 1.096 Å, which is very close to the calculated C–H bond length in the CH4 molecule of 1.09 Å. The local atomic geometries of Hi and CO–Hi are illustrated in Fig. 3.
We also calculated the binding energy of the CO–Hi complex, defined as
| Eb[(CO–Hi)q] = Ef[COq′] + Ef[H+i] − Ef[(CO–Hi)q], | (4) |
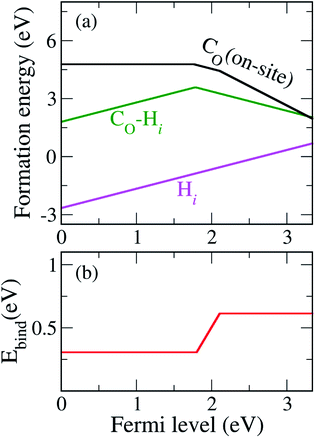 | ||
| Fig. 4 (a) Formation energies of CO, Hi, and the CO–Hi complex under the O-poor limit. (b) The calculated binding energy (Ebind) of the CO–Hi complex as a function of the Fermi level. | ||
3.4 Optical absorption and emission
Here we focus on CO and CO–Hi, which introduce deep levels in the band gap and could give rise to optical transitions with lower energy than the band gap of TiO2. The optical properties of CO were determined through the configuration coordinate diagram shown in Fig. 5. The optical transition associated with CO occurs through the process C2−O + hν → C−O + e−, as represented in Fig. 5(a). C2−O absorbs a photon and is converted to C−O with an electron in the conduction band. The absorption energy was obtained by calculating the difference in the formation energy between C−O in the C2−O lattice geometry and C2−O. The calculated absorption energy corresponds to the CO-related absorption peak centered at 1.83 eV, in which an electron is excited from the fully occupied state of C2−O to the conduction band. The calculated emission energy, representing the recombination of the electron in the conduction band with the hole in C−O, i.e. C−O + e− → C2−O + hν, is 0.74 eV.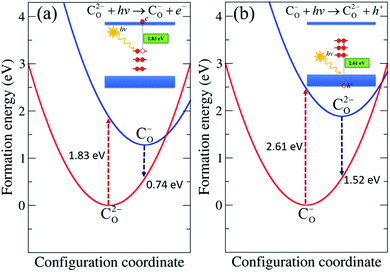 | ||
| Fig. 5 Configuration coordinate diagram for CO in rutile TiO2. The formation energies correspond to the similar O-poor condition in Fig. 2 and εF at (a) CBM for the C2−O + hν → C−O + e− process and at (b) VBM for the C−O + hν → C2−O + h+ process. | ||
Besides, another optical transition of CO occurs through the process C−O + hν → C0O + e−, in which C−O absorbs a photon, converting it to C0O with an electron in the conduction band. The absorption energy was obtained by calculating the difference in the formation energy between C−O and C0O in the C−O lattice geometry. The calculated absorption energy for this process is 2.18 eV. The calculated emission energy for C0O + e− → C−O + hν is 0.34 eV.
We also considered the transition through the process C−O + hν → C2−O + h+, as depicted in Fig. 5(b), in which an electron is transferred to C−O, converting it into C2−O with a hole in the valence band. The analogous transition process C0O + hν → C−O + h+ also takes place. The absorption energies of both processes were calculated by constructing the configuration coordinate diagram, yielding values of 2.61 eV and 3.01 eV, respectively. The absorption energies associated with valence band electron exchange were slightly higher than those associated with conduction band electron exchange. The emission energies are 1.52 eV for C2−O + h+ → C−O + hν and 1.17 eV for C−O + h+ → C0O + hν.
In addition, we consider the optical transition associated with (CO–Hi) through the process (CO–Hi)− + hν → (CO–Hi)0 + e−, in which an electron is excited from (CO–Hi)− to the conduction band, yielding an absorption energy of 2.16 eV. Another transition process, (CO–Hi)0 + hν → (CO–Hi)− + h+, gives an absorption energy of 2.40 eV. These absorption energies are slightly higher than the absorption energy associated with CO. All the plausible optical transition processes and absorption and emission energies associated with CO and the (CO–Hi) complex are listed in Table 2.
| Procedure | Type | eV | Color |
|---|---|---|---|
| C2−O + hν → C−O + e− | Absorption, CBM | 1.83 | Red |
| C−O + hν → C0O + e− | Absorption, CBM | 2.18 | Yellow |
| C−O + e− → C2−O + hν | Emission, CBM | 0.74 | IR |
| C0O + e− → C−O + hν | Emission, CBM | 0.34 | IR |
| C−O + hν → C2−O + h+ | Absorption, VBM | 2.61 | Blue |
| C0O + hν → C−O + h+ | Absorption, VBM | 3.01 | Violet |
| C2−O + h+ → C−O + hν | Emission, VBM | 1.52 | IR |
| C−O + h+ → C0O + hν | Emission, VBM | 1.17 | IR |
| (CO–Hi)− + hν → (CO–Hi)0 + e− | Absorption, CBM | 2.16 | Yellow |
| (CO–Hi)0 + hν → (CO–Hi)+ + e− | Absorption, CBM | 1.60 | Red |
| (CO–Hi)+ + e− → (CO–Hi)0 + hν | Emission, CBM | 1.41 | IR |
| (CO–Hi)0 + e− → (CO–Hi)− + hν | Emission, CBM | 0.94 | IR |
| (CO–Hi)+ + hν → (CO–Hi)0 + h+ | Absorption, VBM | 1.94 | Red |
| (CO–Hi)0 + hν → (CO–Hi)− + h+ | Absorption, VBM | 2.40 | Green |
| (CO–Hi)− + h+ → (CO–Hi)0 + hν | Emission, VBM | 1.17 | IR |
| (CO–Hi)0 + h+ → (CO–Hi)+ + hν | Emission, VBM | 1.74 | Red |
Our calculated optical absorption energies listed in Table 2 elucidate that both CO and the (CO–Hi) complex give rise to optical absorption in the visible-light region. Most of the emission energies associated with CO and the (CO–Hi) complex are in the infrared region. These C-related impurities become predominant in n-type rutile TiO2 under highly O-deficient conditions. In experiments, C-doped TiO2 samples often exhibit mixed-phase structures (anatase–rutile, anatase–brookite or anatase–rutile–brookite).49–52 An effort to prepare C-doped rutile TiO2 has also been reported; however, C dopants were not successfully incorporated into the lattice sites.53 Pure C-doped rutile TiO2 samples are still very scarce. Recently, black carbon-doped rutile TiO2 was reported to have been successfully synthesized by the substitution of O at C sites in TiC film.54 However, it is ambiguous whether C atoms were atomically dispersed in the TiO2 lattice sites, as indicated by the dominant C–C bond characteristics in the X-ray photoemission spectroscopy peaks. Therefore, we do not directly compare our calculated optical absorption energies with the available experimental values. Our results presented here are provided to support future experimental identification of C impurities using optical-transition measurement techniques.
4 Conclusions
In summary, we employed hybrid density-functional calculations to investigate the thermodynamic stability and the effects of C impurities on optical absorption in rutile TiO2. We find that, among other C impurities, only substitutional CO introduces defect levels in the band gap and gives rise to optical absorption in the visible region. Our calculated formation energies show that CO is a deep donor and energetically stable in n-type TiO2 under the O-poor limit. When the oxygen partial pressure increases, Ci–VTi becomes energetically stable in n-type TiO2; however, it is electrically and optically inactive. We also find that hydrogen can bind with CO in a (CO–Hi) complex which is stable up to relatively high temperature. This complex does not completely passivate the visible-light absorption induced by CO but leads to a net red-shift in the absorption edge.In addition, we find that Ci and Ci–VO are shallow donors and can act as compensating centers for CO acceptor and p-type dopants in rutile TiO2. Therefore, substrates, precursors or growth processes containing carbon should be avoided for the efficient fabrication of p-type rutile TiO2. Our results presented in this work reveal the true nature of C impurities and the C impurity–H complex in rutile TiO2. They not only serve as a guide for C impurity identification in rutile TiO2 but also pave the way for new applications of TiO2 in optoelectronics and photovoltaics.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Graduate School of Kasetsart University and the Thailand Research Fund (Grant No. RSA6280068). We thank I. Chatratin and A. Janotti for fruitful discussions. We wish to thank the high-performance computing facilities at the Synchrotron Light Research Institute (SLRI, Thailand) and King Mongkut’s University of Technology Thonburi (KMUTT, Thailand) for their hospitality.Notes and references
- M. Ni, M. K. Leung, D. Y. Leung and K. Sumathy, Renewable Sustainable Energy Rev., 2007, 11, 401–425 CrossRef CAS.
- L. Hao, J. Wang, F.-Q. Bai, M. Xie and H.-X. Zhang, Eur. J. Inorg. Chem., 2015, 2015, 5563–5570 CrossRef CAS.
- T.-F. Lu, W. Li, F.-Q. Bai, R. Jia, J. Chen and H.-X. Zhang, J. Mater. Chem. A, 2017, 5, 15567–15577 RSC.
- L. Liu, H. Zhao, J. M. Andino and Y. Li, ACS Catal., 2012, 2, 1817–1828 CrossRef CAS.
- T. Ohno, K. Sarukawa and M. Matsumura, New J. Chem., 2002, 26, 1167–1170 RSC.
- S. Mahshid, M. Askari, M. S. Ghamsari, N. Afshar and S. Lahuti, J. Alloys Compd., 2009, 478, 586–589 CrossRef CAS.
- D. A. Hanaor, I. Chironi, I. Karatchevtseva, G. Triani and C. C. Sorrell, Adv. Appl. Ceram., 2012, 111, 149–158 CrossRef CAS.
- A. Amtout and R. Leonelli, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 51, 6842 CrossRef CAS PubMed.
- V. E. Henrich and R. L. Kurtz, Phys. Rev. B: Condens. Matter Mater. Phys., 1981, 23, 6280–6287 CrossRef CAS.
- D. Duonghong, E. Borgarello and M. Graetzel, J. Am. Chem. Soc., 1981, 103, 4685–4690 CrossRef CAS.
- E. Bae, W. Choi, J. Park, H. S. Shin, S. B. Kim and J. S. Lee, J. Phys. Chem. B, 2004, 108, 14093–14101 CrossRef CAS.
- H. Kisch, L. Zang, C. Lange, W. F. Maier, C. Antonius and D. Meissner, Angew. Chem., Int. Ed., 1998, 37, 3034–3036 CrossRef CAS PubMed.
- C.-y. Wang, D. W. Bahnemann and J. K. Dohrmann, Chem. Commun., 2000, 1539–1540 RSC.
- H. Yamashita, M. Honda, M. Harada, Y. Ichihashi, M. Anpo, T. Hirao, N. Itoh and N. Iwamoto, J. Phys. Chem. B, 1998, 102, 10707–10711 CrossRef CAS.
- R. Asahi, T. Morikawa, T. Ohwaki, K. Aoki and Y. Taga, Science, 2001, 293, 269–271 CrossRef CAS PubMed.
- Y. Park, W. Kim, H. Park, T. Tachikawa, T. Majima and W. Choi, Appl. Catal., B, 2009, 91, 355–361 CrossRef CAS.
- S. Livraghi, M. C. Paganini, E. Giamello, A. Selloni, C. Di Valentin and G. Pacchioni, J. Am. Chem. Soc., 2006, 128, 15666–15671 CrossRef CAS PubMed.
- S. U. Khan, M. Al-Shahry and W. B. Ingler, Science, 2002, 297, 2243–2245 CrossRef CAS PubMed.
- Y. Choi, T. Umebayashi and M. Yoshikawa, J. Mater. Sci., 2004, 39, 1837–1839 CrossRef CAS.
- H. Irie, Y. Watanabe and K. Hashimoto, Chem. Lett., 2003, 32, 772–773 CrossRef CAS.
- S.-W. Hsu, T.-S. Yang, T.-K. Chen and M.-S. Wong, Thin Solid Films, 2007, 515, 3521–3526 CrossRef CAS.
- Y. Li, D.-S. Hwang, N. H. Lee and S.-J. Kim, Chem. Phys. Lett., 2005, 404, 25–29 CrossRef CAS.
- W. Ren, Z. Ai, F. Jia, L. Zhang, X. Fan and Z. Zou, Appl. Catal., B, 2007, 69, 138–144 CrossRef CAS.
- T. Ohno, T. Tsubota, K. Nishijima and Z. Miyamoto, Chem. Lett., 2004, 33, 750–751 CrossRef CAS.
- S. Sakthivel and H. Kisch, Angew. Chem., Int. Ed., 2003, 42, 4908–4911 CrossRef CAS PubMed.
- R. Klaysri, M. Ratova, P. Praserthdam and P. J. Kelly, Nanomaterials, 2017, 7, 113 CrossRef PubMed.
- C. Di Valentin, G. Pacchioni and A. Selloni, Chem. Mater., 2005, 17, 6656–6665 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- P. Mori-Sánchez, A. J. Cohen and W. Yang, J. Chem. Phys., 2006, 125, 201102 CrossRef PubMed.
- V. Polo, E. Kraka and D. Cremer, Mol. Phys., 2002, 100, 1771–1790 CrossRef CAS.
- B. G. Janesko, T. M. Henderson and G. E. Scuseria, Phys. Chem. Chem. Phys., 2009, 11, 443–454 RSC.
- C. Freysoldt, B. Grabowski, T. Hickel, J. Neugebauer, G. Kresse, A. Janotti and C. G. Van de Walle, Rev. Mod. Phys., 2014, 86, 253 CrossRef.
- J. Varley, A. Janotti and C. Van de Walle, Adv. Mater., 2011, 23, 2343–2347 CrossRef CAS PubMed.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207 CrossRef CAS.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- S. Lany and A. Zunger, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 085202 CrossRef.
- P. Deák, B. Aradi and T. Frauenheim, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 155207 CrossRef.
- J. Paier, M. Marsman, K. Hummer, G. Kresse, I. C. Gerber and J. G. Ángyán, J. Chem. Phys., 2006, 124, 154709 CrossRef CAS PubMed.
- S. Lany and A. Zunger, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 235104 CrossRef.
- R. A. Parker, Phys. Rev., 1961, 124, 1719 CrossRef CAS.
- G. L. Humphrey, J. Am. Chem. Soc., 1951, 73, 1587–1590 CrossRef CAS.
- C. G. Van de Walle and J. Neugebauer, J. Appl. Phys., 2004, 95, 3851–3879 CrossRef CAS.
- A. Janotti, J. Varley, P. Rinke, N. Umezawa, G. Kresse and C. Van de Walle, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 085212 CrossRef.
- F. A. Grant, Rev. Mod. Phys., 1959, 31, 646–674 CrossRef CAS.
- P. Reunchan, N. Umezawa, A. Janotti, T. Jiraroj and S. Limpijumnong, et al., Phys. Rev. B, 2017, 95, 205204 CrossRef.
- F. Filippone, G. Mattioli, P. Alippi and A. A. Bonapasta, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 245203 CrossRef.
- J. B. Bates, J. Wang and R. Perkins, Phys. Rev. B: Condens. Matter Mater. Phys., 1979, 19, 4130 CrossRef CAS.
- M. Ratova, R. Klaysri, P. Praserthdam and P. J. Kelly, Vacuum, 2018, 149, 214–224 CrossRef CAS.
- Y.-T. Lin, C.-H. Weng, Y.-H. Lin, C.-C. Shiesh and F.-Y. Chen, Sep. Purif. Technol., 2013, 116, 114–123 CrossRef CAS.
- J. Jia, D. Li, J. Wan and X. Yu, J. Ind. Eng. Chem., 2016, 33, 162–169 CrossRef CAS.
- A. Bai, W. Liang, G. Zheng and J. Xue, J. Wuhan Univ. Technol., Mater. Sci. Ed., 2010, 25, 738–742 CrossRef CAS.
- E. M. Neville, J. Ziegler, J. D. MacElroy, K. R. Thampi and J. A. Sullivan, Appl. Catal., A, 2014, 470, 434–441 CrossRef CAS.
- S. Guan, L. Hao, H. Yoshida, Y. Lu and X. Zhao, Mater. Express, 2017, 7, 509–515 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: (1) Chemical potential diagram for equilibrium growth of rutile TiO2; (2) band structures and corresponding Brillouin zone; and (3) density of states of CO. See DOI: 10.1039/d0ra02709j |
| This journal is © The Royal Society of Chemistry 2020 |