Open Access Article
Open Access ArticleHydrogenated Ψ-graphene as an ultraviolet optomechanical sensor
Mahdi Faghihnasiri ac,
S. Hannan Mousavia,
Farzaneh Shayeganfar
ac,
S. Hannan Mousavia,
Farzaneh Shayeganfar b,
Aidin Ahmadia and
Javad Beheshtian
b,
Aidin Ahmadia and
Javad Beheshtian *c
*c
aComputational Materials Science Laboratory, Nano Research and Training Center, NRTC, Iran
bDepartment of Physics and Energy Engineering, Amirkabir University of Technology, Tehran, Iran
cFaculty of Science, Shahid Rajaee Teacher Training, 16875-163, Tehran, Iran,. E-mail: j.beheshtian@sru.ac.ir
First published on 10th July 2020
Abstract
PSI (ψ)-graphene is a dynamically and thermally stable two-dimensional (2D) allotrope of carbon composed of 5-6-7 carbon rings. Herein, we study the opto/mechanical behavior of two graphene allotropes, Ψ-graphene and its hydrogenated form, Ψ-graphane under uniaxial and biaxial strain using density functional theory (DFT) calculations. We calculated the elastic constants and second Piola-Kirchhoff (PK2) stresses, in which both nanostructures indicate a similar elasticity behavior to graphene. Also, the plasmonic behavior of these structures in response to various strains has been studied. As a result, plasmonic peaks varied up to about 2 eV under strain. Our findings reveal that these two structures have a large peak in the ultraviolet (UV) region and can be tuned by different applied strain. In addition, Ψ-graphene has smaller peaks in the IR and UV regions. Therefore, both Ψ-graphene and Ψ-graphane can be used as UV optomechanical sensors, whereas Ψ-graphene could be used as an infrared (IR) and visible sensor.
1. Introduction
Carbon has always been the focus of scientists and researchers considerations, especially after it appeared as a 2D material during experimentation with graphene.1 Graphene, has a hexagonal structure of carbon atoms, due to its intrinsic unique specifications,2 e.g. a semiconductor with zero bandgap energy, high carrier mobility, bipolar transport, and strong sp2 junctions. These specifications excited the curiosity of scientists to produce nanoelectronic devices, especially graphene-based transistors.3,4 Carbon-based 2D materials also have other applications including e.g. biosensing,5–7 catalysts in fuel cells,8,9 solar cells,10,11 energy generation and storage,12,13 medicine,14 metal-ion batteries15,16 and water treatment.17,18Despite the theoretical efforts, different graphene allotropes are very challenging. Carbine, graphene, graphane, and biphenylene have been investigated both in a practical and theoretical manner19,20 i.e. at first, the existence of a structure has been predicted and then through a certain method, it has been synthesized.
Although unique specifications like zero-gap can create an advantage in certain kinds of devices such as optical detectors,21 the use of gapless materials such as graphene in a transistor is impossible or extremely difficult, because of meager Ion/Ioff ratio.22,23 Therefore, the existence of such restrictions led researchers to focus on either optimizing structures24 or the other allotropes of graphene, which will not have gapless limitation, while maintaining graphene strengths, simultaneously.
The existence of advanced synthesizing nanostructures technologies e.g. chemical vapor deposition (CVD) and epitaxy,25 allows us to build a suitable structure in terms of its practical need. Various allotropes of graphene have been reported and predicted until now; one can refer to Ψ-graphene,26 popgraphene,15 pentagraphene,27 graphane and graphyne.28 Some of these allotropes are hydrogenated forms of graphene (graphane) and some are different in the crystalline structure such as popgraphene. Based on the total energy calculations of a structure, all allotropes of graphene have less stability than graphene itself. As it is reported, graphenes' total energy is −9.23 to −9.28 eV per atom,29–31 while this value for biphenylene is −8.82 eV per atom30,32 and for graphyne is −8.3 to −8.51 eV per atom.31,32 Nevertheless, allotropes of graphene have more strain sustainability than graphene itself; e.g. fracture strain for graphyne, biphenylene, and graphene is 0.29–0.28 (ref. 33) and 0.22 (ref. 29) respectively.
Recently, Xiaoyin Li et al.26 theoretically studied the Ψ-graphene, which has a structure of 5-6-5 carbon rings and one-atomic thickness like graphene sheets. Moreover, Ψ-graphene has metallic properties and maintains its characteristic against external strain as reported in ref. 25. Another interesting characteristic of Ψ-graphene is a Li diffusion barrier about 0.265–0.313 eV, which is 0.31 eV for graphene. Due to a large number of hexagonal structures in its composition, its thermodynamic stability is high. According to studies conducted, Ψ-graphene has a total energy of −9.07 eV per atom; more than other different carbon allotropes. The Young's modulus of Ψ-graphene, graphene, and penta-graphene have been reported as 283.49, 342.2, and 263.8 N m−1 respectively,26 so Ψ-graphene is the most similar structure to graphene in terms of mechanical properties and features.
One of the challenges with graphene for use in electronic and optoelectronics devices is that there is no bandgap in its electronic structure.34 One way for overcome this issue is functionalization of graphene with hydrogen. Studies have shown that the graphene lattice vector does not change significantly with temperature after hydrogenation and indicates application of graphene is in hydrogen storage.35 So in this paper, we have carried out a systematic investigation of the structural stability and mechanical properties of Ψ-graphene and hydrogenated Ψ-graphene (Ψ-graphane) under external strain. Subsequently, we will survey electronic and optical properties in both cases under strain. The optical properties such as the dielectric function, absorption spectrum, plasmonic effects were analyzed in detail.
2. Computational method
To investigate the structural stability including total energy, the energy of structures under strain, and applied force to each atom, we use the Quantum ESPRESSO package.36 In these calculations, a 12-atom unit cell of Ψ-graphene was with P2mg plane symmetry (plane group no. 7). To increase the accuracy of calculations, PAW37 pseudopotential and PBEsol exchange–correlation function were used.38 In this case, the plane wave energy cutoff was chosen as 950 eV with 8 × 8 × 1 k-point in reciprocal space. The relaxation of the structure was performed through the Broyden–Fletcher–Goldfarb–Shanno (BFGS) method.39 Moreover, the total energy applied to each ion was considered to be below 1 × 10−7 eV Å−1. To remove influence from the parallel planes, a vacuum space in the vertical direction to Ψ-graphene plane was considered which obtained 15 Å. In addition, we have performed a similar calculation on the hydrogenated structure of this carbon allotrope, which was named as Ψ-graphane.3. Results and discussion
3.1. Lattice specifications
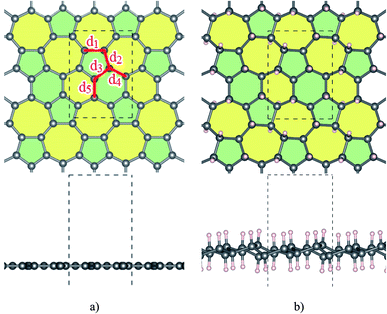
Our study begins with the optimization of Ψ-graphene and Ψ-graphane as plotted in Fig. 1a and b respectively. A detailed description of optimized structures is brought in Table 1 and compared with other reports. Our computation indicates that lattice constants of a and b are 6.68 Å and 4.82 Å respectively, which are almost equal to 6.70 Å and 4.84 Å in Li, et al. paper.26| sp2 | a | b | c | dC–C | |||||
|---|---|---|---|---|---|---|---|---|---|
| d1 | d2 | d3 | d4 | d5 | |||||
| Ψ-Graphene (this work) | ✓ | 6.68 | 4.82 | 13.96 | 1.5 | 1.43 | 1.41 | 1.41 | 1.42 |
| Ψ-Graphene (ref. 26) | • | 6.76 | 4.93 | 15.84 | 1.58 | 1.53 | 1.51 | 1.51 | 1.53 |
| Ψ-Graphane | 6.7 | 4.84 | 14 | 1.53 | 1.51 | 1.52 | 1.53 | 1.52 | |
| T-Graphene40 | 3.42 | 3.42 | 10 | 1.383–1.468 | |||||
| Phagraphene31 | • | 8.09 | 6.65 | 9.62 | 1.40–1.52 | ||||
| Biphenylene41,42 | • | 9.00 | 7.49 | — | 1.40–1.45 | ||||
| Tetrahexadodectite42,43 | • | 6.78 | 6.69 | — | 1.37–1.49 | ||||
| Pentahexaoctite42,44 | • | 3.78 | 5.85 | 15 | 1.37–1.49 | ||||
| Pentaheptite42,45 | • | 4.78 | 4.78 | — | 1.39–1.50 | ||||
Atomic distances, except d1 which equals 1.5 Å, have values between 1.41 to 1.43 Å. The different lattice constant values in this work have lesser quantities in comparison to similar ones in ref. 26; which is originated from PBEsol in this work instead of PBE. PBEsol is intended to improve on PBE for equilibrium properties such as bond lengths and lattice parameters.38 PBEsol functional will give better results for elastic properties including lattice parameters. All of these parameters are reported in Table 1.
Fig. 1b shows the structure of optimized Ψ-graphane obtained through the DFT calculations. Moreover, similar to Ψ-graphene detailed optimized lattice constants are presented in Table 1.
3.2. Elastic properties
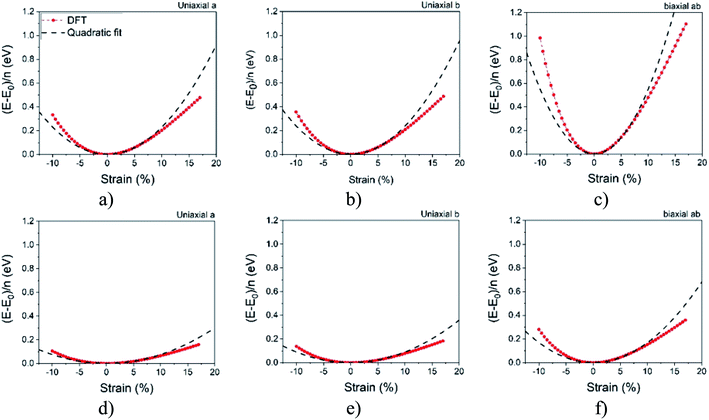
In order to calculate the elastic properties of these materials, we put them under three deformations tensors (Di, i = 1, 2, 3). D1 and D2 constants are used for applied stresses in directions a and b respectively. The D3 constant is used for symmetrical stress in the ab direction. The elastic constants are calculated from the stress matrix elements according to the percentage of the harmonic area which has a value between −2.5% to 7% as can be seen in Fig. 2. In the harmonic area, strain energy and applied strain have a quadratic relation, although, beyond it, an area which is known as the anharmonic area, the degree of this relation will be increased. The width and depth of these well like curves, respectively, indicate the flexibility and strength of each structure.Fig. 2 reveals that the depth of Ψ-graphane is less than Ψ-graphene, and confirms that Ψ-graphene is more strength than Ψ-graphane.
In order to study on the elastic behavior of Ψ-graphene and Ψ-graphane, second-order elastic constants are considered trough eqn (1). Afterward, elastic energy is calculated by using eqn (2). In Table 2, the elastic constants for some allotropes of graphene are reported. Constants in this table have defined as:46
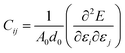 | (1) |
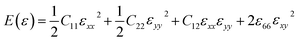 | (2) |
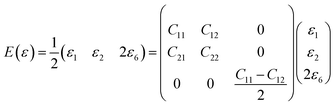 | (3) |
| C66 = (C11 − C12)/2 | (4) |
| C11 | C12 | C22 | C66 | Unit | |
|---|---|---|---|---|---|
| Ψ-Graphene (this work) | 266.78 | 70.72 | 276.27 | 98.03 | N m−1 |
| Ψ-Graphene (ref. 26) | 306.73 | 84.44 | 302.42 | 111.15 | N m−1 |
| Ψ-Graphane (this work) | 164.64 | 21.25 | 199.27 | 71.7 | N m−1 |
| Graphene (experimental) | 340 (ref. 48) | N m−1 | |||
| Graphene (DFT) | 354.6 (ref. 48) | 52 (ref. 49) | 354.6 | 151.3 | N m−1 |
| C-Graphane | 230 (ref. 49) | 50 (ref. 49) | 230 | 90 | N m−1 |
| Penta-graphene | 265 (ref. 50) | −18 (ref. 50) | 141.5 | N m−1 |
Graphene is still the hardest 2D carbon compound, according to the elastic coefficients reported in Table 2. In the Ψ-graphene the presence of pentagonal and hexagonal rings reduced its symmetry and stability compared to graphene. Even though Ψ-graphene does not have the same hardness as graphene, it has a relatively good hardness compared to other carbon compounds and has even higher elastic coefficients than penta-graphene.
In addition, Ψ-graphene has lower elastic coefficients than Ψ-graphane. The reason for this difference is the presence of sp2 and sp3 hybridization as well as the buckling of the atoms in Ψ-graphane makes it 61% less stiff than Ψ-graphene. This difference can be used to distinguish graphene and graphane materials.
In order to consider the influence of large strain on the nonlinear behavior of a structure, the second Piola-Kirchhoff (PK2) stresses (Σ) should be used. To find the PK2 we use the eqn (5):51
| Σ = JF−1σ(F−1)T | (5) |
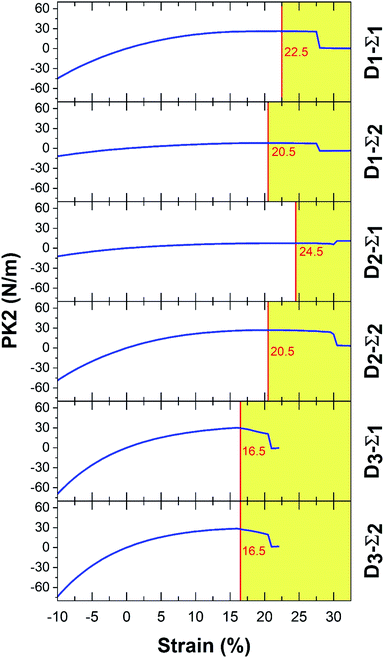
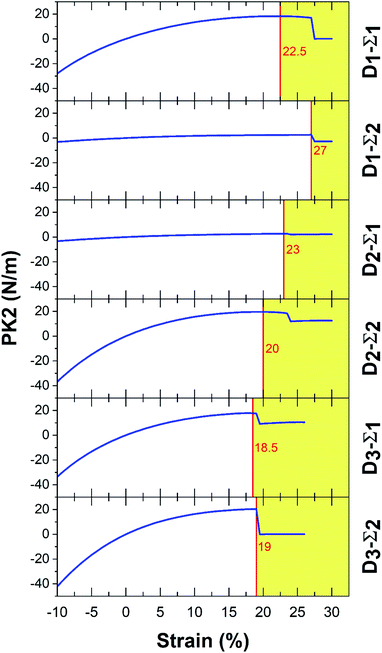
In Fig. 3 and 4, Σ1 and Σ2 are 11 and 22 elements in the main diagonal of the stress matrix respectively. The red line in these figures shows the boundary between the “elastic region”, left side, and the “plastic region”, right side. The maximum of the elastic region indicates the ultimate strain, which a material can withstand under the strain. In the elastic region, a structure can return to its initial state after removing the ultimate strain. It should be taken into consideration, due to the existence of some imperfections e.g. defects; the mentioned boundary is placed in fewer strain values. In Table 3, PK2 values are reported. As a result, Ψ-graphane has more ultimate strain values than Ψ-graphene. However, the elastic region of Ψ-graphene and Ψ-graphane is almost similar to that of graphene and has similar flexibility.
| D1–Σ1 | D1–Σ2 | D2–Σ1 | D2–Σ2 | D3–Σ1 | D3–Σ2 | Unit | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Strain (%) | PK2 | Strain (%) | PK2 | Strain (%) | PK2 | Strain (%) | PK2 | Strain (%) | PK2 | Strain (%) | PK2 | ||
| Ψ-Graphene | 22.5 | 2.62 | 20.5 | 8.17 | 24.5 | 7.69 | 20.5 | 26.91 | 16.5 | 29.56 | 16.5 | 27.63 | N m−1 |
| Ψ-Graphane | 22.5 | 18.27 | 27 | 2.57 | 23 | 2.79 | 20 | 19.54 | 18.5 | 17.77 | 19 | 20.3 | |
| Graphene52 | 23 | 7 | 23 | 30.4 | 19 | 28.6 | 19 | 5.5 | 23 | 32.1 | 23 | 32.1 | |
| Graphane52 | 25 | 3 | 25 | 21.4 | 17 | 18.9 | 17 | 1.2 | 23 | 20.8 | 23 | 20.8 | |
| Graphyne53 | 20 | 17.84 | 20 | 10.4 | 20 | 8.8 | 20 | 18.83 | 18 | 20.64 | 18 | 20.64 | |
3.3. Band structure
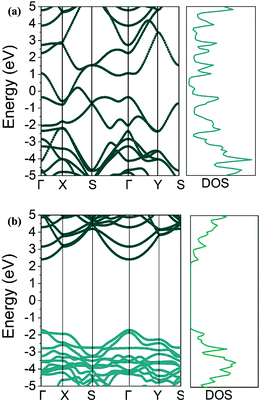
From a different perspective, the electronic properties of Ψ-graphene and Ψ-graphane are considered in this work. Fig. 5a shows the electronic band structure and density of states (DOS) of Ψ-graphene and Fig. 5b shows the same characters for Ψ-graphene.As can be seen in Fig. 5b, Ψ-graphane has a 4.13 eV bandgap, while Ψ-graphene has no bandgap. As mentioned, the structure of Ψ-graphene maintains its metallicity under any kind of deformation and strains.
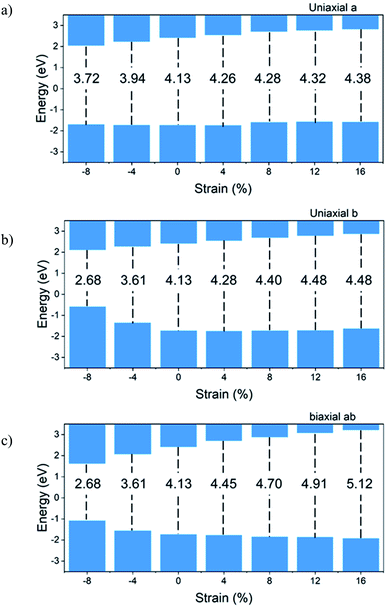
Fig. 6 shows the bandgap versus strain for the Ψ-graphane. Due to the metallic and gapless properties of Ψ-graphene under strain, Fig. 6 shows the bandgap variations for Ψ-graphane only.
To compare tensile and compressive strained Ψ-graphane, the bandgap of unstrained Ψ-graphane, 4.13 eV is set to be a reference. For direction, a (Fig. 6a), this value has been decreased to 3.72 eV over −8% compression, and it has been increased to 4.38 eV for tensile strain up to +16% strain. In other words, under compression, the bandgap is decreased and under tensile strain is increased. It should be noted that the contribution of the conduction band (CB) in these changes is more than the valence band (VB) (Fig. 6a). From −8% to +4% strain, the variations growth is constant and in hundreds of meV. One can see for +8% strain, VB moves toward positive energies around 140 meV. Meanwhile, from this point onwards, the variation enhances around tens of meV.
Previous studies have shown that biaxial strain do not form a bandgap in the electron structure of graphene.54 However, under the influence of uniaxis strain in the direction of zigzag and armchair, breaking the symmetry of the structure leads to a very small band gap. The greatest gap in zigzag strain occurred at 24%, which is 0.5 eV. Also, in the direction of armchair, the maximum gap occurs in the strain of 13%, which is 0.16 eV. In contrast, the graphane is a semiconductor with a direct gap of 3.54 eV.55 The bandgap of graphane increases under the influence of uniaxis strain and reaches 5.5 eV at 15% strain, which is approximately equal to the amount of Ψ-graphane bandgap at 16% strain.
For direction b, from −8% to +16% of strain, the bandgap changes from 2.68 eV to 4.48 eV, respectively. It should be noted that the behavior of CB is different from the VB. The CB shift for bandgap closing or opening is almost homogeneous. For VB, we divide variations into three parts. The VB moves toward positive energy with increasing compression. From an unstrained structure up to +8% tensile strain, there is almost no variation. And beyond this point, VB shows a slight increase in direction to positive energies. For biaxial ab direction, the bandgap opening happens from −8% to +16% strain and takes values from 2.68 eV up to 5.12 eV for the above strain.
In practice, such a shift in the bandgap due to the increase in system temperature could appear. Also, the distance between valence and conduction band due to increasing the temperature and energy band broadening will be reduced; therefore, the absorption probability of photons with lesser energies could be increased. The variation of the electronic bandgap related to temperature is called the Varshni equation.56
3.4. Optical properties
Complex dielectric function is used to define a solids linear optical specification,57 which relates its macroscopic properties to its microscopic ones. In other words, the dielectric constant of each system is a gauge to measure applied field linear responsibility of each of those systems.58 The dielectric constant relates to an applied field and defines the level of polarization related to different parameters e.g. frequency, field, etc. The imaginary part of the dielectric function (ε2), assuming a single-particle system, obtains from the eqn (6):59
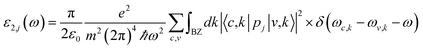 | (6) |
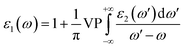 | (7) |
Using eqn (7) the Cauchy principal value, VP, is attained. From dielectric function, one can obtain some optical properties e.g. absorption coefficient and refractive index.
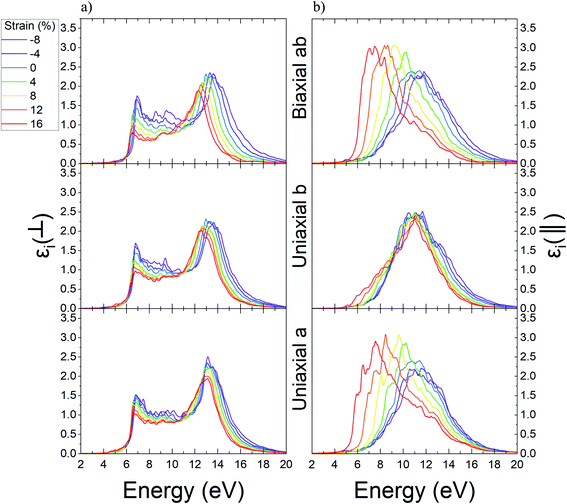
In the next step, we computed the real and imaginary parts of the dielectric function of Ψ-graphene and Ψ-graphane. The real part of dielectric function for compressive and tensile strained Ψ-graphene from −8% to 16% in a, b, and ab directions have been reported in Fig. 7. In these figures, the ⊥ symbol is used for out-of-plane or vertical polarization, and the ‖ symbol is used for in-plane or horizontal polarization.
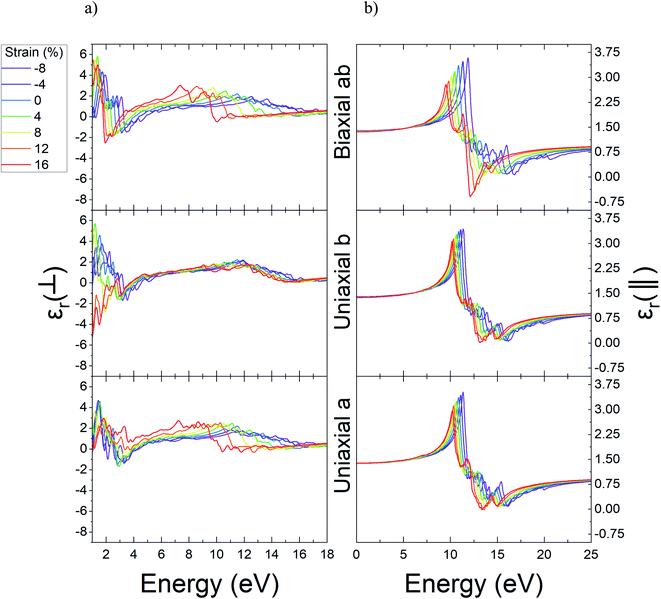 | ||
| Fig. 7 The real part of dielectric function of unstrained and strained Ψ-graphene; (a) out-of-plane (b) in-plane. | ||
From these figures, one can obtain the variations of static dielectric constant in order to study the polarizability of a structure.61 Since Ψ-graphene is a conductor, same as graphene, the real part of its' dielectric function for in-plane polarizations and energies near zero eV, has singularities. For energies over one eV, the real part of dielectric function fluctuations encounter redshift and blue-shift with increasing tensile and compressive strain, respectively.
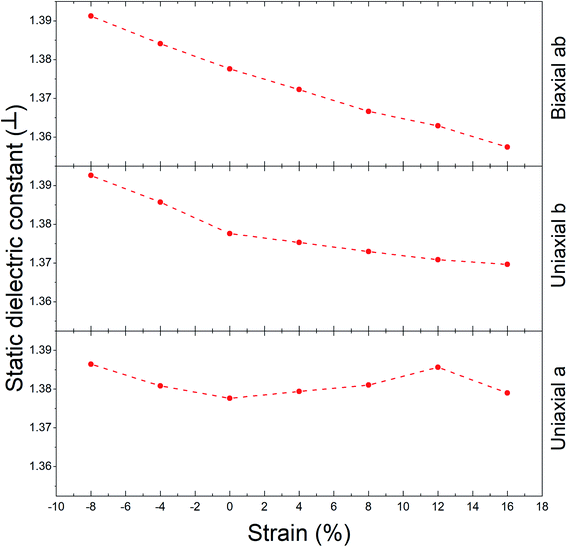
The static dielectric constant for out-of-plane polarizations in equilibrium for Ψ-graphene has obtained 1.38. This value, as can be seen in Fig. 8, also experienced a slight variation between about 1.36 and 1.39 for related strain range and various directions.
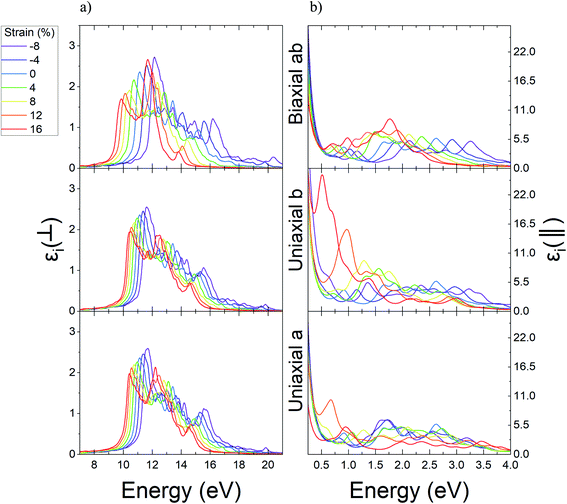
The real part of the dielectric function shows the response of the material to the applied variable electric field while the electric field hasn't been absorbed but its energy could be stored and remitted or in terms the ability to permit the electric field through the material. Fig. 7 shows that pick of the real part of the dielectric function of Ψ-graphene has blueshift under compressive strains and redshift under tensile strain for both in-plane and out-of-plane polarizations. The energy variations for applied electromagnetic waves under in-plane polarization and a, b, and ab directions in the range of −8% to +16% strain are 11.36–10.23 eV, 11.38–10.19 eV, and 11.89–9.53 eV respectively. Meanwhile, for out-of-plane polarization, these variations are 11.5–7.25 eV, 11.9–9.06 eV, and 12.61–7.37 eV correspondingly.
From the imaginary part of the dielectric function diagram, one can acquire information about the optical absorption of a structure. The peak of the aforementioned diagram defines the optical absorption between valence and conduction bands of that structure. The imaginary part of dielectric function diagrams can be viewed in Fig. 9. According to this figure, the equilibrium state of Ψ-graphene has two peaks in 11.14 eV and 13.42 eV. For a strain of −8%, these two peaks convert to one peak in 11.71 eV, 11.62 eV, and 12.16 eV for the directions a, b, and ab respectively. For strain up to 16%, the mentioned peaks move to 10.42 eV and 12.22 eV for a direction, 10.52 eV and 12.51 eV for b direction and 9.87 eV and 11.7 eV for ab direction. Also, the in-plane absorption peak placed at 0.005 eV and any change related to various types of strain for this peak is observable.
Through a similar study, the variations result for the real part of dielectric function related to Ψ-graphane under different values of strain are reported in Fig. 10. Ψ-Graphane due to its 4.13 eV band gap has different optical behavior in comparison with gapless Ψ-graphene. The real part of dielectric function diagram for both polarizations has negative quantities. This diagram for out-of-plane polarizations has two peaks in 6.43 and 12.39 eV energies, whilst, for in-plane polarizations has one peak in 9.33 eV energy and related to in and out-of-plane polarizations, after 13.9 and 13.14 eV energies goes to negative amounts.
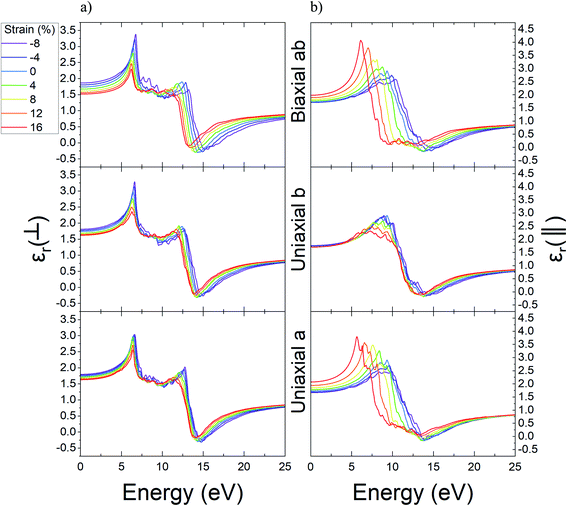 | ||
| Fig. 10 The real part of dielectric function of unstrained and strained Ψ-graphane; (a) out-of-plane, (b) in-plane. | ||
The real part of Ψ-graphane dielectric function for in-plane polarizations under uniaxial a and biaxial ab strain has noticeable variations. The peak of the diagram under tensile strain directed to greater energies has about 0.58 and 1.11 eV blue-shift up to 16% strain and under compression ones has about 3.68 and 3.21 eV red-shift up to −8% leading to lesser energies. Also, under uniaxial b strain in the range of −8% to 16% its peak has poor variations about 1.54 eV.
As mentioned before, the real part of Ψ-graphane dielectric function for out-of-plane polarization has two peaks in 6.43 and 12.39 eV energies. The place of the first peak, unlike its intensity, isn't influenced by any kind of strain. Under compression and tensile strain, the peaks' intensity will be decreased and increased relatively. The second peak for a, b, and ab directions, respectively, under tensile strain has 0.38, 0.28, and 0.82 eV red-shift to lesser energies and under compression strain has 1.53, 1.02, and 2.16 eV blue-shift to greater energies.
Using Fig. 10, the static dielectric constant variations progression is acquired as Fig. 11a for out-of-plane polarization. Decreasing this constant is the result of increasing the tensile strain; meanwhile, opposing behavior is displayed from compression strain. Increasing the static dielectric constant is the result of increasing the compression strain. According to Fig. 11a, the variation range for mentioned constant related to different directions is as follows: 1.63 < a direction < 1.79, 1.62 < b direction < 1.81 and 1.51 < ab direction < 1.86.
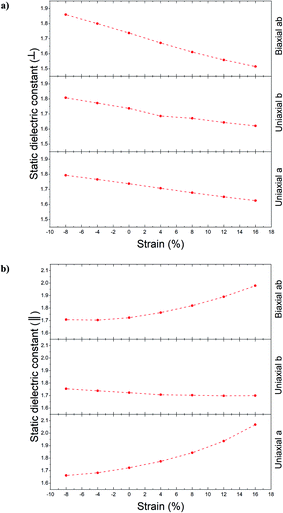 | ||
| Fig. 11 The static dielectric function for unstrained and strained Ψ-graphane and different directions, (a) out-plane polarization, (b) in-plane polarization. | ||
For in-plane polarizations, two different progressions can be seen. One progression (for b direction) is almost similar to an out-of-plane one, with a range between 1.7 to 1.75 values. However, a and ab directions behave completely differently. By increasing the tensile strain, the static dielectric constant increased, and with increasing the compression strain it experienced decreasing. The variation range according to Fig. 11b is as follows: 1.66 < a direction < 2.07 and 1.71 < ab direction < 1.98.
The imaginary part of dielectric functions diagrams for Ψ-graphane, related to different polarization and directions are reported in Fig. 12. The imaginary part of dielectric function under in-plane polarizations for Ψ-graphane has a peak in 11.45 eV. The mentioned peak for a and ab directions has noticeable shifts. Tensile strain up to 16% in a and ab directions move the peak to 7.56 and 7.52 eV energies, respectively. Whereas for compression strain up to −8%, it moves to 11.04 and 11.83 eV energies related to the cited directions.
 | ||
| Fig. 12 The imaginary part of dielectric function for unstrained and strained Ψ-graphane; (a) out-of-plane, (b) in-plane. | ||
In accordance with Fig. 12, there are two peaks for out-of-plane polarization, which are placed in 6.93 and 13.14 eV points. Under tensile and compression strain over the range of −8% to 16%, the first peak doesn't have a noticeable shift. The maximum shift is about 0.36 eV, which is occurred in the ab direction. Whilst, the second peak under some kinds of strain has more shifts. Although it doesn't have any significant shifts for direction a, for b and ab directions it has a 0.63 eV red-shift up to 16% for tensile strain and 0.64 eV blue-shift up to −8% for compression strain in ab direction. Also, for direction b, for strain up to −8% and 16%, it has 0.59 and 0.37 eV blue-shift and red-shift in that order.
3.5. Absorption spectrum
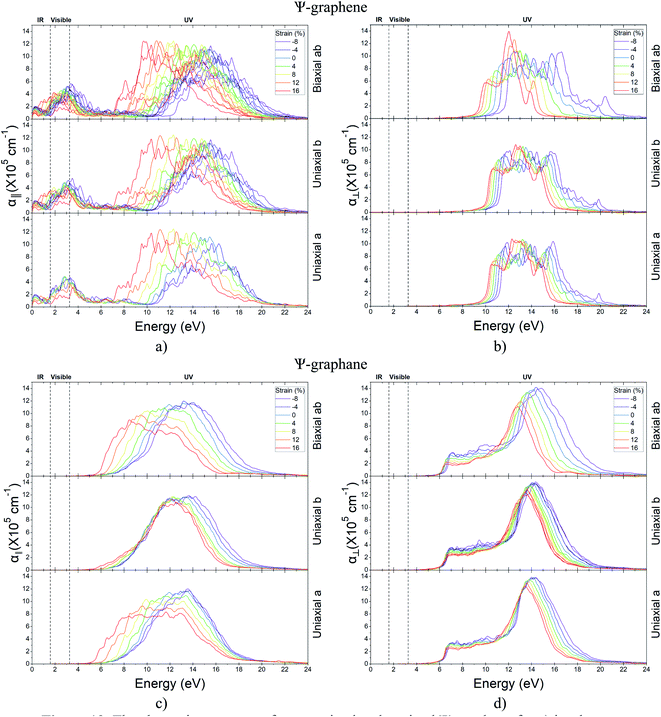
Using the complex dielectric function, one can obtain the absorption coefficient, according to eqn (8).62 This optical parameter is studied for both Ψ-graphene and Ψ-graphane under mentioned polarizations and directions.
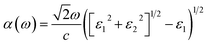 | (8) |
Throughout in-plane polarization, the structure of Ψ-graphene has an absorption coefficient in all three IR, visible and UV regions. In unstrained structure, there are three main peaks at 0.28 eV, 2.8 eV, and 15.47 eV in relation to the mentioned regions respectively. According to Fig. 13a, the place of the peak in the IR region has almost remained constant. It should be noted, one peak has been added to the IR region in relation to the b direction and tensile strain, i.e. in about 1.5 eV. The peak which is placed in the visible region, under compressive strain, moves to 3.3 eV, 3.5 eV, and 3.36 eV for a, b and ab directions respectively. All movements are directed to the NUV region. The situation for the tensile strain is completely different. For +16% tensile strain, this peak moves to 3.53 eV, which is within the NUV region. Meanwhile, for b and ab directions this shift is still occurred in the visible region, i.e. 3.1 eV and 1.9 eV, respectively. It should be also noted, there are still stronger peaks in the UV region.
 | ||
| Fig. 13 The absorption spectrum for unstrained and strained Ψ-graphane for (a) in-plane polarization (b) out-plane polarization and Ψ-graphene (c) in-plane polarization (d) out-plane polarization. | ||
According to Fig. 13b, Ψ-graphene also has a peak in the UV region in relation to out-of-plane polarization and various directions. The mentioned peak for tensile and compressive strained structure indicates red-shift and blue-shift energy displacements, respectively.
The absorption diagram of Ψ-graphane, due to the existence of an in-plane polarization, has a peak at 13.17 eV for unstrained structure. This main peak for a, b and ab directions moves to 13.56 eV, 13.66 eV and 13.79 eV under −8% compressive strain, and shift to 11.56 eV, 12.55 eV and 8.48 eV for 16% tensile strain. In other words, the absorption of Ψ-graphane, relating to tensile strain, moves from Extreme Ultraviolet (EUV) to Vacuum Ultraviolet (VUV) region. Therefore, one can say Ψ-graphane, which has no absorption in the infrared (IR) region, is suitable for ultraviolet (UV) detection (Fig. 13c).
Due to out-of-plane polarization, unstrained Ψ-graphane has a peak at 14.17 eV. This main peak for compressive strain in b and ab directions transfers to 14.36 eV and 14.83 eV, while for the direction a is almost the same value. Under tensile strain, this peak transfers to 13.47 eV, 13.65 eV, and 12.82 eV for a, b, and ab directions, respectively. Similar to other optical parameters of Ψ-graphane, the absorption diagram under tensile strain have red-shift to low energies, whilst under compressive strain has blue-shift towards high-level energies. In other words, Ψ-graphane under out-of-plane polarization is also a UV detector with a slight difference. According to Fig. 13d, the detection amount between Deep Ultraviolet (DUV) and EUV regions, compared to parallel polarization, has been decreased.
In addition to the ultraviolet absorption of Ψ-graphane, the intensity of its optical absorption is an interesting point. The absorption is in noticeable order of 105 cm−1. Therefore, Ψ-graphane is a UV absorber and visible wavelengths could be transmitted without any absorption.
3.6. Surface plasmon
Light with polarization parallel to the surface of 2D structures can lead to a massive movement of electrons in matter. These conditions are known as plasmonic behavior.59 As a result, the reaction of the material to in-plane polarization is very important. When the real part of dielectric function is zero and the imaginary part has a very small amount, according to eqn (9),63 electron energy loss function (EELF) is maximized and surface plasmon will be formed in the material.
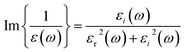 | (9) |
Theoretical63,64 and practical65 studies have shown, graphene EELF has two peaks in 4.6 eV and 14.6 eV for in-plane polarization. As the graphene band structure analysis has revealed, the peak of EELF at 4.6 eV is related to π → π* electron transition. In this transition, π is the Pz orbitals in VB, and π* is the empty Pz orbitals of CB around the point M in graphene first Brillouin zone (BZ). The existence of van Hove singularity in the Pz orbital of CB and VB near point M is the cause of this transition and concluded from the PDOS graph.66 In this case, the collective behavior of electrons, under the influence of the in-plane electric field of the incident electromagnetic wave, leads to the formation of π + σ plasmon in graphene. Also, the 14.6 eV EELF is according to σ → π* transition which is known to as π + σ plasmon.64 Since π + σ plasmon appears at high frequencies, researchers have been less concerned. Wider the EELF graph in these plasmons is the main difference from π plasmons which is leading to plasmon lifetime difference.66
Since the study of the behavior of surface plasmons in the fabrication of photonic circuits is very important, the behavior of Ψ-graphene and Ψ-graphane plasmons has been studied in the continuation of this section. As can be seen in Fig. 14, only Ψ-graphene for in-plane polarization has two EELF diagram peaks that are placed in 4.22 and 17.65 eV (Fig. 14a) and other structures have only one peak. Therefore, the peak of Ψ-graphene for out-of-plane polarization placed in 15.91 eV (Fig. 14b). Likewise, Ψ-graphane for in-plane and out-of-plane polarization has a peak in 16.01 eV (Figure 14c) and 16.20 eV (Fig. 14d) respectively. After that, variations of these peaks related to strain have been studied for both structures. As a result, one can say the previous peak condition remained constant i.e. Ψ-graphene for in-plane polarization has two peaks whilst other situations have one peak in their EELF diagram. Tables 4–6 show the influence of strain on the peaks of EELF briefly.
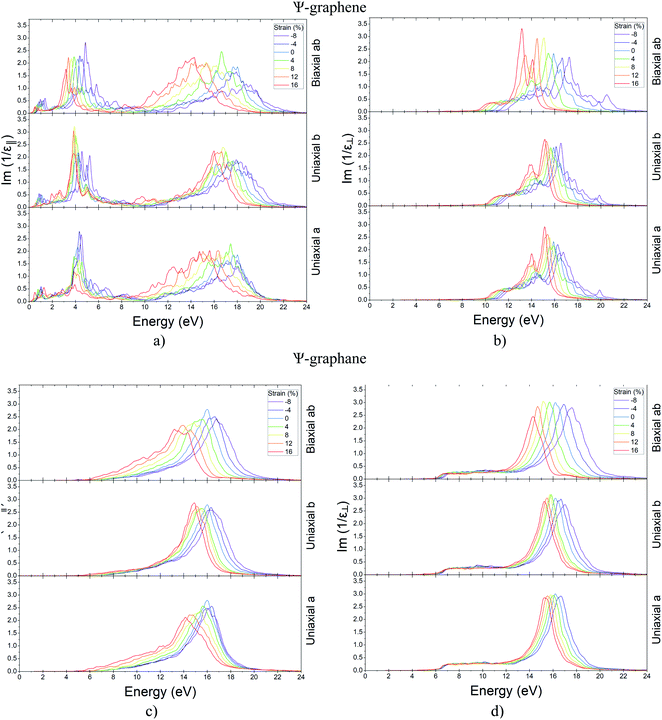 | ||
| Fig. 14 EELF for unstrained and strained Ψ-graphene for (a) in-plane polarization (b) out-plane polarization and Ψ-graphane (c) in-plane polarization (d) out-plane polarization. | ||
| Structure | Polarization | Strain (%) | Unit | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| −8 | −4 | 0 | 4 | 8 | 12 | 16 | ||||||||||
| Ψ-Graphene | In-plane | 4.5 | 18.05 | 4.35 | 17.99 | 4.22 | 17.65 | 3.88 | 17.42 | 4.33 | 16.44 | 3.93 | 16.28 | 3.94 | 15.61 | eV |
| Out-of-plane | — | 16.75 | — | 16.26 | — | 15.91 | — | 15.87 | — | 15.54 | — | 15.38 | — | 15.14 | ||
| Ψ-Graphane | In-plane | — | 16.08 | — | 16.37 | — | 16.01 | — | 15.63 | — | 15.47 | — | 14.51 | — | 14.15 | |
| Out-of-plane | — | 15.28 | — | 16.68 | — | 16.20 | — | 16.04 | — | 15.82 | — | 15.53 | — | 15.28 | ||
| Peak | 1st | 2nd | 1st | 2nd | 1st | 2nd | 1st | 2nd | 1st | 2nd | 1st | 2nd | 1st | 2nd | ||
| Structure | Polarization | Strain (%) | Unit | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| −8 | −4 | 0 | 4 | 8 | 12 | 16 | ||||||||||
| Ψ-Graphene | In-plane | 5.24 | 17.92 | 4.99 | 17.23 | 4.22 | 17.65 | 4 | 17.02 | 3.91 | 16.77 | 3.85 | 16.63 | 3.86 | 15.99 | eV |
| Out-of-plane | — | 16.54 | — | 16.12 | — | 15.91 | — | 15.65 | — | 15.65 | — | 15.29 | — | 15.15 | ||
| Ψ-Graphane | In-plane | — | 16.24 | — | 16.33 | — | 16.01 | — | 15.5 | — | 15.46 | — | 15.11 | — | 14.90 | |
| Out-of-plane | — | 17.02 | — | 16.67 | — | 16.20 | — | 15.83 | — | 15.73 | — | 15.49 | — | 15.25 | ||
| Peak | 1st | 2nd | 1st | 2nd | 1st | 2nd | 1st | 2nd | 1st | 2nd | 1st | 2nd | 1st | 2nd | ||
| Structure | Polarization | Strain (%) | Unit | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| −8 | −4 | 0 | 4 | 8 | 12 | 16 | ||||||||||
| Ψ-Graphene | In-plane | 4.87 | 18.78 | 4.38 | 17.92 | 4.22 | 17.65 | 3.89 | 16.65 | 3.66 | 15.32 | 3.4 | 14.36 | 3.18 | 14.28 | eV |
| Out-of-plane | — | 17.26 | — | 16.65 | — | 15.91 | — | 15.45 | — | 15.07 | — | 14.48 | — | 14.09 | ||
| Ψ-Graphane | In-plane | — | 16.79 | — | 16.66 | — | 16.01 | — | 15.62 | — | 14.89 | — | 13.95 | — | 13.21 | |
| Out-of-plane | — | 17.60 | — | 16.92 | — | 16.20 | — | 15.70 | — | 15.17 | — | 14.69 | — | 14.31 | ||
| Peak | 1st | 2nd | 1st | 2nd | 1st | 2nd | 1st | 2nd | 1st | 2nd | 1st | 2nd | 1st | 2nd | ||
4. Conclusions
In conclusion, we have presented a detailed description of opto/mechanical behavior of Ψ-graphene and its hydrogenated, i.e. Ψ-graphane by using the DFT approach. Our findings show that the elastic region of Ψ-graphene and Ψ-graphane are intended in the range of 16.5% to 27%, which are similar to the range of 17% to 25% for graphene and graphane. Moreover, all unstrained and strained structures for various polarizations have absorption coefficient in the UV region, except Ψ-graphene, which its response is in the range of IR to UV regions. Therefore, Ψ-graphene could be an IR and visible detector if in-plane polarization had performed, otherwise, it can be used as a UV detector. Only Ψ-graphene in response to in-plane polarization, similar to graphene, has two 4.22 eV and 17.65 eV plasmonic peaks, which could be varied about 1 eV and 3.4 eV for strained structures.The static dielectric constant of strained Ψ-graphene for in-plane polarization doesn't show any distinguishable variations, while out-of-plane polarization decrease with applied strain. Also, the static dielectric constant of compressive strained Ψ-graphane for in-plane polarization decreases with strain, while for tensile strained structure increases with strain. Our findings of opto/mechanical behavior of Ψ-graphene and its hydrogenated are key conceptual and fundamental advances, which have important implications for the science-based engineering of optomechanical sensors based on graphene.
Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
Javad Beheshtian would like to acknowledge the Research Council of Shahid Rajaee Teacher Training University for their support.References
- A. H. C. Neto and K. Novoselov, Two-Dimensional Crystals: Beyond Graphene, Mater. Express, 2011, 1(1), 10–17 CrossRef.
- A. K. Geim and K. S. Novoselov, The rise of graphene, in Nanoscience and Technology: A Collection of Reviews from Nature Journals, 2010, World Scientific, pp. 11–19 Search PubMed.
- F. Schwierz, Graphene transistors, Nat. Nanotechnol., 2010, 5(7), 487 CrossRef CAS PubMed.
- M. Faghihnasiri, et al., The temperature effect on mechanical properties of silicon carbide sheet based on density functional treatment, Solid State Commun., 2016, 227, 40–44 CrossRef CAS.
- Y. Wang, et al., Nitrogen-Doped Graphene and Its Application in Electrochemical Biosensing, ACS Nano, 2010, 4(4), 1790–1798 CrossRef CAS PubMed.
- M. Pumera, Graphene in biosensing, Mater. Today, 2011, 14(7), 308–315 CrossRef CAS.
- P. Suvarnaphaet and S. Pechprasarn, Graphene-Based Materials for Biosensors: A Review, Sensors, 2017, 17(10), 2161 CrossRef PubMed.
- P. Wu, et al., Graphyne as a promising metal-free electrocatalyst for oxygen reduction reactions in acidic fuel cells: a DFT study, J. Phys. Chem. C, 2012, 116(38), 20472–20479 CrossRef CAS.
- S. H. Hur and J. N. Park, Graphene and its application in fuel cell catalysis: a review, Asia-Pac. J. Chem. Eng., 2013, 8(2), 218–233 CrossRef CAS.
- X. Wang, L. Zhi and K. Müllen, Transparent, conductive graphene electrodes for dye-sensitized solar cells, Nano Lett., 2008, 8(1), 323–327 CrossRef CAS PubMed.
- U. Mehmood, et al., Nanocomposites of carbon allotropes with TiO2 as effective photoanodes for efficient dye-sensitized solar cells, Mater. Lett., 2018, 228, 125–128 CrossRef CAS.
- M. Notarianni, et al., Synthesis and applications of carbon nanomaterials for energy generation and storage, Beilstein J. Nanotechnol., 2016, 7, 149–196 CrossRef CAS PubMed.
- R. Raccichini, et al., The role of graphene for electrochemical energy storage, Nat. Mater., 2015, 14(3), 271 CrossRef CAS PubMed.
- B. Vedhanarayanan, et al., Hybrid materials of 1D and 2D carbon allotropes and synthetic π-systems, NPG Asia Mater., 2018, 10(4), 107–126 CrossRef CAS.
- S. Wang, et al., Popgraphene: a new 2D planar carbon allotrope composed of 5–8–5 carbon rings for high-performance lithium-ion battery anodes from bottom-up programming, J. Mater. Chem. A, 2018, 6(16), 6815–6821 RSC.
- Z. Xiong, Y. S. Yun and H.-J. Jin, Applications of Carbon Nanotubes for Lithium Ion Battery Anodes, Materials, 2013, 6(3), 1138–1158 CrossRef CAS PubMed.
- M. Bartolomei, et al., Penetration barrier of water through graphynes' pores: first-principles predictions and force field optimization, J. Phys. Chem. Lett., 2014, 5(4), 751–755 CrossRef CAS PubMed.
- Y. Liu, et al., A graphene-based electrochemical filter for water purification, J. Mater. Chem. A, 2014, 2(39), 16554–16562 RSC.
- J. Lüder, et al., The electronic characterization of biphenylene—Experimental and theoretical insights from core and valence level spectroscopy, J. Chem. Phys., 2015, 142(7), 074305 CrossRef PubMed.
- A. M. Ilyin, et al., Computer simulation and experimental study of graphane-like structures formed by electrolytic hydrogenation, Phys. E, 2011, 43(6), 1262–1265 CrossRef CAS.
- F. Xia, et al., Ultrafast graphene photodetector, Nat. Nanotechnol., 2009, 4(12), 839 CrossRef CAS PubMed.
- P. Avouris, Graphene: Electronic and Photonic Properties and Devices, Nano Lett., 2010, 10(11), 4285–4294 CrossRef CAS PubMed.
- I. Meric, et al., Current saturation in zero-bandgap, top-gated graphene field-effect transistors, Nat. Nanotechnol., 2008, 3, 654 CrossRef CAS PubMed.
- M. S. Jang, et al., Graphene field effect transistor without an energy gap, Proc. Natl. Acad. Sci. U. S. A., 2013, 110(22), 8786–8789 CrossRef CAS PubMed.
- S. Park and R. S. Ruoff, Chemical methods for the production of graphenes, Nat. Nanotechnol., 2009, 4, 217 CrossRef CAS PubMed.
- X. Li, Q. Wang and P. Jena, ψ-Graphene: A New Metallic Allotrope of Planar Carbon with Potential Applications as Anode Materials for Lithium-Ion Batteries, J. Phys. Chem. Lett., 2017, 8(14), 3234–3241 CrossRef CAS PubMed.
- B. Xiao, et al., Penta-graphene: a promising anode material as the Li/Na-ion battery with both extremely high theoretical capacity and fast charge/discharge rate, ACS Appl. Mater. Interfaces, 2016, 8(51), 35342–35352 CrossRef CAS PubMed.
- Q. Peng, et al., New materials graphyne, graphdiyne, graphone, and graphane: review of properties, synthesis, and application in nanotechnology, Nanotechnol., Sci. Appl., 2014, 7, 1 CAS.
- Q. X. Pei, Y. W. Zhang and V. B. Shenoy, A molecular dynamics study of the mechanical properties of hydrogen functionalized graphene, Carbon, 2010, 48(3), 898–904 CrossRef CAS.
- O. Rahaman, et al., Metamorphosis in carbon network: from penta-graphene to biphenylene under uniaxial tension, FlatChem, 2017, 1, 65–73 CrossRef CAS.
- Z. Wang, et al., Phagraphene: A Low-Energy Graphene Allotrope Composed of 5–6–7 Carbon Rings with Distorted Dirac Cones, Nano Lett., 2015, 15(9), 6182–6186 CrossRef CAS PubMed.
- L. E. F. F. Torres, S. Roche, and J. C. Charlier, Introduction to Graphene-Based Nanomaterials: From Electronic Structure to Quantum Transport, Cambridge University Press, 2014 Search PubMed.
- Y. Li, et al., Mechanical properties of hydrogen functionalized graphene allotropes, Comput. Mater. Sci., 2014, 83, 212–216 CrossRef CAS.
- J. O. Sofo, A. S. Chaudhari and G. D. Barber, Graphane: A two-dimensional hydrocarbon, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75(15), 153401 CrossRef.
- L. Feng Huang and Z. Zeng, Lattice dynamics and disorder-induced contraction in functionalized graphene, J. Appl. Phys., 2013, 113(8), 083524 CrossRef.
- P. Giannozzi, et al., QUANTUM ESPRESSO: a modular and open-source software project for quantum simulations of materials, J. Phys.: Condens. Matter, 2009, 21(39), 395502 CrossRef PubMed.
- P. E. Blöchl, Projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50(24), 17953 CrossRef PubMed.
- J. P. Perdew, et al., Restoring the density-gradient expansion for exchange in solids and surfaces, Phys. Rev. Lett., 2008, 100(13), 136406 CrossRef PubMed.
- J. D. Head and M. C. Zerner, A Broyden—Fletcher—Goldfarb—Shanno optimization procedure for molecular geometries, Chem. Phys. Lett., 1985, 122(3), 264–270 CrossRef CAS.
- Y. Liu, et al., Structural and Electronic Properties of T Graphene: A Two-Dimensional Carbon Allotrope with Tetrarings, Phys. Rev. Lett., 2012, 108(22), 225505 CrossRef PubMed.
- M. A. Hudspeth, et al., Electronic Properties of the Biphenylene Sheet and Its One-Dimensional Derivatives, ACS Nano, 2010, 4(8), 4565–4570 CrossRef CAS PubMed.
- A. Lherbier, et al., Lithiation properties of sp2 carbon allotropes, Phys. Rev. Mater., 2018, 2(8), 085408 CrossRef CAS.
- G. Brunetto, et al., Nonzero Gap Two-Dimensional Carbon Allotrope from Porous Graphene, J. Phys. Chem. C, 2012, 116(23), 12810–12813 CrossRef CAS.
- B. R. Sharma, A. Manjanath and A. K. Singh, Pentahexoctite: a new two-dimensional allotrope of carbon, Sci. Rep., 2014, 4, 7164 CrossRef CAS PubMed.
- V. H. Crespi, et al., Prediction of a pure-carbon planar covalent metal, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 53(20), R13303–R13305 CrossRef CAS PubMed.
- S. Thomas, et al., Assessment of the mechanical properties of monolayer graphene using the energy and strain-fluctuation methods, RSC Adv., 2018, 8(48), 27283–27292 RSC.
- M. Faghihnasiri, et al., Nonlinear elastic behavior and anisotropic electronic properties of two-dimensional borophene, J. Appl. Phys., 2019, 125(14), 145107 CrossRef.
- K. Choudhary, et al., Elastic properties of bulk and low-dimensional materials using van der Waals density functional, Phys. Rev. B, 2018, 98(1), 014107 CrossRef CAS PubMed.
- L. Ottaviano and V. Morandi, GraphITA 2011: Selected papers from the Workshop on Fundamentals and Applications of Graphene, Springer, Berlin Heidelberg, 2012 Search PubMed.
- Z. Shunhong, et al., Penta-graphene: a new carbon allotrope, Radio Electronics Nanosystems Information Technology, 2015, 7(2), 191–207 CrossRef.
- H. Sun, S. Mukherjee and C. V. Singh, Mechanical properties of monolayer penta-graphene and phagraphene: a first-principles study, Phys. Chem. Chem. Phys., 2016, 18(38), 26736–26742 RSC.
- Q. Peng, et al., A theoretical analysis of the effect of the hydrogenation of graphene to graphane on its mechanical properties, Phys. Chem. Chem. Phys., 2013, 15(6), 2003–2011 RSC.
- Q. Peng, W. Ji and S. De, Mechanical properties of graphyne monolayers: a first-principles study, Phys. Chem. Chem. Phys., 2012, 14(38), 13385–13391 RSC.
- G. Gui, J. Li and J. Zhong, Band structure engineering of graphene by strain: first-principles calculations, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78(7), 075435 CrossRef.
- M. Topsakal, S. Cahangirov and S. Ciraci, The response of mechanical and electronic properties of graphane to the elastic strain, Appl. Phys. Lett., 2010, 96(9), 091912 CrossRef.
- Y. P. Varshni, Temperature dependence of the energy gap in semiconductors, Physica, 1967, 34(1), 149–154 CrossRef CAS.
- D. N. Quang, B. Esser and R. Keiper, On the theory of the complex dielectric function of a heavily doped degenerate semiconductor, Phys. Status Solidi B, 1979, 94(1), 115–123 CrossRef.
- S. De Leeuw, J. W. Perram and E. Smith, Computer simulation of the static dielectric constant of systems with permanent electric dipoles, Annu. Rev. Phys. Chem., 1986, 37(1), 245–270 CrossRef CAS PubMed.
- F. Zheng, J. Tao and A. M. Rappe, Frequency-dependent dielectric function of semiconductors with application to physisorption, Phys. Rev. B, 2017, 95(3), 035203 CrossRef.
- O. Stenzel, The Physics of Thin Film Optical Spectra: An Introduction, Springer, 2005 Search PubMed.
- R. T. Cygan and A. C. Lasaga, Dielectric and polarization behavior of forsterite at elevated temperatures, Am. Mineral., 1986, 71(5–6), 758–766 CAS.
- B. Qiu, et al., Optical Properties of Graphene/MoS2 Heterostructure: First Principles Calculations, Nanomaterials, 2018, 8(11), 962 CrossRef PubMed.
- B. Mohan, A. Kumar and P. K. Ahluwalia, A first principle study of interband transitions and electron energy loss in mono and bilayer graphene: effect of external electric field, Phys. E, 2012, 44(7), 1670–1674 CrossRef CAS.
- O. V. Sedelnikova, L. G. Bulusheva and A. V. Okotrub, Ab initio study of dielectric response of rippled graphene, J. Chem. Phys., 2011, 134(24), 244707 CrossRef CAS PubMed.
- T. Eberlein, et al., Plasmon spectroscopy of free-standing graphene films, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77(23), 233406 CrossRef.
- P. Li, X. Ren and L. He, First-principles calculations and model analysis of plasmon excitations in graphene and graphene/hBN heterostructure, Phys. Rev. B, 2017, 96(16), 165417 CrossRef.
| This journal is © The Royal Society of Chemistry 2020 |