Open Access Article
Open Access ArticleDirect hybridization gap from intersite and onsite electronic interactions in CeAg2Ge2
Soma Banik *ab,
A. Aryac and
A. K. Sinha
*ab,
A. Aryac and
A. K. Sinha ab
ab
aSynchrotron Utilization Section, Raja Ramanna Centre for Advanced Technology, Indore, 452013, India. E-mail: soma@rrcat.gov.in
bHomi Bhabha National Institute, Training School Complex, Anushakti Nagar, Mumbai, 400094, India
cGlass and Advanced Materials Division, Bhabha Atomic Research Centre, Mumbai, 400085, India
First published on 25th June 2020
Abstract
Electronic and crystal structure studies are presented to describe the role of intersite and onsite interactions for antiferromagnetic ordering in CeAg2Ge2. The crystal structure showed a prominent magnetovolume effect with anomalous negative thermal expansion at low temperature as a consequence of itinerant electron magnetism. The direct hybridization gap with a V-shaped band observed in the angle resolved photoemission data at room temperature, indicates that spin polarized quasiparticle states exist in the gapped region. Valence band broadening and enhanced localization effects at low temperature indicate strong hybridization of the valence orbitals of Ce atoms with the near neighbor Ge atoms. We find that the intersite interaction between the Ce atoms at high temperature stabilizes the onsite interaction at low temperature that leads to the spin density wave type antiferromagnetism in CeAg2Ge2.
1 Introduction
In Ce based intermetallic compounds the 4f electron lies at the boundary between the itinerant and localized character which gives rise to a variety of ground state properties, such as heavy fermion superconductivity, quantum phase transitions, valence fluctuations and magnetically ordered ground state with varying degree of renormalized quasiparticle masses.1–4 In the iso-structural CeT2Ge2 (T = Ru, Au and Ag), ferromagnetic, antiferromagnetic (AFM) and incommensurate structures have been inferred from neutron scattering.5 In particular, the variation of the magnetic relaxation rate with temperature in CeAg2Ge2 was explained by the hybridization of 4f electrons with the delocalized band states, leading to the existence of renormalized electronic quasiparticles and antiferromagnetic order. From the residual linewidth at low temperature, a Kondo lattice temperature of 3 ± 1 K was inferred in CeAg2Ge2 which orders antiferromagnetically at TN = 4.6 K.6 The quasielastic scattering in CeAg2Ge2 was found to have onsite (Kondo) and intersite (RKKY) correlations. Later work on single crystalline CeAg2Ge2 revealed a spin density wave (SDW) structure of Ce moments along the [001] direction which fluctuate spatially along the b-axis.7 A shallow minimum in the electrical resistivity at 20 K and an entropy release of Rln4 at 20 K were attributed to the short range antiferromagnetic order and/or residual weak Kondo interaction that lead to the quasiquartet ground state in CeAg2Ge2.6Magnetism in Ce based heavy fermion systems depends on the intrinsic strong Coulomb correlation (U) within the 4f shell which gives rise to the local moment and the initial mixing of the 4f localized states with the 5d band states through f–d hybridization, which in turn gives rise to the spin polarised quasiparticle states. It is well known that the Ce based intermetallic compounds may exhibit a hybridization gap in their electronic spectra which can be indirect or direct.8 The hybridization gap is the absence of quasiparticle states between the conduction band and the localized 4f states.9 In the case of an indirect hybridization gap as reported in heavy-fermion semiconductors and Kondo insulators, the chemical potential will lie within the gap. For the direct hybridization gap, the chemical potential will lie outside the hybridization gap and the ground state can either be metallic or semimetallic.8 From our earlier photoemission measurements we found that Ce exists in the metallic γ-Ce phase in CeAg2Ge2.10–12 We have experimentally determined the Coulomb correlation energy within the Ce 4f shell (U ≈ 4.2 eV) and the hybridization interaction between the Ce 4f and the 5d electrons (Δ ≈ 0.19 eV) which corroborates with the single impurity Anderson model.10,11 Here we further extended our photoemission work to estimate the hybridization gap present in this system and to understand its origin. We have reported a comparative study of experimental band structure and LSDA + U calculations to explain the role of intersite and onsite interactions in the origin of both spin density wave aniferromagnetism and the hybridization gap in CeAg2Ge2.
2 Methods: experimental and theory
A CeAg2Ge2 single crystal was grown by the self-flux method.6 High resolution angle resolved photoemission measurement with 10 meV energy resolution and 0.2° angular resolution was performed at the experimental station of angle resolved photoelectron spectroscopy (ARPES), Indus-2, India. The CeAg2Ge2 single crystal was cleaved in situ to obtain an atomically clean surface at room temperature and at the base vacuum of 6 × 10−11 mbar. The typical dimensions of the flat single crystalline [001] surface after cleaving are about 3 mm × 4 mm. For the consistency of the results we performed the photoemission measurements on the same cleaved surface at the paramagnetic phase at 300 K (RT) and at 15 K near TN, which we shall call the low temperature (LT) phase. The LT in the ARPES set-up has been achieved using a 4 K closed cycle refrigerator with a temperature stability of 0.2 K. Core levels were studied using X-ray photoemission spectroscopy (XPS) with Mg Kα source from SPECS (XR 50). Valence band angle integrated photoelectron spectroscopy (AIPES) and angular resolved photoelectron spectroscopy (ARPES) were studied using a monochromatic helium-1 source from SPECS (UVS 300). The spot size of the He source is 0.8 mm and it has been ensured that the spot of the He source falls on the flat surface of the single crystal during the measurement. All the AIPES valence band, XPS and ARPES data were recorded with a SPECS Phoibos 150 electron energy analyzer. The base vacuum during the measurement was 7 × 10−11 mbar. Temperature dependent X-ray diffraction (XRD) measurements were performed at the angle-dispersive X-ray diffraction (ADXRD) beamline with an Indus-2 synchrotron radiation source. LT was achieved using a liquid helium based flow-type cryostat with temperature stability of 0.15 K. A high spectral resolution of about 1 eV at 10 keV was achieved using a Si(111) based double crystal monochromator.13 Powder XRD of the CeAg2Ge2 single crystal was recorded at 15 keV excitation energy using an Image plate Mar-345 detector. The photon energy and the sample to detector distance were accurately calibrated using LaB6 NIST standard. Fit2D software was used to generate the XRD pattern from the diffraction rings obtained by Image plate data. Le Bail decomposition of the XRD pattern was carried out using the JANA2000 package.14Ab initio planewave-based calculations are performed employing the Vienna Ab initio Simulation Package (VASP)15 within the generalized gradient approximation (GGA) using Perdew–Burke–Ernzerhof parameterization for exchange correlation.16 Projected augmented wave (PAW) potentials are used which treats Ge 3d4s4p states, Ag 4d5s5p states and Ce 5d4f6s states as valence states. We have performed spin-polarized calculations including the Coulomb correlation (U) under the local spin density approximation (LSDA + U) scheme as proposed by Dudarev et al.17 including the spin–orbit coupling (SOC). We have referred this calculation as the onsite calculation. In another configuration the spin-up and spin-down moments are considered on the two different Ce sites including the Coulomb correlation (U) and the SOC under the same LSDA + U scheme and are referred to in the intersite calculation. The U–J parameter is kept fixed at 4.5 eV in all the LSDA + U calculations.
3 Results and discussion
3.1 Crystal structure of CeAg2Ge2
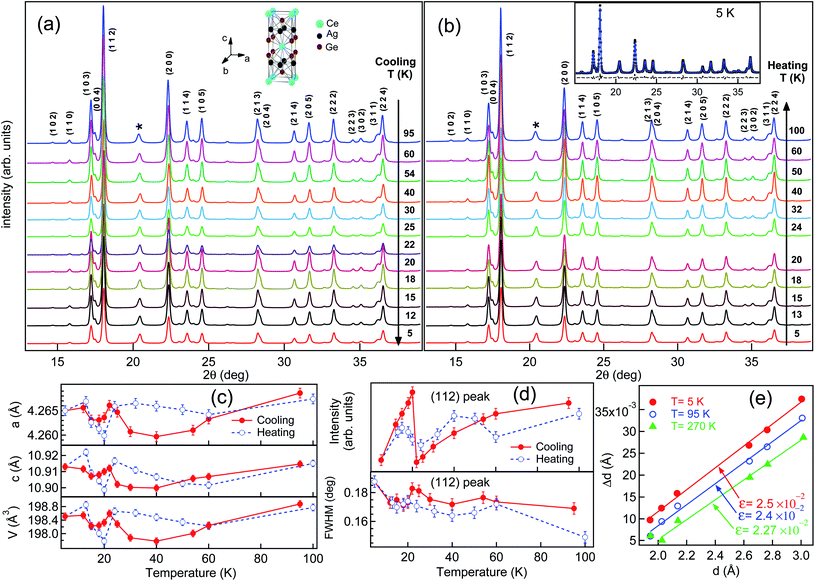
CeAg2Ge2 crystallizes in a ThCr2Si2-type crystal structure with a tetragonal I4/mmm space group.6 The crystal structure is shown in the inset of Fig. 1(a). We have performed the temperature dependent XRD measurements to understand the influence of magnetic interactions on the crystal structure. The XRD measurements were performed on the powder sample in both the cooling and the heating cycles as shown in Fig. 1(a) and (b). We have observed a peak corresponding to the Ag![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ge eutectic phase at 20.45° (marked by a star in Fig. 1(a) and (b)). Such a eutectic phase peak has been reported for single crystals grown by the flux method, for example in CeAg2Si2,18 EuPd2P219 etc. Since, this eutectic phase peak is non-magnetic, it is considered as the reference peak, and the normalization of all the XRD patterns at different temperatures have been performed at this peak position. In Fig. 1(a) and (b) a clear intensity variation in heating and cooling cycles are observed in the diffraction peaks. We used the Le Bail method to determine the lattice parameters at all temperatures. The representative Le Bail fitting of the XRD pattern at 5 K is shown in the inset of Fig. 1(b). We find that there is an isostructural change across the magnetic transition and hence the lattice parameters a and c in Fig. 1(c) follow similar spectral behaviour in both heating and cooling cycles. Decreasing the temperature causes both lattice parameters a and c to decrease down to 60 K followed by anomalous behaviour due to the onset of magnetic transitions. The anomalous negative thermal expansion is expected in magnetic materials which is a result of the magnetovolume effect due to the change in volume resulting from the amplitude variation of a magnetic moment.20 We have observed hysteresis in the lattice parameters as well as in the volume, indicating that the magnetic transition is a first order type. A dip observed in the lattice parameters and volume at around 20 K is related to the short range antiferromagnetic ordering.6 The lattice constants estimated at the RT phase (300 K) are: a = 4.276 and c = 10.915; and at the LT phase (5 K), a = 4.265 and c = 10.913. So, the total volume contraction at the LT phase is just 0.5%. However, the lattice change along the a, and b axis is 5.5 times larger than the c-axis which indicates that the magnetic interaction between the Ce atoms is more on the ab-plane which is responsible for the anisotropic magnetic properties present in this system.6,7
Ge eutectic phase at 20.45° (marked by a star in Fig. 1(a) and (b)). Such a eutectic phase peak has been reported for single crystals grown by the flux method, for example in CeAg2Si2,18 EuPd2P219 etc. Since, this eutectic phase peak is non-magnetic, it is considered as the reference peak, and the normalization of all the XRD patterns at different temperatures have been performed at this peak position. In Fig. 1(a) and (b) a clear intensity variation in heating and cooling cycles are observed in the diffraction peaks. We used the Le Bail method to determine the lattice parameters at all temperatures. The representative Le Bail fitting of the XRD pattern at 5 K is shown in the inset of Fig. 1(b). We find that there is an isostructural change across the magnetic transition and hence the lattice parameters a and c in Fig. 1(c) follow similar spectral behaviour in both heating and cooling cycles. Decreasing the temperature causes both lattice parameters a and c to decrease down to 60 K followed by anomalous behaviour due to the onset of magnetic transitions. The anomalous negative thermal expansion is expected in magnetic materials which is a result of the magnetovolume effect due to the change in volume resulting from the amplitude variation of a magnetic moment.20 We have observed hysteresis in the lattice parameters as well as in the volume, indicating that the magnetic transition is a first order type. A dip observed in the lattice parameters and volume at around 20 K is related to the short range antiferromagnetic ordering.6 The lattice constants estimated at the RT phase (300 K) are: a = 4.276 and c = 10.915; and at the LT phase (5 K), a = 4.265 and c = 10.913. So, the total volume contraction at the LT phase is just 0.5%. However, the lattice change along the a, and b axis is 5.5 times larger than the c-axis which indicates that the magnetic interaction between the Ce atoms is more on the ab-plane which is responsible for the anisotropic magnetic properties present in this system.6,7
Interestingly, we find that the dependence of temperature also has influence on the diffraction peak intensity and the full width at half maximum (FWHM) of the peaks. In Fig. 1(d) the intensity variation of the (112) peak is plotted for both heating and cooling cycles (top panel). The intensity of the (112) peak is found to decrease with the decrease in temperature followed by a sharp kink at 20 K. Moreover, the FWHM of the (112) peak in Fig. 1(d) (bottom panel) is found to increase with the decrease in temperature showing a dip at around 20 K. The broadening of the diffraction peaks with the decrease in temperature as well as the variation of the peak intensity21 indicates the presence of residual strain in CeAg2Ge2. This residual strain is associated with the magnetic interactions between the Ce atoms at different sites and is responsible for the anomalous negative thermal expansion and magnetovolume effect in this system. The residual microstrain (ε) which is independent of the grain size can be calculated in the ambient stress free conditions using the formula ε = Δd/d, where d is the peak position and Δd = (Δdobserved2 − Δdinstrumental2)1/2 is the width of the peak after subtracting the instrumental broadening.21 The instrumental broadening has been obtained from the LaB6 NIST standard sample. The value of ε can be estimated from the slope of the straight line fitting in the Δd vs. d plot as shown in Fig. 1(e) for 5 K, 95 K and 270 K in the cooling cycle. We find that ε at 5 K (≈2.5 × 10−2) is larger than at 270 K (≈2.27 × 10−2). The decrease in the value of ε at higher temperatures clearly indicates that the residual strain gets relaxed at higher temperatures. The magnetovolume effect and magnetostriction are well reported in rare earth based antiferromagnetic systems22 and in several other magnetic systems.20,23,24 The magnetovolume effect in the magnetic systems is associated mainly with itinerant electron magnetism22,23,25 where the electrons responsible for magnetism are also responsible for chemical bonding. The temperature induced strain may arise as the overlap of the electronic orbitals is expected to enhance at low temperature and is responsible for the changes in the chemical bonding between the atoms which will modify the hybridization of the valence electrons. Hence, there is a need to explore the electronic structure of CeAg2Ge2 as a function of temperature to understand the changes in the chemical bonding responsible for the itinerant electron magnetism in this system.
3.2 AIPES studies and LSDA + U calculations
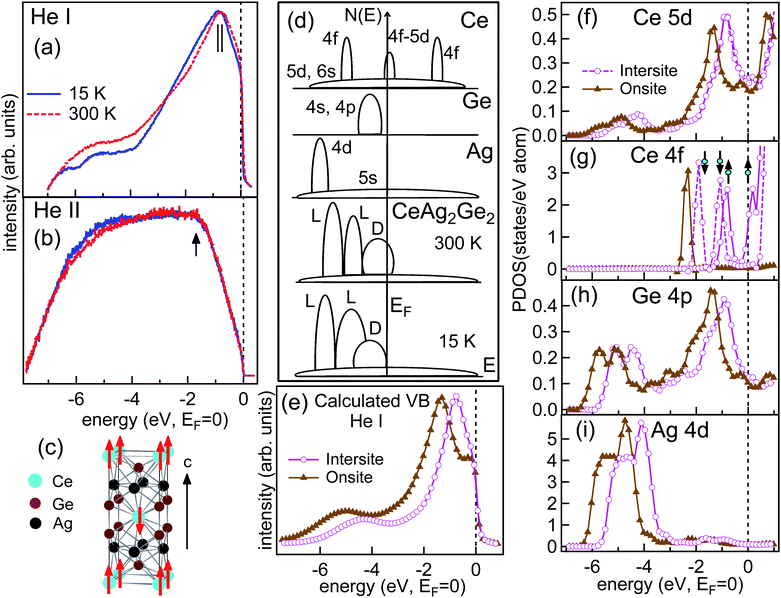
To understand the role of chemical bonding we have performed the core level studies at RT and LT phases. The inelastic background has been subtracted from the raw data by the Tougaard procedure.26 The Ce 3d core level spectra in Fig. 2(a) show that the spin–orbit splitting in CeAg2Ge2 is ∼18.6 eV at both RT and LT phases, and is higher than that of elemental Ce, ∼18.1 eV.27 The Ce 3d core level has contributions from 3d9f1 and 3d9f2 states marked as f1 and f2, respectively. The f1 feature arises when the screening is produced in the 5d6s2 band, and the f2 feature arises when the screening occurs in the 4f band which pulls the additional 4f state below the Fermi energy (EF) such that there is filling of the core hole due to the Coulomb interaction.31 Appearance of the f2 feature signifies that the 4f states have a delocalized character due to the hybridization with the conduction electrons.11 We performed the deconvolution of the Ce 3d core level to extract the information about the delocalized valence electrons (the f2 feature as shown in Fig. 2(b)). The intensity ratio (r) of the f1 and f2 peaks can be used to determine the total hybridization parameter (Δ) such that r = I(f2)/(I(f1) + I(f2)). The value of r is estimated to be ≈0.37 ± 0.005 and ≈0.15 ± 0.003 at RT and LT, respectively. Using the correlation between Δ and r as outlined by Fuggle et al.,11,28 the estimated value of Δ at the RT phase is ≈0.190 ± 0.005 eV and the LT phase is ≈0.085 ± 0.001 eV. A higher value of Δ at RT indicates that the quasiparticle state which arises due to the hybridization between the Ce 4f and the conduction electrons has higher density at RT. We have observed a shift in the 3d core level of Ag and Ge towards a lower binding energy at RT as shown in Fig. 2(c) and (d), respectively. However, both Ag 3d and Ge 3d core levels lie at the same energy position at the LT when compared with the pure elemental Ag 3d and Ge 3d core levels.27 The shift of 3d peaks between LT and RT for Ag is about 0.65 eV and for Ge is about 0.6 eV. The reason for the shift in the 3d peaks of Ag and Ge towards lower binding energy at RT is associated with the change in the density of conduction electrons at EF with temperature, which can happen as the higher thermal energy at RT increases the hopping probability of the valence electrons into the conduction band while at LT the valence electrons will try to remain in the lowest energy state. This is typical semiconductor-like activation behavior due to the Ge atoms. Hence, temperature dependence of the electronic states indicates that the orbitals of the Ge atoms must be overlapped with the orbitals of the Ce and the Ag atoms. A similar kind of temperature dependence on the core levels has been observed in MnSi1.75 which was attributed to the strong hybridization between the Mn 3d and Si 3p states.29 In CeAg2Ge2, we expect that the quasiparticle states of Ce must be strongly hybridized with the valence electrons of Ge and Ag to obtain the metallic bond.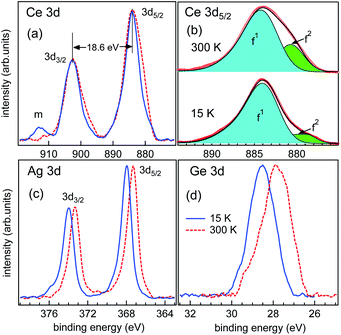 | ||
| Fig. 2 Core levels of CeAg2Ge2 at 300 K (dashed line) and 15 K (solid line) shown for (a) Ce 3d (c) Ag 3d and (d) Ge 3d. (b) Shows the Ce 3d5/2 fitted with the f1, f2 contribution at 300 K and 15 K. | ||
In Fig. 2(a), a broad shake-up satellite feature marked by m is observed at around 913 eV. The most frequent shake-up satellites are either plasmon losses or discrete excitations like the sharp f0 peak in α-Ce systems.31 We find that the intensity of the f0 peak in the Ce 3d core level is almost negligible for Ce 3d5/2 which indicates that Ce exists in the stable trivalent state in this compound in the whole temperature range, and the shake-up satellite is related to plasmonic losses. A similar broad shake-up satellite is also observed for γ-type Ce metal,30 CeSe31 and CeMIn5 where M = Ir, Co, Rh.32 The enhancement of the plasmonic excitation at LT is also reported in CeMIn5 systems32 which is related to a more free electron-like character at EF. So, the origin of plasmonic excitation in CeAg2Ge2 at LT indicates strong hybridization between the quasiparticle Ce 4f states and the near neighbor Ge states which will lead to opening of the activation-type hybridization gap. Hence, the EF is expected to lie in the conduction band with more free electron-like states that leads to the metallic properties.
AIPES valence band spectra of CeAg2Ge2 at RT and LT phases recorded using 21.2 eV (He I) and 40.8 eV (He II) excitation energies are shown in Fig. 3(a) and (b), respectively. The photoionization cross-section of Ce 5d is higher than Ce 4f in the He I spectra while the photoionization cross-section of the Ce 4f state is higher than Ce 5d in the He II spectra. We observed the centroid position in the He I spectra at −0.75 eV for RT which shifted to −0.95 eV for LT (shown by vertical markers) in Fig. 3(a). The He II valence band in Fig. 3(b) does not show any shift of the centroid position and lies at −1.7 eV which corresponds to the position of the localized Ce 4f0 state. There are a further three important observations in the He II spectra: (1) the energy position of the Ce 4f state, (2) the valence band spectral shape and (3) the electronic states at the vicinity of EF, all confirm that the Ce is in the γ-type Ce phase in this system over the whole temperature range, which is in agreement with our earlier resonant photoemission work in ref. 10. Interestingly we observe that there is not only an increase in the valence band width at LT in the region between EF and −3 eV binding energy (see Fig. 3(a)) but also there is depletion of the electronic states near EF. All the above measurements indicate that there is strong Ce 4f, 5d and Ge 4s, 4p hybridization present that leads to valence band broadening and hence, enhances the screening effect.
The mechanism of localization and delocalization phenomena in CeAg2Ge2 can be understood from the schematic diagram of density of states [N(E)] for elemental Ce, Ge and Ag as shown in Fig. 3(d). In elemental Ce it is known that the localized state is purely a 4f state governed by the Coulomb correlation U, while the delocalized quasiparticle state is the 4f–5d hybridized state near EF. With the increase in hybridization in elemental Ce at LT the density of the delocalized 4f–5d state will enhance because of the direct overlap of the delocalized 4f orbitals of one atom with the other Ce atoms. In elemental Ge, 4s–4p states are localized and lie away from EF with a band gap of ≈0.7 eV. The band gap in Ge opens at LT while at RT the thermal energy excites the electrons from the valence band to the conduction band, and hence the 4p electrons have delocalized character at RT. The elemental Ag has more localized 4d states which lie well below EF (≈5.5 eV) with free electron-like 5s states at EF. The scenario of localized and delocalized bands in CeAg2Ge2 are marked by L and D, respectively, and are shown for the present experimental conditions at RT and LT in Fig. 3(d). From the crystal structure of CeAg2Ge2 in Fig. 3(c) we find that the Ce atom has first near neighbor Ge atoms while the Ag atoms are strongly bonded with the Ge atoms. Due to the metallic bonding in CeAg2Ge2 in the whole temperature range, the valence electrons of Ce, Ge and Ag will hybridize to have more delocalized states. Hence, the delocalized 4p orbitals of Ge atoms are expected to hybridize with the delocalized 4f–5d orbitals of the near neighbor Ce atoms as well as with the 5s orbitals of Ag atoms. So, the delocalized broad feature near EF arises due to the hybridization of conduction electrons of Ce, Ge and Ag while there are two localized bands arising due to the Ce 4f and Ag 4d states which are also hybridized with the localized Ge 4p states. Hence, the drastic variation observed in the valence band and the core levels in CeAg2Ge2 at RT and LT is mainly due to the temperature dependence of the Ge states that are strongly hybridized with the Ce and the Ag states. Moreover the magnetic interaction in this system will depend on the intersite and the onsite interactions of the Ce atoms which has the local moment.
To understand the effect of orbital overlap at different temperatures, and hence the change in the hybridization in CeAg2Ge2, we performed density of states (DOS) calculations using the LSDA + U method. As hybridization is not the input parameter in the DFT calculations, we adopted two models based on the theory of Anderson’s kinetic exchange interactions33 like: (1) intersite exchange interaction with the local moments on Ce atoms where the indirect exchange interaction is between the local moments through the spin polarization of the conduction electrons (RKKY-type); and (2) onsite Coulomb interactions where the local moments are screened by the spin polarized conduction electrons (Kondo-type). From our He II data in Fig. 3(b) we find that the position of the Ce 4f0 state marked by an arrow remains the same at both RT and LT which indicates that the local moment due to 4f localization (U) remains constant across the magnetic transition while the density of delocalized electrons have been found to change drastically, as observed in He I (Fig. 3(a)). The intersite exchange interaction model is generally considered for a many body system with one spin-up and one spin-down electron at two different sites. We have considered spin-up and spin-down orientations at the two different sites of Ce atoms along the c-axis as shown in Fig. 3(c), based on the neutron scattering results where the maximum change along the c-axis has been attributed to the presence of intrinsic SDW.7 In the second model of onsite spin polarization, the localization governed by U, is due to the interaction between the antiparallel spin states at the same site. The SOC has been incorporated in both the calculations. The PDOS of Ce 5d, Ce 4f, Ge 4p and Ag 4d states which have the larger photoionization cross-section in the photoemission valence band, are shown in Fig. 3(f), (g), (h) and (i), respectively, for both the intersite and onsite calculations. In the onsite calculation Ce 4f states lie at −2.2 eV below EF (Fig. 3(g)) indicating the more localized nature, while the delocalized Ce 4f states near EF are absent. In the intersite calculation the localized Ce 4f state with the spin-down orientation appears at −1.8 eV and the spin-up state, which has the delocalized character, appears near the EF. The SOC in the intersite calculation not only causes the splitting of the spin degenerate states in the 2 different Ce sites (Fig. 3(g)), but also induces hybridization between the spin-up and spin-down states. Clear energy shift in the density of all the valence states has been observed between the intersite and onsite calculations which is consistent with the experimental core levels and valence band at RT and LT. It is quite clear from the LSDA + U calculations that the electronic states up to −3 eV from EF, have the dominant contribution due to the hybridized Ce 4f, 5d and Ge 4p states, while the electronic states below −3 eV up to −7 eV are mostly the hybridized Ag 4d and Ge 4p states.
Theoretical DOS calculations are broadened in Fig. 3(e) for direct comparison with the experimental He I data (Fig. 3(a)). He-I spectra have a higher photoionization cross-section of Ce 5d and Ge 4p states, hence the broadening has been carried out by adding the PDOS of Ce 5d and Ge 4p states. The added DOS then multiplies with the Fermi function at the measurement temperature and convoluted with a Voigt function. The FWHM of the Gaussian component is taken to be 0.1 eV of the Voigt function which represents the maximum instrumental resolution at 300 K. The energy dependent Lorentzian FWHM that represents the life-time broadening is 0.3E, where E is the energy with respect to EF.11 The inelastic background and the matrix elements are not considered. All the broadened DOS are normalized at the maximum peak position. We find that both the centroid position at RT (−0.75 eV) and LT (−0.95 eV), and the spectral shape observed in the experiment (Fig. 3(a)), show very good consistency with the calculation (Fig. 3(e)) for intersite interactions (−0.83 eV) and onsite interactions (−1.3 eV). Moreover the valence band broadening and the depletion of states are also quite prominent for the onsite interaction, similar to the experimental LT spectra (Fig. 3(a)). There are small differences between experimental and theory because of the sample related strain effects which are not considered in the calculations. Moreover the theoretical calculations are performed at 0 K considering ideal conditions, which may not be the case in the experiment.
3.3 ARPES studies and LSDA + U calculations
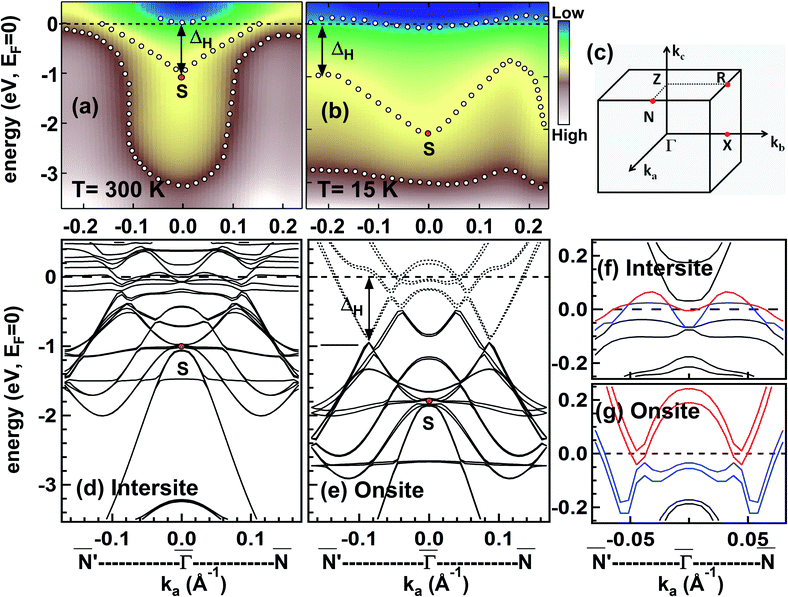
The magnetic interaction between the Ce atoms is found to be more along the ab-plane as obtained in our XRD measurement, hence we have performed ARPES along the ka (![[N with combining macron]](https://www.rsc.org/images/entities/i_char_004e_0304.gif) ′–
′–![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) –
–![[N with combining macron]](https://www.rsc.org/images/entities/i_char_004e_0304.gif) ) direction using He I excitation at the RT and the LT phases as shown in Fig. 4(a) and (b). In Fig. 4(c) the Brillouin zone with high symmetry points on the projected 2D surface are shown. Near EF the conduction band is observed at RT (Fig. 4(a)) and LT (Fig. 4(b)). A V-shaped band and van Hove singularity (marked by S) at the
) direction using He I excitation at the RT and the LT phases as shown in Fig. 4(a) and (b). In Fig. 4(c) the Brillouin zone with high symmetry points on the projected 2D surface are shown. Near EF the conduction band is observed at RT (Fig. 4(a)) and LT (Fig. 4(b)). A V-shaped band and van Hove singularity (marked by S) at the ![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) point has been observed at −1.1 eV in both the RT ARPES data (Fig. 4(a)) and the intersite calculation (Fig. 4(d)). The origin of S at RT can be understood from the Ce 4f PDOS calculation for intersite (Fig. 3(g)), where we find that the spin-up states (solid line with circles) and spin-down states (dashed line with circles) cross each other at around −1 eV which gives rise to the singularity (Fig. 4(a)). The V-shaped band at RT is a clear signature of the SOC and the magnetocrystalline anisotropy present in this system. A large parabolic band with minimum around −3 eV and flat ends, appears in the RT data (Fig. 4(a)) but is not present in the intersite calculation (Fig. 4(d)). Such bands have been seen in other rare-earth based systems and arise due to the bulk surface correspondence where electrons or holes on the surface of the material interact due to the non-trivial topology of the electronic spectra in the bulk.34 ARPES data at the LT phase (Fig. 4(b)) show good agreement with the onsite calculations (Fig. 4(e)) where S is shifted to a higher binding energy (≈−2 eV). Temperature dependence on the conduction electrons and opening of the hybridization gap at LT is quite clear in the ARPES data. We find a direct hybridization gap ΔH ≈ 1 eV (marked with an arrow in Fig. 4(a) and (b)) that has activation-type behavior present in CeAg2Ge2. In rare earth based systems the activation-type hybridization gap is reported to arise between the localized 4f band and the 5d conduction band.35 The opening of the activation-type hybridization gap indicates the absence of the quasiparticle state which is clearly observed in the experimental ARPES data at LT (Fig. 4(b)). The V-shaped band which appears inside the hybridization gap is the quasiparticle state that arises due to the Ce 4f–5d hybridization at RT (see Fig. 3(f) and (g)). We also find that the Ce 5d conduction electrons are also strongly hybridized with the Ge 4p conduction electrons in the PDOS in Fig. 3(f) and (h). At LT, the onsite interactions of the Ce atoms give rise to a separate hole-like valence band (solid bands in Fig. 4(e)) and electron-like conduction band (dotted bands in Fig. 4(e)). The conduction band minimum is obtained at ≈−1 eV (shown by arrow in Fig. 4(e)) from EF. We find that the quasiparticle state which arises due to the Ce 4f–5d hybridization is absent in this region (see Fig. 3(f) and (g)) for the onsite interaction and hence confirms the presence of a hybridization gap in the calculation (marked by an arrow in Fig. 4(e)). In the onsite calculation, the spin polarized electronic states near EF are the hybridized Ce 5d and Ge 4p states. Such free electron-like states are responsible for the enhanced plasmonic excitation as observed in the Ce 3d core level in Fig. 2(a). The enhanced localization effect observed in the experiments at LT is due to the hybridization of the Ce 4f, 5d with the Ge 4p states (see Fig. 3(f), (g) and (h)). We find that the opening of the hybridization gap at LT is governed by the onsite interaction in Ce atoms, but the activation-like behavior present in the Ge atoms with strong hybridization between Ge 4p and Ce 5d states enhances the screening of the localized 4f moment by the 5d conduction electrons and stabilizes the Kondo lattice-like behavior in this system. Hence, the interplay between the Kondo and the RKKY-type interactions gives rise to the magnetic ordering in this system. Some differences have been observed in the experimental band structure as compared to the theoretical calculations as we find a larger number of bands in theory corresponding to all the valence band states including Ce 4f, Ce 5d, Ag 4d and Ge 4p, but in the experiment the photoionization cross-section of Ce 5d and Ge 4p states is higher with He I excitation, hence, all the bands are not observed in the experimental ARPES data which enables us to determine the actual ΔH present in CeAg2Ge2. The optical transition gap of about ∼1 eV has been reported in ref. 36 for CeAg2Ge2 from optical conductivity measurement which supports the present results.
point has been observed at −1.1 eV in both the RT ARPES data (Fig. 4(a)) and the intersite calculation (Fig. 4(d)). The origin of S at RT can be understood from the Ce 4f PDOS calculation for intersite (Fig. 3(g)), where we find that the spin-up states (solid line with circles) and spin-down states (dashed line with circles) cross each other at around −1 eV which gives rise to the singularity (Fig. 4(a)). The V-shaped band at RT is a clear signature of the SOC and the magnetocrystalline anisotropy present in this system. A large parabolic band with minimum around −3 eV and flat ends, appears in the RT data (Fig. 4(a)) but is not present in the intersite calculation (Fig. 4(d)). Such bands have been seen in other rare-earth based systems and arise due to the bulk surface correspondence where electrons or holes on the surface of the material interact due to the non-trivial topology of the electronic spectra in the bulk.34 ARPES data at the LT phase (Fig. 4(b)) show good agreement with the onsite calculations (Fig. 4(e)) where S is shifted to a higher binding energy (≈−2 eV). Temperature dependence on the conduction electrons and opening of the hybridization gap at LT is quite clear in the ARPES data. We find a direct hybridization gap ΔH ≈ 1 eV (marked with an arrow in Fig. 4(a) and (b)) that has activation-type behavior present in CeAg2Ge2. In rare earth based systems the activation-type hybridization gap is reported to arise between the localized 4f band and the 5d conduction band.35 The opening of the activation-type hybridization gap indicates the absence of the quasiparticle state which is clearly observed in the experimental ARPES data at LT (Fig. 4(b)). The V-shaped band which appears inside the hybridization gap is the quasiparticle state that arises due to the Ce 4f–5d hybridization at RT (see Fig. 3(f) and (g)). We also find that the Ce 5d conduction electrons are also strongly hybridized with the Ge 4p conduction electrons in the PDOS in Fig. 3(f) and (h). At LT, the onsite interactions of the Ce atoms give rise to a separate hole-like valence band (solid bands in Fig. 4(e)) and electron-like conduction band (dotted bands in Fig. 4(e)). The conduction band minimum is obtained at ≈−1 eV (shown by arrow in Fig. 4(e)) from EF. We find that the quasiparticle state which arises due to the Ce 4f–5d hybridization is absent in this region (see Fig. 3(f) and (g)) for the onsite interaction and hence confirms the presence of a hybridization gap in the calculation (marked by an arrow in Fig. 4(e)). In the onsite calculation, the spin polarized electronic states near EF are the hybridized Ce 5d and Ge 4p states. Such free electron-like states are responsible for the enhanced plasmonic excitation as observed in the Ce 3d core level in Fig. 2(a). The enhanced localization effect observed in the experiments at LT is due to the hybridization of the Ce 4f, 5d with the Ge 4p states (see Fig. 3(f), (g) and (h)). We find that the opening of the hybridization gap at LT is governed by the onsite interaction in Ce atoms, but the activation-like behavior present in the Ge atoms with strong hybridization between Ge 4p and Ce 5d states enhances the screening of the localized 4f moment by the 5d conduction electrons and stabilizes the Kondo lattice-like behavior in this system. Hence, the interplay between the Kondo and the RKKY-type interactions gives rise to the magnetic ordering in this system. Some differences have been observed in the experimental band structure as compared to the theoretical calculations as we find a larger number of bands in theory corresponding to all the valence band states including Ce 4f, Ce 5d, Ag 4d and Ge 4p, but in the experiment the photoionization cross-section of Ce 5d and Ge 4p states is higher with He I excitation, hence, all the bands are not observed in the experimental ARPES data which enables us to determine the actual ΔH present in CeAg2Ge2. The optical transition gap of about ∼1 eV has been reported in ref. 36 for CeAg2Ge2 from optical conductivity measurement which supports the present results.
The local magnetic moment determined in the intersite calculation for the Ce 4f spin-up is ≈0.954 μB and the spin-down is ≈1.109 μB. The fully degenerate J = 5/2 ground-state of Ce3+ ion has the moment of 2.15 μB along the c-axis5,7 which is in good agreement with the total moment obtained in the intersite calculation (2.06 μB). In the onsite calculation the change in Ce moment along different directions depends on the SOC. The highest magnetic moment is obtained along the a-axis (1.192 μB) than the b-axis (1.173 μB) and the c-axis (0.797 μB). Hence, the a-axis is the easy axis of magnetization and the calculated moment along the a-axis (1.192 μB) is in good agreement with the moment determined in the neutron scattering experiments (1.23 μB) at LT (1.5 K).7 In the intersite calculation we find that the doublet band intersects the EF (Fig. 4(f)) which is responsible for the doublet state in the RT paramagnetic phase. It was observed that the magnetic susceptibility does not obey the simple Curie–Weiss law in CeAg2Ge2, due to the doublet states present in this system.6 In the onsite calculation we find two doublet bands cross the EF (Fig. 4(g)) which are responsible for the quasi quartet ground state as reported at 20 K in CeAg2Ge2.6 As the magnetic interaction proceeds via the conduction electrons so at RT the Ce 4f electrons which are hybridized with the Ce 5d and Ge 4p states, are responsible for the SDW in this system. While at LT, the SDW stabilizes and gives rise to the antiferromagnetic ordering due to enhanced localization, where the Ce 4f is well screened by the Ce 5d and Ge 4p conduction electrons, which not only open up the direct hybridization gap in this system but also give rise to spin polarised itinerant states at EF.
4 Conclusion
We conclude that the itinerant electron magnetism in metallic CeAg2Ge2 is due to the interplay between intersite and onsite electronic interactions and is associated with a temperature dependent change in the hybridization. The magnetovolume effect with anomalous negative thermal expansion observed in the crystal structure at low temperature is associated with the itinerant electron magnetism as the electrons which take part in the chemical bonding also give rise to the magnetism. Temperature dependent variation of density of states and the increase in valence band width at low temperature indicates that the 5d conduction electrons of Ce are strongly hybridized with the near neighbour 4p electrons of Ge. The spin polarized quasiparticle states which arise due to the intersite interaction between the Ce atoms give rise to SDW in this system. However, the localization effect due to onsite interactions stabilizes SDW and gives rise to the itinerant antiferromagnetic ordering in this system. The material with negative thermal expansion has high technological demand in the precision instruments which indicates CeAg2Ge2 is a potential material for technological applications. Moreover the temperature dependence of density variation of the itinerant electrons with antiferromagnetic correlations and magnetostriction effects make this material important for applications in spintronics and thermoelectricity.Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationships that could have influenced the work reported in this paper. There are no conflicts to declare.Acknowledgements
The authors wish to thank Dr Tapas Ganguli for helpful discussions and support for the photoemission experiments. Prof. A. Thamizhavel and Prof. S. K. Dhar are thanked for the single crystal samples and helpful discussions. Dr Archana Sagdeo, Mr M. N. Singh and Mr Anuj Upadhyay are thanked for the low temperature XRD measurements.Notes and references
- D. Malterre, M. Grioni and Y. Baer, Adv. Phys., 1996, 45, 299 CrossRef CAS.
- C. Petrovic, R. Movshovich, M. Jaime, P. G. Pagliuso, M. F. Hundley, J. L. Sarrao, Z. Fisk and J. D. Thompson, Europhys. Lett., 2001, 53, 354 CrossRef CAS.
- M. V. Lalić, J. M. Filho, A. W. Carbonari and R. N. Saxena, J. Phys.: Condens. Matter, 2004, 16, 6685 CrossRef.
- E. Bauer, G. Hilscher, H. Michor, Ch. Paul, E. W. Scheidt, A. Gribanov, Yu. Seropegin, H. Noe, M. Sigrist and P. Rogl, Phys. Rev. Lett., 2004, 92, 027003 CrossRef CAS PubMed.
- A. Loidl, K. Knorr, G. Knopp, A. Krimmel, R. Caspary, A. Böhm, G. Sparn, C. Geibel, F. Steglich and A. P. Murani, Phys. Rev. B, 1992, 46, 9341 CrossRef CAS PubMed.
- A. Thamizhavel, R. Kulkarni and S. K. Dhar, Phys. Rev. B, 2007, 75, 144426 CrossRef.
- D. K. Singh, A. Thamizhavel, S. Chang, J. W. Lynn, D. A. Joshi, S. K. Dhar and S. Chi, Phys. Rev. B, 2011, 84, 052401 CrossRef.
- X. Yang, P. S. Riseborough and T. Durakiewicz, J. Phys.: Condens. Matter, 2011, 23, 094211 CrossRef PubMed.
- M. Miyazawa and K. Yamada, J. Phys. Soc. Jpn., 2003, 72, 2033 CrossRef CAS.
- S. Banik, A. Arya, A. Bendounan, M. Maniraj, A. Thamizhavel, I. Vobornik, S. K. Dhar and S. K. Deb, J. Phys.: Condens. Matter, 2014, 26, 335502 CrossRef PubMed.
- S. Banik, A. Chakrabarti, D. A. Joshi, A. Thamizhavel, D. M. Phase, S. K. Dhar and S. K. Deb, Phys. Rev. B, 2010, 82, 113107 CrossRef.
- S. Banik, A. Chakrabarti, S. K. Deb, S. N. Jha, S. V. N. Bhaskara Rao, D. A. Joshi, A. Thamizhavel and S. K. Dhar, Solid State Commun., 2010, 150, 1936 CrossRef CAS.
- A. K. Sinha, M. N. Singh, A. Upadhyay and A. Sagdeo, J. Phys.: Conf. Ser., 2013, 425, 072017 CrossRef.
- V. Petřiček and M. Dušek, Jana2000 Crystallographic computing system, 2003 Search PubMed.
- G. Kresse and J. Furthmüller, Phys. Rev. B, 1996, 54, 11169 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed; J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396 CrossRef.
- S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Phys. Rev. B, 1998, 57, 1505 CrossRef CAS.
- B. H. Grier, J. M. Lawrence, V. Murgai and R. D. Parks, Phys. Rev. B, 1984, 29, 2664 CrossRef CAS.
- G. Drachuck, A. E. Böhmer, S. L. Budko and P. C. Canfield, J. Magn. Magn. Mater., 2016, 417, 420 CrossRef CAS.
- J. Chen, L. Hu, J. Deng and X. Xing, Chem. Soc. Rev., 2015, 44, 3522 RSC.
- Y. Zhao and J. Zhang, J. Appl. Crystallogr., 2008, 41, 1095 CrossRef CAS.
- M. Doerr, M. Rotter and A. Lindbaum, Adv. Phys., 2005, 54, 1–66 CrossRef CAS.
- K. Takenaka, M. Ichigo, T. Hamada, A. Ozawa, T. Shibayama, T. Inagaki and K. Asano, Sci. Technol. Adv. Mater., 2014, 15, 015009 CrossRef PubMed.
- P. Miao, et al., Adv. Mater., 2017, 29, 1605991 CrossRef PubMed.
- Y. Takahashi, J. Jpn. Soc. Powder Powder Metall., 2016, 64, 159 CrossRef.
- S. Tougaard, Surf. Sci., 1989, 216, 343 CrossRef CAS.
- C. D. Wagner, W. M. Riggs, J. F. Moulder and L. E. Davis, Handbook of X-ray Photoelectron spectroscopy, Perkin-Elmer Corporation, 1979 Search PubMed.
- J. C. Fuggle, et al., Phys. Rev., 1983, 27, 7330 Search PubMed; J. C. Fuggle, O. Gunnarsson, G. A. Sawatzky and K. Schönhammer, Phys. Rev. B, 1988, 37, 1103 CrossRef CAS PubMed.
- S. Banik and P. P. Kumar, Solid State Commun., 2020, 307, 113807 CrossRef CAS.
- E. Wuilloud, H. R. Moser, W. D. Schneider and Y. Baer, Phys. Rev. B, 1983, 78, 7354 CrossRef.
- S. Hüfner, Photoelectron Spectrocopy Principles and Applications, Springer-Verlag, Berlin, 1995 Search PubMed.
- M. Sundermann, et al., J. Electron Spectrosc. Relat. Phenom., 2016, 209, 1–8 CrossRef CAS.
- P. W. Anderson, Phys. Rev., 1959, 115, 2 CrossRef CAS.
- S. Banik, P. K. Das, A. Bendounan, I. Vobornik, A. Arya, N. Beaulieu, J. Fujii, A. Thamizhavel, P. U. Sastry, A. K. Sinha, D. M. Phase and S. K. Deb, Sci. Rep., 2017, 7, 4120 CrossRef PubMed.
- M. Park and J. Hong, J. Korean Phys. Soc., 1998, 33, 480 CAS.
- S.-i. Kimura, Y. S. Kwon, Y. Matsumoto, H. Aoki and O. Sakai, J. Phys. Soc. Jpn., 2016, 85, 083702 CrossRef.
| This journal is © The Royal Society of Chemistry 2020 |