First-principles study of the adsorption behaviors of Li atoms and LiF on the CF_x (x = 1.0, 0.9, 0.8, 0.5, ∼0.0) surface

Abstract

Based on first principles calculation, the adsorption properties of Li atoms and LiF molecules on the fluorographene (CF_x) surface with different F/C ratios (x = 1.0, 0.9, 0.8, 0.5 and ∼0.0) have been studied in the present work. The calculated binding energy of Li and CF_x is greater than 2.29 eV under different F/C ratios, indicating that the battery has the potential to maintain a high discharge platform during the whole discharge process. But the adsorption energies of LiF on a CF_x layer for different F/C ratios are 0.12–1.04 eV, which means LiF is not easy to desorb from a CF_x surface even at room temperature. It will stay on the surface for a long time and affect the subsequent discharge. Current calculations also show the structure of the CF_x-skeleton will change greatly during the reaction, when there are many unsaturated carbon atoms on the CF_x surface, such as at x = 0.8 and 0.5. Moreover, the discharge voltage is strongly dependent on the discharge site. After discharge, the CF_x-skeleton may continue to relax and release a lot of heat energy.

---

Introduction

Rechargeable Li ion batteries have become the dominant power source for portable electronics applications, particulary for primary lithium batteries, but they cannot be recharged in certain situations. Primary lithium batteries are an important class of energy storage devices, which are widely used due to their excellent performance.^1–3 In particular, fluorinated carbon CF_x (x ≈ 0.13–1.5) is commercialized as a high energy density material in Li primary cells.^4,5 Li/CF_1.0 provides a theoretical capacity of 865 mA h g⁻¹ with a high discharge plateau voltage of ∼3.0 V vs. Li⁺/Li, providing an energy density of about 2600 W h kg⁻¹.^6–9 This performance is much better than that of other primary lithium batteries.^10–14 Thus, primary Li/CF_x batteries are used in military as defence tools, medical implants, long time spatial exploratory missions, and cameras etc.^15,16

The carbon fluoride cathode has many unique advantages, such as a high theoretical potential, a wide operational temperature range, and a flat discharge potential.^17–21 Lithium batteries with graphite fluoride cathode were commercialized in 1973. Since then, it has been shown that fluorine compounds are useful and attractive materials for lithium batteries.^22,23

However, Li/CF_x batteries are used mainly in low power applications due to the slow kinetics at the CF_x cathode. The main contributors to the slow kinetics are poor electronic conductivity of CF_x. The main challenge for CF_x cathodes is still their poor rate performance. A lot of strategies have been employed to enhance the rate performance by adding conductive carbon or oxide,^24–29 and to enhance the combination of Li atom and specific capacity by using dopant, defect and grain in graphene.³⁰ A number of experimental measurements have also shown that batteries performance is strongly influenced by the rate of discharge, the F/C ratio of CF_x and the electrolyte composition.^31–33 Lewandowski proposed that the rate-determine step in Li/CF_x cell is charge transfer rate.³⁴

Despite these encouraging advances, the problems of voltage decreasing rapidly at the high discharge rates have not been resolved. In 2019, Zhou and others found that fluorinated nanographite with different F/C ratio was prepared via direct fluorination. Because of its wide surface area, short diffusion length and continuous conduction path, it can effectively improve the low rate performance and initial voltage delay of Li/CF_x batteries.^35–39 For example, fluorinated graphene prepared at 450 °C can be discharged at a high rate of about 3.6C, delivering a high power density of 5460 W kg⁻¹ with a remaining energy density of 1030.5 W h kg⁻¹.³⁹

The Li/CF_x cell is known to produce a significant amount of thermal power during high rate discharge and cathode swelling that can result in mechanical deformation of the cell.⁴⁰ In 2011, Zhang's results support a mechanism where the discharge product is LiF deposited on the internal surfaces of the carbon layers left behind after electrochemical reduction with this deposition leading directly to the measured cathode swelling.⁴¹

In order to better improve the battery performance, it is necessary to study the physical mechanism of the main reaction process of Li/CF_x batteries. In such cases, F atoms of CF_x serve as electron acceptors, which can generate charge transfer from the coupled 2D materials to CF_x, and hence yield p-type doping.⁴² The ionized fluorinated graphene is combined with a lithium ion Li⁺ to form lithium fluoride particles LiF according to the following reactions:^43,44

CF_x + e⁻ → (CF_x)⁻ (1)

Li → Li⁺ + e⁻ (2)

xLi + CF_x → xLiF + C (3)

The discharge reactions include the formation of C and LiF. Li/CF_x batteries exhibit variable capacities, because CF_x compounds can be non-stoichiometric with x values. Research focuses on the performance of fluorinated graphene materials in lithium batteries.^45,46 Rao et al.⁴⁷ have studied adsorption energy of Li atom on CF_x surface by first-principles calculations. The obtained values are in agrement with experimental finding.⁴⁸ Furthermore, the volume of the anode material changes greatly, which affects the electrochemical performance and safety performance of lithium batteries. In addition to theoretical reports of the effect of strain on the adsorption of Li atoms on graphene,⁴⁹ LiF further blocks the electron conduction and deteriorates discharge performance. For the study of battery safety performance, the mechanical–electrochemical–thermal coupling behavior of batteries⁵⁰ and the safety parameters of the battery short-circuit are reported by some authors.⁵¹

The main work of this paper is to calculate the adsorption energy of Li/LiF on CF_x surface. It is proved that the fluorinated graphene can maintain the high discharge platform when it is used as the cathode material of lithium primary batteries. Furthermore, the theoretical exploration of the problem of rapid voltage drop of primary lithium batteries is expected to improve the discharge performance of the batteries. The adsorption properties and electron transfer mechanism of Li atom on CF_x surface with different F/C ratio, as well as the desorption behavior and transfer mechanism of LiF on CF_x surface are systematically studied by theoretical method, which are helpful to improve the efficiency of the batteries.

Computational details

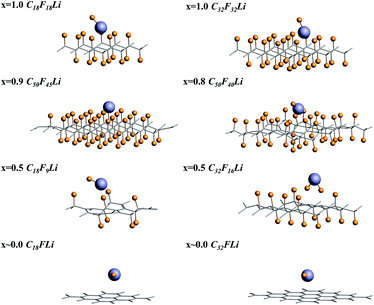
Fluorinated graphene was examined with the use of Density Functional Theory (DFT) formalism. And DFT calculations were performed on the generalized-gradient approximation (GGA) level using periodic boundary conditions (PBC).⁵² All the calculations were performed in Amsterdam Modeling Suite 2019.104 (ref. 53 and 54) using the Perdew–Burke–Ernzerhof (PBE) functional and 5 × 5 k-grid. To calculate the adsorption energy of Li/LiF on the CF_x surface, eight different supercells were chosen. C_mF_nLi (C₁₈F₁₈Li, C₃₂F₃₂Li, C₅₀F₄₅Li, C₅₀F₄₀Li, C₁₈F₉Li, C₃₂F₁₆Li, C₁₈FLi and C₃₂FLi) structures mean different F/C ratio. When F/C ratio x = 0.8/0.9, C₅₀F₄₅Li and C₅₀F₄₀Li systems contain about 100 atoms, which will lead to a large computational cost. For reducing the computational cost, the frozen core approximation was applied in our optimized calculations. The optimized structures were taken from the PBE-DZP calculations in AMS-BAND. The single point calculation and energy decomposition analysis (pEDA) were performed with a TZP basis set.⁵⁵ Partial adsorption energy calculation was performed using the PBE-D dispersion-correction scheme for consider the van der Waals interaction.^56,57

For all of the selected systems, the chair configuration has the lowest energy structure. The optimized structures of the selected systems are shown in Fig. 1. And C–C and C–F bond lengths in the optimized C₁₈F₁₈Li structure are 1.51 and 1.38 Å, respectively.^58,59 The side view of the optimized structures of C_mF_nLi are shown in Fig. 2. The optimized Li–F bond lengths, as well as absorption energies of Li and LiF on the CF_x surface are listed in Table 1.⁶⁰

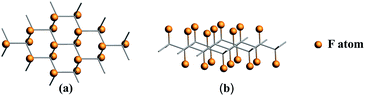Fig. 1 Optimized structures for CF_x (x = 1.0) system. (a) Top view, (b) side view. The orange spheres represent F atoms adsorbed on the side to graphene.

Fig. 2 The side view of the optimized structures of C_mF_nLi.

Table 1 The optimized Li–F bond lengths (unit: Å); the absorption energies of Li (ΔE) and LiF (ΔE′) on the CF_x surface, respectively (unit: eV). I and II represent the cases of sufficient relaxation and fixed nonreactive atomic coordinates, respectively

	x = 1.1	x = 1.0				x = 0.9	x = 0.8		x = 0.5			x ∼ 0.0
	Expt^26	C18F18Li	C32F32Li	C18F18Li^47	Expt^61	C50F45Li	C50F40Li	Expt^26	C18F9Li	C32F16Li	Expt^26	C18FLi	C32FLi
Li–F	—	1.70	1.71	—	—	1.87–1.91	1.71	—	1.72	1.38	—	1.71	1.60
										1.71
I
ΔE	2.60	2.30	2.29	2.29	2.50	2.61–3.32	4.98	∼3.0	4.86	12.36	∼2.9	4.13	4.59
		2.47#	2.56#							5.00*
ΔE′	—	0.51	0.48	—	—	—	0.58	—	0.50	—	—	0.36#	0.02
		1.04#	1.02#						0.76#				0.12#
II
ΔE	—	—	—	—	—	—	3.87	—	3.53	4.04	—	3.31	3.74
ΔE′	—	—	—	—	—	—	—	—	0.32	0.33	—	0.37#	−0.02
													0.06#

---

Results and discussion

The performance of the high energy density primary batteries of Li/CF_x depends on the value of x strongly, so the interaction energy between the Li and CF_x layers is a very important parameter. In order to quantitatively describe the interactions between the adsorbate and Li atoms, we adopt a common definition of the binding energies:⁴⁷

E_LiCnFm = E(Li) + E(C_nF_m) − E(LiC_nF_m)

where n and m represent the number of C and F atoms in the supercell. E_LiCnFm is the binding energy of Li on CF_x layers.

E(Li) + E(C_nF_m) is the energy of Li/CF_x system when Li atom is 10 Å away from CF_x, and E(LiC_nF_m) is the energy when the system is optimized to stable structure. The optimized structures and the adsorption energies of the different F/C ratio x cases are shown in Fig. 2 and Table 1, respectively.

For x = 1.0, the calculated binding energies are 2.30 and 2.29 eV for C₁₈F₁₈Li and C₃₂F₃₂Li species respectively. It means that the size effect of the supercell is very small. At the same time, the result of our calculation is consistent with Rao's result which is calculated by VASP package. It is noted that the calculation of VASP uses pseudo two-dimensional model, AMS uses real two-dimensional model. Unlike the program of plane wave basis set used by VASP, AMS uses the all electron theory which combines numerical basis set and slater basis set. It can deal with all electrons accurately, and can deal with the two-dimensional system in the true sense, without worrying about the reliability of the system due to the accuracy of the pseudopotential. While the difference between the two calculation results is only 0.01 eV, which can be ignored. The discharge plateau voltage of a real Li/CF_x cell (x = 1.0) is 2.50 V.⁶¹ And the discharge plateau of the Li/CF_1.1 batteries appears near 2.60 V when the x in CF_x equals 1.1 in the experimental observation. The calculated results of PBE-D functional are 2.47 and 2.56 eV, respectively, and are recorded in Table 1 by the symbol “#”. The calculation results are closer to the experimental values, but due to the ionization and solvent effect of Li atoms are not considered in the theoretical calculation, the difference between the experimental and theoretical results is reasonable. The computational Li–F bond length of the optimized structure are 1.70 and 1.71 Å for C₁₈F₁₈Li and C₃₂F₃₂Li species, which is close to the bond length of 1.80 Å of LiF molecule. From the corresponding optimal structure shown in Fig. 2, it can be seen that the F atom has separated from the CF_x surface for x = 1.0.

When x = 0.9, there are many combinations of defect sites and adsorption sites, and the calculated binding energy must vary with the change of binding sites.⁶² In this paper, the defect sites of F atoms in the C₅₀F₄₅Li system are randomly selected, and five configurations with random structures are calculated. Fig. 3 shows a schematic diagram of different optimized adsorption structure. The corresponding Li–F bond length and binding energy are listed in Table 2. The adsorption energy of different structures is between 2.72 and 3.32 eV, and the change range of bond length is about 0.04 Å. Obviously, the binding energy has a clear relationship with the discharge position. The actual voltage of the batteries may be related to the discharge site. Additionally, when x = 0.9, the calculated Li–F bond length is about 1.90 Å. This is 0.2 Å longer than the Li–F bond when x takes other values. The five configurations of C₅₀F₄₅Li are randomly selected representative structures. The bond lengths and adsorption energy properties of other configurations should not be much different from these calculation results. From the optimized structure shown in Fig. 2, it can be seen that the orientation of LiF at x = 0.9 is obviously different from other situations. This will help to solve the deposition problem of LiF on CF_x surface.

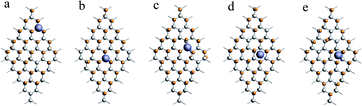Fig. 3 Five different optimized adsorption structures of the C₅₀F₄₅Li system, and the corresponding binding energies are listed in Table 2.

Table 2 The Li–F bond lengths of the optimized structures (unit: Å) and the binding energies of Li atom attacking CF from different positions when x = 0.9. (unit: eV)

C50F45Li	(a)	(b)	(c)	(d)	(e)
Li–F	1.91	1.89	1.87	1.91	1.90
ΔE	2.72	2.82	3.22	2.92	3.31

---

When x is 0.8, 20% of the carbon atoms are unsaturated, which makes the flexibility of the system much greater than the cases of x = 1.0 and x = 0.9. Therefore, the binding energy of a single Li atom in C₅₀F₄₀Li reaches 4.98 eV and it is strongly dependent on site. In contrast, the experimental discharge energy is far lower than the calculated value, only about 3.0 eV.²⁶ In the calculation of binding energy, the structure of the system is fully relaxed, and the configuration of the space has also changed greatly. In order to consider the effect of relaxation, the Li atom and the F atom which involved in the reaction are allowed to participate in the energy optimization process. The calculated binding energy of C₅₀F₄₀Li systems is 3.87 eV. However, in the experimental the discharge process, especially the rapid discharge process, the system has no time and space to fully relax, it will cause the discharge voltage to be greatly reduced. On the other hand, how to plan the discharge behavior to optimize the batteries performance is worth studying.

If x takes 0.5, the reaction of the system is going to be more complicated. The binding energy calculated from C₁₈F₉Li is 4.86 eV, which is close to the result of x = 0.8. More specially, the binding energy of C₃₂F₁₆Li is 12.36 eV, which is much larger than the bond energy of Li–F (6.00 eV) and C–F (1.95 eV). Sufficient relaxation of the C₃₂F₁₆Li system enables the Li atom to interact with multiple F and C atoms at the same time. If the coordinates of non-reactive atoms are fixed in the optimization process, the calculated binding energies of C₁₈F₉Li and C₃₂F₁₆Li systems are 3.53 and 4.04 eV. Li atom binding with two adjacent F atoms in C₃₂F₁₆Li species gives a relatively high binding energy of 4.04 eV. In the actual batteries, the relaxation of CF-skeleton is limited, which will definitely lead to the decrease of discharge capacity. While the release of relaxation energy will cause the batteries to heat up.

If there is only one F atom on the graphene fragment, we define this case as x ∼ 0.0. Although the actually F/C ratio of C₁₈FLi system is 0.06, and that of C₃₂FLi system is 0.03.When the systems are fully relaxed, the calculated binding energies for C₁₈FLi and C₃₂FLi are 4.13 and 4.59 eV respectively. If we only allow geometry coordinate of Li and F atoms to be optimized, the binding energies of C₁₈FLi and C₃₂FLi are 3.31 and 3.74 eV. On the other hand, if PBE-D functional was used in the calculation, the adsorption energies of LiF on C₁₈FLi and C₃₂FLi systems are 0.36 and 0.12 eV, respectively. And the LiF adsorption energies calculated after fixing non-reactive atoms are 0.37 and 0.06 eV, respectively. These results were recorded and marked by “#” in Table 1.

It is obvious that the binding energies of Li and CF_x are greater than 2.29 eV under different F/C ratio in the theoretical calculations. But in the experimental measurement, the discharge platform will change a lot with the discharge speed.²⁶ We know that the binding energy reflects the thermodynamic characteristics of the system, and the dynamic characteristics will also greatly affect the actual efficiency of the batteries.

First of all, we can consider one of the cases that affects the dynamic behavior of discharge. Is it possible to affect the performance of the batteries if multiple Li atoms are adsorbed by CF_x at the same time? Because we use the algorithm of periodic system calculation, this algorithm automatically includes the simultaneous adsorption of many Li atoms. However, the actual calculation results show that the synergistic adsorption behavior has little effect on the batteries performance if we use the supercell with different size. For example, we use C₁₈F₁₈Li and C₃₂F₃₂Li species to calculate the binding energy for the case of x = 1.0, the energy difference is only 0.01 eV. In addition, the disordered adsorption of Li atoms with different concentrations on single CF_x layer is considered. Theoretical calculations show that the more Li atoms are adsorbed on the CF_x layer, the more C–F bonds are broken.⁴⁷

Another dynamic factor that may affect the efficiency of the batteries is the desorption process of LiF. In Table 1, the adsorption energies of LiF on CF_x layer for different F/C ratio are listed. The calculated adsorption energy is about 0.50 eV for the cases of x is not equal to 0.0 using PBE functional. At room temperature, the desorption rate of LiF with 0.50 eV adsorption energy is about 10⁴ s⁻¹. When the temperature decreases, the desorption rate will decrease significantly, which will affect the discharge behavior. According to the results calculated by the PBE-D functional for considering the van der Walls interaction, the adsorption energy of LiF ranges from 0.12 to 1.04 eV for different F/C ratios. The related desorption rate of LiF is sometimes about 10⁻⁵ s⁻¹ at room temperature, LiF tends to stay on the surface of CF_x all the time, thus affecting the discharge behavior of the battery continuously.⁶³ Theoretically, choosing the appropriate discharge temperature may be beneficial to the improvement of batteries efficiency. Of course, the optimal temperature corresponding to different discharge stages may be different. For LiF adsorbed on the surface of CF_x, in addition to leaving the CF_x surface directly, it may also move on the surface. Our calculation shows that LiF moves almost freely on the graphene surface, and the translation energy barrier between different adsorption sites is about 0.04 eV only. The voltage of discharge platform reported in many papers²⁶ decreases rapidly with the increase of current, and the residual of LiF on CF_x surface may be an important reason. Rao' work discusses the accumulation of LiF on CF_x surface. Their work also shows that LiF prefers to stay near the CF_x surface, this will affect the subsequent batteries performance.⁴⁷ Of course, according to our calculation, the adsorption energy of LiF of about 0.50 eV is not particularly large. At a higher temperature, LiF can be easily desorbed and migrated.

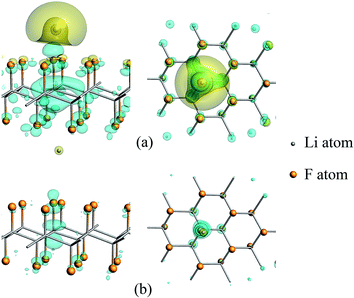
According to the calculation results listed in Table 1, in the presence of a certain amount of unsaturated carbon, the relaxation of CF_x will affect the discharge process. At this time, the distance of Li–F is a very important factor for electron transfer. In addition, the charge density difference between the CF_x and the Li atom in C₁₈F₁₈Li system are calculated and plotted, as seen in Fig. 4, to clarify the electronic gain and loss in space. The Li–F distances in the upper (a) and lower (b) panels are 1.71 and 3.00 Å, respectively. The blue/yellow contour corresponds to accumulation/depletion of electron density, it's clear that charge transfer occurs when Li is close enough to the surface.

Fig. 4 Charge density difference of Li atom adsorbed on CF_x surface, with the iso-surface level of 0.0015. The space enclosed by the blue and yellow iso-surfaces are the electron gaining and losing regions, respectively. (a) and (b) show the cases when the Li–F distance are 1.71 and 3.00 Å, respectively. Left and right are side view and top view of the system.

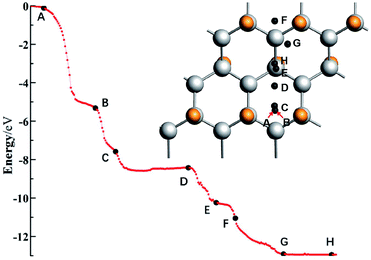
For the system with geometry changes greatly during the reaction process, such as C₃₂F₁₆Li for the F/C ratio is equal to 0.5, its reaction dynamics and electron transfer process are very complicated. When x = 0.8 and x = 0.5, the calculated adsorption energy deviates greatly from the experimental value, and there is a significant relaxation phenomenon of non-fully CF_x. Especially when x = 0.5, the adsorption energy of the Li atom in system C₃₂F₁₆Li is about 12.36 eV. Fig. 5 shows the energy curve of the Li atoms starting from a distance and reaching the CF_x surface along the direction of potential energy gradient, and then arriving the optimal structure of C₃₂F₁₆Li system. Several important nodes on the energy curve are marked by characters of A–H. The energy at point A refers to energy of the C₃₂F₁₆Li when the CF_x surface is 10 Å away from the Li atom, namely E_A, which is taken as the relative energy zero. And the energy at point H refers to the energy of the optimized structure of the system, namely E_H. The relative positions of different energy points are also shown in Fig. 5. The graph on the upper right is the motion of the Li atom on the CF_x surface as the C₃₂F₁₆Li system searches for the most stable structure. At the same time, in Fig. 6, the side view and top view of the corresponding structure of each A–H energy point are plotted. And the charge distribution using Hirshfeld's description for reactive Li and F atoms are listed in Fig. 6.⁶⁴

Fig. 5 An energy curve indicates that the Li atom starts from far away, along the gradient direction of potential energy to CF_x surface, and then reaches the optimal structure of C₃₂F₁₆Li system. And several important nodes A–H are marked.

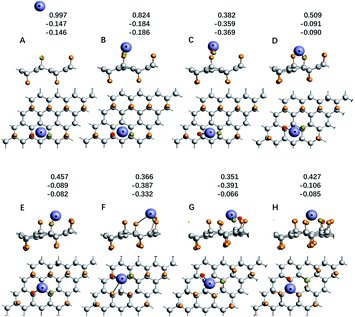Fig. 6 The side view and top view of structure diagram of each node in Fig. 5, and the Hirshfeld charge population of lithium atom and the two fluorine atoms is listed too.

In Fig. 5, Li atom approaches CF_x rapidly from A to B point along the direction of vertical surface firstly. The Li atom goes from 8.29 Å away from the F atom that it's reacting with to 1.72 Å away directly, and the system energy goes down by 5.17 eV. The previous calculations showed that electron transfer occurred when the Li–F distance was about 1.89 Å. Although the subsequent process from B to H has a great release of energy, it will not be converted into electric energy of the batteries, but into heat energy of the system. Studying the effect of such a large energy change on the system will help people understand how to improve the battery's performance in dynamics viewpoint. Fig. 6 shows the geometry of C₃₂F₁₆Li system changing from A to H points continuously. From point B to point C, the system releases energy of 2.27 eV. Furthermore, two F atoms adjacent to Li atom gradually separate from the CF_x surface and bond with the Li atom. At point C, the bond lengths between the two F atoms and Li atom are 1.68 Å and 1.70 Å, respectively. When the Li atom moves to the D point, the two F atoms linked to it will be attracted by the CF_x surface, which makes the energy of the system reduce about 1.03 eV. In this way, the Li atom, F atoms and CF_x surface reach the lowest energy point by constantly adjusting their positions. From point D to H, the energy of the system continues to decrease by nearly 3.89 eV. Specially, the side view structure of the G-point shown in Fig. 6 shows that the CF_x framework has changed greatly, while the structure of the H-point shows that multiple F atoms tend to combine with Li atom. At the same time, from the top view, the trajectories of Li atom on the surface of CF_x move back again at point F, which is due to the change of stable structure caused by the significant relaxation of carbon skeleton. In general, in the whole process of the combination of Li atom and CF_x, the energy of the system decreases by about 12.36 eV, in which about 5.00 eV energy will be converted into the electric energy of the batteries, the remaining about 7.00 eV energy will be converted into heat, and the temperature of the batteries will rise.

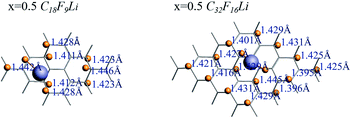
The length of the C–F bond can reflect the interaction status between C and F, the range of C–F bond length of each C_nF_mLi system is listed in Table 3. In addition to the F atom bonded with Li atom, the biggest difference in the length of other C–F bonds is less than 0.05 Å, which has little effect on the bond energy of C–F bond. Fig. 7 shows the C–F bond lengths of C₁₈F₉Li and C₃₂F₁₆Li systems when the F/C ration x is equal to 0.5.

Table 3 The longest (L) and shortest (S) bond lengths of C–F in Li/CF_x systems. (unit: Å)

	x = 1.0		x = 0.9	x = 0.8	x = 0.5
	C18F18Li	C32F32Li	C50F45Li	C50F40Li	C18FLi	C32FLi
L	1.407	1.406	1.507	1.493	1.599	1.445
S	1.376	1.377	1.359	1.398	1.411	1.395

---

Fig. 7 The C–F bond lengths in C₁₈F₉Li and C₃₂F₁₆Li systems.

Conclusions

In this work, we computed the interactions between Li/LiF and CF_x with different F/C ratio (x = 1.0, 0.9, 0.8, 0.5, and ∼0.0) using DFT method in AMS-BAND package. In general, the discharge behavior of the battery and the diffusion behavior of LiF on the CF_x surface are F/C ration dependent. The calculated binding energy of Li and CF_x is greater than 2.29 eV under different F/C ratio, indicating that the batteries have the potential to maintain a high discharge platform during the whole discharge process. The calculation also shows that when the F/C ratio is low, there will be a lot of unsaturated carbon, the Li atom and CF_x-skeleton relax a lot of heat during the reaction. When the relaxation of carbon skeleton releases a lot of heat, its structure also changes greatly. This situation will lead to the inevitable expansion of battery volume. However, in the actual batteries discharge process, the CF_x system cannot fully relax, which may be the reason for the decline of the discharge plateau of the batteries during rapid discharge.

The calculated adsorption energy of LiF on CF_x layer for different F/C ratios is 0.12–1.04 eV. At room temperature, the corresponding desorption rate varies in a wide range from 10⁻⁵ to 10¹¹ s⁻¹, which has a great probability to cause the accumulation of LiF on the CF_x surface, thus affecting the discharge performance of the battery. Since the calculation results of LiF adsorption energy are closely related to the selection of functional, our calculation may overestimate the adsorption energy. But how to control the desorption process of LiF is one of the problems that must be considered to improve the performance of the battery.

The C–F bond length is the direct expression of F activity. The calculation shows that the change range of C–F bond length does not change greatly under different F/C ratio, indicating that the reactivity of F atom and Li atom is relatively stable.

For optimizing the performance of the fluorinated graphene primary lithium batteries, it is very important to further study the dynamics process related to the adsorption behavior of Li atom and LiF on CF surface. We will carry out this research in the future work.

Conflicts of interest

No conflict of interest exits in the submission of this manuscript, and manuscript is approved by all authors for publication. I would like to declare on behalf of my co-authors that the work described was original research that has not been published previously, and not under consideration for publication elsewhere, in whole or in part.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (Grant No. 21903057 to H. R. and No. 91841301 to J. M.).

References

1. K. Guérin, M. Dubois, A. Houdayer and A. Hamwi, Applicative Performances of Fluorinated Carbons through Fluorination Routes: A Review, J. Fluorine Chem., 2012, 134, 11–17.
2. C. X. Zu and H. Li, Thermodynamic Analysis on Energy Densities of Batteries, Energy Environ. Sci., 2011, 4, 2614–2624.
3. M. Inagaki and F. Kang, Graphene Derivatives: Graphane, Fluorographene, Graphene Oxide, Graphyne and Graphdiyne, J. Mater. Chem. A, 2014, 2, 13193–13206.
4. N. Watanabe and M. Fukuda, Primary Cell for Electric Batteries, US Pat., US3536532A, 1970.
5. G. Eichinger and J. O. Besenhard, High Energy Density Lithium Cells: Part Ii. Cathodes and Complete Cells, J. Electroanal. Chem. Interfacial Electrochem., 1976, 72, 1–31.
6. M. A. Reddy, B. Breitung and M. Fichtner, Improving the Energy Density and Power Density of CF_x by Mechanical Milling: A Primary Lithium Battery Electrode, ACS Appl. Mater. Interfaces, 2013, 5, 11207–11211.
7. S. F. Schuster, M. J. Brand, P. Berg, M. Gleissenberger and A. Jossen, Lithium-Ion Cell-to-Cell Variation During Battery Electric Vehicle Operation.(Report), J. Power Sources, 2015, 297, 242.
8. C. Peng, Y. Li, F. Yao, H. Fu, R. Zhou, Y. Feng and W. Feng, Ultrahigh-Energy-Density Fluorinated Calcinated Macadamia Nut Shell Cathodes for Lithium/Fluorinated Carbon Batteries, Carbon, 2019, 153, 783–791.
9. A. Markevich, R. Jones and P. R. Briddon, Doping of Fluorographene by Surface Adsorbates, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 115439.
10. S. Peng, S. Yan, N. Wang, W. Nan, J. Wang, X. Chen, C. Wang, X. Qi and S. Dai, Fluorinated Graphene/Sulfur Hybrid Cathode for High Energy and High Power Density Lithium Primary Batteries, RSC Adv., 2018, 8, 12701–12707.
11. Y. Dai, S. Cai, L. Wu, W. Yang, J. Xie, W. Wen, J. C. Zheng and Y. Zhu, Surface Modified CF_x Cathode Material for Ultrafast Discharge and High Energy Density, J. Mater. Chem. A, 2014, 2, 20896–20901.
12. M. Yiwen, Z. Hongzhang, W. Baoshan, W. Meiri, L. Xianfeng and Z. Huamin, Lithium Sulfur Primary Battery with Super High Energy Density: Based on the Cauliflower-Like Structured C/S Cathode, Sci. Rep., 2015, 5, 14949.
13. Q. Zhang, K. J. Takeuchi, E. S. Takeuchi and A. C. Marschilok, Progress Towards High-Power Li/CF_X Batteries: Electrode Architectures Using Carbon Nanotubes with CF_X, Phys. Chem. Chem. Phys., 2015, 17, 22504–22518.
14. M. Makaremi, B. Mortazavi and C. V. Singh, Carbon Ene-Yne Graphyne Monolayer as an Outstanding Anode Material for Li/Naion Batteries, Appl. Mater. Today, 2018, 10, 115–121.
15. I. Ali, A. A. Basheer, X. Y. Mbianda, A. Burakov, E. Galunin, I. Burakova, E. Mkrtchyan, A. Tkachev and V. Grachev, Graphene Based Adsorbents for Remediation of Noxious Pollutants from Wastewater, Environ. Int., 2019, 127, 160–180.
16. D. Damien, P. M. Sudeep, T. N. Narayanan, M. R. Anantharaman, P. M. Ajayan and M. M. Shaijumon, Fluorinated Graphene Based Electrodes for High Performance Primary Lithium Batteries, RSC Adv., 2013, 3, 25702–25706.
17. P. Lazar, E. Otyepkova, F. Karlicky, K. Cepe and M. Otyepka, The Surface and Structural Properties of Graphite Fluoride, Carbon, 2015, 94, 804–809.
18. A. Hamwi, Fluorine Reactivity with Graphite and Fullerenes. Fluoride Derivatives and Some Practical Electrochemical Applications, J. Phys. Chem. Solids, 1996, 57, 677–688.
19. T. Nakajima, R. Hagiwara, K. Moriya and N. Watanabe, Discharge Characteristics of Graphite Fluoride Prepared Via Graphite Oxide, J. Power Sources, 1987, 20, 93–98.
20. T. Nakajima, Discharge Characteristics of Poly(Carbon Monofluoride) Prepared from the Residual Carbon Obtained by Thermal Decomposition of Poly(Dicarbon Monofluoride) and Graphite Oxide, J. Electrochem. Soc., 1986, 133, 1761.
21. P. Gong, Z. Wang, J. Wang, H. Wang, Z. Li, Z. Fan, Y. Xu, X. Han and S. Yang, One-Pot Sonochemical Preparation of Fluorographene and Selective Tuning of Its Fluorine Coverage, J. Mater. Chem., 2012, 22, 16950–16956.
22. T. Nakajima, Fluorine Compounds as Energy Conversion Materials, J. Fluorine Chem., 2013, 149, 104–111.
23. X. Xie, S. Wang, K. Kretschmer and G. Wang, Two-Dimensional Layered Compound Based Anode Materials for Lithium-Ion Batteries and Sodium-Ion Batteries, J. Colloid Interface Sci., 2017, 499, 17–32.
24. W. Liu, Y. Li, B.-X. Zhan, B. Shi, R. Guo, H.-J. Pei, J.-Y. Xie and Z.-W. Fu, Amorphous, Highly Disordered Carbon Fluorides as a Novel Cathode for Sodium Secondary Batteries, J. Phys. Chem. C, 2016, 120, 25203–25209.
25. D. Xu, X. Yu, L. Zuo and D. Yang, Interface Engineering and Efficiency Improvement of Monolayer Graphene–Silicon Solar Cells by Inserting an Ultra-Thin Lif Interlayer, RSC Adv., 2015, 5, 46480–46484.
26. G. Zhong, H. Chen, X. Huang, H. Yue and C. Lu, High-Power-Density, High-Energy-Density Fluorinated Graphene for Primary Lithium Batteries.(Brief Article), Front. Chem., 2018, 6, 50.
27. N. Leifer, V. S. Johnson, R. Benari, H. Gan, J. M. Lehnes, R. Guo, W. Lu, B. C. Muffoletto, T. B. Reddy and P. E. Stallworth, Solid-State Nmr Studies of Chemically Lithiated CF_x, J. Electrochem. Soc., 2010, 157, A148–A154.
28. Y. Li, Y. Chen, W. Feng, F. Ding and X. Liu, The Improved Discharge Performance of Li/CF_x Batteries by Using Multi-Walled Carbon Nanotubes as Conductive Additive, J. Power Sources, 2011, 196, 2246–2250.
29. H. Che, J. Liu, H. Wang, X. Wang, S. S. Zhang, X.-Z. Liao and Z.-F. Ma, Rubidium and Cesium Ions as Electrolyte Additive for Improving Performance of Hard Carbon Anode in Sodium-Ion Battery, Electrochem. Commun., 2017, 83, 20–23.
30. S. S. Zhang, D. Foster and J. Read, Carbothermal Treatment for the Improved Discharge Performance of Primary Li/CF_x Battery, J. Power Sources, 2009, 191, 648–652.
31. Y. Ahmad, K. Guérin, M. Dubois, W. Zhang and A. Hamwi, Enhanced Performances in Primary Lithium Batteries of Fluorinated Carbon Nanofibers through Static Fluorination, Electrochim. Acta, 2013, 114, 142–151.
32. K. Guérin, M. Dubois and A. Hamwi, Electrochemical Discharge Mechanism of Fluorinated Graphite Used as Electrode in Primary Lithium Batteries, J. Phys. Chem. Solids, 2006, 67, 1173–1177.
33. H. Groult, C. M. Julien, A. Bahloul, S. Leclerc, E. Briot and A. Mauger, Improvements of the Electrochemical Features of Graphite Fluorides in Primary Lithium Battery by Electrodeposition of Polypyrrole, Electrochem. Commun., 2011, 13, 1074–1076.
34. L.-F. Wang, T.-B. Ma, Y.-Z. Hu, H. Wang and T.-M. Shao, Ab Initio Study of the Friction Mechanism of Fluorographene and Graphane, J. Phys. Chem. C, 2013, 117, 12520–12525.
35. P. F. Fulvio, et al., Fluorination of “Brick and Mortar” Soft-Templated Graphitic Ordered Mesoporous Carbons for High Power Lithium-Ion Battery, J. Mater. Chem. A, 2013, 1, 9414.
36. Y. Li, L. Yang, Q. Meng, X. Qiu and Y. Feng, Emission Characteristics of Microbial Aerosols in a Municipal Sewage Treatment Plant in Xi’an, China, Aerosol Air Qual. Res., 2013, 13, 343–349.
37. R. Yazami, A. Hamwi, K. Guérin, Y. Ozawa, M. Dubois, J. Giraudet and F. Masin, Fluorinated Carbon Nanofibres for High Energy and High Power Densities Primary Lithium Batteries, Electrochem. Commun., 2007, 9, 1850–1855.
38. P. Meduri, H. Chen, J. Xiao, J. J. Martinez, T. Carlson, J.-G. Zhang and Z. D. Deng, Tunable Electrochemical Properties of Fluorinated Graphene, J. Mater. Chem. A, 2013, 1, 7866.
39. L. Wang, Y. Li, S. Wang, P. Zhou, Z. Zhao, X. Li, J. Zhou and S. Zhuo, Fluorinated Nanographite as a Cathode Material for Lithium Primary Batteries, ChemElectroChem, 2019, 6, 2201–2207.
40. Y. Wang, B. Liu, Q. Li, S. Cartmell, S. Ferrara, Z. D. Deng and J. Xiao, Lithium and Lithium Ion Batteries for Applications in Microelectronic Devices: A Review, J. Power Sources, 2015, 286, 330–345.
41. J. Read, E. Collins, B. Piekarski and S. Zhang, Lif Formation and Cathode Swelling in the Li/CF_x Battery, J. Electrochem. Soc., 2011, 158, A504.
42. Y. Li, F. Li and Z. Chen, Graphane/Fluorographene Bilayer: Considerable C–H···F–C Hydrogen Bonding and Effective Band Structure Engineering, J. Am. Chem. Soc., 2012, 134, 11269–11275.
43. T. Nakajima, Carbon–Fluorine Compounds as Battery Materials, J. Fluorine Chem., 1999, 100, 57–61.
44. Y. Ahmad, M. Dubois, K. Guérin, A. Hamwi and W. Zhang, Pushing the Theoretical Limit of Li–CF_x Batteries Using Fluorinated Nanostructured Carbon Nanodiscs, Carbon, 2015, 94, 1061–1070.
45. P. Lam and R. Yazami, Physical Characteristics and Rate Performance of (CF_x)N (0.33 < X < 0.66) in Lithium Batteries, J. Power Sources, 2006, 153, 354–359.
46. K. Guérin, J. P. Pinheiro, M. Dubois, Z. Fawal, F. Masin, R. Yazami and A. Hamwi, Synthesis and Characterization of Highly Fluorinated Graphite Containing sp² and sp³ Carbon, Chem. Mater., 2004, 16, 1786–1792.
47. F. Rao, Z. Wang, B. Xu, L. Chen and C. Ouyang, First-Principles Study of Lithium and Sodium Atoms Intercalation in Fluorinated Graphite, Engineering, 2015, 1, 243–246.
48. K. Guérin, J. P. Pinhero, M. Dubois, Z. Fawal, F. Masin, R. Yazami and A. Hamwi, Synthesis and Characterization of Highly Fluorinated Graphite Containing sp² and sp³ Carbon, Chem. Mater., 2004, 16, 1786–1792.
49. C. Chang, S. Yin and J. Xu, Exploring High-Energy and Mechanically Robust Anode Materials Based on Doped Graphene for Lithium-Ion Batteries: A First-Principles Study, RSC Adv., 2020, 10, 13662–13668.
50. B. Liu, Y. Jia, C. Yuan, L. Wang, X. Gao, S. Yin and J. Xu, Safety Issues and Mechanisms of Lithium-Ion Battery Cell Upon Mechanical Abusive Loading: A Review, Energy Storage Mater., 2020, 24, 85–112.
51. J. Xu, Y. Wu and S. Yin, Investigation of Effects of Design Parameters on the Internal Short-Circuit in Cylindrical Lithium-Ion Batteries, RSC Adv., 2017, 7, 14360–14371.
52. B. P. Klein, et al., Enhanced Bonding of Pentagon–Heptagon Defects in Graphene to Metal Surfaces: Insights from the Adsorption of Azulene and Naphthalene to Pt(111), Chem. Mater., 2020, 32.
53. E. J. Baerends and G. te Velde, Precise Density-Functional Method for Periodic Structures, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 44, 7888–7903.
54. M. Raupach and R. Tonner, A Periodic Energy Decomposition Analysis (Peda) Method for the Investigation of Chemical Bonding in Extended Systems, J. Chem. Phys., 2015, 142, 194105.
55. D. C. Graham, K. J. Cavell and B. F. Yates, Oxidative Addition of 2-Substituted Azolium Salts to Group-10 Metal Zero Complexes-a Dft Study, Dalton Trans., 2003, 2007, 4650.
56. P. Janthon, F. Viñes, S. M. Kozlov, J. Limtrakul and F. Illas, Theoretical Assessment of Graphene-Metal Contacts, J. Chem. Phys., 2013, 138, 244701.
57. M. Petr, et al., Thermally Reduced Fluorographenes as Efficient Electrode Materials for Supercapacitors, Nanoscale, 2019, 11, 21364–21375.
58. O. Leenaerts, H. Peelaers and A. D. Hernandez-Nieves, First-principles investigation of graphene fluoride and graphane, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 195436.
59. S. S. Han, T. H. Yu, B. V. Merinov, A. C. T. van Duin, R. Yazami and W. A. Goddard, Unraveling Structural Models of Graphite Fluorides by Density Functional Theory Calculations, Chem. Mater., 2010, 22, 2142–2154.
60. C.-K. Yang, A Metallic Graphene Layer Adsorbed with Lithium, Appl. Phys. Lett., 2009, 94, 163115.
61. C. Pang, F. Ding, W. Sun, J. Liu, M. Hao, Y. Wang, X. Liu and Q. Xu, A Novel Dimethyl Sulfoxide/1,3-Dioxolane Based Electrolyte for Lithium/Carbon Fluorides Batteries with a High Discharge Voltage Plateau, Electrochim. Acta, 2015, 174, 230–237.
62. R. B. dos Santos, R. Rivelino, F. d. B. Mota and G. K. Gueorguiev, Exploring Hydrogenation and Fluorination in Curved 2D Carbon Systems: A Density Functional Theory Study on Corannulene. (Report), J. Phys. Chem. A, 2012, 116, 9080–9087.
63. H. Tachikawa, A Direct Molecular Orbital-Molecular Dynamics Study on the Diffusion of the Li Ion on a Fluorinated Graphene Surface, J. Phys. Chem. C, 2008, 112, 10193–10199.
64. F. Hirshfeld, Bonded-Atom Fragments for Describing Molecular Charge Densities, Theor. Chim. Acta, 1977, 44, 129–138.

---