Open Access Article
Open Access ArticleStructural, electronic and optical properties of pristine and functionalized MgO monolayers: a first principles study
D. M. Hoat *ab,
Vo Van On*c,
Duy Khanh Nguyenc,
Mosayeb Naseri
*ab,
Vo Van On*c,
Duy Khanh Nguyenc,
Mosayeb Naseri d,
R. Ponce-Péreze,
Tuan V. Vu
d,
R. Ponce-Péreze,
Tuan V. Vu fg,
J. F. Rivas-Silvah,
Nguyen N. Hieu
fg,
J. F. Rivas-Silvah,
Nguyen N. Hieu bi and
Gregorio H. Cocoletzih
bi and
Gregorio H. Cocoletzih
aInstitute of Theoretical and Applied Research, Duy Tan University, Hanoi 100000, Vietnam. E-mail: dominhhoat@duytan.edu.vn
bFaculty of Natural Sciences, Duy Tan University, Da Nang 550000, Vietnam
cGroup of Computational Physics and Simulation of Advanced Materials, Institute of Applied Technology, Thu Dau Mot University, Binh Duong Province, Vietnam. E-mail: onvv@tdmu.edu.vn; nguyenduykhanh@tdmu.edu.vn
dDepartment of Physics, Kermanshah Branch, Islamic Azad University, P.O. Box 6718997551, Kermanshah, Iran. E-mail: m.naseri@iauksh.ac.ir
eUniversidad Nacional Autónoma de México, Centro de Nanociencias y Nanotecnología, Apartado Postal 14, Ensenada, Baja California Código Postal 22800, México. E-mail: rponce@cnyn.unam.mx
fDivision of Computational Physics, Institute for Computational Science, Ton Duc Thang University, Ho Chi Minh City, Vietnam. E-mail: vuvantuan@tdtu.edu.vn
gFaculty of Electrical & Electronics Engineering, Ton Duc Thang University, Ho Chi Minh City, Vietnam
hBenemérita Universidad Autónoma de Puebla, Instituto de Física, Apartado Postal J-48, Puebla 72570, Mexico. E-mail: rivas@ifuap.buap.mx; cocoletz@ifuap.buap.mx
iInstitute of Research and Development, Duy Tan University, Da Nang 550000, Vietnam. E-mail: hieunn@duytan.edu.vn
First published on 6th November 2020
Abstract
In this paper, we present a detailed investigation of the structural, electronic, and optical properties of pristine, nitrogenated, and fluorinated MgO monolayers using ab initio calculations. The two dimensional (2D) material stability is confirmed by the phonon dispersion curves and binding energies. Full functionalization causes notable changes in the monolayer structure and slightly reduces the chemical stability. The simulations predict that the MgO single layer is an indirect semiconductor with an energy gap of 3.481 (4.693) eV as determined by the GGA-PBE (HSE06) functional. The electronic structure of the MgO monolayer exhibits high sensitivity to chemical functionalization. Specifically, nitrogenation induces metallization of the MgO monolayer, while an indirect–direct band gap transition and band gap reduction of 81.34 (59.96)% are achieved by means of fluorination. Consequently, the functionalized single layers display strong optical absorption in the infrared and visible regimes. The results suggest that full nitrogenation and fluorination may be a quite effective approach to enhance the optoelectronic properties of the MgO monolayer for application in nano-devices.
1 Introduction
The discovery of graphene in 2004 by Novoselov and co-workers,1 with extremely outstanding physical, chemical, and mechanical properties,2,3 was the beginning of the boom in two dimensional (2D) materials research. So far, researchers have explored a large variety of 2D layered materials through experimental synthesis and characterization as well as theoretical predictions. For example, silicene,4,5 phosphorene,6,7 transition metal dichalcogenides,8,9 and monolayers belonging to the II–VI,10–12 III–V,13–15 IV–IV,13,16,17 and MXene18,19 families have been investigated. In recent years, the 2D heterostructures formed by stacking two different monolayers17,20–22 and Janus monolayers23,24 have been widely investigated. In general, these 2D layers possess electronic band gaps and are classified as semiconductors or insulators, presenting better optoelectronic suitability than graphene, whose applications are limited because of its zero band gap.Experimentally, bulk II–VI compounds, for example, ZnO,25 CdO,26 ZnS27 and MgO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Cd28 among others, are important materials for optoelectronic applications. However, the growth and characterization of II–VI monolayers have not been well studied, so far. Instead, the physical properties of these 2D materials have been predicted using first principles calculations. For example, the graphene-like MgO monolayer was predicted by Zheng et al.29 The results indicated that the MgO single layer has good dynamical stability and an indirect band gap of 3.60 eV. Later, promising piezoelectric properties for the 2D II–VI family of compounds were predicted by Menderes et al.30 Moghadam et al.31 have also studied the electronic, magnetic and optical properties of the MgO monolayer doped with B, C, N and F. As a result, an indirect energy gap of 3.8 eV was obtained for the pristine MgO single layer. B, C and N single atom doping induces significant magnetization in the monolayer, generating half-metallic and magnetic semiconductor behavior, while non-magnetic properties are induced with F doping. In addition, efforts have been made to obtain a more accurate band gap for the MgO monolayer. Recently, mBJ potential calculations carried out by Nourozi et al.32 yielded a larger band gap of 4.2 eV. Luo et al.33 performed first principles calculations based on the pseudopotential plus hybrid functional HSE06 to investigate the electronic structure of the graphene-like MgO monolayer, and obtained a band gap of 4.76 eV. To the best of our knowledge, the electronic properties, including band structure formation and chemical bonding, as well as the optical properties of the MgO monolayer have not been well investigated, so far. Therefore, it is worth carrying out a detailed investigation to address this lack of knowledge.
Cd28 among others, are important materials for optoelectronic applications. However, the growth and characterization of II–VI monolayers have not been well studied, so far. Instead, the physical properties of these 2D materials have been predicted using first principles calculations. For example, the graphene-like MgO monolayer was predicted by Zheng et al.29 The results indicated that the MgO single layer has good dynamical stability and an indirect band gap of 3.60 eV. Later, promising piezoelectric properties for the 2D II–VI family of compounds were predicted by Menderes et al.30 Moghadam et al.31 have also studied the electronic, magnetic and optical properties of the MgO monolayer doped with B, C, N and F. As a result, an indirect energy gap of 3.8 eV was obtained for the pristine MgO single layer. B, C and N single atom doping induces significant magnetization in the monolayer, generating half-metallic and magnetic semiconductor behavior, while non-magnetic properties are induced with F doping. In addition, efforts have been made to obtain a more accurate band gap for the MgO monolayer. Recently, mBJ potential calculations carried out by Nourozi et al.32 yielded a larger band gap of 4.2 eV. Luo et al.33 performed first principles calculations based on the pseudopotential plus hybrid functional HSE06 to investigate the electronic structure of the graphene-like MgO monolayer, and obtained a band gap of 4.76 eV. To the best of our knowledge, the electronic properties, including band structure formation and chemical bonding, as well as the optical properties of the MgO monolayer have not been well investigated, so far. Therefore, it is worth carrying out a detailed investigation to address this lack of knowledge.
On the other hand, chemical functionalization has been experimentally and theoretically demonstrated to be an effective method to fine tune the electronic structure and related properties of low-dimensional materials.34–39 Results have shown that half-functionalization may induce important magnetism, while fully functionalized single layers exhibit no magnetic properties.40 Motivated by such observations, in this work we investigate systematically the structural, electronic and optical properties of pristine, nitrogenated and fluorinated MgO monolayers. Calculations show that the MgO single layer is a semiconductor with a wide indirect band gap of 3.481 eV, therefore in order to make it suitable for optoelectronic applications, it is necessary to reduce its energy gap. Reviewing the literature, we realized that fluorination may decrease the electronic band gap of 2D materials,40,41 therefore, fluorine (F) is chosen as a functionalization agent in this work. Moreover, we also examine the effects of nitrogenation and find that it induces metallization of the monolayer. We focus on analyzing the effects of functionalization on the structural and optoelectronic properties of the MgO monolayer. It is anticipated that functionalizing the MgO single layer with N and F atoms leads to enhancement of its optoelectronic properties, making it more suitable for practical applications in nano-devices.
2 Computational approach
First principles density functional theory (DFT)-based42 calculations are performed using the WIEN2k simulation code,43 which makes use of the full-potential linearized augmented plane wave (FP-LAPW) method to solve the self-consistent Kohn–Sham equations. The electron exchange–correlation interactions are determined by the generalized gradient approximation with the Perdew–Burke–Ernzerhof (PBE) functional.44 In addition, for reliable calculation of the energy gap, the hybrid functional HSE06 (ref. 45) is also employed. Within the spherical muffin-tin, the maximum quantum number lmax = 10 is used for the base functions of the spherical harmonics. While the basis set of the plane wave expansion is limited by the product of the smallest muffin-tin radius RMT and the maximum wave vector Kmax so that RMTKmax = 7 in the interstitial regions. The maximum Gaussian parameter Gmax = 12 is set for the charge and potential expansion. In the calculations, the core states and valence states are determined separately with a cut-off energy of −6.0 Ry. In the structural optimization process, the force is set to 1 mRy/a.u. and the Brillouin zone is sampled with an 8 × 8 × 1 k-mesh.46 While a denser 16 × 16 × 1 mesh is employed for the electronic properties calculations. In order to get self-consistent energy convergency, an energy criterion of 0.0001 Ry is used. In the periodic calculations of low dimensional materials, it is necessary to generate a large enough vacuum gap to prevent interlayer interactions. In this work, the layers are separated by an empty region larger than 14 Å to avoid interlayer interactions.3 Results
3.1 Structural properties
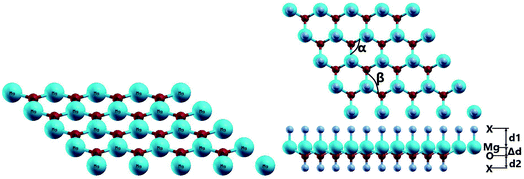
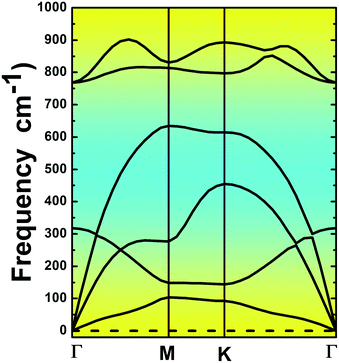
The MgO monolayer is formed by alternating Mg and O atoms in a hexagonal honeycomb structure, with space group P![[6 with combining macron]](https://www.rsc.org/images/entities/char_0036_0304.gif) m2 (no. 187). Fig. 1 shows a 4 × 4 × 1 supercell of the MgO monolayer atomic structure. The calculations give a lattice constant of 3.29 Å, which is in good agreement with previous theoretical results,29,30 generating the interatomic distance dMg–O = 1.90 Å. The interatomic Mg–O–Mg and O–Mg–O angles are 120°, which results from the structural planarity of the single layer. The phonon dispersion curves displayed in Fig. 2 show that the MgO monolayer is dynamically stable due to the absence of imaginary frequencies in the phonon modes.
m2 (no. 187). Fig. 1 shows a 4 × 4 × 1 supercell of the MgO monolayer atomic structure. The calculations give a lattice constant of 3.29 Å, which is in good agreement with previous theoretical results,29,30 generating the interatomic distance dMg–O = 1.90 Å. The interatomic Mg–O–Mg and O–Mg–O angles are 120°, which results from the structural planarity of the single layer. The phonon dispersion curves displayed in Fig. 2 show that the MgO monolayer is dynamically stable due to the absence of imaginary frequencies in the phonon modes.
Fig. 1 also shows a schematic 4 × 4 × 1 supercell of the fully functionalized MgO monolayer (X–MgO–X, X = N and F). The optimized structural parameters of the nitrogenated and fluorinated MgO single layers are given in Table 1. Note that the Mg–X bond length (X = N and F) is larger than the O–X one, suggesting that the former bond is considerably weaker than the latter. This behavior can be attributed to the ionicity of the Mg–X chemical bond due to the large electronegativity difference between the Mg and X atoms, while the O–X bond may be predominantly covalent. Also, the functionalization induces an important change in the MgO single layer structure. Specifically, a buckling appears, destroying the structural planarity, and consequently the interatomic distance dMg–O increases while the Mg–O–Mg and O–Mg–O angles decrease considerably.
| dMg–O (Å) | d1 (Å) | Δd (Å) | d2 (Å) | α (°) | β (°) | Eb (eV per atom) | |
|---|---|---|---|---|---|---|---|
| MgO | 1.900 | — | 0 | — | 120 | 120 | −5.420 |
| N–MgO–N | 2.130 | 1.994 | 0.964 | 1.324 | 101.113 | 101.113 | −4.340 |
| F–MgO–F | 2.007 | 1.742 | 0.648 | 1.518 | 110.109 | 110.109 | −4.000 |
In order to examine the stability of the pristine and functionalized MgO monolayers, the binding energy Eb is determined using the following expression:
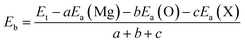 | (1) |
3.2 Electronic properties
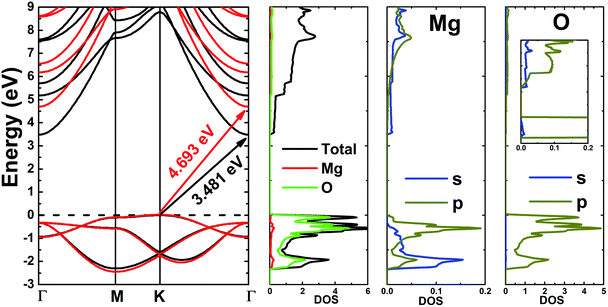
Fig. 3 shows the band structure, total density of states (TDOS) and partial density of states (PDOS) of the pristine MgO monolayer in an energy range from −3 to 9 eV, in which the Fermi level is set at 0 eV. The MgO single layer is predicted to be an indirect band gap material given that the highest point of the valence band is found at the K point, while the lowest conduction band point appears at the center of the Brillouin zone, that is the Γ point. PBE- and HSE06-based calculations provide electronic band gaps of 3.481 and 4.693 eV, respectively. Our results are in good agreement with those previously reported.29,31–33 Undoubtedly, the HSE06 hybrid functional produces better results given that the standard GGA-PBE functional frequently underestimates the energy gaps of materials. The electronic configurations of elemental Mg and O are [Ne]3s2 and 1s22s22p4, respectively. Due to the large electronegativity difference, it is expected that the Mg atom gives two electrons to the O atom to totally fill the O-2p orbital, giving rise to the major presence of the O-2p state in the upper part of the valence band and the Mg-3s state in the lower part of the conduction band. Consequently, the Mg–O chemical bond is predominantly ionic. However in the case of the MgO monolayer, Fig. 3 indicates that the O-p state is the main contributor to the valence band in the energy range from −2.30 to 0 eV, in which a small contribution from the Mg-s and Mg-p states can also be noted. While the conduction band from 3.481 to 9 eV is formed mainly by the O-p, Mg-s, and Mg-p states. The PDOS profile suggests s–p hybridization in the single layer to yield an sp2 state. The valence charge distribution in the pristine MgO monolayer is illustrated in Fig. 4a and 5a. Note that a large charge density is centered around the O atom, indicating a high electron concentration, and consequently an ionic chemical bond is generated. However, significant charge density is also distributed in the Mg–O bridge regions, which is a result of the sp2 hybridization, creating a covalent bond. The analyzed results provide evidence that the chemical bond in the pristine MgO single layer is a mixture of ionic and covalent in nature.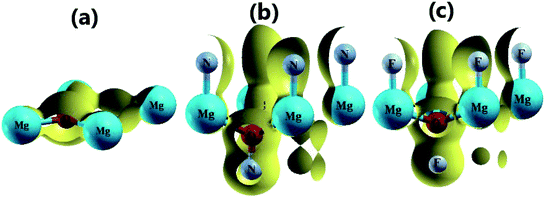 | ||
| Fig. 4 3D valence charge density of the (a) pristine, (b) N-functionalized and (c) F-functionalized MgO monolayers (isosurface 0.2 e bohr−3). | ||
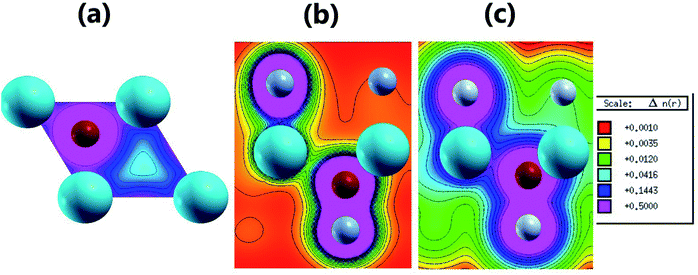 | ||
| Fig. 5 2D valence charge density along (a) the (001) plane of the pristine MgO monolayer, and the (110) planes of the (b) N-functionalized and (c) F-functionalized MgO monolayers. | ||
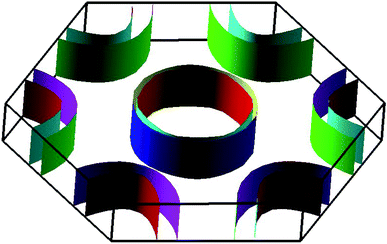
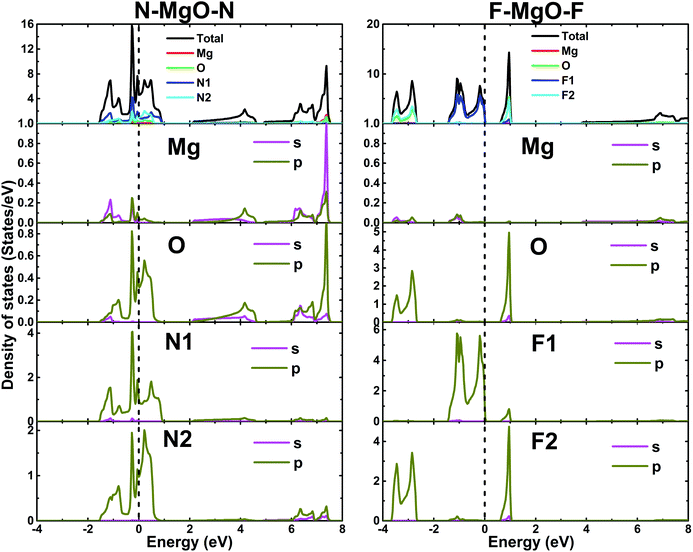
The electronic band structures of the nitrogenated and fluorinated MgO monolayers are presented in Fig. 6. Note that nitrogenation induces metallization of the MgO single layer given that the upper part of the valence band crosses the Fermi level, with the highest point located at an energy of 0.771 eV above the Fermi level. Specifically, there are four subband lines that intercept the Fermi level, which are called “V1”, “V2”, “V3” and “V4” (see Fig. 6a). To show more clearly the metallic nature of the N–MgO–N monolayer, its Fermi surface is calculated, and the results are given in Fig. 7. From the figure, it can be observed that there are four separate Fermi surfaces. Specifically, those of the V1 and V2 lines are found centered at the Brillouin zone center, while the surfaces centered at the zone corners (K point) correspond to the V3 and V4 energy lines. It is important to mention that the N–MgO–N metallicity is also predicted by the HSE06 functional, however, hybrid functionals may falsely predict the fundamental properties of metallic materials.47 Therefore, in the case of nitrogenation only the results obtained with the PBE potential are presented and discussed. In the case of the fluorinated MgO monolayer, the valence band maximum touches the Fermi level at the Γ point, while a flat subband appears in the lower part of the conduction band, considerably reducing the electronic band gap. To be precise, the F–MgO–F monolayer has a Γ–Γ band gap of 0.648 (1.879) eV as obtained with the PBE (HSE06) functional, corresponding to a reduction of 81.34 (59.96)% as compared with the pristine MgO case. It is worth mentioning that chemical functionalization of the MgO monolayer with F and N atoms may lead to enhancement of sunlight harvesting, as well as avoiding the energy loss favored by the direct nature of the band gap. The TDOS and PDOS of the functionalized MgO single layers are given in Fig. 8. In the figure, the labels “1” and “2” indicate that the functionalization agent is bound to the Mg and O atoms, respectively. The DOS profiles demonstrate that the nitrogen electronic states exhibit almost no participation in the conduction band formation in the N–MgO–N monolayer. While the valence band is built mainly by the N1-p, N2-p and O-p states, where the metallic nature can be attributed mainly to the p states of the nitrogen atoms which range from −1.5 to 0.771 eV, and the presence of the O-p state is less important. In the energy range from −4 to 0 eV, the valence band of the F–MgO–F monolayer is divided into two separate subbands, and a similar feature is noted in the conduction band up to 8 eV. The lower valence subband from −3.68 to −2.64 eV and the flat conduction subband from 0.65 to 1.09 eV are dominated mainly by the O-p and F2-p states, suggesting strong hybridization of the 2p orbitals in the O–F2 bond. While the F1-p state forms the upper valence band from −1.45 to 0 eV.
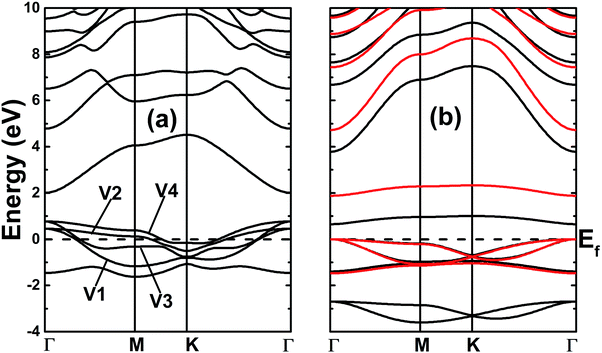 | ||
| Fig. 6 Band structures of the (a) N- and (b) F-functionalized MgO monolayers (black lines and red lines represent the results obtained with the PBE and HSE06 functionals, respectively). | ||
Fig. 4b and c and 5b and c show the valence charge distributions of the functionalized MgO monolayers. As expected, the strong hybridization of the O-2p and X2-2p (X2 = N2 or F2) orbitals gives rise to a large charge density in the bridge regions between the O and X2 atoms and the distribution is quite symmetric, generating a covalent O–X2 chemical bond. In the N–MgO–N monolayer, the N1–Mg and Mg–O chemical bonds are predominantly ionic given that there is only small charge density in the interatomic regions. Unlike the N–MgO–N monolayer, the F1–Mg and Mg–O bonds in the F–MgO–F monolayer may contain a portion of covalence as significant charge density is noted in the bridge regions. However, we can conclude that these last-mentioned chemical bonds are predominantly ionic given that the distribution is considerably directed toward the F1 and O atoms, respectively.
3.3 Optical properties
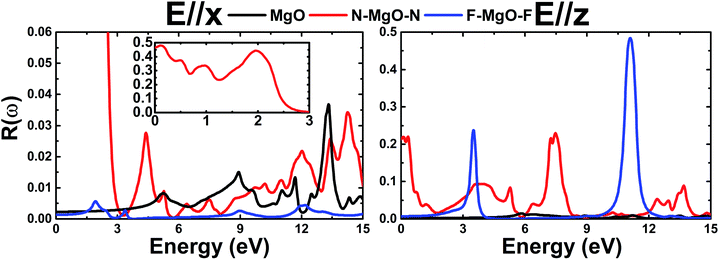
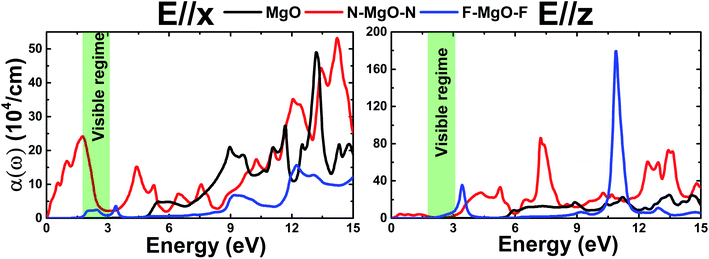
In this section, we discuss the optical response of the pristine and functionalized MgO monolayers to electromagnetic radiation by determining and analyzing the optical properties. Electronic transitions can be categorized into interband transitions and intraband transitions, which are responsible for the optical response in semiconductors and metals, respectively. As a first step, the complex dielectric function ε(ω) = ε1(ω) + iε2(ω), which contains the reflective character (real part) and absorptive character (imaginary part), is calculated. Then, the optical properties including reflectivity R(ω), absorption coefficient α(ω), and refractive index n(ω) are deduced from the known dielectric function.48 Hexagonal symmetry generates isotropy along the in-plane x- and y-directions, therefore for all optical quantities the effect of incident light (electromagnetic radiation) polarized along the x- (E//x) and z-axes (E//z) is discussed.
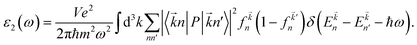 | (2) |
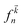 denotes the Fermi distribution function, and energy conservation is introduced through the Dirac function
denotes the Fermi distribution function, and energy conservation is introduced through the Dirac function 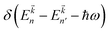 .
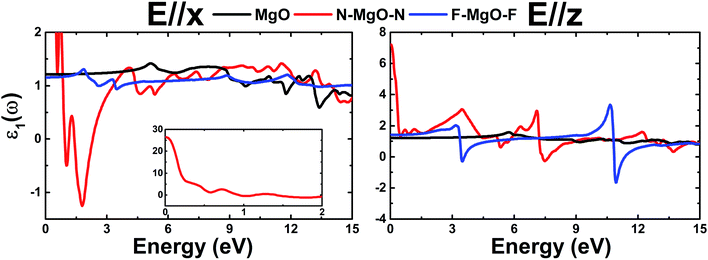
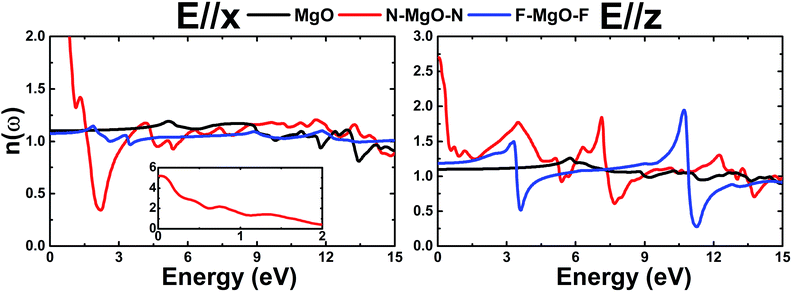
.Fig. 9 shows ε2(ω) plots of the pristine and functionalized MgO monolayers as a function of energy. As mentioned above, interband transitions may provide the main contribution in the case of pristine and fluorinated MgO single layers due to their semiconducting nature. Meanwhile intraband transitions are manifested in the nitrogenated monolayer due to the metallicity, in which no energy is required to excite the electrons from the valence band to the conduction band. Therefore, at extremely low energies, the ε2(ω) value of N–MgO–N takes high values of 7.741 and 1.238 in the case of E//x and E//z, respectively. On the contrary, the ε2(ω) edges of MgO and F–MgO–F start near their respective band gaps, above which the energy is sufficient for electronic excitations. ε2(ω) increases dramatically to reach maximum values at 5.455 (6.571), 0.150 (0.340) and 2.054 (3.388) eV in the case of the MgO, N–MgO–N and F–MgO–F monolayers, respectively, when the incident light is polarized in the x (z) direction. After that, ε2(ω) fluctuates in the ultraviolet regime, exhibiting some prominent peaks. It appears that the ε2(ω) value of MgO for E//x is slightly larger than that for E//z. Moreover, in the infrared regime the ε2(ω) value of N–MgO–N takes very large values, reaching 18.505 at 0.150 eV. However, in most of the considered energy range, z-polarized light may be more efficient in promoting electronic transitions in the functionalized single layers given that ε2(ω) takes values considerably larger than those observed in the case of x-polarization. This behavior can be attributed to the orientation of the functionalization agents, which are aligned vertically with respect to the MgO single layer host.
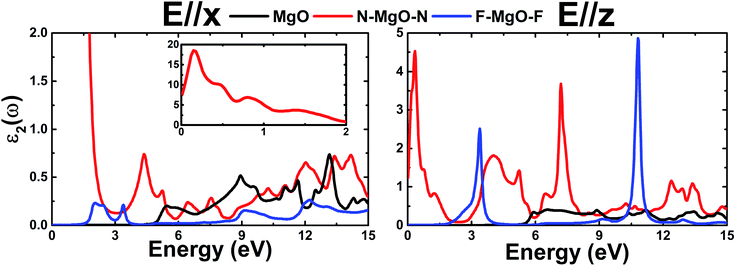 | ||
| Fig. 9 Imaginary part of the dielectric function of the pristine, N- and F-functionalized MgO monolayers. | ||
The real part ε1(ω) represents the electronic polarizability, and it is linked with the imaginary part ε2(ω) as follows:50
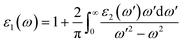 | (3) |
ε1(ω) of the pristine and functionalized MgO monolayers is plotted in Fig. 10 as a function of energy. At the zero frequency limit, the static dielectric constants of the MgO, N–MgO–N and F–MgO–F monolayers are 1.212 (1.207), 26.419 (7.211) and 1.156 (1.404), respectively, in the case of E//x (E//z). Similar to ε2(ω), for N–MgO–N, ε1(ω) has large values in the infrared region, and it shows decreasing behavior above zero energy. In contrast, the ε1(ω) values of the pristine and fluorinated monolayers increase to reach maximum values of 1.417 at 5.156 eV (and 1.576 at 5.726 eV) and 1.310 at 1.865 eV (and 2.024 at 3.170 eV), respectively, when the incident light is x-polarized (and z-polarized). After that, ε1(ω) presents an obvious fluctuation. It is important to mention that for N–MgO–N, ε1(ω) decreases to negative values, and the most negative value is −1.253 at 1.782 eV for E//x. For E//z, a similar feature is noted for the fluorinated single layer. Specifically, there are two negative peaks at 3.497 and 10.926 eV, whose values are −0.292 and −1.663, respectively. Negative ε1(ω) values indicate the interaction of free electrons with the incident light, and the reflection may be large. Functionalization may enhance the electronic polarizability of the MgO monolayer under z-polarized incident electromagnetic radiation given that the ε1(ω) values are increased considerably, and the opposite trend is noted for E//x.
4 Conclusions
In summary, the structural, electronic, and optical properties of the MgO, N–MgO–N, and F–MgO–F monolayers have been comprehensively investigated using the FP-LAPW technique within the DFT scheme. The planar honeycomb MgO single layer is proven to be structurally and dynamically stable. Chemical functionalization induces the appearance of buckling and reduction of the interatomic angles Mg–O–Mg and O–Mg–O. The Mg–X1 (X = N and F) bond is predominantly ionic and is weaker than the covalent O–X2 bond, and consequently the length of the former is considerably smaller than that of the latter. The MgO single layer possesses an indirect K–Γ gap of 4.693 eV, and the s and p states of both constituents form the valence band and conduction band. In contrast, the N–MgO–N monolayer has a metallic nature that is attributed mainly to the N-p state, whose Fermi surfaces are centered at the center and corners of the Brillouin zone. A band gap reduction to 0.648 eV is a consequence of full fluorination, which is regulated mainly by the F1-p state and the F2(p)–O(p) hybridized state given that they compose the upper valence band and lower conduction band. The results suggest that the N–MgO–N and F–MgO–F monolayers may be more promising 2D optoelectronic materials than the pristine MgO single layer given that they possess the ability to absorb light lying in a wide energy range from visible to ultraviolet with large absorption coefficients. The results presented herein are expected to provide good theoretical guidance for the application of MgO monolayers in nano optoelectronic devices.Conflicts of interest
There are no conflicts to declare.References
- K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Science, 2004, 306, 666–669 CrossRef CAS.
- M. J. Allen, V. C. Tung and R. B. Kaner, Chem. Rev., 2010, 110, 132–145 CrossRef CAS.
- S. Dutta and S. K. Pati, J. Mater. Chem., 2010, 20, 8207–8223 RSC.
- Y. Cai, C.-P. Chuu, C. Wei and M. Chou, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 245408 CrossRef.
- N. W. Johnson, P. Vogt, A. Resta, P. De Padova, I. Perez, D. Muir, E. Z. Kurmaev, G. Le Lay and A. Moewes, Adv. Funct. Mater., 2014, 24, 5253–5259 CrossRef CAS.
- A. H. Woomer, T. W. Farnsworth, J. Hu, R. A. Wells, C. L. Donley and S. C. Warren, ACS Nano, 2015, 9, 8869–8884 CrossRef CAS.
- A. Carvalho, M. Wang, X. Zhu, A. S. Rodin, H. Su and A. H. C. Neto, Nat. Rev. Mater., 2016, 1, 1–16 Search PubMed.
- C. Cong, J. Shang, X. Wu, B. Cao, N. Peimyoo, C. Qiu, L. Sun and T. Yu, Adv. Opt. Mater., 2014, 2, 131–136 CrossRef.
- K. M. McCreary, A. T. Hanbicki, J. T. Robinson, E. Cobas, J. C. Culbertson, A. L. Friedman, G. G. Jernigan and B. T. Jonker, Adv. Funct. Mater., 2014, 24, 6449–6454 CrossRef CAS.
- M. Naseri, D. Hoat, J. Rivas-Silva and G. H. Cocoletzi, Optik, 2020, 210, 164567 CrossRef CAS.
- M. Topsakal, S. Cahangirov, E. Bekaroglu and S. Ciraci, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 235119 CrossRef.
- M. Abutalib, Superlattices Microstruct., 2020, 106570 CrossRef CAS.
- H. Şahin, S. Cahangirov, M. Topsakal, E. Bekaroglu, E. Akturk, R. T. Senger and S. Ciraci, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 155453 CrossRef.
- V. Wang, N. Ma, H. Mizuseki and Y. Kawazoe, Solid State Commun., 2012, 152, 816–820 CrossRef CAS.
- D. C. Camacho-Mojica and F. López-Urías, Chem. Phys. Lett., 2016, 652, 73–78 CrossRef CAS.
- E. Bekaroglu, M. Topsakal, S. Cahangirov and S. Ciraci, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 075433 CrossRef.
- T.-Y. Lü, X.-X. Liao, H.-Q. Wang and J.-C. Zheng, J. Mater. Chem., 2012, 22, 10062–10068 RSC.
- Y. Gogotsi and B. Anasori, ACS Nano, 2019, 13, 8491–8494 CrossRef CAS.
- J. D. Gouveia, F. Viñes, F. Illas and J. R. Gomes, Phys. Rev. Mater., 2020, 4, 054003 CrossRef CAS.
- F. Khan, H. Din, S. Khan, G. Rehman, M. Bilal, C. V. Nguyen, I. Ahmad, L.-Y. Gan and B. Amin, J. Phys. Chem. Solids, 2019, 126, 304–309 CrossRef CAS.
- S. Wang, C. Ren, H. Tian, J. Yu and M. Sun, Phys. Chem. Chem. Phys., 2018, 20, 13394–13399 RSC.
- T. V. Vu, N. V. Hieu, H. V. Phuc, N. N. Hieu, H. Bui, M. Idrees, B. Amin and C. V. Nguyen, Appl. Surf. Sci., 2020, 507, 145036 CrossRef CAS.
- D. Hoat, M. Naseri, N. N. Hieu, R. Ponce-Pérez, J. Rivas-Silva, T. V. Vu and G. H. Cocoletzi, J. Phys. Chem. Solids, 2020, 144, 109490 CrossRef CAS.
- S.-D. Guo, X.-S. Guo, R.-Y. Han and Y. Deng, Phys. Chem. Chem. Phys., 2019, 21, 24620–24628 RSC.
- A. Tsukazaki, M. Kubota, A. Ohtomo, T. Onuma, K. Ohtani, H. Ohno, S. F. Chichibu and M. Kawasaki, Jpn. J. Appl. Phys., 2005, 44, L643 CrossRef CAS.
- S. Cheemadan, A. Rafiudeen and M. C. S. Kumar, J. Nanophotonics, 2016, 10, 033007 CrossRef.
- J. S. McCloy, R. Korenstein and B. Zelinski, J. Am. Ceram. Soc., 2009, 92, 1725–1731 CrossRef CAS.
- K. Kaviyarasu and P. A. Devarajan, Adv. Appl. Sci. Res., 2011, 2, 131–138 CAS.
- H. Zheng, X.-B. Li, N.-K. Chen, S.-Y. Xie, W. Q. Tian, Y. Chen, H. Xia, S. Zhang and H.-B. Sun, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 115307 CrossRef.
- M. M. Alyörük, Phys. Status Solidi B, 2016, 253, 2534–2539 CrossRef.
- A. D. Moghadam, P. Maskane and S. Esfandiari, Phys. C, 2018, 549, 33–36 CrossRef CAS.
- B. Nourozi, A. Aminian, N. Fili, Y. Zangeneh, A. Boochani and P. Darabi, Results Phys., 2019, 12, 2038–2043 CrossRef.
- B. Luo, Y. Yao, E. Tian, H. Song, X. Wang, G. Li, K. Xi, B. Li, H. Song and L. Li, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 17213–17218 CrossRef CAS.
- T. Kuila, S. Bose, A. K. Mishra, P. Khanra, N. H. Kim and J. H. Lee, Prog. Mater. Sci., 2012, 57, 1061–1105 CrossRef CAS.
- K. Balasubramanian and M. Burghard, Small, 2005, 1, 180–192 CrossRef CAS.
- S.-H. Cheng, K. Zou, F. Okino, H. R. Gutierrez, A. Gupta, N. Shen, P. Eklund, J. O. Sofo and J. Zhu, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 205435 CrossRef.
- D. Hoat, M. Naseri, N. T. Binh, J. Rivas-Silva, T. V. Vu and G. H. Cocoletzi, Phys. Lett. A, 2020, 126444 CrossRef CAS.
- Q. Li, Q. Zhou, X. Niu, Y. Zhao, Q. Chen and J. Wang, J. Phys. Chem. Lett., 2016, 7, 4540–4546 CrossRef CAS.
- D. Hoat, M. Naseri, N. N. Hieu, R. Ponce-Pérez, J. Rivas-Silva and G. H. Cocoletzi, Superlattices Microstruct., 2020, 137, 106320 CrossRef CAS.
- L. Chen, Y. Cui, Z. Xiong, M. Zhou and Y. Gao, RSC Adv., 2019, 9, 21831–21843 RSC.
- D. Hoat, M. Naseri, R. Ponce-Péreze, N. N. Hieu, J. Rivas-Silva, T. V. Vu, H. D. Tong and G. H. Cocoletzi, Mater. Res. Express, 2019, 7, 015013 CrossRef.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133 CrossRef.
- K. Schwarz and P. Blaha, Comput. Mater. Sci., 2003, 28, 259–273 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207–8215 CrossRef CAS.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188 CrossRef.
- W. Gao, T. A. Abtew, T. Cai, Y. Sun, S. Zhang and P. Zhang, 2015, arXiv preprint arXiv:1504.06259.
- J. R. Silva, A. M. Blas and D. Hoat, J. Phys. Chem. Solids, 2019, 128, 310–315 CrossRef CAS.
- C. Ambrosch-Draxl and J. O. Sofo, Comput. Phys. Commun., 2006, 175, 1–14 CrossRef CAS.
- J. S. Toll, Phys. Rev., 1956, 104, 1760 CrossRef.
| This journal is © The Royal Society of Chemistry 2020 |