Open Access Article
Open Access ArticleDFT study of α-Keggin, lacunary Keggin, and ironII–VI substituted Keggin polyoxometalates: the effect of oxidation state and axial ligand on geometry, electronic structures and oxygen transfer†
Soheila
Mir
,
Bahram
Yadollahi
 *,
Reza
Omidyan
and
Gholamhasan
Azimi
*,
Reza
Omidyan
and
Gholamhasan
Azimi
Department of Chemistry, University of Isfahan, Isfahan 81746-73441, Iran. E-mail: yadollahi@chem.ui.ac.ir; yadollahi.b@gmail.com
First published on 11th September 2020
Abstract
Herein, the geometry, electronic structure, Fe–ligand bonding nature and simulated IR spectrum of α-Keggin, lacunary Keggin, iron(II/III)-substituted and the important oxidized high-valent iron derivatives of Keggin type polyoxometalates have been studied using the density functional theory (DFT/OPTX-PBE) method and natural bond orbital (NBO) analysis. The effects of different Fe oxidation states (II–VI) and H2O/OH−/O2− ligand interactions have been addressed concerning their geometry and electronic structures. It has been revealed that the d-atomic orbitals of Fe and 2p orbitals of polyoxometalate's oxygen-atoms contribute in ligand binding. Compared with other high valent species, the considered polyoxometalate system of [PW11O39(FeVO)]4−, possesses a high reactivity for oxygen transfer.
1. Introduction
Polyoxometalates (POMs) represent a diverse class of inorganic metal-oxide anion clusters with defined structures based on MO6 octahedra mostly containing tungsten and/or molybdenum in their highest oxidation states.1–3 Owing to their attractive structure along with chemical and electronic versatility, they have found different applications in catalysis, medicine and materials sciences.4–6 Among a wide variety of heteropoly compounds, Keggin type POMs, [XM12O40]n−, are the most stable and available species. Substitution of addenda atoms (W or Mo) in Keggins with other transition metals generates transition metal substituted Keggin type POMs (TMSPOMs). This type of substitution, as one of the main source of diversity, improves redox and acid/base properties of POMs in a variety of chemical processes.2 Some of the TMSPOMs, such as high-valent iron–oxo species in heme enzymes (or metalloporphyrin complexes)7,8 and nonheme reagents,9 are used as oxidation catalyst in different organic reactions.Understanding the effect of various properties, such as the roles of transition metals, framework metal atoms MFM, and type of heteroatom X and counter ions, in TMSPOMs stability and reactivity could be useful in designing efficient POM-based materials in emerging technologies. Electronic structure and reactivity of this growing class of inorganic compounds need to comprehensive experimental and theoretical investigations.
As stated above, POMs and especially TMSPOMs have been used extensively in different catalytic oxidation reactions using environmentally friendly oxidants such as hydrogen peroxide. These compounds and some of their derivatives, which could be produced in the reaction medium, with respect to stability, energy and their properties, possibly will contribute in catalytic processes.
The structural and reactivity differences in high-valent metal derivatives of TMSPOMs allow the researchers to resort the computational examinations in this field. There are a vast number of reports devoted on theoretical exploration of POMs with focus on understanding the electronic structure, redox property, magnetism, and reaction mechanisms.10–27 For example, the essential role of [(Xn+O4)MIII2(OH)2(MFW)10O32](8−n)− chemical composition – where M = Fe, Mn, Ru, MFW = Mo and W, and X = AlIII, SiIV, PV, and SVI – in the geometry, electronic structure, magnetic properties and defining lower-lying electronic state of these species were investigated. This, in turn, would possibly have an impact on their reactivity.28,29 The molecular geometry, electronic structure, redox properties and metal-functional group bonding nature of a series of transition metal nitrido and dinitrogen derivatives of Keggin type POMs were also analyzed by density functional theory (DFT) and natural bond orbital (NBO) analysis. Their findings indicate that the electrophilic/nucleophilic reactivity and interaction between metal and functional group in these POMs is directly related to the transition metal substitution.30–32 The systematic DFT and NBO analysis were employed to investigate the electronic structures and bonding features of the ruthenium(II) atom and SO2 molecule in the two ruthenium–sulfur dioxide (SO2) adducts of trans-Ru(NH3)4(SO2)Cl+ and [(SiW11O39)RuII(SO2)].6–33 The DFT method has also been employed to design a new [Mo5O18Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O]3− catalyst, which would act as selective C–H hydroxylation reagent34 and adopted to identify the electronic and redox properties, protonation, and stability of five [α-PTi2W10O40]7− isomers.35 All of these valuable studies shed more light on the application of POMs in different realms.
O]3− catalyst, which would act as selective C–H hydroxylation reagent34 and adopted to identify the electronic and redox properties, protonation, and stability of five [α-PTi2W10O40]7− isomers.35 All of these valuable studies shed more light on the application of POMs in different realms.
The theoretical study of TMSPOMs derivatives is difficult because of multiple lower lying electronic states, high negative charges and large sizes. In this study, high level density functional theoretical method has been applied to study a Keggin POM, α-[PW12O40]3− (PW12), lacunary Keggin POM, [PW11O39]7− (PW11), FeII/III substituted Keggin POMs, [PW11O39(Fen+)](7−n)− (PWFen+) (n = 2, 3), FeII/III/IV substituted Keggin POMs with H2O ligand, [PW11O39(Fen+OH2)](7−n)− (PWFen+OH2) (n = 2, 3, 4), and other high valent FeIV/V/VI POMs with OH− and O2− ligands as potential active POM species. The significance of the work could be unravelled when the difficulties associated with theoretical studies of organometallic, owing to strong spin contamination problems would be taken into account. Fortunately, recent development in deMon2K code,36 by implementing the auxiliary DFT approaches and robust algorithms made it feasible to study such heavy systems.
2. Results and discussion
2.1. Ground state geometries, charge distribution, electronic structure, and simulated infrared spectra of PW12 and PW11 anions
The most common Keggin heteropoly anions like PW12, [SiW12O40]4− and [PMo12O40]3− are formed from simple oxoanions and required heteroatoms through a self-assembly process upon acidification in aqueous solutions.| 12WO42− + HPO42− + 23H+ → [PW12O40]3− + 12H2O |
Adding controlled amounts of hydroxide ions to the aqueous solution of these heteropoly anions could generate the lacunary (defect) POMs. These POM anions encompass one or more vacancies due to loss of addenda atom(s) from the structure. At the pH = 2, this process is expressed as follows:37,38
| [PW12O40]3− ⇄ [PW11O39]7− + WO4+ |
The mono lacunary Keggin POMs could act as pentadentate ligands and so frequently applied in preparing TMSPOMs. These compounds come in a big variety and are used as acid or oxidation catalysts.
In this study, attempts are made to investigate the geometry, electronic structure and simulation of IR spectra of the mentioned POMs. The process begins with study on PW12 and followed by PW11, where one WO4+ unit is removed, Fe substituted PW11 as PWFen+ (n = 2 and 3) and ended by PWFen+OH2 (n = 2 and 3) with H2O as the axial ligand. Since this TMSPOMs could be used as catalyst in oxidation reactions through the interaction between oxidant and catalyst, different types of high oxidation state Fe substituted Keggin POMs along with various axial ligands have been considered.
| Exp.a | PW11 | PW12 | ||
|---|---|---|---|---|
| Selected bond | Bond length | Selected bond | Bond length | |
| a The experimental values were adapted from ref. 21 and 35. | ||||
| 1.530 | P1–Oa13 | 1.563 | P1–Oa14 | 1.597 |
| — | P1–Oa14 | 1.563 | P1–Oa15 | 1.561 |
| 2.430 | W2–Oa13 | 2.428 | W2–Oa14 | 2.375 |
| — | W6–Oa13 | 2.429 | W6–Oa14 | 2.516 |
| 1.900 | W2–Ob24 | 1.867 | W2–Ob25 | 2.061 |
| 1.900 | W6–Ob28 | 1.868 | W6–Ob29 | 1.912 |
| 1.910 | W2–Oc33 | 1.881 | W2–Oc34 | 1.893 |
| 1.910 | W6–Oc39 | 1.881 | W6–Oc40 | 1.902 |
| 1.690 | W2–Od41 | 1.700 | W2–Od42 | 1.745 |
| 1.690 | W6–Od44 | 1.700 | W6–Od45 | 1.741 |
Bond length is a good parameter for evaluation of interaction strength between two atoms. By removing a WO4+ moiety from PW12, the system's charge is varied from −3 to −7 in PW11. As a result, the P1–Oa13 (1.597 Å), W6–Oa13 (2.516 Å), W6–Ob28 (1.912 Å), W6–Oc39 (1.902 Å) and W6–Od44 (1.741 Å) bond lengths in PW11 elongate respect to P1–Oa14 (1.563 Å), W6–Oa14 (2.429 Å), W6–Ob29 (1.868 Å), W6–Oc40 (1.881 Å) and W6–Od45 (1.70 Å) bond lengths in PW12, respectively (see Scheme 1 for numbering). These results indicate a few weakening of binding interactions in PW11 for bonds far from lacuna position and larger changes in the bond lengths around cavity (lacuna). The bond lengths of W (4, 5, 9 and 10) atoms with O (25, 19, 32 and 38) atoms in PW11 respect to PW12 are shortened from 1.920 to 1.730 Å. This bond length shortening could be related to the high electronic density on O (25, 19, 32 and 38) atoms after removal of WO4+. As mentioned, O atom's electronic density could be shifted to W and thus, strengthening of interactions.
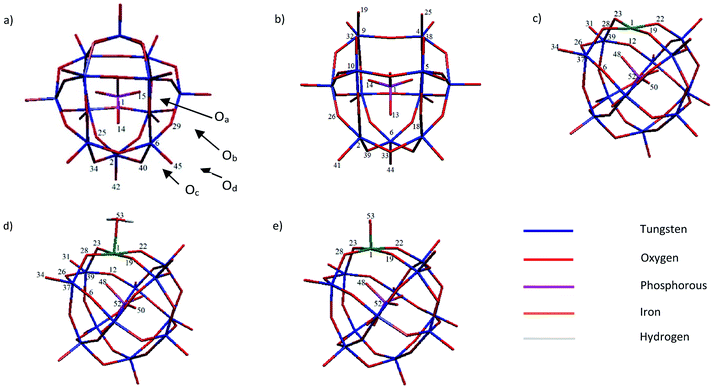 | ||
| Scheme 1 The relevant numbering pattern of studied systems: (a) PW12, (b) PW11, (c) PWFen+ (n = 2, 3), (d) PWFen+OH2 (n = 2, 3 and 4) and (e) PWFen+O (n = 4, 5 and 6). | ||
For PW12, it has been predicted that the singlet spin state (S = 0) is the most stable state, while the triplet (S = 1) and quintet (S = 2) spin states are 57.30 and 125.50 kcal mol−1 higher in energy than the singlet state, respectively (Table S1†). Also, in PW11 the triplet spin state is 55.86 kcal mol−1 higher in energy than corresponding singlet spin state.
| POM | PO43− | W | Ob | Oc | Od |
|---|---|---|---|---|---|
| PW12 | −0.98 | +1.98 | −0.82 | −0.77 | −0.56 |
| PW11 | −1.06 | +1.67 to +1.92 | −0.70 to −0.87 | −0.70 to −0.82 | −0.69 |
Atomic charges of PW12 and PW11 were calculated at UOPBE/6-31G(d) level (LANL2DZ basis set on the metal atom). Although in computational context, the absolute Mulliken charges are not so accurate, their variations could be quite reliable.21 According to the theoretical studies by Courcot and Bridgeman, the Mulliken atomic charges – compared to Hirshfeld, Voronoi Deformation Density (VDD), Quantum Theory of Atoms in Molecules (QTAIM) and the Net Total Voronoi (NTV) charges – could show the best convergence during the calculation with experimental data for several polyanions and provide a good description of Coulomb potential and their chemistry properties.39–43 For PW12, an electronic charge of −0.98e is assigned for the central PO43− moiety, which increases slightly by −0.08e for PW11 (i.e. q = −1.06e, q is the net charge of central PO43− in PW11), and in turn constitutes the difference between local charge of central PO43− in PW11 and PW12. High differences between the net charges for Od in PW11 (−0.69e) and PW12 (−0.56e) have not changed the local charge of central PO43−. This high charge density is accumulated in the W11O35 framework of POM, especially in the terminal oxygen atoms, and increases the basicity of them.
Other prominent changes occur in atoms near the lacuna, which the positive charge of W (4, 5, 9 and 10) atoms in PW12 decreased from 1.98e to 1.67e in PW11. This is related to the charge transfer from O (19, 25, 32 and 38) atoms in PW11 which bearing the high charge density after removal of WO4+ moiety (more information on Mulliken charges of PW12 and PW11 is presented in Table S6†).
Moreover, in order to determine the effect of additional negative charge on the valence orbital energies, six valence orbitals (α and β-spin) were selected for PW12 and PW11 compounds (Fig. 1). From Fig. 1a, among six selected α and β orbitals for PW12, there are only two orbitals with negative energy and four MOs with energy close to zero. However, for PW11, all mentioned orbitals possess high positive energy (Fig. 1b). The results also indicate positive energy for the interior orbitals (up to HOMO−118; no. 127). So, it can be deduced that an additional negative charge on PW11 increases the orbital energy. As a result, in PW11, electrons are better available for stabilizing transition metals in different oxidation states and so PW11 converts to a better electron donor ligand.
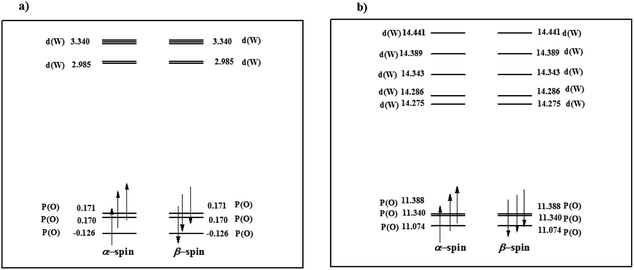 | ||
| Fig. 1 Energy level expressions of frontier molecular orbitals (FMOs) for (a) PW12 and (b) PW11 in the ground state. The orbital energy values have been represented in eV. | ||
Also, by removal of WO4+ moiety the molecular symmetry of PW12 reduces from Td to C3 in PW11. Decent in symmetry leads to lifting the doublet-triplet degeneracy in dxy-like orbitals21 of PW12 and singlet degeneracy for all orbitals performs in PW11 (Fig. 1).
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Od, W–Ob–W and W–Oc–W bond lengths in PW11, which are far from lacuna site, would increase. IR spectroscopy being able to detect small structural differences and so, is a sufficient probe for investigation of the variation of Keggin-type POM structures. Keggin-type POMs, as metal–oxygen clusters, contain some of metal–oxygen stretching vibrational modes at 500–1100 cm−1. Accordingly, based on vibrational frequency calculations, simulation of IR spectrum of PW12 and PW11 have been done at OPTX-PBE/DZVP-GGA level.
Od, W–Ob–W and W–Oc–W bond lengths in PW11, which are far from lacuna site, would increase. IR spectroscopy being able to detect small structural differences and so, is a sufficient probe for investigation of the variation of Keggin-type POM structures. Keggin-type POMs, as metal–oxygen clusters, contain some of metal–oxygen stretching vibrational modes at 500–1100 cm−1. Accordingly, based on vibrational frequency calculations, simulation of IR spectrum of PW12 and PW11 have been done at OPTX-PBE/DZVP-GGA level.
For PW12 structure, four infrared absorption bands at 1067, 963, 863 and 790 cm−1 have been assigned to P–Oa, W![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Od, W–Ob–W and W–Oc–W stretching bonds, respectively. From literature, it has been established that DFT methods generate IR vibrational frequencies with a slight shift towards low energies.44 As to PW11, the P–Oa stretching mode exhibits a splitting to two components at 1060 and 1050 cm−1 which is approved by experimental data.45 Moreover, the vibrational frequencies of P–Oa, W
Od, W–Ob–W and W–Oc–W stretching bonds, respectively. From literature, it has been established that DFT methods generate IR vibrational frequencies with a slight shift towards low energies.44 As to PW11, the P–Oa stretching mode exhibits a splitting to two components at 1060 and 1050 cm−1 which is approved by experimental data.45 Moreover, the vibrational frequencies of P–Oa, W![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Od, W–Ob–W and W–Oc–W bonds in PW11 at 1060, 1050, 871, 800 and 706 cm−1, in comparison with PW12, are appeared at lower frequencies. The results of IR spectrum calculations, that verify the modification in PW11 geometry, are tabulated in Table 3 (and also Fig. S3 and S4†).
Od, W–Ob–W and W–Oc–W bonds in PW11 at 1060, 1050, 871, 800 and 706 cm−1, in comparison with PW12, are appeared at lower frequencies. The results of IR spectrum calculations, that verify the modification in PW11 geometry, are tabulated in Table 3 (and also Fig. S3 and S4†).
| Stretching mode | Vibrational frequency/cm−1 | |
|---|---|---|
| PW11 | PW12 | |
| ν (P–Oa)1 | 1060 | 1067 |
| ν (P–Oa)2 | 1050 | — |
ν
(W![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Od) Od)
|
871 | 963 |
| ν (W–Ob–W) | 800 | 863 |
| ν (W–Oc–W) | 706 | 790 |
2.2. Ground state geometries, charge distribution, electronic structure, and simulated infrared spectra of PWFen+ and PWFen+OH2 (n = 2 and 3)
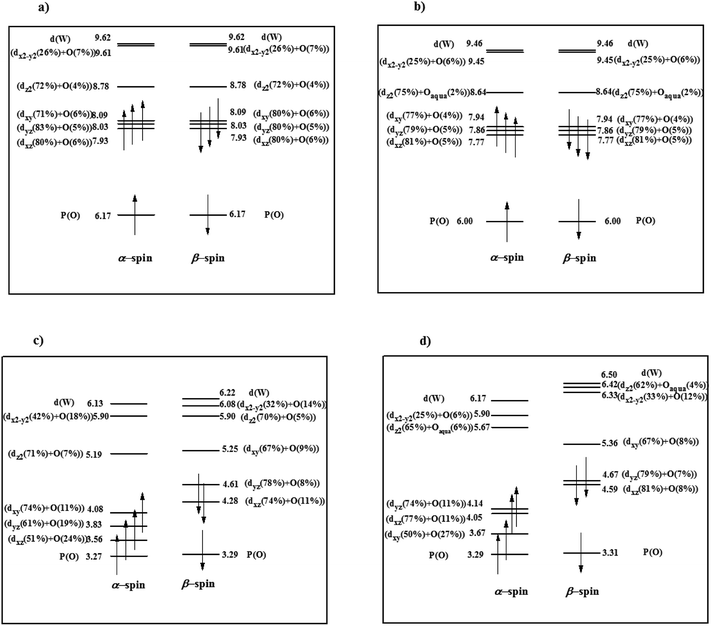
In respect to the role of TMSPOMs in different reactions like oxidative and acid/base processes46–50 and also the effective role of iron substituted POMs,51 various Fe oxidation states in iron substituted Keggin type POMs have been studied in this work. As stated above, truncation of PW12 by removing of WO4+ moiety leaves behind a lacunary PW11 which act as a ligand and in combination with Fe generates PWFen+ (n = 2 and 3) as iron substituted POMs. By locating a H2O ligand at the sixth octahedral coordination position, the PWFen+OH2 (n = 2 and 3) cluster would be formed.Also, the structure of PWFeIIOH2 was optimized in three spin states singlet (S = 0), triplet (S = 1) and quintet (S = 2). From the results, it has been unravelled that quintet state (S = 2) is the most stable while singlet (S = 0) and triplet (S = 1) spin states are 23.53 and 12.49 kcal mol−1 less stable, respectively. Our attempts failed in determination a local minimum for interacting of H2O and FeII in triplet and quintet spin states since the weak iron–water interaction results in separation of H2O following optimization and then their interaction with O28 of POM through hydrogen bond has been exhibited. Consequently, the singlet spin state is more favourable for this Fe substituted POM in an oxidation process, because Fe interacts directly with H2O ligand. At higher spin states, electron transfer from FeII d orbitals of antibonding MOs of Fe–OH2 bond leads to weakening the interaction between H2O and Fe, and so dissociation of H2O following optimization of corresponding geometry. The same holds true for PWFeIIIOH2 at doublet, quartet and sextet spin states, where doublet spin state is more appropriate because Fe interacts directly with H2O. As shown in Fig. 2, PWFen+OH2 (n = 2 and 3) which is generated through replacing WO4+ moiety with [Fe–OH2] in PW12 is optimized at doublet, quartet and sextet spin states for FeIII and singlet, triplet and quintet spin states for FeII (see ESI† for xyz coordinates of studied systems).
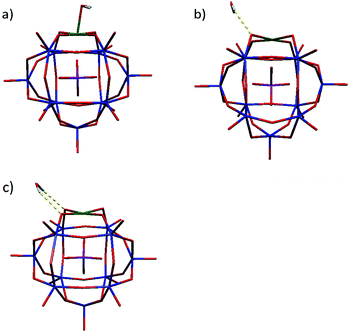 | ||
| Fig. 2 The optimized geometry of PWFeIIOH2 (a) in the singlet, (b) in the triplet and (c) in the quintet spin states obtained by OPTX-PBE/DZVP-GGA calculation. | ||
Key geometry parameters of PWFen+ and PWFen+OH2 (n = 2 and 3) are tabulated in Table S2.† In PWFeII, as the total charge reduced from −7 to −5 respect to PW11, the bond lengths are also shortened, while these are still long respect to PW12. This implies that by changing the electron density on atoms the whole system remained stable but some of the bond lengths are altered. The most important alterations in the bond lengths have been predicted in the bonds around lacuna region in POM. The W–O bond length nearby the lacuna, which their oxygen atoms are ligated to FeII, increases from 1.730 Å in PW11 to 1.808 Å in PWFeII (Table S2†). Substitution of Fe in PW11 is along with significant charge distribution from oxygen atoms to Fe. The charges of Fe, W (35, 37, 39 and 44) and O donor atoms (19, 22, 23 and 28) in PWFeII are 0.67e, 1.86e and −0.69e respectively, which in compare with charges of W (4, 5, 9 and 10) and O donor atoms (19, 25, 32 and 38) in PW11 (1.70e and −0.63e respectively), the positive charge of W atoms is increased. Thus the bond length for W37–Oc28 (1.808 Å) is predicted to be shorter and stronger with respect to Fe1–Oc28 (1.932 Å). The difference predicted between Fe1–Oa48 (1.938 Å) and W37–Oa48 (2.460 Å) bond lengths shows the stronger interaction between Fe and Oa48 (centre tetrahedral oxygen) respect to W37–Oa48, even though FeII and WVI radiuses are almost equal. This is because the bond length depends on both of the M–O interaction and metal radius. Also, the stronger interaction can be related to the favourable orientation of Fe dz2 orbital with Oa48 pz orbital and not to the charge distribution, because the charge of Oa48 (−0.76) in PWFeII compared with Oa13 (−0.74) in PW11 was not changed significantly. In PWFeIII, single electron oxidation of FeII into FeIII caused the shortening of all above mentioned bond lengths. This implies that bonding interaction between FeIII atom and four oxygen atoms of POM lacuna is stronger than that of FeII.
Our calculation also shows small structural differences between PWFen+ and PWFen+OH2 (n = 2 and 3) (Table S2†). A slight structural change has been exhibited when H2O ligated on Fe and so Fe1–Oa48 (see Scheme 1 for labelling) bond length become longer in PWFen+OH2 (n = 2 and 3) (i.e. q = 0.044 Å) and is the difference in Fe1–Oa48 bond length between PWFeII and PWFeIIOH2. The large Fe1–Oa48 length shows a weak bonding interaction which provides an unsaturated metal atom in pseudo-octahedral coordinated sphere.19,30,31 Thus, Fe has an additional ability for binding to H2O ligand. It is well-known that POMs have excellent structural stability while accepting or donating one or several electrons in various chemical mediums. Along with our study, the geometric parameters of POMs were checked for single electron oxidation of iron in POM (FeII to FeIII). As expected, no significant structural changes were predicted and only the geometric parameters of Fe–OH2 bond have been influenced. The FeII–Oaqua and FeIII–Oaqua bond lengths were 2.113 Å and 2.060 Å respectively, and Δr(FeIII/II–Oaqua) = 0.053 Å.
The bonding nature has also been investigated using NBO analysis. The calculated WBI (Wiberg Bond Index) values for FeII–OH2 and FeIII–OH2 are 0.3358 and 0.3759, respectively (Table S2†). Thus, there is a single and weak bonding interaction between FeII and FeIII with H2O molecule.
| Atom/group | PWFeII | PWFeIIOH2 | PWFeIII | PWFeIIIOH2 |
|---|---|---|---|---|
| PO4 | −0.96 | −0.96 | −0.97 | −0.94 |
| Od | −0.63 | −0.63 | −0.60 | −0.60 |
| O48 | −0.78 | −0.76 | −0.76 | −0.74 |
| Ob (W2) | −0.82 | −0.82 | −0.83 | −0.82 |
| Ob (FeW) | −0.70 | −0.70 | −0.72 | −0.72 |
| Oc (W2) | −0.78 | −0.78 | −0.78 | −0.77 |
| Oc (FeW) | −0.67 | −0.69 | −0.68 | −0.70 |
| Fe | 0.67 | 0.64 | 0.85 | 0.66 |
| W | 1.90 | 1.91 | 1.95 | 1.95 |
| Oaqua | — | −0.90 | — | −0.75 |
(i) The Ob(W2) and Oc(W2) charges in Fe-substituted systems are similar to that of PW12 and PW11. The higher negative charges of bridged oxygen atoms, Ob(W2) and Oc(W2) with values between −0.82e and −0.77e, than terminal oxygen atoms have revealed higher basicity of bridged oxygen atoms.
(ii) In these systems, because of shorter bond lengths, favourable orientations and so higher negative overlap in terminal metal–oxygen bonds are expected. Also, transfer charges from Od (−0.63e) to tungsten are predicted to be more than those of Ob (−0.82e) and Oc (−0.78e) as bridged oxygen atoms. These results state that W![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Od bond (1.720 Å) is stronger and shorter than W–Ob (1.945 Å) and W–Oc (1.967 Å) bonds.
Od bond (1.720 Å) is stronger and shorter than W–Ob (1.945 Å) and W–Oc (1.967 Å) bonds.
(iii) The negative charges on bridge and corner oxygen atoms in Ob (W2) and Oc (W2) are larger than those of bridge and corner oxygen atoms in Ob (FeW) and Oc (FeW). This indicates more charge transfer effect from these oxygen atoms to Fe.
(iv) For PW12, the Mulliken analysis assigns an electronic charge of −0.98e on PO43−. Slightly decreasing in the negative charge on PO43− in Fe-substituted POM indicates that Fe substitution in POM does not change the net charge on PO43−. So, additional charges from substitution of Fen+ (n = 2 and 3) instead of WO4+ moiety in Keggin POM may be directed to W11O35 framework of POM and specially concentrated in terminal oxygen atoms. As it could be seen, the charges on terminal oxygen atoms in these systems are greater than those of PW12. Accumulation of charge density in the terminal oxygen atoms of Keggin POMs shows a relationship between the basicity of terminal oxygen atoms and the number and type of substituted metals. Also, in electron transfer reactions of Keggin POMs, additional electron transfers to the terminal oxygen atoms and the POM structure occur without significantly deforming in the framework. For this reason, the Keggin POMs are of interest in oxidation catalysis.21,54–56
(v) Different atoms in PWFen+ resemble the charges on PWFen+OH2 (n = 2 and 3), except the positive charge on Fe which decreases after H2O placing. The charge reduction for oxidation state III is more than oxidation state II. This implies a charge reorganization or transfer from O atom of H2O ligand to Fe and reduction of positive charge on Fe atom.
Compared with the free metal ion, lower magnitude of positive charge on Fe indicates charge reorganization or transfer from Keggin-type POM cage to the transition metal center, which is in well agreement with the MO prediction. Increasing of the Fe oxidation state from II to III is along with an increasing in oxygen 2p-orbital contribution (19, 22, 23 and 28) in PW11 indicating a stronger interaction between FeIII and PW11. This is mainly due to lower energy gaps between FeIII d orbitals and oxygen 2p orbitals in PW11 than that of FeII ion. By linking H2O ligand to iron, the orbital energies and configuration of electronic structure in PWFeIIOH2 do not change, in respect to PWFeII (Fig. 3b). Bonding interaction between Fe and H2O ligand is accompanied by overlapping between σ(b2) non-bonding orbital of H2O ligand and 3dz2 orbital of Fe leading to a weak σ bonding interaction. A charge transfer from H2O oxygen atom to Fe could be occurred after this σ interaction,57,58 and so, in PWFeIII the interaction of metal center with H2O becomes stronger. Moreover, orbital energies for PWFen+ and PWFen+OH2 (n = 2 and 3) decrease by changing the FeII to FeIII in a significant manner (Fig. 3).
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Od and W–Ob–W vibrations, compared to α-PW12, shifted to lower energies. Therefore, five characteristic bands could easily be employed to identify the structure of PWFen+ (n = 2 and 3) POMs.59 For simulated vibrational spectrum of PWFen+OH2 compared with that of PWFen+ (n = 2 and 3), the IR band of P–Oa is predicted to shift by 12 cm−1 upon linking to H2O (Table 5, and Fig. S5–S8†). However, W
Od and W–Ob–W vibrations, compared to α-PW12, shifted to lower energies. Therefore, five characteristic bands could easily be employed to identify the structure of PWFen+ (n = 2 and 3) POMs.59 For simulated vibrational spectrum of PWFen+OH2 compared with that of PWFen+ (n = 2 and 3), the IR band of P–Oa is predicted to shift by 12 cm−1 upon linking to H2O (Table 5, and Fig. S5–S8†). However, W![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Od, W–Ob–W, W–Oc–Fe and W–Oc–W vibrations are not significantly shifted which indicate that these vibrational bands are not sensitive to H2O ligation.
Od, W–Ob–W, W–Oc–Fe and W–Oc–W vibrations are not significantly shifted which indicate that these vibrational bands are not sensitive to H2O ligation.
| POM | 2S + 1 | ν (P–Oa) |
ν
(W![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Od) Od)
|
ν (W–Ob–W) | ν (W–Oc–W) | ν (W–Oc–Fe) | ν (H–O–H) | ν (H–O–H) | ν (H–O–H) |
|---|---|---|---|---|---|---|---|---|---|
| PWFeIII | 2 | 1092 | 942 | 843 | 778 | 756 | — | — | — |
| PWFeIIIOH2 | 2 | 1080 | 941 | 844 | 777 | 756 | 1684 | 3636 | 3732 |
| PWFeII | 1 | 1072 | 921 | 831 | 769 | 738 | — | — | — |
| PWFeIIOH2 | 1 | 1061 | 921 | 834 | 775 | 731 | 1689 | 3635 | 3716 |
According to the simulated IR spectrum of PWFen+OH2 (n = 2 and 3), the symmetric stretching and bending vibrational frequencies of H2O are similar in both complexes. This is mainly due to weak interaction between H2O and iron atoms in both of Fe oxidation states. By increasing the Fe oxidation state (from +2 to +3), all vibrational frequencies of P–Oa, W![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Od, W–Ob–W and W–Oc–W bonds in simulated IR spectrum move towards higher frequencies which is compatible with corresponded bond lengths.
Od, W–Ob–W and W–Oc–W bonds in simulated IR spectrum move towards higher frequencies which is compatible with corresponded bond lengths.
2.3. High-valent PWFeIV(OH2/OH) and PWFeIV/V/VI(O) substituted POMs
TMSPOMs are of major importance in oxygenation of organic compounds.3,4,60–66 In the oxidative process, high-valent TMSPOMs are usually generated by interaction of low-valent substituted transition metals with oxidant or other species available in the reaction medium and exhibited improved catalytic behaviours. Study on these high-valent TMSPOMs is essential for determining and characterizing their active species in reaction mediums. To our knowledge, rare studies on geometry, electronic structure and activity of high-valent TMSPOMs have been reported in literature. The quantum chemistry calculations based on DFT are applicable tools to shed more light on this context. A detailed DFT study on geometry, electronic structure and chemical bonding features of important high-valent species consist of [PW11O39(FeIVOH2)]3− (PWFeIVOH2), [PW11O39(FeIVOH)]4− (PWFeIVOH), [PW11O39(FeIVO)]5− (PWFeIVO), [PW11O39(FeVO)]4− (PWFeVO), and [PW11O39(FeVIO)]3− (PWFeVIO) were done at the OPTX-PBE/DZVP-GGA level. High-valent [PW11O39(Fen+O)](9−n)− (PWFen+O; n = 4, 5, 6) species constitute important intermediates in oxidation processes. These oxidized species could have terminal Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond as an essential active site in catalytic oxygenation reactions. For terminal W
O bond as an essential active site in catalytic oxygenation reactions. For terminal W![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bonds, because of π*-antibonding unoccupied orbitals, their bonding interactions lie in very high energy and so are not available for interaction with substrates.32 In this section, at first the geometry, electronic structure and chemical bonding features of seven considered species will be deliberated, and then favourable species for oxidation reactions will be addressed.
O bonds, because of π*-antibonding unoccupied orbitals, their bonding interactions lie in very high energy and so are not available for interaction with substrates.32 In this section, at first the geometry, electronic structure and chemical bonding features of seven considered species will be deliberated, and then favourable species for oxidation reactions will be addressed.
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond could not exist in PWFeIVOH2. As previously mentioned, POMs can accept or donate one or several electrons with minimal structural changes,27,30 thus our focus was not concentrated on bond lengths in this POMs (Table S3†). To verify, similarity in the IR frequencies of high-valent TMSPOMs have been shown by calculation (Table S4 and Fig. S9–S13†).
O bond could not exist in PWFeIVOH2. As previously mentioned, POMs can accept or donate one or several electrons with minimal structural changes,27,30 thus our focus was not concentrated on bond lengths in this POMs (Table S3†). To verify, similarity in the IR frequencies of high-valent TMSPOMs have been shown by calculation (Table S4 and Fig. S9–S13†).
Bond length and bonding interaction in FeIV–OH2 has not much difference with those of low-oxidation state species PWFeIIIOH2. Thus, Fe–Oligand bond length is decreased from 2.060 Å in PWFeIIIOH2 to 2.047 Å in PWFeIVOH2 (Δr(Fe–OH2) = 0.013 Å) and so the electronic structures of PWFeIIIOH2 and PWFeIVOH2 are almost similar. From the orbital energies of PWFeIVOH2 calculated through UOPBE/6-31G(d) level (LANL2DZ basis set on the metal atom), five MOs of HOMO−2, HOMO−1, HOMO, LUMO and LUMO+1 (Fig. S2a†) are metal-based d orbitals with antibonding character. These are originated from the overlapping between d orbitals of Fe and oxygen p orbitals (19, 22, 23 and 28). From the interaction between Fe 3dz2 orbital and σ(b2) non-bonding orbital of H2O, a σ* molecular orbital could be formed.
Also, the inspection of molecular orbital diagram in this compound indicates that the π*-antibonding orbital, which is responsible for Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond, is not formed (Fig. S2a†). This expression of electronic configuration which made by molecular orbital analysis could be confirmed by Mulliken spin population. Obviously, the spin densities contribute in determining the electronic structure in all POM compounds. The spin density of PWFeIVOH2 in its triplet ground state is mainly localized on FeIV (1.6) and partly on the four coordinated oxygen atoms of PW11 (0.085). No spin density resides on Oaqua (−0.015) being in well agreement with the MO prediction (Table 6).
O bond, is not formed (Fig. S2a†). This expression of electronic configuration which made by molecular orbital analysis could be confirmed by Mulliken spin population. Obviously, the spin densities contribute in determining the electronic structure in all POM compounds. The spin density of PWFeIVOH2 in its triplet ground state is mainly localized on FeIV (1.6) and partly on the four coordinated oxygen atoms of PW11 (0.085). No spin density resides on Oaqua (−0.015) being in well agreement with the MO prediction (Table 6).
| POM | Charge of Oligand | Charge of Fe | Spin density of Oligand | Spin density of Fe |
|---|---|---|---|---|
| PWFeIIOH2 | −0.90 | 0.64 | 0 | 0 |
| PWFeIIIOH2 | −0.75 | 0.66 | −0.008 | 0.924 |
| PWFeIVOH2 | −0.73 | 0.82 | −0.01 | 1.595 |
| PWFeIVOH | −0.64 | 0.87 | 0.10 | 1.713 |
| PWFeIVO | −0.43 | 0.86 | 0.76 | 3.072 |
| PWFeVO | −0.37 | 0.96 | 0.81 | 1.986 |
| PWFeVIO | −0.31 | 1.11 | 0.46 | 1.332 |
Geometry structure of the other high oxidation state Fe substituted POMs, PWFeIVOH, was also optimized at OPTX-PBE/DZVP-GGA level. As results show, triplet state (S = 1) is the most stable and for singlet (S = 0) and quintet (S = 2) spin states lower stabilities up to 11.1 and 4.8 kcal mol−1 were obtained, respectively. From the key geometrical parameters tabulated in Table S3,† by OH ligand in place of H2O, interaction between FeIV and OH in a significant manner is improved. Thus, the optimized FeIV–Oligand bond length is decreased from 2.047 Å in PWFeIVOH2 to 1.815 Å in PWFeIVOH (Δr(Fe–Oligand) = 0.232 Å). The calculated WBI value for FeIV–OH is 0.9089 and so FeIV–OH bond is a strong single bond.
According to our calculations, significant change on the Fe–OH bond in PWFeIVOH demonstrates different electronic structure from FeII/III/IV–OH2 POMs (Fig. S2b†). Among five frontier molecular orbitals that are metal-based d orbitals, two are responsible for Fe–OH bonding interaction. The σ(p–d) orbital come from overlapping between 2pz orbital of OH ligand with 3dz2 orbital of Fe.
Also, the π*-antibonding orbitals arise from the interaction among 3dxz orbital of Fe and 2px from oxygen in OH. It is well known that Fe–Oligand π*-antibonding unoccupied orbital is closely correlated to the catalytic oxygenation processes, because it provides an electronic clue for reactivity in oxygen transfer reactions. Therefore, PWFeIVOH with unoccupied 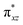 -antibonding orbital may have a better reactivity for oxygen transfer reaction.67,68
-antibonding orbital may have a better reactivity for oxygen transfer reaction.67,68
In PWFeIVO, decreasing in FeIV–Oligand bond length to 1.641 Å in the triplet ground state, compared to 1.815 Å for PWFeIVOH, could be confirmed by calculation of WBI value for FeIV–Oligand which is 1.46. Moreover, this shows a significant double bond feature for FeIV–Oligand (Table S3†). Analysis of FeIV–O bonding interaction by electronic structure shows that HOMO and HOMO−1 orbitals are responsible for metal–oxygen binding interaction (Fig. S2c†). Both orbitals are obtained from significant contribution of oxygen 2px/y orbitals and 3dxz/yz orbitals of FeIV. It should be noted that, these orbitals have important Fe–Oligand π*-antibonding character. Among that, 3dxy orbital is destabilized by antibonding interactions with p orbitals of four donor oxygen atoms at lacuna POM. As mentioned above, this important unoccupied Fe–Oligand π*-antibonding orbitals do not exist in FeII/III/IV–OH2 POMs.
In PWFeVO, optimized structure of the low energy triplet spin state show that FeV–Oligand bond length decreases to 1.635 Å from 1.641 Å in FeIV–O. This demonstrates minor changes in FeV–Oligand compared to FeIV–Oligand bond. This is mainly due to electron removing from nonbonding 3dxy orbital (β-HOMO) in FeV–O respect to FeV–Oligand bond. From the previous experimental studies by Rong and co-workers, [PW11O39(RuVO)]4− possesses high capability in oxygen-transfer reaction.69,70 It is worth mentioning that in the most of oxygen transfer reactions, at first, one electron transfers from πc![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) c orbital of alkene to
c orbital of alkene to 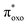 orbital of M
orbital of M![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O. This would weaken the M
O. This would weaken the M![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond and then oxygen transfer from M
O bond and then oxygen transfer from M![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O group to alkene will happen.71,72 Hence, PWFeVO could be a favourable species in these reactions due to some of advantages that will be discussed in the following.
O group to alkene will happen.71,72 Hence, PWFeVO could be a favourable species in these reactions due to some of advantages that will be discussed in the following.
For optimized PWFeVIO, the FeVI–Oligand bond length decreases to 1.601 Å in the triplet ground state from 1.635 Å in PWFeVO (Δr(FeV/VI–Oligand) = 0.034 Å). Also, calculated WBI value for FeVI–Oligand was 1.542 which indicates a significant double bond feature (Table S3†). In view of that, PWFeVIO bonding interaction and subsequently their electronic structure are similar to PWFeIV/VO.
As mentioned above, the important unoccupied Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O π*-antibonding orbitals are absent in PWFeII/III/IVOH2 while they appear in PWFeIV/V/VIO. Mulliken spin population analysis also supports these interactions and electronic structures. Spin density in these compounds is mostly localized on Fe
O π*-antibonding orbitals are absent in PWFeII/III/IVOH2 while they appear in PWFeIV/V/VIO. Mulliken spin population analysis also supports these interactions and electronic structures. Spin density in these compounds is mostly localized on Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O moiety and some of that on four oxygen in lacuna position of PW11, while the rest of POM cage carry a small negative spin density (Table 6).
O moiety and some of that on four oxygen in lacuna position of PW11, while the rest of POM cage carry a small negative spin density (Table 6).
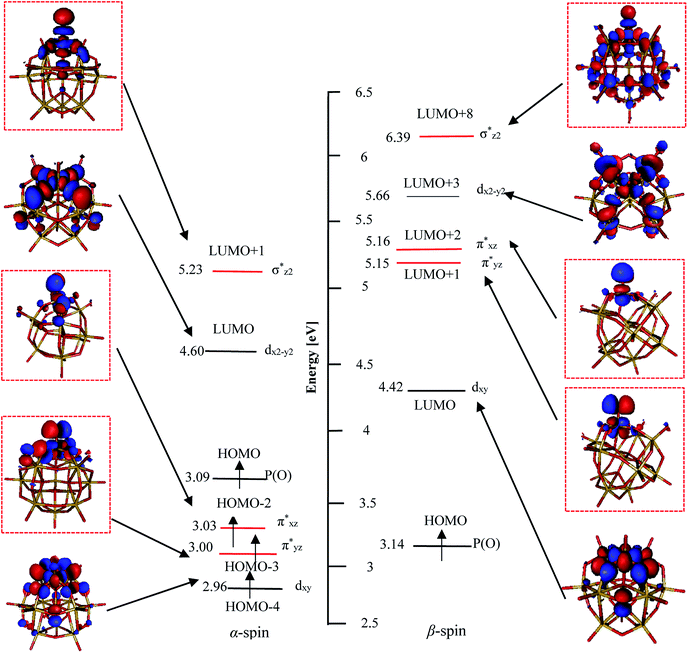
Now the question is: which of these high-oxidation states Fe substituted POMs would be favourable for oxidation process. According to frontier molecular orbital (FMO) theory, a suitable oxidation catalyst requires unoccupied orbitals with low energy and high orbital contribution of reactive atom at LUMO to achieve an appropriate overlap with the reagent FMOs.67,68,73,74 The energy expression and participation percentage of Fe and oxygen in unoccupied Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O π*-antibonding orbitals are shown in Fig. 4.
O π*-antibonding orbitals are shown in Fig. 4.
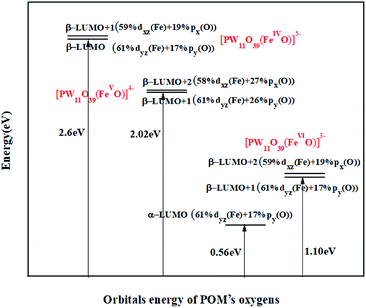 | ||
Fig. 4 Unoccupied Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O π*-antibonding orbitals for high-oxidation states PWFeIV/V/VIO determined based on UOPBE/6-31G(d) level (LANL2DZ basis set on the metal atom). O π*-antibonding orbitals for high-oxidation states PWFeIV/V/VIO determined based on UOPBE/6-31G(d) level (LANL2DZ basis set on the metal atom). | ||
As it could be seen in Fig. 4, in PWFeIV/VO species, unoccupied Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O π*-antibonding orbitals consist of β spin orbitals. In PWFeVIO, unoccupied Fe
O π*-antibonding orbitals consist of β spin orbitals. In PWFeVIO, unoccupied Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O π*-antibonding orbitals consist of α and β spin orbitals. Respect to HOMO, which contains oxygen p-orbitals, the energies of unoccupied Fe
O π*-antibonding orbitals consist of α and β spin orbitals. Respect to HOMO, which contains oxygen p-orbitals, the energies of unoccupied Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O π*-antibonding orbitals decrease in the following order: PWFeIVO > PWFeVO > PWFeVIO (Fig. 4). This order could be attributed to the POM charges reducing.75–77 Contribution of oxygen atom orbitals in these unoccupied Fe
O π*-antibonding orbitals decrease in the following order: PWFeIVO > PWFeVO > PWFeVIO (Fig. 4). This order could be attributed to the POM charges reducing.75–77 Contribution of oxygen atom orbitals in these unoccupied Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O π*-antibonding orbitals decreases as following: PWFeVO > PWFeIVO > PWFeVIO (Fig. 4).
O π*-antibonding orbitals decreases as following: PWFeVO > PWFeIVO > PWFeVIO (Fig. 4).
Calculated atomic charges and spin density values of oxygen bonded Fe in PWFeIV/V/VIO species are tabulated in Table 6. Results in Table 6 show lower negative charge for O2− ligand in these TMSPOMs than free O2−. Lesser negative charge on O2− ligand indicates the charge transfer from oxygen to Fe. Therefore, polarization of Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond could be an important factor for determining the activity differences in these TMSPOMs. The absolute values of atomic charges decrease in the following order: PWFeIVO (−0.43) > PWFeVO (−0.37) > PWFeVIO (−0.31) (Table 6). This is mainly along with increasing in the oxidation state of Fe atom. Moreover, decreasing in the spin density of O2− ligand for these high-oxidation state species is as following: PWFeVO > PWFeIVO > PWFeVIO (Table 6). In both of PWFeIV/VO species, with high spin density on the O2− (0.76 and 0.81 respectively), the O2− ligand possess substantial radical character. In experimental reports, radical complexes are regarded as suitable catalysts for closure of the epoxide rings.20 In contrary, radical character of oxygen in PWFeVIO is weakened considerably where the calculated spin density on the O2− decreased to 0.46.
O bond could be an important factor for determining the activity differences in these TMSPOMs. The absolute values of atomic charges decrease in the following order: PWFeIVO (−0.43) > PWFeVO (−0.37) > PWFeVIO (−0.31) (Table 6). This is mainly along with increasing in the oxidation state of Fe atom. Moreover, decreasing in the spin density of O2− ligand for these high-oxidation state species is as following: PWFeVO > PWFeIVO > PWFeVIO (Table 6). In both of PWFeIV/VO species, with high spin density on the O2− (0.76 and 0.81 respectively), the O2− ligand possess substantial radical character. In experimental reports, radical complexes are regarded as suitable catalysts for closure of the epoxide rings.20 In contrary, radical character of oxygen in PWFeVIO is weakened considerably where the calculated spin density on the O2− decreased to 0.46.
According to above mentioned points, PWFeVO would be favorable for oxidation processes owing to unoccupied π*-antibonding orbitals (β-LUMO+1 and β-LUMO+2) with low energy and high contribution of O2− respect to PWFeII/III/IVOH2, PWFeIVOH and PWFeIV/VIO. From the FMOs energy expression of PWFeVO in Fig. 5, it could be revealed that: α and β occupied and unoccupied orbitals with π* symmetry (α-HOMO−2, α-HOMO−3, β-LUMO+1, β-LUMO+2) and α and β unoccupied orbitals with σ* symmetry (α-LUMO+1 and β-LUMO+8) are responsible for Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bonding interaction in PWFeVO. The π*-antibonding orbitals are formed from overlapping between 3dxz/yz orbitals of FeV and 2px/y orbitals of oxygen, while the σ*-antibonding orbitals are made from combining the 3dz2 orbital of FeV and 2pz orbital of O2− ligand. Due to their lower energy, unoccupied π* orbitals are more important than σ* ones. According to DFT results, unoccupied Fe
O bonding interaction in PWFeVO. The π*-antibonding orbitals are formed from overlapping between 3dxz/yz orbitals of FeV and 2px/y orbitals of oxygen, while the σ*-antibonding orbitals are made from combining the 3dz2 orbital of FeV and 2pz orbital of O2− ligand. Due to their lower energy, unoccupied π* orbitals are more important than σ* ones. According to DFT results, unoccupied Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O π*-antibonding orbitals comprise from β-LUMO+1 and β-LUMO+2 in which β-LUMO+1
O π*-antibonding orbitals comprise from β-LUMO+1 and β-LUMO+2 in which β-LUMO+1 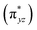 contain 26% contribution of O2− py orbital and 61% FeV dyz orbital and β-LUMO+2
contain 26% contribution of O2− py orbital and 61% FeV dyz orbital and β-LUMO+2 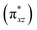 contains 27% contribution of O2− px orbital and 58% of FeV dxz orbital which are mostly classified as Fe
contains 27% contribution of O2− px orbital and 58% of FeV dxz orbital which are mostly classified as Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O functional group (Fig. 4).
O functional group (Fig. 4).
3. Computational details
All DFT computations of this work were performed with deMon2k program.36 We used the OPTX exchange functional proposed by Cohen and Handy,78,79 coupled with the Perdew–Becke–Ernzerhof (PBE) correlation functional.80 This Generalized-Gradient-Approximation (GGA) functional has been shown adequacy for modeling iron–porphyrin and cobalt porphyrin complexes.81–84 The Keggin type POM compounds were investigated by OPTX-PBE functional by assuming its adequacy based on previous studies.26,34,85 The DFT energies and gradients were corrected by an empirical expression to indicate dispersion.86 The Kohn–Sham equations were solved within the auxiliary DFT framework, where variationaly fitted auxiliary electron densities are applied in calculating both the Coulomb and the exchange-correlation (XC) potential.87,88 An adaptive grid of fine mesh (tolerance 10−7 a.u.) was chosen for the numerical integration of the XC potential.89 The basis set of DZVP-GGA (double-zeta-valence-polarization calibrated for generalized-gradient-approximation functional) on Fe, O, P, W and H was applied for geometry optimizations, frequency and electronic structure analyses.90 The auxiliary electron density was expanded with the GEN-A2 auxiliary basis set on Fe, W, P, O and H.91 The self-consistent-field iterations were run with convergence criteria of 10−8 hartree on the DFT energies. The geometry optimizations were performed with 1 × 10−5 hartree per bohr tolerance criteria on the energy gradients. No molecular symmetry was applied in geometry optimizations. Vibrational frequencies were obtained at the same level in this work. Cartesian coordinates of the optimized geometries of the complexes are presented in ESI.† Natural bond orbital (NBO) analysis at the OPBE/6-31G(d) level (LANL2DZ basis set on the metal atom)92–94 was performed to assign the atomic charges, spin densities and effective bond order/Wiberg Bond Indices (WBI). The NBO calculations were done with the Gaussian 09 package,95 considering only the ions without either counter cations or solvent molecules.4 Conclusion
DFT/OPTX-PBE method has been employed to investigate the geometry, electronic structure, Fe–ligand bonding nature, and simulated IR spectrum of α-Keggin, lacunary Keggin, FeII/III substituted and the important oxidized high-valent iron derivatives of Keggin type POMs. The most significant finding is briefed as follows:(i) Increasing in the POM charge, like PW11, results in no significant alteration of local charge at central PO43−. This high charge density is accumulated in W11O35 framework of the POM and specially concentrated on the terminal oxygen atoms which increase their basicity.
(ii) The electronic structures provide basis for understanding the bonding interactions between FeII and POM ligand. Bonding MOs result from contribution of 3d atomic orbitals of FeII and 2p orbitals of oxygen in POM.
(iii) The simulated IR spectra show that four characteristic peaks of PW12 split into five owing to substitution of Fe atom in PWFen+ (n = 2 and 3).
(iv) The PWFeII/III/IVOH2 derivatives show the weak Fe–Oligand single bond and PWFeIV/V/VIO derivatives display the strong Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O double bond. So, it could be predicted that Fe oxidation state affect the antibonding interaction between Fe and ligand, which is the main character of these derivatives, and increase their activity in oxygen transfer processes.
O double bond. So, it could be predicted that Fe oxidation state affect the antibonding interaction between Fe and ligand, which is the main character of these derivatives, and increase their activity in oxygen transfer processes.
(v) Relevant to other high-valent species, PWFeVO would be favourable for oxidation process because of low energy unoccupied π*-antibonding orbitals and high contribution of oxygen.
(vi) The FMO analysis indicated that Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bonding interaction mainly comes from an effective overlapping between 2px/y orbitals of O2− ligand and 3dxz/yz orbitals of Fe, thus an electron transfer from oxygen to Fe atom could be occurred.
O bonding interaction mainly comes from an effective overlapping between 2px/y orbitals of O2− ligand and 3dxz/yz orbitals of Fe, thus an electron transfer from oxygen to Fe atom could be occurred.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors are thankful of University of Isfahan for financially support of this research. We are also grateful from Prof. Aurelien de La Lande (Laboratoire de Chimie Physique, LCP, CNRS) and the University of Paris-Sud for supporting our computations at Styx.Notes and references
- P. Gouzerh and A. Proust, Chem. Rev., 1998, 98, 77–112 CrossRef CAS PubMed.
- J. T. Rhule, C. L. Hill, D. A. Judd and R. F. Schinazi, Chem. Rev., 1998, 98, 327–358 CrossRef CAS.
- S.-S. Wang and G.-Y. Yang, Chem. Rev., 2015, 115, 4893–4962 CrossRef CAS PubMed.
- I. V. Kozhevnikov, Chem. Rev., 1998, 98, 171–198 CrossRef CAS.
- A. Proust, R. Thouvenot and P. Gouzerh, Chem. Commun., 2008, 1837–1852 RSC.
- T. Yamase, Chem. Rev., 1998, 98, 307–326 CrossRef CAS.
- M. Sono, M. P. Roach, E. D. Coulter and J. H. Dawson, Chem. Rev., 1996, 96, 2841–2888 CrossRef CAS.
- C. Wang, K. V. Shalyaev, M. Bonchio, T. Carofiglio and J. T. Groves, Inorg. Chem., 2006, 45, 4769–4782 CrossRef CAS.
- J. Kaizer, E. J. Klinker, N. Y. Oh, J. U. Rohde, W. J. Song, A. Stubna, J. Kim, E. Münck, W. Nam and L. Que, J. Am. Chem. Soc., 2004, 126, 472–473 CrossRef CAS PubMed.
- N. S. Antonova, J. J. Carbó, U. Kortz, O. A. Kholdeeva and J. M. Poblet, J. Am. Chem. Soc., 2010, 132, 7488–7497 CrossRef CAS PubMed.
- S. P. de Visser, D. Kumar, R. Neumann and S. Shaik, Angew. Chem., Int. Ed., 2004, 43, 5661–5665 CrossRef CAS.
- P. Jiménez-Lozano, I. Y. Skobelev, O. A. Kholdeeva, J. M. Poblet and J. J. Carbó, Inorg. Chem., 2016, 55, 6080–6084 CrossRef.
- K. Kamata, T. Hirano, S. Kuzuya and N. Mizuno, J. Am. Chem. Soc., 2009, 131, 6997–7004 CrossRef CAS PubMed.
- K. Kamata, R. Ishimoto, T. Hirano, S. Kuzuya, K. Uehara and N. Mizuno, Inorg. Chem., 2010, 49, 2471–2478 CrossRef CAS.
- K. Kamata, Y. Nakagawa, K. Yamaguchi and N. Mizuno, J. Am. Chem. Soc., 2008, 130, 15304–15310 CrossRef CAS.
- A. E. Kuznetsov, Y. V. Geletii, C. L. Hill, K. Morokuma and D. G. Musaev, Inorg. Chem., 2009, 48, 1871–1878 CrossRef CAS.
- Z. L. Lang, G. C. Yang, M. N. Ma, S. Z. Wen, L. K. Yan, W. Guan and Z. M. Su, Dalton Trans., 2013, 42, 10617–10625 RSC.
- C. G. Liu, W. Guan, L. K. Yan and Z. M. Su, Eur. J. Inorg. Chem., 2011, 489–494 CrossRef.
- C. G. Liu, W. Guan, L. K. Yan, P. Song and Z. M. Su, Dalton Trans., 2009, 6208–6213 RSC.
- C. G Liu, X. M. Jiang and Z. M. Su, Inorg. Chem., 2017, 56, 10496–10504 CrossRef.
- J. M. Maestre, X. Lopez, C. Bo, J.-M. Poblet and N. Casan-Pastor, J. Am. Chem. Soc., 2001, 123, 3749–3758 CrossRef CAS PubMed.
- D. G. Musaev, K. Morokuma, Y. V. Geletii and C. L. Hill, Inorg. Chem., 2004, 43, 7702–7708 CrossRef CAS.
- Y. Nakagawa and N. Mizuno, Inorg. Chem., 2007, 46, 1727–1736 CrossRef CAS.
- R. Prabhakar, K. Morokuma, C. L. Hill and D. G. Musaev, Inorg. Chem., 2006, 45, 5703–5709 CrossRef CAS PubMed.
- J. Wang, C. Hu, M. Jian, J. Zhang and G. Li, J. Catal., 2006, 240, 23–30 CrossRef CAS.
- H. N. Wu, J. Wang, H. Li, N. N. Ma, T. Zhang, S. Q. Shi, L. K. Yan and Z. M. Su, Comput. Theor. Chem., 2016, 1089, 28–34 CrossRef CAS.
- M. X. Jiang and C. G. Liu, J. Phys. Chem. C, 2017, 121, 12735–12744 CrossRef CAS.
- D. Quiñonero, Y. Wang, K. Morokuma, L. A. Khavrutskii, B. Botar, Y. V. Geletii, C. L. Hill and D. G. Musaev, J. Phys. Chem. B, 2006, 110, 170–173 CrossRef PubMed.
- Y. Wang, G. Zheng, K. Morokuma, Y. V. Geletii, C. L. Hill and D. G. Musaev, J. Phys. Chem. B, 2006, 110, 5230–5237 CrossRef CAS PubMed.
- C.-G. Liu, S. Liu and T. Zheng, Inorg. Chem., 2015, 54, 7929–7935 CrossRef CAS PubMed.
- C. G. Liu, Z. M. Su, W. Guan and L. K. Yan, Inorg. Chem., 2009, 48, 541–548 CrossRef CAS.
- S. Romo, N. S. Antonova, J. J. Carbó and J. M. Poblet, Dalton Trans., 2008, 5166–5172 RSC.
- B. Zhu, Z. L. Lang, M. N. Ma, L. K. Yan and Z. M. Su, Phys. Chem. Chem. Phys., 2014, 16, 18017–18022 RSC.
- E. Derat, D. Kumar, R. Neumann and S. Shaik, Inorg. Chem., 2006, 45, 8655–8663 CrossRef CAS PubMed.
- W. Guan, L. Yan, Z. Su, S. Liu, M. Zhang and X. Wang, Inorg. Chem., 2005, 44, 100–107 CrossRef CAS.
- A. Koster, G. Geudtner, P. Calaminici, M. Casida, V. Dominguez, R. Flores-Moreno, G. Gamboa, A. Goursot, T. Heine and A. Ipatov, DeMon2k, Version 3, The deMon Developers, Cinvestav, Mexico City, Mexico, 2011 Search PubMed.
- R. Neumann and A. M. Khenkin, J. Mol. Catal. A: Chem., 1996, 114, 169–180 CrossRef CAS.
- P. Souchay, Polyanions et polycations, Gauthier-Villars, 1963 Search PubMed.
- X. Lo'pez, J. J. Carbo', C. Bo and J. M. Poblet, Chem. Soc. Rev., 2012, 41, 7537–7571 RSC.
- B. Courcot and A. J. Bridgeman, Int. J. Quantum Chem., 2010, 110, 2155–2161 CrossRef CAS.
- B. Courcot and A. J. Bridgeman, J. Comput. Chem., 2011, 32, 240–247 CrossRef CAS PubMed.
- B. Courcot and A. J. Bridgeman, J. Comput. Chem., 2011, 32, 1703–1710 CrossRef CAS PubMed.
- B. Courcot and A. J. Bridgeman, J. Comput. Chem., 2011, 32, 3143–3153 CrossRef CAS.
- M. R. Farsani and B. Yadollahi, J. Mol. Catal. A: Chem., 2014, 392, 8–15 CrossRef CAS.
- I. Böschen, B. Buss and B. Krebs, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1974, 30, 48–56 CrossRef.
- C. L. Hill and R. B. Brown, J. Am. Chem. Soc., 1986, 108, 536–538 CrossRef CAS PubMed.
- M. Colladon, A. Scarso, P. Sgarbossa, R. A. Michelin and G. Strukul, J. Am. Chem. Soc., 2007, 129, 7680–7689 CrossRef CAS PubMed.
- N. Mizuno and M. Misono, Chem. Rev., 1998, 98, 199–218 CrossRef CAS PubMed.
- N. Mizuno, K. Yamaguchi and K. Kamata, Coord. Chem. Rev., 2005, 249, 1944–1956 CrossRef CAS.
- Y. Sawada, K. Matsumoto and T. Katsuki, Angew. Chem., Int. Ed., 2007, 46, 4559–4561 CrossRef CAS PubMed.
- D. Mansuy, J. F. Bartoli, P. Battioni, D. K. Lyon and R. G. Finke, J. Am. Chem. Soc., 1991, 113, 7222–7226 CrossRef CAS.
- T. A. Betley and J. C. Peters, J. Am. Chem. Soc., 2004, 126, 6252–6254 CrossRef CAS PubMed.
- M. D. Fryzuk, S. A. Johnson, B. O. Patrick, A. Albinati, S. A. Mason and T. F. Koetzle, J. Am. Chem. Soc., 2001, 123, 3960–3973 CrossRef CAS.
- A. Hiskia and E. Papaconstantinou, Inorg. Chem., 1992, 31, 163–167 CrossRef CAS.
- L. Eberson, New J. Chem., 1992, 16, 151–156 CAS.
- I. A. Weinstock, Chem. Rev., 1998, 98, 113–170 CrossRef CAS PubMed.
- R. Tonner, F. Öxler, B. Neumüller, W. Petz and G. Frenking, Angew. Chem., Int. Ed., 2006, 45, 8038–8042 CrossRef CAS.
- H. Chen, M. Ikeda-Saito and S. Shaik, J. Am. Chem. Soc., 2008, 130, 14778–14790 CrossRef CAS PubMed.
- F. M. Santos, S. P. Magina, H. I. Nogueira and A. M. Cavaleiro, New J. Chem., 2016, 40, 945–953 RSC.
- S. Afewerki and A. Cordova, Chem. Rev., 2016, 116, 13512–13570 CrossRef CAS.
- F. G. Gelalcha, Chem. Rev., 2007, 107, 3338–3361 CrossRef CAS PubMed.
- T. Mallat and A. Baiker, Chem. Rev., 2004, 104, 3037–3058 CrossRef CAS.
- V. C. C. Wang, S. Maji, P. P. Y. Chen, H. K. Lee, S. S. F. Yu and S. I. J. C. R. Chan, Chem. Rev., 2017, 117, 8574–8621 CrossRef CAS.
- B. Zhang, H. Asakura, J. Zhang, J. Zhang, S. De and N. Yan, Angew. Chem., Int. Ed., 2016, 55, 8319–8323 CrossRef CAS.
- C. L. Hill and C. M. Prosser-McCartha, Coord. Chem. Rev., 1995, 143, 407–455 CrossRef CAS.
- J. Roithova and D. Schroder, Chem. Rev., 2009, 110, 1170–1211 CrossRef PubMed.
- S. Shaik, H. Hirao and D. Kumar, Acc. Chem. Res., 2007, 40, 532–542 CrossRef CAS PubMed.
- S. Shaik, D. Kumar, S. P. de Visser, A. Altun and W. Thiel, Chem. Rev., 2005, 105, 2279–2328 CrossRef CAS PubMed.
- R. Neumann and C. Abu-Gnim, J. Am. Chem. Soc., 1990, 112, 6025–6031 CrossRef CAS.
- C. Rong and M. T. Pope, J. Am. Chem. Soc., 1992, 114, 2932–2938 CrossRef CAS.
- M. T. Pope and A. Müller, Angew. Chem., Int. Ed., 1991, 30, 34–48 CrossRef.
- M. Sadakane and E. Steckhan, Chem. Rev., 1998, 98, 219–238 CrossRef CAS PubMed.
- A. Decker, M. S. Chow, J. N. Kemsley, N. Lehnert and E. I. Solomon, J. Am. Chem. Soc., 2006, 128, 4719–4733 CrossRef CAS PubMed.
- A. Decker, J.-U. Rohde, L. Que and E. I. Solomon, J. Am. Chem. Soc., 2004, 126, 5378–5379 CrossRef CAS PubMed.
- J. A. Fernández, X. López, C. Bo, C. de Graaf, E. J. Baerends and J. M. Poblet, J. Am. Chem. Soc., 2007, 129, 12244–12253 CrossRef PubMed.
- X. López, J. A. Fernández and J. M. Poblet, Dalton Trans., 2006, 1162–1167 RSC.
- S. Romo, J. A. Fernández, J. M. Maestre, B. Keita, L. Nadjo, C. de Graaf and J. M. Poblet, Inorg. Chem., 2007, 46, 4022–4027 CrossRef CAS.
- N. C. Handy and A. J. Cohen, Mol. Phys., 2001, 99, 403–412 CrossRef CAS.
- M. Swart, A. W. Ehlers and K. Lammertsma, Mol. Phys., 2004, 102, 2467–2474 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- A. de la Lande, M.-H. Ha-Thi, S. Chen, B. Soep and N. Shafizadeh, Phys. Chem. Chem. Phys., 2016, 18, 16700–16708 RSC.
- M. M. Conradie, J. Conradie and A. Ghosh, J. Inorg. Biochem., 2011, 105, 84–91 CrossRef CAS PubMed.
- M. Aarabi, R. Omidyan, S. Soorkia, G. Grégoire, M. Broquier, M.-E. Crestoni, A. de La Lande, B. Soep and N. Shafizadeh, Phys. Chem. Chem. Phys., 2019, 21, 1750–1760 RSC.
- M. Aarabi, S. Soorkia, G. Grégoire, M. Broquier, A. de la Lande, B. Soep, R. Omidyan and N. Shafizadeh, Phys. Chem. Chem. Phys., 2019, 21, 21329–21340 RSC.
- C. G. Liu, Mol. Phys., 2011, 109, 1851–1857 CrossRef CAS.
- A. Goursot, T. Mineva, R. Kevorkyants and D. Talbi, J. Chem. Theory Comput., 2007, 3, 755–763 CrossRef CAS PubMed.
- R. Flores-Moreno and A. M. Köster, J. Chem. Phys., 2008, 128, 134105 CrossRef PubMed.
- A. Vela, V. Medel and S. Trickey, J. Chem. Phys., 2009, 130, 244103 CrossRef CAS PubMed.
- M. Krack and A. M. Köster, J. Chem. Phys., 1998, 108, 3226–3234 CrossRef CAS.
- P. Calaminici, F. Janetzko, A. M. Köster, R. Mejia-Olvera and B. Zuniga-Gutierrez, J. Chem. Phys., 2007, 126, 044108 CrossRef PubMed.
- T. Clark, J. Chandrasekhar, G. W. Spitznagel and P. V. R. Schleyer, J. Comput. Chem., 1983, 4, 294–301 CrossRef CAS.
- P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 270–283 CrossRef CAS.
- P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 299–310 CrossRef CAS.
- W. R. Wadt and P. J. Hay, J. Chem. Phys., 1985, 82, 284–298 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 09, Gaussian, Inc., Wallingford CT, 2013 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ra05189f |
| This journal is © The Royal Society of Chemistry 2020 |