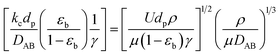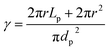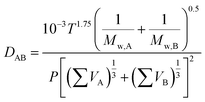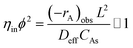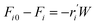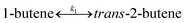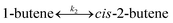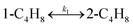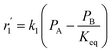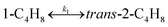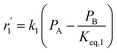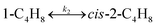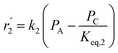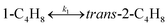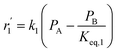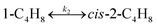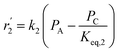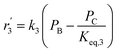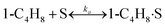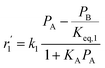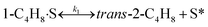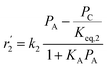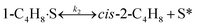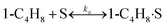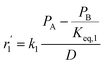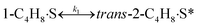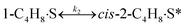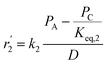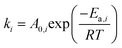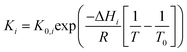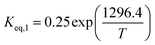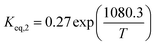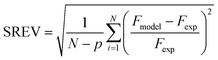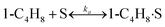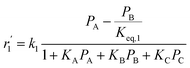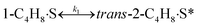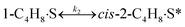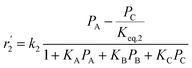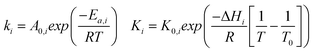DOI:
10.1039/D0RA05453D
(Paper)
RSC Adv., 2020,
10, 36667-36677
Intrinsic kinetic study of 1-butene isomerization over magnesium oxide catalyst via a Berty stationary catalyst basket reactor†
Received
22nd June 2020
, Accepted 15th September 2020
First published on 6th October 2020
Abstract
In this work, we studied the intrinsic kinetics of 1-butene isomerization over a commercial MgO catalyst using a Berty-type reactor (gradient-less recycle reactor). The Berty-type reactor has a behavior equivalent to a continuous stirred tank reactor (CSTR) with perfect mixing. The experimental results from this reactor were selected in a range in the absence of external and internal mass- and heat-transfer resistances, thereby representing the intrinsic kinetics. The 1-butene isomerization was carried out under atmospheric pressure, a WHSV of 1.05–5.47 h−1, and the reaction temperature from 350 °C to 450 °C. The kinetic models were established on the basis of different mechanisms for 1-butene isomerization over MgO. The results showed that the LHHW kinetic model provided the best agreement with the experimental data. The reactions involve three steps, including (1) adsorption of 1-butene on the active site, (2) the chemical surface reactions of 1-butene to trans- and cis-2-butene, and (3) the desorption of trans- and cis-2-butene. The surface reactions were assumed to be the rate-determining step. The percentage error of all predicted values was less than 5% under the studied operating conditions.
Introduction
The double bond isomerization of 1-butene is an essential part of a complex reaction network in olefin metathesis technology discovered by Anderson and Merckling at Dupont in 1955.2 The olefin metathesis technology was commercialized by the Phillips Petroleum Company and was called the Phillips Triolefin Process for propylene production.1,2 Currently, the increasing demand of end-user industries such as e-commerce and logistics, construction sector, and packaging industry has led to the growth of the propylene market.3 In recent years, olefin metathesis technology has becomes one of interesting methods for propylene production as it converts low-value olefins such as butene to high-value olefins via double bond rearrangement of hydrocarbon molecules.4 This process interconverts propylene with ethylene and 2-butene.5 Propylene is mainly produced by the cross-metathesis between 1-butene and 2-butene or between ethylene and 2-butene.6 Moreover, a non-ethylene feed can be used to produce propylene with bi-functional catalysts due to the occurrence of both the metathesis reaction and n-butene isomerization.6,7 Therefore, the double bond isomerization between 1-butene and 2-butene plays an important role in the olefin metathesis technology.
At present, the ABB Lummus Company has established olefin conversion technology (OCT) for propylene production using a WO3/SiO2 catalyst, which is inexpensive and resilient to poisoning compared with the conventional Mo- and Re-based catalysts.6,8 However, in order to improve the catalytic activity of metathesis, catalysts for n-butene isomerization such as MgO, CaO, ZnO, and ZrO2 can be added during the OCT process to enhance the reaction rate of isomerization and enable more 2-butene to be consumed in the metathesis reaction.6,9 Moreover, according to Kasempremchit et al. (2016), isomerization and metathesis reactions over MgO and WO3/SiO2 bi-functional catalysts can be used to generate propylene only from 1-butene alternative feed.7 Among the common isomerization catalysts, MgO was selected due to its high catalytic activity and stability for use in the commercial process. In addition, they found that the separated bed of MgO and WO3/SiO2 is more effective than a physically mixed bed.7
In this research, we focus on the reaction kinetics of 1-butene double bond isomerization over MgO catalyst. The reaction kinetics of n-butene isomerization has been widely investigated by many researchers over many solid base catalysts for a long time.10–17 In order to predict the product compositions accurately, knowledge of the reaction rate and rate expression based on intrinsic kinetics is necessary for fundamental understanding of the translation of laboratory data to pilot and commercial scales, respectively.18–20 Intrinsic kinetics is a multi-scale approach performing only chemical reactions at the catalyst surface.21 However, it is well-known that the reaction kinetics is affected by internal and external mass transfer resistances.22 Therefore, the key challenge of the intrinsic kinetic model primarily depends on the reliability of experimental data in the absence of limitations of the mass- and heat-transfer regimes.23
Due to the rate-limiting effects of the mass and heat transfer associated with standard thermogravimetric analysis (TGA) and fixed bed reactors over the years, the Berty stationary basket catalyst reactor was investigated in this research.24 The limiting effects of mass- and heat-transfer can be diminished in this Berty-type reactor; moreover, the intrinsic kinetics may be revealed.21,24,25 According to Al-Saleh et al. (1988) and Raghuveer et al. (2016), these Berty-type reactors can test gas phase heterogeneous catalytic reactions without the resistances of heat transfer and internal and external mass transfer due to recirculation within the reactor.25,26 Furthermore, Al-Saleh et al. (1988) found that the activation energies of partial and complete ethylene oxidation reactions over a silver catalyst were higher than previously reported data by other researchers. They mentioned the reason that the strong or medium internal and external mass limitations can dominate the true activation energies.26 Hannounf and Regalbuto (1992) showed that their micro-Berty catalytic reactor can also offer ideal mixing characteristics in some operating conditions by step change tracer experiments over a Ni/Al2O3 catalyst in CO methanation.27 In addition, because Berty reactors show the same behaviour as CSTR, the mathematical models to describe the mole, energy, and momentum balances can be represented with the equations for CSTR. For these reasons, Berty reactors have been extensively investigated for laboratory-scale reactions.25,28–30
According to the literature to date, there have only been a few studies on 1-butene isomerization over MgO catalyst from the aspect of intrinsic kinetics. Therefore, in this research, intrinsic kinetic modelling using a Berty-type reactor (gradientless recycle reactor) for 1-butene isomerization over a commercial MgO catalyst was investigated. Different mechanisms for the double bond isomerization of 1-butene were also proposed in order to determine the proper intrinsic kinetic model. Moreover, the activation energies, adsorption coefficients, and rate constants were explored with both power law and Langmuir Hinshelwood Hougen Watson (LHHW) models.
Experimental set-up
To determine the kinetic parameters of 1-butene isomerization in a Berty-type reactor, commercial cylindrical MgO catalysts were used with an average diameter of 4.818 mm and height of 4.732 mm. A schematic of the experimental apparatus for the Berty-type reactor is shown in Fig. 1. The instrument symbols are summarized in Table 1. The experimental apparatus can be divided into three parts: a gas feeding system with mass flow controllers, the reactor units, and an analytical system. A catalyst basket (2-inch inner diameter) was filled with 2.5 g of the commercial MgO catalyst with inert balls and installed at the center of the vessel. The temperature of the catalytic bed was kept constant at the desired temperature using an electric furnace jacket on the outside wall of the vessel. Initially, the MgO catalyst was pretreated with N2 (99.9% purity, 200 mL min−1) at 500 °C under atmospheric pressure for 2 hours in order to decrease the humidity of the catalyst. In addition, the motor was set at an impeller speed of 1500 rpm. Then, the reactor was cooled to the desired reaction temperature, and the gaseous feed of pure 1-butene was fed at the bottom of the vessel. The impeller inside the reactor acting to provide perfect mixing was rotated at 1500 rpm below the catalytic bed. After that, the effluent streams were analyzed by an on-line gas chromatograph instrument with a flame ionization detector (FID) to measure the exit gas compositions. For the operating conditions, 1-butene isomerization was carried out under atmospheric pressure and three reaction temperatures of 350 °C, 400 °C and 450 °C for 3 hours. The feed flow rates of 1-butene were investigated in the range of 2.62 to 13.68 g h−1 (WHSV of 1.05 to 5.47 h−1). All inlet flow rates were controlled by mass flow controllers with 0.1% full scale precision.
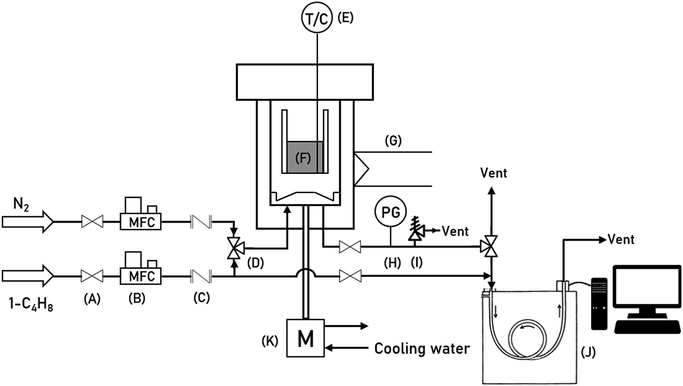 |
| | Fig. 1 A schematic of the experimental apparatus for 1-butene isomerization in the Berty-type reactor. | |
Table 1 Instrument symbols in the schematics of the experimental apparatus (Fig. 1)
| Symbol |
Instrument |
| A |
Ball valve |
| B |
Mass flow controller |
| C |
Check valve |
| D |
3-Way valve |
| E |
Thermocouple |
| F |
Catalytic bed |
| G |
Heater |
| H |
Pressure gauge |
| I |
Relief valve |
| J |
Gas chromatograph |
| K |
Motor |
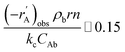
For investigation of the external mass transfer limitation in the Berty-type reactor, the effect of the impeller speed on the catalytic activity of 1-butene isomerization was performed with pure 1-butene feed and 2.5 g of catalyst at a temperature of 450 °C, atmospheric pressure, and a WHSV of 1.05 h−1. The external mass transfer resistance can be minimized by increasing the number of revolutions per minute (rpm).26 Therefore, the different impeller speeds were studied at 0, 250, 500, 1000, 1500, 2000, and 2500 rpm to determine the appropriate rate of stirring. Moreover, the Mears criterion was used to consider the mass transfer from the bulk gas to the external catalyst surface or the external mass transfer limitation, as illustrated in eqn (1). If this value is below 0.15, the external mass diffusion can be neglected.
| |
 | (1) |
The mass transfer coefficient was calculated by the Thoenes–Kramers correlation, as shown in eqn (2) and (3).31 The shape factor (γ) used to calculate the mass transfer coefficient for a cylindrical pellet is the external surface area divided by πdp2, as illustrated in eqn (4), and dp is the volume-average particle diameter.
| | |
Sh′ = (Re′)1/2(Sc)1/3
| (2) |
| |
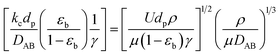 | (3) |
| |
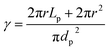 | (4) |
The binary gas phase diffusion coefficient (DAB) can be predicted by Fuller correlation, as expressed in eqn (5).32
| |
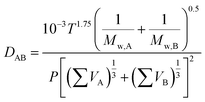 | (5) |
Furthermore, the Weisz–Prater criterion was used to determine the internal mass transfer limitation in the Berty-type reactor.33 This criterion is shown in eqn (6). When the value is much less than 1, it can be considered that there is no internal diffusion limitation or concentration gradient within the catalyst pellet. The characteristic length (L) of the cylindrical pellet can be calculated by the radius of the pellet divided by two (r/2), and the concentration at the catalyst surface (CAs) can be approximated by the bulk concentration. The effective diffusion coefficient (Deff) can be estimated by Deff = εpDAB/τ.
| |
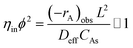 | (6) |
Kinetic modelling
| |
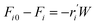 | (7) |
| |
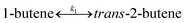 | (8) |
| |
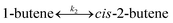 | (9) |
To model a Berty reactor, due to the identical behaviour of a Berty reactor and a continuous stirred tank reactor (CSTR), the mole balance equations of species i for the CSTR model can be used and written as an algebraic equation in eqn (7). Steady state conditions and perfect mixing were assumed. In addition, the energy balance was neglected because the temperature in these reactors was considered to be isothermal. The difference in the temperatures between the top and bottom of catalyst bed in the Berty reactor was measured and was found to be within 2 °C, as shown in the section below. In this research, catalyst deactivation was not considered due to the very low coke content in the spent MgO catalyst. The reaction pathway of 1-butene isomerization over the MgO catalyst performed in this research was assumed based on that reported by Baird and Lunsford (1972), as shown in Fig. 2.9 They found that 1-butene was physically adsorbed on MgO and retained its olefinic character.9 According to Wang et al. (2011), a periodic DFT study of double bond isomerization of butene over the surface of MgO showed that the isomerization process includes two steps: (1) the abstraction of H atom from 1-butene to form chemisorbed 2-butenide with an allyl group, and (2) the addition of H atom to this species to form 2-butene.34 This mechanism also corresponds to the work of Baird and Lunsford (1972). Trans-2-butene and cis-2-butene are produced by different pathways over the surface of MgO catalyst. In order to determine a suitable kinetic model, different mechanisms for 1-butene isomerization over MgO catalyst were proposed, as illustrated in Table 2. For this research, the two steps of the isomerization process described by Wang et al. (2011) were combined into the surface chemical reaction step, as shown by eqn (8) and (9).
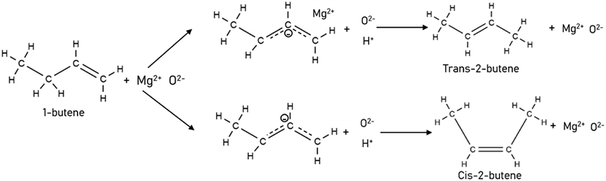 |
| | Fig. 2 Mechanism for 1-butene isomerization over the MgO catalyst.9 | |
Table 2 The different mechanisms for 1-butene isomerization over MgO catalysta
| No. |
Proposed mechanisms |
Rate expressions |
Eqn |
| A, B, and C are 1-butene, trans-2-butene, and cis-2-butene, respectively. For LHHW, the surface reaction step (*) is the rate-determining step. |
| Mechanism I (P-L model) |
 |
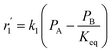 |
(14) |
| Mechanism II (P-L model) |
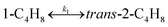 |
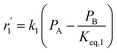 |
(15) |
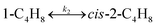 |
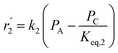 |
(16) |
| Mechanism III (P-L model) |
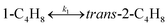 |
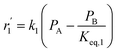 |
(17) |
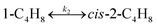 |
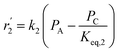 |
(18) |
 |
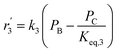 |
(19) |
| Mechanism IV (LHHW) |
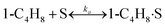 |
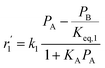 |
(20) |
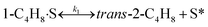 |
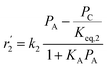 |
(21) |
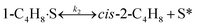 |
| Mechanism V (LHHW) |
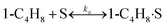 |
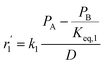 |
(22) |
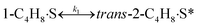 |
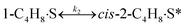 |
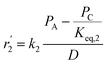 |
(23) |
 |
 |
D = 1 + KAPA + KBPB + KCPC |
|
In mechanism I, the chemical reactions in eqn (8) and (9) were grouped into a single chemical reaction, as shown in eqn (14), while mechanism II involves the same chemical reactions as in eqn (8) and (9). Mechanism III includes a chemical reaction of trans-2-butene to cis-2-butene. The 1st order power law model with reversible reactions was used in the three mechanisms above, as illustrated in eqn (14) to (19). For mechanism IV, the adsorption of 1-butene on the catalyst surface and the surface chemical reactions to form trans- and cis-2-butene were applied without the desorption step. Meanwhile, the desorption of trans- and cis-2-butene was also included in mechanism V. The Langmuir Hinshelwood Hougen Watson (LHHW) model was used as the rate expression for mechanisms IV and V, as illustrated in eqn (20) to (23). Note that no other products (such as isobutene and 1,3-butadiene) were detected from the 1-butene isomerization over MgO catalyst, and no inhibitor was found in the catalytic sites.
The kinetic rate constants and adsorption coefficients can be represented by Arrhenius's equation and the van't Hoff expression, given in eqn (10) and (11), respectively:
| |
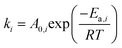 | (10) |
| |
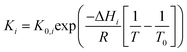 | (11) |
where
Ea,i is the activation energy,
R is a gas constant (8.31451 J mol
−1 K
−1), and
A0,i is the pre-exponential factor according to Arrhenius's equation. Δ
Hi is the adsorption enthalpy.
K0,i and
T0 are the adsorption coefficient and temperature at reference (450 °C), respectively.
The equilibrium constant (Keq,i) was calculated via Aspen Plus software. The REquil reactor module with the non-random to liquid (NRTL) method was simulated to investigate the thermodynamic equilibrium of 1-butene, trans-2-butene, and cis-2-butene at temperatures from 350 °C to 450 °C and atmospheric pressure. According to this model, the conversions of 1-butene at thermodynamics equilibrium and temperatures of 350 °C, 400 °C, and 450 °C are equal to 78%, 76%, and 73%, respectively. The thermodynamics equilibrium constants can be calculated by eqn (12) and (13) for isomerization of 1-butene to trans-2-butene and cis-2-butene, respectively.
| |
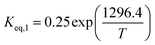 | (12) |
| |
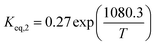 | (13) |
Numerical analysis
For the Berty reactor, the non-linear equations with the rate expressions of 1-butene isomerization mentioned above were computed by a solver function based on the Levenberg–Marquardt algorithm in order to find the outlet flow rate of each species (Fi). During the calculations, the objective function as the square root of the error variance (SREV) was minimized simultaneously in order to determine the kinetic constants at the lowest value of the objective function. The SREV is written in eqn (24) as follows:| |
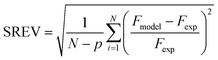 | (24) |
where N is the number of experimental points and p is the number of kinetic parameters of each model. Fmodel and Fexp are the predicted and experimental mole flow rates of each species at the outlet of the reactor, respectively.
Then, the sets of kinetic parameters were determined at each reaction temperature. The activation energies, adsorption coefficients and rate constants were evaluated by Arrhenius plots. Furthermore, the percentage error was calculated to compare the accuracy of the different mechanisms in order to find the most suitable method, as shown below.
| |
 | (25) |
Results and discussion
Characterization
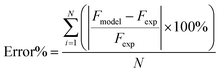
0.11 g of the spent MgO catalysts used to carry out 1-butene isomerization under a pressure of 1 bar and an impeller speed of 1500 rpm at the maximum and minimum reaction temperatures (350 °C and 450 °C) were characterized by the temperature programmed oxidation (TPO) technique to measure the coke contents of the spent catalysts. Fig. 3 shows that the species of coke on the catalyst surface of MgO can be divided into three species, and the coke contents at the temperatures of 350 °C and 450 °C were estimated to be equal to 0.247 and 0.268% wt/wt, respectively. Therefore, it can be summarized that the coke content in the MgO catalyst can be neglected, and a deactivation model for 1-butene isomerization over the MgO catalyst was not used for this research.
 |
| | Fig. 3 TPO profiles generated for the spent MgO catalyst at 350 °C and 450 °C. | |
Mass- and heat-transfer limitations
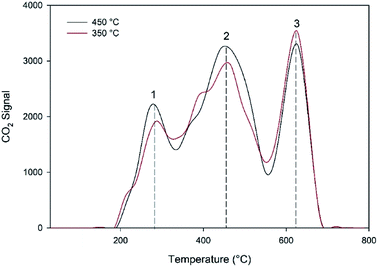
In order to determine the intrinsic kinetics, the effects of mass- and heat-transfer limitations must be extracted from the experimental data to perform only the chemical surface reaction of the catalyst. To achieve this aim, the effects of all transport resistances on the catalytic activity were investigated in this research. Firstly, the effect of the impeller speed inside the Berty-type reactor on the catalytic activity was investigated under a temperature of 450 °C, inlet flow rate of 2.62 g h−1 and pressure of 1 atm. Fig. 4 shows that the 1-butene conversion and the selectivities of both trans-2-butene and cis-2-butene were significantly affected by external mass transfer in the range of impeller speeds of about 0 to 500 rpm. Increasing the impeller speed improves the 1-butene conversion due to good mixing within the vessel and reduction of the external mass transfer limitation. The resistance film could be reduced when the velocity around the catalyst pellets increases due to an increment of the mixing degree. For impeller speeds between 1000 and 2500 rpm, the conversion and the product selectivity are slightly influenced owing to the decreasing external mass transfer resistance. From these results, an impeller speed of 1500 rpm was selected to investigate the kinetic experiments for this research.
 |
| | Fig. 4 Conversion of 1-butene and selectivity of trans-2-butene and cis-2-butene at different impeller speeds (rpm) at a temperature of 450 °C, inlet flow rate of 2.62 g h−1 and 1 atm pressure. | |
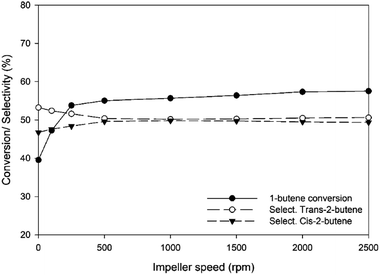
Moreover, the Mears criterion and Weisz–Prater criterion, as shown in eqn (1) and (6), were calculated to determine the external and internal mass diffusions, respectively, at different inlet flow rates and temperatures under atmospheric pressure and an impeller speed of 1500 rpm. Fig. 5 shows that all values calculated by the Weisz–Prater criterion (blue point) are below 1 (blue dash line). Under WHSV of 1.05 to 5.47 h−1, this criterion can be estimated to be in the range of 0.118 to 0.694. Therefore, the intraparticle concentration gradient or internal mass transfer resistance is not significant under the operation in this Berty reactor. Furthermore, reducing the feed flow rate diminishes the effect of the internal mass transfer limitation on the catalytic activity. On the other hand, the red dashed line represents the Mears criterion for external mass transfer limitation, and the values of all the red points are in the range from 1.29 × 10−6 to 1.49 × 10−5, which are below 0.15. Therefore, no external mass transfer resistance or concentration gradient exists between the bulk gas and the external surface of the catalyst pellet. Moreover, these results substantiate the absence of external mass diffusion in the data in Fig. 4.
 |
| | Fig. 5 The Weisz–Prater and Mears criteria for internal and external mass transfer limitations under a pressure of 1 bar and 1500 rpm impeller speed. | |
For the heat transfer limitation, a thermocouple was used to measure the temperature profiles at different heights of the catalytic bed, as shown in Fig. 6. The observed temperature difference between the top and bottom bed was within 2 °C. Therefore, an isothermal condition can be considered, and the effects of heat transfer resistance can be neglected.
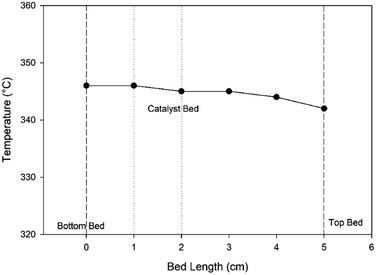 |
| | Fig. 6 The temperature profile of the catalytic bed in the Berty-type reactor at a set point temperature of 400 °C, pressure of 1 bar, and impeller speed of 1500 rpm. | |
In addition, for the catalytic activities, the effects of temperature on the 1-butene conversion and the selectivity are illustrated in Fig. 7. The highest 1-butene conversion can be observed at the maximum temperature (450 °C), corresponding to the Arrhenius equation, in which the reaction rate rises at elevated temperature. The trans-2-butene selectivity is also enhanced at elevated temperature, whereas the selectivity of cis-2-butene decreases. The selectivity characteristics of the product isomers for the base catalyst rely on the relative stability of the two allylic carbanions, which are the intermediate forms.16 According to Fig. 7, the selectivity of cis-2-butene is higher than that of trans-2-butene because the allylic carbanion of the cis form is more stable than that of the trans form on the surface of the solid base catalyst. However, the selectivity of trans-2-butene can increase at elevated temperature.
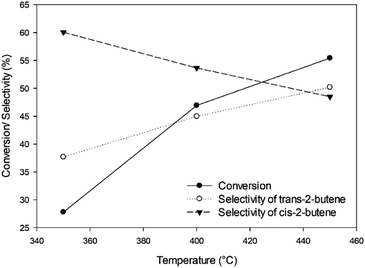 |
| | Fig. 7 The conversion of 1-butene and selectivities of trans-2-butene and cis-2-butene under pressure of 1 bar, inlet flow rate of 2.62 g h−1, and impeller speed of 1500 rpm at different temperatures. | |
Selection of the kinetic model
To find a suitable kinetic model for 1-butene isomerization over the MgO catalyst, the rate constants were estimated via regression with the experimental data at three temperatures (350 °C, 400 °C, and 450 °C). The feed flow rate was varied in a range of 2.62 to 13.68 g h−1 with an impeller speed of 1500 rpm under atmospheric pressure. After reaching the steady state, the outlet mole flow rates were analyzed together with the kinetic models mentioned in the section above. The objective function performed as the square root of the error variance (SREV) in eqn (24) was minimized to find the intrinsic kinetic parameters. The accuracy of the predicted outlet mole flow rates depends on the lowest objective function value calculated.
Fig. 8 shows the percentage error calculated by eqn (25) at different temperatures of each mechanism (I–V). It was found that the mechanism V provided the lowest percentage error, followed by mechanisms III, II, IV and I, sequentially. The percentage errors of mechanism V at three temperatures of 350 °C, 400 °C, and 450 °C were estimated to be equal to 2.38, 5.39, and 3.12%, respectively. Consequently, mechanism V involving 1-butene adsorption on the active site, the surface chemical reactions of 1-butene to trans- and cis-2-butene, and the desorption of trans- and cis-2-butene with the LHHW model provides a suitable intrinsic kinetic model for 1-butene isomerization over MgO catalyst. Furthermore, the rate constants and adsorption coefficients of mechanism V at different temperatures are tabulated in Table 3.
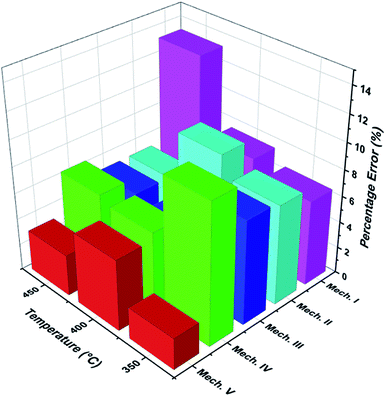 |
| | Fig. 8 The percentage error of each proposed mechanism at different temperatures. | |
Table 3 Estimated reaction rate constants and adsorption coefficients for 1-butene isomerization
| Reaction rate constants and adsorption coefficients |
| T (°C) |
350 |
400 |
450 |
| K1 |
2.242 × 10−6 |
7.810 × 10−6 |
1.816 × 10−5 |
| k2 |
4.149 × 10−6 |
1.107 × 10−5 |
2.132 × 10−5 |
| KA |
0.891 |
0.758 |
0.570 |
| KB |
3.577 |
3.134 |
2.493 |
| KC |
3.931 |
3.429 |
2.729 |
The experimental and predicted molar flow rates of different gases for 1-butene isomerization at different temperatures are shown in Fig. 9. The symbols refer to the experimental exit mole flow rates under steady state conditions, whereas the different lines represent the predicted exit mole flow rates in the steady state. These results reveal that the exit mole flow rates obtained from the intrinsic kinetic model (mechanism V) can predict the experimental exit mole flow rates accurately. In addition, the effects of the feed flow rate on the catalytic activity in the Berty-type reactor were investigated. The conversion of 1-butene can be reduced when the feed flow rate increases owing to the reduction of the contact time between 1-butene and the MgO catalyst. This results in increases in the exit mole flow rates of the different gases. Remarkably, the exit mole flow rates at high temperature (450 °C) in Fig. 9c are significantly affected by the feed flow rate due to the high catalytic activity when the temperature increases.
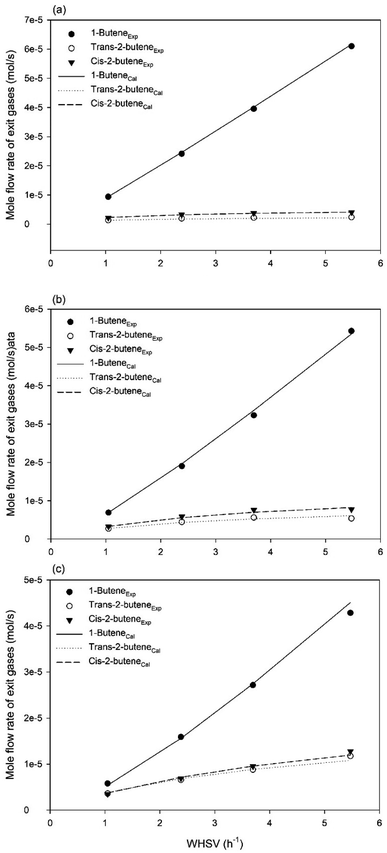 |
| | Fig. 9 Experimental and predicted molar flow rates of different gases for 1-butene isomerization under a pressure of 1 bar and impeller speed of 1500 rpm at different temperatures: (a) T = 350 °C, (b) T = 400 °C, and (c) T = 450 °C, respectively. | |
Table 3 summarizes the values of the rate constants (ki) and adsorption coefficients (Ki) obtained from mechanism V at different temperatures. The ki and Ki values were used to plot the Arrhenius-like expression (ln(k) versus 1000/T), as illustrated in Fig. 10. The straight line of the Arrhenius plot in each rate constant confirms the consistency of the present LHHW model. Moreover, Fig. 10 was used to determine four different parameters: the adsorption enthalpy (ΔHi), the adsorption coefficient at the reference temperature (K0,i), the pre-exponential factor according to Arrhenius's equation (A0,i), and the activation energies (Ea,i). The slopes and intersections of the linear equations of ln(k1) and ln(k2) according to the Arrhenius's equation were used to determine Ea,i and A0,i, as demonstrated in the ESI (eqn S1–S5†). On the other hand, ΔHi in the van't Hoff expression was interpreted from the linear equations of the adsorption coefficients, as shown in eqn S6–S10.† For this research, the reference temperature was 723.15 K; therefore, K0,i was represented by the adsorption coefficients at 723.15 K. In addition, all values of the slopes and intersections in Fig. 10 are provided in Table S1.† In summary, the values of A0,i, Ea,i, ΔHi, and K0,i for mechanism V are summarized in Table 4.
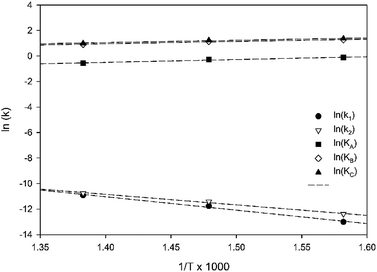 |
| | Fig. 10 Arrhenius plot of 1-butene isomerization (Mechanism V). | |
Table 4 Values of the kinetic and adsorption parameters and the rate expressions for the chosen modelsa
| Mechanism V (LHHW) |
Rate expressions |
| The reference temperature (T0) was defined at 723.15 K. |
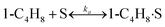 |
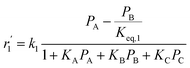 |
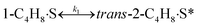 |
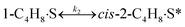 |
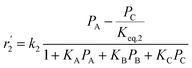 |
 |
 |
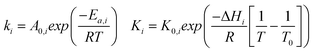 |
| Parameter |
A0,i |
Ea,i (kJ mol−1) |
R2 |
Parameter |
K0,i |
ΔHi (kJ mol−1) |
R2 |
| K1(mol g−1 s−1) |
9.052 |
78.608 |
0.995 |
KA (bar−1) |
0.570 |
−16.610 |
0.960 |
| K2 (mol g−1 s−1) |
0.615 |
61.520 |
0.995 |
KB (bar−1) |
2.493 |
−13.420 |
0.962 |
| KC(bar−1) |
2.729 |
−13.556 |
0.965 |
Furthermore, the exit mole flow rates of different gases between the experimental data and model predictions were compared, as shown in Fig. 11. It can be summarized that the model prediction with mechanism V and the experimental data are in good agreement for 1-butene isomerization over MgO catalyst at 350 °C, 400 °C, and 450 °C.
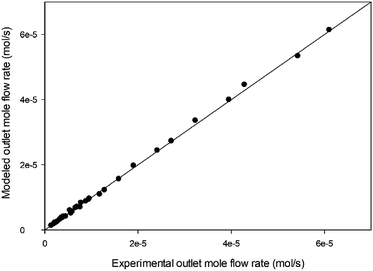 |
| | Fig. 11 Comparison between experimental results and model predictions for 1-butene isomerization at all reaction temperatures (350 °C, 400 °C, and 450 °C). | |
In addition, Fig. 12 summarizes the activation energy values for 1-butene isomerization reported in previous work over many solid catalysts. The orange colour represents the activation energies for the reaction of 1-butene isomerization to all 2-butenes. The green and purple colours represent the conversion of 1-butene to form trans-2-butene and cis-2-butene, respectively. For this research, we focused on the activation energies of 1-butene isomerization over MgO catalyst. Although the same MgO catalyst was studied by Baird and Lunsford (1972), Kasempremchit et al. (2016), and in our research, the activation energies obtained in each study were different.7,9
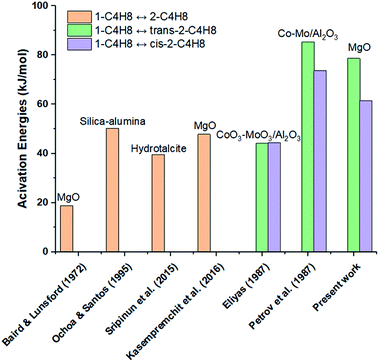 |
| | Fig. 12 Activation energies for 1-butene isomerization reaction in this and previous work.7,9,11,14,16,35 | |
The first hypothesis is that the physical and chemical properties of the MgO catalyst in each study were different. Suttibut et al. (2015) studied the effects of the pre-treatment temperature on MgO catalyst in 1-butene isomerization. They found that the basicity, pore volume, and average pore size changed under different pre-treatment temperature conditions, resulting in different catalytic activities of the MgO catalyst and different activation energies as well.36 Moreover, the differences may be due to differences in the transport phenomena involving pore and bulk diffusion and flow in the reactor. A U-tube reactor, fixed bed reactor, and Berty-type reactor were used in work by Baird and Lunsford (1972), by Kasempremchit et al. (2016), and in our research, respectively.7,9 For a Berty reactor, perfect mixing can be performed inside the reactor because it has the same recirculation behaviour as a CSTR, resulting in low bulk mass transfer limitation.26 On the other hand, the fixed bed reactor can be considered as a plug flow criterion. The heat- and mass-transfer in a fixed bed reactor rely on the reactor size, catalyst volume, and space velocity.21 Moreover, in fact, axial dispersion probably exists in the fixed bed reactor and deviates from the ideal plug flow.37 Due to the abovementioned factors, the reactors could fundamentally measure the kinetics under different process conditions. Remarkably, the activation energies for 1-butene isomerization over MgO catalyst studied in the Berty reactor are higher than those in a U-tube reactor (Baird and Lunsford, 1972) and a fixed bed reactor (Kasempremchit et al., 2016).7,9 This is probably because the data observed in the latter reactors were measured under some limitations of external and internal mass transfer.26 According to Fogler (2006), when the measured activation energy is influenced by internal mass transfer resistance, the true activation energy can be approximately twice the apparent activation energy (ET = 2EApp).31 The true activation energy is higher than the apparent activation energy.26,31 Therefore, this Berty reactor may demonstrate the intrinsic kinetics for 1-butene isomerization over MgO catalyst.
Conclusion
Intrinsic kinetic modelling of 1-butene isomerization over MgO catalyst was investigated via a Berty-type reactor. The results showed that external and internal mass transfer resistance and heat transfer resistance could not be found in this reactor. Therefore, the obtained activation energies, adsorption coefficients, and rate constants are not dominated by these transport limitations. For the effects of the operating conditions, 1-butene conversion can be enhanced by an increase in reaction temperature, corresponding to Arrhenius's equation, whereas 1-butene conversion is decreased by increasing the feed flow rate due to the lower contact time. Moreover, the product selectivity is significantly affected by the reaction temperature but only slightly influenced by the feed flow rate or WHSV.
For kinetic modelling, the TPO technique was used to confirm the absence of coke formation over the MgO catalyst. The coke contents in the spent catalysts were very low; therefore, there is no deactivation model for this research. Different mechanisms of the isomerization process were proposed. The LHHW kinetic model with the mechanism (V) involves three steps: (1) 1-butene adsorption on the active site, (2) the surface chemical reactions of 1-butene to trans- and cis-2-butene (rate-determining step), and (3) the desorption of trans- and cis-2-butene, and it is considered to be an appropriate intrinsic kinetics model for 1-butene isomerization over a commercial MgO catalyst. This proposed mechanism also corresponds to the mechanisms of Baird and Lunsford (1972) and Wang et al. (2011), who studied catalytic sites for the isomerization of 1-butene over MgO.9,34 The error percentages of this mechanism (V) at three temperatures of 350 °C, 400 °C, and 450 °C were calculated to be equal to 2.38%, 5.39%, and 3.12%, respectively. The experimental and predicted exit mole flow rates also demonstrated good agreement with this mechanism (V). Finally, the activation energies for 1-butene isomerization to trans- and cis-2-butene are 78.61 and 61.52 kJ mol−1, respectively.
Nomenclature
| A0,i | Pre-exponential factor according to Arrhenius's equation (mol g−1 s−1) |
| CAb | Concentration at the bulk fluid (mol m−3) |
| CAs | Concentration at the external surface of species A (mol m−3) |
| dp | Volume average particle diameter (m) |
| DAB | Binary gas phase diffusion coefficient (m2 s−1) |
| Deff | Effective diffusion coefficient (m2 s−1) |
| Ea,i | Activation energy (kJ mol−1) |
| Fi0 | Inlet mole flow rate (mol s−1) |
| Fi | Outlet mole flow rate (mol s−1) |
| Fexp | Experimental exit mole flow rate (mol s−1) |
| Fmodel | Predicted exit mole flow rate (mol s−1) |
| ΔHi | Adsorption enthalpy (kJ mol−1) |
| kc | Mass transfer coefficient (m s−1) |
| ki | Kinetic rate constant (mol g−1 s−1) |
| Ki | Adsorption coefficient (bar−1) |
| K0,i | Adsorption coefficient at the reference temperature (bar−1) |
| Keq,i | Thermodynamic equilibrium constant (—) |
| L | Characteristic particle size (m) |
| Lp | Particle length (m) |
| Mw,i | Molecular weight of species i (kg mol−1) |
| n | reaction order (—) |
| N | Number of experimental points (—) |
| p | Number of kinetic parameters (—) |
| P | Total pressure (bar) |
| Pi | Partial pressure (bar) |
| R | Gas constant (J mol−1 K−1) |
| r | Radius of the catalyst pellet (m) |
| rAobs | Observed volumetric reaction rate (mol m−3 s−1) |
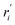 | Reaction rate based on the unit mass of the solid (mol kg−1 s−1) |
| T | Temperature (K) |
| T0 | Reference temperature (K) |
| U | Superficial velocity (m s−1) |
| Vi | Diffusion volume of species i (—) |
| W | Weight of the catalyst (kg) |
Greek symbols
| ηin | Internal effectiveness factor (—) |
| ϕ | Thiele modulus (—) |
| ρ | Density of fluid (kg m−3) |
| ρb | Bulk density (kg m−3) |
| μ | Viscosity of fluid (Pa s) |
| γ | Shape factor (—) |
| εb | Bulk porosity (—) |
| εp | Particle porosity of the catalyst (—) |
| τ | Tortuosity (—) |
Abbreviations
| CSTR | Continuous stirred tank reactor |
| WHSV | Weight hour space velocity |
| SREV | Square root of the error variance |
| rpm | Revolutions per minute |
| LHHW | Langmuir Hinshelwood Hougen Watson |
| P-L | Power law model |
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
The authors would like to acknowledge the financial support from SCG Chemicals Co., Ltd.
References
- J. Mol, J. Mol. Catal. A: Chem., 2004, 213, 39–45 CrossRef CAS.
- S. Lwin and I. E. Wachs, ACS Catal., 2014, 4, 2505–2520 CrossRef CAS.
- J. Watson, Propylene Market To Reach USD 137.02 Billion By 2027, accessed June 3, 2020, https://www.globenewswire.com/news-release/2020/04/15/2016731/0/en/Propylene-Market-To-Reach-USD-137-02-Billion-By-2027-Reports-and-Data.html Search PubMed.
- D. Hua, Z. Zhou, Q. Hua, J. Li, X. Lu, Y. Xie, H. Xiao, M. Li and J. Yang, Catalysts, 2018, 8, 585–596 CrossRef.
- V. Blay, E. Epelde, R. Miravalles and L. A. Perea, Catal. Rev., 2018, 60, 278–335 CrossRef CAS.
- W. Jiang, R. Huang, P. Li, S. Feng, G. Zhou, C. Yu, H. Zhou, C. Xu and Q. Xu, Appl. Catal., A, 2016, 517, 227–235 CrossRef CAS.
- N. Kasempremchit, P. Praserthdam and S. Assabumrungrat, Korean J. Chem. Eng., 2016, 33, 2842–2848 CrossRef CAS.
- T. I. Bhuiyan, P. Arudra, M. M. Hossain, M. N. Akhtar, A. M. Aitani, R. H. Abudawoud and S. S. Al-Khattaf, Can. J. Chem. Eng., 2014, 92, 1271–1282 CrossRef CAS.
- M. J. Baird and J. H. Lunsford, J. Catal., 1972, 26, 440–450 CrossRef CAS.
- V. R. Choudhary and L. K. Doraiswamy, Ind. Eng. Chem. Process Des. Dev., 1975, 14, 227–235 CrossRef CAS.
- A. Eliyas, L. Petrov, C. Vladov and D. Shopov, Appl. Catal., 1987, 33, 295–307 CrossRef.
- T. Grupp, V. Kohl, H. Schlifer and H. Hofmann, Appl. Catal., 1991, 76, 61–77 CrossRef CAS.
- M. W. Simon, S. L. Suib and C.-L. O'Young, J. Catal., 1994, 147, 484–493 CrossRef CAS.
- F. Garcia-Ochoa and A. Santos, AIChE J., 1995, 41, 286–300 CrossRef CAS.
- A. G. Gayubo, F. J. Llorens, E. A. Cepeda, M. Olazar and J. Bilbao, Chem. Eng. Sci., 1997, 52, 2829–2835 CrossRef CAS.
- S. Sripinun, K. Suriye, S. Kunjara Na Ayudhyab, P. Praserthdam and S. Assabumrungrat, Open Science Index, Environmental and Ecological Engineering, 2015, 9, 599–602 Search PubMed.
- M. L. Ferreira and E. H. Rueda, J. Mol. Catal. A: Chem., 2002, 178, 147–160 CrossRef CAS.
- Y. Schuurman, Catal. Today, 2008, 138, 15–20 CrossRef CAS.
- G. Ertl, H. Knozinger and J. Weitkamc, in Handbook of Heterogeneous Catalysis, 1997, ch. 6, pp. 1190–1260 Search PubMed.
- S. Mondal, H. Malviya and P. Biswas, React. Chem. Eng., 2019, 4, 595–609 RSC.
- R. J. Berger, E. H. Stitt, G. B. Marin, F. Kapteijn and J. A. Moulijn, Cattech, 2001, 5, 36–60 CrossRef.
- X. Gao, Q. Ding, Y. Wu, Y. Jiao, J. Zhang, X. Li and H. Li, React. Chem. Eng., 2020, 5, 485–494 RSC.
- S. Vernuccio, R. Goy, P. Rudolf von Rohr, J. Medlock and W. Bonrath, React. Chem. Eng., 2016, 1, 445–453 RSC.
- R. Pretorius, J. le Roux, K. Wagener, D. van Vuuren and P. Crouse, React. Chem. Eng., 2019, 4, 1400–1409 RSC.
- C. S. Raghuveer, J. W. Thybaut and G. B. Marin, Fuel, 2016, 171, 253–262 CrossRef CAS.
- M. A. Al-Saleh, M. S. Al-Ahmadi and M. A. Shalabi, Chem. Eng. J., 1988, 37, 35–41 CrossRef CAS.
- H. Hannounf and J. R. Regalbuto, Ind. Eng. Chem. Res., 1992, 31, 1288–1292 CrossRef.
- G. Zwahlen Andreas and B. Agnew John, Ind. Eng. Chem. Res., 1992, 31, 2088–2093 CrossRef.
- A. N. R. Bos, E. S. Bootsma, F. Foeth, H. W. J. Sleyster and K. R. Westerterp, Chem. Eng. Process., 1993, 32, 53–63 CrossRef CAS.
- F. G. Botes, Appl. Catal., A, 2005, 284, 21–29 CrossRef CAS.
- H. S. Fogler, in Elements of Chemical Reaction Engineering, Pearson Education, Inc., 2006 Search PubMed.
- E. N. Fuller, P. D. Schettler and J. C. Giddings, Ind. Eng. Chem, 1966, 58, 18–27 CrossRef CAS.
- P. B. Weisz and C. D. Prater, in Advances in Catalysis, ed. W. G. Frankenburg, V. I. Komarewsky and E. K. Rideal, Academic Press, 1954, vol. 6, pp. 143–196 Search PubMed.
- C.-M. Wang, Y.-D. Wang, J. Dong, S. Liu and Z.-K. Xie, Comput. Theor. Chem., 2011, 974, 52–56 CrossRef CAS.
- L. Petrov, A. Eliyas, C. Vladov and D. Shopov, Appl. Catal., 1987, 29, 219–234 CrossRef CAS.
- P. Suttibut, K. Suriye, S. Kunjara Na Ayudhya, P. Praserthdam and J. Panpranot, Asia-Pac. J. Chem. Eng., 2015, 10, 248–258 CrossRef CAS.
- L. R. de Souza Jr and L. Lorenz, the Proceedings of the 2014 COMSOL Conference in Curitiba, Brazil, 2014 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ra05453d |
|
| This journal is © The Royal Society of Chemistry 2020 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article a and
Suttichai Assabumrungrat
a and
Suttichai Assabumrungrat *ac
*ac