Open Access Article
Open Access ArticleUnderstanding the crystal structure-dependent electrochemical capacitance of spinel and rock-salt Ni–Co oxides via density function theory calculations†
Xuan Sun,
Jinfeng Sun,
Lingzhi Guo,
Linrui Hou * and
Changzhou Yuan*
* and
Changzhou Yuan*
School of Materials Science & Engineering, University of Jinan, Jinan, 250022, P. R. China. E-mail: mse_houlr@ujn.edu.cn; mse_yuancz@ujn.edu.cn; ayuancz@163.com
First published on 28th September 2020
Abstract
The spinel NiCo2O4 and rock-salt NiCoO2 have been well established as attractive electrodes for supercapacitors. However, what is the intrinsic role of the congenital aspect, i.e., crystal structure and the surface and/or near-surface controlled electrochemical redox behaviors, if the acquired features (i.e., morphology, specific surface area, pore structure, and so on) are wholly ignored? Herein, we purposefully elucidated the underlying influences of unique crystal structures of NiCo2O4 and NiCoO2 on their pseudocapacitance from mechanism analysis through the density function theory based first-principles calculations, along with the experimental validation. Systematic theoretical calculation and analysis revealed that more charge carriers near the Fermi-level, stronger affinity with OH− in the electrolyte, easier deprotonation process, and the site-enriched characteristic for low-index surfaces of NiCoO2 enable its faster redox reaction kinetics and greater charge transfer, when compared to the spinel NiCo2O4. The in-depth understanding of crystal structure–property relationship here will guide rational optimization and selection of appropriate electrodes for advanced supercapacitors.
1 Introduction
To date, supercapacitors have shown great potential for electrochemical energy storage due to their higher power density and longer lifespan than rechargeable batteries.1 From the intrinsic energy storage mechanism point of view, supercapacitors are typically categorized into electric double-layer capacitors (EDLCs) depending upon fast ad/desorption of ions on the electrode surface, and pseudocapacitors originating from rapid faradaic redox reactions on/near the surface of the electrodes.2,3 However, the low specific capacitances (SCs) of EDLCs, to a great extent, limit their utilization in high energy applications. As a result, enormous amounts of research have been greatly stimulated to develop high-performance electrode materials with pseudocapacitive characteristics.4,5Binary transition metal oxides (BTMOs) have been intensively investigated as active materials for supercapacitors due to their easy availability, environmental friendliness, and multiple oxidation states for efficient charge storage.6,7 Especially, spinel NiCo2O4 and rock-salt NiCoO2, stand out from others, owing to their more than two orders of magnitude higher electrical conductivity than their parent cobalt oxides.8,9 In general, inherent electronic conductivity and ionic adsorption capability of abundant active sites are key points influencing electrochemical performance of pseudocapacitive electrodes, except for the acquired aspects including specific surface area (SSA) and pore structure.10,11 Although extensive investigations into structural and/or compositional designs towards enhancing electrochemical properties of NiCo2O4 and/or NiCoO2 electrodes have already been made,6,12–17 no any reports can be retrieved to figure out which one possesses even better electrochemical activities. In fact, it is yet difficult to draw a definitive conclusion according to the previous contributions about the two for supercapacitors, since all the reported electrochemical properties are based on their different acquired characteristics (i.e., morphology/SSA/pore structure).6,9,12–17 In this regard, a thought-provoking question comes to the fore: what is the role of the congenital aspect, i.e., crystal structures of spinel NiCo2O4 and rock-salt NiCoO2, in their surface and/or near-surface controlled electrochemical redox behaviors if the aforementioned acquired features are wholly ignored? There is no doubt that the in-depth understanding of crystal structure–property relationship will render instructive insights into future optimal choice of appropriate electrodes for advanced supercapacitors.
With comprehensive considerations above in mind, herein, we elucidated the underlying influences of unique crystal structures of NiCo2O4 and NiCoO2 on their pseudocapacitances from mechanism analysis through the density function theory (DFT) based first-principles calculations, along with the experimental validation. Systematic theoretical calculation and analysis revealed that more charge carriers near the Fermi-level, stronger affinity with hydroxyls in the electrolyte, easier deprotonation process, and the site-enriched characteristic for low-index surfaces of NiCoO2 enable its faster redox reaction kinetics and more charge transfer, when compared to the spinel NiCo2O4. As expected, the NiCoO2 exhibited enhanced electrochemical behaviors especially at high rates.
2 Computational methods
Spin-polarized density functional theory calculations were carried out based on the Cambridge Sequential Total Energy Package known as CASTEP,18 using the projector augmented wave (PAW) potentials.19 we used the Perdew–Burke–Ernzerhof with Hubbard U (PBE + U) form within the generalized gradient approximation (GGA) for exchange–correlation energy.19,20 Notably, different values between U = 0 and 8 have been used in the Ni/Co compounds in the literature. Herein, we have chosen U values of 5.5 for Ni ions, and 4.5/3.3 eV for Co ions at tetrahedral/octahedral sites, respectively, to obtain the correct electronic and magnetic state of bulk NiCoO2 and NiCo2O4. The number of plane wave was collected by a 500 eV. The Brillouin zones were represented by a Monkhorst–Pack mesh of 7 × 7 × 7 k-points for crystals and 3 × 3 × 1 k-points for studied surface slabs.21 The stoichiometric surfaces were modeled by a (1 × 1) unit cell for NiCo2O4 and (2 × 2) for NiCoO2, which were separated in the z-direction by a 15 Å vacuum. The convergence criterion of Hellmann–Feynman forces and total energy were 0.015 eV Å−1 and 10−5 eV, respectively. For accurate results, we compared band structures between NiCo2O4 and NiCoO2 using HSE06 hybrid functional.22 To model the magnetic state of NiCo2O4 and NiCoO2, we used antiparallel spins for Co and Ni atoms in NiCoO2 due to its high Néel temperature according to Du et al.23 In addition, the Co atoms at tetrahedral sites have antiparallel state with Ni atoms for NiCo2O4, where the Co ions at octahedral sites have no spin polarization due to the fully occupied t2g states.24The surface energy (γ), was computed as γ = (Eslab − nEbulk)/2A, where Eslab, Ebulk, n and A were the energy of the slab supercell, the bulk energy per unit cell, the number of bulk cells contained in the surface slab, and the surface area of each side for the slab, respectively. For the surface with different hydroxyl coverage, the average adsorption energy could be defined as Eads = [E(nOH/slab) − E(slab) − nE(OH)]/n.25,26 The deprotonation energy was calculated by Ede = [E(O/slab) − E(nOH/slab) + 0.5nE(H2)]/n, where E(nOH/slab), E(O/slab), E(slab), E(OH)/E(H2) and n were the energies of the adsorbed systems, the energy of the deprotonation system, the energy of the clean surface, the energies for an isolated hydroxyl/H2 molecules, and the number of adsorbed hydroxyls or desorbed protons, respectively. To have a profound understanding about charge transfer, the Bader charge method, where an amount of each charge was considered in the region separated by the minimum of electronic charge density between each atom, was used.27,28
3 Results and discussion
3.1 Crystal structures
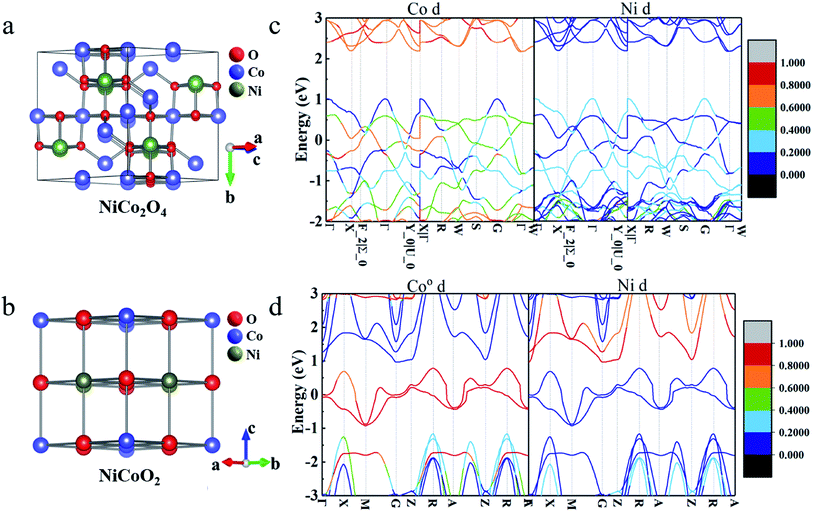
As schematically shown in Fig. 1a and b, the crystal structures of NiCo2O4 and NiCoO2, typically contain 56 and 8 atoms in the unit cells, respectively. According to the site performance theory, the crystal structure of NiCo2O4 and NiCoO2 can be constructed by substituting cobalt atoms located at octahedral sites in spinel Co3O4 and rock-salt CoO unit cells with elemental nickel, respectively.7,24,29 Evidently, the spinel NiCo2O4 contains two kinds of Co atoms located at octahedrally coordinated sites (Coo) and tetrahedrally coordinated sites (Cot), respectively, coupled with alternating layers of –Coo–O– and –Ni–O– along the z direction,24 as described in Fig. 1a. The rock-salt NiCoO2, as shown in Fig. 1b, only possesses the octahedral sites both for Co and Ni atoms. The optimized lattice constant values of NiCo2O4 and NiCoO2 (Table S1, ESI†) are 8.22 and 4.26 Å, just with ∼1.4% and ∼0.5% error, respectively, when compared to their standard files. In addition, the computed magnetic moments of Cot and Ni are 2.77 and −1.43 μB in spinel NiCo2O4, respectively, and 2.74 and −1.80 μB for Co and Ni in rock-salt NiCoO2, which are in good agreement with the reported calculational and/or experimental values.24,303.2 Electronic properties
According to the pseudocapacitive system, the electrolyte ions diffuse from the electrolyte to the electrode/electrolyte interface under the effect of external circuit in the charging process, and then, the redox reaction occurs. Thus, the states near the Fermi-level, especially the contribution of d-orbital of metal ions, are considered to be related with the charge storage ability.31,32 As discerned from the total band structures of NiCo2O4 (Fig. 1c) and NiCoO2 (Fig. 1d), the occupied and unoccupied electronic states are visualized near the Fermi-level, favoring for their rapid electronic transport. To gain more insights into specific electronic structure around the Fermi-level, the projected band structures of d-orbital from the active Ni/Co atoms were calculated. Clearly, the bands near the Fermi-level are mainly contributed by the d-orbital of Co atoms, in which the Ni atoms contribute little. In addition, for spinel NiCo2O4, two kinds of atoms, i.e., Coo and Cot both contribute the bands near the Fermi-level (Fig. S1, ESI†), where the contribution of Cot can be wholly negligible. One thing worth noting is that the contributions of d-orbital near the Fermi-level are greatly conducive to the enhanced electron mobility for rapid redox process of pseudocapacitive electrodes.33,34 On account of more contributions from d-orbital of metal atoms to the bands near the Fermi-level of rock-salt NiCoO2, it can be rationally anticipated that the NiCoO2 will exhibit higher electroactivities than spinel NiCo2O4.353.3 Charge-storage mechanism analysis
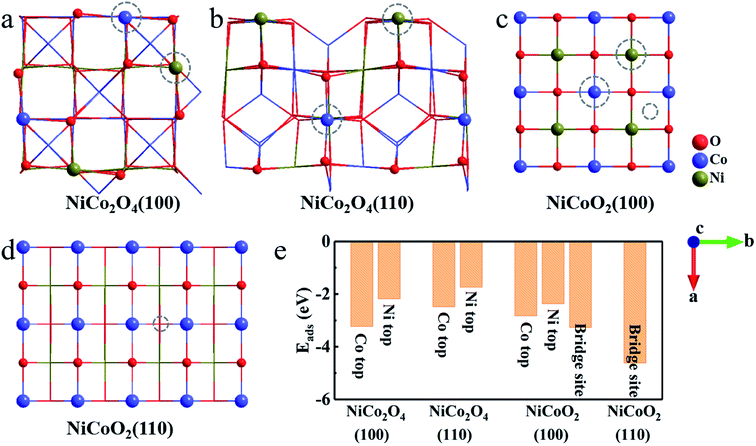
As for the surface modeling, we here consider three low-index, (100), (110) and (111), planes of NiCo2O4 and NiCoO2 with the largest interplanar spacing, as they are predicted to be the most stable in the cubic crystals.36,37 Among the three surfaces, the (111) plane, both for spinel and rock salt structure, is not truly stable surfaces, which can be expected to undergo surface reconstruction.36,38 Therefore, we finally study the (100) and (110) surfaces. The surface energy values of (100)/(110) for NiCo2O4 and NiCoO2 are 1.03/1.25 and 0.95/1.99 J m−2, respectively. Notably, the (110) surface, both for NiCo2O4 and NiCoO2, has two different stable non-polar surface configurations (Fig. 2). Accordingly, we choose the Oh(top) (Fig. 2a) of the NiCo2O4(110) for further calculation, since its total energy is 0.23 eV, lower than those of Th/Oh(top) (Fig. 2b) according to the DFT calculation. And the Co(top) (Fig. 2c), whose total energy is 0.66 eV, lower than that of Ni(top) (Fig. 2d), is chosen for the NiCoO2(110). Corresponding surface lattice constants are summarized as well (Table S1, ESI†).According to the established charge-storage mechanism of NiCo2O4 and NiCoO2 in alkaline KOH solution, the pseudocapacitance always takes place as following two steps.10,14,39,40 First, the redox reaction occurring on the exposed surface generally starts from the OH− adsorption, thus leading to the formation of *OH species. And then, the reaction of adsorbed *OH with the OH− in the solution partially forms the adsorbed *O species, and releases a H2O molecule meanwhile, which is generally ascribed as a deprotonation process. Since the pseudocapacitance originates from the fast redox reactions through the chemisorption of electrolyte ions, the binding energy can act as one of the descriptors for evaluating electrochemical performance. After simple analysis, there are two kinds of stable adsorbed sites, that is, the top sites of Co and Ni atoms both in (100) and (110) surfaces of NiCo2O4 (Fig. 3a and b). For the case of NiCoO2(100), the OH− can be adsorbed stably both on the top sites of Ni/Co and bridge site between them (Fig. 3c). In contrast, the OH− adsorbs only on the bridge site of two Co atoms in NiCoO2(110) (Fig. 3d). As collected in Fig. 3e, the binding energy between hydroxyls and active surfaces of NiCo2O4/NiCoO2 is an exothermic and spontaneous process, due to their negative adsorption energy. The Co sites in NiCo2O4 display stronger absorption capacity for OH− on both two surfaces, as indicated by even more negative Eads for (100) (−3.23 eV) and (110) (−2.48 eV) than those of Ni sites (−2.18 and −1.74 eV) (Fig. S2a–d, ESI†). As regards the NiCoO2(100), the bridge site between Co and Ni (Fig. S2e, ESI†) is a more preferred site, which shows the Eads of −3.26 eV for OH−, lower than those at the top of single Co (−2.83 eV) and Ni (−2.37 eV) ions (Fig. S2f and g, ESI†). The NiCoO2(110) shows the most negative Eads of −4.62 eV when adsorbed on the bridge site between two Co atoms (Fig. S2h, ESI†). Clearly, compared with those of NiCo2O4, the (100) and (110) surfaces of NiCoO2 both exhibit more negative Eads in the case of low coverage (Fig. 3e), which indeed favors for high faradaic reaction kinetics, thanks to the fast and stable OH− adsorption on the two surfaces.
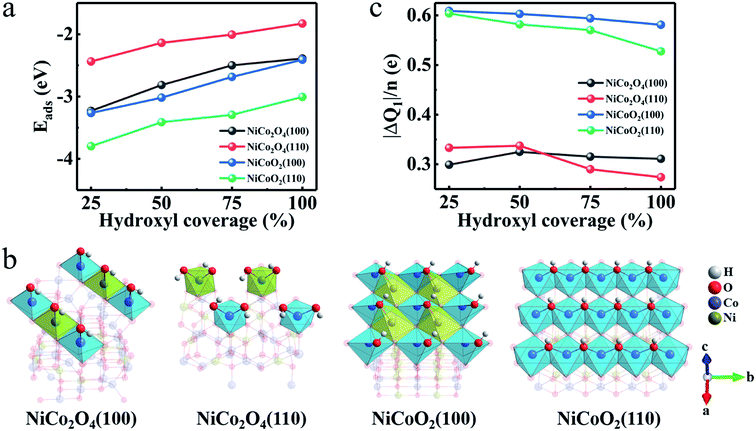
Then, we investigate how OH− pattern varies when its coverage is changed. Fig. 4a presents the Eads as function of hydroxyl coverage for the most stable adsorption sites of the NiCo2O4 and NiCoO2. It's clear that the Eads decreases as the hydroxyl coverage increases for both the (100) and (110) surfaces due to the gradual saturation of the surface. The Eads values of the (100)/(110) surfaces for NiCoO2 are larger than those of NiCo2O4 at all values of hydroxyls coverage. Corresponding relaxation configurations (Fig. S3a–d, ESI†) are summarized as well. According to the coordination configurations of the surface atoms, the Ni/Co atoms display octahedral coordination geometry when the OH− coverage is full (Fig. 4b). Evidently, two hydroxyls are adsorbed on each Ni and Co sites in NiCo2O4(110) due to two oxygen atoms loss in the coordination of octahedral Ni and Co.
Besides the binding ability between electrode surfaces and electrolyte ions, a superior electrode material fundamentally requires rich active sites and high electron-donating capability,35 which are always related to the charge transfer originating from the hydroxyl adsorption. From the lattice constants aforementioned (Table S1, ESI†), the exposed surfaces of NiCoO2 own higher concentration of active atoms (CAAs) of Ni and Co, which will bond directly to the hydroxyls in the reaction process. The CAAs are calculated as ∼11.02 and ∼7.57 atoms per nm for (100) and (110) surfaces of NiCoO2, respectively, approximately twice of those for (100) (5.92 atoms per nm) and (110) (4.19 atoms per nm) of NiCo2O4 (Fig. S4a, ESI†). Therefore, the preponderant reaction surface of NiCoO2 promotes a greater proportion of Ni and Co atoms involved in electrochemical reactions, which would provide high electron-donating capability. By performing the calculations on charge density difference (Fig. S4b–e, ESI†), we can deduce that most electrons tend to transfer from electrodes to hydroxyls when the Ni/Co TMOs are charged, indicating that the adsorption process is an oxidation process of surface metal atoms. We further explore the charge transfer (ΔQ1) versus the hydroxyl coverage according to the Bader charge analysis (Fig. 4c). The average charge values (ΔQ1/n), that is the adsorbed OH−, obtained on the NiCoO2(100) and (110) surfaces are larger than those in the NiCo2O4(100) and NiCo2O4(110) at any hydroxyl coverage. It confirms a tendency that a better electron donation of surface Ni/Co atoms ensures their higher oxidation states. All analysis above therefore can deduce the exceptionally high pseudocapacitance of the rock-salt NiCoO2 in alkaline KOH electrolyte.
The deprotonation process can be described as MOOH + OH− ↔ MO2 + H2O (M is Co or Ni). However, the general observation is that the deprotonation process cannot occur at octahedral coordinate Ni ions, at the limited work potential window for supercapacitors, due to the higher transition potential than that of Co ions.40,41 As shown in Fig. 5, the deprotonation, is a relatively unfavorable process compared to adsorption process due to the high deprotonation energy values (Ede), which means that the reaction involved in the second step needs even higher driving force. The DFT calculation also authenticates that the Ede values on (100) (1.72 eV) and (110) (1.70 eV) surfaces of NiCoO2 are lower than those of NiCo2O4, i.e., 2.65/2.22 eV for the (100)/(110) surfaces (Fig. 5b). Hence, the formed *OH has much more opportunities to desorb protons from the surfaces of NiCoO2 than the NiCo2O4 to form *O. While, there are more electrons transfer from electrodes to adsorbed molecules due to the deprotonation process, which demonstrates that the surface/subsurface metal atoms are further oxidized. But for NiCoO2(100), the number of charge transfer decreases after hydrogen desorption, which is related to the fact that the adsorption sites deviate from the bridge sites to the top of cobalt, decreasing the charge donation of nickel atoms (Fig. 5c).
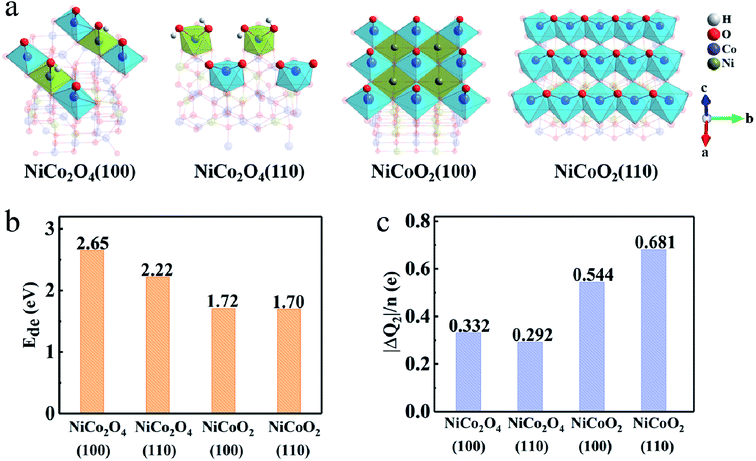 | ||
| Fig. 5 (a) Surface configuration, (b) average deprotonation energy (Ede) and (c) charge transfer (ΔQ2) after the complete deprotonation. | ||
The first-principles calculation results, as discussed above, corroborate more attractive innate merits of NiCoO2 serving as the electrode material for supercapacitors as follows. First, the large electronic state contribution from Co atoms of NiCoO2 near the Fermi-level provides more charge carriers for faradaic redox reactions, thus enhancing the redox activities. Second, the much easier OH− adsorption and deprotonation processes will accelerate the surface reaction dynamics. The two aspects synergistically facilitate the rate behaviors of the NiCoO2 electrode. Third, the surfaces of NiCoO2 show high concentration of redox active sites and higher electron donation capability than NiCo2O4, realizing a large degree of oxidation after reaction, which is helpful to obtain large SCs. It is thanks to these appealing congenital advantages that the rock-salt NiCoO2 can be reasonably anticipated with even better electrochemical performance than the spinel NiCo2O4.
3.4 Electrochemical properties
To experimentally support the above viewpoint, we purposefully chose our synthesized two Ni–Co binary oxides, i.e., flower-shaped NiCoO2 (ref. 14) and NiCo2O4 (Fig. S5 and S6, ESI†), and comparatively study their capacitive performance. The distinct redox peaks in cyclic voltammetry (CV) curves of both NiCo2O4 (Fig. 6a) and NiCoO2 (ref. 14) verify their typical pseudocapacitance mainly, which typically results from fast and reversible redox processes of Co2+/Co3+/Co4+ and Ni2+/Ni3+ in 2 M KOH aqueous solution.9,14,15,42,43 As derived from the chronopotentiometry (CP) plots (Fig. 6b), the spinel NiCo2O4 electrode with a mass loading 5 mg cm−2 exhibits reversible SCs of ∼262, ∼260, ∼258, ∼256, ∼222 and ∼133 F g−1 at the current densities of 2, 3, 4, 5, 10 and 20 A g−1, respectively. By sharp contrast, the rock-salt NiCoO2 obtains ultrahigh SCs of ∼836 and ∼415 F g−1 at 2 and 20 A g−1, respectively,14 which are both higher than three times those of the NiCo2O4 electrode, as plotted in Fig. 6c.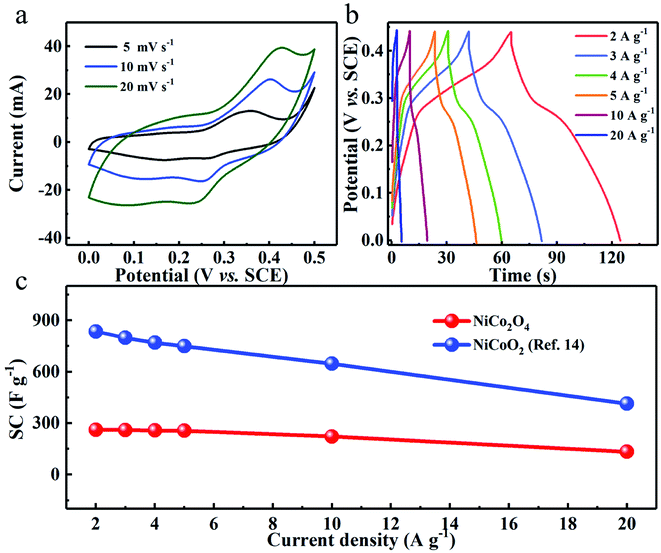 | ||
| Fig. 6 (a) CV and (b) CP curves of the NiCo2O4 electrode. (c) Comparison of SCs between NiCo2O4 and NiCoO2 electrodes at various current densities. | ||
4 Conclusions
In summary, we have comprehensively conducted the first-principle DFT calculations to shed light on the distinguished advantages of rock-salt NiCoO2 from its crystal structure. The faster hydroxyls adsorption/deprotonation kinetics and higher electron donation capability enable the rock-salt NiCoO2 as a more competitive electrode for supercapacitors when compared to its spinel counterpart of NiCo2O4. Furthermore, electrochemical evaluation experimentally authenticated the theoretical simulation and calculation. The contribution here will guide rational optimization and selection of pseudocapacitive electrodes for advanced supercapacitors.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We appreciate the financial support from National Natural Science Foundation of China (Grant No. 51772127 and 51772131), Major Program of Shandong Province Natural Science Foundation (Grant No. ZR2018ZB0317), Taishan Scholars (Grant No. ts201712050), and Collaborative Innovation Center of Technology and Equipment for Biological Diagnosis and Therapy in Universities of Shandong.References
- J. Sun, C. Wu, X. Sun, H. Hu, C. Zhi, L. Hou and C. Yuan, J. Mater. Chem. A, 2017, 5, 9443–9464 RSC.
- J. Chen, Y. Han, X. Kong, X. Deng, H. J. Park, Y. Guo, S. Jin, Z. Qi, Z. Lee, Z. Qiao, R. S. Ruoff and H. Ji, Angew. Chem., Int. Ed., 2016, 55, 13822–13827 CrossRef CAS.
- L. Liu, H. P. Zhao and Y. Lei, InfoMat, 2019, 1, 74–84 CrossRef CAS.
- H. S. Kim, J. B. Cook, H. Lin, J. S. Ko, S. H. Tolbert, V. Ozolins and B. Dunn, Nat. Mater., 2017, 16, 454–460 CrossRef CAS.
- R. Wang, M. Yao and Z. Niu, InfoMat, 2020, 2, 113–125 CrossRef CAS.
- X. Li, L. Jiang, C. Zhou, J. Liu and H. Zeng, NPG Asia Mater., 2015, 7, e165 CrossRef CAS.
- S. Liu, D. Ni, H.-F. Li, K. N. Hui, C.-Y. Ouyang and S. C. Jun, J. Mater. Chem. A, 2018, 6, 10674–10685 RSC.
- C. Yuan, H. B. Wu, Y. Xie and X. Lou, Angew. Chem., Int. Ed., 2014, 53, 1488–1504 CrossRef CAS.
- B. B. Liu, J. G. Liu, T. T. Zhang, C. X. Xu and H. Liu, J. Mater. Chem. A, 2019, 7, 16222–16230 RSC.
- J. Li, Z. Liu, Q. Zhang, Y. Cheng, B. Zhao, S. Dai, H.-H. Wu, K. Zhang, D. Ding, Y. Wu, M. Liu and M.-S. Wang, Nano Energy, 2019, 57, 22–33 CrossRef CAS.
- X. Li, L. Jiang, C. Zhou, J. Liu and H. Zeng, NPG Asia Mater., 2015, 7, e165 CrossRef CAS.
- D. P. Dubal, P. Gomez-Romero, B. R. Sankapal and R. Holze, Nano Energy, 2015, 11, 377–399 CrossRef CAS.
- X. Xu, H. Zhou, S. Ding, J. Li, B. Li and D. Yu, J. Power Sources, 2014, 267, 641–647 CrossRef CAS.
- Z. Wang, Z. Zhao, Y. Zhang, G. Pang, X. Sun, J. Zhang, L. Hou and C. Yuan, J. Alloys Compd., 2019, 779, 81–90 CrossRef CAS.
- Y. Zhu, H. Huang, G. Li, X. Liang, W. Zhou, J. Guo, W. Wei and S. Tang, Electrochim. Acta, 2017, 248, 562–569 CrossRef CAS.
- J. Xiao and S. Yang, J. Mater. Chem., 2012, 22, 12253–12262 RSC.
- H. W. Wang, Z. A. Hu, Y. Q. Chang, Y. L. Chen, H. Y. Wu, Z. Y. Zhang and Y. Y. Yang, J. Mater. Chem., 2011, 21, 10504–10511 RSC.
- M. C. Payne, T. A. Arias and J. D. Joannopoulos, Rev. Mod. Phys., 1992, 64, 1045–1097 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS.
- S. L. Dudarev, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505–1509 CrossRef CAS.
- H. J. Monkhorst, Phys. Rev. B: Solid State, 1977, 16, 1748–1749 CrossRef.
- J. Heyd, G. E. Scuseria and M. J. Ernzerhof, Chem. Phys., 2003, 118, 8207–8215 CAS.
- Y.-Z. Jin, Z. Li, J.-Q. Wang, R. Li, Z.-Q. Li, H. Liu, J. Mao, C.-K. Dong, J. Yang, S.-Z. Qiao and X.-W. Du, Adv. Energy Mater., 2018, 8, 1703469 CrossRef.
- X. Shi, S. L. Bernasek and A. Selloni, J. Phys. Chem. C, 2016, 120, 14892–14898 CrossRef CAS.
- X. Yu, Y. Li, Y.-W. Li, J. Wang and H. Jiao, J. Phys. Chem. C, 2013, 117, 7648–7655 CrossRef CAS.
- K. Shojaee, A. Montoya and B. S. Haynes, Comput. Mater. Sci., 2013, 72, 15–25 CrossRef CAS.
- E. Sanville, S. D. Kenny, R. Smith and G. Henkelman, J. Comput. Chem., 2007, 28, 899–908 CrossRef CAS.
- W. Tang, E. Sanville and G. Henkelman, J. Phys.: Condens. Matter, 2009, 21, 084204 CrossRef CAS.
- J. Wu, P. Guo, R. Mi, X. Liu, H. Zhang, J. Mei, H. Liu, W. M. Lau and L.-M. Liu, J. Mater. Chem. A, 2015, 3, 15331–15338 RSC.
- K. Fominykh, G. C. Tok, P. Zeller, H. Hajiyani, T. Miller, M. Dblinger, R. Pentcheva, T. Bein and D. Fattakhova-Rohlfing, Adv. Funct. Mater., 2017, 27, 1605121 CrossRef.
- Y. F. Zhang, F. Vines, Y. J. Xu, Y. Li, J. Q. Li and F. Illas, J. Phys. Chem. B, 2006, 110, 15454–15458 CrossRef CAS.
- L. Zhang, J. Fischer, Y. Jia, X. Yan, W. Xu, X. Wang, J. Chen, D. Yang, H. Liu, L. Zhuang, M. Hankel, D. J. Searles, K. Huang, S. Feng, C. L. Brown and X. Yao, J. Am. Chem. Soc., 2018, 140, 10757–10763 CrossRef CAS.
- C. Xiang, Y. Liu, Y. Yin, P. Huang, Y. Zou, M. Fehse, Z. She, F. Xu, D. Banerjee, D. Hermida Merino, A. Longo, H.-B. Kraatz, D. F. Brougham, B. Wu and L. Sun, ACS Appl. Energy Mater., 2019, 2, 3389–3399 CrossRef CAS.
- Y. F. Zhang, F. Vines, Y. J. Xu, Y. Li, J. Q. Li and F. Illas, J. Phys. Chem. B, 2006, 110, 15454–15458 CrossRef CAS.
- Z. Zhang, L. Wang, W. Wang, J. Liu, Z. Hong, K. Cho and W. Wang, J. Mater. Chem. A, 2019, 7, 16231–16238 RSC.
- F. Zasada, J. Gryboś, P. Indyka, W. Piskorz, J. Kaczmarczyk and Z. Sojka, J. Phys. Chem. C, 2014, 118, 19085–19097 CrossRef CAS.
- S. C. Parker, P. M. Oliver, N. H. De Leeuw, J. O. Titiloye and G. W. Watson, Phase Transitions, 1997, 61, 83–107 CrossRef CAS.
- W. Zhao, M. Bajdich, S. Carey, A. Vojvodic, J. K. Nørskov and C. T. Campbell, ACS Catal., 2016, 6, 7377–7384 CrossRef CAS.
- Q. Zhang, Z. Liu, B. Zhao, Y. Cheng, L. Zhang, H.-H. Wu, M.-S. Wang, S. Dai, K. Zhang, D. Ding, Y. Wu and M. Liu, Energy Storage Materials, 2019, 16, 632–645 CrossRef.
- Z. Wu, Y. Zhu and X. Ji, J. Mater. Chem. A, 2014, 2, 14759–14772 RSC.
- P. Rasiyah, A. C. C. Tseung and D. B. Hibbert, J. Electrochem. Soc., 1982, 129, 1724–1727 CrossRef CAS.
- T. Y. Wei, C. H. Chen, H. C. Chien, S. Y. Lu and C. C. Hu, Adv. Mater., 2010, 22, 347–351 CrossRef CAS.
- R. Wang, M. Yao and Z. Niu, InfoMat, 2020, 2, 113–125 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ra05578f |
| This journal is © The Royal Society of Chemistry 2020 |