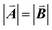Nanoleite: a new semiconducting carbon allotrope predicted by density functional theory

Abstract

In this report, a new carbon allotrope named nanoleite is proposed. Its crystal structure is constructed by embedding carbon nanotubes into the matrix of lonsdaleite periodically, leading to a hexagonal primitive unit cell. The equilibrium structure of nanoleite is fully relaxed by density functional theory calculation, and we demonstrate that nanoleite is a semiconductor with an indirect energy bandgap of 2.06 eV. Furthermore, it has a high absorption coefficient in the visible spectrum range, which is comparable to that of the gallium arsenide and indium phosphide. X-ray diffraction patterns and phonon modes are also studied.

---

Introduction

The search for carbon allotropes beyond graphite and diamond has never ceased in the past few decades. Zero-dimensional fullerene,¹ one-dimensional carbon nanotubes (CNTs),² and two-dimensional graphene³ are some of the most common and widely studied allotropic forms of carbon, and have found applications in solar cells, field-effect transistors, sensors, electromagnetic interference shielding, batteries and supercapacitors.^4–8 Other emerging forms of carbon allotropes, such as D-carbon,⁹ T-carbon,¹⁰ penta-graphene,¹¹ protomene,¹² novamene,¹³ and zayedene¹⁴ have been predicted by theorists and some have been confirmed by the experimentalists. Some of the reported carbon allotropes have extraordinary properties, such as ultra-high hardness,¹⁵ direct bandgap,¹⁰ ferromagnetic,¹⁶ and so on, which makes them highly prominent for various applications.

In this report, we borrow the concept of metamaterials to construct a new carbon allotrope. For metamaterials, elements are periodically arranged to obtain extraordinary properties, such as negative refractive index,¹⁷ and perfect absorption.¹⁸ To construct our carbon allotrope, metallic armchair CNTs (6,6) are periodically embedded into the matrix of another carbon allotrope, lonsdaleite, which is also called hexagonal diamond.¹⁹ The combination of the crystal structure of CNTs and lonsdaleite, we therefore name it nanoleite. Density functional theory calculation shows that nanoleite is an indirect bandgap semiconductor with an energy bandgap of 2.06 eV, which also has a high absorption coefficient comparable to that of the gallium arsenide (GaAs) and indium phosphide (InP) in the visible spectrum range.

Crystal structure

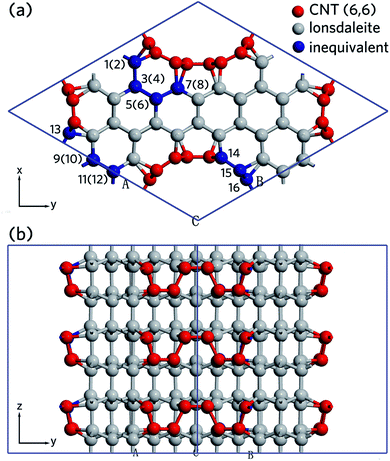
The crystal structure of nanoleite shares a similar building procedure with that of our previously reported carbon sp chains in hexagonal diamond nanocavities.¹⁴ To construct the crystal model of nanoleite, the lonsdaleite is hollowed out to form a single layer hexagonal shell cavity, and then an armchair metallic CNT with chirality index number of (6,6) is placed in the middle of the shell cavity to form the nanoleite structure. Because of the crystal structure symmetry of lonsdaleite (3-fold symmetry axis), it requires the carbon nanotube to have the same symmetry axis, which means that only the (3n,3n) tubes can fulfill the constraint. Furthermore, crystal lattice match requires the size of the hexagonal shell cavity to accommodate the diameter of the inside tubes, making the tube with a chirality index number of (6,6) and a pristine diameter of 8.14 Å the best fit. The first three structure combinations of lonsdaleite and (3,3), (6,6) and (9,9) CNTs are shown in Fig. S1.‡ Fig. S2‡ shows a 3 × 3 × 1 supercell, in which the relative position between CNTs and lonsdaleite can be identified.

Fig. 1 shows the primitive cell of nanoleite relaxed in its lowest energy configuration. It has a 3-fold symmetry axis, which is compatible with crystallization in a hexagonal lattice. Fig. 1a is the view down the 3-fold symmetry z-axis, wherein the carbon atoms belonging to CNTs are highlighted in red, and the ones belonging to lonsdaleite are in grey. As indicated by the dark grey rhombus region, there are 84 carbon atoms in the primitive cell, only 16 are inequivalent and are highlighted in blue. The numbers in parenthesis indicate the carbon atoms are located underneath the top ones. The space group describes the symmetry operations and Wyckoff positions of a specific crystal. Nanoleite is found to have a space group of P31m (157#). Given this space group symmetry, one obtains all 84 atomic positions in terms of 16 inequivalent ones. The fractional coordinates, symmetry multiplicity, and Wyckoff label of the 16 inequivalent atoms are summarized in Table 1. Fig. 1b shows the side view of the crystal structure in the x-direction, where the top carbon atoms and its underneath ones are displaced.

Fig. 1 A ball-stick model of the relaxed crystal structure of nanoleite. (a) A view down the 3-fold symmetry z-axis; (b) a side view in the x-direction. The hexagonal primitive cell is highlighted by dark grey rhombus and contains 84 carbon atoms. The lattice vectors , , are indicated, in which , and γ = 120°. The CNT (6,6) carbon atoms are highlighted in red, while the lonsdaleite carbon atoms are in grey. The 16 inequivalent carbon atoms are highlighted in blue. The labeled numbers in parenthesis indicate the carbon atoms located underneath the top ones.

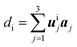Table 1 The fractional coordinates, symmetry multiplicity, and Wyckoff label of the 16 inequivalent atoms in the relaxed structure. Columns 2, 3, and 4 reports the uⁱ_j components of the 16 symmetry inequivalent carbon atoms at positions d_i in the cell, along the primitive vectors a_j of the hexagonal lattice, according to . The cell parameters (a = |a₁| = |a₂| and c = |a₃|) are provided in Table 2. Column 5 reports the number n_symm and Wyckoff label (parenthesized) of equivalent atoms generated by applying symmetry operations

Atom	a1	a2	a3	nsymm (Wyckoff)
1	0.88937	0.55518	0.19620	6 (d)
2	0.89347	0.55732	0.82741	6 (d)
3	0.77681	0.44403	0.32274	6 (d)
4	0.77852	0.44715	0.69635	6 (d)
5	0.66610	0.44303	0.19707	6 (d)
6	0.66696	0.44558	0.82655	6 (d)
7	0.65945	0.54763	0.32500	6 (d)
8	0.65673	0.55038	0.70199	6 (d)
9	0.55531	0.00000	0.32704	3 (c)
10	0.55144	0.00000	0.70543	3 (c)
11	0.44602	0.00000	0.19834	3 (c)
12	0.44844	0.00000	0.83317	3 (c)
13	0.73937	0.05983	0.66126	6 (d)
14	0.22554	0.34689	0.35113	6 (d)
15	0.11916	0.33878	0.34409	6 (d)
16	0.06045	0.31516	0.67124	6 (d)

---

Results and discussion

Structure properties

To obtain the equilibrium configuration and electronic properties of nanoleite, the well-established density functional theory (DFT) is employed.^{9–14,20–24} Density functionals including the general gradient approximation (GGA)²⁵ and hybrid functional (HSE06) are used in the Perdew–Burke–Ernzerhof (PBE) formulation,²⁶ with the norm-conserving PseudoDojo²⁷ pseudopotential as implemented in the quantum simulation package QuantumATK.²⁸ The wave functions are expanded on a plain-waves basis with a wave function cut-off of 35 hartree for both of GGA and HSE06, which guarantees the convergence of the total energy of nanoleite structure within 10⁻⁵ hartree.

The Brillouin zone of nanoleite is sampled with a 6 × 6 × 12 Monkhorst–Pack k-point grid,²⁹ with a density of ∼10 points per angstrom and shifted to Γ. The occupation method of Fermi–Dirac with a broadening of 300 K is used during the numerical simulation.

We performed simulations to fully relax the atomic positions d_i, also allowing the cell primitive vectors to change to get rid of the overall stress. Atomic relaxation is performed until the following criteria are reached: the total force must be less than 10⁻⁵ eV per angstrom and stress error less than 10⁻³ GPa. The fully relaxed crystal structure file is provided as ESI.‡

Table 1 reports the fractional coordinates of the 16 inequivalent atoms. Table 2 shows the structural parameters, such as the lattice vectors, space group, Young's modulus, and bandgap of nanoleite. The corresponding structure parameters of lonsdaleite, CNT (6,6), and fcc-diamond are summarized for comparison.

Table 2 The structural properties of nanoleite, compared to those of lonsdaleite, CNT (6,6), and fcc-diamond. Bandgaps calculated by TB (parenthesized) are summarized for comparison. Binding energy differences ΔE_b = E_nanoleite − E_diamond, where the reference binding energy of diamond E^GGA_b = −8.92 eV is reported per carbon atom

Structure parameter	Nanoleite HSE06 (TB)	Lonsdaleite HSE06 (TB)	CNT (6,6) HSE06 (TB)	Diamond HSE06 (TB)
Natoms per cell	84	4	24	2
ΔEb per atom	0.21	0.03	−0.02	0
Space group	157#	194#	84#	227#
H–M notation	P31m	P63/mmc	P42/m	Fd3̄m
Band gap (eV)	2.06 (2.31)	5.43 (5.33)	0.20 (0.06)	5.33 (5.48)
Young's modulus (GPa)	477.27 (x)	1225.28 (x)	—	1057.43 (x)
	477.56 (y)	1225.11 (y)	—	1057.43 (y)
	674.73 (z)	1288.61 (z)	1293.08 (z)	1057.43 (z)
Lattice a (pm)	1323.74	252	—	357
Lattice c (pm)	419.40	412	—	—

---

Simulated diffraction pattern

Fig. 2 shows the calculated X-ray diffraction pattern (XRD) of nanoleite in its lowest energy configuration. Meanwhile, the patterns of CNT (6,6) and the lonsdaleite are presented for comparison. To identify the peaks, the data of CNT (6,6) and nanoleite in a specific range is multiplied by 10 and 40 times, respectively. The rectangle is used to highlight the zoomed diffraction angle range. It shows that the main XRD features of the lonsdaleite can still be observed in the nanoleite, though extremely weak in the diffraction angle range of 40–100 degrees. However, the characteristic peaks of CNT (6,6) can not be identified in the nanoleite, which stems from the fact that the CNT has to change its structure to accommodate the crystal structure of the lonsdaleite. Fig. S3‡ shows that the diameter of the CNT (6,6) shrinks from 8.14 Å, in the pristine state, to 7.98 Å, in the fully relaxed nanoleite configuration, about 2% decrease.

Fig. 2 Calculated XRD diffraction pattern of nanoleite (purple) in the DFT-GGA lowest energy configuration, compared to those of the CNT (red) and lonsdaleite (blue). The data of CNT and nanoleite is multiplied by 10 and 40 times, respectively. The patterns are computed for the standard radiation wavelength λ = 154 pm of the Cu K_α line.

Thermal stability

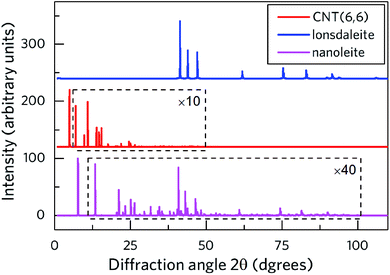
Ab initio molecular dynamics is used to study the structural stability of nanoleite. The NPT Martyna–Tobias–Klein barostat is used to keep the pressure of 1 bar and Maxwell–Boltzmann temperature of 300 K is used to initiate the velocity. Fig. 3a shows the temperature and energy variation during 10 ps simulation time, which shows a slight shock. At the end of the simulation, the last image is captured and shown in Fig. 3b, which confirms the stability of nanoleite without structural change.

Fig. 3 Molecular dynamic simulation. (a) Change of temperature (top panel) and energy (lower panel) of nanoleite during the ab initio molecular dynamics simulation of 10 ps under 300 K and 1 bar. (b) Last image at the end of molecular dynamic simulation.

Electronic properties

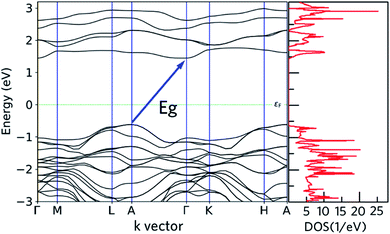
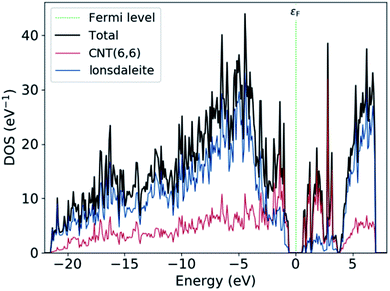
Both of the DFT-HSE06 and semi-empirical (tight binding) have been used to calculate the band structure of nanoleite. The band gaps from these two theory levels are close to each other, within 12%, thus only the DFT-HSE06 results are reported. Fig. 4 reports the calculated band structure and its density of states (DOS) around the Fermi level. The band structure depicted in Fig. 4 shows that nanoleite is an indirect semiconductor, with a bandgap of 2.06 eV.

Fig. 4 Calculated electronic states of nanoleite, the dashed line is the position of the Fermi level. Left: DFT-HSE06 Kohn–Sham band structure along the high symmetry path in the first Brillouin zone. Right: the density of states corresponding to the band structure.

Fig. 5 shows the projected density of states (PDOS) on the atom sites of CNT (6,6) and the lonsdaleite. The PDOS is used to visualize the contribution of different orbitals to the density of states. It is noted that around the Fermi level ε_F, the main contribution to the conduction band comes from CNT (6,6). In comparison, both of the CNT (6,6) and lonsdaleite comparatively contribute to the valence band. This decomposition proves that the semiconducting behavior of nanoleite arises due to the presence of CNT (6,6).

Fig. 5 The PDOS on the CNT (6,6), which is highlighted in red, and on the lonsdaleite that is in blue.

Phonon band structure

As limited by computational capability, the phonon frequencies of nanoleite are calculated by forcefield method, with an optimized Tersoff and Brenner empirical potential parameters for lattice dynamics are used.³⁰ Fig. 6 shows the phonon band structure, which is calculated along the same k-points path as for the electronic band structure. The acoustic branches are visible as they depart from zero frequency at the point of Γ. It is found that the lower acoustic branch has a 3-fold degeneracy along the Γ–K high symmetry line. At a higher frequency range of 250–1350 cm⁻¹, the optical phonon branches are observed to cluster and intersect with each other. Apart from the majority branches of optical phonon, four additional optical branches can be observed above the frequency of 1600 cm⁻¹.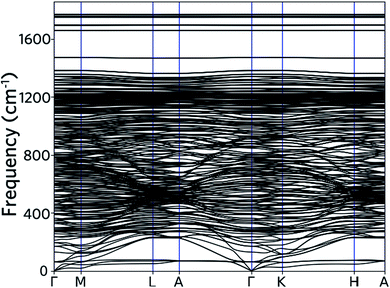

Fig. 6 Phonon dispersion computed along the same Brillouin zone path as drawn for the electron bands in Fig. 4.

The vibration mode is analyzed at q point with coordinates at (0,0,0). This shows that the first mode has a wavenumber of 59.42 cm⁻¹, which is contributed primarily by carbon atoms that belonging to CNT (6,6). The movement direction of the carbon atoms is shown as Fig. 7, which is indicated by red arrows. Fig. 7a shows the view from z-direction, and Fig. 7b is an x-direction view. It is found that 50% of the carbon atoms move in the +z direction, while the other 50% move in the −z direction. This, results in a tangential mode, can be used as a signature to identify the nanoleite structure experimentally.

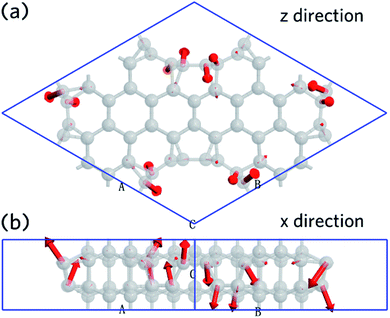Fig. 7 The first vibration mode calculated at the point of q (0,0,0). (a) A view down from z-direction, and a view from x-direction (b), the movement direction is highlighted in red.

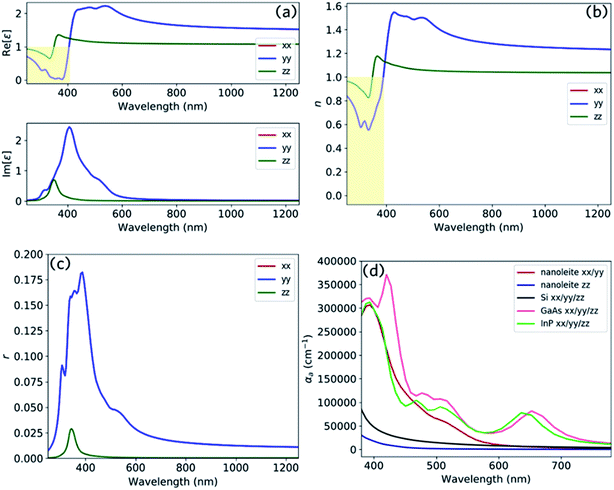
Optical spectrum

Fig. 8 reports the optical spectrum of nanoleite. It clearly shows that nanoleite is an anisotropic material, as the properties in the z direction are different from that of in the x/y direction. Fig. 8a shows the dielectric constant calculated in the range of 250–1250 nm by HSE06 functional. The real part dielectric constant is less than unity in the range of 250–375 nm in the z direction, and the range 250–406 nm in x/y direction. Furthermore, it has a refractive index less than unity in the range of 250–347 nm in the z direction, and the range of 250–388 nm in x/y direction, as shown in Fig. 8b. This distinct feature might comes from the unique structure of nanoleite, the CNTs (6,6) are periodically embedded in the matrix of lonsdaleite, which can be regarded as a metamaterial. In metamaterial, due to the electric or magnetic resonances, the values of ε or μ can be made to approach zero, leading to a near-zero refractive index (n ∼ 0).³¹ However, if the electric or magnetic resonances are close, but not too close, to strong optically active resonances, it will result in the reduction of the refractive index to below that of vacuum (i.e., 0 < n < 1).³² The reflectivity is reported in Fig. 8c and has a peak that appears near 380 nm. To compare the absorption performance of nanoleite to commonly used semiconductors, such as Si, GaAs, and InP, we calculated their absorption coefficient and summarized them in Fig. 8d. This confirms that nanoleite has an absorption coefficient comparable to that of the direct bandgap semiconductors, such as GaAs and InP. The absorption coefficient for the z direction is much lower than that of the x/y direction due to the tube structure of CNT (6,6), which is aligned in the z direction, shown as Fig. 1a.

Fig. 8 The optical spectrum of nanoleite and its comparison with commonly used semiconductors, the calculation is carried out by HSE06 hybrid functional. The calculated dielectric constant (a), refractive index (b), and reflectivity (c) of nanoleite in the wavelength range of 250–1250 nm. (d) A comparison of the absorption coefficient between nanoleite, Si, GaAs, and InP in the visible range of 380–780 nm, xx/yy/zz are tensors.

Conclusions

Nanoleite reported in this study qualifies as a new potentially-useful indirect semiconductor. The predicted energy bandgap, see Table 2, is comparable to that of the Si, GaAs, and InP. Furthermore, it has a high absorption coefficient comparable to that of the GaAs and InP in the visible range. Both of the appropriate energy bandgap and the high absorption coefficient make nanoleite as a good candidate for solar cell applications. The embedded CNT (6,6) renders nanoleite as a through-hole structure, which can be used as a platform to load other semiconducting organic molecular, such as poly 3-hexylthiophene,³³ poly p-phenylene vinylene,³⁴ etc. to form semiconducting heterojunctions at the interface, which could find applications for heterojunction optoelectronic devices.

Conflicts of interest

The authors declare no conflicts of interest in the development of this research work.

Acknowledgements

This work was supported by the research project entitled as “Development of the Emirates Advanced Materials Research Program” under the Visiting Scientist Agreement between Khalifa University of Science &Technology and Alfields Inc., signed in 2018.

Notes and references

1. H. W. Kroto, J. R. Heath, S. C. O'Brien, R. F. Curl and R. E. Smalley, Nature, 1985, 318, 162–163.
2. S. Iijima and T. Ichihashi, Nature, 1993, 363, 603–605.
3. K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Science, 2004, 306, 666–669.
4. J. Li, Y. Lu, Q. Ye, M. Cinke, J. Han and M. Meyyappan, Nano Lett., 2003, 3, 929–933.
5. Y. Wang, D. Liu, H. Zhang, J. Wang, R. Du, T.-T. Li, J. Qian, Y. Hu and S. Huang, Nano Lett., 2020, 20, 496–501.
6. Q. Huang, Y. Guo, X. Wang, L. Chai, J. Ding, L. Zhong, T.-T. Li, Y. Hu, J. Qian and S. Huang, Nanoscale, 2020, 12, 10019–10025.
7. Y. Liu, J. Zhao, Z. Li, C. Mu, W. Ma, H. Hu, K. Jiang, H. Lin, H. Ade and H. Yan, Nat. Commun., 2014, 5, 5293.
8. Y.-M. Lin, C. Dimitrakopoulos, K. A. Jenkins, D. B. Farmer, H.-Y. Chiu, A. Grill and P. Avouris, Science, 2010, 327, 662.
9. D. Fan, S. Lu, A. A. Golov, A. A. Kabanov and X. Hu, J. Chem. Phys., 2018, 149, 114702.
10. X.-L. Sheng, Q.-B. Yan, F. Ye, Q.-R. Zheng and G. Su, Phys. Rev. Lett., 2011, 106, 155703.
11. S. Zhang, J. Zhou, Q. Wang, X. Chen, Y. Kawazoe and P. Jena, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 2372–2377.
12. F. Delodovici, N. Manini, R. S. Wittman, D. S. Choi, M. Al Fahim and L. A. Burchfield, Carbon, 2018, 126, 574–579.
13. L. A. Burchfield, M. A. Fahim, R. S. Wittman, F. Delodovici and N. Manini, Heliyon, 2017, 3, e00242.
14. F. Delodovici, D. S. Choi, M. Al Fahim, L. A. Burchfield and N. Manini, Phys. Chem. Chem. Phys., 2019, 21, 21814–21823.
15. Z. Pan, H. Sun, Y. Zhang and C. Chen, Phys. Rev. Lett., 2009, 102, 055503.
16. J. Narayan and A. Bhaumik, J. Appl. Phys., 2015, 118, 215303.
17. D. R. Smith, J. B. Pendry and M. C. K. Wiltshire, Science, 2004, 305, 788–792.
18. N. I. Landy, S. Sajuyigbe, J. J. Mock, D. R. Smith and W. J. Padilla, Phys. Rev. Lett., 2008, 100, 207402.
19. D. Kraus, A. Ravasio, M. Gauthier, D. O. Gericke, J. Vorberger, S. Frydrych, J. Helfrich, L. B. Fletcher, G. Schaumann, B. Nagler, B. Barbrel, B. Bachmann, E. J. Gamboa, S. Göde, E. Granados, G. Gregori, H. J. Lee, P. Neumayer, W. Schumaker, T. Döppner, R. W. Falcone, S. H. Glenzer and M. Roth, Nat. Commun., 2016, 7, 10970.
20. Y. Liu, R. O. Jones, X. Zhao and Y. Ando, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 125413.
21. I. E. Castelli, P. Salvestrini and N. Manini, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 214110.
22. F. Zhang, B. Sahu, H. Min and A. H. MacDonald, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 035409.
23. Z. Wang, X. F. Zhou, X. Zhang, Q. Zhu, H. Dong, M. Zhao and A. R. Oganov, Nano Lett., 2015, 15, 6182–6186.
24. Y. Liu, G. Wang, Q. Huang, L. Guo and X. Chen, Phys. Rev. Lett., 2012, 108, 225505.
25. A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100.
26. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
27. M. J. van Setten, M. Giantomassi, E. Bousquet, M. J. Verstraete, D. R. Hamann, X. Gonze and G. M. Rignanese, Comput. Phys. Commun., 2018, 226, 39–54.
28. S. Smidstrup, T. Markussen, P. Vancraeyveld, J. Wellendorff, J. Schneider, T. Gunst, B. Verstichel, D. Stradi, P. A. Khomyakov, U. G. Vej-Hansen, M.-E. Lee, S. T. Chill, F. Rasmussen, G. Penazzi, F. Corsetti, A. Ojanperä, K. Jensen, M. L. N. Palsgaard, U. Martinez, A. Blom, M. Brandbyge and K. Stokbro, J. Phys.: Condens. Matter, 2019, 32, 015901.
29. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192.
30. L. Lindsay and D. A. Broido, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 205441.
31. I. Liberal and N. Engheta, Nat. Photonics, 2017, 11, 149–158.
32. A. Shahsafi, Y. Xiao, J. Salman, B. S. Gundlach, C. Wan, P. J. Roney and M. A. Kats, Phys. Rev. Appl., 2018, 10, 034019.
33. E. Orgiu, N. Crivillers, M. Herder, L. Grubert, M. Patzel, J. Frisch, E. Pavlica, D. T. Duong, G. Bratina, A. Salleo, N. Koch, S. Hecht and P. Samori, Nat. Chem., 2012, 4, 675–679.
34. I. H. Campbell and B. K. Crone, Adv. Mater., 2006, 18, 77–79.

---

Footnotes

† The genesis of this proposed new class of allotropes began with a simple “ball & stick” model proposed in March of 2020 by one of the authors (Larry A. Burchfield) of this work. This in turn leads to the concept of an entirely new classification of carbon allotropes, which is based on the possibility of having multiple nanotubes in a single hexagonal diamond cage. Additionally, an alternative class of allotropes is proposed having different diameter carbon nanotubes housed in a hexagonal diamond cage.

‡ Electronic supplementary information (ESI) available: Supercell crystal structure, carbon nanotube diameter variation, structure combination of lonsdaleite and (3,3), (6,6) and (9,9) carbon nanotubes. CCDC 2034541. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d0ra05593j

---