Open Access Article
Open Access ArticleDroplet fluid infusion into a dust layer in relation to self-cleaning
Ghassan Hassanabc,
Bekir Sami Yilbas *abc and
Hussain Al-Qahtania
*abc and
Hussain Al-Qahtania
aMechanical Engineering Department, King Fahd University of Petroleum & Minerals, Dhahran, Saudi Arabia. E-mail: bsyilbas@kfupm.edu.sa
bCenter of Research Excellence in Renewable Energy (CoRE-RE), King Fahd University of Petroleum and Minerals (KFUPM), Dhahran 31261, Saudi Arabia
cK.A.CARE Energy Research & Innovation Center, Dhahran, Saudi Arabia
First published on 28th August 2020
Abstract
Wettability of a droplet liquid on a dusty hydrophobic plate is considered and the fluid infusion into the dust layer is studied pertinent to dust removal from the hydrophobic surfaces via rolling/sliding droplets. Influence of droplet hydrostatic pressure on the fluid infusion into dust layer is also investigated towards exploring the dust removal mechanisms. Environmental dust characteristics are evaluated and their interface with the droplet fluid is assessed. Sets of experiments are carried out to examine: (i) droplet fluid infusion into the dust layer, (ii) droplet fluid cloaking of dust, and (iii) evaluate the weight gain of the dust particles during cloaking. The findings reveal that droplet fluid (water) spreads onto the dusty surface and infuses on the dust particles. Cloaking velocity decays sharply with time and the weight gain of the dust particles is about 17% of the original dust weight after cloaking. The dust particles have a large area of nano-size open-pores-sites on the surface; however, capillary diffusion through these sites is limited with shallow depths and the weight gain of a dust particle via capillary diffusion is about 1% of the particle weight. The maximum infusion depth of the droplet fluid in the dust layer is about 74 μm, which is slightly less than the dust layer thickness on the surface. The rolling droplet picks up all the dust from the 150 μm thick dust layer on the surface.
Introduction
Increased frequency of dust storms causes excessive environmental dust settlement on surfaces, which influences the operation and efficiency of many devices. In particular, environmental dust accumulation on solar energy reaping devices, such as photovoltaics, reduces performance of the device significantly and the cost-effective dust removal from such device surfaces becomes challenging. Several methods are tailored for removing the dust from surfaces and some of these include gas assisted removal,1 water jet spraying,2 electrostatic repelling,3 acoustic excitation,4 mechanical scrubbing5 and water droplet self-cleaning. Most of the cleaning processes introduced require external power sources and the sustainable operation of the processes remains costly because of the required pumping/compression and electric power. The small size dust, which are stuck to the surfaces, possess significant pinning force as created via adhesion between the surfaces.6 This requires high repelling forces to remove such particles. In some cases, the formation of non-stoichiometric compounds in dust particles, such as sodium, potassium, and chlorine, creates ionic charges on the dust surfaces,7 which enhances the pinning force on the settled surfaces.This becomes more apparent for small size dust particles. Moreover, self-cleaning process mimics the nature while repelling dust from the surfaces. In most of the self-cleaning applications, a water droplet rolls/slides on the surface and dust on the path of the droplet are picked up by the droplet fluid.8 However, large size droplets are used to secure large droplet path on the soiled surface because of achieving large area of cleaning on the surface per rolling of the droplet. In general, the large droplets on the hydrophobic surfaces suffer from bulging and increased droplet puddling becomes unavoidable on the surface. This gives rise to striations like dust residues along the droplet path rather than parallelly formed droplet path.9 In addition, dust thickness on the surface causes droplet kinetic energy dissipation and the rolling speed reduces on the dusty surface. Increasing the rolling speed enables to improve the rolling length of the droplet. Hence, investigation of the droplet speed on the dusty hydrophobic surface becomes essential.
Creating an electrostatic effect on dust provides repelling of dust from surfaces; in addition, air assisting gas as used with the electrostatic repelling enhances the dust cleaning process. However, removal of small dust is requires additional efforts such as boosted charging potential and increased assisting gas flow.3 This is mainly because of the small size dust having enhanced adhesion onto the solid surfaces. Introducing electrodynamic screening system creates a dust cleaning effects on solid surfaces. The designing of a such system enabling an efficient dust removing operation is difficult to achieve because of involvement of the various parameters such as inter-electrode spacing, applied voltage settings, assessment of dust particles' charges, and etc.10 Application of electrostatic screening on dust removal can be extended for cleaning of solar thermal troughs and photovoltaic solar panels. Although the screening system provides particle solution for dust removal, the gravitational influence only allows almost 50% of the dust remaining on the surface.11 However, the design of electrostatic screen can be modified generating a reciprocator behavior of the particles in electrodes spacing via applying an AC current to screening system.12 This improves the amount of dust repelled from the photovoltaic panel surfaces. Moreover, water droplet cleaning of surfaces via mimicking the nature becomes important because of less amount of clean water usage as compared to water jet cleaning, which is particularly true for the regions where water is scarcely available. Rolling/sliding action of droplet requires hydrophobic surfaces with low contact angle hysteresis.13 To achieve such wetting characteristics, hierarchical distributed nano/micro size pillars with low surface free energies need to be created on the surface.14 Although several techniques are adopted to generate hydrophobic surfaces, the solution crystallization15 and dip coating16 techniques become popular because of easiness and clean processes involved. In general, large droplets on hydrophobic surfaces undergoes puddling because of the gravity and droplet wetting size on the soiled hydrophobic surface changes due to droplet bulging. This changes the parallel droplet path towards the striation droplet path feature on the surfaces; therefore, the area cleaned by the droplet on the hydrophobic surface reduces via striations.9 This shortcoming can be minimized via reducing the droplet size on the surfaces. Moreover, droplet fluid cloaks the dust particle prior to picking up from surfaces. This forms the bases for dust removal by a rolling/sliding droplet on the hydrophobic surfaces. In the case of thick dust layers, the cloaking and droplet residence time on the surface become critical and cleaning can be partly achieved while leaving significant amount of dust on the surfaces. In order to explore dust particles cloaking via droplet liquid further investigation of the liquid spreading and cloaking onto dust particle becomes essential.
Dust accumulation on surfaces forms thick dust layer over the time and self-cleaning of thick dust layer becomes challenging. Recent changes in harsh weather conditions contribute to the excessive dust settlements on surfaces in short durations. This increases the frequency of cleaning process and brings the extra cost operating the energy harnessing devices. On the other hand, droplet rolling and the mechanism of the dust picking from hydrophobic surfaces was studied earlier,8,9 however, cloaking of droplet fluid over thick dust layer is left for future study. In the current study, water cloaking of dust at various thicknesses is considered in relation to water droplet cleaning of hydrophobic surfaces. An experiment is conducted to monitor cloaking velocity of the water for various shapes of dust columns. The dust columns are considered to be porous like sites and formulation of liquid height along the dust columns is presented in relation to droplet fluid cloaking on dust particles. To assess the gravitational influence on the liquid diffusion and spreading on the dust, tests are repeated incorporating the liquid on the top and bottom of the columns. A high speed and thermal imaging systems are used to monitor the liquid diffusion length and wetting site along the dust columns.
Experimental
Environmental dusts were gathered from photovoltaic (PV-panel) surfaces in the local region of Dammam in Saudi Arabia. Soft-brushes were utilized to gather the dust from PV-panel surfaces and later they are stored in vacuum tight containers. The collection of dust was repeated every three months period to minimize the effect of seasonal influence on the dust characteristics. The dust particles were characterized using scanning electron microscopy (JEOL 6460) and X-ray diffraction (Bruker D8). To evaluate the dissolution of dust compounds in water, dust were stirred with desalinated water. Later, the solution in the liquid form was obtained from the mixture solution and evaluated via a quadrupole inductively coupled plasma mass spectrometer (Thermo Scientific, XSeries 2). The surface tension of the liquid solution obtained from the solution mixture was measured using force tensiometer (Kruss, K100). Surface free energy of the dust pellets are measured using droplet contact angle method. Contact angle measurements are performed employing a Kyowa (DM 501) goniometer with the volume steps of 0.1 μL. The sessile droplet images were recorded by 25× magnification and temperature of measuring ambient was let at 20 ± 0.18 °C. After settling a liquid drop on the sample surfaces, the contact angles of sessile droplet both sides were recorded. High-precision drop shape analysis (HPDSA) was conducted evaluating the recorded contact angles adopting the early work.17 The tests were repeated 10 times to ensure the measurement repeatability. Moreover, water, ethylene glycol, and diiodomethane are used evaluating the surface energy of dust pellets (15 mm diameter and 4 mm thickness), which are formed slightly pressing the collected dusts. The contact angles for water, ethylene glycol, and diiodomethane on the dust pellet using Kyowa (DM 501) goniometer are 36° ± 3°, 86° ± 4°, and 127° ± 5°, respectively. Circular dust columns (5 mm diameter and 15 mm height) are also produced in a similar way of the pellets to assess the droplet fluid infusion into the dust column. A high-speed optical video system (Speed Sense 9040) was operated at 5000 frames-per-second (fps) with the image resolution 1280 × 800 recording the data.To test and evaluate the rolling droplet picking dust form the dusty hydrophobic surface, glass plate surfaces were hydrophobized through deposition of functionalized nano-silica particles.18 Mixture of ethanol (14.2 mL), desalinated water (1.2 mL), and ammonium hydroxide (24 mL) was stirred at 350 rpm for 55 minutes. Tetraethyl orthosilicate (TOES) (1 mL TOES in 4 mL ethanol) was added in the stirred solution. The silane 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 molar ratio was used as a modifier agent into the mixture solution and, later, magnetically stirred over 16 hours. Later, the reactants in the mixture were eliminated through centrifugation. A dip coating method was employed for laying the prepared solution onto glass surfaces. The dip coating provided a uniform thickness of deposited layer (500 ± 30 nm).
4 molar ratio was used as a modifier agent into the mixture solution and, later, magnetically stirred over 16 hours. Later, the reactants in the mixture were eliminated through centrifugation. A dip coating method was employed for laying the prepared solution onto glass surfaces. The dip coating provided a uniform thickness of deposited layer (500 ± 30 nm).
Results and discussion
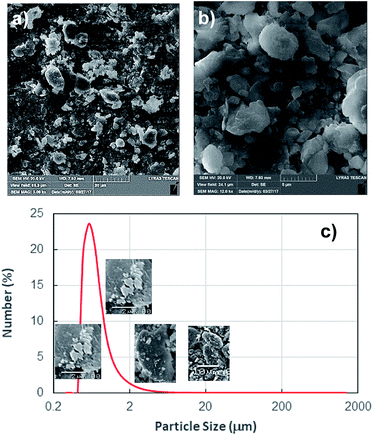
Since the dust settles on the surfaces in dusty environment, dust removing by rolling/sliding water droplets while mimicking the natural rain becomes important. To achieve droplet rolling/sliding on surfaces, hydrophobic wetting state of the surface becomes critical. Nevertheless, the characteristics of the dust remain equally important for the removal process. Hence, dust flakes characterization becomes necessary. Fig. 1a and b show SEM micrographs of the dust collected while Fig. 1c shows the dust particle size distribution. The dust flakes has various sizes and shapes (Fig. 1a). Small flakes form cluster-like structure among the large flakes (Fig. 1b) and some of small flakes attach onto large dust flake surfaces (Fig. 1a). The size of dust varies from sub-microns to tens of microns (Fig. 1c). The dust particles average size is about 1.2 μm. The clustering and attachment of small dust particles reveals that these particles have charges, which enable them to cluster. The possible explanation for the charges on these particles is the prolonged duration of exposing the sun close to sea environment. The small size dust particle sustain in air for long duration and interacting solar radiation to small size dust results in charge forming on surfaces.Dust flakes compose various elements, which can be observed from Fig. 2a, in which XRD data of dust places is shown. The peaks of Na, K, Ca, S, Si, and Fe are apparent. The peaks corresponding to iron and silicon coincide and presence of Na and K can be attributed to the sea-salts, i.e. the dust flakes are gathered from the region (Dammam) close to the Arabian Gulf. Sulfur could be associated with anhydrite or gypsum (CaSO4) and iron may be related to clay-aggregated hematite (Fe2O3). Table 1 gives elemental data obtained from energy dispersive spectroscopy of the dust flakes. The geological formation of the landscape plays an important role on the elemental distribution in the dust flakes. As the size of the particle reduces (≤2 μm), concentration of elements becomes different than that of large size flakes (≥4 μm). Change of elemental concentrations, particularly for Na and K, between the large and small flakes are because of the small flakes, which stay prolonged duration in atmosphere in the sea environment. The salt ions may attach and form compounds with small dust flakes. The molar ratio of chlorin in NaCl and KCl does not satisfy the stoichiometric ratio, which suggest that these compounds are not salt crystals rather chlorin dissolve in these structures. Moreover, the density of dust varies with size and elemental content. The flakes with small sizes (≤2 μm) has the density of about 1200–1600 kg m−3 while large flakes (≥4 μm) have the density of about 2200–2800 kg m−3.
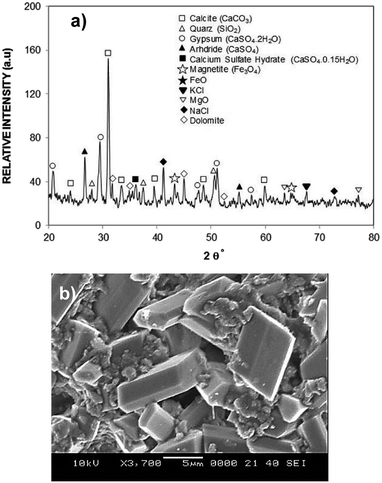 | ||
| Fig. 2 X-ray data and dried mixture solution: (a) X-ray data of dust particles, and (b) SEM micrograph of crystals formed due to dried dust and desalinated water mixture (solution). | ||
| Si | Ca | Na | S | Mg | K | Fe | Cl | O | |
|---|---|---|---|---|---|---|---|---|---|
| Size ≥ 1.2 μm | 12 | 8.3 | 2.2 | 1.3 | 2.5 | 0.8 | 1.2 | 0.4 | BL |
| Size < 1.2 μm | 10 | 7.3 | 2.7 | 2.5 | 1.3 | 1.2 | 1.1 | 1.1 | BL |
| Dust residues | 9.5 | 7.1 | 1.9 | 1.3 | 2.4 | 0.9 | 0.9 | 0.4 | BL |
| Dried solution | 0.7 | 18 | 1.4 | 4.2 | 0.4 | 0.6 | 0.6 | 6.1 | BL |
In the humid-air, water undergoes condensation on dust flakes and some of the dust content may dissolve in the condensate water. To determine the solubility of dust compounds in water, further experiments are carried out. Dust flakes with mass ratio of 0.2 (mass of dust over mass of water) are mixed with desalinated water and pH of the mixture is monitored with time. The mixture pH increases reaching 7.8 with short duration while demonstrating that the mixture resembles the basic solution. This is attributed to the dissolved compounds of Na, K, and Cl; hence, the dissolved compounds in water cause the creation of OH− ions towards basic solution. In order to evaluate the decomposition concentration in the mixture, inductively coupled plasma spectrometry (ICP) is carried out. Table 2 provides the ICP data. The presence of Na, K, and Cl in the ICP data reveals the dissolution of these flakes compounds in the mixture. The properties of the mixture solution, such as surface tension, changes because of presence of Na, K, and Cl.
| Ca | Na | Mg | K | Fe | Cl |
|---|---|---|---|---|---|
| 308700 | 45![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 300 |
69![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 500 |
34![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 100 |
1870 | 36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 800 |
To evaluate the surface tension variation because of dissolution of such content, surface tension measurement of the mixture solution having different dust concentration is realized. Table 3 gives the surface tension of the mixture solution for various dust concentrations. Surface tension of the mixture solution slightly increases with increasing dust concentration. As compared to distilled water, surface tension increases by 3%, i.e. it changes from 0.072 N m−1 to 0.0742 N m−1. Increasing dust concentration within 15% to 20%, the surface tension of the mixture solution remains same. Moreover, the variation of surface tension of the mixture solution does not notably alter the liquid droplet contact angle on the surface.
| Concentration (weight%) | Surface tension (N m−1) |
|---|---|
| 0 | 0.0720 |
| 5% | 0.0725 |
| 10% | 0.0737 |
| 15% | 0.0742 |
| 20% | 0.0742 |
Since rolling droplet on dusty surface picks the dust flakes from the surface, these fakes alter the surface tension of the droplet liquid. Altering the surface tension of the droplet fluid changes the droplet adhesion on the hydrophobic surface, since the adhesion force related to the rolling/sliding droplet is,19 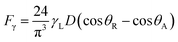 where γL represents surface tension of the droplet liquid, D is the droplet diameter, θR and θA are the receding and advancing angles, respectively. Hence, the droplet adhesion enhances with same amount of increased in surface tension of the liquid. Moreover, further examinations for the mixture solution is conducted. The solution is extracted from the mixture and it is deposited onto a glass plate and being allowed to dry in the laboratory environments while mimicking the outdoor atmospheric conditions (308 K, 101
where γL represents surface tension of the droplet liquid, D is the droplet diameter, θR and θA are the receding and advancing angles, respectively. Hence, the droplet adhesion enhances with same amount of increased in surface tension of the liquid. Moreover, further examinations for the mixture solution is conducted. The solution is extracted from the mixture and it is deposited onto a glass plate and being allowed to dry in the laboratory environments while mimicking the outdoor atmospheric conditions (308 K, 101![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 348 kPa, and relative humidity 85%) for one hour. Fig. 2b shows SEM image of the dried solution and dust-particle-residuals on the glass plate. The dried solution possesses crystals with different orientations and dust residues are also seen on the glass. The energy spectroscopic analysis of the dried solution and the dust residues are given in Table 1 The calcium and chlorine contents of the dried solution increase significantly while silicon content in the dried solution reduces considerably, i.e., Ca and Cl contents increases to 18.1% and 6.1% in the dried solution while silicon content reduces to 0.7% in the dried solution. Hence, the crystals appeared on the surface following drying the mixture are mainly calcium chloride crystals.
348 kPa, and relative humidity 85%) for one hour. Fig. 2b shows SEM image of the dried solution and dust-particle-residuals on the glass plate. The dried solution possesses crystals with different orientations and dust residues are also seen on the glass. The energy spectroscopic analysis of the dried solution and the dust residues are given in Table 1 The calcium and chlorine contents of the dried solution increase significantly while silicon content in the dried solution reduces considerably, i.e., Ca and Cl contents increases to 18.1% and 6.1% in the dried solution while silicon content reduces to 0.7% in the dried solution. Hence, the crystals appeared on the surface following drying the mixture are mainly calcium chloride crystals.
On the other hand, it is demonstrated that the droplet can fluid cloak the dust on the hydrophobic surface prior to picking from the surface. Hence, the droplet fluid (water) spreading and cloaking on the dust flakes become important. To assess the spreading of water on the dust layer, further tests are carried out. In this case, the pellets are formed from the dust flakes and droplet contact angle method20–22 is adopted to evaluate the surface free energy of dust pellets. Hence, diiodomethane, water, and glycerol are used to evaluate the surface free energy of the dust pellets. The surface energy is:
| γ = γL + γP | (1) |
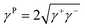 | (2) |
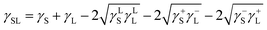 | (3) |
γL![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ = γS − γSL − PeL θ = γS − γSL − PeL
| (4) |
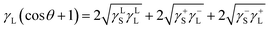 | (5) |
The data for γLL, γ+L, and γ−L can be found from literature for water, ethylene glycol, and diiodomethane, which are given in Table 4.20–22 Incorporating eqn (1), (2) and (5) with the data in Table 4, the surface free energy of dust pellet (γS) can be evaluated, which are given in Table 5. The surface free energy of the dust pellets is evaluated as 114 ± 5.5 mJ m−2. It is worth to mention that the standard deviation of surface free energy is estimated from: 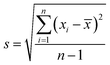 , here n is the number of data points (measurements), xi is the surface free energy determined and
, here n is the number of data points (measurements), xi is the surface free energy determined and ![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) is the mean value of the surface free energy. The standard deviation (s) is determined as 5.5 mJ m−2 and the mean value (
is the mean value of the surface free energy. The standard deviation (s) is determined as 5.5 mJ m−2 and the mean value (![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) ) is 114 mJ m−2. The measurements were repeated to secure the minimum experimental errors. The measurement errors estimated after 12 repeats of the experiments is about 5%. In addition, the Washburn method23 is used to assess contact angle measurements on the dust pellet surfaces. A glass-tube of 3 mm diameter is used to fill the loose dust particles. The selected liquid (water) is made in contact with tube. This enables to draw-up the liquid in the tube under the capillary force. The mass increase in the tube and the time for the mass increase is related through the Washburn equation, i.e.
) is 114 mJ m−2. The measurements were repeated to secure the minimum experimental errors. The measurement errors estimated after 12 repeats of the experiments is about 5%. In addition, the Washburn method23 is used to assess contact angle measurements on the dust pellet surfaces. A glass-tube of 3 mm diameter is used to fill the loose dust particles. The selected liquid (water) is made in contact with tube. This enables to draw-up the liquid in the tube under the capillary force. The mass increase in the tube and the time for the mass increase is related through the Washburn equation, i.e. 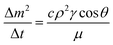 , here Δm is the mass gain, Δt represents the duration for the mass gain (flow time), c is the capillary constant of the dust, ρ is the fluid density, θ is the contact angle, μ is the fluid viscosity. The capillary constant of dust is obtained using n-hexane as a liquid, which results in zero contact angle (θ = 0). The change of mass gain square (Δm)2 with corresponding time (Δt) provides the contact angle of the fluid. The capillary constant for the dust particles is estimated as 5.82 × 10−16–6.54 × 10−16 m−5. However, the variation of dust particle size influences the capillary constant.24 Hence, the capillary constant variation may be attributed to the dust particle sizes variation. The contact angle determined from the Washburn method differs slightly from that obtained from the dust pellet surface, i.e., the water contact angle obtained on the dust pellet surface is almost 36° ± 3° however, it is 37.4° ± 3° from the Washburn method. Nevertheless, the difference is small. Moreover, water spreading on the dust surface remains important during droplet rolling on dusty surface. The droplet liquid (water) spreading should satisfy the hemi-wicking criteria25 to spread on dusty surface. The spreading coefficient can be expressed as: S = γS − γL − γSL, here, γS is the free energy of dusty surface, γL resembles the liquid surface tension, and γSL is the interfacial tension at water and the dusty surface at the interface. The interfacial tension is formulated to be:
, here Δm is the mass gain, Δt represents the duration for the mass gain (flow time), c is the capillary constant of the dust, ρ is the fluid density, θ is the contact angle, μ is the fluid viscosity. The capillary constant of dust is obtained using n-hexane as a liquid, which results in zero contact angle (θ = 0). The change of mass gain square (Δm)2 with corresponding time (Δt) provides the contact angle of the fluid. The capillary constant for the dust particles is estimated as 5.82 × 10−16–6.54 × 10−16 m−5. However, the variation of dust particle size influences the capillary constant.24 Hence, the capillary constant variation may be attributed to the dust particle sizes variation. The contact angle determined from the Washburn method differs slightly from that obtained from the dust pellet surface, i.e., the water contact angle obtained on the dust pellet surface is almost 36° ± 3° however, it is 37.4° ± 3° from the Washburn method. Nevertheless, the difference is small. Moreover, water spreading on the dust surface remains important during droplet rolling on dusty surface. The droplet liquid (water) spreading should satisfy the hemi-wicking criteria25 to spread on dusty surface. The spreading coefficient can be expressed as: S = γS − γL − γSL, here, γS is the free energy of dusty surface, γL resembles the liquid surface tension, and γSL is the interfacial tension at water and the dusty surface at the interface. The interfacial tension is formulated to be: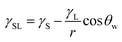 ,26 here θw is contact angle of water on the dust-pellet surface and r represents the roughness parameter of the dusty surface. Moreover, 3-dimensional micro-optical imager is used to evaluate r, which results an average value of r = 0.62. It is worth to mention that the roughness parameter assessment is repeated several times on the different locations of the dust pellet surface and the roughness parameter varies on the surface within the range of 0.58 to 0.66 with an average of 0.62. θw for the dust-pellet surface is 36° ± 3°. Hence, γS–L = 20.55 mJ m−2 and introducing in spreading coefficient (S) equation, it results in S = 21.95 mJ m−2, i.e. S becomes greater than 0; therefore, water spreads on the dust-pellet surface, i.e. it spreads on the dusty surface. The spreading fluid can form a liquid ridge almost wrapping the dust particle surface. The liquid ridge further infuses onto the dust surface while encapsulating the particle. This is identified as liquid cloaking of a particle.27
,26 here θw is contact angle of water on the dust-pellet surface and r represents the roughness parameter of the dusty surface. Moreover, 3-dimensional micro-optical imager is used to evaluate r, which results an average value of r = 0.62. It is worth to mention that the roughness parameter assessment is repeated several times on the different locations of the dust pellet surface and the roughness parameter varies on the surface within the range of 0.58 to 0.66 with an average of 0.62. θw for the dust-pellet surface is 36° ± 3°. Hence, γS–L = 20.55 mJ m−2 and introducing in spreading coefficient (S) equation, it results in S = 21.95 mJ m−2, i.e. S becomes greater than 0; therefore, water spreads on the dust-pellet surface, i.e. it spreads on the dusty surface. The spreading fluid can form a liquid ridge almost wrapping the dust particle surface. The liquid ridge further infuses onto the dust surface while encapsulating the particle. This is identified as liquid cloaking of a particle.27
| γL (mJ m−2) | γLL (mJ m−2) | γ+L (mJ m−2) | γ−L (mJ m−2) | |
|---|---|---|---|---|
| Water | 72.8 | 21.8 | 25.5 | 25.5 |
| Diodomethane | 50.8 | 50 | 0 | 0 |
| Ethylene glycol | 48 | 19 | 0.41 | 1.28 |
| γS (mJ m−2) | γ+S (mJ m−2) | γ−S (mJ m−2) | |
|---|---|---|---|
| Dust | 114.2 | 63.29 | 50.49 |
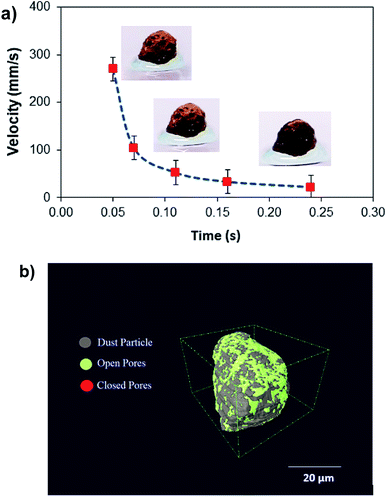
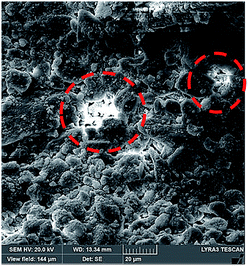
Hence, further tests are carried out to measure the velocity of droplet liquid cloaking on dust particle surface. A high speed optical imaging system is adopted to record the ridge height variation with time on a dust particle. Fig. 3a depicts the cloaking velocity with time. The cloaking velocity decays steeply with time resembling an exponential decay, which can be expressed as ∼Ke−nt, here K represents a constant and n is the parameter, which is about 0.25 s−1. The similar cloaking velocity decay is as well presented previously.28 The variation of cloaking velocity occurs depending on the particle shape. In general, the force equilibrium, due to the gravity, liquid surface tension, interfacial tension, solid surface free energy, and shear resistance, defines the cloaking velocity.29 Moreover, the shear rate during cloaking causes fluid energy loss and it can be in the form of the Ohnesorge number 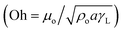 ; here, γL represents liquid surface tension and a corresponds to particle size.30 For the dust particle of 1.2 μm (average size), the resulting Ohnesorge number remains smaller than one (Oh ∼ 0.057). This demonstrates that the influence of the viscous dissipation during cloaking is not significant on the force balance. The dust particle possesses open pores on the surface, which can be observed from Fig. 3b, in which computerized tomography image of the particle is shown. Hence, it is possible that the weight of the dust particle increases by the liquid film formed on the surface after liquid wrapping of the entire particle.
; here, γL represents liquid surface tension and a corresponds to particle size.30 For the dust particle of 1.2 μm (average size), the resulting Ohnesorge number remains smaller than one (Oh ∼ 0.057). This demonstrates that the influence of the viscous dissipation during cloaking is not significant on the force balance. The dust particle possesses open pores on the surface, which can be observed from Fig. 3b, in which computerized tomography image of the particle is shown. Hence, it is possible that the weight of the dust particle increases by the liquid film formed on the surface after liquid wrapping of the entire particle.
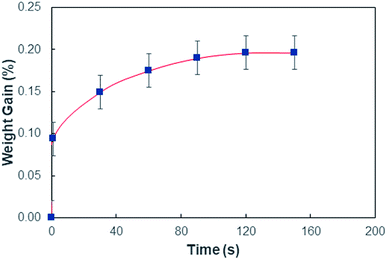
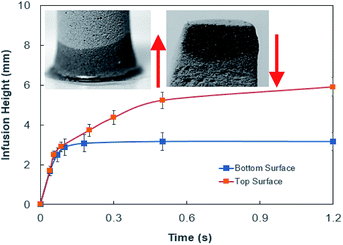
In order to assess weight gain of a dust particle during the cloaking experiments are carried out using the sensitive weight scale (Thomas Scientific). The percentage of weight gain of the particle is measured after the complete cloaking. The weight gain of the dust particle is found to be almost 17.8%. It is worth to mention that the work of adhesion of the liquid is related to the weight gain of the dust particle. The work of adhesion for a liquid–solid (dust particle) combination can be presented in terms of Dupre equation,31,32 which is: Wadd = γL + γS − γSL. Since, the interfacial surface tension is determined as γSL = 20.55 mJ m−2, the surface free energy of the dust particle is about γS = 114 mJ m−2, the work adhesion becomes in the order of Wadd = 166.25 mJ m−2. Hence, liquid strongly adhere on the surface of the dust particle, which causes weight gain of the particle after the liquid cloaking completes. In addition, some liquid diffuse into the dust particle via pores sites under the capillary influence. To evaluate the amount of liquid diffusion under capillary influence, further experiments are carried out. The dust particle kept into the liquid for 400 s after completing of cloaking (liquid rapping the entire surface of the dust particle). Fig. 4 depicts the percentage of the weight gain of the dust particle of 1.25 μm size with time due to capillary diffusion. The percentage of weight gain is determined through the relation 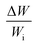 , where ΔW is the weight difference of the dust particle for 400 s after accomplishing cloaking and onset of cloaking, and Wi is the weight of the dry dust particle (on set of cloaking). The weight gain of the particle, during the period of 400 s, is less than 0.1%. The weight gain of the particle due to the capillary diffusion is negligibly small. Therefore, the weight gain of the individual dust particle, which is wetted and picked up by the rolling and/or sliding droplet, is considerably small. Since the dust layer on the hydrophobic surface composes of many dust particles and their settlement on the surface forms like a porous layer.
, where ΔW is the weight difference of the dust particle for 400 s after accomplishing cloaking and onset of cloaking, and Wi is the weight of the dry dust particle (on set of cloaking). The weight gain of the particle, during the period of 400 s, is less than 0.1%. The weight gain of the particle due to the capillary diffusion is negligibly small. Therefore, the weight gain of the individual dust particle, which is wetted and picked up by the rolling and/or sliding droplet, is considerably small. Since the dust layer on the hydrophobic surface composes of many dust particles and their settlement on the surface forms like a porous layer.
The consideration of porous layer resembling the settled dust on the surface becomes more appropriate for the analysis. To evaluate the droplet fluid penetration into the dust layer during droplet rolling on the dusty surface, the sets of experiments are carried out. The pellets like dust columns with 8 mm diameter and 12 mm height are made and the infusion of water film into the dust column is monitored using high speed imaging and thermal camera. Firstly, the dust column is located in contact with the water film of 500 μm spread on a glass plate. Secondly, the experiment is repeated as the droplet of 30 μL volume is formed on the top of the dust column. This arrangement enables to observe the gravitational influence on the water infusion into the dust columns. Fig. 5 shows the optical image of the dust column and desalinated water infusion height with time (liquid is on bottom and top of dust column) while Fig. 6 shows the SEM micrograph of dried columns.
 | ||
| Fig. 5 Desalinated water infusion height in dust column for water location at cone top and cone bottom surfaces. Arrows show flow direction. | ||
 | ||
| Fig. 6 SEM micrograph of dust column cross-section after drying. Dotted circles show dried mixture solution in dust column cross-section. | ||
The pattern of the wetted region across the dust column changes slightly (Fig. 5) and some residues of small size dried solution, composing of dissolved dust compounds, are observable (Fig. 6). This indicates that water dissolve some dust compounds as it infuse into the dust column. Moreover, it can be observed that infused fluid height in the dust column increases rapidly with time and as the time progresses the rise of infused liquid height becomes small. In addition, the infused liquid height corresponding to the case one (liquid film is at column bottom) attains lower values than that of the case two (liquid film is at the top of the column top). Consequently, gravity enhances the infused liquid height in the column. The infusion of water into the dust column is related to mainly liquid film height, capillary pressure in porous (wick) structure, and flow/capillary resistance force in porous (wick) structure of the column. The capillary pressure in the wick structure is: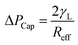 ,33 here, γL represents liquid surface tension and Reff is the effective capillary radius. Moreover, the pressure drop takes place during infusion of the fluid into the porous (wick) structure, which is related to friction resistance due to pores structure and gravitation (hydrostatic influence). The pressure drop or loss (ΔPloss) can be written in line with the previous formulation:
,33 here, γL represents liquid surface tension and Reff is the effective capillary radius. Moreover, the pressure drop takes place during infusion of the fluid into the porous (wick) structure, which is related to friction resistance due to pores structure and gravitation (hydrostatic influence). The pressure drop or loss (ΔPloss) can be written in line with the previous formulation: 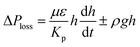 ,33 here μ represents the fluid viscosity, ε corresponds to the porosity, Kp is permeability, h is the infused liquid height (liquid wetting height) in the porous structure, ρ is the density of the liquid, and g is the gravity. Here, ± is associated with the location of the fluid film/droplet on the dust column. It takes positive (−) for the liquid on the top of the column while it becomes negative (+), if the liquid is at the dust column bottom. The porosity of dust column is estimated from the SEM images at the dust column cross-section (Fig. 6). Hence, the porosity is determined the area ratio of total pores area to the dust column cross-sectional area, i.e. it is determined as 0.28 ± 0.04. The permeability meter is used to evaluate the dust column permeability (Kp), which is measured as about 10–12 m2. The measurement of the dust column permeability is repeated for ten different columns and the data obtained from permeability varies within almost 20%. Infusion of the liquid via porous structure requires that the capillary force should overcome the pressure drop and in the limit the force generated by the pressure drop could be similar order to the capillary force. This allows to balance of these forces, i.e. πR2effΔPCap = 2πReffLeffΔPloss, here Leff represents the effective capillary length. Hence, the pressure loss ΔPloss becomes
,33 here μ represents the fluid viscosity, ε corresponds to the porosity, Kp is permeability, h is the infused liquid height (liquid wetting height) in the porous structure, ρ is the density of the liquid, and g is the gravity. Here, ± is associated with the location of the fluid film/droplet on the dust column. It takes positive (−) for the liquid on the top of the column while it becomes negative (+), if the liquid is at the dust column bottom. The porosity of dust column is estimated from the SEM images at the dust column cross-section (Fig. 6). Hence, the porosity is determined the area ratio of total pores area to the dust column cross-sectional area, i.e. it is determined as 0.28 ± 0.04. The permeability meter is used to evaluate the dust column permeability (Kp), which is measured as about 10–12 m2. The measurement of the dust column permeability is repeated for ten different columns and the data obtained from permeability varies within almost 20%. Infusion of the liquid via porous structure requires that the capillary force should overcome the pressure drop and in the limit the force generated by the pressure drop could be similar order to the capillary force. This allows to balance of these forces, i.e. πR2effΔPCap = 2πReffLeffΔPloss, here Leff represents the effective capillary length. Hence, the pressure loss ΔPloss becomes 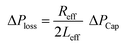 . Introducing the capillary pressure
. Introducing the capillary pressure 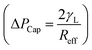 in the pressure loss term, it yields:
in the pressure loss term, it yields: 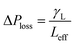 . Replacing the pressure loss in
. Replacing the pressure loss in 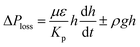 , it yields:
, it yields:
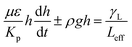 | (6) |
On the other hand, measuring the effective capillary length of the dust columns is rather difficult, since we do not have an equipment with high measurement accuracy to achieve this measurement. However, the effective capillary length can be estimated using eqn (6) and the experimental data for infusion behavior. Moreover, Fig. 7 shows temporal variation of desalinated water infusion velocity for two cases (liquid film is at the top and at the bottom, respectively). The infusion velocity increases to reach its peak prior to decreasing and attending a steady value, which is considerably small. Hence, almost after 0.3 s, desalinated water infusion into the dust column becomes gradual. Therefore, using eqn (6) and Fig. 6 and 7 allow to determine the effective infusion depth. The estimated effective capillary length from eqn (6) becomes almost same after 0.4 s of infusion time for two cases where the liquid film is at the dust column bottom (case one) and the liquid film at the top of the dust column (case two), i.e. the effective capillary length for the dust column is 0.074 mm after 0.4 s of infusion time for two cases. Moreover, further increasing infusion period (≥0.4) does not alter significantly the effective capillary length.
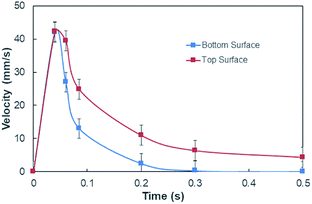 | ||
| Fig. 7 Desalinated water infusion velocity with time for water locations at the top and bottom of the dust columns. | ||
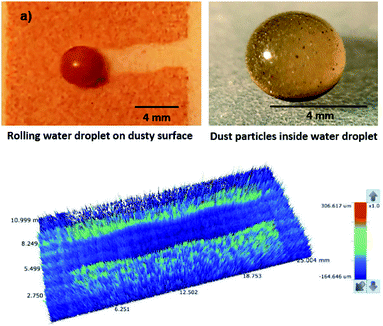
Although the capillary length is less than the dust layer thickness, which is formed due to dust settlement in outdoor environment after two weeks (150 μm), during droplet rolling the transition period remains longer the infusion period. Consequently, dust removal by rolling droplet from the surface becomes possible for the dust layer thickness of 150 μm during the droplet transition on the dusty surface. The further study is conducted assessing the cleaning of dusty hydrophobic surface by a rolling water droplet of 30 μL. The dust layer thickness is set at 150 μm resembling the dust settlement over a period of two weeks and tilt angle of the hydrophobic surface is kept at 5°. Fig. 8a shows the optical image of the dust particles inside the droplet fluid while Fig. 8b shows optical image of the droplet path on the dusty hydrophobic surface. It is evident that the dust particles are removed by the rolling droplet (Fig. 8a) and the droplet path remains clean (Fig. 8b). In this case, the droplet fluid fully infuses and wets the dust layer on the hydrophobic surface during its rotational/sliding transition.
The durability of the hydrophobic surfaces in harsh environments (high temperature, high humidity, and dusty) is one of the challenges of self-cleaning applications. The coating produced currently for hydrophobizing the glass surfaces can resists temperatures as high as 200 °C; however, the dissolution of dust compounds, such as NaCl and KCl, in humid ambient can locally damage the coated surface while limiting the coating durability. Hence, future studies are planned to minimize such limitations.
Conclusion
Wetting state of the droplet fluid (water) on dusty hydrophobic surface is considered and infusion of water into dust layer is examined in line with the rolling/sliding droplet cleaning of dusty hydrophobic surfaces. Environmental dust particles are examined in details and dust characteristics including composition, shape, surface free energy, and surface morphology are presented. Water spreading on dusty surface is assessed and droplet fluid cloaking of dust is evaluated. The dust layer is considered to be a porous-like structure and water infusion into dust layer is formulated including the influence of capillary, gravitational, porous resistance forces. The effective length of infusion height in the dust layer is estimated incorporating the experimental data. High speed and thermal cameras are used to monitor the infusion front velocity in the dust layer. The findings revealed that dust particles posses various elements and compounds. Elemental structure of the dust changes depending on the dust size; hence, small size dust has large weight concentration of Na, K, and Cl. Some of dust compounds can dissolve in water and sharply elevates basic content (pH = 7.8). Dried dissolved solution forms mainly CaCl crystals on the surface. Water spreads onto dust layer and wets the surface. Water cloaking velocity remains high in the during the ridge formation around the dust particles, as the cloaking progresses, the cloaking velocity attains almost steady behavior. Water infuses into the dust layer; however, weight gain of the dust particle is almost limited with the wrapping layer of the fluid aver the particle surface. Dust particle surface has large open-pore-sites with nano-sizes. Weight gain of the dust particle via liquid diffusion from open-pore-sites during cloaking is negligibly small, which is less than 1%. The hydrostatic influence of droplet fluid significantly alters the liquid infusion into the dust layer. The penetration speed (infusion speed) of the fluid attains larger values for the case as the liquid is located at the top of the dust column than that of the case as the liquid at the bottom of the dust column. The maximum depth of liquid infusion in the dust column remains same for both cases of liquid locations at the dust column. The maximum depth of infusion (0.074 mm) well exists the dust layer thickness of 150 μm. It should be noted that dust settlement on surfaces in the outdoor condition over two weeks period creates a dust layer of about 150 μm. Hence, rolling droplet liquid infuses the dust layer thickness on the hydrophobic surface and cleans the surface via removing the dust particles. The current study sheds light onto the droplet fluid infusion into the environmentally formed dust layer on the hydrophobic surfaces and provides useful information on the droplet liquid infusion depth for the rolling/sliding droplets in relation to droplet-cleaning applications of dusty surfaces.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors wish to acknowledge the support of the Deanship of Research, King Fahd University of Petroleum and Minerals (KFUPM), through project #IN171001, and the funding support provided by the King Abdullah City for Atomic and Renewable Energy (K.A.CARE).Notes and references
- X. Du, F. Jiang, E. Liu, C. Wu and F. H. Ghorbel, J. Aerosol Sci., 2019, 130, 32–44 CrossRef CAS.
- T. Charinpanitkul and W. Tanthapanichakoon, Sep. Purif. Technol., 2011, 77, 382–388 CrossRef CAS.
- M. Gao, Y. Zhu, X. Yao, J. Shi and W. Shangguan, Powder Technol., 2019, 348, 13–23 CrossRef CAS.
- K. Zu, Y. Yao, M. Cai, F. Zhao and D. L. Cheng, J. Aerosol Sci., 2017, 114, 62–76 CrossRef CAS.
- S. Zarei, E. Jamshidi and A. Afshar Ebrahimi, Chem. Eng. Process., 2010, 49, 1193–1198 CrossRef CAS.
- B. S. Yilbas, H. Ali, M. Khaled, N. Al-Aqeeli, N. Abu-Dheir and K. Varanasi, Sci. Rep., 2015, 5, 15833 CrossRef CAS PubMed.
- B. S. Yilbas, H. Ghassan, H. Ali and N. Al-Aqeeli, Sci. Rep., 2017, 7, 45999 CrossRef CAS PubMed.
- B. S. Yilbas, G. Hassan, H. Al-Qahtani, S. Bahatab, A. Z. Sahin, A. Al-Sharafi and A. A. Abubakara, Dust removal from a hydrophobic surface by rolling fizzy water droplets, RSC Adv., 2020, 10, 19811–19821 RSC.
- G. Hassan, B. S. Yilbas, A. Al-Sharafi, H. Al-Qahtani and N. Al-Aqeeli, RSC Adv., 2019, 9, 3582–3596 RSC.
- A. Sayyah, D. R. Crowell, A. Raychowdhury, M. N. Horenstein and M. K. Mazumder, J. Electrost., 2017, 87, 173–179 CrossRef.
- C.-Y. Chen, J. K. W. Chesnutt, C.-H. Chien, B. Guo and C.-Y. Wu, Sol. Energy, 2019, 187, 341–435 CrossRef.
- H. Kawamoto, J. Electrost., 2019, 98, 11–16 CrossRef.
- J. Zhu and X. Dai, AIP Adv., 2019, 9, 065309 CrossRef.
- B. S. Yilbas, H. Ali, M. Khaled, N. Al-Aqeeli, N. Abu-Dheir and K. K. Varanasi, Appl. Surf. Sci., 2015, 351, 880–888 CrossRef CAS.
- B. S. Yilbas, H. Ali, N. Al-Aqeeli, N. Abu-Dheir and M. Khaled, Sol. Energy, 2016, 125, 282–293 CrossRef CAS.
- A. Al-Sharafi, B. S. Yilbas and H. Ali, Appl. Therm. Eng., 2018, 128, 92–106 CrossRef.
- F. Heib and M. Schmitt, Coatings, 2016, 6, 57–74 CrossRef.
- W. Y. D. Yong, Z. Zhang, G. Cristobal and W. S. Chin, Colloids Surf., A, 2014, 460, 151–157 CrossRef CAS.
- A. Sharafi, B. S. Yilbas, H. Ali and N. Al-Aqeeli, Sci. Rep., 2018, 8, 3061 CrossRef PubMed.
- C. Van Oss, R. Good and M. Chaudhury, J. Chromatogr. A, 1987, 391, 53–65 CrossRef CAS PubMed.
- M. Gindl, G. Sinn, W. Gindl, A. Reiterer and S. Tschegg, Colloids Surf., A, 2001, 181(1–3), 279–287 CrossRef CAS.
- B. JanAczuk, W. WoAjcik and A. Zdziennicka, Mater. Chem. Phys., 1999, 58, 166–171 CrossRef.
- E. W. Washburn, Phys. Rev., 1921, 17, 374 CrossRef CAS.
- L. Galet, S. Patry and J. A. Dodds, J. Colloid Interface Sci., 2010, 346(2), 470–475 CrossRef CAS PubMed.
- S. Anand, K. Rykaczewski, S. B. Subramanyam, D. Beysens and K. K. Varanasi, Soft Matter, 2015, 11, 69–80 RSC.
- J. D. Smith, R. Dhiman, S. Anand, E. Reza-Garduno, R. E. Cohen, G. H. McKinley and K. K. Varanasi, Soft Matter, 2013, 9, 1772–1780 RSC.
- C. Howell, A. Grinthal, S. Sunny, M. Aizenberg and J. Aizenberg, Adv. Mater., 2018, 30, 1802724 CrossRef PubMed.
- F. Brochard-Wyart, H. Hervet, C. Redon and F. Rondelez, J. Colloid Interface Sci., 1991, 142, 518–527 CrossRef CAS.
- V. Bergeron and D. Langevin, Phys. Rev. Lett., 1996, 76, 3152–3155 CrossRef CAS PubMed.
- A. Carlson, P. Kim, G. Amberg and H. A. Stone, EPL, 2013, 104, 34008 CrossRef.
- J. F. Lancaster, The use of adhesives for making structural joints, in Metallurgy of Welding, 6th edn, 1999, pp. 54–84 Search PubMed.
- S. Ebnesajjad and A. H. Landrock, Adhesive Technology Handbook, 2011, pp. 21–30 Search PubMed.
- Y. Tang, D. Deng, L. Lu, M. Pan and Q. Wang, Exp. Therm. Fluid Sci., 2010, 34, 190–196 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2020 |