DOI:
10.1039/D0RA05979J
(Paper)
RSC Adv., 2020,
10, 35039-35048
Are disulfide bonds resilient to double ionization? Insights from coincidence spectroscopy and ab initio calculations†
Received
8th July 2020
, Accepted 14th September 2020
First published on 22nd September 2020
Abstract
Disulfide bonds (–S–S–) are commonly present in biomolecules and have also been detected in astrophysical environments. In this work, the stability of the disulfide bond towards double ionization is investigated using quantum chemical calculations and photoelectron photoion photoion coincidence (PEPIPICO) spectroscopy measurements on the prototype dimethyl disulfide (CH3SSCH3, DMDS) molecule. The experiments were performed using high energy synchrotron radiation photons before (2465.0 eV) and at (2470.9 eV) the first sigma resonance around the S 1s edge. We applied the multivariate normal distribution analysis to identify the most plausible ionic fragmentation mechanisms from the doubly ionized DMDS. By mapping the minimum energy structures on the dicationic C2H6S22+ potential energy surface, we show that disulfide bonds are only present in high-lying isomers, in contrast to their analogous neutral systems. Our results also indicate that the number of fragment ions containing a disulfide bond for both photon energies is negligible. Taken together, our results reveal that the disulfide bond is severely damaged as a consequence of sulfur core–shell ionization processes, due to the lowering of its thermodynamic stability in multiply-charged systems.
1 Introduction
Sulfur is one of the most abundant chemical elements in the universe. As a consequence, distinct classes of sulfur-bearing molecules are detected in a variety of astrophysical environments – from protostellar outflows,1 protoplanetary disks,2 photodissociation regions3 and infrared dark clouds4 to interstellar ice analogs,5,6 planetary atmospheres7,8 and meteorites.9 The element is also considered crucial for the emergence and development of life on Earth. Organosulfur compounds and amino acids, for example, are easily formed in experiments simulating an H2S-containing prebiotic atmosphere, related to early planetary volcanism.10,11 It is also the basis of the chemo-autotrophic iron–sulfur world origin of life theory developed by Wächtershäuser,12,13 where the exoergic transformation of FeS into pyrite (FeS2) in the presence of H2S is proposed as a key energy-delivering source for early metabolism on primitive Earth.14
Similarly to carbon, sulfur makes strong bonds with itself. It is the element with the largest number of solid allotropes, exhibiting a pronounced tendency for catenation.15,16 A large number of stable Sn clusters have been described by computational17–20 and experimental21–24 tools, most of them containing either rings or chains. The octamer S8 crown ring with D4d symmetry is the most stable Sn cluster,19 and also the most common species in sulfur melts below the polymerization temperature.25,26 Additionally, iron–sulfur clusters27 represent another important class of sulfur-containing molecules, which are present in a variety of metalloproteins with distinct functionalities.28
The S2 unit, the smallest motif containing a sulfur–sulfur chemical bond, is known as the disulfide bond (–S–S–). The first interstellar molecule containing such a feature, S2H, was only recently observed by Fuente and co-workers29 in the Horsehead nebula, possibly resulting from the proton detachment of an HSSH+ intermediate.30 Moreover, the disulfide bond plays a very important role in the stability, solubility and folding of proteins, being present in around 10% of the proteins produced by mammalian cells.31–35 In some cases, disulfide bonds are also directly involved in the enzyme activity, mediating thiol-disulfide interchange reactions in subsequent oxidation/reduction cycles.36 The allosteric disulfides33 comprise a third type of disulfide bond, controlling protein function by triggering conformational changes in the three-dimensional biomolecular structure. Finally, disulfide bonds may also have played a role in non-enzymatic routes for the prebiotic formation of deoxynucleotides.37 Taken together, these results point out that understanding the stability of the disulfide bond towards external agents, such as radiation, is of crucial interest for biochemical processes, astrochemistry and early Earth studies.
In the past years, our group has been investigating the absorption and ionic fragmentation of sulfur-containing molecules after core electron excitations38 using synchrotron radiation,39,40 high-energy electrons41 and ions.42 The excitation and ionization of core electrons may lead to breakage of chemical bonds and dissociation of molecules. This is attributed to Auger-type processes, in which relaxation after the core-hole formation leads to the ejection of one (or even more) valence electron(s). As a consequence, a multiply-charged species is formed, usually unstable and possessing dissociative character.
Herein, we focus our attention on dimethyl disulfide (CH3SSCH3, DMDS), which can be considered as a prototype for systems containing covalent disulfide bonds. A brief review of valence-shell photoionization of DMDS can be found in Bernini et al.39 Borkar et al.43 discuss the fragmentation, both theoretically and experimentally, at low photon energies (9.5 eV to 14.4 eV) using photoelectron–photoion coincidence (PEPICO) measurements. Single dissociation pathways of DMDS at lower energies were also studied by Butler et al.44 and Chiang et al.45 In a previous work, we investigated the ion–ion coincidence spectrum of DMDS obtained at an incident electron energy of 800 eV (valence-shell study due to the energy transferred after the impact).46
In this work, we extend this analysis to high-energy photon impact (∼ 2400 eV). Photoelectron–photoion–photoion coincidence (PEPIPICO) experiments47,48 were employed in order to investigate the most relevant mechanisms of ionic fragmentation after double ionization starting from excitation around the S 1s edge. For analyzing the PEPIPICO data, we applied a multivariate normal distribution methodology adapted by our group to study coincidence techniques.46 Additionally, we apply quantum chemical calculations in order to elucidate the structure and relative stability of C2H6S22+ isomers, aiming at investigating the stability of the disulfide bond after production of a doubly ionized dimethyl disulfide. Density functional theory and coupled-cluster calculations were used for mapping the minimum energy geometries of the dicationic C2H6S22+ potential energy surface. A comparison between the most stable doubly-charged species with the neutral ones gives insights on the thermodynamic stability of the S–S linkage after double ionization. Our results are discussed in the context of understanding the radiation damage of sulfur-containing proteins and the survival of species bearing disulfide bonds in astrochemical and prebiotic scenarios.
2 Methods
Initially, we obtained Near Edge X-ray Absorption Fine Structure (NEXAFS) spectra and performed PEPICO measurements around the S 1s edge of DMDS using the Soft X-ray Spectroscopy beamline (SXS) in the Laboratório Nacional de Luz Síncrotron (LNLS), Campinas, Brazil. These results were published in early works of our group46,49 and will not be discussed herein. Details of the experimental setup are also described elsewhere.46,49
At high photon energy regimes, there is a large probability of double (or multiple) ionization, whose molecular states are usually highly dissociative. PEPIPICO experiments were employed to characterize the main ionic fragments from such events. The basic principle of the PEPIPICO technique consists in the detection, following photon absorption, of two positive ions resulting from a single Coulomb explosion process. The start measurement of ions arrival times is provided by the photoelectron.50 With such measurements it is possible to obtain the component of the ion linear momentum along the spectrometer axis. Depending on the momentum balance, for a limited number of linear and sequenced reactions,51 it is possible to relate the ion coincidence spectra with the molecular fragmentation mechanism,48,52 whose dynamics could involve two-, three- and four-body dissociations (for a description of such mechanisms see Simon et al.52).
In the present study we apply the multivariate normal distribution analysis to identify viable ionic fragmentation mechanisms. A complete description of the method can be found elsewhere.46 Briefly, the ion–ion coincidence spectrum is considered as a linear combination of Gaussian-type multivariate functions. The full width at half maximum (FWHM) for a Gaussian function is given by:53
| |
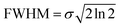 | (1) |
The Gaussian probability function only depends on two parameters: the standard deviation (σ) and the expected time-of-flight value (μ) of the mass peaks. According to the momentum balance, a given fragmentation reaction can be described by a system of linear equations. The parameters of this linear system are the FWHM of the mass peaks in the PEPIPICO spectra, which are proportional to the kinetic energy of the ion. Thus, the ratio between the standard deviations are calculated and can be compared with the island slopes (see e.g. Eland 1987 (ref. 48)).
The normal density function Gij of each set of i, j ion–ion coincidence peak is expressed as a function of μ and Σ:
| |
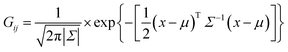 | (2) |
where
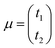
is the vector of the expected time values (
t1 and
t2 for the bivariate case) of the projection plot;
x = (
t1,
t2) describes the mutually independent time variables; and
Σ is the variance–covariance matrix between
t1 and
t2:
| |
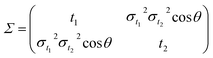 | (3) |
with
σt12 and
σt22 being the variances of the time vector variables and
θ the angle between them. Considering that the probability density function for each dissociation (Coulomb explosion) is given by
Gij, the total law of probability,
G, considering all dissociation processes, can be expressed as follows:
| |
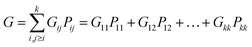 | (4) |
the
Pij given by the following relation:
| |
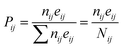 | (5) |
The above equation is the relation among all the events in the Coulomb ion–ion explosion spectra, given by Nij, whereas nij is the number of total counts of a particular ion–ion coincidence (or island) and eij the detector efficiency of each event. Detection efficiencies and high-order aborted coincidences were taken into account during the data analysis by using a protocol developed by the LNLS team for the TOF spectrometer used in our experiments.54
As for the quantum chemical calculations, from thirty different initial structures, geometry optimizations and frequency calculations of the C2H6S2 dication at the (U)M06-2X/cc-pVTZ level for singlet and triplet multiplicities were performed. The initial structures were built varying the presence of rings (open-chain or cyclic), the type of chain (straight or branched), the CS bonding arrangement (CCSS, CSCS, CSSC, SCCS), and the position of the hydrogen atoms and formal positive charges. Hessian calculations were only performed for structures with electronic energy in the range of 0–30 kcal mol−1 from the least energetic structure. Since this was not the case for any of the triplet species, only singlet geometries were characterized by the frequency analysis. Single-point calculations at the CCSD(T)/aug-cc-pVTZ were performed at the optimized structures. The isomers were organized by their relative enthalpy values at 298 K (H298) in the ascending order (1 denotes the most stable dication whereas 14 denotes the highest energy isomer described herein). We also studied the thermochemistry of selected dissociation pathways taking the minimum energy structure (13) – which most closely resembles the neutral DMDS molecule – as reference. Geometry optimizations and frequency analyses of all fragments were obtained following the same methodology as for C2H6S22+. All calculations were performed using the Gaussian 16 program package.55
3 Results and discussion
3.1 Structure and stability of C2H6S22+ isomers
Fig. 1 shows the formal Lewis structure of the C2H6S2 dications in the enthalpy ascending order. The relative enthalpy value of each isomer is shown in parenthesis, in kcal mol−1. Fig. 2, on the other hand, shows the optimized C2H6S22+ molecular structures obtained in this work classified by the type of carbon–sulfur skeleton.
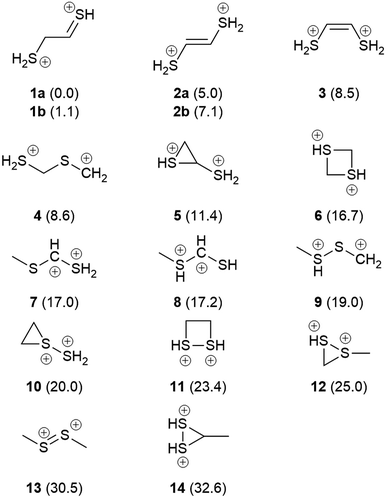 |
| | Fig. 1 The most stable C2H6S2 dication (1a) and its low-lying isomers. The H298 values (kcal mol−1) relative to 1a at the CCSD(T)/aug-cc-pVTZ//M06-2X/cc-pVTZ level of theory are shown in parenthesis. | |
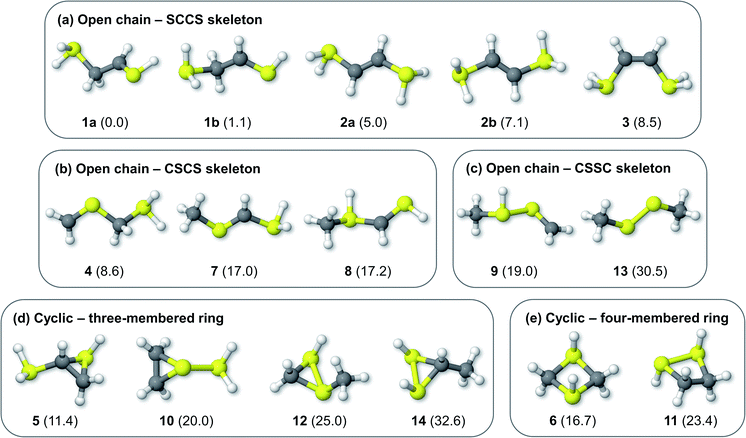 |
| | Fig. 2 Optimized C2H6S22+ structures bearing open chain (a) SCCS, (b) CSCS, and (c) CSSC skeleton bonding motifs, and cyclic (d) three- and (e) four-membered rings. The H298 values (kcal mol−1) relative to 1a at the CCSD(T)/aug-cc-pVTZ//M06-2X/cc-pVTZ level of theory are shown in parenthesis. | |
The most stable isomers of C2H6S22+ are open-chain structures, featuring either SCCS or CSCS skeletons and formal charges at the terminal atoms. 1a (0.0 kcal mol−1) and 1b (1.1 kcal mol−1) are two distinct rotamers of an out-of-plane SCCS motif related to the 2-mercaptoethanethial molecule, with protonation at both terminals. This energy difference is close to the expected average errors of CCSD(T)/aug-cc-pVTZ for isomerization energies of organic compounds.56 The low-lying isomers 2a and 2b, on the other hand, lay 5.0 and 7.1 kcal mol−1 above 1a. While for the former species the bond distances suggest the presence of a carbon–sulfur double bond in one of the terminals and a single sp3–sp2-like carbon–carbon central bond (1a: C–C = 1.495 Å; C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S = 1.624 Å), for 2a and 2b a central carbon–carbon double bond (2a: C
S = 1.624 Å), for 2a and 2b a central carbon–carbon double bond (2a: C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C = 1.320 Å) and terminal single C–S bonds (1.802 Å) are observed. This set of rotamers are related to the trans-ethylenedithiol molecule, protonated at both SH terminal groups. The next low-lying isomer (3, 8.5 kcal mol−1) is also analogous to the ethylenedithiol molecule, but in a cis-type configuration. Isomer 4 (8.6 kcal mol−1) is the most stable one in which a primary carbon is at the terminal of a straight chain. This structure is related to the mercaptomethylthiomethylium ion, protonated at the terminal SH. Other straight chain isomers containing one terminal primary carbon atom are 7 (17.0 kcal mol−1) and 8 (17.2 kcal mol−1).
C = 1.320 Å) and terminal single C–S bonds (1.802 Å) are observed. This set of rotamers are related to the trans-ethylenedithiol molecule, protonated at both SH terminal groups. The next low-lying isomer (3, 8.5 kcal mol−1) is also analogous to the ethylenedithiol molecule, but in a cis-type configuration. Isomer 4 (8.6 kcal mol−1) is the most stable one in which a primary carbon is at the terminal of a straight chain. This structure is related to the mercaptomethylthiomethylium ion, protonated at the terminal SH. Other straight chain isomers containing one terminal primary carbon atom are 7 (17.0 kcal mol−1) and 8 (17.2 kcal mol−1).
Isomer 5 is the most stable cyclic C2H6S2 dication, lying 11.4 kcal mol−1 above 1a. It presents a thiirane ring protonated at the S atom, and a SH+2 substituent bonded to a carbon atom. Other isomers containing a three-membered ring are 10 (20.0 kcal mol−1), 12 (25.0 kcal mol−1), and 14 (32.6 kcal mol−1). Four-membered rings, related to the regioisomers 1,3- (6) and 1,2-dithiethane (11) protonated at both S atoms were also found, with enthalpy values of 16.7 and 23.4 kcal mol−1 above the 1a structure, respectively.
Finally, only two isomers containing a disulfide bridge within a straight chain have been found. The most stable one (9, 19.0 kcal mol−1) is related to the methyldisulfanylmethylium ion, protonated at the CH3–S sulfur. Isomer 13, on the other hand, is the trans-dimethylsulfene dication, analogous to the neutral dimethyldisulfide (DMDS) molecule. It lies 13.3 kcal mol−1 higher in enthalpy than its regioisomer 9, and 30.5 kcal mol−1 above 1a. Contrary to the neutral DMDS molecule, the skeleton atoms of 13 are in the same plane, in a trans-form configuration. Moreover, the S–S bond distance at the M06-2X/cc-pVTZ level of theory is 1.909 Å, smaller than a typical single S–S bond (2.022 Å).57 These results suggest that the sulfur atoms of the trans-dimethylsulfene dication are connected by a double bond.
From these results, a qualitative analysis on the resiliency of the disulfide bridge to double ionization processes in an RSSR molecule can be made. The removal of two electrons from the S2 moiety dramatically changes the molecular structure towards the disulfide bridge, and the RSSR dihedral angle increases from ∼90° to ∼180°. A similar torsional change is observed in the CH3SSCH3+ cation, as early shown by Butler.58 Moreover, the S–S bond length becomes shorter, and a double bond between two atoms with formal positive charges is achieved. However, while the twisted CH3SSCH3 and CH3CH2SSH (ethyl hydrodisulfide) isomers are among the most stable neutral structures due to the presence of the strong disulfide bond, their respective doubly-charged planar structures with trans configuration are energetically higher than several other open chain and cyclic C2H6S2 isomers. Therefore, a molecular reorganization of the undissociated dication is expected in order to transform the doubly-charged RSSR moiety into a more stable minimum, in which the disulfide bond is broken. Ultimately, this suggests that a substantial loss of molecular integrity should occur in the parent dication after the double ionization of DMDS, evidencing the high vulnerability of the disulfide bond with respect to oxidation. Given the importance of disulfide bonds to the three-dimensional structure of biomolecules, it seems reasonable to expect that a double ionization process could promote the breakage of the S–S bond, which will open distinct dissociation channels but also might lead to a considerable structural change in the undissociated systems. This picture is in line with previous findings by Chiang45 and Butler,58 which revealed that isomerization pathways preceding bond cleavage are common processes related to dissociative photoionization of DMDS in the low photon energy domain.
3.2 Ion–ion coincidences and fragmentation mechanisms
After analyzing the minimum energy structures of the C2H6S2 dication, we focus our attention on the ion–ion coincidences and possible fragmentation mechanisms of DMDS that follow ionization from the K-shell and Auger electron release. As shown by Ankerhold et al.59 for the CS2 and OCS molecules, the ion–ion coincidence spectra contour plots do not depend on the incident energy around the sulfur K edge. We obtain similar results for the present molecule, as the i-variances of each m/z peak in the multivariate normal distribution analysis do not vary with the incidence energy. If the incident energy changes, differences among the PEPIPICO spectra would affect the probability of occurrence (intensity counts), but not their shape (neither the variance) within the S K-shell range. As a consequence, the same channels of ion dissociation are achieved, with variations only in their intensities.
Table 1 shows the parameters for the Coulomb explosion and the probability associated with the fragmentation of the DMDS molecule at 2465.0 eV and 2470.9 eV, following eqn (1)–(5). The mechanisms that involve the release of an H+ ion at the beginning of the reaction were not taken into account because its low mass would not affect the overall mass balance statistically. The probability function that we pursued is related to the C and S atoms, aiming at understanding the disulfide stability. Additionally, we also performed quantum chemical calculations on selected fragmentation pathways, which were classified by their distinct overall ion coincidences. By obtaining the exoergicity of each reaction channel after calculating their ΔH298 values and combining these results with the statistical parameters following the work of Varas et al. 2015,46 we could discriminate which are the most probable DMDS fragmentation mechanisms after the dication formation from core shell ionization. A similar approach was used by Ruhl et al.60 to investigate the charge separation following double ionization of organic methyl compounds. The ΔH298 values are shown in Table 2. The ion–ion coincidence mass spectra of the DMDS molecule are presented in Table 1 and Fig. 3.
Table 1 Parameters of the multivariate normal distribution function
| Coincidence |
μ |
Σ |
Gij |
Pij |
| 2465.0 eV |
2470.9 eV |
2465.0 eV |
2470.9 eV |
| [S]+/[CHn]+ |
 |
 |
62![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 234 234 |
12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 917 917![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 950 950 |
0.704 |
0.918 |
| [CHn]+/[HCS]+ |
 |
 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 717 717 |
417![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 210 210 |
0.121 |
0.030 |
| [CHn]+/[SS]+ |
 |
 |
5968 |
18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 558 558 |
0.067 |
0.001 |
| [CH3]+/[CHnSS]+ |
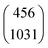 |
 |
744 |
2568 |
0.008 |
>0.001 |
| [S]+/[HCS]+ |
 |
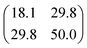 |
8703 |
713![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 342 342 |
0.098 |
0.051 |
Table 2 Heats of reactions for selected fragmentation pathways obtained at the CCSD(T)/aug-cc-pVTZ//(U)M06-2X/cc-pVTZ level
| Reaction pathway |
Coincidence |
ΔH298 (kcal mol−1) |
ΔH298 (eV) |
| C2H6S22+ (13) → C2H6S22+ (1a) |
— |
−30.5 |
−1.32 |
| C2H6S22+ (13) → S+ (4S) + C+ (2P) + CH4 + H2S |
[S]+/[C]+ |
183.1 |
7.94 |
| C2H6S22+ (13) → S+ (4S) + C+ (2P) + CH3SH + H2 |
[S]+/[C]+ |
200.7 |
8.70 |
| C2H6S22+ (13) → S+ (4S) + CH+ + CH4 + SH |
[S]+/[CH]+ |
179.2 |
7.77 |
| C2H6S22+ (13) → S+ (4S)+ CH+ + CH3S + H2 |
[S]+/[CH]+ |
192.3 |
8.34 |
| C2H6S22+ (13) → S+ (4S) + CH+ + CH3 + H2S |
[S]+/[CH]+ |
193.2 |
8.38 |
| C2H6S22+ (13) → S+ (4S) + CH+ + CH3SH + H (2S) |
[S]+/[CH]+ |
210.5 |
9.13 |
| C2H6S22+ (13) → S+ (4S) + CH2+ + CH3SH |
[S]+/[CH2]+ |
105.4 |
4.57 |
| C2H6S22+ (13) → S+ (4S) + CH2+ + H2CS + H2 |
[S]+/[CH2]+ |
139.9 |
6.07 |
| C2H6S22+ (13) → S+ (4S) + CH2+ + CH4 + S (3P) |
[S]+/[CH2]+ |
156.1 |
6.77 |
| C2H6S22+ (13) → S+ (4S) + CH2+ + CH3 + SH |
[S]+/[CH2]+ |
177.5 |
7.70 |
| C2H6S22+ (13) → S+ (4S) + CH2+ + CH2 + H2S |
[S]+/[CH2]+ |
197.1 |
8.55 |
| C2H6S22+ (13) → S+ (4S) + CH3+ + CH3S |
[S]+/[CH3]+ |
69.0 |
2.99 |
| C2H6S22+ (13) → S+ (4S) + CH3+ + H2CS + H (2S) |
[S]+/[CH3]+ |
121.6 |
5.27 |
| C2H6S22+ (13) → S+ (4S) + CH3+ + CH3 + S |
[S]+/[CH3]+ |
138.2 |
5.99 |
| C2H6S22+ (13) → S+ (4S) + CH3+ + CH2 + SH |
[S]+/[CH3]+ |
165.1 |
7.16 |
| C2H6S22+ (13) → S+ (4S) + CH3+ + CH + H2S |
[S]+/[CH3]+ |
175.1 |
7.59 |
| C2H6S22+ (13) → S+ (4S) + HCS+ + H (2S) + CH4 |
[S]+/[HCS]+ |
58.9 |
2.55 |
| C2H6S22+ (13) → S+ (4S) + HCS+ + H2 + CH3 |
[S]+/[HCS]+ |
59.2 |
2.57 |
| C2H6S22+ (13) → CH+2 + HCS+ + SH + H2 |
[CH2]+/[HCS]+ |
90.2 |
3.91 |
| C2H6S22+ (13) → CH2+ + HCS+ + H2S + H (2S) |
[CH2]+/[HCS]+ |
103.8 |
4.50 |
| C2H6S22+ (13) → CH3+ + HCS+ + H2S |
[CH3]+/[HCS]+ |
−17.5 |
−0.76 |
| C2H6S22+ (13) → CH3+ + HCS+ + H2 + S (3P) |
[CH3]+/[HCS]+ |
50.8 |
2.20 |
| C2H6S22+ (13) → CH3+ + HCS+ + H (2S) + SH |
[CH3]+/[HCS]+ |
71.9 |
3.12 |
| C2H6S22+ (13) → CH3+ + S2+ + CH3 |
[CH3]+/[S2]+ |
26.1 |
1.13 |
| C2H6S22+ (13) → CH3+ + S2+ + CH + H2 |
[CH3]+/[S2]+ |
131.4 |
5.70 |
| C2H6S22+ (13) → CH3+ + S2+ + CH2 + H |
[CH3]+/[S2]+ |
135.1 |
5.86 |
| C2H6S22+ (13) → CH3+ + CH3S2+ |
[CH3]+/[CH3S2]+ |
−37.9 |
−1.64 |
| C2H6S22+ (13) → 2SCH3+ |
[SCH3]+/[SCH3]+ |
0.8 |
0.03 |
| C2H6S22+ (13) → S+ (4S) + S+ (4S) + C2H6 |
[S]+/[S]+ |
58.4 |
2.53 |
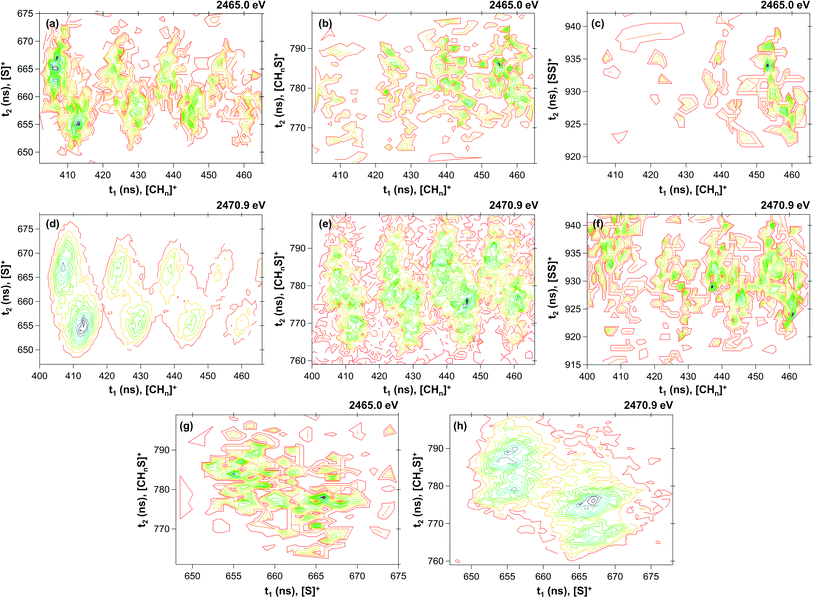 |
| | Fig. 3 Contour plot of coincidence islands at 2465.0 eV ((a) [CHn]+/[S]+; (b) [CHn]+/[CHnS]+; (c) [CHn]+/[SS]+; (g) [S]+/[CHnS]+) and at 2470.9 eV ((d) [CHn]+/[S]+; (e) [CHn]+/[CHnS]+; (f) [CHn]+/[SS]+; (h) [S]+/[CHnS]+). | |
By inspecting Table 1, we could distinguish four probability density functions contributions that taken together account for more than 99% of the Coulomb explosion processes before the sulfur S 1s sigma resonance. These functions are related to the [S]+/[CHn]+ (Pij = 0.704), [CHn]+/[HCS]+ (Pij = 0.121), [S]+/[HCS]+ (Pij = 0.098) and [CHn]+/[SS]+ (Pij = 0.067) coincidence channels. At the resonance (2470.9 eV), the probability of the doubly charged DMDS system to dissociate through the [S]+/[CHn]+ channel increases substantially (Pij = 0.917), while all other channels are depleted. The probability of the [S]+/[HCS]+ channel drops down to 5.1%, while [CHn]+/[HCS]+ channel is merely 3.0%. All other channels contribute to less than 1% for the Coulomb explosion processes at the first sigma resonance. A detailed description of each one of the probability density functions is shown in the next sections.
3.2.1 The [CHn]+/[S]+ ion coincidences. The [CHn]+/[S]+ probability density function is dominant in both energies, accounting for around 70% (Pij = 0.704) of the PEPIPICO spectra at 2465.0 eV and more than 90% (Pij = 0.918) at 2470.9 eV. The fragmentation enhancement observed as one moves from a photon energy (2465.0 eV, below resonance) at which only direct photoionization processes are allowed, to a photon energy (2470.9 eV) at which a resonant process is induced, demonstrates the importance of resonant Auger processes towards the fragmentation of the molecule.61 Furthermore, rearrangement processes observed herein are the result of extremely fast (femtosecond or attosecond regime) chemical reactions.62 The [CHn]+/[S]+ coincidences appear as well-defined and hydrogen-resolved islands, each one with two maximum regions, as shown in Fig. 3(a) and (d). The most intense contribution comes from the [C]+/[S]+ coincidence, followed by [CH]+/[S]+, [CH2]+/[S]+ and [CH3]+/[S]+. The relation of the variances for this coincidence group is 0.47 ± 0.1 (see Table 1; for details of the method, see Varas et al.46). A distinct number of mechanisms could explain the formation of such ions in coincidence. For [C]+/[S]+, the most plausible mechanism from the variance analysis is the four-body secondary decay after a deferred charge separation, as depicted in eqn (6a)–(6c).| | |
C2H6S22+ (13) → CH3CHS2+ + H2S
| (6a) |
| | |
CH3CHS2+ → [S]+ + CH3CH+
| (6b) |
In the first step, there is a release of neutral H2S, and the remaining doubly-charged [CH3CHS]2+ species is then dissociated into [S]+ and [CH3CH]+. The latter ion finally decomposes into CH4 and [C]+. This mechanism is also supported by our thermochemistry calculations, which revealed that the formation of neutral CH4 and H2S as a consequence of dissociation from DMDS2+ is the least endoergic pathway (7.94 eV) associated to the [C]+/[S]+ coincidence. Similar mechanisms could be proposed for the other CHn+ ions, as shown in eqn (7)–(9):
| | |
C2H6S22+ (13) → CH3CHS2+ + H2S
| (7a) |
| | |
CH3CHS2+ → [S]+ + CH3CH+
| (7b) |
| | |
CH3CH+ → CH3 + [CH]+
| (7c) |
| | |
C2H6S22+ (13) → CH3CH2S2+ + SH
| (8a) |
| | |
CH3CH2S2+ → [S]+ + CH3CH2+
| (8b) |
| | |
CH3CH2+ → CH3 + [CH2]+
| (8c) |
| | |
C2H6S22+ (13) → CH3CH2SH2+ + S
| (9a) |
| | |
CH3CH2SH2+ → [S]+ + CH3CH3+
| (9b) |
| | |
CH3CH3+ → CH3 + [CH3]+
| (9c) |
To the best of our knowledge, H2S or SH dissociation from a doubly-charged DMDS molecule has not been studied computationally up to date. Different fragmentation routes for neutral SH loss from the monocationic DMDS species, however, have been described by Borkar and coworkers.43 From their results, the least endergonic pathway involves initial methyl migration to form an SS(CH3)2+ intermediate, followed by C–H activation of one of the hydrogen atoms of the methyl group by the terminal S atom. The S–S bond of the HSS(CH2)(CH3)+ intermediate is then cleaved, leading to neutral SH and CH2SCH3+. As none of these intermediates were found for the dication, our results suggest that this particular route is not allowed for the doubly-charged DMDS molecule. On the other hand, both the global minimum 1a and most of the low-lying isomers possess terminal H2S groups, indicating that these are all suitable structures for further fragmentation through H2S loss.
The mechanisms depicted in eqn (6) and (7) are also in agreement with the previous work by Butler,58 which observed that the release of neutral S species competes with the direct H3CS–SCH3 bond cleavage. The enthalpies of these fragmentation pathways are 7.77 eV, 6.77 eV and 5.99 eV, respectively. For the [CH]+/[S]+ coincidence the depicted pathway is also the least endoergic one, as revealed by the thermochemistry calculations. However, this is not the case for the [CHn]+/[S]+ coincidences related to the [CH2]+ and [CH3]+ ions, where the most stable pathways are three-body dissociations that involve the formation of only one neutral species. The relation of the variances suggests that three-body secondary decay processes could also occur for the [CHn]+/[S]+, leading to the following set of equations:
| | |
C2H6S22+ (13) → [CH3]+ + CH3SS+
| (10a) |
| | |
CH3SS+ → [S]+ + CH3S
| (10b) |
| | |
C2H6S22+ (13) → [CH2]++CH3SSH+
| (11a) |
| | |
CH3SSH+ → [S]+ + CH3SH
| (11b) |
The homolytic charge dissociation of the doubly-charged DMDS molecule leading to [CH3]+ and [CH3SS]+ is the most stable fragmentation pathway as revealed by our calculations, being exoergic by −37.9 kcal mol−1 (−1.64 eV). This comes from the fact that the C–S bond is weaker than the S–S bond in DMDS,63 and also could explain the high yields of the [CH3SS]+ ion in mass spectra of valence ionization processes.64 Taken together, our results suggest that the main fragmentation mechanism leading to [C]+ and [CH]+ are processes related to four-body secondary decay after a deferred charge separation, while [CH2]+ and [CH3]+ are formed mainly through a three-body secondary decay.
3.2.2 The [CHn]+/[HCS]+ ion coincidence. The [CHn]+/[HCS]+ probability density function accounts for around 12% of the PEPIPICO spectra at 2465.0 eV and merely 3% at 2470.9 eV. As in the previous case, these coincidences are observed as well-defined and hydrogen-resolved islands, each one also presenting two maximum regions, as shown in Fig. 3(b) and (e). The most intense contribution comes from the [CH2]+/[S]+ and [CH3]+/[S]+ coincidences, and the relation of the variances for the group is 0.94 ± 0.1 (see Table 1). This value, in combination to the thermochemistry calculations, suggests the mechanisms depicted in eqn (12) and (13), which are also related to a four-body secondary decay after a deferred charge separation:| | |
C2H6S22+ (13) → CH3SCH22+ + SH
| (12a) |
| | |
CH3SCH22+ → CH3S+ + [CH2]+
| (12b) |
| | |
CH3S+ → [HCS]+ + H2
| (12c) |
| | |
C2H6S22+ (13) → CH3SCH32+ + S
| (13a) |
| | |
CH3SCH32+ → CH3S+ + [CH3]+
| (13b) |
| | |
CH3S+ → [HCS]+ + H2
| (13c) |
The enthalpy value for the first mechanism is 3.91 eV, while for the latter is 2.20 eV. A three-body dissociation into [CH3]+, [HCS]+ and H2S is exoergic by −17.5 kcal mol−1 (−0.76 eV), suggesting that it could also be a relevant dissociation pathway.
3.2.3 The [S]+/[HCS]+ ion coincidence. The [S]+/[HCS]+ probability density function is the third most important contribution for the PEPIPICO spectra at 2465.0 eV, accounting for around 10% of the overall coincidences. At the first sigma resonance, its contribution lowers to 5%, being then the second most relevant coincidence at 2470.9 eV. The coincidence islands at both energies are shown in Fig. 3(g) and (h). The relation of the variances is 0.60 ± 0.1, which leads to the following mechanism:| | |
C2H6S22+ (13) → CH3SSCH22+ + H
| (14a) |
| | |
CH3SSCH22+ → [HCS]+ + CH3SH+
| (14b) |
| | |
CH3SH+ → [S]+ + CH4
| (14c) |
Or, analogously:
| | |
C2H6S22+ (13) → CH3SSCH2+ + H2
| (15a) |
| | |
CH3SSCH2+ → [HCS]+ + CH3S+
| (15b) |
The enthalpy values for the dissociation pathways are 58.9 kcal mol−1 (2.55 eV) and 59.2 kcal mol−1 (2.57 eV), respectively. Therefore, the calculations suggest that both mechanisms seem plausible for accounting to the [S]+/[HCS]+ coincidence.
3.2.4 The [CHn]+/[SS]+ ion coincidence. The [CHn]+/[SS]+ probability density function has the smallest contribution among the ones described herein. It accounts for less than 1% in both energies. At 2465.0 eV (Fig. 3(c)), only contributions coming from the [CH3]+/[SS]+ are observed, while less pronounced coincidence islands from [CH2]+/[SS]+, [CH]+/[SS]+ and [C]+/[SS]+ are also obtained at 2470.9 eV (Fig. 3(f)). The following mechanism is proposed for the [CH3]+/[SS]+ coincidence:| | |
C2H6S22+ (13) → CH3SS2+ + CH3
| (16a) |
| | |
CH3SS2+ → [CH3]+ + [SS]+
| (16b) |
With the electron gun at 800 eV,46 the most probable dissociation channel involves the formation of the CH3SS+ ion, which contains a disulfide bond. The main differences between the low-energy fragmentation studies and those presented herein are related to the nature of the inelastic collisions (electrons losing energy and producing valence ionization instead of inner-shell processes) as well as the energy absorbed by the molecule after the ionization. As a consequence, it is expected that these processes will give rise to distinct molecular fragmentation channels, and also to distinct fragment branching ratios. For valence ionization, the most probable double coincidence channels for DMDS are related to the [CH3SS]+/[CH3]+ and [CH3]+/[SS]+, whereas for inner-shell ionization the yields of fragments containing the S2 moiety are negligible.
Chemical bonding is usually thought as being solely related to valence electrons, with core electrons playing only a minor role. Conversely, a vast body of literature has demonstrated that the excitation and ionization of core electrons may lead to an extensive breakage of chemical bonds, and consequently to molecular dissociation.65–67 However, the effectiveness of bond breaking after inner-shell excitation depends not only on the impact energies and the nature of the atom that is being ionized, but also on the chemical bond itself. By comparing the yields of the fragmentation products of DMDS after ionization using photon energies around the sulfur K-shell resonance obtained herein, it is possible to see that the S–S bond is significantly more affected than the C–S bond, as S2-bearing fragments are negligible. This trend is the opposite than what is expected from the corresponding bond strengths, as the S–S bond in DMDS is stronger than C–S.63 Additionally, our calculations reveal that the global minimum and the low-lying isomers of the doubly-charged parent ion with C2H6S2 stoichiometry do not present disulfide bonding, indicating that their stabilizing effect is severely weakened after double ionization. Taken together, these results evidence that the S–S bond is not stable enough to compensate for a double ionization event, and that any parent DMDS dication that may avoid fragmentation should undergo a severe isomerization process and loss of structural integrity during the time-of-flight.
4 Conclusions
In summary, we studied the resilience of the disulfide bond in the dimethyl disulfide (DMDS) molecule subjected to doubly ionization process combining coincidence spectroscopy and quantum chemical calculations. Initially, we mapped the minimum energy structures of the C2H6S22+ dication, and showed that, in contrast to their analogous neutral systems, disulfide bonds are only present in high-lying isomers. The global minimum (1) at the CCSD(T)/aug-cc-pVTZ//M06-2X/cc-pVTZ level of theory is the protonated dimercaptoethanylium system, which contains terminal H2S+ and HS+ groups. In opposition to neutral DMDS, the doubly-charged CH3SSCH32+ system (13) presents a planar backbone and a short S–S bond of merely 1.909 Å, and the resulting structure is 30.5 kcal mol−1 less stable than 1. By using a multivariate normal distribution protocol, we were able to discriminate the most plausible fragmentation mechanisms that contribute to the two-dimensional photoelectron–photoion–photoion coincidence (PEPIPICO) spectra of DMDS following photon impact with energies around the S 1s resonance. Furthermore, we showed that the branching ratios of DMDS fragmentation with high energy photons are dependent on whether the hole is created in resonance or not. Our results revealed that the disulfide bond is severely damaged as a consequence of sulfur core–shell ionization processes, and this is related to the low thermodynamic stability of such a bonding in multiply-charged systems. Further double fragmentation experiments are being conducted for the dimethyl sulfide (DMS) and methyl propyl disulfide (MPDS) molecules.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
The authors acknowledge CNPq, CAPES, Universidad de Costa Rica and FAPERJ for financial support. We are grateful to the Brazilian Synchrotron Light Facility (LNLS) for financial and technical assistance. We are particularly indebted to Tamires M. Gallo, Flavio Vicentin and Paulo T. Fonseca for their help during the course of the experiments. F. F. acknowledges CAPES and the Alexander von Humboldt Foundation for a Capes-Humboldt fellowship for postdoctoral researchers.
References
- J. Holdship, I. Jimenez-Serra, S. Viti, C. Codella, M. Benedettini, F. Fontani, M. Tafalla, R. Bachiller, C. Ceccarelli and L. Podio, Astrophys. J., 2019, 878, 64 CrossRef CAS
 .
. - R. Le Gal, K. I. Öberg, R. A. Loomis, J. Pegues and J. B. Bergner, Astrophys. J., 2019, 876, 72 CrossRef CAS
 .
. - J. R. Goicoechea, J. Pety, M. Gerin, D. Teyssier, E. Roueff, P. Hily-Blant and S. Baek, Astron. Astrophys., 2006, 456, 565–580 CrossRef CAS
 .
. - P. P. B. Beaklini, E. Mendoza, C. M. Canelo, I. Aleman, M. Merello, S. Kong, F. Navarete, E. Janot-Pacheco, Z. Abraham, J. R. D. Lépine, A. A. de Almeida and A. C. S. Friaça, Mon. Not. R. Astron. Soc., 2020, 491, 427–439 CrossRef
 .
. - S. Maity and R. I. Kaiser, Astrophys. J., 2013, 773, 184 CrossRef
 .
. - A. Ruf, A. Bouquet, P. Boduch, P. Schmitt-Kopplin, V. Vinogradoff, F. Duvernay, R. G. Urso, R. Brunetto, L. Le Sergeant d'Hendecourt, O. Mousis and G. Danger, Astrophys. J., 2019, 885, L40 CrossRef CAS
 .
. - X. Zhang, M. C. Liang, F. P. Mills, D. A. Belyaev and Y. L. Yung, Icarus, 2012, 217, 714–739 CrossRef CAS
 .
. - V. A. Krasnopolsky, Icarus, 2016, 274, 33–36 CrossRef CAS
 .
. - P. Schmitt-Kopplin, Z. Gabelica, R. D. Gougeon, A. Fekete, B. Kanawati, M. Harir, I. Gebefuegi, G. Eckel and N. Hertkorn, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 2763–2768 CrossRef CAS
 .
. - E. T. Parker, H. J. Cleaves, M. P. Callahan, J. P. Dworkin, D. P. Glavin, A. Lazcano and J. L. Bada, Origins Life Evol. Biospheres, 2011, 41, 569–574 CrossRef CAS
 .
. - E. T. Parker, H. J. Cleaves, J. P. Dworkin, D. P. Glavin, M. Callahan, A. Aubrey, A. Lazcano and J. L. Bada, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 5526–5531 CrossRef CAS
 .
. - G. Wächtershäuser, Prog. Biophys. Mol. Biol., 1992, 58, 85–201 CrossRef
 .
. - G. Wachtershauser, Science, 2000, 289, 1307–1308 CrossRef CAS
 .
. - J. Thiel, J. M. Byrne, A. Kappler, B. Schink and M. Pester, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 6897–6902 CrossRef CAS
 .
. - B. Meyer, Chem. Rev., 1976, 76, 367–388 CrossRef CAS
 .
. - R. Steudel and B. Eckert, Elem. Sulfur Sulfur-Rich Compd. I. Top. Curr. Chem., Springer, Berlin, Heidelberg, 230th edn, 2003, pp. 1–79 Search PubMed
 .
. - D. Hohl, R. O. Jones, R. Car and M. Parrinello, J. Chem. Phys., 1988, 89, 6823–6835 CrossRef CAS
 .
. - K. Raghavachari, C. M. Rohlfing and J. S. Binkley, J. Chem. Phys., 1990, 93, 5862–5874 CrossRef CAS
 .
. - R. O. Jones and P. Ballone, J. Chem. Phys., 2003, 118, 9257–9265 CrossRef CAS
 .
. - R. Gleiter, G. Haberhauer and F. Rominger, Eur. J. Inorg. Chem., 2019, 2019, 3846–3853 CrossRef CAS
 .
. - G. D. Brabson, Z. Mielke and L. Andrews, J. Phys. Chem., 1991, 95, 79–86 CrossRef CAS
 .
. - R. Steudel, O. Schumann, J. Buschmann and P. Luger, Angew. Chem., Int. Ed., 1998, 37, 2377–2378 CrossRef CAS
 .
. - R. Steudel, J. Steidel, J. Pickardt, F. Schuster and R. Reinhardt, Z. Naturforsch., B: Anorg. Chem., Org. Chem., 1980, 35, 1378–1383 Search PubMed
 .
. - S. Matsuno, M. Yamashina, Y. Sei, M. Akita, A. Kuzume, K. Yamamoto and M. Yoshizawa, Nat. Commun., 2017, 8, 749 CrossRef
 .
. - R. Steudel, R. Strauss and L. Koch, Angew. Chem., Int. Ed. Engl., 1985, 24, 59–60 CrossRef
 .
. - R. Ludwig, J. Behler, B. Klink and F. Weinhold, Angew. Chem., Int. Ed., 2002, 41, 3199–3202 CrossRef CAS
 .
. - H. Beinert, Science, 1997, 277, 653–659 CrossRef CAS
 .
. - J. Liu, S. Chakraborty, P. Hosseinzadeh, Y. Yu, S. Tian, I. Petrik, A. Bhagi and Y. Lu, Chem. Rev., 2014, 114, 4366–4469 CrossRef CAS
 .
. - A. Fuente, J. R. Goicoechea, J. Pety, R. Le Gal, R. Martín-Doménech, P. Gratier, V. Guzmán, E. Roueff, J. C. Loison, G. M. Muñoz Caro, V. Wakelam, M. Gerin, P. Riviere-Marichalar and T. Vidal, Astrophys. J., 2017, 851, L49 CrossRef
 .
. - R. C. Fortenberry and J. S. Francisco, Astrophys. J., 2018, 856, 30 CrossRef
 .
. - S. F. Betz, Protein Sci., 1993, 2, 1551–1558 CrossRef CAS
 .
. - W. J. Wedemeyer, E. Welker, M. Narayan and H. A. Scheraga, Biochemistry, 2000, 39, 4207–4216 CrossRef CAS
 .
. - B. Schmidt, L. Ho and P. J. Hogg, Biochemistry, 2006, 45, 7429–7433 CrossRef CAS
 .
. - M. Trivedi, J. Laurence and T. Siahaan, Curr. Protein Pept. Sci., 2009, 10, 614–625 CrossRef CAS
 .
. - N. Samainukul, A. K. Linn, M. B. Javadi, S. Sakdee, C. Angsuthanasombat and G. Katzenmeier, Biochem. Biophys. Res. Commun., 2019, 514, 365–371 CrossRef CAS
 .
. - H. Kadokura, F. Katzen and J. Beckwith, Annu. Rev. Biochem., 2003, 72, 111–135 CrossRef CAS
 .
. - I. Dragičević, D. Barić, B. Kovačević, B. T. Golding and D. M. Smith, Chem.–Eur. J., 2015, 21, 6132–6143 CrossRef
 .
. - G. G. B. de Souza and J. C. Gonzalez, Radiat. Bioanal., Springer, Cham, 8th edn, 2019, pp. 287–312 Search PubMed
 .
. - R. B. Bernini, L. B. G. da Silva, F. N. Rodrigues, L. H. Coutinho, A. B. Rocha and G. G. B. de Souza, J. Chem. Phys., 2012, 136, 144307 CrossRef CAS
 .
. - J. Gonzalez, G. Simões, R. Bernini, L. Coutinho, F. Stedile, C. Nunez, F. Vicentin and G. de Souza, J. Braz. Chem. Soc., 2019, 30, 1887–1896 CAS
 .
. - G. Simões, F. Rodrigues, R. Bernini, C. Castro and G. de Souza, J. Electron Spectrosc. Relat. Phenom., 2014, 193, 21–26 CrossRef
 .
. - R. C. M. Salles, L. H. Coutinho, A. G. da Veiga, M. M. Sant'Anna and G. G. B. de Souza, J. Chem. Phys., 2018, 148, 045107 CrossRef CAS
 .
. - S. Borkar, B. Sztáray and A. Bodi, J. Electron Spectrosc. Relat. Phenom., 2014, 196, 165–172 CrossRef CAS
 .
. - J. J. Butler, T. Baer and S. A. Evans, J. Am. Chem. Soc., 1983, 105, 3451–3455 CrossRef CAS
 .
. - S.-Y. Chiang, C.-I. Ma and D.-J. Shr, J. Chem. Phys., 1999, 110, 9056–9063 CrossRef CAS
 .
. - L. R. Varas, F. C. Pontes, A. C. F. Santos, L. H. Coutinho and G. G. B. de Souza, Rapid Commun. Mass Spectrom., 2015, 29, 1571–1576 CrossRef CAS
 .
. - L. Fransinski, K. Codling and P. Hatherly, Phys. Lett. A, 1989, 142, 499–503 CrossRef
 .
. - J. Eland, Mol. Phys., 1987, 61, 725–745 CrossRef CAS
 .
. - L. R. Varas, L. H. Coutinho, R. B. Bernini, A. M. Betancourt, C. E. V. de Moura, A. B. Rocha and G. G. B. de Souza, RSC Adv., 2017, 7, 36525–36532 RSC
 .
. - L. J. Frasinski, M. Stankiewicz, K. J. Randall, P. A. Hatherly and K. Codling, J. Phys. B: At. Mol. Phys., 1986, 19, L819–L824 CrossRef CAS
 .
. - M. Lavollée and V. Brems, J. Chem. Phys., 1999, 110, 918–926 CrossRef
 .
. - M. Simon, T. Lebrun, R. Martins, G. G. B. de Souza, I. Nenner, M. Lavollee and P. Morin, J. Phys. Chem., 1993, 97, 5228–5237 CrossRef CAS
 .
. - E. W. Weisstein, Gaussian function, 2002 Search PubMed
 .
. - F. Burmeister, L. Coutinho, R. Marinho, M. Homem, M. De Morais, A. Mocellin, O. Björneholm, S. Sorensen, P. d. T. Fonseca and A. Lindgren, et al., J. Electron Spectrosc. Relat. Phenom., 2010, 180, 6–13 CrossRef CAS
 .
. - M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Revision C.01, Gaussian Inc., Wallingford CT, 2016 Search PubMed
 .
. - S. Grimme, M. Steinmetz and M. Korth, J. Org. Chem., 2007, 72, 2118–2126 CrossRef CAS
 .
. - B. Beagley and K. T. McAloon, Trans. Faraday Soc., 1971, 67, 3216 RSC
 .
. - J. J. Butler, T. Baer and S. A. Evans Jr, J. Am. Chem. Soc., 1983, 105, 3451–3455 CrossRef CAS
 .
. - U. Ankerhold, B. Esser and F. von Busch, J. Phys. B: At., Mol. Opt. Phys., 1997, 30, 1207–1222 CrossRef CAS
 .
. - E. Ruhl, S. Price, S. Leach and J. Eland, J. Phys. B: At., Mol. Opt. Phys., 1990, 97, 175–201 CAS
 .
. - M. Piancastelli, J. Electron Spectrosc. Relat. Phenom., 2000, 107, 1–26 CrossRef CAS
 .
. - T. Marchenko, S. Carniato, L. Journel, R. Guillemin, E. Kawerk, M. Žitnik, M. Kavčič, K. Bučar, R. Bohinc and M. Petric, et al., Phys. Rev. X, 2015, 5, 031021 Search PubMed
 .
. - S. W. Benson, Chem. Rev., 1978, 78, 23–35 CrossRef CAS
 .
. - S. Stein, NIST/EPA/NIH Mass Spectral Library with Search Program, NIST Standard Reference Database 1A, 2005 Search PubMed
 .
. - I. Nenner and P. Morin, VUV and Soft X-ray Photoionization ed U. Becker and D. A. Shirley, 1996 Search PubMed
 .
. - R. Feifel and M. N. Piancastelli, J. Electron Spectrosc. Relat. Phenom., 2011, 183, 10–28 CrossRef CAS
 .
. - M. Quack and F. Merkt, Handbook of high-resolution spectroscopy, Wiley-Blackwell, 2011 Search PubMed
 .
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ra05979j |
|
| This journal is © The Royal Society of Chemistry 2020 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *a,
Felipe Fantuzzi
*a,
Felipe Fantuzzi bcd,
Lúcia Helena Coutinho
bcd,
Lúcia Helena Coutinho e,
Rafael B. Bernini
e,
Rafael B. Bernini f,
Marco Antonio Chaer Nascimento
f,
Marco Antonio Chaer Nascimento b and
G. G. B. de Souza*b
b and
G. G. B. de Souza*b
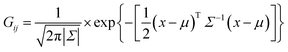
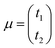 is the vector of the expected time values (t1 and t2 for the bivariate case) of the projection plot; x = (t1, t2) describes the mutually independent time variables; and Σ is the variance–covariance matrix between t1 and t2:
is the vector of the expected time values (t1 and t2 for the bivariate case) of the projection plot; x = (t1, t2) describes the mutually independent time variables; and Σ is the variance–covariance matrix between t1 and t2: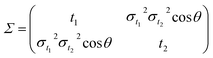
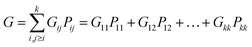
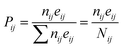

![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S = 1.624 Å), for 2a and 2b a central carbon–carbon double bond (2a: C
S = 1.624 Å), for 2a and 2b a central carbon–carbon double bond (2a: C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C = 1.320 Å) and terminal single C–S bonds (1.802 Å) are observed. This set of rotamers are related to the trans-ethylenedithiol molecule, protonated at both SH terminal groups. The next low-lying isomer (3, 8.5 kcal mol−1) is also analogous to the ethylenedithiol molecule, but in a cis-type configuration. Isomer 4 (8.6 kcal mol−1) is the most stable one in which a primary carbon is at the terminal of a straight chain. This structure is related to the mercaptomethylthiomethylium ion, protonated at the terminal SH. Other straight chain isomers containing one terminal primary carbon atom are 7 (17.0 kcal mol−1) and 8 (17.2 kcal mol−1).
C = 1.320 Å) and terminal single C–S bonds (1.802 Å) are observed. This set of rotamers are related to the trans-ethylenedithiol molecule, protonated at both SH terminal groups. The next low-lying isomer (3, 8.5 kcal mol−1) is also analogous to the ethylenedithiol molecule, but in a cis-type configuration. Isomer 4 (8.6 kcal mol−1) is the most stable one in which a primary carbon is at the terminal of a straight chain. This structure is related to the mercaptomethylthiomethylium ion, protonated at the terminal SH. Other straight chain isomers containing one terminal primary carbon atom are 7 (17.0 kcal mol−1) and 8 (17.2 kcal mol−1)..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.




![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 234
234