Pyrazinamide resistance of novel mutations in pncA and their dynamic behavior

Abstract

Pyrazinamide (PZA) is one of the essential anti-mycobacterium drugs, active against non-replicating Mycobacterium tuberculosis (MTB) isolates. PZA is converted into its active state, called pyrazinoic acid (POA), by action of pncA encoding pyrazinamidase (PZase). In the majority of PZA-resistance isolates, pncA harbored mutations in the coding region. In our recent report, we detected a number of novel variants in PZA-resistance (PZA^R) MTB isolates, whose resistance mechanisms were yet to be determined. Here we performed several analyses to unveil the PZA^R mechanism of R123P, T76P, G150A, and H71R mutants (MTs) through molecular dynamics (MD) simulations. In brief, culture positive MTB isolates were subjected to PZA susceptibility tests using the WHO recommended concentration of PZA (100 μg ml⁻¹). The PZA^R samples were screened for mutations in pncA along sensitive isolates through polymerase chain reactions and sequencing. A large number of variants (GeneBank accession no. MH461111), including R123P, T76P, G150A, and H71R, have been spotted in more than 70% of isolates. However, the mechanism of PZA^R for mutants (MTs) R123P, T76P, G150A, and H71R was unknown. For the MTs and native PZase structures (WT), thermodynamic properties were compared using molecular dynamics simulations for 100 ns. The MTs structural activity was compared to the WT. Folding effect and pocket volume variations have been detected when comparing between WT and MTs. Geometric matching further confirmed the effect of R123P, T76P, G150A, and H71R mutations on PZase dynamics, making them vulnerable for activating the pro-drug into POA. This study offers a better understanding for management of PZA^R TB. The results may be used as alternative diagnostic tools to infer PZA resistance at a structural dynamics level.

---

1. Introduction

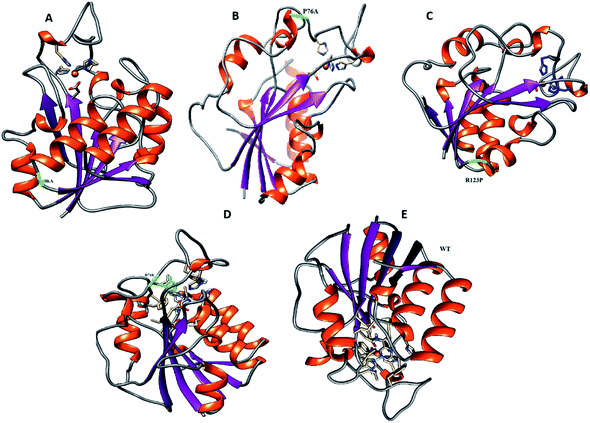
Pyrazinamide (PZA) is one of the essential anti-mycobacterium drugs effective against only isolates in latent Mycobacterium tuberculosis (MTB) isolates. The drug in combination has reduced tuberculosis (TB) therapy to 6 months.¹ According to the world health organization (WHO), about 1.7 billion of the world’s population are infected with latent TB. Among the anti-TB drugs, PZA activation into the active form pyrazinoic acid (POA) depends on pyrazinamidase (PZase) activity. The common mechanism behind PZA-resistance (PZA^R) is mutations in the pncA gene.^2–5 The PZase crystal structure consists of four α-helices surrounding six parallel β-sheets.⁶ At the metal binding site, Fe²⁺ establishes hydrogen interactions with His51, His57, His71 and Asp49 (ref. 7) while residues Asp8, Lys96, and Cys138 form catalytic triads, close to β-strand 3 and 1 and the N-terminal of α-helix 3.

Amino acid locations 132–142, 61–85, and 3–17 of PZase are frequently mutated.^8,9 However, mutations may occur elsewhere than these sites and may alter the protein folding.^1,37 Mutations may produce an allosteric effect.¹⁰ Investigations exploring the dynamics behavior of variants using molecular dynamics simulations (MD) are a time efficient approach.

Ligand–protein interactions are widely investigated using MD approaches. MD simulations are a widely used approach to provide insight into mechanisms of changes in drug targets that can result in resistance among infectious diseases. Although experimental procedures are considered as the gold standard, MD simulations have a certain useful aspect for unveiling the resistance mechanism at the level of molecules and atoms where molecular interactions are addressed and the level of effect is observed for better understanding of the mechanism.¹¹ The structural change aspects of proteins have a particular importance in depicting the residues level information that could be useful in many industrial level applications. MD simulation^12–14 is an ideal approach to explore the molecular level information.

In recent studies, the sequencing of the pncA genes from PZA^R isolates revealed novel mutations⁴ whose mechanism of resistance has not been investigated. Using MD simulations, MTs R123P, T76P and G150A in comparison with WT were observed to dig out the mechanism of PZA^R. In the present study, the dynamics behaviors of WT and MTs R123P, T76P, G150A, and H71R have been studied and compared to explore the changes in PZase, effecting the conversion of PZA into the active form.

2. Material and methods

2.1. Crystal structure preparation

The crystal structure was retrieved from the Protein Data Bank (PDB ID 3pl1).¹⁵ Mutations H71R, R123P, T76P, and G150A were induced using PyMOL.¹⁶

The chemical structure of PZA was retrieved from PubChem, an online database for chemical compounds using PubChem CID: 1046.¹⁷ The molecular operating system (MOE)¹⁸ has been applied for generating the docking complexes prior to MD simulation.

2.2. Molecular docking and binding pocket analysis

The PatchDock server was used to dock the WT and MTs in order to observe the protein–drug interactions. PatchDock measures the geometric features of the receptor and small molecules. Binding pockets of WT and MTs were measured through the online server Computed Atlas Surface Topography of proteins (CASTp). The CASTp server locates, delineates and computes concave areas on protein 3D structures. These regions comprise pockets sited on surfaces and spaces buried inside of proteins. The PatchDock performs molecular docking of protein–ligand complexes with a geometry-based docking algorithm. The server finds the docking transformations, yielding good molecular shape complementarity. The transformations induce wide interface areas. A widespread interface includes several local matched features of the docked biomolecules possessing complementary characteristics. The Connolly dot surface molecules are represented as convex, concave, and flat patches. A good geometric surface is calculated with high matching scores.

2.3. Validation via molecular dynamics (MD) simulation

The wild type and mutant types of the proteins were investigated using molecular dynamics (MD) simulation studies using the Amber package,³⁹ using Amber14ff. The TIP3P water model was used to solvate the systems while to neutralize the system Na⁺ ions were added.⁴⁰ The system was energy minimized by using the steepest descent algorithm. The minimized complexes were heated up to 300 K in 0.2 ns. Subsequently, each system was equilibrated by a two step procedure at constant 1 atm and 300 K. Restraining simulation of the position was employed to equilibrate the ions and solvent around the protein before the actual simulation. Constant number of atoms, volume, pressure, and temperature (NPT and NVT) ensembles were applied to the system for the MD simulation studies. The Particle Mesh Ewald (PME) algorithm was used to calculate the long-range electrostatics interactions. Short-range Coulomb and Van der Waals interactions were set for cutoff values. A cutoff distance of 10.0 Å was used. Periodic boundary conditions were applied in all the three dimensions. A total of 100 ns of MD simulation has been used for the protein–ligand complex to analyze the behavior of WT and MTs complexes. The resulting structural coordinates were saved at intervals of every 2 ps.

2.4. Principal Component Analysis (PCA) and internal motion of system

Principal Component Analysis (PCA) has been performed on the mass-weighted cartesian coordinates to obtain internal motion of the system. PCA clusters the motion of different trajectories and shows its distribution along the principal axis. A set of transformed variables z1, z2…, zp, known as principal components (PCs), are generated.^41,42 The first two components known as PC1 and PC2 give the trajectories on the initial two principal components of motion. The following equation was used to draw clusters of the trajectories and understand the distribution pattern.

ΔG(X) = −k_BT ln P(X)

where X indicates the response of the two principal components, k_B is the Boltzmann constant, and P(X) is the dispersion of the framework’s likelihood on the first two principal components.

2.5. Binding free energy calculation

The script MMPBSA.PY was used to calculate the free binding energy for all the protein–ligand complexes^38,43–46 considering 2500 snapshots from the MD trajectories using the following equation.

The free energy of each component was estimated using the following equation:

ΔG_bind = ΔG_complex − [ΔG_receptor + ΔG_ligand]

ΔG_bind: total binding free energy. The free energy of each component was estimated using the following equation:

G = G_bond + G_ele + G_vdW + G_pol + G_npol-TS

where G_bond, G_ele, and G_vdW denote bonded, electrostatic, and van der Waals interactions, respectively. G_pol and G_npol are polar and nonpolar solvated free energies. The G_pol and G_npol are calculated by the Generalized Born (GB) implicit solvent method with the solvent-accessible surface area SASA term.

2.6. Dynamic cross-correlation

A time subordinate movement of Cα atoms was obtained by using the dynamics cross-correlation maps (DCCM) approach.^27,47 Thus, to understand the correlated and anti-correlated motions of the Cα atoms of all the system’s residues, the correlation matrix was obtained. The following equation was used for DCCM calculations.

C_ij = 〈Δr_i × Δr_j〉/(〈Δr_i²〉〈Δr_j²〉)²

The matrix (C_ij) represents the time-correlated data of the protein between the i and j atoms. Cα atoms from the 5000 snapshots were chosen to construct the matrix at 0.002 ns intervals. In the plot, the positive values specify correlated motions, whereas negative values indicate anti-correlated motion during the simulation.

3. Results

3.1. Binding pocket and free energy calculation of WT and mutant PZase

The binding pocket contains residues Asp8, Lys96, and Cys138 and forms catalytic triads close to β-strand 3 and 1 and the N-terminal of α-helix 3. The binding pocket volume of WT has been considered as the most suitable for interactions with the drug. Any deviations in the pocket volume may result in weak or loss of binding with the drug. The CASTp server analyzed and computed the binding pocket of WT and MTs (Table 1). The server computed pocket volumes for MTs show variations compared to the server computed pocket volume of 525.641 Å for WT. The pocket volumes of MTs H71R and T76P have been highly affected. This deviation may impede the binding affinity. The total free energies of WT and MTs have also been detected to have significant variations. WT has been detected as the most stable based on total free energy, SASA and also van der Waals interactions.

Table 1 Binding pocket volume and thermodynamic WT and MTs PZase^a

Complex name	PatchDock score	Pocket volume (Å)	MMGBSA
			ΔvdW	ΔElec	ΔPs	ΔSASA	ΔGTotal
a ΔGTotal = total binding free energy; Elec = electrostatic energy; SASA = solvent accessible surface area; Ps = polar solvation; vdW = van der Waals; MMGBSA = molecular mechanics generalized Born solvent accessibility.
Wild	2386	525.641	−21.671	−18.992	26.685	−3.699	−19.839
H71R	2377	158.181	−19.431	−23.646	32.782	−2.801	−15.414
T76P	2382	333.695	−19.675	−22.019	33.119	−2.786	−16.342
R123P	2382	525.641	−18.334	−20.132	30.231	−1.098	−13.782
G150A	2420	481.240	−20.546	−19.898	27.928	−2.990	−17.134

---

3.2. PZase and PZA shape complementarity

Shape complementarity between drug (PZA) and target (PZase) has been computed, using PatchDock. WT exhibited a good molecular shape complementarity score as compared to MTs (Table 1). The variation in shape complementarity scores, where WT exhibited a higher matching than the MTs, shows the intensity of the effect on the geometry of the PZase structure during binding with small molecules (Table 1).

3.3. Flexibility and stability of WT and MTs

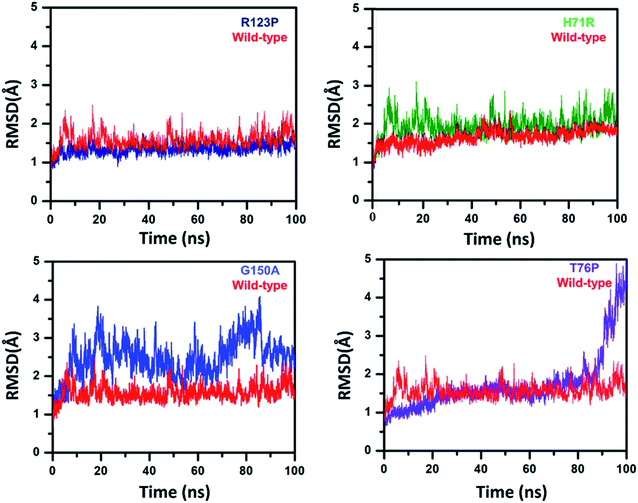
To analyze the conformational fluctuations due to mutations, the RMSD and RMSF for R123P, T76P, G150A, H71R and WT, were compared. WT exhibited an RMSD between 1 Å and 2 Å which remains fairly consistent over 100 ns (Fig. 2). The T76P seems highly unstable even with a 100 ns simulation period.

Fig. 1 Location of mutations has been highlighted in PZase before MD simulation. (A) G150A. (B) T76P. (C, D and E) R123P, H71R, and WT. These mutations are mainly present in the loop regions which are functionally considered important.

Fig. 2 RMSD of WT and MTs. WT and MTs attained a significant difference in RMSDs. WT is seen to be stable throughout the simulation while R123P, T76P, G150A, and H71R exhibited high RMSD and more deviation.

On the other hand, MTs attained a significant difference in their overall stability. MTs R123P, T76P, G150A, and H71R exhibited an RMSD between 1 Å and 4.5 Å (Fig. 2) and remain unstable at the end of the simulation period as compared to the WT.

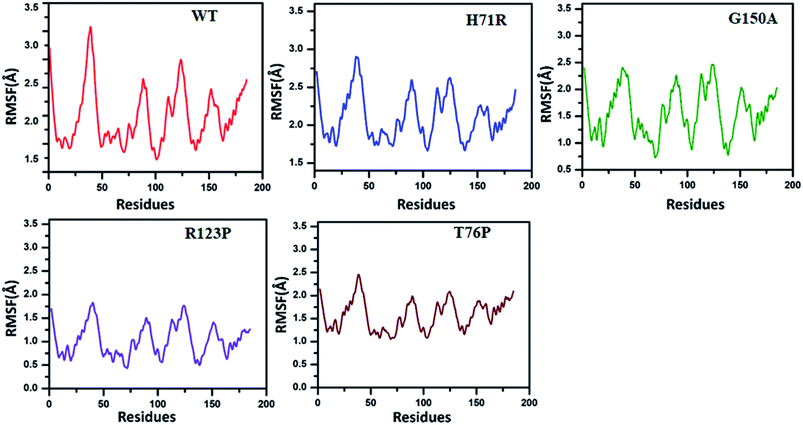
The RMSF exhibited by MTs is higher than for the WT (Fig. 3). The WT RMSF value ranges from 2.5–3.4 Å. The uppermost RMSF has been observed at residue locations 25–50. The main differences have been detected at the residual region 75–150 where the RMSD value could be observed in comparison with WT. Similarly the residues’ fluctuation could be seen at the terminal, which is more flexible in WT than MTs. However, the residues’ fluctuations in MTs beyond 50 seems a little different when compared with WT.

Fig. 3 RMSF comparison between WT and MTs. Higher RMSF has been observed in MTs (0.5–2.9 Å) at residues 25–150 than WT (2.5–3.4 Å). WT attained an RMSF between 1.4 Å and 3.3 Å. In comparison with WT, H71R exhibited an RMSF between 1.7 Å and 2.7 Å. G150A attained a fluctuation between 0.7 Å and 2.2 Å while R123P (between 0.5 Å and 1.7 Å) and T76P (between 1.2 Å and 2.2 Å) exhibited very low RMSF when compared with WT.

3.4. Radius of gyration

To determine the impact of the mutations on the compactness of the protein, R_g was calculated. As given in Fig. 4, the wild type and R123P mutant showed similar patterns of R_g, which is in uniformity with the results from the patch dock cavity volume prediction. The average R_g for the wild type was observed to be 16.2 Å. The R_g for the wild type remained uniform until 80 ns but a sudden increase and then decrease afterward was observed. In the case of H71R the average R_g was observed to be 15.4 Å, however a major drift at 60 ns was observed and the R_g increased up to 16.2 Å. For G150A, with a relatively higher R_g (∼16 Å), major R_g shifts were observed at different intervals. Furthermore, T76P also showed a relative increase in the R_g at different intervals such as 75 ns and 95 ns. These results imply that the mutants affected the compactness of the protein when compared to the wild type.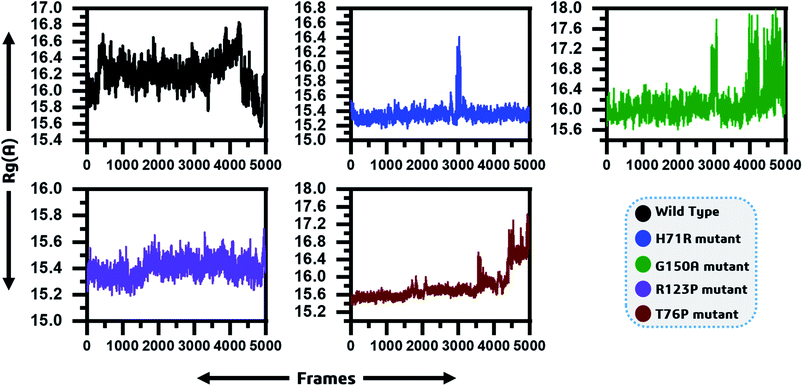

Fig. 4 Radius of gyration as function of time is given and represented by different colours. The x-axis shows the total frames while the y-axis shows R_g in Angstroms.

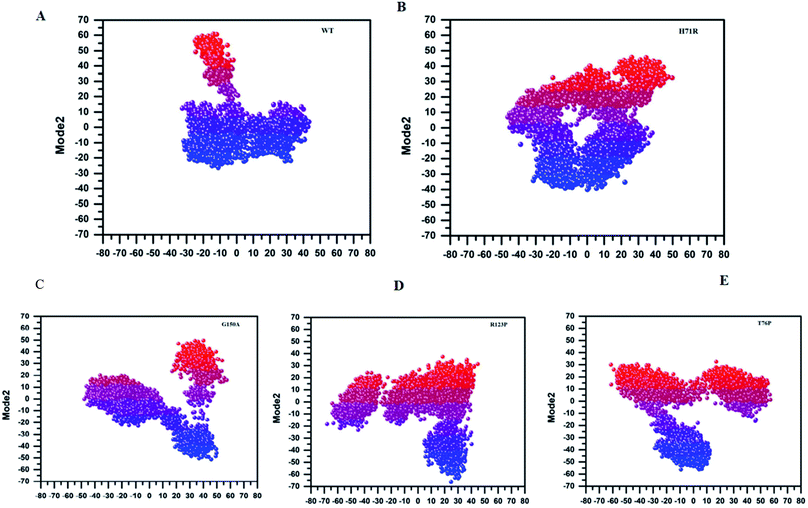
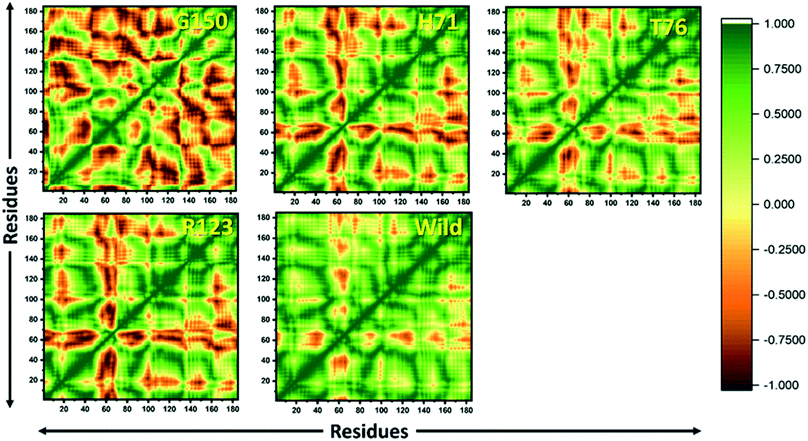
MTs displayed a more scattered category of motion than native PZase, scattered over a large area on PC1 between −60 and 50 and PC2, −40 and 40 (Fig. 5B). MTs G150A, R123P, and T76P showed a wider and more scattered type of motion on PC2 between −50 and 50, −70 and 30, −60 and 30, respectively (Fig. 5). Residues’ positive and negative correlated motions were observed through dynamic cross correlated motion (DCCM) as shown in Fig. 6. WT revealed a more interrelated motion as compared to MTs. Amino acids at all positions except at locations 50–60 exhibited a negative correlation in WT. The highest negative correlated motion was observed in G150A (residues 5–180). DCCM shows that this increase in negative correlated motion in residues might be involved in changing the dynamics of PZase, resulting in PZA resistance.

Fig. 5 Principal Component Analysis (PCA) of WT and MTs. PCA of MTs is scattered on PC1 and PC2, depicting a wider range of motions. The MTs are of a more significantly dispersed type as compared to WT.

Fig. 6 DCCM of WT and MTs. (a) G150A, (b) H71R, (c) T76P, (d) R123P, and (e) WT shows more correlated motions of residues. The green color depicts positive correlation while red color shows negative correlation. The color slopes show a gradual decline in the correlation.

4. Discussion

Among the first-line drugs, PZA has high potential against non-replicated MTB isolates. However, PZA^R is major obstacle towards the TB end program. Resistance to PZA is most commonly associated with pncA gene mutations, encoding PZase. The prodrug PZA is converted into the active form POA by the interaction of PZase. Recently we have detected some novel mutations (Accession MH461111-17)⁴ in the pncA of PZA^R isolates from the Northern areas, Khyber Pakhtunkhwa province of Pakistan. Although these mutations have been detected in pncA among phenotypically confirmed PZA^R isolates, however, the molecular mechanism of resistance of R123P, T76P, G150A, and H71R has not been explored. To unveil the molecular mechanism of PZA^R arising from these mutations, multiple analysis was performed, using MD simulation approaches. The MTs and WT PZase structure dynamics have been compared.

The function of the protein is highly dependent upon the structure.^19–22 Any change in the coding region of pncA may cause conformational drifts, affecting the protein functions. The effects of R123P, T76P, G150A, and H71R on PZase dynamics as well as on the thermodynamics properties have been detected (Table 1). The effect of these mutations has also been observed on the geometry of the protein structure that may affect the optimum binding with PZA, resulting in PZA^R.³⁷ The effects of these variants have also been found on the PZase stability (RMSD) and flexibility (RMSF) which is consistent with the previous reports.^21,23–26

For all structures, the RMSD and RMSF of R123P, T76P, G150A, and H71R seem more elevated in comparison with WT, indicating a level of instability for the PZase function (Fig. 2). These outcomes were similar to the previous reports.^4,27–31 Although these mutations were present in the loop regions (Fig. 1), far from the PZA binding pocket, their effects could be seen to not only modulate the allosteric site but may also change the dynamics of the enzyme, resulting in drug resistance.

The thermodynamic properties of biomolecules, and the other main forces including hydrogen bonds, van der Waals, and electrostatic forces, are mainly involved in the protein–ligand interactions.³² These forces were detected to vary between WT and MTs (Table 1). Computational investigation of the mutations’ effects on proteins and ligand interaction energies, highlights the link between variants and drug resistance in infectious diseases. The free energy has remained an important characteristic of proteins to infer stability and protein’s wild-type function. The changes in the protein’s stability due to mutations may cause diseases.³³ The current study also confirmed the destabilizing effect of the R123P, T76P, G150A, and H71R using PCA which shows larger randomized movement for MTs compared to the WT system. These findings are very similar to the most recent study,³⁴ suggesting low binding affinity for the PZA to be converted into the active form POA. The binding free energy also showed a difference in binding energy between WT and MTs, signifying the effect of mutations on PZase thermodynamics.

The binding pocket volume of WT has been considered optimum for a good binding affinity and any deviation in pocket volume may cause a weak or loss of interaction.³⁵ Changes in pocket volume have also been detected in MTs PZase, as compared to WT, when subjected to pocket volume calculation.

In conclusion, our study uses molecular dynamics simulation findings to assess the molecular mechanisms of PZA resistance affecting TB therapy. Mutations R123P, T76P, G150A, and H71R in PZase may have a significant role in PZA resistance for which the experimental results have already been provided.³⁶ These mutations have already been detected in PZA-resistance isolates while the mechanism of resistance was explored in the current study. These mutations might be involved in deviating PZase activity, flexibility, stability, and folding. The current analysis supports PZA-resistance arising from A46V and H71Y. Thus, this study might be helpful in understanding the mutation effect on overall PZase activity and may be used for better management of latent TB, toward a global end 2030.

Author contributions

Conceptualization: DQW, AA, MTK; data curation: AA, SC, AK, AS; formal analysis: AA, SA, SC, MTK, AK; funding acquisition: DQW; approval: DQW.

Funding

The current research study was supported by Dong-Qing Wei through grants from the National Natural Science Foundation of China (Contract no. 61832019, 61503244), the Ministry of Science and Technology of China (2016YFA0501703), Science and Technology Commission of Shanghai Municipality through grant 19430750600, the Joint Research Funds for Medical and Engineering and Scientific Research at Shanghai Jiao Tong University (YG2017ZD14), the Natural Science Foundation of Henan Province (162300410060). The computations were partially performed at the Pengcheng Lab, and the Center for High-Performance Computing, Shanghai Jiao Tong University.

Conflicts of interest

The authors declare that they have no competing interests.

Acknowledgements

The current study was technically supported by Director PTRL KP, Peshawar, Dr Sajid Ali, molecular biologist and Anwar Sheed Khan, microbiologist.

References

1. A. N. Yadon, K. Maharaj, J. H. Adamson, Y.-P. Lai, J. C. Sacchettini and T. R. Ioerger, et al. A comprehensive characterization of PncA polymorphisms that confer resistance to pyrazinamide, Nat. Commun., 2017, 8 DOI:10.1038/s41467-017-00721-2.
2. A. Akhmetova, U. Kozhamkulov, V. Bismilda, L. Chingissova, T. Abildaev and M. Dymova, et al., Mutations in the pncA and rpsA genes among 77 Mycobacterium tuberculosis isolates in Kazakhstan, Int. J. Tuberc. Lung Dis., 2015, 19, 179–184.
3. D. C. Alexander, J. H. Ma, J. L. Guthrie, J. Blair, P. Chedore and F. B. Jamieson, Reply to “Role of rpsA Gene Sequencing in Diagnosis of Pyrazinamide Resistance”, J. Clin. Microbiol., 2013, 51, 383,  DOI:10.1128/JCM.02760-12.
4. M. T. Khan, S. I. Malik, S. Ali, N. Masood, T. Nadeem and A. S. Khan, et al., Pyrazinamide resistance and mutations in pncA among isolates of Mycobacterium tuberculosis from Khyber Pakhtunkhwa, Pakistan, BMC Infect. Dis., 2019, 19, 116,  DOI:10.1186/s12879-019-3764-2.
5. S. Zhang, J. Chen, W. Shi, W. Liu, W. Zhang and Y. Zhang, Mutations in panD encoding aspartate decarboxylase are associated with pyrazinamide resistance in Mycobacterium tuberculosis, Emerging Microbes Infect., 2013, 2, e34.
6. S. Petrella, N. Gelus-Ziental, A. Maudry, C. Laurans, R. Boudjelloul and W. Sougakoff, Crystal structure of the pyrazinamidase of Mycobacterium tuberculosis: insights into natural and acquired resistance to pyrazinamide, PLoS One, 2011, 6, e15785.
7. C. Vats, J. Dhanjal, S. Goyal, A. Gupta, N. Bharadvaja and A. Grover, Mechanistic analysis elucidating the relationship between Lys96 mutation in Mycobacterium tuberculosis pyrazinamidase enzyme and pyrazinamide susceptibility, BMC Genomics, 2015, 16, S14.
8. N. Lemaitre, I. Callebaut, F. Frenois, V. Jarleir and W. Sougakof, Study of the structure–activity relationships for the pyrazinamidase (PncA) from Mycobacterium tuberculosis, Biochem. J., 2001, 353, 453–458.
9. P. Sheen, P. Ferrer, R. H. Gilman, J. López-Llano, P. Fuentes and E. Valencia, et al., Effect of pyrazinamidase activity on pyrazinamide resistance in Mycobacterium tuberculosis, Tuberculosis, 2009, 89, 109–113.
10. M. Kosloff and R. Kolodny, Sequence-similar, structure-dissimilar protein pairs in the PDB, Proteins, 2008, 71, 891–902,  DOI:10.1002/prot.21770.
11. H. Liu and X. Yao, Molecular basis of the interaction for an essential subunit PA-PB1 in influenza virus RNA polymerase: insights from molecular dynamics simulation and free energy calculation, Mol. Pharm., 2010, 7, 75–85,  DOI:10.1021/mp900131p.
12. W. Xue, D. Pan, Y. Yang, H. Liu and X. Yao, Molecular modeling study on the resistance mechanism of HCV NS3/4A serine protease mutants R155K, A156V and D168A to TMC435, Antiviral Res., 2012, 93, 126–137,  DOI:10.1016/j.antiviral.2011.11.007.
13. T. Hou, W. A. McLaughlin and W. Wang, Evaluating the potency of HIV-1 protease drugs to combat resistance, Proteins, 2008, 71, 1163–1174,  DOI:10.1002/prot.21808.
14. B. Ding, N. Li and W. Wang, Characterizing binding of small molecules. II. Evaluating the potency of small molecules to combat resistance based on docking structures, J. Chem. Inf. Model., 2013, 53, 1213–1222,  DOI:10.1021/ci400011c.
15. H. M. Berman, The Protein Data Bank: a historical perspective, Acta Crystallogr., Sect. A: Found. Crystallogr., 2008, 64, 88–95,  DOI:10.1107/S0108767307035623.
16. L. W. DeLano, The PyMOL Molecular Graphics System, DeLano Scientific, Palo Alto, CA, USA, 2002, http://www.pymol.org.
17. E. E. Bolton, Y. Wang, P. A. Thiessen and S. H. Bryant. Chapter 12 - PubChem: Integrated Platform of Small Molecules and Biological Activities, in Annu. Rep. Comput. Chem., ed. R. A. Wheeler and D. C. Spellmeyer, Elsevier; 2008, vol. 4, pp. 217–41.
18. S. Vilar, G. Cozza and S. Moro, Medicinal chemistry and the molecular operating environment (MOE): application of QSAR and molecular docking to drug discovery, Curr. Top. Med. Chem., 2008, 8, 1555–1572.
19. M. Bhattacharya, A. Hota, A. Kar, D. Sankar Chini, R. Chandra Malick and B. Chandra Patra, et al., In silico structural and functional modelling of Antifreeze protein (AFP) sequences of Ocean pout (Zoarces americanus, Bloch & Schneider 1801), J. Genet. Eng. Biotechnol., 2018, 16, 721–730.
20. S. Khan and M. Vihinen, Spectrum of disease-causing mutations in protein secondary structures, BMC Struct. Biol., 2007, 7, 56,  DOI:10.1186/1472-6807-7-56.
21. N. Nagasundaram, H. Zhu, J. Liu, V. Karthick, C. George Priya Doss and C. Chakraborty, et al., Analysing the Effect of Mutation on Protein Function and Discovering Potential Inhibitors of CDK4: Molecular Modelling and Dynamics Studies, PLoS One, 2015, 10 DOI:10.1371/journal.pone.0133969.
22. B. Reva, Y. Antipin and C. Sander, Predicting the functional impact of protein mutations: application to cancer genomics, Nucleic Acids Res., 2011, 39, e118,  DOI:10.1093/nar/gkr407.
23. S. K. Ali, P. Sneha, J. P. Christy, H. Zayed and C. G. P. Doss, Molecular dynamics-based analyses of the structural instability and secondary structure of the fibrinogen gamma chain protein with the D356V mutation, J. Biomol. Struct. Dyn., 2017, 35, 2714–2724,  DOI:10.1080/07391102.2016.1229634.
24. K. Amine, L. Miri, A. Naimi, R. Saile, A. El Kharrim and A. Mikou, et al., Molecular Dynamics Approach in the Comparison of Wild-Type and Mutant Paraoxonase-1 Apoenzyme Form, Bioinf. Biol. Insights, 2015, 9, 129–140,  DOI:10.4137/BBI.S25626.
25. C. G. P. Doss, B. Rajith, N. Garwasis, P. R. Mathew, A. S. Raju and K. Apoorva, et al., Screening of mutations affecting protein stability and dynamics of FGFR1—A simulation analysis, Appl. Transl. Genomics, 2012, 1, 37–43,  DOI:10.1016/j.atg.2012.06.002.
26. R. Kumar, R. Kumar, P. Tanwar, G. K. Rath, R. Kumar and S. Kumar, et al., Deciphering the impact of missense mutations on structure and dynamics of SMAD4 protein involved in pathogenesis of gall bladder cancer, J. Biomol. Struct. Dyn., 2020, 1–15,  DOI:10.1080/07391102.2020.1740789.
27. M. T. Khan, A. Khan, A. U. Rehman, Y. Wang, K. Akhtar and S. I. Malik, et al., Structural and free energy landscape of novel mutations in ribosomal protein S1 (rpsA) associated with pyrazinamide resistance, Sci. Rep., 2019, 9, 7482,  DOI:10.1038/s41598-019-44013-9.
28. M. Junaid, M. T. Khan, S. I. Malik and D.-Q. Wei, Insights into the mechanisms of pyrazinamide resistance of three pyrazinamidase mutants N11K, P69T and D126N, J. Chem. Inf. Model., 2018, 59, 498–508,  DOI:10.1021/acs.jcim.8b00525.
29. C. Vats, J. Dhanjal, S. Goyal, A. Gupta, N. Bharadvaja and A. Grover, Mechanistic analysis elucidating the relationship between Lys96 mutation in Mycobacterium tuberculosis pyrazinamidase enzyme and pyrazinamide susceptibility, BMC Genomics, 2015, 16(Suppl 2), S14,  DOI:10.1186/1471-2164-16-S2-S14.
30. M. He, W. Li, Q. Zheng and H. Zhang, A molecular dynamics investigation into the mechanisms of alectinib resistance of three ALK mutants, J. Cell. Biochem., 2018, 119, 5332–5342,  DOI:10.1002/jcb.26666.
31. M. Aggarwal, A. Singh, S. Grover, B. Pandey, A. Kumari and A. Grover, Role of pnc A gene mutations W68R and W68G in pyrazinamide resistance, J. Cell. Biochem., 2017, 13, 593.
32. N. Nagasundaram, H. Zhu, J. Liu, V. Karthik, C. George Priya Doss and C. Chakraborty, et al., Analysing the Effect of Mutation on Protein Function and Discovering Potential Inhibitors of CDK4: Molecular Modelling and Dynamics Studies, PLoS One, 2015, 10 DOI:10.1371/journal.pone.0133969.
33. Z. Zhang, L. Wang, Y. Gao, J. Zhang, M. Zhenirovskyy and E. Alexov, Predicting folding free energy changes upon single point mutations, Bioinformatics, 2012, 28, 664–671,  DOI:10.1093/bioinformatics/bts005.
34. R. Chitongo, A. E. Obasa, S. G. Mikasi, G. B. Jacobs and R. Cloete, Molecular dynamic simulations to investigate the structural impact of known drug resistance mutations on HIV-1C Integrase-Dolutegravir binding, PLoS One, 2020, 15, e0223464,  DOI:10.1371/journal.pone.0223464.
35. L. J. Y. M. Swier, L. Monjas, F. Reeßing, R. C. Oudshoorn, Aisyah and T. Primke, et al., Insight into the complete substrate-binding pocket of ThiT by chemical and genetic mutations, MedChemComm, 2017, 8, 1121–1130,  10.1039/C7MD00079K.
36. M. T. Khan, S. I. Malik, S. Ali, N. Masood, T. Nadeem and A. S. Khan, et al., Pyrazinamide resistance and mutations in pncA among isolates of Mycobacterium tuberculosis from Khyber Pakhtunkhwa, Pakistan, BMC Infect. Dis., 2019, 19, 116,  DOI:10.1186/s12879-019-3764-2.
37. Characterization of pncA mutations in pyrazinamide-resistant Mycobacterium tuberculosis isolates from Korea and analysis of the correlation between the mutations and pyrazinamidase activity.
38. B. R. Miller III, MMPBSA. py: an efficient program for end-state free energy calculations, J. Chem. Theory Comput., 2012.
39. H. J. Berendsen, D. van der Spoel and R. van Drunen, GROMACS: a message-passing parallel molecular dynamics implementation, Comput. Phys. Commun., 1995, 91(1–3), 43–56.
40. D. J. Mermelstein, C. Lin, G. Nelson, R. Kretsch, J. A. McCammon and R. C. Walker, Fast and flexible gpu accelerated binding free energy calculations within the amber molecular dynamics package, J. Comput. Chem., 2018, 39(19), 1354–1358.
41. S. Iida, T. Mashimo, T. Kurosawa, H. Hojo, H. Muta, Y. Goto, Y. Fukunishi, H. Nakamura and J. Higo, Variation of free – energy landscape of the p53 C – terminal domain induced by acetylation: Enhanced conformational sampling, J. Comput. Chem., 2016, 37(31), 2687–2700.
42. S. Tripathi, G. Srivastava and A. Sharma, Molecular dynamics simulation and free energy landscape methods in probing L215H, L217R and L225M βI-tubulin mutations causing paclitaxel resistance in cancer cells, Biochem. Biophys. Res. Commun., 2016, 476(4), 273–279.
43. T. Hou, J. Wang, Y. Li and W. Wang, Assessing the performance of the MM/PBSA and MM/GBSA methods. 1 The accuracy of binding free energy calculations based on molecular dynamics simulations, J. Chem. Inf. Model., 2011, 51(1), 69–82.
44. B. R. Miller III, T. D. McGee Jr, J. M. Swails, N. Homeyer, H. Gohlke and A. E. Roitberg, MMPBSA. py: an efficient program for end-state free energy calculations, J. Chem. Theory Comput., 2012, 8(9), 3314–3321.
45. H. Sun, Y. Li, M. Shen, S. Tian, L. Xu, P. Pan, Y. Guan and T. Hou, Assessing the performance of MM/PBSA and MM/GBSA methods. 5 Improved docking performance using high solute dielectric constant MM/GBSA and MM/PBSA rescoring, Phys. Chem. Chem. Phys., 2014, 16(40), 22035–22045.
46. X. Liu, D. Shi, S. Zhou, H. Liu, H. Liu and X. Yao, Molecular dynamics simulations and novel drug discovery, Expert Opin. Drug Discovery, 2018, 13(1), 23–37.
47. V. Gosu and S. Choi, Structural dynamic analysis of apo and ATP-bound IRAK4 kinase, Sci. Rep., 2014, 4(1), 1–3.

---

Footnote

† These authors contributed equally.

---