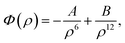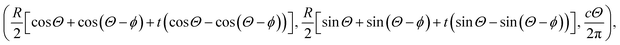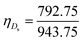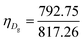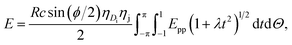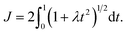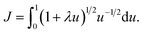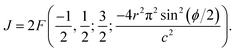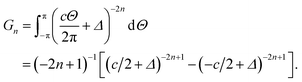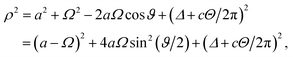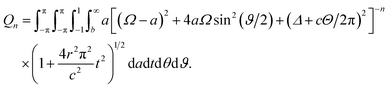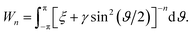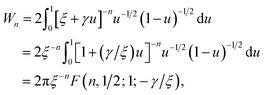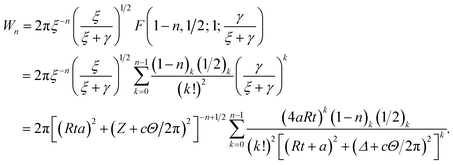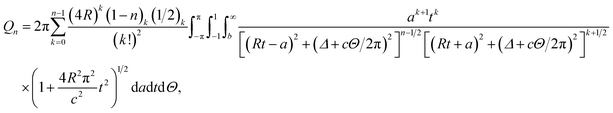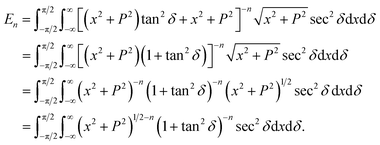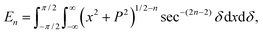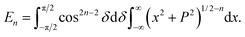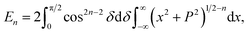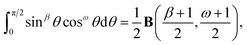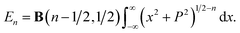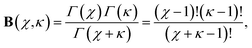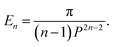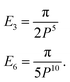Open Access Article
Open Access ArticleInstability and translocation through nanopores of DNA interacting with single-layer materials
Mansoor H. Alshehri *a,
Faisal Z. Duraihema and
Mohammed A. Aba Oudb
*a,
Faisal Z. Duraihema and
Mohammed A. Aba Oudb
aDepartment of Mathematics, College of Science, King Saud University, Riyadh-11451, Saudi Arabia. E-mail: mhalshehri@ksu.edu.sa
bDepartment of Mathematics and Statistics, Al Imam Mohammad Ibn Saud Islamic University (IMSIU), Riyadh, Kingdom of Saudi Arabia
First published on 7th October 2020
Abstract
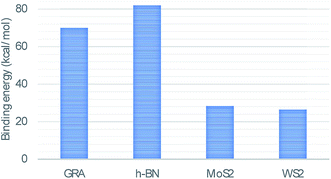
In this study, we use classical applied mathematical modelling to employ the 6–12 Lennard-Jones potential function along with the continuous approximation to investigate the interaction energies between a double-stranded deoxyribonucleic acid (dsDNA) molecule and two-dimensional nanomaterials, namely graphene (GRA), hexagonal boron nitride (h-BN), molybdenum disulphide (MoS2), and tungsten disulphide (WS2). Assuming that the dsDNA molecule has a perpendicular distance Δ above the nano-sheet surface, we calculated the molecular interaction energy and determined the relation between the location of the minimum energy and Δ. We also investigated the interaction of a dsDNA molecule with the surface of each nano-sheet in the presence of a circular hole simulating a nanopore. The radius of the nanopore that results in the minimum energy was determined. Our results show that the adsorption energies of the dsDNA molecule with GRA, h-BN, MoS2, and WS2 nano-sheets corresponding to the perpendicular distance Δ = 20 Å are approximately 70, 82, 28, and 26 (kcal mol−1), respectively, and we observed that the dsDNA molecule moves through nanopores of radii greater than 12.2 Å.
1 Introduction
Owing to their small size and geometric and mechanical properties, nanomaterials have been used in many fields, including commercial applications, biomedicine, gene and drug delivery, clean energy, gas storage, gas separation, and materials science.1–7 Graphene (GRA) and graphene-like materials such as hexagonal boron nitride (h-BN), molybdenum disulphide (MoS2), and tungsten disulphide (WS2) have a two-dimensional (2D) atomic layer structure, as shown in Fig. 1. Such 2D nanomaterials have elicited increasing interest owing to their unique structures and exceptional properties, and they have been significantly promoted for many potential applications, including those in the fields of electronics, photonics, biomedical, and bioassays.9–12 2D nanomaterials have essential features that remain unchanged upon adsorption of deoxyribonucleic acid (DNA); thus, they could prove to be promising for many applications such as self-assembly, therapeutic nucleic acids, and biosensors.14,35Although GRA, h-BN, MoS2, and WS2 sheets have structural similarities, the four nanomaterials have different properties that may lead them to behave differently from one another. For instance, the bond lengths in the B–N bonds in h-BN, C–C bonds in GRA, Mo–S bonds in MoS2 and W–S bonds in WS2 are 1.45 Å, 1.42 Å, 2.40 Å, and 2.43 Å, respectively.20 In addition, h-BN has a large ionicity, it is a good 2D insulator with a broad band gap, and its B–N bonds have an asymmetric distribution of charge. Moreover, h-BN has a smooth surface without any charge traps, and it also has a low dielectric constant and high temperature stability.13
Nanopores are very small gaps that biomolecules can use for transport through membranes, and could provide substantial opportunities to create the next generation of nanomaterial devices for various applications, especially in the nanomedical field and scanning microscopy.23,36,40 Numerous experiments and simulations have been conducted to explore the behaviour of DNA molecules interacting with nano-sheets, and the transfer mechanisms of DNA molecules through nanopores in such sheets.20,23–30,35,37–39
Although previous studies have investigated interactions between DNA molecules and nano-sheets or nanopores, more research on the DNA sequencing by 2D materials is necessary. Mathematical modelling plays an important role in providing a description of experimental results and can help forecast new phenomena and new results. Additionally, mathematical modelling can be leveraged to accurately predict optimal configurations and physical parameters. In this study, we examine the interactions between a double-stranded DNA (dsDNA) molecule and monolayers of GRA, h-BN, MoS2, and WS2, and we determine the behaviour of a dsDNA molecule as it moves through a nanopore. We employ classical applied mathematical modelling using the basic principles of mechanics to exploit the continuous approximation with the 6–12 Lennard-Jones potential, which has been successfully used in several studies to determine the energy behaviours of nanostructures (for example, ref. 15–19). By minimising the binding energies, we determine the distance of the dsDNA molecule above the surface of each nano-sheet when the helix axis of the dsDNA molecule is perpendicular to the surface of the sheet. Additionally, we minimise the molecular interaction energy of the dsDNA molecules, which are assumed to move through a nanopore, to determine the radius b of the pore. Moreover, a comparison of the adsorption and the translocation of a dsDNA molecule through the nanopores of the four nanomaterials is provided.
2 Modelling approach
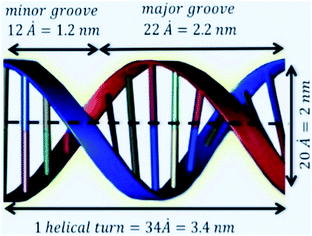
The unit cell of B-DNA as shown in Fig. 2 is used in this study. This form of DNA is predominantly found in cells.8 Double-stranded DNA is assumed to contain 10.5 base-pairs, which gives an average of 792.75 atoms, in one complete helix rotation. Due to the large number of atoms in the dsDNA molecules and 2D-nanomaterials, they might be modelled using the continuous approximation, which assumes that the atoms are uniformly distributed over their entire surfaces, to formulate analytical expressions for their interactions. Thus, the interaction energy may be obtained as a double integral over the surface of each molecule, and it is given as
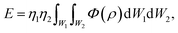 | (1) |
where A = 4εσ6 and B = 4εσ12 are the attractive and the repulsive constants, respectively. The attractive and the repulsive constants can be calculated using the empirical mixing laws ε12 = (ε1ε2)1/2, and σ12(σ1 + σ2)/2,31,32 where ε is the well depth and σ is the van der Waals diameter, which are taken from Rappi et al.21 The double integral and all the subsequent integrals in this study are surface integrals that are evaluated over the surfaces of molecules, and as shown in Kreyszig [ref. 33, pp. 443–452] and Kaplan [ref. 34, pp. 313–319], these surface integrals can be evaluated. Here, mathematical modelling is utilised to determine the molecular interaction energies between a dsDNA molecule and 2D-nanomaterials, by adopting the 6–12 Lennard-Jones potential and the continuous approximation. Surface integration is utilised to calculate the total interaction energy of the nano-sheets with the dsDNA molecule due to the continuous approximation, which assumes that intermolecular interactions can be approximated by average atomic surface densities. The Cartesian coordinate system (x, y, z) is used as a reference to model the two interacting molecules - the nano-sheets and the dsDNA molecule. Thus, the coordinates of a typical point on the surface of a nano-sheet can be given by (x, y, 0), and the parametric equation of a typical point on the surface of the dsDNA may be given by
where ϕ is the helical phase angle parameter which can be either the special case ϕ = π or the physical value that leads to the measured locations of the major and minor grooves ϕ = 12π/17. R = 10 Å is the radius of the dsDNA helix, c = 34 Å is the unit cell length of the dsDNA helix, and the parametric variables Θ and t are such that −π < Θ < π and −1 < t < 1. The adsorption onto nano-sheet surfaces and the translocation through nanopores by the dsDNA molecule are presented in the following sub-sections, respectively.
2.1 Interactions of dsDNA molecules and nano-sheets
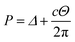 . Now, by using eqn (1) we calculate the binding energy from the integral expression
. Now, by using eqn (1) we calculate the binding energy from the integral expression
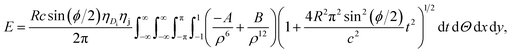 | (2) |
 , is the atomic surface density of the dsDNA molecule, and
, is the atomic surface density of the dsDNA molecule, and  is the atomic surface density of the sheets, and they can obtained from
is the atomic surface density of the sheets, and they can obtained from 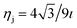 where ι is the bonds length of the elements of the nano-sheets, they have listed in Table 1, and ρ2 = x2 + y2 + P2 denotes the distance between two typical points on the sheet and the dsDNA molecule. First, we find the interaction of a plane with point P, which is given by
where ι is the bonds length of the elements of the nano-sheets, they have listed in Table 1, and ρ2 = x2 + y2 + P2 denotes the distance between two typical points on the sheet and the dsDNA molecule. First, we find the interaction of a plane with point P, which is given by
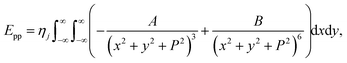 | (3) |
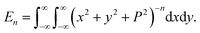 | (4) |
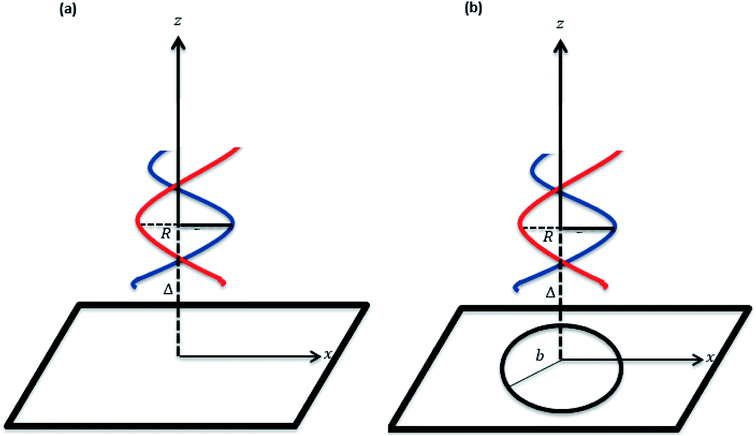 | ||
| Fig. 3 Schematic for a dsDNA molecule (a) being adsorbed by the nanosheet and (b) penetrating a nanopore in the sheet. | ||
The details for the analytical evaluation of En are presented in the Appendix. Therefore, the total interaction E may be written as
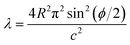 . To evaluate the integral E over t, we introduce the integral J as follows
. To evaluate the integral E over t, we introduce the integral J as followsMaking the substitution t2 = u yields the following
This integral can be written in a standard hypergeometric form as
Now we need only to evaluate the integral E over Θ, so we introduce the integral Gn
Thus, the total binding energy between the dsDNA molecule and h-BN sheet surface is given by
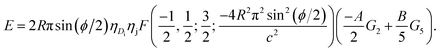 | (5) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ, a
ϑ, a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ, 0) and the hole in the surface of the plane is assumed to be located at z = 0 so that the coordinates of a typical point of the hole can be given by (b
ϑ, 0) and the hole in the surface of the plane is assumed to be located at z = 0 so that the coordinates of a typical point of the hole can be given by (b![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ, b
ϑ, b![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ, 0) where b < a < ∞. Without loss of generality, and owing to the symmetry of the sheet, the coordinates of a typical point on the dsDNA molecule may be given from (Ω, 0, Δ + cΘ/2π), where Ω2 = R2[cos2(ϕ/2) + t2
ϑ, 0) where b < a < ∞. Without loss of generality, and owing to the symmetry of the sheet, the coordinates of a typical point on the dsDNA molecule may be given from (Ω, 0, Δ + cΘ/2π), where Ω2 = R2[cos2(ϕ/2) + t2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin2(ϕ/2)]. The distance ρ from a typical point of the plane to a typical point of the dsDNA is given by
sin2(ϕ/2)]. The distance ρ from a typical point of the plane to a typical point of the dsDNA is given byand the total potential energy of the dsDNA of general helical angle ϕ = 12π/17 with respect to the nanopore is given by
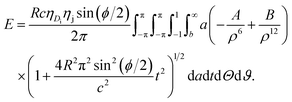 | (6) |
Now, we consider a case where only the interaction energy for the special helical phase angle ϕ = π is considered. In this case, the formal analytical details are slightly simpler than for the general case. Thus, in this case we have Ω = Rt and the total energy E is given by
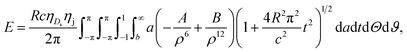 | (7) |
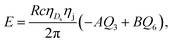 | (8) |
By letting ξ = (Ω − a)2 + (δ + cθ/2π)2 and γ = 4aΩ, we define the integral Wn as
Making the substitution sin2(ϑ/2) = u ⇒ dϑ = u−1/2(1 − u)−1/2du, the integral Wn becomes
Thus, the integral Qn has three remaining integrals over a, t and Θ as
3 Results and discussion
We evaluated eqn (5) and (8) using the algebraic computer package MAPLE together with the constant values in Tables 1 and 2. The relationship between the binding energy and the perpendicular distance Δ in the interactions between a dsDNA molecule and nano-sheets of the four 2D-nanomaterials GRA, h-BN, MoS2, and WS2, for two cases of the helical phase angle ϕ, are shown in Fig. 4 and Table 3. It is clear from Fig. 4 and Table 3 that the profile of the adsorption for the h-BN nano-sheet is significantly different from that for the other materials. The results show that the interaction between dsDNA and the h-BN nano-sheet is stronger than those between dsDNA and the other three materials, as the former reaches the lowest minimum energy. The comparison of binding energies of dsDNA with GRA, h-BN, MoS2, and WS2 is shown in Fig. 5, where the order of binding energy of the dsDNA molecule with the nano-sheets is h-BN > GRA > MoS2 > WS2. However, as shown in Table 3, the perpendicular distances Δ for these four materials to the centre of the dsDNA molecule is not significantly different, and the distance from the edge of the dsDNA to the surface of the sheets is given by (Δ − c/2 ≈ 3.2 Å), which is similar to that of GRA found in an earlier study.17 We note that the same equilibrium spacing profile is observed for the dsDNA molecule from the surface of each nano-sheet, and that only the magnitude of the energy differs. Our results for interaction energies with respect to the perpendicular distance of a dsDNA molecule from the nano-sheet surfaces are in good agreement with those given in the literature.20,22 We note from the difference of the results that the binding energies are sensitive to the Lennard-Jones constants (A and B), which are obtained using the values of the well depth ε and the van der Waals diameter σ. Herein, we comment that although the structures of the four nano-sheets are similar, h-BN possesses different properties. For example, h-BN sheets may be more uniform with regard to electronic properties than other nano-sheets, which might affect the interactions with DNA molecules. In addition, Fig. 6 graphically shows the relation between the total potential energy and the perpendicular distance Δ for different values of the pore radius b. We observe that the dsDNA does not penetrate a nanopore in any nano-sheet type when the radius of the pore b < 12.1 Å, and the interaction energy tends to infinity, which corresponds to a positive value of Δ. These results are in good agreement with the results of other works, as shown in Table 4. Furthermore, we observe that the dsDNA molecule moves closer to the sheet surface as the hole radius increases, due to the lower repulsive force from the sheet surface, and the fact that the dsDNA molecule has more space to move through the gap. Once the gap radius is larger than 12.2 Å, the dsDNA molecule can penetrate the surface of the sheet, which corresponds to negative values of Δ. These results are similar to those observed for GRA in an earlier study,18 and they are consistent with other experimental results, as shown in Table 4. Our results show that the optimal value of the gap radius b, where the minimum energy occurs, is b ≈ 12.8 Å.| Interaction | A (Å6 kcal mol−1) | B (Å12 kcal mol−1) |
|---|---|---|
| GRA–DNA | 791.8154556 | 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 424 424![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 599.652 599.652 |
| h-BN–DNA | 903.6818110 | 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 571 571![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 946.879 946.879 |
| MoS2–DNA | 772.7401758 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 772 772![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 395.061 395.061 |
| WS2–DNA | 739.1353066 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 690 690![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 802.161 802.161 |
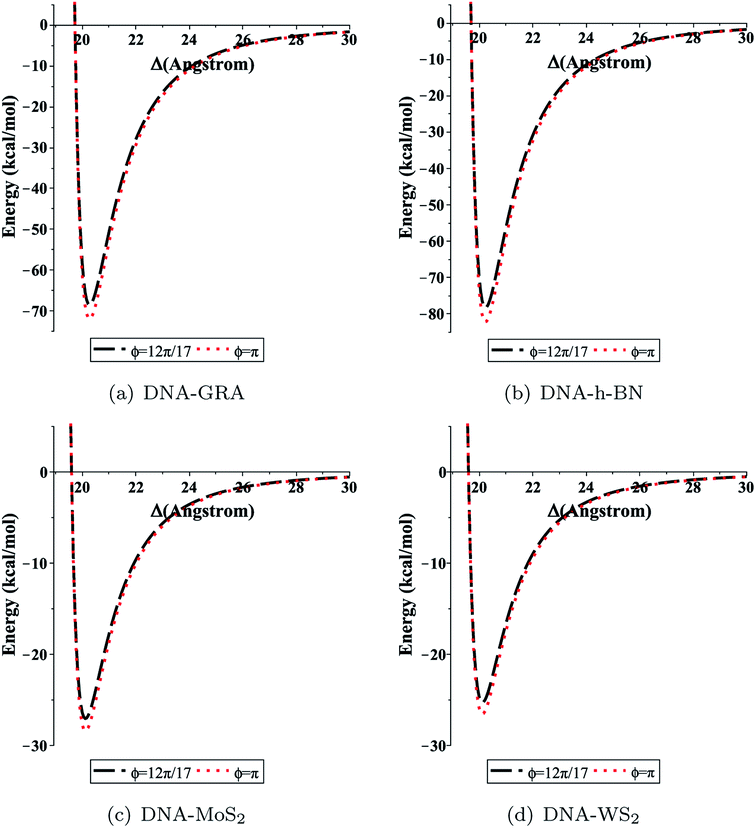 | ||
| Fig. 4 Total interaction energy between dsDNA and the nano-sheets with respect to the perpendicular distance Δ for both cases ϕ = 12π/17 (black dashed lines), and ϕ = π (red dotted lines). | ||
| Interaction | Interaction energy, E (kcal mol−1) | Perpendicular distance, Δ (Å) | ||
|---|---|---|---|---|
| ϕ = 12π/17 | ϕ = π | ϕ = 12π/17 | ϕ = π | |
| DNA–GRA | −68.56763 | −71.97261 | 20.27102 | 20.27102 |
| DNA–h-BN | −78.28127 | −82.16862 | 20.23138 | 20.23139 |
| DNA–MoS2 | −27.05815 | −28.40183 | 20.11723 | 20.11723 |
| DNA–WS2 | −25.29527 | −26.55140 | 20.11584 | 20.11584 |
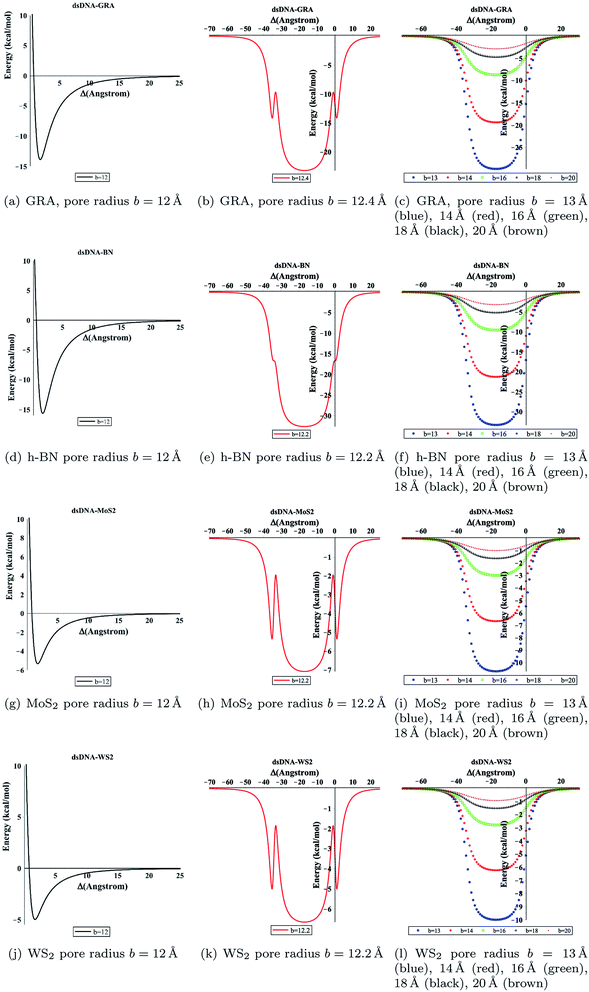 | ||
| Fig. 6 Total energy associated with the interaction of dsDNA with pores showing different values of radius b with respect to the perpendicular distance Δ. | ||
4 Conclusions
In summary, the molecular interaction energies of a dsDNA molecule with 2D monolayers of GRA, h-BN, MoS2, and WS2, as well as the translocation of the dsDNA through nanopores in these materials, have been investigated using applied mathematical modelling. Comparison of the calculated adsorption characteristics shows that the interaction between dsDNA and the h-BN nano-sheet is stronger than those between dsDNA and the other three materials, with the order of interactions being h-BN > GRA > MoS2 > WS2. By minimising the binding energies, we obtained the equilibrium distances of the dsDNA to the nano-sheets in the case where the helix axis of the dsDNA molecule is perpendicular to the sheet surface. We found that the minimum energies occur for distances Δ ≈ 20 Å. In addition, our results show that the dsDNA molecule passes through nanopores with radii b larger than 12.2 Å in these materials. Moreover, the fundamental results in this study can provide promising guidance for designing new 2D nanomaterial-based devices for several applications, particularly in biomedical and biological fields.Appendix: analytical evaluation of (4)
In this appendix, we present the analytical details for the evaluation of eqn (4). We begin by defining the integral En (n = 3, 6), as
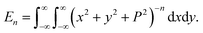 | (9a) |
We first integrate eqn (9a) with respect to y by making the substitution  , when y = −∞ ⇒ δ = −π/2, and when y = ∞ ⇒ δ = π/2, thus integral En becomes
, when y = −∞ ⇒ δ = −π/2, and when y = ∞ ⇒ δ = π/2, thus integral En becomes
Using sec2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ = 1 + tan2
δ = 1 + tan2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ, the integral En is given by
δ, the integral En is given by
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ = cos(2n−2)
δ = cos(2n−2)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ, En becomes
δ, En becomesSince cosine is an even symmetric function, we can rewrite the integral as
where B(χ, κ) is the beta function (in this case β = 0 and ω = 2n − 2 and note that B(χ, κ) = B(κ, χ)). Thus, the integral En becomes
We make a further substitution of x = P![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) tan
tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ and proceed as in the previous integral, so the integral becomes
ϕ and proceed as in the previous integral, so the integral becomes
| En = P2−2nB(n − 1/2, 1/2)B(n − 1, 1/2). |
We may evaluate the beta function given above using
Thus, for (n = 3, 6) we have
Conflicts of interest
The authors declare that there is no conflict of interest.Acknowledgements
The authors extend their appreciation to the Deanship of Scientific Research at King Saud University for funding this work through research group no. RG-1441-439.References
- J. M. Bonard, N. Weiss, H. Kind, T. Stckli, L. Forr, K. Kern and A. Hteain, Adv. Mater., 2001, 13, 184–188 CrossRef CAS.
- H. Gao and Y. Kong, Annu. Rev. Mater. Res., 2004, 34, 123–150 CrossRef CAS.
- D. Cui, Biomolecules functionalized carbon nanotubes and their applications, in Medicinal Chemistry and Pharmacological Potential of Fullerenes and Carbon Nanotubes, Carbon Materials: Chemistry and Physics, Springer Netherlands, 2008, vol. 1, pp. 181–221 Search PubMed.
- X. Xu, R. Li, M. Ma, X. Wang, Y. Wang and H. Zou, Soft Matter, 2012, 8, 2915–2923 RSC.
- K. Kamiya and S. Okada, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 155444 CrossRef.
- Y. Benenson, T. Paz-Elizur, R. Adar, E. Keinan, Z. Livneh and E. Shapiro, Nature, 2001, 414, 430–434 CrossRef CAS.
- C. M. Niemeyer, Appl. Phys. A: Mater. Sci. Process., 1999, 68, 119–124 CrossRef CAS.
- B. Alberts, A. Johnson, J. Lewis, M. Raff, K. Roberts, and P. Walter, Molecular Biology of the Cell, Garland Science, New York, 2008 Search PubMed.
- X. Chen, L. Zhang, C. Park, C. C. Fay, X. Wang and C. Ke, Appl. Phys. Lett., 2015, 107, 253105 CrossRef.
- H. Liu and C. H. Turner, Phys. Chem. Chem. Phys., 2014, 16, 22853–22860 RSC.
- X. Li, X. Wu, X. C. Zeng and J. Yang, ACS Nano, 2012, 6, 4104–4112 CrossRef CAS.
- Q. Weng, W. Xuebin, W. Xi, B. Yoshio and G. Dmitr, Chem. Soc. Rev., 2016, 45, 3989 RSC.
- A. Rubio, J. L. Corkill and M. L. Cohen, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 5081–5084 CrossRef CAS.
- C. Lu, Y. Liu, Y. Ying and J. Liu, Langmuir, 2017, 33, 630–637 CrossRef CAS.
- N. Thamwattana, D. Baowan and B. J. Cox, RSC Adv., 2013, 3(45), 23482 RSC.
- D. Baowan, B. J. Cox and J. M. Hill, RSC Adv., 2015, 5, 5508 RSC.
- M. H. Alshehri, B. J. Cox and J. M. Hill, Eur. Phys. J. D, 2013, 67, 226 CrossRef.
- M. H. Alshehri, B. J. Cox and J. M. Hill, J. Theor. Biol., 2015, 387, 68–70 CrossRef CAS.
- M. H. Alshehri, J. Comput. Theor. Nanosci., 2018, 15, 311–316 CrossRef CAS.
- H. Vovushaab and B. Sanyal, RSC Adv., 2015, 5, 67427 RSC.
- A. K. Rappi, C. J. Casewit, K. S. Colwell, W. A. Goddard III, W. M. Skid and J. Am, J. Am. Chem. Soc., 1992, 114(25), 10024–10035 CrossRef.
- M. Kabelac, O. Kroutil, M. Predota, F. Lankas and M. Sip, Phys. Chem. Chem. Phys., 2012, 14, 4217 RSC.
- C. Sathe, X. Zou, J.-P. Leburton and K. Schulten, ACS Nano, 2011, 5, 8842–8851 CrossRef CAS.
- G. F. Schneider, S. W. Kowalczyk, V. E. Calado, G. Pandraud, H. W. Zandbergen, L. M. Vandersypen and C. Dekker, Nano Lett., 2010, 10, 3163–3167 CrossRef CAS.
- S. Garaj, W. Hubbard, A. Reina, J. Kong, D. Branton and J. A. Golovchenko, Nature, 2010, 467, 190–193 CrossRef CAS.
- Z. Gu, Y. Zhang, B. Luanb and R. Zhou, Soft Matter, 2016, 12, 817 RSC.
- Y. Zhang, Y. Zhou, Z. Li, H. Chen, L. Zhang and J. Fan, Nanoscale, 2020, 12, 10026–10034 RSC.
- A. B. Farimani, K. Min and N. R. Aluru, ACS Nano, 2014, 8, 7914–7922 CrossRef CAS.
- J. Feng, K. Liu, R. D. Bulushev, S. Khlybov, D. Dumcenco, A. Kis, and A. Radenovic, 2015, arXiv Prepr. arXiv 1505, 01608.
- G. Danda, P. M. Das, Y. C. Chou, J. T. Mlack, W. M. Parkin, C. H. Naylor, K. Fujisawa, T. Zhang, L. B. Fulton, M. Terrones, A. T. C. Johnson and M. Drndic, ACS Nano, 2017, 11, 1937–1945 CrossRef CAS.
- L. A. Girifalco, M. Hodak and R. S. Lee, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, 104–110 CrossRef.
- J. O. Hirschfelder, C. F. Curtiss, and R. B. Bird, Molecular Theory of Gases and Liquids, Wiley, New York, 1954 Search PubMed.
- E. Kreyszig, Advanced Engineering Mathematics, John Wiley and Sons, 10th edn, 2011 Search PubMed.
- W. Kaplan, Advanced Calculus, Addison-Wesley, 3rd edn, 1984 Search PubMed.
- Q. Lin, X. Zou, G. Zhou, R. Liu, J. Wu, J. Li and W. Duan, Phys. Chem. Chem. Phys., 2011, 13, 12225–12230 RSC.
- G. Ciofani, G. G. Genchi, I. Liakos, A. Athanassiou, D. Dinucci, F. Chiellini and V. Mattoli, J. Colloid Interface Sci., 2012, 374, 308 CrossRef CAS.
- L. Zhang and X. Wang, Nanomaterials, 2016, 6, 111 CrossRef.
- J. Lee, Y. Choi, H. Kim, R. H. Scheicher and J. Cho, J. Phys. Chem. C, 2013, 117, 13435–13441 CrossRef CAS.
- S. Mukhopadhyay, S. Gowtham, R. H. Scheicher, R. Pandey and S. P. Karna, Nanotechnology, 2010, 21, 165703 CrossRef.
- S. Liu, B. Lu, Q. Zhao, J. Li, T. Gao, Y. Chen, Y. Zhang, Z. Liu, Z. Fan, F. Yang, L. You and D. Yu, Adv. Mater., 2013, 25, 4549–4554 CrossRef CAS.
- I. S. Gradshteyn and I. M. Ryzhik, Table of Integrals, Series, and Products, Academic Press, New York, 7th edn, 2007 Search PubMed.
| This journal is © The Royal Society of Chemistry 2020 |