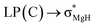On single-electron magnesium bonding formation and the effect of methyl substitution

Abstract

The complexes formed between MgX₂ (X = F, H) molecules and alkyl radicals Y [Y = CH₃, CH₂CH₃, CH(CH₃)₂, and C(CH₃)₃] have been characterized by using quantum chemical methods. The binding distance in all cases is less than the sum of vdW radii of Mg and C, indicating the formation of a non-covalent interaction, namely single-electron magnesium bond. Energy decomposition analysis reveals that electrostatic and polarization contributions are the major components responsible for the stability of the studied complexes. According to interaction energy, atoms in molecules, and independent gradient model analyses, methyl substitution on electron donor Y imposes a positive effect on its complexation with MgX₂. When compared with other nonbonded interactions, the single-electron magnesium bond is found to have strength comparable to those of the single-electron beryllium bond and π-magnesium bond.

---

1. Introduction

Weak interactions, different from traditional chemical bonds, are much weaker and have longer interaction distance than corresponding covalent bonds. Nevertheless, they are no less important and play crucial roles in chemical and biochemical research^1–5 including molecular recognition,^6,7 molecular medicine,⁸ functional materials design,⁹ catalysis,¹⁰ etc. Besides, weak interactions such as van der Waals forces, hydrogen bonding, π–π stacking effect, etc., are of great significance in the formation of supramolecular systems.¹¹ In recent work, halogen bonding has been used as an efficient tool to control the emission color of bimetallic sliver-gold structures.¹² Lieffrig and co-workers reported the supramolecular self-assembled isostructural crystalline salts PT(1)X (X = Cl, Br) which are formed through halogen bonding interactions.¹³ Weak interactions were also proved to play a part in transporting K⁺ cations across lipid bilayer membranes.¹⁴ In addition, it has been found that the cooperative effects of multiple weak interactions help to reinforce each other.^15–17 The extensive applications of weak interactions have been invoking a growing number of related research studies, which not only put forward various new forms of intermolecular or intramolecular interactions, but aid in understanding their origins.^18–20

Hydrogen bonding is one of the most common weak interactions and was first proposed in early 20th century, and is still an active topic of scientific research due to its importance in many chemical and biological processes.^21,22 In general, a hydrogen bond has the form of X–H⋯Y, where the Y moiety interacts with the proton donor through its lone pair(s). Hydrogen bond interaction has an intrinsic directionality, and is characterized by saturability. In recent years, many different types of untraditional hydrogen bonds have been developed by involving diverse electron donors including conjugated molecules, radicals, metal hydrides, and even a localized electron. Correspondingly, the concepts of π-hydrogen bond,^23,24 single-electron hydrogen bond,²⁵ dihydrogen bond,²⁶ and electron hydrogen bond^27,28 have been raised successively.

Owing to the electronic similarity among lithium, sodium, and hydrogen elements, efforts have also been devoted to exploring the possibility that lithium or sodium salt molecules serve as Lewis acids to interact with electron donors. Consequently, the existence of lithium bonding^29–31 and sodium bonding^32,33 interactions has been put forward. In 2009, Yáñez and co-workers further enriched the study of non-covalent interactions with a series of beryllium bonding systems in which the BeX₂ (X = H, F, Cl, OH) molecules take the role of electron acceptor.³⁴ As an analog of beryllium bonds, magnesium bond was theoretically predicted shortly afterwards.^35,36 Different from beryllium and its compounds, the magnesium-containing complexes are non-toxic, which renders their experimental identification much more practicable. Besides, magnesium is an indispensable element in all the organisms and takes part in many important biochemical processes.^37,38 Thus, the in-depth study of all sorts of magnesium bonding systems may provide meaningful references for biological and environmental chemistry studies.

In the present work, we aim to gain a fundamental understanding of the interaction between magnesium salt molecules and free radicals since the latter are known to play a crucial role in chemistry, especially organic chemistry,^39,40 atmospheric chemistry^41,42 and biochemistry.^43,44 By using quantum chemical calculations, the formation of single-electron magnesium bond between MgX₂ (X = F, H) and a series of alkyl radicals (methyl, ethyl, isopropyl, and tertiary butyl) was characterized in detail and compared with other noncovalent interactions. Besides, methyl substitution effect on structure and bonding of the resulting complexes was analyzed as well.

2. Computational details

The geometries of the X₂Mg⋯Y [X = F, H; Y = CH₃, CH₂CH₃, CH(CH₃)₂, and C(CH₃)₃] complexes and involved monomers were optimized at the MP2/aug-cc-pVTZ level with using the counterpoise procedure.⁴⁵ Harmonic vibrational frequency analysis was performed at the same level to affirm that these structures are local minima on their respective potential energy surfaces. Natural bond orbital (NBO) analysis⁴⁶ was performed at the MP2 level to examine the charge transfer between MgX₂ (X = F, H) and the alkyl radicals. In this work, the 〈S²〉 values are 0.7501 for all the open-shell calculations, indicating negligible spin contamination. The above calculations were carried out by using the GAUSSIAN 09 program.⁴⁷

The Bader's quantum theory of atoms-in-molecules (QTAIM)^48,49 was carried out to characterize the chemical bonding of the studied complexes. By the aid of Multiwfn program,⁵⁰ the bond critical points (BCPs) were found through the analysis of wave function.⁵¹ Meanwhile, the electron density ρ(r) and its corresponding Laplacian (∇²ρ) at the BCPs were obtained. To intuitively show the studied single-electron magnesium bond in real space, we applied the independent gradient model (IGM) method⁵² (embedded in the Multiwfn program) in combination with the visual molecular dynamics (VMD) program.⁵³ With basis set superposition error (BSSE)⁵⁴ correction, intermolecular interaction energies of the X₂Mg⋯Y complexes were obtained at the CCSD(T)//MP2/aug-cc-pVTZ level. To provide more insight into on the nature of interaction between MgX₂ and radical molecules, the localized molecular orbital energy decomposition analysis (LMOEDA)⁵⁵ were performed by using the GAMESS program package.⁵⁶ According to LMOEDA, the total interaction energy of a complex is composed of electrostatic (ΔE_elstat), exchange-repulsion (ΔE_ex+rep), polarization (ΔE_pol), and correlation (ΔE_disp) contributions, as shown in eqn (1)

ΔE_int = ΔE_elstat + ΔE_ex+rep + ΔE_pol + ΔE_disp (1)

In this work, the first three components were computed at the SCF level while the ΔE_disp term was obtained at the MP2 level.

3. Results and discussion

3.1 Geometric structures and single-electron magnesium bonds

The optimized structures of the X₂Mg⋯Y [X = F, H; Y = CH₃, CH₂CH₃, CH(CH₃)₂, and C(CH₃)₃] complexes are shown in Fig. 1, and the important geometrical parameters are presented in Table 1. For comparison, the geometrical structures of corresponding monomers are presented in ESI (Fig. S1†). The NPA charges of the complexes and monomers are collected in Table 2.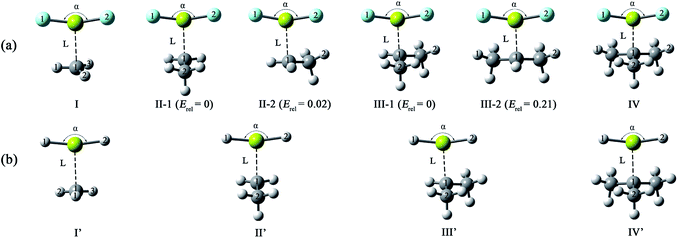

Fig. 1 Optimized structures of the (a) F₂Mg⋯Y and (b) H₂Mg⋯Y [Y = CH₃, CH₂CH₃, CH(CH₃)₂, C(CH₃)₃] complexes and the relative energies of isomers (E_rel, in kcal mol⁻¹) at the MP2/aug-cc-pVTZ level.

Table 1 Optimized geometrical parameters of the X₂Mg⋯Y [X = F, H; Y = CH₃, CH₂CH₃, CH(CH₃)₂, C(CH₃)₃] complexes at the MP2/aug-cc-pVTZ level. L and α represent the Mg⋯C1 distance and the X–Mg–X angle, respectively. Bond lengths in Å and bond angles in degrees (the Mg–F bond length is 1.768 Å for the MgF₂ monomer. The Mg–H bond length is 1.706 Å for the MgH₂ monomer)

Complex	Symmetry	L	α	RMg–X1	RMg–X2	DX1–Mg–C1–H1
I	Cs	2.573	163.0	1.778	1.779	0.0
II-1	Cs	2.509	160.1	1.781	1.781	32.2
II-2	C1	2.521	160.1	1.780	1.783	12.3
III-1	C1	2.485	158.3	1.782	1.785	28.0
III-2	Cs	2.498	157.8	1.783	1.783	89.1
IV	Cs	2.478	156.7	1.785	1.785
I′	Cs	2.707	166.6	1.717	1.717	89.9
II′	Cs	2.644	164.3	1.719	1.719	31.8
III′	C1	2.615	163.0	1.720	1.722	24.9
IV′	C1	2.623	161.5	1.722	1.722

---

Table 2 NPA charges for the X₂Mg⋯Y [X = F, H; Y= CH₃, CH₂CH₃, CH(CH₃)₂, C(CH₃)₃] complexes at the MP2/aug-cc-pVTZ level (NPA charges are 1.863|e| and 0.932|e| for Mg and F atoms, respectively, in the MgF₂ monomer. NPA charges are 1.428|e| and −0.714|e| for Mg and H atoms, respectively, in the MgH₂ monomer)

Complex	C1		Radical in complex	Mg		X1/X2 in complex
	In monomer	In complex		In complex	Δq
I	−0.467	−0.527	0.019	1.842	−0.021	−0.931
II-1	−0.260	−0.344	0.019	1.832	−0.031	−0.926
II-2		−0.347	0.018	1.841	−0.022	−0.931/−0.930
III-1	−0.072	−0.165	0.015	1.835	−0.028	−0.926/−0.925
III-2		−0.166	0.018	1.833	−0.030	−0.925
IV	0.102	0.011	0.004	1.844	−0.019	−0.924
I′	−0.467	−0.510	0.011	1.425	−0.003	−0.717
II′	−0.260	−0.323	0.011	1.429	0.001	−0.720
III′	−0.072	−0.140	0.012	1.433	0.005	−0.720/−0.723
IV′	0.102	0.046	0.003	1.439	0.011	−0.721

---

From Fig. 1 and Table 1, both F₂Mg⋯CH₃ (I) and H₂Mg⋯CH₃ (I′) complexes possess C_s symmetry. Their structural difference mainly comes from different interaction orientation between X₂Mg molecule and methyl, which is reflected in the ∠X1MgC1H1 dihedral angle (0° for I and 89.9° for I′). The binding distances (L), defined as the distance between Mg and C1 atoms, are 2.573 and 2.707 Å for I and I′, respectively. The interaction between F₂Mg and ethyl, isopropyl, and tertiary butyl results in five complexes. The II-1 and II-2 complexes can be regarded as being obtained when the H2 and H3 atoms of F₂Mg⋯CH₃ are replaced by methyl, respectively. The energy difference between them is only 0.02 kcal mol⁻¹. Similarly, the III-1 and III-2 isomers can be obtained when two of the methyl hydrogen atoms in F₂Mg⋯CH₃ are substituted. III-2 is 0.21 kcal mol⁻¹ higher in total energy relative to III-1. The situation is somewhat different for the BeH₂-based system. From Fig. 1, MgH₂ binding with ethyl (or isopropyl) leads to only one structure. It can be seen that isomer II′ resembles II-1 in geometry, while the structure of III′ parallels that of III-1. The F₂Mg⋯C(CH₃)₃ (IV) and H₂Mg⋯C(CH₃)₃ (IV′) complexes share a similar geometry, and the ∠F1MgC1C2 dihedral angle of 88.5° is close to the ∠H1MgC1C2 dihedral angle of 88.9°.

Besides, to evaluate the performance of modern DFT functionals for characterizing such magnesium-bonding system, structure optimizations of the X₂Mg⋯CH₃ and X₂Mg⋯CH₂CH₃ complexes were also performed by using the wB97XD, M06-2X, B3LYP-D3(BJ), and B2LYPD3 methods with the aug-cc-pVTZ basis set. The results are compared with those of the MP2 method in Table S1 in ESI.† It can be found that all these DFT functionals tend to underestimate the Mg⋯C binding distance (by 0.034–0.156 Å). For the MgF₂-based system, the wB97XD and M06-2X functionals overestimate the F–Mg–C angle while the other two underestimate it. For the MgH₂-based system, the H–Mg–C angle is always underestimated by these functionals. It is worth noting that the wB97XD and M06-2X functionals can only yield the II-1 isomer, but fail to predict the II-2 isomer. In contrast, the B3LYP-D3(BJ) and B2LYPD3 functionals are able to predict both structures. Hence, it can be concluded that the B3LYP-D3(BJ) and B2LYPD3 methods can be used to describe the structures of the studied species and yield basically consistent results with those obtained at the MP2 level.

From Table 1, the binding distances of the studied X₂Mg⋯Y species vary in the range of 2.478–2.707 Å, which are far shorter than 3.9 Å, namely the sum of van der Waals radii of Mg and C atoms.⁵⁷ This fact indicates a certain interaction between MgF2/MgH2 and the radicals. To illustrate this, the potential energy surfaces of the F₂Mg⋯CH₃ and H₂Mg⋯CH₃ complexes have been roughly obtained by scanning the Mg⋯C distance and the X–Mg–C (X = F, H) angle at the MP2/aug-cc-pVTZ level (see Fig. S2†). Herein, the Mg⋯C distance varies from 5.0 Å to 2.0 Å in steps of −0.3 Å, and the X–Mg–C angle increases from 90° to 102° with increments of 1.2°. As can be seen from the PES plot, the total energies of both dimers decrease as the MgX₂ molecule approaches the methyl radical, showing an attraction interaction between two species. Ultimately, minimum potential energy structures have been reached, which are basically consistent with the optimized structures of complexes I and I′. The singly occupied molecular orbitals (SOMOs) of the complexes and their corresponding free radicals are shown in Fig. 2, where the orbital energies are also included. It can be seen that the SOMOs of complexes are mainly contributed from those of radicals, and the MgX₂ molecule acts as the single electron acceptor. Thereby the interaction between the two monomers of the X₂Mg⋯Y complexes can be defined as a single-electron magnesium bond. Furthermore, the SOMO orbital energies of complexes are lower by 0.019–0.038 eV compared with corresponding free radicals, revealing that the formation of single-electron Mg bond enhances the stability of the radicals.

Fig. 2 The singly occupied molecular orbitals and corresponding orbital energies (in eV) of the single-electron magnesium bonding complexes and corresponding monomers at the MP2/aug-cc-pVTZ level.

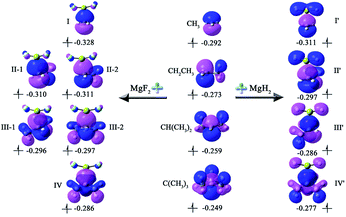
To intuitively show the bonding between MgX₂ molecule and Y radicals, the independent gradient model (IGM) analysis of the X₂Mg⋯Y complexes was performed. A descriptor (δg^inter) is then derived that uniquely defines intermolecular interaction regions. The resulting δg^inter isosurfaces are presented in Fig. 3. It is known that the blue and green colors on the isosurfaces stand for strong intermolecular attractive interaction and weak van der Waals interaction, respectively. As shown in Fig. 3, the single-electron Mg bond, which mainly lies between Mg and C1 atoms, is represented by blue-green isosurfaces. Note that there are also small green regions between F of MgF₂ and methyl H atom of the radicals in the II-2, III-1, III-2 and IV complexes, reflecting a weak intermolecular attraction. This can be understood given the relatively shorter F⋯H2 distances (2.706–2.762 Å) in these four dimers and the negative charge of the F atom (0.924–0.931|e|). The overall size of the isosurface increases as the number of methyl substituents increases, implying an increasing bonding strength. Note that the isosurfaces have more blue component for the F₂Mg⋯Y complexes compared with the H₂Mg-based series, indicating that the bonding strength of the former is stronger than that of the latter. This is consistent with the shorter L values of the former (2.478–2.573 Å) than those of the latter (2.623–2.707 Å).

Fig. 3 The isosurfaces of δg^inter (isovalue = 0.01) for the X₂Mg⋯Y [X = F, H; Y = CH₃, CH₂CH₃, CH(CH₃)₂, C(CH₃)₃] complexes.

From Table 1, the binding distance decreases in the sequence F₂Mg⋯CH₃ (2.573 Å) > F₂Mg⋯CH₂CH₃ (2.509 and 2.521 Å for II-1 and II-2, respectively) > F₂Mg⋯CH(CH₃)₂ (2.485 and 2.498 Å for III-1 and III-2, respectively) > F₂Mg⋯C(CH₃)₃ (2.478 Å). Hence, the methyl substitution effect on the formation of single-electron Mg bond is positive. Similarly, the Mg⋯C1 distance of the H₂Mg-based series varies in the order H₂Mg⋯CH₃ (2.707 Å) > H₂Mg⋯CH₂CH₃ (2.644 Å) > H₂Mg⋯CH(CH₃)₂ (2.615 Å). Compared with H₂Mg⋯CH(CH₃)₂, the H₂Mg⋯C(CH₃)₃ complex has a slightly longer binding distance of 2.623 Å, which can be attributed to steric-hindrance effect. The case is similar to previously reported results of single-electron Be bonding systems.⁵⁸ Note that the Mg–X bond of MgX₂ is elongated by 0.010–0.017 Å upon the interaction with the Y radicals. Hence, the formation of single-electron Mg bond renders the Mg–X bonds weakened. In addition, the MgX₂ subunit bends from the linear geometry, and the bending angles (α) are 156.7–166.6° (see Fig. 1 and Table 1). From Table 1, the more methyl groups the Y radical contains, the more the MgX₂ molecule is bent.

From natural population analysis (NPA), the Y moieties carry 0.003–0.019|e| positive charges in the complexes (see Table 2), confirming that the radical plays the role of electron donor and MgX₂ serves as electron acceptor during the formation of single-electron Mg bond. To shed more light on the charge transfer interaction between MgF₂/MgH₂ and Y radicals, the related orbitals and corresponding second-order stabilization energies are listed in Table 3. For the F₂Mg-based series, the main charge transfer arises from the unpaired electron of C1 atom (LP(C)) to the empty 3s orbital (s*(Mg)) of Mg. For the F₂Mg⋯C(CH₃)₃ complex, there is an additional electron donation from LP(C) to the empty 3p orbital of Mg. As for the H₂Mg-based complexes, the LP(C) → p*(Mg) orbital interaction is dominant in intermolecular charge transfer. Besides, there are some minor charge transfer contributions, for example, from LP(C) to 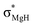antibonding orbital, from σ_CH bonding orbital to the empty 3s and 3p orbitals of Mg, and from the σ_CC bonding orbital to p*(Mg) orbital (only for the IV′ complex).

Table 3 Second order stabilization energies (kcal mol⁻¹) of the orbital interactions in the X₂Mg⋯Y [X = F, H, O; Y = CH₃, CH₂CH₃, CH(CH₃)₂, C(CH₃)₃] complexes

	LP(C) → s*(Mg)	LP(C) → p*(Mg)		σCH1 → p*(Mg)	σCH2 → s*(Mg)	σCH3 → p*(Mg)	σCC → p*(Mg)
I	20.11
II-1	9.34
II-2	19.08
III-1	13.82
III-2	9.30
IV	9.36	2.49
I’		14.37	2.47/2.47	1.21	1.06	1.06
II’		13.82	2.33/2.33	1.38	1.38
III’		11.69	2.46/1.99	1.76
IV’		8.88	1.90/1.90				1.18

---

3.2 Interaction energies

Table 4 shows the interaction energies (E_int) of the studied single-electron magnesium bonding complexes. Clearly, basis set superposition error (BSSE) is not ignorable for interaction energy calculations. From the table, the BSSE values are 0.5–1.51 kcal mol⁻¹ and 0.19–0.52 kcal mol⁻¹ for the MgF₂- and MgH₂-based complexes, respectively. Besides, the BSSE values increase as the number of methyl groups in the radical increases and account for 9.7% and 5.5% of the CCSD(T) interaction energy for the MgF₂⋯C(CH₃)₃ and MgH₂⋯C(CH₃)₃ complexes, respectively. The MP2 interaction energies show a similar trend and close values to the CCSD(T) results, and their difference is less than 6.1%. Thus, the MP2 method is also reliable in calculating single-electron magnesium bonding energies. The HF method, on the other hand, is not so satisfying in interaction energy prediction, especially when it comes to the MgH₂⋯Y series. From Table 4, the electron correlation contribution contributes 14.8–27.0% and 48.4–57.6% to the CCSD(T) interaction energies of the MgF₂- and MgH₂-based complexes, respectively. From the previous reports, the electron correlation contributes 5.2%, 43.7% and 81.6% to the interaction energies of single-electron lithium bonding H₃C⋯LiH,²⁹ single-electron hydrogen bonding H₃C⋯HF²⁵ and single-electron beryllium bonding H₃C⋯BeH₂ (ref. 58) complexes, respectively. Hence, the electron correlation contribution to single-electron magnesium bonds is comparable to that to single-electron hydrogen bonds.

Table 4 BSSE-corrected interaction energies (in kcal mol⁻¹) and electron correlation effect (EC = [CCSD(T)-SCF]/CCSD(T) × 100%) of the X₂Mg⋯Y [X = F, H; Y = CH₃, CH₂CH₃, CH(CH₃)₂, C(CH₃)₃] complexes. The electron density (ρ, in au.) and its Laplacian (∇²ρ, in au.) at the Mg⋯C1 BCP at the MP2/aug-cc-pVTZ level

	SCF	MP2	CCSD(T)	BSSE	EC	ρ(r)	∇^2ρ(r)
I	−7.34	−8.18	−8.61	0.54	14.8%	0.014	0.060
II-1	−9.21	−11.05	−11.52	0.89	20.1%	0.017	0.073
II-2	−9.48	−11.18	−11.70	0.81	19.0%	0.016	0.071
III-1	−10.53	−13.33	−13.81	1.21	23.8%	0.018	0.080
III-2	−10.90	−13.52	−14.06	1.09	22.5%	0.018	0.078
IV	−11.36	−15.12	−15.56	1.51	27.0%	0.019	0.084
I′	−2.71	−4.93	−5.25	0.19	48.4%	0.012	0.039
II′	−3.62	−6.94	−7.13	0.30	49.2%	0.013	0.048
III′	−4.12	−8.53	−8.60	0.41	52.1%	0.015	0.054
IV′	−4.05	−9.23	−9.55	0.52	57.6%	0.015	0.054

---

With a lower-lying LUMO orbital, MgF₂ presents a higher acidity than MgH₂ molecule. Thus, a stronger interaction can be expected when the former serves as electron acceptor instead of the latter. From Table 4 and Fig. S3a,† the interaction energy of a F₂Mg⋯Y complex is 3.36–6.01 kcal mol⁻¹ larger than that of corresponding H₂Mg⋯Y complex. In addition, the absolute interaction energies of the MgF₂-containing complexes follow the order F₂Mg⋯CH₃ (8.61 kcal mol⁻¹) < F₂Mg⋯CH₂CH₃ (11.52 and 11.70 kcal mol⁻¹ for II-1 and II-2, respectively) < F₂Mg⋯CH(CH₃)₂ (13.81 and 14.06 kcal mol⁻¹ for III-1 and III-2, respectively) < F₂Mg⋯C(CH₃)₃ (15.56 kcal mol⁻¹). This trend also applies to the MgH₂-based series. Obviously, the interaction energy of an X₂Mg⋯alkyl complex becomes larger as more methyl substituents are involved in the alkyl radical. Note that the interaction energy of isomer II-2 is 0.18 kcal mol⁻¹ larger than that of II-1, which might be attributed to the additional F2^δ−⋯H2^δ+ interaction in II-2. Similarly, isomer III-2 contains one more F^δ−⋯H^δ+ secondary interaction compared with III-1, justifying its slightly larger interaction energy.

From Table 4, the interaction energies vary from −8.61 to −15.56 kcal mol⁻¹ for the F₂Mg⋯Y complexes, and from −5.25 to −9.55 kcal mol⁻¹ for the H₂Mg⋯Y series. Note that these values are comparable to those (−6.13 to −14.92 kcal mol⁻¹)⁵⁸ of the X₂Be⋯Y [X = F, H; Y = CH₃, CH₂CH₃, CH(CH₃)₂, and C(CH₃)₃] complexes. Meanwhile, the interaction energies are −13.47 ∼ −15.80 kcal mol⁻¹ for F₂Mg⋯π and −7.22 ∼ −8.91 kcal mol⁻¹ for H₂Mg⋯π interactions where the π electron donors are acetylene, ethylene and benzene molecules.³⁶ Hence, it can be concluded that single-electron magnesium bond, single-electron beryllium bond, and π-magnesium bond are comparable in strength.

To deepen the understanding of the nature of single-electron Mg bond, the interaction energies of the X₂Mg⋯Y complexes have been further analyzed by using the LMOEDA method. The energy decomposition results present considerable electrostatic and polarization interactions in the complexation between MgX₂ and radical molecules. The former accounts for approximately half of the total attractive interaction energy, and the latter makes up 27.6–38.1% (see Table 5). Besides, the dispersion energy contributes 5.7–21.6% to the stabilization of the studied complexes, especially for the MgH₂-based series. From the table, all the terms, namely the electrostatic, polarization, exchange-repulsion and dispersion energies, increase with the growth of number of methyl groups in the system except that III-2 has a slightly higher electrostatic energy than IV. The LMOEDA analysis also reveals that a F₂Mg⋯Y complex possesses larger attractive interaction energy and smaller exchange-repulsion energy than corresponding H₂Mg⋯Y complex, giving rise to the larger E_int value of the former.

Table 5 LMOEDA partition terms (in kcal mol⁻¹) and the percentage contribution of electrostatic, polarization and dispersion components to the total attractive interaction energy for the X₂Mg⋯Y [X = F, H; Y = CH₃, CH₂CH₃, CH(CH₃)₂, C(CH₃)₃] complexes

	Eelst	Eex+rep	Epol	Edisp
I	−8.73 (57.8%)	6.95	−5.51 (36.5%)	−0.86 (5.7%)
II-1	−11.52 (54.2%)	10.17	−7.86 (37.0%)	−1.86 (8.8%)
II-2	−12.26 (56.6%)	10.73	−7.66 (35.4%)	−1.73 (8.0%)
III-1	−12.98 (51.3%)	11.94	−9.48 (37.5%)	−2.82 (11.2%)
III-2	−14.02 (54.5%)	12.20	−9.07 (35.3%)	−2.63 (10.2%)
IV	−13.92 (48.7%)	13.48	−10.90 (38.1%)	−3.78 (13.2%)
I′	−8.32 (55.8%)	9.95	−4.36 (29.3%)	−2.22 (14.9%)
II′	−10.50 (54.3%)	12.37	−5.50 (28.5%)	−3.33 (17.2%)
III′	−12.23 (53.0%)	14.51	−6.42 (27.8%)	−4.42 (19.2%)
IV′	−13.10 (50.8%)	16.14	−7.11 (27.6%)	−5.58 (21.6%)

---

3.3 Harmonic vibrational frequencies

Main harmonic vibrational frequencies and their corresponding infrared intensities of the X₂Mg⋯Y complexes are shown in Table 6. From the table, the magnesium bond stretching vibration of the F₂Mg⋯Y complexes occurs in the 200.8–258.5 cm⁻¹ region, comparable to that of 208.0–240.7 cm⁻¹ for the F₂Mg⋯π bonding species.³⁶ The Mg⋯C1 stretching vibrational frequency of the H₂Mg⋯Y series, on the other hand, shows an apparent increase as more methyl groups are involved in the electron donor.

Table 6 Main harmonic vibrational frequencies [v (cm⁻¹)] and corresponding infrared intensity of the X₂Mg⋯Y [X = F, H; Y = CH₃, CH₂CH₃, CH(CH₃)₂, C(CH₃)₃] complexes at the MP2/aug-cc-pVTZ level (the X-Mg-X symmetric stretching frequencies are 551.5 cm⁻¹ and 1636.2 cm⁻¹ in the MgF₂ and MgH₂ monomers, respectively; the X-Mg-X antisymmetric stretching frequencies are 861.3 cm⁻¹ and 1659.0 cm⁻¹ in the MgF₂ and MgH₂ monomers, respectively)

	X–Mg–X sym. stretch			X–Mg–X antisym. stretch			Mg⋯C stretch v
	v in complex	Δv	IR intensity	v in complex	Δv	IR intensity
I	544.7	−6.8	17.4	830.6	−30.7	152.5	209.5
II-1	544.1	−7.4	24.5	825.0	−36.3	96.0	229.2
II-2	543.6	−7.9	25.0	822.4	−38.9	146.5	224.5
III-1	542.5	−9.0	31.5	815.7	−45.6	140.3	258.5
III-2	543.2	−8.3	32.1	815.5	−45.8	142.5	249.7
IV	541.7	−9.8	34.2	809.9	−51.4	134.4	200.8
I′	1601.9	−34.3	13.4	1621.0	−38.0	484.3	150.4
II′	1594.7	−41.5	21.7	1612.5	−46.5	485.3	175.3
III′	1588.7	−47.5	33.6	1606.5	−52.5	473.0	231.9
IV′	1586.1	−50.1	38.1	1602.7	−56.3	465.6	352.8

---

From Table 6, both X–Mg–X symmetric and antisymmetric stretching vibrational frequencies decrease as a result of the complexation between MgX₂ and radical molecules, which accords well with the lengthening of the Mg–X bonds. The antisymmetric X–Mg–X and symmetric H–Mg–H stretching vibration frequencies are red-shifted by 30.7 to 56.3 cm⁻¹ in the complexes. In contrast, the F–Mg–F symmetric stretching frequency has a minor redshift of less than 10 cm⁻¹. This may be attributed to the stronger intermolecular interaction of the F₂Mg⋯Y complexes and the bent structure of the MgF₂ subunit, which bring about coupling of the symmetric stretch of the F–Mg–F bond with the stretching Mg⋯C1 bond. Note that the similar vibrational-mode coupling even results in abnormal blue-shifted F–Be–F symmetric stretch in the studies of beryllium bonding systems.^34,58 In addition, it has been found that the antisymmetric stretching vibration of the MgX₂ subunit has larger IR intensity than symmetric stretching vibration, especially in the MgH₂-based complexes.

3.4 AIM analysis

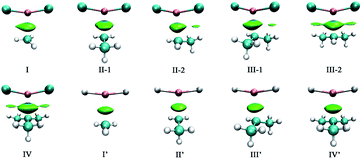
Bader's quantum theory of atoms in molecules (QTAIM) was applied to the topic complexes to gain more insight into the nature of single-electron magnesium bond. The electron densities (ρ) and their Laplacians (∇²ρ) at the Mg⋯C1 bond critical points (BCPs) have been obtained, which are listed in Table 4. The molecular graphs of the complexes are presented in Fig. 4.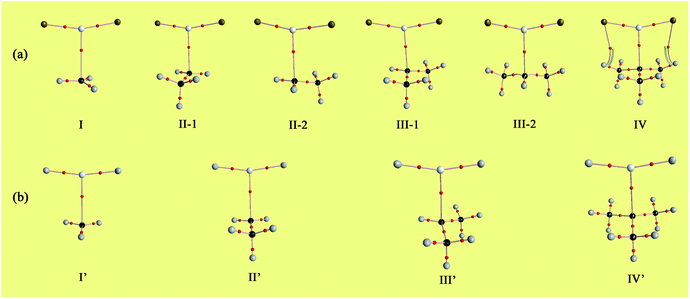

Fig. 4 Molecular graphs of the (a) F₂Mg⋯Y and (b) H₂Mg⋯Y [Y = CH₃, CH₂CH₃, CH(CH₃)₂, C(CH₃)₃] complexes.

From Fig. 4, there are bond critical points between MgX₂ and radicals in all the cases, indicating the formation of single-electron magnesium bond therein. It is worth mentioning that there are also interaction paths between F of MgF₂ and H of the C(CH₃)₃ radical in complex IV, only their corresponding electron density (ρ = 0.006 au.) is quite small. As shown in Table 4, the values of electron density and Laplacians at the Mg⋯C1 BCPs are in the range of 0.012–0.019 and 0.039–0.084 au, respectively. Besides, both ρ and ∇²ρ values increase gradually with the increasing number of methyl groups involved in the X₂Mg⋯Y complexes. From Fig. S3b,† the evolution of electron density at the Mg⋯C1 BCP shows a similar trend to that of interaction energy. This again reflects the positive role of the methyl substituent in the single-electron magnesium bond formation. According to a previous study of π-magnesium bond, the values of electron density at the π⋯Mg BCPs also range from 0.012 to 0.019 au.,³⁶ also reflecting that π-magnesium bond and single-electron magnesium bond are close to each other in strength.

4. Conclusions

According to quantum chemical calculations, the MgX₂ (X = F, H) molecules are able to serve as Lewis acids and form complexes with alkyl radicals Y [Y = CH₃, CH₂CH₃, CH(CH₃)₂, and C(CH₃)₃]. The existence of single-electron magnesium bond is thereby proposed. Upon the interaction with radicals, the MgX₂ molecule becomes bent, accompanied by elongated Mg–X bonds and red-shifted X–Mg–X stretching vibrations. LMOEDA analysis demonstrates that the electrostatic and polarization interactions make dominant contributions to the stability of the topic complexes. Besides, there is 0.003–0.019|e| electron transfer from the radical molecules to MgX₂ during complexation and the main electron donation takes place from the SOMO orbital of the radicals to the 3s or 3p orbital of Mg. It has been found that, the more methyl groups are involved in electron donor Y, the shorter the binding distance and the larger the interaction energy of the X₂Mg⋯Y complex, showing the positive effect of methyl substitution on single-electron magnesium bonding formation. We hope that the results of this study can further enrich the knowledge of intermolecular weak interactions, and may provide meaningful references for biological and chemical processes that involve radicals.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (Grant No. 21573089, 51872057) and the “13th Five-Year” Science and Technology Research Project of Jilin provincial education department (JJKH20190117KJ).

Notes and references

1. R. W. Saalfrank, H. Maid and A. Scheurer, Angew. Chem., Int. Ed., 2008, 47, 8794–8824.
2. A. Llanes-Pallas, C.-A. Palma, L. Piot, A. Belbakra, A. Listorti, M. Prato, P. Samorì, N. Armaroli and D. Bonifazi, J. Am. Chem. Soc., 2009, 131, 509–520.
3. A. Priimagi, G. Cavallo, P. Metrangolo and G. Resnati, Acc. Chem. Res., 2013, 46, 2686–2695.
4. A. Bauzá and A. Frontera, Angew. Chem., Int. Ed., 2015, 54, 7340–7343.
5. P. Politzer, J. S. Murray and T. Clark, J. Mol. Model., 2015, 21, 52.
6. G. Jones, P. Willett and R. C. Glen, J. Mol. Biol., 1995, 245, 43–53.
7. M. G. Chudzinski, C. A. McClary and M. S. Taylor, J. Am. Chem. Soc., 2011, 133, 10559–10567.
8. J. Itskovitz-Eldor, M. Schuldiner, D. Karsenti, A. Eden, O. Yanuka, M. Amit, H. Soreq and N. Benvenisty, Mol. Med., 2000, 6, 88–95.
9. R. B. Walsh, C. W. Padgett, P. Metrangolo, G. Resnati, T. W. Hanks and W. T. Pennington, Cryst. Growth Des., 2001, 1, 165–175.
10. V. N. Lindsay, C. Nicolas and A. B. Charette, J. Am. Chem. Soc., 2011, 133, 8972–8981.
11. P.-P. Zhou and W.-Y. Qiu, J. Phys. Chem. A, 2009, 113, 10306–10320.
12. A. Laguna, T. Lasanta, J. M. López-de-Luzuriaga, M. Monge, P. Naumov and M. E. Olmos, J. Am. Chem. Soc., 2010, 132, 456–457.
13. J. Lieffrig, H. M. Yamamoto, T. Kusamoto, H. Cui, O. Jeannin, M. Fourmigué and R. Kato, Cryst. Growth Des., 2011, 11, 4267–4271.
14. N. Sakai, J. Mareda and S. Matile, Acc. Chem. Res., 2005, 38, 79–87.
15. Q. Li, Q. Lin, W. Li, J. Cheng, B. Gong and J. Sun, ChemPhysChem, 2008, 9, 2265–2269.
16. A. Ebrahimi, M. Habibi, R. S. Neyband and A. R. Gholipour, Phys. Chem. Chem. Phys., 2009, 11, 11424–11431.
17. J. K. Khedkar, M. M. Deshmukh, S. R. Gadre and S. P. Gejji, J. Phys. Chem. A, 2012, 116, 3739–3744.
18. E. Rossi, M. De Santis, D. Sorbelli, L. Storchi, L. Belpassi and P. Belanzoni, Phys. Chem. Chem. Phys., 2020, 22, 1897–1910.
19. P. R. Varadwaj, A. Varadwaj and H. M. Marques, Inorganics, 2019, 7, 40.
20. P. R. Varadwaj, Molecules, 2019, 24, 3166.
21. Y. Nishiyama, P. Langan and H. Chanzy, J. Am. Chem. Soc., 2002, 124, 9074–9082.
22. Y. Nishiyama, J. Sugiyama, H. Chanzy and P. Langan, J. Am. Chem. Soc., 2003, 125, 14300–14306.
23. K. P. Gierszal, J. G. Davis, M. D. Hands, D. S. Wilcox, L. V. Slipchenko and D. Ben-Amotz, J. Phys. Chem. Lett., 2011, 2, 2930–2933.
24. A. Bajpai, M. Lusi and M. J. Zaworotko, Chem. Commun., 2017, 53, 3978–3981.
25. B.-Q. Wang, Z.-R. Li, D. Wu, X.-Y. Hao, R.-J. Li and C.-C. Sun, Chem. Phys. Lett., 2003, 375, 91–95.
26. H. Cybulski, E. Tymińska and J. Sadlej, ChemPhysChem, 2006, 7, 629–639.
27. X.-Y. Hao, Z.-R. Li, D. Wu, Z.-S. Li and C.-C. Sun, J. Chem. Phys., 2003, 118, 10939–10943.
28. T. Tsurusawa and S. Iwata, J. Chem. Phys., 2000, 112, 5705–5710.
29. Y. Li, D. Wu, Z.-R. Li, W. Chen and C.-C. Sun, J. Chem. Phys., 2006, 125, 084317.
30. K. Yuan, Y.-Z. Liu, L.-L. LÜ, Y.-C. Zhu, J. Zhang and J.-Y. Zhang, Chin. J. Chem., 2009, 27, 697–702.
31. Q. Li, Y. Wang, W. Li, J. Cheng, B. Gong and J. Sun, Phys. Chem. Chem. Phys., 2009, 11, 2402–2407.
32. Z.-F. Li, Y.-C. Zhu and H.-X. Li, Phys. Chem. Chem. Phys., 2009, 11, 11113–11120.
33. Z. Li, X. Zhang, H. Li, Y. Zhu and X. Yang, Chem. Phys. Lett., 2011, 510, 273–277.
34. M. Yáñez, P. Sanz, O. Mó, I. Alkorta and J. Elguero, J. Chem. Theory Comput., 2009, 5, 2763–2771.
35. X. Yang, Q. Li, J. Cheng and W. Li, J. Mol. Model., 2013, 19, 247–253.
36. S.-Y. Li, D. Wu, Y. Li, D. Yu, J.-Y. Liu and Z.-R. Li, RSC Adv., 2016, 6, 102754–102761.
37. C.-Y. Li, E. A. Hemmig, J. Kong, J. Yoo, S. Hernández-Ainsa, U. F. Keyser and A. Aksimentiev, ACS Nano, 2015, 9, 1420–1433.
38. E. P. Gates, J. K. Jensen, J. N. Harb and A. T. Woolley, RSC Adv., 2015, 5, 8134–8141.
39. J. W. Tucker, J. D. Nguyen, J. M. Narayanam, S. W. Krabbe and C. R. Stephenson, Chem. Commun., 2010, 46, 4985–4987.
40. H. G. Yayla and R. R. Knowles, Synlett, 2014, 25, 2819–2826.
41. F. Hasager, S. T. Andersen, S. A. Hass, M. P. Sulbaek Andersen and O. J. Nielsen, J. Phys. Chem. A, 2019, 123, 10315–10322.
42. A. M. Arangio, H. Tong, J. Socorro, U. Poschl and M. Shiraiwa, Atmos. Chem. Phys., 2016, 16, 13105–13119.
43. C. Prescott and S. E. Bottle, Cell Biochem. Biophys., 2017, 75, 227–240.
44. V. Marchand, N. Charlier, J. Verrax, P. Buc-Calderon, P. Levêque and B. Gallez, PLoS One, 2017, 12, e0172998.
45. S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553–566.
46. J. E. Carpenter and F. Weinhold, J. Mol. Struct.: THEOCHEM, 1988, 169, 41–62.
47. M. J. Frisch, G. Trucks, H. Schlegel, G. Scuseria, M. Robb, J. Cheeseman, G. Scalmani, V. Barone, B. Mennucci and G. Petersson, Gaussian 09, Gaussian Inc., Wallingford, CT, 2009.
48. R. F. W. Bader and C. F. Matta, J. Phys. Chem. A, 2004, 108, 8385–8394.
49. F. Cortés-Guzmán and R. F. W. Bader, Coord. Chem. Rev., 2005, 249, 633–662.
50. E. R. Johnson, S. Keinan, P. Mori-Sánchez, J. Contreras-García, A. J. Cohen and W. Yang, J. Am. Chem. Soc., 2010, 132, 6498–6506.
51. T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592.
52. C. Lefebvre, G. Rubez, H. Khartabil, J.-C. Boisson, J. Contreras-García and E. Hénon, Phys. Chem. Chem. Phys., 2017, 19, 17928–17936.
53. W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38.
54. S. F. Boys and F. d. Bernardi, Mol. Phys., 1970, 19, 553–566.
55. P. Su and H. Li, J. Chem. Phys., 2009, 131, 014102.
56. M. W. Schmidt, K. K. Baldridge, J. A. Boatz, S. T. Elbert, M. S. Gordon, J. H. Jensen, S. Koseki, N. Matsunaga, K. A. Nguyen and S. Su, J. Comput. Chem., 1993, 14, 1347–1363.
57. S. S. Batsanov, Inorg. Mater., 2001, 37, 871–885.
58. D. Yu, D. Wu, Y. Li and S.-Y. Li, Theor. Chem. Acc., 2016, 135, 112.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ra06591a

---