Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Unspecified verticality of Franck–Condon transitions, absorption and emission spectra of cyanine dyes, and a classically inspired approximation
Joseph D. Alia *a and
Joseph A. Flackb
*a and
Joseph A. Flackb
aDivision of Science and Mathematics, University of Minnesota Morris, 600 E 4th St, USA. E-mail: aliaj@morris.umn.edu; Tel: +1-320-589-6345
bNYITCOM at Arkansas State University, P. O. Box 2206, State University, AR 72467, USA
First published on 26th November 2020
Abstract
The computed vertical energy, Ev,a/f, from the equilibrium geometry of the initial electronic state is frequently considered as representative of the experimental excitation/emission energy, Eabs/fl = hc/λmax. Application of the quantum mechanical version of the Franck–Condon principle does not involve precise specification of nuclear positions before, after, or during an electronic transition. Moreover, the duration of an electronic transition is not experimentally accessible in spectra with resolved vibrational structure. It is shown that computed vibronic spectra based on TDDFT methods and application of quantum mechanical FC analysis predict Eabs = hc/λmax with a 10-fold improvement in accuracy compared to Ev,a for nine cyanine dyes. It is argued that part of the reason for accuracy when this FC analysis is compared to experiment as opposed to Ev,a/f is the unspecified verticality of transitions in the context of the quantum version of the FC principle. Classical FC transitions that preserve nuclear kinetic energy before and after an electronic transition were previously found to occur at a weighted average of final and initial electronic state molecular geometries known as the r-centroid. Inspired by this approach a qualitative method using computed vertical and adiabatic energies and the harmonic approximation is developed and applied yielding a 5-fold improvement in accuracy compared to Ev,a. This improvement results from the dominance of low frequency vibronic transitions in the cyanine dye major band. The model gives insight into the nature of the redshift when qPCR dye EvaGreen is complexed to λDNA and is applicable to the low frequency band of similar non cyanine dyes such as curcumin. It is found that the computed vibronic cyanine dye spectra from time-dependent FC analysis at 0 K and 298 K show decreased intensity at higher temperature suggestive of increased intensity with restricted motion shown when cyanine dyes are used in biomedical imaging. A 2-layer ONIOM model of the DNA minor groove indicates restricted motion of the TC-1 dye excited state in this setting indicative of enhanced fluorescence.
Introduction
How should one think of the motion of nuclei during an electronic transition of a molecule? Usual statements of the Franck–Condon principle tell us change in position of nuclei is negligible during an electronic transition. Quantum and classical versions of the FC principle differ on this and whether there is even a meaningful answer. We propose that examination of this question in the context of computed vibronic absorption and fluorescence spectra of cyanine dyes helps to reveal a source of systematic error in comparison of TDDFT vertical energies to experimental spectra. We develop a qualitative classically inspired approach to a vertical energy that gives closer agreement to experiment for nine cyanine dye examples than do vertical TDDFT energies calculated from the optimized geometry of the initial electronic state. We find our applications both of the quantum mechanical FC principle and of our newly developed classically inspired approach yield high accuracy compared to experiment for the dyes studied.Unspecified verticality in the quantum FC principle
Franck in 1926 showed how different possible ground and excited state bond potential energy curves are the basis for understanding variation in band structure of diatomic molecules of different composition.1 Condon's 1926 paper builds on Franck's work showing favorable vibronic transitions to be those for which classically specified positions and momenta of nuclei have negligible change during the electronic transition.2 These two papers from 1926 comprise the classical Franck–Condon principle. Condon was already aware in 1926 that this treatment was provisional and would be superseded by an approach based on “the newer kinematics of Heisenberg, Born, and Jordan”. In 1928, Condon explains the “inexactness” of his previous approach and develops what is now known as the quantum mechanical Franck–Condon principle which avoids “violation of the Heisenberg indeterminacy principle” by not requiring specification of nuclear positions during a transition but instead bases the probability of a given transition on the overlap between wavefunctions of vibrations involved.3 Schwartz (1973) concisely summarizes this aspect of Condon's 1928 paper, “… as Condon pointed out (3), the uncertainty principle precludes the precise specification of the nuclear position and momentum. For this reason, Condon rejected the earlier statement of the Franck–Condon principle”.4 Schwartz goes on to show that because of energy-lifetime uncertainty, the supposed duration of an electronic transition, “10−15 or even 10−18 s depending on the authors”, is not experimentally accessible using methods yielding vibrational structure.4 He concludes it is not possible to experimentally compare duration of an electronic transition with period of vibrations in the transition and such a comparison is meaningless from the point of view of energy-lifetime uncertainty.4 The classical concept of vertical transitions is useful under some circumstances. Noda and Zare (1982) show that an averaged molecular geometry, 〈r〉 = 〈v′|r|v′′〉/〈v′|v′′〉, known as the r-centroid, gives the position of a vertical transition that preserves the kinetic energy due to motion of the nuclei before and after an electronic transition consistent with the classical Franck–Condon principle.5 This approach applies where one would expect a classical approach to work well, i.e., small energy spacing between vibrational energy levels. Noda and Zare give several diatomic molecule examples.5 The Franck–Condon principle also applies to molecules with more than two atoms.The Duschinsky transformation
Application of the Franck–Condon principle to molecules with more than two atoms requires common normal mode coordinates between initial and final electronic states. This is accomplished with Duschinsky transformation, Q′′ = JQ′ + K, describing vibrational coordinates, Q′′, of the initial electronic state as linear combinations of those of the final electronic state, Q′, through application of Duschinsky rotation matrix, J, and shifted by the difference between initial and final electronic state equilibrium geometries along normal modes of the initial electronic state by Duschinsky shift vector K. Franck–Condon factors can be computed once a common normal coordinate system has been established but before this is possible, the displacement between final and initial states and their respective potential energy surfaces must be computed. There are several ways of accomplishing these goals.Adiabatic and vertical approximations
Approaches that account for the displacement between electronic state geometries and their respective potential energy surfaces fall into two main categories, adiabatic and vertical.6,7 Adiabatic methods require optimized equilibrium geometries for both states. Vertical methods extrapolate final state displacement and vibrations from the initial state optimized geometry.Adiabatic Hessian (AH) methods include normal modes of each electronic state according to the Hessian at their respective equilibrium geometries. For adiabatic shift (AS) methods, the two electronic states are taken to have the same PES only displaced.
Vertical Hessian (VH) methods extrapolate the displacement between electronic state geometries and the vibrational modes of the final electronic state based on the final state PES at the equilibrium geometry of the initial electronic state while vertical gradient (VG) methods make a similar extrapolation for the final state but assuming both states have the same PES but displaced.7
The Duschinsky shift vector is explicitly calculated if adiabatic methods are used while it is only approximated in vertical methods. Adiabatic approximations, moreover, apply the harmonic approximation where it is most valid and may therefore be expected to give more appropriate computed overlap between final and initial state wavefunctions. Vertical methods, correspond to the short-time picture of spectroscopy, and can describe higher frequency lines resolved at shorter time scales but if low frequency lines, the 0–0 transition for example, are needed, adiabatic methods are needed.6 Cyanine dyes, the focus of this work, have intense major peak consisting of low lying vibronic transitions appropriate for an adiabatic FC approach.
Cyanine dyes
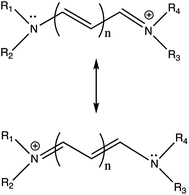
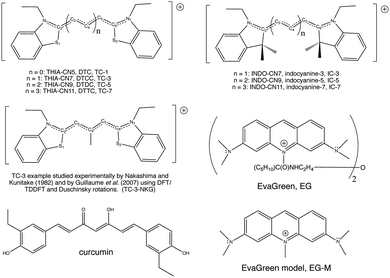
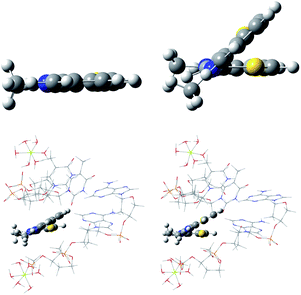
Cyanine dye model systems are referred to by the number of atoms in the conjugated system including nitrogen atoms. For example, if in Fig. 1 n = 1 the dye is CN5 or if n = 2, the dye is CN7 etc. The nitrogen atoms are frequently part of heterocyclic ring end groups in which case the dyes are referred to by the number of carbon atoms in the conjugated chain between end groups. Examples that are the focus of this paper are shown in Fig. 2. THIA and INDO dyes and modifications based on them have applications in biomedical imaging. TC-1 shows enhanced fluorescence in the presence of bacterial cells.9 Nakashima and Kunitake (1982) found enhanced fluorescence of the TC-3-NKG example (Fig. 2 middle left) in the presence of aqueous lipid bilayers.10 TC-3 and TC-3-NKG show enhanced fluorescence in the presence of DNA relevant to the study of gene regulation,11 and an analogue of TC-3 and TC-3-NKG was shown to have fluorescence sensitive to oligomeric and fibrillar α-synuclein relevant to Parkinson's disease.12 TC-7 has been used in in vivo studies to quantify nerve cell myelination and to measure DNA helicity and sequence.13,14 Variations of IC-3 and IC-5 are used as covalent labeling dyes to monitor the budding and fusion events of viruses in living cells.15 These two indocyanine dyes have also been found useful in targeting mitochondria in cancer cells and delivering cargoes to them.16 EvaGreen, also shown in Fig. 2, displays enhanced and redshifted fluorescence when bound in the DNA minor groove and is an effective reagent for detection of autoimmune antibodies in qPCR methods.17–19 Both THIA and INDO dyes are subjects of study for use in DSSCs.20,21 We will refer to these dyes and their analogues with H or methyl substituted for ethyl on the nitrogen atoms according to abbreviations given in Fig. 2. Curcumin, also shown in Fig. 2 in its keto–enol form, is not a cyanine dye. Its seven-carbon conjugated chain and aromatic end groups give curcumin a similar structure to the THIA and INDO dyes. Electron delocalization contributing to curcumin's strong absorption at 425 nm and fluorescence at 542 nm in ethanol does not involve nitrogen atoms as in cyanine dyes. Moreover, curcumin has neutral charge and the oxygen substitution of its conjugated chain is a central feature contributing to its chemical and photophysical properties. Curcumin is included in this study to compare and contrast with results on cyanine dyes.
The π-system electron delocalization between the nitrogen atoms is the basis of the success of Kuhn's 1949 application of the particle-in-a-box model toward understanding the increase in absorption λmax with increased number of carbons in the polymethine chain.23 Polymethine chain bond length alternation (BLA) broadens peaks in electronic spectra and can shift the position of λmax.
BLA in cyanine dyes with the polymethine chain length of seven or more carbon atoms has been observed under some circumstances and has been the subject of both experimental and theoretical interest. Ragni et al. (2019) found the large stokes shift of some C7 dyes to be explained by ground state BLA sensitive to substitution and the central carbon of the polymethine chain and solvent polarity followed by relaxation to a symmetric exited state.24 Gierschner et al. (2020) showed similar C7 cyanine dyes also with substitution at the central carbon to have BLA sensitive to counter ions in solution and in their crystal structures and found this to cause broadened and redshifted absorption spectrum.25 Crossover from symmetric to BLA structures depends on dye functionality, polymethine chain length and media. Yesudas (2013) found agreement between results using DFT (their custom density functionals and M06HF) and experiments showing that cyanine dyes, including the TC dyes shown in Fig. 2, are symmetric in solution and show BLA with chain lengths of eleven or more carbon atoms.26 Potenza et al. (1978) using X-ray crystallography found that TC-7 iodide crystals have BLA.27 The published literature indicates the dyes that are the focus of this article are symmetric in solution, even in polar solvents. This is an important consideration in regard to the accuracy of TDDFT results compared to experimental spectra as electronic and vibrational properties depend strongly on this symmetry.
Guillaume et al. (2007) using TDDFT and Franck–Condon analysis based on Duschinsky rotations found good agreement to the experimentally observed shoulders in absorption and emissions spectra of TC-3-NKG and vibrational assignments indicating these shoulders result from a collection of singly excited vibrations rather than a unique dominant vibrational mode as argued by Mustroph (2018).28,29 There does not seem to be disagreement that many low frequency vibrations contribute to the dominant band.28,29 The computations of Guillaume et al. (2007) are in vacuo and they conclude the remaining differences between their computed vibronic spectra and experiment are due to media and the limitation of the XC density functional.28
The limitations of a variety of density functional and wavefunction approaches applied to cyanine dyes have been the subject of a number of studies. Comparison between computed vertical transitions from a variety of TDDFT and wavefunction methods and with experiment for the simplest cyanine dye examples (R1 = R2 = R3 = R4 = H in Fig. 1) has been a topic of interest and debate. Send et al. (2011) concluded comparison of computed vertical energies to experiment is unreliable due to non-vertical transitions and cite Dierksen and Grimme (2004) who found Franck–Condon and Herzberg–Teller analysis based on TDDFT computations give results in good agreement with experiment for a number of polyene and aromatic examples.30,31 According to Send et al. (2011), vertical energies from quantum Monte Carlo, single reference and multi-reference wavefunction methods, and B2PLYP methods give reasonably close excitation values which are improvements on GGA, hybrid GGA, and meta hybrid GGA methods.30 Truhlar et al. (2012) subsequently showed these classes of TDDFT give errors in a similar range as wavefunction methods, 0.10–0.36 eV and 0.16–0.34 eV respectively, with respect to quantum Monte Carlo results which are considered to be the best estimate and found M06HF to be most accurate among the Minnesota density functionals for this application.32 Later work by Jacquemin et al. (2015) indicates TDDFT methods systematically overestimate cyanine dye excitation energies “irrespective of the details of the computational protocol” and continuing effort to accurately describe their photophysical properties. They report wavefunction methods to be more accurate but not feasible for “real-life” cyanines.33 Interest in practical applications of cyanine dyes has prompted computations beyond these simplest cases including the TC dyes studied here.
Cole et al. (2016) found vertical excitation energies for TC-3, TC-5, and TC-7 with H- and Me-substituted for the nitrogen ethyl groups and the TC-3 analogue with oxygen substituted for sulfur, calculated using TDDFT with the M06HF meta hybrid density functional overestimated excitation energy of 0.51 eV on average compared to experiment and improved to 0.35 eV with solvent effects included while LT-DF-DCC2 computations corrected for solvent effects gave vertical excitation energies greater than experimental Eabs by an average of 0.15 eV.21 We note that the error of 0.35 eV reported by Cole et al. using M06HF is smaller than that found using other functionals BHandHLYP for example.25 TDDFT methods are widely available and computationally accessible and this has motivated the use of empirical corrections to their results when applied to cyanine dyes.
Spichty et al. (2011) devised a conceptually informed four-parameter empirical approach for predicting absorption wave-length of cyanine dyes from their computed TDDFT vertical energies, Ev,a in Fig. 3, and zero point vibrational energies.34 Nakano et al. (2019) compared λ from TDDFT Ev,a to experimental absorption λmax for 70 polymethine dyes including the methyl analogues of TC-3, TC-5, TC-7, IC-3, and IC-5 and found strong linear relationships and also confirmed the systematic underestimation of λmax when this comparison is made using a wide range of fourteen density functionals including GGAs, hybrid-GGAs, meta-GGAs, hybrid-meta GGAs, and a hybrid-meta-NGA.35 There is enough consistency in results across these functionals that the averaged regression curve from combined results can be used to quantitatively predict λmax. These empirical approaches are of practical value because they allow predictions to be made based on computed ground state properties without the more time consuming task of finding an optimized excited state geometry and carrying frequency analysis on it. Still, the nature of the systematic error in comparing computed Ev,a to experiment is not fully accounted for.
We propose the error resulting from comparison of TDDFT Ev,a to experimental Eabs = hc/λmax is based, in part, on the fact that electronic transitions from an exactly specified molecular geometry are not a well-defined idea in the context of the quantum mechanical Franck–Condon principle.3,4 The computed vibronic spectra would then be expected to give improved accuracy in Eabs = hc/λmax provided the band shape predicted for the major peak is reasonable. One might expect a vertical transition from an averaged molecular geometry to be an appropriate comparison to experimental spectra in cases where classical approximations are appropriate and classically vertical transitions conserve kinetic energy due to nuclear motion as Zare and Noda demonstrated for the r-centroid.5 The contribution of low frequency vibrations to the major band in cyanine dye electronic spectra may make them a class of molecules conducive to such a classical approximation for their most intense spectral peak.
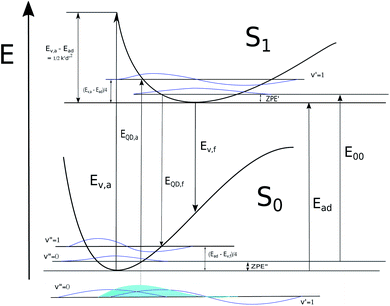
In this work we perform Franck–Condon analysis on N-methyl versions of cyanine dyes in Fig. 2 to find vibronic absorption and emission spectra with solvents described by implicit solvation. Curcumin, a non-cyanine dye, is included for the sake of comparison. Computed absorption and emission λmax, Stokes shifts, and E00 are compared with those from experiment. The major peak in the computed vibronic spectra is found to consist of numerous low frequency transitions. A simple model is developed utilizing computed vertical energies from the optimized geometries of the initial electronic state, Ev,a and Ev,f, for absorption and fluorescence respectively, the adiabatic energy, Ead and zero-point vibrational energies of both states involved in the transition. These energies are depicted in Fig. 3. The approach is based on the harmonic approximation and the idea that a classical approximation would represent vibronic transitions as taking place vertically from an averaged molecular geometry. This simple model gives absorption and fluorescence energies with only slightly less accuracy than spectra computed from FC analysis and both methods are found to have high accuracy compared to experiment.
Computational methods
Geometry optimization and FC analysis
Methyl analogues of the THIA and INDO dyes, curcumin, and EG-M, in Fig. 2 were the subject of computations carried out using Gaussian 09, Revision B.01 (ref. 36) and Gaussian 16, Revision A.03 (ref. 37) software. B3LYP38–41 and M06HF42 hybrid and meta hybrid density functionals were used with the 6-31G(d) basis set for most examples. A wide variety of density functionals have been used in TDDFT studies of cyanine dyes and with consistent overestimation of vertical energies as discussed in the introduction. B3LYP and M06HF are among the functionals found to give correct BLA predictions and by using them, we avoid the larger error in TDDFT vertical energy expected from BHandHLYP but not the overall systematic error in comparison of vertical energies from the optimized geometry of the initial electronic state to experimental λmax.24–26 BHandHLYP computations were carried out on TC-3-NKG using 6-31G(d), 6-311G(d), and SVP basis sets for the sake of comparing to results in the literature. We found Ev,a and Ev,f for curcumin to be far more sensitive to % HF exchange than for cyanine dyes and we found M06 to give the most accurate results for this case.In choosing density functionals for the purpose of computing vibrationally resolved spectra of dye molecules one should keep in mind that band shape can have an effect on λmax and functionals that predict accurate band shape in vibronic spectra are not necessarily well suited for predicting accurate overall position in the spectrum. In their study of coumarin dyes, Bloino et al. (2015) found use of two functionals, ωB97x for accurate band shape shifted by PBE0 wavelengths for accurate position in the spectrum, gave best agreement with experiment.7 They found PBE0, M06, and B3LYP functionals to result in vibronic spectra drastically underestimating the intensity of bands due to higher frequency vibrations. We found that for application to cyanine dyes in this study, B3LYP and M06HF give reasonably good vibronic band shape and position in the spectrum compared to experiment and to other functionals used in the literature. Perhaps the dominant peak in cyanine dyes near the 0–0 transition and broadened and shifted by low frequency transitions is less sensitive to choice of density functional. Our B3LYP and BHandHLYP calculations on TC-3-NKG and results reported in the literature on a wider range of cyanine dyes indicate predicted λmax for this peak is fairly insensitive to choice of basis set.34
Ground and excited state molecular geometries were optimized in solution according to a polarization continuum model, PCM in Gaussian software packages used.43–59 Effects of nonequilibrium solvation were approximated using a linear response correction to absorption energies, Ev,a, calculated from the ground state equilibrium geometry. The nonequilibrium linear response solvation method includes this solvation effect directly in the TDSCF vertical absorption energy for the specified CI-singles excited state.55,60,61 This option is not available for calculation of Ev,f for which equilibrium solvation was used.60 State specific nonequilibrium solvation, a method that entails iterative optimization of the final electronic state charge distribution and interaction with solvent based on the input solvent reaction field from the initial electronic state, was applied to TC-3 for the purpose of comparison.62,63 It was found that, for absorption, the linear response method gave results closer to experiment. Nonequilibrium state specific solvation for TC-3 emission was close to results using equilibrium solvation so it was concluded that nonequilibrium solvation effects are small for emissions processes for this example.
Ground state and excited state geometries were optimized using “tight” convergence and ultrafine grid integration criteria. Local minima in ground electronic state geometries were confirmed with all real vibrational frequencies. Vertical excitation energies, Ev,a, were computed from the optimized ground state geometries using TDSCF with the same density functionals, integration, and solvent as used for the ground state geometry optimization and corresponding geometry optimization of the lowest energy singlet excited state. Local minima were verified with all positive real vibrational frequencies for all examples except TD M06HF for TC-5 and TC-7 for which two imaginary frequencies remained. The problematic vibrational modes for these two cases involved symmetric and antisymmetric rotation of the methyl groups coupled to lowest wavenumber symmetric and antisymmetric flexing modes of the polymethine chain. Adjustment in geometry and recalculation were not successful in removing these imaginary frequency modes and these results could not be used for FC analysis. The M06HF ground state optimized geometry of TC-7 showed BLA in contrast to the observed experimental spectra of this dye in solution so these computational results were not used for further analysis.64
Methods of Barone et al. (2007–2009) were used to carry out time-independent Franck–Condon analysis corresponding to temperature of 0 K.65–68 Vibrationally resolved spectra were computed for the absorption spectrum of TC-3 based on M06HF results and absorption and emission spectra for TC-5, TC-7, and IC-5 using B3LYP results. In vacuo computations were performed for TC-3-NKG in order to compare with results of similar calculations in the literature.28 Vibronic spectra were computed for curcumin in vacuo but did not achieve sufficient spectral progression for curcumin in ethanol. Time dependent FC analyses were computed at temperatures of 0 K and 298.15 K.
ONIOM model of TC-1 and EG-M in the DNA minor groove
A two-base-pair model of DNA with a backbone consisting five ribose phosphate diesters was constructed to approximate the environment of the DNA minor groove. Two magnesium dications octahedrally solvated with six water molecules each were used to partially balance the charge of the five phosphate diesters so the total charge of the DNA fragment was −1. The TC-1 and EG-M dyes have charge of +1 so the entire model had neutral charge. The dyes were placed in the minor groove and the complex was optimized using UFF69 and QEq70 charges on atoms before ONIOM71–74 calculations were carried out. The ONIOM calculations had 2 layers. The DNA layer was low and used UFF and the high layer used B3LYP/6-31G(d). The TC-1 excited state twisted and puckered indicative of a biradical state similar to the first excited electronic state of ethylene.75 MN15 was then used because it is parameterized for use in both single and multireference circumstances.76 A less twisted ES geometry resulted using MN15. B3LYP/6-31G(d) optimization of EG-M in the DNA minor groove model gave a geometry with two excited states close in energy, also an indication that MN15 may be a more appropriate method for this case. Optimization using MN15 resulted in a different excited state geometry without other nearby excited states. Both B3LYP and MN15 optimizations of EG-M excited state in the DNA minor groove gave a negative vibrational frequency precluding Franck–Condon analysis.The classically inspired QD model
(1) Duschinsky shift vector, K, in distance coordinates rather than mass weighted coordinates, defines the displacement d, from the equilibrium geometry of the initial state to that of the final state.
(2) The sum of harmonic displacement energies is equal to Ev,a − Ead for absorption and Ead − Ev,f for fluorescence, that is, 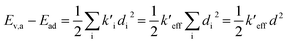 for absorption and
for absorption and 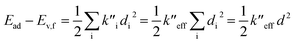 for fluorescence.
for fluorescence.
(3) The position specified by d/2 is about equal to the vector sum of r-centroids along each mode.
(4) The energy difference between final and initial electronic state energies at d/2 corresponds to a classically vertical transition.
Though this classically inspired model is defined in terms of the Duschinsky transformation, which is generally an explicit part of AH and AS methods, the following equations show how the current model, also an adiabatic approximation requiring optimization of both electronic state geometries, is applied for estimation of λmax without the use of d = K and the effective force constants discussed above. These, however, are useful for understanding what kinds of effects are included and where the model applies and will be discussed after its basic application is described. Our model can be applied in reference to Ead or E00 but the results are better if ZPE energies are accounted for in ground and excited states so E00 is preferable if available.
| E00 = Ead − ZPE′′ + ZPE′ | (1) |
From the harmonic approximation the geometry at displacement d/2 would have energy above the equilibrium geometry of the final electronic state as shown be eqn (2) and (3). See Fig. 3.
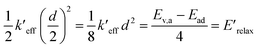 | (2) |
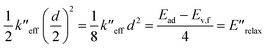 | (3) |
Eqn (2) and (3) are estimates of relaxation energy after excitation or after emission and allow calculation of EQD,a and EQD,f in eqn (4) intended as estimates of absorbance and fluorescence energies. See Fig. 3.
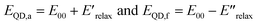 | (4) |
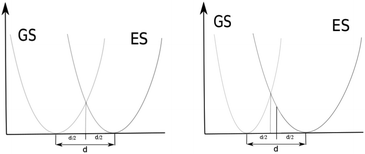
The QD model corresponds most closely to an AS approximation as PES curves that are the same only displaced intersect at d/2. See Fig. 4 (left). Their ZPEs in this case are equal and therefore they have equal total vibrational energy in their v = 0 states. With total vibrational energy and total vibrational potential energy both equal, their total vibrational kinetic energy must also be equal, i.e. vibrational kinetic energy is conserved in a classically vertical transition from this position. If the harmonic potential of one electronic state is more narrow than the other, the point of intersection between the potentials shifts toward the minimum of the narrower potential. See Fig. 4 right. In this case, the ZPE of the state with the narrower potential is greater. The two states have the same vibrational potential energy at their intersection but the state with narrower potential has greater total vibrational energy in its v = 0 state and therefore greater vibrational kinetic energy according to the virial theorem. Moving back toward d/2, the classical vibrational potential energy increases so the classical kinetic energy must decrease for the narrower potential. This shift toward d/2 in the broader potential causes classical potential energy to decrease and classical kinetic energy to increase. The position at which classical vibrational kinetic energy is the same for both states is shifted back toward d/2. Transitions from v = 0 in the state with the narrower potential to overtones in the wider potential would be at classical positions with less shift from d/2 in order to have kinetic energy conserved in a classically vertical transition. Though the QD model shows a more direct correspondence to AS approximations for their 0–0 transitions, comparison of the QD model to AH approximations seems reasonable. We will refer to EQD that use Ead as the reference as EQD − AS and those that use E00 as the reference as EQD − AH. EQD − AS will still include some effects of different GS and ES potential energy surfaces from definition (2) in the previous subsection.
EQD,a implicitly includes nonequilibrium effect of solvent and according to the definitions enumerated according to the Duschinsky transformation, this means the effective force constant, 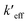 , absorbs this effect. PCM solvation has an effect on computed vibrations and not all vibrations will be effected in the same way. Normal modes with greater displacement in the Duschinsky vector have greater contribution to the vibronic spectrum and are weighted more in their contribution to Ev,a − Ead or Ead − Ev,f therefore the effect of PCM solvation on vibrations contributing to the vibronic spectrum is also implicit in the QD model. Solvent effects cause initial and final electronic states to have different equilibrium geometries than they do in vacuo causing the displacement to be different and likely greater in which case the effects of anharmonicity would be greater in solvent. These differences are also absorbed into energy differences Ev,a − Ead or Ead − Ev,f and absorbed into the QD model through the effective force constants given that the anharmonicities do not result in significantly different mode mixing than predicted by use of the harmonic approximation at ground and excited state equilibrium geometries. This is more likely true for rigid or semi-rigid molecules.
, absorbs this effect. PCM solvation has an effect on computed vibrations and not all vibrations will be effected in the same way. Normal modes with greater displacement in the Duschinsky vector have greater contribution to the vibronic spectrum and are weighted more in their contribution to Ev,a − Ead or Ead − Ev,f therefore the effect of PCM solvation on vibrations contributing to the vibronic spectrum is also implicit in the QD model. Solvent effects cause initial and final electronic states to have different equilibrium geometries than they do in vacuo causing the displacement to be different and likely greater in which case the effects of anharmonicity would be greater in solvent. These differences are also absorbed into energy differences Ev,a − Ead or Ead − Ev,f and absorbed into the QD model through the effective force constants given that the anharmonicities do not result in significantly different mode mixing than predicted by use of the harmonic approximation at ground and excited state equilibrium geometries. This is more likely true for rigid or semi-rigid molecules.
Results and discussion
Accuracy of absorption and fluorescence energies from computed vibronic spectra
Computed vertical excitation and emission energies, Ev,a and Ev,f compared to Eabs/fl = hc/λmax from experiment are presented in Table 1. The mean error in comparison of Ev,a and Ev,f to experimental Eabs/fl = hc/λmax is 0.4 eV for absorptions and 0.2 eV for fluorescence. These errors are consistent with the literature and somewhat smaller than that reported in some cases. Gierschner et al. (2020) for example report 0.5 eV in their TDDFT application of BHandHLYP/6-311G*.25| Dye | Ev,a comp. | Eabs exp. | Ev,f comp. | Efl exp. |
|---|---|---|---|---|
| a M06HF/6-31G(d) and PCM nonequilibrium linear response solvation.b B3LYP/6-31G(d) and PCM nonequilibrium linear response solvation.c M06HF/6-31G(d) and PCM equilibrium solvation.d B3LYP/6-31G(d) and PCM equilibrium solvation.e PhotochemCAD77–79 https://www.photochemcad.com.f West and Pearce (1965).80g Sorokin et al. (1967).64 | ||||
| TC-3 ethanol | 2.652a | 2.220e | 2.198c | 2.170e |
| TC-5 water | 2.319b | 1.91f | 1.912d | |
| TC-5 ethanol | 2.304b | 1.891e | 1.931d | 1.831e |
| TC-7 water | 2.075b | 1.647f | 1.682d | |
| TC-7 methanol | 2.077b | 1.638f | 1.695d | 1.553g |
| TC-7 2-propanol | 2.057b | 1.642e | 1.710d | |
| TC-7 DMSO | 2.043b | 1.605f | 1.688d | 1.52g |
| IC-5 methanol | 2.353b | 1.945e | 1.956d | 1.887e |
| Mean error | 0.4 ± 0.2 | 0.1 ± 0.06 | ||
Eabs/fl = hc/λmax from the major peak in the computed vibronic absorption and emissions spectra show better agreement with those from experimental spectra and give mean errors of 0.04 eV for absorption and 0.05 eV for fluorescence. See Table 2. We believe the high degree of accuracy of Eabs/fl = hc/λmax from our computed vibronic spectra compared to experiment as opposed to Ev,a and Ev,f which are more frequently compared in the literature is due to the error in comparing the vertical energy from the optimized geometry of the initial electronic state to experimental Eabs/fl = hc/λmax. Our computed vibronic spectra allow us to predict where and if vertical energies from the equilibrium geometry may occur in the Franck–Condon region and how well they compare to computed and experimental vibronic peaks. See Fig. 5.
| Dye | Eabs comp. | Eabs exp. | Efl comp. | Efl exp. |
|---|---|---|---|---|
| a M06HF/6-31G(d) and PCM nonequilibrium linear response solvation, time-independent FC analysis at 0 K.b B3LYP/6-31G(d) and PCM nonequilibrium linear response solvation, time-independent FC analysis at 0 K.c B3LYP/6-31G(d) and PCM equilibrium solvation, time-independent FC analysis at 0 K.d PhotochemCAD https://www.photochemcad.com.77–79e West and Pearce (1965).80f Sorokin et al. (1967).64 | ||||
| TC-3 ethanol | 2.231a | 2.220d | 2.170d | |
| TC-5 water | 1.916b | 1.91e | 1.879c | |
| TC-5 ethanol | 1.932b | 1.891d | 1.894c | 1.831d |
| TC-7 water | 1.683b | 1.647e | 1.636c | |
| TC-7 methanol | 1.694b | 1.638f | 1.587c | 1.553f |
| TC-7 2-propanol | 1.708b | 1.624d | 1.663c | |
| TC-7 DMSO | 1.668b | 1.605f | 1.645c | 1.52f |
| IC-5 | 1.962b | 1.945f | 1.935c | 1.887f |
| Mean error | 0.04 ± 0.02 | 0.05 ± 0.05 | ||
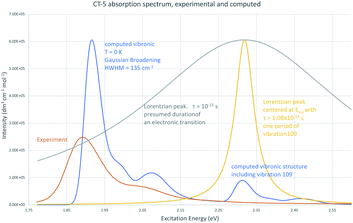
An experimental spectrum of CT-5 in ethanol is shown in Fig. 5 along with its computed vibronic absorption spectrum.77–79 The position of the vertical excitation energy from the ground state equilibrium geometry, Ev,a, is shown as the maximum of a Lorentzian peak with width based on the period of a vibration contributing to the nearest computed vibronic peak, mode 109, a C–H stretching mode on the N1 and N7 methyl groups. Higher frequency vibrations have shorter periods of vibration and would therefore be shown as wider Lorentzian peaks. A fluorescence lifetime on order of picoseconds, typical for cyanine dyes, would allow for about 100 periods of this vibration so an appropriate natural line width would likely be narrower. The width of the corresponding computed vibronic peak as displayed is based on the large number of predicted vibronic transitions contributing to it and Gaussian broadening of 135 cm−1, a default used by the GaussView 6.1 program. There are two goals to showing Ev,a in this way (1) to demonstrate that Ev,a is in the Franck–Condon region of the computed vibronic spectrum but does not correspond to vibrational structure that agrees well with λmax in the experimental spectrum and, (2) to illustrate the arguments of Schwartz (1973),4 i.e., lifetimes on order of the period of molecular vibrations are consistent with vibronic peaks whereas measurements based on a presumed duration for an electronic transition, 10−18 s to 10−15 s do not allow sufficient resolution to show vibronic peaks as shown by the Lorentzian curve also centered at Ev,a but corresponding to a lifetime of 10−15 s. Shorter lifetimes result in even broader peaks; a lifetime of 10−18 s would appear as a horizontal line. The duration of an electronic transition is neither necessary nor well-defined in the context of the quantum mechanical version of the Franck–Condon principle. Specifying the position from which an excitation occurs as the equilibrium geometry of the initial electronic state and Ev,a/f as most appropriate for comparison to experiment is therefore not well-founded. The major peak shown in the computed vibronic spectrum in Fig. 5 results from vibronic transitions involving lower frequency vibrations and shows good agreement with experiment while peaks resulting from vibronic transitions involving higher frequency vibrations are not apparent in the experimental spectrum.
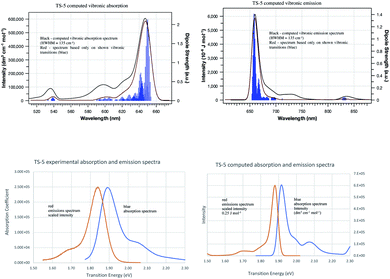
Computed vibronic spectra for TC-5 are shown alongside experimental ones in Fig. 6.77–79 Vibronic transition sticks of 0.0005% intensity and greater in blue show how the contours of the computed spectra result from the predicted vibronic transitions. Agreement between the computed and experimental spectra suggests the contours in the experimental absorption and emissions spectra are due to vibrational structure. Intersection of the experimental absorption and emissions spectra indicates E00 = 1.87 eV, different from E00 = 1.91 eV from computations, 2.1% error. The vibronic transitions responsible for maximum intensity are close in energy to E00 and are due to low frequency breathing and bending modes in ground and excited state. The higher energy vibronic transitions are largely due to symmetric C–C stretching modes and the highest from C–H stretching modes. Duschinsky matrices for the examples studied here are an indication of the mixing of normal modes due to geometric distortion between ground and excited state geometries. These are largely diagonal indicating a small degree of mixing of normal modes. Many of the predicted vibronic transitions involve simultaneous vibronic excitation of two and in some cases three vibrational modes. These would seem to also be important in computed spectra at typical laboratory temperatures. Computational memory constraints precluded use of time-independent FC methods to compute vibronic spectra at 298 K.
Computed spectra at 0 K and 298 K
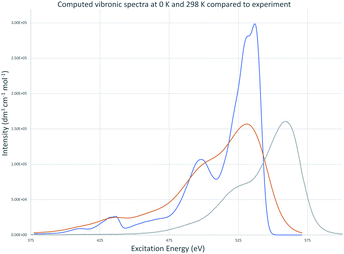
Vibronic spectra were also computed using time-dependent FC analysis. This approach allowed prediction of spectra at temperatures higher than 0 K with less computational demand by reducing the amount of memory needed which made time-independent computations inaccessible to us. The large memory demands found for room temperature time-independent FC computations is likely due to the large number of initial state low frequency vibrational energy levels that are thermally accessible at 298 K. The vibronic transitions due to low frequency vibrations make the major contributions to the major peak for cyanine dyes and are the focus of the QD method so cannot be neglected for the purposes of this work. TD vibronic spectra at 0 K matched those computed using time-dependent FC analysis while those at 298 K had lower intensity and showed less well-defined vibrational structure giving a closer match to the intensity of peaks in experimental spectra. The absorbance spectra of TC-3 in ethanol are shown in Fig. 7 as an example. The contours of the computed TC-3 absorption spectrum shown in Fig. 7 are a good match to the experimental spectrum. This was true to varying degrees for the examples studied. Computed vibronic spectra at 298 K tended to overestimate intensity at higher/lower excitation/emission energy compared to experimental spectra from the literature. While temperature had a pronounced effect on intensity and appearance of vibrational structure in the computed spectra, effect on λmax was negligible. The lower intensity with more thermally accessible vibrations at 298 K compared to 0 K in the computed spectra is suggestive of the enhanced fluorescence intensity of cyanine dyes with motions restricted by viscous media, aggregation, or binding to biomolecules.9,10,17,81Time-dependent FC methods do not give assignments for vibronic transitions. The good agreement between time-dependent and time-independent FC spectra at T = 0 K and analogous appearance of the spectra at room temperature suggest the low frequency vibrations continue to make an important contribution to the spectra at 298 K. The major peak in the computed vibronic absorption and emissions spectra for the examples presented here involves low frequency transitions and are presumably amenable to application of classical concepts which do not entail vertical excitation from the equilibrium geometry of the initial electronic state but from a position resulting from a weighted average between states in the transition similar to the r-centroid, 〈r〉 = 〈v′|r|v′′〉/〈v′|v′′〉, as discussed by Noda and Zare.5 The QD method developed and applied here is drastically simplified in comparison, only requiring use of Ev,a/f, Ead, and E00 and corresponds to an averaging between initial and final state optimized geometries. Results based on this approach are presented next.
Results from the quarter difference method
Absorption and fluorescence energies calculated from the QD method are compared with experimental values in Table 3. QD-AH include the effect of different ZPE in initial and final electronic states and QD-AS do not. Mean errors included in the bottom row of Table 3 indicate both approaches are more accurate than the vertical energies from the equilibrium geometry of the initial electronic state (Table 1) and only slightly less accurate than predictions made using computed vibronic spectra, Table 2. QD-AH are more accurate than QD-AS which overestimate transition energies by an average of about 0.06 eV due to the fact that excited state ZPEs are less than ground state ones by this amount on average for these examples. The improved accuracy of EQD,a from QD-AH compared to Ev,a is greater than EQD,f compared to Ev,f which are only slightly more accurate. Both Eabs/fl = hc/λmax from the computed vibronic spectra and the results from the QD method show excellent accuracy compared to results we have found in the literature from similar examples.21,28| Dye/solvent | EQD,a − AH | EQD,a − AS | Eabs exp. | EQD,f − AH | EQD,f − AS | Efl exp. |
|---|---|---|---|---|---|---|
| a M06HF/6-31G(d) and PCM nonequilibrium linear response solvation.b B3LYP/6-31G(d) and PCM nonequilibrium linear response solvation.c M06HF/6-31G(d) and PCM equilibrium solvation.d B3LYP/6-31G(d) and PCM equilibrium solvation.e PhotochemCAD https://www.photochemcad.com accessed July 2020.71–73f West and Pearce (1965).80g Sorokin et al. (1967).64h MN15/6-31G(d) and PCM nonequilibrium linear response solvation.i Thomas et al. (2010).9j MN15/6-31G(d) and PCM equilibrium solvation.k 2-Layer ONIOM MN15 for dye and UFF for DNA minor groove model.l B3LYP/6-31G(d) no solvent model used.m Eabs = hc/λmax from B3LYP/6-31G(d) computed vibronic spectrum also in vacuo.n Nakashima and Kunitake (1982).10o Xin et al. (2007).18p Eabs/fl = hc/λmax from M06/6-31G(d) in vacuo. | ||||||
| TC-1 water | 2.975h | 3.056h | 2.917i | 2.810j | 2.890j | 2.638i |
| TC-1 DNA | 3.044k | 3.152k | 2.948k | 3.055k | ||
| TC-3 ethanol | 2.286b | 2.367b | 2.220e | 2.198d | 2.270d | 2.170e |
| TC-3 ethanol | 2.388a | 2.386a | 2.220e | 2.247c | 2.273c | 2.170e |
| TC-3 water | 2.377b | 2.357b | 2.242f | 2.2534f | ||
| TC-3 water | 2.377a | 2.375a | 2.242f | 2.256c | 2.253c | |
| TC-3-NKG in vacuo | 2.587l | 2.672l | 2.583m | 2.551l | 2.668l | 2.555m |
| TC-3-NKG water | 2.295b | 2.369b | 2.292n | 2.195d | 2.270d | |
| TC-5 water | 1.985b | 2.051b | 1.91f | 1.896d | 21.873d | |
| TC-5 ethanol | 1.993b | 2.062b | 1.891e | 1.900d | 1.968d | 1.831e |
| TC-7 water | 1.747b | 1.808b | 1.647f | 1.649d | 1.710d | |
| TC-7 methanol | 1.756b | 1.819b | 1.638g | 1.660d | 1.723d | 1.553g |
| TC-7 2-propanol | 1.761b | 1.825b | 1.624g | 1.660d | 1.739d | |
| TC-7 DMSO | 1.743b | 1.805b | 1.605g | 1.654d | 1.716d | 1.523g |
| IC-3 methanol | 2.305b | 2.397b | 2.279e | 2.192d | 2.284d | 2.218e |
| IC-5 methanol | 2.028b | 2.107b | 1.945e | 1.929d | 2.008d | 1.884e |
| IC-7 ethanol | 1.800b | 1.870b | 1.667e | 1.712d | 1.783d | 1.610e |
| EG-M water | 2.533b | 2.640b | 2.638o | 2.463d | 2.569d | 2.362o |
| Curcumin in vacuo | 2.904p | 3.024p | 2.883p | 2.847p | 2.968p | 2.869p |
| Mean error | 0.08 ± 0.03 | 0.14 ± 0.01 | 0.07 ± 0.08 | 0.14 ± 0.02 | ||
To study these effects of solvent and anharmonicity in more detail we compared harmonic displacements energies from the computed normal modes and elements of the Duschinsky shift vector for TC-5 absorption and emission in the gas phase and in PCM ethanol and for curcumin in PCM ethanol and compared these with Ev,a − Ead and Ead − Ev,f on which the QD model is based. For TC-5 absorbance in ethanol Ev,a − Ead = 0.323 eV and 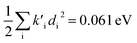 indicate a large effect due to solvent not included in the computed normal modes. For TC-5 fluorescence in ethanol Ead − Ev,f = 0.050 eV and
indicate a large effect due to solvent not included in the computed normal modes. For TC-5 fluorescence in ethanol Ead − Ev,f = 0.050 eV and 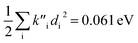 were found, a much smaller difference. For TC-5 in vacuo Ev,a − Ead = 0.0435 eV and
were found, a much smaller difference. For TC-5 in vacuo Ev,a − Ead = 0.0435 eV and 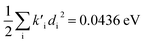 were found for absorbance and Ead − Ev,f = 0.0453 eV and
were found for absorbance and Ead − Ev,f = 0.0453 eV and 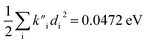 for fluorescence. It is unclear how much of the difference between these TC-5 absorption results in ethanol and in vacuum are due to nonequilibrium solvation and how much due anharmonicity from the larger displacement in ethanol. For TC-5, rms displacement in ethanol is 1.71 Å while in vacuo it is 0.799 Å. The error for QD-AH for TC-5 in ethanol is 0.102 eV compared to 0.041 eV from the computed vibronic spectrum both typical of these methods applied to the molecules studied here. To see if the agreement in vacuo would be equally as close for a similarly shaped molecule but not a cyanine dye, the same approach was used for curcumin in vacuo resulting in Ev,a − Ead = 0.112 eV and
for fluorescence. It is unclear how much of the difference between these TC-5 absorption results in ethanol and in vacuum are due to nonequilibrium solvation and how much due anharmonicity from the larger displacement in ethanol. For TC-5, rms displacement in ethanol is 1.71 Å while in vacuo it is 0.799 Å. The error for QD-AH for TC-5 in ethanol is 0.102 eV compared to 0.041 eV from the computed vibronic spectrum both typical of these methods applied to the molecules studied here. To see if the agreement in vacuo would be equally as close for a similarly shaped molecule but not a cyanine dye, the same approach was used for curcumin in vacuo resulting in Ev,a − Ead = 0.112 eV and 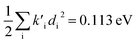 for absorption and Ead − Ev,f = 0.115 eV and
for absorption and Ead − Ev,f = 0.115 eV and 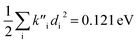 for fluorescence.
for fluorescence.
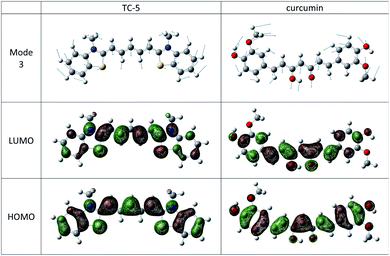
The THIA and INDO cyanine dyes and curcumin have similar molecular structures, a conjugated carbon chain with aromatic end groups on either end. These examples have the same low frequency vibration, mode 3 with wavenumber of about 22 cm−1 that makes the most significant vibronic contribution to the major peak and has the largest Duschinsky shift contribution. Mode 3 in these cases consists of a flexing motion with the middle of the conjugated chain and end groups moving in opposite directions. See Fig. 8. Movement along this mode from initial to final state equilibrium geometries is understandable based on the phase of the HOMO and LUMO for the electronic transitions studied here which are well characterized as HOMO–LUMO. Contour plots of these orbitals for TC-5 and curcumin are also shown in Fig. 8.
Mode 1 in EG-M (36 cm−1) has a similar motion but out of plane, a motion that would seem to make a strong contribution along the path from ground to first excited state. A vibronic spectrum was not obtained for EG-M but errors using the QD model were similar to other examples except EQD,a underestimates Eabs compared to experiment rather than overestimating it as in the other examples. This is an indication that higher frequency modes may make a stronger contribution to the vibronic lineshape of the dominant peak in EG-M. When EvaGreen is complexed to λDNA a longer wavelength peak which is only a shoulder in the spectrum of free EvaGreen becomes the dominant peak.18 EQD,a = 2.53 eV for EG-M is close to this lower energy peak that emerges when EG is complexed with λDNA with experimental Eabs = hc/λmax = 2.50 eV. By analogy to other cyanine dyes, the higher frequency dominant peak in EG may be due to vibrations of N-substituents, the tether in the case of EG, and these may be damped when the two EG-M moieties are complexed in the DNA minor groove.
FC analysis for curcumin in ethanol did not result in a vibronic spectrum due to poor spectral progression. Ev,a is very sensitive to % HF exchange in the XC functional used for this example. M06 gave the best Ev,a and Ev,f values of the functionals tried which were not exhaustive, 2.93 eV (423 nm) compared to 2.92 eV (425 nm) from experiment for absorption and 2.47 eV (502 nm) compared to 2.287 eV (542 nm) from experiment for fluorescence.77–79 The large predicted fluorescence redshift is explainable by a shift of electron density onto keto–enol oxygen atoms causing pronounced stabilization by the PCM ethanol. The even larger fluorescence redshift found in experiment is ascribed to solvent dynamics involving solvent molecule disruption of the enol–keto H-bond leading to nonradiative decay and coupling between dark and emissive excited states resulting in longer emitted wavelength.82 Experimental absorption and fluorescence spectra of curcumin in ethanol at room temperature show broad peaks with no apparent vibronic structure.77–79 Application of the QD method using the M06–PCM ethanol results gave large underestimation of Eabs = hc/λmax, with an error of −0.307 eV. This error will be analysed in the next section.
Accuracy of the QD method for cyanine dyes and limitations in extending application to other classes of molecules
The accuracy of λmax from computed vibronic spectra and the corresponding predictions from the QD model for cyanine dyes and curcumin in vacuo highlight cases where these methods can be applied with accurate results. The example of curcumin in ethanol highlights effects that need to be considered when applying the model to other classes of molecules.The results of FC analysis and the QD-AH method when applied to the THIA and INDO dyes are accurate when compared to experimental Eabs/fl = hc/λmax with mean errors less than 0.1 eV, a much higher degree of accuracy than results when vertical energies from the equilibrium geometry of the initial state, Ev,a/fl, are compared to experimental Eabs/fl = hc/λmax. In vacuo computations on TC-3-NKG were performed using BHandHLYP and SVP, 6-31G(d), and 6-311G(d) basis sets to compare with results from the literature and to investigate improvements gained from use of a solvent model as well a possible cancellation of errors which may be contributing to the accuracy of the results.
Our computed vibronic spectrum of TC-3-NKG in vacuo are similar to the results Guillaume et al. (2007) who found Ev,a of 3.01 eV, Ead of 2.93 eV (423 nm) and E00 of 2.84 (437 nm).28 Guillaume et al. concluded the remaining error to be due to the media, methanol 2.29 eV (542 nm) or bilayer membrane 2.19 eV (565 nm), and the XC density functional. We performed BHandHLYP/SVP computations in vacuo to confirm Guillaume et al.'s results and then used BHandHLYP/SVP in PCM methanol to distinguish errors ascribable to this functional and to media. We found Ev,a of 2.87 eV, Ead of 2.53 eV and E00 of 2.48 (499 nm) showing marked improvement when solvent is accounted for. Our results using B3LYP/6-31G* gave in vacuo results of Ev,a = 2.75 eV, Ead of 2.69 eV, and E00 of 2.57 eV improved to Ev,a = 2.62 eV, Ead of 2.28 eV, and E00 of 2.21 eV in PCM water in closer agreement with experimental Eabs = hc/241 nm of 2.29 eV with water as the solvent. B3LYP/6-31G* gives markedly more accurate results than BHandLYP/SVP so far as Ev,a, Ead, and E00 are appropriate for comparison to experimental spectra.
EQD,a, calculated from our B3LYP/6-31G* results further improves accuracy predicting Eabs = 2.30 eV, 0.13% error compared to experiment, small compared to our average from Table 3, 3.8%, which is still less than the error form BHandHLYP/SVP in PCM methanol, 9.2%.
To investigate the effects of solvent in more detail, state specific nonequilibrium solvation methods were applied to TC-3 in ethanol resulting in an increase in Ev,a = 2.79 eV compared to the nonequilibrium linear response model Ev,a = 2.60 eV using B3LYP. Results were similar using M06HF. If the linear response solvation method underestimates effects of nonequilibrium solvation on excitation energies by about 0.2 eV, this would put the errors in excitation energies from FC and QD methods more in the range one expects for M06HF applied to C3, C5, and C7 cyanine dyes.32 It's possible some of the accuracy of FC and QD results presented here is due to underestimation nonequilibrium solvation from linear response theory compensating overestimation of excitation energies from the DFT methods we employ. Results here show less accurate results for the TC-3-NKG example if BHandLYP is used. State specific nonequilibrium solvation applied to TC-3 fluorescence with ethanol the solvent gave similar results to equilibrium solvation indicating nonequilibrium solvation effects are small for fluorescence in this case.
Part of the error in comparing computed Ev,a to experimental Eabs = hc/λmax is the implicit assumption that electronic excitations occur from an exactly specified molecular geometry. The error can be avoided if λmax from a computed vibronic spectrum is used however, there can be difficulties with this comparison because electronic structure methods that predict accurate band shape due to vibronic transitions may not also predict accurate position in the spectrum. Bloino et al. (2015) found that functionals that give accurate position in the spectrum vastly underestimate the intensity of the major peak indicated by experiment for four coumarin dyes but give accurate results for the low frequency peak with maximum near E00.7 The situation is simpler for cyanine dyes for which this low frequency band is also the most intense one in experimental spectra and one can predict λmax for the spectrum based on this band that is also described well by functionals that give accurate position in the spectrum. Our finding that AH FC analysis and the QD method give more accurate λmax when B3LYP is used rather than BHandHLYP may be due to the fact that for cyanine dyes, the low frequency peak in the vibronic spectrum has the highest intensity. The QD method if applied to coumarin dyes would be appropriate for predicting λmax for this lowest frequency band but not the band corresponding to the most intense peak in the experimental spectrum.
Alternatively, following the example of Bloino et al. (2015), one might use two basis sets, for example, ωB97x for accurate overall band shape shifted by PBE0 results for accurate λmax. Translation of this approach to the QD model would mean using Ev,a/f and Ead from ωB97x to compute EQD,a/f and then shifting their position in the spectrum by Δλ = λVE,PBE0 − λVE,XCF where XCF, the functional used for more accurate vibronic structure, might be ωB97x. Using Ev,a/f and Ead from ωB97x would implicitly include effects of contributions from the vibrations contributing to the higher frequency peak more accurately described by ωB97x than by PBE0 which gives more accurate position. This approach may give better accuracy in comparison to a vibronic spectrum for which symmetric Gaussian broadening due to solvent does not allow these peaks to be distinguished.
The reliance of the QD method on only Ev,a/f, Ead, and E00 precludes its description of temperature dependent effects that cause both broadening of spectral lines and shifting in the spectrum. The TD-FC spectra we present show broadening at 298 K compared to 0 K but do not include temperature dependent solvent effects. Santoro et al. (2015) present a simple classically based approach to estimate solvent broadening based on a symmetric Gaussian distribution of solvent energies. The standard deviation in solvent energies is estimated according to temperature and difference in vertical transitions with nonequilibrium and equilibrium implicit solvation, σ2 = 2kBT(Eneqv − Eeqv).83 The results of state specific nonequilibrium solvation for TC-3 plugged into this equation give σ = 0.15 eV from B3LYP and σ = 0.14 eV from M06HF. The Gaussian peak from the B3LYP σ is shown in Fig. 9 compared to the experimental fluorescence spectrum of TC-3.
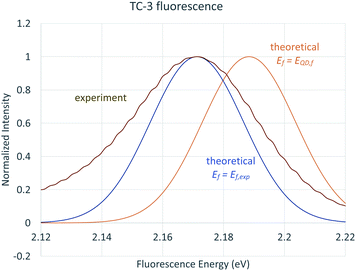 | ||
| Fig. 9 Experimental fluorescence (brown), theoretical Gaussian broadening centered at the experimental fluorescence energy (blue), theoretical Gaussian broadening centered at EQD,f (orange). | ||
In addition to solvent broadening with increased temperature, temperature dependent solvent effects may cause shifts in λmax. Huppert et al. (2011) show the spectrum of curcumin in ethanol at 84 K to include three peaks similar to the coumarin dyes, the central peak being the most intense and having λmax at 2.44 eV (509 nm) in excellent agreement with Ev,f = 2.47 eV (502 nm) from M06. They report the 0–0 peak at Ev,f = 2.59 eV (478 nm) while QD model gives QDv,f = 2.50 eV (496 nm) and an error of ≈ 0.1 eV much like the cyanine dye examples. Huppert et al. report the peaks in the curcumin vibronic emissions spectrum are separated by 1270 cm−1, 0.157 eV. Assuming the same band structure for the vibronic absorption spectrum at 84 K and λmax as reflecting the central peak, allows an estimate of the 0–0 peak in the absorption spectrum to be at 2.76 eV and an error in EQD,a of − 0.15 eV. Given that QD method applies to the low frequency peak, these errors are similar to those for the cyanine dyes.
Huppert et al. (2011) explain the dramatic redshift to 2.20 eV (563 nm) with increase in temperature to 298 K according to solvent dynamics that disrupt the intramolecular H-bond in the curcumin keto–enol system causing nonradiative decay by allowing the ring systems on either end to twist with respect to each other.82 They report the position and shape of the spectrum are nearly temperature independent at temperatures less than 165 K at which solvent dynamics have time scales similar to the excited state lifetime.
Temperature dependent solvation effects are more of a concern for curcumin and coumarin dyes than for cyanine dyes because curcumin and cyanine dyes have fluorescent life times in ethanol on order of nanoseconds, two order of magnitude greater than for cyanine dyes in ethanol.82,84,85 Temperature dependent solvent effects for cyanine dyes therefore would require much higher temperature.
Excited state twisting of molecules consisting of aromatic groups bridged by a conjugated carbon chain is a mechanism of nonradiative decay leading to lower fluorescence intensity. Prevention of such twisting at low temperatures or in an environment where the dye has more restricted movement enhances fluorescence and this property can be used in biosensors. This motivated computations with TC-1 in a DNA minor grove model to see if this environment would restrict the twisting found in the TC-1 excited state geometry in PCM water. EG has an enhanced and redshifted fluorescence in the DNA minor groove EG-M was also the subject of calculations in our DNA minor groove model.
ONIOM TC-1 and EG-M in the DNA minor groove model
The TC-1 cation in its ground state was predicted to have a twist along the methine chain when complexed in the DNA minor groove according to the ONIOM model used here. This is in contrast to its planar geometry predicted in water. See Fig. 10. The excited state, while optimizing with B3LYP and water as the PCM solvent drastically twists with puckering similar to the ethylene first excited state.75 A minimum energy geometry was not found. The first excited state of ethylene is an example used to test DFT methods designed for use in cases that are multireference in the context of wavefunction methods.75 Excited state geometries were successfully optimized for TC-1 in PCM water and in the ONIOM DNA minor groove model using ONIOM MN15:UFF. See Fig. 10. The change in excited state twisting is less for TC-1 in the DNA minor groove (change in dihedral S1C2C6S2 17° → 28° GS → ES) than in water (change in dihedral S1C2C6S2 0° → 43° GS → ES) indicating a more restricted geometry in the DNA minor groove setting consistent with enhanced fluorescence displayed by TC-1 in a biological setting. Attempts at calculating a vibronic spectrum for TC-1 in the DNA minor groove and in water were not successful. Large expected errors in the ZPE due to a large number of normal modes in the DNA model precluded use of the QD method. EG-M showed one imaginary vibrational frequency in its excited state in the ONIOM DNA minor groove calculations precluding further analysis by FC or QD methods. The QD model results for EG-M still allow some interpretation as to the nature of the redshift of EG when complexed to λDNA though our DNA model does not contribute to this interpretation.Possible explanation of redshift in EvaGreen absorbance in presence of λDNA
The fused ring structure of EG-M is different than the THIA and INDO cyanine dyes and the underestimation by EQD,a of EG-M experimental Eabs for free EG seems to imply higher frequency vibronic transitions contribute to the major band for this molecule similar to the curcumin and coumarin examples. If this is the case, the dominant low frequency band that emerges when EG is complexed to λDNA with Eabs = hc/λmax = 2.50 eV may be due to a low frequency band well described by EQD,a = 2.53 eV.Conclusions
Vertical transition energies, Ev,a/f from the equilibrium geometry of the initial electronic state in a transition are frequently considered to be representative of the Eabs/fl = hc/λmax from experiment. It is shown here Ev,a/f for THIA and INDO cyanine dyes occur in the Franck–Condon region predicted by TDDFT and FC analysis but correspond to vibrations far from the most intense peak and to vibrational structure that is mostly washed out in experimental spectra in solution. Low wavenumber vibrations contribute to the major peak in the computed vibronic spectra with Eabs/fl = hc/λmax showing a 10-fold improvement in accuracy compared to Ev,a. The computed vibronic spectra are based on the quantum version of the FC principle which relies neither on exactly specified molecular geometries before, during, or after a transition nor specified duration for an electronic transition in comparison to the period of molecular vibrations involved in it.A classically inspired approach is developed which corresponds to vertical transitions from an averaged molecular geometry appropriate in a way analogous to the r-centroid that preserves kinetic energy before and after an electronic transition in accord with the classical version of the FC principle. We refer to this classically inspired approach as the quarter difference (QD) method based on the way it utilizes the harmonic approximation. Application of the quantum FC and QD methods give better accuracy than Ev,a/f showing a 5-fold improvement in accuracy compared experiment.
The QD model is an implementation of an adiabatic approximation appropriate for low frequency vibronic transitions near the 0–0 transition as appropriate for a classical approximation. This is the major peak in spectra of cyanine dyes so the approach is particularly well suited for them. Extension of the QD model to non-cyanine dyes was tested using M06 computations which gave accurate position in the spectrum for curcumin, but with inaccurate overall band shape due to underestimation of the intensity of higher frequency bands as seen in the literature for coumarin dyes. Though the vibronic spectrum of curcumin in ethanol was not obtained, the QD model applied to the low frequency band and compared to the low frequency band from experiment gave similar accuracy as for cyanine dyes. Dyes with long lifetimes compared to solvent dynamics such as curcumin and coumarin dyes are more prone to temperature dependent solvation effects on their spectra and comparisons to results from the QD model is more complicated but not impossible as was demonstrated with the curcumin example.
Computed vibronic spectra at 298 K show reduced intensity at this temperature compared to 0 K suggestive of experimental spectra where solvent viscosity, aggregation, or complexation to biomolecules restrict motion of the dye. A 2-layer ONIOM model of the DNA model shows the geometry of the TC-1 dye excited state has a restricted twist in its geometry compared to that in water and perhaps conducive to enhance fluorescence in this setting. EQD,a for EG-M matches the longer wavelength peak that becomes dominant when EG is bound to λDNA. This could indicate a change in EvaGreen vibrations due to this complexation perhaps damping those responsible for the higher frequency peak in free EG and enhancing low frequency vibronic transitions well described by the QD model.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors are grateful to the UMN Morris Chemistry Discipline, Division of Science and Mathematics, and Dean's Office for the sabbatical during which a major part of the work presented here was completed. We thank the UMN Morris Dean's Office, Grant's Developement Office, and FREF committee for the FREF funds that paid the open access fee for this publicaiton.Notes and references
- J. Franck, Z. Phys. Chem., Stoechiom. Verwandtschaftsl., 1926, 120, 144–156 Search PubMed.
- E. Condon, Phys. Rev., 1926, 28, 1182–1201 CrossRef CAS.
- E. U. Condon, Phys. Rev., 1928, 32, 0858–0872 CrossRef CAS.
- S. E. Schwartz, J. Chem. Educ., 1973, 50, 608–610 CrossRef CAS.
- C. Noda and R. N. Zare, J. Mol. Spectrosc., 1982, 95, 254–270 CrossRef CAS.
- A. Hazra, H. H. Chang and M. Nooijen, J. Chem. Phys., 2004, 121, 2125–2136 CrossRef CAS.
- F. Muniz-Miranda, A. Pedone, G. Battistelli, M. Montalti, J. Bloino and V. Barone, J. Chem. Theory Comput., 2015, 11, 5371–5384 CrossRef CAS.
- W. H. Mills and R. S. Wishart, J. Chem. Soc., 1920, 117, 579–587 RSC.
- M. S. Thomas, V. Nunez, S. Upadhyayula, E. R. Zielins, D. Bao, J. M. Vasquez, B. Bahmani and V. I. Vullev, Langmuir, 2010, 26, 9756–9765 CrossRef CAS.
- N. Nakashima and T. Kunitake, J. Am. Chem. Soc., 1982, 104, 4261–4262 CrossRef CAS.
- H. S. Mohammed, J. O. Delos Santos and B. A. Armitage, Artif. DNA PNA XNA, 2011, 2, 43–49 CrossRef.
- V. B. Kovalska, M. Y. Losytskyy, O. I. Tolmachev, Y. L. Slominskii, G. M. Segers-Nolten, V. Subramaniam and S. M. Yarmoluk, J. Fluoresc., 2012, 22, 1441–1448 CrossRef CAS.
- J. K. Choi, A. D'Urso, M. Trauernicht, M. Shabbir-Hussain, A. E. Holmes and M. Balaz, Int. J. Mol. Sci., 2011, 12, 8052–8062 CrossRef CAS.
- C. Wang, C. Wu, D. C. Popescu, J. Zhu, W. B. Macklin, R. H. Miller and Y. Wang, J. Neurosci., 2011, 31, 2382–2390 CrossRef CAS.
- S. L. Liu, Z. G. Wang, H. Y. Xie, A. A. Liu, D. C. Lamb and D. W. Pang, Chem. Rev., 2020, 120, 1936–1979 CrossRef CAS.
- A. R. Nodling, E. M. Mills, X. F. Li, D. Cardella, E. J. Sayers, S. H. Wu, A. T. Jones, L. Y. P. Luk and Y. H. Tsai, Chem. Commun., 2020, 56, 4672–4675 RSC.
- I. Domljanovic, A. Carstens, A. Okholm, J. Kjems, C. T. Nielsen, N. H. H. Heegaard and K. Astakhova, Sci. Rep., 2017, 7, 1925 CrossRef.
- F. Mao, W. Y. Leung and X. Xin, BMC Biotechnol., 2007, 7, 76 CrossRef.
- L. Falzone, N. Musso, G. Gattuso, D. Bongiorno, C. I. Palermo, G. Scalia, M. Libra and S. Stefani, Int. J. Mol. Med., 2020, 46, 957–964 CrossRef CAS.
- C. I. Oprea, P. Panait, Z. M. Essam, R. M. Abd El-Aal and M. A. Girtu, Nanomaterials, 2020, 10, 662 CrossRef CAS.
- G. Pepe, J. M. Cole, P. G. Waddell and S. McKechnie, Mol. Syst. Des. Eng., 2016, 1, 86–98 RSC.
- C. R. Bury, J. Am. Chem. Soc., 1935, 57, 2115–2117 CrossRef CAS.
- H. Kuhn, J. Chem. Phys., 1949, 17, 1198–1212 CrossRef CAS.
- C. Sassa, A. Painelli, F. Terenziani, M. Trotta and R. Ragni, Phys. Chem. Chem. Phys., 2019, 7, 444–445 Search PubMed.
- M. Eskandari, J. C. Roldao, J. Cerezo, B. Milián-Medina and J. Gierschner, J. Am. Chem. Soc., 2020, 142, 2835–2843 CrossRef CAS.
- K. Yesudas, Phys. Chem. Chem. Phys., 2013, 15, 19456 RSC.
- J. A. Potenza, L. Zyontz and W. Rorowski, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1978, 34, 193–199 CrossRef.
- M. Guillaume, V. Liegeois, B. Champagne and F. Zutterman, Chem. Phys. Lett., 2007, 446, 165–169 CrossRef CAS.
- H. Mustroph and A. Towns, ChemPhysChem, 2018, 19, 1016–1023 CrossRef CAS.
- R. Send, O. Valsson and C. Filippi, J. Chem. Theory Comput., 2011, 7, 444–455 CrossRef CAS.
- M. Dierksen and S. Grimme, J. Chem. Phys., 2004, 120, 3544–3554 CrossRef CAS.
- D. Jacquemin, Y. Zhao, R. Valero, C. Adamo, I. Ciofini and D. G. Truhlar, J. Chem. Theory Comput., 2012, 8, 1255–1259 CrossRef CAS.
- B. Le Guennic and D. Jacquemin, Acc. Chem. Res., 2015, 48, 530–537 CrossRef CAS.
- K. Meguellati, S. Ladame and M. Spichty, Dyes Pigm., 2011, 90, 114–118 CrossRef CAS.
- K. Nakano, T. Konishi and Y. Imamura, Chem. Phys., 2019, 518, 15–24 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, 2013 Search PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. J. Montgomery, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 2016 Search PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- C. T. Lee, W. T. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS.
- S. H. Vosko, L. Wilk and M. Nusair, Can. J. Phys., 1980, 58, 1200–1211 CrossRef CAS.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627 CrossRef CAS.
- Y. Zhao and D. G. Truhlar, J. Phys. Chem. A, 2006, 110, 13126–13130 CrossRef CAS.
- S. Miertuš, E. Scrocco and J. Tomasi, Chem. Phys., 1981, 55, 117–129 CrossRef.
- S. Miertuš and J. Tomasi, Chem. Phys., 1982, 65, 239–245 CrossRef.
- J. L. Pascual-Ahuir, E. Silla and I. Tuñón, J. Comput. Chem., 1994, 15, 1127–1138 CrossRef CAS.
- M. Cossi, V. Barone, R. Cammi and J. Tomasi, Chem. Phys. Lett., 1996, 225, 327–335 CrossRef.
- V. Barone, M. Cossi and J. Tomasi, J. Chem. Phys., 1997, 107, 3210–3221 CrossRef CAS.
- E. Cancès, B. Mennucci and J. Tomasi, J. Chem. Phys., 1997, 107, 3032–3041 CrossRef.
- B. Mennucci and J. Tomasi, J. Chem. Phys., 1997, 106, 5151–5158 CrossRef CAS.
- B. Mennucci, E. Cancès and J. Tomasi, J. Phys. Chem. B, 1997, 101, 10506–10517 CrossRef CAS.
- V. Barone and M. Cossi, J. Phys. Chem. A, 1998, 102, 1995–2001 CrossRef CAS.
- M. Cossi, V. Barone, B. Mennucci and J. Tomasi, Chem. Phys. Lett., 1998, 286, 253–260 CrossRef CAS.
- J. Tomasi, B. Mennucci and E. Cancès, J. Mol. Struct.: THEOCHEM, 1999, 464, 211–226 CrossRef CAS.
- M. Cossi and V. Barone, J. Chem. Phys., 2000, 112, 2427–2435 CrossRef CAS.
- M. Cossi and V. Barone, J. Chem. Phys., 2001, 115, 4708–4717 CrossRef CAS.
- M. Cossi, N. Rega, G. Scalmani and V. Barone, J. Chem. Phys., 2001, 114, 5691–5701 CrossRef CAS.
- M. Cossi, G. Scalmani, N. Rega and V. Barone, J. Chem. Phys., 2002, 117, 43–54 CrossRef CAS.
- M. Cossi, N. Rega, G. Scalmani and V. Barone, J. Comput. Chem., 2003, 24, 669–681 CrossRef CAS.
- G. Scalmani and M. J. Frisch, J. Chem. Phys., 2010, 132, 114110 CrossRef.
- R. Cammi, B. Mennucci and J. Tomasi, J. Phys. Chem. A, 2000, 104, 5630–5637 Search PubMed.
- G. Scalmani, M. J. Frisch, B. Mennucci, J. Tomasi, R. Cammi and V. Barone, J. Chem. Phys., 2006, 124, 94107 CrossRef.
- R. Improta, V. Barone, G. Scalmani and M. J. Frisch, J. Chem. Phys., 2006, 125, 054103 CrossRef.
- R. Improta, G. Scalmani, M. J. Frisch and V. Barone, J. Chem. Phys., 2007, 127, 074504 CrossRef.
- P. P. Sorokin, J. R. Lankard, E. C. Hammond and V. L. Moruzzi, IBM J. Res. Dev., 1967, 11, 130 CAS.
- F. Santoro, R. Improta, A. Lami, J. Bloino and V. Barone, J. Chem. Phys., 2007, 126, 084509 CrossRef.
- F. Santoro, A. Lami, R. Improta and V. Barone, J. Chem. Phys., 2007, 126, 184102 CrossRef.
- F. Santoro, A. Lami, R. Improta, J. Bloino and V. Barone, J. Chem. Phys., 2008, 128, 224311 CrossRef.
- V. Barone, J. Bloino, M. Biczysko and F. Sanroro, J. Chem. Theory Comput., 2009, 5, 540–554 CrossRef CAS.
- A. K. Rappé, K. S. Colwell, W. A. Goddard, W. M. Skiff and C. J. Casewit, J. Am. Chem. Soc., 1992, 114, 10024–10035 CrossRef.
- A. K. Rappé, L. M. Bormann-Rochotte, D. C. Wiser, J. R. Hart, M. A. Pietsch and C. J. Casewit, Mol. Phys., 2007, 105, 301–324 CrossRef.
- S. Dapprich, I. Komaromi, K. S. Byun, K. Morokuma and M. J. Frisch, J. Mol. Struct.: THEOCHEM, 1999, 461, 1–21 CrossRef.
- T. Vreven and K. Morokuma, Annu. Rep. Comput. Chem., 2006, 2, 35–51 CAS.
- T. Vreven, K. S. Byun, I. Komaromi, S. Dapprich, J. A. Montgomery, K. Morokuma and M. J. Frisch, Abstr. Pap. Am. Chem. Soc., 2006, 232, 408 Search PubMed.
- F. R. Clemente and T. Vreven, Quantum Biochemistry, Wiley VCH, Weinheim, 2010 Search PubMed.
- A. D. Becke, Mol. Phys., 2015, 113, 1884–1889 CrossRef CAS.
- H. Y. S. Yu, X. He, S. H. L. Li and D. G. Truhlar, Chem. Sci., 2016, 7, 5032–5051 RSC.
- M. Taniguchi, H. Du and J. S. Lindsey, Photochem. Photobiol., 2018, 94, 277–289 CrossRef CAS.
- M. Taniguchi and J. S. Lindsey, Photochem. Photobiol., 2018, 94, 290–327 CrossRef CAS.
- M. Taniguchi, J. S. Lindsey and H. Du, PhotochemCAD, accessed July 2020 Search PubMed.
- W. West and S. Pearce, J. Phys. Chem., 1965, 69, 1894 CrossRef CAS.
- S. Ozcelik and D. L. Akins, J. Phys. Chem. B, 1999, 103, 8926–8929 CrossRef.
- Y. Erez, I. Presiado, R. Gepshtein and D. Huppert, J. Phys. Chem. A, 2011, 115, 10962–10971 CrossRef CAS.
- J. Cerezo, F. J. A. Ferrer, G. Prampolini and F. Santoro, J. Chem. Theory Comput., 2015, 11, 5810–5825 CrossRef CAS.
- C. A. Guarin, J. P. Villabona-Monsalve, R. Lopez-Arteaga and J. Peon, J. Phys. Chem. B, 2013, 117, 7352–7362 CrossRef CAS.
- G. Jones, W. R. Jackson, C. Choi and W. R. Bergmark, J. Phys. Chem., 1985, 89, 294–300 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2020 |