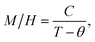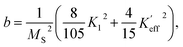Open Access Article
Open Access ArticleSmart magnetic nanopowder based on the manganite perovskite for local hyperthermia†
A. V. Pashchenkoabc,
N. A. Liedienov *ab,
I. V. Fesychd,
Quanjun Lia,
V. G. Pitsyugae,
V. A. Turchenkobf,
V. G. Pogrebnyakc,
Bingbing Liu
*ab,
I. V. Fesychd,
Quanjun Lia,
V. G. Pitsyugae,
V. A. Turchenkobf,
V. G. Pogrebnyakc,
Bingbing Liu a and
G. G. Levchenko
a and
G. G. Levchenko *ab
*ab
aState Key Laboratory of Superhard Materials, International Center of Future Science, Jilin University, 130012 Changchun, China. E-mail: nikita.ledenev.ssp@gmail.com
bDonetsk Institute for Physics and Engineering named after O.O. Galkin, NAS of Ukraine, 03028 Kyiv, Ukraine. E-mail: g-levch@ukr.net
cIvano-Frankivsk National Technical University of Oil and Gas, MESU, 76019 Ivano-Frankivsk, Ukraine
dTaras Shevchenko National University of Kyiv, 01030 Kyiv, Ukraine
eVasyl' Stus Donetsk National University, 21021 Vinnytsia, Ukraine
fFrank Laboratory of Neutron Physics, Joint Institute for Nuclear Research, 141980 Dubna, Russia
First published on 20th August 2020
Abstract
For many medical applications related to diagnosis and treatment of cancer disease, hyperthermia plays an increasingly important role as a local heating method, where precise control of temperature and parameters of the working material is strongly required. Obtaining a smart material with “self-controlled” heating in a desirable temperature range is a relevant task. For this purpose, the nanopowder of manganite perovskite with super-stoichiometric manganese has been synthesized, which consists of soft spherical-like ferromagnetic nanoparticles with an average size of 65 nm and with a narrow temperature range of the magnetic phase transition at 42 °C. Based on the analysis of experimental magnetic data, a specific loss power has been calculated for both quasi-stable and relaxation hysteresis regions. It has been shown that the local heating of the cell structures to 42 °C may occur for a short time (∼1.5 min.) Upon reaching 42 °C, the heating is stopped due to transition of the nanopowder to the paramagnetic state. The obtained results demonstrate the possibility of using synthesized nanopowder as a smart magnetic nanomaterial for local hyperthermia with automatic heating stabilization in the safe range of hyperthermia without the risk of mechanical damage to cell structures.
1. Introduction
In modern science, medical applications related to (i) magnetic separation,1 (ii) targeted drug delivery to diseased tissues,2 (iii) the creation of new MRI contrast agents working at the cellular and molecular level for tumor theranostics,3,4 (iv) tissue engineering and regenerative medicine,5,6 (v) magnetic hyperthermia7,8 are of great interest. In each of these applications, a unique combination of the properties for magnetic nanoparticles (MNPs) is to have a small size and to generate heat under an alternating magnetic field (AMF). The MNP size is in the range of ∼1–100 nm, which is comparable with the sizes of intracellular biological structures of ∼10–100 nm, viruses ∼10–200 nm, proteins ∼4–50 nm and genes ∼2–100 nm.9 This allows MNP to penetrate into the tissue and affect the physiological processes of the body at the cellular level. The intensity of heating depends both on the properties of the magnetic nanomaterial (dispersion, Curie temperature, coercivity, magnetization), and on the characteristics of the external influence (temperature, exposure time, AMF amplitude and frequency). While local heating above 44 °C, necrosis of muscle tissue occurs in 10 min.10 To avoid overheating, it is necessary to strictly control exposure time, AMF amplitude and nanoparticle concentration.11 The risk of tissue overheating is minimized by the intelligent control system for magnetic hyperthermia. The work of the intelligent system is based on the fact that the Curie temperature of the particles is in the safe hyperthermia range of 42–44 °C. Above the Curie temperature, the particle goes into the paramagnetic (PM) state and its heating ceases. Such a nanopowder exhibits the properties of a smart nanomaterial, since it automatically changes its properties depending on external conditions.The synthesis of such smart nanopowder allows us to solve another complex problem that is associated with intracellular (local) hyperthermia.12,13 In magnetic hyperthermia, heating of a particle occurs as a result of losses associated with both frictional heating of a particle during its rotation under AMF (Brownian relaxation) and relaxation of magnetization without rotation of the particle (Néel relaxation).14 In intracellular hyperthermia, a particle via the core–shell structure is modified with biocompatible agents and is rigidly attached to the protein structures of the cell.15 The rotation of such a particle under AMF can lead to mechanical damage and cell death.16 In order to avoid mechanical damage to cell structures, heating should be carried out only as a result of Néel relaxation. The temperature dependence of the specific loss power (SLP) during the Néel relaxation has a resonant form and increases sharply near the temperature of the magnetic phase transition.17 Since, the Curie temperature of smart magnetic nanopowder is in the hyperthermia range of 42–44 °C, such powder with the necessary set of magnetic properties can be used for local hyperthermia without the risk of mechanical damage to cell structures. The search for such smart magnetic nanopowder is a topical task for materials science, physics, nanomedicine and nanotechnology.
2. Heating mechanism and composition choice
In the magnetometric method, which is used to estimate the heating efficiency in hyperthermia,18 the SLP can be obtained from hysteresis losses during magnetization reversal.19 The hysteresis heating can be observed both in the quasi-stable hysteresis and in the relaxation hysteresis. The main difference in the heating mechanisms is that dissipative processes appear in the relaxation region, which are associated with the appearance of a phase difference between the AMF and magnetization.20,21 The SLP in single-domain (SD) particles under the AMF is significantly higher than in multidomain (MD) particles.22 Thus, it is advisable to use a magnetic powder, which should consist of SD soft MNPs with a large magnetization near FM transition temperature.For SD monodisperse spherical particles in the quasi-stable region, the magneto-field dependence of the specific hysteresis loss wsw is approximated by the following expression:23
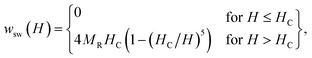 | (1) |
| SLP(H, f) = wsw(H) × f. | (2) |
Heating MNPs in the relaxation hysteresis is associated with the relaxation processes of magnetization. The relaxation time τR for soft magnetic particles, which do not rotate and do not move in the AMF, is equal to the Néel relaxation time τR = τN = τ0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(KeffV/kBT), where τ0 ∼ 10−9 to 10−13 s is the characteristic relaxation time.20,24–26 On the hysteresis curves M(H), the inclusion of the relaxation magnetization processes manifests itself in increasing the area of the hysteresis region A, which has an ellipsoidal shape with an increase in the AMF frequency f.27 In the magnetic hyperthermia for nanosystems with the parameter σ = KeffV/kBT, the specific hysteresis loss wsw in the relaxation region is calculated by the following expressions:20
exp(KeffV/kBT), where τ0 ∼ 10−9 to 10−13 s is the characteristic relaxation time.20,24–26 On the hysteresis curves M(H), the inclusion of the relaxation magnetization processes manifests itself in increasing the area of the hysteresis region A, which has an ellipsoidal shape with an increase in the AMF frequency f.27 In the magnetic hyperthermia for nanosystems with the parameter σ = KeffV/kBT, the specific hysteresis loss wsw in the relaxation region is calculated by the following expressions:20
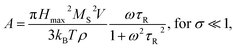 | (3) |
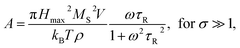 | (4) |
With an increase in the temperature, the heating efficiency of SLP in a quasi-stable hysteresis region decreases in proportion to the multiplication of MR and HC (see eqn (1) and (2)) and equals zero at TC. However, the SLP increases for the relaxation hysteresis near the temperature of the magnetic phase transition (see eqn (4)). This heating mechanism of particles to a Curie temperature is advisable to use as the main mechanism for heating magnetic nanoparticles in local hyperthermia. The search for a soft magnetic material with a Curie temperature tC = 42–44 °C, a high saturation magnetization near the Curie temperature, and a narrow temperature FM–PM phase transitions is a topical task for both hyperthermia and material science. Summarizing the above, it is possible to establish requirements for the choice of the composition and characteristics of nanopowder that can be used as a smart magnetic material for local hyperthermia: (i) the nanopowder should be a soft magnetic material, (ii) the magnetic nanoparticles should be predominantly in the SD state, (iii) the Curie temperature should be in the tC = 42–44 °C range, (iv) the nanopowder should have a narrow temperature range of the magnetic phase transition FM–PM, (v) the magnetic nanoparticles should have a large saturation magnetization MS near tC, and (vi) the nanopowder should have a lower HC coercivity with respect to the AMF (Hmax > HC).
This list of functional properties may be satisfied by rare-earth manganites La1−xAxMnO3 with a perovskite structure ABO3,28,29 where A is a mono- or divalent large A-cation, such Ca2+, Sr2+, Ba2+, K+, Na+, or Ag+. The Curie temperature of these compounds strongly depends on the ratio MnB3+/MnB4+, so it is quite easy to control it by changing the concentration and valence state of the A-cation to obtain tC = 42–44 °C.
Great difficulties in finding the magnetic material for local hyperthermia are connected with the fact that they should have a narrow temperature range of the FM–PM magnetic phase transition. An increase in the temperature range of the magnetic phase transition is associated with both the appearance of local antiferromagnetic interactions caused by the Jahn–Teller electron–phonon interaction with orthorhombic distortions,30 and the magnetic inhomogeneity of the local environment of manganese as a result of the presence of cation V(c) and anion V(a) vacancies.31,32 Superstoichiometric manganese is an excess manganese, for which the filling factor of the B-position in the molar formula exceeds one. Using NMR 55Mn method,31 it was shown that super-stoichiometric manganese, which fills cation vacancies and completes the B-sublattice of manganese, increases magnetic homogeneity and reduces the temperature range of magnetic ordering. It should be noted that among the compositions with super-stoichiometric manganese of La1−xMn1+xO3−δ,33 La0.7Sr0.3Mn1.1O3,34 La0.7Sr0.3−xBixMn1.1O3,35 (La0.7Ca0.3)1−xMn1+xO3,36,37 (Nd0.7Sr0.3)1−xMn1+xO3−δ,31 and La0.9−xAgxMn1.1O3,38 the Ag-containing manganites have a Curie temperature which most close to the necessary functional properties of the magnetic material for hyperthermia, i.e. tC = 42–44 °C.39 Therefore, the non-stoichiometric La0.6Ag0.2Mn1.2O3 composition with an increased content of super-stoichiometric manganese is considered here as the basis for the production of smart magnetic nanopowder for local hyperthermia. In addition, on the toxicity of the investigated nanopowder, it should be added that the manganite perovskite nanoparticles show a better colloidal stability, good biocompatibility with cell lines and do not have toxic effects.40
3. Methods
The pyrolytic synthesis of La0.6Ag0.2Mn1.2O3 nanopowder was used. As initial components, aqueous solutions of lanthanum nitrate (0.5 mol L−1), manganese nitrate (0.6 mol L−1), and silver nitrate (0.1 mol L−1) were used. The nitrate solutions were mixed in a stoichiometric ratio and evaporated in a water bath at 80 °C for 6 h. Pyrolysis of the dried mixture was carried out at 600 °C. After grinding in an agate mortar, the powder was calcined in an alundum crucible at 800 °C (10 h). Additional synthesizing annealing was performed at 900 °C (20 h). The powder was cooled under conditions of natural heat exchange between the furnace and the environment.X-ray diffraction studies were performed on a Shimadzu LabX XRD-6000 X-ray diffractometer in Cu Kα-radiation. Additionally, the phase composition and the type of crystal structure of the studied powder was analyzed by X-ray diffractometer MicroMax-007 HF (Rigaku, Japan) in Mo-Kα radiation, λ = 0.71146 Å. The refinement of crystal structure was carried out with Rietveld analysis,41 using the FullProf software.42 The microstructural characterization of the La0.6Ag0.2Mn1.2O3 nanopowder was performed using JEOL JEM-2200FS transmission electron microscopy (TEM). High-resolution TEM (HRTEM) with accelerating voltage of 200 kV was also used to image La0.6Ag0.2Mn1.2O3 nanoparticles. A sample for the TEM analysis was prepared by placing a drop of diluted suspension of particles in acetone onto a carbon coated copper grid. Particle morphology and particle size were determined by scanning electron microscopy (SEM) on an FEI MAGELLAN 400 Scanning Electron Microscope. Magnetic measurements were carried out on a Quantum Design SQUID MPMS 3 SQUED magnetometer in the temperature range from 2 to 400 K and in magnetic fields up to 70 kOe.
4. Results and discussion
4.1. Structure, phase composition, morphology, and the size of nanoparticles
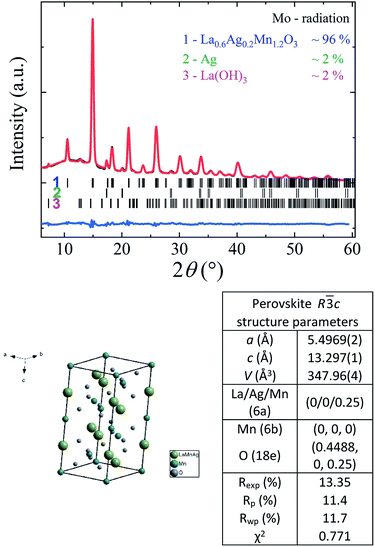
According to X-ray data (see Fig. 1), the crystal structure of the La0.6Ag0.2Mn1.2O3 nanopowder is well described in the framework of rhombohedral R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c space group (No. 167). The sample has a small quantity of impurities: Ag (∼2%) and La(OH)3 (∼2%). The parameters and volume of perovskite unit cell in the hexagonal setup are equal to a = 5.4969(2) Å, c = 13.297(1) Å and V = 347.96(4) Å, respectively. The X-ray density of La0.6Ag0.2Mn1.2O3 with a molar mass of 218.8 g mol−1 and an amount of Z = 6 molar formulas per unit cell is ρx = 6.266 g cm−3. The preservation of structural single-phase up to 96% with a large amount of 20% super-stoichiometric manganese and its absence in minor phases indicates its complete dissolution in the perovskite structure with completed manganese B-sublattice.
c space group (No. 167). The sample has a small quantity of impurities: Ag (∼2%) and La(OH)3 (∼2%). The parameters and volume of perovskite unit cell in the hexagonal setup are equal to a = 5.4969(2) Å, c = 13.297(1) Å and V = 347.96(4) Å, respectively. The X-ray density of La0.6Ag0.2Mn1.2O3 with a molar mass of 218.8 g mol−1 and an amount of Z = 6 molar formulas per unit cell is ρx = 6.266 g cm−3. The preservation of structural single-phase up to 96% with a large amount of 20% super-stoichiometric manganese and its absence in minor phases indicates its complete dissolution in the perovskite structure with completed manganese B-sublattice.
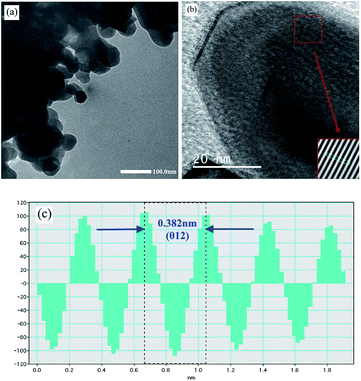
According to the SEM and TEM studies, the La0.6Ag0.2Mn1.2O3 nanopowder consists of spherical-like nanoparticles with an average particle size of DSEM0 = 65 ± 1 nm (see ESI 2†) and DTEM0 ∼ 60 nm (see Fig. 2a), which is in agreement with the XRD, since an average size of the coherent scattering regions is DXRD0 = 62 ± 2 nm (see ESI 1†). HRTEM image of the sample (Fig. 2b) clearly shows the lattice interplanar distance of the La0.6Ag0.2Mn1.2O3 nanoparticles. The Fast Fourier Transform (FFT) using Gatan Microscopy Suite software was used to measure the interplanar distance (see insert in Fig. 2b). Fig. 2c demonstrates the corresponding lattice plane intensity profile. The interplanar distance of 0.382 nm (012) obtained from FFT is in a good agreement with the XRD data.
The availability of even a slight dispersion in the size D can lead to the magnetic particles being in both the SD and MD states. The magnetic state of a particle affects the magnetic loss of the nanopowder. Establishment of boundary sizes for the La0.6Ag0.2Mn1.2O3 nanopowder, when the transition is observed from one magnetic state to another one, is of interest from a practical point of view for hyperthermia. For this purpose, it is necessary to study the magnetic properties of the La0.6Ag0.2Mn1.2O3 nanopowder in wide temperature and magnetic field ranges.
4.2. Magnetic properties of La0.6Ag0.2Mn1.2O3 nanopowder
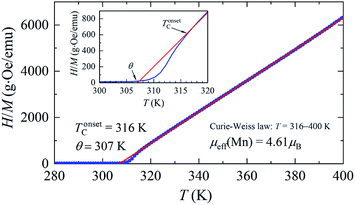
The temperature dependences of the (M/H)ZFC(T) and (M/H)FC(T) magnetic susceptibility (see Fig. 3) correspond to a typical manifestation of the magnetic properties of a nanopowder that consists of non-interacting SD FM nanoparticles with randomly oriented uniaxial magnetic anisotropy.43–45 The Curie temperature TC = 308 K was determined from the temperature dependences of the d(M/H)/dT derivative (see inset on Fig. 3). The blocking temperature TB = 301 K is the maximum of the ZFC curve.46 For T < TB, the MNPs are in the blocked state. At T > TB, the particles go into superparamagnetic (SPM) unblocked state and the ZFC and FC curves should coincide.47 Usually, the effective anisotropy constant Keff is determined using a simple its connection with the temperature TB:48| KeffV ≈ 25kBTB. | (5) |
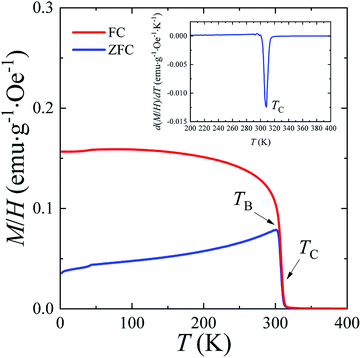 | ||
| Fig. 3 The temperature dependencies of (M/H)ZFC(T) and (M/H)FC(T) magnetic susceptibility, the Curie temperature TC and the blocking temperature TB at H = 50 Oe for the La0.6Ag0.2Mn1.2O3 nanopowder. | ||
From eqn (5), the constant Keff = 7.123 × 103 erg cm−3 is calculated for the La0.6Ag0.2Mn1.2O3 nanopowder with the blocking temperature TB = 301 K and the average size of D0 = 65.3 nm for spherical particles.
A more detailed analysis of the ZFC/FC curves made it possible to determine the irreversibility temperature Tirr = 315 K above of which the temperature hysteresis in the magnetization dependences is completely absent. The TB ≠ Tirr condition confirms the result of the SEM studies because there is size dispersion in the La0.6Ag0.2Mn1.2O3 nanopowder. In the ideal case for non-interacting MNPs with the same size D, the blocking temperature TB and the irreversibility temperature Tirr should coincide. In real cases, due to the size dispersion of the particles, the temperature is TB < Tirr. It is associated with particles with a large size D, where the blocking temperature TB is higher according to eqn (5). However, a slight difference between the temperatures of TB and Tirr allows concluding that MNPs with almost the same size take part in the formation of the magnetic properties of the La0.6Ag0.2Mn1.2O3, so the studied nanopowder can be considered to be monodisperse.
Above the temperature TC, the particles in the La0.6Ag0.2Mn1.2O3 nanopowder go into the PM state, for which the Curie–Weiss law is fulfilled (see Fig. 4):
A very sharp transition to the FM state with a narrow temperature interval ΔTC (see Fig. 3) due to the influence of super-stoichiometric Mn is of interest because it satisfies the requirements for magnetic powder with an intelligent local hyperthermia control system. The A- and B-structural positions, valence, and magnetic states of manganese in the nanopowder of non-stoichiometric La0.6Ag0.2Mn1.2O3 composition are determined and given in (see ESI 3†).
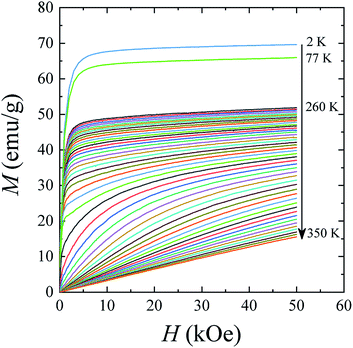
The magnetic hysteresis loops M(H) in the La0.6Ag0.2Mn1.2O3 nanopowder were measured in a magnetic field up to H = 70 kOe at temperatures of T = 2, 77, 300, and 400 K (see ESI 3†). The magnetic parameters obtained from hysteresis curves are shown in Table S4 of ESI 3.† With an increase in temperature, the saturation magnetization MS decreases from MS = 69.7 emu g−1 at T = 2 K to 65.9 emu g−1 at T = 77 K and 34.1 emu g−1 at T = 300 K. At T = 400 K, the dependence M(H) is linear, as it should be for the PM state. The coercivity HC and the residual magnetization MR also decrease from HC = 172 Oe and MR = 7.5 emu g−1 at T = 2 K to HC = 109 Oe and MR = 4.9 emu g−1 at T = 77 K, and to HC = 51 Oe and MR = 1.1 emu g−1 at T = 300 K.
The magnetization isotherms M(H) of the La0.6Ag0.2Mn1.2O3 nanopowder are presented in Fig. 5. The magnetization process of the MNPs ensemble can be considered as the magnetization of a uniaxial polycrystalline material, for which the law of approximation to the saturation magnetization MS is valid in a magnetic field H:49
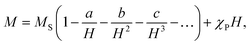 | (6) |
where K1 is the magnetocrystalline anisotropy constant,
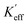 is the effective anisotropy constant that includes the shape anisotropy constant and the magnetostriction constant. For systems with uniaxial anisotropy, the upper limit of K1 can be obtained from the equality:51
is the effective anisotropy constant that includes the shape anisotropy constant and the magnetostriction constant. For systems with uniaxial anisotropy, the upper limit of K1 can be obtained from the equality:51
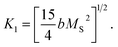 | (7) |
While approximating the isotherm M(H) for T = 2 K by the dependence (6) (see Fig. 6), the coefficient b = 131.38 Oe2 was obtained. Using eqn (7) with a saturation magnetization MS = 426.8 emu cm−3 (69.7 emu g−1), the magnetocrystalline anisotropy constant K1 = 9.5 × 103 erg cm−3 was obtained.
Using above received parameters of La0.6Ag0.2Mn1.2O3, for making conclusion about possibility to use its for local hypothermia, all necessary for that characteristics were calculated (see ESI 4†) and presented here: magnetic hardness parameter k = 0.008, FM exchange length lex = 5.476 × 10−7 cm, exchange hardness constant A = 3.432 × 10−7 erg cm−1, exchange integral Jex = 4.63 × 10−15 erg and the critical sizes of DSDcr = 39 nm for the SD state and of DMDcr = 51 nm for the MD state. The values of the parameter k satisfy criterion for the soft magnetic particles. The sizes of DSDcr and DMDcr fully agree with the results of the fundamental work,52 where the DMDcr/DSDcr ratio for the soft magnetic materials should increase with an increase in the parameter k from 1.2562 at k = 0 to ∞ at k = 0.3253. Comparing the obtained results with conditions of the magnetic state of nanoparticle, it can be concluded that particles with sizes up to 39 nm are in the SD state (7%), sizes from 39 to 51 nm are in the VS state (17%), and sizes of greater than 51 nm are in the MD state (76%) at T = 2 K (see ESI 2 and 4†).
According to the Stoner–Wohlfarth model,53 which considers the properties of non-interacting SD particles with a regular ellipsoidal shape, the anisotropy field HA can be written as:
| HA = 2K1/MS. | (8) |
In the Stoner–Wohlfarth model for spherical SD particles at T = 0, the anisotropy field coincides with the coercivity, i.e. HA = HC. According to eqn (8), the anisotropy field equals HA = 44 Oe in the La0.6Ag0.2Mn1.2O3 nanopowder with MS = 426.8 emu cm−3 and K1 = 9.5 × 103 erg cm−3. For spherical particles with a magnetization of ∼400 emu cm−3, even a small deviation from sphericity (the semiaxis ratio in the ellipsoid is 0.9) will lead to an increase in HC by ∼200 Oe.53 Therefore, the discrepancy between the calculated HA and experimental HC is due to the influence of shape anisotropy.
4.3. Heating and temperature stabilization in the La0.6Ag0.2Mn1.2O3 nanopowder
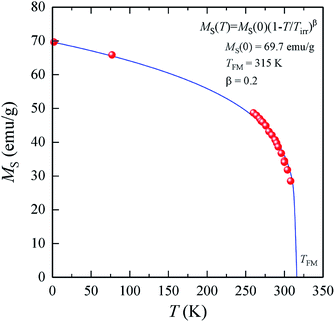
The features of the magnetic behavior of nanoparticles near the magnetic phase transition temperature are of great importance when choosing a smart magnetic nanomaterial for local hyperthermia. Fig. 6 shows the temperature dependence of the saturation magnetization MS(T), which was plotted based on the analysis of the magnetization isotherms M(H) (see Fig. 5). In the FM region, the MS(T) curve has the form of a power law:47
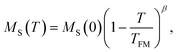 | (9) |
In magnetic hyperthermia, a sinusoidal magnetic field can affect the stimulation of peripheral nerves and cardiac tissue.54 In case of choosing the optimal ranges of the frequency f and the amplitude of the magnetic field Hmax, it is necessary to take into account their boundary limits, above which the effect of AMF on nervous excitement disappears. The upper stimulation threshold is limited by the range from Hmax = 10 Oe at f = 100 kHz to Hmax = 10 kOe at f = 10 Hz.55 This means that for therapeutic purposes it is not recommended to use a sinusoidal magnetic field with low values of f and Hmax.
On the other hand, in order to avoid the harmful effects of electromagnetic fields on the human body, the upper limit of f × H should not exceed the maximum value of (f × H)max. In clinical trials, it was found that during hyperthermia for one hour, the subjects did not experience severe discomfort if (f × H)max = 6.3 × 107 Oe s−1 (5 × 109 A m−1 s−1).54 AMF with a high frequency causes nonspecific heating in tissues due to the induced eddy currents, which should be minimized. Therefore, it is advisable to consider the possibility of carrying out the hyperthermia procedure in the range of not too high frequencies f with amplitude AMF, which satisfies the condition f × Hmax ≤ (f × H)max. The results of preclinical studies showed56 that there were no adverse effects under AFM (f = 153 kHz and Hmax = 700 Oe) even with continuous magnetic hyperthermia for 20 minutes. The use of magnetic field with Hmax = 1300 Oe was also acceptable, but keeping heat removal mode with using suitable variations in the duration of electromagnetic pulses.
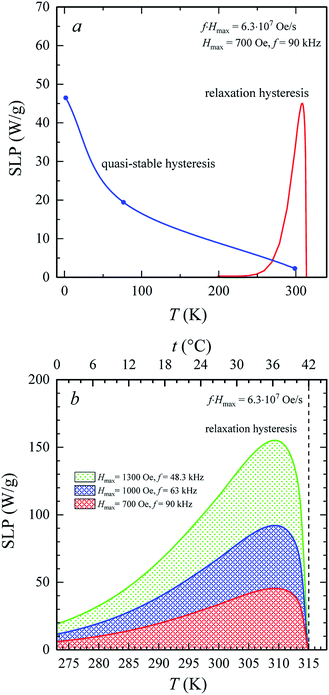
The heating of SD and monodisperse soft magnetic nanoparticles in the AMF is a result of the hysteresis losses. Fig. 7a shows the temperature changes in the specific loss power, SLP(T), for the La0.6Ag0.2Mn1.2O3 nanopowder under AMF with Hmax = 700 Oe and f = 90 kHz. At low temperatures, the SLP values were obtained from experimental hysteresis loops (see Table S4†) for the quasi-stable hysteresis region using eqn (1) and (2). With an increase in the temperature, the SLP decreases from SLP = 46 W g−1 at T = 2 K to 19 W g−1 at T = 77 K, 2 W g−1 at T = 300 K and 0 W g−1 at T = 316 K. Such a mechanism for heating the magnetic particles does not consider the relaxation processes of magnetization.
The SLP in the relaxation hysteresis region was determined using eqn (2) and (4). In the case, when the relaxation time τR depends not only on the volume V of the particle, but also on the magnetic anisotropy K, the temperature dependence τR(T) has the form:57
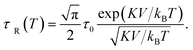 | (10) |
For SPM nanoparticles of lanthanum manganites, the characteristic relaxation time τ0 is 1.7 × 10−12 s.58 Calculating SLP near the magnetic phase transition, it is necessary to consider the parameter σ ≫ 1 and the magnetic anisotropy K = Keff for the La0.6Ag0.2Mn1.2O3 nanopowder at T = 300 K. The magnetization MS(T) is a power law dependence (9) with the temperature TFM = 315 K and parameter β = 0.2. As seen from Fig. 7a, at temperatures T ≥ 250 K, the specific loss power appears and increases. The SLP increases to a maximum value of 44 W g−1 at T = 310 K and then reduces dramatically to zero at T = 315 K. The resulting SLP for the La0.6Ag0.2Mn1.2O3 nanopowder are in good agreement with the specific absorption rate SAR = 48–54 W g−1 for manganite La1−xSrxMnO3 nanoparticles with 0.2 < x < 0.4.57 However, lanthanum–strontium manganite is not suitable to the smart material for magnetic hyperthermia, since it does not have a sharp magnetic phase transition at TC and the Curie temperature is above the range of 42–44 °C of hyperthermia.59
A nonmonotonic behavior of the SLP(T) dependence follows from the relation between the spontaneous magnetization MS(T) and the relaxation time τR(T) in eqn (4). In the La0.6Ag0.2Mn1.2O3 nanopowder with τ0 = 1.7 × 10−12 s, Keff = 7.123 × 103 erg cm−3 and D0 = 65.3 nm, the relaxation time decreases from τR = 3.243 s at T = 250 K to 0.024 s at T = 300 K and 0.007 s at T = 315 K. At a frequency f = 90 kHz, taking into account the resonance condition 2πf0 × τR(T) = 1, it follows that SLP(T) should take the maximum value at T = 490 K. However, the SLP increases inversely with a decrease in τR(T) within the temperature range from 250 to 310 K, since MS(T) varies slightly. In the range from 310 to 315 K, a sharp decrease in the SLP is due to a sharp drop in MS2 to 0 (see eqn (4)).
Fig. 7b shows three temperature dependences of SLP(T) in the relaxation hysteresis region for three pairs of values of f and Hmax. Each SLP(T) curve satisfies the condition for the safe influence of AMF on biological subject, i.e. (f × Hmax) = (f × H)max = 6.3 × 107 Oe s−1. In all curves, the maximum of SLP is observed at a temperature T = 310 K (37 °C). The maximum temperature is independent of Hmax and f. With an increase in Hmax, the maximum of SLP increases from 44 W g−1 for Hmax = 700 Oe and f = 90 kHz to 91 W g−1 for Hmax = 1000 Oe and f = 63 kHz and up to 153 W g−1 for Hmax = 1300 Oe and f = 48.3 kHz. Such an increase in SLP by more than 3 times means the possibility of a significant increase in the heating intensity during hyperthermia. This is due to an increase in the amplitude of AMF when heating occurs in the relaxation hysteresis region. It should be also noted that such an increase in SLP occurs without violating the safe influence of AMF on the vital functions of an organism.
For a complete analysis of the functional properties of the smart magnetic La0.6Ag0.2Mn1.2O3 nanopowder, an unclear question remains regarding whether the such power SLP is sufficient to self-heat of MNP and to heat of the cell structures to the therapeutic range at local hyperthermia. Using equation:
The obtained values of SLP = 44–153 W g−1 for the La0.6Ag0.2Mn1.2O3 with a heating rate of 0.1–0.3 °C s−1 are comparable to SLP = 26–380 W g−1 with a heating rate of 0.3–0.7 °C s−1 for Fe3O4 and MnFe2O4 nanoparticles,61 which are currently used commercially in medical hyperthermia applications. However, the high Curie temperature of TC = 585 °C for Fe3O4,62 and 277–347 °C for MnFe2O4,63 does not allow to automatically stabilize heating in the safe range of hyperthermia (42–44 °C). In addition, the La0.6Ag0.2Mn1.2O3 nanoparticles have an order of magnitude lower coercivity with magnetic hardness parameter k = 0.008 in comparison with Fe3O4 and MnFe2O4, k = 0.01–0.09,64 that greatly increases the risk of mechanical damage to cells in AMF during intracellular hyperthermia due to using Fe3O4 and MnFe2O4 nanoparticles.
It should be also noted that there are two 55Mn and 139La centers of the NMR signal in the synthesized smart magnetic La0.6Ag0.2Mn1.2O3 nanopowder. In the FM state at T < TC (42 °C), the formation of the NMR spectrum on 55Mn nuclei (the gyromagnetic ratio γMn = 10.560 MHz/T)65 occurs under the influence of the hyperfine interaction field HHIF = 34–38 T.36 The field on 139La nuclei (γLa = 6.014 MHz/T)66 has a dipole–dipole character and is in the range Hdd = 2.3–3.7 T.65,67 In the PM state (T > TC), during MRI studies, the field on the 55Mn and 139La NMR nuclei decreases to ∼1.5 T of the tomograph field. Such a variety of magnetic resonance properties of the synthesized La0.6Ag0.2Mn1.2O3 nanopowder operating at the intracellular level additionally opens up great prospects for its use as novel MRI contrast agents for tumor theranostics, which combine the properties of both therapeutic and diagnostic agents.
5. Conclusions
The main ratios of the magnetic and shape-forming parameters of the smart La0.6Ag0.2Mn1.2O3 material suitable for local (intracellular) hyperthermia have been determined. It has been established that the synthesized La0.6Ag0.2Mn1.2O3 nanopowder consists of spherical-like particles with an average size of 65 nm. The main magnetic properties, such as: magnetic hardness parameter, k = 0.008; effective anisotropy constant, Keff = 7.123 × 103 erg cm3; magnetocrystalline anisotropy constant, K1 = 9.5 × 103 erg cm3; anisotropy field, HA = 44 Oe (at T = 0); critical size of SD state, DSDcr = 39 nm (at T = 2 K); critical size of MD state, DMDcr = 51 nm (at T = 2 K); Curie temperature, TC = 308 K; blocking temperature, TB = 301 K; and temperature of appearance of FM fluctuations, TonsetC = 316 K have been determined for the La0.6Ag0.2Mn1.2O3 nanopowder. These magnetic parameters clearly demonstrate the possibility of using La0.6Ag0.2Mn1.2O3 as a smart magnetic nanomaterial for local (intracellular) hyperthermia. In AMF, the appearance and increase in the SLP near TC are associated with the influence of the Néel relaxation. Intensive heating of MNPs in the relaxation hysteresis continues up to temperature 42 °C with a maximum value of SLP at t = 37 °C. Such thermomagnetic properties allow locally heating cell structures to 42 °C for a short time, stabilizing this temperature and carrying out magnetic hyperthermia without the risk of overheating and mechanical damage to biological tissue. Obtaining such necessary functional properties has become possible due to the use of the La0.6Ag0.2Mn1.2O3 composition with a super-stoichiometric manganese which demonstrates relaxation hysteresis of magnetization in the temperature range of the magnetic phase transition. Moreover, the presence of 55Mn and 139La NMR centers, as well as unique variety and combination of functional properties in the La0.6Ag0.2Mn1.2O3 nanopowder expand the functionality of using this smart material.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was partially supported by The Thousand Talents Program for Foreign Experts program of China (project WQ20162200339) and Grant of NAS of Ukraine for research laboratories/groups of young scientists of NAS of Ukraine 2020–2021 (grant agreement no. 08/01-2020).References
- K. Y. Castillo-Torres, E. S. McLamore and D. P. Arnold, Micromachin., 2020, 11, 16, DOI:10.3390/mi11010016.
- D. Lombardo, M. A. Kiselev and M. T. Caccamo, J. Nanomater., 2019, 2019, 26, DOI:10.1155/2019/3702518.
- J. Chen, H.-H. Xiang, Z.-Z. Zhao, Y.-K. Wu, M.-Y. Fei and M.-M. Song, RSC Adv., 2020, 10, 18054–18061, 10.1039/d0ra01807d.
- X. Cai, Q. Zhu and Y. Zeng, Int. J. Nanomed., 2019, 14, 8321, DOI:10.2147/fijn.s218085.
- M. Fathi-Achachelouei, H. Knopf-Marques and C. E. Ribeiro da Silva, Front. Bioeng. Biotech., 2019, 7, 113, DOI:10.3389/ffbioe.2019.00113.
- M. Banobre-Lopez, Y. Pineiro-Redondo and M. Sandri, IEEE Trans. Magn., 2014, 50, 1, DOI:10.1109/tmag.2014.2.
- V. M. Kulkarni, D. Bodas and K. M. Paknikar, RSC Adv., 2015, 5, 60254, 10.1039/c5ra02731d.
- D. Chang, M. Lim and J. A. Goos, Front. Pharmacol., 2018, 9, 831, DOI:10.3389/fphar.2018.00831.
- J. Owens Frank and P. Poole Charles, Physics and Chemistry of Nanosolids, 2008, vol. 539 Search PubMed.
- M. Dewhirst, B. L. Viglianti and M. Lora-Michiels, Thermal Treatment of Tissue: Energy Delivery and Assessment II, 2003, vol. 4954, p. 37, DOI:10.1117/12.476637.
- L. Asín, M. R. Ibarra and A. Tres, Pharm. Res., 2012, 29, 1319, DOI:10.1007/s11095-012-0710-z.
- X. Liu, Y. Zhang and Y. Wang, Theran., 2020, 10, 3793, DOI:10.7150/thno.40805.
- C. Blanco-Andujar, D. Ortega and P. Southern, Nanomedicine, 2016, 12, 121, DOI:10.2217/nnm.15.185.
- V. M. Kalita, A. I. Tovstolytkin and S. M. Ryabchenko, Phys. Chem. Chem. Phys., 2015, 17, 18087, 10.1039/c5cp02822a.
- N. Zhu, H. Ji and P. Yu, Nanomaterials, 2018, 8, 810, DOI:10.3390/nano8100810.
- D.-H. Kim, E. A. Rozhkova, I. V. Ulasov, S. D. Bader, T. Rajh, M. S. Lesniak and V. Novosad, Nat. Mater., 2010, 9, 165, DOI:10.1038/nmat2591.
- G. Barrera, P. Allia and P. Tiberto, Nanoscale, 2020, 12, 6360, 10.1039/c9nr09503a.
- Z. Nemati, J. Alonso, L. M. Martinez, H. Khurshid, E. Garaio, J. A. Garcia, M. A. Phan and H. Srikanth, J. Phys. Chem. C, 2016, 120, 8370, DOI:10.1021/acs.jpcc.6b01426.
- A. J. Giustini, A. A. Petryk, S. M. Cassim, J. A. Tate, I. Baker and P. J. Hoopes, Nano LIFE, 2010, 1, 17, DOI:10.1142/s1793984410000067.
- J. Carrey, B. Mehdaoui and V. Respaud, J. Appl. Phys., 2011, 109, 083921, DOI:10.1063/1.3551582.
- V. M. Kalita, I. Dzhezherya Yu and G. G. Levchenko, Soft Matter, 2019, 15, 5987, 10.1039/c9sm00735k.
- A. Jordan, P. Wust, H. Fahlin, W. John, A. Hinz and R. Felix, Int. J. Hyperthermia, 1993, 9, 51, DOI:10.3109/02656739309061478.
- R. Hergt, S. Dutz and M. Roder, J. Phys.: Condens. Matter, 2008, 20, 385214, DOI:10.1088/0953-8984/20/38/385214.
- E. Lima, E. De Biasi, R. D. Zysler, M. S. Mansilla, M. L. Mojica-Pisciotti, T. E. Torres, M. P. Calatayud, C. Marquina, M. R. Ibarra and G. F. Goya, J. Nanopart. Res., 2014, 16, 2791, DOI:10.1007/s11051-014-2791-6.
- E. A. Perigo, G. Hemery, O. Sandre, D. Ortega, E. Garaio, F. Plazaola and F. J. Teran, Appl. Phys. Rev., 2015, 2, 041302, DOI:10.1063/1.4935688.
- E. Lima, T. E. Torres, L. M. Rossi, H. R. Rechenberg, T. S. Berquo, A. Ibarra, C. Marquina, M. R. Ibarra and G. F. Goya, J. Nanopart. Res., 2013, 15, 1654, DOI:10.1007/s11051-013-1654-x.
- N. A. Usov, M. S. Nesmeyanov and V. P. Tarasov, Sci. Rep., 2018, 8, 1224, DOI:10.1038/s41598-017-18162-8.
- V. Markovich, A. Wisniewski and H. Szymczak, Chapter One Magnetic Properties of Perovskite Manganites and Their Modifications, Handbook of Magnetic Materials, Elsevier, 2014, DOI:10.1016/b978-0-444-63291-3.00001-5.
- O. A. Shlyakhtin, V. G. Leontiev, O. Young-Jei and A. A. Kuznetsov, Smart Mater. Struct., 2007, 16, N35, DOI:10.1088/0964-1726/16/5/n02.
- J.-M. Li, C. H. A. Huan, Y.-W. Du, F. Duan and Z. X. Shen, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 63, 024416, DOI:10.1103/physrevb.63.024416.
- A. V. Pashchenko, V. P. Pashchenko, V. K. Prokopenko, F. Revenko Yu, S. Prylipko Yu, N. A. Ledenev, G. G. Levchenko, V. P. Dyakonov and H. Szymczak, Acta Mater., 2014, 70, 218, DOI:10.1016/j.actamat.2014.02.014.
- А. V. Pashchenko, V. P. Pashchenko, V. K. Prokopenko, Y. F. Revenko, А. S. Мazur, V. V. Burchovetskii, V. А. Тurchenko, N. A. Liedienov, V. G. Pitsyuga, G. G. Levchenko, V. P. Dyakonov and H. Szymczak, J. Magn. Magn. Mater., 2016, 416, 457, DOI:10.1016/j.jmmm.2016.05.010.
- A. V. Pashchenko, V. P. Pashchenko, Y. F. Revenko, V. K. Prokopenko, A. A. Shemyakov, V. А. Тurchenko, V. Y. Sycheva, B. M. Efros, V. P. Komarov and L. G. Gusakova, Metallofiz. Noveishie Tekhnol., 2010, 32, 487 CAS.
- A. V. Pashchenko, V. P. Pashchenko, Y. F. Revenko, V. K. Prokopenko, A. A. Shemyakov, G. G. Levchenko, N. E. Pismenova, V. V. Kitaev, Y. M. Gufan, A. G. Sil'cheva and V. P. Dyakonov, J. Magn. Magn. Mater., 2014, 369, 122, DOI:10.1016/j.jmmm.2014.06.009.
- A. V. Pashchenko, V. P. Pashchenko, Y. F. Revenko, V. K. Prokopenko, A. S. Mazur, V. A. Turchenko, V. V. Burkhovetskii, A. G. Sil'cheva, P. P. Konstantinov and Y. M. Gufan, Phys. Solid State, 2013, 55, 321, DOI:10.1134/s1063783413020236.
- V. P. Pashchenko, A. V. Pashchenko, V. K. Prokopenko, F. Revenko Yu, A. A. Shemyakov and A. G. Sil'cheva, Tech. Phys., 2012, 57, 1508, DOI:10.1134/s1063784212110217.
- A. Sazanovich, J. Pietosa, A. Pashchenko, E. Zubov, V. Dyakonov and H. Szymczak, Acta Phys. Pol., A, 2012, 122, 162, DOI:10.12693/aphyspola.122.162.
- A. V. Pashchenko, V. P. Pashchenko, N. A. Liedienov, V. K. Prokopenko, Y. F. Revenko, N. E. Pismenova, V. V. Burhovetskii, V. Y. Sycheva, A. V. Voznyak, G. G. Levchenko, V. P. Dyakonov and H. Szymczak, J. Alloys Compd., 2017, 709, 779, DOI:10.1016/j.jallcom.2017.03.093.
- N. A. Liedienov, V. M. Kalita, A. V. Pashchenko, I. Dzhezherya Yu, I. V. Fesych, Q. Li and G. G. Levchenko, J. Alloys Compd., 2020, 836, 155440, DOI:10.1016/j.jallcom.2020.155440.
- N. D. Thorat, R. M. Patil, V. M. Khot, A. B. Salunkhe, A. I. Prasad, K. C. Barick, R. S. Ningthoujam and S. H. Pawar, New J. Chem., 2013, 372733–372742, 10.1039/c3nj00007a.
- H. Rietveld, J. Appl. Crystallogr., 1969, 2, 65–71, DOI:10.1107/s0021889869006558.
- J. Rodrguez-Carvajal, Phys. B, 1993, 192, 55–69, DOI:10.1016/0921-4526(93)90108-i.
- F. Tournus and E. Bonet, J. Magn. Magn. Mater., 2011, 323, 1109, DOI:10.1016/j.jmmm.2010.11.056.
- F. Tournus and A. Tamion, J. Magn. Magn. Mater., 2011, 323, 1118, DOI:10.1016/j.jmmm.2010.11.057.
- J.-M. Li, X.-L. Zeng and Z.-A. Xu, Appl. Phys. Lett., 2013, 103, 232410, DOI:10.1063/1.4840320.
- I. J. Bruvera, P. Mendoza Zelis, M. Pilar Calatayud, G. F. Goya and F. H. Sanchez, J. Appl. Phys., 2015, 118, 184304, DOI:10.1063/1.4935484.
- A. V. Bodnaruk, V. M. Kalita, M. M. Kulyk, S. M. Ryabchenko, A. I. Tovstolytkin, S. O. Solopan and A. G. Belous, J. Phys.: Condens. Matter, 2019, 31, 375801, DOI:10.1088/1361-648x/ab26fa.
- C. P. Bean and J. D. Livingston, J. Appl. Phys., 1959, 30, 120S, DOI:10.1063/1.2185850.
- K.-Y. Ho, X.-Y. Xiong, J. Zhi and L. -Z. Cheng, J. Appl. Phys., 1993, 74, 6788, DOI:10.1063/1.355078.
- D. H. Manh, P. T. Phong, P. H. Nam, D. K. Tung, N. X. Phuc and I.-J. Lee, Phys. B, 2014, 444, 94, DOI:10.1016/j.physb.2014.03.025.
- D. H. Manh, P. T. Phong and T. D. Tung, J. Alloys Compd., 2011, 509, 1373, DOI:10.1016/j.jallcom.2010.10.104.
- W. F. Brown, J. Appl. Phys., 1968, 39, 993, DOI:10.1063/1.1656363.
- E. C. Stoner and E. P. Wohlfarth, IEEE Trans. Magn., 1991, 27, 3475, DOI:10.1109/tmag.1991.1183750.
- Q. A. Pankhurst, T. K. Thanh and S. K. Jones, J. Phys. D: Appl. Phys., 2009, 42, 224001, DOI:10.1088/0022-3727/42/22/224001.
- J. P. Reilly, Stimulation via Electric and Magnetic Fields, in Applied Bioelectricity, Springer, New York, NY, DOI:10.1007/978-1-4612-1664-3_9.
- R. Ivkov, S. J. DeNardo and W. Daum, Clin. Cancer Res., 2005, 11, 7093, DOI:10.1158/1078-0432.ccr-1004-0016.
- R. E. Rosensweig, J. Magn. Magn. Mater., 2002, 252, 370, DOI:10.1016/s0304-8853(02)00706-0.
- A. Rostamnejadi, H. Salamati, P. Kameli and H. Ahmadvand, J. Magn. Magn. Mater., 2009, 321, 3121, DOI:10.1016/j.jmmm.2009.05.035.
- Z. Wei, A. V. Pashchenko, N. A. Liedienov, I. V. Zatovsky, D. S. Butenko, Q. Li, I. V. Fesych, V. A. Turchenko, E. E. Zubov, P. Y. Polynchuk, V. G. Pogrebnyak, V. M. Poroshin and G. G. Levchenko, Phys. Chem. Chem. Phys., 2020, 22, 11817, 10.1039/d0cp01426e.
- A. G. Gamzatov, B. Abdulvagidov Sh and A. M. Aliev, Phys. Solid State, 2007, 49, 1769, DOI:10.1134/s1063783407090260.
- F. Soetaert, S. K. Kandala, A. Bakuzis and R. Ivkov, Sci. Rep., 2017, 7, 6661, DOI:10.1038/s41598-017-07088-w.
- S. Tikadzumi, Physics of Ferromagnetism. Magnetic Properties and Practice Applications [in Russian], Moscow, Mir, 1987 Search PubMed.
- I. Sharifi, H. Shokrollahi and S. Amiri, J. Magn. Magn. Mater., 2012, 324, 903–915, DOI:10.1016/j.jmmm.2011.10.017.
- Y. O. Tykhonenko-Polishchuk and A. I. Tovstolytkin, J. Nano- Electron. Phys., 2017, 9, 1–17, DOI:10.21272/jnep.9(2).02028.
- A. V. Pashchenko, V. P. Pashchenko, V. K. Prokopenko, A. G. Sil'cheva, Y. F. Revenko, A. A. Shemyakov, N. G. Kisel', V. P. Komarov, V. Y. Sycheva, S. V. Gorban' and V. G. Pogrebnyak, Phys. Solid State, 2012, 54, 767, DOI:10.1134/s106378341204021x.
- G. H. Fuller, J. Phys. Chem. Ref. Data, 1976, 5, 835, DOI:10.1063/1.555544.
- V. P. Pashchenko, A. V. Pashchenko, A. V. Prokopenko, F. Revenko Yu, V. V. Burkhovetskii, A. A. Shemyakov, A. G. Sil'cheva and G. G. Levchenko, J. Exp. Theor. Phys., 2012, 114, 503, DOI:10.1134/s1063776112030193.
Footnote |
| † Electronic supplementary information (ESI) available: Definition of coherent scattering size in the La0.6Ag0.2Mn1.2O3 nanopowder; definition of the particle size distribution function in the magnetic La0.6Ag0.2Mn1.2O3 nanopowder; The A- and B-structural positions, valence and magnetic states of manganese in non-stoichiometric La0.6Ag0.2Mn1.2O3 nanopowder; calculation of the main magnetic characteristics of the La0.6Ag0.2Mn1.2O3 composition for local hyperthermia. See DOI: 10.1039/d0ra06779b |
| This journal is © The Royal Society of Chemistry 2020 |