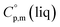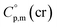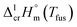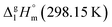Open Access Article
Open Access ArticleError or exemption to the rule? Development of a diagnostic check for thermochemistry of metal–organic compounds†
Kseniya V. Zherikova *a and
Sergey P. Verevkin
*a and
Sergey P. Verevkin *bc
*bc
aNikolaev Institute of Inorganic Chemistry of Siberian Branch of Russian Academy of Sciences, 630090 Novosibirsk, Russia. E-mail: ksenia@niic.nsc.ru
bChemical Technological Department, Samara State Technical University, Samara 443100, Russia. E-mail: sergey.verevkin@uni-rostock.de
cDepartment of Physical Chemistry and Department of “Science and Technology of Life, Light and Matter”, University of Rostock, Rostock, 18059, Germany
First published on 15th October 2020
Abstract
Volatile metal β-diketonates are well-known precursors used in Metal–Organic Chemical Vapour Deposition (MOCVD) for manufacturing film materials. Knowledge of vapour pressures and sublimation/vaporization thermodynamics of the MOCVD precursors is indispensable for optimization of deposition. However, the spread of available data could be unacceptably large for the same precursor for several reasons related to its chemical nature or incorrectly configured conditions of tensimetric investigation. In this work, we have developed an algorithm for a general diagnostic check, based on principles of group-additivity, for thermochemistry on solid–gas, liquid–gas, and solid–liquid phase transitions of metal–organic compounds and applied it to tris(beta-diketonato)iron complexes. The diagnostic tool helps to localize general “healthy” thermochemical interconnected data, and, subsequently, isolate molecules with definitely “ill” properties from the data pool. This diagnostic tool could be expanded and adapted for β-diketonate complexes with metals other than iron.
1. Introduction
Metal β-diketonates are the oldest1 and still one of the most preferred precursors for manufacturing film materials by using Metal–Organic Chemical Vapour Deposition (MOCVD).2–4 The technological parameters of the deposition process are determined by the physical and chemical properties of the precursors used. The quality of precursors is mainly assessed based on their volatility and thermal stability in both the condensed and gaseous phases. The volatility of the metal-containing precursor is quantified by its vapour pressure at a given temperature. This parameter is crucial in MOCVD, since it determines the optimal concentration of the metal source in the reaction zone and defines the deposition rate, responsible for microstructure and functional properties of the target film material.Vapour pressures of a precursor, pi, are usually measured by using different techniques in possibly large, but generally limited temperature ranges. A large amount of experimental vapour pressures for metal–organic compounds can be found in the literature.5,6 Experimental vapour pressures are usually approximated by various types of simple or sophisticated equations.7 Of these, equations with three setting parameters are the most convenient, because they adequately correspond to the accuracy of typical measurement techniques (as a rule, the typical accuracy is on the level of 3–10%). Moreover, they are practically important for a reliable vapour pressure extrapolation outside the experimental temperature range, because the third coefficient is responsible for the curvature of the vapour pressure temperature dependence. This feasibility is especially valuable for the MOCVD, because it extends the frame for the process optimization. Last decades we are favoring the following three parameter equation8
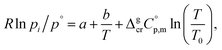 | (1) |
 is the difference of the isobaric molar heat capacities of the gaseous,
is the difference of the isobaric molar heat capacities of the gaseous,  and the crystal,
and the crystal,  phases; T0 appearing in eqn (1) is an arbitrarily chosen reference temperature (T = 298 K has been chosen in this work) and R is the ideal gas constant. Eqn (1) is equally valid for the treatment of vapour pressure temperature dependence measured over the solid or liquid precursor. In the case of the liquid precursor, a parameter
phases; T0 appearing in eqn (1) is an arbitrarily chosen reference temperature (T = 298 K has been chosen in this work) and R is the ideal gas constant. Eqn (1) is equally valid for the treatment of vapour pressure temperature dependence measured over the solid or liquid precursor. In the case of the liquid precursor, a parameter 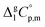 is used, which is derived with help of the liquid phase isobaric molar heat capacity
is used, which is derived with help of the liquid phase isobaric molar heat capacity 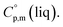 9,10 Eqn (1) is broadly used for vapour pressures approximations of organic compounds, where
9,10 Eqn (1) is broadly used for vapour pressures approximations of organic compounds, where 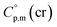 data and
data and 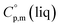 data are readily available.11–14 Recently, we have successfully applied eqn (1) for metal–organic compounds (ferrocene15 and its derivatives16) as well. However, this equation seems to be unfeasible for the metal β-diketonates, because the available
data are readily available.11–14 Recently, we have successfully applied eqn (1) for metal–organic compounds (ferrocene15 and its derivatives16) as well. However, this equation seems to be unfeasible for the metal β-diketonates, because the available 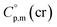 values are scarce and, even worse, the data on
values are scarce and, even worse, the data on 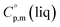 and
and 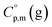 are virtually absent. In the absence of these data, eqn (1) is shrinking into the classic two-parameter linear Clausius–Clapeyron equation. Admittedly, the extrapolation potential of the Clausius–Clapeyron equation is very limited. This leads to an obvious loss of vapour pressure prediction quality for the MOCVD processes. Nevertheless, the current status quo is that all available in the literature vapour pressures for the metal–organic compounds were approximated with the Clausius–Clapeyron equation. Coefficients a and b of this equation are responsible for the enthalpy and entropy of sublimation/vaporization processes and they are referenced to the average temperature, Tav, of the experimental interval. These data are usually reported in the original literature and mostly used for practical optimization of the MOCVD processes. However, the spread of available data is unacceptably large. Thus, it is generally not easy to rationalize and even compare the available sublimation/vaporization thermodynamic data due to the following reasons.
are virtually absent. In the absence of these data, eqn (1) is shrinking into the classic two-parameter linear Clausius–Clapeyron equation. Admittedly, the extrapolation potential of the Clausius–Clapeyron equation is very limited. This leads to an obvious loss of vapour pressure prediction quality for the MOCVD processes. Nevertheless, the current status quo is that all available in the literature vapour pressures for the metal–organic compounds were approximated with the Clausius–Clapeyron equation. Coefficients a and b of this equation are responsible for the enthalpy and entropy of sublimation/vaporization processes and they are referenced to the average temperature, Tav, of the experimental interval. These data are usually reported in the original literature and mostly used for practical optimization of the MOCVD processes. However, the spread of available data is unacceptably large. Thus, it is generally not easy to rationalize and even compare the available sublimation/vaporization thermodynamic data due to the following reasons.
At first, the available Tav values demonstrate significant variations depending on the experimental technique, specific properties, and thermal stability of the precursor. As a consequence, the comparison of sublimation enthalpies even for a single compound is not possible, because Tav values frequently differ by 80–100 K.
Secondly, it is difficult to rule out a possible systematic error that is inherent in the data. Indeed, the metal β-diketonates are chemically active compounds and this feature can heavily aggravate the experimental study. For example, it was established that all vapour pressure measurements on metal β-diketonates performed by using isoteniscope in the middle of the last century were in serious error, because the sample vapour reacted with the mercury used as the manometer's fluid.17–21 There are also more complex examples of the influence of the chemical nature of the precursor on the experimental results. For instance, the association of precursor molecules in the gas phase, observed by using the static method, has to be taken into account in order to avoid results misinterpretation.22
The third essential and critical issue is a purity attestation of precursors. It is well-known, that the insufficient chemical and phase purity of precursors may affect results of thermodynamic measurements drastically.23 For example, even small amount of impurity significantly decreases the melting point of precursor, which is decisive for correct configuration of conditions of sublimation and vaporization e.g. tensimetric investigation.
The possible interference of all three aforementioned reasons is resulting in experimental thermodynamic data sets on vapour pressures, fusion temperatures, sublimation/vaporization, and fusion enthalpies, which are significantly spreading for the same precursor, as measured by different techniques and in different laboratories. For instance, in the case of vapour pressure – the variation in available data sets can be a factor of tenth.24 Such a broad scatter of thermodynamic data does not facilitate optimization of the MOCVD process and deposition experiments are inevitably conducted under ill-defined and empirically selected conditions.
How to deal with such an ill-determined and questionable collection of experimental thermodynamic properties on metal β-diketonates? First of all, we need to develop a kind of general diagnostic tool, in order to localize a rational “healthy” level of the property, and, subsequently, isolate molecules with the definitely “ill” property from the data pool. Such a diagnostic tool doubtlessly should be related to structure–property relationships. This is the only way to generate an expectation of a “reasonable” level for the property of interest, based on the reliable data available for the structurally parent molecules.
One of the most useful manifestations of the structure–property relationships is group-additivity (GA) procedure. The basic idea is to divide molecules into smaller units, assigning them “group additive values (GAVs)”, and use an additive scheme to obtain thermochemical data based on contributions from these groups.25 The crucial advantage of the GA method is that it enables a direct diagnosis of the faulty property. The simple deviation from additivity could be seen as an indicator of the “sick” property. However, similar to everyday life, the diagnosis can be right or wrong. Indeed, the deviation from the level established by the group additivity rule cannot only be due to pure experimental errors. It is well-known, that numerous structural peculiarities in the molecule are responsible for “non-additive” contributions. For example, for cycloalkanes (cyclopropane, cyclobutane, etc.), an individual non-additive “ring-strain” correction is contemplated to improve the GA method. It is evident that molecules of metal beta-diketonates also contain ring structures that do not comply with the group additivity rules. As a consequence, we always have to deal with the same challenging question for each metal β-diketonate: error or exemption to the rule? To answer this question, we have developed an algorithm for the diagnostic check of thermochemical properties of metal–organic compounds.
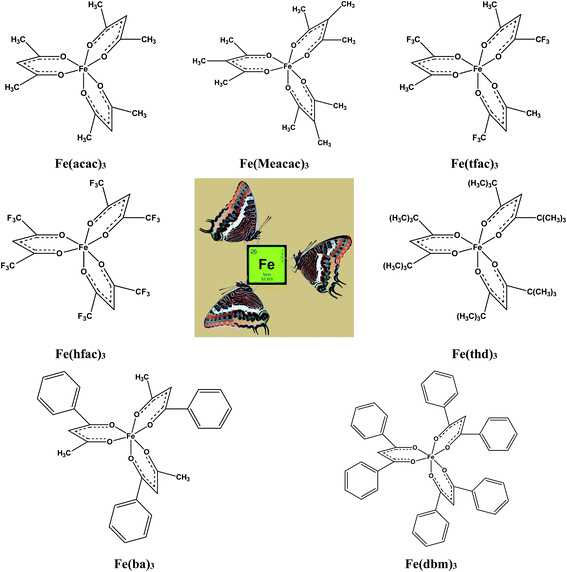
In focus of this paper is energetics of solid–gas, liquid–gas, solid–liquid phase transitions. A series of iron(III) tris-β-diketonates (Fig. 1) was taken first in order to rationalize the structure–property relationships within the group of similarly shaped molecules with the pronounced structural unit – iron atom surrounded by three ligands.
This choice is due to two main factors. On the one hand, this series represents a variety of molecules with different types of substitutions in the end groups and at γ-carbon of the β-diketonate ligand. There is a lot of literature on the thermodynamics of phase transitions that are necessary for the development and validation of structure–property correlations. The available for iron(III) tris-β-diketonates data set contains experimental data of significantly different quality. Thus, this set is a very suitable hardness test for the reliable diagnostic check for the really “sick” data pool, where values, e.g. of vapour pressure obtained by different researchers for the same compound, can differ by orders of magnitude. In addition, preference for a particular result is often not always obvious when the available data are very limited. In this case, the specification of the respective value as “error” can be regrettable, since this can also be the “exemption to the rule”.
The main goal of this work is to develop such a diagnostic tool that would allow verification of available thermochemical data on solid–gas, liquid–gas, and solid–liquid phase transitions for iron(III) tris-β-diketonates (Fig. 1). This diagnostic tool could be expanded and adapted for β-diketonate complexes with metals other than iron. Moreover, this diagnostic tool could be also adapted for the evaluation of experimental data sets of standard molar enthalpies of formation of metal β-diketonates.
2. Results and discussion
Thermodynamic studies of the MOCVD precursors in Novosibirsk have a long history that began in the middle of the last century. A significant amount of own experimental data on phase transition properties have now been accumulated from measurements by using tensimetry, effusion and transpiration techniques.5,6,22–24 The relevant literature data have been collected and evaluated in order to optimise the MOCVD conditions. A comprehensive compilation of the sublimation and vaporization enthalpies is given in Table 1. for tris(β-diketonato)iron(III) complexes available in the literature
for tris(β-diketonato)iron(III) complexes available in the literature
| Complex (state) CAS | Techniquea | T-range, K | b, kJ mol−1 | c, kJ mol−1 | Ref. |
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 |
a Techniques: IT = isoteniscope; T = transpiration; SB = sublimation bulb; S = static method; C = calorimetry; K = Knudsen effusion method with weighing of the cell; K/MS = Knudsen effusion method with mass spectrometric registration of gas phase; TE = torsion-effusion method; TGA = thermal gravimetric analysis; LT = Langmuir technique; DC = drop calorimetry; GC = gas chromatography.b Values of the sublimation/vaporization enthalpy and uncertainties (if available) were listed as they given in literature source.c Uncertainty of the sublimation/vaporization enthalpy 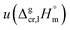 is the standard uncertainty (at 0.68 level of confidence, k = 1). We assessed the uncertainty based on our experience.d Weighted mean value. We used the experimental uncertainty as the weighing factor. Values in parenthesis were excluded from the calculation of the mean. Values in bold are recommended for further thermochemical calculations. Uncertainty of these sublimation/vaporization enthalpies is the standard uncertainty (at 0.68 level of confidence, k = 1). We assessed the uncertainty based on our experience.d Weighted mean value. We used the experimental uncertainty as the weighing factor. Values in parenthesis were excluded from the calculation of the mean. Values in bold are recommended for further thermochemical calculations. Uncertainty of these sublimation/vaporization enthalpies 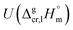 is the expanded uncertainty (0.95 level of confidence, k = 2).e Uncertainty is the expanded uncertainty (0.95 level of confidence, k = 2).e Uncertainty 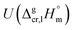 is expressed as the expanded uncertainty (0.95 level of confidence, k = 2).f Vapour pressures were studied in the temperature range that encompassed the melting temperature, which lead to a significant systematic error.g The temperature range of vapour pressure measurements was assessed. is expressed as the expanded uncertainty (0.95 level of confidence, k = 2).f Vapour pressures were studied in the temperature range that encompassed the melting temperature, which lead to a significant systematic error.g The temperature range of vapour pressure measurements was assessed. |
|||||
| Fe(acac)3 (cr) 14024-18-1 | IT | 323–355 | 20 | (23 ± 20) | Ref. 17 |
| IT | 350–403 | 23 | (28 ± 20) | Ref. 18 | |
| IT | 378–388 | 65 | (71 ± 20) | Ref. 19 | |
| IT | 318–443 | 20 | (25 ± 20) | Ref. 20 | |
| SB | 378–405 | 99.0 ± 0.8 | 105 ± 10 | Ref. 26 | |
| T | 363–423 | 114 | 120 ± 8 | Ref. 27 | |
| TGA | 335–356 | 115 | 118 ± 10 | Ref. 28 | |
| K | 406–441 | 117 ± 16 | 125 ± 16 | Ref. 29 | |
| SB | 373–402 | 121 ± 5 | 127 ± 5 | Ref. 30 | |
| IT | 381–402 | 112 ± 6 | 118 ± 8 | Ref. 30 | |
| T | 400–458 | 100 | 109 ± 20 | Ref. 31 | |
| C | 298 | — | 138 ± 5 | Ref. 32 | |
| K | 309–360 | 126.4 ± 3.1 | 128.8 ± 3.1 | Ref. 33 | |
| LT | 338–355 | 114.2 ± 1.5 | 117 ± 10 | Ref. 34–36 | |
| GC | 453–488 | 132.9 | 144 ± 10 | Ref. 37 | |
| TE | 369–388 | 124.6 ± 1.3 | 129.8 ± 1.9 | Ref. 38 | |
| K | 369–388 | 124.7 ± 1.2 | 129.9 ± 1.8 | Ref. 38 | |
| TGA | 430–450 | 118 | 127 ± 10 | Ref. 39 | |
| TGA | 413–443 | 112 | 120 ± 10 | Ref. 40 | |
| K/MS | 340–405 | 130.5 ± 2.5 | 135.4 ± 2.6 | Ref. 41 | |
| T | 400–458 | 124.1 ± 1.2 | 132.6 ± 1.4 | Ref. 42 | |
| K | 353–411 | 130.8 ± 2.5 | 136.3 ± 2.6 | Ref. 42 | |
| 131.3 ± 1.5d | |||||
| Fe(acac)3 (liq) 14024-18-1 | GC | 465 | 20 | (42 ± 20) | Ref. 43 |
| TGA | 452–535 | 82 ± 1 | 108 ± 5 | Ref. 44 | |
| GC | 488–548 | 93.3 | 122 ± 10 | Ref. 37 | |
| 110.8 ± 8.9d | |||||
| Fe(Meacac)3 (cr) 13978-46-6 | DC | 422 | 227.2 ± 1.4 | 164.5 ± 10e | Ref. 45 |
| Fe(tfac)3 (cr) 14526-22-8 | IT | 323–373 | 87 | (91 ± 20) | Ref. 17 |
| IT | 311–333 | 87 | (89 ± 20) | Ref. 20 | |
| T | 329–373 | 128.9 | 133.1 ± 3.1 | Ref. 27 | |
| T | 379–390 | 122.7 ± 5.0 | 129.5 ± 5.5 | Ref. 46 | |
| T | 380–387 | 104.6 ± 0.8 | 112 ± 15 | Ref. 47 | |
| DC | 389 | 183 ± 5 | 138 ± 10 | Ref. 48 | |
| TGA | 373–403f | 96 | 103 ± 20 | Ref. 40 | |
| 131.5 ± 5.1d | |||||
| Fe(tfac)3 (liq) 14526-22-8 | S | 392–428 | 87.0 ± 1.2 | 104.3 ± 1.6 | Ref. 49 |
| GC | 433 | 80.3 | 101 ± 10 | Ref. 43 | |
| T | 393–438 | 79.9 ± 0.5 | 98.0 ± 1.2 | Ref. 47 | |
| GC | 398–453 | 84.2 | 103.8 ± 10 | Ref. 37 | |
| 100.3 ± 1.9d | |||||
| Fe(hfac)3 (cr) 17786-67-3 | LT | 293–307 | 118.5 ± 2.4 | 118.7 ± 8.0 | Ref. 35 |
| T | 303–326 | 104.1 ± 1.3 | 105.7 ± 1.5 | Ref. 42 | |
| 106.1 ± 3.0d | |||||
| Fe(hfac)3 (liq) 17786-67-3 | S | 348–380 | 59.8 ± 0.8 | 72.2 ± 2.0 | Ref. 50 |
| GC | 363–403 | 79.4 | 95 ± 10 | Ref. 37 | |
| TGA | 333–363 | 60.0 | 69 ± 10 | Ref. 40 | |
| T | 326–352 | 71.1 ± 0.9 | 78.8 ± 1.0 | Ref. 42 | |
| 77.6 ± 1.8d | |||||
| Fe(ba)3 (cr) 14323-17-2 | IT | 378–418g | 11 | (20 ± 20) | Ref. 20 |
| DC | 501 | 337 ± 2.5 | 200 ± 10e | Ref. 48 | |
| Fe(dbm)3 (cr) 14405-49-3 | IT | 367–384 | 38 | (48 ± 20) | Ref. 19 |
| IT | 373–403g | 32 | (43 ± 20) | Ref. 18 | |
| K | 455–530 | 141.6 ± 3.9 | 164.7 ± 8.0e | Ref. 42 | |
| Fe(thd)3 (cr) 14876-47-2 | K | 390–430 | 107 ± 5 | 122 ± 10 | Ref. 51 |
| DC | 396 | 235 ± 2.5 | 146 ± 10 | Ref. 48 | |
| LT | 316–330 | 136.1 ± 1.9 | 139.4 ± 2.3 | Ref. 34–36 | |
| TE | 360–378 | 126.4 ± 1.2 | 135.9 ± 1.8 | Ref. 38 | |
| K | 360–378 | 125.2 ± 1.2 | 134.7 ± 1.8 | Ref. 38 | |
| TGA | 413–443f | 111 | 128 ± 10 | Ref. 40 | |
| T | 388–436 | 120.6 ± 0.8 | 135.8 ± 1.1 | Ref. 42 | |
| K | 341–408 | 131.9 ± 2.6 | 142.1 ± 2.7 | Ref. 52 | |
| 136.4 ± 1.5d | |||||
| Fe(thd)3 (liq) 14876-47-2 | T | 436–453 | 85.3 ± 0.3 | 121.8 ± 3.1e | Ref. 42 |
2.1 Temperature adjustment of sublimation/vaporization enthalpies of tris(β-diketonato)iron(III) complexes to T = 298.15 K
It is obvious from Table 1, that vapour pressures for each tris(β-diketonato)iron(III) complexes were measured in significantly different temperature intervals. The adjustment of thermochemical properties to the reference temperature T = 298.15 K is common practice.9,10 It is usually required to compare and reconcile experimental results measured with different methods and authors. Data properly adjusted to T = 298.15 K also help to reveal structure–property relationships present in structurally parent series of compounds. The temperature adjustment of the energetic values is generally based on the Kirchhoff's law. The following equations are used to adjust the sublimation/vaporization enthalpies:
 | (2) |
 | (3) |
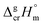 and
and 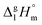 are the standard molar sublimation and vaporization enthalpies, respectively. Values of
are the standard molar sublimation and vaporization enthalpies, respectively. Values of  and
and 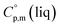 are usually derived from the adiabatic calorimetry (AC), differential scanning calorimetry (DSC), or they can easily be estimated (e.g. for organic compounds) by the group additivity procedure.9,10 Unfortunately, the
are usually derived from the adiabatic calorimetry (AC), differential scanning calorimetry (DSC), or they can easily be estimated (e.g. for organic compounds) by the group additivity procedure.9,10 Unfortunately, the 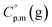 values of low volatile compounds can be obtained only from quantum chemical calculations53 or from the GA methods,54 but the reliability of the
values of low volatile compounds can be obtained only from quantum chemical calculations53 or from the GA methods,54 but the reliability of the  estimates and (as a consequence)
estimates and (as a consequence)  values remains questionable without the appropriate validation. Last decade, a pure empirical way to assess
values remains questionable without the appropriate validation. Last decade, a pure empirical way to assess  values was suggested by Chickos and Acree.10 This approach is based either on the experimental or estimated values on
values was suggested by Chickos and Acree.10 This approach is based either on the experimental or estimated values on  and it has been broadly used for organic compounds. However, the parametrization of the Chickos and Acree procedure is still absent for the metal-containing compounds. In our previous works on ferrocene and alkylferrocenes,15,16 we have launched a modification of the Chickos and Acree GA procedure towards organometallic compounds. In order to calculate the
and it has been broadly used for organic compounds. However, the parametrization of the Chickos and Acree procedure is still absent for the metal-containing compounds. In our previous works on ferrocene and alkylferrocenes,15,16 we have launched a modification of the Chickos and Acree GA procedure towards organometallic compounds. In order to calculate the 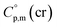 and
and  values of the ferrocene derivatives, we have suggested to define the ferrocene moiety [C5H5–Fe–C5H5] as the single increment, but all other groups, adjacent to the ferrocene moiety (e.g. increments CH3, CH2, CH, etc.), could be taken from the original work by Chickos and Acree.10 Such a simple modification was tested with reliable data on alkyl-substituted ferrocenes successfully.16 In a similar way we decided to calculate the
values of the ferrocene derivatives, we have suggested to define the ferrocene moiety [C5H5–Fe–C5H5] as the single increment, but all other groups, adjacent to the ferrocene moiety (e.g. increments CH3, CH2, CH, etc.), could be taken from the original work by Chickos and Acree.10 Such a simple modification was tested with reliable data on alkyl-substituted ferrocenes successfully.16 In a similar way we decided to calculate the  and
and  values of tris(β-diketonato)iron(III) complexes.
values of tris(β-diketonato)iron(III) complexes.
The adaptation of the algorithm is based on the reliable 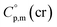 value for Fe(acac)3 measured by AC.55 At the first step of the GA parametrization we have suggested to define the Fe(acac)3-moiety as a single increment, keeping the general definition of groups attached to the ligand (e.g. increments CH3, CF3, C6H5, etc.) and their heat capacity contributions as they given in compilation.10 For the crystal phase contribution of the [Fe(acac)3]-moiety, we have assigned the value of
value for Fe(acac)3 measured by AC.55 At the first step of the GA parametrization we have suggested to define the Fe(acac)3-moiety as a single increment, keeping the general definition of groups attached to the ligand (e.g. increments CH3, CF3, C6H5, etc.) and their heat capacity contributions as they given in compilation.10 For the crystal phase contribution of the [Fe(acac)3]-moiety, we have assigned the value of  = 429.9 J K−1 mol−1 (ref. 55) (see Table 2). To the best of our knowledge, the liquid phase heat capacities
= 429.9 J K−1 mol−1 (ref. 55) (see Table 2). To the best of our knowledge, the liquid phase heat capacities 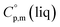 of tris(β-diketonato)iron(III) complexes are not known at all. The contribution of
of tris(β-diketonato)iron(III) complexes are not known at all. The contribution of 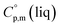 = 429.9 + 31.0 = 460.9 J K−1 mol−1 for the liquid phase heat capacity of the [Fe(acac)3]-moiety has been assessed according to the general trend, where
= 429.9 + 31.0 = 460.9 J K−1 mol−1 for the liquid phase heat capacity of the [Fe(acac)3]-moiety has been assessed according to the general trend, where  >
> 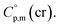 The complementary term of 31 J K−1 mol−1 has been derived from
The complementary term of 31 J K−1 mol−1 has been derived from  = 191 J K−1 mol−1 and
= 191 J K−1 mol−1 and 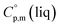 = 222 J K−1 mol−1 evaluated from the solid and the liquid heat capacities of ferrocene.15 It has been found that the level of the difference between
= 222 J K−1 mol−1 evaluated from the solid and the liquid heat capacities of ferrocene.15 It has been found that the level of the difference between 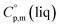 and
and  around 30 J K−1 mol−1 is also common for the large and complex molecules, like e.g. ionic liquids (see Table S1†). Thus, given the complete lack of data on
around 30 J K−1 mol−1 is also common for the large and complex molecules, like e.g. ionic liquids (see Table S1†). Thus, given the complete lack of data on 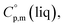 it seems reasonable to propagate the same trend (
it seems reasonable to propagate the same trend ( >
> 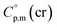 of 31 J K−1 mol−1) for the tris(β-diketonato)iron(III) complexes.
of 31 J K−1 mol−1) for the tris(β-diketonato)iron(III) complexes.
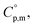 and heat capacity differences,
and heat capacity differences,  for tris(β-diketonato)iron(III) complexes at 298.15 K (in J K−1 mol−1)
for tris(β-diketonato)iron(III) complexes at 298.15 K (in J K−1 mol−1)
| Complex | a | b | c | b |
|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 |
a Calculated by group contribution method by Chickos et al.9,10 with the contributions adjusted for the tris(β-diketonato)iron(III) complexes derivatives (see text).b Calculated according to eqn (4) and (5).c Calculated as  = = 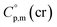 + 31 J K−1 mol−1. The contribution of 31 J K−1 mol−1 was derived from experimental data on + 31 J K−1 mol−1. The contribution of 31 J K−1 mol−1 was derived from experimental data on  and and  for ferrocene15 and was assumed to be valid for tris(β-diketonato)iron(III) complexes. for ferrocene15 and was assumed to be valid for tris(β-diketonato)iron(III) complexes. |
||||
| Fe(acac)3 | 429.9 (ref. 55) | 65.2 | 460.9 | 130.4 |
| Fe(Meacac)3 | 512.7 | 77.7 | 543.7 | 151.9 |
| Fe(tfac)3 | 521.4 | 79.0 | 552.4 | 154.2 |
| Fe(hfac)3 | 654.9 (ref. 55) | 99.0 | 685.9 | 188.9 |
| Fe(ba)3 | 608.1 | 92.0 | 639.1 | 176.7 |
| Fe(dbm)3 | 786.2 | 118.7 | 817.2 | 223.1 |
| Fe(thd)3 | 887.7 (ref. 55) | 133.9 | 918.7 | 249.4 |
Using the numerical values for  and
and 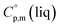 assigned for the [Fe(acac)3]-moiety, calculations of heat capacities of other tris(β-diketonato)iron(III) complexes is simple and straightforward. For example, to estimate heat capacity of Fe(Meacac)3, it is necessary to subtract three contributions of [CaH] = 17.5 J K−1 mol−1 from the basic molecule value of
assigned for the [Fe(acac)3]-moiety, calculations of heat capacities of other tris(β-diketonato)iron(III) complexes is simple and straightforward. For example, to estimate heat capacity of Fe(Meacac)3, it is necessary to subtract three contributions of [CaH] = 17.5 J K−1 mol−1 from the basic molecule value of 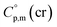 = 429.9 J K−1 mol−1 for [Fe(acac)3] and add three contributions of [CaC] = 8.5 J K−1 mol−1 and three contributions of [CH3] = 36.6 J K−1 mol−1 as it is presented in Fig. 2. The resulting value of
= 429.9 J K−1 mol−1 for [Fe(acac)3] and add three contributions of [CaC] = 8.5 J K−1 mol−1 and three contributions of [CH3] = 36.6 J K−1 mol−1 as it is presented in Fig. 2. The resulting value of  = 512.7 J K−1 mol−1 (see Table 2) was estimated for [Fe(Meacac)3] and we used it to derive value of
= 512.7 J K−1 mol−1 (see Table 2) was estimated for [Fe(Meacac)3] and we used it to derive value of 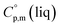 = 512.7 + 31.0 = 543.7 J K−1 mol−1 (see Table 2). Another example is estimation of the heat capacity of Fe(tfac)3: again we start with the
= 512.7 + 31.0 = 543.7 J K−1 mol−1 (see Table 2). Another example is estimation of the heat capacity of Fe(tfac)3: again we start with the  = 429.9 J K−1 mol−1 for the basic molecule [Fe(acac)3], subtract three contributions of [CH3] = 36.6 J K−1 mol−1 and add three contributions of [CF3] = 67.1 J K−1 mol−1 as it is shown in Fig. 2. The resulting value of
= 429.9 J K−1 mol−1 for the basic molecule [Fe(acac)3], subtract three contributions of [CH3] = 36.6 J K−1 mol−1 and add three contributions of [CF3] = 67.1 J K−1 mol−1 as it is shown in Fig. 2. The resulting value of 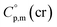 = 521.4 J K−1 mol−1 is used for estimation of
= 521.4 J K−1 mol−1 is used for estimation of  = 521.4 + 31.0 = 552.4 J K−1 mol−1 for Fe(tfac)3 (see Table 2). Reliable
= 521.4 + 31.0 = 552.4 J K−1 mol−1 for Fe(tfac)3 (see Table 2). Reliable 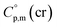 values for Fe(acac)3, Fe(hfac)3, and Fe(thd)3 are available from the literature.55 For Fe(Meacac)3, Fe(tfac)3, Fe(ba)3, and Fe(dbm)3 the
values for Fe(acac)3, Fe(hfac)3, and Fe(thd)3 are available from the literature.55 For Fe(Meacac)3, Fe(tfac)3, Fe(ba)3, and Fe(dbm)3 the 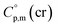 values were estimated (see Table 2) using the algorithm shown in Fig. 2.
values were estimated (see Table 2) using the algorithm shown in Fig. 2.
The next step is to calculate the 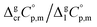 values required for the adjustment of sublimation/vaporization enthalpies to the reference temperature according to eqn (2) and (3). In our previous work on ferrocene15 we described four approaches for assessment of these heat capacity differences. The application of the individual approaches is only determined by the availability of the required input data. With the very limited thermodynamic data for the tris(β-diketonato)iron(III) complexes, the only empirical correlations for
values required for the adjustment of sublimation/vaporization enthalpies to the reference temperature according to eqn (2) and (3). In our previous work on ferrocene15 we described four approaches for assessment of these heat capacity differences. The application of the individual approaches is only determined by the availability of the required input data. With the very limited thermodynamic data for the tris(β-diketonato)iron(III) complexes, the only empirical correlations for 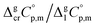 values suggested by Chickos and Acree10 can be used:
values suggested by Chickos and Acree10 can be used:
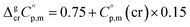 | (4) |
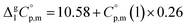 | (5) |
It should be noted that both correlations were developed for molecules that do not contain metal as a structural unit. However, in our recent works15,16 on ferrocene and its alkyl derivatives, we were able to demonstrate with help of reliable experimental 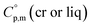 values and quantum-chemical calculations, that these equations are also valid for the metal-containing compounds. In the current study we also used eqn (4) and (5) for calculation of the
values and quantum-chemical calculations, that these equations are also valid for the metal-containing compounds. In the current study we also used eqn (4) and (5) for calculation of the 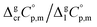 values of tris(β-diketonato)iron(III) complexes (see Table 2, column 3 and column 5). We used these values to adjust the
values of tris(β-diketonato)iron(III) complexes (see Table 2, column 3 and column 5). We used these values to adjust the 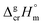 and
and 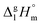 values reported at Tav (Table 1, column 4) to the reference temperature T = 298.15 K (Table 1, column 5) and begin to develop the structure–property relationships for this family of metal–organic compounds.
values reported at Tav (Table 1, column 4) to the reference temperature T = 298.15 K (Table 1, column 5) and begin to develop the structure–property relationships for this family of metal–organic compounds.
2.2 Indirect assessment of fusion enthalpies of tris(β-diketonato)iron(III) complexes
Last decades the fusion enthalpies of materials are commonly measured by commercially available DSC. However, the metal β-diketonates (see Fig. 1) are volatile and can escape from the standard alumina pan or even blast the pan at elevated temperatures. Moreover, the metal β-diketonates can undergo solid–solid transformations before the melting or decompose at relatively low temperatures. Available results on melting temperatures and fusion enthalpies for tris(β-diketonato)iron(III) complexes are collected in Table 3.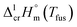 for tris(β-diketonato)iron(III) complexesa
for tris(β-diketonato)iron(III) complexesa
| Complex | Tfus/K | /kJ mol−1 | b/kJ mol−1 |
|---|---|---|---|
| 1 | 2 | 3 | 4 |
a Uncertainties in this table are expressed as expanded uncertainties at a level of confidence of 0.95 (k = 2). Complete compilation of melting temperatures for tris(β-diketonato)iron(III) complexes available in the literature is given in Table S2.b The enthalpies of fusion, 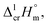 at Tfus were adjusted to 298.15 K (see eqn (6)). Uncertainties in the temperature adjustment of fusion enthalpies from Tfus to the reference temperature are estimated to account with 30% to the total adjustment.58c Average value.d Weighted mean value. We used the experimental uncertainty as the weighing factor. Values in parenthesis were excluded from the calculation of the mean.e Calculated by the multiplication of the fusion temperature Tfus with the Walden constant of 69 ± 2 J K−1 mol−1 (see Table 4) with uncertainty assessed to be ±3.0 kJ mol−1.f The enthalpies of fusion, at Tfus were adjusted to 298.15 K (see eqn (6)). Uncertainties in the temperature adjustment of fusion enthalpies from Tfus to the reference temperature are estimated to account with 30% to the total adjustment.58c Average value.d Weighted mean value. We used the experimental uncertainty as the weighing factor. Values in parenthesis were excluded from the calculation of the mean.e Calculated by the multiplication of the fusion temperature Tfus with the Walden constant of 69 ± 2 J K−1 mol−1 (see Table 4) with uncertainty assessed to be ±3.0 kJ mol−1.f The enthalpies of fusion,  at 298.15 K derived as the difference between experimental sublimation and vaporization enthalpies (see Table 1, column 5, values in bold) were adjusted to Tfus. Uncertainties in the temperature adjustment of fusion enthalpies from the reference temperature to Tfus are estimated to account with 30% to the total adjustment.58g The enthalpies of fusion, at 298.15 K derived as the difference between experimental sublimation and vaporization enthalpies (see Table 1, column 5, values in bold) were adjusted to Tfus. Uncertainties in the temperature adjustment of fusion enthalpies from the reference temperature to Tfus are estimated to account with 30% to the total adjustment.58g The enthalpies of fusion, 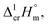 at 298.15 K were calculated as the differences at 298.15 K were calculated as the differences  (see eqn (7)) taken from Table 1 (column 5, values in bold). (see eqn (7)) taken from Table 1 (column 5, values in bold). |
|||
| Fe(acac)3 | 454 | (25.9 ± 0.5)26 | 20.5 ± 3.3 |
| 461 | 34.1 ± 0.9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 44 44 |
||
| 462 | (22.6 ± 0.5)56 | ||
| 460 | (25.3 ± 1.0)57 | ||
| 459 | 30.1 ± 0.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 57 57 |
||
| 459c | 31.0 ± 0.9d | ||
| Fe(Meacac)3 | 461 | 31.8 ± 3.0e | 19.7 ± 4.7 |
| Fe(tfac)3 | 389 | 38.0 ± 5.5f | 31.2 ± 5.4g |
| Fe(hfac)3 | 329 | 31.3 ± 3.6f | 28.5 ± 3.5g |
| Fe(ba)3 | 496 | 34.2 ± 3.0e | 17.4 ± 5.9 |
| Fe(dbm)3 | 539 | 37.3 ± 3.0e | 12.2 ± 8.1 |
| Fe(thd)3 | 438 | 30.8 ± 5.9f | 14.6 ± 3.4g |
The spread of fusion enthalpies,  from 22.6 kJ mol−1 to 34.1 kJ mol−1 is an obvious manifestation of faulty experimental conditions. The reason for the discrepancies observed was explained by Sabolovic et al.57 They studied thermal behaviour for Fe(acac)3 on two different calorimeters, with and without high-pressure sample pans used. The smaller value of
from 22.6 kJ mol−1 to 34.1 kJ mol−1 is an obvious manifestation of faulty experimental conditions. The reason for the discrepancies observed was explained by Sabolovic et al.57 They studied thermal behaviour for Fe(acac)3 on two different calorimeters, with and without high-pressure sample pans used. The smaller value of  = 25.3 kJ mol−1 was measured with the standard sample pan. The larger value of
= 25.3 kJ mol−1 was measured with the standard sample pan. The larger value of  = 30.1 kJ mol−1 was measured with the high-pressure sample pans and this result is similar to that obtained by Beech and Lintonbon,44 who used the same calorimeter type (DSC-1B) equipped with the high-pressure pan. In order to get more confidence, the weighted mean value of
= 30.1 kJ mol−1 was measured with the high-pressure sample pans and this result is similar to that obtained by Beech and Lintonbon,44 who used the same calorimeter type (DSC-1B) equipped with the high-pressure pan. In order to get more confidence, the weighted mean value of  = 31.0 ± 0.9 kJ mol−1 was calculated for Fe(acac)3 and used for thermochemical calculations (see Table 4).
= 31.0 ± 0.9 kJ mol−1 was calculated for Fe(acac)3 and used for thermochemical calculations (see Table 4).
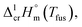 of tris(β-diketonato)iron(III) complexesa
of tris(β-diketonato)iron(III) complexesa
| Complex | b, kJ mol−1 | Tfus/Kb, K | Walden constantc, J K−1 mol−1 |
|---|---|---|---|
a Uncertainties in this table are expressed as expanded uncertainties at a level of confidence of 0.95 (k = 2).b From Table 3.c Calculated as follows: Walden constant = 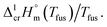 d Weighted mean value. We used the uncertainty as the weighing factor. d Weighted mean value. We used the uncertainty as the weighing factor. |
|||
| Fe(acac)3 | 31.0 ± 0.9 | 459 | 68 ± 2 |
| Fe(tfac)3 | 38.0 ± 5.5 | 389 | 98 ± 14 |
| Fe(hfac)3 | 31.3 ± 3.6 | 329 | 95 ± 11 |
| Fe(thd)3 | 30.8 ± 5.9 | 438 | 73 ± 14 |
| 69 ± 2d | |||
As a rule, thermochemical calculations are commonly performed at T = 298.15 K. The adjustment of  to this temperature is performed according to the Kirchhoff's law:
to this temperature is performed according to the Kirchhoff's law:
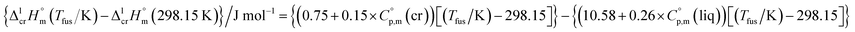 | (6) |
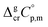 and
and  were taken from Table 2. With this adjustment, the molar enthalpy of fusion of
were taken from Table 2. With this adjustment, the molar enthalpy of fusion of  = 20.5 ± 3.3 kJ mol−1 was calculated for Fe(acac)3. Uncertainties in the temperature adjustment of fusion enthalpy from Tfus to the reference temperature were estimated to account with 30% to the total adjustment.58 Uncertainty of
= 20.5 ± 3.3 kJ mol−1 was calculated for Fe(acac)3. Uncertainties in the temperature adjustment of fusion enthalpy from Tfus to the reference temperature were estimated to account with 30% to the total adjustment.58 Uncertainty of  comprises experimental uncertainty and uncertainty due to temperature adjustment.
comprises experimental uncertainty and uncertainty due to temperature adjustment.
The fusion enthalpies, 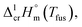 for other tris(β-diketonato)iron(III) complexes listed in Fig. 1 are not found in the literature. However, for some of them, they can be indirectly derived from the results of vapour pressure measurements performed below
for other tris(β-diketonato)iron(III) complexes listed in Fig. 1 are not found in the literature. However, for some of them, they can be indirectly derived from the results of vapour pressure measurements performed below  and above
and above  the melting temperature according to the general thermochemical equation:
the melting temperature according to the general thermochemical equation:
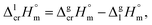 | (7) |
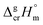 and
and  results for Fe(tfac)3, Fe(hfac)3, and Fe(thd)3 to this temperature (see Table 1). Consequently, the differences
results for Fe(tfac)3, Fe(hfac)3, and Fe(thd)3 to this temperature (see Table 1). Consequently, the differences  calculated for these iron β-diketonates are the fusion enthalpies,
calculated for these iron β-diketonates are the fusion enthalpies,  referenced to T = 298.15 K (see Table 3, column 4). We collected Tfus values for Fe(tfac)3, Fe(hfac)3, and Fe(thd)3 available in the literature (see Table S2†) and calculated the average ones (see Table 3, column 2). The
referenced to T = 298.15 K (see Table 3, column 4). We collected Tfus values for Fe(tfac)3, Fe(hfac)3, and Fe(thd)3 available in the literature (see Table S2†) and calculated the average ones (see Table 3, column 2). The 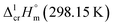 values derived from experimental data according to eqn (7) were re-adjusted to the fusion temperature by Kirchhoff's law (see eqn (6)) with help of the
values derived from experimental data according to eqn (7) were re-adjusted to the fusion temperature by Kirchhoff's law (see eqn (6)) with help of the  and
and 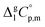 taken from Table 2. With this adjustment, the standard molar enthalpies of fusion at Tfus have been indirectly derived and they are given in Table 3 (column 3). These
taken from Table 2. With this adjustment, the standard molar enthalpies of fusion at Tfus have been indirectly derived and they are given in Table 3 (column 3). These  values can be now applied for further thermochemical calculations as follows.
values can be now applied for further thermochemical calculations as follows.
In series of our recent works, we have gathered experiences with implementation of the Walden's rule:59
 | (8) |
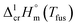 values. The classic empirical Walden-constant = 56.5 J K−1 mol−1 was suggested for estimations irrespective to the structure of the organic molecules. To our surprise, this empirical constant is valid even for the strongly associated compounds like amides,60 nucleobases,61 and even for organometallic compounds like alkylferrocenes.16 In this work we calculated the Walden-constant using the empirical fusion enthalpies,
values. The classic empirical Walden-constant = 56.5 J K−1 mol−1 was suggested for estimations irrespective to the structure of the organic molecules. To our surprise, this empirical constant is valid even for the strongly associated compounds like amides,60 nucleobases,61 and even for organometallic compounds like alkylferrocenes.16 In this work we calculated the Walden-constant using the empirical fusion enthalpies,  and Tfus of Fe(acac)3, Fe(tfac)3, Fe(hfac)3, and Fe(thd)3, (see Table 4).
and Tfus of Fe(acac)3, Fe(tfac)3, Fe(hfac)3, and Fe(thd)3, (see Table 4).
We have derived the Walden-constant = 69 ± 2 J K−1 mol−1 as weighted mean value using the uncertainty as the weighing factor for these tris(β-diketonato)iron(III) complexes. This value somewhat higher, but it is essentially the same as the original value suggested by Walden. As a consequence, having reliable experimental data on Tfus for the metal β-diketonates, their enthalpies of fusion can be quickly assessed with the Walden-constant settled at the level of 69 J K−1 mol−1. This approximation is helpful for deduction of vaporization enthalpies of the metal β-diketonates and development of group-additivity procedure for the  value prediction as it follows in the forthcoming chapters.
value prediction as it follows in the forthcoming chapters.
2.3 Structure–property relationships in tris(β-diketonato)iron(III) complexes
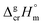 values is a vain endeavor. This statement is easy to support with help of sublimation enthalpy data on pairs of similarly structured compounds. For example, values of
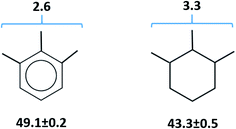
values is a vain endeavor. This statement is easy to support with help of sublimation enthalpy data on pairs of similarly structured compounds. For example, values of  of benzene (44.7 ± 0.2 kJ mol−1 (ref. 63)) and methylbenzene (48.0 ± 1.1 kJ mol−1 (ref. 63)) allow for an estimation of the methyl-group contribution of [CH3] = 3.3 kJ mol−1 (see Fig. 3). Is the [CH3] contribution similar in size in the biphenyl system? Comparison of
of benzene (44.7 ± 0.2 kJ mol−1 (ref. 63)) and methylbenzene (48.0 ± 1.1 kJ mol−1 (ref. 63)) allow for an estimation of the methyl-group contribution of [CH3] = 3.3 kJ mol−1 (see Fig. 3). Is the [CH3] contribution similar in size in the biphenyl system? Comparison of  values for biphenyl (81.8 ± 0.4 kJ mol−1 (ref. 64)) and 4-methyl-biphenyl (80.2 ± 1.4 kJ mol−1 (ref. 65)) provides to some extend different methyl-group contribution of [CH3] = −1.6 kJ mol−1 (see Fig. 3).
values for biphenyl (81.8 ± 0.4 kJ mol−1 (ref. 64)) and 4-methyl-biphenyl (80.2 ± 1.4 kJ mol−1 (ref. 65)) provides to some extend different methyl-group contribution of [CH3] = −1.6 kJ mol−1 (see Fig. 3).
What about metal–organic compounds? Let us compare the sublimation enthalpies of Fe(acac)3 and Fe(Meacac)3 listed in Table 1. The difference between  values for both complexes renders the methyl-group contribution of [CH3] = (164.5 − 131.3)/3 = 11.1 kJ mol−1 (see Fig. 3). The latter value is significantly different from [CH3] contribution in organic compounds discussed above. It is reasonable to suppose that the larger [CH3] contribution can be attributed to peculiarities of metal β-diketonates. However, this supposition is hardly correct as it can be demonstrated by comparison the sublimation enthalpies of Fe(acac)3 and Fe(ba)3 listed in Table 1. The difference between
values for both complexes renders the methyl-group contribution of [CH3] = (164.5 − 131.3)/3 = 11.1 kJ mol−1 (see Fig. 3). The latter value is significantly different from [CH3] contribution in organic compounds discussed above. It is reasonable to suppose that the larger [CH3] contribution can be attributed to peculiarities of metal β-diketonates. However, this supposition is hardly correct as it can be demonstrated by comparison the sublimation enthalpies of Fe(acac)3 and Fe(ba)3 listed in Table 1. The difference between  values for both complexes after subtraction of three increments of [CH3] = 11.1 kJ mol−1 results in contribution for the phenyl-group [C6H5] = 200 − (131.3 − 3 × 11.1) = 101.9/3 = 34.0 kJ mol−1 (see Fig. 3). Such of [C6H5]-contribution to the sublimation enthalpy just derived for metal β-diketonates seems to be rather too low, since it is quite similar to the contribution of [C6H5] = 32.4 kJ mol−1 ascribed for the vaporization enthalpy in simple organic compounds or calculated by using increments from ref. 25 (5 × Ca–(H) + Ca–(C) = 32.4 kJ mol−1). This observation contradicts to the reasonable expectation for considerably larger contribution of the phenyl group to the sublimation enthalpy as compared to those to the vaporization enthalpy. All of the examples discussed provide clear evidence that group additivity does not correctly predict the enthalpy of sublimation. An apparent reason for GA failure is that according to the general thermochemical equation eqn (7), the sublimation enthalpy incorporates two independent contributions: the non-additive contribution for the fusion enthalpy,
values for both complexes after subtraction of three increments of [CH3] = 11.1 kJ mol−1 results in contribution for the phenyl-group [C6H5] = 200 − (131.3 − 3 × 11.1) = 101.9/3 = 34.0 kJ mol−1 (see Fig. 3). Such of [C6H5]-contribution to the sublimation enthalpy just derived for metal β-diketonates seems to be rather too low, since it is quite similar to the contribution of [C6H5] = 32.4 kJ mol−1 ascribed for the vaporization enthalpy in simple organic compounds or calculated by using increments from ref. 25 (5 × Ca–(H) + Ca–(C) = 32.4 kJ mol−1). This observation contradicts to the reasonable expectation for considerably larger contribution of the phenyl group to the sublimation enthalpy as compared to those to the vaporization enthalpy. All of the examples discussed provide clear evidence that group additivity does not correctly predict the enthalpy of sublimation. An apparent reason for GA failure is that according to the general thermochemical equation eqn (7), the sublimation enthalpy incorporates two independent contributions: the non-additive contribution for the fusion enthalpy,  and the additive contribution for the vaporization enthalpy,
and the additive contribution for the vaporization enthalpy, 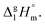 As can be seen from Table 3, the non-additive input from fusion enthalpy is especially significant for metal–organic compounds. Thus, any structure–property correlations in terms of sublimation enthalpies
As can be seen from Table 3, the non-additive input from fusion enthalpy is especially significant for metal–organic compounds. Thus, any structure–property correlations in terms of sublimation enthalpies 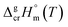 are generally restricted only to similarly shaped molecules, where the non-additive contributions from the fusion enthalpy
are generally restricted only to similarly shaped molecules, where the non-additive contributions from the fusion enthalpy 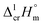 could be occasionally not too much different.66,67
could be occasionally not too much different.66,67
 are well established in the current literature.68,69 Well then, having the credible methods for the assessment of the non-additive fusion enthalpies already established in this work (as it described in Section 2.2), we are going to develop the GA approach for the prediction of vaporization enthalpies,
are well established in the current literature.68,69 Well then, having the credible methods for the assessment of the non-additive fusion enthalpies already established in this work (as it described in Section 2.2), we are going to develop the GA approach for the prediction of vaporization enthalpies, 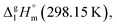 of tris(β-diketonato)iron(III) complexes.
of tris(β-diketonato)iron(III) complexes.The vaporization enthalpies were derived according to equation:
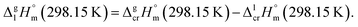 | (9) |
We used the sublimation enthalpies, 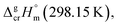 evaluated in Table 1 together with
evaluated in Table 1 together with  for these complexes collected in Table 3. The standard molar enthalpies of vaporization of tris(β-diketonato)iron(III) complexes at the reference temperature of T = 298.15 K calculated according to eqn (9) or those derived from the vapour pressure measurements above the melting temperature (see Table 1) are given in Table 5, column 4. Are these values thermodynamically consistent? A simple way to establish the data consistency is structure–property correlations in series of similarly shaped compounds as it described in the next section.
for these complexes collected in Table 3. The standard molar enthalpies of vaporization of tris(β-diketonato)iron(III) complexes at the reference temperature of T = 298.15 K calculated according to eqn (9) or those derived from the vapour pressure measurements above the melting temperature (see Table 1) are given in Table 5, column 4. Are these values thermodynamically consistent? A simple way to establish the data consistency is structure–property correlations in series of similarly shaped compounds as it described in the next section.
| Complex | b | c | b,d | e | Df |
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 |
| a Uncertainties in this table are expressed as expanded uncertainties at a level of confidence of 0.95 (k = 2).b From Table 1, column 5, in bold.c From Table 3, column 4.d Difference between column 2 and 3 in this table.e Calculated by using the group-additivity procedure (see text).f Difference between column 4 and 5 in this table. | |||||
| Fe(acac)3 | 131.3 ± 1.5 | 20.5 ± 3.3 | 110.8 ± 3.6d | 105.8 | 5.0 ± 3.6 |
| 110.8 ± 8.9b | |||||
| Fe(Meacac)3 | 164.5 ± 10 | 19.7 ± 4.7 | 145 ± 11d | 131.8 | 13 ± 11 |
| Fe(tfac)3 | 131.5 ± 5.1 | 31.2 ± 5.4 | 100.3 ± 1.9b | 100.3 | 0.0 ± 1.9 |
| Fe(ba)3 | 200.0 ± 10 | 17.4 ± 5.9 | 183 ± 12d | 183.7 | −1 ± 12 |
| Fe(hfac)3 | 106.1 ± 3.0 | 28.5 ± 3.5 | 77.6 ± 1.8b | 94.7 | −17.1 ± 1.8 |
| Fe(thd)3 | 136.4 ± 1.5 | 14.6 ± 3.4 | 121.8 ± 3.1b | 153.5 | −31.7 ± 3.1 |
| Fe(dbm)3 | 164.7 ± 8.0 | 12.2 ± 8.1 | 153 ± 11d | 261.5 | −109 ± 11 |
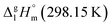 for the HL and Fe(L)3 series considered for structure–property correlations are collected in Table 6.
for the HL and Fe(L)3 series considered for structure–property correlations are collected in Table 6.
| CAS | β-Diketone | Complex | a | |
|---|---|---|---|---|
| a Data from Table 5, column 4.b Weighted average from two results given in Table 5, column 4. | ||||
| 123-54-6 | Acetylacetone | 41.8 ± 0.2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 72 72 |
Fe(acac)3 | 110.8 ± 3.3b |
| 815-57-6 | 3-Methyl-2,4-pentanedione | 48.5 ± 5.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 45 45 |
Fe(Meacac)3 | 145 ± 11 |
| 367-57-7 | Trifluoroacetylacetone | 37.3 ± 0.2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 72 72 |
Fe(tfac)3 | 100.3 ± 1.9 |
| 1522-22-1 | Hexafluoroacetylacetone | 30.7 ± 0.2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 72 72 |
Fe(hfac)3 | 77.6 ± 1.8 |
It has turned out, that a very good linear correlation (see Fig. S1†) has been observed between experimental 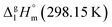 values as follows:
values as follows:
 | (10) |
Such a good quality of correlation can be considered as an indicator of internal data consistency within each series of organic and metal–organic compounds. These consistent values can be used now for development of the group-additivity method for prediction of vaporization enthalpies, 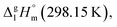 for metal–organic compounds under study.
for metal–organic compounds under study.
 of organic compounds are well established and broadly used in the literature.25,68,69 For the purpose of this work we extracted from our previous work68 an essential number of group-additivity values (GAVs), which are extended in this study and compiled in Table 7.
of organic compounds are well established and broadly used in the literature.25,68,69 For the purpose of this work we extracted from our previous work68 an essential number of group-additivity values (GAVs), which are extended in this study and compiled in Table 7.
| GAV | |
|---|---|
| a Parametrization is presented in Fig. 7.b Parametrization is presented in Fig. 10.c Parametrization is presented in Fig. 11.d Parametrization is presented in Fig. 9. | |
| C-(C)(H)3 or [CH3] | 5.65 |
| C–(C)2(H)2 | 4.98 |
| C–(C)3(H) | 3.01 |
| C–(C)4 | 0.01 |
| C–(C)2(H)2 (cyclic) | 5.5a |
| O–(C)2 (cyclic) | 7.9 |
| C–(O)(H)(C)2(cyclic) | 0.62 |
| C–(O)2(H)2 (cyclic) | 8.7a |
| CF3 | 3.8b |
| C6H5 | 31.6b |
| C(CH3)3 | 13.6b |
| [1,2,3-CH3] | 3.0c |
| Fe | 4.4d |
| Ca–(H) | 5.65 |
| Ca–(C) | 4.10 |
Despite the fact that the GA method was generally developed for organic substances there were also attempts to apply it for metal-containing compounds. For example, Sevast'yanov et al.73,74 calculated the enthalpies of vaporization of molecular organometallic compounds of strontium and titanium by the method of group contributions, but due to the differences between the experiment and estimation up to 60 kJ mol−1, these efforts could be hardly designate as successful. From our experiences, the apparent reason for such failure is insufficient experimental database, as well as difficulties with a proper definition of structural unites required for the parametrization of the GA method. We also have to overcome these difficulties with parametrization of vaporization enthalpy of tris(β-diketonato)iron(III) complexes. Indeed, considering the structure of e.g. Fe(acac)3, we immediately have to face the question how to parametrise the oxygen atoms surrounding iron atom (see Fig. 4, left).
From one hand, it is obvious that structures of ligands adjacent to the iron atom should be regarded as aromatic, from the other hand, we are not able to conduct any parametrization of the “aromatic” oxygens attached to the Fe atom (see Fig. 4, middle), because more simple molecules suitable for incrementation are absent in the nature (see Fig. 4, right). Anyway, the idea to represent the structure of metal β-diketonate complexes as the sum of contributions assigned to the metal (e.g. Fe in this study) and to the three adjacent ligands (see Fig. 4, middle), seems to be the simplest and the most attractive for practical realisation. But the question with quantification of energetics of the six-membered “aromatic” unit still remains unsolved (see Fig. 4, right).
By the way, how different could the energetics of the six-membered “aromatic” and the six-membered “aliphatic” unite be? In order to answer this question, we have collected and compared vaporization enthalpies of benzene, cyclohexene, cyclohexane, as well as of toluene and methyl-cyclohexene (Fig. 5). It is obvious from Fig. 5, that vaporization enthalpies, 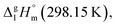 of “aromatic” and “aliphatic” cyclic molecules are very similar, in spite of well-known conformational diversity of substituted aliphatic six-membered rings.
of “aromatic” and “aliphatic” cyclic molecules are very similar, in spite of well-known conformational diversity of substituted aliphatic six-membered rings.
 | ||
Fig. 5 Comparison of experimental vaporization enthalpies,  of benzene, cyclohexene, and cyclohexene (upper-level), as well as toluene and methyl-cyclohexene (low-level), modelling systems with the six-membered “aromatic” and the six-membered “aliphatic” cycles (numeric values of vaporization enthalpies in kJ mol−1 were taken from ref. 72). of benzene, cyclohexene, and cyclohexene (upper-level), as well as toluene and methyl-cyclohexene (low-level), modelling systems with the six-membered “aromatic” and the six-membered “aliphatic” cycles (numeric values of vaporization enthalpies in kJ mol−1 were taken from ref. 72). | ||
This observation has prompted an assumption, that the 4,6-dimethyl-1,3-dioxane (see Fig. 6, left) could be considered as a suitable model compound, which imitates the vaporization energetics of the non-existing six-membered “aromatic” cycle (see Fig. 6, right). Vaporization enthalpies, 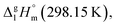 of both cis- (41.7 ± 0.4 kJ mol−1) and trans-4,6-dimethyl-1,3-dioxane (42.5 ± 0.6 kJ mol−1) have been measured just recently.75 Since vaporization enthalpies of both isomers are indistinguishable within the boundaries of their experimental uncertainties, we used vaporization enthalpy of trans-4,6-dimethyl-1,3-dioxane (42.5 ± 0.6 kJ mol−1) for thermochemical calculations along this manuscript.
of both cis- (41.7 ± 0.4 kJ mol−1) and trans-4,6-dimethyl-1,3-dioxane (42.5 ± 0.6 kJ mol−1) have been measured just recently.75 Since vaporization enthalpies of both isomers are indistinguishable within the boundaries of their experimental uncertainties, we used vaporization enthalpy of trans-4,6-dimethyl-1,3-dioxane (42.5 ± 0.6 kJ mol−1) for thermochemical calculations along this manuscript.
 | ||
Fig. 6 Comparison of the vaporization enthalpies,  of the model molecule 4,6-dimethyl-1,3-dioxane with the of the model molecule 4,6-dimethyl-1,3-dioxane with the  value of the corresponding ligand (in kJ mol−1). value of the corresponding ligand (in kJ mol−1). | ||
However, the envisaged model molecule of 4,6-dimethyl-1,3-dioxane does not represent the corresponding ligand correctly. As it can be seen in Fig. 6, we have to cut the “nose” in the 4,6-dimethyl-1,3-dioxane structure in order to reproduce the required fragment correctly. In terms of group-additivity it means that we need to subtract the enthalpic increment C–(O)2(H)2 (cyclic) = 8.7 kJ mol−1 (see Fig. 7 and Table 7) from  = 42.5 ± 0.6 kJ mol−1 of 4,6-dimethyl-1,3-dioxane. Now the desired resulting fragment (see Fig. 6, right) properly representing the [L] ligand adjacent to the iron in the Fe(acac)3 has the numerical contribution to the vaporization enthalpy of [L](acac) = (42.5 − 8.7) = 33.8 kJ mol−1 (see Fig. 6).
= 42.5 ± 0.6 kJ mol−1 of 4,6-dimethyl-1,3-dioxane. Now the desired resulting fragment (see Fig. 6, right) properly representing the [L] ligand adjacent to the iron in the Fe(acac)3 has the numerical contribution to the vaporization enthalpy of [L](acac) = (42.5 − 8.7) = 33.8 kJ mol−1 (see Fig. 6).
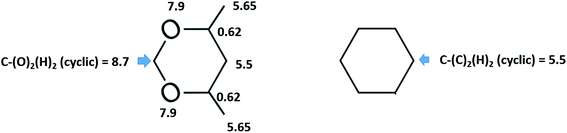 | ||
Fig. 7 Parametrization of specific group contributions required for prediction of vaporization enthalpy (in kJ mol−1). The contribution C–(O)2(H)2 (cyclic) is derived from the experimental value of  = 42.5 ± 0.6 kJ mol−1 of 4,6-dimethyl-1,3-dioxane. The contribution C–(C)2(H)2 (cyclic) = 5.5 kJ mol−1 is derived from the experimental value of = 42.5 ± 0.6 kJ mol−1 of 4,6-dimethyl-1,3-dioxane. The contribution C–(C)2(H)2 (cyclic) = 5.5 kJ mol−1 is derived from the experimental value of  = 33.1 ± 0.2 kJ mol−1 (ref. 72) of cyclohexane, where six such increments are present. = 33.1 ± 0.2 kJ mol−1 (ref. 72) of cyclohexane, where six such increments are present. | ||
This ligand, [L](acac) = 33.8 kJ mol−1, is suggested now as a building block to construct a theoretical  value of Fe(acac)3 as it shown in Fig. 8. However, in order to complete this construction, we need a numerical contribution to the vaporization enthalpy coming from the central atom iron [Fe] in Fe(acac)3.
value of Fe(acac)3 as it shown in Fig. 8. However, in order to complete this construction, we need a numerical contribution to the vaporization enthalpy coming from the central atom iron [Fe] in Fe(acac)3.
 = 60.9 ± 1.9 kJ mol−1 of ferrocene was evaluated and shown to be thermodynamically consistent. In order to extract the numerical contribution to the vaporization enthalpy coming from the central atom iron, [Fe], we have to assume (see Fig. 9) that the group-contribution CaH = 5.65 kJ mol−1 in benzene (one of six C atoms in the benzene aromatic ring) is equivalent to CaH in ferrocene (one of ten C atoms in both five-membered aromatic rings). With this assumption applied to the experimental vaporization enthalpy of ferrocene, the required contribution of [Fe] = 4.4 kJ mol−1 (see Table 7 and Fig. 9) is derived and it is assumed to be also valid for the vaporization enthalpy estimations for tris(β-diketonato)iron(III) complexes.
= 60.9 ± 1.9 kJ mol−1 of ferrocene was evaluated and shown to be thermodynamically consistent. In order to extract the numerical contribution to the vaporization enthalpy coming from the central atom iron, [Fe], we have to assume (see Fig. 9) that the group-contribution CaH = 5.65 kJ mol−1 in benzene (one of six C atoms in the benzene aromatic ring) is equivalent to CaH in ferrocene (one of ten C atoms in both five-membered aromatic rings). With this assumption applied to the experimental vaporization enthalpy of ferrocene, the required contribution of [Fe] = 4.4 kJ mol−1 (see Table 7 and Fig. 9) is derived and it is assumed to be also valid for the vaporization enthalpy estimations for tris(β-diketonato)iron(III) complexes.
 of tris(β-diketonato)iron(III) complexes is now completed. The road map for estimations is given in Fig. 10. The compilation of increments necessary for work with iron β-diketonates is given in Table 7. Generally, there are two options to commence the GA procedure. The first option is based on any reliable experimental thermochemical property (e.g. enthalpy of vaporization, enthalpy of formation, heat capacity, etc.) of a “core” molecule. In the current study it is for sure the vaporization enthalpy of Fe(acac)3 (see the consistent results in Table 5, column 4). The H atoms (or the CH3 groups) in the ligands surrounding the Fe atom can be consequently exchanged with an arbitrary R substituent (see Fig. 10, left) having an energetic contribution ΔH(H → R) specific for each type of R. The approach for parametrization of ΔH(H → R) contributions for the exchange of R substituent on the ligand ring is graphically presented in Fig. 10 (right). The numerical values are listed in Table 7. This option could be helpful for the data evaluation and consistency test for β-diketonate chelates with metal other than iron provided that complex with reliable experimental vaporization enthalpy can be found and appointed as the “core” molecule.
of tris(β-diketonato)iron(III) complexes is now completed. The road map for estimations is given in Fig. 10. The compilation of increments necessary for work with iron β-diketonates is given in Table 7. Generally, there are two options to commence the GA procedure. The first option is based on any reliable experimental thermochemical property (e.g. enthalpy of vaporization, enthalpy of formation, heat capacity, etc.) of a “core” molecule. In the current study it is for sure the vaporization enthalpy of Fe(acac)3 (see the consistent results in Table 5, column 4). The H atoms (or the CH3 groups) in the ligands surrounding the Fe atom can be consequently exchanged with an arbitrary R substituent (see Fig. 10, left) having an energetic contribution ΔH(H → R) specific for each type of R. The approach for parametrization of ΔH(H → R) contributions for the exchange of R substituent on the ligand ring is graphically presented in Fig. 10 (right). The numerical values are listed in Table 7. This option could be helpful for the data evaluation and consistency test for β-diketonate chelates with metal other than iron provided that complex with reliable experimental vaporization enthalpy can be found and appointed as the “core” molecule.
 | ||
Fig. 10 The road map for estimation of  of tris(β-diketonato)iron(III) complexes based on the [L](acac) ligand (the idea – left and the result – middle). Approach for parametrization of contributions H → R for the exchange of R substituent on the ligand ring (right). Experimental data involved in the approach are collected in Table S3.† of tris(β-diketonato)iron(III) complexes based on the [L](acac) ligand (the idea – left and the result – middle). Approach for parametrization of contributions H → R for the exchange of R substituent on the ligand ring (right). Experimental data involved in the approach are collected in Table S3.† | ||
The second option is completely based on the GAVs established in Table 7 and the ligand, [L](acac) = 33.8 kJ mol−1 (see Fig. 6). The main idea is equivalent with the first option, but the consecutive exchanged of H atoms (or the CH3 groups) with the arbitrary R substituent is executed only on the [L](acac) ligand. The result is multiplied by three and supplemented with the increment for iron [Fe] (or another metal of interest). Contributions ΔH(H → R) specific for each type of substituent R are given in Table 7. This option could only be used if no additional interactions between substituents within the complex are assumed.
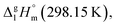 of metal–organic compounds under study. For the validation procedure we used the second option (see Section 2.3.6) based on modifications of the ligand [L](acac) = 33.8 kJ mol−1 (see Fig. 6).
of metal–organic compounds under study. For the validation procedure we used the second option (see Section 2.3.6) based on modifications of the ligand [L](acac) = 33.8 kJ mol−1 (see Fig. 6).
Calculations for Fe(acac)3. To pursue the design drawing presented in Fig. 8, we are ready now to estimate the theoretical vaporization enthalpy value of Fe(acac)3:
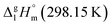 = 33.8 × 3 + 4.4 = 105.8 kJ mol−1 (Table 5, column 5), which is in very good agreement with the experimental value of
= 33.8 × 3 + 4.4 = 105.8 kJ mol−1 (Table 5, column 5), which is in very good agreement with the experimental value of  = 110.8 ± 8.9 kJ mol−1 as well as with the value of
= 110.8 ± 8.9 kJ mol−1 as well as with the value of 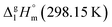 = 110.8 ± 3.6 kJ mol−1 calculated as the difference between experimental results on sublimation and fusion enthalpies (Table 5, column 4). Such a good agreement between theoretical and experimental results has encouraged further validation of the GA procedure.
= 110.8 ± 3.6 kJ mol−1 calculated as the difference between experimental results on sublimation and fusion enthalpies (Table 5, column 4). Such a good agreement between theoretical and experimental results has encouraged further validation of the GA procedure.
Calculations for Fe(Meacac)3. This complex has the additional CH3 group on each ligand in comparison to the Fe(acac)3 (see Fig. 3, third line). From our experience, the arrangement of three CH3 groups in the sequence 1,2,3 on the aromatic or aliphatic ring may cause an additional contribution (see Fig. 11) due to the so-called “buttress”-effect.76 In order to evaluate this [1,2,3-CH3] contribution, we used experimental vaporization enthalpies of benzene, toluene and 1,2,3-trimethylbenzene, as well as vaporization enthalpies of cyclohexene, methylcyclohexene, and 1,2,3-trimethylcyclohexane. All experimental data except for 1,2,3-trimethylcyclohexane were taken from ref. 72. Vaporization enthalpy of 1,2,3-trimethylcyclohexane was derived from correlation of experimental vaporization enthalpies of alkyl-substituted cyclohexanes with their Kovat's retention indices (Table S4†). As it apparent from Fig. 11, the [1,2,3-CH3] contributions for aromatic and aliphatic cycles are quite similar in size on the level of 3.0 kJ mol−1.
 | ||
| Fig. 11 Estimation of the [1,2,3-CH3] group contribution from arrangement of three CH3 groups in the sequence 1,2,3 on the aromatic or aliphatic ring, based on vaporization enthalpies (kJ mol−1) of 1,2,3-trimethylbenzene72 and 1,2,3-trimethylcyclohexane (see Table S3 and Fig. S2†). | ||
This empirical correction was applied for calculation of vaporization enthalpy of the ligand in Fe(Meacac)3, based on the starting value of [L](acac) = 33.8 kJ mol−1 and two additional contributions for [CH3] = 5.65 kJ mol−1 and [1,2,3-CH3] = 3.0 kJ mol−1. The resulting numerical value for the ligand in Fe(Meacac)3, [L](Meacac) = 42.5 kJ mol−1, was multiplied by three and after summation with the [Fe] = 4.4 kJ mol−1, the theoretical value of 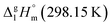 = 131.8 kJ mol−1 for the Fe(Meacac)3 complex was calculated (see Table 5, column 5). This result is in fair agreement with the experimental value of
= 131.8 kJ mol−1 for the Fe(Meacac)3 complex was calculated (see Table 5, column 5). This result is in fair agreement with the experimental value of  = 145 ± 11 kJ mol−1 (see Table 5, column 4) taking into account the significant experimental uncertainties.
= 145 ± 11 kJ mol−1 (see Table 5, column 4) taking into account the significant experimental uncertainties.
Calculations for Fe(tfac)3. For calculation of vaporization enthalpy of the ligand in Fe(tfac)3 we begin again with the ligand [L](acac) = 33.8 kJ mol−1, then subtract the contributions for [CH3] = 5.65 kJ mol−1 and add the increment [CF3] = 3.8 kJ mol−1 (see Fig. 10 right). The ligand [L](tfac) = 32.0 kJ mol−1 was multiplied by three and complemented with the [Fe] = 4.4 kJ mol−1. The resulting theoretical value of
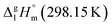 = 100.3 kJ mol−1 for the Fe(tfac)3 complex (Table 5, column 5) is in excellent agreement with the experimental value of
= 100.3 kJ mol−1 for the Fe(tfac)3 complex (Table 5, column 5) is in excellent agreement with the experimental value of  = 100.3 ± 1.9 kJ mol−1 (Table 5, column 4). And again a good agreement between theoretical and experimental result has proved the reliability of the GA procedure.
= 100.3 ± 1.9 kJ mol−1 (Table 5, column 4). And again a good agreement between theoretical and experimental result has proved the reliability of the GA procedure.
Calculations for Fe(ba)3. The contribution for vaporization enthalpy of the ligand in Fe(ba)3 was calculated by subtraction of substituent [CH3] = 5.65 kJ mol−1 from [L](acac) = 33.8 kJ mol−1, adding [C6H5] = 31.6 kJ mol−1 (see Fig. 10 right). The ligand [L]tfac(ba) = 59.8 kJ mol−1 was multiplied by three and complemented with the [Fe] = 4.4 kJ mol−1. The resulting theoretical value of
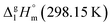 = 183.7 kJ mol−1 for the Fe(ba)3 complex (Table 5, column 5) is still in agreement with the experimental value of
= 183.7 kJ mol−1 for the Fe(ba)3 complex (Table 5, column 5) is still in agreement with the experimental value of 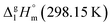 = 183 ± 12 kJ mol−1 (Table 5, column 4) taking into account relatively high experimental uncertainty.
= 183 ± 12 kJ mol−1 (Table 5, column 4) taking into account relatively high experimental uncertainty.Summing up, the group additivity calculations carried out on four tris(β-diketonato)iron(III) complexes, Fe(acac)3, Fe(Meacac)3, Fe(tfac)3, and Fe(ba)3, have demonstrated a fair agreement between theoretical and experimental results and verified the reliability of the GA procedure for prediction of vaporization enthalpies developed in this work. We are going to elaborate and generalize this procedure for β-(diketonato)metal complexes in the forthcoming work. Moreover, having established the degree of reliance on this GA procedure we intend to apply this method for detection and explanation of a non-additive effects inherent for β-(diketonato)metal complexes, which are stipulating an exceedingly high volatility of organometallic complexes containing e.g. branched substituents.
It is self-evident, that the dispersion forces are emerging as the consequence of nearest-neighbor and non-nearest-neighbor interactions between substituents placed in the close proximity on the ligands surrounding the metal in the middle of the complex. This diversity of the collective interactions is definitely non-additive and it cannot be captured by the summation of GAVs. In contrast, the experimental thermodynamic property (vaporization enthalpy in this case) naturally comprises all existing additive and non-additive interactions. The apparent conclusion from this specification of the dispersion forces is that the difference between the experimental vaporization enthalpy of Fe(L)3 and its theoretical additive value, could be considered as the measure for the amount of dispersion forces contributing to vaporization enthalpy. Following this idea, we calculated the aforementioned differences D, defined as the quantity of possible dispersion forces inherent in differently shaped metal–organic complexes (see Table 5, column 6). Analysis of these differences D, corroborates with conclusions drawn by development of GA procedure and with the well-established CVD experiences. The dispersion forces are practically absent in Fe(acac)3, Fe(Meacac)3, and Fe(tfac)3 complexes. Also the value of D = −1 ± 12 kJ mol−1 (see Table 5, column 6) for Fe(ba)3 does not arose suspicion on weak stabilization due to the attractive repulsions of phenyl π-orbitals. However, this stabilization could be in shadow of the large uncertainty. But already impressive stabilisation of D = −17.1 ± 1.8 kJ mol−1 is apparent in the Fe(hfac)3 complex. The significantly more profound stabilization of D = −31.7 ± 3.1 kJ mol−1 is evident in the Fe(thd)3 complex. However, the most surprising stabilization of D = −109 ± 11 kJ mol−1 is derived for the Fe(dbm)3 complex. Such enormous rise of dispersion forces could be attributed to the intensive attractive repulsions between π-orbitals of phenyl substituents located in very close proximity. Otherwise, there is only the single experimental study of the Fe(dbm)3 complex,42 and additional experimental efforts are highly desired in order to ascertain the discussion on dispersion forces present in this complex.
3. Conclusion
According to the title of this paper “Error or exemption to the rule?” we have confronted with ill-defined massive of experimental data on phase transitions solid–gas, liquid–gas, and solid–liquid. The enormous spread of available results has thwarted reasonable selection of reliable values. For this reason, we have developed a diagnostic check for thermochemistry of metal–organic compounds, based on principles of group-additivity. This diagnostic tool served in two ways. From one hand we have been able to separate and reject the “ill” data for each compound. From the other hand this diagnostic tool has helped to reveal the “exemption to the rule?”, where the deviation from the additivity rules has manifested appearance of the strong dispersion forces, responsible for elevated volatility of complexes with branched substituents. The diagnostic tool was developed and checked for the β-(diketonato)iron(III) complexes. The amplification of this method for the β-(diketonato)metal(III) complexes is under construction.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work has been supported by the German Science Foundation (DFG) in the frame of the special priority program SPP 1807 “Control of London Dispersion Interactions in Molecular Chemistry”, (grant VE 265-9/2 for SPV). KZ are grateful to the Ministry of Science and Education of the Russian Federation for supporting the research (Nikolaev Institute of Inorganic Chemistry SB RAS).References
- M. Leskelä, H. Mölsä and L. Niinistö, Supercond. Sci. Technol., 1993, 6, 627–656 CrossRef and references therein.
- G. G. Condorelli, G. Malandrino and I. L. Fragalà, Coord. Chem. Rev., 2007, 251, 1931–1950 CrossRef CAS.
- A. Devi, Coord. Chem. Rev., 2013, 257, 3332–3384 CrossRef CAS.
- G. Carraro, C. Maccato, A. Gasparotto, D. Barreca, M. Walter, L. Mayrhofer, M. Moseler, A. Venzo, R. Seraglia and C. Marega, Phys. Chem. Chem. Phys., 2015, 17, 11174–11181 RSC.
- I. K. Igumenov, T. V. Basova and V. R. Belosludov, in Application of thermodynamics to biological and materials science, ed. T. Mizutani, InTech, Rijeka, Croatia, 2011, pp. 521–546 Search PubMed.
- I. K. Igumenov, J. Phys. IV, 1995, 05, C5-489–C5-496 CrossRef.
- T. G. Hicks and N. P. Chopey, Handbook of Chemical Engineering Calculations, McGraw-Hill, United States, Fourth Edition, 2012 Search PubMed.
- D. Kulikov, S. P. Verevkin and A. Heintz, J. Chem. Eng. Data, 2001, 46, 1593–1600 CrossRef CAS.
- J. S. Chickos, S. Hosseini, D. G. Hesse and J. F. Liebman, Struct. Chem., 1993, 4, 271–278 CrossRef CAS.
- W. Acree, Jr and J. S. Chickos, J. Phys. Chem. Ref. Data, 2017, 46, 013104 CrossRef.
- S. P. Verevkin, V. N. Emel'yanenko, M. A. Varfolomeev, B. N. Solomonov and K. V. Zherikova, Fluid Phase Equilib., 2014, 380, 67–75 CrossRef CAS.
- S. P. Verevkin, S. V. Melkhanova, V. N. Emel'yanenko, D. H. Zaitsau, M. A. Varfolomeev, B. N. Solomonov and K. V. Zherikova, J. Phys. Chem. B, 2014, 118, 14479–14492 CrossRef CAS.
- T. Reschke, K. V. Zherikova, S. P. Verevkin and C. Held, J. Pharm. Sci., 2016, 105, 1050–1058 CrossRef CAS.
- K. V. Zherikova, A. A. Svetlov, N. V. Kuratieva and S. P. Verevkin, Chemosphere, 2016, 161, 157–166 CrossRef CAS.
- K. V. Zherikova and S. P. Verevkin, Fluid Phase Equilib., 2018, 472, 196–203 CrossRef CAS.
- S. P. Verevkin, V. N. Emel'yanenko, K. V. Zherikova, L. N. Zelenina, D. H. Zaitsau and A. A. Pimerzin, Chem. Phys. Lett., 2020, 739, 136911 CrossRef CAS.
- E. W. Berg and J. T. Truemper, J. Phys. Chem., 1960, 64, 487–490 CrossRef CAS.
- D. T. Farrar and M. M. Jones, J. Phys. Chem., 1964, 68, 1717–1721 CrossRef CAS.
- J. L. Wood and M. M. Jones, Inorg. Chem., 1964, 3, 1553–1557 CrossRef CAS.
- E. W. Berg and J. T. Truemper, Anal. Chim. Acta, 1965, 32, 245–252 CrossRef CAS.
- L. Komissarova, M. Gurevich, T. Sas and B. Stepin, Zh. Neorg. Khim., 1978, 23, 3145–3147 CAS.
- K. V. Zherikova, L. N. Zelenina, T. P. Chusova, N. V. Gelfond and N. B. Morozova, J. Chem. Thermodyn., 2016, 101, 162–167 CrossRef CAS.
- S. Sysoev, T. Cheremisina, L. Zelenina, S. Tkachev, K. Zherikova, N. Morozova and N. Kuratieva, J. Therm. Anal. Calorim., 2010, 101, 41–44 CrossRef CAS.
- L. N. Zelenina, K. V. Zherikova, T. P. Chusova, S. V. Trubin, R. A. Bredikhin, N. V. Gelfond and N. B. Morozova, Thermochim. Acta, 2020, 689, 178639 CrossRef CAS.
- S. P. Verevkin, V. N. Emel'yanenko, V. Diky, C. D. Muzny, R. D. Chirico and M. Frenkel, J. Phys. Chem. Ref. Data, 2013, 42, 033102 CrossRef.
- T. P. Melia and R. Merrifield, J. Inorg. Nucl. Chem., 1970, 32, 2573–2579 CrossRef CAS.
- H.-J. Götze, K. Bloss and H. Molketin, Z. Phys. Chem., 1970, 73, 314–320 CrossRef.
- S. J. Ashcroft, Thermochim. Acta, 1971, 2, 512–514 CrossRef CAS.
- Kozyrkin B. I., et al., Presented in part at II All-Union Conference on the Thermodynamics of Organic Compounds, Gorky, 1976, as cited in ref. 42.
- J. Sachinidis and J. O. Hill, Thermochim. Acta, 1980, 35, 59–66 CrossRef CAS.
- J. Maslowska and J. B. Baranowski, Chem. Anal., 1981, 26, 1017–1027 CAS , cited in https://webbook.nist.gov.
- S. Murata, M. Sakiyama and S. Seki, Thermochim. Acta, 1985, 88, 121–126 CrossRef CAS.
- I. P. Malkerova, A. S. Alikhanyan, V. G. Sevast'yanov, Y. K. Grinberg and V. I. Gorgoraki, Zh. Neorg. Khim., 1990, 35(2), 413–418 CAS.
- P. A. Gerasimov, A. I. Gerasimova, N. E. Fedotova, N. B. Morozova and I. K. Igumenov, Izv. Vyssh. Uchebn. Zaved., Khim. Khim. Tekhnol., 1992, 35, 38–44 Search PubMed.
- N. E. Fedotova, N. B. Morozova, I. K. Igumenov, P. A. Gerasimov and A. I. Gerasimova, Koord. Khim., 1993, 19, 622–629 CAS.
- P. A. Gerasimov, A. I. Gerasimova, N. B. Morozova and I. K. Igumenov, Sib. Khim. Zh., 1991, 1, 87–91 Search PubMed.
- E. A. Mazurenko and A. I. Gerasimchuk, Ukr. Khim. Zh. (Russ. Ed.), 1993, 59, 526–536 CAS.
- M. A. V. Ribeiro da Silva, M. J. S. Monte and J. Huinink, J. Chem. Thermodyn., 1996, 28, 413–419 CrossRef CAS.
- E. G. Gillan, S. G. Bott and A. R. Barron, Chem. Mater., 1997, 9, 796–806 CrossRef CAS.
- B. D. Fahlman and A. R. Barron, Adv. Mater. Opt. Electron., 2000, 10, 223–232 CrossRef CAS.
- P. P. Semyannikov, I. K. Igumenov, S. V. Trubin and I. P. Asanov, J. Phys. IV, 2001, 11, Pr3/995–Pr3/1003 CAS.
- P. A. Stabnikov, S. V. Sysoev, N. S. Vanina, S. V. Trubin, P. P. Semyannikov and I. K. Igumenov, Electronic Journal “Investigated in Russia”, 2001 Search PubMed , http://zhurnal.ape.relarn.ru/articles/2001/023.pdf.
- S. V. Volkov, E. A. Mazurenko and Z. N. Bublik, in Str., Svoistva Primen. β-Diketonatov Met., ed. V. I. Spitsyn, Nauka, Moscow, 1978, pp. 119–122 Search PubMed.
- G. Beech and R. M. Lintonbon, Thermochim. Acta, 1971, 3, 97–105 CrossRef CAS.
- M. A. V. Ribeiro da Silva, M. L. C. C. H. Ferrao and R. M. G. Esteves da Silva, J. Chem. Thermodyn., 1992, 24, 1293–1298 CrossRef CAS.
- N. Matsubara and T. Kuwamoto, Thermochim. Acta, 1985, 83, 193–202 CrossRef CAS.
- N. Matsubara and T. Kuwamoto, Inorg. Chem., 1985, 24, 2697–2701 CrossRef CAS.
- M. A. V. Ribeiro da Silva and M. L. C. C. H. Ferrao, J. Chem. Thermodyn., 1988, 20, 79–85 CrossRef CAS.
- Y. V. Chumachenko, I. K. Igumenov and S. V. Zemskov, Zh. Fiz. Khim., 1978, 52, 2416–2418 CAS.
- I. K. Igumenov, T. Yu. Gerasimenko and N. B. Morozova, Saturated vapor pressure of tris-hexafluoroacetylacetonates of metals of the first transition row, Izv. Sib. Otd. Acad. Nauk SSSR, Ser. Khim. Nauk, 1986, 2, 54–57 Search PubMed.
- H. R. Brunner and B. J. Curtis, J. Therm. Anal., 1973, 5, 111–115 CrossRef CAS.
- M. A. Siddiqi, R. A. Siddiqui and B. Atakan, J. Chem. Eng. Data, 2010, 55, 2149–2154 CrossRef CAS.
- E. L. Croker and S. A. Basu-Dutt, Chem. Educ., 2002, 7, 136–141 CrossRef CAS.
- E. S. Domalski and E. D. Hearing, J. Phys. Chem. Ref. Data, 1993, 22, 805–1159 CrossRef CAS.
- M. A. Bespyatov and V. N. Naumov, J. Chem. Eng. Data, 2010, 55, 46–51 CrossRef CAS.
- J. P. Murray and J. O. Hill, Thermochim. Acta, 1984, 72, 341–347 CrossRef CAS.
- J. Sabolovic, Z. Mrak, S. Kostrun and A. Janekovic, Inorg. Chem., 2004, 43, 8479–8489 CrossRef CAS.
- C. Gobble, J. Chickos and S. P. Verevkin, J. Chem. Eng. Data, 2014, 59, 1353–1365 CrossRef CAS.
- P. Walden, Z. Elektrochem. Angew. Phys. Chem., 1908, 14, 713–724 CrossRef CAS.
- C. Held, J. Brinkmann, A.-D. Schröder, M. I. Yagofarov and S. P. Verevkin, Fluid Phase Equilib., 2018, 455, 43–53 CrossRef CAS.
- A. Abdelaziz, D. H. Zaitsau, N. V. Kuratieva, S. P. Verevkin and C. Schick, Phys. Chem. Chem. Phys., 2019, 21, 12787–12797 RSC.
- Chemical Vapour Deposition (CVD): Advances, Technology and Applications, ed. K.-L. Choy, CRC Press/Taylor & Francis Group, Boca Raton, FL, 1st Edition, 2019 Search PubMed.
- M. V. Roux, M. Temprado, J. S. Chickos and Y. Nagano, J. Phys. Chem. Ref. Data, 2008, 37, 1855–1996 CrossRef CAS.
- D. H. Zaitsau, V. N. Emel’yanenko, A. A. Pimerzin and S. P. Verevkina, J. Chem. Thermodyn., 2018, 122, 1–12 CrossRef CAS.
- M. A. V. Ribeiro da Silva, M. A. R. Matos, C. M. A. do Rio and V. M. F. Morais, J. Chem. Soc., Faraday Trans., 1997, 93, 3061–3065 RSC.
- C. M. Matveev, A. Y. Timoshkin and P. A. Stabnikov, Vestn. S.-Peterb. Univ., Ser. 4: Fiz., Khim., 2011, 37–47 Search PubMed.
- N. B. Morozova, K. V. Zherikova, P. P. Semyannikov, S. V. Trubin and I. K. Igumenov, J. Therm. Anal. Calorim., 2009, 98, 395–399 CrossRef CAS.
- S. P. Verevkin, J. Chem. Eng. Data, 2002, 47, 1071–1097 CrossRef CAS.
- S. P. Verevkin, J. Therm. Anal. Calorim., 2000, 60, 437–451 CrossRef CAS.
- S. P. Verevkin, V. N. Emel'yanenko and D. H. Zaitsau, ChemPhysChem, 2018, 19, 619–630 CrossRef CAS.
- G. Pilcher, Systematics of metal-ligand binding energies, Pure Appl. Chem., 1989, 61, 855–860 CAS.
- V. Majer and V. Svoboda and H. V. Kehiaian, Enthalpies of Vaporization of Organic Compounds: A Critical Review and Data Compilation, Blackwell Scientific Publications, Oxford, 1985 Search PubMed.
- V. G. Sevast'yanov, E. P. Simonenko, D. V. Sevast'yanov and N. T. Kuznetsov, Russ. J. Coord. Chem., 2004, 30, 755–758 CrossRef.
- V. G. Sevast'yanov, D. V. Sevast'yanov, E. V. Peresypkina, V. A. Blatov and N. T. Kuznetsov, Rus. J. Coord. Chem., 2004, 30, 679–684 CrossRef.
- S. P. Verevkin, M. E. Konnova, K. V. Zherikova and A. A. Pimerzin, Fluid Phase Equilib., 2020, 510, 112503 CrossRef CAS.
- S. P. Verevkin, Thermochemistry of phenols: buttress effects in steric hindered phenols, J. Chem. Thermodyn., 1999, 31, 1397–1416 CrossRef CAS.
- D. H. Zaitsau, N. Plechkova and S. P. Verevkin, J. Chem. Thermodyn., 2019, 130, 204–212 CrossRef CAS.
- D. H. Zaitsau, V. N. Emel'yanenko, P. Stange, S. P. Verevkin and R. Ludwig, Angew. Chem., Int. Ed., 2019, 58, 8589–8592 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ra06880b |
| This journal is © The Royal Society of Chemistry 2020 |