Open Access Article
Open Access ArticleProbing the supramolecular features via π–π interaction of a di-iminopyrene-di-benzo-18-crown-6-ether compound: experimental and theoretical study†
Adina Coroaba a,
Dragos-Lucian Isac*a,
Cristina Al-Matarneha,
Tudor Vasiliua,
Sorin-Alexandru Ibanescua,
Radu Zondaa,
Rodinel Ardeleanua,
Andrei Neamtuab,
Daniel Timpuc,
Alina Nicolescuc,
Francesca Mocci
a,
Dragos-Lucian Isac*a,
Cristina Al-Matarneha,
Tudor Vasiliua,
Sorin-Alexandru Ibanescua,
Radu Zondaa,
Rodinel Ardeleanua,
Andrei Neamtuab,
Daniel Timpuc,
Alina Nicolescuc,
Francesca Mocci ad,
Stelian S. Maierae,
Aatto Laaksonenaf,
Marc Jean Médard Abadieag and
Mariana Pinteala
ad,
Stelian S. Maierae,
Aatto Laaksonenaf,
Marc Jean Médard Abadieag and
Mariana Pinteala *a
*a
aCentre of Advanced Research in Bionanoconjugates and Biopolymers, “Petru Poni” Institute of Macromolecular Chemistry, 41A Grigore Ghica Voda Alley, 700487 Iasi, Romania. E-mail: pinteala@icmpp.ro; isac.dragos@icmpp.ro
bCenter of Fundamental Research and Experimental Development in Translational Medicine, Regional Institute of Oncology, General Henri Mathias Berthelot St, 700483 Iasi, Romania
cPhysics of Polymers and Polymeric Materials, “Petru Poni” Institute of Macromolecular Chemistry, 41A Grigore Ghica Voda Alley, 700487 Iasi, Romania
dDepartment of Chemical and Geological Sciences, University of Cagliari, I-09042 Monserrato, Italy
ePolymers Research Center, “Gheorghe Asachi” Technical University of Iasi, 73 Mangeron Blvd., 700050 Iasi, Romania
fDepartment of Materials and Environmental Chemistry, Division of Physical Chemistry, Arrhenius Laboratory, Stockholm University, SE-106 91 Stockholm, Sweden
gFaculy of Science, University of Montpellier, Place E. Bataillon, 34095 Montpellier, France
First published on 16th October 2020
Abstract
A novel DPyDB-C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N-18C6 compound was synthesised by linking a pyrene moiety to each phenyl group of dibenzo-18-crown-6-ether, the crown ether, through –HC
N-18C6 compound was synthesised by linking a pyrene moiety to each phenyl group of dibenzo-18-crown-6-ether, the crown ether, through –HC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N– bonds and characterized by FTIR, 1H-NMR, 13C-NMR, TGA, and DSC techniques. The quantitative 13C-NMR analysis revealed the presence of two position isomers. The electronic structure of the DPyDB-C
N– bonds and characterized by FTIR, 1H-NMR, 13C-NMR, TGA, and DSC techniques. The quantitative 13C-NMR analysis revealed the presence of two position isomers. The electronic structure of the DPyDB-C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N-18C6 molecule was characterized by UV-vis and fluorescence spectroscopies in four solvents with different polarities to observe particular behavior of isomers, as well as to demonstrate a possible non-bonding chemical association (such as ground- and excited-state associations, namely, to probe if there were forming dimers/excimers). The interpretation of the electronic structure was realized through QM calculations. The TD-CAM-B3LYP functional, at the 6-311+G(d,p) basis set, indicated the presence of predominant π → π* and mixed π → π* + n → π* transitions, in line with the UV-vis experimental data. Even though DPyDB-C
N-18C6 molecule was characterized by UV-vis and fluorescence spectroscopies in four solvents with different polarities to observe particular behavior of isomers, as well as to demonstrate a possible non-bonding chemical association (such as ground- and excited-state associations, namely, to probe if there were forming dimers/excimers). The interpretation of the electronic structure was realized through QM calculations. The TD-CAM-B3LYP functional, at the 6-311+G(d,p) basis set, indicated the presence of predominant π → π* and mixed π → π* + n → π* transitions, in line with the UV-vis experimental data. Even though DPyDB-C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N-18C6 computational studies revealed a π-extended conjugation effect with predominantly π → π* transitions, thorough fluorescence analysis was observed a weak emission, as an effect of PET and ACQ. In particular, the WAXD analysis of powder and thin films obtained from n-hexane, 1,2-dichloroethane, and ethanol indicated an amorphous organization, whereas from toluene a smectic ordering was obtained. These results were correlated with MD simulation, and it was observed that the molecular geometry of DPyDB-C
N-18C6 computational studies revealed a π-extended conjugation effect with predominantly π → π* transitions, thorough fluorescence analysis was observed a weak emission, as an effect of PET and ACQ. In particular, the WAXD analysis of powder and thin films obtained from n-hexane, 1,2-dichloroethane, and ethanol indicated an amorphous organization, whereas from toluene a smectic ordering was obtained. These results were correlated with MD simulation, and it was observed that the molecular geometry of DPyDB-C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N-18C6 molecule played a defining role in the pyrene stacking arrangement.
N-18C6 molecule played a defining role in the pyrene stacking arrangement.
1 Introduction
Supramolecular chemistry has seen significant development over last decades, earning a lead role in the scientific research. Whilst in classical chemistry the focus is mainly on covalent bonds, in supramolecular chemistry the spotlight is on reversible interactions. The concept of self-assembly is defined by the spontaneous formation or development of some systems without exterior intervention, other than environmental conditions. Controlling this phenomenon is of great interest in the synthesis of materials with complex properties at the nano- and micro-scale. The control over self-assembly process has proved to be even more essential in developing supramolecular structures with biological functions, in understanding natural systems and for their synthetic implementation.1–3 The self-assembly of molecules is mainly based on noncovalent interactions between different parts of the molecules. This involves attraction and repulsive forces such as ion–ion interactions, van der Waals interactions, dipole–dipole or ion–dipole interactions, coordinative bonds, hydrogen bonds, and π–π stacking.4–8The functionality of a supramolecular structure is endowed by some of the chemical groups belonging to the constituent molecules, which are capable of selectively interacting with various entities in the proximal environment. It is already known that crown ethers selectively interact with alkaline ions, based on the correlation between the size of the crown ether cycle and the ionic radius.9,10 Exploiting this uniqueness, crown ether derivatives are often used as sensors,11,12 ion channels,13–16 or carriers17 for metallic ions. For some of the mentioned functions, it is useful to integrate functionalized crown ethers in supramolecular structures.18–21
A particular way to create supramolecular structures is to use π-conjugated molecules. Studying charge transfer interactions, Koshkakaryan et al.22 developed a stable supramolecular assembly containing intercalated crown-ethers and naphthalene diimide-based molecules in 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 ratio, when naphthalene groups were situated in- and out-side of the crown ether ring. However, the use of π-conjugated molecules as binders represents an attractive way to build supramolecular structures. For this purpose, pyrene is a good choice, thanks to its propensity to self-aggregate by π-stacking, which can be visualized resorting to fluorescence emission spectroscopy. In this respect, pyrene excimers are often used as fluorescence markers for studying the systems' microheterogeneity. Pinteala et al.23 investigated the conformational changes and the aggregation of hydrophobic-hydrophilic copolymers, using pyrene as a dye. They recorded the spectra of pyrene molecules captured in the space nearby copolymers and evaluated the local hydrophobicity of the microenvironment by evaluating the intensity ratio between the first and the third vibronic band in pyrene fluorescence emission spectra. Szajdzinska-Pietek et al.24 used pyrene and a pyrene derivate, 1,3-bis(1-pyrenyl)propane, to continue the study of the same copolymer.23 According to them, the self-assembly of the chains leads to the formation of hydrophobic domains, determining an increase in the local concentration of fluorescent probes due to the π-stacking, a phenomenon revealed by excimer formation at a longer wavelengths (in the range of 420–550 nm). Moreover, they observed that the dyeing effect of the pyrene derivative is more sensitive and stronger than that of pyrene. Because of its characteristic photophysical behavior such as its prominent and typical absorption bands and fluorescence emission,25,26 pyrene was involved in numerous supramolecular studies. The first two excited states of pyrene compounds, 1La and 1Lb, π → π*, corresponding to S0 → S1 and S0 → S2 excitations, proved to have the main role in the photophysical processes involving such molecular systems.25,27–30 The band's intensity variation (including their appearance or disappearance), together with the wavelength shifts in UV-vis and fluorescence spectra varies from one pyrene derivative to another. The studies indicate that pyrene compounds are able to form dimers (by the weak association in the ground state), excimers (by the strong association in the excited states), and/or π–π stacking aggregates.25,29,31–37 Computational approaches such as density functional theory (DFT), time-dependent density functional theory (TD-DFT), and molecular dynamics (MD) simulations facilitate the understanding of the nature of electronic structure in the ground and excited states (presence of π → π* transitions described by molecular orbitals), and of the supramolecular interactions (π–π stacking associations) of pyrene derivatives. The presence of specific functional groups such as imine bond (–HC
2 ratio, when naphthalene groups were situated in- and out-side of the crown ether ring. However, the use of π-conjugated molecules as binders represents an attractive way to build supramolecular structures. For this purpose, pyrene is a good choice, thanks to its propensity to self-aggregate by π-stacking, which can be visualized resorting to fluorescence emission spectroscopy. In this respect, pyrene excimers are often used as fluorescence markers for studying the systems' microheterogeneity. Pinteala et al.23 investigated the conformational changes and the aggregation of hydrophobic-hydrophilic copolymers, using pyrene as a dye. They recorded the spectra of pyrene molecules captured in the space nearby copolymers and evaluated the local hydrophobicity of the microenvironment by evaluating the intensity ratio between the first and the third vibronic band in pyrene fluorescence emission spectra. Szajdzinska-Pietek et al.24 used pyrene and a pyrene derivate, 1,3-bis(1-pyrenyl)propane, to continue the study of the same copolymer.23 According to them, the self-assembly of the chains leads to the formation of hydrophobic domains, determining an increase in the local concentration of fluorescent probes due to the π-stacking, a phenomenon revealed by excimer formation at a longer wavelengths (in the range of 420–550 nm). Moreover, they observed that the dyeing effect of the pyrene derivative is more sensitive and stronger than that of pyrene. Because of its characteristic photophysical behavior such as its prominent and typical absorption bands and fluorescence emission,25,26 pyrene was involved in numerous supramolecular studies. The first two excited states of pyrene compounds, 1La and 1Lb, π → π*, corresponding to S0 → S1 and S0 → S2 excitations, proved to have the main role in the photophysical processes involving such molecular systems.25,27–30 The band's intensity variation (including their appearance or disappearance), together with the wavelength shifts in UV-vis and fluorescence spectra varies from one pyrene derivative to another. The studies indicate that pyrene compounds are able to form dimers (by the weak association in the ground state), excimers (by the strong association in the excited states), and/or π–π stacking aggregates.25,29,31–37 Computational approaches such as density functional theory (DFT), time-dependent density functional theory (TD-DFT), and molecular dynamics (MD) simulations facilitate the understanding of the nature of electronic structure in the ground and excited states (presence of π → π* transitions described by molecular orbitals), and of the supramolecular interactions (π–π stacking associations) of pyrene derivatives. The presence of specific functional groups such as imine bond (–HC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–), phenyl ring, or crown ethers in the moiety of pyrene units is able to induce new electron transitions (such as n → π* ones38), or different association interactions.
N–), phenyl ring, or crown ethers in the moiety of pyrene units is able to induce new electron transitions (such as n → π* ones38), or different association interactions.
The published studies that address the π–π interaction in the pyrene–crown ether systems mainly refer to the changes in the molecular geometry of the assembly as a result of the binding of two pyrene units, in different chemical environments. Jarolímová et al.39 studied crown ethers of different sizes, functionalized with pyreneamide derivatives, as potassium ion-selective nanosensors. The complexation of the cation with the crown ether ring determines the molecule unfolding, and consequently, the disappearance of the excimer emission in an on-off manner, which makes the compound usable as a chemosensor.39
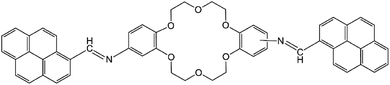
The present work reports the synthesis of di-iminopyrene-dibenzo-18-crown-6-ether (named as DPyDB–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–18C6 in the present paper), a novel compound including crown ether and pyrene moieties linked by –HC
N–18C6 in the present paper), a novel compound including crown ether and pyrene moieties linked by –HC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N– bonds (Fig. 1). The aim of the present study was to prove, based on photophysical properties measurements, the formation of a potential supramolecular arrangement mediated by inter- and intramolecular interactions between the DPyDB–C
N– bonds (Fig. 1). The aim of the present study was to prove, based on photophysical properties measurements, the formation of a potential supramolecular arrangement mediated by inter- and intramolecular interactions between the DPyDB–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–18C6 molecules. The experimental results were correlated with the molecular dynamics and with quantum mechanics calculations. For photophysical investigations, solvents with different polarities (n-hexane, toluene, 1,2-dichloroethane, and ethanol) were chosen.
N–18C6 molecules. The experimental results were correlated with the molecular dynamics and with quantum mechanics calculations. For photophysical investigations, solvents with different polarities (n-hexane, toluene, 1,2-dichloroethane, and ethanol) were chosen.
2 Experimental section
2.1 Reagents and solutions
All reagents and solvents were purchased from Sigma-Aldrich (Merck KGaA, Darmstadt, Germany) and used without further purification.2.2 Instrumentation and measurements
Analytical thin-layer chromatography was performed with commercial silica gel plates 60 F254 (Merck Darmstadt, Germany) and visualized with UV light (λmax = 254 or 365 nm). The nuclear magnetic resonance (NMR) spectra were recorded using a Bruker Avance Neo 400 MHz spectrometer (Bruker, Germany). Chemical shifts were reported in delta (δ) units, part per million (ppm). The following abbreviations were used to designate chemical shift multiplicities: s = singlet, d = doublet, t = triplet, q = quartet, m = multiplet, as = apparent singlet. The Fourier-transform infrared (FTIR) spectra were recorded using a Bruker VERTEX 70 FT-IR spectrometer (Bruker, Germany) at ambient temperature, in potassium bromide (KBr) pellets. The thermogravimetric analysis (TGA) was performed using STA 449F1 Jupiter equipment (Netzsch, Germany). The measurements were made in the temperature range 20–700 °C under nitrogen flow (50 mL min−1) at a heating rate of 10 °C min−1. Differential scanning calorimetry (DSC) measurements were conducted using a DSC 200 F3 Maia device (Netzsch, Germany). A mass of 15 mg of each sample was heated in a pierced and sealed aluminum crucible at a heating rate of 10 °C min−1 under a nitrogen stream at a flow rate of 50 mL min−1. The temperature against heat flow was recorded. The device was calibrated using indium according to standard procedures. Wide-angle X-ray diffraction (WAXD) analyses were performed using a D8 ADVANCE diffractometer (Bruker AXS, Germany) with Cu-Kα radiation (λ = 0.1541 nm), a parallel beam with a Göbel mirror, and a dynamic scintillation detector. All the samples were investigated for a 2θ diffraction angle ranging from 0.8° to 60°, in a step scan mode of 2 s per step, with a step size of 0.02°, at 40 kV and 35 mA, at room temperature. The calculation of 2θ values, the interplanar distance (d), and peak heights were carried out using the Bruker “DIFFRAC-PLUS Evaluation – EVA” software. The Bruker “TOPAS” software was used for crystallite size data processing. UV-vis measurements were performed using a Lambda 35 device (PerkinElmer, USA). The absorption spectra were recorded in the 200–700 nm range for identical sample volumes (3 mL) with the following parameters: slit width 1 nm, scan speed 480 nm min−1, and 1 nm data interval. The spectra of the samples were recorded at room temperature using 1 cm path length quartz cuvettes. Fluorescence measurements were carried out using a FluoroMax-4 spectrophotometer (Horiba, Japan). The emission spectra were recorded using an excitation wavelength of 360 nm. The concentrations of the solution obtained were determined by Quartz Crystal Microbalance with Dissipation (QCM-D) using a QSense Pro instrument (Biolin Scientific, Sweden). QSX 301 Gold sensors, acquired from Scientific Biolin Scientific AB, Sweden, were cleaned by placing them in a 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture of Milli-Q water, ammonia (25%), and hydrogen peroxide (30%) at 75 °C for 5 minutes. The sensors were then rinsed with Milli-Q water and dried with nitrogen gas. The resonance frequency of a clean QCM sensor (f0) was measured in air. Then, on gold QCM chips, a known volume of the solutions (100 μL for ethanol and toluene and 150 μL for n-hexane and 1,2-dichloroethane) with unknown concentrations were added drop by drop and dried under a nitrogen stream. The sensors were mounted again in the instrument and the resonance frequency after deposition (f1) was measured also in the air atmosphere.
1 mixture of Milli-Q water, ammonia (25%), and hydrogen peroxide (30%) at 75 °C for 5 minutes. The sensors were then rinsed with Milli-Q water and dried with nitrogen gas. The resonance frequency of a clean QCM sensor (f0) was measured in air. Then, on gold QCM chips, a known volume of the solutions (100 μL for ethanol and toluene and 150 μL for n-hexane and 1,2-dichloroethane) with unknown concentrations were added drop by drop and dried under a nitrogen stream. The sensors were mounted again in the instrument and the resonance frequency after deposition (f1) was measured also in the air atmosphere.
2.3 Synthesis of di-iminopyrene-dibenzo-18-crown-6-ether (DPyDB-C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/h3_char_e001.gif) N-18C6)
N-18C6)
To a solution of diaminodibenzo-18-crown-6-ether (200 mg, 0.51 mmol) in ethanol (20 mL), acetic acid (200 μL, 2.80 mmol, 4 equiv.) and 1-pyrenecarboxaldehyde (260 mg, 1.15 mmol, 2.1 equiv.) were added. The resulting mixture was stirred at room temperature for 24 h. The crude product was filtrated and then purified by centrifugation for separation from dichloromethane and ethyl ether. Yellow solid, yield 80%, IR: 3035, 2922, 2868, 1909, 1508, 1276, 1263, 1130, 1055 cm−1. 1H-NMR (400 MHz, CDCl3): δ = 4.14 (as, 8H), 4.35 (dd, 8H), 7.02 (d, 4H), 7.08 (s, 2H), 8.08 (d, 2H), 8.15 (d, 2H), 8.18 (d, 2H), 8.28 (m, 8H), 8.77 (d, 2H), 9.05 (d, 2H), 9.54 (s, 2H). 13C-NMR (100 MHz, DMSO): δ = 69.5, 106.6, 113.1, 114.6, 123.1, 123.7, 124.3, 124.6, 125.6, 126.4, 126.9, 127.1, 127.9, 129.2, 130.3, 131.2, 131.4, 133.1, 145.3, 147.5, 149.0, 157.0.
2.4 Molecular dynamics (MD) simulations
The behavior of the molecular system in different solvents and the ability of the target compound to establish intermolecular interactions between di-iminopyrene-dibenzo-18-crown-6-ether and polar solvents (using ethanol as an explicit model) were investigated by molecular dynamics (MD) simulations. All MD simulations were done using the GROMACS 2018 program.40 The initial structure of the molecules was built using the AVOGADRO software.41 The molecules were parameterized using the following protocol. The GAUSSIAN 16 software42 and RED-Tools43 software were used to calculate the partial atomic charge distribution and to optimize the molecular geometry of the compounds. The method used for calculations was HF/6-31G* with the Connoly surface algorithm. The force field used to describe the system was AMBER force field. The parameters for bonds, angles, and dihedrals were calculated using the Ambertools18 software44 and the GAFF parameters. All simulations were carried out using the Beskow supercomputer from the KTH Royal Institute of Technology, PDC Center for high-performance computing.The details of the simulations are presented in Table 1. The simulations were performed with the NPT ensemble at T = 293 K and P = 1 atm under isotropic conditions. The temperature was controlled using the Noose–Hoover thermostat and the pressure was controlled using the Parinello–Rahman barostat. The equations of motions were integrated with a time step of 2.5 fs. Before starting each simulation, energy minimization was performed using the steepest descent algorithm. Periodic boundary conditions (PBCs) were used for all simulations. The Van der Waals interactions were selected by the particle mesh Ewald (PME) method with a cut-off of 1 nm.
| System | Number of crown ether molecules/Na+/K+/Ca2+/Cl- | Number of solvent molecules | Simulation box size (nm3) | Simulation duration |
|---|---|---|---|---|
DPyDB–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–18C6 system N–18C6 system |
80 molecules (40 molecules of each isomer)/0/0/0/0 | 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 278 ethanol 278 ethanol |
13.363 | 800 ns |
| Ions system | 10 molecules/10/10/10/40 | Water | 8 | 40 ns |
2.5 Quantum mechanics calculations
In this work, the quantum mechanics calculations were performed using the Gaussian (G16) package42 by density functional theory (DFT) and time-dependent density functional theory (TD-DFT) in order to investigate both the ground and excited states. The optimization of the calculations using the DFT method was employed with the PBE0/6-311+G(d,p) level of theory. The equilibrium geometry has been first optimized to the ground-state level. A conformational search was performed to identify if the equilibrium geometry corresponds to the local minimum of the potential energy surface. Then, the Hessian frequencies have been computed for the equilibrium geometry and no eigenvalues have been obtained, indicating that the molecular geometry structure corresponds to the local minimum on the potential energy surface.Excited states and theoretical absorption spectra were computed with TD-CAM-B3LYP functional and 6-311+G(d,p) basis sets. To obtain a comparison between theoretical and experimental results, as well as a good estimation of the first electronic transitions, ten states were included in the TD-DFT calculations. Thus, the TD-DFT calculations at three different levels of theory, namely, TD-CAM-B3LYP/6-311+G(d,p), TD-PBE0/6-311+G(d,p), and TD-B3LYP/6-311+G(d,p) have been further used for comparison. All TD-DFT calculations were performed in gas phase and solvent environments with different polarities: n-hexane (ε = 1.9), toluene (ε = 2.34), 1,2-dichloroethane (ε = 10.1), and ethanol (ε = 24.3) in order to simulate the experimental UV-vis absorption spectra. The polarized continuum model (PCM)45 was used to mimic the solvent's environment.
Both density functionals, PBE0 (ref. 46 and 47) and CAM-B3LYP,48 were used in the present theoretical calculations to explore the electronic structure of di-iminopyrene-dibenzo-18-crown-6-ether. Moreover, PBE0, TD-BE0, and TD-CAM-B3LYP functionals were used in the theoretical calculations to explore the electronic structure of organic49,50 and inorganic51,52 compounds providing reliable geometries and good estimated values of the transition energies. Likewise, the TD-B3LYP/6-311+G(d,p) method was also included to study the theoretical electronic absorption spectra. This supplementary level of theory was employed because this method gives good results regarding the optoelectronic properties of π-conjugated compounds53 and of 3-methoxy-2-((pyren-2yl-imino)methyl) phenol.38 Quantum mechanics calculations were carried out on the Tetralith supercomputer from the KTH Royal Institute of Technology, PDC Center for High-Performance Computing.
3 Results and discussions
3.1. Synthesis and physicochemical characterization of di-iminopyrene-dibenzo-18-crown-6-ether
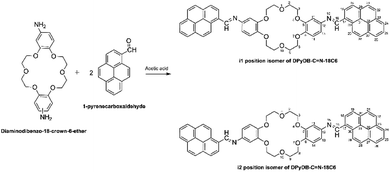
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/b_char_e001.gif) N–18C6. Di-iminopyrene-dibenzo-18-crown-6-ether was prepared by the direct reaction between the amino groups of diaminodibenzo-18-crown-6-ether and the aldehyde group of 1-pyrenecarboxaldehyde, in an acidic medium, with the formation of imine bonds between the two precursors, as presented in Scheme 1. Diaminodibenzo-18-crown-6-ether was synthesized as described by Ardeleanu et al.,54 as a mixture of two position isomers (noted as i1 and i2) in regard to the amino position on the phenyl ring, and was used without further separation.
N–18C6. Di-iminopyrene-dibenzo-18-crown-6-ether was prepared by the direct reaction between the amino groups of diaminodibenzo-18-crown-6-ether and the aldehyde group of 1-pyrenecarboxaldehyde, in an acidic medium, with the formation of imine bonds between the two precursors, as presented in Scheme 1. Diaminodibenzo-18-crown-6-ether was synthesized as described by Ardeleanu et al.,54 as a mixture of two position isomers (noted as i1 and i2) in regard to the amino position on the phenyl ring, and was used without further separation.
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–18C6 (Fig. S1†) showed absorption bands between 2922–2868 and 1130–1055 cm−1, characteristic for O–C–C–O and C–O–C ether bonds from the crown ether, and two intense absorption bands at 1610–1583 cm−1, characteristic of the in-phase stretching vibrations of the newly formed –HC
N–18C6 (Fig. S1†) showed absorption bands between 2922–2868 and 1130–1055 cm−1, characteristic for O–C–C–O and C–O–C ether bonds from the crown ether, and two intense absorption bands at 1610–1583 cm−1, characteristic of the in-phase stretching vibrations of the newly formed –HC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–imine bond. It was also noticed that the disappearance of the intense absorption bands at 2712, 1797, and 1678 cm−1, characteristic of 1-pyrenecarboxaldehyde, is one more proof that the reaction took place.
N–imine bond. It was also noticed that the disappearance of the intense absorption bands at 2712, 1797, and 1678 cm−1, characteristic of 1-pyrenecarboxaldehyde, is one more proof that the reaction took place.![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–18C6 (Fig. S2†), the signals at δ = 4.14–4.35 ppm have been assigned to aliphatic atoms from the crown ether structure. Protons H18 give a signal at δ = 9.05 ppm, and protons H19 at δ = 8.77 ppm, under the influence of the electron-withdrawing neighbors. The most deshelled proton is the one corresponding to the imine, H16, at 9.54 ppm. The disappearance of the characteristic protons for the amino group in the crown ether (4.68 ppm) and of the aldehyde group in 1-pyrenecarboxaldehyde (10.7 ppm) further confirm the structure of DPyDB–C
N–18C6 (Fig. S2†), the signals at δ = 4.14–4.35 ppm have been assigned to aliphatic atoms from the crown ether structure. Protons H18 give a signal at δ = 9.05 ppm, and protons H19 at δ = 8.77 ppm, under the influence of the electron-withdrawing neighbors. The most deshelled proton is the one corresponding to the imine, H16, at 9.54 ppm. The disappearance of the characteristic protons for the amino group in the crown ether (4.68 ppm) and of the aldehyde group in 1-pyrenecarboxaldehyde (10.7 ppm) further confirm the structure of DPyDB–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–18C6. 13C-NMR spectra (Fig. S3†) showed signals in accordance with the proposed structure, with emphasis on the two different signals for the aliphatic zone corresponding to the atoms from the crown ether structure at δ = 69.5 ppm, and a signal at δ = 157.0 ppm corresponding to the C16 imine carbon. The quantitative 13C-NMR study (Fig. S4†) for diaminodibenzo-18-crown-6-ether revealed an approximatively 1
N–18C6. 13C-NMR spectra (Fig. S3†) showed signals in accordance with the proposed structure, with emphasis on the two different signals for the aliphatic zone corresponding to the atoms from the crown ether structure at δ = 69.5 ppm, and a signal at δ = 157.0 ppm corresponding to the C16 imine carbon. The quantitative 13C-NMR study (Fig. S4†) for diaminodibenzo-18-crown-6-ether revealed an approximatively 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio between the two isomers, and it was assumed that the final compound, DPyDB–C
1 ratio between the two isomers, and it was assumed that the final compound, DPyDB–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–18C6, has the same isomer ratio as the starting compound.
N–18C6, has the same isomer ratio as the starting compound.![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–18C6. Two thermal decomposition stages with a maximum weight loss in the range of 340–568 °C are present. The first stage was assigned to the loss of solvent molecules (ethanol and water) (1.07; 1.46 wt%). The second step, with initial temperatures between 340 and 420 °C, corresponds to the loss of 29.4% weight (crown ether moiety and 13.8% corresponding to the benzo amino structure at 420–568 °C). The more stable remaining structural entities thermally decompose in the domain 568–700 °C, leaving a residue that corresponds to the pyrene moiety.
N–18C6. Two thermal decomposition stages with a maximum weight loss in the range of 340–568 °C are present. The first stage was assigned to the loss of solvent molecules (ethanol and water) (1.07; 1.46 wt%). The second step, with initial temperatures between 340 and 420 °C, corresponds to the loss of 29.4% weight (crown ether moiety and 13.8% corresponding to the benzo amino structure at 420–568 °C). The more stable remaining structural entities thermally decompose in the domain 568–700 °C, leaving a residue that corresponds to the pyrene moiety.Fig. S6† reveals that the differential scanning calorimetry (DSC) curves corresponding to the heating and cooling runs of the studied sample. The heating curve presented a peak at 185 °C, which is rather a heat anomaly or expresses a complex phase transition,55 before sample degradation. No defined melting point was registered on the cooling curve, suggesting the amorphous character of the product.
3.2 The ability of supramolecular arrangement investigated by wide-angle X-ray diffraction (WAXD) analysis and simulated using molecular dynamics (MD)
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–18C6, WAXD analysis was performed on the product powder, revealing an amorphous material. Moreover, WAXD was used to determine whether the solvent can influence the supramolecular arrangement of the compound. In this respect, solvents with different polarities were used: n-hexane (ε = 1.9), toluene (ε = 2.4), 1,2-dichloroethane (ε = 10.1), and ethanol (ε = 24.3). Four highly concentrated solutions of DPyDB–C
N–18C6, WAXD analysis was performed on the product powder, revealing an amorphous material. Moreover, WAXD was used to determine whether the solvent can influence the supramolecular arrangement of the compound. In this respect, solvents with different polarities were used: n-hexane (ε = 1.9), toluene (ε = 2.4), 1,2-dichloroethane (ε = 10.1), and ethanol (ε = 24.3). Four highly concentrated solutions of DPyDB–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–18C6 were prepared in each solvent and were left to rest for 24 hours. The resulting precipitates were collected, dropwise deposited on silicon wafer substrates, and left to dry by slow evaporation. The obtained films were then subjected to WAXD analysis. The results revealed that n-hexane, 1,2-dichloroethane, and ethanol solvents do not influence the supramolecular arrangement of the compound, the same amorphous character being put in evidence. However, the film obtained from toluene showed a crystalline character, as presented in Fig. 2 and Table 2. The broad peaks obtained at 2θ values of 12.4° and 22.8° belong to the silicon wafer substrate. The full width at half maximum (FWHM) of the peaks and the crystallite sizes were calculated using the Debye–Scherrer equation using the highest peak P1 as the reference; the following values were respectively obtained: 0.127 for FWHM and 69.74 nm for crystallite size. The scattering vector ratio (Table 2, q/reciprocal lattice vector) of approximatively 1
N–18C6 were prepared in each solvent and were left to rest for 24 hours. The resulting precipitates were collected, dropwise deposited on silicon wafer substrates, and left to dry by slow evaporation. The obtained films were then subjected to WAXD analysis. The results revealed that n-hexane, 1,2-dichloroethane, and ethanol solvents do not influence the supramolecular arrangement of the compound, the same amorphous character being put in evidence. However, the film obtained from toluene showed a crystalline character, as presented in Fig. 2 and Table 2. The broad peaks obtained at 2θ values of 12.4° and 22.8° belong to the silicon wafer substrate. The full width at half maximum (FWHM) of the peaks and the crystallite sizes were calculated using the Debye–Scherrer equation using the highest peak P1 as the reference; the following values were respectively obtained: 0.127 for FWHM and 69.74 nm for crystallite size. The scattering vector ratio (Table 2, q/reciprocal lattice vector) of approximatively 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3
3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 indicates a smectic ordering.56 Based on this fact, it can be assumed that π–π, multipole, induced-multipole, and dispersion force interactions between toluene molecules and pyrene units57 lead to a potential supramolecular arrangement of DPyDB–C
4 indicates a smectic ordering.56 Based on this fact, it can be assumed that π–π, multipole, induced-multipole, and dispersion force interactions between toluene molecules and pyrene units57 lead to a potential supramolecular arrangement of DPyDB–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–18C6.
N–18C6.
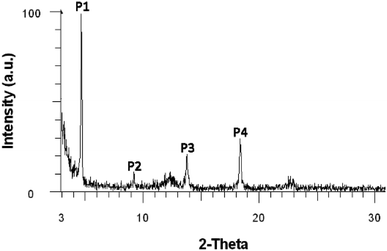 | ||
Fig. 2 Wide-angle X-ray diffraction (WAXD) diffractogram of the DPyDB–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–18C6 film obtained from the toluene solution. N–18C6 film obtained from the toluene solution. | ||
| Peak | Angle (2-theta°) | d value (Å) | q (Å−1) | q ratio |
|---|---|---|---|---|
| P1 | 4.626 | 19.09 | 0.328430 | 1.00 |
| P2 | 9.191 | 9.61 | 0.652008 | 1.99 |
| P3 | 13.753 | 6.43 | 0.974339 | 2.97 |
| P4 | 18.365 | 4.83 | 1.298631 | 3.95 |
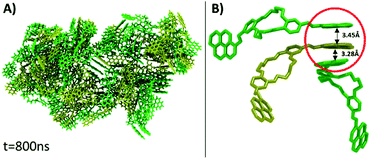
The visual analysis of the simulation trajectory showed that the molecules started to aggregate as soon as the simulation was initiated. The fast aggregation was due to the high concentration simulated, which was much higher than the experimental one. The reason for the need to work under high-concentration conditions is that the simulation of the experimental concentration is impossible in a feasible amount of time, due to the high number of solvent molecules, which must be considered (108 solvent molecules). Therefore, to put in evidence the intermolecular interactions that govern the aggregation process, a system that would aggregate and reach equilibrium in a reasonable amount of time must be chosen.
Under the simulation conditions, DPyDB–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–18C6 formed a single aggregate that includes 80 molecules (40 molecules of each position isomer). Fig. 4 depicts the final structure of the aggregate of DPyDB–C
N–18C6 formed a single aggregate that includes 80 molecules (40 molecules of each position isomer). Fig. 4 depicts the final structure of the aggregate of DPyDB–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–18C6, with a detail of the interaction between molecules.
N–18C6, with a detail of the interaction between molecules.
Visual analysis of the simulated aggregate shows an amorphous structure (Fig. 4A), in good agreement with the WAXD findings. Despite the high disorder degree of the aggregate, it can be seen that pyrene units are still capable of forming intermolecular π–π stacks between three or four near-by molecules. The results of MD computation indicated the existence of an almost isoenergetic structure, as a slipped-parallel aggregate, with interaction distances of about 3.45 and 3.28 Å. The ordered pyrene units are developed only at one side of the molecule, the pyrene moieties on the other side being either not-aggregated or involved in stacks with pyrene groups belonging to totally different molecules (Fig. 4B). Due to the high degree of disorder, there was no way to determine whether the presence of two isomers has any effect on the final structure of the aggregate.
The inability of the compound to align its both pyrene cycles with the two pyrenes of the same partner molecule is due to the dihedral angle in –C–HC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–C–, which includes the imine –HC
N–C–, which includes the imine –HC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N– bond. It induces a twist between the planes of pyrenes and phenyl cycles respectively, which is propagated towards the plane of the second pyrene moiety. Another motivation of the inability to form more systematic intermolecular π–π stacks is the presence of a C–H bond (held by a –HC
N– bond. It induces a twist between the planes of pyrenes and phenyl cycles respectively, which is propagated towards the plane of the second pyrene moiety. Another motivation of the inability to form more systematic intermolecular π–π stacks is the presence of a C–H bond (held by a –HC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N– unit) in the vicinity of a lone pair (belonging to the nitrogen atom of the same unit), which may induce a hindrance repulsion between neighboring molecules. In order to confirm the existence of the twisted dihedral angle (–C–HC
N– unit) in the vicinity of a lone pair (belonging to the nitrogen atom of the same unit), which may induce a hindrance repulsion between neighboring molecules. In order to confirm the existence of the twisted dihedral angle (–C–HC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–C–), quantum mechanics (QM) molecular geometry optimization, presented later in the paper (see Section 3.3.2), was performed. The computational results also evidenced that hydrogen interactions were formed between nitrogen atoms of imine bonds (–HC
N–C–), quantum mechanics (QM) molecular geometry optimization, presented later in the paper (see Section 3.3.2), was performed. The computational results also evidenced that hydrogen interactions were formed between nitrogen atoms of imine bonds (–HC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–) and the –O–H moiety of ethanol. A similar interaction was also observed between the –OH group of ethanol with the oxygen atom of the crown ether segment in DPyDB–C
N–) and the –O–H moiety of ethanol. A similar interaction was also observed between the –OH group of ethanol with the oxygen atom of the crown ether segment in DPyDB–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–18C6 molecules. The hydroxyl group of ethanol plays the role of hydrogen bond donor, while the nitrogen atoms belonging to imine groups, together with the oxygen atoms held by the crown ether, act as hydrogen bond acceptors.
N–18C6 molecules. The hydroxyl group of ethanol plays the role of hydrogen bond donor, while the nitrogen atoms belonging to imine groups, together with the oxygen atoms held by the crown ether, act as hydrogen bond acceptors.
3.3. Photophysical properties: experimental and theoretical studies
3.3.1.1 UV-vis absorption spectra. To demonstrate the photophysical properties DPyDB–C
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–18C6, the UV-vis absorption of its solutions in the same solvents was examined. Regardless of the solvent, the compound presented low solubility, possibly due to an aggregation effect that occurs as a consequence of the inter- and intra-molecular interactions. In order to determine the concentrations of the compound in the investigated solutions, quartz crystal microbalance with dissipation (QCM-D) measurements were performed. In this respect, based on the QCM-D-measured change in frequency Δf = f1 − f0, the areal-mass difference (Δm) was calculated using the Sauerbrey equation:58,59 Δm = −CΔf/n, where C (17.7 ng (cm−2 Hz)−1) represents a numerical constant related to the properties of quartz, and n (=7 in our case) is the harmonic overtone number which was considered. The results were normalized taking into account the volume of the solution, leading to the concentrations presented in Table S1.†
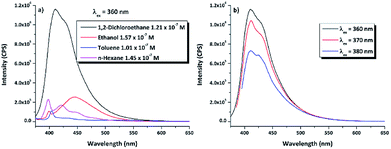
N–18C6, the UV-vis absorption of its solutions in the same solvents was examined. Regardless of the solvent, the compound presented low solubility, possibly due to an aggregation effect that occurs as a consequence of the inter- and intra-molecular interactions. In order to determine the concentrations of the compound in the investigated solutions, quartz crystal microbalance with dissipation (QCM-D) measurements were performed. In this respect, based on the QCM-D-measured change in frequency Δf = f1 − f0, the areal-mass difference (Δm) was calculated using the Sauerbrey equation:58,59 Δm = −CΔf/n, where C (17.7 ng (cm−2 Hz)−1) represents a numerical constant related to the properties of quartz, and n (=7 in our case) is the harmonic overtone number which was considered. The results were normalized taking into account the volume of the solution, leading to the concentrations presented in Table S1.†The experimental UV-vis spectra of DPyDB–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–18C6, at different concentrations in solvents of different polarities (n-hexane, toluene, 1,2-dichloroethane, and ethanol) are presented in Fig. 5. The vibronic effects, related to the presence of both pyrene and phenyl rings, appear in two ranges: 200–300 nm and 310–475 nm. The bands in the first range may be assigned to π → π* transitions, while the broad band in the second one could be ascribed to a mixture of π → π* and n → π* electronic transitions.38 Remarkably, the structure observed in 310–475 nm range in n-hexane was lost in the polar solvents. For each solvent, the spectral shape does not change with the increasing concentration of the solute and does not reveal any new peaks at longer wavelengths.
N–18C6, at different concentrations in solvents of different polarities (n-hexane, toluene, 1,2-dichloroethane, and ethanol) are presented in Fig. 5. The vibronic effects, related to the presence of both pyrene and phenyl rings, appear in two ranges: 200–300 nm and 310–475 nm. The bands in the first range may be assigned to π → π* transitions, while the broad band in the second one could be ascribed to a mixture of π → π* and n → π* electronic transitions.38 Remarkably, the structure observed in 310–475 nm range in n-hexane was lost in the polar solvents. For each solvent, the spectral shape does not change with the increasing concentration of the solute and does not reveal any new peaks at longer wavelengths.
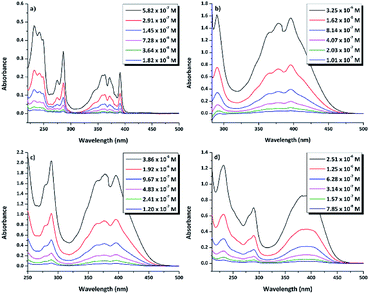 | ||
| Fig. 5 UV-vis absorption spectra of di-iminopyrene-dibenzo-18-crown-6-ether in: (a) n-hexane, (b) toluene, (c) 1,2-dicholoroethane, and (d) ethanol. | ||
3.3.1.2 Fluorescence spectroscopy. The photophysical properties of emission for the DPyDB–C
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–18C6 compound have been investigated by fluorescence spectroscopy at 360 nm excitation wavelength, in the same four solvents as for the UV-vis and WAXD analyses (Fig. 6a). Comparing the profiles of the emission spectra, it was found that DPyDB–C
N–18C6 compound have been investigated by fluorescence spectroscopy at 360 nm excitation wavelength, in the same four solvents as for the UV-vis and WAXD analyses (Fig. 6a). Comparing the profiles of the emission spectra, it was found that DPyDB–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–18C6 has a weak fluorescence emission, regardless of the chosen solvent. However, a slight increase in fluorescence emission can be seen in 1,2-dichloroethane, due to a different organization of the entire molecular system, interactions between the solvent and the molecules, as well as the increase in the stability of pyrene-type functional groups in this solvent.60 This is also sustained by the QM calculations when it was found that the values of the oscillator strength (f) for the π → π* transitions are higher in this solvent (Table S2†). A weak fluorescence in solution could have many possible reasons, such as aggregation-caused quenching (ACQ) effect,61,62 concentration quenching, photoinduced electron transfer (PET), energy transfer, and a double bond in the imine groups.62–64 According to references,38,62–64 the most probable explanation for the weak fluorescence in our system may be mainly related to a PET effect, which arises from the imine nitrogen atom to the large π-conjugation system of the pyrene moiety. Other explanations could be an ACQ effect, concentration quenching, as well as the presence of both pyrene units on the sides of the crown ether that leads to a quenching of the fluorescence emission. The weak fluorescence emission was confirmed by a low photoluminescence quantum yield (PLQY), similarly to the results obtained for other pyrene derivatives.62–64 Table 3 resumes the PLQY values for the DPyDB–C
N–18C6 has a weak fluorescence emission, regardless of the chosen solvent. However, a slight increase in fluorescence emission can be seen in 1,2-dichloroethane, due to a different organization of the entire molecular system, interactions between the solvent and the molecules, as well as the increase in the stability of pyrene-type functional groups in this solvent.60 This is also sustained by the QM calculations when it was found that the values of the oscillator strength (f) for the π → π* transitions are higher in this solvent (Table S2†). A weak fluorescence in solution could have many possible reasons, such as aggregation-caused quenching (ACQ) effect,61,62 concentration quenching, photoinduced electron transfer (PET), energy transfer, and a double bond in the imine groups.62–64 According to references,38,62–64 the most probable explanation for the weak fluorescence in our system may be mainly related to a PET effect, which arises from the imine nitrogen atom to the large π-conjugation system of the pyrene moiety. Other explanations could be an ACQ effect, concentration quenching, as well as the presence of both pyrene units on the sides of the crown ether that leads to a quenching of the fluorescence emission. The weak fluorescence emission was confirmed by a low photoluminescence quantum yield (PLQY), similarly to the results obtained for other pyrene derivatives.62–64 Table 3 resumes the PLQY values for the DPyDB–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–18C6 compound in each solvent. The exception was the measurement of the quantum yield in toluene, where a higher value was obtained as compared to the other solvents, maybe due to the interactions that develop between toluene molecules and the pyrene units.57 Moreover, when the excitation wavelength was increased toward the visible region, there was a decrease in the intensity of the emission spectra regardless of the chosen solvent (Fig. 6b). This fact could be attributed to the low-lying n → π* electronic transition.
N–18C6 compound in each solvent. The exception was the measurement of the quantum yield in toluene, where a higher value was obtained as compared to the other solvents, maybe due to the interactions that develop between toluene molecules and the pyrene units.57 Moreover, when the excitation wavelength was increased toward the visible region, there was a decrease in the intensity of the emission spectra regardless of the chosen solvent (Fig. 6b). This fact could be attributed to the low-lying n → π* electronic transition.
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–18C6 in n-hexane, toluene, 1,2-dichloroethane, and ethanol
N–18C6 in n-hexane, toluene, 1,2-dichloroethane, and ethanol
| Solvent | Photoluminescence quantum yield (PLQY) |
|---|---|
| n-Hexane | 0.39% |
| Toluene | 0.99% |
| Ethanol | 0.31% |
| 1,2-Dichloroethane | 0.56% |
3.3.2.1 Ground state. In order to explain the inability of DPyDB–C
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–18C6 to form good intermolecular π–π stacks revealed by MD simulations, quantum mechanics (QM) calculations in the ground state (GS) were performed. Moreover, the equilibrium geometries of both position isomers, predicted by quantitative 13C-NMR were studied to investigate if there are differences in the energy, dipole moments, as well as the intramolecular parameters (such as dihedral and valence angles, and bond length).
N–18C6 to form good intermolecular π–π stacks revealed by MD simulations, quantum mechanics (QM) calculations in the ground state (GS) were performed. Moreover, the equilibrium geometries of both position isomers, predicted by quantitative 13C-NMR were studied to investigate if there are differences in the energy, dipole moments, as well as the intramolecular parameters (such as dihedral and valence angles, and bond length).All equilibrium geometries of both position isomers (i1 and i2) reached after the completion of QM calculations using the PBE0/6-311+G(d,p) method are depicted in Fig. 7 and 8. DFT calculations were carried out in the ground state, considering the singlet state S0 as a fundamental level. The conformational effect has been studied by rotating the plane of the pyrene moiety following a clockwise direction, while the plane of the phenyl moiety was orientated counter clockwise, by small steps of 10°. The conformational effect of the studied compounds was estimated along the potential energy surface (PES). The motions of both fragments (pyrene and phenyl rings) were performed keeping the plane of double bond –HC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N– fixed (Fig. S7†). The scan procedure was operated for a single plane, the one in which were included the pyrene moiety, the double bond fragment –HC
N– fixed (Fig. S7†). The scan procedure was operated for a single plane, the one in which were included the pyrene moiety, the double bond fragment –HC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–, the phenyl ring, and a few atoms belonging to the crown ether fragment (not the all them). The crown ether fragment was reduced because this sequence can have multiple conformational effects, and to be close to the local minimum given by the QM calculations, a cut of atoms has been made. The new molecular geometry obtained for these scans was previously optimized by the DFT – PBE0/6-311+G(d,p) method, which suffered a conformational search (Fig. S7 and S8†). The computational results after PES scan indicate that the equilibrium geometry from the GS minimum has the same orientations of sequences as the entire system considered in our study (Fig. S8†).
N–, the phenyl ring, and a few atoms belonging to the crown ether fragment (not the all them). The crown ether fragment was reduced because this sequence can have multiple conformational effects, and to be close to the local minimum given by the QM calculations, a cut of atoms has been made. The new molecular geometry obtained for these scans was previously optimized by the DFT – PBE0/6-311+G(d,p) method, which suffered a conformational search (Fig. S7 and S8†). The computational results after PES scan indicate that the equilibrium geometry from the GS minimum has the same orientations of sequences as the entire system considered in our study (Fig. S8†).
 | ||
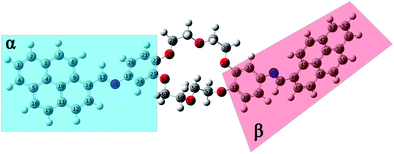
| Fig. 7 Equilibrium geometries into the GS for the i1 isomer computed using the PBE0/6-311+G(d,p) method. | ||
 | ||
| Fig. 8 Equilibrium geometries into the GS for the i2 isomer computed using the PBE0/6-311+G(d,p) method. | ||
The DFT-PBE0/6-311+G(d,p) method indicates that the i2 molecular system was stable in energy as compared to i1 (around 0.42 kcal mol−1 for i1), according to the data in Table S3.† The calculated dipole moment was of 4.59 D for i1 and of about 4.52 D for i2 (see Table S3†). Small differences in the energy stability of molecular systems, as well as into the values of dipole moments indicated that these compounds are hard to be isolated from the solution.
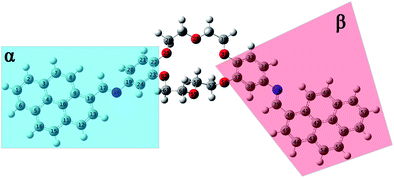
The structural parameters of these compounds, such as dihedral and valence angles, and bond lengths, were extracted after the DFT-PBE0/6-311+G(d,p) calculations. For easier comparison, both position isomers have been separated into two major regions, marked further in text with α and β symbols (Fig. 7 and 8). The α-section (including the pyrene unit, central linking –HC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N– bond, and phenyl fragment) is evidenced with blue color. The β-section (which includes the second phenyl moiety, second central bridge double bond, and second pyrene aromatic ring) is shown in a red color frame.
N– bond, and phenyl fragment) is evidenced with blue color. The β-section (which includes the second phenyl moiety, second central bridge double bond, and second pyrene aromatic ring) is shown in a red color frame.
Based on the values resulting after the optimization using the PBE0/6-311+G(d,p) method performed for GS of i1, a slight variation in the C9–C14–C17![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N18 dihedral angle around 4.2° (tending to planarity) was obtained in the case of α-section. On the contrary, the value of the C36–C35–N38
N18 dihedral angle around 4.2° (tending to planarity) was obtained in the case of α-section. On the contrary, the value of the C36–C35–N38![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C39 dihedral angle in the β-section was 33.3°. The dihedral angles of fragment sequences are linking the pyrene and phenyl units (C14–C17
C39 dihedral angle in the β-section was 33.3°. The dihedral angles of fragment sequences are linking the pyrene and phenyl units (C14–C17![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N18–C19 and C35–N38
N18–C19 and C35–N38![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C39–C40, respectively) lost to planarity. The C14–C17
C39–C40, respectively) lost to planarity. The C14–C17![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N18–C19 dihedral angle from the α-section has a value around 176.2°, while the C35–N38
N18–C19 dihedral angle from the α-section has a value around 176.2°, while the C35–N38![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C39–C40 dihedral angle from the β-section was orientated with −177.5°. The C17
C39–C40 dihedral angle from the β-section was orientated with −177.5°. The C17![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N18–C19–C24 dihedral angle has a value of around 145.4°, being twisted from planarity with 34.6°. The orientation of the N38
N18–C19–C24 dihedral angle has a value of around 145.4°, being twisted from planarity with 34.6°. The orientation of the N38![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C39–C40–C41 dihedral angle tends to be close to planarity (around 3.6°) (Table S4†).
C39–C40–C41 dihedral angle tends to be close to planarity (around 3.6°) (Table S4†).
The optimization results in the case of i2 isomer showed that the C9–C14–C17![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N18 dihedral angle (from α-section) is close to planarity (175.2°), while the C35–C34–N38
N18 dihedral angle (from α-section) is close to planarity (175.2°), while the C35–C34–N38![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C39 dihedral angle (from the β-section) is twisted with 39.4°. The values in Table S4† indicated that both bridge dihedral angles, which are linking α- and β-sections (C14–C17
C39 dihedral angle (from the β-section) is twisted with 39.4°. The values in Table S4† indicated that both bridge dihedral angles, which are linking α- and β-sections (C14–C17![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N18–C19 and C34–N38
N18–C19 and C34–N38![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C39–C40), are close to planarity, having values around 176.2° and −177.1°, respectively. In the case of the β-section, the N38
C39–C40), are close to planarity, having values around 176.2° and −177.1°, respectively. In the case of the β-section, the N38![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C39–C40–C41 dihedral angle has a small value of about 4.8°. Therefore, the orientations of dihedral angles have the same trends for both i1 and i2 compounds.
C39–C40–C41 dihedral angle has a small value of about 4.8°. Therefore, the orientations of dihedral angles have the same trends for both i1 and i2 compounds.
To estimate the interatomic distance values, it was considered that the –HC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N– bond length represents the reference value for both i1 and i2 isomers. The computational results resumed in Table S5† indicate that, in the case of i1 isomer, the –C17
N– bond length represents the reference value for both i1 and i2 isomers. The computational results resumed in Table S5† indicate that, in the case of i1 isomer, the –C17![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N18– bond length in the α-section is slightly higher (with 0.001 Å) than the –N38
N18– bond length in the α-section is slightly higher (with 0.001 Å) than the –N38![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C39– length in the β-section. The same trend resulted in the case of the –HC
C39– length in the β-section. The same trend resulted in the case of the –HC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N– bonds in the i2 isomer. No significant differences in the values were observed by comparing the –HC
N– bonds in the i2 isomer. No significant differences in the values were observed by comparing the –HC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N– central bridge from i1 with the same bond belonging to i2. In this case, both compounds were isoelectronic, and differences appear at the position isomers.
N– central bridge from i1 with the same bond belonging to i2. In this case, both compounds were isoelectronic, and differences appear at the position isomers.
The results of the PBE0/6-311+G(d,p) calculation in Table S5† predict that the adjacent bonds have different lengths in the α-section, compared with those in the β-section, for both i1 and i2 isomers. The intramolecular bond length variations appear due to the extended conjugation system. In the case of i1, the length of the adjacent bonds positioned in the α-section was higher in value than the β-section. On the contrary, in compound i2, the results are reversed (Table S5†).
Regarding the valence angles, all computational data results are presented in Table S6.† Analysing the obtained results, it can be asserted that the values for i1 and i2 isomers were comparable. Moreover, the computational data from Table S6† indicate a slight difference in valence angle values between the two positions. However, considering the valence angle values, as well as the values of central double bonds, both i1 and i2 isomers, with respect to the trigonal plane geometry, are in the sp2 hybridization state.
In conclusion, it can be affirmed that the molecular geometry is not influenced by variations in bond length and valence angles. Moreover, because the dihedral angles between the pyrene unit and the phenyl aromatic ring of the crown ether (–C–HC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NC–) can vary up to 40°, the assembly in the π–π stacking can be hindered (as discussed in the MD simulations) (as shown in Section 3.2.2).
NC–) can vary up to 40°, the assembly in the π–π stacking can be hindered (as discussed in the MD simulations) (as shown in Section 3.2.2).
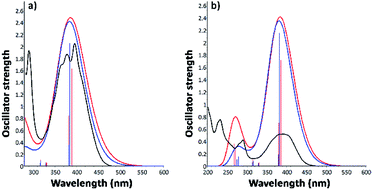
3.3.2.2. Excitation electronic transitions. The assignments of the excitation electronic transitions from the experimental spectra have been described and correlated with the TD-DFT calculations. The theoretical absorption spectra were calculated for both i1 and i2 position isomers. The equilibrium geometries optimized with the PBE0/6-311+G(d,p) level of theory were used in the TD-DFT computations. The TD-DFT absorption spectrum for each isomer was calculated in the gas phase and then into the implicit solvents: n-hexane, toluene, 1,2-dichloroethane, and ethanol, respectively. TD-DFT calculations were made using the PBE0/6-311+G(d,p), TD-CAM-B3LYP/6-311+G(d,p), TD-B3LYP/6-311+G(d,p) methods. The theoretical data such as values of absorption band maxima (λabs) and the oscillator strength (f) obtained from TD-DFT calculations are given in Table S2.† The results reveal that the TD-CAM-B3LYP/6-311+G(d,p) method predicts results closer to the experimental data, especially for the wavelengths located in the visible region. Moreover, a good correlation was obtained of electronic theoretical absorption spectra calculated at the TD-CAM-B3LYP/6-311+G(d,p) level of theory in toluene and ethanol solvents as compared to the experimental data (Fig. 9). However, TD-PBE0/6-311+G(d,p) and TD-B3LYP/6-311+G(d,p) overestimated the results in comparison with the experimental measurements (Table S2†).
Experimental and TD calculations indicated a strong intensity of the absorption band in the visible region. Comparing the TD calculations results with the experimental measurements illustrated in Fig. 9, no significant shift ranges of the maximum absorption wavelengths were observed. Moreover, the results presented in Fig. 9 indicated that both isomers can absorb at the same wavelength. The oscillator strength values (f) of the i2 isomer calculated with TD-CAM-B3LYP in all solvents (Table S2†) are higher than those of the i1 isomer, suggesting that the i2 isomer has a slightly hyperchromic effect.
Molecular orbitals corresponding to the excitation electronic transitions involved have been extracted from the TD-CAMB3LYP calculation in the gas phase. The surfaces of molecular orbitals were drawn at the 0.02 a.u. iso level, and they describe the electron density in both the GS and the excited state. The excitation character for the first six transitions of i1 and i2 isomers has been selected for representations (Fig. 10 and 11). The first six transitions have been selected for representation because they give the most intense signals in the electronic absorption spectra. The rest of the transitions have lower values of intensity due to the oscillator strength; hence these transitions are not expected to influence the theoretical absorption band structure. All first six excited state transitions represented in Fig. 10 and 11 suggested π → π* and mixed π → π* and n → π* characters, which are in good agreement with the experimental absorption data. The mixed excited state transitions appear as an effect of energy levels being near degenerate, as well as due to the presence of intramolecular interactions (existence of electron density transfer). The electron densities in all cases were localized on the pyrene sequence.
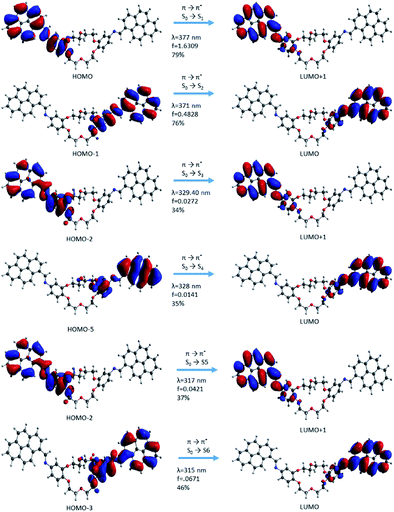 | ||
| Fig. 10 Molecular orbital representation of the i1 isomer using TD-CAMB3LYp/6-31+G(d,p) in the gas phase. | ||
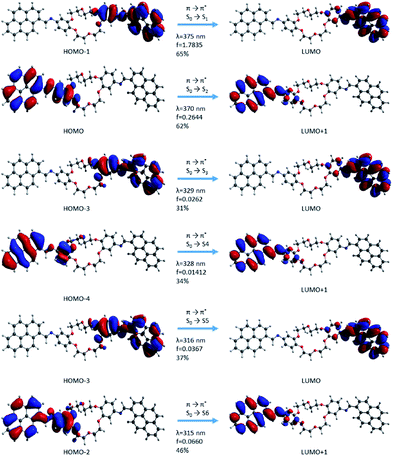 | ||
| Fig. 11 Molecular orbital representation of the i2 isomer using TD-CAMB3LYp/6-31+G(d,p) in the gas phase. | ||
In the case of the i1 isomer, the first transition was π → π* (S0 → S1) and the electron density was localized on the pyrene-phenyl and the imine bond (–HC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–) sequences from the α-section (Fig. 7). The molecular orbital that characterizes this π → π* transition is HOMO → LUMO+1. The photophysical process during this transition includes a slight delocalization of electron density from the phenyl ring (in the ground state, (π) up to antibonding orbitals of pyrene, as well as on the –HC
N–) sequences from the α-section (Fig. 7). The molecular orbital that characterizes this π → π* transition is HOMO → LUMO+1. The photophysical process during this transition includes a slight delocalization of electron density from the phenyl ring (in the ground state, (π) up to antibonding orbitals of pyrene, as well as on the –HC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N– bond and partially on the phenyl bond corresponding to the excited state (π*)). This delocalization suggests that the compound has a π-extended conjugation during the photophysical process. The second transition π → π* (S0 → S2) occurred when the process was localized on the sequences from the β-section. The molecular frontier was localized here between HOMO-1 → LUMO (Fig. 10). The third transition has a mixed character, π → π* and n → π*, but with predominantly π → π* excitation. This type of transition confirms that the lone pair electrons from the nitrogen atom (belonging to the –HC
N– bond and partially on the phenyl bond corresponding to the excited state (π*)). This delocalization suggests that the compound has a π-extended conjugation during the photophysical process. The second transition π → π* (S0 → S2) occurred when the process was localized on the sequences from the β-section. The molecular frontier was localized here between HOMO-1 → LUMO (Fig. 10). The third transition has a mixed character, π → π* and n → π*, but with predominantly π → π* excitation. This type of transition confirms that the lone pair electrons from the nitrogen atom (belonging to the –HC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N– bond) can participate in the electron density conjugation effect. Only the first two excited state transitions have a major contribution (up to 75%, S0 → S1 and S0 → S2) and a higher oscillator strength value, which indicates that these are predominant in the absorption electronic spectra. The other transitions have small contribution and a small oscillator strength (f) value.
N– bond) can participate in the electron density conjugation effect. Only the first two excited state transitions have a major contribution (up to 75%, S0 → S1 and S0 → S2) and a higher oscillator strength value, which indicates that these are predominant in the absorption electronic spectra. The other transitions have small contribution and a small oscillator strength (f) value.
In the case of the i2 isomer, the first transition occurs from the phenyl–HC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–pyrene sequences and corresponds to the occupied orbital π (HOMO−1) → unoccupied orbital π* (LUMO) in the same fragments. This excitation takes place in the β-section contrary to the situation from the i1 isomer (Fig. 10 and 11). Similar to the i1 isomer, the i2 isomer showed a π-extended electron density conjugation during the photophysical process. The π-extended electron density conjugation appears as an effect of an intramolecular interaction between phenyl, –HC
N–pyrene sequences and corresponds to the occupied orbital π (HOMO−1) → unoccupied orbital π* (LUMO) in the same fragments. This excitation takes place in the β-section contrary to the situation from the i1 isomer (Fig. 10 and 11). Similar to the i1 isomer, the i2 isomer showed a π-extended electron density conjugation during the photophysical process. The π-extended electron density conjugation appears as an effect of an intramolecular interaction between phenyl, –HC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–, and pyrene moieties. The second transition includes an π-extended conjugation during the photophysical process of group moieties from the α-section and the nature of this excitation was π (HOMO−1) → π* (LUMO) and S0 → S2 (Fig. 11). Both first (S0 → S1) and second transitions (S0 → S2) have a major contribution in the absorption electronic spectra because the oscillator strength values (f) were higher than the rest of the transitions. The other transitions have small oscillator strength values, and the contributions are less than 46%.
N–, and pyrene moieties. The second transition includes an π-extended conjugation during the photophysical process of group moieties from the α-section and the nature of this excitation was π (HOMO−1) → π* (LUMO) and S0 → S2 (Fig. 11). Both first (S0 → S1) and second transitions (S0 → S2) have a major contribution in the absorption electronic spectra because the oscillator strength values (f) were higher than the rest of the transitions. The other transitions have small oscillator strength values, and the contributions are less than 46%.
In summary, both pyrene units from the α- and β-sections have a major contribution to observed transitions, but only S0 → S1 and S0 → S2 transitions act with a major contribution on the absorption electronic spectra. The nature of transitions, predicted by the TD-DFT calculations, was also observed in other pyrene derivative studies.25,29,30,37,65 In the case of the DPyDB–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–18C6 compound, no transfer of electron density between pyrene–pyrene fragments (a transfer from pyrene moiety from the α-section to the pyrene unit belonging to the β-section) was observed. Possibly, this potential situation was stopped by the presence of the crown ether sequence, which interrupts the extended conjugation. It can be assumed that if the electronic density was localized on pyrene units from the α- and β-sections, clear π–π stacking interactions would have been observed. The electronic density was localized only on one side of the crown ether sequence (α- or β-section) and this led to a perturbation, forming a well-ordered intermolecular π–π stack.
N–18C6 compound, no transfer of electron density between pyrene–pyrene fragments (a transfer from pyrene moiety from the α-section to the pyrene unit belonging to the β-section) was observed. Possibly, this potential situation was stopped by the presence of the crown ether sequence, which interrupts the extended conjugation. It can be assumed that if the electronic density was localized on pyrene units from the α- and β-sections, clear π–π stacking interactions would have been observed. The electronic density was localized only on one side of the crown ether sequence (α- or β-section) and this led to a perturbation, forming a well-ordered intermolecular π–π stack.
3.3.2.2.1. MD simulations of ion selectivity. Envisioning a chemo-sensor application for our novel compound was performed a molecular dynamic simulation of 10 DPyDB–C
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–18C6 molecules in a mixed ion solution to test the ion selectivity. The molecules were distributed randomly in an 8 × 8 × 8 nm box. Then, 10 of each Na+, K+ and Ca2+ ions and 40 Cl− ions were added, and the entire system was solvated with water. To prevent the aggregation of the DPyDB–C
N–18C6 molecules in a mixed ion solution to test the ion selectivity. The molecules were distributed randomly in an 8 × 8 × 8 nm box. Then, 10 of each Na+, K+ and Ca2+ ions and 40 Cl− ions were added, and the entire system was solvated with water. To prevent the aggregation of the DPyDB–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–18C6 compound, a position restraint was applied to one of the C atoms from the crown ether. This restrained position allowed the molecule to twist and turn freely in the solution, but at the same time preventing diffusion in the solvent. Two simulations for 40 ns each were performed, starting from two different randomly dispersed structures in order to investigate what ions interact with DPyDB–C
N–18C6 compound, a position restraint was applied to one of the C atoms from the crown ether. This restrained position allowed the molecule to twist and turn freely in the solution, but at the same time preventing diffusion in the solvent. Two simulations for 40 ns each were performed, starting from two different randomly dispersed structures in order to investigate what ions interact with DPyDB–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–18C6 and to eliminate any bias that may have been induced by the initial position of the simulated molecules. The final structures obtained after the simulation are presented in Fig. S9.†
N–18C6 and to eliminate any bias that may have been induced by the initial position of the simulated molecules. The final structures obtained after the simulation are presented in Fig. S9.†
By visually analysing both simulations, it was observed that the DPyDB–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–18C6 molecules interacted only with K+ ions, forming stable complexes. Fig. 12 depicts one of the DPyDB–C
N–18C6 molecules interacted only with K+ ions, forming stable complexes. Fig. 12 depicts one of the DPyDB–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–18C6 molecule with a K+ ion trapped in the crown ether.
N–18C6 molecule with a K+ ion trapped in the crown ether.
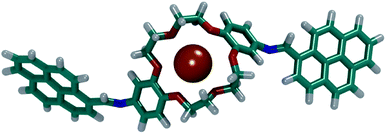 | ||
Fig. 12 Example of a complex formed between DPyDB–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–18C6 and a K+ ion. C atoms are shown in teal, O atoms in red, N atoms in blue, K+ atoms in orange and H atoms in white. N–18C6 and a K+ ion. C atoms are shown in teal, O atoms in red, N atoms in blue, K+ atoms in orange and H atoms in white. | ||
These simulations point towards a successful usage of the DPyDB–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–18C6 molecules as a chemo-sensor selective for K+ ions. A detailed study of the complexation of DPyDB–C
N–18C6 molecules as a chemo-sensor selective for K+ ions. A detailed study of the complexation of DPyDB–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–18C6 with different cations and the effect that the complexation has on the photophysical properties will be detailed in a future study.
N–18C6 with different cations and the effect that the complexation has on the photophysical properties will be detailed in a future study.
4 Conclusions
In this work, a novel compound was synthesised by linking two pyrene moieties to diaminodibenzo-18-crown-6-ether through –HC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N– bonds, resulting in DPyDB–C
N– bonds, resulting in DPyDB–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–18C6 product. The synthesis was confirmed by FTIR, 1H-NMR, 13C-NMR, TGA, and DSC techniques. The quantitative 13C-NMR analysis revealed the presence of the two position isomers. WAXD technique and MD simulations were used to evaluate the possibility of the supramolecular arrangement of DPyDB–C
N–18C6 product. The synthesis was confirmed by FTIR, 1H-NMR, 13C-NMR, TGA, and DSC techniques. The quantitative 13C-NMR analysis revealed the presence of the two position isomers. WAXD technique and MD simulations were used to evaluate the possibility of the supramolecular arrangement of DPyDB–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–18C6. Both experimental and theoretical methods showed that the compound forms an aggregate with weak π–π interactions. The MD simulation results revealed the existence of almost isoenergetic structures as a slipped-parallel aggregate with an interaction distance around 3.45 and 3.28 Å. Through the QM calculations, it was observed that –C–HC
N–18C6. Both experimental and theoretical methods showed that the compound forms an aggregate with weak π–π interactions. The MD simulation results revealed the existence of almost isoenergetic structures as a slipped-parallel aggregate with an interaction distance around 3.45 and 3.28 Å. Through the QM calculations, it was observed that –C–HC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–C– dihedral angle, which links the pyrene units to the phenyl rings of the crown ether, was twisted around 40°. This situation explains the inability to align both pyrenes from the same DPyDB–C
N–C– dihedral angle, which links the pyrene units to the phenyl rings of the crown ether, was twisted around 40°. This situation explains the inability to align both pyrenes from the same DPyDB–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–18C6 molecule with the pyrenes from another molecule, as observed from the MD simulation results. This incapacity is also governed by the presence of a C–H bond and lone pairs of nitrogen from the –HC
N–18C6 molecule with the pyrenes from another molecule, as observed from the MD simulation results. This incapacity is also governed by the presence of a C–H bond and lone pairs of nitrogen from the –HC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N– bond, inducing a hindrance repulsion between individual molecules. Furthermore, the DPyDB–C
N– bond, inducing a hindrance repulsion between individual molecules. Furthermore, the DPyDB–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–18C6 compound was investigated from the point of view of its photophysical properties. In order to understand the electronic structure, the UV-vis and fluorescence experiments together with the theoretical studies (QM calculations) were performed in solvents with different polarities (n-hexane, toluene, 1,2-dichloroethane, and ethanol). From the results, we observed the presence of π → π* and n → π* transitions, among which the π → π* transition due to π-extended conjugation is predominant. By contrast, through fluorescence analysis, a weak emission was observed and could be explained by photoinduced electron transfer (PET) and aggregation-caused quenching (ACQ) effects. The frontier molecular orbitals into the ground state demonstrated that the electronic density of DPyDB–C
N–18C6 compound was investigated from the point of view of its photophysical properties. In order to understand the electronic structure, the UV-vis and fluorescence experiments together with the theoretical studies (QM calculations) were performed in solvents with different polarities (n-hexane, toluene, 1,2-dichloroethane, and ethanol). From the results, we observed the presence of π → π* and n → π* transitions, among which the π → π* transition due to π-extended conjugation is predominant. By contrast, through fluorescence analysis, a weak emission was observed and could be explained by photoinduced electron transfer (PET) and aggregation-caused quenching (ACQ) effects. The frontier molecular orbitals into the ground state demonstrated that the electronic density of DPyDB–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–18C6 was localized only on one pyrene–CH
N–18C6 was localized only on one pyrene–CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–phenyl sequence of the crown ether, leading to a perturbation of a well-ordered intermolecular π–π stacking.
N–phenyl sequence of the crown ether, leading to a perturbation of a well-ordered intermolecular π–π stacking.
Author contributions
A. C., D.-L. I., and M. P. conceived and planned the experiments; C. A.-M., R. Z., and R. A. performed the synthesis of di-iminopyrene-dibenzo-18-crown-6-ether compound; C. A.-M., S.-A. I., D. T., and A. N. performed the physico-chemical characterization of the di-iminopyrene-dibenzo-18-crown-6-ether compound; A. C. performed the photophysical properties measurements; T. V. performed the MD simulations; D.-L. I. performed the QM calculations; A. C., D.-L. I., C. A.-M., T. V., and M. P. wrote and revised the manuscript; F. M., A. L., M. J. M. A., and M. P. supervised the experimental and theoretical studies. All authors have been involved in checking the data, and have given approval to the final version of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This publication received funding from the European Union's Horizon 2020 Research and Innovation Program under Grant Agreement No. 667387, WIDESPREAD 2-2014 “SupraChem Lab”, and PN-III-P4-ID-PCCF-2016-0050 grant, funded by the Ministry of Research and Innovation, CNCS/CCCDI–UEFISCDI, within the PNCDI III program.References
- S. Zhang, Nat. Biotechnol., 2003, 21, 1171–1178 CrossRef CAS.
- A. Aliprandi, M. Mauro and L. De Cola, Nat. Chem., 2016, 8, 10 CrossRef CAS.
- D. Nieckarz, W. Rżysko and P. Szabelski, Phys. Chem. Chem. Phys., 2018, 20, 23363–23377 RSC.
- J. W. Steed, J. L. Atwood and P. A. Gale, in Supramolecular Chemistry: From Molecules to Nanomaterials, 2012 Search PubMed.
- D. González-Rodríguez and A. P. H. J. Schenning, Chem. Mater., 2011, 23, 310–325 CrossRef.
- M. Blomenhofer, S. Ganzleben, D. Hanft, H.-W. Schmidt, M. Kristiansen, P. Smith, K. Stoll, D. Mäder and K. Hoffmann, Macromolecules, 2005, 38, 3688–3695 CrossRef CAS.
- J. B. Bodapati and H. Icil, Photochem. Photobiol. Sci., 2011, 10, 1283–1293 RSC.
- T. Shu, J. Wu, M. Lu, L. Chen, T. Yi, F. Li and C. Huang, J. Mater. Chem., 2008, 18, 886–893 RSC.
- J. W. Steed, Coord. Chem. Rev., 2001, 215, 171–221 CrossRef CAS.
- G. W. Gokel, Crown Ethers and Cryptands, Royal Society of Chemistry, Cambridge, 1991 Search PubMed.
- S. H. Kim, K. C. Song, S. Ahn, Y. S. Kang and S.-K. Chang, Tetrahedron Lett., 2006, 47, 497–500 CrossRef CAS.
- H. Maeda, K. Nakamura, T. Furuyama and M. Segi, Photochem. Photobiol. Sci., 2019, 18, 2397–2410 RSC.
- G. W. Gokel and S. Negin, Acc. Chem. Res., 2013, 46, 2824–2833 CrossRef CAS.
- A. L. Sisson, M. R. Shah, S. Bhosale and S. Matile, Chem. Soc. Rev., 2006, 35, 1269–1286 RSC.
- N. Sakai and S. Matile, Langmuir, 2013, 29, 9031–9040 CrossRef CAS.
- R. Zonda, A. Coroaba, S. Ibanescu, T. Vasiliu, A. Neamtu, M. Silion, T. Rusu and M. Pinteala, Rev. Roum. Chim., 2018, 63, 665–672 Search PubMed.
- J. Lamb, R. Izatt, P. Robertson and J. Christensen, J. Am. Chem. Soc., 1980, 102, 2452–2454 CrossRef CAS.
- F. Otis, C. Racine-Berthiaume and N. Voyer, J. Am. Chem. Soc., 2011, 133, 6481–6483 CrossRef CAS.
- A. Gilles and M. Barboiu, J. Am. Chem. Soc., 2016, 138, 426–432 CrossRef CAS.
- D. R. Rueda, A. Nogales, J. J. Hernández, M.-C. García-Gutiérrez, T. A. Ezquerra, S. V. Roth, M. G. Zolotukhin and R. Serna, Langmuir, 2007, 23, 12677–12681 CrossRef CAS.
- P. Staffeld, M. Kaller, P. Ehni, M. Ebert, S. Laschat and F. Giesselmann, Crystals, 2019, 9, 74 CrossRef.
- G. Koshkakaryan, L. M. Klivansky, D. Cao, M. Snauko, S. J. Teat, J. O. Struppe and Y. Liu, J. Am. Chem. Soc., 2009, 131, 2078–2079 CrossRef CAS.
- M. Pinteala, V. Epure, V. Harabagiu, B. C. Simionescu and S. Schlick, Macromolecules, 2004, 37, 4623–4634 CrossRef CAS.
- E. Szajdzinska-Pietek, M. Pinteala and S. Schlick, Polymer, 2004, 45, 4113–4120 CrossRef CAS.
- S. Shirai and S. Inagaki, RSC Adv., 2020, 10, 12988–12998 RSC.
- T. M. Figueira-Duarte and K. Müllen, Chem. Rev., 2011, 111, 7260–7314 CrossRef CAS.
- J. R. Platt, J. Chem. Phys., 1949, 17, 484–495 CrossRef CAS.
- T. M. Cardozo, A. P. Galliez, I. Borges, F. Plasser, A. J. A. Aquino, M. Barbatti and H. Lischka, Phys. Chem. Chem. Phys., 2019, 21, 13916–13924 RSC.
- J. Hoche, H.-C. Schmitt, A. Humeniuk, I. Fischer, R. Mitrić and M. I. S. Röhr, Phys. Chem. Chem. Phys., 2017, 19, 25002–25015 RSC.
- M. Baba, M. Saitoh, Y. Kowaka, K. Taguma, K. Yoshida, Y. Semba, S. Kasahara, T. Yamanaka, Y. Ohshima, Y.-C. Hsu and S. H. Lin, J. Chem. Phys., 2009, 131, 224318 CrossRef.
- R. Andriessen, M. Ameloot, N. Boens and F. C. D. Schryver, J. Phys. Chem., 1992, 96, 314–326 CrossRef CAS.
- N. J. Silva, F. B. C. Machado, H. Lischka and A. J. A. Aquino, Phys. Chem. Chem. Phys., 2016, 18, 22300–22310 RSC.
- F. H. Herbstein, M. Kapon and V. Shteiman, Acta Crystallogr., Sect. B: Struct. Sci., 2001, 57, 692–696 CrossRef CAS.
- S. K. Kim, J. H. Bok, R. A. Bartsch, J. Y. Lee and J. S. Kim, Org. Lett., 2005, 7, 4839–4842 CrossRef CAS.
- E. J. Jun, H. N. Won, J. S. Kim, K.-H. Lee and J. Yoon, Tetrahedron Lett., 2006, 47, 4577–4580 CrossRef CAS.
- H. Yan, P. Cui, C.-B. Liu and S.-L. Yuan, Langmuir, 2012, 28, 4931–4938 CrossRef CAS.
- S. Shirai, S. Iwata, T. Tani and S. Inagaki, J. Phys. Chem. A, 2011, 115, 7687–7699 CrossRef CAS.
- M. Shyamal, P. Mazumdar, S. Maity, G. P. Sahoo, G. Salgado-Morán and A. Misra, J. Phys. Chem. A, 2016, 120, 210–220 CrossRef CAS.
- Z. Jarolímová, M. Vishe, J. Lacour and E. Bakker, Chem. Sci., 2016, 7, 525–533 RSC.
- H. Bekker, H. Berendsen, E. Dijkstra, S. Achterop, R. Vondrumen, D. Vanderspoel, A. Sijbers, H. Keegstra and M. Renardus, in Physics Computing '92, World Scientific Publishing, Singapore, 1993, pp. 252–256 Search PubMed.
- M. D. Hanwell, D. E. Curtis, D. C. Lonie, T. Vandermeersch, E. Zurek and G. R. Hutchison, J. Cheminf., 2012, 4, 17 CAS.
- M. Frisch, G. Trucks, H. Schlegel, G. Scuseria, M. Robb, J. Cheeseman, G. Scalmani, V. Barone, G. Petersson, H. Nakatsuji, X. Bao, M. Caricato, A. Marenich, J. Bloino, B. Janesko, R. Gomperts, B. Mennucci, H. Hratchian, J. Ortiz, A. Izmaylov, J. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. Montgomery Jr, J. Peralta, F. Ogliaro, M. Bearpark, J. Heyd, E. Brothers, K. Kudin, V. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. Burant, S. Iyengar, J. Tomasi, M. Cossi, J. Millam, M. Klene, C. Adamo, R. Cammi, J. Ochterski, R. Martin, K. Morokuma, O. Farkas, J. Foresman and D. Fox, Gaussian 16, Gaussian Inc., Wallingford CT, 2016 Search PubMed.
- F.-Y. Dupradeau, A. Pigache, T. Zaffran, C. Savineau, R. Lelong, N. Grivel, D. Lelong, W. Rosanski and P. Cieplak, Phys. Chem. Chem. Phys., 2010, 12, 7821–7839 RSC.
- Amber Tools 18, http://ambermd.org/AmberTools.php.
- J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3094 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS.
- T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57 CrossRef CAS.
- D. L. Isac, A. Airinei, D. Maftei, I. Humelnicu, F. Mocci, A. Laaksonen and M. Pinteală, J. Phys. Chem. A, 2019, 123, 5525–5536 CrossRef CAS.
- A. Airinei, D. L. Isac, M. Homocianu, C. Cojocaru and C. Hulubei, J. Mol. Liq., 2017, 240, 476–485 CrossRef CAS.
- Y. Xie, N. Du, S. Yu, L. Zhang and M. Yang, J. Phys. Chem. C, 2019, 123, 30714–30722 CrossRef CAS.
- N. Du, S. Yu, Y. Xie, Y. Cui, L. Zhang and M. Yang, Eur. Phys. J. B, 2019, 92, 1–12 CrossRef.
- K. Khayer and T. Haque, ACS Omega, 2020, 5, 4507–4531 CrossRef CAS.
- R. Ardeleanu, N. Voiculescu, M. Marcu, G. Roman, C. Buchidau, L. Sacarescu and G. Sacarescu, Macromol. Rapid Commun., 1997, 18, 739–746 CrossRef CAS.
- Y. Liu, Y. Chen, M. Xu, C.-L. Zhu and Z. Liu, J. Mol. Struct., 2017, 1148, 429–434 CrossRef CAS.
- V. K. Thakur and M. R. Kessler, Liquid Crystalline Polymers: Volume 1 – Structure and Chemistry, Springer, 2015 Search PubMed.
- P. Lianos and S. Georghiou, Photochem. Photobiol., 1979, 30, 355–362 CrossRef CAS.
- G. Sauerbrey, Z. Phys., 1959, 155, 206–222 CrossRef CAS.
- A. K. Dutta and G. Belfort, Langmuir, 2007, 23, 3088–3094 CrossRef CAS.
- S. Yousefinejad, F. Honarasa and M. Chaabi, New J. Chem., 2016, 40, 10197–10207 RSC.
- S. A. Jenekhe and J. A. Osaheni, Science, 1994, 265, 765–768 CrossRef CAS.
- A. Kathiravan, K. Sundaravel, M. Jaccob, G. Dhinagaran, A. Rameshkumar, D. Arul Ananth and T. Sivasudha, J. Phys. Chem. B, 2014, 118, 13573–13581 CrossRef CAS.
- A. K. Gupta, A. Dhir and C. P. Pradeep, Dalton Trans., 2013, 42, 12819–12823 RSC.
- L. Zang, D. Wei, S. Wang and S. Jiang, Tetrahedron, 2012, 68, 636–641 CrossRef CAS.
- A. T. Haedler, H. Misslitz, C. Buehlmeyer, R. Q. Albuquerque, A. Köhler and H.-W. Schmidt, ChemPhysChem, 2013, 14, 1818–1829 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ra06929a |
| This journal is © The Royal Society of Chemistry 2020 |