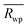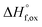Open Access Article
Open Access ArticleDisorder in Ho2Ti2−xZrxO7: pyrochlore to defect fluorite solid solution series
Devon L. Drey a,
Eric C. O'Quinna,
Tamilarasan Subramanib,
Kristina Lilovab,
Gianguido Baldinozzic,
Igor M. Gusseva,
Antonio F. Fuentes
a,
Eric C. O'Quinna,
Tamilarasan Subramanib,
Kristina Lilovab,
Gianguido Baldinozzic,
Igor M. Gusseva,
Antonio F. Fuentes d,
Joerg C. Neuefeinde,
Michelle Everette,
David Sprouster
d,
Joerg C. Neuefeinde,
Michelle Everette,
David Sprouster f,
Alexandra Navrotskyb,
Rodney C. Ewingg and
Maik Lang*a
f,
Alexandra Navrotskyb,
Rodney C. Ewingg and
Maik Lang*a
aDepartment of Nuclear Engineering, University of Tennessee, Knoxville, TN 37996, USA. E-mail: mlang2@utk.edu
bSchool of Molecular Sciences, Center for Materials of the Universe, Arizona State University, Tempe, AZ 85287, USA
cLaboratoire Structures, Propriétés et Modélisation des Solides, CNRS, Centrale Supélec, Université Paris-Saclay, F-91190 Gif-sur-Yvette, France
dCinvestav Unidad Saltillo, 25900 Ramos Arizpe, Coahuila, Mexico
eNeutron Scattering Division, Oak Ridge National Laboratory, Oak Ridge, TN 37831, USA
fDepartment of Materials Science and Chemical Engineering, State University of New York, Stony Brook, NY 11794, USA
gDepartment of Geological Sciences, Stanford University, Stanford, CA 94305, USA
First published on 18th September 2020
Abstract
Pyrochlore (A2B2O7) is an important, isometric structure-type because of its large variety of compositions and structural derivatives that are generally related to different disordering mechanisms at various spatial scales. The disordering is key to understanding variations in properties, such as magnetic behavior or ionic conduction. Neutron and X-ray total scattering methods were used to investigate the degree of structural disorder in the Ho2Ti2−xZrxO7 (x = 0.0–2.0, Δx = 0.25) solid solution series as a function of the Zr-content, x. Ordered pyrochlores (Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) disorder to defect fluorite (Fm
m) disorder to defect fluorite (Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) via cation and anion disordering. Total scattering experiments with sensitivity to the cation and anion sublattices provide unique insight into the underlying atomic processes. Using simultaneous Rietveld refinement (long-range structure) and small-box refinement PDF analysis (short-range structure), we show that the series undergoes a rapid transformation from pyrochlore to defect fluorite at x ≈ 1.2, while the short-range structure exhibits a linear increase in a local weberite-type phase, C2221, over the entire composition range. Enthalpies of formation from the oxides
m) via cation and anion disordering. Total scattering experiments with sensitivity to the cation and anion sublattices provide unique insight into the underlying atomic processes. Using simultaneous Rietveld refinement (long-range structure) and small-box refinement PDF analysis (short-range structure), we show that the series undergoes a rapid transformation from pyrochlore to defect fluorite at x ≈ 1.2, while the short-range structure exhibits a linear increase in a local weberite-type phase, C2221, over the entire composition range. Enthalpies of formation from the oxides 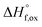 determined using high temperature oxide melt solution calorimetry support the structural data and provide insight into the effect of local ordering on the energetics of disorder. The measured enthalpies of mixing are negative and are fit by a regular solution parameter of W = −31.8 ± 3.7 kJ mol−1. However, the extensive short-range ordering determined from the structural analysis strongly suggests that the entropies of mixing must be far less positive than implied by the random mixing of a regular solution. We propose a local disordering scheme involving the pyrochlore 48f to 8a site oxygen Frenkel defect that creates 7-coordinated Zr sites contained within local weberite-type coherent nanodomains. Thus, the solid solution is best described as a mixture of two phases, with the weberite-type nanodomains triggering the long-range structural transformation to defect fluorite after accumulation above a critical concentration (50% Ti replaced by Zr).
determined using high temperature oxide melt solution calorimetry support the structural data and provide insight into the effect of local ordering on the energetics of disorder. The measured enthalpies of mixing are negative and are fit by a regular solution parameter of W = −31.8 ± 3.7 kJ mol−1. However, the extensive short-range ordering determined from the structural analysis strongly suggests that the entropies of mixing must be far less positive than implied by the random mixing of a regular solution. We propose a local disordering scheme involving the pyrochlore 48f to 8a site oxygen Frenkel defect that creates 7-coordinated Zr sites contained within local weberite-type coherent nanodomains. Thus, the solid solution is best described as a mixture of two phases, with the weberite-type nanodomains triggering the long-range structural transformation to defect fluorite after accumulation above a critical concentration (50% Ti replaced by Zr).
1. Introduction
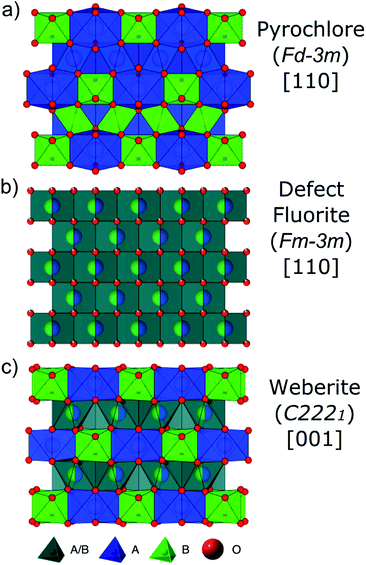
Defect formation, defect mobility, and associated disorder profoundly affect the physical properties of many materials and affect material performance in both ambient and extreme environments. As a result, there is a need for a better understanding of order–disorder transformations in these technologically important materials. Pyrochlore oxides with general formula A2B2O7 have exceptional chemical versatility and structural flexibility,1–6 as well as unique defect dynamics,6–12 that have made pyrochlore structures the center of investigation for a wide variety of energy related applications. Some pyrochlore compounds exhibit useful properties such as catalytic activity, piezoelectricity, ferro- and ferrimagnetism, luminescence, and giant magnetoresistance.1,4,13,14 The electronic properties of pyrochlores vary from being superconducting, metallic, or semiconducting to having a high ionic conductivity.4,13 Pyrochlore compositions are being developed for use as electrolytes in solid oxide fuel cells,9,15 thermal barrier coatings (TBCs) for high wear/high temperature components,16 oxygen gas sensors,17 and nuclear waste forms for the immobilization of Pu and other actinides.2,7,18–20The ideal fully ordered cubic pyrochlore structure (Fig. 1a) is given by the formula A2B2X6YZ with A and B being cations, X and Y anions, and Z a constitutional vacancy (Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m). Pyrochlore is a 2 × 2 × 2 superstructure of the fluorite unit cell AX2 (Fm
m). Pyrochlore is a 2 × 2 × 2 superstructure of the fluorite unit cell AX2 (Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) with two cation sites and three anion sites containing one-eighth fewer anions (M
m) with two cation sites and three anion sites containing one-eighth fewer anions (M![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) X ratio 4
X ratio 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 vs. 1
7 vs. 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2).21,22 The eight-coordinated A-site (16d) is occupied by the larger cation, often a trivalent rare earth element with ionic radius ∼1 Å,23 and the six-coordinated B-site (16c) by the smaller cation, usually a tetravalent 3d, 4d, or 5d transition metal or IVa group element with ionic radius ∼0.6 Å.23 Oxygen atoms occupy the X (48f) and Y (8b) sites with constitutional vacancies on the Z (8a) site. The presence of multiple cations with different valences drives the cations to order themselves in the structure. The coordination environments of the cations are AX6Y2 and BX6Z2, while the anions are each coordinated by four cations (XA2B2, YA4, and ZB4). This structure is highly symmetric, with the free parameters being the unit-cell parameter (a) and the 48f anion x-position (x48f).
2).21,22 The eight-coordinated A-site (16d) is occupied by the larger cation, often a trivalent rare earth element with ionic radius ∼1 Å,23 and the six-coordinated B-site (16c) by the smaller cation, usually a tetravalent 3d, 4d, or 5d transition metal or IVa group element with ionic radius ∼0.6 Å.23 Oxygen atoms occupy the X (48f) and Y (8b) sites with constitutional vacancies on the Z (8a) site. The presence of multiple cations with different valences drives the cations to order themselves in the structure. The coordination environments of the cations are AX6Y2 and BX6Z2, while the anions are each coordinated by four cations (XA2B2, YA4, and ZB4). This structure is highly symmetric, with the free parameters being the unit-cell parameter (a) and the 48f anion x-position (x48f).
The ordered pyrochlore structure (e.g., Ho2Ti2O7, Fig. 1a) is susceptible to disordering, which proceeds over the longer length scales by randomization of the cation and anion sublattices and results in a disordered, defect fluorite structure (e.g., Ho2Zr2O7, Fig. 1b).8 The A- and B-site coordination number (CN) changes from 8 and 6 in pyrochlore, respectively, to on average 7 for both. This order–disorder transformation can be induced by chemical substitution (achieved via synthesis/doping),24,25 temperature or pressure,10,24,26 or ion irradiation.26,27 Whether a pyrochlore composition disorders to defect fluorite, or not, has been shown to be predominantly controlled by the energetics of defect formation and disordering.7,28,29 The propensity for antisite defects (A and B cation exchange) to form is strongly correlated with the A and B cation radii ratio, rA/rB.1,3,7,12,19,30 If cation radii are similar (rA/rB < 1.46), formation of antisite defects is more energetically favorable and the disordered, defect fluorite atomic arrangement is preferred.
The effect of direct chemical substitution of the B-site cation on the pyrochlore-to-defect fluorite transformation has been studied extensively using a variety of solid solution series, such as Y2B2−xB′xO7 (B and B′ = Ti, Sn, or Zr, B ≠ B′) and Ho2Ti2−xZrxO7.9,15,24,25,31–36 These studies utilized X-ray and neutron diffraction to probe the long-range structure and used X-ray absorption spectroscopy to probe short-range effects, observing how disordering proceeds as a function of chemical composition. Probing the local structure of Y2B2−xZrxO7 (B = Ti or Sn) pyrochlore compounds using Raman and NMR spectroscopy confirms a gradual order–disorder transition from pyrochlore to defect fluorite with increasing Zr-content.33–35,37 Additional spectroscopic studies using Raman, magic-angle spinning nuclear magnetic resonance (MAS NMR), and X-ray absorption near-edge structure (XANES), supported by density functional theory (DFT) calculations, have revealed short- and intermediate range compositional and structural modulations that indicate retention of pyrochlore-like ordering well into the Zr-rich defect fluorite phase.38,39 Utilizing diffraction methods, Wuensch et al.9,15,24,32 and Shafique et al.36 reported that the Y2Sn2−xZrxO7, Y2Ti2−xZrxO7, and Ho2Ti2−xZrxO7 solid solution series disorder progressively with increasing Zr-content, with disorder on the cation and anion sublattices proceeding at different rates and seemingly independently. As Zr replaces Ti or Sn, oxygen anions from 48f sites, and later the 8b sites at higher fractions of Zr, begin to occupy the vacant 8a sites. The cation sublattice remains ordered until the Zr-content reaches more than 50% (x = 1.0), at which point the exchange of A and B site cations occurs much more efficiently. The differences in disordering behavior on each sublattice is even larger for Y2Sn2−xZrxO7, with only 31% of Sn occupying the A-site at x = 1.6 while the anions are nearly fully disordered. In both the Y2Ti2−xZrxO7 and Y2Sn2−xZrxO7 systems, the anion sublattice disorders before the cation sublattice, and the complete transition to defect fluorite is not attained until the Zr-content is substantial (x > 1.6).
Studies of disordered pyrochlores over the past two decades suggest that the short-range structure is more ordered than is implied by the observable long-range defect fluorite structure.25,31,35,40,41 Recent studies using neutron total scattering experiments with pair distribution function (PDF) analysis of disordered pyrochlore (e.g., Ho2Zr2O7) have uncovered that the local atomic arrangement of the defect fluorite phase is actually described by a partially ordered orthorhombic phase,42 the structure of which can be described by a weberite-type (C2221) structural model that is isostructural to Y3TaO7.42–47 The weberite-type structure is another derivative of the fluorite structure with a 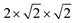 superstructure that contains a higher degree of ordered arrangements of different valence cations and ordered anion vacancies as compared with defect fluorite but is distinct from pyrochlore (Fig. 1c). In a weberite-type structure, the cation sublattice is split unequally into three cation sublattices, with the trivalent cation occupying the eight-coordinated 4b sites, the tetravalent cation occupying the six-coordinated 4b sites, and both cations occupying the seven-coordinated 8c sites randomly. The anions are distributed onto two sets of 8c sites and three sets of 4c sites, with constitutional vacancies on additional 4c sites. The general formula for weberite can be written as ABC2X4Y2Z. Compounds that exhibit the long-range weberite structure display a pronounced chemical selectivity. A recent computational study by Solomon et al. shows that low-energy, long-range weberite-type configurations are favored at low values of the ionic radius ratio of A- and B-site cations rA/rB.48 Random averaging of weberite-type local configurations leads to a long-range disordered, defect fluorite structure when averaged over many unit cells.44,46 Heterogeneous disordering processes with different short- and long-range structural motifs have been similarly observed for other ceramics, such as spinel,49 and different disordering processes through intrinsic (nonstoichiometry and chemical composition15,50) and extrinsic (ball milling and irradiation43,51) means. This behavior is consistent with Pauling's rules which have been shown to dictate the local atomic arrangements in disordered ceramics.46
superstructure that contains a higher degree of ordered arrangements of different valence cations and ordered anion vacancies as compared with defect fluorite but is distinct from pyrochlore (Fig. 1c). In a weberite-type structure, the cation sublattice is split unequally into three cation sublattices, with the trivalent cation occupying the eight-coordinated 4b sites, the tetravalent cation occupying the six-coordinated 4b sites, and both cations occupying the seven-coordinated 8c sites randomly. The anions are distributed onto two sets of 8c sites and three sets of 4c sites, with constitutional vacancies on additional 4c sites. The general formula for weberite can be written as ABC2X4Y2Z. Compounds that exhibit the long-range weberite structure display a pronounced chemical selectivity. A recent computational study by Solomon et al. shows that low-energy, long-range weberite-type configurations are favored at low values of the ionic radius ratio of A- and B-site cations rA/rB.48 Random averaging of weberite-type local configurations leads to a long-range disordered, defect fluorite structure when averaged over many unit cells.44,46 Heterogeneous disordering processes with different short- and long-range structural motifs have been similarly observed for other ceramics, such as spinel,49 and different disordering processes through intrinsic (nonstoichiometry and chemical composition15,50) and extrinsic (ball milling and irradiation43,51) means. This behavior is consistent with Pauling's rules which have been shown to dictate the local atomic arrangements in disordered ceramics.46
In addition to structural and computational evidence of short-range ordering in disordered pyrochlore, thermodynamic data obtained by Navrotsky and coworkers using high temperature oxide melt solution calorimetry suggests the occurrence of short-range ordering in disordered pyrochlore,40,41 the fluorite related ZrO2–RE2O3, HfO2–RE2O3, and CeO2–RE2O3 (RE = rare earth) solid solutions,52–57 and recently in the zircon Th1−xUxSiO4 solid solution.58 The finding of weberite-type short-range ordering in nominally disordered pyrochlores by Shamblin et al.42 has led to many thermodynamic studies aimed at understanding the mechanism and energetics of order–disorder transitions in pyrochlores, weberites, and other compounds with fluorite-derived structures.52,59–62
While the local atomic arrangement and long-range structure in fully disordered complex oxides has been studied in detail, little information is available on the behavior at both length scales in partially disordered materials. In this study, neutron and X-ray total scattering experiments were performed on nine members of the solid solution series Ho2Ti2−xZrxO7 (0 ≤ x ≤ 2.0) to comprehensively characterize the chemically induced order–disorder transformation across both short and long length scales. Analysis of the PDFs and structure functions provides insight into the role that specific local defects (and associated correlated disorder) play in the long-range order–disorder transformation. The scattering experiments were complemented by oxide melt solution calorimetry to determine enthalpies of formation (ΔHf) and mixing (ΔHmix) of the solid solution series. Both structural and thermodynamic results provide strong evidence for a complex short-range ordering scheme that drives the long-range behavior observable by conventional diffraction analysis.
2. Methods
2.1 Sample synthesis
Polycrystalline samples of Ho2Ti2−xZrxO7 (x = 0.0, 0.25, 0.5, 0.75, 1.0, 1.25, 1.5, 1.75, and 2.0) were synthesized using standard solid-state techniques. High purity reagent oxides (TiO2, ZrO2 and Ho2O3) were purchased from Sigma-Aldrich and mixed via the following solid-state reaction:| (2 − x)TiO2 + xZrO2 + Ho2O3 → Ho2Ti2−xZrxO7 | (1) |
The powders were mixed thoroughly in an agate mortar and were uniaxially pressed into pellets in a hydraulic press with a pressure of 315 MPa, resulting in pellets 1 cm in diameter and approximately 2–3 mm thick. The pellets were subsequently fired in air at 1500 °C for 72 hours, with intermediate grinding and pressing every 12 hours. The pellets were allowed to cool at the natural cooling rate of the furnace following each firing cycle. After the final firing/cooling cycle, the pellets were hand-ground into a fine powder for use in neutron and X-ray total scattering experiments. The resulting powders were all a light pink-orange color, darkening very slightly with increasing x.
2.2 Neutron and X-ray total scattering measurements
Neutron total scattering measurements were performed at the Nanoscale Ordered Materials Diffractometer (NOMAD) beamline at the Spallation Neutron Source (SNS),63 located at Oak Ridge National Laboratory (ORNL). NOMAD's high intensity neutron beam combined with a large accessible momentum transfer range and good momentum transfer resolution make it ideal for the study of disordered, low-mass samples. Approximately 200 mg of each composition were loaded into quartz capillaries with diameters of 2 mm and wall thicknesses of 0.01 mm. Measurements of diamond and silicon powders were used to calibrate NOMAD's time-of-flight detector banks and to determine instrument parameters for use in structural refinement software. NOMAD's detection system consists of six banks of over 300 3He linear position sensitive detectors that can routinely reach maximum momentum transfer values of 50 Å−1 and greater. Each sample and an empty quartz capillary were measured for approximately 60 minutes at room temperature. The total scattering structure functions, S(Q), were produced by combining diffraction data from all six banks and after background subtraction (from the empty quartz capillary) and normalization of the sample scattering intensity to the scattering intensity from a solid vanadium rod. The pair distribution functions, G(r), were obtained through the Fourier transform of S(Q) with Qmin = 0.2 Å−1 and Qmax = 31.4 Å−1:
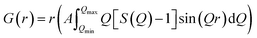 | (2) |
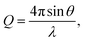 | (3) |
X-ray total scattering characterization was performed at the 28-ID-2 (XPD) beamline at the National Synchrotron Light Source-II (NSLS-II)65,66 at Brookhaven National Laboratory (BNL). All nine series members' powders were placed in Kapton tube capillaries with an outer diameter of 1.11 mm and a wall thickness of 50.8 μm which serve as sample containers. The capillaries were filled to a height of 3.0 cm with sample powder and sealed with approximately 0.5 cm long polymer stoppers inserted into both ends. Measurements of a LaB6 660a standard powder were used for the calibration of XPD's 2D detector and to determine the instrument parameters for use in structural refinement software. All measurements were performed at room temperature with an exposure time of 10 seconds per sample and photon wavelength of 0.18754 Å (∼66.1 keV). An empty Kapton tube as well as a LaB6 standard were measured to correctly subtract the capillary's scattering contribution as background and properly scale each sample's scattering intensity. The X-ray scattering from each sample was recorded as 2D diffractograms gathered using a PerkinElmer XRD 1621 digital imaging detector with an active area of 16′′ × 16′′ and resolution of 2048 × 2048 pixels which in XPD's detector setup can collect reasonably good quality data up to maximum momentum transfer values of 27.0 Å−1. Resulting 2D diffraction images were transformed into structure functions S(Q), with the scattering vector Q varying from Qmin = 0.5 Å−1 to Qmax = 25.0 Å−1. Pair distribution functions, G(r), were obtained through eqn (2) using the software PDFgetX3.67 Unlike the neutron PDFs, no Lorch function was applied to the X-ray PDFs as the first few peaks, where truncation ripples are most prominent, were not used in the small-box refinements of these PDFs.
2.3 Structure data analysis
The long-range structure Rietveld refinements of neutron and X-ray data were performed using the GSAS-II software package.68 Structural refinement of the measured Ho2Ti2−xZrxO7 samples were performed using the Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m and/or Fm
m and/or Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group (Table 1), depending on which space group fit the diffraction pattern best. For the Fd
m space group (Table 1), depending on which space group fit the diffraction pattern best. For the Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m structural model, the unit cell parameter aP and the 48f anion x-position x48f were refined. All three oxygen sites (48f, 8b, and 8a) occupancies ni were refined. To maintain oxygen balance among the three sites, the occupancies were constrained using the following relation:
m structural model, the unit cell parameter aP and the 48f anion x-position x48f were refined. All three oxygen sites (48f, 8b, and 8a) occupancies ni were refined. To maintain oxygen balance among the three sites, the occupancies were constrained using the following relation:| 48n48f + 8n8b + 8n8a = 56 | (4) |
| Wyckoff equipoint (CN) | Occupancy | x | y | z |
|---|---|---|---|---|
| a Free parameters are in bold. | ||||
Fd![[3 with combining macron]](https://www.rsc.org/images/entities/b_char_0033_0304.gif) m (pyrochlore, space group no. 227) m (pyrochlore, space group no. 227) |
||||
| 16d (8) | Ho | 0.5 | 0.5 | 0.5 |
| 16c (6) | Ti1−x/2Zrx/2 | 0 | 0 | 0 |
| 48f | O(1−i)/6 | 0.3317 | 0.125 | 0.125 |
| 8b | O′ | 0.375 | 0.375 | 0.375 |
| 8a | Oi | 0.125 | 0.125 | 0.125 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
Fm![[3 with combining macron]](https://www.rsc.org/images/entities/b_char_0033_0304.gif) m (defect fluorite, space group no. 225) m (defect fluorite, space group no. 225) |
||||
| 4a (7) | Ho0.5Tix/4Zr1−x/4 | 0 | 0 | 0 |
| 8c | O0.875 | 0.25 | 0.25 | 0.25 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| C2221 (weberite, space group no. 20) | ||||
| 4b (8) | Ho | 0 | 0.4956 | 0.25 |
| 8c (7) | Ho1/2Zr1/2 | 0.2360 | 0.2374 | 0 |
| 4b (6) | Zr | 0 | 0 | 0.25 |
| 8c | O | 0.139 | 0.181 | 0.304 |
| 8c | O | 0.121 | 0.770 | 0.267 |
| 4a | O | 0.131 | 0.5 | 0 |
| 4a | O | 0.131 | 0.5 | 0.5 |
| 4a | O | 0.072 | 0 | 0 |
This accounts for oxygen anions shifting from the occupied 48f and 8b sites to the vacant 8a site. The isotropic thermal parameters for the 8b and 8a oxygen sites were refined to be equal (u8b = u8a). The cation sublattice was constrained to have fully occupied sites. For the Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m structural model, the unit cell parameter, aDF, was refined. The distribution of the three atomic species (Ho, Ti, Zr) over the two crystallographically distinct A- and B-sites in Fd
m structural model, the unit cell parameter, aDF, was refined. The distribution of the three atomic species (Ho, Ti, Zr) over the two crystallographically distinct A- and B-sites in Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m cannot be uniquely determined from diffraction experiments alone; rather, it is only possible to determine the average scattering lengths of each site with the added limitation of reasonable isotropic thermal parameters, with the highest thermal parameter refined for all fits being approximately 0.04 for the 8c oxygen site. This is further complicated by the somewhat similar neutron scattering lengths of Ho and Zr (Table 2). Therefore, it was assumed for the pyrochlore fits that Ho fully occupies the A-site and not the B-site and vice versa for Ti and Zr, though Ti and Zr occupancies on the B-site were allowed to vary with changing Zr-content to match the stoichiometry of each sample. For both space group refinements, the isotropic thermal parameters were refined independently, with the exception of the 8b and 8a sites in the Fd
m cannot be uniquely determined from diffraction experiments alone; rather, it is only possible to determine the average scattering lengths of each site with the added limitation of reasonable isotropic thermal parameters, with the highest thermal parameter refined for all fits being approximately 0.04 for the 8c oxygen site. This is further complicated by the somewhat similar neutron scattering lengths of Ho and Zr (Table 2). Therefore, it was assumed for the pyrochlore fits that Ho fully occupies the A-site and not the B-site and vice versa for Ti and Zr, though Ti and Zr occupancies on the B-site were allowed to vary with changing Zr-content to match the stoichiometry of each sample. For both space group refinements, the isotropic thermal parameters were refined independently, with the exception of the 8b and 8a sites in the Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m refinements. The background was fitted using a shifted, 16-term Chebyshev polynomial.
m refinements. The background was fitted using a shifted, 16-term Chebyshev polynomial.
| Element/ion | Ionic radius (Å)23 | Neutron scattering length (bni) (fm)69 | X-ray scattering length (bxi = ref1)a,b (fm)70 |
|---|---|---|---|
| a Classical electron radius re; real part of the atomic scattering factor f1.b X-ray energy of 66.1 keV. | |||
| Ho3+ | 0.901 (VI) | 8.01 | 187.8 |
| 1.015 (VIII) | |||
| Zr4+ | 0.72 (VI) | 7.16 | 112.9 |
| 0.78 (VII) | |||
| 0.84 (VIII) | |||
| Ti4+ | 0.605 (VI) | −3.44 | 62.2 |
| 0.74 (VIII) | |||
| O2− | 1.38 (IV) | 5.80 | 22.6 |
In GSAS-II, a “background” can be defined to be subtracted from diffraction patterns. Normally diffuse scattering is discarded with this background. However, the diffuse scattering changes with composition and provides additional information on the short- and medium-range behaviors beyond the PDF analysis. To subtract the background associated with the measurement and retain the diffuse scattering from the sample, the fully ordered pyrochlore Ho2Ti2O7 endmember was assumed to have no diffuse scattering. The refined background polynomial for this composition was then used as universal background associated with the measurement (with slight modifications to account for peak position shifts for the different chemical compositions). Rietveld refinement was then repeated with the previously determined structural models but with the new background polynomial. The subsequent increase in the goodness-of-fit (Rw) parameter was then used as a measure of the impact that diffuse scattering has on the quality of the fit.
Local structure characterizations were obtained from small-box refinements of the PDFs using the software package PDFgui.71 The small-box refinements were performed using: (i) the cubic Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m structure, (ii) the orthorhombic weberite C2221 structure, and (iii) a local two-phase mixed structural model consisting of (i) and (ii).
m structure, (ii) the orthorhombic weberite C2221 structure, and (iii) a local two-phase mixed structural model consisting of (i) and (ii).
Nine parameters were refined for the fully ordered pyrochlore endmember, Ho2Ti2O7, with cubic Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m symmetry: the unit cell parameter (a = b = c), the scale factor, the linear correlated motion factor, atomic displacement parameters (ADPs) for the 16c, 16d, and 8b sites (u11 = u22 = u33), the x-position for the 48f site, and the ADPs for the 48f site (u11 ≠ u22 = u33). The anisotropic ADPs for the 16c and 16d sites (u12 = u23 = u13) and the 48f site (u23 ≠ 0) were fixed. Thirty-three parameters were refined for the fully disordered endmember, Ho2Zr2O7, with orthorhombic C2221 symmetry (weberite-type): the unit cell parameters (a ≠ b ≠ c), the scale factor, the linear correlated motion factor, the ADPs for the two 4b sites (u11 = u22 = u33), the ADPs for the three 8c sites and three 4a sites (u11 ≠ u22 ≠ u33), the y-positions for the two 4b sites, the x-, y-, and z-positions for the three 8c sites, and the x-positions for the three 4a sites. It is more correct to model the system as harmonic (refining u12, u23, u13 where appropriate), but this was forgone in favor of a more isotropic treatment of the ADPs to simplify the model and improve convergence of the calculations. The two-phase model used for the intermediate compositions retained the same parameters listed for the two endmember models, but with the addition of a weberite-type phase fraction parameter, totaling 49 parameters. All refinements resulted in no highly correlated parameters.
m symmetry: the unit cell parameter (a = b = c), the scale factor, the linear correlated motion factor, atomic displacement parameters (ADPs) for the 16c, 16d, and 8b sites (u11 = u22 = u33), the x-position for the 48f site, and the ADPs for the 48f site (u11 ≠ u22 = u33). The anisotropic ADPs for the 16c and 16d sites (u12 = u23 = u13) and the 48f site (u23 ≠ 0) were fixed. Thirty-three parameters were refined for the fully disordered endmember, Ho2Zr2O7, with orthorhombic C2221 symmetry (weberite-type): the unit cell parameters (a ≠ b ≠ c), the scale factor, the linear correlated motion factor, the ADPs for the two 4b sites (u11 = u22 = u33), the ADPs for the three 8c sites and three 4a sites (u11 ≠ u22 ≠ u33), the y-positions for the two 4b sites, the x-, y-, and z-positions for the three 8c sites, and the x-positions for the three 4a sites. It is more correct to model the system as harmonic (refining u12, u23, u13 where appropriate), but this was forgone in favor of a more isotropic treatment of the ADPs to simplify the model and improve convergence of the calculations. The two-phase model used for the intermediate compositions retained the same parameters listed for the two endmember models, but with the addition of a weberite-type phase fraction parameter, totaling 49 parameters. All refinements resulted in no highly correlated parameters.
To study the Rwp values of the Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m and Fm
m and Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m models to the local structure, PDF “boxcar” refinements were performed. PDF small-box refinements were carried out in the 1.7–11.7 Å r-range using the structural parameters found during Rietveld refinement as the initial parameters. Once the Rwp for that range was obtained, successive 10 Å refinements were repeated in progressively higher r-space, with the final values of each refinement becoming the initial parameters of the next fitting, like train “boxcars”. The goodness of fit in PDFgui is defined as
m models to the local structure, PDF “boxcar” refinements were performed. PDF small-box refinements were carried out in the 1.7–11.7 Å r-range using the structural parameters found during Rietveld refinement as the initial parameters. Once the Rwp for that range was obtained, successive 10 Å refinements were repeated in progressively higher r-space, with the final values of each refinement becoming the initial parameters of the next fitting, like train “boxcars”. The goodness of fit in PDFgui is defined as
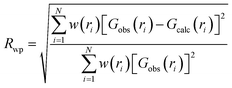 | (5) |
An approach developed by Neder et al. allows for the modelling of the diffuse scattering observed in the structure functions, S(Q), by including the contributions of coherent nanodomains to the scattering.74 This approach splits the overall diffracted intensity into the sum of two contributions: (i) a long-range average structure, where the atoms have weighted occupancies from averaging all nanodomain variants, and (ii) a “difference” structure, where the atom occupancies and positions account for the difference between the nanodomain ordered structure and the long-range configurational average. A Scherrer-type finite size broadening was used to describe the broadening produced by the finite correlation length of the nanodomain structure and the spatial average extension of the correlation giving rise to diffuse scattering. The Rietveld software GSAS-II was used to implement this approach and scattering data gathered with NOMAD detector bank 2 was chosen for fitting to best capture both the Bragg and the diffuse scattering.
2.4 High temperature oxide melt solution calorimetry
High temperature calorimetry was performed using a Tian Calvet twin-calorimeter AlexSYS (Setaram, Cailure, France) to determine the enthalpies of formation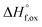 of all nine members of the Ho2Ti2−xZrxO7 solid solution series. The solvent used was sodium molybdate (3Na2O·4MoO3) prepared according to ref. 75 using MoO3 (Fisher, 99.5% purity) and Na2MoO4·2H2O (Emdmillipore, 99.5% purity) as reagents. The calorimeter was calibrated against the heat content of 5 mg pellets of α-Al2O3.76 Sample powders were preheated to 800 °C for 8 hours to remove potential residue water, pressed into 5–8 mg pellets, and dropped at room temperature into a platinum crucible containing 20 g of molten solvent at 800 °C. A constant flow rate of O2 was flushed over the solvent at 90 ml min−1 to create a stable environment above the solvent and bubbled through it at 5 ml min−1 to ensure an oxidative environment.76 The enthalpy of drop solution, ΔHds, which is the measured heat effect of dropping a room temperature pellet into the solvent and is the sum of the heat content of the sample and the heat released during its dissolution, was calculated by integrating the heat flow curve using CALISTO software provided by Setaram. This procedure and methodology have been used extensively on other similar materials and described in detail previously.76–79 The thermochemical cycle used for the calculation of the enthalpies of formation,
of all nine members of the Ho2Ti2−xZrxO7 solid solution series. The solvent used was sodium molybdate (3Na2O·4MoO3) prepared according to ref. 75 using MoO3 (Fisher, 99.5% purity) and Na2MoO4·2H2O (Emdmillipore, 99.5% purity) as reagents. The calorimeter was calibrated against the heat content of 5 mg pellets of α-Al2O3.76 Sample powders were preheated to 800 °C for 8 hours to remove potential residue water, pressed into 5–8 mg pellets, and dropped at room temperature into a platinum crucible containing 20 g of molten solvent at 800 °C. A constant flow rate of O2 was flushed over the solvent at 90 ml min−1 to create a stable environment above the solvent and bubbled through it at 5 ml min−1 to ensure an oxidative environment.76 The enthalpy of drop solution, ΔHds, which is the measured heat effect of dropping a room temperature pellet into the solvent and is the sum of the heat content of the sample and the heat released during its dissolution, was calculated by integrating the heat flow curve using CALISTO software provided by Setaram. This procedure and methodology have been used extensively on other similar materials and described in detail previously.76–79 The thermochemical cycle used for the calculation of the enthalpies of formation, 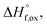 from ΔHds are summarized in Table 3. The needed ΔHds values for Ho2O3 and TiO2 were acquired from literature ref. 76 and 80, respectively, and that of ZrO2 was measured in this study. Up to 8 drops were performed for each sample to reduce the uncertainty in the measurement.
from ΔHds are summarized in Table 3. The needed ΔHds values for Ho2O3 and TiO2 were acquired from literature ref. 76 and 80, respectively, and that of ZrO2 was measured in this study. Up to 8 drops were performed for each sample to reduce the uncertainty in the measurement.
| Reaction | ΔH (kJ mol−1) | |
|---|---|---|
| a Ref. 76.b Ref. 80.c Measured as part of this work, s = solid, sln = solution, ds = drop solution, f,ox = formation from oxides, 25 = 25 °C, and 800 = 800 °C. | ||
| Ho2Ti2−xZrxO7(s,25) → Ho2O3(sln,800) + (2 − x)TiO2(sln,800) + xZrO2(sln,800) | {1} ΔHds – Ho2Ti2−xZrxO7 | Table 7 |
| Ho2O3(s,25) → Ho2O3(sln,800) | {2} ΔHds – Ho2O3 | −109.4 ± 1.8a |
| TiO2(s,25) → TiO2(sln,800) | {3} ΔHds – TiO2 | 73.4 ± 0.4b |
| ZrO2(s,25) → ZrO2(sln,800) | {4} ΔHds – ZrO2 | 29.2 ± 1.6c |
| Ho2O3(s,25)+(2 − x)TiO2(s,25) + xZrO2(s,25) → Ho2Ti2−xZrxO7(s,25) | {5} 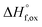 – Ho2Ti2−xZrxO7 – Ho2Ti2−xZrxO7 |
Table 7 |
| ΔH{5} = −ΔH{1} + ΔH{2} + (2 − x)ΔH{3} + xΔH{4} | ||
3. Results
3.1 Long-range structure – neutron and X-ray reciprocal space analysis
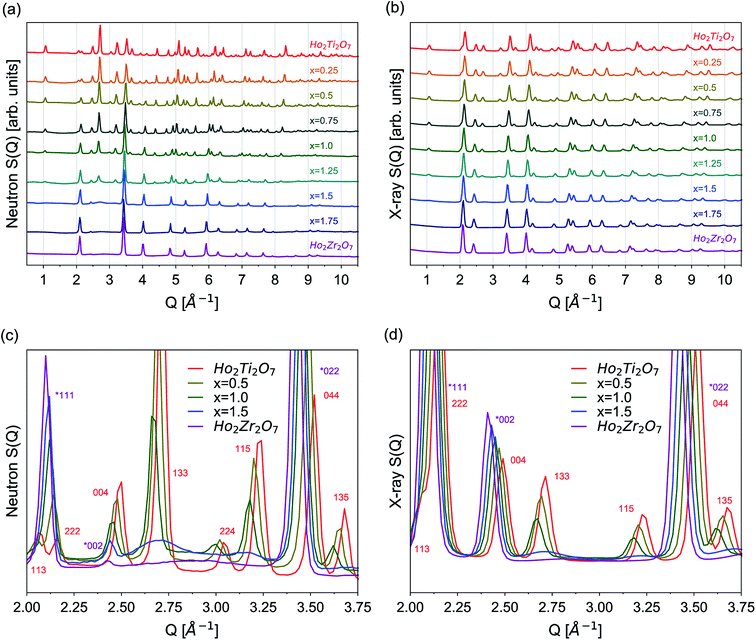
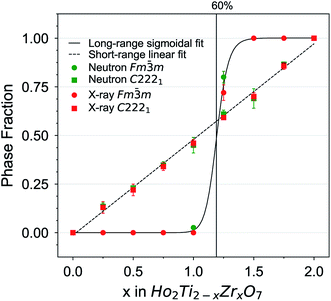
The as-collected neutron and X-ray structure functions for all Ho2Ti2−xZrxO7 compositions are shown in Fig. 2. The structure functions indicate that the samples are well-crystallized, and no detectable peaks associated with impurities are present. A gradual shift in common Bragg peaks to lower Q marks the expansion of the unit cell with increasing Zr-content, x. Disorder of the cation and anion sublattices across the series is observed as distinct changes in the relative intensities of various Bragg peaks. Disordering of the cation sublattice results in pyrochlore superstructure diffraction peaks with odd Miller indices to have reduced intensities across the entire Q-range (e.g., (111), (113), (133), (115), and (135)). Conversely, most pyrochlore diffraction peaks with even Miller indices exhibit marked increases in intensities (e.g., (222) and (044)). The disappearance of most superstructure peaks is consistently observed in the neutron and X-ray diffraction patterns between x = 1.25 and 1.5, indicating the total conversion from ordered pyrochlore to disordered, defect fluorite. This behavior is in agreement with previous diffraction studies on the Ho2Ti2−xZxO7 and Y2B2−xZrxO7 (B = Ti or Sn) solid solution series.15,25,35,36 Disordering of the anion sublattice is complex and is more effectively observed using neutrons, as neutron total scattering is sensitive to the oxygen sublattice. Neutron scattering lengths, unlike X-ray scattering lengths, are independent of the number of electrons around the ion, making some diffraction peaks associated to the oxygen sublattice highly visible to neutrons, e.g., (224) in Fig. 2c and d. In some cases, neutrons are also able to discern the different species of cations better than X-rays (e.g., Zr and Ti) (Table 2).Rietveld refinements were performed on all neutron and X-ray diffraction patterns using the pyrochlore (Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) and/or defect fluorite (Fm
m) and/or defect fluorite (Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) structural models described in Table 1. Refinements of the endmembers yielded structural parameters that are in agreement with previous neutron scattering studies,36,42 with the long-range structure of Ho2Ti2O7 being best described as an ordered pyrochlore structure and Ho2Zr2O7 by a fully disordered, defect fluorite structure. For the intermediate compositions, the pyrochlore structure best fit the diffraction patterns for the compositions x = 0.25, 0.5, and 0.75, while the disordered, defect fluorite was the best fit for the compositions x = 1.5, 1.75, and 2.0. Both phases were found to coexist at x = 1.25 in both neutron and X-ray patterns and at x = 1.0 in the neutron pattern. The values obtained from refinements of all intermediate series members, including the defect fluorite Fm
m) structural models described in Table 1. Refinements of the endmembers yielded structural parameters that are in agreement with previous neutron scattering studies,36,42 with the long-range structure of Ho2Ti2O7 being best described as an ordered pyrochlore structure and Ho2Zr2O7 by a fully disordered, defect fluorite structure. For the intermediate compositions, the pyrochlore structure best fit the diffraction patterns for the compositions x = 0.25, 0.5, and 0.75, while the disordered, defect fluorite was the best fit for the compositions x = 1.5, 1.75, and 2.0. Both phases were found to coexist at x = 1.25 in both neutron and X-ray patterns and at x = 1.0 in the neutron pattern. The values obtained from refinements of all intermediate series members, including the defect fluorite Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phase fraction, unit cell parameters, a, for both structures, refined 48f x-position parameter x48f, 8a oxygen occupancy of the pyrochlore structure n8a, and Rw values for each refinement, are summarized in Table 4. These parameters were found to agree acceptably with those of a previous neutron diffraction study.36 A defect pyrochlore unit cell, where the 48f and 8b oxygens are allowed to shift and occupy the vacant 8a site, was found to best fit the diffraction patterns for the compositions x = 0.25, 0.5, 0.75, and 1.0. The x48f and n8a parameters increase across this range, a trend that is qualitatively similar to the behavior previously reported for the disordering processes in Ho2Ti2−xZxO7 and Y2B2−xZrxO7 (B = Ti or Sn) solid solution series.15,25,35,36 The x48f parameter increases for x values up to 1.25 by 3.2% and 4.3% in the neutron and X-ray refinements, respectively. The parameter n8a increases for x values up to 1.0 from 0 to 0.20 (neutrons) and from 0 to 0.28 (X-rays), which corresponds to 0, 1.6, and 2.24 out of 8 oxygen anions on the 8a site. Upon extensive formation of the defect fluorite structure at x = 1.25, the n8a parameter drastically decreases to 0.09 (neutrons) and 0 (X-rays), corresponding to 0.72 oxygen anions. The 8b site remains fully occupied at all pyrochlore-containing compositions. For the mixed-phase compositions, the Ti and Zr occupancy levels in the defect fluorite phase were allowed to vary under the constraint of fully occupied cation sites. The refined defect fluorite phase was found to contain primarily Zr, with the Ti content increasing from 0% at x = 1.0, to approximately 7% at x = 1.25, to stoichiometric values at x = 1.5 where the pyrochlore phase was no longer evident in the structure functions and part of the structural refinement.
m phase fraction, unit cell parameters, a, for both structures, refined 48f x-position parameter x48f, 8a oxygen occupancy of the pyrochlore structure n8a, and Rw values for each refinement, are summarized in Table 4. These parameters were found to agree acceptably with those of a previous neutron diffraction study.36 A defect pyrochlore unit cell, where the 48f and 8b oxygens are allowed to shift and occupy the vacant 8a site, was found to best fit the diffraction patterns for the compositions x = 0.25, 0.5, 0.75, and 1.0. The x48f and n8a parameters increase across this range, a trend that is qualitatively similar to the behavior previously reported for the disordering processes in Ho2Ti2−xZxO7 and Y2B2−xZrxO7 (B = Ti or Sn) solid solution series.15,25,35,36 The x48f parameter increases for x values up to 1.25 by 3.2% and 4.3% in the neutron and X-ray refinements, respectively. The parameter n8a increases for x values up to 1.0 from 0 to 0.20 (neutrons) and from 0 to 0.28 (X-rays), which corresponds to 0, 1.6, and 2.24 out of 8 oxygen anions on the 8a site. Upon extensive formation of the defect fluorite structure at x = 1.25, the n8a parameter drastically decreases to 0.09 (neutrons) and 0 (X-rays), corresponding to 0.72 oxygen anions. The 8b site remains fully occupied at all pyrochlore-containing compositions. For the mixed-phase compositions, the Ti and Zr occupancy levels in the defect fluorite phase were allowed to vary under the constraint of fully occupied cation sites. The refined defect fluorite phase was found to contain primarily Zr, with the Ti content increasing from 0% at x = 1.0, to approximately 7% at x = 1.25, to stoichiometric values at x = 1.5 where the pyrochlore phase was no longer evident in the structure functions and part of the structural refinement.
| Neutron Rietveld refinement (fit range Q = 3.3–14.2 Å−1) | |||||||
|---|---|---|---|---|---|---|---|
| Composition | Structure | Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m fraction, f m fraction, f |
a [Å] | x48f | n8a | Rw (%) −DSd | Rw (%) +DSd |
a Equivalent x48f in Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m is 0.375.b Equivalent n8a in Fm m is 0.375.b Equivalent n8a in Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m is 0.875.c Two measurements were taken yielding a values 0.3% of each other.d Denotes whether the diffuse scattering was discarded with the background (−DS) or included in the refinement (+DS). m is 0.875.c Two measurements were taken yielding a values 0.3% of each other.d Denotes whether the diffuse scattering was discarded with the background (−DS) or included in the refinement (+DS). |
|||||||
| Ho2Ti2O7 | Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
0 | 10.1013(2) | 0.3289(1) | 0 | 5.81 | 5.81 |
| Ho2Ti1.75Zr0.25O7 | Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
0 | 10.1469(2) | 0.3300(1) | 0.03(1) | 6.03 | 6.16 |
| Ho2Ti1.50Zr0.50O7 | Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
0 | 10.1871(3) | 0.3324(2) | 0.10(1) | 5.57 | 5.73 |
| Ho2Ti1.25Zr0.75O7 | Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
0 | 10.2300(2) | 0.3348(2) | 0.12(1) | 5.74 | 5.96 |
| Ho2Ti1.00Zr1.00O7 | Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m + Fm m + Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
0.026(2) | 10.2725(4) | 0.3395(3) | 0.20(6) | 5.00 | 5.24 |
| 5.160(7) | 0.375a | 0.875b | |||||
| Ho2Ti0.75Zr1.25O7 | Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m + Fm m + Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
0.80(3) | 10.284(1) | 0.3380(5) | 0.09(4) | 5.55 | 6.43 |
| 5.1593(3) | 0.375a | 0.875b | |||||
| Ho2Ti0.50Zr1.50O7 | Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
1 | 5.1633(2) | 0.375a | 0.875b | 7.20 | 9.10 |
| Ho2Ti0.25Zr1.75O7 | Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
1 | 5.1922(1) | 0.375a | 0.875b | 7.31 | 11.92 |
| Ho2Zr2O7 | Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
1 | 5.2289(3)c | 0.375a | 0.875b | 7.98 | 9.62 |
| X-ray Rietveld refinement (fit range Q = 0.8–25 Å−1) | |||||||
|---|---|---|---|---|---|---|---|
| Composition | Structure | Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m fraction, f m fraction, f |
a0 [Å] | x48f | 8a site fraction | Rw (%) | |
| Ho2Ti2O7 | Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
0 | 10.1024(4) | 0.330(1) | 0 | 1.76 | |
| Ho2Ti1.75Zr0.25O7 | Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
0 | 10.1422(3) | 0.334(1) | 0 | 1.20 | |
| Ho2Ti1.50Zr0.50O7 | Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
0 | 10.1857(4) | 0.339(1) | 0.06(7) | 1.40 | |
| Ho2Ti1.25Zr0.75O7 | Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
0 | 10.2266(5) | 0.340(2) | 0.12(7) | 1.57 | |
| Ho2Ti1.00Zr1.00O7 | Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
0 | 10.2741(6) | 0.341(2) | 0.28(9) | 1.68 | |
| Ho2Ti0.75Zr1.25O7 | Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m + Fm m + Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
0.73(4) | 10.273(2) | 0.345(3) | 0 | 1.75 | |
| 5.1588(6) | 0.375a | 0.875b | |||||
| Ho2Ti0.50Zr1.50O7 | Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
1 | 5.1703(4) | 0.375a | 0.875b | 2.48 | |
| Ho2Ti0.25Zr1.75O7 | Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
1 | 5.1918(3) | 0.375a | 0.875b | 2.07 | |
| Ho2Zr2O7 | Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
1 | 5.2104(4) | 0.375a | 0.875b | 2.38 | |
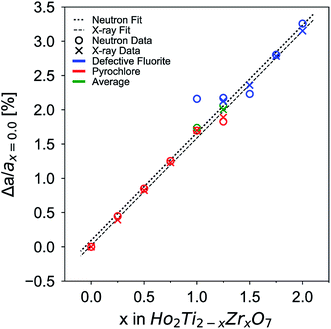
The change in unit cell parameter with respect to the pyrochlore endmember Ho2Ti2O7 Δa/ax=0 (a = aP and 2aDF) across the series exhibits a linear increase with increasing Zr-content, x, that resembles a trend following Vegard's law,81 as expected from substituting the larger Zr cation for Ti (Fig. 3). There is a slight change in the slope of the unit cell parameters upon the phase change from pyrochlore to defect fluorite that deviates from Vegard's law. This behavior has been observed in other pyrochlore to defect fluorite solid solution series.36,50,82 Linear fits through the neutron and X-ray data points reveal oversized defect fluorite and undersized pyrochlore unit cell parameters for the two-phase compositions at x = 1.0 and 1.25. When these two points are averaged using their corresponding phase fractions, the resulting unit cell parameters lie very close to the linear fits. The sample composition x = 1.5 has a slightly undersized unit cell parameter based on the neutron data, which may indicate the continued existence of a small amount of the pyrochlore phase beyond x = 1.25 or a small deviation from the x value.
Diffuse scattering is observed in the structure functions as background beneath and between the Bragg peaks, which is a result of short-range deviations from the long-range structure (Fig. 2c and d).83 Increasing the Zr-content gradually to x = 1.0 increases the background baseline of the structure functions, and broad, low intensity peaks are apparent for larger x values. This is particularly evident for the x = 1.5 composition as two broad peaks are observed between Q = 2.5 and 2.9 Å−1 and between Q = 3.0 and 3.3 Å−1, approximately underneath the (133) and (115) peaks. The positions of the two new diffuse peaks do not follow the trend of the pyrochlore superlattice peaks, but rather adopt positions that are independent of the pyrochlore members. These two peaks merge into a single peak seen between Q = 2.5 and 3.3 Å−1 in the Ho2Zr2O7 structure function. A consistent increase in diffuse scattering in the predominately pyrochlore members (x = 0.0 to 1.0) indicate that despite the pyrochlore long-range structure, local deviations from pyrochlore are increasingly present. Conversely, the diffuse scattering peaks in the disordered members (x = 1.25 to 2.0) signal local structural order that is distinct from defect fluorite. These trends are also observed at high Q where many small peaks merge with increasing x (not shown). The diffuse scattering is much more prominent in the neutron scattering patterns than the X-ray scattering patterns. The local ordering in the system is heavily influenced by the oxygen sublattice, which is better observed with neutrons. This gives the Bragg peaks in the neutron scattering patterns a broadened appearance as the diffuse scattering increases and overlaps the bases of the Bragg peaks. Simple analysis of the diffuse scattering was performed through manipulation of the background polynomial used in Rietveld refinements by monitoring the quality of the fits (Table 4). The background polynomial of the Ho2Ti2O7 endmember was applied to the patterns of the other members to include the diffuse scattering in the refinements. All members that were refined primarily with the pyrochlore structure (x = 0.25–1.0) exhibited small decreases in fit quality (<0.3% increase in Rw). Compositions refined primarily with the defect fluorite structure (x = 1.25–2.0) whose structure functions had distinct diffuse scattering peaks exhibited the greatest decrease in fit quality (2–4% increase in Rw). A more detailed understanding of the origin of the diffuse scattering is obtained with Fourier analysis of the structure functions in the form of PDFs.
3.2 Short-range structure – neutron and X-ray real space (PDF) analysis
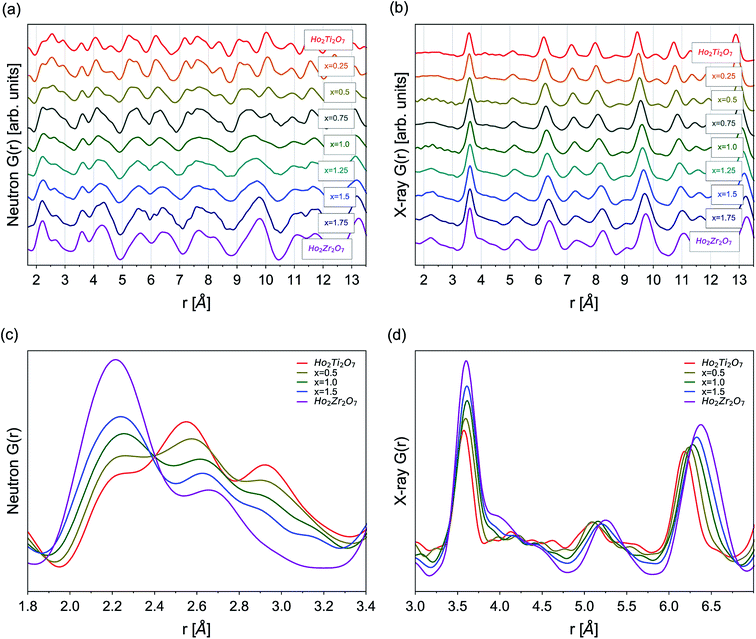
Neutron and X-ray PDFs are an intuitive, real-space representation of the atomic configuration and were used to gain further insight into the nature of disorder across the solid solution series over the short- and intermediate-range length scales (Fig. 4). Peak positions in the PDFs give information on interatomic distances, peak areas on coordination numbers, and peak widths on the atomic thermal vibrations and accumulated disorder. Single peaks can contain information on multiple atomic pairs, such as the negative peak at 1.95 Å in the neutron PDF of Ho2Ti2O7 which gives information on the nearest neighbor Ti–O octahedral correlations (Fig. 4a). Increasing disorder is apparent in the PDFs across all r-space as several distinct, sharp peaks merge into fewer broad peaks with increasing Zr-content, x. For example, multiple peaks associated with various atomic correlations in the region from 9.0 to 10.5 Å merge together with increasing x (Fig. 4a and b). Peak intensities increase across r-space due to the negatively scattering Ti being replaced by the positively scattering Zr (Table 1). Furthermore, peaks at higher r-space are broader and less numerous than at lower r-space due to very large atomic shells with many atoms that average together. The long-range PDFs (r > 25 Å, not shown) of compositions with higher x values indicate more disorder than the short-range PDFs, indicating there is some degree of local order associated with these compositions.Analysis of the nearest neighbor cation–anion correlations at low r-space in the neutron PDFs (1.7 to 3.5 Å) (Fig. 4c) that form the coordination polyhedra give direct insight into the local atomic configuration. The negative scattering length of Ti leads to a negative partial PDF, gTi–X(r), highlighting atomic correlations that are only associated with Ti–X (X = Ho, Zr, O) distances. When Ti is replaced by Zr its negative scattering contribution is reduced, decreasing the intensity of the negative Ti–O peak at 1.95 Å. As the Zr-content increases, Zr not only replaces Ti but also occupies sites regularly filled by Ho, seen in the PDFs as the broadening and intensifying of the peak at 2.2 Å, which contains many of the nearest neighbor cation–oxygen bond correlations. The O–O peaks at 2.6 Å and 2.95 Å broaden and reduce in intensity with increasing x due to the O–O bonds adopting a more varied distribution of lengths. The cation–cation correlations at slightly higher r-space are best analyzed in the X-ray PDFs (1.7 to 7.0 Å) that are highly sensitive to cation position (Fig. 4d). The first few peaks from 1.7 Å to 3.2 Å have extremely low intensities due to the weak cation–anion and anion–anion correlations. Only a general increase of intensity of these peaks with increasing Zr-content, x, can be observed with no discernable shape changes. Truncation ripples are present in the x = 0.5 and 1.0 samples, likely due to experimental differences such as reduced packing fraction of these powders. The first prominent peak at 3.57 Å contains all nearest-neighbor cation–cation correlations and the peak intensity gradually increases as Zr replaces Ti. A broad shoulder at ∼4.0 Å indicates that the incorporation of Zr lengthens a portion of these distances significantly beyond what would be observed for different cation sites. Peaks at higher r-values exhibit significant broadening with increasing disorder and little shape change, such as the development of new peaks and shoulders or peak merging. This is not the case in the neutron PDFs where the peaks are constantly changing shape with increasing Zr-content across the entire r-range, which indicates that the oxygen sublattice is subject to more changes than the cation sublattice as Ti is replaced with Zr and disorder accumulates.
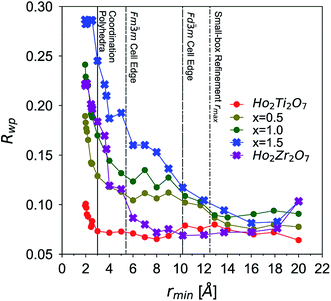
The long-range structural models determined using Rietveld refinement for each composition were applied to the PDF via small-box refinement from r = 1.7 to 50 Å (Table 4). This resulted in, except for the Ho2Ti2O7 endmember, poor fits for all compositions (Rwp > 25%), especially at low r-values where local distortions exist. “Boxcar” refinements were used to determine the spatial range of the local deviations in the long-range structure (Fig. 5). The exclusion of the PDF region that contains the coordination polyhedra bond correlations (solid line) significantly improved the goodness-of-fit values of small-box refinements beyond the dimensions of the Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m ordered pyrochlore unit cell (long dashed line) and larger. The PDFs of the compositions whose diffraction patterns were consistent with the ordered pyrochlore structure (circles) were in general better modelled at low rmin values than those that exhibit the Fm
m ordered pyrochlore unit cell (long dashed line) and larger. The PDFs of the compositions whose diffraction patterns were consistent with the ordered pyrochlore structure (circles) were in general better modelled at low rmin values than those that exhibit the Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m disordered, defect fluorite long-range structure (crosses). The goodness-of-fit values at all rmin values tend to worsen with increasing Zr-content, with the exception of the Ho2Zr2O7 endmember which exhibits high Rwp values at low rmin that fall to similar values as the Ho2Ti2O7 endmember beyond the dimensions of the defect fluorite unit cell (short dashed line). Additionally, the two endmembers' Rwp values were lower as compared to the intermediate series members that share the same long-range phase.
m disordered, defect fluorite long-range structure (crosses). The goodness-of-fit values at all rmin values tend to worsen with increasing Zr-content, with the exception of the Ho2Zr2O7 endmember which exhibits high Rwp values at low rmin that fall to similar values as the Ho2Ti2O7 endmember beyond the dimensions of the defect fluorite unit cell (short dashed line). Additionally, the two endmembers' Rwp values were lower as compared to the intermediate series members that share the same long-range phase.
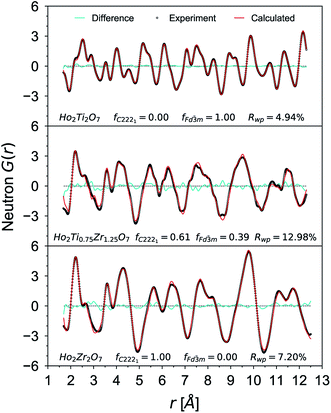
Small-box refinements were performed on the neutron and X-ray PDFs with refinement limits that were established from the “boxcar” analysis (r = 1.7–12.5 Å, Fig. 5 dotted dashed line). Only the PDF for the Ho2Ti2O7 endmember was fully refined using solely the pyrochlore Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group (Fig. 6). The intermediate compositions that are well-modelled over the long-range with the pyrochlore structure (x = 0.25 to 0.75) deviate from the ordered pyrochlore structure over short length scales (r < 12.5 Å). In contrast, all PDFs associated with sample compositions that are best refined on the long-range with the defect fluorite structure (x = 1.5 to 2.0) cannot be modelled locally with the Fm
m space group (Fig. 6). The intermediate compositions that are well-modelled over the long-range with the pyrochlore structure (x = 0.25 to 0.75) deviate from the ordered pyrochlore structure over short length scales (r < 12.5 Å). In contrast, all PDFs associated with sample compositions that are best refined on the long-range with the defect fluorite structure (x = 1.5 to 2.0) cannot be modelled locally with the Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group. Furthermore, the two members that exhibit two phases on the long-range (x = 1.0 and 1.25) cannot be locally refined using the pyrochlore/defect fluorite two-phase model. The PDF of the fully disordered Ho2Zr2O7 endmember is best refined using a weberite-type structural model.41 Among the many forms of weberite-type ordering,84 the best fit in this study was obtained with a model isostructural with Y3TaO7 (C2221). This model is described in depth elsewhere.45,46 This structure is very similar to Ccmm and has been previously used to describe the local atomic arrangement in A3BO7 defect fluorite materials.43 The 16h oxygen site is split into two 8c sites and most cations and anions in the structure have more positional and vibrational degrees of freedom than in Ccmm. The unit cell parameters used for both the Fd
m space group. Furthermore, the two members that exhibit two phases on the long-range (x = 1.0 and 1.25) cannot be locally refined using the pyrochlore/defect fluorite two-phase model. The PDF of the fully disordered Ho2Zr2O7 endmember is best refined using a weberite-type structural model.41 Among the many forms of weberite-type ordering,84 the best fit in this study was obtained with a model isostructural with Y3TaO7 (C2221). This model is described in depth elsewhere.45,46 This structure is very similar to Ccmm and has been previously used to describe the local atomic arrangement in A3BO7 defect fluorite materials.43 The 16h oxygen site is split into two 8c sites and most cations and anions in the structure have more positional and vibrational degrees of freedom than in Ccmm. The unit cell parameters used for both the Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m and C2221 structural models are reported in Table 1. Although the C2221 space group has more degrees of structural freedom than Fd
m and C2221 structural models are reported in Table 1. Although the C2221 space group has more degrees of structural freedom than Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m, the two cations and the anion vacancy are more ordered than in Fm
m, the two cations and the anion vacancy are more ordered than in Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m. Similar to the results by Shamblin et al., this weberite-type model fits the PDF of the Ho2Zr2O7 endmember very well out to an r-value of 12.5 Å, beyond which the PDF is best fit by the long-range Fm
m. Similar to the results by Shamblin et al., this weberite-type model fits the PDF of the Ho2Zr2O7 endmember very well out to an r-value of 12.5 Å, beyond which the PDF is best fit by the long-range Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m model.42
m model.42
The details of the two-phase model and site occupancies were constructed based on the neutron PDF data by assigning the Ti sites to the Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phase and the Zr sites to C2221. This configuration provided the best fit results and other model permutations resulted in poor fits with large average Rwp values, unphysical coordination polyhedra geometries, and non-stoichiometric compositions (Table 5). Permutations where Ti was forced into a weberite-type configuration resulted in the least agreement between model and data, followed by permutations where Zr was forced into a pyrochlore arrangement. Refinement of both the neutron and X-ray PDFs of the fully disordered Ho2Zr2O7 endmember with the C2221 model yielded a fit of poorer quality than the ordered pyrochlore Ho2Ti2O7 endmember which was refined with the Fd
m phase and the Zr sites to C2221. This configuration provided the best fit results and other model permutations resulted in poor fits with large average Rwp values, unphysical coordination polyhedra geometries, and non-stoichiometric compositions (Table 5). Permutations where Ti was forced into a weberite-type configuration resulted in the least agreement between model and data, followed by permutations where Zr was forced into a pyrochlore arrangement. Refinement of both the neutron and X-ray PDFs of the fully disordered Ho2Zr2O7 endmember with the C2221 model yielded a fit of poorer quality than the ordered pyrochlore Ho2Ti2O7 endmember which was refined with the Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m model (Table 6). All intermediate compositions of the solid-solution series were best described by a “two-phase” Fd
m model (Table 6). All intermediate compositions of the solid-solution series were best described by a “two-phase” Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m/C2221 model as shown in Fig. 6 representative for the x = 1.25 composition. The C2221 phase fraction systematically increased with Zr-content over the compositional range. The same two-phase model was applied to neutron and X-ray data but the Rwp values of the X-ray PDF fits were consistently lower for all intermediate compositions. Since X-rays are more sensitive to the cation positions, the trend in the goodness-of-fit values indicates that the cationic arrangement, with Zr and Ho occupying the 7-coordinated sites and Ti remaining in the 6-coordinated sites, is a good model for the cation sublattice. Conversely, X-rays have poor sensitivity to the anion sublattice and thus the neutron fits are necessary to completely evaluate the effectiveness of the two-phase model. The increase in the Rwp values of the neutron PDF fits with increasing Zr-content shows that the disorder present is more complex than can be fully captured by this model.
m/C2221 model as shown in Fig. 6 representative for the x = 1.25 composition. The C2221 phase fraction systematically increased with Zr-content over the compositional range. The same two-phase model was applied to neutron and X-ray data but the Rwp values of the X-ray PDF fits were consistently lower for all intermediate compositions. Since X-rays are more sensitive to the cation positions, the trend in the goodness-of-fit values indicates that the cationic arrangement, with Zr and Ho occupying the 7-coordinated sites and Ti remaining in the 6-coordinated sites, is a good model for the cation sublattice. Conversely, X-rays have poor sensitivity to the anion sublattice and thus the neutron fits are necessary to completely evaluate the effectiveness of the two-phase model. The increase in the Rwp values of the neutron PDF fits with increasing Zr-content shows that the disorder present is more complex than can be fully captured by this model.
| Neutron total scattering (fit range r = 1.7–12.5 Å) | |||
|---|---|---|---|
| Composition | Structure | C2221 fraction, y | Rwp (%) |
| Ho2Ti2O7 | Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
0 | 4.94 |
| Ho2Ti1.75Zr0.25O7 | Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m + C2221 m + C2221 |
0.14(2) | 9.01 |
| Ho2Ti1.50Zr0.50O7 | Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m + C2221 m + C2221 |
0.23(2) | 9.16 |
| Ho2Ti1.25Zr0.75O7 | Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m + C2221 m + C2221 |
0.35(2) | 12.91 |
| Ho2Ti1.00Zr1.00O7 | Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m + C2221 m + C2221 |
0.45(4) | 10.48 |
| Ho2Ti0.75Zr1.25O7 | Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m + C2221 m + C2221 |
0.61(2) | 12.98 |
| Ho2Ti0.50Zr1.50O7 | Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m + C2221 m + C2221 |
0.69(5) | 11.58 |
| Ho2Ti0.25Zr1.75O7 | Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m + C2221 m + C2221 |
0.87(1) | 13.04 |
| Ho2Zr2O7 | C2221 | 1 | 7.20 |
| X-ray total scattering (fit range r = 3.2–12.5 Å) | |||
|---|---|---|---|
| Composition | Structure | C2221 fraction, y | Rwp (%) |
| Ho2Ti2O7 | Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
0 | 6.89 |
| Ho2Ti1.75Zr0.25O7 | Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m + C2221 m + C2221 |
0.13(3) | 5.29 |
| Ho2Ti1.50Zr0.50O7 | Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m + C2221 m + C2221 |
0.22(3) | 4.93 |
| Ho2Ti1.25Zr0.75O7 | Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m + C2221 m + C2221 |
0.34(2) | 4.59 |
| Ho2Ti1.00Zr1.00O7 | Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m + C2221 m + C2221 |
0.46(2) | 5.69 |
| Ho2Ti0.75Zr1.25O7 | Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m + C2221 m + C2221 |
0.59(2) | 6.40 |
| Ho2Ti0.50Zr1.50O7 | Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m + C2221 m + C2221 |
0.70(2) | 7.37 |
| Ho2Ti0.25Zr1.75O7 | Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m + C2221 m + C2221 |
0.86(2) | 8.29 |
| Ho2Zr2O7 | C2221 | 1 | 8.82 |
3.3 Enthalpy of formation and mixing – high temperature oxide melt solution calorimetry
After non-destructive neutron and X-ray characterization, all Ho2Ti2−xZrxO7 sample compositions were analyzed using high temperature solution calorimetry. Fig. 7a shows the measured enthalpies of drop solution, ΔHds, versus Zr-content, x. These values are summarized in Table 7. The enthalpy of drop solution is the highest for the fully ordered Ho2Ti2O7 endmember with a value of 126.0 ± 0.5 kJ mol−1 and systematically decreases with increasing x to −16.4 ± 0.8 kJ mol−1 for the fully disordered Ho2Zr2O7 endmember. The dissolution behavior of the series is decreasingly endothermic with Ho2Zr2O7 being the only member that dissolves exothermically. The trend in ΔHds deviates from an ideal linear behavior and is best described as a function of increasing mole fraction of Ho2Zr2O7 (x/2) with a second-degree polynomial equation:
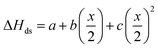 | (6) |
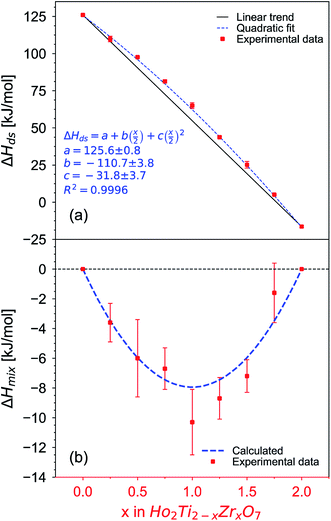 | ||
| Fig. 7 (a) Enthalpy of drop solution, ΔHds, as a function of Zr-content, x, in Ho2Ti2−xZrxO7 (Table 7). Error bars are smaller than the symbol for some compositions. The blue dashed curve is a fit to the data points using a second-degree polynomial function (eqn (6) with fit values given) and the black solid line represents ideal linear behavior between the two endmembers. (b) Corresponding enthalpies of mixing, ΔHmix, determined using eqn (7) (red data points) and ΔHmix calculated from the quadratic fit to ΔHds (blue dashed curve) (Table 8) using the formula ΔHmix (calc.) = W × (x/2) × (1 − x/2), where W = interaction parameter and x/2 = mole fraction of Ho2Zr2O7. Uncertainties of ΔHmix are propagated ΔHds errors. | ||
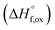 in the solid solution series Ho2Ti2−xZrxO7 (0 ≤ x ≤ 2.00)a
in the solid solution series Ho2Ti2−xZrxO7 (0 ≤ x ≤ 2.00)a
| x in Ho2Ti2−xZrxO7 | ΔHds (kJ mol−1) | (kJ mol−1) |
|---|---|---|
| a 4,6,7,8 number of drops. | ||
| 0 | 126.08 ± 0.5 | −88.7 ± 2.0 |
| 0.25 | 109.88 ± 1.8 | −83.6 ± 2.7 |
| 0.50 | 97.66 ± 0.6 | −82.4 ± 2.2 |
| 0.75 | 81.38 ± 1.1 | −77.2 ± 2.5 |
| 1.00 | 65.08 ± 2.0 | −72.0 ± 2.7 |
| 1.25 | 43.77 ± 1.0 | −61.7 ± 3.0 |
| 1.50 | 25.24 ± 2.3 | −54.3 ± 3.9 |
| 1.75 | 5.14 ± 0.3 | −45.2 ± 3.4 |
| 2.00 | −16.47 ± 0.8 | −34.8 ± 3.8 |
From the measured ΔHds the enthalpies of mixing (formation of solid solutions from the two endmembers), ΔHmix, as a function of x were determined using the following equation:
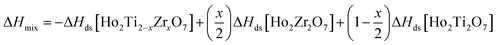 | (7) |
The enthalpies of mixing decrease with increasing Zr-content x to a minimum at −10.3 ± 2.2 kJ mol−1 for the intermediate composition x = 1.0 and then increase again with further substitution of Ti by Zr (Fig. 7b and Table 8). The trend of ΔHmix is very similar in shape and magnitude to those reported for the aforementioned binary oxide solid solutions.50–55 This behavior was attributed to the formation of ordered nanoscale clusters involving cations, oxygen, and oxygen vacancies.52–57 A fit of the ΔHmix data was produced by calculating ΔHmix values from the quadratic fit of ΔHds using eqn (7). This results in a smooth parabola that better predicts the magnitude of the minimum at x = 1.0, which is −7.9 kJ mol−1 (Table 8). The endmembers' structures have different symmetries but are related as they are both derived from fluorite, with the ordered structure being a subgroup of the disordered defect fluorite structure. Thus, the accumulation of disorder may be gradual, and the observed phase transition could be second order. The enthalpy of mixing in the Ho2Ti2O7–Ho2Zr2O7 solid solution series portrays no anomaly near the order–disorder transition point where the symmetry changes and we consider the system to form a continuous solid solution with a gradually increasing degree of disorder. The negative heat of mixing fit by a regular solution parameter is consistent with this behavior and with some amount of short-range ordering.
| x in Ho2Ti2−xZrxO7 | ΔHmixa (kJ mol−1) | Calculated ΔHmixc (kJ mol−1) | Phase fraction of weberite-type, y | ΔHmixb (kJ mol−1) | Calculated ΔHmixc (kJ mol−1) |
|---|---|---|---|---|---|
| a ΔHmix (kJ mol−1) (experimental) considering mole fraction of Ho2Zr2O7 (x/2) obtained using eqn 7.b ΔHmix (kJ mol−1) (experimental) considering phase fraction of weberite-type (y) obtained using ΔHmix = −ΔHds[Ho2Ti2−xZrxO7] + yΔHds[Ho2Zr2O7] + (1 − y)ΔHds[Ho2Ti2O7].c Calculated from values of the second-degree fits of the ΔHds data using eqn 7. | |||||
| 0 | 0 | 0 | 0 | 0 | 0 |
| 0.25 | −3.6 ± 1.3 | −3.5 | 0.14(2) | −3.2 ± 1.7 | −1.9 |
| 0.50 | −6.0 ± 2.6 | −6.0 | 0.23(2) | −4.3 ± 1.0 | −2.8 |
| 0.75 | −6.7 ± 1.4 | −7.4 | 0.35(2) | −4.7 ± 1.4 | −3.6 |
| 1.00 | −10.3 ± 2.2 | −7.9 | 0.45(4) | −5.1 ± 1.4 | −3.9 |
| 1.25 | −8.7 ± 1.4 | −7.4 | 0.61(2) | −4.5 ± 1.2 | −3.8 |
| 1.50 | −7.2 ± 1.1 | −6.0 | 0.69(5) | −3.0 ± 1.6 | −3.4 |
| 1.75 | −1.6 ± 2.0 | −3.5 | 0.87(7) | −2.4 ± 1.4 | −1.8 |
| 2.00 | 0 | 0 | 1 | 0 | 0 |
The enthalpies of formation from binary oxides, 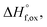 for the Ho2Ti2−xZrxO7 system are all exothermic (Table 7), suggesting enhanced stability relative to the binary oxides, but they become less exothermic with increasing Zr-content, ranging from −88.7 ± 2.0 kJ mol−1 for the ordered Ho2Ti2O7 endmember to −34.8 ± 3.8 kJ mol−1 for the disordered Ho2Zr2O7 endmember (Table 7).
for the Ho2Ti2−xZrxO7 system are all exothermic (Table 7), suggesting enhanced stability relative to the binary oxides, but they become less exothermic with increasing Zr-content, ranging from −88.7 ± 2.0 kJ mol−1 for the ordered Ho2Ti2O7 endmember to −34.8 ± 3.8 kJ mol−1 for the disordered Ho2Zr2O7 endmember (Table 7).
4. Discussion
4.1 Structural data
Combined neutron and X-ray total scattering provide unique insight into the pyrochlore-to-defect fluorite disordering process and how it proceeds at the long- and short-range scales across the Ho2Ti2−xZrxO7 solid solution series through comparison of the Rietveld and small-box refinements. While previous investigations have addressed this order–disorder transition with different local and long-range analytical probes, total scattering experiments with PDF analysis allow simultaneous study, and thus direct comparison, of the atomic structure at different length scales. The C2221 weberite-type phase fraction (determined through PDF analysis) is a measure for the short-range disorder, while the long-range Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m defect fluorite phase fraction, the pyrochlore 8a oxygen occupancy n8a, and the pyrochlore 48f oxygen x-position x48f (determined through Rietveld refinement) are measures of the long-range disorder. The transition from the fully ordered pyrochlore structure (Ho2Ti2O7) to the fully disordered, defect fluorite structure (Ho2Zr2O7) is complex and has a distinct dependence on the Zr-content, x, across different length scales (Fig. 8). The long-range structure exhibits a fairly abrupt change in ordering, with the defect fluorite phase fraction following sigmoidal behavior. The diffraction patterns of almost all samples were fully refined with either the Fd
m defect fluorite phase fraction, the pyrochlore 8a oxygen occupancy n8a, and the pyrochlore 48f oxygen x-position x48f (determined through Rietveld refinement) are measures of the long-range disorder. The transition from the fully ordered pyrochlore structure (Ho2Ti2O7) to the fully disordered, defect fluorite structure (Ho2Zr2O7) is complex and has a distinct dependence on the Zr-content, x, across different length scales (Fig. 8). The long-range structure exhibits a fairly abrupt change in ordering, with the defect fluorite phase fraction following sigmoidal behavior. The diffraction patterns of almost all samples were fully refined with either the Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (Ti-rich compositions) or the Fm
m (Ti-rich compositions) or the Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (Zr-rich compositions) phase, and only the intermediate compositions x = 1.0 and 1.25 exhibited coexistence of both phases. With increasing Zr-content, the ordered pyrochlore phase persists until more than 50% of Ti is replaced by Zr which then triggers over the long-range a nearly complete disordering to defect fluorite across a narrow compositional range centered around x ≈ 1.2 (Fig. 8). The oxygen site parameters (x48f and n8a), which indicate the degree of disorder of the anion sublattice, increase in a similar manner to the defect fluorite phase fraction (not shown). This would suggest that both the cation and anion sublattices disorder together over the same compositional regimes. This behavior is in agreement with previous studies on the Y2Ti2−xZrxO7 and Ho2Ti2−xZrxO7 systems which show a similar abrupt transition from pyrochlore to defect fluorite with the two phases coexisting around x ≈ 1.2.31,36 In the present solid solution series, the more step-like order–disorder transition across the long-range is in clear contrast to the more gradual accumulation of disorder at the local scale. The weberite-type phase fraction increases linearly at the expense of the pyrochlore phase (Fig. 8) and apart from the two endmembers, both phases coexist locally for all compositions measured. Such a gradual increase in short-range modifications has been observed in previous studies on Y2B2−xZrxO7 (B = Ti or Sn) pyrochlore using Raman spectroscopy, magic angle spinning nuclear magnetic resonance (MAS NMR), and X-ray absorption near-edge structure (XANES).38,39 While it has been shown before that fully ordered compositions are pyrochlore on both the long- and short-range and that fully disordered compositions are defect fluorite on the long-range and weberite-type on the short-range,42 this study reveals a complex behavior for intermediate compositions. The degree of disorder is, for a given composition, distinct at different length scales and the evolution of the structure on the long- and short-range with changes in composition appears to be decoupled. Compositions which are ordered over the long-range (e.g., x = 0.75 with 37.5% Zr) still locally contain a large fraction of the weberite-type phase (∼35%).
m (Zr-rich compositions) phase, and only the intermediate compositions x = 1.0 and 1.25 exhibited coexistence of both phases. With increasing Zr-content, the ordered pyrochlore phase persists until more than 50% of Ti is replaced by Zr which then triggers over the long-range a nearly complete disordering to defect fluorite across a narrow compositional range centered around x ≈ 1.2 (Fig. 8). The oxygen site parameters (x48f and n8a), which indicate the degree of disorder of the anion sublattice, increase in a similar manner to the defect fluorite phase fraction (not shown). This would suggest that both the cation and anion sublattices disorder together over the same compositional regimes. This behavior is in agreement with previous studies on the Y2Ti2−xZrxO7 and Ho2Ti2−xZrxO7 systems which show a similar abrupt transition from pyrochlore to defect fluorite with the two phases coexisting around x ≈ 1.2.31,36 In the present solid solution series, the more step-like order–disorder transition across the long-range is in clear contrast to the more gradual accumulation of disorder at the local scale. The weberite-type phase fraction increases linearly at the expense of the pyrochlore phase (Fig. 8) and apart from the two endmembers, both phases coexist locally for all compositions measured. Such a gradual increase in short-range modifications has been observed in previous studies on Y2B2−xZrxO7 (B = Ti or Sn) pyrochlore using Raman spectroscopy, magic angle spinning nuclear magnetic resonance (MAS NMR), and X-ray absorption near-edge structure (XANES).38,39 While it has been shown before that fully ordered compositions are pyrochlore on both the long- and short-range and that fully disordered compositions are defect fluorite on the long-range and weberite-type on the short-range,42 this study reveals a complex behavior for intermediate compositions. The degree of disorder is, for a given composition, distinct at different length scales and the evolution of the structure on the long- and short-range with changes in composition appears to be decoupled. Compositions which are ordered over the long-range (e.g., x = 0.75 with 37.5% Zr) still locally contain a large fraction of the weberite-type phase (∼35%).
The immediate formation of a local weberite-type phase in Ho2Ti2O7 pyrochlore upon the substitution of any amount of Zr can be understood by a detailed comparison of the two structures. Observation of pyrochlore along the [110] direction reveals repeating layers of distinct 6- and 8-fold sites (Fig. 1a). This is similar to the weberite-type structure which also contains 6- and 8-fold site layers but with intermediate layers of 7-fold sites occupied by a random mix of Ho and Zr cations and an ordered arrangement of oxygen anion defects (Fig. 1c). Indeed, Zr is coordinated by seven oxygen anions in monoclinic zirconia88,89 and has been previously observed to adopt a 7-coordinated environment within the pyrochlore matrix.25,31,35 Recent work using Pauling's rules has proposed that the formation of 7-coordinated sites is driven by either the direct movement of 48f oxygen anions into 8a sites, or through an indirect path where the 8b oxygen anions migrate into 8a sites and then are immediately occupied by 48f oxygen anions.46 Both atomic-scale movements explain the retention of oxygen in the 8b site deduced using Rietveld refinement. This movement creates a short-range polyhedral arrangement that is nearly indistinguishable from the weberite model in A3BO7 oxides and provides a coordination environment that is better suited to accommodate the larger Zr cations. First-principles calculations support this theory and show the lowest energy structures are attained by oxygen relaxations that allow for 7-coordinated Zr cations.90 O'Quinn et al. show these short-range polyhedral arrangements (essentially weberite-type nanodomains) form in the pyrochlore matrix such that the configurational average of all potential orientations yields the long-range defect fluorite structure.46 This behavior can also be understood based on a weberite-type building block model. Movement of an oxygen anion forms a weberite-type building block within the pyrochlore matrix, but limits the motion of other nearby oxygen anions, establishing a minimum distance between weberite-type building blocks. This is a direct result of applying Pauling's rules, which dictates that the other oxygen anions associated with this building block must remain with this 7-coordinated Zr cation.46 A direct comparison of the short- and long-range behavior in the present solid solution series reveals that weberite-type building blocks will gradually form until a critical density is reached (50% of Ti replaced by Zr) which triggers the long-range transformation to an average defect fluorite (Fig. 8). A similar behavior has been previously observed in ion-irradiated sesquioxides (A2O3) in which oxygen defects are formed under irradiation far from each other and trigger a phase transformation (cubic-to-monoclinic) upon reaching a critical density.91
The diffuse scattering observed in the neutron structure functions, S(Q), of the Ho2Ti2−xZrxO7 series (Fig. 2) gives further insight on how the local structural arrangements translate to the long-range structure. Individual weberite-type building blocks formed from a single oxygen defect within the pyrochlore matrix are on the order of a nanometer as shown by the boxcar refinement (Fig. 5). The diffuse scattering is likely produced by the correlated differences between randomly oriented larger weberite-type nanodomains and the average crystal matrix. An approach developed by Neder et al.74 was used to model coherent weberite-type and pyrochlore nanodomains to replicate diffuse scattering in the neutron total scattering data of the x = 1.75 composition with an average defect fluorite structure (Fig. 9). This composition was chosen as its S(Q) shows distinct diffuse scattering with several prominent peak-like features. The integral diffracted intensity was split into the long-range average structure (Bragg peaks) and a “difference” structure (diffuse scattering, i.e., nanodomains). The model using weberite-type (C2221) nanodomains in a defect fluorite Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m matrix (Fig. 9a) replicated both the diffuse scattering peaks and the Bragg peaks well (Rw = 5.15%). The model using a pyrochlore (Fd
m matrix (Fig. 9a) replicated both the diffuse scattering peaks and the Bragg peaks well (Rw = 5.15%). The model using a pyrochlore (Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) nanodomain model (Fig. 9b) replicated diffuse features at Q = 3.2 and 4.7 Å−1, but captured less of the diffuse scattering (Q = 2.7, 3.7, 4.5–5.1 Å−1), over and under fit several Bragg peaks (Q = 2.1 and 5.3 Å−1), and in general produced a lower quality fit (Rw = 9.20%). This behavior reflects the short-range structure obtained for this composition using PDF small-box modeling, showing a predominantly weberite-type atomic arrangement with the retention of some character of pyrochlore ordering. These goodness-of-fit values (Rw) should not be directly compared to those of the standard Rietveld refinement results as difference modelling uses significantly more parameters. The nanodomain modeling shows that while weberite-type and pyrochlore building blocks are responsible for the short-range structure in the PDF, larger nanodomains of both phases are responsible for the diffuse scattering observed at high Zr-content. Therefore, this diffuse scattering represents the intermediate-range structure which is important in understanding the formation of the long-range defect fluorite. Further work using advanced reverse Monte Carlo (RMC) and molecular dynamics (MD) modelling may help elucidate these processes and describe the structural heterogeneity in disordered pyrochlore oxides.
m) nanodomain model (Fig. 9b) replicated diffuse features at Q = 3.2 and 4.7 Å−1, but captured less of the diffuse scattering (Q = 2.7, 3.7, 4.5–5.1 Å−1), over and under fit several Bragg peaks (Q = 2.1 and 5.3 Å−1), and in general produced a lower quality fit (Rw = 9.20%). This behavior reflects the short-range structure obtained for this composition using PDF small-box modeling, showing a predominantly weberite-type atomic arrangement with the retention of some character of pyrochlore ordering. These goodness-of-fit values (Rw) should not be directly compared to those of the standard Rietveld refinement results as difference modelling uses significantly more parameters. The nanodomain modeling shows that while weberite-type and pyrochlore building blocks are responsible for the short-range structure in the PDF, larger nanodomains of both phases are responsible for the diffuse scattering observed at high Zr-content. Therefore, this diffuse scattering represents the intermediate-range structure which is important in understanding the formation of the long-range defect fluorite. Further work using advanced reverse Monte Carlo (RMC) and molecular dynamics (MD) modelling may help elucidate these processes and describe the structural heterogeneity in disordered pyrochlore oxides.
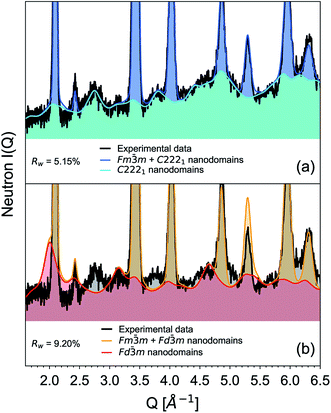 | ||
Fig. 9 Diffuse scattering analysis using neutron scattering data (black) and Rietveld refinement using the approach by Neder et al.74 (a) Defect fluorite (Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m, blue) plus weberite-type nanodomains (C2221, cyan) refinement. (b) Defect fluorite (Fm m, blue) plus weberite-type nanodomains (C2221, cyan) refinement. (b) Defect fluorite (Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m, orange) plus pyrochlore nanodomains (Fd m, orange) plus pyrochlore nanodomains (Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m, red). Key features not fit are marked with a diamond. The coherent nanodomains were modelled to be 4 nm. m, red). Key features not fit are marked with a diamond. The coherent nanodomains were modelled to be 4 nm. | ||
4.2 Thermodynamic data
The thermodynamic data provide further insight into the role of local atomic arrangements associated with the disordering process across the Ho2Ti2−xZrxO7 solid solution series. Several factors contribute to ΔHds and ΔHmix in binary and pseudobinary solid solutions, four of which were considered by Davies and Navrotsky:92 (i) size difference, (ii) valence of cations being mixed, (iii) electronic configuration, and (iv) covalency difference. The first two factors are most significant for the Ho2Ti2−xZrxO7 system and hinder cationic mixing as Ti4+ and Zr4+ have different ionic sizes (Table 2) and high valences. Since the electronic configuration of Ti4+ and Zr4+ and the ionic character of the M–O bond for each cation are similar, these terms are considered less important. Following the approach developed by Davies and Navrotsky,92 one obtains a positive interaction parameter of +25 kJ mol−1 for ΔHds resulting from the size difference of the two cations being fully mixed (Zr4+ and Ti4+). The experimentally determined interaction parameter of −32 kJ mol−1 (eqn (6)) suggests that disordering in this solid solution series can be associated to a value of −57 kJ mol−1 (−57 kJ mol−1 + 25 kJ mol−1 = −32 kJ mol−1) which is quite exothermic, indicating these rearrangements are highly favorable. Such a strongly exothermic interaction parameter weakens the strict applicability of a regular solution approach because the large extent of short-range order will diminish the entropy of mixing significantly from that of a random distribution of cations, anions, and vacancies. Thus, the interaction parameter for Ho2Ti2−xZrxO7 should be considered more as a convenient fitting parameter than as a stringent physical description of the system. For a full thermodynamic description, more complex mixing models are required.Realizing the importance of the weberite-type domains in the disordering process, ΔHds was plotted against the fraction of the local weberite-type phase, y, determined from structural analysis (Fig. 10a). The new ΔHds data is also fit by a second-degree polynomial equation:
| ΔHds = a′ + b′y + c′y2 | (8) |
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phase fraction, f, the behavior deviates dramatically from a linear trend and shows a sigmoidal evolution (Fig. 10a). Since there is no evidence for a sharp change in enthalpy near the critical composition of the pyrochlore-to-defect fluorite transition (x ≈ 1.2), it can be concluded that the long-range structure is not the driving force for the thermodynamics of the system.
m phase fraction, f, the behavior deviates dramatically from a linear trend and shows a sigmoidal evolution (Fig. 10a). Since there is no evidence for a sharp change in enthalpy near the critical composition of the pyrochlore-to-defect fluorite transition (x ≈ 1.2), it can be concluded that the long-range structure is not the driving force for the thermodynamics of the system.
 | ||
Fig. 10 (a) Enthalpy of drop solution, ΔHds, of Ho2Ti2−xZrxO7 as a function of phase fraction of weberite-type C2221, y (red), and defect fluorite Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m, f (black). Error bars are smaller than the symbol for some compositions. The blue dashed curve is a fit to the data points versus y using a second-degree polynomial function (eqn (8) with fit values given) and the black solid line represents ideal linear behavior based on the two endmembers. (b) Corresponding enthalpies of mixing, ΔHmix, determined using eqn (7) (red data points) and ΔHmix calculated from the quadratic fit to ΔHds versus y (blue dashed curve) (Table 8). Uncertainties of ΔHmix are propagated ΔHds errors. Fig. 10 plotted on the same scale as Fig. 7 for direct comparison. m, f (black). Error bars are smaller than the symbol for some compositions. The blue dashed curve is a fit to the data points versus y using a second-degree polynomial function (eqn (8) with fit values given) and the black solid line represents ideal linear behavior based on the two endmembers. (b) Corresponding enthalpies of mixing, ΔHmix, determined using eqn (7) (red data points) and ΔHmix calculated from the quadratic fit to ΔHds versus y (blue dashed curve) (Table 8). Uncertainties of ΔHmix are propagated ΔHds errors. Fig. 10 plotted on the same scale as Fig. 7 for direct comparison. | ||
While the weberite-type structure is more ordered than defect fluorite, it is still partially disordered and may have less order than in reported clusters of rare earth stabilized fluorite phases, which may explain the less negative interaction parameter. Alternatively, the substitution of rare earth cations in other defect fluorite phases, such as yttria-stabilized zirconia (YSZ), involves the creation and ordering of charge-balanced defects (trivalent cations and oxygen anion vacancies), while in the system studied here the total number of vacancies and charge on the cation sublattices are fixed by the A2B2O7 stoichiometry, with only their ordering and distribution varying. Thus, electrostatic factors may be less important, consistent with less exothermic mixing. In addition, the weberite-type structure is not constrained to have the same composition as the matrix, with a given bulk composition, x, being the only overall compositional constraint. To further analyze the thermodynamic data in the complex Ho2Ti2−xZrxO7 system, quantitative atomistic models are needed that describe the heats, entropies, and free energies of mixing. How much configurational entropy remains in these partially ordered structures remains a major question. High temperature in situ diffraction and differential scanning calorimetry studies can be done in the future to find the temperature dependence of the equilibrium degree of disorder and provide a more realistic thermodynamic model, as has been done for other pyrochlore compounds.93 However, since at present we have data only for one series of quenched materials, we cannot say anything definitive about the equilibrium degree of ordering and resulting configurational entropy. Further local structure and calorimetry studies of more fluorite-related systems would provide insights about the relation between local structure and thermodynamics.
5. Conclusions
We have investigated in detail how disordering proceeds across the Ho2Ti2−xZrxO7 solid solution series from the long-range structure to the local atomic configuration. Combined neutron and X-ray total scattering, with high sensitivity to both cation and anion sublattices, reveal a complex order–disorder transition across different length scales induced by chemical substitution of Ti by Zr. Disordering proceeds locally through gradual accumulation of a weberite-type (C2221) phase (linearly with increasing Zr-content x), which is in stark contrast to the step-like transition over the long-range from the pyrochlore structure (Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) to the defect fluorite structure (Fm
m) to the defect fluorite structure (Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) at x ≈ 1.2. Comparison of the local and average phase behavior and the polyhedral layering patterns in pyrochlore and weberite indicates that weberite-type building blocks are created at a distance from each other when Zr replaces Ti through the introduction of oxygen Frenkel defects. Weberite-type building blocks increase in number with increasing Zr-content until a critical concentration, which is followed by the appearance of defect fluorite in the long-range structure (when approximately 50% of Ti is replaced by Zr). The weberite-type building blocks (essentially weberite-type nanodomains) form within the pyrochlore matrix such that the configurational average of all potential orientations yields the long-range defect fluorite structure beyond the critical accumulation point. Analysis of the diffuse scattering supports this claim and further suggests that intermediate-range interactions play a critical role in the progression of the order–disorder transition. The thermodynamic data obtained from high temperature oxide melt solution calorimetry indicate that the energetics across the solid solution series closely follow the short-range phase behavior (phase fraction of weberite domains) rather than the transformation from pyrochlore to defect fluorite. The large extent of short-range ordering implies that one should not apply simple models, like regular solution, to these systems because of the inherent complexity of the entropy of mixing term. This complexity must be considered when analyzing other similar systems and when seeking new materials with desirable properties.
m) at x ≈ 1.2. Comparison of the local and average phase behavior and the polyhedral layering patterns in pyrochlore and weberite indicates that weberite-type building blocks are created at a distance from each other when Zr replaces Ti through the introduction of oxygen Frenkel defects. Weberite-type building blocks increase in number with increasing Zr-content until a critical concentration, which is followed by the appearance of defect fluorite in the long-range structure (when approximately 50% of Ti is replaced by Zr). The weberite-type building blocks (essentially weberite-type nanodomains) form within the pyrochlore matrix such that the configurational average of all potential orientations yields the long-range defect fluorite structure beyond the critical accumulation point. Analysis of the diffuse scattering supports this claim and further suggests that intermediate-range interactions play a critical role in the progression of the order–disorder transition. The thermodynamic data obtained from high temperature oxide melt solution calorimetry indicate that the energetics across the solid solution series closely follow the short-range phase behavior (phase fraction of weberite domains) rather than the transformation from pyrochlore to defect fluorite. The large extent of short-range ordering implies that one should not apply simple models, like regular solution, to these systems because of the inherent complexity of the entropy of mixing term. This complexity must be considered when analyzing other similar systems and when seeking new materials with desirable properties.
Author contributions
D. D., E. O., and M. L. conceived and designed the study. A. F. provided samples for the study. D. D., E. O., J. N., M. E., I. G., and M. L. performed the neutron total scattering experiments and analyzed the data. D. D., I. G., D. S., and M. L. performed the X-ray total scattering experiments and analyzed the data. T. S., K. L., and A. N. performed the high temperature melt solution calorimetry and analyzed the data. D. D. and G. B. performed diffuse scattering analysis on all total scattering data. D. D., E. O., T. S., A. N., G. B., R. E., and M. L. interpreted the data. D. D. drafted the manuscript with input from and critical review by all authors.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the U.S. Department of Energy, Office of Science, Basic Energy Sciences, under Award DE-SC0020321. This material is based upon work supported under an Integrated University Program Graduate Fellowship (D. L. D). E. C. O. acknowledges support from the U.S. Department of Energy, Office of Science, Office of Workforce Development for Teachers and Scientists, Office of Science Graduate Student Research (SCGSR) program. The SCGSR program is administered by the Oak Ridge Institute for Science and Education for the DOE under contract number DE-SC0014664. The calorimetric work at UC Davis was supported by the U. S. Department of Energy, Office of Basic Energy Sciences, under Award DE-FG02-03ER46053. A. F. F. thanks Mexican Conacyt, for the financial support given to this work (Grant No. CB2013-01-221701). The research at ORNL's Spallation Neutron Source was sponsored by the Scientific User Facilities Division, Office of Basic Energy Sciences, U.S. Department of Energy. This research used The X-ray Powder Diffraction beamline of the National Synchrotron Light Source II, a U.S. Department of Energy (DOE) Office of Science User Facility operated for the DOE Office of Science by Brookhaven National Laboratory under Contract No. DE-SC0012704.References
- M. A. Subramanian, G. Aravamudan and G. V. Subba Rao, Prog. Solid State Chem., 1983, 15, 55–143 CrossRef CAS.
- R. C. Ewing, W. J. Weber and J. Lian, J. Appl. Phys., 2004, 95, 5949–5971 CrossRef CAS.
- B. C. Chakoumakos, J. Solid State Chem., 1984, 53, 120–129 CrossRef CAS.
- B. J. Kennedy, Phys. B, 1997, 241–243, 303–310 CrossRef CAS.
- H. Nyman, S. Andersson, B. G. Hyde and M. O'Keeffe, J. Solid State Chem., 1978, 26, 123–131 CrossRef CAS.
- P. J. Wilde and C. R. A. Catlow, Solid State Ionics, 1998, 112, 173–183 CrossRef CAS.
- K. E. Sickafus, L. Minervini, R. W. Grimes, J. A. Valdez, M. Ishimaru, F. Li, K. J. McClellan and T. Hartmann, Science, 2000, 289, 748–751 CrossRef CAS.
- L. Minervini, R. W. Grimes and K. E. Sickafus, J. Am. Ceram. Soc., 2000, 83, 1873–1878 CrossRef CAS.
- B. J. Wuensch, K. W. Eberman, C. Heremans, E. M. Ku, P. Onnerud, E. M. E. Yeo, S. M. Haile, J. K. Stalick and J. D. Jorgensen, Solid State Ionics, 2000, 129, 111–133 CrossRef CAS.
- F. X. Zhang, M. Lang, Z. Liu and R. C. Ewing, Phys. Rev. Lett., 2010, 105, 015503 CrossRef CAS.
- F. X. Zhang, J. W. Wang, J. Lian, M. K. Lang, U. Becker and R. C. Ewing, Phys. Rev. Lett., 2008, 100, 045503 CrossRef CAS.
- W. R. Panero, L. Stixrude and R. C. Ewing, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 054110 CrossRef.
- M. T. Weller, R. W. Hughes, J. Rooke, C. S. Knee and J. Reading, Dalton Trans., 2004, 3032–3041, 10.1039/b401787k.
- Y. Shimakawa and Y. Kubo, Mater. Sci. Eng., B, 1999, 63, 44–48 CrossRef.
- C. Heremans, B. J. Wuensch, J. K. Stalick and E. Prince, J. Solid State Chem., 1995, 117, 108–121 CrossRef CAS.
- X. Cao, J. Mater. Sci. Technol., 2007, 23, 15–35 CrossRef CAS.
- P. K. Moon and H. L. Tuller, Sens. Actuators, B, 1990, 1, 199–202 CrossRef CAS.
- S. X. Wang, B. D. Begg, L. M. Wang, R. C. Ewing, W. J. Weber and K. V. G. Kutty, J. Mater. Res., 1999, 14, 4470–4473 CrossRef CAS.
- K. E. Sickafus, R. W. Grimes, J. A. Valdez, A. Cleave, M. Tang, M. Ishimaru, S. M. Corish, C. R. Stanek and B. P. Uberuaga, Nat. Mater., 2007, 6, 217 CrossRef CAS.
- S. Finkeldei, M. C. Stennett, P. M. Kowalski, Y. Ji, E. de Visser-Týnová, N. C. Hyatt, D. Bosbach and F. Brandt, J. Mater. Chem. A, 2020, 8, 2387–2403 RSC.
- M. Lang, M. Toulemonde, J. Zhang, F. Zhang, C. L. Tracy, J. Lian, Z. Wang, W. J. Weber, D. Severin, M. Bender, C. Trautmann and R. C. Ewing, Nucl. Instrum. Methods Phys. Res., Sect. B, 2014, 336, 102–115 CrossRef CAS.
- D. M. Strachan, R. D. Scheele, E. C. Buck, J. P. Icenhower, A. E. Kozelisky, R. L. Sell, R. J. Elovich and W. C. Buchmiller, J. Nucl. Mater., 2005, 345, 109–135 CrossRef CAS.
- R. D. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751–767 CrossRef.
- B. J. Wuensch and K. W. Eberman, JOM, 2000, 52, 19–21 CrossRef CAS.
- S. T. Norberg, S. Hull, S. G. Eriksson, I. Ahmed, F. Kinyanjui and J. J. Biendicho, Chem. Mater., 2012, 24, 4294–4300 CrossRef CAS.
- M. Lang, F. Zhang, J. Zhang, J. Wang, J. Lian, W. J. Weber, B. Schuster, C. Trautmann, R. Neumann and R. C. Ewing, Nucl. Instrum. Methods Phys. Res., Sect. B, 2010, 268, 2951–2959 CrossRef CAS.
- M. Lang, J. Lian, J. Zhang, F. Zhang, W. J. Weber, C. Trautmann and R. C. Ewing, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 224105 CrossRef.
- J. Lian, K. B. Helean, B. J. Kennedy, L. M. Wang, A. Navrotsky and R. C. Ewing, J. Phys. Chem. B, 2006, 110, 2343–2350 CrossRef CAS.
- Y. Li, P. M. Kowalski, G. Beridze, A. R. Birnie, S. Finkeldei and D. Bosbach, Scr. Mater., 2015, 107, 18–21 CrossRef CAS.
- C. Jiang, C. R. Stanek, K. E. Sickafus and B. P. Uberuaga, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 104203 CrossRef.
- Y. Liu, R. L. Withers and L. Norén, J. Solid State Chem., 2004, 177, 4404–4412 CrossRef CAS.
- E. M. Ku, E. M. E. Yeo and B. J. Wuensch, MRS Proc., 1998, 547, 327 CrossRef.
- N. Kim and C. P. Grey, J. Solid State Chem., 2003, 175, 110–115 CrossRef CAS.
- M. de los Reyes, K. R. Whittle, Z. Zhang, S. E. Ashbrook, M. R. Mitchell, L.-Y. Jang and G. R. Lumpkin, RSC Adv., 2013, 3, 5090–5099 RSC.
- Z. Zhang, S. C. Middleburgh, M. de los Reyes, G. R. Lumpkin, B. J. Kennedy, P. E. R. Blanchard, E. Reynolds and L.-Y. Jang, J. Phys. Chem. C, 2013, 117, 26740–26749 CrossRef CAS.
- M. Shafique, B. J. Kennedy, Y. Iqbal and R. Ubic, J. Alloys Compd., 2016, 671, 226–233 CrossRef CAS.
- M. Glerup, O. F. Nielsen and F. W. Poulsen, J. Solid State Chem., 2001, 160, 25–32 CrossRef CAS.
- P. E. R. Blanchard, R. Clements, B. J. Kennedy, C. D. Ling, E. Reynolds, M. Avdeev, A. P. J. Stampfl, Z. Zhang and L.-Y. Jang, Inorg. Chem., 2012, 51, 13237–13244 CrossRef CAS.
- P. E. R. Blanchard, S. Liu, B. J. Kennedy, C. D. Ling, M. Avdeev, J. B. Aitken, B. C. C. Cowie and A. Tadich, J. Phys. Chem. C, 2013, 117, 2266–2273 CrossRef CAS.
- S. V. Ushakov, A. Navrotsky, J. A. Tangeman and K. B. Helean, J. Am. Ceram. Soc., 2007, 90, 1171–1176 CrossRef CAS.
- M. P. Saradhi, S. V. Ushakov and A. Navrotsky, RSC Adv., 2012, 2, 3328–3334 RSC.
- J. Shamblin, M. Feygenson, J. Neuefeind, C. L. Tracy, F. Zhang, S. Finkeldei, D. Bosbach, H. Zhou, R. C. Ewing and M. Lang, Nat. Mater., 2016, 15, 507 CrossRef CAS.
- G. King, C. M. Thompson, J. E. Greedan and A. Llobet, J. Phys. Chem. A, 2013, 1, 10487–10494 CAS.
- J. Shamblin, C. L. Tracy, R. I. Palomares, E. C. O'Quinn, R. C. Ewing, J. Neuefeind, M. Feygenson, J. Behrens, C. Trautmann and M. Lang, Acta Mater., 2018, 144, 60–67 CrossRef CAS.
- I. M. Gussev, E. C. O'Quinn, G. Baldinozzi, J. Neuefeind, R. C. Ewing, F. Zhang and M. Lang, Acta Mater., 2020, 196, 704–709 CrossRef CAS.
- E. C. O'Quinn, K. E. Sickafus, R. C. Ewing, G. Baldinozzi, J. C. Neuefeind, M. G. Tucker, A. F. Fuentes, D. Drey and M. K. Lang, Sci. Adv., 2020, 6, eabc2758 CrossRef.
- M. Wakeshima, H. Nishimine and Y. Hinatsu, J. Phys.: Condens. Matter, 2004, 16, 4103–4120 CrossRef CAS.
- J. M. Solomon, J. Shamblin, M. Lang, A. Navrotsky and M. Asta, Sci. Rep., 2016, 6, 38772 CrossRef CAS.
- E. C. O'Quinn, J. Shamblin, B. Perlov, R. C. Ewing, J. Neuefeind, M. Feygenson, I. Gussev and M. Lang, J. Am. Chem. Soc., 2017, 139, 10395–10402 CrossRef.
- S. Finkeldei, P. Kegler, P. M. Kowalski, C. Schreinemachers, F. Brandt, A. A. Bukaemskiy, V. L. Vinograd, G. Beridze, A. Shelyug, A. Navrotsky and D. Bosbach, Acta Mater., 2017, 125, 166–176 CrossRef CAS.
- E. C. O'Quinn, J. L. Bishop, R. Sherrod, J. Neuefeind, S. M. Montemayor, A. F. Fuentes and M. Lang, J. Mater. Sci., 2018, 53, 13400–13410 CrossRef.
- T. A. Lee and A. Navrotsky, J. Mater. Res., 2004, 19, 1855–1861 CrossRef CAS.
- T. A. Lee, A. Navrotsky and I. Molodetsky, J. Mater. Res., 2003, 18, 908–918 CrossRef CAS.
- A. Navrotsky, J. Mater. Chem., 2010, 20, 10577–10587 RSC.
- A. Navrotsky, P. Simoncic, H. Yokokawa, W. Chen and T. Lee, Faraday Discuss., 2007, 134, 171–180 RSC.
- P. Simoncic and A. Navrotsky, J. Am. Ceram. Soc., 2007, 90, 2143–2150 CrossRef CAS.
- P. Simoncic and A. Navrotsky, J. Mater. Res., 2007, 22, 876–885 CrossRef CAS.
- X. Guo, S. Szenknect, A. Mesbah, N. Clavier, C. Poinssot, D. Wu, H. Xu, N. Dacheux, R. C. Ewing and A. Navrotsky, Chem. Mater., 2016, 28, 7117–7124 CrossRef CAS.
- C.-K. Chung, J. Shamblin, E. C. O'Quinn, A. Shelyug, I. Gussev, M. Lang and A. Navrotsky, Acta Mater., 2018, 145, 227–234 CrossRef CAS.
- C.-K. Chung, E. C. O’Quinn, J. C. Neuefeind, A. F. Fuentes, H. Xu, M. Lang and A. Navrotsky, Acta Mater., 2019, 181, 309–317 CrossRef CAS.
- C.-K. Chung, M. Lang, H. Xu and A. Navrotsky, Acta Mater., 2018, 155, 386–392 CrossRef CAS.
- T. Subramani and A. Navrotsky, Inorg. Chem., 2019, 58, 16126–16133 CrossRef CAS.
- J. Neuefeind, M. Feygenson, J. Carruth, R. Hoffmann and K. K. Chipley, Nucl. Instrum. Methods Phys. Res., Sect. B, 2012, 287, 68–75 CrossRef CAS.
- A. K. Soper and E. R. Barney, J. Appl. Crystallogr., 2012, 45, 1314 CrossRef CAS.
- S. G. Eric Dooryhee, M. Rehak and X. Shi, Preliminary Design Report for the X-ray Powder Diffraction (XPD) Beamline at NSLS-II, NSLS-II, Brookhaven National Lab, 2010 Search PubMed.
- X. Shi, S. Ghose and E. Dooryhee, J. Synchrotron Radiat., 2013, 20, 234–242 CrossRef CAS.
- P. Juhas, T. Davis, C. L. Farrow and S. J. L. Billinge, J. Appl. Crystallogr., 2013, 46, 560–566 CrossRef CAS.
- R. B. Von Dreele and B. H. Toby, J. Appl. Crystallogr., 2013, 46, 544–549 CrossRef.
- V. F. Sears, Neutron News, 1992, 3, 26–37 CrossRef.
- X-ray Form Factor, Attenuation and Scattering Tables (version 2.1), http://physics.nist.gov/ffast, accessed March 2020 Search PubMed.
- C. L. Farrow, P. Juhas, J. W. Liu, D. Bryndin, E. S. Božin, J. Bloch, T. Proffen and S. J. L. Billinge, J. Phys.: Condens. Matter, 2007, 19, 335219 CrossRef CAS.
- G. Paglia, E. S. Božin, D. Vengust, D. Mihailovic and S. J. L. Billinge, Chem. Mater., 2006, 18, 100–106 CrossRef CAS.
- V. Petkov, S. J. L. Billinge, P. Larson, S. D. Mahanti, T. Vogt, K. K. Rangan and M. G. Kanatzidis, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 092105 CrossRef.
- R. B. Neder, F. Frey and H. Schulz, Acta Crystallogr., Sect. A: Found. Crystallogr., 1990, 46, 792–798 CrossRef.
- A. Navrotsky and O. J. Kleppa, Inorg. Chem., 1967, 6, 2119–2121 CrossRef CAS.
- A. Navrotsky, J. Am. Ceram. Soc., 2014, 97, 3349–3359 CrossRef CAS.
- A. Navrotsky, Phys. Chem. Miner., 1977, 2, 89–104 CrossRef CAS.
- A. Navrotsky, Phys. Chem. Miner., 1997, 24, 222–241 CrossRef CAS.
- A. Navrotsky, Am. Mineral., 2015, 100, 674–680 CrossRef.
- S. Hayun and A. Navrotsky, J. Solid State Chem., 2012, 187, 70–74 CrossRef CAS.
- V. L. Vegard, J. Mater. Sci., 1921, 1, 79–90 Search PubMed.
- K. R. Whittle, L. M. D. Cranswick, S. A. T. Redfern, I. P. Swainson and G. R. Lumpkin, J. Solid State Chem., 2009, 182, 442–450 CrossRef CAS.
- T. Egami and S. J. L. Billinge, Underneath the Bragg Peaks: Structural Analysis of Complex Materials, Pergamon, Oxford, 2012 Search PubMed.
- L. Cai and J. C. Nino, Acta Crystallogr., Sect. B: Struct. Sci., 2009, 65, 269–290 CrossRef CAS.
- J. H. Hildebrand, J. Am. Chem. Soc., 1929, 51, 66–80 CrossRef CAS.
- J. Ganguly, EMU Notes in Mineralogy, 2001, vol. 3, pp. 37–69 Search PubMed.
- R. A. Swalin, Am. J. Phys., 1962, 30, 778 CrossRef.
- D. K. Smith and W. Newkirk, Acta Crystallogr., 1965, 18, 983–991 CrossRef CAS.
- J. D. McCullough and K. N. Trueblood, Acta Crystallogr., 1959, 12, 507–511 CrossRef CAS.
- G. Pilania, B. Puchala and B. Uberuaga, npj Comput. Mater., 2019, 5, 7 CrossRef.
- C. L. Tracy, M. Lang, F. Zhang, C. Trautmann and R. C. Ewing, Phys. Rev. B, 2015, 92, 174101 CrossRef.
- P. K. Davies and A. Navrotsky, J. Solid State Chem., 1983, 46, 1–22 CrossRef CAS.
- P. S. Maram, S. V. Ushakov, R. J. K. Weber, C. J. Benmore and A. Navrotsky, Sci. Rep., 2018, 8, 1–11 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2020 |