Open Access Article
Open Access ArticleScreening of metal–organic frameworks for water adsorption heat transformation using structure–property relationships†
Min Xu *ab,
Zhangli Liuab,
Xiulan Huaiab,
Lanting Louab and
Jiangfeng Guoab
*ab,
Zhangli Liuab,
Xiulan Huaiab,
Lanting Louab and
Jiangfeng Guoab
aInstitute of Engineering Thermophysics, Chinese Academy of Sciences, Beijing, 100190, China. E-mail: xumin@iet.cn; Fax: +86-10-82543035; Tel: +86-10-82543035
bUniversity of Chinese Academy of Sciences, Beijing 100049, China
First published on 18th September 2020
Abstract
It is of great importance to correlate the water adsorption performance of MOFs to their physicochemical features in order to design and prepare MOFs for applications in adsorption heat transformation. In this work, both data analysis from existing studies and Grand Canonical Monte Carlo molecular simulation investigations were carried out. The results indicated that the highest water adsorption capacity was determined by the pore volume of MOF adsorbents, while there was a linear correlation interrelationship between isosteric heats of adsorption and the water adsorption performance at a low relative pressure. More detailed analysis showed that the charge distribution framework and pore size of MOFs contributed together to the hydrophilicity. Electrostatic interaction between water molecules and the framework atoms played a key role at low relative water pressure. A quantitative structure–property relationship model that can correlate the hydrophilicity of MOFs to their pore size and atomic partial charge was established. Along with some qualitative considerations, the screening methodology is proposed and is used to screen proper MOFs in the CoRE database. Seven MOFs were detected, and four of them were synthesized to validate the screening principle. The results indicated that these four MOFs possessed outstanding water adsorption performance and could be considered as promising candidates in applications for adsorption heating and cooling.
1. Introduction
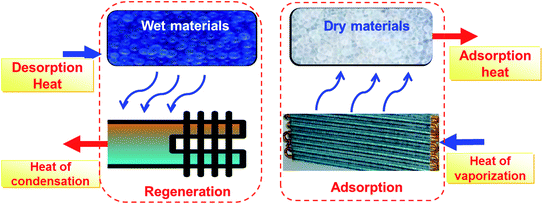
Energy is the foundation for human life and is an important resource for economic development. Recent decades have witnessed a huge increase in energy demand with the development of economy and increased resident living level in China. Energy consumption for space heating and cooling is a major proportion. By the end of 2016, the total heating area of urban and rural buildings in northern China was about 20.6 billion square meters, and the number is growing continuously. However, up to 83% of the energy demand for space heating is provided by coal. At present, about 400 million ton of standard coal is needed for heating in both rural and urban households.1 This clearly highlights the importance of fuel substitution and the transition to cleaner fuels for heating and cooling as a tool to decrease fossil fuel consumption and associated environmental issues. The utilization of solar energy has huge potential for heating and cooling purposes due to its intrinsic characteristics of wide distribution, abundant, clean, and renewable resource. Thermally driven adsorption heat transformation utilizing solar energy can be employed due to its advantages such as low driven or regeneration temperatures, extremely little electrical power demand, environment-friendly working medium and the potential of energy storage.2–4Fig. 1 shows the thermodynamic principle of an adsorption heat transformation (AHT). For the adsorption process, a working fluid (usually water) is evaporated when evaporation heat Qevap is introduced, and consequently adsorbed at porous materials where adsorption heat Qads is released. For the regeneration process, after saturation of the adsorbent, regeneration heat (solar thermal energy or waste heat) Qdes is applied, and water desorbs from adsorbents with the vapor condenser, releasing condensation heat Qcond. In the cooling case, Qevap serves as useful cold, and Qads + Qcond are rejected into the environment. In the heat pump and thermal energy storage case, Qevap is taken from the environment and Qads + Qcond is the useful heat. Water is the best green working fluid given its non-toxicity and high enthalpy of evaporation.
The porous materials, as the adsorbent, play an important role in the performance of the heat transformation. The water uptake, hydrophilicity, and desorption hysteresis of the used materials directly determine the available driving temperatures, relative working pressure, price and efficiency of the heat transformation. Silica gel, zeolites and composite superabsorbent polymers5–10 have been widely used for adsorption-based heat pumps and chillers. However, some drawbacks of these adsorbents have been identified, such as an insufficient adsorption capacity at a low relative pressure and/or a high regeneration temperature. In recent years, porous metal–organic frameworks (MOFs) have been considered a new class of water adsorbents due to the fact that MOFs exhibit a distinct tunability of their structural and hydrophilic properties. By using MOF/water working pairs, much significant progress has been achieved in the fields of adsorption heat transformation.11–13 Furukawa et al.14 prepared a series of zirconium(IV) MOFs by using various organic linkers. Among these materials, MOF-801 and MOF-841 showed the highest water adsorption performance. Cadiau et al.15 designed a hydrophilic Al-based MOF, named MIL-160, by using a linker with an aromatic ring incorporating a polar heteroatom (2,5-furandicarboxylic acid). This material possesses a high water uptake of 0.35 g g−1 at low pressure (below p/p0 < 0.2) and excellent hydrothermally stability. Sohail et al.16 synthesized NH2-MIL-125 (Ti) derived from Ti(BuO)4 with high hydrothermal stability, showing a high water uptake of 0.55 g g−1 under p/p0 = 0.3. More recently, Wang et al.17 prepared a large-pore Zr-based MOF, MIP-200, which showed a high water uptake of 0.39 g g−1 under p/p0 = 0.25, facile regeneration at low temperatures (<70 °C) and stable cycling. Lenzen et al.18 designed and synthesized an aluminum-based MOF (CAU-23) that showed a water adsorption capacity of 0.37 g g−1 around p/p0 = 0.3 and excellent cooling performance under driving temperatures down to 60 °C. Lee et al.19 developed three isostructural metal–organic frameworks (MOFs), named M-CUK-1 (where M = Co2+, Ni2+, or Mg2+), which showed step-like water adsorption isotherms, relatively high water sorption capacities (0.3 g g−1) at low p/p0, stable cycling, facile regeneration, and benchmark coefficient of performance values for cooling and heating at a low driving temperature. Luna-Triguero et al.20 found that a recently synthesized Zr-based MOF, ZJNU-30,21 showed record-breaking water sorption capacity (1.2 g g−1), cooling capacity (550 kW h m−3), and COP for cooling applications (0.948) through GCMC simulation. Besides these new synthesized MOFs, some considerable work has been devoted to the performance enhancement of the existing materials, such as MIL-101, UiO-66,22 MOF-801![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 23 and CAU-11. For example, the group of Prof. Janiak24,25 carried many studies to modify the Al-based MOFs to improve their performance for the application of AHT.
23 and CAU-11. For example, the group of Prof. Janiak24,25 carried many studies to modify the Al-based MOFs to improve their performance for the application of AHT.
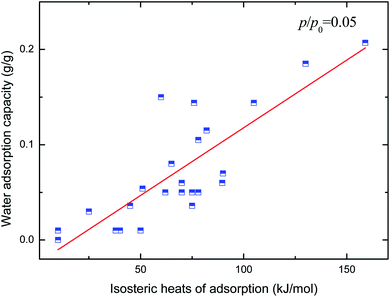
Although the above-mentioned MOFs possess good potential for application as adsorption heat pumps or chillers, there is still a long way to go to obtain practical materials with excellent performance. The best approach to guide the design and preparation of the materials is still unclear. It is necessary to understand the quantitative relationship between the water adsorption performance and the physicochemical features of the MOFs. Based on a set of 15 MOFs exhibiting various pore sizes, topology and surface functions, Canivet et al.26 investigated the water uptake and the hydrophobicity–hydrophilicity of the materials. In addition, the influences of the surface chemistry and pore size were discussed. Recently, the high-throughput screening of MOFs for gas sorption or storage has been reported with the help of GCMC simulations due to the enhancement of the power and speed of computing.27–30 However, the calculation of detailed adsorption isotherms for thousands of structures is still an expensive computational cost. Also, the GCMC computation accuracy is hugely dependent on the force field used for MOFs or adsorbate molecules. The reliability of the simulation results may be in doubt without experimental verification. Therefore, a simple and quantitative understanding of the structure–property relationship, which can directly evaluate the performance of the porous materials based on their physicochemical features, is needed based on a large library of MOF materials. Simply put, deriving the quantitative structure–property relationship models that could rationalize the performance of a large series of MOFs for a targeted application could be invaluable for not only predicting the characteristics of a given MOF, but for further guiding the design and preparation of advanced materials with enhanced performance.
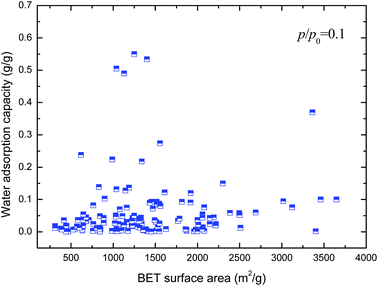
In light of the above considerations, this paper aims to understand the relations of the pore volumes, surface areas, pore sizes, and heat of adsorption of the MOFs with their calculated and experimental water adsorption capacities (include maximum water uptake, pressure at which pore filling occurs and so on) based on a set of 230 experimental and simulation data. The Grand Canonical Monte Carlo (GCMC) molecular simulation investigations were also performed to further reveal the detailed connection between the physicochemical features of MOFs and their water adsorption properties at the molecular scale. Quantitative structure–property relationship models were obtained. Subsequently, a simple screening method to find the advanced materials with enhanced water adsorption performances is proposed, which is verified by using the CoRE MOF database. Finally, 7 MOFs with predicted remarkable water sorption performance were obtained, and 4 of them were prepared. All of these synthesized materials exhibited excellent water adsorption performance.
2. Method
2.1. Data collection
Water adsorption capacities reported in the literature for various MOFs with open-metal sites were taken into consideration in this study to reveal quantitative relationships between the structural characteristics of these materials and their measured/simulated adsorption capacities. 230 data available for 55 different MOFs were utilized in the investigations, as shown in Table S1 in the ESI.† Most of these were obtained from the review of de Lange et al.,11 and the latest reported data in recent years were included. The structure properties, such as pore volumes, surface areas and pore size that can be directly measured and/or evaluated based on a specified MOF, were collected. The maximum water uptake, heats of adsorption, and relative pressure for which half of the largest water adsorption capacity (represents hydrophilicity) was reached were also collected for the corresponding MOFs.2.2. GCMC simulation
Grand Canonical Monte Carlo (GCMC) simulations were employed to calculate the adsorption of water in the MOFs at 298 K. We placed an emphasis on the influence of electrostatic interactions and pore size. UiO-66(Zr) and Na-rho-ZMOF were used in this study due to their different physicochemical features and pore size. Their framework structures were constructed from their corresponding experimental single-crystal diffraction data.31,32 All of the MOFs were treated as rigid frameworks with atoms frozen at their crystallographic positions. A cutoff radius was set to 1.2 nm for the LJ interactions, while the long-range electrostatic interactions were handled by the Ewald summation technique. Periodic boundary conditions were considered in all three dimensions. For each state point, GCMC simulations consisted of 1 × 107 steps to ensure the equilibration, followed by 1 × 107 steps to sample the desired thermodynamic properties. In addition, to obtain accurate ensemble averages in GCMC simulations, at least millions of configurations generated by random translation, rotation, regrowth, and swap moves were sampled in each simulation. The reliable force fields for the adsorbed molecules and MOFs, as well as the atomic partial charges for the atoms in UiO-66(Zr)33 and Na-rho-ZMOF (ref. 34) used in this study are listed in the ESI.†In this study, the TIP4P and TIP3P water model was used to describe the water–water interactions for UiO-66(Zr) and Na-rho-ZMOF, respectively. Table S2 and Fig. S1† list the corresponding LJ parameters and atomic charges. For both MOFs, a combination of the LJ and coulombic potential was employed to calculate the interactions between adsorbents and frameworks. The LJ potential parameters for the framework atoms were taken from the Dreiding force field,35 and the missing parameters for the metal were taken from the Universal force field36 for the water adsorption in UiO-66(Zr). It should be noted that the LJ parameters of the force field were rescaled in this work by reducing or increasing their values by 30% (εused = 0.70ε and σused = 1.30σ) to better represent the experimental adsorption isotherms of water in UiO-66(Zr). However, all parameters were taken from the Universal force field for that in Na-rho-ZMOF as listed in Table S2 in the ESI.†
3. Results and Discussion
3.1. Structure–property relationships
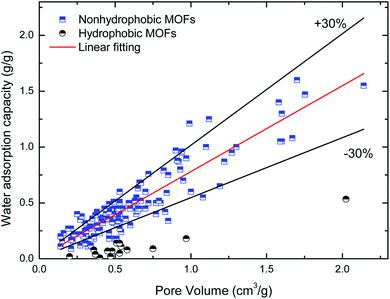
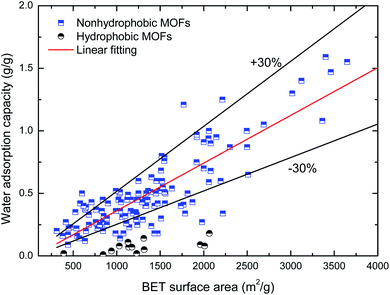
| qmax = 0.781Vp + 0.012 | (1) |
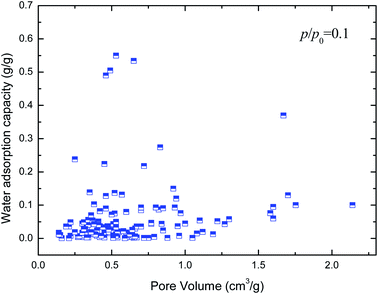
Unfortunately, the isosteric heats of adsorption cannot be directly obtained through the structural properties of the porous materials. Therefore, it is necessary to identify the structural parameters that can be related to the hydrophilicity. As we all know, the smaller pore size of a porous material leads to a deeper overlap of the potential, thus resulting in the stronger adsorption of adsorbates. Also, electrostatic interactions (Coulomb interactions) are an important factor due to the fact that water is a highly polar molecule and the atomic charge distribution of MOFs is significantly varied.41–43 Therefore, the influence of pore size and atomic charge distribution of MOFs on the water uptake must be investigated. In this work, a GCMC study was carried out on the adsorption of water in two types of MOFs with various pore sizes and charge distribution of frameworks, i.e., UiO-66(Zr) and Na-rho-ZMOF. The former possesses pore sizes of 6–11 Å, while the latter exhibits larger pore diameters (18.2 Å), and an anionic framework and charge-balancing non-framework ions, which enhance the non-uniformity of the atomic charge distribution. To determine the effect of the electrostatic interactions on the water adsorption isotherm, additional GCMC simulations were performed, that is, the electrostatic interactions between the water molecules and the MOFs were switched off. The results are shown in Fig. 7. The comparison of the GCMC results in our study and the experimental or simulation data in the literature is also depicted for both MOFs, and the results are acceptable, except for the water uptake values of UiO-66(Zr) at higher pressure. The center-of-mass distributions of H2O adsorbed on UiO-66(Zr) and Na-rho-ZMOF at 298 K and various relative pressures are shown in Fig. 8 and 9, respectively. For UiO-66(Zr), water molecules are preferentially adsorbed on the unsaturated metal sites and the neighboring areas of H atoms in the ligand at a low relative pressure. With increasing relative pressure, the adsorbed amounts of water increase gradually due to the interaction between water molecules. The situation changes for Na-rho-ZMOF, where the adsorbed water molecules interact more strongly with the non-framework Na ions even at a fairly low relative pressure. This illustrates the critical influence of electrostatic interactions on the water adsorption.
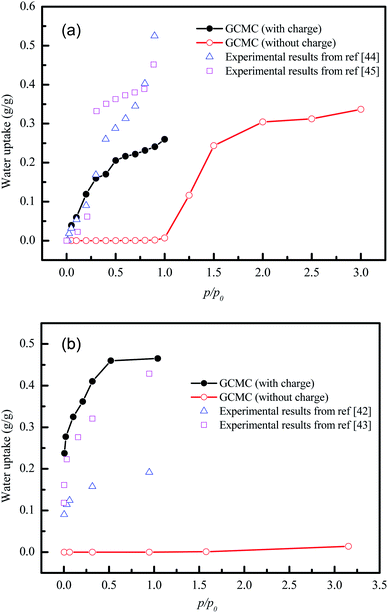 | ||
| Fig. 7 Water adsorption isotherms from GCMC simulation of UiO-66(Zr) (a) and Na-rho-ZMOF (b) with and without charge. | ||
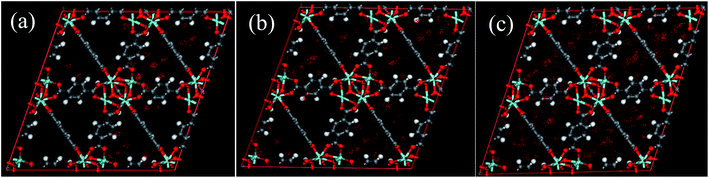 | ||
| Fig. 8 The center-of-mass distributions of H2O adsorbed UiO-66(Zr) at 298 K. (a) p/p0 = 0.1; (b) p/p0 = 0.3; (c) p/p0,a = 0.9. | ||
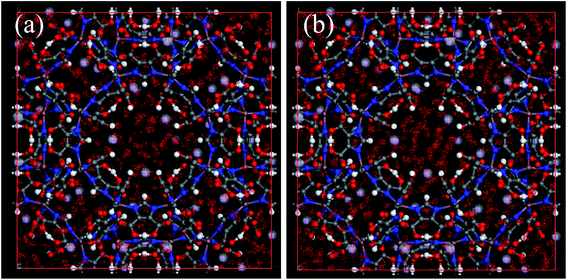 | ||
| Fig. 9 The center-of-mass distributions of H2O adsorbed Na-rho-ZMOF at 298 K. (a) p/p0 = 0.01; (b) p/p0 = 0.3. | ||
Also, it is shown that huge differences in the water isotherm are found when all atomic charges are zero for both MOFs, demonstrating that the electrostatic interactions play a significant role in the hydrophilicity. The polarity of water leads to this phenomenon. It can also be concluded that the greater effect of electrostatic interactions is shown for water sorption in Na-rho-ZMOF, which exhibits few adsorption sites even at p/p0 > 3 when the atomic charges are zero. However, UiO-66(Zr) without atomic charges can adsorb a large number of water molecules at p/p0 > 1.5. This can be attributed to the influence of pore size. UiO-66(Zr) with smaller pore sizes shows a higher adsorption capacity of water at low relative pressure when all atomic charges are set to zero. These results illustrate the influence of pore size and atomic charge distributions on hydrophilicity once again.
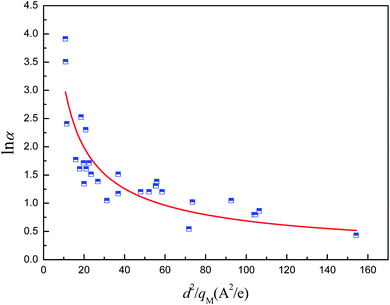
To address the issues mentioned above, the relationship between α (relative pressure for which capacity is 50% of qmax) and both pore size and atomic charges was studied. The metal partial charge and the pore limited diameter were used to simplify the correlation. The results are depicted in Fig. 10. It can be shown that ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α is related to d2/qM with the R2 of 0.776, demonstrating that the hydrophilicity can be predicted by the metal partial charge and the pore limited diameter. The correlation for ln
α is related to d2/qM with the R2 of 0.776, demonstrating that the hydrophilicity can be predicted by the metal partial charge and the pore limited diameter. The correlation for ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α and d2/qM at the maximum is shown in eqn (2). It should be noted that the presence of hydrophilic or hydrophobic functional groups could reduce the predicted accuracy of this correlation. The hydrophilicity should be overestimated when the MOFs were constructed with ligands with hydrophobic functional groups. For example, the α for MIL-101(Cr)-NH2 can be overestimated by a factor of 6.95%, which may be acceptable for the screening.
α and d2/qM at the maximum is shown in eqn (2). It should be noted that the presence of hydrophilic or hydrophobic functional groups could reduce the predicted accuracy of this correlation. The hydrophilicity should be overestimated when the MOFs were constructed with ligands with hydrophobic functional groups. For example, the α for MIL-101(Cr)-NH2 can be overestimated by a factor of 6.95%, which may be acceptable for the screening.
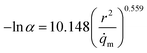 | (2) |
3.2. Screening methodology
In this section, a simple method is built to screen the promising MOFs or evaluate the performance of a given MOF by considering the quantitative analysis of the structure–property relationship mentioned above and some qualitative investigations. Four steps were needed in our study. The detailed description of the screening methodology is presented below.3.3. Verification
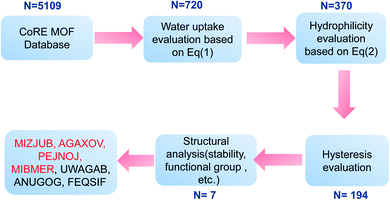
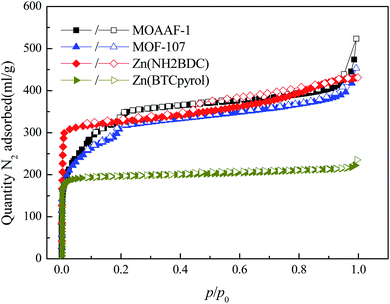
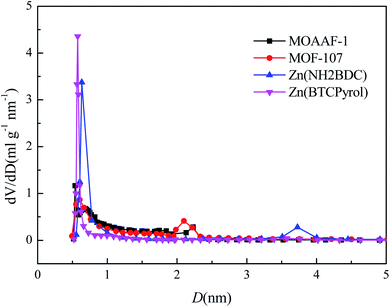
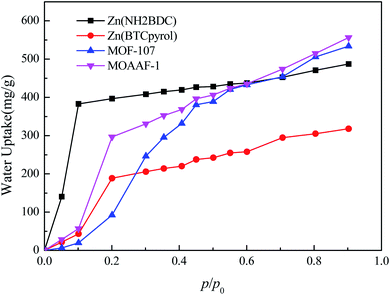
The Computation-Ready, Experimental (CoRE) database46 containing geometric data for 5109 structures was used to verify the screening method mentioned above. The workflow of the simple screening strategy employed in this work is shown in Fig. 11. In step 1, maximum water adsorption capacities of all MOFs in the database were evaluated based on eqn (1). The results indicate that 720 MOFs remained that exhibit a water uptake of up to 0.6 g g−1, and the other were eliminated with no more consideration. In step 2, α was evaluated based on eqn (2), in which PLD was used as pore diameter d and the atomic charges were calculated through the CBAC method.47 After this step, 370 MOFs remained. In steps 3 and 4, hysteresis evaluation and structural analysis were carried out and only 7 MOFs (MIZJUB, AGAXOV, PEJNOJ, MIBMER, UWAGAB, ANUGOG, and FEQSIF) were screened and considered as the potential materials for adsorption heat pumps.To further verify the availability of the screening method, 4 MOFs (MOAAF-1(Zn),48 MOF-107(Cu),49 Zn(NH2BDC),50 and Zn(BTCpyrol)51) among these screened materials were prepared, and the synthesis and activation methods are shown in the ESI.† The other 3 MOFs were not synthesized since the required ligands were expensive and difficult to obtain. The XRD patterns and SEM pictures of the as-prepared MOFs are shown in Fig. S2–S6.† Nitrogen adsorption/desorption isotherms and pore diameter distributions for the as-prepared MOFs are shown in Fig. 12 and 13. The results indicate that the N2 adsorption isotherms of the samples belong to type I with excellent microporosity, and a few mesopores also appear in MOAAF-1(Zn), MOF-107(Cu), and Zn(NH2BDC). The comparison of pore structure between the theoretical predicted results and the experimental data from the as-prepared MOFs is depicted in Table 1. It can be seen that the experimental BET surface areas of the as-prepared MOFs are lower than those of the ideal values while their total pore volumes are similar, except for Zn(BTCpyrol). This highlights the deviation between the ideal crystal and the as-synthesized one and/or the inappropriate activation methods. Fig. 14 depicts the water sorption isotherms for the as-prepared MOFs at 298 K. The water sorption isotherms of all 4 MOFs possess a sigmoidal shape. Most of the water uptake occurs at p/p0 < 0.2, except for MOF-107(Cu). The maximum water uptake at 298 K progresses as MOAAF-1(Zn) (0.557 g g−1) > MOF-107(Cu) (0.534 g g−1) > Zn(NH2BDC) (0.487 g g−1) > Zn(BTCpyrol) (0.318 g g−1). The hydrophilicity of the MOFs ranks as Zn(NH2BDC) > MOAAF-1(Zn) > Zn(BTCpyrol) > MOF-107(Cu). Zn(NH2BDC) and MOAAF-1(Zn) are recommended as potential materials for adsorption heat pumps due to their excellent water uptake and appropriate hydrophilicity. Zn(NH2BDC) exhibits a high equilibrium water uptake of 0.408 g g−1 at 25 °C and p/p0 = 0.3. This uptake is higher than those of the selected benchmark water adsorbents: 0.29 g g−1 (SAPO-34),11 0.20 g g−1 (silica gel),11 0.35 g g−1 (MIL-160),15 0.30 g g−1(CAU-10),11 0.28 g g−1 (MOF-801),14 0.30 g g−1 (Co-CUK-1),19 0.37 g g−1 (LTA-AlPO4),52 0.375 g g−1 (CAU-23)18 and 0.39 g g−1 (MIP-200).17 It should also be noted that no obvious loss of crystallinity was observed for Zn(NH2BDC) after an adsorption–desorption cycle, demonstrating its application prospect, although more work should be carried out.
| Samples | Sta (m2 g−1) | SBETb (m2 g−1) | Vp,tc (mL g−1) | Vp,ed (mL g−1) | qmax,pe (g g−1) | qmax,pf (g g−1) | qmax,eg (g g−1) | αph (—) | αei (—) |
|---|---|---|---|---|---|---|---|---|---|
| a Theoretical surface area.b Experimental BET surface area.c Theoretical pore volume.d Experimental pore volume.e Predicted qmax based on the theoretical pore volume.f Predicted qmax based on the experimental pore volume.g Experimental qmax.h Predicted α based on theoretical pore size.i Experimental α. | |||||||||
| MOAAF-1(Zn) | 2943.50 | 1221.78 | 0.884 | 0.780 | 0.692 | 0.620 | 0.557 | 0.133 | ∼0.18 |
| MOF-107(Cu) | 2760.67 | 1002.29 | 0.801 | 0.581 | 0.632 | 0.466 | 0.534 | 0.184 | ∼0.30 |
| Zn(NH2BDC) | 2078.60 | 827.03 | 0.773 | 0.666 | 0.605 | 0.532 | 0.487 | 0.160 | ∼0.08 |
| Zn(BTCpyrol) | 2251.23 | 555.65 | 0.766 | 0.343 | 0.600 | 0.280 | 0.318 | 0.133 | ∼0.15 |
Table 1 also lists the comparison of experimental and predicted water adsorption performance of as-prepared MOFs. The results indicate that the experimental maximum water uptake of the four MOFs is lower than the predicted values based on the theoretical pore volume with deviation within 30%, except for Zn(BTCpyrol), while all of them are close to the predicted values based on the experimental pore volume. The experimental α of the four MOFs is similar to the predicted ones, except for MOF-107(Cu) and Zn(NH2BDC). The experimental α of MOF-107(Cu) is higher than the calculated one due to the larger pore size of the as-prepared sample, while that of Zn(NH2BDC) is lower than the evaluated one due to the presence of hydrophilic –NH2 groups.
Although some materials were undoubtedly missed, it may be concluded that the screening method proposed in this work is available to identify potential materials or evaluate the performance of a MOF with the given structural properties quickly for the application of adsorption heat transformation, especially when the computing power is limited.
4. Conclusions
Focusing on the screening of more appropriate MOFs with better water adsorption performance for the application of adsorption heat pumps, we investigated the structure–property relationships of MOFs for water adsorption with the aid of GCMC molecular modeling combined with data analysis reported in the literature. This study shows that pore volume is a crucial feature of the MOFs that determines the adsorption capacities of the MOFs at high relative water pressure. The results further highlight that there is a linear correlation interrelationship between the heats of adsorption and the water adsorption capacities of the MOFs at low humidity. Specifically, the electrostatic interactions and pore size play a dominant role in the water adsorption capacities at low relative water pressures. The GCMC study shows that the electrostatic interactions produced by the atomic charges of the frameworks largely dominate the adsorption of water molecules with intrinsic polarities at the initial stage of the adsorption. Moreover, two structure–property relationship models and a simple screening methodology were proposed to quantitatively and qualitatively guide the screening of potential MOFs with excellent water adsorption performance, which was tested and verified by using the CoRE MOF database. Finally, seven potential MOFs for the application of adsorption heat pumps and chillers were identified. Four of them were synthesized, and their water isotherms were measured. The results demonstrated the utility of the screening methodology in this work and two MOFs, i.e., Zn(NH2BDC) and MOAAF-1(Zn), were recommended as promising materials for adsorption-driven heat pumps and chillers.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Key R&D Program of China (No. 2016YFB0601701) and the National Natural Science Foundation of China (No. 51836009 and 51776202).References
- Winter clean heating plan in northern China (2017–2021), 2017, http://www.nea.gov.cn/2017-12/27/c_136854721.htm Search PubMed.
- P. Goyal, P. Baredar, A. Mittal and A. R. Siddiqui, Adsorption refrigeration technology-An overview of theory and its solar energy applications, Renew. Sustain. Energy Rev., 2016, 53, 1389–1410 CrossRef CAS.
- H. Demir, M. Mobedi and S. Ülkü, A review on adsorption heat pump: Problems and solutions, Renew. Sustain. Energy Rev., 2008, 12, 2381–2403 CrossRef.
- Y. I. Aristov, Adsorptive transformation and storage of renewable heat: Review of current trends in adsorption dynamics, Renewable Energy, 2017, 110, 105–114 CrossRef.
- P. Vivekh, M. Kumja, D. T. Bui and K. J. Chua, Recent developments in solid desiccant coated heat exchangers–A review, Appl. Energy, 2018, 229, 778–803 CrossRef.
- P. Vivekh, D. T. Bui, M. R. Islam, K. Zaw and K. J. Chua, Experimental performance and energy efficiency investigation of composite superabsorbent polymer and potassium formate coated heat exchangers, Appl. Energy, 2020, 275, 115428 CrossRef CAS.
- P. Vivekh, D. T. Bui, M. R. Islam, K. Zaw and K. J. Chua, Experimental performance evaluation of desiccant coated heat exchangers from a combined first and second law of thermodynamics perspective, Energy Convers. Manage., 2020, 207, 112518 CrossRef.
- P. Vivekh, M. R. Islam and K. J. Chua, Experimental performance evaluation of a composite superabsorbent polymer coated heat exchanger based air dehumidification system, Appl. Energy, 2020, 260, 114256 CrossRef CAS.
- P. Vivekh, D. T. Bui, M. Kumja, M. R. Islam and K. J. Chua, Theoretical performance analysis of silica gel and composite polymer desiccant coated heat exchangers based on a CFD approach, Energy Convers. Manage., 2019, 187, 423–446 CrossRef CAS.
- P. Vivekh, D. T. Bui, Y. Wong, M. Kumja and K. J. Chua, Performance evaluation of PVA-LiCl coated heat exchangers for next-generation of energy-efficient dehumidification, Appl. Energy, 2019, 237, 733–750 CrossRef CAS.
- M. F. de Lange, K. J. F. M. Verouden, T. J. H. Vlugt, J. Gascon and F. Kapteijn, Adsorption-Driven Heat Pumps: The Potential of Metal-Organic Frameworks, Chem. Rev., 2015, 115, 12205–12250 CrossRef CAS.
- A. Karmakara, V. Prabakaranb, D. Zhao and K. J. Chua, A review of metal–organic frameworks (MOFs) as energy-efficient desiccants for adsorption driven heat-transformation applications, Appl. Energy, 2020, 269, 115070 CrossRef.
- A. Karmakar, P. G. M. Mileo, I. Bok, S. B. Peh, J. Zhang, H. Yuan, G. Maurin and D. Zhao, Thermo-Responsive MOF/Polymer Composites for Temperature-Mediated Water Capture and Release, Angew. Chem., Int. Ed., 2020, 59, 11003–11009 CrossRef CAS.
- H. Furukawa, F. Gándara, Y. B. Zhang, J. Jiang and W. L. Queen, Water adsorption in porous metal–organic frameworks and related materials, J. Am. Chem. Soc., 2014, 136, 4369–4381 CrossRef CAS.
- A. Cadiau, J. S. Lee, D. D. Borges, P. Fabry, T. Devic, M. T. Wharmby, C. Martineau, D. Foucher, F. Taulelle, C. H. Jun, Y. K. Hwang, N. Stock, M. F. de Lange, F. Kapteijn, J. Gascon, G. Maurin, J. S. Chang and C. Serre, Design of hydrophilic metal–organic framework water adsorbents for heat reallocation, Adv. Mater., 2015, 27, 4775–4780 CrossRef CAS.
- M. Sohail, Y. N. Yun, E. Lee, S. K. Kim, K. Cho, J. N. Kim, T. W. Kim, J. H. Moon and H. Kim, Synthesis of Highly Crystalline NH2-MIL-125 (Ti) with S-shaped water isotherms for adsorption heat transformation, Cryst. Growth Des., 2017, 17, 1208–1213 CrossRef CAS.
- S. Wang, J. S. Lee, M. Wahiduzzaman, J. Park, M. Muschi, C. Martineau-Corcos, A. Tissot, K. H. Cho, J. Marrot, W. Shepard, G. Maurin, J. S. Chang and C. Serre, A robust large-pore zirconium carboxylate metal–organic framework for energy-efficient water-sorption-driven refrigeration, Nat. Energy, 2018, 3, 985–993 CrossRef CAS.
- D. Lenzen, J. Zhao, S. J. Ernst, M. Wahiduzzaman, A. K. Inge, D. Fröhlich, H. Xu, H. J. Bart, C. Janiak, S. Henninger, G. Maurin, X. Zou and N. Stock, A metal–organic framework for efficient water-based ultra-low-temperature-driven cooling, Nat. Commun., 2019, 10, 3025 CrossRef.
- J. S. Lee, J. W. Yoon, P. G. M. Mileo, K. H. Cho, J. Park, K. Kim, H. Kim, M. F. de Lange, F. Kapteijn, G. Maurin, S. M. Humphrey and J. S. Chang, Porous metal–organic framework CUK-1 for adsorption heat allocation toward green applications of natural refrigerant water, ACS Appl. Mater. Interfaces, 2019, 11, 25778–25789 CrossRef CAS.
- A. Luna-Triguero, A. Sławek, H. P. Huinink, T. J. H. Vlugt, A. Poursaeidesfahani, J. M. Vicent-Luna and S. Calero, Enhancing the water capacity in Zr-Based metal–organic framework for heat pump and atmospheric water generator applications, ACS Appl. Nano Mater., 2019, 2, 3050–3059 CrossRef CAS.
- H. Liu, Y. He, J. Jiao, D. Bai, D. L. Chen, R. Krishna and B. Chen, A Porous Zirconium-based metal–organic framework with the potential for the separation of butene isomers, Chem.–Eur. J., 2016, 22, 1–11 CrossRef CAS.
- B. Han and A. Chakraborty, Advanced cooling heat pump and desalination employing functional UiO-66 (Zr) metal–organic frameworks, Energy Convers. Manage., 2020, 213, 112825 CrossRef CAS.
- B. Han and A. Chakraborty, Adsorption characteristics of methyl-functional ligand MOF-801 and water systems: Adsorption chiller modelling and performances, Appl. Therm. Eng., 2020, 175, 115393 CrossRef CAS.
- C. Schlüsener, M. Xhinovci, S.-J. Ernst, A. Schmitz, N. Tannert and C. Janiak, Solid-Solution mixed-minker synthesis of isoreticular Al-based MOFs for an easy hydrophilicity tuning in water-sorption heat transformations, Chem. Mater., 2019, 31, 4051–4062 CrossRef.
- N. Tannertx, C. Jansenx, S. Nießing and C. Janiak, Robust synthesis routes and porosity of Al-based metal–organic frameworks Al-fumarate, CAU-10-H and MIL-160, Dalton Trans., 2019, 48, 2967–2976 RSC.
- J. Canivet, J. Bonnefoy, C. Daniel, A. Legrand, B. Coasne and D. Farrusseng, Structure–property relationships of water adsorption in metal–organic frameworks, New J. Chem., 2014, 38, 3102–3111 RSC.
- C. E. Wilmer, M. Leaf, C. Y. Lee, O. K. Farha, B. G. Hauser, J. T. Hupp and R. Q. Snurr, Large-scale screening of hypothetical metal–organic frameworks, Nat. Chem., 2012, 4, 83–89 CrossRef CAS.
- M. Erdős, M. F. de Lange, F. Kapteijn, O. A. Moultos and T. J. H. Vlugt, In silico screening of metal–organic frameworks for adsorption-driven heat pumps and chillers, ACS Appl. Mater. Interfaces, 2018, 10, 27074–27087 CrossRef.
- F. Zhou, B. Zheng, D. Liu, Z. Wang and Q. Yang, Large-scale structural refinement and screening of zirconium metal–organic frameworks for H2S/CH4 separation, ACS Appl. Mater. Interfaces, 2019, 11, 46984–46992 CrossRef CAS.
- L. Wilbraham, E. Berardo, L. Turcani, K. E. Jelfs and M. A. Zwijnenburg, High-throughput screening approach for the optoelectronic properties of conjugated polymers, J. Chem. Inf. Model., 2018, 58, 2450–2459 CrossRef CAS.
- J. H. Cavka, S. Jakobsen, U. Olsbye, N. Guillou, C. Lamberti, S. Bordiga and K. P. Lillerud, A new zirconium inorganic building brick forming metal–organic frameworks with exceptional stability, J. Am. Chem. Soc., 2008, 130, 13850–13851 CrossRef.
- Y. Liu, V. C. Kravtsov, R. Larsen and M. Eddaoudi, Molecular building blocks approach to the assembly of zeolite-like metal–organic frameworks (ZMOFs) with extra-large cavities, Chem. Commun., 2006, 1488–1490 RSC.
- Q. Yang, A. D. Wiersum, P. L. Llewellyn, V. Guillerm, C. Serre and G. Maurin, Functionalizing porous zirconium terephthalate UiO-66(Zr) for natural gas upgrading: A computational exploration, Chem. Commun., 2011, 47, 9603–9605 RSC.
- R. Babarao and J. Jiang, Upgrade of natural gas in rho zeolite-like metal–organic framework and effect of water: a computational study, Energy Environ. Sci., 2009, 2, 1088–1093 RSC.
- S. L. Mayo, B. D. Olafson and W. A. Goddard III, A generic force field for molecular simulations, J. Phys. Chem., 1990, 94, 8897–8909 CrossRef CAS.
- A. K. Rappe, C. J. Casewit, K. S. Colwell, W. A. Goddard III and W. M. Skiff, UFF, a full periodic table force field for molecular mechanics and molecular dynamics simulations, J. Am. Chem. Soc., 1992, 114, 10024–10035 CrossRef CAS.
- S. Wang, Comparative molecular simulation study of methane adsorption in metal–organic frameworks, Energy Fuels, 2007, 21, 953–956 CrossRef CAS.
- H. Frost, T. Düren and R. Q. Snurr, Effects of surface area, free volume, and heat of adsorption on hydrogen uptake in metal–organic frameworks, J. Phys. Chem. B, 2006, 110, 9565–9570 CrossRef CAS.
- Q. Yang and C. Zhong, Electrostatic-Field-Induced enhancement of gas mixture separation in metal–organic frameworks: A computational study, ChemPhysChem, 2006, 7, 1417–1421 CrossRef CAS.
- Q. Yang, C. Zhong and J. F. Chen, Computational study of CO2 storage in Metal-Organic Frameworks, J. Phys. Chem. C, 2008, 112, 1562–1569 CrossRef CAS.
- X. Peng, L. C. Lin, W. Sun and B. Smit, Water adsorption in metal–organic frameworks with open-metal sites, AIChE J., 2015, 61, 677–687 CrossRef CAS.
- A. Nalaparaju, X. S. Zhao and J. W. Jiang, Molecular understanding for the adsorption of water and alcohols in hydrophilic and hydrophobic zeolitic metal–organic frameworks, J. Phys. Chem. C, 2010, 114, 11542–11550 CrossRef CAS.
- A. Nalaparaju, R. Babarao, X. S. Zhao and J. W. Jiang, Atomistic insight into adsorption, mobility, and vibration of water in ion-exchanged zeolite-like metal–organic frameworks, ACS Nano, 2009, 3, 2563–2572 CrossRef CAS.
- F. Jeremias, V. Lozan, S. K. Henninger and C. Janiak, Programming MOFs for water sorption: amino-functionalized MIL-125 and UiO-66 for heat transformation and heat storage applications, Dalton Trans., 2013, 42, 15967–15973 RSC.
- P. M. Schoenecker, C. G. Carson, H. Jasuja, C. J. J. Flemming and K. S. Walton, Effect of water adsorption on retention of structure and surface area of metal–organic frameworks, Ind. Eng. Chem. Res., 2012, 51, 6513–6519 CrossRef CAS.
- Y. G. Chung, J. Camp, M. Haranczyk, B. J. Sikora, W. Bury, V. Krungleviciute, T. Yildirim, O. K. Farha, D. S. Sholl and R. Q. Snurr, Computation-ready, experimental metal–organic frameworks: A tool to enable high-throughput screening of nanoporous crystals, Chem. Mater., 2014, 26, 6185–6192 CrossRef CAS.
- Q. Xu and C. Zhong, A general approach for estimating framework charges in metal–organic frameworks, J. Phys. Chem. C, 2010, 114, 5035–5042 CrossRef CAS.
- M. J. Manos, E. E. Moushi, G. S. Papaefstathiou and A. J. Tasiopoulos, New Zn2+ metal–organic frameworks with unique network topologies from the combination of trimesic acid and amino-alcohols, Cryst. Growth Des., 2012, 12, 5471–5480 CrossRef CAS.
- M. Eddaoudi, J. Kim, D. Vodak, A. Sudik, J. Wachter, M. O'Keeffe and O. M. Yaghi, Geometric requirements and examples of important structures in the assembly of square building blocks, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 4900–4904 CrossRef CAS.
- X. F. Wang, Y. B. Zhang, X. N. Cheng and X. M. Chen, Two microporous metal–organic frameworks with different topologies constructed from linear trinuclear M3(COO)n secondary building units, CrystEngComm, 2008, 10, 753–758 RSC.
- H. Yang, H. X. Zhang, D. C. Hou, T. H. Li and J. Zhang, Assembly between various molecular-building-blocks for network diversity of zinc–1,3,5-benzenetricarboxylate frameworks, CrystEngComm, 2012, 14, 8684–8688 RSC.
- A. Krajnc, J. Varlec, M. Mazaj, A. Ristić, N. Z. Logar and G. Mali, Superior performance of microporous aluminophosphate with LTA topology in solar-energy storage and heat reallocation, Adv. Energy Mater., 2017, 7, 1601815 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ra06363k |
| This journal is © The Royal Society of Chemistry 2020 |