Open Access Article
Open Access ArticleEfficiency of liquid tin(II) n-alkoxide initiators in the ring-opening polymerization of L-lactide: kinetic studies by non-isothermal differential scanning calorimetry†
Montira Sriyai abc,
Tawan Chaiwonac,
Robert Molloyd,
Puttinan Meepowpan
abc,
Tawan Chaiwonac,
Robert Molloyd,
Puttinan Meepowpan abd and
Winita Punyodom
abd and
Winita Punyodom *abd
*abd
aDepartment of Chemistry, Faculty of Science, Chiang Mai University, Chiang Mai 50200, Thailand
bCenter of Excellence for Innovation in Chemistry (PERCH-CIC), Faculty of Science, Chiang Mai University, Chiang Mai 50200, Thailand
cGraduate School, Chiang Mai University, Chiang Mai 50200, Thailand
dCenter of Excellence in Materials Science and Technology, Chiang Mai University, Chiang Mai 50200, Thailand. E-mail: winitacmu@gmail.com
First published on 8th December 2020
Abstract
Novel soluble liquid tin(II) n-butoxide (Sn(OnC4H9)2), tin(II) n-hexoxide (Sn(OnC6H13)2), and tin(II) n-octoxide (Sn(OnC8H17)2) initiators were synthesized for use as coordination–insertion initiators in the bulk ring-opening polymerization (ROP) of L-lactide (LLA). In order to compare their efficiencies with the more commonly used tin(II) 2-ethylhexanoate (stannous octoate, Sn(Oct)2) and conventional tin(II) octoate/n-alcohol (SnOct2/nROH) initiating systems, kinetic parameters derived from monomer conversion data were obtained from non-isothermal differential scanning calorimetry (DSC). In this work, the three non-isothermal DSC kinetic approaches including dynamic (Kissinger, Flynn–Wall, and Ozawa); isoconversional (Friedman, Kissinger–Akahira–Sunose (KAS) and Ozawa–Flynn–Wall (OFW)); and Borchardt and Daniels (B/D) methods of data analysis were compared. The kinetic results showed that, under the same conditions, the rate of polymerization for the 7 initiators/initiating systems was in the order of liquid Sn(OnC4H9)2 > Sn(Oct)2/nC4H9OH > Sn(Oct)2 ≅ liquid Sn(OnC6H13)2 > Sn(Oct)2/nC6H13OH ≅ liquid Sn(OnC8H17)2 > Sn(Oct)2/nC8H17OH. The lowest activation energies (Ea = 52, 59, and 56 kJ mol−1 for the Kissinger, Flynn–Wall, and Ozawa dynamic methods; Ea = 53–60, 55–58, and 60–62 kJ mol−1 for the Friedman, KAS, and OFW isoconversional methods; and Ea = 76–84 kJ mol−1 for the B/D) were found in the polymerizations using the novel liquid Sn(OnC4H9)2 as the initiator, thereby showing it to be the most efficient initiator in the ROP of L-lactide.
1. Introduction
Biodegradable aliphatic polyesters have attracted much interest as replacements for petroleum-based materials due to their environmentally friendly properties and derivability from renewable resources. The most popular and important biodegradable aliphatic polyesters are poly(L-lactide) (PLLA), polyglycolide (PGA), poly(ε-caprolactone) (PCL), and their other high molecular weight co- or terpolymers. Among these, PLA-based materials are of the most interest due to their biocompatibility and biodegradability in a broad range of applications, especially biomedical applications such as absorbable surgical sutures, controlled drug delivery systems, and bone fixation devices.1–5 Poly(lactic acid) (PLA) can be produced from lactic acid derived from the fermentation of renewable starch-containing resources such as corn, sugar beet, and cassava.6–8 Lactide (L) monomer is prepared by condensing lactic acid to low molecular weight PLA which is then thermally cracked to yield the six-membered ring lactide monomer. The crude lactide monomer can be purified by repeated recrystallization before being polymerized in bulk to form high molecular weight PLA.9Tin(II) 2-ethylhexanoate or stannous octoate (Sn(Oct)2) is the most common initiator used in the ROP of lactones and lactides due to its effectiveness and versatility. It is also easy to handle and is soluble in most common organic solvents and monomers.10–12 Moreover, it has been approved for use as a food additive by the US Food and Drug Administration (FDA). However, in order to improve its effectiveness, Sn(Oct)2 is usually used in combination with an alcohol co-initiator (ROH) as the initiating system.
Mechanistically, Kricheldorf and co-workers proposed the coordination of the Sn(Oct)2 and the alcohol with the cyclic ester monomer followed by ROP.13 In this mechanism, the Sn(Oct)2 serves as a catalyst while the alcohol is an initiator, as depicted in Fig. 1(a). However, Penczek et al. later suggested that the Sn(Oct)2 and the alcohol react together resulting in the formation of a tin(II) monoalkoxide ((Oct)Sn(OR)) and tin(II) dialkoxide (Sn(OR)2) which then become the ‘true’ initiators as shown in Fig. 1(b).14 This latter mechanism is now widely accepted as the true initiation pathway. Therefore, in order to produce high molecular weight polyesters via ROP, it is vitally important to know the exact concentration of the tin(II) alkoxide initiator which should be easily and completely soluble in the cyclic ester monomer.
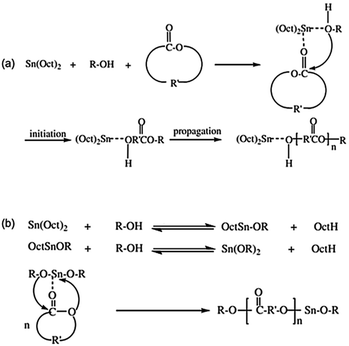 | ||
| Fig. 1 Comparison of the old (a) and the new (b) mechanistic proposals using Sn(Oct)2: (a) complexation of the monomer and alcohol prior to ROP and (b) formation of tin(II) alkoxide before ROP.13,14 | ||
As previously mentioned, it is now widely accepted that the tin(II) monoalkoxide, (Oct)Sn(OR), and/or the dialkoxide, Sn(OR)2, are the true initiators formed in situ via the reaction between Sn(Oct)2 and ROH. Since the coupled reactions in Fig. 1(b) are both reversible and interdependent, the exact initiator concentrations will be unknown. Moreover, stannous octoate is well known to be an effective transesterification catalyst, ROH can act as a chain transfer agent, and the octanoic acid (OctH) by-product can also catalyze other unwanted side-reactions. Thus, the kinetics of the ROP and the final molecular weight of the polymer cannot be accurately predicted. Therefore, in order to overcome this problem, it is logical to synthesize the tin(II) dialkoxide (Sn(OR)2) separately so that it can be used directly in an accurately known concentration.
The synthesis of solid tin(II) alkoxides has been known for over 50 years.15,16 However, they have been found to have their drawbacks as initiators, in particular their difficult solubility in cyclic ester monomers and common organic solvents and their instability in contact with air and moisture which is caused by their solid-state molecular self-aggregations as shown in Fig. 2(a) and (b). According to their low solubility in most organic solvents and cyclic ester monomers of these solid tin(II) alkoxides, the polymerizations of monomers such as L-lactide, D-lactide, DL-lactide, ε-caprolactone and other cyclic esters are relatively slow and ineffective.
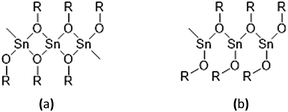 | ||
| Fig. 2 Molecular self-aggregations in solid tin(II) alkoxides: (a) angular aggregation and (b) linear aggregation. | ||
Consequently, in this work, some novel liquid soluble tin(II) alkoxides were prepared for use in the ROP of L-lactide in order to overcome the molecular self-aggregation difficulties found in previous works with solid tin(II) alkoxides. Meepowpan and co-workers have proposed a method for synthesizing soluble liquid Sn(OR)2 using stoichiometric amounts of anhydrous tin(II) chloride (SnCl2), diethylamine ((C2H5)2NH), and an alcohol (ROH).17 Because the liquid Sn(OR)2 is completely soluble, it leads to more reproducible results which, in turn, leads to a more detailed understanding of the kinetics and mechanism of the ROP reaction. Using the Sn(OR)2 initiator directly instead of generating it in situ should give more reproducible and predictable results in terms of both kinetic and molecular weight control compared with the Sn(Oct)2/ROH initiating system or Sn(Oct)2 alone.
In order to investigate the efficiency of the liquid tin(II) alkoxide initiators, the kinetics of the ROP of LA were investigated by measuring the decrease in the monomer concentration as a function of time. This can be done by a variety of methods such as dilatometry, gravimetry, proton-nuclear magnetic resonance (1H-NMR) spectroscopy, infrared (IR) spectroscopy, Raman spectroscopy, and differential scanning calorimetry (DSC).18–23
Among those aforementioned methods, DSC has been found to be a fast and convenient method for studying polymerization kinetics and for determining kinetic parameters such as monomer conversion (α), rate of polymerization (dα/dt), order of reaction (n), and activation energy (Ea) of the ROP of both liquid and solid cyclic ester monomers. Furthermore, with the advent of convenient software-based data analysis programs, the ability to obtain such kinetic information has become more practical compared to other techniques.24–27
DSC kinetic experiments can be performed under either isothermal or non-isothermal conditions. In isothermal DSC, the polymerization is conducted at a constant temperature while in non-isothermal DSC, polymerization occurs during a temperature scan at a constant heating rate. The conversion of monomer to polymer can be determined from the amount of heat released from the reaction at any time t (ΔHt) divided by the total heat of reaction (ΔHm). Then, from the monomer conversion, various kinetic parameters such as rate of polymerization (dα/dt), activation energy (Ea), and rate constant (k) can be determined.
However, due to the overlap of the endothermic lactide melting peak and the exothermic peak from its polymerization in isothermal DSC, as reported in previous work,24 only non-isothermal DSC studies of the ROP of LLA polymerization in bulk were carried out in this work.
2. Experimental
2.1. Purification of L-lactide monomer
Crude L-lactide (Bioplastic Production Laboratory for Medical Applications, ISO 13485:2016 Accredited Laboratory, Chiang Mai University) was purified by repeated (approximately three times) recrystallization from distilled ethyl acetate to yield pure L-lactide as a white, needle-like, crystalline solid. It was then dried to constant weight in a vacuum oven at 55 °C prior to being transferred to a controlled atmosphere glove box (Labconco) for use in synthesis. The final product of >99.9% purity was obtained in a percentage yield of 40–55%.2.2. Purification of Sn(Oct)2 initiator
Sn(Oct)2 (Sigma-Aldrich) was purified by bulb-to-bulb vacuum distillation. Firstly, Sn(Oct)2 was stirred under reduced pressure (high vacuum) at room temperature to remove residual water. Then, the 2-ethylhexanoic acid impurity was removed under vacuum distillation at 120–126 °C/15 Torr (boiling point = 140 °C/23 Torr).28 The purified Sn(Oct)2 remaining in the heating flask was obtained as a colorless viscous liquid and was stored over molecular sieves type 4 Å.2.3. Synthesis of liquid tin(II) n-alkoxide initiators
In this work, the synthesis of liquid tin(II) alkoxides for use as initiators in the ROP of L-lactide was as described in the novel modified method by Meepowpan et al.17 and shown in eqn (1):
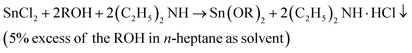 | (1) |
The synthesis process employed anhydrous tin(II) chloride (SnCl2, Sigma-Aldrich) dissolved in n-heptane (nC7H16, Sigma-Aldrich) mixed with dry diethylamine ((C2H5)2NH, Panreac). An alcohol, n-ROH, in which the R group was either n-C4H9, n-C6H13, or n-C8H17 (Labscan) was added to the reaction mixture and stirred for 12 hours. The reaction mixture of the diethylamine hydrochloride salt, the n-heptane solvent plus any residual alcohol, ROH, and diethylamine was then filtered under a nitrogen atmosphere before being evaporated to dryness. All of the three tin(II) alkoxides, namely: tin(II) n-butoxide (Sn(OnC4H9)2), tin(II) n-hexoxide (Sn(OnC6H13)2), and tin(II) n-octoxide (Sn(OnC8H17)2) were obtained as viscous, dark yellow liquids which were readily soluble in most common organic solvents such as chloroform, toluene, and n-heptane. Moreover, they could all be stored under an inert atmosphere for long periods i.e. up to 1 month without any significant change in their reactivity and, therefore, in their efficiency as initiators for the ROP of L-lactide. Fig. 3 shows chemical structures of stannous octoate and the three liquid tin(II) n-alkoxides synthesized in this work.
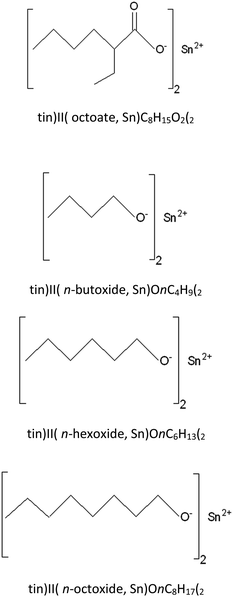 | ||
| Fig. 3 Chemical structures of: tin(II) octoate; tin(II) n-butoxide; tin(II) n-hexoxide; and tin(II) n-octoxide initiators. | ||
2.4. Kinetic studies by DSC
Non-isothermal DSC kinetic studies of the ROP of L-LA using the Sn(Oct)2; Sn(OnR)2 initiators and Sn(Oct)2/nROH initiating systems were performed on a PerkinElmer DSC 7 Differential Scanning Calorimeter under a flowing nitrogen (N2) atmosphere (20 mL min−1). Prior to measurement, the instrument was calibrated using high purity (>99.999%) indium and tin standards (Tm = 156.60 °C, ΔHf = 28.45 J g−1 and Tm = 231.88 °C, ΔHf = 60.46 J g−1 respectively).29,30 The data obtained were analyzed by using Pyris 1 software. For each experiment, 5–10 mg of the well-mixed monomer-initiator sample was weighed into a 50 μL aluminium pan and hermetically sealed. Measurements were performed at heating rates of 5, 10, 15, and 20 °C min−1 over the temperature range of 20 to 240 °C. The experimental data were analyzed by the three so-called dynamic; isoconversional; and B/D approaches.2.4.1.1. Dynamic methods. In general, the polymerization rate can be described by the following rate eqn (2):
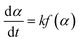 | (2) |
The dependence of a rate constant (k) on temperature (T) is given by the Arrhenius eqn (3):31
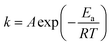 | (3) |
The activation energy (Ea) of the polymerization reaction can be determined by using peak methods which consider using the peak temperature at maximum rate (Tp) such as the Kissinger and Ozawa methods and using the temperature at 50% conversion (T50%) such as the Flynn–Wall method. The Kissinger, Flynn–Wall, and Ozawa methods are DSC dynamic methods which rely on approximating the so-called temperature integral and require data on temperature only.32,33
The Kissinger method uses the temperature at which the rate of polymerization is at the maximum (Tp) and the activation energy, Ea, is obtained from the maximum reaction rate where d(dα/dt)/dt is zero under a constant heating rate condition leading to eqn (4) as follows:34,35
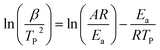 | (4) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (β/TP2) against 1/Tp.
(β/TP2) against 1/Tp.
The Flynn–Wall method is an integral method for determining the activation energies without any reaction order.36 This method combining with Doyle's approximation leads to eqn (5):37
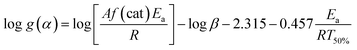 | (5) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β against 1/T50% at a constant g(α). Therefore, activation energy Ea determination from dynamic DSC polymerization only requires determining the temperature at which 50% polymerization is achieved.
β against 1/T50% at a constant g(α). Therefore, activation energy Ea determination from dynamic DSC polymerization only requires determining the temperature at which 50% polymerization is achieved.
Similar to the Flynn–Wall method, the Ozawa method uses the temperature at which the rate of polymerization is at the maximum which, when combined with Doyle's approximation, leads to eqn (6):38
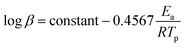 | (6) |
In this method, plots of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β against 1/Tp are used to determine the energy of activation (Ea) from the slopes.
β against 1/Tp are used to determine the energy of activation (Ea) from the slopes.
2.4.1.2. Isoconversional methods. Isoconversional methods are amongst the most reliable methods for the calculation of activation energy of thermally activated reactions. Isoconversional methods can be categorized into two main groups of methods.33 The first group are considered as Type A methods (or rate-isoconversional methods). A well-known method of this type is the Friedman method which makes no mathematical approximations. The second group are considered as Type B methods which apply a range of approximations for the temperature integral p(x) such as the Kissinger–Akahira–Sunose (KAS) method and the Flynn–Wall–Ozawa method.36,38–40
These isoconversional methods employ multiple temperature programs (e.g., different heating rates) in order to obtain data from various rates at a constant fraction of conversion (extent of reaction), α. In other words, isoconversional methods allow complex (i.e., multi-step) processes to be determined via a variation in activation energy (Ea) with conversion α.41 This means that, if a significant variation in Ea occurs with conversion α, the process is complex. On the other hand, if Ea is independent of conversion α, then the reaction is a single-step process. Isoconversional methods are based exclusively on dynamic DSC analysis.
Based on eqn (2) and (3), the kinetic approach proposed by Friedman expresses the logarithm of reaction rate, ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (dα/dt), as a function of the reciprocal temperature, as shown in eqn (7).42 This enables the activation energy Ea to be determined for each fraction of conversion, α:
(dα/dt), as a function of the reciprocal temperature, as shown in eqn (7).42 This enables the activation energy Ea to be determined for each fraction of conversion, α:
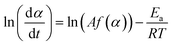 | (7) |
This equation implies that the reaction rate is only a function of temperature at a constant value of α. It is obvious that if the function f(α) is constant for a particular value of α, then ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (Af(α)) is constant as well. Therefore, by plotting ln
(Af(α)) is constant as well. Therefore, by plotting ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (dα/dt) against 1/T, a value for −Ea/R, and hence Ea, can be obtained.
(dα/dt) against 1/T, a value for −Ea/R, and hence Ea, can be obtained.
The Kissinger–Akahira–Sunose (KAS) method is based on eqn (8) as follows:
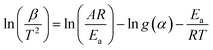 | (8) |
The activation energy Ea can then be obtained from the slope of a semi-log plot of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (β/T2) against 1/T at constant conversion.
(β/T2) against 1/T at constant conversion.
The Ozawa–Flynn–Wall (OFW) isoconversional method uses Doyle's approximation leading to eqn (9):43,44
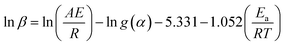 | (9) |
2.4.1.3. Borchardt and Daniels method45–48. The Borchardt and Daniels (B/D) approach gives the calculation of activation energy (Ea), pre-exponential factor (A), heat of reaction (ΔH), reaction order (n), and rate constant (k) from a single DSC scan.45–48 This approach assumes that the reaction follows nth order kinetics and obeys the general rate eqn (10):
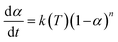 | (10) |
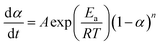 | (11) |
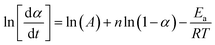 | (12) |
Eqn (12) can be solved with a multiple linear regression of the general form: z = a + bx + cy (where z ≅ ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [dα/dt]; ln
[dα/dt]; ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (A) ≅ a; b ≅ n; x ≅ ln
(A) ≅ a; b ≅ n; x ≅ ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [1 − α]; c ≅ −Ea/R; and y ≅ 1/T). The values for dα/dt; α; and T are experimental parameters obtained from a single linear heating rate DSC experiment scanning through the temperature region of the reaction exotherm as shown in Fig. 4.
[1 − α]; c ≅ −Ea/R; and y ≅ 1/T). The values for dα/dt; α; and T are experimental parameters obtained from a single linear heating rate DSC experiment scanning through the temperature region of the reaction exotherm as shown in Fig. 4.
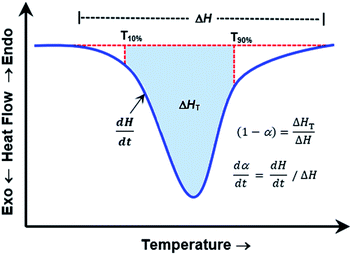 | ||
| Fig. 4 Idealized DSC curve for kinetic parameters determination by using Borchardt and Daniels (B/D) method. | ||
In this B/D method, assume a value for n = 1, then the value for ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [k(T)] can be calculated using eqn (13):
[k(T)] can be calculated using eqn (13):
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [k(T)] = ln [k(T)] = ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [dα/dt] − n [dα/dt] − n![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [1 − α] [1 − α]
| (13) |
Then Ea can be obtained from the slope of a plot of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [k(T)] against 1/T at constant conversion (α = 0.1–0.9).
[k(T)] against 1/T at constant conversion (α = 0.1–0.9).
2.5. Synthesis and characterization of poly(L-lactide) using liquid tin(II) n-butoxide as an initiator
In this work, ring-opening polymerization of L-lactide using liquid Sn(OnC4H9)2 initiator was conducted in the bulk phase. Prior to polymerization, L-lactide monomer of a purity of >99.5% was dried under vacuum at 55 °C for at least 8 h. All glasswares and apparatus used were dried at 120 °C overnight and cooled in a controlled atmosphere glove box prior to use. For each polymerization, approximately 3 g of purified and dried L-lactide monomer were accurately weighed into a 10 mL round bottom flask with a magnetic stirring bar. Then required concentration of tin(II) n-butoxide, Sn(OnC4H9)2, initiator in toluene was added. The reaction flask was then sealed and immersed in a silicone oil-bath for 24 h. At the end of the polymerization period, the reaction flask was removed from the oil-bath and allowed to cool to room temperature. After that, the polymerisate was dissolved in chloroform as solvent and the polymer precipitated from solution by dropwise addition with efficient stirring into ice-cooled absolute methanol. The polymer products obtained were white tough solid and were characterized by the combination of instrumental methods of: FTIR (Bruker Tensor 27 FTIR spectrometer), 1H-NMR (400 MHz Bruker Avance II NMR spectrometer), DSC (PerkinElmer DSC 7 Differential Scanning Calorimeter) and dilute-solution viscometry (Schott-Geräte AVS 300, Ubbelohde viscometer no. 532 00 0c) respectively. Table 1 shows the synthesized polymer codes and conditions used in this work.| Polymer code | [Sn(OnC4H9)2] (mol%) | Temperature (°C) | Polymerization time (h) |
|---|---|---|---|
| PLLA 1 | 0.01 | 100 | 24 |
| PLLA 2 | 0.01 | 110 | 24 |
| PLLA 3 | 0.01 | 120 | 24 |
| PLLA 4 | 0.01 | 130 | 24 |
| PLLA 5 | 0.01 | 140 | 24 |
| PLLA 6 | 0.01 | 150 | 24 |
| PLLA 7 | 0.05 | 100 | 24 |
| PLLA 8 | 0.05 | 110 | 24 |
| PLLA 9 | 0.05 | 120 | 24 |
| PLLA 10 | 0.05 | 130 | 24 |
| PLLA 11 | 0.05 | 140 | 24 |
| PLLA 12 | 0.05 | 150 | 24 |
| PLLA 13 | 0.10 | 100 | 24 |
| PLLA 14 | 0.10 | 110 | 24 |
| PLLA 15 | 0.10 | 120 | 24 |
| PLLA 16 | 0.10 | 130 | 24 |
| PLLA 17 | 0.10 | 140 | 24 |
| PLLA 18 | 0.10 | 150 | 24 |
| PLLA 19 | 0.50 | 100 | 24 |
| PLLA 20 | 0.50 | 110 | 24 |
| PLLA 21 | 0.50 | 120 | 24 |
| PLLA 22 | 0.50 | 130 | 24 |
| PLLA 23 | 0.50 | 140 | 24 |
| PLLA 24 | 0.50 | 150 | 24 |
| PLLA 25 | 1.00 | 100 | 24 |
| PLLA 26 | 1.00 | 110 | 24 |
| PLLA 27 | 1.00 | 120 | 24 |
| PLLA 28 | 1.00 | 130 | 24 |
| PLLA 29 | 1.00 | 140 | 24 |
| PLLA 30 | 1.00 | 150 | 24 |
3. Results and discussion
3.1. Synthesis of liquid tin(II) n-alkoxides
All three synthesized liquid tin(II) n-alkoxides products namely: tin(II) n-butoxide (Sn(OnC4H9)2), tin(II) n-hexoxide (Sn(OnC6H13)2), and tin(II) n-octoxide (Sn(OnC8H17)2) were obtained as viscous, dark yellow liquids of approximately 70–85% yield. The physical appearances, solubility test results, and structural confirmations by various techniques of these three liquid initiator products were stated elsewhere.173.2. Kinetic analyses
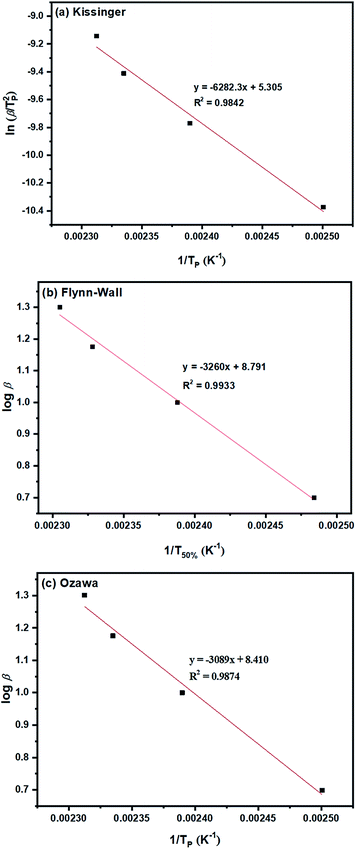 | ||
| Fig. 6 Ea determinations based on dynamic methods of: (a) Kissinger; (b) Flynn–Wall; and (c) Ozawa for the ROP of L-lactide using 1.0 mol% liquid Sn(OnC4H9)2 as an initiator. | ||
| Initiators/initiating systems | Heating rate, β (°C min−1) | Tp (°C) | T50% (°C) | Ea (kJ mol−1) | ||
|---|---|---|---|---|---|---|
| Kissingera | Flynn–Wallb | Ozawac | ||||
a Kissinger: d[ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (β/Tp2)]/d(1/Tp) = −Ea/R = slope.b Flynn–Wall: log (β/Tp2)]/d(1/Tp) = −Ea/R = slope.b Flynn–Wall: log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) g(α) = log g(α) = log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (Af(cat)Ea/R) − log (Af(cat)Ea/R) − log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β − 2.315 − 0.457 (Ea/RT50%), slope = −0.457 (Ea/R).c Ozawa: log β − 2.315 − 0.457 (Ea/RT50%), slope = −0.457 (Ea/R).c Ozawa: log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β = constant − 0.4567 (Ea/RTp), slope = −0.4567 (Ea/R). β = constant − 0.4567 (Ea/RTp), slope = −0.4567 (Ea/R). |
||||||
| Sn(Oct)2 | 5 | 142.0 | 141.8 | 57 | 65 | 61 |
| 10 | 157.8 | 157.0 | ||||
| 15 | 167.3 | 166.0 | ||||
| 20 | 176.0 | 173.0 | ||||
| Liquid Sn(OnC4H9)2 | 5 | 128.9 | 131.1 | 52 | 59 | 56 |
| 10 | 145.3 | 147.2 | ||||
| 15 | 150.8 | 152.5 | ||||
| 20 | 160.3 | 161.7 | ||||
| Sn(Oct)2/nC4H9OH | 5 | 139.2 | 138.8 | 60 | 67 | 64 |
| 10 | 152.3 | 151.7 | ||||
| 15 | 161.5 | 160.3 | ||||
| 20 | 170.0 | 169.0 | ||||
| Liquid Sn(OnC6H13)2 | 5 | 144.8 | 144.2 | 57 | 60 | 61 |
| 10 | 157.5 | 157.1 | ||||
| 15 | 170.0 | 167.3 | ||||
| 20 | 177.0 | 174.3 | ||||
| Sn(Oct)2/nC6H13OH | 5 | 148.8 | 148.5 | 61 | 67 | 66 |
| 10 | 160.0 | 159.0 | ||||
| 15 | 174.3 | 173.3 | ||||
| 20 | 179.3 | 178.0 | ||||
| Liquid Sn(OnC8H17)2 | 5 | 152.3 | 152.8 | 65 | 71 | 69 |
| 10 | 168.5 | 167.3 | ||||
| 15 | 175.5 | 175.8 | ||||
| 20 | 185.3 | 184.0 | ||||
| Sn(Oct)2/nC8H17OH | 5 | 160.3 | 158.3 | 71 | 74 | 72 |
| 10 | 169.3 | 168.0 | ||||
| 15 | 177.5 | 176.5 | ||||
| 20 | 187.0 | 186.7 | ||||
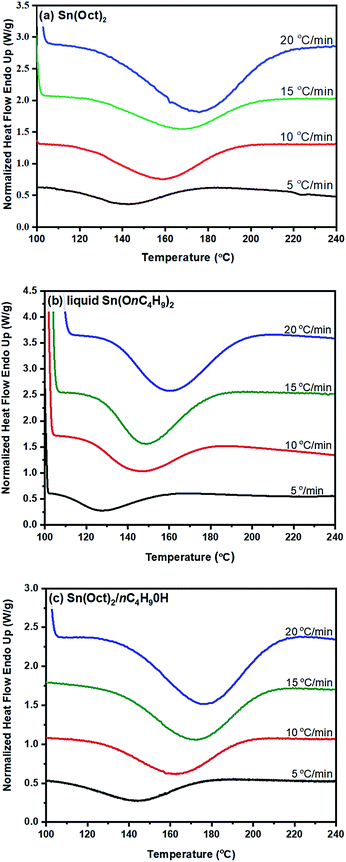
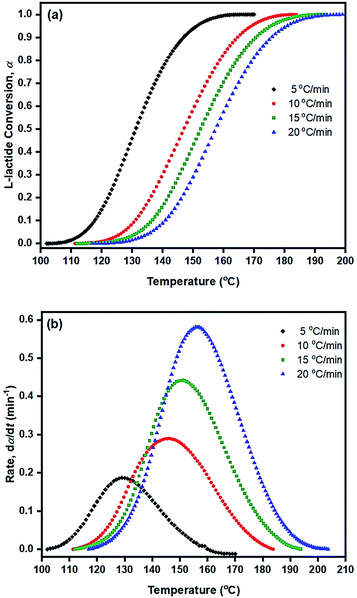
From the original DSC thermograms of heat flow (normalized, W g−1) against temperature (°C) at the four different heating rates of 5, 10, 15, and 20 °C min−1, it was found that the temperature at the maximum peak (Tp) and the temperature of 50% L-lactide monomer conversion (T50%) were found to increase with increasing heating rate.
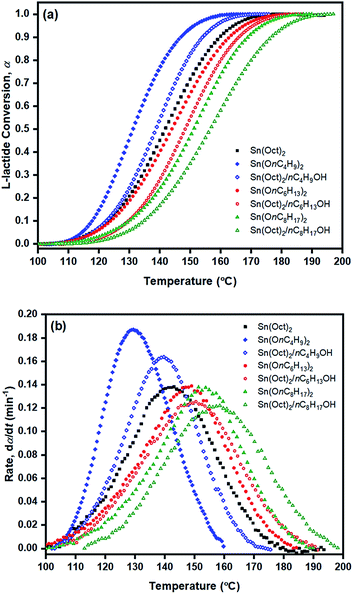
However, when considering the initial temperatures (i.e. onset temperatures, Tonset), it was found that Tonset only slightly increased when increasing the heating rate. This observation was seen for almost every initiator/initiating system. Interestingly, the lowest Tonset polymerization temperature of ∼108 °C was found using the liquid Sn(OnC4H9)2 initiator (Fig. 5(b)) indicating its potential as an initiator to synthesize the PLA at low temperature and yielding the polymer with controlled molecular weight and narrow molecular weight distribution in a short period of time.
Furthermore, the Ea values for the L-lactide polymerizations using the seven initiators/initiating systems can be obtained from the slopes of the plots of (a) ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (β/Tp2) as a function of 1/Tp, (b) log
(β/Tp2) as a function of 1/Tp, (b) log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β as a function of 1/T50% and (c) log
β as a function of 1/T50% and (c) log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β as a function of 1/Tp based on the Kissinger, Flynn–Wall and Ozawa methods respectively. The Ea (kJ mol−1) values obtained from linear equation fitting for these three dynamic methods are compared in Table 2 as previously mentioned.
β as a function of 1/Tp based on the Kissinger, Flynn–Wall and Ozawa methods respectively. The Ea (kJ mol−1) values obtained from linear equation fitting for these three dynamic methods are compared in Table 2 as previously mentioned.
From the results obtained, the Ea values are seen to be in the order of liquid Sn(OnC4H9)2 < Sn(Oct)2/nC4H9OH < Sn(Oct)2 ≅ liquid Sn(OnC6H13)2 < Sn(Oct)2/nC6H13OH ≅ liquid Sn(OnC8H17)2 < Sn(Oct)2/nC8H17OH.
According to isoconversional methods, values of Ea of the ROP of L-lactide were determined from the non-isothermal DSC data by the three methods of Friedman, KAS, and OFW. The plots of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (dα/dt), ln
(dα/dt), ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (β/dT2), and ln
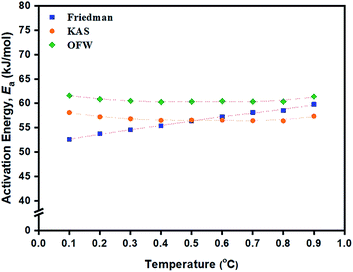
(β/dT2), and ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β against 1/T (K−1) based on these methods for the ROP of L-lactide using 1.0 mol% liquid Sn(OnC4H9)2 as an initiator are shown in Fig. 8(a)–(c). In general, linear plots were obtained for each of the initiating systems although the Friedman plots showed more scattering of the points than those of the KAS and OFW. The values of Ea at a particular conversion, α, can be obtained from the slopes of these linear plots and the values are summarized in Table 3. Again, the Friedman plots showed more variation in Ea with α than the KAS and OFW plots, indicating that the isoconversional KAS and OFW methods are more suitable for Ea determination in L-lactide polymerization. From Fig. 9, similar smaller Ea variations with α were observed for the KAS and OFW methods with the former being consistently <5 kJ mol−1 lower than the latter. The consistency of the Ea values over almost the complete range of conversion is an indication that the coordination–insertion mechanism ring-opening polymerization under the conditions is the sole mechanism which is operational in L-lactide employed in this study.
β against 1/T (K−1) based on these methods for the ROP of L-lactide using 1.0 mol% liquid Sn(OnC4H9)2 as an initiator are shown in Fig. 8(a)–(c). In general, linear plots were obtained for each of the initiating systems although the Friedman plots showed more scattering of the points than those of the KAS and OFW. The values of Ea at a particular conversion, α, can be obtained from the slopes of these linear plots and the values are summarized in Table 3. Again, the Friedman plots showed more variation in Ea with α than the KAS and OFW plots, indicating that the isoconversional KAS and OFW methods are more suitable for Ea determination in L-lactide polymerization. From Fig. 9, similar smaller Ea variations with α were observed for the KAS and OFW methods with the former being consistently <5 kJ mol−1 lower than the latter. The consistency of the Ea values over almost the complete range of conversion is an indication that the coordination–insertion mechanism ring-opening polymerization under the conditions is the sole mechanism which is operational in L-lactide employed in this study.
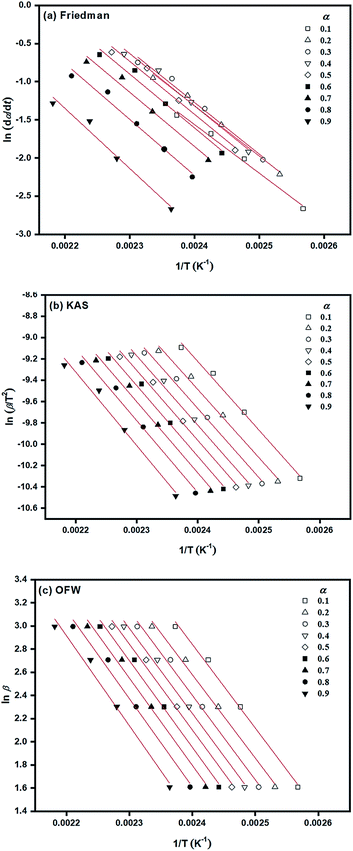 | ||
| Fig. 8 Determination of Ea based on isoconversional methods of: (a) Friedman; (b) KAS; and (c) OFW for the ROP of L-lactide using 1.0 mol% liquid Sn(OnC4H9)2 as an initiator. | ||
| Initiator/initiating system | Ea range (kJ mol−1) | ||
|---|---|---|---|
| Friedmana | KASb | OFWc | |
a Friedman: ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (dα/dt) = ln (dα/dt) = ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (Af(α)) − (Ea/RT), slope = −Ea/R.b KAS: ln (Af(α)) − (Ea/RT), slope = −Ea/R.b KAS: ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (β/T2) = ln (β/T2) = ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [(AR)/Ea] − ln [(AR)/Ea] − ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) g(α) − Ea/RT, slope = −Ea/R.c OFW: ln g(α) − Ea/RT, slope = −Ea/R.c OFW: ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β = ln β = ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [(AE)/R] − ln [(AE)/R] − ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) g(α) − 5.331 − 1.052 (Ea/RT), slope = 1.052 (−Ea/R). g(α) − 5.331 − 1.052 (Ea/RT), slope = 1.052 (−Ea/R). |
|||
| Sn(Oct)2 | 58–63 | 59–74 | 63–77 |
| Sn(OnC4H9)2 | 53–60 | 55–58 | 60–62 |
| Sn(Oct)2/nC4H9OH | 56–63 | 56–64 | 60–67 |
| Sn(OnC6H13)2 | 56–61 | 56–60 | 60–64 |
| Sn(Oct)2/nC6H13OH | 60–63 | 63–71 | 67–74 |
| Sn(OnC8H17)2 | 66–76 | 66–72 | 70–76 |
| Sn(Oct)2/nC8H17OH | 68–81 | 65–74 | 69–78 |
From Table 3, Ea values were found to be the lowest for the Sn(OnC4H9)2 initiator (Ea = 53–60, 55–58, and 60–62 kJ mol−1 for Friedman; KAS; and OFW respectively) and the highest for Sn(Oct)2/nC8H17OH (Ea = 68–81, 65–74, and 69–78 kJ mol−1 for Friedman, KAS, and OFW respectively). When comparing the results at the same heating rate of 5 °C min−1 (see Fig. 10(a) and (b)), the conversion and rate plots showed different values of Tonset with different conversions or rates of polymerization in the order of: liquid Sn(OnC4H9)2 > Sn(Oct)2/nC4H9OH > Sn(Oct)2 ≅ liquid Sn(OnC6H13)2 > Sn(Oct)2/nC6H13OH ≅ liquid Sn(OC8H17)2 > Sn(Oct)2/nC8H17OH.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [k(T)] versus 1/T. Table 4 shows values obtained from ROP of L-lactide using all seven initiators/initiating systems at heating rates of 5, 10, 15, and 20 °C min−1 respectively.
[k(T)] versus 1/T. Table 4 shows values obtained from ROP of L-lactide using all seven initiators/initiating systems at heating rates of 5, 10, 15, and 20 °C min−1 respectively.
| Initiators/initiating systems | Heating rate, β (°C min−1) | Kinetic parameters | ||
|---|---|---|---|---|
| Eaa (kJ mol−1) | Ab (min−1) | kapp, 150 °Cc (min−1) | ||
a B/D: multiple linear regression of eqn (12), −Ea/R = slope.b ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (A) = intercept.c kapp = apparent rate constant at 150 °C = dα/dt/(1 − α)n. (A) = intercept.c kapp = apparent rate constant at 150 °C = dα/dt/(1 − α)n. |
||||
| Sn(Oct)2 | 5 | 79 | 5.42 × 1010 | 0.3150 |
| 10 | 89 | 2.35 × 109 | 0.3162 | |
| 15 | 89 | 1.49 × 109 | 0.3747 | |
| 20 | 91 | 6.32 × 108 | 0.4163 | |
| Liquid Sn(OnC4H9)2 | 5 | 76 | 3.40 × 1010 | 0.5057 |
| 10 | 78 | 2.65 × 1010 | 0.5742 | |
| 15 | 80 | 2.19 × 1010 | 0.6729 | |
| 20 | 84 | 2.87 × 1010 | 0.7696 | |
| Sn(Oct)2/nC4H9OH | 5 | 78 | 7.82 × 109 | 0.4230 |
| 10 | 84 | 2.59 × 1010 | 0.4322 | |
| 15 | 87 | 3.05 × 1010 | 0.4346 | |
| 20 | 88 | 2.57 × 1010 | 0.4936 | |
| Liquid Sn(OnC6H13)2 | 5 | 80 | 2.63 × 1011 | 0.2323 |
| 10 | 87 | 3.40 × 1011 | 0.2352 | |
| 15 | 87 | 2.19 × 1011 | 0.2458 | |
| 20 | 87 | 2.07 × 1011 | 0.2773 | |
| Sn(Oct)2/nC6H13OH | 5 | 89 | 3.64 × 1011 | 0.1710 |
| 10 | 90 | 3.79 × 1011 | 0.1722 | |
| 15 | 92 | 4.63 × 1011 | 0.1975 | |
| 20 | 94 | 1.13 × 109 | 0.2172 | |
| Liquid Sn(OnC8H17)2 | 5 | 90 | 3.52 × 1011 | 0.1446 |
| 10 | 91 | 4.36 × 109 | 0.1475 | |
| 15 | 96 | 9.56 × 109 | 0.1617 | |
| 20 | 97 | 9.48 × 109 | 0.1639 | |
| Sn(Oct)2/nC8H17OH | 5 | 97 | 7.66 × 108 | 0.0372 |
| 10 | 98 | 3.44 × 109 | 0.0943 | |
| 15 | 98 | 7.84 × 1010 | 0.1077 | |
| 20 | 100 | 1.27 × 1010 | 0.1082 | |
Similar to previous dynamic and isoconversional approaches, liquid tin(II) n-butoxide shown to be the most efficient initiator due to its lowest activation energy range (76–84 kJ mol−1) with highest apparent rate constant values.
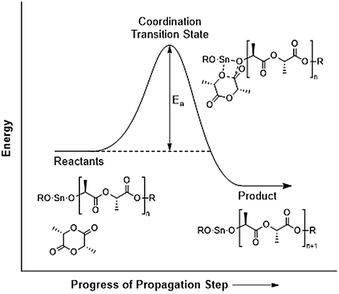
What the Ea value for L-lactide ring-opening polymerization in bulk means essentially is the Ea value for the propagation step since the number of propagation steps far outnumber the initiation and termination steps. Therefore, the actual meaning of Ea can be visualized as shown in the energy diagram in Fig. 11.
3.3. Synthesis and characterization of poly(L-lactide) using liquid tin(II) n-butoxide as an initiator
From the DSC kinetic studies, liquid tin(II) n-butoxide, Sn(OnC4H9)2, has shown to be the most efficient initiator in terms of rate, therefore, it was chosen for a more detailed study of how it can be used to control molecular weight in the ring-opening polymerizaition in bulk of L-lactide by varying its concentration and also the polymerization temperature (Table 1). From the results obtained, structures of all synthesized poly(L-lactide) products using liquid Sn(OnC4H9)2 as an initiator at various conditions were confirmed by FTIR and 1H-NMR respectively.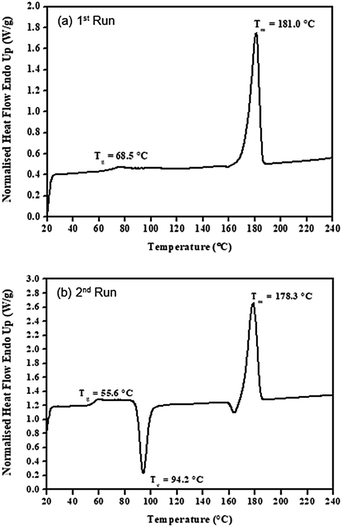 | ||
| Fig. 12 DSC thermograms for (a) 1st run and (b) 2nd run of the purified poly(L-lactide) (PLLA 1) using 0.01 mol% liquid Sn(OnC4H9)2 as an initiator at 100 °C for 24 h. | ||
Information on the DSC thermal transition temperatures (i.e. the glass transition temperature (Tg), the crystallisation temperature (Tc), and the melting temperature (Tm)) as well as the heat of crystallization (ΔHc) and the heat of melting (ΔHm) from all synthesized PLLA polymer products were summarized in Table 5.
| Polymer code | Tg (°C) | Tc (°C) | Tm (°C) | ΔHc (J g−1) | ΔHm (J g−1) | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1st | 2nd | 1st | 2nd | 1st | 2nd | 1st | 2nd | 1st | 2nd | |
| PLLA 1 | 68.5 | 56.6 | — | 94.2 | 181.0 | 178.3 | — | 41.0 | 64.1 | 76.0 |
| PLLA 2 | 67.0 | 54.3 | — | 98.8 | 178.0 | 175.5 | — | 40.4 | 64.5 | 70.5 |
| PLLA 3 | 69.9 | 55.6 | — | 103.0 | 179.8 | 179.5 | — | 38.6 | 46.4 | 56.1 |
| PLLA 4 | 68.6 | 59.8 | — | 106.8 | 177.8 | 177.7 | — | 34.2 | 38.0 | 45.9 |
| PLLA 5 | 63.7 | 58.7 | — | 108.8 | 176.0 | 175.7 | — | 40.5 | 43.3 | 47.1 |
| PLLA 6 | — | 59.1 | — | 105.3 | 176.5 | 176.8 | — | 36.2 | 42.2 | 50.9 |
| PLLA 7 | 54.2 | 51.6 | — | 95.2 | 178.5 | 174.8 | — | 38.6 | 72.1 | 68.1 |
| PLLA 8 | 69.9 | 55.2 | — | 118.0 | 178.7 | 177.0 | — | 53.6 | 52.5 | 47.5 |
| PLLA 9 | 68.6 | 55.8 | — | 106.7 | 178.2 | 178.7 | — | 39.3 | 52.3 | 46.4 |
| PLLA 10 | 72.3 | 60.1 | — | 108.7 | 178.8 | 178.8 | — | 32.1 | 34.1 | 36.9 |
| PLLA 11 | — | 57.6 | — | 106.7 | 174.3 | 174.5 | — | 35.9 | 41.2 | 43.2 |
| PLLA 12 | 71.0 | 59.1 | — | 107.5 | 176.0 | 176.5 | — | 36.6 | 43.2 | 41.5 |
| PLLA 13 | 68.3 | 43.4 | — | 90.2 | 176.2 | 168.2 | — | 40.0 | 60.5 | 55.7 |
| PLLA 14 | 67.0 | 51.7 | — | 99.3 | 177.2 | 173.9 | — | 37.8 | 64.0 | 56.1 |
| PLLA 15 | 69.4 | 54.8 | — | 106.2 | 176.0 | 176.5 | — | 43.2 | 44.8 | 46.6 |
| PLLA 16 | 71.7 | 60.2 | — | 109.3 | 179.5 | 180.2 | — | 35.1 | 39.0 | 45.6 |
| PLLA 17 | 70.3 | 57.1 | — | 112.2 | 171.7 | 171.0 | — | 42.4 | 43.5 | 38.5 |
| PLLA 18 | 69.0 | 58.2 | — | 108.2 | 174.2 | 176.2 | — | 37.0 | 51.6 | 40.2 |
| PLLA 19 | 62.6 | 42.1 | — | 80.2 | 166.5 | 160.8 | — | 37.6 | 67.7 | 56.8 |
| PLLA 20 | 60.4 | 39.6 | — | 86.3 | 169.3 | 163.7 | — | 40.4 | 63.4 | 47.5 |
| PLLA 21 | 68.1 | 40.2 | — | 85.2 | 175.0 | 167.3 | — | 37.2 | 56.0 | 53.8 |
| PLLA 22 | 74.7 | 48.8 | — | 95.0 | 175.5 | 169.0 | — | 38.5 | 50.5 | 48.1 |
| PLLA 23 | 70.7 | 45.4 | — | 91.7 | 173.0 | 166.5 | — | 34.6 | 49.8 | 43.0 |
| PLLA 24 | — | 43.9 | — | 87.3 | 173.3 | 166.0 | — | 31.6 | 49.3 | 45.2 |
| PLLA 25 | — | 36.5 | — | 73.0 | 164.3 | 157.7 | — | 33.7 | 63.6 | 47.2 |
| PLLA 26 | 61.9 | 37.0 | — | 77.0 | 165.0 | 157.0 | — | 34.9 | 67.8 | 50.3 |
| PLLA 27 | — | 39.0 | — | 78.8 | 171.5 | 164.2 | — | 33.6 | 60.1 | 53.9 |
| PLLA 28 | 75.6 | 38.8 | — | 78.8 | 172.3 | 162.3 | — | 27.3 | 49.3 | 45.3 |
| PLLA 29 | — | 43.6 | — | 83.5 | 171.8 | 163.0 | — | 31.0 | 51.0 | 45.2 |
| PLLA 30 | 69.4 | 41.9 | — | 80.8 | 171.2 | 163.2 | — | 29.1 | 50.6 | 46.8 |
| Concentration (g dL−1) | Flow-time (sec) | ηrel | ηsp | ηred (dL g−1) |
|---|---|---|---|---|
| 0 | 132.4 | — | — | — |
| 0.2012 | 207.6 | 1.567 | 0.567 | 2.819 |
| 0.4120 | 301.8 | 2.278 | 1.278 | 3.103 |
| 0.6056 | 423.6 | 3.198 | 2.198 | 3.630 |
| 0.8012 | 562.0 | 4.243 | 3.243 | 4.048 |
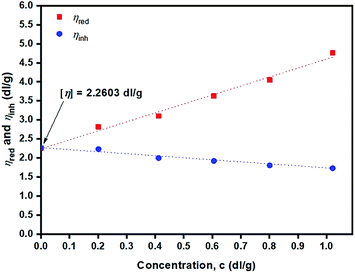
Fig. 13 depicts plots of reduced viscosity (ηred) and inherent viscosity (ηinh) against concentration (g dL−1). Double extrapolating to zero concentration giving a value of intrinsic viscosity [η] of the PLLA sample of 2.26 dL g−1 was obtained.
From the value of [η] = 2.26 dL g−1 (Fig. 13), the polymer's viscosity-average molecular weight, ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) v, can be calculated from the Mark–Houwink–Sakurada49 eqn (14) for PLLA in chloroform at 25 ± 0.1 °C:
v, can be calculated from the Mark–Houwink–Sakurada49 eqn (14) for PLLA in chloroform at 25 ± 0.1 °C:
[η] = 5.45 × 10−4 ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) v−0.73 dL g−1 v−0.73 dL g−1
| (14) |
[2.26] = 5.45 × 10−4 ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) v−0.73 dL g−1 v−0.73 dL g−1 |
![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) v = 9.03 × 104 v = 9.03 × 104 |
Therefore, the number-average molecular weight (![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) n), can be calculated from the gamma function50 eqn (15); assuming an approximately “most probable” molecular weight distribution, as:
n), can be calculated from the gamma function50 eqn (15); assuming an approximately “most probable” molecular weight distribution, as:
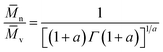 | (15) |
![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) v = 9.03 × 104, therefore giving:
v = 9.03 × 104, therefore giving:![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) n = 4.80 × 104 g mol−1 n = 4.80 × 104 g mol−1 |
The values of [η], ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) v, and
v, and ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) n obtained from dilute-solution viscometry for PLLA products were provided in Table 7.
n obtained from dilute-solution viscometry for PLLA products were provided in Table 7.
![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) v and
v and ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) n obtained from dilute-solution viscometry for all synthesized PLLAs using liquid tin(II) n-butoxide as an initiator
n obtained from dilute-solution viscometry for all synthesized PLLAs using liquid tin(II) n-butoxide as an initiator
| Polymer code | Intrinsic viscosity, [η] (dL g−1) | Viscosity-average molecular weight, ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) v (g mol−1) v (g mol−1) |
Number-average molecular weight, ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) n (g mol−1) n (g mol−1) |
|---|---|---|---|
| PLLA 1 | 0.66 | 2.22 × 104 | 1.18 × 104 |
| PLLA 2 | 1.05 | 3.15 × 104 | 1.68 × 104 |
| PLLA 3 | 2.15 | 8.42 × 104 | 4.48 × 104 |
| PLLA 4 | 1.69 | 6.09 × 104 | 3.24 × 104 |
| PLLA 5 | 1.92 | 7.20 × 104 | 3.83 × 104 |
| PLLA 6 | 1.90 | 7.12 × 104 | 3.79 × 104 |
| PLLA 7 | 0.98 | 2.89 × 104 | 1.54 × 104 |
| PLLA 8 | 1.67 | 5.98 × 104 | 3.18 × 104 |
| PLLA 9 | 2.26 | 9.03 × 104 | 4.80 × 104 |
| PLLA 10 | 2.35 | 9.51 × 104 | 5.05 × 104 |
| PLLA 11 | 1.84 | 6.83 × 104 | 3.63 × 104 |
| PLLA 12 | 2.17 | 8.52 × 104 | 4.53 × 104 |
| PLLA 13 | 0.85 | 2.36 × 104 | 1.25 × 104 |
| PLLA 14 | 1.01 | 2.99 × 104 | 1.59 × 104 |
| PLLA 15 | 2.38 | 9.67 × 104 | 5.14 × 104 |
| PLLA 16 | 2.02 | 7.73 × 104 | 4.11 × 104 |
| PLLA 17 | 1.58 | 5.51 × 104 | 2.93 × 104 |
| PLLA 18 | 1.65 | 5.90 × 104 | 3.14 × 104 |
| PLLA 19 | 0.31 | 6.06 × 103 | 3.22 × 103 |
| PLLA 20 | 0.48 | 1.07 × 104 | 5.71 × 103 |
| PLLA 21 | 0.84 | 2.31 × 104 | 1.23 × 104 |
| PLLA 22 | 1.05 | 3.17 × 104 | 1.68 × 104 |
| PLLA 23 | 0.89 | 2.53 × 104 | 1.35 × 104 |
| PLLA 24 | 0.85 | 2.35 × 104 | 1.25 × 104 |
| PLLA 25 | 0.23 | 4.06 × 103 | 2.16 × 103 |
| PLLA 26 | 0.29 | 5.48 × 103 | 2.91 × 103 |
| PLLA 27 | 0.63 | 1.56 × 104 | 8.32 × 103 |
| PLLA 28 | 0.73 | 1.91 × 104 | 1.02 × 104 |
| PLLA 29 | 0.64 | 1.61 × 104 | 8.55 × 103 |
| PLLA 30 | 0.52 | 1.42 × 104 | 6.86 × 103 |
4. Conclusions
In conclusion, these kinetic studies of the ring-opening polymerization of L-lactide in bulk by dynamic (Kissinger; Flynn–Wall; Ozawa), isoconversional (Friedman, KAS, and OFW) and Borchardt and Daniels (B/D) methods have indicated that the efficiency of the various initiators/initiating systems used in this work is in the order of liquid tin(II) n-butoxide (Sn(OnC4H9)2) > tin(II) octoate/n-butanol (Sn(Oct)2/C4H9OH) > tin(II) octoate (Sn(Oct)2) ≅ liquid tin(II) n-hexoxide (Sn(OnC6H13)2) > tin(II) octoate/n-hexanol (Sn(Oct)2/nC6H13OH) ≅ liquid tin(II) n-octoxide (Sn(OnC8H17)2) > tin(II) octoate/n-octanol (Sn(Oct)2/nC8H17OH).Therefore, liquid tin(II) n-butoxide (Sn(OnC4H9)2) is regarded as being the most efficient initiator for ring-opening polymerization of L-lactide via coordination–insertion mechanism as confirmed by the non-isothermal DSC kinetic studies which gave the lowest Ea values and the fastest rates of polymerization at the lowest temperature.
The results also confirm that the use of liquid tin(II) n-alkoxide (Sn(OR)2) initiator directly is more efficient than generating it in situ via the Sn(Oct)2/ROH reaction. It also has the important advantages of (a) knowing the [Sn(OR)2] concentration accurately for the purpose of being able to predict polymerization rates and polymer molecular weights and (b) to avoid any unwanted side-reactions due to the use of Sn(Oct)2 alone and/or Sn(Oct)2/ROH system.
Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
The authors wish to thank the Center of Excellence for Innovation in Chemistry (PERCH CIC), the Center of Excellence in Materials Science and Technology, Basic Research Fund and the Graduate School of Chiang Mai University, Thailand for funding this research work. The authors would also like to thank the Department of Chemistry, Faculty of Science, Chiang Mai University for providing the laboratory facilities.References
- J. C. Middleton and A. J. Tipton, Biomaterials, 2000, 21(23), 2335–2346 CrossRef CAS.
- M. Srisa-ard, R. Molloy, N. Molloy, J. Siripitayananon and M. Sriyai, Polym. Int., 2001, 50(8), 891–896 CrossRef CAS.
- Y. Baimark, R. Molloy, N. Molloy, J. Siripitayananon, W. Punyodom and M. Sriyai, J. Mater. Sci.: Mater. Med., 2005, 16(8), 699–707 CrossRef CAS.
- W. Channuan, J. Siripitayananon, R. Molloy, M. Sriyai, F. J. Davis and G. R. Mitchell, Polymer, 2005, 46(17), 6411–6428 CrossRef CAS.
- S. Ruengdechawiwat, J. Siripitayananon, R. Molloy, R. Somsunan, P. D. Topham and B. J. Tighe, Int. J. Polym. Mater., 2016, 65(6), 277–284 CrossRef.
- W. H. Carothers, G. L. Dorough and F. J. van Natta, J. Am. Chem. Soc., 1932, 54(2), 761–772 CrossRef CAS.
- A. P. Gupta and V. Kumar, Eur. Polym. J., 2007, 43(10), 4053–4074 CrossRef CAS.
- W. Groot, J. van Krieken, O. Sliekersl and S. de Vos, Production and Purification of Lactic acid and Lactide, in Poly(lactic acid) Synthesis, Structures, Properties, Processing, and Applications, ed. R. Auras, L. Loong-Tak, S. E. M. Selke and T. Hideto, John Wiley & Sons, Inc., Hoboken, New Jersey, 2010, pp. 3–16 Search PubMed.
- O. Dechy-Cabaret, B. Martin-Vaca and D. Bourissou, Polyesters from Dilactones, in Handbook of Ring-Opening Polymerization ed. P. Dubois, O. Coulembier and J.-M. Raquez, Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, 2009, pp. 255–280 Search PubMed.
- H. R. Kricheldorf, K. Bornhorst and H. Hachmann-Thiessen, Macromolecules, 2005, 38(12), 5017–5024 CrossRef CAS.
- S. Kaihara, S. Matsumura, A. G. Mikos and J. P. Fisher, Nat. Protoc., 2007, 2(11), 2767–2771 CrossRef CAS.
- J.-P. Puaux, I. Banu, I. Nagy and G. Bozga, Macromol. Symp., 2007, 259(1), 318–326 CrossRef CAS.
- H. R. Kricheldorf, I. Kreiser-Suanders and C. Boettcher, Polymer, 1995, 36(6), 1253–1259 CrossRef CAS.
- A. Kowalski, A. Duda and S. Penczek, Macromol. Rapid Commun., 1998, 19(11), 567–572 CAS.
- J. S. Morrison and H. M. Haendler, J. Inorg. Nucl. Chem., 1967, 29(2), 393–400 CrossRef CAS.
- R. Gsell and M. Zeldin, J. Inorg. Nucl. Chem., 1975, 37(5), 1133–1137 CrossRef CAS.
- P. Meepowpan, W. Punyodom and R. Molloy, Process for the preparation of liquid tin(II) alkoxides, US Pat., 9637507B2, USPTO, USA, 2017.
- A. Kleawkla, R. Molloy, W. Naksata and W. Punyodom, Adv. Mater. Res., 2008, 55–57, 757–760 CAS.
- C. Yu, L. Zhang, K. Tu and Z. Shen, Polym. Bull., 2004, 52(5), 329–337 CrossRef CAS.
- K. Stridsberg, M. Ryner and A.-C. Albertsson, Macromolecules, 2000, 33(8), 2862–2869 CrossRef CAS.
- B. Braun, J. R. Dorgan and S. F. Dec, Macromolecules, 2006, 39(26), 9302–9310 CrossRef CAS.
- S. Parnell, K. Min and M. Cakmak, Polymer, 2003, 44(18), 5137–5144 CrossRef CAS.
- W. Meelua, R. Molloy, P. Meepowpan and W. Punyodom, J. Polym. Res., 2012, 19, 9799 CrossRef.
- R. Mazarro, A. de Lucas, I. Gracia and J. F. Rodriguez, Macromol. Chem. Phys., 2008, 209(8), 818–824 CrossRef CAS.
- M. Arasa, X. Ramis, J. M. Salla, A. Mantecón and A. Serra, Thermochim. Acta, 2008, 479(1–2), 37–44 CrossRef CAS.
- S. Y. Reyes-López and A. M. Richa, Macromol. Symp., 2013, 325–326(1), 21–37 CrossRef.
- N. G. Sedush and S. N. Chvalun, Eur. Polym. J., 2015, 62, 198–203 CrossRef CAS.
- S.-H. Lee, B.-S. Kim, S. H. Kim, S. W. Choi, S. I. Jeong, I. K. Kwon, S. W. Kang, J. Nikolovski, D. J. Mooney, Y.-K. Han and Y. H. Kim, J. Biomed. Mater. Res., Part A, 2003, 66A(1), 29–37 CrossRef CAS.
- ASTM standard E967, Standard Test Method for Temperature Calibration of Differential Scanning Calorimeters and Differential Thermal Analyzers, ASTM International, West Conshohocken, PA, 2018 Search PubMed.
- ASTM standard E968-02, Standard Practice for Heat Flow Calibration of Differential Scanning Calorimeters, ASTM International, West Conshohocken, PA, 2014 Search PubMed.
- K. J. Laidler, J. Chem. Educ., 1984, 61(6), 494–498 CrossRef CAS.
- J. H. Flynn, Thermochim. Acta, 1997, 300(1–2), 83–92 CrossRef CAS.
- M. J. Starink, Thermochim. Acta, 2003, 404(1–2), 163–176 CrossRef CAS.
- H. E. Kissinger, J. Res. Natl. Bur. Stand., 1956, 57(4), 217–221 CrossRef CAS.
- H. E. Kissinger, Anal. Chem., 1957, 29(11), 1702–1706 CrossRef CAS.
- J. H. Flynn and L. A. Wall, J. Polym. Sci., Part C: Polym. Lett., 1966, 4(5), 323–328 CAS.
- C. D. Doyle, J. Appl. Polym. Sci., 1962, 6(24), 639–642 CrossRef CAS.
- T. Ozawa, J. Therm. Anal. Calorim., 1970, 2(3), 301–324 CrossRef CAS.
- S. Vyazovkin, Isoconversional Methodology, in Isoconversional Kinetics of Thermally Stimulated Processes, ed. S. Vyazovkin, Springer International Publishing Switzerland, 2015, pp. 27–62 Search PubMed.
- E. J. Mittemeijer, J. Mater. Sci., 1992, 27(15), 3977–3987 CrossRef CAS.
- S. Vyazovkin, J. Therm. Anal., 1997, 49(3), 1493–1499 CrossRef CAS.
- H. L. Friedman, J. Polym. Sci., Part C: Polym. Symp., 1964, 6(1), 183–195 CrossRef.
- T. Ozawa, Bull. Chem. Soc. Jpn., 1965, 38(11), 1881–1886 CrossRef CAS.
- J. H. Flynn and L. A. Wall, J. Polym. Sci., Part B: Polym. Lett., 1966, 4(5), 323–328 CrossRef CAS.
- H. J. Borchardt and F. Daniels, J. Am. Chem. Soc., 1957, 79(1), 41–46 CrossRef CAS.
- S. J. Swarin and A. M. Wims, Anal. Calorim., 1977, 4(5), 155–171 CAS.
- ASTM standard E2041, Standard Test Method for Estimating Kinetic Parameters by Differential Scanning Calorimeters Using the Borchardt and Daniels Method, ASTM International, West Conshohocken, PA, 2013 Search PubMed.
- R. S. F. Paula, I. M. Figueredo, R. S. Vieira, T. L. Nascimento, C. L. Cavalcante Jr, Y. L. Machado and M. A. S. Rios, SN Appl. Sci., 2019, 1(884), 1–7 CAS.
- D. R. Witzke and R. Narayan, Macromolecules, 1997, 30(23), 7075–7085 CrossRef CAS.
- P. J. Flory, Determination of Molecular Weights, in Principles of Polymer Chemistry, ed. P. J. Flory, Cornell University Press, Ithaca, New York, 1995, p. 313 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ra07635j |
| This journal is © The Royal Society of Chemistry 2020 |