Open Access Article
Open Access ArticleHighly efficient radiative recombination in intrinsically zero-dimensional perovskite micro-crystals prepared by thermally-assisted solution-phase synthesis†
Wei-Long Xuab,
Siobhan J. Bradley a,
Yang Xua,
Fei Zheng
a,
Yang Xua,
Fei Zheng a,
Christopher R. Hall
a,
Christopher R. Hall a,
Kenneth P. Ghiggino
a,
Kenneth P. Ghiggino a and
Trevor A. Smith
a and
Trevor A. Smith *a
*a
aARC Centre of Excellence in Exciton Science, School of Chemistry, The University of Melbourne, Parkville, Victoria 3010, Australia. E-mail: trevoras@unimelb.edu.au
bSchool of Photoelectric Engineering, Changzhou Institute of Technology, Changzhou, Jiangsu 213002, China
First published on 8th December 2020
Abstract
Zero-dimensional (0D) quantum confinement can be achieved in perovskite materials by the confinement of electron and hole states to single PbX64− perovskite octahedra. In this work, 0D perovskite (Cs4PbBr6) micro-crystals were prepared by a simple thermally-assisted solution method and thoroughly characterized. The micro-crystals show a high level of crystallinity and a high photoluminescence quantum yield of 45%. The radiative recombination coefficient of the 0D perovskite micro-crystals, 1.5 × 10−8 s−1 cm3, is two orders of magnitude higher than that of typical three-dimensional perovskite and is likely a strong contributing factor to the high emission efficiency of 0D perovskite materials. Temperature dependent luminescence measurements provide insight into the role of thermally-activated trap states. Spatially resolved measurements on single 0D perovskite micro-crystals reveal uniform photoluminescence intensity and emission decay behaviour suggesting the solution-based fabrication method yields a high-quality and homogenous single-crystal material. Such uniform emission reflects the intrinsic 0D nature of the material, which may be beneficial to device applications.
Introduction
Low-dimensional perovskite materials have considerable potential for applications in optical devices due to the advantages associated with the spatial confinement of the excitons. One way to achieve such confinement is to reduce the particle size to several nanometres, commonly referred to as quantum dots.1–3 The main preparation methods of perovskite quantum dots are hot injection or ligand-assisted anti-solvent precipitation.4–6 The band gap and optical properties of these quantum dots depend on their size. Perovskite quantum dots exhibit high photoluminescence (PL) quantum efficiency (up to ∼90% for the red and >50% in the violet spectral regions), which is advantageous for potential luminescence applications such as thin film displays.7,8 However, in solid-state thin-films, the PL efficiency decreases dramatically owing to efficient non-radiative recombination channels introduced by particle aggregation and surface trap states. An alternative way to achieve quantum confinement in perovskite materials is to reduce the structural dimension.9–12 Zero-dimensional (0D) perovskites can be achieved by introducing structural barriers between the octahedral units of PbBr6. The 0D structure of these perovskites can extend over large (mm) areas, similar to bulk materials.10 Such structures have been shown to exhibit high PL efficiency (up to 45%).12 However, the source of the luminescence in these materials is still hotly debated. It has been suggested the emission arises from a low density of CsPbBr3 impurities, while others suggest that the luminescence originates from carriers confined to 0D unit-cells with confinement imposed by the intrinsic 0D structure.13–17In this work, we have synthesized 0D perovskite micro-crystals by a simple thermally-assisted solution synthesis method. The PL quantum efficiency of the 0D perovskite micro-crystals reaches 45%. The radiative recombination coefficient of the 0D perovskite material is almost two orders of magnitude higher than that of the corresponding three-dimensional perovskite. The increased exciton–phonon interactions originating from strong lattice vibrations at high temperature make the PL spectrum broaden and blue shift, and the emission lifetime increase. The high PL intensity at low temperature is attributed to an increasing dominance of radiative recombination over non-radiative deactivation. Spatial and temporal PL mapping of single 0D perovskite microcrystals reveals this synthesis method yields high-quality microcrystals with uniform and intense emission from intrinsic zero-dimensional perovskites.
Results and discussion
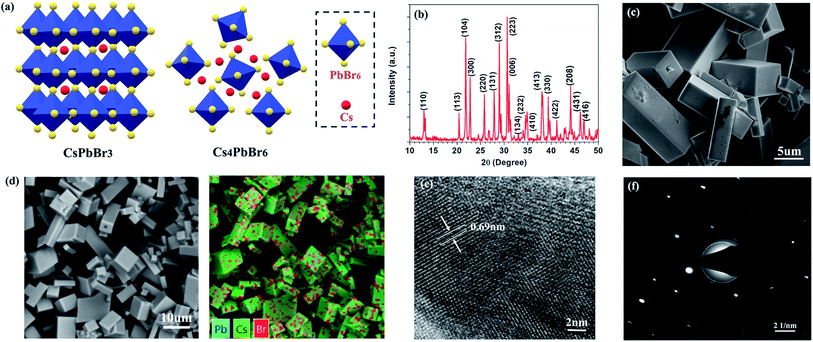
The fabrication procedures of zero-dimensional perovskite micro-crystals are shown in Scheme 1. CsBr solution was added to a glass substrate on a hot plate at 110 °C. When the solution had evaporated to the saturated state, PbBr2 solution was injected. The reaction was allowed to continue until the solvent had evaporated completely. Detailed information about the sample fabrication is provided in the ESI.†Fig. 1a shows the crystalline structures for three-dimensional (CsPbBr3) and zero-dimensional (PbBr6) perovskite materials. PbBr6 comprises isolated octahedral units that do not share common halide atoms, serving to confine band-edge excitons within these small units. Fig. 1b shows results of X-ray diffraction (XRD) measurements, with the main specific crystallization peaks marked, revealing the rhombohedral phase of Cs4PbBr6 consistent with earlier reports (JCPDS no. 73-2478).15,18,19 The scanning electron microscopy (SEM) image (Fig. 1c) shows that the perovskite micro-crystals maintain a regular cuboidal structure over several micrometres. The energy-dispersive X-ray spectroscopy (EDS) mapping image (Fig. 1d) shows that Cs, Pb and Br are distributed in the perovskite crystals with a ratio of 23.8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5.9
5.9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 35.2 (Fig. S1†), which is in good agreement with the stoichiometry of Cs4PbBr6. This result further verifies the perovskite micro-crystals are Cs4PbBr6. The high-resolution transmission electron microscopy (HRTEM) image (Fig. 1e) shows clear periodic lattice fringes. The measured d-spacing of 0.69 nm matches well with the (110) facets of Cs4PbBr6.14,17 The selected-area electron diffraction (SAED) image (Fig. 1f) verifies the single crystalline rhombohedral nature of the perovskite micro-crystals.
35.2 (Fig. S1†), which is in good agreement with the stoichiometry of Cs4PbBr6. This result further verifies the perovskite micro-crystals are Cs4PbBr6. The high-resolution transmission electron microscopy (HRTEM) image (Fig. 1e) shows clear periodic lattice fringes. The measured d-spacing of 0.69 nm matches well with the (110) facets of Cs4PbBr6.14,17 The selected-area electron diffraction (SAED) image (Fig. 1f) verifies the single crystalline rhombohedral nature of the perovskite micro-crystals.
The photoluminescence spectra collected at room temperature are shown in Fig. S2.† The PL peak of the perovskite micro-crystals is at 2.38 eV. Intensity dependent measurements reveal the PL intensity increases in a roughly logarithmic (negative exponential) manner (inset, Fig. S2†) over several hundreds of μW in excitation power with no spectral shift. The PL quantum yield (QY) of the perovskite micro-crystals, measured in an integrating sphere, is 45%. The QY measurement results are shown in Fig. S3.†
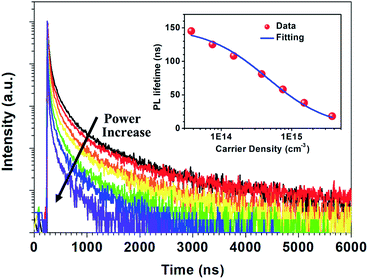
Fig. 2 shows the time-resolved photoluminescence (TRPL) profiles of zero-dimensional perovskite micro-crystals at room temperature. The emission is very long-lived, spanning 6 μs at low excitation powers. As the excitation power is increased from 0.1 nJ cm−2 to 10 nJ cm−2 the timescale decreases significantly, with the signal decaying within 2 μs. The emission decays non-exponentially, as is usual for perovskite materials.12,17 In this work the emission decay profiles were analysed with a function comprising a simple sum of exponential terms:
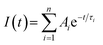 | (1) |
The intensity weighted average lifetime20 is calculated using the equation:
 | (2) |
The average emission decay time can be assumed to be proportional to the inverse of the sum of the rate constants for radiative, kr, and non-radiative, knr, deactivation of the excited state:
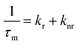 | (3) |
The radiative relaxation rate is assumed to be constant for a given molecule, so the decreased average PL lifetime at higher excitation intensity may be related to an increase in multi-body interactions such as exciton–exciton annihilation.21,22 The high density of excitons generated at the higher excitation intensity can result in increased annihilation and non-radiative recombination rates. The relationship between PL lifetime and carrier density can be expressed as:23,24
| τPL = (A + Bradn0)−1 | (4) |
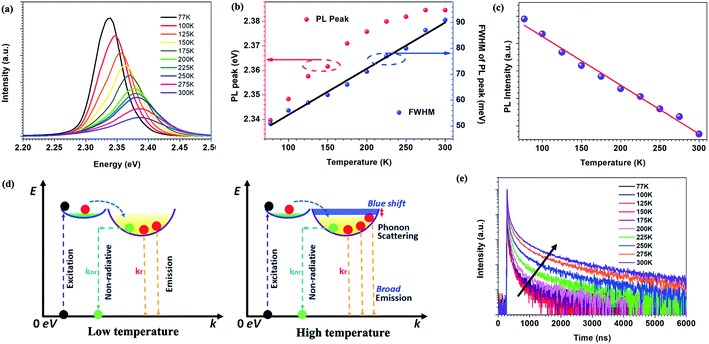
Temperature dependent PL spectra of perovskite micro-crystals are shown in Fig. 3a. With increasing temperature, the PL peak position blue-shifts and its full width at half maximum (FWHM) gradually broadens (Fig. 3b). Meanwhile, the PL intensity decreases linearly, as shown in Fig. 3c. We describe the photo-physical processes within perovskite micro-crystals at different temperatures with the aid of the schematics in Fig. 3d. Following photo-excitation, excitons relax to the ground state through radiative or non-radiative pathways. Phonon-assisted non-radiative recombination processes will be restricted at low temperature owing to weak lattice vibrations. The radiative recombination mechanism plays the dominant role, leading to the higher PL intensity, which is consistent with previous reports.11,25,26 As the temperature is increased, phonons are thermally activated and scatter the excitons, broadening the exciton linewidth. Both acoustic and optical photon scattering could cause the emission peak broadening.29 The increase in temperature also leads to an expansion of the perovskite lattice, leading to a blue-shift in the exciton bandgap.27,28 Some defects exist in perovskite crystals that can capture excitons, leading to a decrease in PL intensity, which is more prevalent at higher temperatures. However, the linear variation of the FWHM with temperature indicates that the scattering from ionized impurities does not play a dominant role.29–31
The temperature dependence of the TRPL of 0D perovskite micro-crystals is shown in Fig. 3e. Unusually, the timescale of the emission increases significantly with increasing temperature, whereas the PL intensity decreases with increasing temperature (Fig. 3c). Since ϕPL = krτ, these observations suggest that the radiative recombination rate, kr, decreases while knr increases disproportionally, as the temperature increases. Fig. S4† shows that the TRPL is nearly independent of the excitation intensity at 77 K. This behaviour suggests that the excitons can radiatively recombine immediately without the impact of additional non-radiative recombination mechanisms such as exciton–exciton annihilation, even at high excitation intensity. The radiative recombination pathway plays the dominant role since the role of thermally activated trap-states is negligible and phonon scattering of excitons is weakened at low temperature, reducing the influence of exciton non-radiative recombination.25
Although the luminescence properties of zero-dimensional perovskites have been examined in several previous studies, the origin of the green emission from zero-dimensional Cs4PbBr6 materials continues to be debated. Several papers suggest the green emission does not emanate from the zero-dimensional material itself.31–38 Reasons leading to this suggestion include; issues relating to the phase of the crystals (e.g. CsPbBr3 ↔ Cs4PbBr6 phase transitions), trace-amounts of CsPbBr3 as an impurity following synthesis, fast recombination of excitons and defect induced emission (such as Br vacancies or the presence of polybromides, self-trapped excitons, and interstitial hydroxyl groups). Recent reviews by Mohammed and co-workers38,39 discuss the various evidence, and the range of techniques used to gain it, for the possible sources of this green emission and suggests that it can be attributed to the existence of three different kinds of Cs4PbBr6 materials (pure, defective and hybrid).
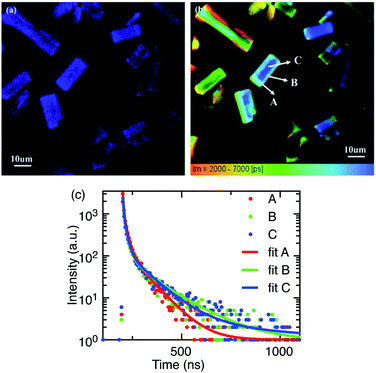
The majority of reported PL spectra of these materials are not spatially resolved. Similarly, the majority of the time-resolved measurements of these materials,11,12,40–45 as summarised by Akkerman et al.,32 report time-resolved PL data integrated over a whole sample, or in some cases from entire single crystals. Such large-area averaging would be insensitive to micrometre sized structural defects or states at crystal boundaries which may be present in these systems. Spatially and temporally resolved optical measurements can provide new information on the luminescence processes in micro-regions within these systems. We have performed time-resolved emission microscopy (TREM) measurements on the zero-dimensional perovskite micro-crystals under discussion. The confocal PL intensity image (Fig. 4a) demonstrates high crystalline uniformity within each crystal since the entire exposed area of the crystals is luminescent. This suggests that the emission originates from the zero-dimensional perovskite itself, rather than a small amount of localized CsPbBr3 impurities, at least on the spatial scales resolvable with current TREM instrumentation. The TREM image and the emission decay profiles corresponding to three typical regions in a single micro-crystal; the corner, the edge, and the body centre (marked A, B, and C, respectively), are shown in Fig. 4b and c. The decay profiles are far from exponential and were parameterized by fitting with sums of 3–4 exponential terms, in the absence of a better fit model. The TREM image (Fig. 4b) displays an amplitude average lifetime map calculated from a triple exponential model (limited by the SPCImage software used). The decay times, relative intensities, and amplitude- and intensity-average emission lifetimes,20 τA and τI, respectively, of the three regions analysed as a sum of four exponential terms are listed in Table 1. The average PL lifetimes in the corner region (A) of this particular micro-crystal are slightly shorter than in the edge or body centre of the crystal (regions B and C), but this is more marked in the intensity-average lifetimes. The variation in the average PL lifetimes from the corner to the rest of the crystal is accounted for by small contributions to the total PL of long-lived components found in the bulk of the micro-crystal (Table 1).
| Decay term | A (corner) | B (edge) | C (centre) |
|---|---|---|---|
| τ1 | 3.6 ns (22%) | 3.5 ns (26%) | 3.9 ns (33%) |
| τ2 | 4.3 ns (21%) | 12.6 ns (63%) | 14.3 ns (57%) |
| τ3 | 17.4 ns (49%) | 50.0 ns (6%) | 96.9 ns (9%) |
| τ4 | 83.1 ns (9%) | 150 ns (5%) | 400 ns (0.3%) |
| τA | 17.4 ns | 19.6 ns | 19.7 ns |
| τI | 43.3 ns | 72.8 ns | 74.6 ns |
Our findings can be compared with previously reported TREM measurements of smaller (∼1–2 μm diameter) phase-pure zero-dimensional Cs4PbBr6 particles17 where the fluorescence was found to be emitted from the entire exposed area of the particles, concurring with our finding that the PL is not due to small quantities of impurity localized in some specific places of the particles. Unlike the uniform PL intensity observed over our micro-crystals (Fig. 4a) the spatial distribution of PL intensity at the central region was found to be significantly higher relative to the edges. Amplitude-average PL lifetimes, very similar to those of the larger microcrystals discussed here, were reported despite the shorter timescale of the measurements, and similarly slightly longer-lived emission was observed towards the centre of the microdisks than the edges. A short decay component with a very similar lifetime to the present case (∼3.4 ns) was observed across the whole microdisk and attributed to trapped exciton recombination inside the crystal, while the long-lived emission (∼19 ns) was ascribed to surface energy state mediated recombination.
There is some indication of slightly longer-lived emission emanating from the centre of the crystals compared to the edges in some of the other microcrystals in the present samples (Fig. 4b), but in comparison with the microdisk work17, the steady-state and time-resolved emission microscopy behaviour of the large zero-dimensional Cs4PbBr6 micro-crystals under investigation here indicates that these crystals are highly uniform in composition and less susceptible to the effects of the surface trap states. The general uniformity of the time-resolved emission behaviour within these crystals suggests that any deep-trap-mediated non-radiative recombinational deactivation is not dominant in these large crystals and the green PL is ascribed to enhanced trap-assisted radiative recombination that is quite uniform over the entire crystal.
Conclusions
In summary, zero-dimensional Cs4PbBr6 micro-crystals of high crystalline quality were prepared by a thermally-assisted solution method and exhibited a high PL quantum yield of 45%. Spatial confinement of the exciton can be achieved within these zero-dimensional perovskite cells despite the overall size of the material spanning several micrometres. The radiative recombination coefficient of the 0D perovskite micro-crystals, 1.5 × 10−8 s−1 cm3, is two orders of magnitude higher than that of the equivalent three-dimensional perovskite, which contributes to the high PL efficiency. At low temperatures, the radiative recombination rate is further increased due to the weak phonon scattering effect. We conclude that the PL properties of zero-dimensional Cs4PbBr6 micro-crystals originate from their intrinsic structural characteristics rather than a small amount of CsPbBr3 impurities. Our investigation provides additional insights into the photophysical dynamics of zero-dimensional perovskite micro-crystals which have potential applications in light-emitting devices and photonics.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the ARC Centre of Excellence in Exciton Science (CE170100026), National Natural Science Foundation of China (No. 61804015), Natural Science Foundation of Jiangsu Province (No. BK20180181) and the Qing Lan Project of the Jiangsu Education Department.References
- H. Wu, S. Wang, F. Cao, J. Zhou, Q. Wu, H. Wang, X. Li, L. Yin and X. Yang, Chem. Mater., 2019, 31, 1936–1940 CrossRef CAS.
- Y. Tong, E. Bladt, M. F. Aygüler, A. Manzi, K. Z. Milowska, V. A. Hintermayr, P. Docampo, S. Bals, A. S. Urban and L. Polavarapu, Angew. Chem., Int. Ed., 2016, 55, 13887–13892 CrossRef CAS.
- A. Swarnkar, R. Chulliyil, V. K. Ravi, M. Irfanullah, A. Chowdhury and A. Nag, Angew. Chem., Int. Ed., 2015, 54, 15424–15428 CrossRef CAS.
- J. Song, J. Li, L. Xu, J. Li, F. Zhang, B. Han, Q. Shan and H. Zeng, Adv. Mater., 2018, 30, 1800764 CrossRef.
- L. Protesescu, S. Yakunin, M. I. Bodnarchuk, F. Krieg, R. Caputo, C. H. Hendon, R. X. Yang, A. Walsh and M. V. Kovalenko, Nano Lett., 2015, 15, 3692–3696 CrossRef CAS.
- B. A. Koscher, J. K. Swabeck, N. D. Bronstein and A. P. Alivisatos, J. Am. Chem. Soc., 2017, 139, 6566–6569 CrossRef CAS.
- S. Zou, C. Liu, R. Li, F. Jiang, X. Chen, Y. Liu and M. Hong, Adv. Mater., 2019, 1900606 CrossRef.
- X. Zhang, X. Bai, H. Wu, X. Zhang, C. Sun, Y. Zhang, W. Zhang, W. Zheng, W. W. Yu and A. L. Rogach, Angew. Chem., Int. Ed., 2018, 57, 3337–3342 CrossRef CAS.
- Z. Bao, H.-C. Wang, Z.-F. Jiang, R.-J. Chung and R.-S. Liu, Inorg. Chem., 2018, 57, 13071–13074 CrossRef CAS.
- X. Chen, F. Zhang, Y. Ge, L. Shi, S. Huang, J. Tang, Z. Lv, L. Zhang, B. Zou and H. Zhong, Adv. Funct. Mater., 2018, 28, 1706567 CrossRef.
- M. De Bastiani, I. Dursun, Y. Zhang, B. A. Alshankiti, X.-H. Miao, J. Yin, E. Yengel, E. Alarousu, B. Turedi, J. M. Almutlaq, M. I. Saidaminov, S. Mitra, I. Gereige, A. AlSaggaf, Y. Zhu, Y. Han, I. S. Roqan, J.-L. Bredas, O. F. Mohammed and O. M. Bakr, Chem. Mater., 2017, 29, 7108–7113 CrossRef CAS.
- M. I. Saidaminov, J. Almutlaq, S. Sarmah, I. Dursun, A. A. Zhumekenov, R. Begum, J. Pan, N. Cho, O. F. Mohammed and O. M. Bakr, ACS Energy Lett., 2016, 1, 840–845 CrossRef CAS.
- Z. Zhang, Y. Zhu, W. Wang, W. Zheng, R. Lin, X. Li, H. Zhang, D. Zhong and F. Huang, Cryst. Growth Des., 2018, 18, 6393–6398 CrossRef CAS.
- Y. Zhang, L. Sinatra, E. Alarousu, J. Yin, A. M. El-Zohry, O. M. Bakr and O. F. Mohammed, J. Phys. Chem. C, 2018, 122, 6493–6498 CrossRef CAS.
- W. Zhai, J. Lin, Q. Li, K. Zheng, Y. Huang, Y. Yao, X. He, L. Li, C. Yu, C. Liu, Y. Fang, Z. Liu and C. Tang, Chem. Mater., 2018, 30, 3714–3721 CrossRef CAS.
- S. Seth and A. Samanta, J. Phys. Chem. Lett., 2017, 9, 176–183 CrossRef.
- S. Seth and A. Samanta, J. Phys. Chem. Lett., 2017, 8, 4461–4467 CrossRef CAS.
- Y. Zhang, M. I. Saidaminov, I. Dursun, H. Yang, B. Murali, E. Alarousu, E. Yengel, B. A. Alshankiti, O. M. Bakr and O. F. Mohammed, J. Phys. Chem. Lett., 2017, 8, 961–965 CrossRef CAS.
- P. Uthirakumar, J.-H. Yun, M. Devendiran, W. W. Lee and I.-H. Lee, J. Lumin., 2019, 209, 163–169 CrossRef CAS.
- A. Sillen and Y. Engelborghs, Photochem. Photobiol., 1998, 67, 475–486 CAS.
- X. Wen, W. Chen, J. Yang, Q. Ou, T. Yang, C. Zhou, H. Lin, Z. Wang, Y. Zhang and G. Conibeer, ACS Appl. Mater. Interfaces, 2018, 10, 31586–31593 CrossRef CAS.
- T. Zhang, Z. Chen, Y. Shi and Q.-H. Xu, Nanoscale, 2019, 11, 3186–3192 RSC.
- V. D'Innocenzo, A. R. Srimath Kandada, M. De Bastiani, M. Gandini and A. Petrozza, J. Am. Chem. Soc., 2014, 136, 17730–17733 CrossRef.
- Y. Yamada, T. Nakamura, M. Endo, A. Wakamiya and Y. Kanemitsu, J. Am. Chem. Soc., 2014, 136, 11610–11613 CrossRef CAS.
- S. D. Stranks, V. M. Burlakov, T. Leijtens, J. M. Ball, A. Goriely and H. J. Snaith, Phys. Rev. Appl., 2014, 2, 034007 CrossRef.
- K. Wu, A. Bera, C. Ma, Y. Du, Y. Yang, L. Li and T. Wu, Phys. Chem. Chem. Phys., 2014, 16, 22476–22481 RSC.
- K. Thirumal, W. K. Chong, W. Xie, R. Ganguly, S. K. Muduli, M. Sherburne, M. Asta, S. Mhaisalkar, T. C. Sum and H. S. Soo, Chem. Mater., 2017, 29, 3947–3953 CrossRef CAS.
- K. Miyata, T. L. Atallah and X.-Y. Zhu, Sci. Adv., 2017, 3, e1701469 CrossRef.
- Z. Guo, X. Wu, T. Zhu, X. Zhu and L. Huang, ACS Nano, 2016, 10, 9992–9998 CrossRef CAS.
- J. Yin, Y. Zhang, A. Bruno, C. Soci, O. M. Bakr, J.-L. Brédas and O. F. Mohammed, ACS Energy Lett., 2017, 2, 2805–2811 CrossRef CAS.
- A. D. Wright, C. Verdi, R. L. Milot, G. E. Eperon, M. A. Pérez-Osorio, H. J. Snaith, F. Giustino, M. B. Johnston and L. M. Herz, Nat. Commun., 2016, 7, 11755 CrossRef.
- Q. A. Akkerman, A. L. Abdelhady and L. Manna, J. Phys. Chem. Lett., 2018, 9, 2326–2337 CrossRef CAS.
- J. Bao and V. G. Hadjiev, Nano-Micro Lett., 2019, 11, 26 CrossRef CAS.
- D. Han, H. Shi, W. Ming, C. Zhou, B. Ma, B. Saparov, Y.-Z. Ma, S. Chen and M.-H. Du, J. Mater. Chem. C, 2018, 6, 6398–6405 RSC.
- J. Yin, H. Yang, K. Song, A. M. El-Zohry, Y. Han, O. M. Bakr, J. L. Bredas and O. F. Mohammed, J. Phys. Chem. Lett., 2018, 9, 5490–5495 CrossRef CAS.
- X. Li, F. Cao, D. Yu, J. Chen, Z. Sun, Y. Shen, Y. Zhu, L. Wang, Y. Wei and Y. Wu, Small, 2017, 13, 1603996 CrossRef.
- Q. A. Akkerman, S. Park, E. Radicchi, F. Nunzi, E. Mosconi, F. De Angelis, R. Brescia, P. Rastogi, M. Prato and L. Manna, Nano Lett., 2017, 17, 1924–1930 CrossRef CAS.
- O. F. Mohammed, J. Phys. Chem. Lett., 2019, 10, 5886–5888 CrossRef CAS.
- L. Wang, H. Liu, Y. Zhang and O. F. Mohammed, ACS Energy Lett., 2019, 5, 87–99 CrossRef.
- J. H. Cha, J. H. Han, W. Yin, C. Park, Y. Park, T. K. Ahn, J. H. Cho and D. Y. Jung, J. Phys. Chem. Lett., 2017, 8, 565–570 CrossRef CAS.
- D. Chen, Z. Wan, X. Chen, Y. Yuan and J. Zhong, J. Mater. Chem. C, 2016, 4, 10646–10653 RSC.
- Y. Ling, L. Tan, X. Wang, Y. Zhou, Y. Xin, B. Ma, K. Hanson and H. Gao, J. Phys. Chem. Lett., 2017, 8, 3266–3271 CrossRef CAS.
- L. N. Quan, R. Quintero-Bermudez, O. Voznyy, G. Walters, A. Jain, J. Z. Fan, X. Zheng, Z. Yang and E. H. Sargent, Adv. Mater., 2017, 29, 1605941–1605946 CrossRef.
- J. Xu, W. Huang, P. Li, D. R. Onken, C. Dun, Y. Guo, K. B. Ucer, C. Lu, H. Wang, S. M. Geyer, R. T. Williams and D. L. Carroll, Adv. Mater., 2017, 29, 1703701–1703710 Search PubMed.
- Z. Gan, F. Zheng, W. Mao, C. Zhou, W. Chen, U. Bach, P. Tapping, T. W. Kee, J. A. Davis, B. Jia and X. Wen, Nanoscale, 2019, 11, 14676–14683 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ra08890k |
| This journal is © The Royal Society of Chemistry 2020 |