Open Access Article
Open Access ArticleDFT investigation of hydrogen atom-abstraction reactions of NHC-boranes by various carbon-centered radicals: barriers and correlation analyses†
Hong-jie Quab,
Lang Yuana,
Cai-xin Jiaa,
Hai-tao Yu *a and
Hui Xu
*a and
Hui Xu *a
*a
aKey Laboratory of Functional Inorganic Material Chemistry (Ministry of Education), School of Chemistry and Materials Science, Heilongjiang University, Harbin 150080, P. R. China
bCollege of Science, Heilongjiang Bayi Agricultural University, Daqing, 163319, P. R. China
First published on 18th September 2020
Abstract
In this study, we employed a quantum-mechanical computational method to investigate the hydrogen-atom abstraction reactions of two nitrogen heterocyclic carbene boranes (NHC-boranes), NHC-BH3 and NHC-BH2CN, by a series of carbon-centered radicals bearing various substituents. We explored the degree of correlation of the activation and free energy barriers to their components. Furthermore, we also investigated the effects of the radical and substituent sizes, nucleophilicity/electrophilicity indices, and the spin density distribution of the radical reactants on the three fundamental barriers and the thermal contribution of the reaction energy to the kinetic barrier. Using the generated data, we assessed the abilities of the various radical reactants to abstract the hydrogen atom from NHC-boranes. Further, we performed a similar analysis after dividing those radical reactants into four groups, which were classified based on the dominant factor affecting their electronic density distribution, which involves the inductive effect, conjugation, hyperconjugation, and the feedback of lone-pair electrons. The results and conclusions of this investigation not only provide insight into the relationships between some of the key kinetic and thermodynamic parameters, which is useful for understanding the dynamics of such hydrogen-abstraction reactions, but also provide information for selecting suitable radical reactants for further experimental investigations.
1. Introduction
Nitrogen heterocyclic carbene boranes (NHC-boranes) can be considered as Lewis acid–base coordination compounds because the NHC donates a pair of electrons to the empty orbital of the boron atom, leading to the formation of a C–B coordinate bond.1,2 Thus, the NHC and borane can be viewed as Lewis base and acid, respectively. The electron-transfer by the NHC renders the borane fragment electron-rich, and hence strongly nucleophilic.3–5 In NHC-boranes, the B–H σ bonding electrons can delocalize into the π-conjugated plane of the NHC ring via σ–π hyperconjugation. This electron donation and delocalization significantly decrease the B–H bond dissociation energy5–7 relative to free trivalent boron species4 and make the B–H bond activation thermodynamically more favorable than that in free BH3. Furthermore, the unpaired electron on the central B atom of the NHC-boryl radical, that results from the homolytic B–H bond cleavage of the NHC-borane, is effectively dispersed on the π-orbital delocalized around the NHC ring.2,8–11 This delocalization significantly improves the thermodynamic stability of the NHC-boryl radical and thus leads to more favorable reaction energy and thermal contribution to kinetic barrier. The reduced kinetic barrier affords a lower B–H activation energy, which renders the B–H activation and the further H-abstraction kinetically more favorable compared to the pristine BH3 and even the N- and P-coordinated amine- and phosphine-boranes.12,13 Thereby, the B–H bond activation of NHC-boranes is kinetically and thermodynamically more favorable and results in the rich chemistry of NHC-boranes.14–16The reactivity of the radical used for the H-atom abstraction of NHC-boranes has a remarkable effect on the rate constant of the process.7,9 For example, the rate constant for the hydrogen atom abstraction with the t-BuO˙ radical is approximately 108 M−1 s−1,3,4,7 whereas the use of alkyl radicals for the same process affords a rate of approximately 104 M−1 s−1.9 Clearly, the polarity effect plays an important role between these two rate constants.11,17 The strongly electrophilic t-BuO˙ radical matches better with the strongly nucleophilic NHC-boranes than the relatively weak electrophilic alkyl radicals, and thus the activation (ΔE‡) and free energy barriers (ΔG‡) are reduced relatively and lead to the higher H-atom abstraction rate constant.
The key parameters for evaluating the relative reactivities of different radical reactants in the H-atom abstractions of NHC-boranes are the kinetic barriers related to the rate constant, such as the intrinsic barrier (ΔE‡0), activation barrier, and free energy barrier.18–20 First, the nucleophilicity and electrophilicity of the radicals used for the H-atom abstractions, which are generally determined by global/local nucleophilicity and electrophilicity indices, are often used as the criterion for evaluating the kinetic barriers.21,22 Such a consideration is based on the polarity-match principle,23–25 wherein the larger the electrophilicity index, or the smaller the nucleophilicity index of the radical, the better is its match with the nucleophilic NHC-boranes, with lower or larger kinetic barriers and corresponding rate constants, respectively. Therefore, the electron-withdrawing and electron-donating groups attached to the radical center make the central atom electron-poor and electron-rich and thus electrophilic and nucleophilic, respectively. However, such an assessment is based more on chemical intuition, because the global nucleophilicity and electrophilicity indices of radicals are determined by their electron affinity and ionization energy.26,27 Alternatively, frontier orbital energies can also be used to determine the radical's local nucleophilicity and electrophilicity indices by taking into account the spin density distribution of the unpaired electron.27–31 Perhaps, such static or thermodynamic parameters can be used to experientially estimate the trends of the relative changes in the rate constants of different H-atom abstraction reactions. However, they are not suitable for describing the strict dynamic behavior, because the reaction dynamics involve not only the radical reactant but also the other NHC-borane reactant, activation transition state (TS), and the relative stabilities of the formed products. The activation barrier can be determined from the total electronic energies of the TS and reactants, and the reaction energy provides the thermodynamic contribution to the kinetic barrier,16 which is a component of the activation barrier. Using the obtained activation barrier and thermodynamic contribution, the intrinsic barrier of a reaction, i.e., the reaction stereoelectronic and steric effects, can be readily separated.32 Further, by combining the activation barrier with the temperature-dependent Gibbs thermal correction, the free energy barrier of the reaction can be determined. Thus, in this approach, the relevance of the radical nucleophilicity or electrophilicity indices for determining the relative rate constants, and the correlations of the barriers to these indices are not clear.
The second method for comparing the relative rate constants of the H-atom abstractions by different radicals involves the use of the charges and/or spin densities on the central atoms of the radical reactants. However, these two approaches still only reflect the electron-loss and electron-addition abilities or trends of the frontier orbitals. When approaching the TS along the reaction coordinate, the redistributions of the charge and spin densities are inevitable. Therefore, it is somewhat unrealistic to derive the kinetic stereoelectronic and steric effects using the charges and spin densities alone, of the energy minimum structures of the radical reactants.33–35 Furthermore, the spin density distribution of the product radical directly affects its thermodynamic stability, and further affects the thermodynamic reaction energy and thermal contribution to the kinetic barrier. Therefore, it is difficult to strictly correlate the relative reactivities of the radicals to their abilities for abstracting H-atoms from the NHC-boranes using their charges and spin density distributions.
The third method is the most chemically intuitive one and uses the size of the radical or its substituent to estimate the effectiveness of the H-atom abstractions from the NHC-boranes. The size of the radical or its substituent may directly reflect the steric hindrance faced during the radical attack. However, this sterics-based judgment is only empirical, because of the multitude of factors involved, such as the variations in the reaction trajectory,36 stereoelectronic and steric effects,33–35 reaction thermodynamics.32 Further, when the steric and electronic hindrances are not the dominant factors related to the H-abstraction kinetics, this method is completely ineffective.
In addition to the evaluation of the effects of the above-mentioned parameters on the three fundamental barriers, i.e., intrinsic, activation, and free energy barriers, it is essential to investigate the correlations among them to understand the H-abstraction kinetics. For a given reaction, this relationship is very clear, as it is well-known that the intrinsic barrier and thermal contribution constitute the activation barrier,32 whereas the free energy barrier is comprised of the activation barrier, activation ZPVE (ΔE‡ZPVE), and activation Gibbs free energy thermal correction (ΔG‡corr) (see next section). However, for the H-abstraction reactions of an NHC-borane by a series of radicals, the degree of statistical correlation among the three barriers appears to be of significant importance in understanding the H-atom abstraction reactivity of a new radical. Furthermore, it is clear that the vibrationally-adiabatic barrier,37 i.e., activation barrier, is made up of the intrinsic barrier and the thermal contribution to the kinetic barrier, in which the former is often understood as the measurement of stereoelectronic and steric effects under the thermoneutral condition, while the latter originates from thermodynamic reaction energy.32,38 However, to the best of our knowledge, the intrinsic barrier and thermal contribution are rather poorly correlated to the activation barrier.
To gain insights into the questions raised in this section on the predictability of H-atom abstraction reactions of NHC-boranes, we selected a series of carbon-centered radicals comprising different substituents as the attacking radicals for performing H-atom abstractions on two given NHC-boranes, NHC-BH3 and NHC-BH2CN. We attempted to build a statistical correlation degree among the intrinsic, activation, and free energy barriers, followed by the investigation of the effects of the radical and substituent sizes, global/local nucleophilicity and electrophilicity indices, and spin density distribution of the unpaired electron in the reactant and product radicals on the three fundamental barriers. The present results and conclusions provide helpful theoretical support for not only the analysis of reaction thermodynamics and dynamics of this type of H-abstraction reactions but also for the selection of radicals for carrying out H-atom abstraction in further experimental investigations.
2. Theoretical and computational details
2.1. Barriers
The free energy barrier is defined as the Gibbs free energy (G) difference between the reaction TS and reactants (R) and can be calculated according to the following equation.
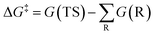 | (1) |
The Gibbs free energy of a species can be calculated using the temperature-dependent thermal correction to the Gibbs free energy (Gcorr) and total electronic energy (E) without the zero-point vibrational energy (ZPVE, EZPVE) correction, and can be calculated according to the following equation.
| G = E + Gcorr | (2) |
Thus, eqn (1) can be rewritten as
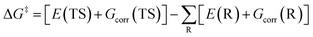 | (3) |
The total electronic energy without ZPVE correction is the difference between the total electronic energy with ZPVE correction (Ecorr) and EZPVE and can be calculated according to the following equation.
| E = Ecorr − EZPVE | (4) |
By substituting eqn (4) into eqn (3), the ΔG‡ can be obtained using the following equations.
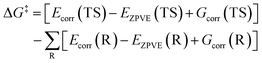 | (5) |
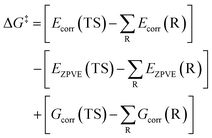 | (6) |
| ΔG‡ = ΔE‡ − ΔE‡ZPVE + ΔG‡corr | (7) |
Notably, the activation barrier ΔE‡ also includes the ZPVE correction, and thus it could also be referred as the vibrationally-adiabatic barrier.
Murdoch et al.39–41 have improved the Marcus equation42–44 and re-expressed the new equation as
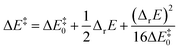 | (8) |
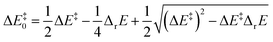 | (9) |
For scenarios where the Marcus intrinsic barrier (ΔG‡0) in the original Marcus equation42–44 becomes the temperature-independent intrinsic barrier (ΔE‡0), the standard reaction Gibbs free energy (ΔrG0) in the original Marcus equation was replaced by the reaction energy (ΔrE, the difference between the ZPVE-corrected electronic total energies of products and reactants). These mathematical and physical treatments significantly expanded the application scope of the Marcus theory in chemical reactions.41,45–47 The latter two terms in eqn (8) can be considered as thermal contributions of the reaction energy to the kinetic barrier (ΔE‡therm). For simplicity, this contribution is abbreviated as thermal contribution in the following discussion. Thus, eqn (8) can be rewritten as
| ΔE‡ = ΔE‡0 + ΔE‡therm | (10) |
By substituting eqn (10) into eqn (7), we obtain
| ΔG‡ = ΔE‡0 + ΔE‡therm − ΔE‡ZPVE + ΔG‡corr | (11) |
It is clear that the free energy barrier consists of the intrinsic barrier, thermal contribution, negative activation ZPVE correction, and activation Gibbs free energy thermal correction.
2.2. Nucleophilicity and electrophilicity indices
Based on Parr's definition,48 the global electrophilicity index (ω) of a radical can be expressed as
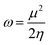 | (12) |
The global nucleophilicity index (N) of a radical is defined as52,53
| N = EαHOMO − EαHOMO(F˙) | (13) |
After obtaining the global electrophilicity and nucleophilicity indices of a radical, its local electrophilicity (ωB) and nucleophilicity (NB) indices can be readily calculated using the spin density (ρs) on the radical center according to the following equations29,53
| ωB = ωρs | (14) |
| NB = Nρs | (15) |
2.3. TST rate constant and activation energy
In this study, we used the traditional transition state theory (TST)54–56 to calculate H-atom abstraction rate constants, and the corresponding equation is57
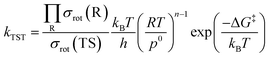 | (16) |
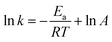 | (17) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k vs. −1/RT.
k vs. −1/RT.
2.4. Computational aspects
The geometries of all stationary points were located using unrestricted computations without any symmetry constraint at the B3LYP/6-311++G(d,p) and M06-2X/6-311++G(d,p) levels of theory.58–62 The density functional theory (DFT) computations were conducted using the Gaussian 09 software package.63 The validity of such a computational level of theory has been proved in previous reports (comparison and explanation of methods, see: ESI†).64–68 Further, frequency computations at the same level of theory were used not only to provide ZPVE and Gibbs free energy thermal correction but also to prove the existence of these located stationary points, i.e., no imaginary frequency for minima and only one imaginary frequency for the TSs. Note that in both geometry optimizations and frequency computations, the solvent effect was considered using the self-consistent reaction field method69,70 with the polarizable continuum model.71–74 The solvent used in computations is benzotrifluoride, which is selected based on the available experiments.17,75,76 Unless otherwise specified, the discussed data were obtained at the B3LYP/6-311++G(d,p) level. When the results are method-dependent or require emphasis and comparison, they are directly discussed at the B3LYP/6-311++G(d,p) and M06-2X/6-311++G(d,p) levels of theory. Furthermore, the electrophilicity/nucleophilicity indices of some minimum structures used in the next discussion were computed at the mPWPW91/6-311+G(d,p) level of theory.773. Results and discussion
Scheme 1 lists the various C-centered free radicals employed for abstracting the hydrogen atoms of NHC-BH3 and NHC-BH2CN. To obtain a more realistic effect of the different radicals on reactions, the substituents were selected based on the size effect and electron-withdrawing and electron-donating properties. The electronic properties involve not only the inductive effect originating from the electronegativity but also the hyperconjugative stabilizations from the different electron delocalization patterns.3.1. Thermal contribution
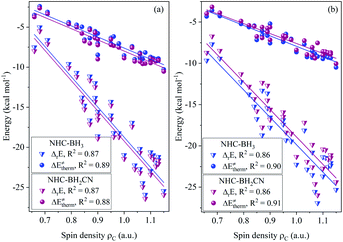
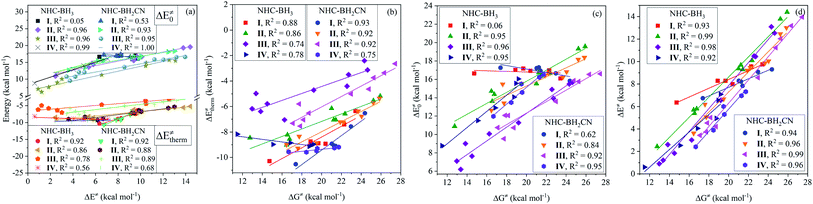
The calculated data (Tables S6–S9†) indicates that all of the H-atom abstraction reactions in our investigation possess negative reaction energy and negative thermal contribution. The negative thermal contribution decreases the activation and free energy barriers and favors B–H bond activation. Furthermore, the exothermicity indicates a more favorable thermodynamic stability of the products compared to the reactants, which is attributed to these two aspects: one is higher C(sp2,sp3)–H bond energy (>90 kcal mol−1) of the closed-shell products78 than the B–H bond energy (<90 kcal mol−1) of the NHC-borane reactants,5–7 while the other is the more effective delocalized stabilization of the unpaired electron of the open-shell NHC-boryl radical products than the open-shell C-centered radical reactants.The fitting results shown in Fig. 1 indicate that the thermal contribution has an acceptable linear dependence on the single-electron spin density of the radical reactant's central C atoms, which is reflected by the coefficients of determination (CODs, R2) of 0.89 and 0.88, for the NHC-BH3 and NHC-BH2CN reaction series, respectively, at the B3LYP level. The values of the negative slopes of the corresponding fitting equations were very close (−14.08 for NHC-BH3 and −14.14 for NHC-BH2CN) and a slightly larger (0.33 kcal mol−1) positive intercept was observed for the NHC-BH3 than for NHC-BH2CN, indicating that the NHC-BH2CN reaction series has a more favorable thermal contribution than that of NHC-BH3. This result is attributed to the lower thermodynamic stability of NHC-˙BH2 than NHC-˙BHCN. Clearly, the single-electron delocalization through p–π conjugation between the –CN and B plays a dominant role in the relatively high thermodynamic stability of NHC-BH2CN. Furthermore, the negative slopes in the two fitting equations imply that the thermal contribution becomes less favorable to the barrier (more positive in value) with decreasing spin density. The decreasing spin density on the C radical center indicates greater delocalization and higher thermodynamic stability, which in turn decreases the reaction energy and thermal contribution. This trend is well supported by the results shown in Fig. 1, wherein, with the reduction of spin density, the reaction energy decreases, and the thermal contribution becomes more positive in value. Thus, the decreasing spin density on the C radical center disfavors the reduction of activation and free energy barriers. Furthermore, the COD (0.87) of spin density vs. reaction energy is very close with those (0.88 and 0.89) of the spin density vs. thermal contribution at the B3LYP level, as shown in Fig. 1. This agreement means that for the present H-atom abstraction reactions, the spin density distribution of the reactant radicals has a strong linear correlation to reaction energy. The reaction energy and thermal contribution can be approximately determined from the spin density distribution of radical reactants.
We found that the higher is the reactivity of the radical reactant, the more negative in value is its thermal contribution (Fig. S1†). Because alkyl radicals and radicals substituted by the groups with only inductive effect have lower thermodynamic stability than the C-centered radicals bearing π-conjugated groups, the latter type of radicals have a less favorable H-atom abstraction thermal contribution than the two former types of radicals. For instance, the methyl radical, which does not have any substituent effects, possesses the most favorable thermal contribution among all tested radicals, while the radicals comprising an unsaturated double bond, such as ˙CH2CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2, ˙CH2–CH
CH2, ˙CH2–CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CF2, ˙CH2–N
CF2, ˙CH2–N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2, ˙CH2Ph, etc., have the smallest (more positive in value) thermal contribution (Fig. S1†). The electron delocalization pattern clearly plays a dominant role in such results.
CH2, ˙CH2Ph, etc., have the smallest (more positive in value) thermal contribution (Fig. S1†). The electron delocalization pattern clearly plays a dominant role in such results.
Different electron delocalization patterns were also found to cause varying nucleophilicities and electrophilicities of the radical reactants (Fig. S2†). The radicals bearing a strong electron-withdrawing group, such as ˙CH2CF3, ˙CH2COOH, ˙CH2CHO, ˙CH2CN, ˙CF2H, ˙CFH2, are relatively strongly electrophilic (weakly nucleophilic), whereas the Et˙, Pr˙, and Bu˙ radicals which bear electron-donating substituents are less electrophilic (strongly nucleophilic) than Me˙. Furthermore, the radicals comprising central C atoms bonded directly to the heteroatom groups (–NH2, –NHMe, –OMe, –OH, etc.) have stronger nucleophilicity than Me˙, implying that the inductive effect originating from the electronegativity is of minor importance, and the dominant factor is the electronic feedback of the lone-pair electrons of the heteroatoms into the p orbital of the central C atoms. Thus, those radicals with heteroatomic substituents display an electron-contributing characteristic. The radicals with the unsaturated groups –N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2, –CH
CH2, –CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2, –CH
CH2, –CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CF2, and –CH2Ph have a similar property, but their electron-transfer pattern does not indicate the feedback of the lone-pair electrons, instead indicating p–π conjugation. Despite the apparent likely relationship between the nucleophilicity/electrophilicity of the radicals and the electron-transfer patterns of substituents, the linear fitting gave a low COD between the spin densities on the C radical centers and the global/local nucleophilicity and electrophilicity indices (Fig. S3†). Even for the spin density vs. local nucleophilicity index, which has the highest COD among the four indices, the COD of the linear fitting was only 0.42.
CF2, and –CH2Ph have a similar property, but their electron-transfer pattern does not indicate the feedback of the lone-pair electrons, instead indicating p–π conjugation. Despite the apparent likely relationship between the nucleophilicity/electrophilicity of the radicals and the electron-transfer patterns of substituents, the linear fitting gave a low COD between the spin densities on the C radical centers and the global/local nucleophilicity and electrophilicity indices (Fig. S3†). Even for the spin density vs. local nucleophilicity index, which has the highest COD among the four indices, the COD of the linear fitting was only 0.42.
Similarly, the thermal contribution had the best linear correlation degree with local nucleophilicity index; however, the COD is somewhat low, as indicated by 0.34 and 0.24 for the NHC-BH3 and NHC-BH2CN reaction series, respectively (Fig. S4†). These results imply that it is difficult to predict the thermal contribution of the H-atom abstraction of a radical, based on its spin density localized at the central C atom. The assessment is only qualitative for the radicals in their extremely nucleophilic and electrophilic states, such as the alkyl radicals and C-centered radicals bearing strong electron-withdrawing substituents (–CHO, –COOH, –COMe, etc.).
3.2. Intrinsic barrier
The definition of the intrinsic barrier is complex and is generally considered to involve the stereoelectronic effect of a reaction.18–20 For some chemical reactions, particularly the bimolecular radical additions and atom/group abstractions, the sizes of the molecules or their substituents bonded to the radical center atoms are often empirically deemed to reflect the stereoelectronic effect; the larger the molecule or substituent, the stronger is the stereoelectronic effect of the reaction, and thus the higher is the corresponding reaction intrinsic barrier, and vice versa. However, if the intrinsic barrier is the only aspect in the composition of the activation barrier other than the thermal contribution, it should include the stereoelectronic effect in addition to the steric effect.79–82 For example, the steric hindrance originating from the van der Waals repulsion, geometric deformation repulsion of the TS, electrostatic action energy, dispersive energy, etc. should contribute to the intrinsic barrier. Therefore, only when the stereoelectronic and steric effects are dominant, and the molecule or group size can reflect them, the intrinsic barrier would have a good correlation degree to the molecule or group size. Obviously, the contribution of the intrinsic barrier is somewhat more complicated than thermal contribution.The results of the calculated intrinsic barriers for the H-abstraction by different radicals clearly indicate that the intrinsic barrier is poorly dependent on the radical size or substituent size (Fig. S5†). The most indicative examples are those of almost all investigated alkyl radicals, including Me˙ which has the smallest size, which have a larger intrinsic barrier than the other substituted radicals, except ˙CH2NH2 and ˙CH2N(CH3)H. For instance, the radical reactants bearing the strong electron-withdrawing groups, such as ˙CH2CF3, ˙CH2COOH, ˙CH2CHO, ˙CH2COMe, have a significantly lower intrinsic barrier than that of the alkyl radicals examined in this study. Such a result is much closely related to the electrophilic and nucleophilic characteristics of the radicals. For ˙CH2NH2 and ˙CH2N(CH3)H, the strong transfer of the lone-pair of electrons from N to the single-electron-occupied p orbital renders the C radical center electron-rich and strongly nucleophilic, while the strong electron-withdrawing groups cause an electron-poor characteristic at the carbon radical center and are thus electrophilic. Electrophilic radicals are better in polarity-matching with nucleophilic NHC-boranes than nucleophilic radicals, and thus the electrophilic radicals such as ˙CH2CF3, ˙CH2COOH, ˙CH2CHO, and ˙CH2COMe, have lower H-atom abstraction intrinsic barriers than the strongly nucleophilic radicals such as ˙CH2NH2 and ˙CH2N(CH3)H.
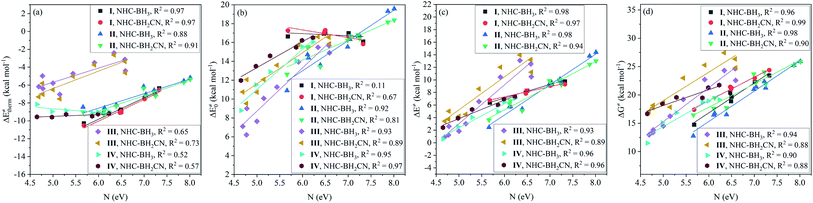
The results of the analysis shown in Fig. 2 indicates the medium linear dependence of the intrinsic barrier on the global/local nucleophilicity and electrophilicity indices, in which those possessing a relatively high COD are the local electrophilicity and global nucleophilicity indices; the former CODs are 0.85 (NHC-BH3) and 0.77 (NHC-BH2CN) and the latter are 0.80 (NHC-BH3) and 0.70 (NHC-BH2CN). It is likely that the local electrophilicity and global nucleophilicity indices can be used to estimate the relative intrinsic barrier heights only between those radicals that have a sufficiently large difference in their nucleophilicity or electrophilicity indexes.
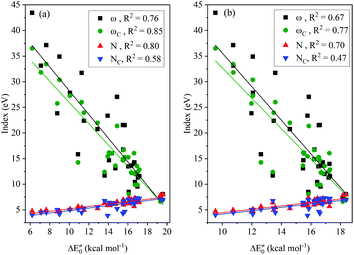 | ||
| Fig. 2 Correlations of nucleophilicity/electrophilicity indexes of the attacking radicals to the intrinsic barriers (ΔE‡0) to the H-abstraction reactions of NHC-BH3 (a) and NHC-BH2CN (b). | ||
3.3. Activation barrier
Activation barrier is comprised of intrinsic barrier and thermal contribution. It should be noted that all of the presently investigated H-atom abstraction reactions are exothermic, which results in a negative thermal contribution. The calculated results (Fig. S6†) revealed that the intrinsic barriers of those H-abstractions account for 52–87% (NHC-BH3) and 56–86% (NHC-BH2CN) of the activation barriers. Thus, the decreased effect of the thermal contribution to the activation barrier exceeds the positive effect of the intrinsic barrier. Furthermore, at the low activation barrier height, the percentage of the intrinsic barrier is close to that of thermal contribution. With an increase in the activation barrier, the proportion of the contribution of the intrinsic barrier and thermal contribution approximately increase and decrease, respectively (Fig. S6†). However, the estimation of the change regularities of the intrinsic barrier and thermal contribution relative to the activation barrier, from their absolute contributions to the activation barrier, is challenging (Fig. S7†). Further analysis indicated that the linear correlation degrees of the activation barrier to the intrinsic barrier and thermal contribution are somewhat low, which is reflected from their CODs of 0.73 (NHC-BH3) and 0.59 (NHC-BH2CN) for the intrinsic barrier and the CODs of 0.19 (NHC-BH3) and 0.47 (NHC-BH2CN) for the thermal contribution (Fig. S8(a)†).Furthermore, we found that the activation barrier has a poor correlation to the global/local nucleophilicity and electrophilicity indices (Fig. S8(b) and (c)†) with CODs of 0.04–0.79. Despite the poor correlation, it is unambiguous that the change of activation barrier approximately obeys the polarity-matching rule for the radicals with strong-withdrawing and strong-donating groups, which leads to their relatively low and high activation barriers, respectively, as shown in Fig. S9.† This trend agrees with the change of the intrinsic barrier relative to the global/local nucleophilicity and electrophilicity indices, as discussed above.
By comparing the results presented in Fig. S9† with those in Fig. S1 and S5,† we explored the variation regularity of the activation barrier relative to the intrinsic barrier and thermal contribution. For ˙CH2NH2 and ˙CH2N(CH3)H, the strong nucleophilicity originating from strong electron-donating groups and weak matching with nucleophilic NHC-boranes led to high intrinsic barriers of their H-abstraction reactions. Further, considering their slightly low thermal contributions, their activation barriers were very high. Thus, the intrinsic barrier dominates their activation barriers. For ˙CH2N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2, ˙CH2Ph, ˙CH2CH
CH2, ˙CH2Ph, ˙CH2CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CF2, and ˙CH2CH
CF2, and ˙CH2CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2, despite their medium intrinsic barriers, the very small thermal contributions arising from their high p–π conjugative stabilization, led to the high activation barriers. However, for the t-Bu˙, i-Pr˙, Et˙, n-Pr˙, and n-Bu˙ radicals with relatively high intrinsic barriers, their very low thermodynamic stabilities result in large thermal contributions and thus activation barriers of a medium-height. Finally, for ˙CH2CF3, ˙CH2COOH, ˙CH2CHO, and ˙CH2COMe, the strong electron-withdrawing groups make their C radical centers strongly electrophilic and afford good agreement with the nucleophilic NHC-boranes, and thus lower their intrinsic barriers. Despite having relatively small thermal contributions, their H-atom abstraction reactions have low activation barriers. Thus, the dominant factor that determines their activation barriers is the intrinsic barrier.
CH2, despite their medium intrinsic barriers, the very small thermal contributions arising from their high p–π conjugative stabilization, led to the high activation barriers. However, for the t-Bu˙, i-Pr˙, Et˙, n-Pr˙, and n-Bu˙ radicals with relatively high intrinsic barriers, their very low thermodynamic stabilities result in large thermal contributions and thus activation barriers of a medium-height. Finally, for ˙CH2CF3, ˙CH2COOH, ˙CH2CHO, and ˙CH2COMe, the strong electron-withdrawing groups make their C radical centers strongly electrophilic and afford good agreement with the nucleophilic NHC-boranes, and thus lower their intrinsic barriers. Despite having relatively small thermal contributions, their H-atom abstraction reactions have low activation barriers. Thus, the dominant factor that determines their activation barriers is the intrinsic barrier.
3.4. Free energy barrier
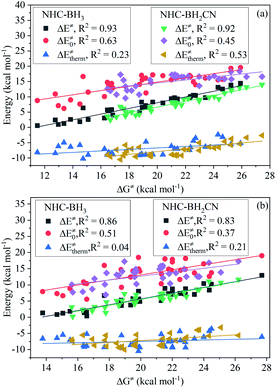
For the H-abstraction reactions investigated in this study, the activation ZPVE correction, intrinsic barrier, and activation Gibbs free energy correction account for less than 4%, 27–54%, and 28–47% of the free energy barrier, respectively; the latter two had over 71% for each reaction (Fig. S10†). Furthermore, the thermal contribution serves to lower the H-abstraction free energy barrier, and its proportion in the free energy barrier varies from 8 to 29% and is less than not only the intrinsic barrier but also the Gibbs free energy thermal correction. However, we did not observe variational regularities of the thermal contribution and intrinsic barrier with the increase in free energy barrier (Fig. S10 and S11†). This trend can be directly observed from the analysis shown in Fig. 3, which involves the linear fitting of the free energy barrier vs. thermal contribution and intrinsic barrier; their respective CODs are only 0.63 and 0.23 for the NHC-BH3 reaction series, and 0.45 and 0.53 for the NHC-BH2CN reaction series.While using eqn (7), we found that upon increasing the free energy barrier, the percentages of the activation barrier and Gibbs thermal correction approximately increase and decrease, respectively (Fig. S12†). However, the contribution of the Gibbs free energy thermal correction to the free energy barrier did not have a significant difference in value (Fig. S11 and S13†). Thus, the free energy barrier should be dominated by the activation barrier. This estimation agrees well with the results of the linear fitting between the activation and free energy barriers (Fig. 3), which gives high CODs of 0.93 (NHC-BH3) and 0.92 (NHC-BH2CN).
Further analysis indicated that the free energy barrier has a poor correlation to the global/local nucleophilicity and electrophilicity indices (Fig. S14†), as noted, that the best dependence is on the global nucleophilicity index with the CODs of 0.74 (NHC-BH3) and 0.52 (NHC-BH2CN). By comparing them with the CODs of 0.80 (NHC-BH3) and 0.70 (NHC-BH2CN) for the intrinsic barrier (Fig. 2) and 0.79 (NHC-BH3) and 0.61 (NHC-BH2CN) for the activation barrier (Fig. S8†), the best correlation to the global nucleophilicity index can be clearly seen to be the intrinsic barrier, followed by the correlations to the activation and free energy barriers. Thus, the electron- and/or orbital-energy-dependent nucleophilicity/electrophilicity indices are much more related to the intrinsic barrier than that of the activation and free energy barriers, including the thermodynamic reaction energy and temperature effect.
Despite the low dependence of the free energy barrier on nucleophilicity/electrophilicity indices, the comparison of the free energy barriers between the two radicals bearing the strong electron-withdrawing and electron-donating groups is abundantly clear (Fig. S13†). For instance, the radicals with relatively small global nucleophilicity index (˙CH2CF3 (4.65), ˙CHF2 (5.66), ˙CH2COOH (4.69), ˙CH2CHO (4.77), ˙CH2COMe (5.00), etc.), caused by the presence of strong electron-withdrawing substituents, have lower free energy barriers than those possessing strongly electron-donating and global nucleophilic groups (t-Bu˙ (7.33), i-Pr˙ (7.01), ˙CH2NHMe (8.01), ˙CH2NH2 (7.87), etc.). This trend can be clearly explained by considering the polarity-matching rule. This regularity is very similar to that displayed in the analysis results for the intrinsic and activation barriers. Furthermore, the free energy barrier distribution (Fig. S13†) with varying radical reactants is very similar to activation barrier distribution (Fig. S9†), which indicates a high correlation between them. Importantly, these results agree well with the analysis results shown in Fig. 3.
3.5. Classification analysis of attacking radicals
The analysis indicates the reasonable predictability of the relative intrinsic, activation, or free energy barrier heights for the H-atom abstractions of an NHC-borane by the radicals with strongly nucleophilic and electrophilic substituents, respectively. However, for the radicals with closely nucleophilicity or electrophilicity indices, the veracity of the judgment of their reactivity is significantly affected by their differing electronic distribution patterns. For alkyl radicals and those with unsaturated groups, the electronic delocalization stabilizations are generally σ–p hyperconjugation and p–π delocalization, respectively. However, for the radicals bearing heteroatomic substituents, the electronic redistribution involves not only the inductive effect but also n → p electronic delocalization. Such complicated electronic delocalization effects lead to a low dependence of barriers on the radical reactants (Fig. 2, S8, and S13†). To understand the effect of electronic delocalization on the H-atom abstraction barrier in greater detail, we divided all of the investigated radical reactants into four groups based on the differences in their electron redistribution patterns. The first type (type-I) is the alkyl radicals, which were Me˙, Et˙, n-Pr˙, i-Pr˙, n-Bu˙, and t-Bu˙. The second type (type-II) radicals are ˙CH2NH2, ˙CH2NHMe, ˙CH2NHCOH, ˙CH2OH, ˙CH2OCH3, ˙CH2SH, ˙CH2SCH3, ˙CH2F, ˙CHF2, and ˙CH2Cl, in which the atoms bonded directly to the C radical centers are heteroatoms. The third type (type-III) radicals include ˙CH2CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CF2, ˙CH2CH
CF2, ˙CH2CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2, ˙CH2N
CH2, ˙CH2N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2, ˙CH2Ph, ˙CH2CN, ˙CH(CH3)CN, ˙CH2CHO, ˙CH2COOH, ˙CH2COMe, and ˙CH2CONH2, among which, the central carbons are bonded to unsaturated bond. The fourth type (type-IV) comprise the (CH2)nCN (n = 2–4) and CH2CFnH3−n (n = 1–3) types, among which the inductive effect is the only prevailing effect.
CH2, ˙CH2Ph, ˙CH2CN, ˙CH(CH3)CN, ˙CH2CHO, ˙CH2COOH, ˙CH2COMe, and ˙CH2CONH2, among which, the central carbons are bonded to unsaturated bond. The fourth type (type-IV) comprise the (CH2)nCN (n = 2–4) and CH2CFnH3−n (n = 1–3) types, among which the inductive effect is the only prevailing effect.
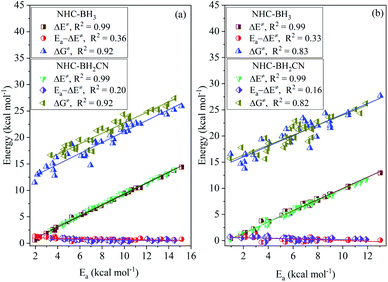
After analyzing the linear dependence of thermal contribution on the global/local nucleophilicity and electrophilicity indices (Fig. S15†), we found that the thermal contribution of the H-abstractions by the type-I radicals has a very high linear dependence on the global nucleophilicity (Fig. 5(a)), global electrophilicity, and local electrophilicity indices of the attacking radicals, and the CODs were higher than 0.97. For the type-II radicals, the thermal contribution had a high correlation to the global nucleophilicity index alone, with CODs of 0.88 and 0.91 for the NHC-BH3 and NHC-BH2CN reaction series, respectively (Fig. 5(a)). No acceptable correlation degree was found between the thermal contribution and global/local nucleophilicity and electrophilicity indices for the type-III and type-IV radicals; the relevant CODs were lower than 0.73 (Fig. 5(a) and S15†).
For the type-I radicals, their intrinsic barriers to H-abstraction reactions are almost independent of the global/local nucleophilicity and electrophilicity indices (Fig. 5(b) and S15†) of the attacking radicals, whereas their activation barriers exhibited a strong linear dependence on the global nucleophilicity index with CODs of 0.98 (NHC-BH3) and 0.97 (NHC-BH2CN) (Fig. 5(c)). Further, considering the significant dependence of the thermal contribution on the global nucleophilicity index (Fig. 5(a)), it is clear that the activation barriers to the H-abstractions of NHC-boranes by various alkyl radicals should be strongly dependent on the thermal contribution, but not on the intrinsic barrier. This trend is well supported by the following linear analysis shown in Fig. 6(a), wherein, a low COD (<0.53) between the activation and intrinsic barriers; however, a high COD (0.92) between activation barrier and thermal contribution was observed. The correlation between the activation barrier and the thermal contribution can be rationalized according to the direct calculated results. As listed in ESI Tables S6 and S8,† the change ranges of the intrinsic barriers to the H-abstractions of NHC-BH3 and NHC-BH2CN by all of the used alkyl radicals are only 1.07 and 1.46 kcal mol−1, respectively, which are at least twice less than those of the thermal contributions (2.53 kcal mol−1 for NHC-BH3 and 4.0 kcal mol−1 for NHC-BH2CN). Thus, the small change range of the intrinsic barrier should be responsible for the weak correlation between the activation barrier and the intrinsic barrier. Clearly, in such H-abstraction reactions, the thermodynamic stabilities of the alkyl radicals play a dominant role in determining the relative activation barrier heights. In contrast, the stereoelectronic and steric effects play only a minor role. Although the relative activation barrier heights can be experientially estimated based on the size or number of the substituents directly bonded to the C centers of the alkyl radicals, such as the trend with Me < n-Bu < n-Pr ≈ Et < i-Pr < t-Bu (NHC-BH3) (Fig. S9†), the results cannot be used to evaluate the relative intrinsic barrier heights (t-Bu < Me < n-Bu < i-Pr ≈ Et < n-Pr for NHC-BH3 series), which account for the stereoelectronic and steric effects.
For the type-II radicals, CODs of 0.92 and 0.81 between the global nucleophilicity index and intrinsic barrier (Fig. 5(b)) are close to 0.88 and 0.91 between the global nucleophilicity index and thermal contribution (Fig. 5(a)), whereas the activation barrier is significantly strongly dependent on the global nucleophilicity index, as noted by the CODs of 0.98 and 0.94 for NHC-BH3 and NHC-BH2CN, respectively (Fig. 5(c)). Furthermore, for the radicals of types III and IV, the global nucleophilicity index is not only strongly dependent on the intrinsic barrier but also the activation barrier, as shown in Fig. 5(b) and (c).
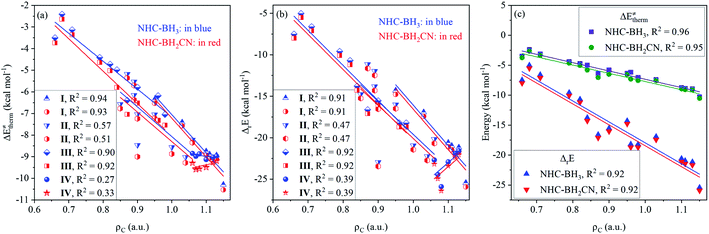
Further analysis indicated that the activation barriers to the H-abstractions by the radicals of types II, III, and IV had a greater correlation to the intrinsic barrier (CODs: 0.93–1.00) than with the thermal contribution (CODs: 0.56–0.89), which is completely opposite from the trend observed for the type-I radicals, as displayed in Fig. 6(a). These results suggest that relative activation barriers for the H-atom abstraction by the radicals of types II, III, and IV are kinetically controlled by the intrinsic barrier; however, for the type-I radicals, they are thermodynamically-controlled by the thermal contribution of the reaction energy.
Fig. 6(b) and (c) display the degree of linear dependence of the free energy barrier on the thermal contribution and intrinsic barrier, respectively. The results indicate that the free energy barriers to the H-atom abstractions by the type-I radicals have a strong correlation to the thermal contribution, but a poor dependence on the intrinsic barrier. This trend is similar to the relationship between the activation barrier and its components, which are the thermal contribution or intrinsic barrier. Apparently, this results from the close intrinsic barriers to the H-atom abstractions of NHC-boranes by different alkyl radicals. For the type-II radicals, the H-abstraction free energy barriers have medium and similar degrees of linear correlation (CODs: 0.84–0.95) to both thermal contribution and intrinsic barrier. The H-abstraction free energy barriers of the type-III and type-IV radicals have a strong linear correlation to the intrinsic barrier with CODs of greater than 0.92 and are weakly dependent on the thermal contribution, with CODs in the 0.72–0.74 range.
When considering the contribution of the activation barrier to free energy barrier according to eqn (7), we found that the free energy barriers of each of the four kinds of radicals possess a strong linear correlation degree to the activation barrier with the CODs larger than 0.92 (Fig. 6(d)). Further, considering the results presented in Fig. 3, it could be known, whether the radical reactants are divided into groups or not, the CODs between the free energy and activation barriers is similar. Furthermore, the slopes in both cases indicated a positive correlation between the free energy and activation barriers. Such a robust quantitative relationship between the free energy and activation barriers is of enormous importance for understanding the H-abstraction reaction kinetics of the reaction series studied herein. When comparing the relative reactivities of the H-atom abstraction reactions of NHC-boranes by different radicals, the results from this study will allow a direct comparison of the temperature-independent activation barriers or relative rate constants without considering the effect of the temperature-dependent Gibbs free energy thermal correction.
3.6. Activation energy
In the computational study, we performed the temperature-dependent Gibbs free energy thermal corrections for all located stationary points and computed the H-abstraction TST rate constants (kH) in the 273–376 K temperature range. Further, we obtained the DFT-based theoretical activation energy of each H-atom abstraction reaction using the standard ln(kH) vs. −1/RT Arrhenius plot (Tables S7 and S9†), which is very important for observing the rate constant changes and understanding thermochemical kinetics in a thermal environment. As shown in Fig. 7, the activation energy is slightly higher than the activation barrier by 0.26–1.34 kcal mol−1 for each H-atom abstraction reaction. Furthermore, the activation energy is rather closely related to the activation and free energy barriers, as noted by the CODs of 0.99 and 0.92 for the former and latter, respectively. Thus, when employing the Arrhenius equation to approximately estimate H-atom abstraction reaction kinetics, the activation barrier can be directly used as a replacement of the activation energy with a simple correction to the Arrhenius pre-exponential factor.4. Summary and conclusions
In this study, we investigated the H-atom abstraction reactions of NHC-BH3 and NHC-BH2CN by various C-centered radicals by employing a DFT-based computational method. Using the results computed at the B3LYP/6-311++G(d,p) level of theory, we performed correlation analysis for the thermal contribution and the three fundamental barriers, the intrinsic, activation, and free energy barriers, which were further explored for revealing their possible dependence on spin density distribution and global/local nucleophilicity and electrophilicity indices of the radical reactants. On the basis of the theoretical computations and correlation analyses, the following conclusions are drawn.(1) Before grouping, the H-atom abstraction reaction energy and thermal contribution have a strong linearly correlation to the spin densities on the central carbon atoms of the attacking radicals. After grouping, the correlation is improved for the alkyl radicals (type-I) and the radicals with the central atoms bonded to unsaturated substituents (type-III). However, relative to the results before grouping, the corresponding correlations weaken for the type-II radicals with the central atoms bonded to heteroatoms and the type-IV radicals, (CH2)nCN (n = 2–4) and CH2CFnH3−n (n = 1–3) with only inductive effect; the inductive effect is believed to play a dominant role in the weakening of the correlation.
(2) Before grouping, we did not find any acceptable dependencies of the activation and free energy barriers on the intrinsic barrier and thermal contribution. After grouping, the activation and free energy barriers of the type-I radicals have a high linear correlation to thermal contribution; however, for the radicals of types II, III, and IV, it is the intrinsic barrier that exhibits a highly linear correlation to the activation and free energy barriers. The relative activation barriers of the type-I radicals are thermodynamically-controlled, whereas for the radicals of types II, III, and IV, the relative activation barriers are kinetically controlled. Whether the radicals are grouped or not, the free energy barrier is highly linearly dependent on the activation barrier.
(3) Before grouping, the global/local nucleophilicity and electrophilicity indices cannot be used to predict thermal contribution and the three fundamental barriers; relatively, the nucleophilicity/electrophilicity indices have a greater correlation to the intrinsic barrier than to the activation and free energy barriers. After grouping, the global nucleophilicity index of the type-I radicals has a strong linear correlation to the thermal contribution, but not to the intrinsic barrier. However, the opposite trend is observed for the other three kinds of radicals, whose global nucleophilicity indexes are much more related to the intrinsic barrier than thermal contribution. Furthermore, the global nucleophilicity index can be used to predict the activation and free energy barriers of each of the four kinds of radicals.
(4) Polarity effect plays an important role in understanding H-abstraction reaction kinetics of NHC-boranes. For a pair of radicals with sufficiently strong electron-withdrawing and electron-donating substituents, their radical center atoms are strongly electrophilic and nucleophilic, respectively. Thus, the former has better polarity-matching with nucleophilic NHC-boranes and lowers the H-atom abstraction intrinsic, activation, and free energy barriers, than the latter. After grouping, the polarity effect can be directly used to predict and address the relative H-abstraction reactivities of each type of radicals, which indicates that the electrophilic or less nucleophilic radicals are better in polarity-matching with strongly nucleophilic NHC-boranes than the nucleophilic or less electrophilic radicals; the former can provide relatively low intrinsic, activation, and free energy barriers.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank Dr Yu-juan Chi for her helpful suggestions on reaction barriers.References
- G. Duret, R. Quinlan, P. Bisseret and N. Blanchard, Chem. Sci., 2015, 6, 5366–5382 RSC.
- V. Nesterov, D. Reiter, P. Bag, P. Frisch, R. Holzner, A. Porzelt and S. Inoue, Chem. Rev., 2018, 118, 9678–9842 CrossRef CAS.
- E. Lacôte, D. P. Curran and J. Lalevée, Chimia, 2012, 66, 382–385 CrossRef.
- M.-A. Tehfe, M. M. Brahmi, J.-P. Fouassier, D. P. Curran, M. Malacria, L. Fensterbank, E. Lacôte and J. Lalevée, Macromolecules, 2010, 43, 2261–2267 CrossRef CAS.
- S. Telitel, A.-L. Vallet, D. M. Flanigan, B. Graff, F. Morlet-Savary, T. Rovis, J. Lalevée and E. Lacôte, Chem.–Eur. J., 2015, 21, 13772–13777 CrossRef CAS.
- S.-H. Ueng, M. M. Brahmi, É. Derat, L. Fensterbank, E. Lacôte, M. Malacria and D. P. Curran, J. Am. Chem. Soc., 2008, 130, 10082–10083 CrossRef CAS.
- M.-A. Tehfe, J. Monot, M. M. Brahmi, H. Bonin-Dubarle, D. P. Curran, M. Malacria, L. Fensterbank, E. Lacôte, J. Lalevée and J.-P. Fouassier, Polym. Chem., 2011, 2, 625–631 RSC.
- D. P. Curran, A. Solovyev, M. M. Brahmi, L. Fensterbank, M. Malacria and E. Lacôte, Angew. Chem., Int. Ed., 2011, 50, 10294–10317 CrossRef CAS.
- F. Barth, F. Achrainer, A. M. Pütz and H. Zipse, Chem.–Eur. J., 2017, 23, 13455–13464 CrossRef CAS.
- T. Matsumoto and F. P. Gabbaï, Organometallics, 2009, 28, 4252–4253 CrossRef CAS.
- J. C. Walton, M. M. Brahmi, J. Monot, L. Fensterbank, M. Malacria, D. P. Curran and E. Lacôte, J. Am. Chem. Soc., 2011, 133, 10312–10321 CrossRef CAS.
- B. Carboni and L. Monnier, Tetrahedron, 1999, 55, 1197–1248 CrossRef CAS.
- A. Staubitz, A. P. M. Robertson, M. E. Sloan and I. Manners, Chem. Rev., 2010, 110, 4023–4078 CrossRef CAS.
- T. Kawamoto, T. Okada, D. P. Curran and I. Ryu, Org. Lett., 2013, 15, 2144–2147 CrossRef CAS.
- S. Telitel, S. Schweizer, F. Morlet-Savary, B. Graff, T. Tschamber, N. Blanchard, J. P. Fouassier, M. Lelli, E. Lacôte and J. Lalevée, Macromolecules, 2013, 46, 43–48 CrossRef CAS.
- S.-C. Ren, F.-L. Zhang, J. Qi, Y.-S. Huang, A.-Q. Xu, H.-Y. Yan and Y.-F. Wang, J. Am. Chem. Soc., 2017, 139, 6050–6053 CrossRef CAS.
- T. Kawamoto, S. J. Geib and D. P. Curran, J. Am. Chem. Soc., 2015, 137, 8617–8622 CrossRef CAS.
- J. P. Richard, T. L. Amyes and M. M. Toteva, Acc. Chem. Res., 2001, 34, 981–988 CrossRef CAS.
- J. P. Richard and K. B. Williams, J. Am. Chem. Soc., 2007, 129, 6952–6961 CrossRef CAS.
- J. M. Mayer, Acc. Chem. Res., 2011, 44, 36–46 CrossRef CAS.
- H. Mayr and M. Patz, Angew. Chem., Int. Ed. Engl., 1994, 33, 938–957 CrossRef.
- G. Hoffmann, V. Tognetti and L. Joubert, J. Phys. Chem. A, 2020, 124, 2090–2101 CrossRef CAS.
- B. P. Roberts, Chem. Soc. Rev., 1999, 28, 25–35 RSC.
- M. H. Shaw, V. W. Shurtleff, J. A. Terrett, J. D. Cuthbertson and D. W. C. MacMillan, Science, 2016, 352, 1304–1308 CrossRef CAS.
- C. Le, Y. Liang, R. W. Evans, X. Li and D. W. C. MacMillan, Nature, 2017, 547, 79–83 CrossRef CAS.
- M. Karelson and V. S. Lobanov, Chem. Rev., 1996, 96, 1027–1044 CrossRef CAS.
- P. K. Chattaraj, U. Sarkar and D. R. Roy, Chem. Rev., 2006, 106, 2065–2091 CrossRef CAS.
- C. Wu, X. Hou, Y. Zheng, P. Li and D. Lu, J. Org. Chem., 2017, 82, 2898–2905 CrossRef CAS.
- P. K. Chattaraj, S. Duley and L. R. Domingo, Org. Biomol. Chem., 2012, 10, 2855–2861 RSC.
- L. R. Domingo, P. Pérez and J. A. Sáez, RSC Adv., 2013, 3, 1486–1494 RSC.
- L. R. Domingo, E. Chamorro and P. Pérez, Eur. J. Org. Chem., 2009, 3036–3044 CrossRef CAS.
- W. H. Saunders Jr, J. Phys. Chem., 1982, 86, 3321–3323 CrossRef.
- A. I. Meyers, M. A. Seefeld, B. A. Lefker, J. F. Blake and P. G. Williard, J. Am. Chem. Soc., 1998, 120, 7429–7438 CrossRef CAS.
- S. M. Behnam, S. E. Behnam, K. Ando, N. S. Green and K. N. Houk, J. Org. Chem., 2000, 65, 8970–8978 CrossRef CAS.
- F.-J. Chen, Y. Lin, M. Xu, Y. Xia, D. J. Wink and D. Lee, Org. Lett., 2020, 22, 718–723 CrossRef CAS.
- V. Reinhardt, M. Winckler and D. Lebiedz, J. Phys. Chem. A, 2008, 112, 1712–1718 CrossRef CAS.
- N. M. Donahue, Chem. Rev., 2003, 103, 4593–4604 CrossRef CAS.
- I. V. Alabugin, K. Gilmore and M. Manoharan, J. Am. Chem. Soc., 2011, 133, 12608–12623 CrossRef CAS.
- D. E. Magnoli and J. R. Murdoch, J. Am. Chem. Soc., 1981, 103, 7465–7469 CrossRef CAS.
- J. R. Murdoch, J. Am. Chem. Soc., 1983, 105, 2667–2672 CrossRef CAS.
- J. Donnella and J. R. Murdoch, J. Am. Chem. Soc., 1984, 106, 4724–4735 CrossRef CAS.
- R. A. Marcus, Annu. Rev. Phys. Chem., 1964, 15, 155–196 CrossRef CAS.
- R. A. Marcus, J. Phys. Chem., 1968, 72, 891–899 CrossRef CAS.
- R. A. Marcus, Rev. Mod. Phys., 1993, 65, 599–601 CrossRef CAS.
- Y. Wang and J. M. Tanko, J. Am. Chem. Soc., 1997, 119, 8201–8208 CrossRef CAS.
- C. F. Bernasconi and M. Pérez-Lorenzo, J. Am. Chem. Soc., 2007, 129, 2704–2712 CrossRef CAS.
- X. Chen and J. I. Brauman, J. Am. Chem. Soc., 2008, 130, 15038–15046 CrossRef CAS.
- R. G. Parr, L. v. Szentpály and S. Liu, J. Am. Chem. Soc., 1999, 121, 1922–1924 CrossRef CAS.
- R. G. Parr, R. A. Donnelly, M. Levy and W. E. Palke, J. Chem. Phys., 1978, 68, 3801–3807 CrossRef CAS.
- M. Franco-Pérez and J. L. Gázquez, J. Phys. Chem. A, 2019, 123, 10065–10071 CrossRef.
- R. G. Parr and R. G. Pearson, J. Am. Chem. Soc., 1983, 105, 7512–7516 CrossRef CAS.
- F. De Vleeschouwer, V. Van Speybroeck, M. Waroquier, P. Geerlings and F. De Proft, Org. Lett., 2007, 9, 2721–2724 CrossRef CAS.
- L. R. Domingo and P. Pérez, Org. Biomol. Chem., 2013, 11, 4350–4358 RSC.
- P. Pechukas and E. Pollak, J. Chem. Phys., 1979, 71, 2062–2068 CrossRef CAS.
- E. Pollak, M. S. Child and P. Pechukas, J. Chem. Phys., 1980, 72, 1669–1678 CrossRef CAS.
- P. Pechukas, Annu. Rev. Phys. Chem., 1981, 32, 159–177 CrossRef CAS.
- A. Fernández-Ramos, B. A. Ellingson, R. Meana-Pañeda, J. M. C. Marques and D. G. Truhlar, Theor. Chem. Acc., 2007, 118, 813–826 Search PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- C. T. Lee, W. T. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS.
- M. J. Frisch, J. A. Pople and J. S. Binkley, J. Chem. Phys., 1984, 80, 3265–3269 CrossRef CAS.
- T. Clark, J. Chandrasekhar, G. W. Spitznagel and P. v. R. Schleyer, J. Comput. Chem., 1983, 4, 294–301 CrossRef CAS.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision A.01, Gaussian, Inc., Wallingford CT, 2009 Search PubMed.
- F. De Vleeschouwer, P. Jaque, P. Geerlings, A. Toro-Labbé and F. De Proft, J. Org. Chem., 2010, 75, 4964–4974 CrossRef CAS.
- W. Dai, D. P. Curran and J. C. Walton, J. Org. Chem., 2019, 84, 2102–2111 CrossRef CAS.
- B. Aubry, D. Subervie, M. Lansalot, E. Bourgeat-Lami, B. Graff, F. Morlet-Savary, C. Dietlin, J.-P. Fouassier, E. Lacôte and J. Lalevée, Macromolecules, 2018, 51, 9730–9739 CrossRef CAS.
- C. Zhu, J. Dong, X. Liu, L. Gao, Y. Zhao, J. Xie, S. Li and C. Zhu, Angew. Chem., 2020, 132, 12917–12921 CrossRef.
- N. Zhou, X.-A. Yuan, Y. Zhao, J. Xie and C. Zhu, Angew. Chem., 2018, 130, 4054–4058 CrossRef.
- J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3094 CrossRef CAS.
- J. Tomasi and M. Persico, Chem. Rev., 1994, 94, 2027–2094 CrossRef CAS.
- V. Barone, M. Cossi and J. Tomasi, J. Comput. Chem., 1998, 19, 404–417 CrossRef CAS.
- S. Miertuš, E. Scrocco and J. Tomasi, Chem. Phys., 1981, 55, 117–129 CrossRef.
- S. Miertus and J. Tomasi, Chem. Phys., 1982, 65, 239–245 CrossRef CAS.
- M. Cossi, V. Barone, R. Cammi and J. Tomasi, Chem. Phys. Lett., 1996, 255, 327–335 CrossRef CAS.
- T. Watanabe, S. J. Geib, D. P. Curran and T. Taniguchi, J. Org. Chem., 2017, 82, 13034–13042 CrossRef CAS.
- W. Dai, D. P. Curran and J. C. Walton, J. Org. Chem., 2019, 84, 2102–2111 CrossRef CAS.
- C. Adamo and V. Barone, J. Chem. Phys., 1998, 108, 664–675 CrossRef CAS.
- R. D. Bach and O. Dmitrenko, J. Am. Chem. Soc., 2004, 126, 4444–4452 CrossRef CAS.
- B. R. Cho and Y. W. Suh, J. Org. Chem., 1989, 54, 2855–2858 CrossRef CAS.
- S. Liu, J. Chem. Phys., 2007, 126, 244103–244107 CrossRef.
- B. Jiang and H. Guo, J. Phys. Chem. C, 2016, 120, 8220–8226 CrossRef CAS.
- M. Alipour and Z. Safari, Phys. Chem. Chem. Phys., 2016, 18, 17917–17929 RSC.
Footnote |
| † Electronic supplementary information (ESI) available: The nucleophilicity and electrophilicity indices, composition of barriers, thermal contribution, and correlation analyses of relevant physical quantities (Fig. S1–S18); comparison and explanation of computational methods (Fig. S19 and S20); computed energies of stationary points and reactions (Tables S1–S9); geometries of located stationary points (Table S10). See DOI: 10.1039/d0ra07638d |
| This journal is © The Royal Society of Chemistry 2020 |