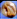Open Access Article
Open Access ArticleSpectroscopic and chromatographic investigation of chiral interactions between tiaprofenic acid and alginate–metal-complexes†
Ghaidaa Alkhayer *a,
Hussein Khudrb and
Yahia Koudsia
*a,
Hussein Khudrb and
Yahia Koudsia
aDepartment of Chemistry, Faculty of Sciences, Damascus University, Syria. E-mail: Ghaidaa.S.AlKhayer@gmail.com
bHigher Institute for Applied Sciences and Technology, Damascus, Syria
First published on 23rd September 2020
Abstract
Alginate–metal-complexes of Ca, Ba, Zn, Fe and Al were prepared in the form of beads. The preparation was based on the ionotropic method to obtain blank beads (unloaded) and beads loaded with tiaprofenic acid. IR spectra of blank beads, drug loaded beads and physical mixtures of the drug with the blank beads were recorded. The comparison of these spectra, especially in the region of hydroxyl group, implied chiral interactions between the drug and the complexes. Additionally, the drug was released from the loaded beads in aqueous phosphate buffer solutions (PBS) at pH = 7.4. Chiral HPLC was used to determine the enantiomeric excess, % ee, of the released drug. The determined % ee values indicated chiral interactions between tiaprofenic acid and alginate–metal-complexes. However, various mathematical models were used to simulate the release kinetics for each enantiomer. The metal content of Na, Ca, Ba, Zn, Fe and Al in the studied materials was measured using atomic absorption spectroscopy.
1. Introduction
Chirality has influenced all areas of drug research, design, development, and applications.1–5 Recently, the global market growth of chiral drugs increased, and chiral materials have been used for enantioselective release purposes.6Drugs are formulated with excipients in different ways to provide the required benefits.7 Currently, chiral excipients represent a substantial part of the commonly used excipients, and alginate has numerous pharmaceutical and medical applications among various chiral excipients.8–10
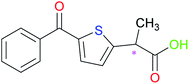
Tiaprofenic acid (Tia) (Fig. 1) is one important non-steroidal anti-inflammatory drug (NSAID) belonging to the 2-aryl-propionic acid family. It is an analgesic and used to treat pain, especially arthritic pain.11 This chiral NSAID has two enantiomeric forms and is usually administrated as a racemate. The S-enantiomer possesses most of the beneficial anti-inflammatory activity, while the R-enantiomer has no significant chiral inversion.12,13
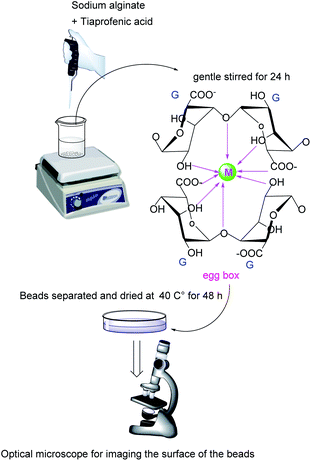
The ionotropic congealing techniques of alginate have developed the use of this chiral excipient in the domain of delivery systems.14,15 These techniques are based on entrapping a drug within cross-linked networks resulted when a multivalent metal ion combines to the uronic acids in different alginate chains. These networks were characterized with “egg-box” structures.16,17
In a previous work,18 as a part of our study on drug-excipient chiral interactions of 2-aryl-propionic acid derivatives, it was demonstrated that congealing alginate with various metal ions affected the enantioselectivity and the rate of released ketoprofen enantiomers in vitro. The present work aims to investigate the existence of chiral interactions between tiaprofenic acid and various kinds of alginate–metal-complexes, and hence, the subsequent effect on the release behaviour and kinetics of R- and S- enantiomers in vitro.
2. Experimental section
2.1. Materials
Alginic acid sodium salt purchased from brown algae bioreagent, suitable for immobilization of microorganisms from Sigma-Aldrich. Racemic tiaprofenic acid was from Sanofi (Sanofi Chimie, France) 100.2%, calcium chloride, iron chloride, aluminium chloride, barium chloride dehydrate and zinc chloride was obtained from Merck. All other chemicals and reagents used were of analytical grade or HPLC grade.2.2. Instrumentations and methods
HPLC conditions were; isocratic, 1 ml min−1 flow rate of mobile phase containing hexane![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) isopropanol
isopropanol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) TFA (90
TFA (90![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.1 v/v%). That mobile phase was degassed prior to use. The column, Kromasil®-5-amy- coat (250 × 4.6 mm i.d) 5 μm, was equilibrated for at least 30 min, at temperature (30 °C), with mobile phase flowing through the chromatographic system before starting the analysis. The samples were monitored at 254 nm.
0.1 v/v%). That mobile phase was degassed prior to use. The column, Kromasil®-5-amy- coat (250 × 4.6 mm i.d) 5 μm, was equilibrated for at least 30 min, at temperature (30 °C), with mobile phase flowing through the chromatographic system before starting the analysis. The samples were monitored at 254 nm.
The blank beads were prepared by dissolving sodium alginate (2% w/v) in phosphate buffer solution (PBS), pH 7.4. After obtaining a clear bubble-free solution, it was droplets using a glassy tube (inner diameter of 1.0 cm) into, the congealing bath, a solution of ion metal chloride (3% w/v) at room temperature. The tube was positioned at 5 cm above the surface of the metal chloride solution. The formed beads were gently stirred in the solution for 24 h. After that, they were separated and washed with PBS, then with distilled water and dried at 40 °C for 48 h.
However, alginate loaded beads were prepared by one-step; racemic tiaprofenic acid (Tia) with a ratio of (1 to 3.75 w/w) to sodium alginate, was dissolved in (PBS, pH 7.4), then, the obtained solution was congealed in the same manner as described above.
Alginate beads containing two metals were prepared by simultaneous and consecutive congealing, which was achieved by alerting the sequence and time of congealing conditions. Table 1 describes congealing conditions of all the prepared beads.
2.3. Beads characterization
The size of beads was measured using a ruler. The diameters were measured using at least ten beads. Table 1 shows obtained results. Optical microscope zoom 2000 from Leica microsystem, Germany was used for imaging the surface of samples. Photos of dried beads were taken with ×40 magnification.| Wres = V × Cres |
| Wl = Wt − Wres |
| Drug loading (Tia%) = (Wl/Wdb) × 100 |
| Loading efficiency L (%) = (Wl/Wt) × 100. |
| Beads name | Before congealing | After congealing | After drying | |||||
|---|---|---|---|---|---|---|---|---|
| WAlg (mg) | Tia, Wt (mg) | Wet beads weight (g) | Tia, Wres (mg) | Tia, Wl (mg) | Tia, L% | Dry beads weight, Wdb (mg) | Tia% | |
| a WAlg: the quantity of alginate used to form the 2% (w/v) solution in PBS. | ||||||||
| ACaT | 321 ± 0.3 | 83 ± 0.4 | 9.114 ± 0.4 | 0.41 ± 1.1 | 82.6 ± 0.2 | 99.4 ± 0.1 | 416 ± 0.3 | 20.3 ± 0.6 |
| ABaT | 317 ± 0.7 | 81 ± 0.1 | 9.071 ± 0.2 | 7.13 ± 0.3 | 73.9 ± 0.9 | 91.2 ± 0.6 | 531 ± 0.4 | 13.9 ± 0.4 |
| AZnT | 304 ± 0.5 | 81 ± 0.2 | 8.125 ± 0.4 | 6.82 ± 0.7 | 74.2 ± 0.3 | 91.6 ± 0.4 | 396 ± 0.4 | 18.7 ± 0.5 |
| AAlT | 319 ± 0.2 | 82 ± 0.5 | 9.851 ± 0.5 | 8.50 ± 0.9 | 73.5 ± 0.5 | 89.6 ± 0.5 | 539 ± 0.3 | 13.6 ± 0.4 |
| AFeT | 325 ± 0.4 | 83 ± 0.4 | 11.733 ± 0.4 | 0.30 ± 0.4 | 72.7 ± 0.6 | 87.6 ± 0.4 | 597 ± 0.4 | 12.2 ± 0.5 |
| A1T | 314 ± 0.7 | 82 ± 0.4 | 10.725 ± 0.3 | 0.86 ± 0.2 | 81.1 ± 0.1 | 98.9 ± 0.1 | 757 ± 0.2 | 10.7 ± 0.7 |
| A2T | 318 ± 0.3 | 84 ± 0.3 | 8.983 ± 0.9 | 23.09 ± 1.4 | 60.9 ± 1.2 | 72.5 ± 1.4 | 537 ± 0.7 | 11.3 ± 0.4 |
| A3T | 316 ± 0.6 | 82 ± 0.2 | 11.372 ± 0.4 | 1.22 ± 0.3 | 80.8 ± 0.4 | 98.5 ± 0.1 | 605 ± 0.1 | 13.3 ± 0.5 |
| S (%) = ((Db − Da)/Db) × 100 |
For non-spherical beads, three dimensions measured represent the length, the width, and the height of the studied beads. Then the mean value of the three measurements was used to calculate the shrinkage ratio.
2.4. In vitro release study
In vitro release of tiaprofenic acid from the beads were carried out in triplicate at room temperature applied for 200–300 mg of dried beads. The dissolution media was 5 ml (PBS, pH 7.4), with a gentle stirred for a period up to 6 h. At pre-set intervals, 0.2 ml of aliquot was withdrawn from release medium and the same volume of fresh medium was replenished immediately to keep the release medium at constant volume. The withdrawn aliquots were analyzed by chiral HPLC.2.5. Drug release kinetic modelling
Five different models; zero-order, first-order, Higuchi, Hixon–Crowell and Korsmeyer–Peppas were investigated to simulate the release kinetic of both Tia enantiomers.3. Results and discussion
3.1. Beads characterization
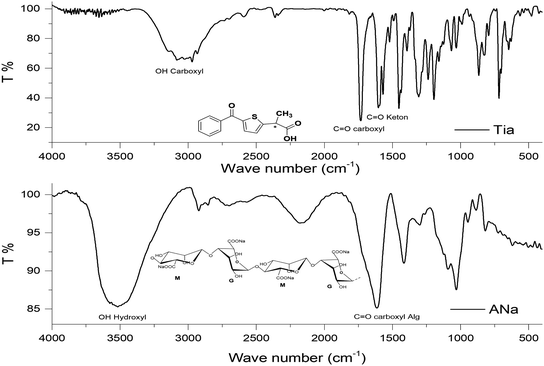
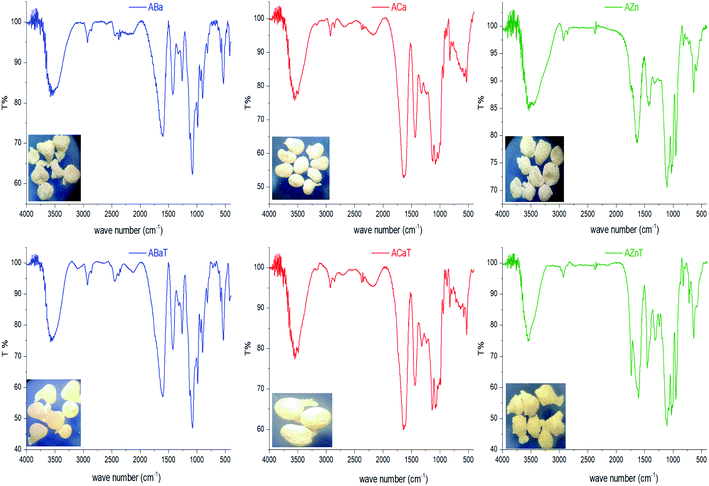
Beads shape and size differed depending on the beads type. ACa, AZn and ABa; the divalent ion metal beads (DivB) looked spherical or spherical-like with mean size of 5–7 mm for wet and 2–3 mm for dry. AFe and AAl; the trivalent ion metal beads (TrivB) were not spherical they had tear-like, wrinkled, collapsed and twisted forms with mean size of 7–9 mm for wet and 2–3.5 mm for dry. However, DivB looked smaller than TrivB with relatively smaller shrinkage ratio. ACa beads showed smaller size and shrinkage ratio compared to those congealed with Fe simultaneously A1T, and consecutively A2T and A3T. Table 1 presents some characteristics of the prepared beads; congealing conditions, bead size and shrinkage ratio.Na content in the starting sodium alginate was determined to be (0.39 mol/100 g). For DivB and TrivB, the metal content was smaller than Na content in the starting alginate with expected values of (0.19 mol/100 g) and (0.13 mol/100 g) respectively. These expected values come from the assumption that the divalent and trivalent metal ions exchanges with Na during beads formation, hence the expected values are the results of dividing Na content by 2 for DivB and 3 for TrivB. However, the obtained values, as shown in Fig. 3, indicate higher contents than the expected ones, except the case of AAlT. Which may due to free ions did not form the egg-box but still entrapped in the resulted network when beads are wet, and consequently when beads dried. Moreover, the results suggest higher metal content for all blank beads in comparison to those loaded beads. Thus, may due to the entrapment of Tia inside the network, which subsequently limit the entrapment of free metal ions. The results also reveal that the metal contents follow the same order for loaded and blank beads, i.e. Ca > Zn > Fe > Ba > Al.
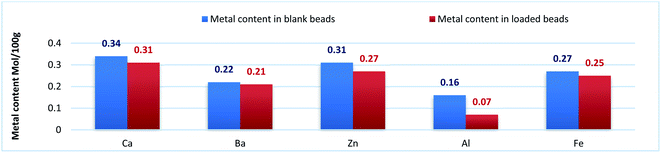 | ||
| Fig. 3 Metal content (mol/100 g) for blank beads (blue column), and metal content for loaded beads (red column). | ||
The results obtained for drug content (Tia%) and drug loading efficiency (L%) are shown in Table 2. For DivB, Tia% values varied from 13.9 for ABaT to 20.3 for ACaT, while TrivB gave 13.6 for AAlT which is comparable to 12.2 for AFeT. Practically, the lowest contents were for A1T, A2T, and A3T.
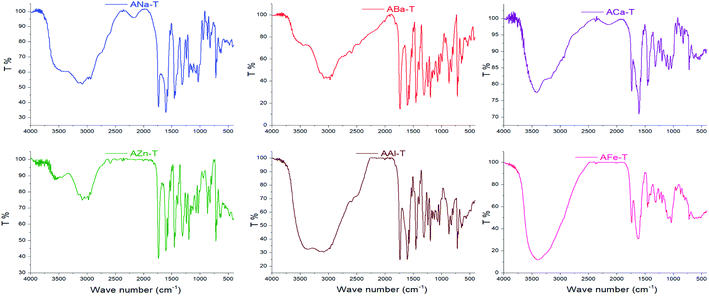
3.2. IR spectroscopy
Interactions between entrapped Tia and alginate complexes can lead to identifiable changes in the FTIR spectra of loaded beads compared with blank beads. Thus, IR spectra were registered for all kinds of prepared beads. For further investigation, physical mixtures of Tia with blank beads were prepared and compared with IR spectra of blank and loaded Tia beads, Table 3 and Fig. 4–7 summaries the results.| OH hydroxyl | OH carboxyl | C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O carboxyl Tia O carboxyl Tia |
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O carboxyl Alg O carboxyl Alg |
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O ketone Tia O ketone Tia |
|
|---|---|---|---|---|---|
| a Carboxylic OH of alginate metal complexes is not expected because the proton OH is replaced with the ion metal making an overall broad signal of hydroxyl OH. OV: the corresponding signal is not resolved but overlapped with other signal in the determined range below. | |||||
| Tia | 2250–3250 | 1741 | 1602 | ||
| ANa | 3523 | a | 1622 | ||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||
| Blank beads | |||||
| ACa | 3434 | a | 1636 (1500–1800) | ||
| ABa | 3445 (3100–3700) | a | 1632 (1500–1800) | ||
| AZn | 3544 | a | 1636 | ||
| AAl | 3419 (3000–3750) | a | 1629 (1500–1800) | ||
| AFe | 3416 | a | 1632 | ||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||
| Loaded beads | |||||
| ACaT | 3489, 3000–3750 | 1734 | 1641 | 1608 | |
| ABaT | 3000–3750 | OV (1500–2000) | OV (1500–1800) | 1602 | |
| AZnT | 2750–3750 | 1734 | 1649 (1500–1850) | 1608 | |
| AAlT | 2750–3750 | 1733 | 1630 | OV (1500–1800) | |
| AFeT | 3482, 3000–3750 | 1751 | 1636 | OV (1500–1800) | |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||
| Physical mixture | |||||
| ANa-T | 3151 (3750–2400) | 1734 | OV (1500–1800) | 1602 | |
| ACa-T | 3420, 2500–3750 | 1739 | 1628 (1500–1800) | 1606 | |
| ABa-T | 2000–3750 | 1734 | OV (1500–1800) | 1602 | |
| AZn-T | 2700–3750 | 1734 | 1626 (1500–1800) | 1606 | |
| AFe-T | 3396, 2500–3750 | 1739 | 1627 | OV (1500–1800) | |
| AAl-T | 2300–3750 | 1739 | OV (1500–1800) | 1611 | |
The spectrum of Tia shows absorption bands at 2250–3250 cm−1 from carboxylic OH, and stretching vibrations at (1741, 1602) cm−1 for C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O carboxyl and C
O carboxyl and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O ketone respectively.
O ketone respectively.
Prepared alginate beads, shows small shift (about 10–15 cm−1) of C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching vibration higher wavenumber compared to initial ANa in the region of 1622 cm−1. Generally, a broad absorption band for OH in the region 3000–3750 cm−1.
O stretching vibration higher wavenumber compared to initial ANa in the region of 1622 cm−1. Generally, a broad absorption band for OH in the region 3000–3750 cm−1.
Alginate loaded beads show IR spectra similar to those of blank beads. However, some variation can be noticed for the spectra of AZnT, AAlT and AFeT in the region of C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O belongs to Tia where the corresponding band appeared at 1734, 1733, and 1741 cm−1 respectively.
O belongs to Tia where the corresponding band appeared at 1734, 1733, and 1741 cm−1 respectively.
In the case of physical mixtures of Tia and bank beads, an overlapping for alginic C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O band was noticed with the C
O band was noticed with the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O band of Tia. On the other hand, a very strong band of Tia hydroxyl (2250–3250 cm−1) beside of alginate complexes (3250–3750 cm−1) led to wide band in the region 2000–3750 cm−1.
O band of Tia. On the other hand, a very strong band of Tia hydroxyl (2250–3250 cm−1) beside of alginate complexes (3250–3750 cm−1) led to wide band in the region 2000–3750 cm−1.
Spectra comparison led to the conclusion that there was not any chemical reaction between Tia and alginate complexes during the preparation of alginate beads, while a physical interaction was observed via hydrogen bonding between C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O carboxyl, C
O carboxyl, C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O ketone and carboxylic OH of Tia and the carboxyl and the hydroxyl groups of alginate. The OH signals for Tia carboxylic OH and alginate hydroxylic OH became one signal due to the hydrogen bonding interaction. The aforementioned results led to chiral interaction suggestions that can explain the enantioselective release during release experiments.
O ketone and carboxylic OH of Tia and the carboxyl and the hydroxyl groups of alginate. The OH signals for Tia carboxylic OH and alginate hydroxylic OH became one signal due to the hydrogen bonding interaction. The aforementioned results led to chiral interaction suggestions that can explain the enantioselective release during release experiments.
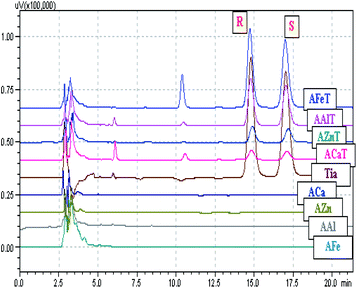
3.3. In vitro tiaprofenic acid enantiomers release study
| Time | ACaT | AZnT | AFeT | AAlT |
|---|---|---|---|---|
| 10 | 10.9 (R) ± 0.4 | 16.7 (R) ± 0.1 | 1.0 (R) ± 0.1 | 1.6 (R) ± 0.4 |
| 20 | 2.0 (R) ± 0.2 | 10.7 (R) ± 0.1 | 1.2 (R) ± 0.1 | 0.2 (R) ± 0.3 |
| 30 | 2.6 (R) ± 0.4 | 6.9 (R) ± 0.1 | 0.5 (S) ± 0.2 | 0.1 (R) ± 0.3 |
| 40 | 1.6 (R) ± 0.3 | 7.1 (R) ± 0.1 | 0.4 (R) ± 0.1 | 0.2 (S) ± 0.3 |
| 50 | 1.6 (R) ± 0.6 | 6.9 (R) ± 0.1 | 0.2 (R) ± 0.2 | 0.5 (S) ± 0.4 |
| 60 | 2.0 (R) ± 0.4 | 7.7 (R) ± 0.1 | 0.8 (R) ± 0.2 | 0.5 (S) ± 0.4 |
| 75 | 2.8 (R) ± 0.1 | 3.6 (R) ± 0.1 | 0.1 (S) ± 0.2 | 0.5 (S) ± 0.3 |
| 90 | 1.4 (R) ± 0.2 | 4.1 (R) ± 0.1 | 0.2 (S) ± 0.2 | 0.5 (S) ± 0.3 |
| 120 | 1.5 (R) ± 0.4 | 1.7 (R) ± 0.2 | 0.3 (S) ± 0.2 | 0.4 (S) ± 0.4 |
| 150 | 1.5 (R) ± 0.4 | 2.8 (R) ± 0.2 | 0.6 (S) ± 0.2 | 0.3 (S) ± 0.4 |
| 210 | 2.3 (R) ± 0.4 | 2.3 (R) ± 0.2 | 0.7 (S) ± 0.2 | 0.1 (S) ± 0.4 |
| 300 | 2.1 (R) ± 0.4 | 0.5 (R) ± 0.2 | 0.9 (S) ± 0.3 | 0.3 (S) ± 0.4 |
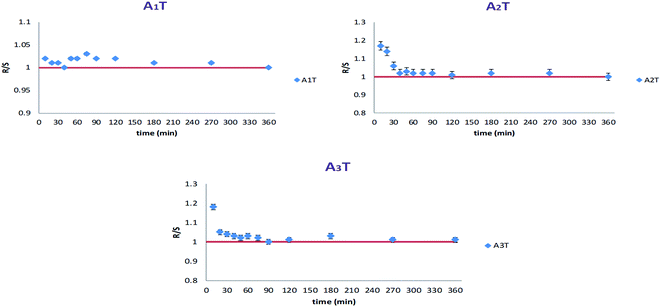
Alginates beads, congealed with two metals, Fe and Ca, showed different behaviors. As presented in Fig. 10, in the case of simultaneous congealing beads A1T, ESR values were practically 1 all over the experiment time. However, for consecutively congealed beads A2T and A3T, ESR values were higher in the first 30 min of the experiment. Thereafter, ESR behaved in a similar fashion to that in A1T.
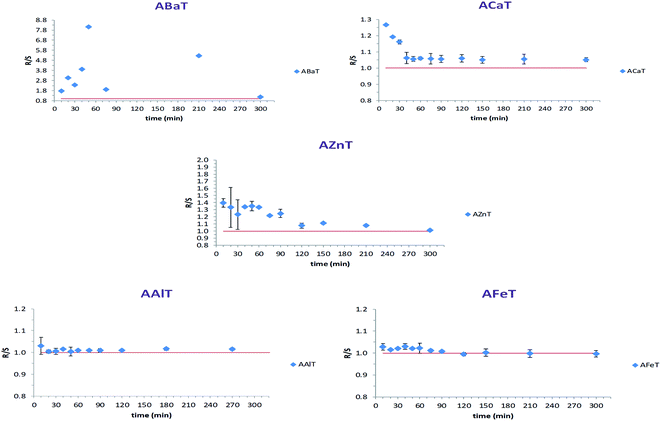
The concentration (μg ml−1) of each enantiomer was plotted against time (hours), bearing in mind that the release medium volume was conserved. Fig. 11 presents the obtained curves for each enantiomer released from the studied beads ACaT, AZnT, AFeT and AAlT. In the case of AAlT and AFeT the obtained curves for S and R enantiomers are practically superimposed because of the minor values of ESR and ee%. However, curves are more distinguishable in the case of ACaT and AZnT. Moreover, the curves behaved differently depending on the metal-complex. For TrivB, AAlT released much more Tia enantiomers than AFeT all over the experiment time. As shown in Fig. 11, enantiomers concentrations are ∼8 μg ml−1 and ∼2 μg ml−1 for AAlT and AFeT, respectively, at the first hour, and they became ∼11 μg ml−1 and ∼3 μg ml−1 at the fifth hour. For DivB, ACaT curves showed different behavior from those of AZnT; the enantiomers, approximately, reached maximum concentrations after one hour, while enantiomers released gradually from AZnT to reach the maximum after five hours. Thus, five kinetic models; zero-order, first-order, Higuchi, Hixson–Crowell and Korsmeyer–Peppas, were used to simulate the release kinetics of Tia enantiomers.
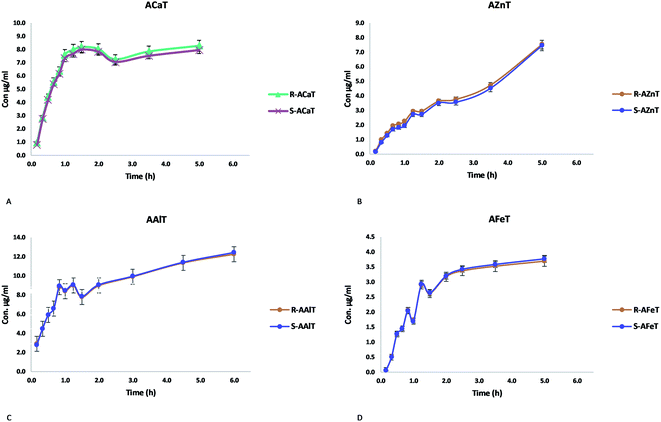 | ||
| Fig. 11 Release behavior of Tia enantiomers, (A) ACaT, (B) AZnT, (C) AAlT, (D) AFeT monitored by chiral HPLC. | ||
Table 5 summarizes the resulted correlation coefficient R2 and the release kinetic constant corresponding to each studied model. The obtained values for ACaT, shows that R and S enantiomer released from the beads according to the best fit model of Korsmeyer–Peppas. However, values obtained for each enantiomer in the case of AZnT did not result in a clear best fit model; zero-order, first-order, and Korsmeyer–Peppas models are all compatible because of R2 = 0.969 (for R enantiomer) and R2 = 0.966 (for S enantiomer). Higuchi model was the best fit model in the case of TrivB for both enantiomers, where, the correlation coefficient was 0.972 and 0.985 for AFeT and AAlT respectively. It is well-known that several factors affect drug release like physicochemical properties of drug, excipient and dosage form design. Release kinetic of a drug is also influenced by other factors; surface area change, pore size, swelling and non-swelling properties of matrix elements and drug content and drug concentration profile in the matrix. The common used models to simulate drug release, such as those used in the manuscript, deals with defined dosage forms i.e. cylindrical, spheres, tablets, patches, … etc19. In fact, the prepared beads, described in the manuscript, differ from those forms mentioned above and they have some particularities: they are not ideal spheres and differ from each other in surface description. The drug content varies depending on the complex type (Table 2) and the drug concentration profile is unknown. The cation size and the cross-linking properties are not the same in all beads kinds. Beads homogeneity is unknown. In brief, the properties of the resulted cross-linked networks with “egg-box” structures vary depending on the properties of the metal ion. Subsequently, surface and core morphologies vary along with physicochemical properties. This could lead to different interactions with the drug and different release mechanisms. The reported exponent n values (Table 5) indicate quasi-Fickian diffusion (n < 0.5) for ACaT and AAlT cases and non-Fickian mechanism for AZnT and AFeT cases (0.5 < n < 1).
| Beads | Released enantiomer | Zero order | First order | Higuchi | Hixson–Crowell | Korsmeyer–Peppas | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| R2 | K0 | R2 | K1 | R2 | KH | R2 | KHC | R2 | n | ||
| ACaT | R | 0.845 | 0.016 | 0.860 | −7 × 10−5 | 0.924 | 0.048 | 0.006 | −0.0001 | 0.942 | 0.279 |
| S | 0.852 | 0.014 | 0.852 | −6 × 10−5 | 0.930 | 0.043 | 0.006 | −0.0005 | 0.936 | 0.264 | |
| AZnT | R | 0.969 | 0.011 | 0.969 | −5 × 10−5 | 0.937 | 0.033 | 0.946 | −0.002 | 0.969 | 0.623 |
| S | 0.966 | 0.012 | 0.966 | −5 × 10−5 | 0.934 | 0.034 | 0.946 | −0.002 | 0.969 | 0.686 | |
| AAlT | R | 0.953 | 0.031 | 0.953 | −0.0001 | 0.984 | 0.101 | 0.795 | −0.002 | 0.973 | 0.308 |
| S | 0.954 | 0.032 | 0.954 | −0.0001 | 0.985 | 0.102 | 0.788 | −0.002 | 0.975 | 0.308 | |
| AFeT | R | 0.914 | 0.031 | 0.915 | −0.0001 | 0.972 | 0.091 | 0.657 | −0.001 | 0.942 | 0.733 |
| S | 0.915 | 0.031 | 0.915 | −0.0001 | 0.972 | 0.092 | 0.669 | −0.001 | 0.941 | 0.741 | |
4. Conclusions
Chiral interactions between tiaprofenic acid and alginate–metal-complexes were investigated using IR spectroscopy, and visualized using chiral HPLC in terms of ESR and ee%. The obtained values of ESR and ee% indicated notable interactions in the case of ACaT and AZnT, but less important in the case of AAlT and AFeT. The concentrations of R and S enantiomers during the release experiment showed different behaviors for the different beads. Thus, the release kinetic was simulated for each enantiomer from the studied beads. Enantiomers showed the same best fit models for the same studied beads. However, the obtained models for DivB were different from those of TrivB. Interestingly, the case of AZnT resulted in three probable models as the corresponding correlation coefficient values are the same. This case implies further investigation to understand the release mechanism. It can be concluded also that the nature of “egg-box”, which depends on the metal ion, plays a substantial role on the possible chiral interactions between the drug and the alginate complex.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors would like to thank the Department of Chemistry, University of Damascus, and the Higher Institute of Applied Sciences and Technology for providing the assistance needed to complete the experiments.References
- I. K. Reddy and R. Mehva, Chirality in Drug Design and Development, USA, 2004 Search PubMed.
- N. Ananthi, Organic & Medicinal Chemistry International Journal, 2018, 5, 1–6 Search PubMed.
- H. Yu, X. Yong, J. Liang, J. Deng and Y. Wu, Ind. Eng. Chem. Res., 2016, 55, 6037–6048 CrossRef CAS.
- M. C. Gohel, Dissolution Technol., 2003, 10, 16–20 CrossRef CAS.
- S. J. Mohan, E. C. Mohan and M. R. Yamsani, Int. J. Pharm. Sci. Nanotechnol., 2009, 1, 309–316 CAS.
- A. Calcaterra and I. D'Acquarica, J. Pharm. Biomed. Anal., 2018, 147, 323–340 CrossRef CAS.
- R. C. Rowe, P. J. Sheskey and M. E. Quinn, Handbook of Pharmaceutical Excipients, Pharmaceutical Press and American Pharmacists Association, USA, 6th edn, 2009 Search PubMed.
- M. S. Hasnain and A. K. Nayak, Alginates Versatile, Versatile Polymers in Biomedical Applications and Therapeutics, 2019, vol. 53 Search PubMed.
- M. Szekalska, A. Puciłowska, E. Szymańska, P. Ciosek and K. Winnicka, Int. J. Polym. Sci., 2016, 2016, 1–18 Search PubMed.
- B. H. A. Rehm, Alginates: Biology and Applications, 2006, vol. 13 Search PubMed.
- K. Baxter, K. Aikman, A. Brayfield, R. Buckingham, C. Cadart, M. Harrison, H. Hayne, M. A. Daya, H. Arnold, N. Bell-Asher, L. C. Sáez, R. Chin, K. Eager, E. Henderson, S. Ho, E. King, S. Ladani, D. Lipanovic, J. MacKershan, J. Martin, A. McFarlane, D. McGuirk, BNF 79, BMA-Royal pharmaceutical society, UK, 79th edn, 2020, vol. March–Sep Search PubMed.
- N. M. Davies, Clin. Pharmacokinet., 1996, 31, 331–347 CrossRef CAS.
- M. Vakily and F. Jama, J. Pharm. Sci., 1994, 83, 495–498 CrossRef CAS.
- P. Patil, D. Chavanke and M. Wagh, Int. J. Pharm. Pharm. Sci., 2012, 4, 27–32 CAS.
- M. Christianah Adeyeye, in Chirality in Drug Design and Development, 2004 Search PubMed.
- L. Li, Y. Fang, R. Vreeker, I. Appelqvist and E. Mendes, Biomacromolecules, 2007, 8, 464–468 CrossRef CAS.
- A. M. du Poset, A. Zitolo, F. Cousin, A. Assifaoui and A. Lerbret, Phys. Chem. Chem. Phys., 2020, 22, 2963–2977 RSC.
- G. Alkhayer, H. Khudr and Y. Koudsi, Anal. Bioanal. Chem. Res., 2020, 7, 61–76 CAS.
- M. P. Paarakh, P. A. N. I. Jose, C. M. Setty and G. V. Peter, International Journal of Pharmacy Research & Technology, 2018, 8, 12–20 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Spectra data. See DOI: 10.1039/d0ra07665a |
| This journal is © The Royal Society of Chemistry 2020 |